| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
4.5. Электромагнитные волны
Свойства электромагнитных волн. Электромагнитной волной называется распространение возмущений электромагнитного поля в пустом пространстве или в среде в отсутствие источников. Существование электромагнитных волн следует из теории Максвелла (см.
разд. 3.15), в которой утверждается, что переменное электрическое поле порождает переменное магнитное поле, а переменное магнитное поле порождает переменное электрическое поле. В случае однородной изотропной среды уравнения Максвелла имеют вид

где  Для электромагнитного поля, зависящего только от координаты х, получаем уравнения:
Для электромагнитного поля, зависящего только от координаты х, получаем уравнения:

В этом случае уравнения для продольных компонент имеют вид  т.е. все продольные компоненты ноля являются постоянными величинами.
т.е. все продольные компоненты ноля являются постоянными величинами.
Нетрудно убедиться, что поперечные компоненты электромагнитного поля подчиняются волновому уравнению:

(таким же уравнениям подчиняются  ). Из этих уравнений следует, что электромагнитные возмущения в среде распространяются со скоростью
). Из этих уравнений следует, что электромагнитные возмущения в среде распространяются со скоростью

где  — скорость электромагнитных волн в вакууме,
— скорость электромагнитных волн в вакууме,  — показатель преломления среды.
— показатель преломления среды.
Рассмотрим плоскую электромагнитную волну определенной частоты (монохроматическую плоскую волну), распространяющуюся вдоль оси  Из (31) получаем:
Из (31) получаем:  Из этих формул можно получить свойства плоской бегущей электромагнитной волны:
Из этих формул можно получить свойства плоской бегущей электромагнитной волны:
1) Электромагнитная волна поперечна.
2) Так как  то
то  Векторы
Векторы  образуют правую тройку векторов (т.е. направление вектора
образуют правую тройку векторов (т.е. направление вектора  совпадает с направлением распространения волны).
совпадает с направлением распространения волны).
3) Величины векторов  и Й в каждый момент времени связаны соотношением
и Й в каждый момент времени связаны соотношением 
От разности фаз  зависит характер поляризации волны. При
зависит характер поляризации волны. При  волна оказывается плоскополяр изованной, т.е. вектор
волна оказывается плоскополяр изованной, т.е. вектор  совершает колебания в одной плоскости (эту плоскость называют плоскостью поляризации волны), а при иной разности фаз — эллиптически поляризованной или
совершает колебания в одной плоскости (эту плоскость называют плоскостью поляризации волны), а при иной разности фаз — эллиптически поляризованной или  и при
и при  поляризованной по кругу (см. разд. 4.1).
поляризованной по кругу (см. разд. 4.1).
Энергия электромагнитных волн. Объемная плотность энергии электромагнитной волны вычисляется по формуле

В случае монохроматической плоскополяризованной волны имеем

Для эллиптически поляризованной волны:

Для волны, поляризованной по кругу  плотность энергии не меняется со временем:
плотность энергии не меняется со временем: 
Плотность потока энергии в электромагнитной волне определяется вектором Пойнтинга (см. разд. 3.15):

который направлен в сторону распространения волны. Интенсивностью электромагнитной волны называется модуль среднего по времени вектора Пойнтинга:

Давление волны. В соответствии с теорией относительности, поток энергии электромагнитного поля в вакууме означает существование импульса электромагнитного поля. Объемная плотность импульса электромагнитного поля равна (по модулю)  поток импульса равен
поток импульса равен  его модуль равен
его модуль равен  При отражении или поглощении волны происходит изменение импульса волны, что должно проявляться в давлении волны на препятствие. При нормальном отражении плоской волны давление равно
При отражении или поглощении волны происходит изменение импульса волны, что должно проявляться в давлении волны на препятствие. При нормальном отражении плоской волны давление равно  где
где  — доля отраженной энергии (коэффициент отражения). В рамках электродинамики давление волны объясняется действием магнитного поля волны на ток, возбуждаемый на отражающей поверхности электрическим полем волны.
— доля отраженной энергии (коэффициент отражения). В рамках электродинамики давление волны объясняется действием магнитного поля волны на ток, возбуждаемый на отражающей поверхности электрическим полем волны.
Излучение плоского тока. Простейшим примером системы, создающей переменные поля и излучающей плоскую электромагнитную волну, является переменный по времени плоский ток. Рассмотрим ток в плоскости  направленный вдоль
направленный вдоль  и изменяющийся по закону
и изменяющийся по закону  Из закона плоского тока для узкого контура, охватывающего ток, получим
Из закона плоского тока для узкого контура, охватывающего ток, получим  где знак
где знак  соответствует полю справа от плоскости (для малых
соответствует полю справа от плоскости (для малых  знак
знак  слева от плоскости. Используя связь между Е и В в плоской волне, получим
слева от плоскости. Используя связь между Е и В в плоской волне, получим  где
где  уосго
уосго  Электрическое поле направлено против тока, его работа над током отрицательна, т.е. ток отдает волне энергию. Поле вдали от плоскости имеет вид
Электрическое поле направлено против тока, его работа над током отрицательна, т.е. ток отдает волне энергию. Поле вдали от плоскости имеет вид  при
при  при
при 

Рис. 58.
Излучение волн движущимися зарядами. Излучение электромагнитных волн происходит при движении зарядов с ускорением. Простейшая излучающая система — электрический диполь, дипольный момент которого быстро меняется со временем (осциллятор, или вибратор Герца). Так как электромагнитные возмущения распространяются со скоростью  то поле излучения на расстоянии
то поле излучения на расстоянии  в момент времени
в момент времени  определяется движением зарядов в диполе в момент
определяется движением зарядов в диполе в момент  Поле излучения выглядит достаточно просто только в волновой зоне) т.е. на расстояниях, больших как по сравнению с размерами диполя, так и по сравнению с
Поле излучения выглядит достаточно просто только в волновой зоне) т.е. на расстояниях, больших как по сравнению с размерами диполя, так и по сравнению с  где
где  — характерное время изменения дипольного момента (в случае гармонических колебаний А — длина волны). Электрическое и магнитное поле в волновой зоне перпендикулярны радиусу-вектору
— характерное время изменения дипольного момента (в случае гармонических колебаний А — длина волны). Электрическое и магнитное поле в волновой зоне перпендикулярны радиусу-вектору  проведенному от диполя к точке наблюдения:
проведенному от диполя к точке наблюдения:


Рис. 59.
Взаимное расположение векторов  изображено на рис. 59. Убывание полей с расстоянием происходит по закону
изображено на рис. 59. Убывание полей с расстоянием происходит по закону  Вектор Пойнтинга в волновой зоне направлен вдоль
Вектор Пойнтинга в волновой зоне направлен вдоль  в направлении, составляющем угол в с вектором
в направлении, составляющем угол в с вектором  он равен:
он равен:

Поток энергии через замкнутую поверхность есть не что иное, как мощность излучения диполя:

Считая, что движется только один из зарядов диполя, получим формулу для мощности излучения ускоренно движущейся частицы:

которая оказывается пропорциональной квадрату ее ускорения.
Линейным гармоническим осциллятором называется электрический диполь, момент которого изменяется по гармоническому закону:  Зависимость интенсивности излученной волны от угла в имеет вид
Зависимость интенсивности излученной волны от угла в имеет вид

Зависимость  (диаграмма направленности) изображена на (рис. 60). Средняя по времени мощность излучения такого осциллятора
(диаграмма направленности) изображена на (рис. 60). Средняя по времени мощность излучения такого осциллятора

пропорциональна четвертой степени его частоты.

Рис. 60.
Пример 1. Свободный электрон в поле плоской электромагнитной волны с амплитудой  совершает вынужденные колебания с амплитудой
совершает вынужденные колебания с амплитудой  (уравнение движения электрона имеет вид:
(уравнение движения электрона имеет вид:  Видно, что мощность излучения свободного электрона в поле электромагнитной волны не зависит от частоты, а сечение рассеяния (отношение мощности излучения к интенсивности падающей волны) равно
Видно, что мощность излучения свободного электрона в поле электромагнитной волны не зависит от частоты, а сечение рассеяния (отношение мощности излучения к интенсивности падающей волны) равно  Другая ситуация возникает, когда в поле электромагнитной волны попадает атомный электрон, собственная частота
Другая ситуация возникает, когда в поле электромагнитной волны попадает атомный электрон, собственная частота  колебаний которого велика по сравнению с частотой падающей (световой) волны. Амплитуда колебаний в этом случае (см. разд. 4.3) равна
колебаний которого велика по сравнению с частотой падающей (световой) волны. Амплитуда колебаний в этом случае (см. разд. 4.3) равна  т.е. почти не зависит от
т.е. почти не зависит от  . В этом случае мощность излучения и сечение рассеяния света пропорциональны
. В этом случае мощность излучения и сечение рассеяния света пропорциональны  что дает качественное объяснение голубому цвету неба (голубой свет рассеивается сильнее).
что дает качественное объяснение голубому цвету неба (голубой свет рассеивается сильнее).
Пример 2. Если представить, что электрон в атоме совершает собственные колебания с частотой  то энергия колебаний равна
то энергия колебаний равна  а мощность излучения равна
а мощность излучения равна  Получаем
Получаем  следовательно, энергия атома изменяется по закону
следовательно, энергия атома изменяется по закону  , где
, где  с называют временем высвечивания атома.
с называют временем высвечивания атома.
Эффект Доплера для электромагнитных волн в вакууме.
Главное отличие от акустического эффекта Доплера (см. разд. 4.4)
состоит в том, что отсутствует система отсчета, связанная со средой, по которой распространяется волна. Поэтому соотношение между частотой излучения  (измеренной в системе отсчета источника
(измеренной в системе отсчета источника  и зарегистрированной частотой и (измеренной в системе отсчета приемника
и зарегистрированной частотой и (измеренной в системе отсчета приемника  может зависеть только от их относительной скорости. Пусть в
может зависеть только от их относительной скорости. Пусть в  источник движется со скоростью
источник движется со скоростью  направленной под углом в к радиусу-вектору, проведенному от приемника к источнику. Повторяя рассуждения, приведенные в разд. 4.4, получим
направленной под углом в к радиусу-вектору, проведенному от приемника к источнику. Повторяя рассуждения, приведенные в разд. 4.4, получим

где  — частота источника, измеренная часами системы
— частота источника, измеренная часами системы  переходя к собственному времени
переходя к собственному времени  или
или  см. разд. 1.11), получим
см. разд. 1.11), получим

Видно, что вследствие преобразования времени наблюдается не только продольный, но и поперечный эффект Доплера (при движении источника перпендикулярно направлению на приемник).

Рис. 61.
Полезно посмотреть на эффект Доплера с иной точки зрения. Поскольку фаза колебания в данной точке волны  должна быть инвариантна по отношению к переходу в другую систему отсчета, то
должна быть инвариантна по отношению к переходу в другую систему отсчета, то  представляет собой
представляет собой  -вектор нулевой длины
-вектор нулевой длины  Если в системе
Если в системе  ось х направить параллельно скорости источника
ось х направить параллельно скорости источника  (рис. 61), то в этой системе отсчета
(рис. 61), то в этой системе отсчета  Применяя для перехода к системе
Применяя для перехода к системе  преобразования Лоренца, имеем:
преобразования Лоренца, имеем:  или
или  Выражая приходим к (35). Этот метод позволяет, записав преобразования Лоренца для волнового вектора получить формулы для явления аберрации света, имеющего важное значение в астрономии.
Выражая приходим к (35). Этот метод позволяет, записав преобразования Лоренца для волнового вектора получить формулы для явления аберрации света, имеющего важное значение в астрономии.
Шкала электромагнитных волн. В зависимости от способов излучения и регистрации электромагнитных волн, в шкале частот  или длин волн в вакууме
или длин волн в вакууме  выделяют несколько диапазонов с условными (перекрывающимися) границами:
выделяют несколько диапазонов с условными (перекрывающимися) границами:
1. Радиоволны  мм).
мм).
2. Оптическое (световое) излучение  мм):
мм):
а) инфракрасное  излучение
излучение  мм),
мм),
б) видимый свет  нм),
нм),
в) ультрафиолетовое  излучение
излучение  нм).
нм).
3. Рентгеновское излучение  нм).
нм).
4. Гамма-излучение (гамма-лучи)  нм).
нм).
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- 1. Аналитическая геометрия на плоскости
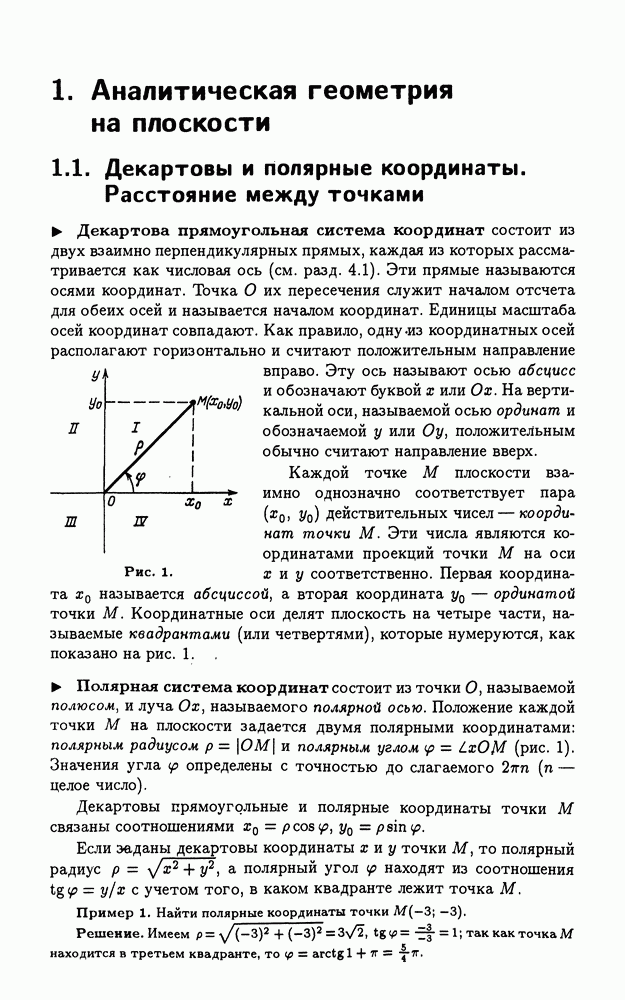
- 1.1. Декартовы и полярные координаты. Расстояние между точками
- 1.2. Деление отрезка в данном отношении. Площадь многоугольника
- 1.3. Различные виды уравнения прямой
- 1.4. Угол между прямыми. Расстояние от точки до прямой
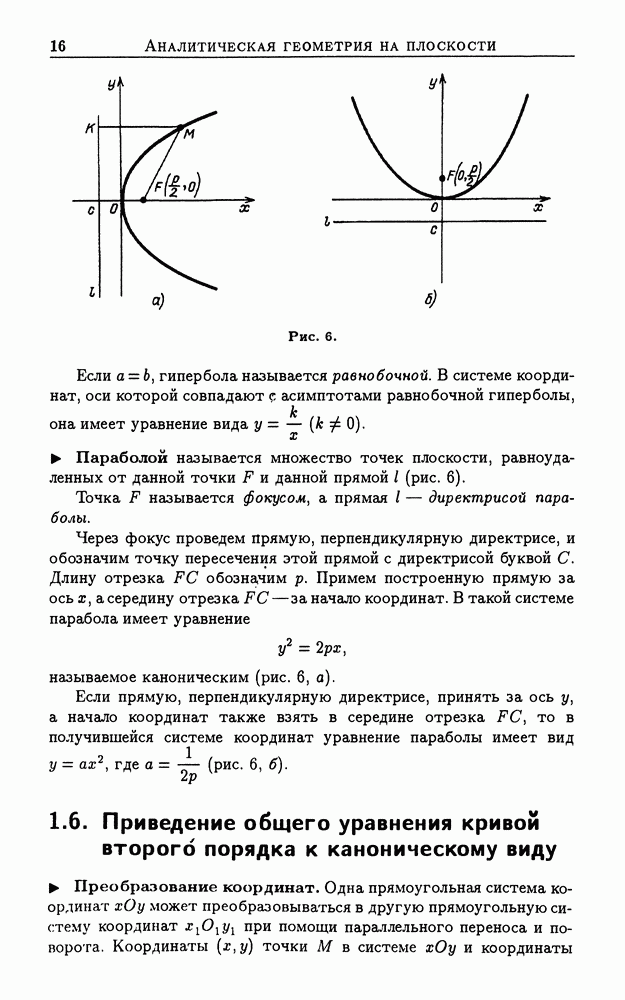
- 1.5. Окружность, эллипс, гипербола и парабола
- 1.6. Приведение общего уравнения кривой второго порядка к каноническому виду
- 2. Аналитическая геометрия в пространстве
- 2.2. Векторы
- 2.3. Действия над векторами. Скалярное произведение
- 2.4. Векторное и смешанное произведения
- 2.5. Плоскость в пространстве
- 2.6. Прямая в пространстве
- 2.7. Прямая и плоскость в пространстве
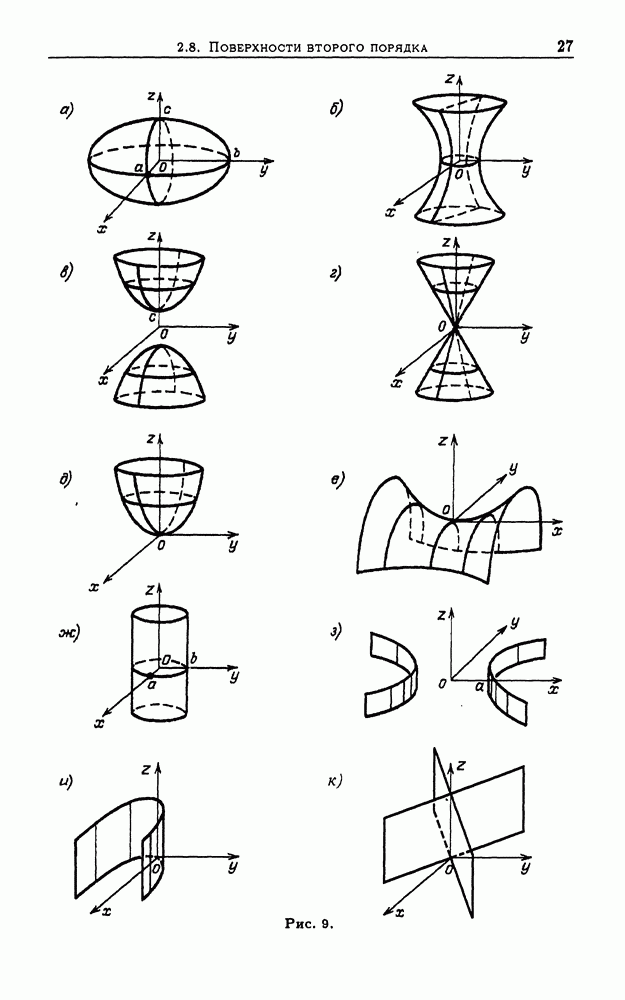
- 2.8. Поверхности второго порядка
- 3. Линейная алгебра
- 3.2. Матрицы
- 3.3. Системы линейных уравнений
- 3.4. Системы n-мерных векторов. Собственные значения и собственные векторы матрицы
- 4. Основные понятия математического анализа
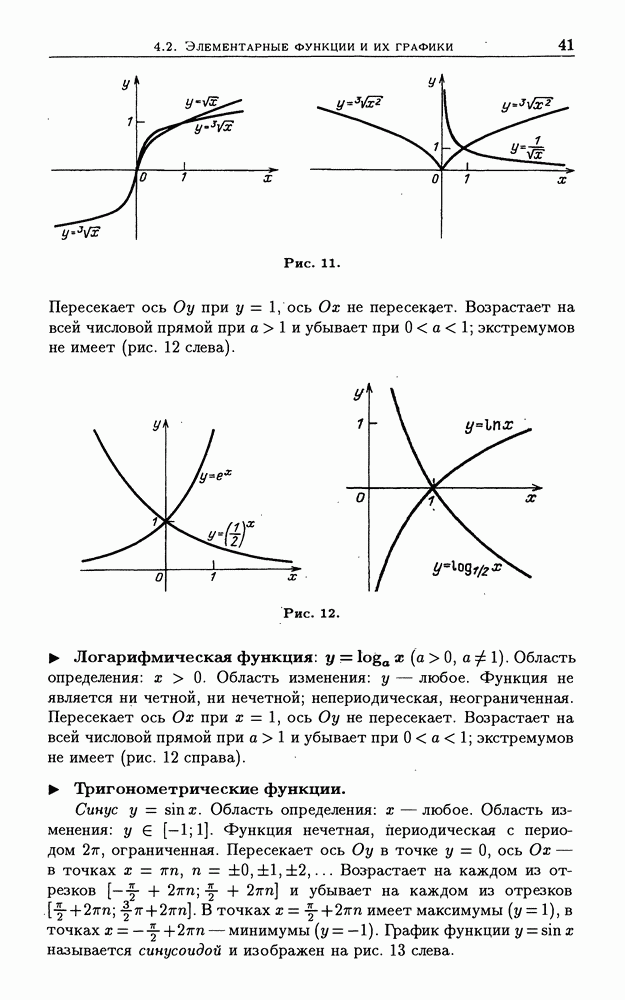
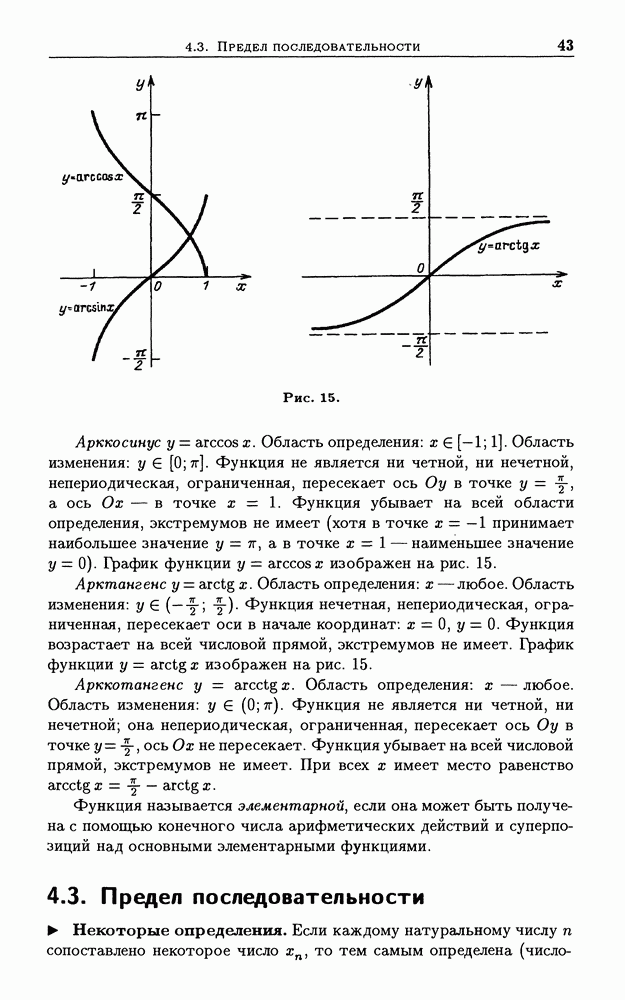
- 4.2. Элементарные функции и их графики
- 4.3. Предел последовательности
- 4.4. Предел функции
- 4.5. Бесконечно малые и бесконечно большие функции
- 4.6. Непрерывность
- 4.7. Асимптоты графика функции
- 5. Дифференциальное исчисление функций одной переменной
- 5.2. Таблица производных и правила дифференцирования
- 5.3. Теоремы о дифференцируемых функциях. Правило Лопиталя
- 5.4. Производные и дифференциалы высших порядков. Формула Тейлора
- 5.5. Экстремумы. Точки перегиба
- 5.6. Общая схема исследования функции и построение графика
- 6. Функции нескольких переменных
- 6.1. Точечные множества. Функции. Предел и непрерывность
- 6.2. Дифференцирование функций нескольких переменных
- 6.3. Производная по направлению. Геометрические приложения
- 6.4. Экстремумы функций нескольких переменных
- 7. Неопределенный интеграл
- 7.1. Первообразная. Неопределенный интеграл и его свойства
- 7.2. Таблица основных интегралов. Примеры интегрирования
- 7.3. Интегрирование по частям. Метод замены переменной
- 7.4. Интегрирование рациональных функций
- 7.5. Интегрирование иррациональных функций
- 7.6. Интегрирование показательных и тригонометрических функций
- 8. Определенный интеграл
- 8.1. Основные определения. Геометрический смысл определенного интеграла
- 8.2. Свойства определенного интеграла
- 8.3. Геометрические и физические приложения определенного интеграла
- 8.4. Несобственные интегралы
- 9. Двойные и тройные интегралы
- 9.1. Определение и свойства двойного интеграла
- 9.2. Вычисление двойного интеграла
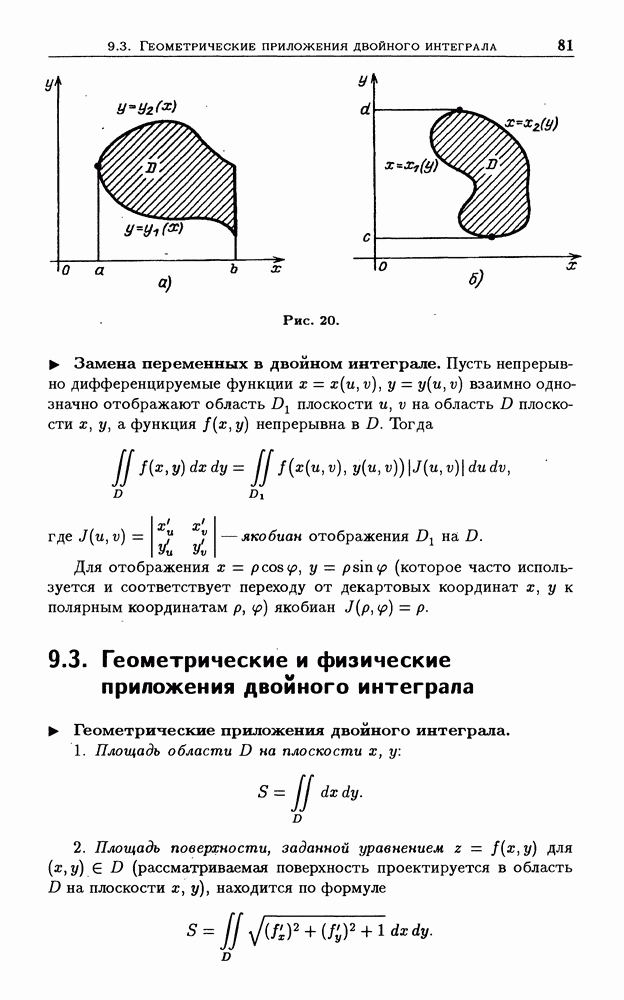
- 9.3. Геометрические и физические приложения двойного интеграла
- 9.4. Определение и свойства тройного интеграла
- 9.5. Вычисление тройного интеграла. Некоторые приложения
- 10. Криволинейные и поверхностные интегралы
- 10.2. Криволинейный интеграл второго рода
- 10.3. Поверхностный интеграл первого рода
- 10.4. Поверхностный интеграл второго рода
- 10.5. Дифференциальные операции и интегральные формулы теории поля
- 11. Ряды
- 11.1. Числовые ряды
- 11.2. Функциональные ряды
- 11.3. Степенные ряды
- 11.4. Ряд Фурье
- 11.5. Интеграл Фурье. Преобразование Фурье
- 12. Обыкновенные дифференциальные уравнения
- 12.2. Дифференциальные уравнения высших порядков
- 12.3. Линейные уравнения n-го порядка
- 12.4. Решение линейных однородных уравнений n-го порядка с постоянными коэффициентами
- 12.5. Линейные неоднородные уравнения n-го порядка
- 12.6. Системы обыкновенных дифференциальных уравнений
- 13. Приближенные вычисления
- 13.1. Метод наименьших квадратов
- 13.2. Приближенное решение алгебраических уравнений
- 13.3. Вычисление определенного интеграла
- 13.4. Численное интегрирование дифференциальных уравнений
- 14. Теория вероятностей
- 14.1. Правила и формулы комбинаторики
- 14.2. Основные понятия теории вероятностей
- 14.3. Условная вероятность. Теоремы и формулы теории вероятностей
- 14.4. Математическое ожидание и дисперсия
- 14.5. Закон больших чисел
- 1. Физические основы механики
- 1.1. Кинематика точки
- 1.2. Кинематика твердого тела
- 1.3. Динамика
- 1.4. Закон сохранения импульса
- 1.5. Закон сохранения энергии
- 1.6. Закон сохранения момента импульса
- 1.7. Задана двух тел и движение в центральном поле
- 1.8. Поле тяготения
- 1.9. Неинерциальные системы отсчета
- 1.10. Динамика твердого тела
- 1.11. Специальная теория относительности
- 2. Молекулярная физика и термодинамика
- 2.2. Первое начало термодинамики
- 2.3. Второе начало термодинамики
- 2.4. Энтропия. Свободная энергия
- 2.5. Кинетическая теория идеального газа
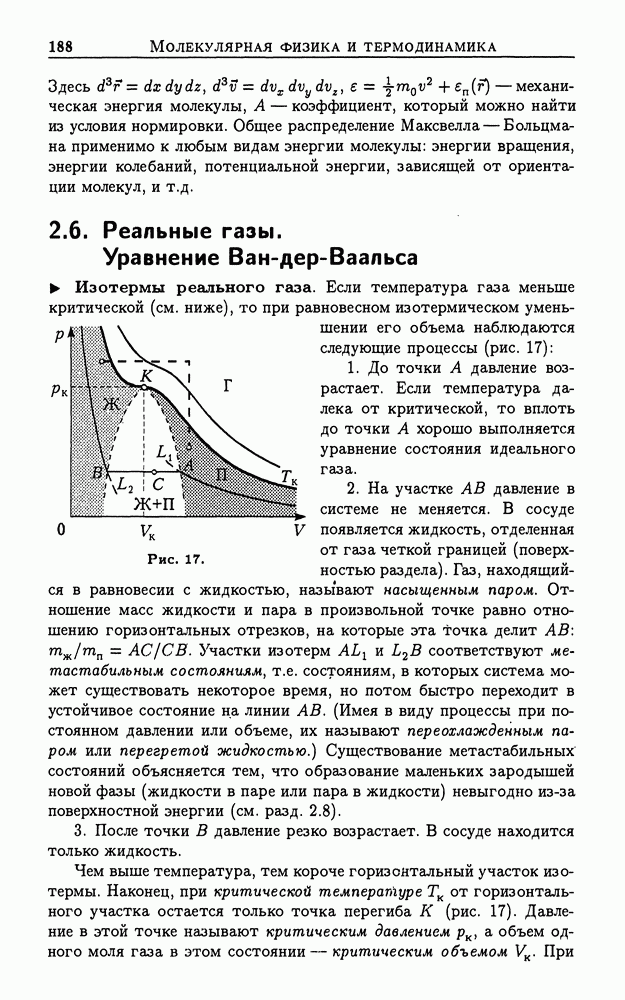
- 2.6. Реальные газы. Уравнение Ван-дер-Ваальса
- 2.7. Равновесие фаз. Фазовые переходы
- 2.8. Поверхностное натяжение
- 2.9. Явления переноса в газах
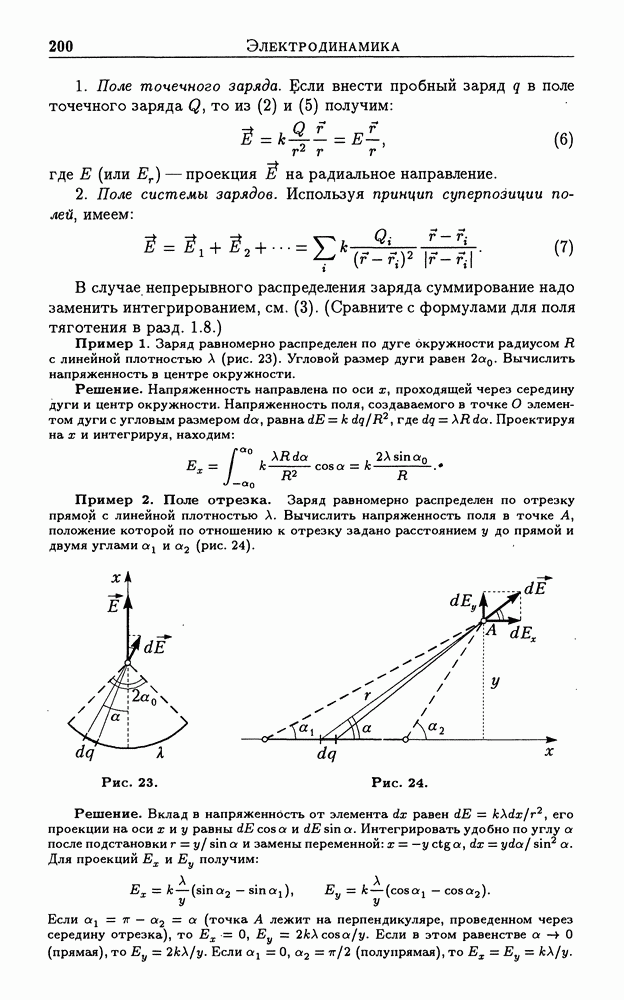
- 3. Электродинамика
- 3.1. Электрический заряд. Закон Кулона
- 3.2. Электрическое поле. Напряженность поля
- 3.3. Электростатическое поле. Принцип суперпозиции для напряженности и потенциала
- 3.4. Теорема Гаусса
- 3.5. Электростатика проводников
- 3.6. Электростатика диэлектриков
- 3.7. Конденсаторы
- 3.8. Энергия электростатического поля
- 3.9. Постоянный ток
- 3.10. Магнитное поле. Сила Лоренца и закон Ампера
- 3.11. Вычисление магнитной индукции
- 3.12. Циркуляция и поток вектора магнитной индукции
- 3.13. Магнитное поле в веществе
- 3.14. Электромагнитная индукция
- 3.15. Уравнения Максвелла
- 4. Колебания и волны
- 4.1. Гармонические колебания. Сложение колебаний
- 4.2. Свободные незатухающие колебания
- 4.3. Затухающие и вынужденные колебания
- 4.4. Упругие волны
- 4.5. Электромагнитные волны
- 5. Оптика
- 5.1. Геометрическая оптика. Фотометрия
- 5.2. Интерференция света
- 5.3. Дифракция
- 5.4. Поляризация света. Формулы Френеля
- 5.5. Дисперсия и поглощение света
- 5.6. Тепловое излучение
- 5.7. Световые кванты
- Список литературы
- 1. Кинематика
- 1.1. Кинематика точки
- 1.2. Кинематика твердого тела
- 1.3. Плоскопараллельное движение твердого тела
- 1.4. Произвольное движение твердого тела
- 1.5. Сложное движение точки
- 2. Основные понятия и аксиомы механики
- 2.2. Аксиомы механики
- 3. Статика
- 3.2. Условия уравновешенности систем сил, приложенных к твердому телу
- 3.3. Решение задан статики
- 3.4. Центр параллельных сил. Центр тяжести твердого тела
- 3.5. Распределенные силы
- 3.6. Законы трения (законы Кулона)
- 4. Динамика материальной точки
- 4.2. Первая и вторая задачи динамики
- 5. Общие теоремы динамики механической системы
- 5.2. Теорема о движении центра масс
- 5.3. Теорема об изменении количества движения
- 5.4. Теорема об изменении кинетического момента
- 5.5. Теорема об изменении кинетической энергии
- 6. Принцип Даламбера. Элементы аналитической механики
- 6.2. Классификация механических связей. Обобщенные координаты
- 6.3. Принцип возможных перемещений
- 6.4. Общее уравнение динамики (принцип Даламбера — Лагранжа)
- 6.5. Уравнения Лагранжа второго рода
- 1. Основные понятия
- 1.1. Введение. Внешние и внутренние силы
- 1.2. Напряжения и деформации в точке
- 1.3. Основные понятия и допущения
- 2. Напряженно-деформированное состояние в точке
- 2.2. Одноосное растяжение и сжатие
- 2.3. Чистый сдвиг
- 3. Центральное растяжение и сжатие
- 3.2. Напряжения и деформации при растяжении или сжатии
- 3.3. Расчеты на прочность при растяжении и сжатии
- 4. Кручение
- 4.2. Напряжения и деформации при кручении
- 4.3. Расчеты на прочность при кручении
- 5. Прямой изгиб
- 5.2. Напряжения и деформации при прямом чистом изгибе
- 5.3. Напряжения и деформации при прямом поперечном изгибе
- 5.4. Расчет на прочность при прямом изгибе
- 6. Сложное сопротивление
- 6.2. Внецентренное растяжение или сжатие
- 6.3. Изгиб с кручением
- 7. Устойчивость сжатых стержней
- 7.2. Формула Эйлера
- 7.3. Влияние способов закрепления концов стержня на величину критической силы
- 7.4. Пределы применимости формулы Эйлера
- 7.5. Расчеты сжатых стержней на устойчивость
- ПРИЛОЖЕНИЯ
- 1. Элементарные функции и их свойства
- 2. Таблица неопределенных интегралов
- 3. Решения обыкновенных дифференциальных уравнений
- 4. Ортогональные криволинейные системы координат
- 5. Некоторые физические постоянные