| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
1.10. Динамика твердого тела
Вращение вокруг неподвижной оси. Момент импульса твердого тела относительно неподвижной оси вращения  (см. разд. 1.6) равен
(см. разд. 1.6) равен

где  — расстояние от точки
— расстояние от точки  до оси вращения, и мы использовали соотношение
до оси вращения, и мы использовали соотношение  Направление проекции совпадает с направлением
Направление проекции совпадает с направлением  т.е. определяется по правилу буравчика. Величина
т.е. определяется по правилу буравчика. Величина

называется моментом инерции твердого тела относительно оси  Продифференцировав (37) по времени и учтя, что
Продифференцировав (37) по времени и учтя, что  где
где  — момент внешних сил относительно оси вращения (уравнение (25)), получим
— момент внешних сил относительно оси вращения (уравнение (25)), получим

где  — угловое ускорение. Это уравнение называют основным уравнением динамики вращательного движения твердого тела вокруг неподвижной оси. Вычислим еще кинетическую энергию вращающегося твердого тела:
— угловое ускорение. Это уравнение называют основным уравнением динамики вращательного движения твердого тела вокруг неподвижной оси. Вычислим еще кинетическую энергию вращающегося твердого тела:

и работу внешней силы при повороте тела:

где 
Пример 1. К концу нити, намотанной на блок с моментом инерции I и радиусом Я, привязали тело массой  и отпустили. Найти угловое ускорение тела.
и отпустили. Найти угловое ускорение тела.
Решение. Запишем второй закон Ньютона для тела:  и уравнение (39) для блока:
и уравнение (39) для блока:  Учтем также кинематическое соотношение
Учтем также кинематическое соотношение  Решая эти уравнения, получим
Решая эти уравнения, получим 
Свойства момента инерции. Момент инерции (38) — скалярная аддитивная величина, характеризующая распределение массы тела по отношению к оси. Из уравнений (39), (40) видно, что момент инерции является мерой инертности твердого тела по отношению к вращательному движению, т.е. играет ту же роль, что масса для поступательного движения.
Пример 2. Вычислить момент инерции однородного диска массой  и радиусом Я относительно оси симметрии.
и радиусом Я относительно оси симметрии.
Решение. Разбив диск на тонкие круговые полоски и интегрируя, получим 

Такой же ответ верен и для сплошного однородного цилиндра.
Теорема Штейнера связывает момент инерции  относительно произвольной оси с моментом инерции
относительно произвольной оси с моментом инерции  относительно параллельной ей оси, проходящей через центр масс твердого тела:
относительно параллельной ей оси, проходящей через центр масс твердого тела:

где  — масса тела, а — расстояние между осями. Например, момент инерции диска относительно оси, перпендикулярной плоскости диска и проходящей через его край, равен
— масса тела, а — расстояние между осями. Например, момент инерции диска относительно оси, перпендикулярной плоскости диска и проходящей через его край, равен  Минимальный момент инерции среди всех параллельных осей получается для оси, проходящей через центр масс.
Минимальный момент инерции среди всех параллельных осей получается для оси, проходящей через центр масс.
Теорема о взаимно перпендикулярных осях: момент инерции плоского тела относительно произвольной оси  перпендикулярной его плоскости, равен сумме моментов инерции относительно двух взаимно перпендикулярных осей х и у, лежащих в плоскости тела и пересекающихся с осью
перпендикулярной его плоскости, равен сумме моментов инерции относительно двух взаимно перпендикулярных осей х и у, лежащих в плоскости тела и пересекающихся с осью 

Например, момент инерции тонкого диска относительно оси симметрии, лежащей в его плоскости, равен 
Приведем моменты инерции некоторых тел различной формы.
1) Тонкий обруч (относительно оси симметрии):  Такой же момент инерции имеет тонкостенный цилиндр (без торцов).
Такой же момент инерции имеет тонкостенный цилиндр (без торцов).
2) Тонкий стержень длиной  (относительно перпендикулярной к стержню оси, проходящей через его середину):
(относительно перпендикулярной к стержню оси, проходящей через его середину):  Такой же момент инерции имеет плоский прямоугольник относительно оси, проходящей через середины противоположных сторон длиной
Такой же момент инерции имеет плоский прямоугольник относительно оси, проходящей через середины противоположных сторон длиной  Относительно края стержня момент инерции равен
Относительно края стержня момент инерции равен 
3) Плоский прямоугольник относительно оси, перпендикулярной его плоскости и проходящей через его центр:  Такой же момент инерции имеет прямоугольный параллелепипед относительно оси, проходящей через середины противоположных граней.
Такой же момент инерции имеет прямоугольный параллелепипед относительно оси, проходящей через середины противоположных граней.
4) Тонкая сфера относительно оси симметрии: 
5) Однородный шар относительно оси симметрии: 
6) Цилиндрический слой с внутренним радиусом  и внешним
и внешним 
Плоское движение твердого тела. Плоское движение есть суперпозиция поступательного движения центра масс и вращательного движения в системе центра масс (см. разд. 1.2). Движение центра масс описывается вторым законом Ньютона и определяется результирующей внешней силой (уравнение (11)). Вращательное движение в системе центра масс подчиняется уравнению (39), в котором надо учитывать только реальные внешние силы, так как момент сил инерции относительно центра масс равен нулю (аналогично моменту сил тяжести, пример 1 из разд. 1.6). Кинетическая энергия плоского движения равна  уравнение
уравнение  Момент импульса относительно неподвижной оси, перпендикулярной плоскости движения, вычисляется по формуле (см. уравнение
Момент импульса относительно неподвижной оси, перпендикулярной плоскости движения, вычисляется по формуле (см. уравнение  где
где  — плечо скорости центра масс относительно оси, а знаки определяются выбором положительного направления вращения.
— плечо скорости центра масс относительно оси, а знаки определяются выбором положительного направления вращения.
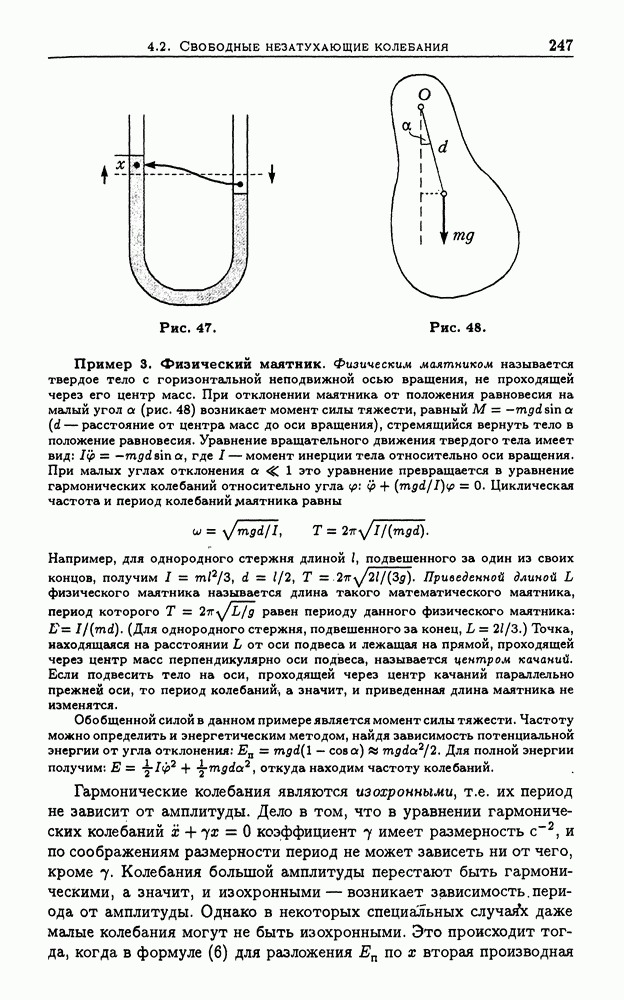
Пример 3. Требуется найти ускорение круглого тела, которое скатывается без проскальзывания по наклонной плоскости (рис. 10).
Решение. Уравнения движения имеют вид:  Условие отсутствия проскальзывания
Условие отсутствия проскальзывания  приводит к уравнению
приводит к уравнению  (см. пример 1 из разд. 1.2). Решая уравнения, находим ускорение:
(см. пример 1 из разд. 1.2). Решая уравнения, находим ускорение:  Так как сила трения покоя работы не совершает, то механическая энергия сохраняется.
Так как сила трения покоя работы не совершает, то механическая энергия сохраняется.

Рис. 10.
Пример 4. При упругом ударе шарика массой  о край неподвижного стержня длиной
о край неподвижного стержня длиной  и массой М, расположенного перпендикулярно его скорости, конечные скорости шарика и, центра стержня V и угловую скорость его вращения
и массой М, расположенного перпендикулярно его скорости, конечные скорости шарика и, центра стержня V и угловую скорость его вращения  определяют из трех уравнений:
определяют из трех уравнений:
1) закона сохранения импульса: 
2) закона сохранения энергии: 
3) закона сохранения момента импульса (например, относительно точки удара): 
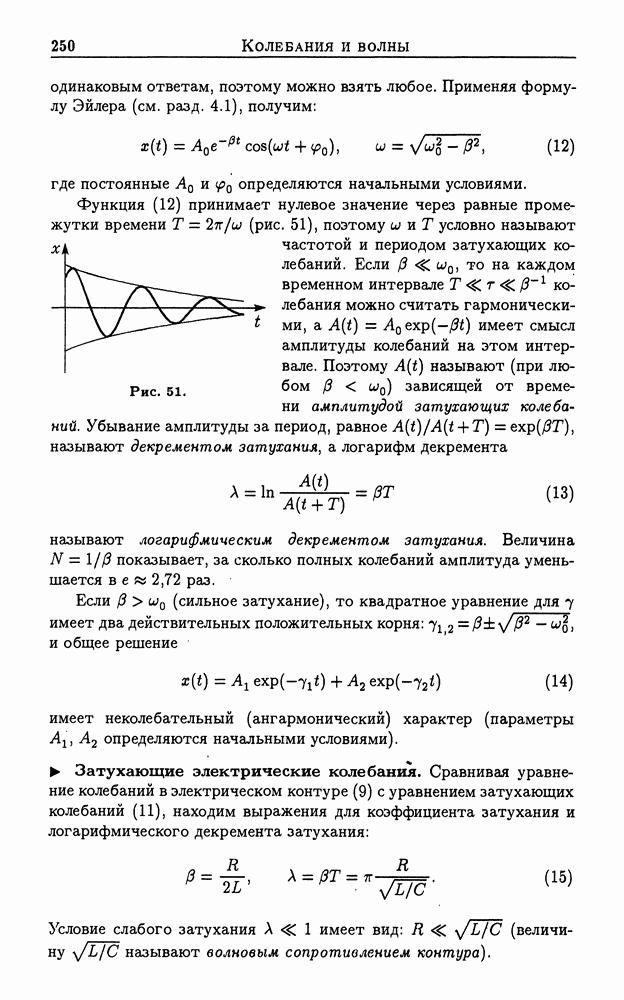
Движение с неподвижной точкой. Угловая скорость вращения, направленная вдоль оси вращения, меняет свое направление как в пространстве, так и по отношению к самому твердому телу. Уравнение движения

которое называют основным уравнением движения твердого тела с неподвижной точкой, позволяетузнать, как изменяется момент импульса  Так как вектор
Так как вектор  в общем случае не параллелен вектору
в общем случае не параллелен вектору  то для
то для

Рис. 11.
замыкания уравнений движения надо научиться связывать эти величины друг с другом.
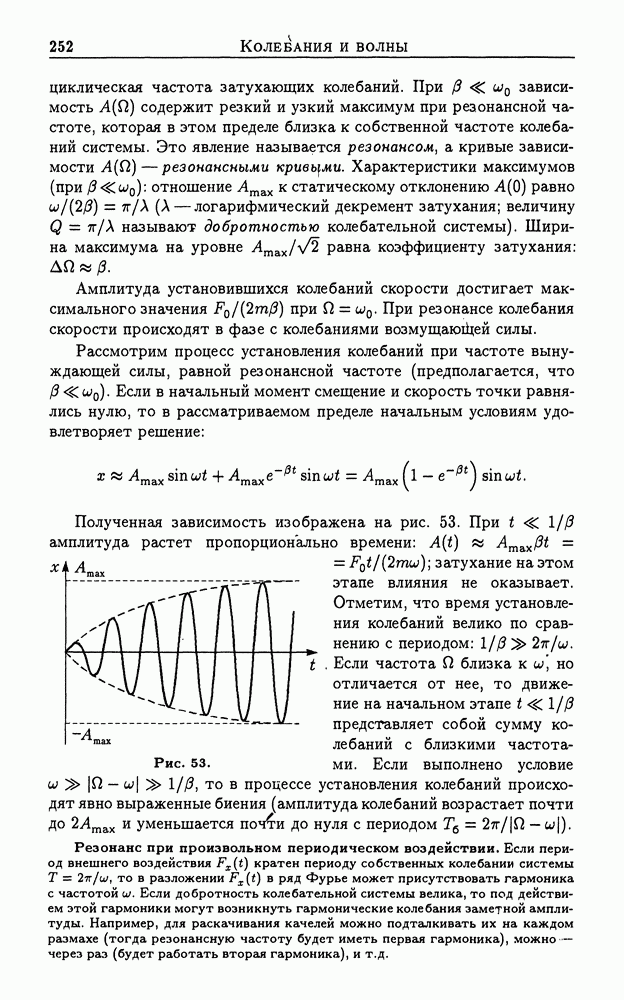
Пример 5. При вращении наклонной гантельки вокруг вертикальной оси (рис. 11) момент импульса  направлен перпендикулярно гантельке, он направлен под углом к оси вращения и сам вращается с угловой скоростью
направлен перпендикулярно гантельке, он направлен под углом к оси вращения и сам вращается с угловой скоростью  .
.
Проблему связи между  решает теорема о главных осях инерции, утверждающая, что для любой точки тела существуют три взаимнодерпендикулярные оси, при врагцении относительно которых вектор
решает теорема о главных осях инерции, утверждающая, что для любой точки тела существуют три взаимнодерпендикулярные оси, при врагцении относительно которых вектор  параллелен оси вращения:
параллелен оси вращения:  Моменты инерции относительно этих осей называют главными моментами инерции. Если вращение происходит вокруг произвольной оси вращения, то, разложив угловую скорость по главным осям
Моменты инерции относительно этих осей называют главными моментами инерции. Если вращение происходит вокруг произвольной оси вращения, то, разложив угловую скорость по главным осям  мы сможем вычислить момент импульса:
мы сможем вычислить момент импульса:  (Аналогично, разложив вектор
(Аналогично, разложив вектор  мы найдем вектор й.) Если главные оси проведены через центр масс (центр инерции) тела, то их называют свободными осями. При вращении вокруг любой из свободных осей сохраняются как импульс, так и момент импульса тела, т.е. для поддержания вращения к телу не надо прикладывать ни внешнюю силу, ни внешний момент сил. (В примере 5 результирующая сила равна нулю, но в точках крепления оси возникает пара сил, момент которых обеспечивает изменение
мы найдем вектор й.) Если главные оси проведены через центр масс (центр инерции) тела, то их называют свободными осями. При вращении вокруг любой из свободных осей сохраняются как импульс, так и момент импульса тела, т.е. для поддержания вращения к телу не надо прикладывать ни внешнюю силу, ни внешний момент сил. (В примере 5 результирующая сила равна нулю, но в точках крепления оси возникает пара сил, момент которых обеспечивает изменение  со временем.) При свободном вращении устойчивым оказывается только вращение относительно двух свободных осей — с минимальным и максимальным главными моментами инерции.
со временем.) При свободном вращении устойчивым оказывается только вращение относительно двух свободных осей — с минимальным и максимальным главными моментами инерции.

Рис. 12.
Гироскопы. Гироскопом называют твердое тело, быстро вращающееся относительно своей оси симметрии. Задачу о движении оси гироскопа можно решать в гироскопическом приближении:  оба вектора направлены вдоль оси симметрии. Уравновешенный гироскоп (закрепленный в центре масс) обладает свойством безынерционно
оба вектора направлены вдоль оси симметрии. Уравновешенный гироскоп (закрепленный в центре масс) обладает свойством безынерционно  его ось перестает двигаться, как только исчезает внешнее воздействие (
его ось перестает двигаться, как только исчезает внешнее воздействие ( обращается в нуль). Это позволяет использовать гироскоп для сохранения ориентации в пространстве.
обращается в нуль). Это позволяет использовать гироскоп для сохранения ориентации в пространстве.
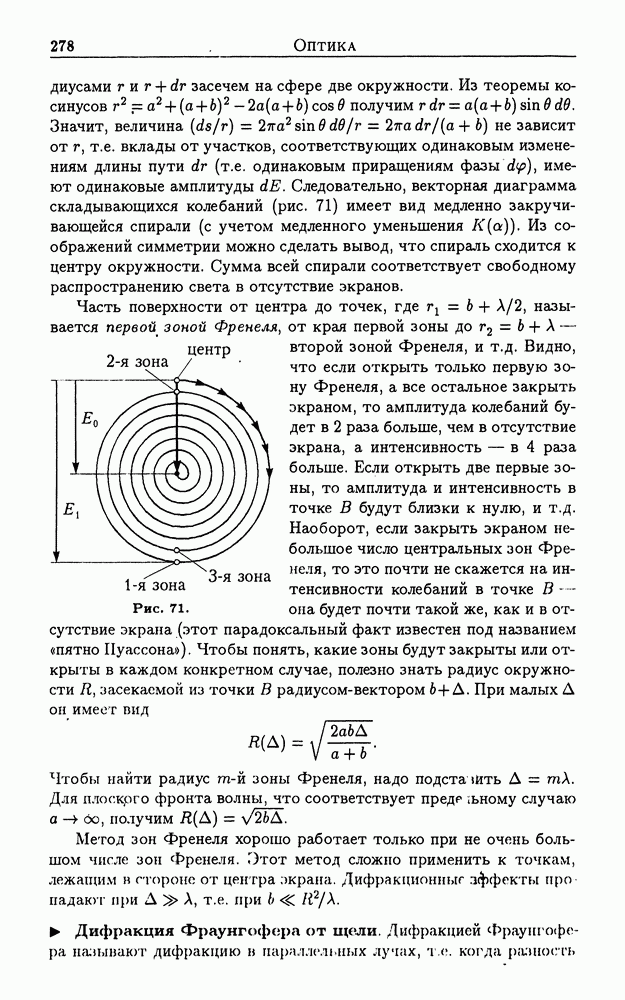
На тяжелый гироскоп (рис. 12), у которого центр масс смещен на расстояние  от точки закрепления действует момент силы тяжедти, направленный перпендикулярно
от точки закрепления действует момент силы тяжедти, направленный перпендикулярно  Так как
Так как  то
то  и ось гироскопа совершают регулярное вращение вокруг вертикальной оси (прецессия гироскопа).
и ось гироскопа совершают регулярное вращение вокруг вертикальной оси (прецессия гироскопа).
Конец вектора  вращается по горизонтальной окружности радиусом
вращается по горизонтальной окружности радиусом  а с угловой скоростью
а с угловой скоростью

Угловая скорость прецессии не зависит от угла наклона оси а.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- 1. Аналитическая геометрия на плоскости
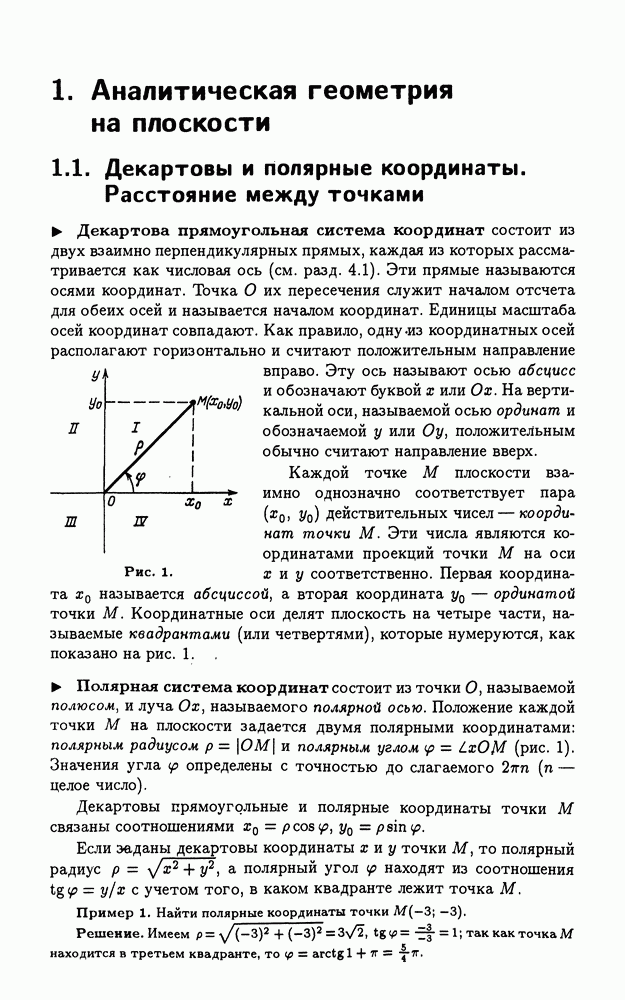
- 1.1. Декартовы и полярные координаты. Расстояние между точками
- 1.2. Деление отрезка в данном отношении. Площадь многоугольника
- 1.3. Различные виды уравнения прямой
- 1.4. Угол между прямыми. Расстояние от точки до прямой
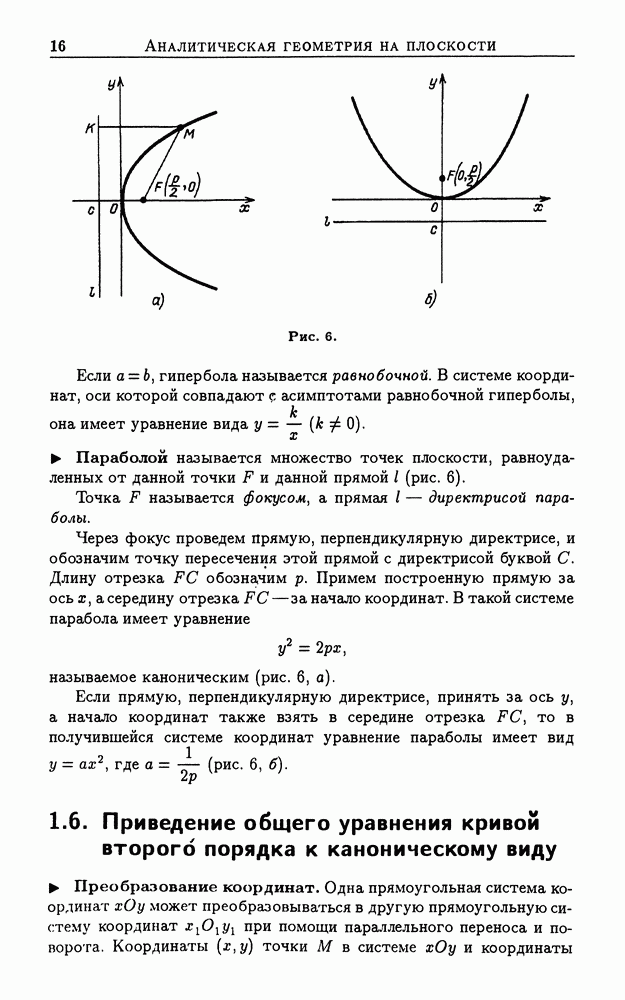
- 1.5. Окружность, эллипс, гипербола и парабола
- 1.6. Приведение общего уравнения кривой второго порядка к каноническому виду
- 2. Аналитическая геометрия в пространстве
- 2.2. Векторы
- 2.3. Действия над векторами. Скалярное произведение
- 2.4. Векторное и смешанное произведения
- 2.5. Плоскость в пространстве
- 2.6. Прямая в пространстве
- 2.7. Прямая и плоскость в пространстве
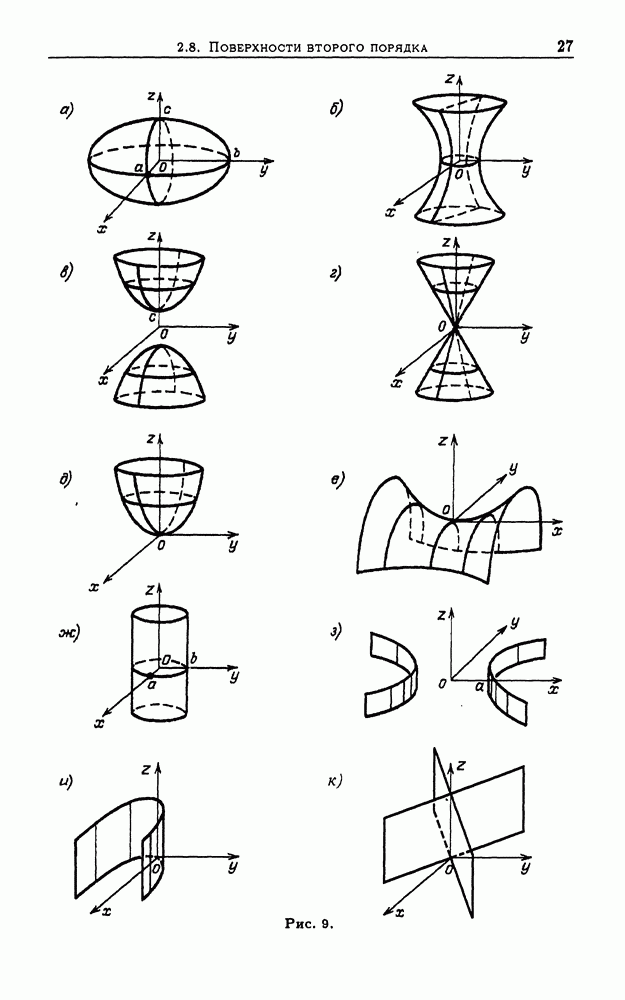
- 2.8. Поверхности второго порядка
- 3. Линейная алгебра
- 3.2. Матрицы
- 3.3. Системы линейных уравнений
- 3.4. Системы n-мерных векторов. Собственные значения и собственные векторы матрицы
- 4. Основные понятия математического анализа
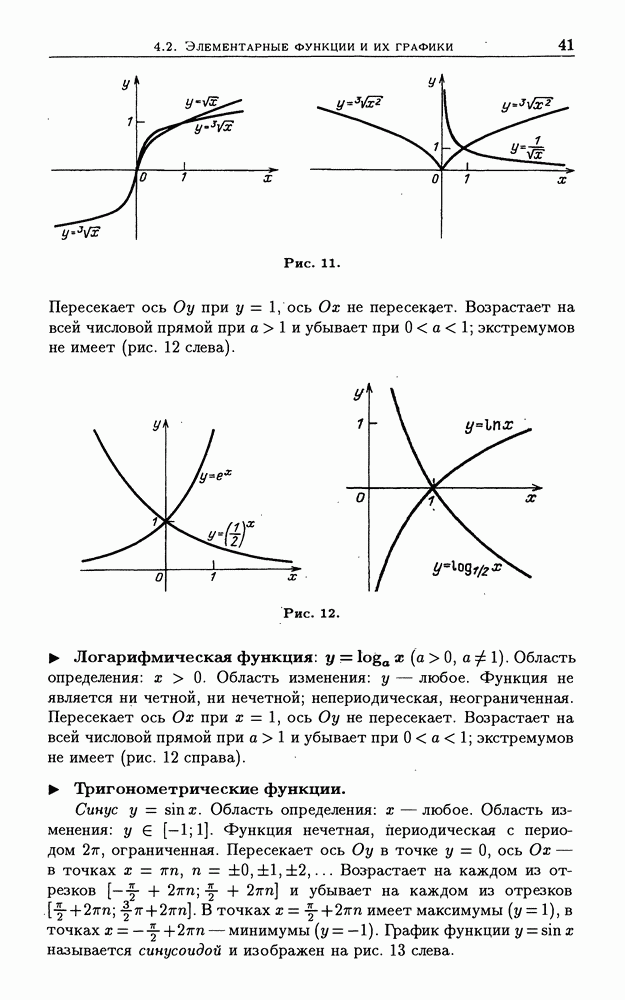
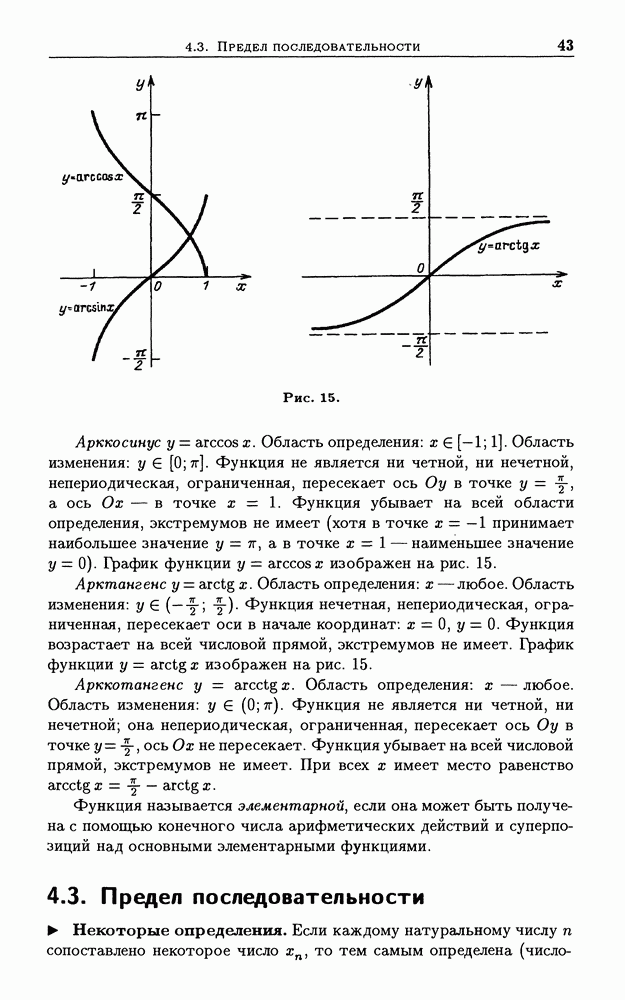
- 4.2. Элементарные функции и их графики
- 4.3. Предел последовательности
- 4.4. Предел функции
- 4.5. Бесконечно малые и бесконечно большие функции
- 4.6. Непрерывность
- 4.7. Асимптоты графика функции
- 5. Дифференциальное исчисление функций одной переменной
- 5.2. Таблица производных и правила дифференцирования
- 5.3. Теоремы о дифференцируемых функциях. Правило Лопиталя
- 5.4. Производные и дифференциалы высших порядков. Формула Тейлора
- 5.5. Экстремумы. Точки перегиба
- 5.6. Общая схема исследования функции и построение графика
- 6. Функции нескольких переменных
- 6.1. Точечные множества. Функции. Предел и непрерывность
- 6.2. Дифференцирование функций нескольких переменных
- 6.3. Производная по направлению. Геометрические приложения
- 6.4. Экстремумы функций нескольких переменных
- 7. Неопределенный интеграл
- 7.1. Первообразная. Неопределенный интеграл и его свойства
- 7.2. Таблица основных интегралов. Примеры интегрирования
- 7.3. Интегрирование по частям. Метод замены переменной
- 7.4. Интегрирование рациональных функций
- 7.5. Интегрирование иррациональных функций
- 7.6. Интегрирование показательных и тригонометрических функций
- 8. Определенный интеграл
- 8.1. Основные определения. Геометрический смысл определенного интеграла
- 8.2. Свойства определенного интеграла
- 8.3. Геометрические и физические приложения определенного интеграла
- 8.4. Несобственные интегралы
- 9. Двойные и тройные интегралы
- 9.1. Определение и свойства двойного интеграла
- 9.2. Вычисление двойного интеграла
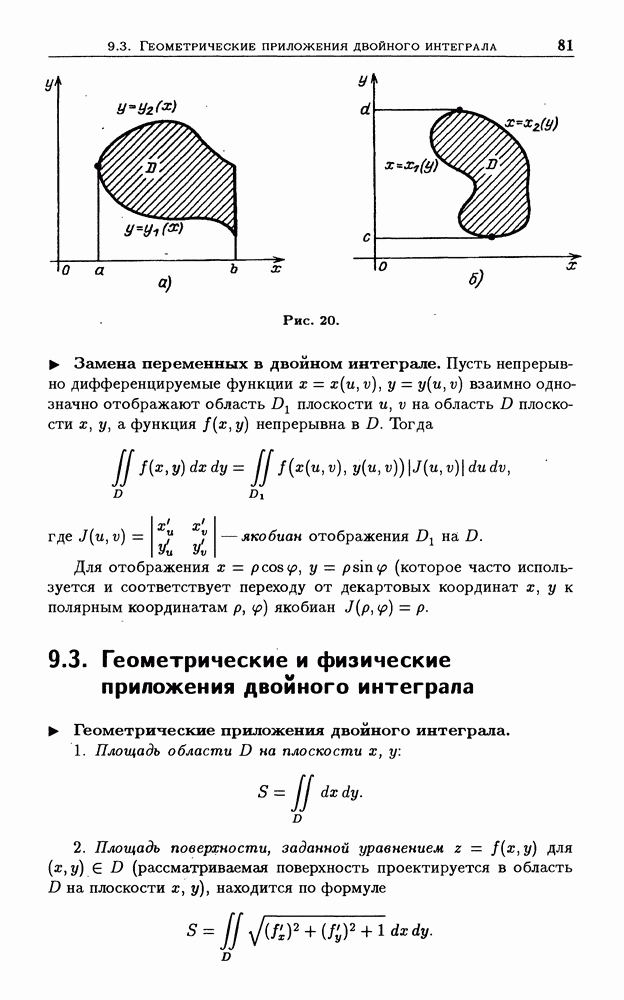
- 9.3. Геометрические и физические приложения двойного интеграла
- 9.4. Определение и свойства тройного интеграла
- 9.5. Вычисление тройного интеграла. Некоторые приложения
- 10. Криволинейные и поверхностные интегралы
- 10.2. Криволинейный интеграл второго рода
- 10.3. Поверхностный интеграл первого рода
- 10.4. Поверхностный интеграл второго рода
- 10.5. Дифференциальные операции и интегральные формулы теории поля
- 11. Ряды
- 11.1. Числовые ряды
- 11.2. Функциональные ряды
- 11.3. Степенные ряды
- 11.4. Ряд Фурье
- 11.5. Интеграл Фурье. Преобразование Фурье
- 12. Обыкновенные дифференциальные уравнения
- 12.2. Дифференциальные уравнения высших порядков
- 12.3. Линейные уравнения n-го порядка
- 12.4. Решение линейных однородных уравнений n-го порядка с постоянными коэффициентами
- 12.5. Линейные неоднородные уравнения n-го порядка
- 12.6. Системы обыкновенных дифференциальных уравнений
- 13. Приближенные вычисления
- 13.1. Метод наименьших квадратов
- 13.2. Приближенное решение алгебраических уравнений
- 13.3. Вычисление определенного интеграла
- 13.4. Численное интегрирование дифференциальных уравнений
- 14. Теория вероятностей
- 14.1. Правила и формулы комбинаторики
- 14.2. Основные понятия теории вероятностей
- 14.3. Условная вероятность. Теоремы и формулы теории вероятностей
- 14.4. Математическое ожидание и дисперсия
- 14.5. Закон больших чисел
- 1. Физические основы механики
- 1.1. Кинематика точки
- 1.2. Кинематика твердого тела
- 1.3. Динамика
- 1.4. Закон сохранения импульса
- 1.5. Закон сохранения энергии
- 1.6. Закон сохранения момента импульса
- 1.7. Задана двух тел и движение в центральном поле
- 1.8. Поле тяготения
- 1.9. Неинерциальные системы отсчета
- 1.10. Динамика твердого тела
- 1.11. Специальная теория относительности
- 2. Молекулярная физика и термодинамика
- 2.2. Первое начало термодинамики
- 2.3. Второе начало термодинамики
- 2.4. Энтропия. Свободная энергия
- 2.5. Кинетическая теория идеального газа
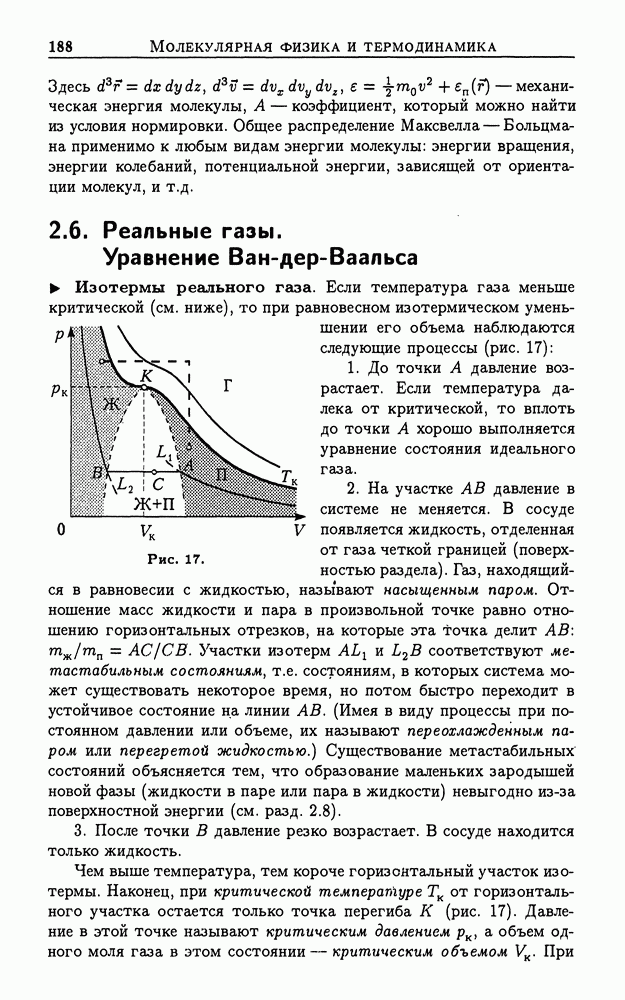
- 2.6. Реальные газы. Уравнение Ван-дер-Ваальса
- 2.7. Равновесие фаз. Фазовые переходы
- 2.8. Поверхностное натяжение
- 2.9. Явления переноса в газах
- 3. Электродинамика
- 3.1. Электрический заряд. Закон Кулона
- 3.2. Электрическое поле. Напряженность поля
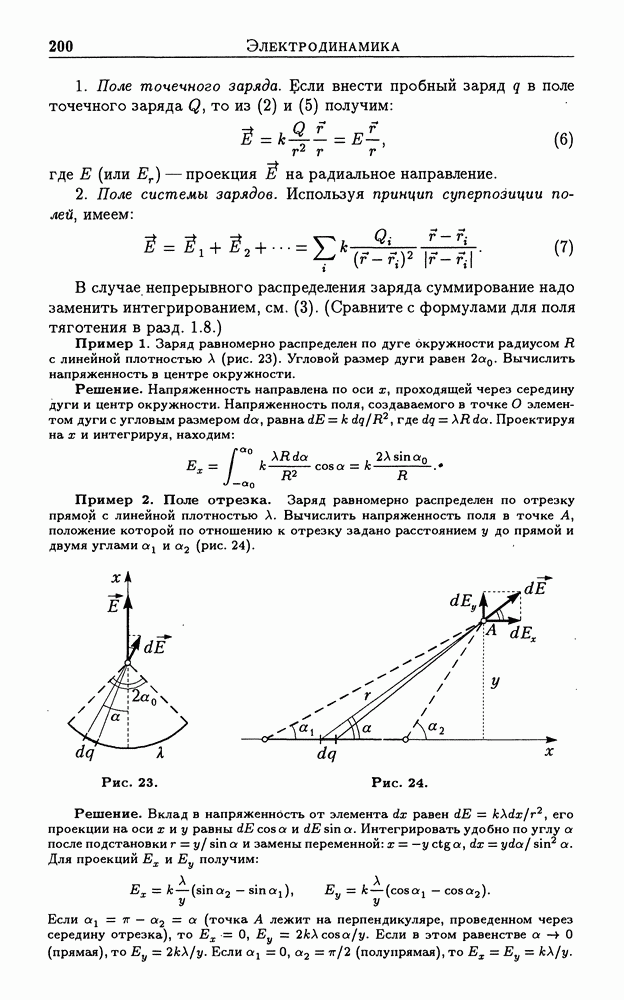
- 3.3. Электростатическое поле. Принцип суперпозиции для напряженности и потенциала
- 3.4. Теорема Гаусса
- 3.5. Электростатика проводников
- 3.6. Электростатика диэлектриков
- 3.7. Конденсаторы
- 3.8. Энергия электростатического поля
- 3.9. Постоянный ток
- 3.10. Магнитное поле. Сила Лоренца и закон Ампера
- 3.11. Вычисление магнитной индукции
- 3.12. Циркуляция и поток вектора магнитной индукции
- 3.13. Магнитное поле в веществе
- 3.14. Электромагнитная индукция
- 3.15. Уравнения Максвелла
- 4. Колебания и волны
- 4.1. Гармонические колебания. Сложение колебаний
- 4.2. Свободные незатухающие колебания
- 4.3. Затухающие и вынужденные колебания
- 4.4. Упругие волны
- 4.5. Электромагнитные волны
- 5. Оптика
- 5.1. Геометрическая оптика. Фотометрия
- 5.2. Интерференция света
- 5.3. Дифракция
- 5.4. Поляризация света. Формулы Френеля
- 5.5. Дисперсия и поглощение света
- 5.6. Тепловое излучение
- 5.7. Световые кванты
- Список литературы
- 1. Кинематика
- 1.1. Кинематика точки
- 1.2. Кинематика твердого тела
- 1.3. Плоскопараллельное движение твердого тела
- 1.4. Произвольное движение твердого тела
- 1.5. Сложное движение точки
- 2. Основные понятия и аксиомы механики
- 2.2. Аксиомы механики
- 3. Статика
- 3.2. Условия уравновешенности систем сил, приложенных к твердому телу
- 3.3. Решение задан статики
- 3.4. Центр параллельных сил. Центр тяжести твердого тела
- 3.5. Распределенные силы
- 3.6. Законы трения (законы Кулона)
- 4. Динамика материальной точки
- 4.2. Первая и вторая задачи динамики
- 5. Общие теоремы динамики механической системы
- 5.2. Теорема о движении центра масс
- 5.3. Теорема об изменении количества движения
- 5.4. Теорема об изменении кинетического момента
- 5.5. Теорема об изменении кинетической энергии
- 6. Принцип Даламбера. Элементы аналитической механики
- 6.2. Классификация механических связей. Обобщенные координаты
- 6.3. Принцип возможных перемещений
- 6.4. Общее уравнение динамики (принцип Даламбера — Лагранжа)
- 6.5. Уравнения Лагранжа второго рода
- 1. Основные понятия
- 1.1. Введение. Внешние и внутренние силы
- 1.2. Напряжения и деформации в точке
- 1.3. Основные понятия и допущения
- 2. Напряженно-деформированное состояние в точке
- 2.2. Одноосное растяжение и сжатие
- 2.3. Чистый сдвиг
- 3. Центральное растяжение и сжатие
- 3.2. Напряжения и деформации при растяжении или сжатии
- 3.3. Расчеты на прочность при растяжении и сжатии
- 4. Кручение
- 4.2. Напряжения и деформации при кручении
- 4.3. Расчеты на прочность при кручении
- 5. Прямой изгиб
- 5.2. Напряжения и деформации при прямом чистом изгибе
- 5.3. Напряжения и деформации при прямом поперечном изгибе
- 5.4. Расчет на прочность при прямом изгибе
- 6. Сложное сопротивление
- 6.2. Внецентренное растяжение или сжатие
- 6.3. Изгиб с кручением
- 7. Устойчивость сжатых стержней
- 7.2. Формула Эйлера
- 7.3. Влияние способов закрепления концов стержня на величину критической силы
- 7.4. Пределы применимости формулы Эйлера
- 7.5. Расчеты сжатых стержней на устойчивость
- ПРИЛОЖЕНИЯ
- 1. Элементарные функции и их свойства
- 2. Таблица неопределенных интегралов
- 3. Решения обыкновенных дифференциальных уравнений
- 4. Ортогональные криволинейные системы координат
- 5. Некоторые физические постоянные