| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2.4. Энтропия. Свободная энергия
Определение энтропии. Уравнение Клаузиуса для обратимого цикла (21) можно переформулировать как условие независимости интеграла

от пути равновесного перехода из состояния А в состояние В. Это позволяет определить функцию состояния — энтропию, точнее, разность энтропий в двух состояниях:

При равновесном процессе без подвода тепла энтропия не меняется (адиабатический процесс можно называть изоэнтропным). Первое начало термодинамики (6) для равновесного процесса в простой системе приобретает вид:

Примеры вычисления энтропии.
1. Процесс с постоянной теплоемкостью. Изменение энтропии при изменении температуры от  до
до  равно
равно

2. Энтропия идеального газа. Подставляя в (23) выражение для внутренней энергии идеального газа (11), с учетом уравнения состояния  получим
получим

Иногда условно записывают  , имея в виду, что в приложениях всегда возникает разность энтропий.
, имея в виду, что в приложениях всегда возникает разность энтропий.
3. Энтропия газа Ван-дер-Ваальса. Подставляя в (23) зависимость (19), с учетом уравнения состояния (3) имеем

Направление неравновесных процессов в теплоизолированной системе. Рассмотрим неравновесный процесс, переводящий
систему из равновесного состояния 1 в равновесное состояние 2. Теперь вернемся из 2 в 1 при помощи любого равновесного процесса, запишем для получившегося циклического процесса неравенство Клаузиуса (20) и учтем определение энтропии (22):

Если неравновесный процесс происходит в адиабатической оболочке, то левая часть равенства обращается в нуль, что дает

т.е. в любом процессе без подвода тепла энтропия не убывает. Равновесное состояние теплоизолированной системы соответствует максимуму энтропии.
Примеры неравновесных процессов.
1. Теплообмен. Рассмотрим простейший пример теплообмена — между двумя телами с одинаковой теплоемкостью С и начальными температурами  Из уравнения теплового баланса следует, что в результате теплообмена оба тела достигнут одинаковой температуры
Из уравнения теплового баланса следует, что в результате теплообмена оба тела достигнут одинаковой температуры  При этом согласно (24) изменение энтропии системы будет положительным:
При этом согласно (24) изменение энтропии системы будет положительным:

(аргумент логарифма больше единицы, так как среднее арифметическое больше среднего геометрического).
2. Расширение идеального газа в пустоту. Внутренняя энергия и, следовательно, температура идеального газа при расширении его в пустоту остаются постоянными. Изменение энтропии находим из формулы (25):

Возрастание энтропии при адиабатическом расширении в пустоту (увеличении V при постоянной  можно доказать для любой простой системы. Если рассматривать
можно доказать для любой простой системы. Если рассматривать  в (23) как функцию переменных, то получим
в (23) как функцию переменных, то получим 
3. Смешение газов. Рассмотрим теплоизолированный сосуд, разделенный перегородкой на две равные части, в каждой из которых содержится по одному молю идеального газа при одинаковых температурах и давлениях. При убирании перегородки газы смешиваются; из формулы (28) следует, что энтропия системы увеличивается
на  (энтропия смешения). В случае различных газов начальное состояние отличается от конечного; газы можно снова разделить, совершая работу над специальными поршнями, пропускающими молекулы только одного сорта. Однако для одинаковых газов начальное и конечное состояния системы тождественны, и энтропия не должна меняться. Отсутствие непрерывного перехода от почти одинаковых к полностью тождественным молекулам называют парадоксом Гиббса.
(энтропия смешения). В случае различных газов начальное состояние отличается от конечного; газы можно снова разделить, совершая работу над специальными поршнями, пропускающими молекулы только одного сорта. Однако для одинаковых газов начальное и конечное состояния системы тождественны, и энтропия не должна меняться. Отсутствие непрерывного перехода от почти одинаковых к полностью тождественным молекулам называют парадоксом Гиббса.
Статистический смысл энтропии. Формула Больцмана

(k — постоянная Больцмана) связывает энтропию макроскопического состояния со статистическим весом этого состояния, т.е. числом различных микроскопических состояний, которые его реализуют. Чем больше П, тем больше вероятность состояния; при неравновесных процессах система переходит от менее вероятных к более вероятным состояниям. Логарифм обеспечивает аддитивность энтропии: статистический вес системы, состоящей из двух независимых подсистем, равен произведению их статистических весов.
Чтобы проиллюстрировать формулу (29), вычислим пространственную часть энтропии газа. Разобьем объем на маленькие ячейки объемом  Каждая молекула может быть помещена в любую из
Каждая молекула может быть помещена в любую из  ячеек, т.е. число независимых состояний равно
ячеек, т.е. число независимых состояний равно  где
где  — число молекул газа. Для энтропии получим
— число молекул газа. Для энтропии получим  Квантовая статистика утверждает, что одинаковые частицы принципиально неразличимы, т.е. П надо разделить на число перестановок между ними
Квантовая статистика утверждает, что одинаковые частицы принципиально неразличимы, т.е. П надо разделить на число перестановок между ними  . В результате для пространственной части энтропии получим выражение
. В результате для пространственной части энтропии получим выражение  Нетрудно убедиться, что таким образом удается разрешить парадокс Гкббса.
Нетрудно убедиться, что таким образом удается разрешить парадокс Гкббса.
Третье начало термодинамики. Третье начало термодинамики (теорема Нернста) утверждает, что при приближении температуры к абсолютному нулю энтропия любой системы стремится к определенному конечному значению, не зависящему от значения остальных термодинамических параметров. Энтропию системы при  принимают равной нулю. Статистическое объяснение: при
принимают равной нулю. Статистическое объяснение: при  система находится в наинизшем энергетическом состоянии, кратность которого (равная статистическому весу системы
система находится в наинизшем энергетическом состоянии, кратность которого (равная статистическому весу системы  при
при  невелика. Значит, в соответствии с формулой Больцмана (29) энтропия пренебрежимо мала. Следствия третьего начала: при Т 0 теплоемкости
невелика. Значит, в соответствии с формулой Больцмана (29) энтропия пренебрежимо мала. Следствия третьего начала: при Т 0 теплоемкости  системы, а также ее температурные коэффициенты объемного расширения а и давления
системы, а также ее температурные коэффициенты объемного расширения а и давления  стремятся к нулю.
стремятся к нулю.
Система в термостате. Свободная энергия. Рассмотрим изменение состояния системы, находящейся в тепловом контакте с термостатом, имеющим постоянную температуру Т. Такую же температуру будет иметь сама система в начальном и конечном равновесных состояниях. Неравенство (26) после «цепочки» преобразований
 принимает вид:
принимает вид:

где  — новая функция состояния, называемая свободной энергией. Если объем системы не меняется, то в рассматриваемом неравновесном процессе
— новая функция состояния, называемая свободной энергией. Если объем системы не меняется, то в рассматриваемом неравновесном процессе

т.е. свободная энергия не возрастает. Другими словами, равновесное состояние системы постоянного объема, находящейся в тепловом контакте с термостатом, соответствует минимуму свободной энергии. Для равновесного процесса неравенство в этих уравнениях превращается в равенство. Из формулы (23) следует, что

Поэтому естественными переменными для свободной энергии являются объем и температура:  .
.
Если у системы в термостате есть механический контакт (лёгкий поршень, гибкая оболочка) с внешней средой, имеющей фиксированное давление  (такое же давление будет у самой системы в равновесном состоянии), то работа против внешних сил равна
(такое же давление будет у самой системы в равновесном состоянии), то работа против внешних сил равна  Из (30) получим
Из (30) получим

где  — термодинамический потенциал Гиббса (при обратимом процессе
— термодинамический потенциал Гиббса (при обратимом процессе  Равновесному состоянию для системы в термостате и гибкой оболочке соответствует минимум
Равновесному состоянию для системы в термостате и гибкой оболочке соответствует минимум  Так как
Так как  то естественными переменными для термодинамического потенциала являются давление и температура:
то естественными переменными для термодинамического потенциала являются давление и температура:  При постоянных давлении и температуре термодинамический потенциал пропорционален количеству вещества:
При постоянных давлении и температуре термодинамический потенциал пропорционален количеству вещества:  — удельный термодинамический потенциал) или
— удельный термодинамический потенциал) или  — термодинамический потенциал в расчете на одну частицу, или химический потенциал).
— термодинамический потенциал в расчете на одну частицу, или химический потенциал).
Канонические уравнения состояния. Естественные переменные. Хотя функции  могут рассматриваться в любых независимых переменных, для каждой из них существуют естественные переменные. Для энтропии это переменные
могут рассматриваться в любых независимых переменных, для каждой из них существуют естественные переменные. Для энтропии это переменные  , для энтальпии —
, для энтальпии —  для свободной энергии — (V, Т), для потенциала Гиббса —
для свободной энергии — (V, Т), для потенциала Гиббса —  . Функция в естественных переменных называется каноническим уравнением состояния. Зная любое каноническое уравнение, можно получить как термическое, так и калорическое уравнения состояния. Например,
. Функция в естественных переменных называется каноническим уравнением состояния. Зная любое каноническое уравнение, можно получить как термическое, так и калорическое уравнения состояния. Например,  дает выражение для
дает выражение для  а выразив
а выразив  найдем
найдем 
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- 1. Аналитическая геометрия на плоскости
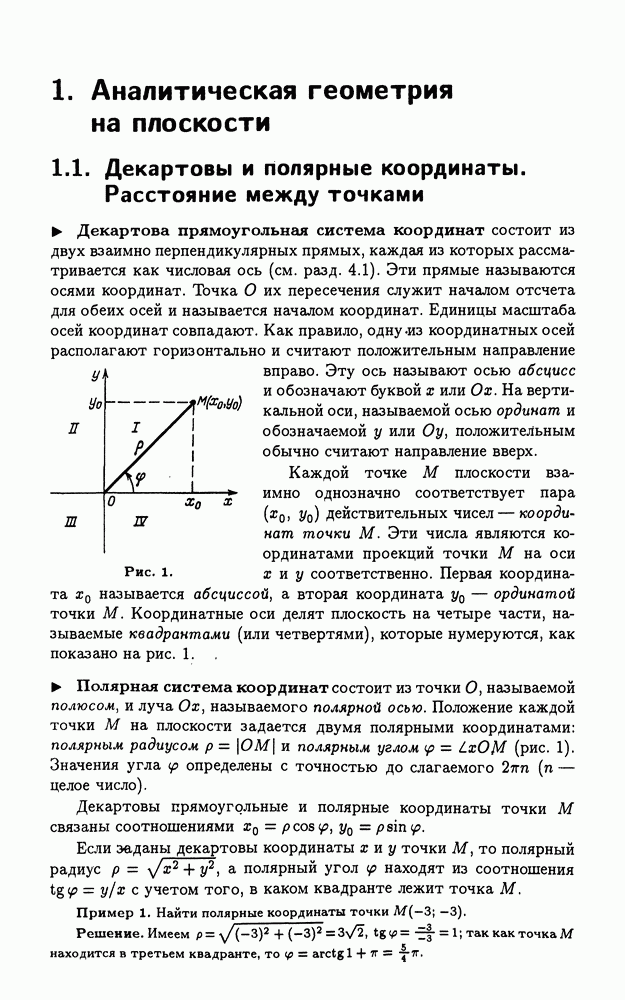
- 1.1. Декартовы и полярные координаты. Расстояние между точками
- 1.2. Деление отрезка в данном отношении. Площадь многоугольника
- 1.3. Различные виды уравнения прямой
- 1.4. Угол между прямыми. Расстояние от точки до прямой
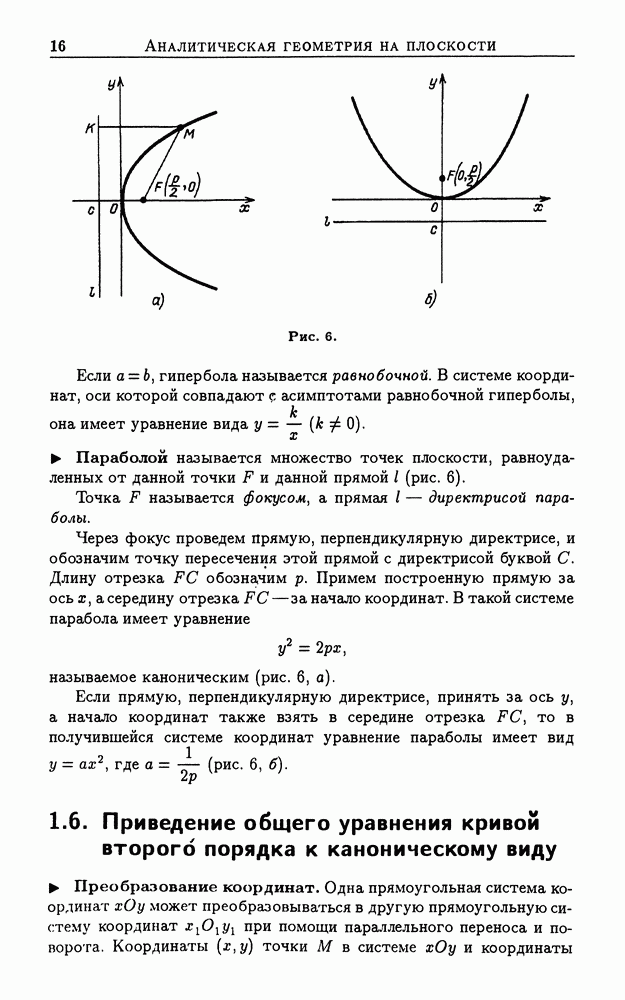
- 1.5. Окружность, эллипс, гипербола и парабола
- 1.6. Приведение общего уравнения кривой второго порядка к каноническому виду
- 2. Аналитическая геометрия в пространстве
- 2.2. Векторы
- 2.3. Действия над векторами. Скалярное произведение
- 2.4. Векторное и смешанное произведения
- 2.5. Плоскость в пространстве
- 2.6. Прямая в пространстве
- 2.7. Прямая и плоскость в пространстве
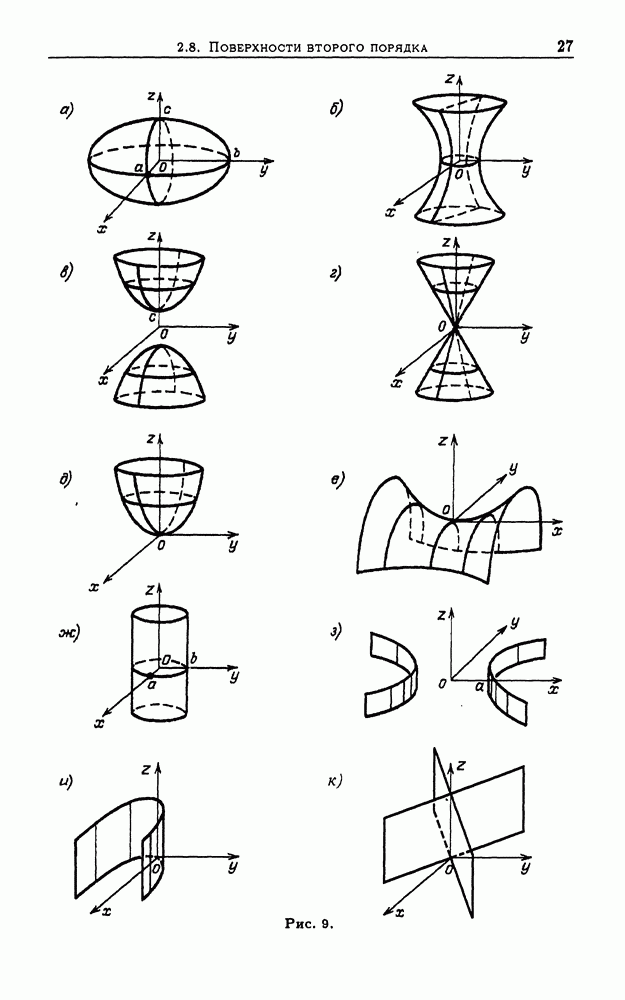
- 2.8. Поверхности второго порядка
- 3. Линейная алгебра
- 3.2. Матрицы
- 3.3. Системы линейных уравнений
- 3.4. Системы n-мерных векторов. Собственные значения и собственные векторы матрицы
- 4. Основные понятия математического анализа
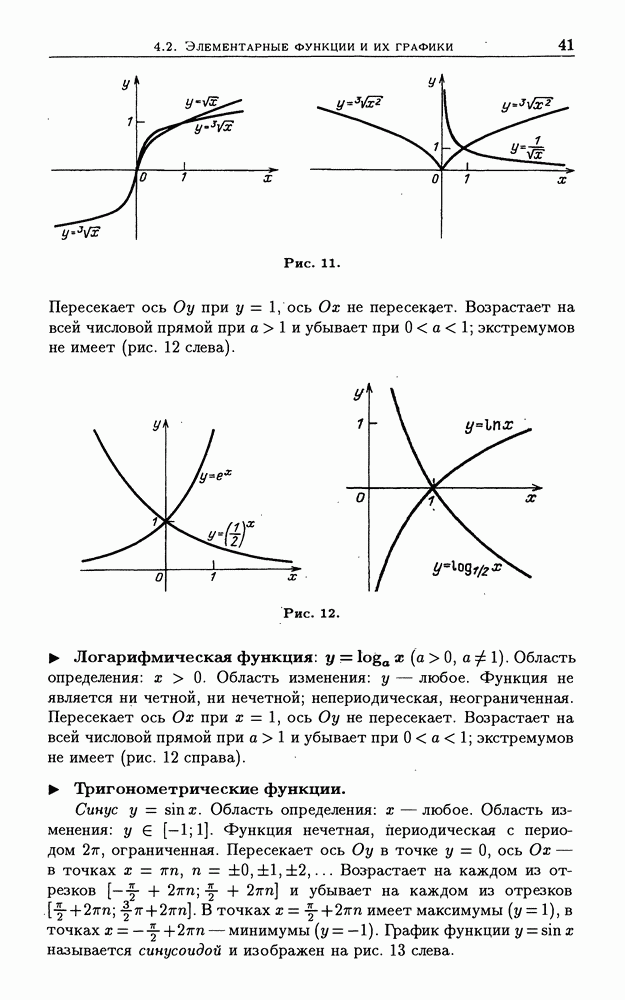
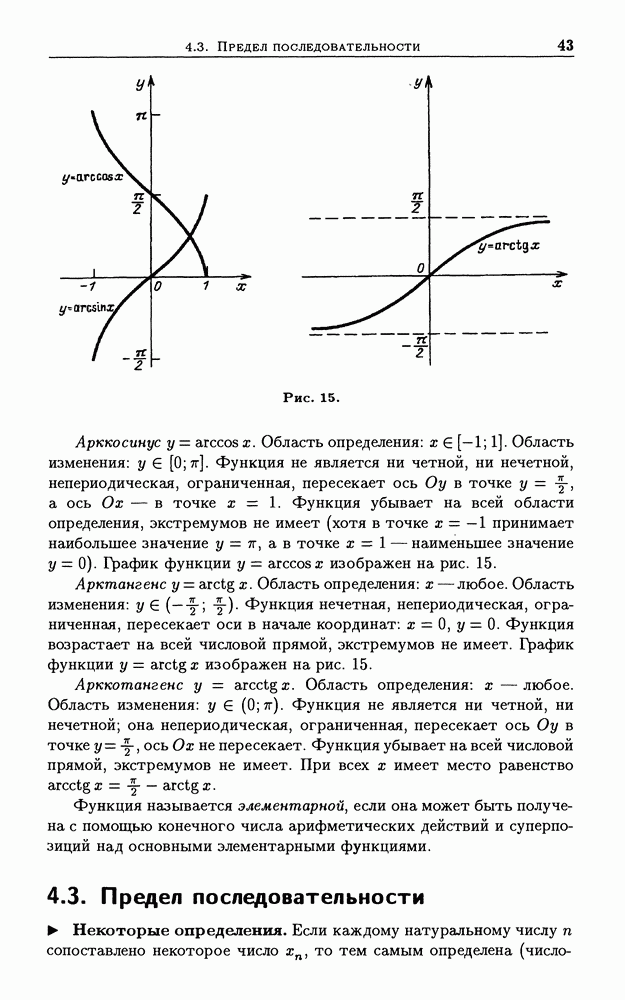
- 4.2. Элементарные функции и их графики
- 4.3. Предел последовательности
- 4.4. Предел функции
- 4.5. Бесконечно малые и бесконечно большие функции
- 4.6. Непрерывность
- 4.7. Асимптоты графика функции
- 5. Дифференциальное исчисление функций одной переменной
- 5.2. Таблица производных и правила дифференцирования
- 5.3. Теоремы о дифференцируемых функциях. Правило Лопиталя
- 5.4. Производные и дифференциалы высших порядков. Формула Тейлора
- 5.5. Экстремумы. Точки перегиба
- 5.6. Общая схема исследования функции и построение графика
- 6. Функции нескольких переменных
- 6.1. Точечные множества. Функции. Предел и непрерывность
- 6.2. Дифференцирование функций нескольких переменных
- 6.3. Производная по направлению. Геометрические приложения
- 6.4. Экстремумы функций нескольких переменных
- 7. Неопределенный интеграл
- 7.1. Первообразная. Неопределенный интеграл и его свойства
- 7.2. Таблица основных интегралов. Примеры интегрирования
- 7.3. Интегрирование по частям. Метод замены переменной
- 7.4. Интегрирование рациональных функций
- 7.5. Интегрирование иррациональных функций
- 7.6. Интегрирование показательных и тригонометрических функций
- 8. Определенный интеграл
- 8.1. Основные определения. Геометрический смысл определенного интеграла
- 8.2. Свойства определенного интеграла
- 8.3. Геометрические и физические приложения определенного интеграла
- 8.4. Несобственные интегралы
- 9. Двойные и тройные интегралы
- 9.1. Определение и свойства двойного интеграла
- 9.2. Вычисление двойного интеграла
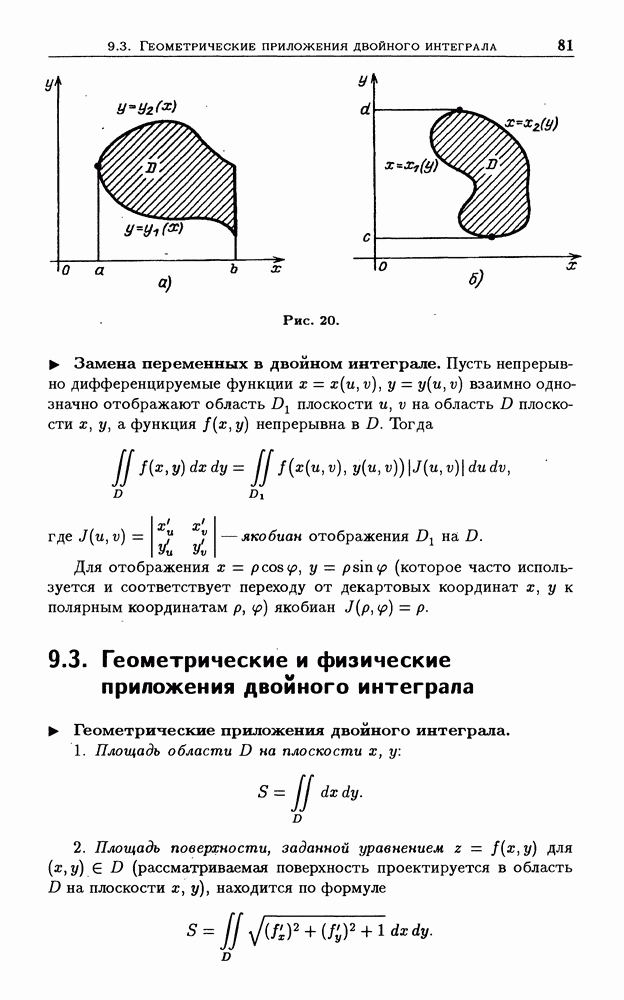
- 9.3. Геометрические и физические приложения двойного интеграла
- 9.4. Определение и свойства тройного интеграла
- 9.5. Вычисление тройного интеграла. Некоторые приложения
- 10. Криволинейные и поверхностные интегралы
- 10.2. Криволинейный интеграл второго рода
- 10.3. Поверхностный интеграл первого рода
- 10.4. Поверхностный интеграл второго рода
- 10.5. Дифференциальные операции и интегральные формулы теории поля
- 11. Ряды
- 11.1. Числовые ряды
- 11.2. Функциональные ряды
- 11.3. Степенные ряды
- 11.4. Ряд Фурье
- 11.5. Интеграл Фурье. Преобразование Фурье
- 12. Обыкновенные дифференциальные уравнения
- 12.2. Дифференциальные уравнения высших порядков
- 12.3. Линейные уравнения n-го порядка
- 12.4. Решение линейных однородных уравнений n-го порядка с постоянными коэффициентами
- 12.5. Линейные неоднородные уравнения n-го порядка
- 12.6. Системы обыкновенных дифференциальных уравнений
- 13. Приближенные вычисления
- 13.1. Метод наименьших квадратов
- 13.2. Приближенное решение алгебраических уравнений
- 13.3. Вычисление определенного интеграла
- 13.4. Численное интегрирование дифференциальных уравнений
- 14. Теория вероятностей
- 14.1. Правила и формулы комбинаторики
- 14.2. Основные понятия теории вероятностей
- 14.3. Условная вероятность. Теоремы и формулы теории вероятностей
- 14.4. Математическое ожидание и дисперсия
- 14.5. Закон больших чисел
- 1. Физические основы механики
- 1.1. Кинематика точки
- 1.2. Кинематика твердого тела
- 1.3. Динамика
- 1.4. Закон сохранения импульса
- 1.5. Закон сохранения энергии
- 1.6. Закон сохранения момента импульса
- 1.7. Задана двух тел и движение в центральном поле
- 1.8. Поле тяготения
- 1.9. Неинерциальные системы отсчета
- 1.10. Динамика твердого тела
- 1.11. Специальная теория относительности
- 2. Молекулярная физика и термодинамика
- 2.2. Первое начало термодинамики
- 2.3. Второе начало термодинамики
- 2.4. Энтропия. Свободная энергия
- 2.5. Кинетическая теория идеального газа
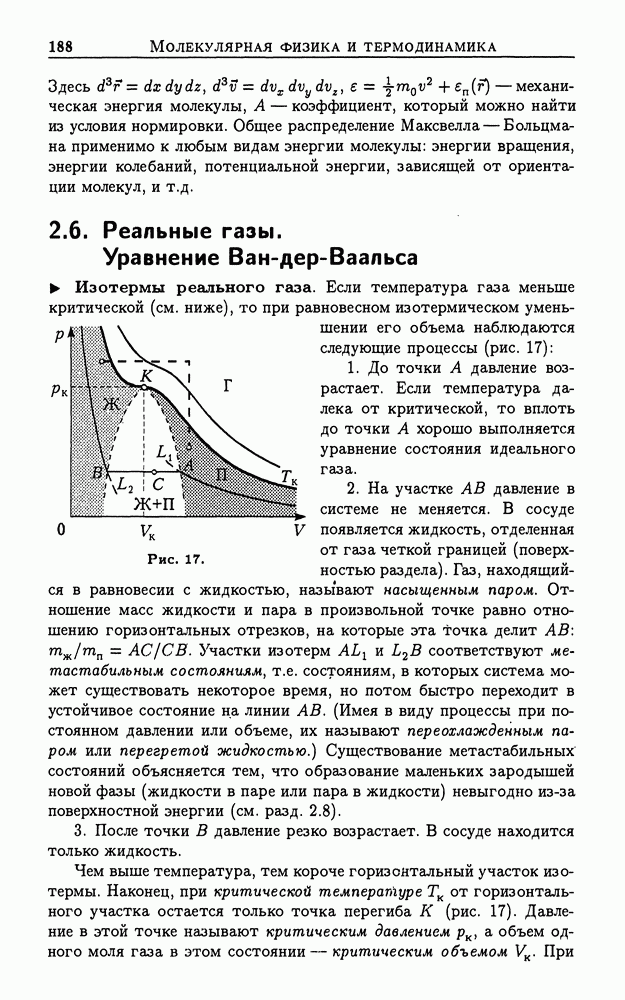
- 2.6. Реальные газы. Уравнение Ван-дер-Ваальса
- 2.7. Равновесие фаз. Фазовые переходы
- 2.8. Поверхностное натяжение
- 2.9. Явления переноса в газах
- 3. Электродинамика
- 3.1. Электрический заряд. Закон Кулона
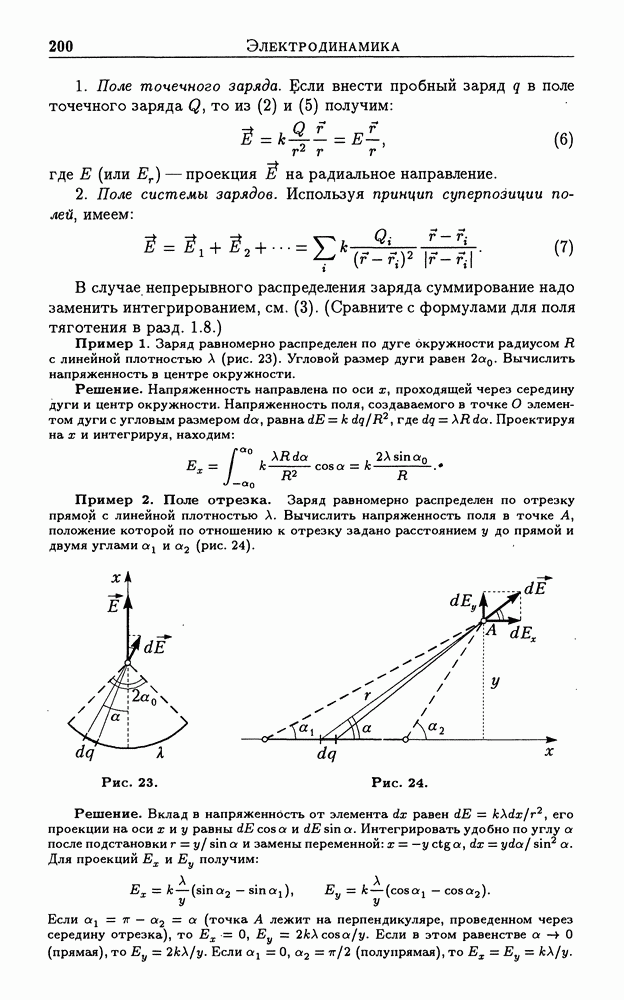
- 3.2. Электрическое поле. Напряженность поля
- 3.3. Электростатическое поле. Принцип суперпозиции для напряженности и потенциала
- 3.4. Теорема Гаусса
- 3.5. Электростатика проводников
- 3.6. Электростатика диэлектриков
- 3.7. Конденсаторы
- 3.8. Энергия электростатического поля
- 3.9. Постоянный ток
- 3.10. Магнитное поле. Сила Лоренца и закон Ампера
- 3.11. Вычисление магнитной индукции
- 3.12. Циркуляция и поток вектора магнитной индукции
- 3.13. Магнитное поле в веществе
- 3.14. Электромагнитная индукция
- 3.15. Уравнения Максвелла
- 4. Колебания и волны
- 4.1. Гармонические колебания. Сложение колебаний
- 4.2. Свободные незатухающие колебания
- 4.3. Затухающие и вынужденные колебания
- 4.4. Упругие волны
- 4.5. Электромагнитные волны
- 5. Оптика
- 5.1. Геометрическая оптика. Фотометрия
- 5.2. Интерференция света
- 5.3. Дифракция
- 5.4. Поляризация света. Формулы Френеля
- 5.5. Дисперсия и поглощение света
- 5.6. Тепловое излучение
- 5.7. Световые кванты
- Список литературы
- 1. Кинематика
- 1.1. Кинематика точки
- 1.2. Кинематика твердого тела
- 1.3. Плоскопараллельное движение твердого тела
- 1.4. Произвольное движение твердого тела
- 1.5. Сложное движение точки
- 2. Основные понятия и аксиомы механики
- 2.2. Аксиомы механики
- 3. Статика
- 3.2. Условия уравновешенности систем сил, приложенных к твердому телу
- 3.3. Решение задан статики
- 3.4. Центр параллельных сил. Центр тяжести твердого тела
- 3.5. Распределенные силы
- 3.6. Законы трения (законы Кулона)
- 4. Динамика материальной точки
- 4.2. Первая и вторая задачи динамики
- 5. Общие теоремы динамики механической системы
- 5.2. Теорема о движении центра масс
- 5.3. Теорема об изменении количества движения
- 5.4. Теорема об изменении кинетического момента
- 5.5. Теорема об изменении кинетической энергии
- 6. Принцип Даламбера. Элементы аналитической механики
- 6.2. Классификация механических связей. Обобщенные координаты
- 6.3. Принцип возможных перемещений
- 6.4. Общее уравнение динамики (принцип Даламбера — Лагранжа)
- 6.5. Уравнения Лагранжа второго рода
- 1. Основные понятия
- 1.1. Введение. Внешние и внутренние силы
- 1.2. Напряжения и деформации в точке
- 1.3. Основные понятия и допущения
- 2. Напряженно-деформированное состояние в точке
- 2.2. Одноосное растяжение и сжатие
- 2.3. Чистый сдвиг
- 3. Центральное растяжение и сжатие
- 3.2. Напряжения и деформации при растяжении или сжатии
- 3.3. Расчеты на прочность при растяжении и сжатии
- 4. Кручение
- 4.2. Напряжения и деформации при кручении
- 4.3. Расчеты на прочность при кручении
- 5. Прямой изгиб
- 5.2. Напряжения и деформации при прямом чистом изгибе
- 5.3. Напряжения и деформации при прямом поперечном изгибе
- 5.4. Расчет на прочность при прямом изгибе
- 6. Сложное сопротивление
- 6.2. Внецентренное растяжение или сжатие
- 6.3. Изгиб с кручением
- 7. Устойчивость сжатых стержней
- 7.2. Формула Эйлера
- 7.3. Влияние способов закрепления концов стержня на величину критической силы
- 7.4. Пределы применимости формулы Эйлера
- 7.5. Расчеты сжатых стержней на устойчивость
- ПРИЛОЖЕНИЯ
- 1. Элементарные функции и их свойства
- 2. Таблица неопределенных интегралов
- 3. Решения обыкновенных дифференциальных уравнений
- 4. Ортогональные криволинейные системы координат
- 5. Некоторые физические постоянные