| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
6.4. Общее уравнение динамики (принцип Даламбера — Лагранжа)
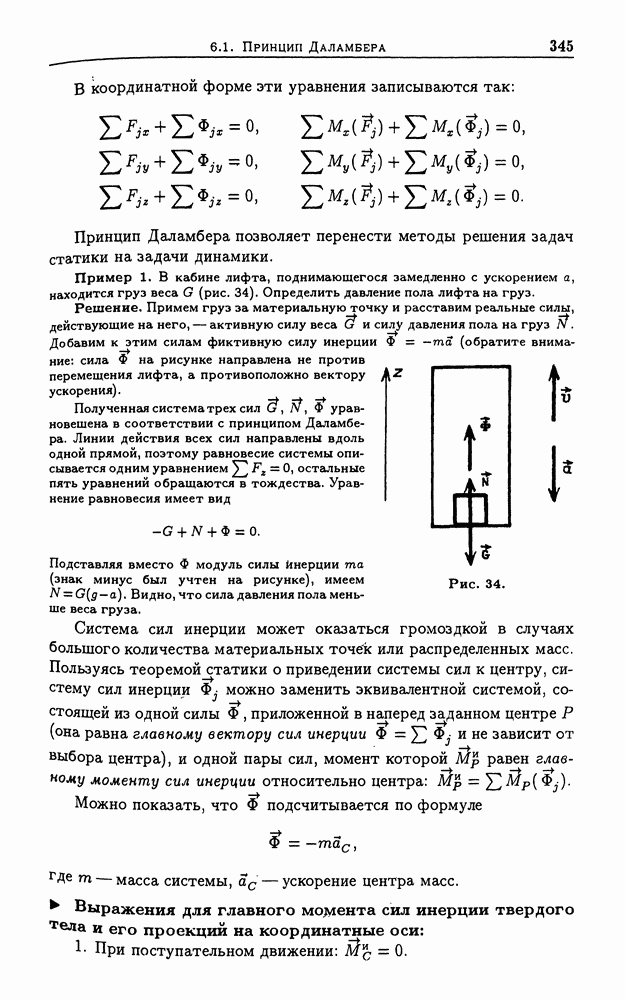
Формулировка общего уравнения динамики: механическая система, на которую наложены идеальные связи, движется так, что в каждый момент времени сумма элементарных работ всех активных сил и сил инерции на любом возможном перемещении системы равна нулю. Математическая формулировка принципа Даламбера — Лагранжа:

Пример. По гладкой горизонтальной поверхности движется прямоугольный параллелепипед массы  по его верхней идеально шероховатой поверхности катится однородный диск массы
по его верхней идеально шероховатой поверхности катится однородный диск массы  и радиуса
и радиуса  к центру которого приложена постоянная горизонтальная сила
к центру которого приложена постоянная горизонтальная сила  (рис. 39, а). Найти ускорения параллелепипеда
(рис. 39, а). Найти ускорения параллелепипеда  и центра диска
и центра диска 
Решение. Рассмотрим систему, состоящую из параллелепипеда и диска. Наложенные связи являются идеальными, и для изучения движения системы можно применить общее уравнение динамики. В качестве координат, определяющих положение системы, выберем абсолютную координату параллелепипеда  и координату
и координату  характеризующую положение диска по отношению к параллелепипеду.
характеризующую положение диска по отношению к параллелепипеду.
Векторы ускорений параллелепипеда  и центра диска
и центра диска  горизонтальны, их величины
горизонтальны, их величины  угловое ускорение диска
угловое ускорение диска  Предполагаемые направления векторов
Предполагаемые направления векторов  и соответствующее им направление дуговой стрелки
и соответствующее им направление дуговой стрелки  изображены на рис. 39, б. К активным силам
изображены на рис. 39, б. К активным силам  силы
силы
весь параллелепипеда и диска) добавим силы инерции  и пару сил инерции с моментом
и пару сил инерции с моментом  (см. рис. 39, б) Сообщим системе возможное перемещение, увеличив координаты
(см. рис. 39, б) Сообщим системе возможное перемещение, увеличив координаты  величины
величины  этом диск повернется на угол
этом диск повернется на угол 

Рис. 39.
Подсчитаем сумму элементарных работ активных сил и сил инерции на возможном перемещении и приравняем ее нулю:

После преобразований получим

Здесь возможные перемещения  могут принимать произвольные независимые между собой значения. Чтобы равенство нулю выполнялось всегда, необходимо, чтобы оба выражения, стоящие множителями при
могут принимать произвольные независимые между собой значения. Чтобы равенство нулю выполнялось всегда, необходимо, чтобы оба выражения, стоящие множителями при  и заключенные в квадратные скобки, были равны нулю. Таким образом, равенство (4) распадается на систему двух уравнений с двумя неизвестными
и заключенные в квадратные скобки, были равны нулю. Таким образом, равенство (4) распадается на систему двух уравнений с двумя неизвестными

Решая систему, найдем

| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- 1. Аналитическая геометрия на плоскости
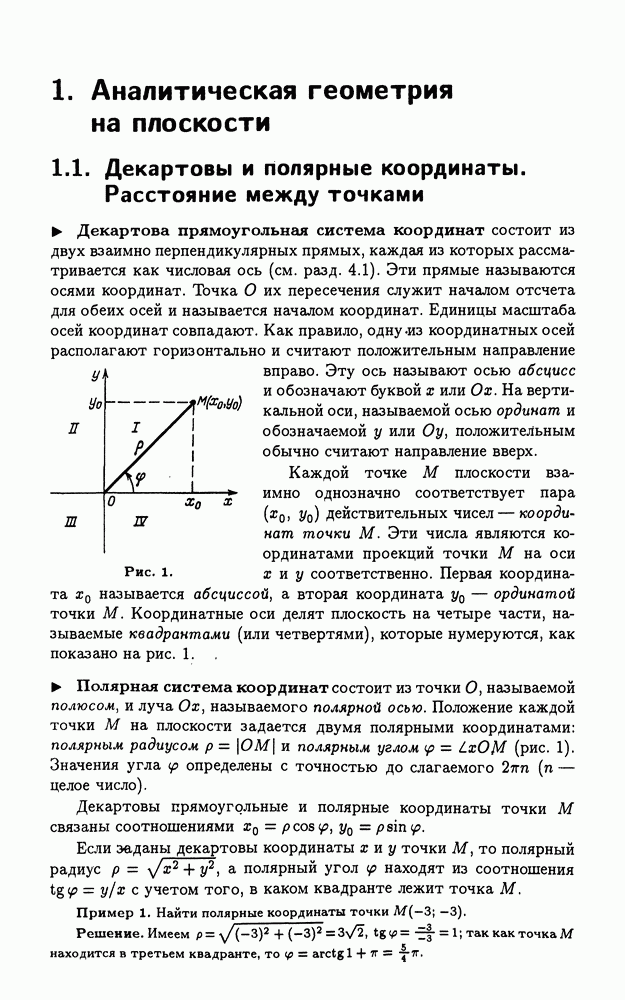
- 1.1. Декартовы и полярные координаты. Расстояние между точками
- 1.2. Деление отрезка в данном отношении. Площадь многоугольника
- 1.3. Различные виды уравнения прямой
- 1.4. Угол между прямыми. Расстояние от точки до прямой
- 1.5. Окружность, эллипс, гипербола и парабола
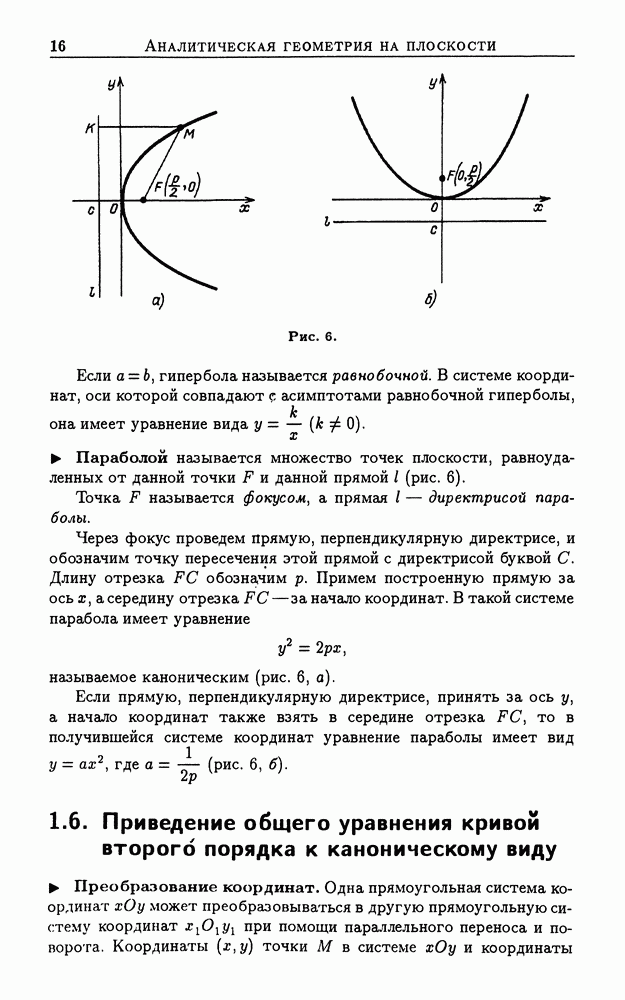
- 1.6. Приведение общего уравнения кривой второго порядка к каноническому виду
- 2. Аналитическая геометрия в пространстве
- 2.2. Векторы
- 2.3. Действия над векторами. Скалярное произведение
- 2.4. Векторное и смешанное произведения
- 2.5. Плоскость в пространстве
- 2.6. Прямая в пространстве
- 2.7. Прямая и плоскость в пространстве
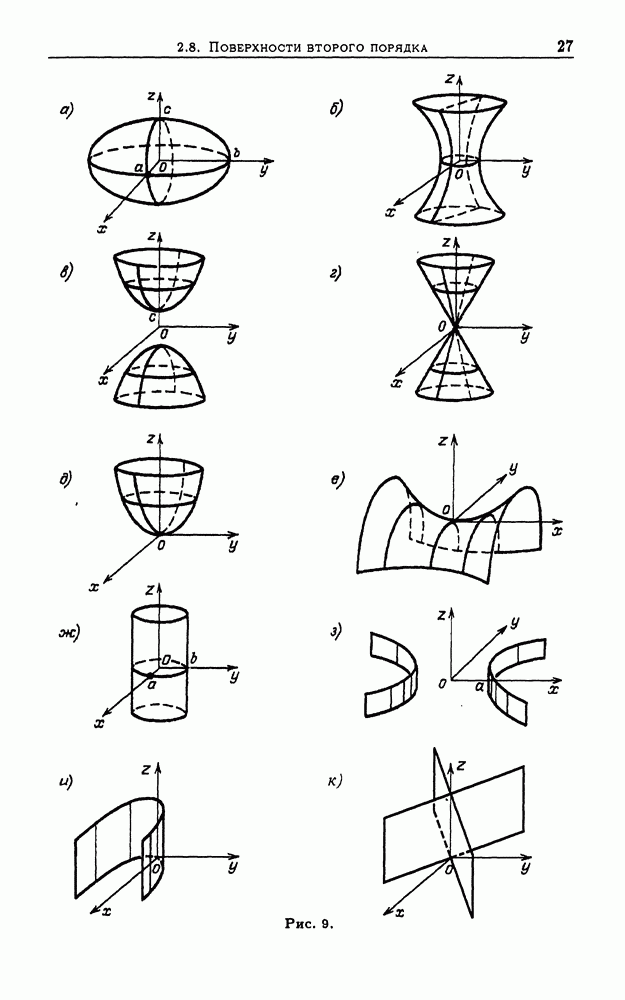
- 2.8. Поверхности второго порядка
- 3. Линейная алгебра
- 3.2. Матрицы
- 3.3. Системы линейных уравнений
- 3.4. Системы n-мерных векторов. Собственные значения и собственные векторы матрицы
- 4. Основные понятия математического анализа
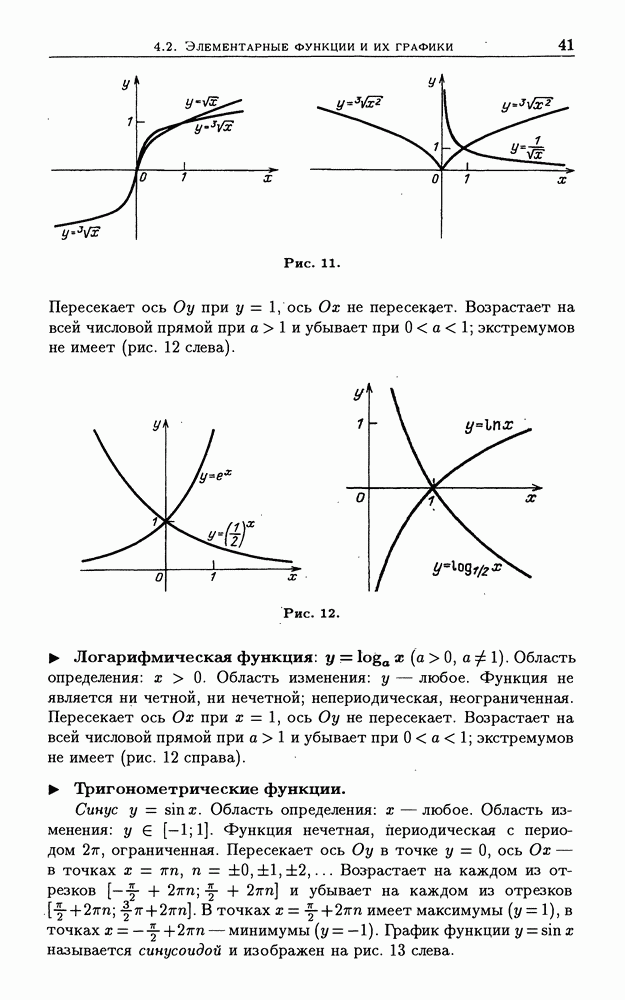
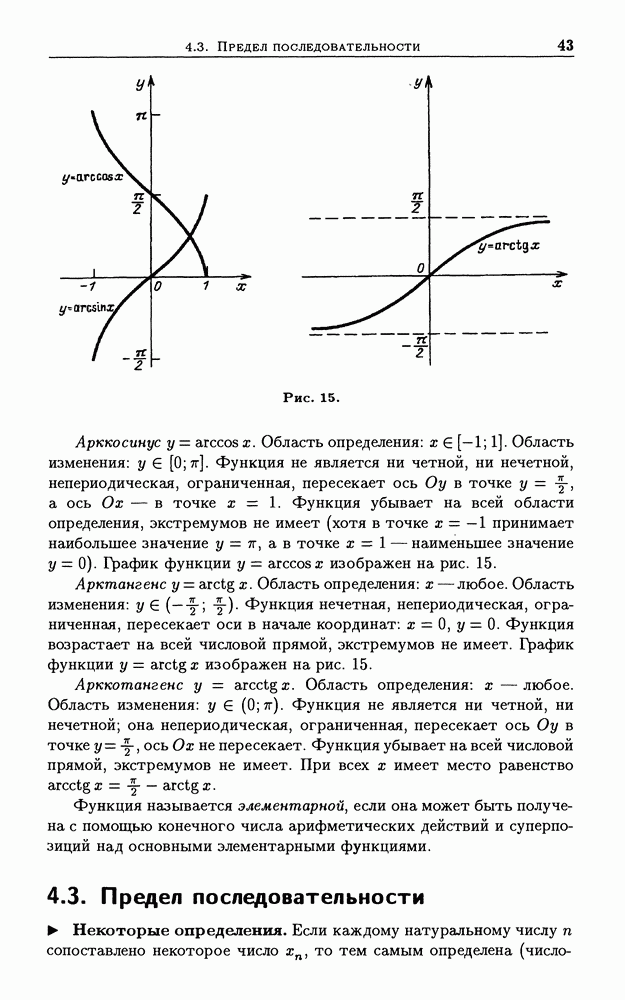
- 4.2. Элементарные функции и их графики
- 4.3. Предел последовательности
- 4.4. Предел функции
- 4.5. Бесконечно малые и бесконечно большие функции
- 4.6. Непрерывность
- 4.7. Асимптоты графика функции
- 5. Дифференциальное исчисление функций одной переменной
- 5.2. Таблица производных и правила дифференцирования
- 5.3. Теоремы о дифференцируемых функциях. Правило Лопиталя
- 5.4. Производные и дифференциалы высших порядков. Формула Тейлора
- 5.5. Экстремумы. Точки перегиба
- 5.6. Общая схема исследования функции и построение графика
- 6. Функции нескольких переменных
- 6.1. Точечные множества. Функции. Предел и непрерывность
- 6.2. Дифференцирование функций нескольких переменных
- 6.3. Производная по направлению. Геометрические приложения
- 6.4. Экстремумы функций нескольких переменных
- 7. Неопределенный интеграл
- 7.1. Первообразная. Неопределенный интеграл и его свойства
- 7.2. Таблица основных интегралов. Примеры интегрирования
- 7.3. Интегрирование по частям. Метод замены переменной
- 7.4. Интегрирование рациональных функций
- 7.5. Интегрирование иррациональных функций
- 7.6. Интегрирование показательных и тригонометрических функций
- 8. Определенный интеграл
- 8.1. Основные определения. Геометрический смысл определенного интеграла
- 8.2. Свойства определенного интеграла
- 8.3. Геометрические и физические приложения определенного интеграла
- 8.4. Несобственные интегралы
- 9. Двойные и тройные интегралы
- 9.1. Определение и свойства двойного интеграла
- 9.2. Вычисление двойного интеграла
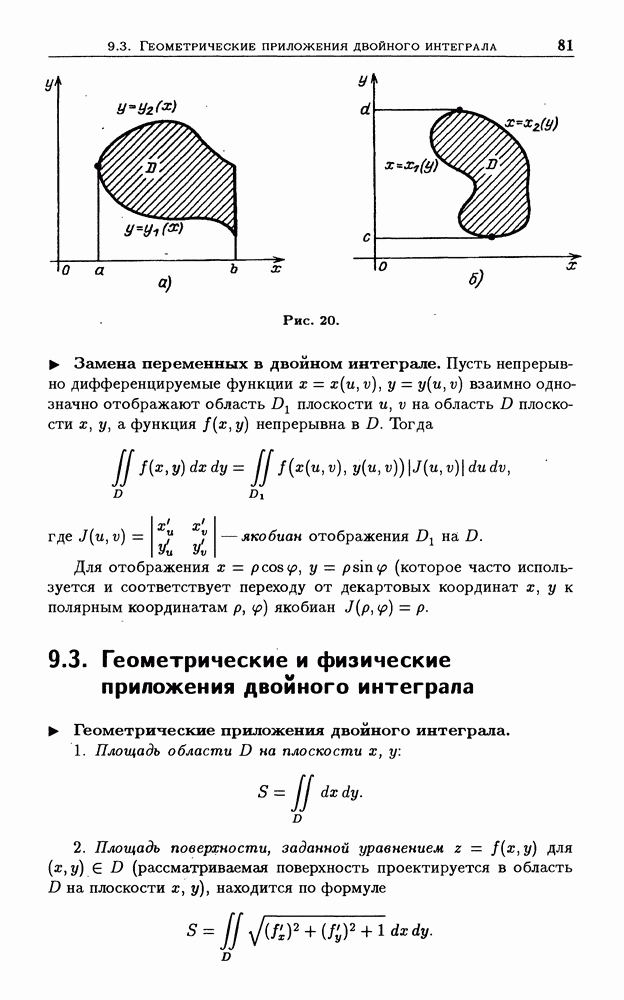
- 9.3. Геометрические и физические приложения двойного интеграла
- 9.4. Определение и свойства тройного интеграла
- 9.5. Вычисление тройного интеграла. Некоторые приложения
- 10. Криволинейные и поверхностные интегралы
- 10.2. Криволинейный интеграл второго рода
- 10.3. Поверхностный интеграл первого рода
- 10.4. Поверхностный интеграл второго рода
- 10.5. Дифференциальные операции и интегральные формулы теории поля
- 11. Ряды
- 11.1. Числовые ряды
- 11.2. Функциональные ряды
- 11.3. Степенные ряды
- 11.4. Ряд Фурье
- 11.5. Интеграл Фурье. Преобразование Фурье
- 12. Обыкновенные дифференциальные уравнения
- 12.2. Дифференциальные уравнения высших порядков
- 12.3. Линейные уравнения n-го порядка
- 12.4. Решение линейных однородных уравнений n-го порядка с постоянными коэффициентами
- 12.5. Линейные неоднородные уравнения n-го порядка
- 12.6. Системы обыкновенных дифференциальных уравнений
- 13. Приближенные вычисления
- 13.1. Метод наименьших квадратов
- 13.2. Приближенное решение алгебраических уравнений
- 13.3. Вычисление определенного интеграла
- 13.4. Численное интегрирование дифференциальных уравнений
- 14. Теория вероятностей
- 14.1. Правила и формулы комбинаторики
- 14.2. Основные понятия теории вероятностей
- 14.3. Условная вероятность. Теоремы и формулы теории вероятностей
- 14.4. Математическое ожидание и дисперсия
- 14.5. Закон больших чисел
- 1. Физические основы механики
- 1.1. Кинематика точки
- 1.2. Кинематика твердого тела
- 1.3. Динамика
- 1.4. Закон сохранения импульса
- 1.5. Закон сохранения энергии
- 1.6. Закон сохранения момента импульса
- 1.7. Задана двух тел и движение в центральном поле
- 1.8. Поле тяготения
- 1.9. Неинерциальные системы отсчета
- 1.10. Динамика твердого тела
- 1.11. Специальная теория относительности
- 2. Молекулярная физика и термодинамика
- 2.2. Первое начало термодинамики
- 2.3. Второе начало термодинамики
- 2.4. Энтропия. Свободная энергия
- 2.5. Кинетическая теория идеального газа
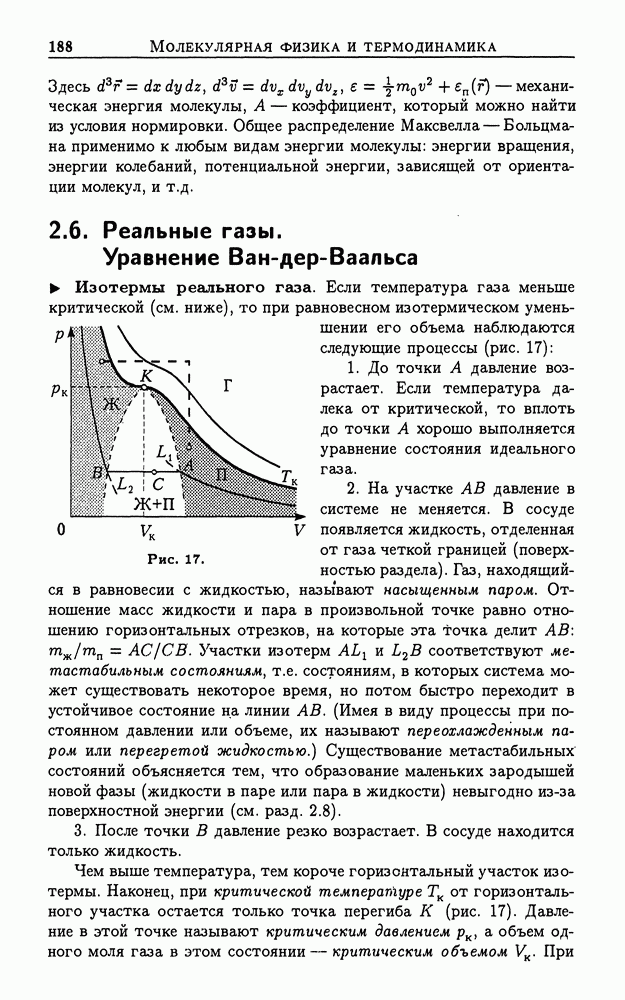
- 2.6. Реальные газы. Уравнение Ван-дер-Ваальса
- 2.7. Равновесие фаз. Фазовые переходы
- 2.8. Поверхностное натяжение
- 2.9. Явления переноса в газах
- 3. Электродинамика
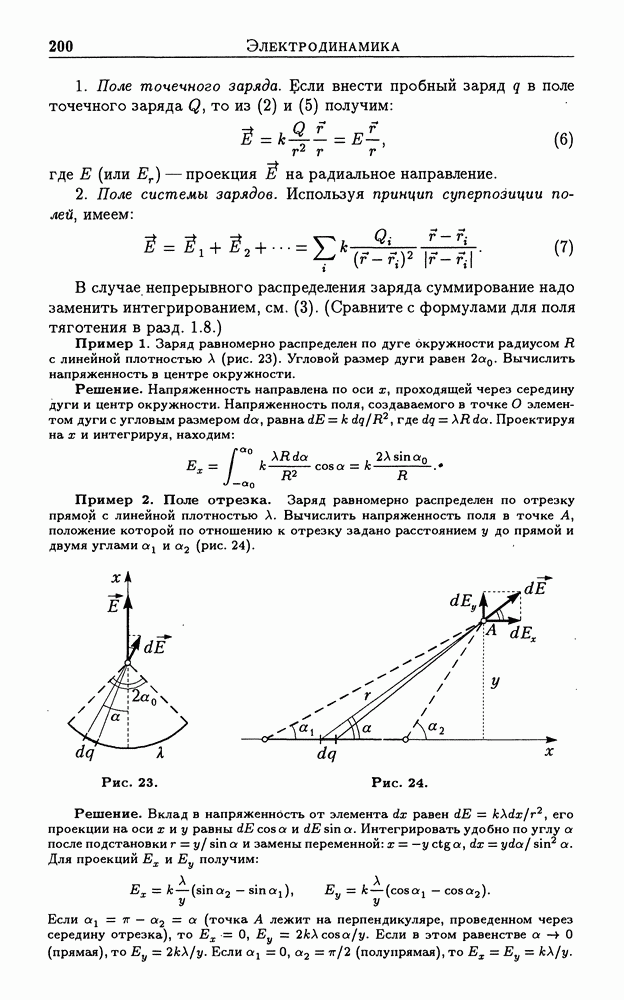
- 3.1. Электрический заряд. Закон Кулона
- 3.2. Электрическое поле. Напряженность поля
- 3.3. Электростатическое поле. Принцип суперпозиции для напряженности и потенциала
- 3.4. Теорема Гаусса
- 3.5. Электростатика проводников
- 3.6. Электростатика диэлектриков
- 3.7. Конденсаторы
- 3.8. Энергия электростатического поля
- 3.9. Постоянный ток
- 3.10. Магнитное поле. Сила Лоренца и закон Ампера
- 3.11. Вычисление магнитной индукции
- 3.12. Циркуляция и поток вектора магнитной индукции
- 3.13. Магнитное поле в веществе
- 3.14. Электромагнитная индукция
- 3.15. Уравнения Максвелла
- 4. Колебания и волны
- 4.1. Гармонические колебания. Сложение колебаний
- 4.2. Свободные незатухающие колебания
- 4.3. Затухающие и вынужденные колебания
- 4.4. Упругие волны
- 4.5. Электромагнитные волны
- 5. Оптика
- 5.1. Геометрическая оптика. Фотометрия
- 5.2. Интерференция света
- 5.3. Дифракция
- 5.4. Поляризация света. Формулы Френеля
- 5.5. Дисперсия и поглощение света
- 5.6. Тепловое излучение
- 5.7. Световые кванты
- Список литературы
- 1. Кинематика
- 1.1. Кинематика точки
- 1.2. Кинематика твердого тела
- 1.3. Плоскопараллельное движение твердого тела
- 1.4. Произвольное движение твердого тела
- 1.5. Сложное движение точки
- 2. Основные понятия и аксиомы механики
- 2.2. Аксиомы механики
- 3. Статика
- 3.2. Условия уравновешенности систем сил, приложенных к твердому телу
- 3.3. Решение задан статики
- 3.4. Центр параллельных сил. Центр тяжести твердого тела
- 3.5. Распределенные силы
- 3.6. Законы трения (законы Кулона)
- 4. Динамика материальной точки
- 4.2. Первая и вторая задачи динамики
- 5. Общие теоремы динамики механической системы
- 5.2. Теорема о движении центра масс
- 5.3. Теорема об изменении количества движения
- 5.4. Теорема об изменении кинетического момента
- 5.5. Теорема об изменении кинетической энергии
- 6. Принцип Даламбера. Элементы аналитической механики
- 6.2. Классификация механических связей. Обобщенные координаты
- 6.3. Принцип возможных перемещений
- 6.4. Общее уравнение динамики (принцип Даламбера — Лагранжа)
- 6.5. Уравнения Лагранжа второго рода
- 1. Основные понятия
- 1.1. Введение. Внешние и внутренние силы
- 1.2. Напряжения и деформации в точке
- 1.3. Основные понятия и допущения
- 2. Напряженно-деформированное состояние в точке
- 2.2. Одноосное растяжение и сжатие
- 2.3. Чистый сдвиг
- 3. Центральное растяжение и сжатие
- 3.2. Напряжения и деформации при растяжении или сжатии
- 3.3. Расчеты на прочность при растяжении и сжатии
- 4. Кручение
- 4.2. Напряжения и деформации при кручении
- 4.3. Расчеты на прочность при кручении
- 5. Прямой изгиб
- 5.2. Напряжения и деформации при прямом чистом изгибе
- 5.3. Напряжения и деформации при прямом поперечном изгибе
- 5.4. Расчет на прочность при прямом изгибе
- 6. Сложное сопротивление
- 6.2. Внецентренное растяжение или сжатие
- 6.3. Изгиб с кручением
- 7. Устойчивость сжатых стержней
- 7.2. Формула Эйлера
- 7.3. Влияние способов закрепления концов стержня на величину критической силы
- 7.4. Пределы применимости формулы Эйлера
- 7.5. Расчеты сжатых стержней на устойчивость
- ПРИЛОЖЕНИЯ
- 1. Элементарные функции и их свойства
- 2. Таблица неопределенных интегралов
- 3. Решения обыкновенных дифференциальных уравнений
- 4. Ортогональные криволинейные системы координат
- 5. Некоторые физические постоянные