| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
4.3. Затухающие и вынужденные колебания
Затухающие колебания. Если в колебательной системе происходят потери энергии, то амплитуда колебаний уменьшается со временем. Если потери энергии механических колебаний определяются силой вязкого трения, которая при малых скоростях пропорциональна скорости, то уравнение движения  приводится к линейному дифференциальному уравнению
приводится к линейному дифференциальному уравнению

которое называется уравнением затухающих колебаний. Здесь  — коэффициент затухания,
— коэффициент затухания,  — циклическая частота собственных колебаний в отсутствие затухания (при
— циклическая частота собственных колебаний в отсутствие затухания (при  Решение этого уравнения удобно искать в виде экспоненты:
Решение этого уравнения удобно искать в виде экспоненты:  Подставляя в (11), получим для
Подставляя в (11), получим для  квадратное уравнение:
квадратное уравнение:  Если
Если  то уравнение имеет два комплексно сопряженных решения:
то уравнение имеет два комплексно сопряженных решения:  которые приводят к
которые приводят к
одинаковым ответам, поэтому можно взять любое. Применяя формулу Эйлера (см. разд. 4.1), получим:

где постоянные  определяются начальными условиями.
определяются начальными условиями.
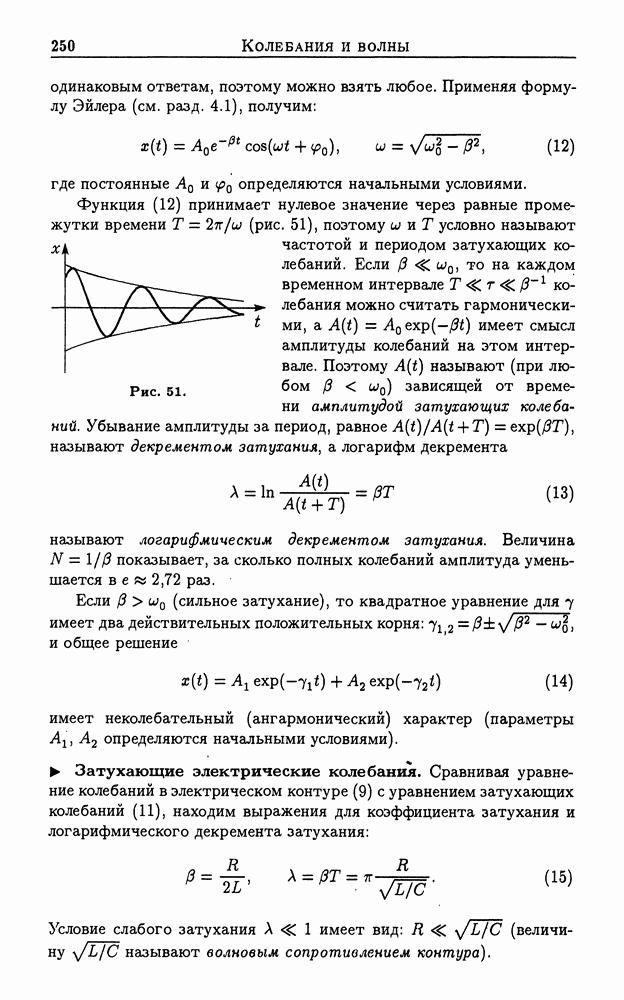
Функция (12) принимает нулевое значение через равные промежутки времени  (рис. 51), поэтому
(рис. 51), поэтому  и Т условно называют частотой и периодом затухающих колебаний. Если
и Т условно называют частотой и периодом затухающих колебаний. Если  то на каждом временном интервале
то на каждом временном интервале  колебания можно считать гармоническими,
колебания можно считать гармоническими,  имеет смысл амплитуды колебаний на этом интервале. Поэтому
имеет смысл амплитуды колебаний на этом интервале. Поэтому  называют (при любом
называют (при любом  зависящей от времени амплитудой затухающих колебаний. Убывание амплитуды за период, равное
зависящей от времени амплитудой затухающих колебаний. Убывание амплитуды за период, равное  называют декрементом затухания, а логарифм декремента
называют декрементом затухания, а логарифм декремента

называют логарифмическим декрементом затухания. Величина  показывает, за сколько полных колебаний амплитуда уменьшается
показывает, за сколько полных колебаний амплитуда уменьшается  раз.
раз.

Рис. 51.
Если  (сильное затухание), то квадратное уравнение для
(сильное затухание), то квадратное уравнение для  имеет два действительных положительных корня:
имеет два действительных положительных корня:  и общее решение
и общее решение

имеет неколебательный (ангармонический) характер (параметры  определяются начальными условиями).
определяются начальными условиями).
Затухающие электрические колебания. Сравнивая уравнение колебаний в электрическом контуре (9) с уравнением затухающих колебаний (11), находим выражения для коэффициента затухания и логарифмического декремента затухания:

Условие слабого затухания  имеет вид:
имеет вид:  (величину
(величину  называют волновым сопротивлением контура).
называют волновым сопротивлением контура).
Вынужденные механические колебания. Движение системы под воздействием внешней периодической силы называют вынужденными колебаниями, саму внешнюю силу называют вынуждающей силой. Из уравнения движения  получим уравнение вынужденных колебаний:
получим уравнение вынужденных колебаний:

где принято обозначение 
Общее решение такого неоднородного (с отличной от нуля правой частью) уравнения может быть представлено в виде суммы частного (т.е. любого) решения неоднородного уравнения и общего решения однородного уравнения. (Общее решение должно содержать свободные параметры, позволяющие удовлетворить любым начальным условиям.) Однородное уравнение представляет собой уравнение затухающих колебаний, его общее решение (формулы (12) и  экспоненциально затухает за время
экспоненциально затухает за время  Затухание собственных колебаний означает окончание переходного режима установления колебаний и наступление режима установившихся вынужденных колебаний, характеристики которого определяются функцией
Затухание собственных колебаний означает окончание переходного режима установления колебаний и наступление режима установившихся вынужденных колебаний, характеристики которого определяются функцией  и параметрами
и параметрами  но не зависят от начальных условий.
но не зависят от начальных условий.
Частное решение уравнения (16) будем искать в виде установившихся колебаний. Так как любая периодическая сила  может быть разложена в ряд Фурье, то естественно исследовать установившиеся вынужденные колебания под действием гармонической вынуждающей силы
может быть разложена в ряд Фурье, то естественно исследовать установившиеся вынужденные колебания под действием гармонической вынуждающей силы  Будем искать их в виде гармонических колебаний такой же частоты, но со сдвигом по фазе:
Будем искать их в виде гармонических колебаний такой же частоты, но со сдвигом по фазе:

Подставляя (17) в уравнение, находим 

При  получим
получим  что соответствует статическому смещению тела вслед за медленно меняющейся силой. При
что соответствует статическому смещению тела вслед за медленно меняющейся силой. При  имеем
имеем  Графики
Графики  приведены на рис. 52.
приведены на рис. 52.

Рис. 52.
Резонанс. Максимальное значение амплитуды установившихся колебаний достигается при резонансной частоте  и равно
и равно  где
где 
циклическая частота затухающих колебаний. При  и 0 зависимость
и 0 зависимость  содержит резкий и узкий максимум при резонансной частоте, которая в этом пределе близка к собственной частоте колебаний системы. Это явление называется резонансом, а кривые зависимости
содержит резкий и узкий максимум при резонансной частоте, которая в этом пределе близка к собственной частоте колебаний системы. Это явление называется резонансом, а кривые зависимости  -резонансными кривыми. Характеристики максимумов
-резонансными кривыми. Характеристики максимумов  отношение Атах к статическому отклонению
отношение Атах к статическому отклонению  равно
равно  логарифмический декремент затухания; величину
логарифмический декремент затухания; величину  называют добротностью колебательной системы). Ширина максимума на уровне
называют добротностью колебательной системы). Ширина максимума на уровне  равна коэффициенту затухания:
равна коэффициенту затухания: 
Амплитуда установившихся колебаний скорости достигает максимального значения  при
при  При резонансе колебания скорости происходят в фазе с колебаниями возмущающей силы.
При резонансе колебания скорости происходят в фазе с колебаниями возмущающей силы.
Рассмотрим процесс установления колебаний при частоте вынуждающей силы, равной резонансной частоте (предполагается, что  Если в начальный момент смещение и скорость точки равнялись нулю, то в рассматриваемом пределе начальным условиям удовлетворяет решение:
Если в начальный момент смещение и скорость точки равнялись нулю, то в рассматриваемом пределе начальным условиям удовлетворяет решение:

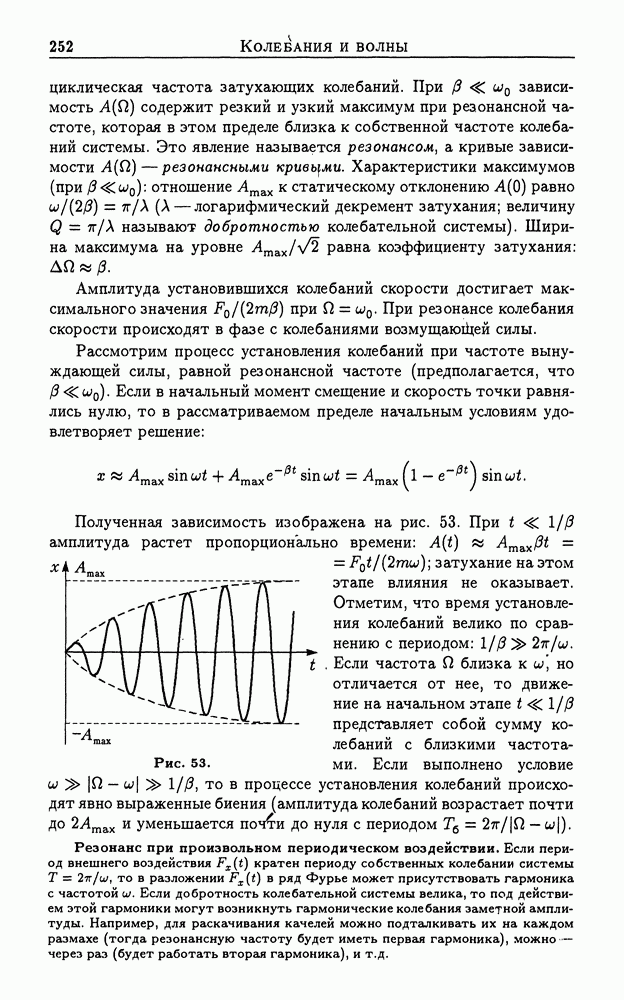
Полученная зависимость изображена на рис. 53. При  амплитуда растет пропорционально времени:
амплитуда растет пропорционально времени:  затухание на этом этапе влияния не оказывает. Отметим, что время установления колебаний велико по сравнению с периодом:
затухание на этом этапе влияния не оказывает. Отметим, что время установления колебаний велико по сравнению с периодом:  Если частота
Если частота  близка к но отличается от нее, то движение на начальном этапе
близка к но отличается от нее, то движение на начальном этапе  представляет собой сумму колебаний с близкими частотами. Если выполнено условие
представляет собой сумму колебаний с близкими частотами. Если выполнено условие  то в процессе установления колебаний происходят явно выраженные биения (амплитуда колебаний возрастает почти до
то в процессе установления колебаний происходят явно выраженные биения (амплитуда колебаний возрастает почти до  и уменьшается почги до нуля с периодом
и уменьшается почги до нуля с периодом 

Рис. 53.
Резонанс при произвольном периодическом воздействии. Если период внешнего воздействия  кратен периоду собственных колебании системы
кратен периоду собственных колебании системы  то в разложении
то в разложении  в ряд Фурье может присутствовать гармоника с частотой и. Если добротность колебательной системы велика, то под действием этой гармоники могут возникнуть гармонические колебания заметной амплитуды. Например, для раскачивания качелей можно подталкивать их на каждом размахе (тогда резонансную частоту будет иметь первая гармоника), можно — через раз (будет работать вторая гармоника), и т. д.
в ряд Фурье может присутствовать гармоника с частотой и. Если добротность колебательной системы велика, то под действием этой гармоники могут возникнуть гармонические колебания заметной амплитуды. Например, для раскачивания качелей можно подталкивать их на каждом размахе (тогда резонансную частоту будет иметь первая гармоника), можно — через раз (будет работать вторая гармоника), и т. д.
Вынужденные электрические колебания. Если в колебательный контур (см. разд. 4.2) включить переменную ЭДС  , то вынужденные колебания будут описываться таким же дифференциальным уравнением, как и для механической системы:
, то вынужденные колебания будут описываться таким же дифференциальным уравнением, как и для механической системы:

Здесь  — заряд на конденсаторе,
— заряд на конденсаторе,  — коэффициент затухания,
— коэффициент затухания,  — циклическая частота собственных колебаний контура. Рассмотрим установившиеся колебания под действием гармонического воздействия
— циклическая частота собственных колебаний контура. Рассмотрим установившиеся колебания под действием гармонического воздействия  Колебания заряда происходят по закону
Колебания заряда происходят по закону  где для амплитуды
где для амплитуды  и сдвига по фазе
и сдвига по фазе  верны выражения (18). Однако в электрической цепи интерес представляют не колебания заряда, а колебания тока
верны выражения (18). Однако в электрической цепи интерес представляют не колебания заряда, а колебания тока  которые происходят по закону
которые происходят по закону  с амплитудой и сдвигом по фазе, равными
с амплитудой и сдвигом по фазе, равными

Максимум амплитуды колебаний тока (резонанс) достигается при значении  и равен
и равен  При резонансе колебания тока происходят в фазе с колебаниями ЭДС.
При резонансе колебания тока происходят в фазе с колебаниями ЭДС.

Рис. 54.
Колебания напряжения на сопротивлении, конденсаторе и катушке индуктивности описываются следующими формулами:

Коэффициенты пропорциональности между амплитудами тока и напряжения называют:  — емкостным сопротивлением,
— емкостным сопротивлением,  — индуктивным сопротивлением. Величину
— индуктивным сопротивлением. Величину  называют реактивным сопротивлением цепи, сопротивление
называют реактивным сопротивлением цепи, сопротивление  — активным сопротивлением (в том смысле, что только на нем рассеивается энергия), величину
— активным сопротивлением (в том смысле, что только на нем рассеивается энергия), величину  — полным сопротивлением. Формулу (20) можно переписать в виде:
— полным сопротивлением. Формулу (20) можно переписать в виде:  . Все эти соотношения становятся очень наглядными при использовании векторных диаграмм (рис. 54). При резонансе
. Все эти соотношения становятся очень наглядными при использовании векторных диаграмм (рис. 54). При резонансе  , т.е. колебания напряжений на емкости и на индуктивности компенсируют друг друга и сопротивление цепи превращается в активное сопротивление
, т.е. колебания напряжений на емкости и на индуктивности компенсируют друг друга и сопротивление цепи превращается в активное сопротивление 
Мощность на участке цепи. Действующим, или эффективным, значением переменного тока (напряжения,  называется такое значение постоянного тока, при котором на активном сопротивлении выделяется за период такое же количество теплоты, как при переменном токе (т.е. среднеквадратичное за период значение):
называется такое значение постоянного тока, при котором на активном сопротивлении выделяется за период такое же количество теплоты, как при переменном токе (т.е. среднеквадратичное за период значение):

Для синусоидального тока  Если сдвиг фазы между током и напряжением равен
Если сдвиг фазы между током и напряжением равен  то средняя за период мощность равна
то средняя за период мощность равна

Для реактивного сопротивления средняя мощность равна нулю.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- 1. Аналитическая геометрия на плоскости
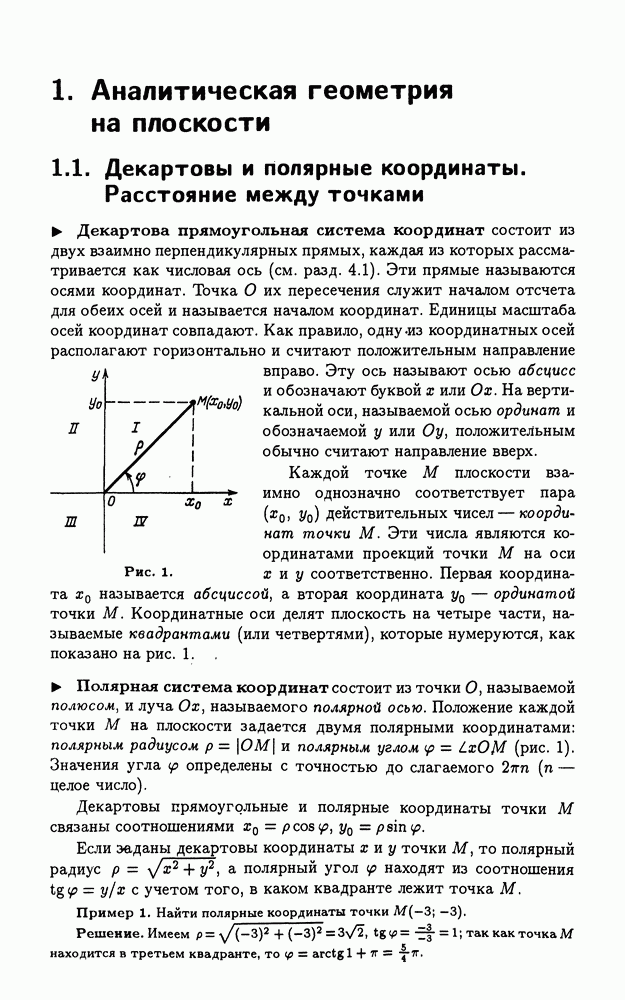
- 1.1. Декартовы и полярные координаты. Расстояние между точками
- 1.2. Деление отрезка в данном отношении. Площадь многоугольника
- 1.3. Различные виды уравнения прямой
- 1.4. Угол между прямыми. Расстояние от точки до прямой
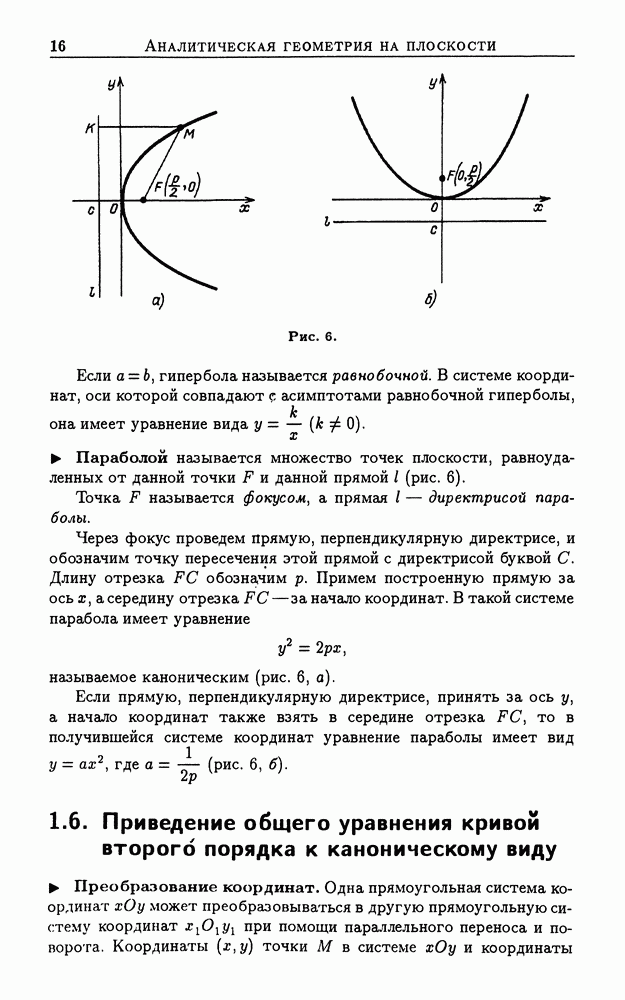
- 1.5. Окружность, эллипс, гипербола и парабола
- 1.6. Приведение общего уравнения кривой второго порядка к каноническому виду
- 2. Аналитическая геометрия в пространстве
- 2.2. Векторы
- 2.3. Действия над векторами. Скалярное произведение
- 2.4. Векторное и смешанное произведения
- 2.5. Плоскость в пространстве
- 2.6. Прямая в пространстве
- 2.7. Прямая и плоскость в пространстве
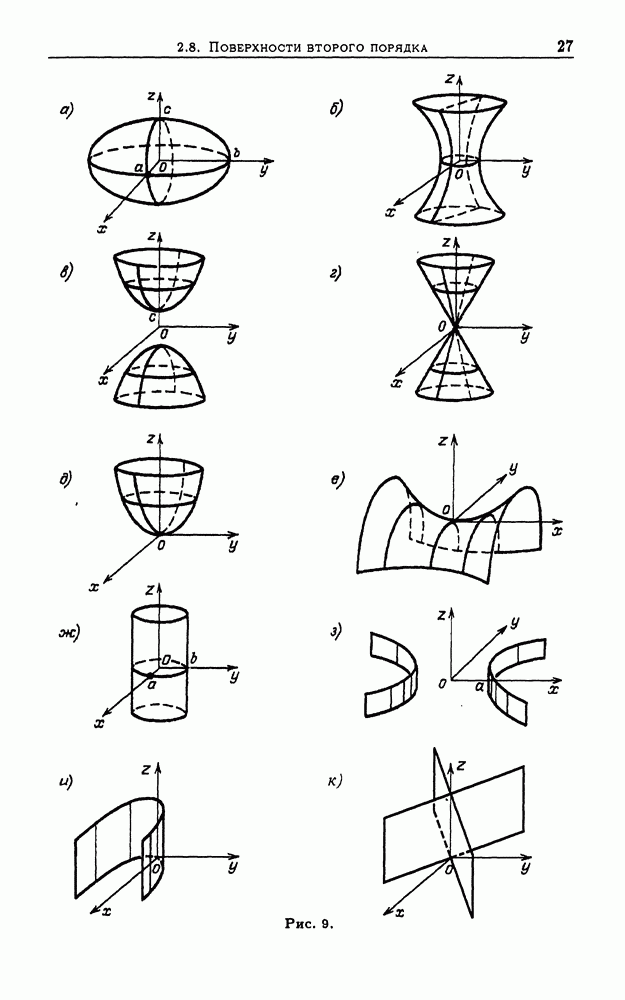
- 2.8. Поверхности второго порядка
- 3. Линейная алгебра
- 3.2. Матрицы
- 3.3. Системы линейных уравнений
- 3.4. Системы n-мерных векторов. Собственные значения и собственные векторы матрицы
- 4. Основные понятия математического анализа
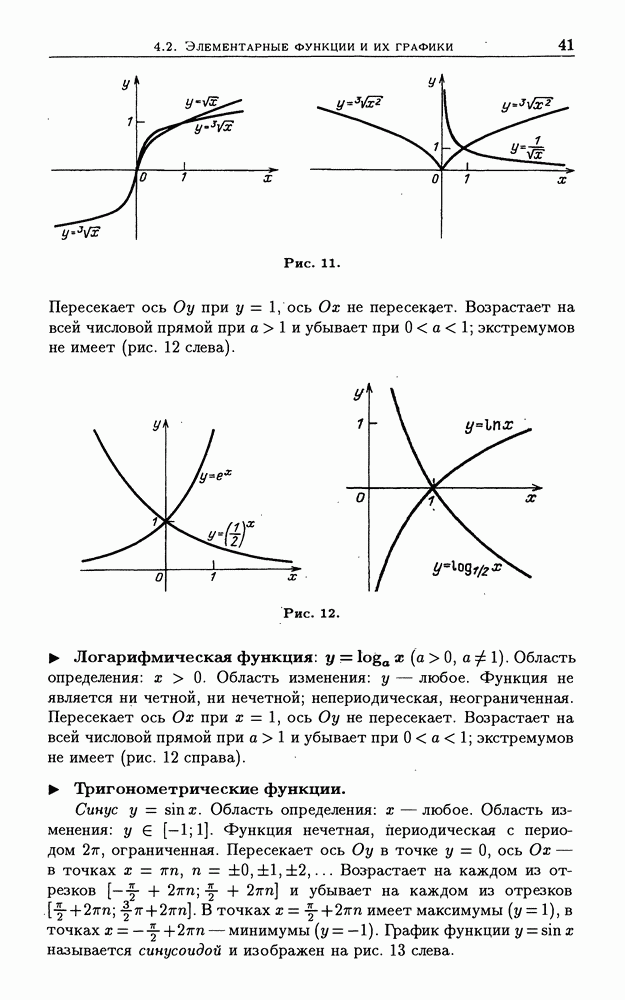
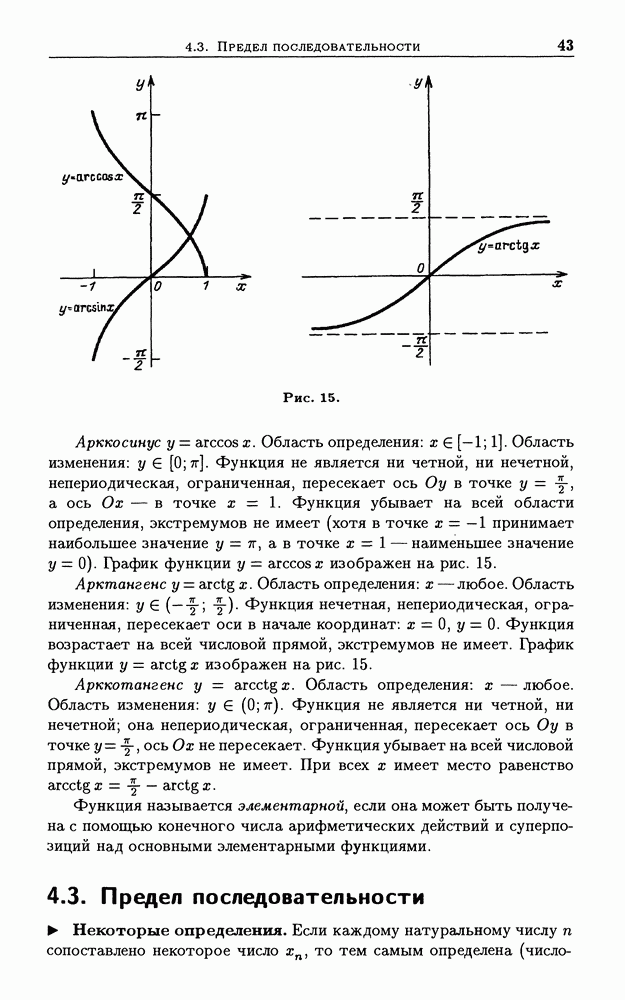
- 4.2. Элементарные функции и их графики
- 4.3. Предел последовательности
- 4.4. Предел функции
- 4.5. Бесконечно малые и бесконечно большие функции
- 4.6. Непрерывность
- 4.7. Асимптоты графика функции
- 5. Дифференциальное исчисление функций одной переменной
- 5.2. Таблица производных и правила дифференцирования
- 5.3. Теоремы о дифференцируемых функциях. Правило Лопиталя
- 5.4. Производные и дифференциалы высших порядков. Формула Тейлора
- 5.5. Экстремумы. Точки перегиба
- 5.6. Общая схема исследования функции и построение графика
- 6. Функции нескольких переменных
- 6.1. Точечные множества. Функции. Предел и непрерывность
- 6.2. Дифференцирование функций нескольких переменных
- 6.3. Производная по направлению. Геометрические приложения
- 6.4. Экстремумы функций нескольких переменных
- 7. Неопределенный интеграл
- 7.1. Первообразная. Неопределенный интеграл и его свойства
- 7.2. Таблица основных интегралов. Примеры интегрирования
- 7.3. Интегрирование по частям. Метод замены переменной
- 7.4. Интегрирование рациональных функций
- 7.5. Интегрирование иррациональных функций
- 7.6. Интегрирование показательных и тригонометрических функций
- 8. Определенный интеграл
- 8.1. Основные определения. Геометрический смысл определенного интеграла
- 8.2. Свойства определенного интеграла
- 8.3. Геометрические и физические приложения определенного интеграла
- 8.4. Несобственные интегралы
- 9. Двойные и тройные интегралы
- 9.1. Определение и свойства двойного интеграла
- 9.2. Вычисление двойного интеграла
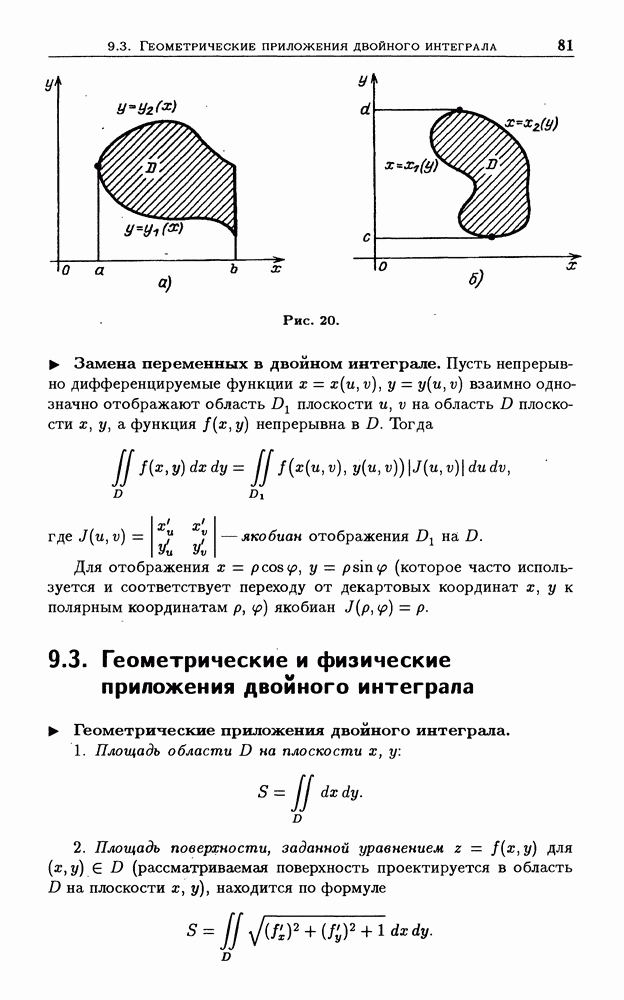
- 9.3. Геометрические и физические приложения двойного интеграла
- 9.4. Определение и свойства тройного интеграла
- 9.5. Вычисление тройного интеграла. Некоторые приложения
- 10. Криволинейные и поверхностные интегралы
- 10.2. Криволинейный интеграл второго рода
- 10.3. Поверхностный интеграл первого рода
- 10.4. Поверхностный интеграл второго рода
- 10.5. Дифференциальные операции и интегральные формулы теории поля
- 11. Ряды
- 11.1. Числовые ряды
- 11.2. Функциональные ряды
- 11.3. Степенные ряды
- 11.4. Ряд Фурье
- 11.5. Интеграл Фурье. Преобразование Фурье
- 12. Обыкновенные дифференциальные уравнения
- 12.2. Дифференциальные уравнения высших порядков
- 12.3. Линейные уравнения n-го порядка
- 12.4. Решение линейных однородных уравнений n-го порядка с постоянными коэффициентами
- 12.5. Линейные неоднородные уравнения n-го порядка
- 12.6. Системы обыкновенных дифференциальных уравнений
- 13. Приближенные вычисления
- 13.1. Метод наименьших квадратов
- 13.2. Приближенное решение алгебраических уравнений
- 13.3. Вычисление определенного интеграла
- 13.4. Численное интегрирование дифференциальных уравнений
- 14. Теория вероятностей
- 14.1. Правила и формулы комбинаторики
- 14.2. Основные понятия теории вероятностей
- 14.3. Условная вероятность. Теоремы и формулы теории вероятностей
- 14.4. Математическое ожидание и дисперсия
- 14.5. Закон больших чисел
- 1. Физические основы механики
- 1.1. Кинематика точки
- 1.2. Кинематика твердого тела
- 1.3. Динамика
- 1.4. Закон сохранения импульса
- 1.5. Закон сохранения энергии
- 1.6. Закон сохранения момента импульса
- 1.7. Задана двух тел и движение в центральном поле
- 1.8. Поле тяготения
- 1.9. Неинерциальные системы отсчета
- 1.10. Динамика твердого тела
- 1.11. Специальная теория относительности
- 2. Молекулярная физика и термодинамика
- 2.2. Первое начало термодинамики
- 2.3. Второе начало термодинамики
- 2.4. Энтропия. Свободная энергия
- 2.5. Кинетическая теория идеального газа
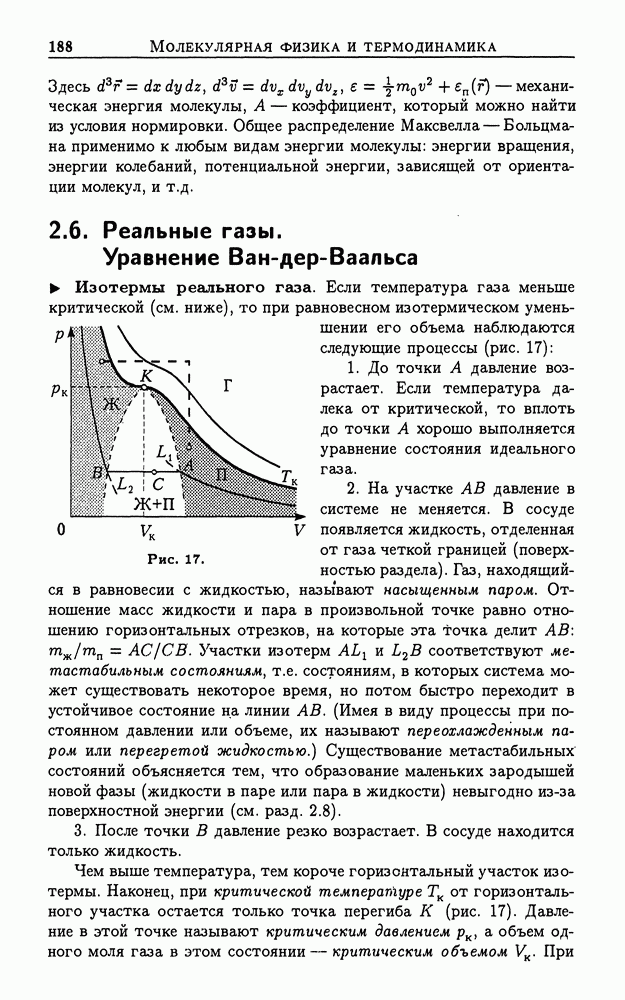
- 2.6. Реальные газы. Уравнение Ван-дер-Ваальса
- 2.7. Равновесие фаз. Фазовые переходы
- 2.8. Поверхностное натяжение
- 2.9. Явления переноса в газах
- 3. Электродинамика
- 3.1. Электрический заряд. Закон Кулона
- 3.2. Электрическое поле. Напряженность поля
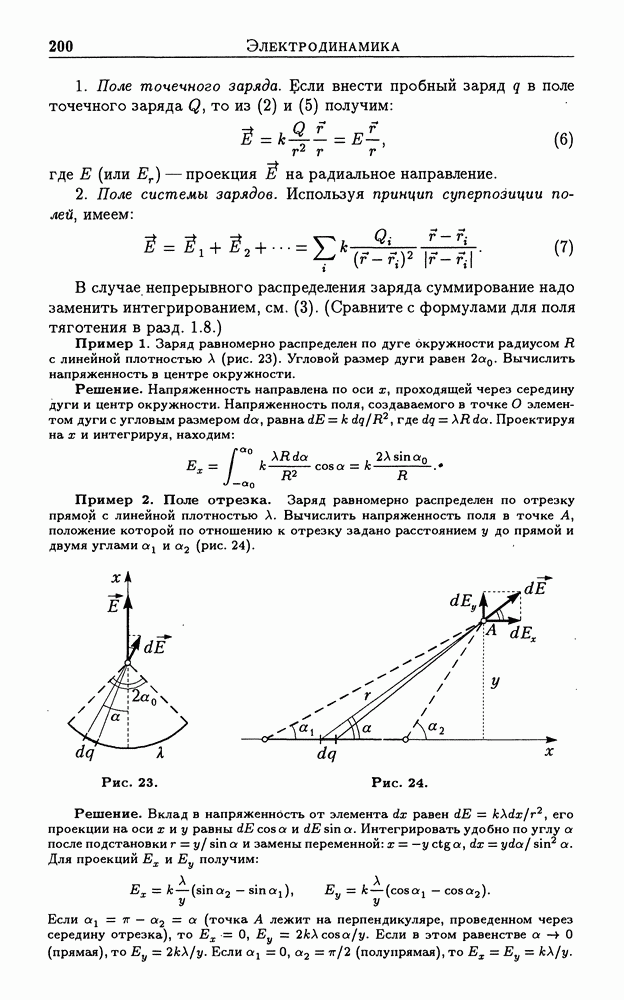
- 3.3. Электростатическое поле. Принцип суперпозиции для напряженности и потенциала
- 3.4. Теорема Гаусса
- 3.5. Электростатика проводников
- 3.6. Электростатика диэлектриков
- 3.7. Конденсаторы
- 3.8. Энергия электростатического поля
- 3.9. Постоянный ток
- 3.10. Магнитное поле. Сила Лоренца и закон Ампера
- 3.11. Вычисление магнитной индукции
- 3.12. Циркуляция и поток вектора магнитной индукции
- 3.13. Магнитное поле в веществе
- 3.14. Электромагнитная индукция
- 3.15. Уравнения Максвелла
- 4. Колебания и волны
- 4.1. Гармонические колебания. Сложение колебаний
- 4.2. Свободные незатухающие колебания
- 4.3. Затухающие и вынужденные колебания
- 4.4. Упругие волны
- 4.5. Электромагнитные волны
- 5. Оптика
- 5.1. Геометрическая оптика. Фотометрия
- 5.2. Интерференция света
- 5.3. Дифракция
- 5.4. Поляризация света. Формулы Френеля
- 5.5. Дисперсия и поглощение света
- 5.6. Тепловое излучение
- 5.7. Световые кванты
- Список литературы
- 1. Кинематика
- 1.1. Кинематика точки
- 1.2. Кинематика твердого тела
- 1.3. Плоскопараллельное движение твердого тела
- 1.4. Произвольное движение твердого тела
- 1.5. Сложное движение точки
- 2. Основные понятия и аксиомы механики
- 2.2. Аксиомы механики
- 3. Статика
- 3.2. Условия уравновешенности систем сил, приложенных к твердому телу
- 3.3. Решение задан статики
- 3.4. Центр параллельных сил. Центр тяжести твердого тела
- 3.5. Распределенные силы
- 3.6. Законы трения (законы Кулона)
- 4. Динамика материальной точки
- 4.2. Первая и вторая задачи динамики
- 5. Общие теоремы динамики механической системы
- 5.2. Теорема о движении центра масс
- 5.3. Теорема об изменении количества движения
- 5.4. Теорема об изменении кинетического момента
- 5.5. Теорема об изменении кинетической энергии
- 6. Принцип Даламбера. Элементы аналитической механики
- 6.2. Классификация механических связей. Обобщенные координаты
- 6.3. Принцип возможных перемещений
- 6.4. Общее уравнение динамики (принцип Даламбера — Лагранжа)
- 6.5. Уравнения Лагранжа второго рода
- 1. Основные понятия
- 1.1. Введение. Внешние и внутренние силы
- 1.2. Напряжения и деформации в точке
- 1.3. Основные понятия и допущения
- 2. Напряженно-деформированное состояние в точке
- 2.2. Одноосное растяжение и сжатие
- 2.3. Чистый сдвиг
- 3. Центральное растяжение и сжатие
- 3.2. Напряжения и деформации при растяжении или сжатии
- 3.3. Расчеты на прочность при растяжении и сжатии
- 4. Кручение
- 4.2. Напряжения и деформации при кручении
- 4.3. Расчеты на прочность при кручении
- 5. Прямой изгиб
- 5.2. Напряжения и деформации при прямом чистом изгибе
- 5.3. Напряжения и деформации при прямом поперечном изгибе
- 5.4. Расчет на прочность при прямом изгибе
- 6. Сложное сопротивление
- 6.2. Внецентренное растяжение или сжатие
- 6.3. Изгиб с кручением
- 7. Устойчивость сжатых стержней
- 7.2. Формула Эйлера
- 7.3. Влияние способов закрепления концов стержня на величину критической силы
- 7.4. Пределы применимости формулы Эйлера
- 7.5. Расчеты сжатых стержней на устойчивость
- ПРИЛОЖЕНИЯ
- 1. Элементарные функции и их свойства
- 2. Таблица неопределенных интегралов
- 3. Решения обыкновенных дифференциальных уравнений
- 4. Ортогональные криволинейные системы координат
- 5. Некоторые физические постоянные