| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
4.2. Свободные незатухающие колебания
Свободные механические колебания. Если смещение консервативной механической системы из положения устойчивого равновесия описывается одним параметром х, то при малых х потенциальная
энергия имеет вид

т.е. при малых отклонениях от устойчивого равновесия система совершает гармонические колебания. Потенциальную энергию колебательной системы принято отсчитывать от положения устойчивого равновесия  при
при  Обобщенная сила
Обобщенная сила  при малых х пропорциональна смещению:
при малых х пропорциональна смещению:  (Если х — линейная координата, то обобщенная сила — проекция силы на направление смещения; если х — угол отклонения, то х — вращательный момент.)
(Если х — линейная координата, то обобщенная сила — проекция силы на направление смещения; если х — угол отклонения, то х — вращательный момент.)
Если механическая система представляет собой материальную точку или поступательно движущееся тело, то кинетическая энергия имеет вид  Уравнение движения
Уравнение движения

имеет такой же вид, как для груза на пружине. Поэтому действующую на тело возвращающую (т.е. направленную в сторону положения равновесия) силу называют при малых х квазиупругой силой:  а коэффициент х — эффективной жесткостью. Циклическая частота и период колебаний имеют вид:
а коэффициент х — эффективной жесткостью. Циклическая частота и период колебаний имеют вид:

Точка совершает гармонические колебания:  а ее кинетическая и потенциальная энергии — гармонические колебания с частотой
а ее кинетическая и потенциальная энергии — гармонические колебания с частотой 

где  — полная механическая энергия, которая пропорциональна квадрату амплитуды. Средняя кинетическая энергия равна средней потенциальной энергии.
— полная механическая энергия, которая пропорциональна квадрату амплитуды. Средняя кинетическая энергия равна средней потенциальной энергии.
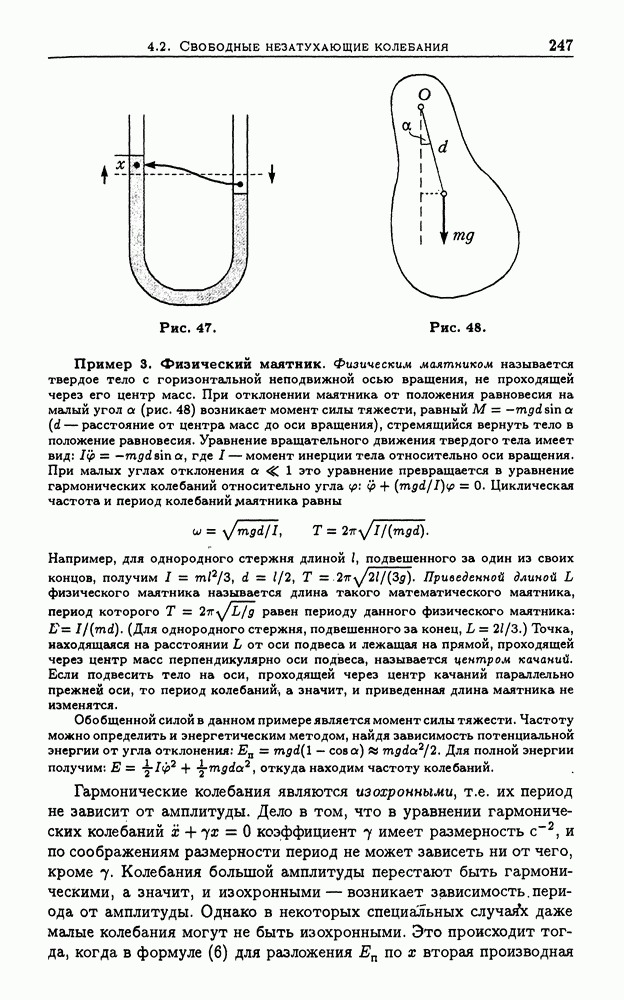
Пример 1. Потенциальная энергия жидкости в  -образной трубке (рис. 47) при смещении жидкости на х увеличивается на
-образной трубке (рис. 47) при смещении жидкости на х увеличивается на  — плотность жидкости,
— плотность жидкости,  — сечение трубки), а кинетическая энергия равна
— сечение трубки), а кинетическая энергия равна  Значит, циклическая частота колебаний равна
Значит, циклическая частота колебаний равна 
Пример 2. В одной из «дорезерфордовских моделей атома водорода положительный заряд предполагался равномерно распределенным по шару радиусом Я, равным радиусу атома, а электрон располагался в центре шара. Найдем частоту колебаний электрона при смещении его из положения равновесия. Сила притяжения при смещении на  равна
равна  (см. разд. 3.4), поэтому при смещении на
(см. разд. 3.4), поэтому при смещении на  будут происходить гармонические колебания с частотой
будут происходить гармонические колебания с частотой 

Рис. 47.

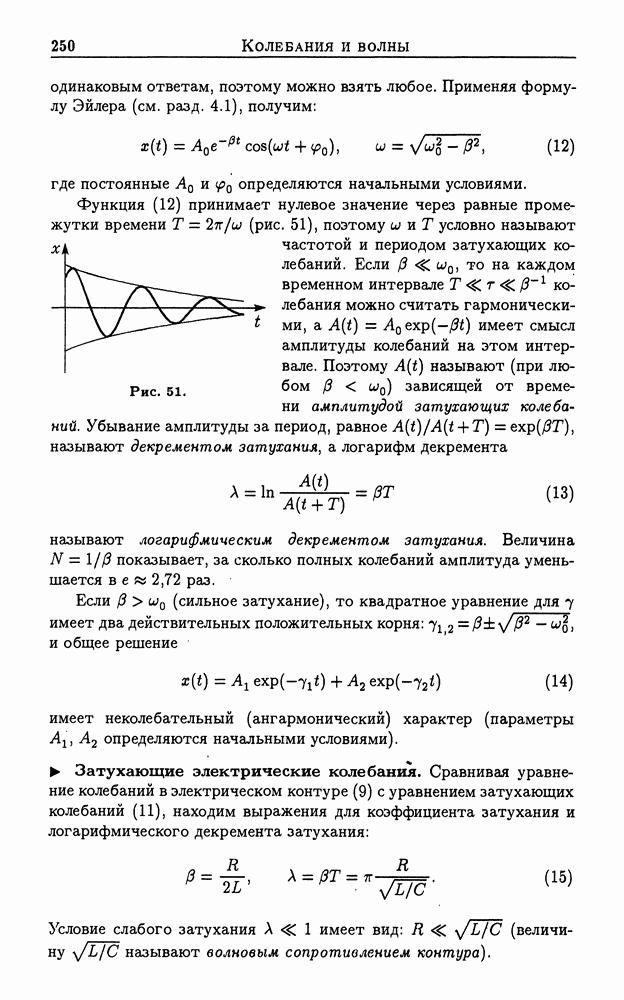
Рис. 48.
Пример 3. Физический маятник. Физическим маятником называется твердое тело с горизонтальной неподвижной осью вращения, не проходящей через его центр масс. При отклонении маятника от положения равновесия на малый угол а (рис. 48) возникает момент силы тяжести, равный  а
а  — расстояние от центра масс до оси вращения), стремящийся вернуть тело в положение равновесия. Уравнение вращательного движения твердого тела имеет вид:
— расстояние от центра масс до оси вращения), стремящийся вернуть тело в положение равновесия. Уравнение вращательного движения твердого тела имеет вид:  , где I — момент инерции тела относительно оси вращения. При малых углах отклонения а 1 это уравнение превращается в уравнение гармонических колебаний относительно угла
, где I — момент инерции тела относительно оси вращения. При малых углах отклонения а 1 это уравнение превращается в уравнение гармонических колебаний относительно угла  Циклическая частота и период колебаний маятника равны
Циклическая частота и период колебаний маятника равны

Например, для однородного стержня длиной  подвешенного за один из своих концов, получим
подвешенного за один из своих концов, получим  Приведенной длиной
Приведенной длиной  физического маятника называется длина такого математического маятника, период которого
физического маятника называется длина такого математического маятника, период которого  равен периоду данного физического маятника:
равен периоду данного физического маятника:  (Для однородного стержня, подвешенного за конец,
(Для однородного стержня, подвешенного за конец,  Точка, находящаяся на расстоянии
Точка, находящаяся на расстоянии  от оси подвеса и лежащая на прямой, проходящей через центр масс перпендикулярно оси подвеса, называется центром качаний. Если подвесить тело на оси, проходящей через центр качании параллельно прежней оси, то период колебаний, а значит, и приведенная длина маятника не изменятся.
от оси подвеса и лежащая на прямой, проходящей через центр масс перпендикулярно оси подвеса, называется центром качаний. Если подвесить тело на оси, проходящей через центр качании параллельно прежней оси, то период колебаний, а значит, и приведенная длина маятника не изменятся.
Обобщенной силой в данном примере является момент силы тяжести. Частоту можно определить и энергетическим методом, найдя зависимость потенциальной энергии от угла отклонения.  Для полной энергии получим:
Для полной энергии получим:  откуда находим частоту колебаний.
откуда находим частоту колебаний.
Гармонические колебания являются изохронными, т.е. их период не зависит от амплитуды. Дело в том, что в уравнении гармонических колебаний  коэффициент 7 имеет размерность
коэффициент 7 имеет размерность  и по соображениям размерности период не может зависеть ни от чего, кроме 7. Колебания большой амплитуды перестают быть гармоническими, а значит, и изохронными — возникает зависимость периода от амплитуды. Однако в некоторых специальных случаях даже малые колебания могут не быть изохронными. Это происходит тогда, когда в формуле (6) для разложения
и по соображениям размерности период не может зависеть ни от чего, кроме 7. Колебания большой амплитуды перестают быть гармоническими, а значит, и изохронными — возникает зависимость периода от амплитуды. Однако в некоторых специальных случаях даже малые колебания могут не быть изохронными. Это происходит тогда, когда в формуле (6) для разложения  по х вторая производная
по х вторая производная
обращается в нуль. Такая ситуация возникает, например, при отклонении груза, прикрепленного к середине недеформированной пружины с закрепленными концами, в перпендикулярном пружине направлении. Потенциальная энергия при малых х пропорциональна  и уравнение движения имеет вид:
и уравнение движения имеет вид:  Размерность 7 в этом случае
Размерность 7 в этом случае  и период колебаний
и период колебаний  обратно пропорционален амплитуде.
обратно пропорционален амплитуде.
Колебательные системы с несколькими степенями свободы. Если смещение системы из устойчивого положения равновесия характеризуется  независимыми параметрами
независимыми параметрами  то при произвольном малом начальном отклонении зависимость
то при произвольном малом начальном отклонении зависимость  не будет гармоническим колебанием. Однако любое движение может быть представлено в виде суммы
не будет гармоническим колебанием. Однако любое движение может быть представлено в виде суммы  специальных движений, называемых нормальными колебательными модами, в каждом из которых все
специальных движений, называемых нормальными колебательными модами, в каждом из которых все  совершают гармонические колебания с некоторой циклической частотой, характеризующей данную моду. В общем случае все
совершают гармонические колебания с некоторой циклической частотой, характеризующей данную моду. В общем случае все  частот могут быть различными.
частот могут быть различными.
Пример 4. Связанные маятники. Рассмотрим два одинаковых математических маятника длиной  грузы которых соединены недеформированной пружиной жесткостью к (рис. 49).
грузы которых соединены недеформированной пружиной жесткостью к (рис. 49).

Рис. 49.
Нормальные моды данной системы позволяет угадать симметрия системы. Гармонические колебания возникают при: а) одинаковом отклонении маятников в одну сторону  и б) при одинаковом отклонении маятников в разные стороны
и б) при одинаковом отклонении маятников в разные стороны  первом случае:
первом случае:  во втором:
во втором:  Если отклонить в сторону только первый маятник, что соответствует начальным условиям (юго)
Если отклонить в сторону только первый маятник, что соответствует начальным условиям (юго)  то такое отклонение можно представить в виде суммы двух нормальных отклонений:
то такое отклонение можно представить в виде суммы двух нормальных отклонений:  Это значит, что движение первого маятника будет совершаться по закону:
Это значит, что движение первого маятника будет совершаться по закону:  а второго маятника — по закону:
а второго маятника — по закону:  Если
Если  то частоты
то частоты  будут близки:
будут близки:  при наложении двух колебании с близкими частотами будут наблюдаться биения (см. разд. 4.1): через время
при наложении двух колебании с близкими частотами будут наблюдаться биения (см. разд. 4.1): через время  второй маятник раскачается, а первый остановится, еще через такое же время энергия снова перейдет к первому маятнику, и т. д.
второй маятник раскачается, а первый остановится, еще через такое же время энергия снова перейдет к первому маятнику, и т. д.

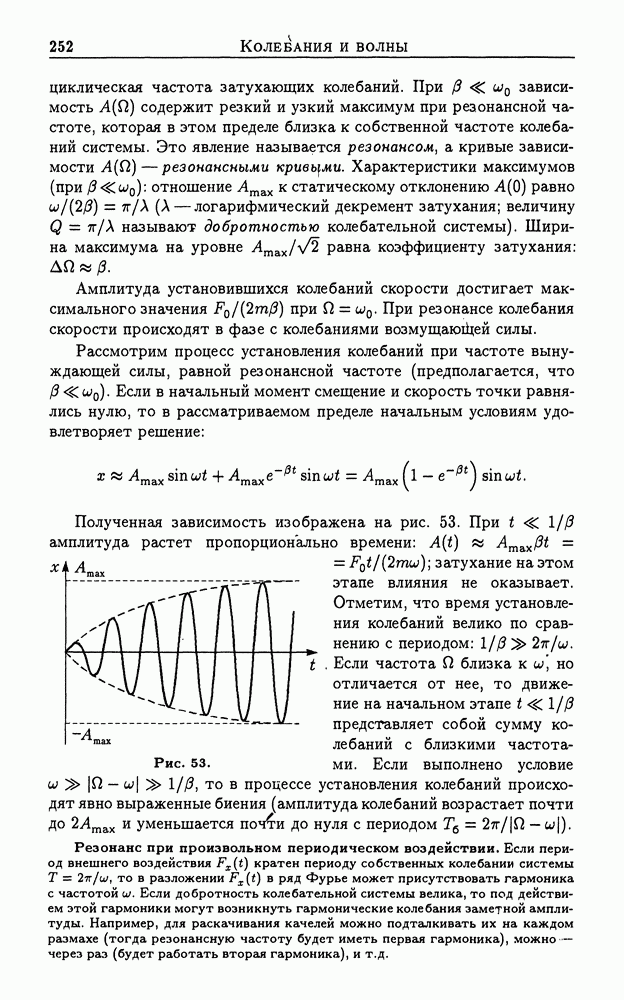
Рис. 50.
Свободные колебания в электрическом контуре. Колебательным контуром называется замкнутая цепь, состоящая из конденсатора емкостью С и катушки индуктивностью  (рис. 50). Процессы в колебательном контуре, как и в цепях переменного тока, исследуются в области частот, где выполняется условие квазистационарности (см. разд. 3.14), т. е. и
(рис. 50). Процессы в колебательном контуре, как и в цепях переменного тока, исследуются в области частот, где выполняется условие квазистационарности (см. разд. 3.14), т. е. и  где I — характерные размеры системы (в этом
где I — характерные размеры системы (в этом
приближении, в частности, можно не учитывать излучение контура). Закон Ома для участка цепи, содержащего индуктивность, при выбранном правиле знаков для обхода контура и для заряда конденсатора имеет вид:  где
где  — сопротивление проводов и катушки. С учетом соотношений: I = q (верного при выбранных знаках),
— сопротивление проводов и катушки. С учетом соотношений: I = q (верного при выбранных знаках),  имеем
имеем  Отсюда получим
Отсюда получим

Если сопротивление контура пренебрежимо мало (что соответствует  то заряд на конденсаторе изменяется по гармоническому закону
то заряд на конденсаторе изменяется по гармоническому закону  с циклической частотой и периодом, равными
с циклической частотой и периодом, равными

Ток в контуре изменяется по гармоническому закону с амплитудой  с опережением по фазе на
с опережением по фазе на  Энергия контура
Энергия контура

переходит из электрической формы в магнитную и обратно: в момент максимальной зарядки конденсатора она равна  а когда заряд конденсатора равен нулю, то
а когда заряд конденсатора равен нулю, то  Для зависимости магнитной и электрической энергии от времени верны такие же соотношения, как для кинетической и потенциальной энергий при механических колебаниях.
Для зависимости магнитной и электрической энергии от времени верны такие же соотношения, как для кинетической и потенциальной энергий при механических колебаниях.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- 1. Аналитическая геометрия на плоскости
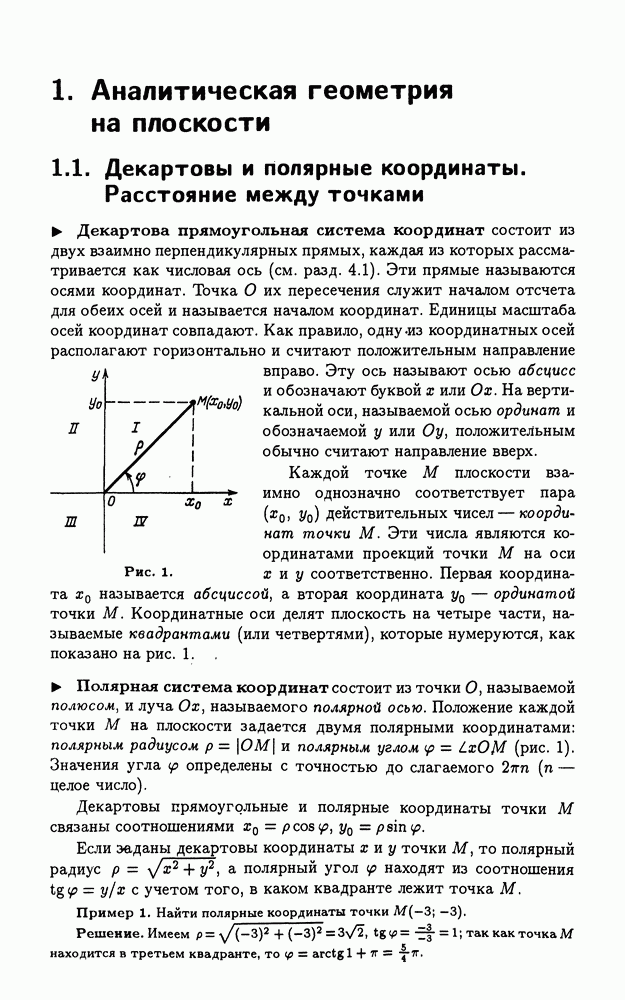
- 1.1. Декартовы и полярные координаты. Расстояние между точками
- 1.2. Деление отрезка в данном отношении. Площадь многоугольника
- 1.3. Различные виды уравнения прямой
- 1.4. Угол между прямыми. Расстояние от точки до прямой
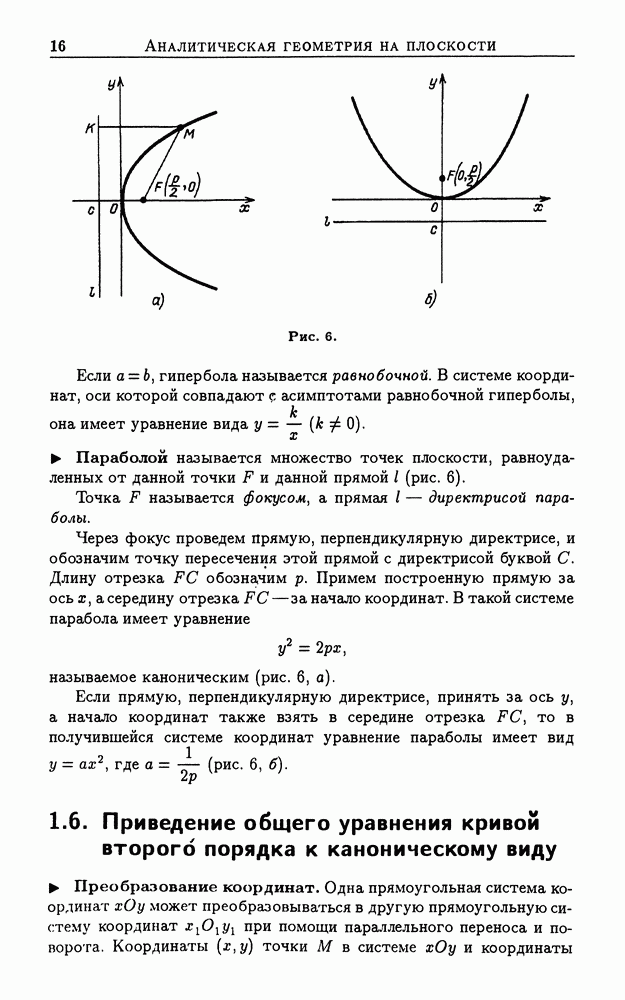
- 1.5. Окружность, эллипс, гипербола и парабола
- 1.6. Приведение общего уравнения кривой второго порядка к каноническому виду
- 2. Аналитическая геометрия в пространстве
- 2.2. Векторы
- 2.3. Действия над векторами. Скалярное произведение
- 2.4. Векторное и смешанное произведения
- 2.5. Плоскость в пространстве
- 2.6. Прямая в пространстве
- 2.7. Прямая и плоскость в пространстве
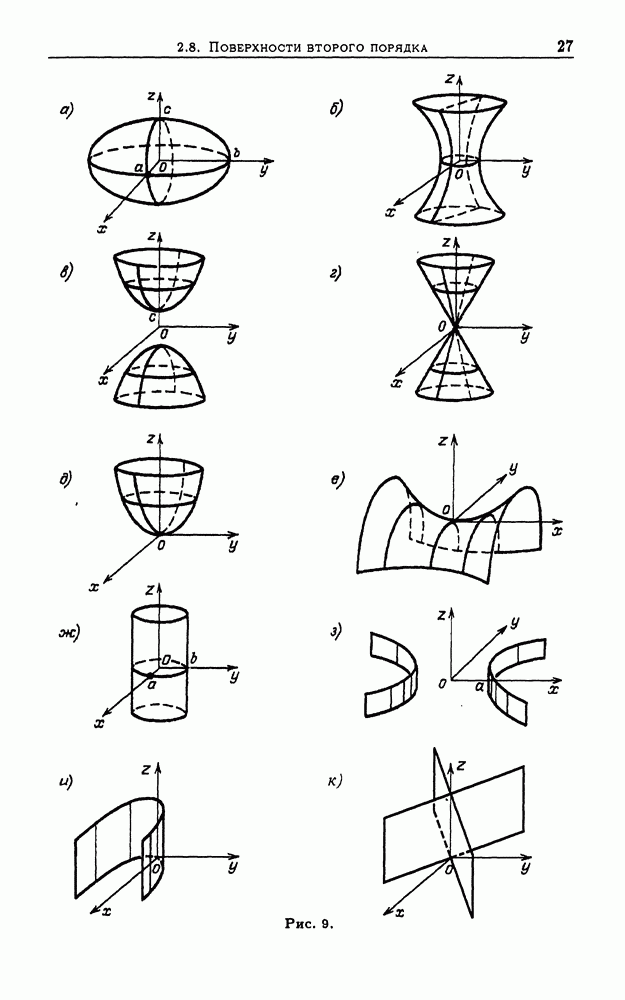
- 2.8. Поверхности второго порядка
- 3. Линейная алгебра
- 3.2. Матрицы
- 3.3. Системы линейных уравнений
- 3.4. Системы n-мерных векторов. Собственные значения и собственные векторы матрицы
- 4. Основные понятия математического анализа
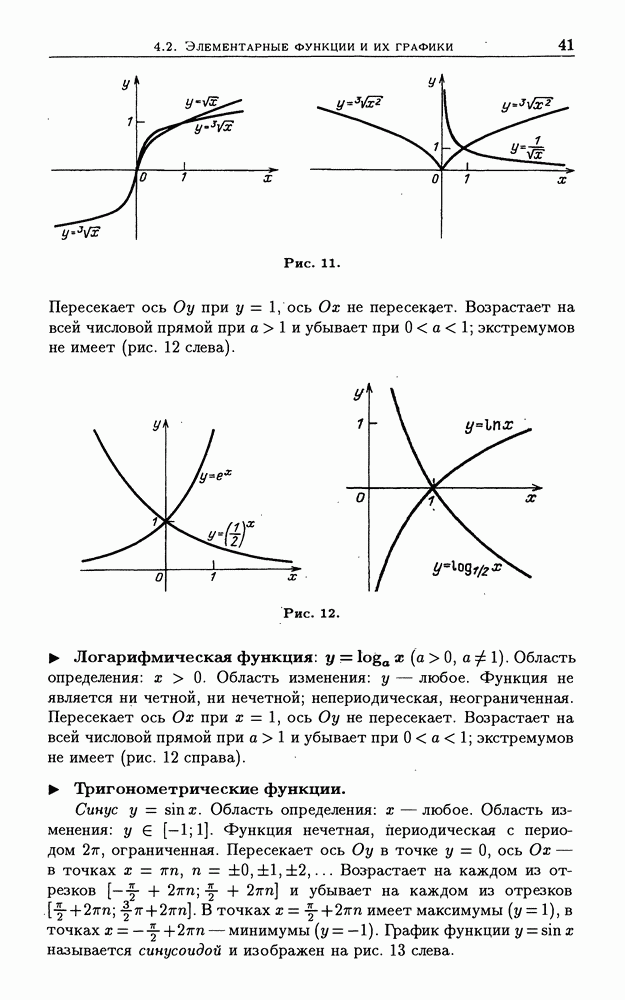
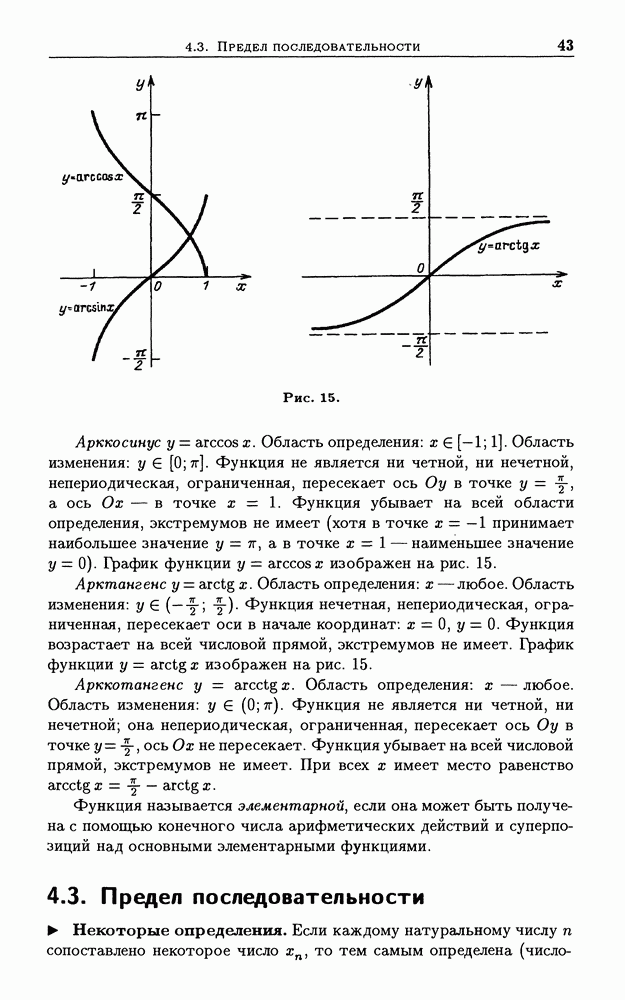
- 4.2. Элементарные функции и их графики
- 4.3. Предел последовательности
- 4.4. Предел функции
- 4.5. Бесконечно малые и бесконечно большие функции
- 4.6. Непрерывность
- 4.7. Асимптоты графика функции
- 5. Дифференциальное исчисление функций одной переменной
- 5.2. Таблица производных и правила дифференцирования
- 5.3. Теоремы о дифференцируемых функциях. Правило Лопиталя
- 5.4. Производные и дифференциалы высших порядков. Формула Тейлора
- 5.5. Экстремумы. Точки перегиба
- 5.6. Общая схема исследования функции и построение графика
- 6. Функции нескольких переменных
- 6.1. Точечные множества. Функции. Предел и непрерывность
- 6.2. Дифференцирование функций нескольких переменных
- 6.3. Производная по направлению. Геометрические приложения
- 6.4. Экстремумы функций нескольких переменных
- 7. Неопределенный интеграл
- 7.1. Первообразная. Неопределенный интеграл и его свойства
- 7.2. Таблица основных интегралов. Примеры интегрирования
- 7.3. Интегрирование по частям. Метод замены переменной
- 7.4. Интегрирование рациональных функций
- 7.5. Интегрирование иррациональных функций
- 7.6. Интегрирование показательных и тригонометрических функций
- 8. Определенный интеграл
- 8.1. Основные определения. Геометрический смысл определенного интеграла
- 8.2. Свойства определенного интеграла
- 8.3. Геометрические и физические приложения определенного интеграла
- 8.4. Несобственные интегралы
- 9. Двойные и тройные интегралы
- 9.1. Определение и свойства двойного интеграла
- 9.2. Вычисление двойного интеграла
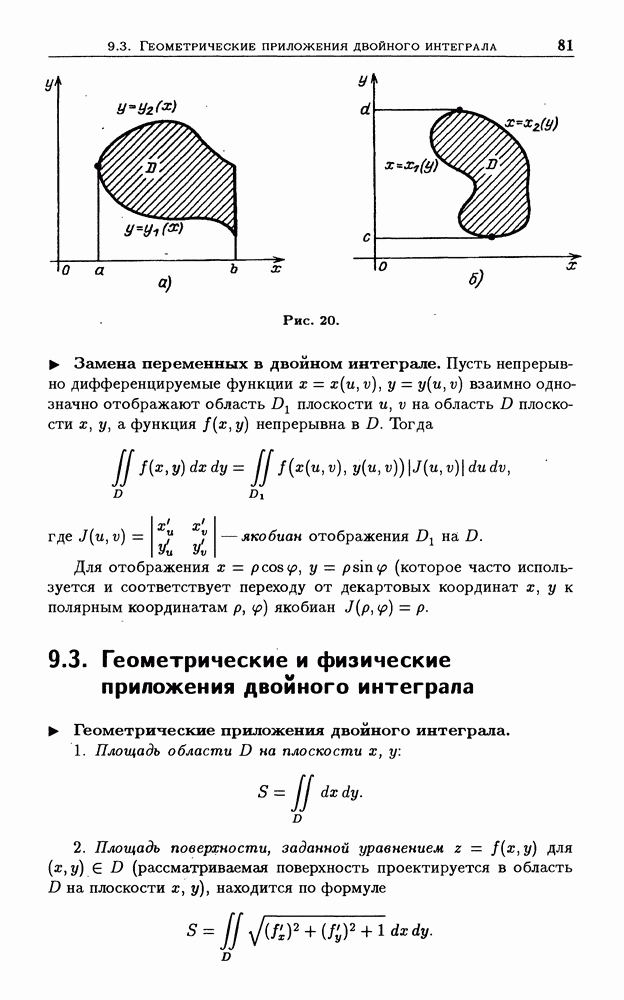
- 9.3. Геометрические и физические приложения двойного интеграла
- 9.4. Определение и свойства тройного интеграла
- 9.5. Вычисление тройного интеграла. Некоторые приложения
- 10. Криволинейные и поверхностные интегралы
- 10.2. Криволинейный интеграл второго рода
- 10.3. Поверхностный интеграл первого рода
- 10.4. Поверхностный интеграл второго рода
- 10.5. Дифференциальные операции и интегральные формулы теории поля
- 11. Ряды
- 11.1. Числовые ряды
- 11.2. Функциональные ряды
- 11.3. Степенные ряды
- 11.4. Ряд Фурье
- 11.5. Интеграл Фурье. Преобразование Фурье
- 12. Обыкновенные дифференциальные уравнения
- 12.2. Дифференциальные уравнения высших порядков
- 12.3. Линейные уравнения n-го порядка
- 12.4. Решение линейных однородных уравнений n-го порядка с постоянными коэффициентами
- 12.5. Линейные неоднородные уравнения n-го порядка
- 12.6. Системы обыкновенных дифференциальных уравнений
- 13. Приближенные вычисления
- 13.1. Метод наименьших квадратов
- 13.2. Приближенное решение алгебраических уравнений
- 13.3. Вычисление определенного интеграла
- 13.4. Численное интегрирование дифференциальных уравнений
- 14. Теория вероятностей
- 14.1. Правила и формулы комбинаторики
- 14.2. Основные понятия теории вероятностей
- 14.3. Условная вероятность. Теоремы и формулы теории вероятностей
- 14.4. Математическое ожидание и дисперсия
- 14.5. Закон больших чисел
- 1. Физические основы механики
- 1.1. Кинематика точки
- 1.2. Кинематика твердого тела
- 1.3. Динамика
- 1.4. Закон сохранения импульса
- 1.5. Закон сохранения энергии
- 1.6. Закон сохранения момента импульса
- 1.7. Задана двух тел и движение в центральном поле
- 1.8. Поле тяготения
- 1.9. Неинерциальные системы отсчета
- 1.10. Динамика твердого тела
- 1.11. Специальная теория относительности
- 2. Молекулярная физика и термодинамика
- 2.2. Первое начало термодинамики
- 2.3. Второе начало термодинамики
- 2.4. Энтропия. Свободная энергия
- 2.5. Кинетическая теория идеального газа
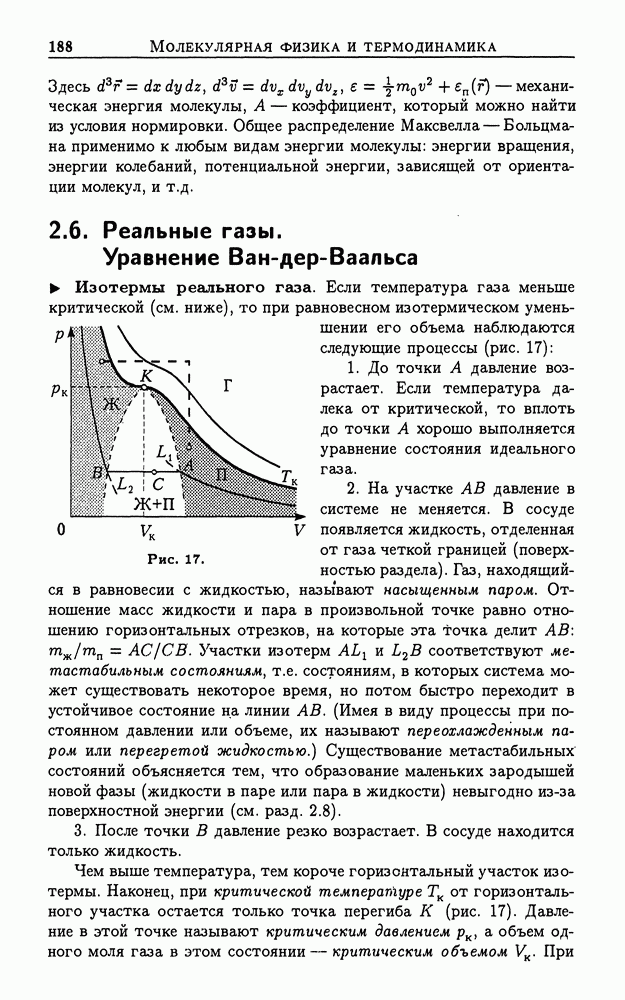
- 2.6. Реальные газы. Уравнение Ван-дер-Ваальса
- 2.7. Равновесие фаз. Фазовые переходы
- 2.8. Поверхностное натяжение
- 2.9. Явления переноса в газах
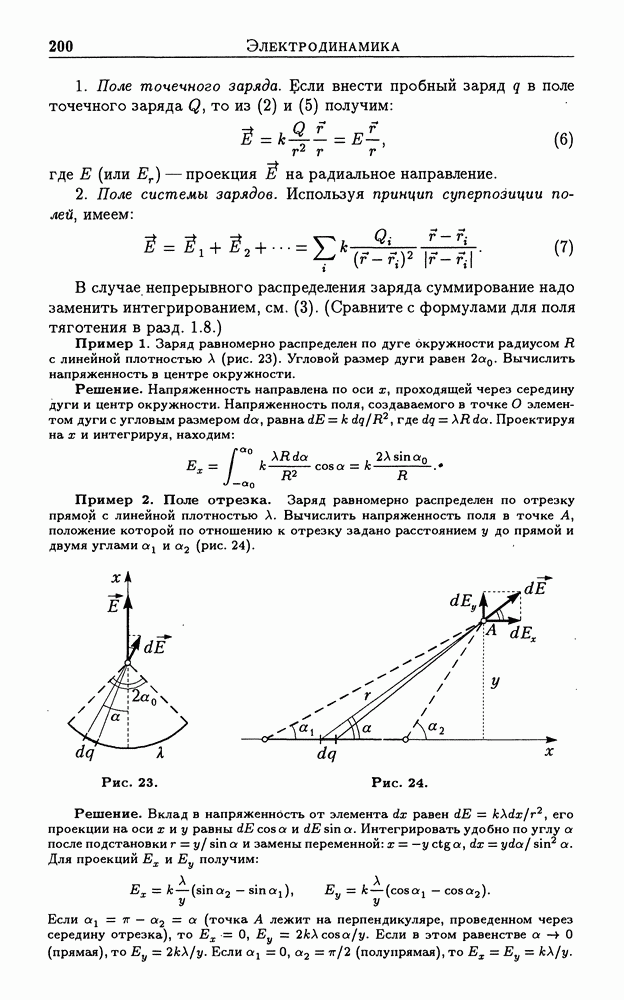
- 3. Электродинамика
- 3.1. Электрический заряд. Закон Кулона
- 3.2. Электрическое поле. Напряженность поля
- 3.3. Электростатическое поле. Принцип суперпозиции для напряженности и потенциала
- 3.4. Теорема Гаусса
- 3.5. Электростатика проводников
- 3.6. Электростатика диэлектриков
- 3.7. Конденсаторы
- 3.8. Энергия электростатического поля
- 3.9. Постоянный ток
- 3.10. Магнитное поле. Сила Лоренца и закон Ампера
- 3.11. Вычисление магнитной индукции
- 3.12. Циркуляция и поток вектора магнитной индукции
- 3.13. Магнитное поле в веществе
- 3.14. Электромагнитная индукция
- 3.15. Уравнения Максвелла
- 4. Колебания и волны
- 4.1. Гармонические колебания. Сложение колебаний
- 4.2. Свободные незатухающие колебания
- 4.3. Затухающие и вынужденные колебания
- 4.4. Упругие волны
- 4.5. Электромагнитные волны
- 5. Оптика
- 5.1. Геометрическая оптика. Фотометрия
- 5.2. Интерференция света
- 5.3. Дифракция
- 5.4. Поляризация света. Формулы Френеля
- 5.5. Дисперсия и поглощение света
- 5.6. Тепловое излучение
- 5.7. Световые кванты
- Список литературы
- 1. Кинематика
- 1.1. Кинематика точки
- 1.2. Кинематика твердого тела
- 1.3. Плоскопараллельное движение твердого тела
- 1.4. Произвольное движение твердого тела
- 1.5. Сложное движение точки
- 2. Основные понятия и аксиомы механики
- 2.2. Аксиомы механики
- 3. Статика
- 3.2. Условия уравновешенности систем сил, приложенных к твердому телу
- 3.3. Решение задан статики
- 3.4. Центр параллельных сил. Центр тяжести твердого тела
- 3.5. Распределенные силы
- 3.6. Законы трения (законы Кулона)
- 4. Динамика материальной точки
- 4.2. Первая и вторая задачи динамики
- 5. Общие теоремы динамики механической системы
- 5.2. Теорема о движении центра масс
- 5.3. Теорема об изменении количества движения
- 5.4. Теорема об изменении кинетического момента
- 5.5. Теорема об изменении кинетической энергии
- 6. Принцип Даламбера. Элементы аналитической механики
- 6.2. Классификация механических связей. Обобщенные координаты
- 6.3. Принцип возможных перемещений
- 6.4. Общее уравнение динамики (принцип Даламбера — Лагранжа)
- 6.5. Уравнения Лагранжа второго рода
- 1. Основные понятия
- 1.1. Введение. Внешние и внутренние силы
- 1.2. Напряжения и деформации в точке
- 1.3. Основные понятия и допущения
- 2. Напряженно-деформированное состояние в точке
- 2.2. Одноосное растяжение и сжатие
- 2.3. Чистый сдвиг
- 3. Центральное растяжение и сжатие
- 3.2. Напряжения и деформации при растяжении или сжатии
- 3.3. Расчеты на прочность при растяжении и сжатии
- 4. Кручение
- 4.2. Напряжения и деформации при кручении
- 4.3. Расчеты на прочность при кручении
- 5. Прямой изгиб
- 5.2. Напряжения и деформации при прямом чистом изгибе
- 5.3. Напряжения и деформации при прямом поперечном изгибе
- 5.4. Расчет на прочность при прямом изгибе
- 6. Сложное сопротивление
- 6.2. Внецентренное растяжение или сжатие
- 6.3. Изгиб с кручением
- 7. Устойчивость сжатых стержней
- 7.2. Формула Эйлера
- 7.3. Влияние способов закрепления концов стержня на величину критической силы
- 7.4. Пределы применимости формулы Эйлера
- 7.5. Расчеты сжатых стержней на устойчивость
- ПРИЛОЖЕНИЯ
- 1. Элементарные функции и их свойства
- 2. Таблица неопределенных интегралов
- 3. Решения обыкновенных дифференциальных уравнений
- 4. Ортогональные криволинейные системы координат
- 5. Некоторые физические постоянные