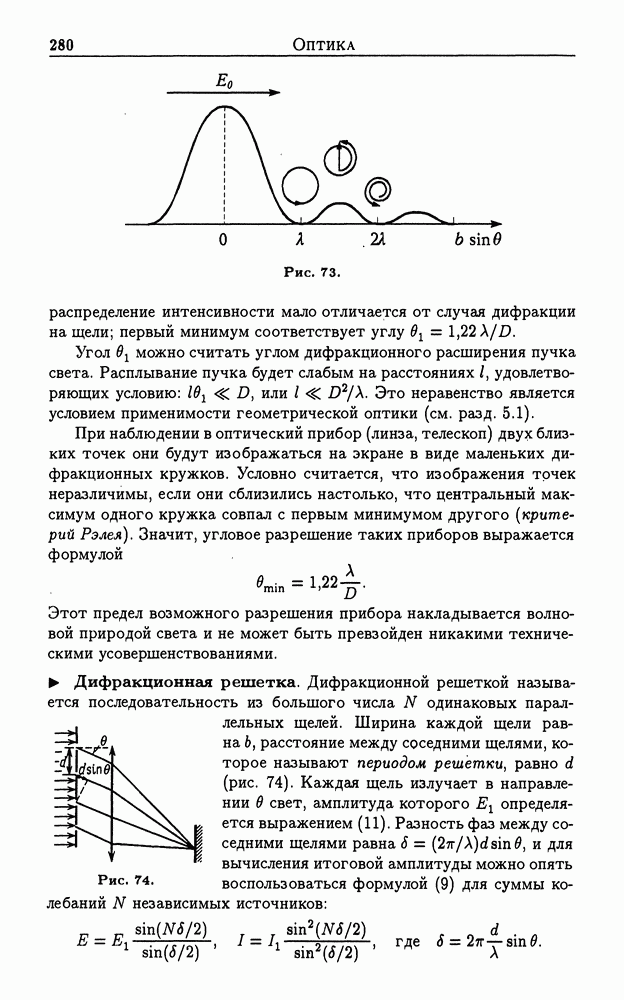
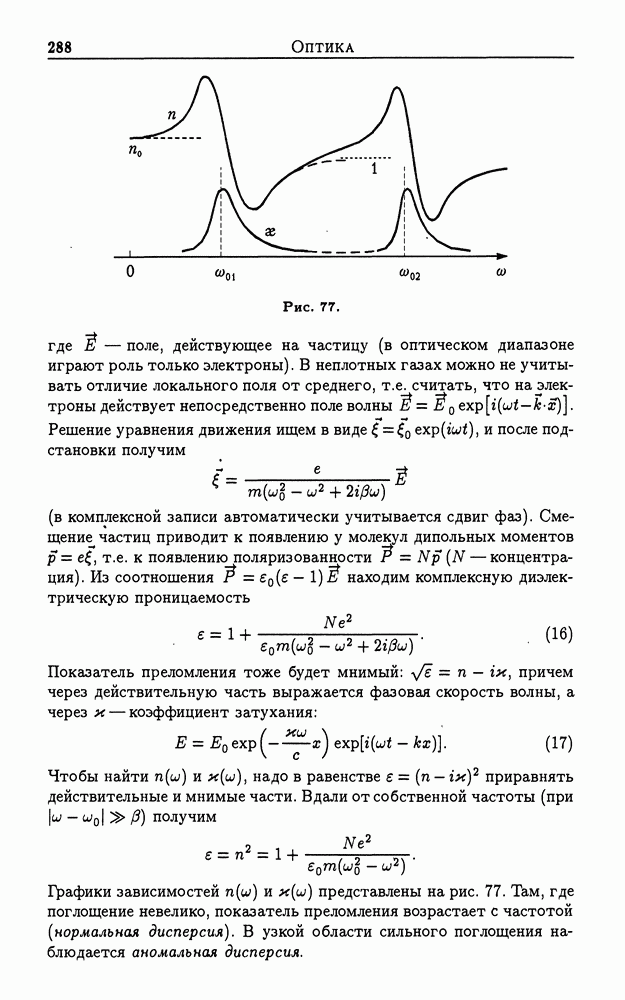
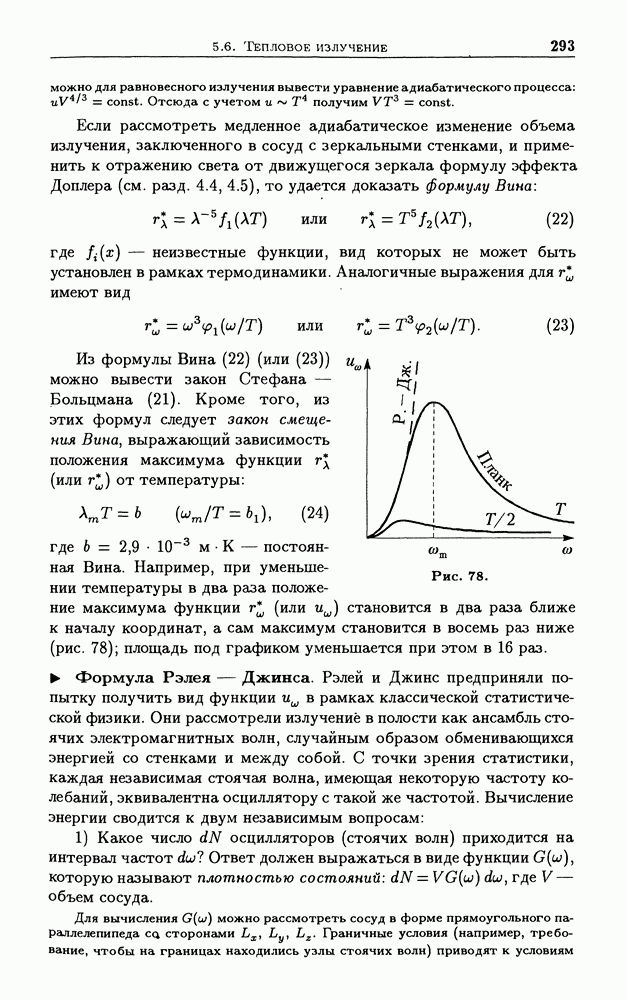
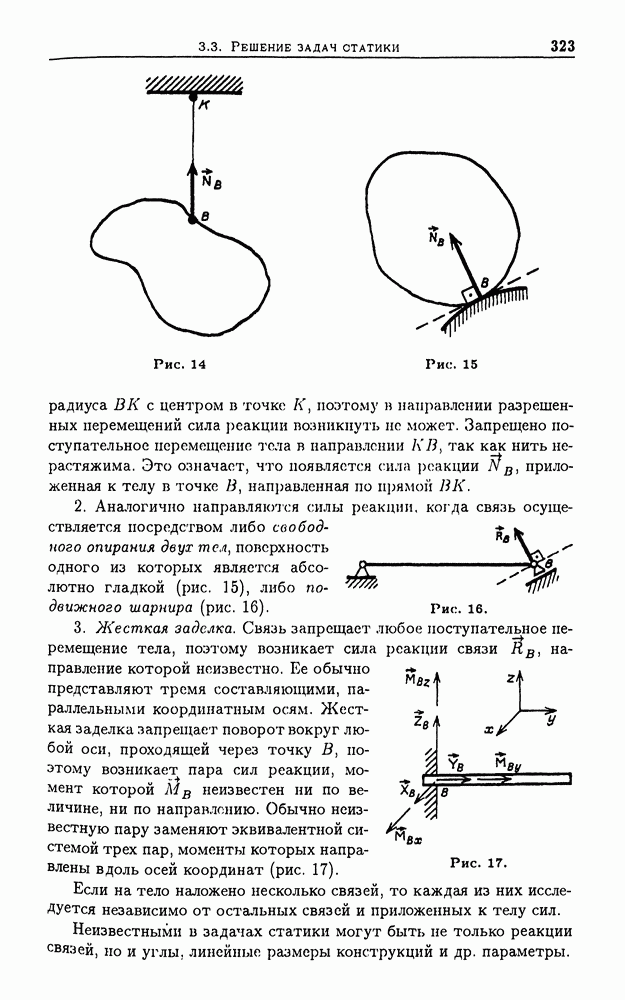
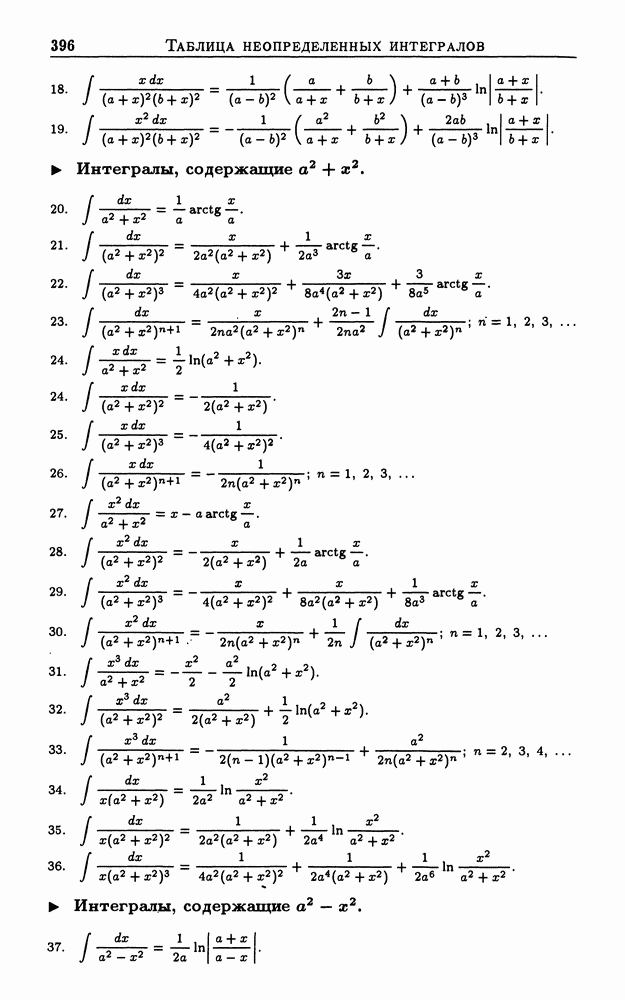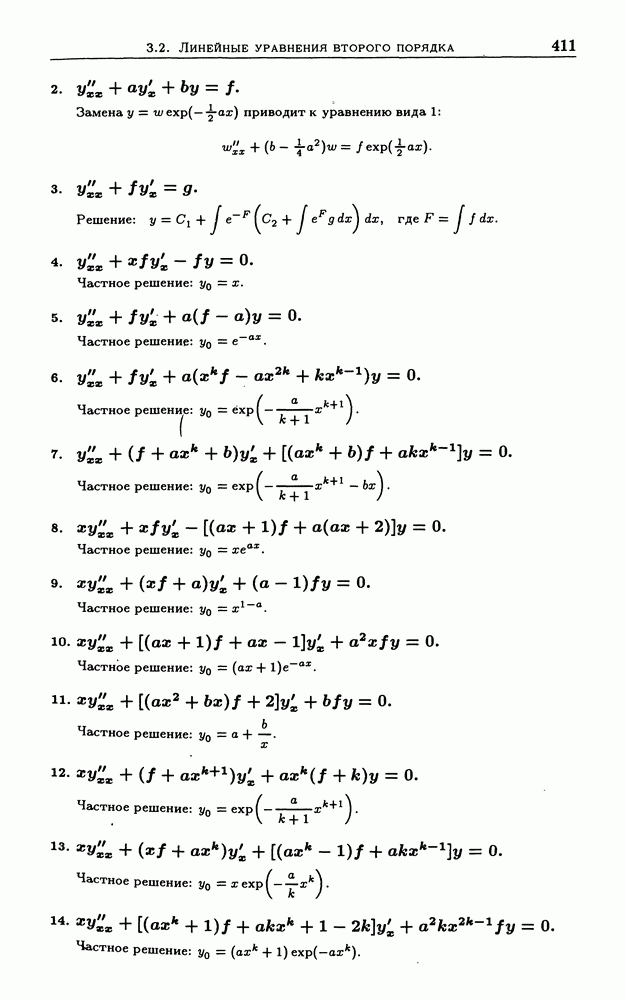| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
1.8. Поле тяготения
Закон всемирного тяготения. Две точечные массы  находящиеся на расстоянии
находящиеся на расстоянии  друг от друга, притягиваются с силой тяготения (гравитационной силой), равной
друг от друга, притягиваются с силой тяготения (гравитационной силой), равной

где  — гравитационная постоянная. Сила тяготения — центральная сила, т.е. она действует вдоль линии, соединяющей частицы.
— гравитационная постоянная. Сила тяготения — центральная сила, т.е. она действует вдоль линии, соединяющей частицы.
Силу, действующую на материальную точку массой  в центральном поле тяготения (гравитационном поле), создаваемым неподвижной точечной массой М, можно записать в виде (см. разд. 1.3):
в центральном поле тяготения (гравитационном поле), создаваемым неподвижной точечной массой М, можно записать в виде (см. разд. 1.3):

Тем самым роль «заряда» для поля тяготения играет инертная масса  . Иногда это свойство формулируют как равенство гравитационной и инертной масс. Потенциальную энергию точки в центральном поле тяготения можно найти, используя соотношение между силой и потенциальной энергией (формула
. Иногда это свойство формулируют как равенство гравитационной и инертной масс. Потенциальную энергию точки в центральном поле тяготения можно найти, используя соотношение между силой и потенциальной энергией (формула  т. е.
т. е.  Константу обычно полагают равной нулю, т.е. принимают за нуль потенциальную энергию на бесконечности:
Константу обычно полагают равной нулю, т.е. принимают за нуль потенциальную энергию на бесконечности:

Принцип суперпозиции. Если поле тяготения создается несколькими точечными массами  то сила, действующая на материальную точку массой
то сила, действующая на материальную точку массой  и ее потенциальная энергия вычисляются по формулам:
и ее потенциальная энергия вычисляются по формулам:

где  — радиус-вектор точки массой
— радиус-вектор точки массой  — радиус-вектор точки массой
— радиус-вектор точки массой  Если источник поля представляет собой непрерывно распределенную массу, то суммирование в (31) надо заменить интегрированием.
Если источник поля представляет собой непрерывно распределенную массу, то суммирование в (31) надо заменить интегрированием.
Напряженность и потенциал поля тяготения. Из уравнений (31) видно, что как сила, действующая на материальную точку массой  в поле тяготения, так и ее потенциальная энергия пропорциональны
в поле тяготения, так и ее потенциальная энергия пропорциональны  Значит, удельные значения массы и энергии (отношения
Значит, удельные значения массы и энергии (отношения  ) не зависят от величины
) не зависят от величины  т.е. представляют собой характеристики поля. Их называют, соответственно, напряженностью и потенциалом поля тяготения:
т.е. представляют собой характеристики поля. Их называют, соответственно, напряженностью и потенциалом поля тяготения:

Напряженность поля имеет простой физический смысл: она представляет собой ускорение свободного падения любой точечной массы, помещенной в данную точку поля. Напряженность и потенциал поля тяготения, создаваемого точечной массой М, имеют вид:

Напряженность и потенциал поля, создаваемого несколькими массами, вычисляются с помощью принципа суперпозиции. Запись уравнения аналогична (31), для разнообразия запишем ответ для случая распределенной массы:

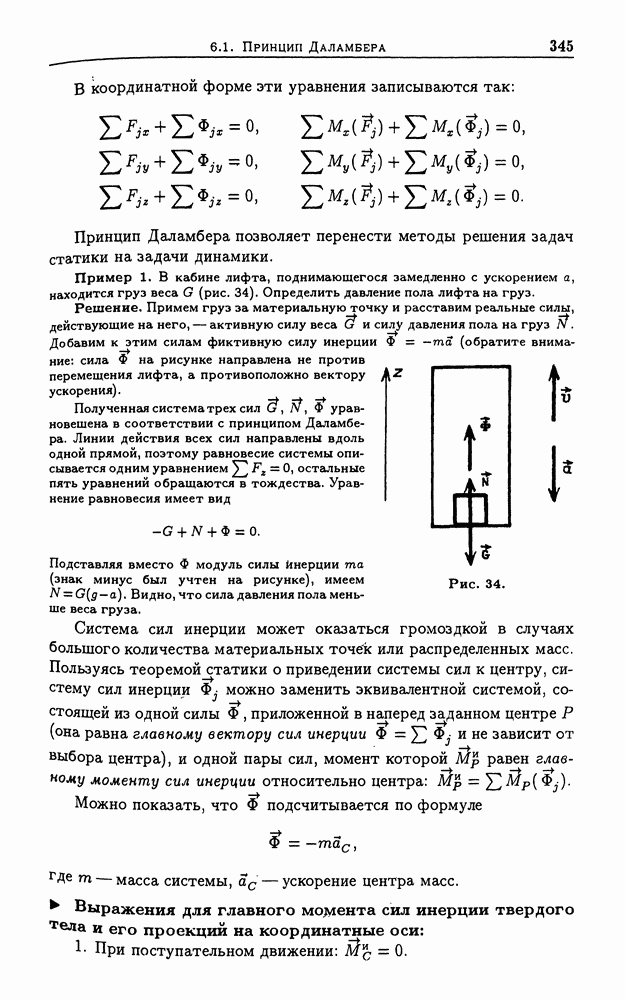
Пример 1. Показать, что напряженность поля тяготения внутри тонкого сферического слоя равна нулю.
Решение. Для доказательства рассмотрим вклад в напряженность поля в точке А небольших участков В и С сферы, отсекаемых от нее тонким конусом с вершиной в точке А (рис. 9). Отношение площадей этих участков, а значит, и отношение их масс, равно отношению квадратов расстояний от этих участков до точки А. Следовательно, напряженности, создаваемые этими участками в точке А, равны по величине.

Рис. 9.
Напряженность поля, создаваемого тонкой сферой массой М вне ее, оказывается равной напряженности, создаваемой точечной массой М, помещенной в центр сферы. Доказательство этого результата требует громоздкого интегрирования (первым его проделал Ньютон). В гл. 3 это утверждение будет доказано с помощью теоремы Гаусса. Такой же ответ годится для любой сферически распределенной массы, в частности, для любой сферической планеты.
Пример 2. Пусть масса М распределена по отрезку длиной  Вычислить напряженность и потенцией! на продолжении отрезка, на расстоянии х от его центра.
Вычислить напряженность и потенцией! на продолжении отрезка, на расстоянии х от его центра.
Решение. Масса  заключенная на отрезке длиной
заключенная на отрезке длиной  равна
равна  Интегрируя, получим
Интегрируя, получим

Видно, что симметричное, но несферическое тело нельзя заменить точечной массой, помещенной в ее центр. Этот пример является также иллюстрацией того, что напряженность и потенциал связаны соотношением  аналогичным соотношению (16).
аналогичным соотношению (16).
Движение в центральном поле тяготения. Законы Кеплера. Движение в центральном поле тяготения подчиняется общим законам движения в центральном поле. Однако оно обладает некоторыми особенностями, отраженными в первом и третьем из законов Кеплера, сформулированных им для планет Солнечной системы.
Первый закон Кеплера утверждает, что финитное движение  материальной точки в центральном поле тяготения происходит по замкнутой траектории — эллипсу, в одном из фокусов которого находится центр силы притяжения (Солнце).
материальной точки в центральном поле тяготения происходит по замкнутой траектории — эллипсу, в одном из фокусов которого находится центр силы притяжения (Солнце).
Второй закон Кеплера фиксирует постоянство секторной скорости, т.е. скорости «заметания» площади радиусом-вектором движущейся точки. Он относится к любому центральному полю и является прямым следствием закона сохранения момента импульса (см. пример 2 из разд. 1.6).
Третий закон Кеплера утверждает, что квадраты периодов движения относятся как кубы больших полуосей эллиптических орбит: 
Дополним первый закон Кеплера утверждением, что инфинитное движение в центральном поле тяготения происходит либо по параболе  либо по гиперболе
либо по гиперболе  . В качестве дополнения к третьему закону Кеплера приведем связь между удельной энергией движения и большой полуосью:
. В качестве дополнения к третьему закону Кеплера приведем связь между удельной энергией движения и большой полуосью:  Видно, что период движения однозначно определяется удельной энергией движущегося тела.
Видно, что период движения однозначно определяется удельной энергией движущегося тела.
Космические скорости. Первой космической скоростью называют скорость движения по круговой орбите вблизи поверхности планеты. Она определяется из уравнения движения спутника  и равна
и равна  (Для Земли
(Для Земли 
Вторая космическая скорость — минимальная скорость, которую надо сообщить телу на поверхности планеты, чтобы оно преодолело силу тяготения и ушло на бесконечность. Как видно из разд. 1.7, условием инфинитности движения является неравенство О, т.е. вторая космическая скорость находится из уравнения  и равна
и равна  (Для Земли
(Для Земли  )
)
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- 1. Аналитическая геометрия на плоскости
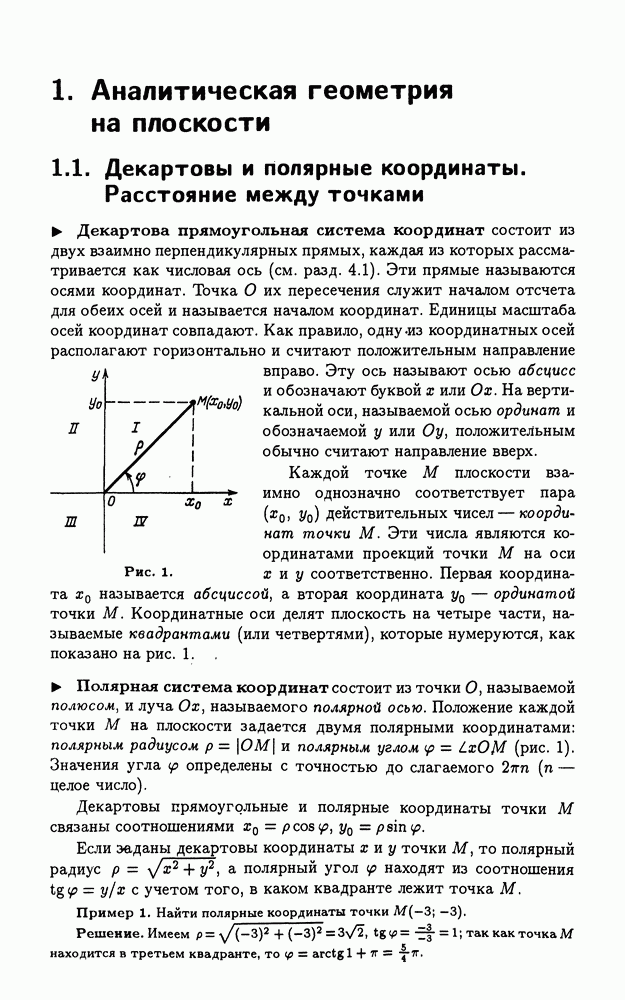
- 1.1. Декартовы и полярные координаты. Расстояние между точками
- 1.2. Деление отрезка в данном отношении. Площадь многоугольника
- 1.3. Различные виды уравнения прямой
- 1.4. Угол между прямыми. Расстояние от точки до прямой
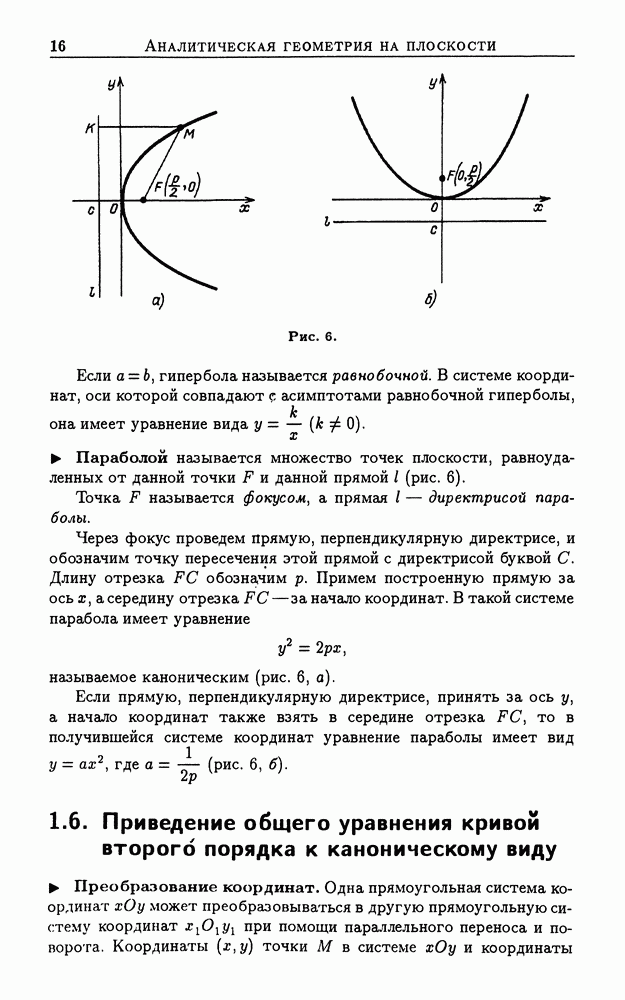
- 1.5. Окружность, эллипс, гипербола и парабола
- 1.6. Приведение общего уравнения кривой второго порядка к каноническому виду
- 2. Аналитическая геометрия в пространстве
- 2.2. Векторы
- 2.3. Действия над векторами. Скалярное произведение
- 2.4. Векторное и смешанное произведения
- 2.5. Плоскость в пространстве
- 2.6. Прямая в пространстве
- 2.7. Прямая и плоскость в пространстве
- 2.8. Поверхности второго порядка
- 3. Линейная алгебра
- 3.2. Матрицы
- 3.3. Системы линейных уравнений
- 3.4. Системы n-мерных векторов. Собственные значения и собственные векторы матрицы
- 4. Основные понятия математического анализа
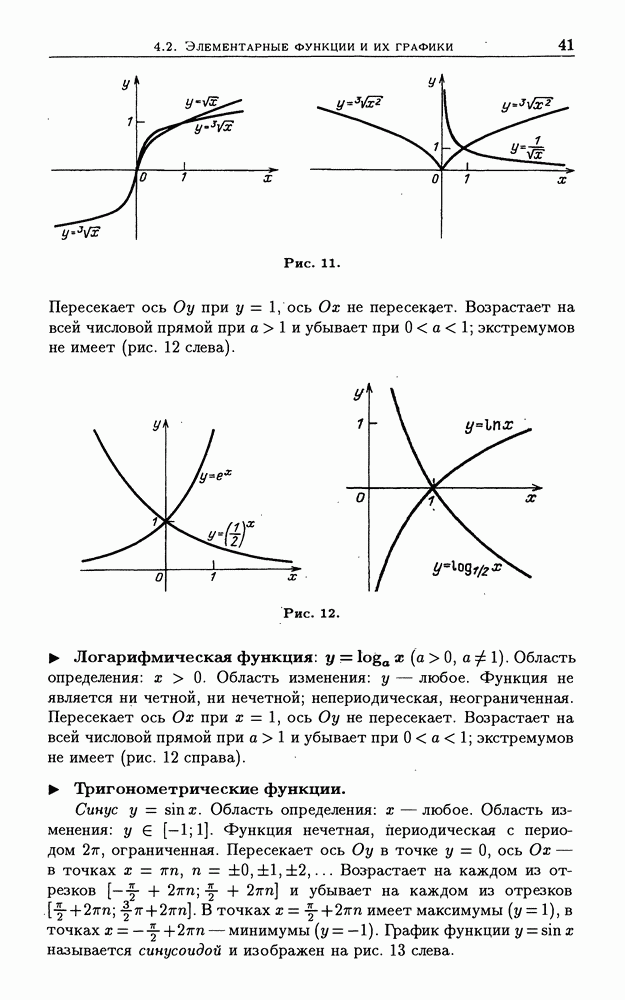
- 4.2. Элементарные функции и их графики
- 4.3. Предел последовательности
- 4.4. Предел функции
- 4.5. Бесконечно малые и бесконечно большие функции
- 4.6. Непрерывность
- 4.7. Асимптоты графика функции
- 5. Дифференциальное исчисление функций одной переменной
- 5.2. Таблица производных и правила дифференцирования
- 5.3. Теоремы о дифференцируемых функциях. Правило Лопиталя
- 5.4. Производные и дифференциалы высших порядков. Формула Тейлора
- 5.5. Экстремумы. Точки перегиба
- 5.6. Общая схема исследования функции и построение графика
- 6. Функции нескольких переменных
- 6.1. Точечные множества. Функции. Предел и непрерывность
- 6.2. Дифференцирование функций нескольких переменных
- 6.3. Производная по направлению. Геометрические приложения
- 6.4. Экстремумы функций нескольких переменных
- 7. Неопределенный интеграл
- 7.1. Первообразная. Неопределенный интеграл и его свойства
- 7.2. Таблица основных интегралов. Примеры интегрирования
- 7.3. Интегрирование по частям. Метод замены переменной
- 7.4. Интегрирование рациональных функций
- 7.5. Интегрирование иррациональных функций
- 7.6. Интегрирование показательных и тригонометрических функций
- 8. Определенный интеграл
- 8.1. Основные определения. Геометрический смысл определенного интеграла
- 8.2. Свойства определенного интеграла
- 8.3. Геометрические и физические приложения определенного интеграла
- 8.4. Несобственные интегралы
- 9. Двойные и тройные интегралы
- 9.1. Определение и свойства двойного интеграла
- 9.2. Вычисление двойного интеграла
- 9.3. Геометрические и физические приложения двойного интеграла
- 9.4. Определение и свойства тройного интеграла
- 9.5. Вычисление тройного интеграла. Некоторые приложения
- 10. Криволинейные и поверхностные интегралы
- 10.2. Криволинейный интеграл второго рода
- 10.3. Поверхностный интеграл первого рода
- 10.4. Поверхностный интеграл второго рода
- 10.5. Дифференциальные операции и интегральные формулы теории поля
- 11. Ряды
- 11.1. Числовые ряды
- 11.2. Функциональные ряды
- 11.3. Степенные ряды
- 11.4. Ряд Фурье
- 11.5. Интеграл Фурье. Преобразование Фурье
- 12. Обыкновенные дифференциальные уравнения
- 12.2. Дифференциальные уравнения высших порядков
- 12.3. Линейные уравнения n-го порядка
- 12.4. Решение линейных однородных уравнений n-го порядка с постоянными коэффициентами
- 12.5. Линейные неоднородные уравнения n-го порядка
- 12.6. Системы обыкновенных дифференциальных уравнений
- 13. Приближенные вычисления
- 13.1. Метод наименьших квадратов
- 13.2. Приближенное решение алгебраических уравнений
- 13.3. Вычисление определенного интеграла
- 13.4. Численное интегрирование дифференциальных уравнений
- 14. Теория вероятностей
- 14.1. Правила и формулы комбинаторики
- 14.2. Основные понятия теории вероятностей
- 14.3. Условная вероятность. Теоремы и формулы теории вероятностей
- 14.4. Математическое ожидание и дисперсия
- 14.5. Закон больших чисел
- 1. Физические основы механики
- 1.1. Кинематика точки
- 1.2. Кинематика твердого тела
- 1.3. Динамика
- 1.4. Закон сохранения импульса
- 1.5. Закон сохранения энергии
- 1.6. Закон сохранения момента импульса
- 1.7. Задана двух тел и движение в центральном поле
- 1.8. Поле тяготения
- 1.9. Неинерциальные системы отсчета
- 1.10. Динамика твердого тела
- 1.11. Специальная теория относительности
- 2. Молекулярная физика и термодинамика
- 2.2. Первое начало термодинамики
- 2.3. Второе начало термодинамики
- 2.4. Энтропия. Свободная энергия
- 2.5. Кинетическая теория идеального газа
- 2.6. Реальные газы. Уравнение Ван-дер-Ваальса
- 2.7. Равновесие фаз. Фазовые переходы
- 2.8. Поверхностное натяжение
- 2.9. Явления переноса в газах
- 3. Электродинамика
- 3.1. Электрический заряд. Закон Кулона
- 3.2. Электрическое поле. Напряженность поля
- 3.3. Электростатическое поле. Принцип суперпозиции для напряженности и потенциала
- 3.4. Теорема Гаусса
- 3.5. Электростатика проводников
- 3.6. Электростатика диэлектриков
- 3.7. Конденсаторы
- 3.8. Энергия электростатического поля
- 3.9. Постоянный ток
- 3.10. Магнитное поле. Сила Лоренца и закон Ампера
- 3.11. Вычисление магнитной индукции
- 3.12. Циркуляция и поток вектора магнитной индукции
- 3.13. Магнитное поле в веществе
- 3.14. Электромагнитная индукция
- 3.15. Уравнения Максвелла
- 4. Колебания и волны
- 4.1. Гармонические колебания. Сложение колебаний
- 4.2. Свободные незатухающие колебания
- 4.3. Затухающие и вынужденные колебания
- 4.4. Упругие волны
- 4.5. Электромагнитные волны
- 5. Оптика
- 5.1. Геометрическая оптика. Фотометрия
- 5.2. Интерференция света
- 5.3. Дифракция
- 5.4. Поляризация света. Формулы Френеля
- 5.5. Дисперсия и поглощение света
- 5.6. Тепловое излучение
- 5.7. Световые кванты
- Список литературы
- 1. Кинематика
- 1.1. Кинематика точки
- 1.2. Кинематика твердого тела
- 1.3. Плоскопараллельное движение твердого тела
- 1.4. Произвольное движение твердого тела
- 1.5. Сложное движение точки
- 2. Основные понятия и аксиомы механики
- 2.2. Аксиомы механики
- 3. Статика
- 3.2. Условия уравновешенности систем сил, приложенных к твердому телу
- 3.3. Решение задан статики
- 3.4. Центр параллельных сил. Центр тяжести твердого тела
- 3.5. Распределенные силы
- 3.6. Законы трения (законы Кулона)
- 4. Динамика материальной точки
- 4.2. Первая и вторая задачи динамики
- 5. Общие теоремы динамики механической системы
- 5.2. Теорема о движении центра масс
- 5.3. Теорема об изменении количества движения
- 5.4. Теорема об изменении кинетического момента
- 5.5. Теорема об изменении кинетической энергии
- 6. Принцип Даламбера. Элементы аналитической механики
- 6.2. Классификация механических связей. Обобщенные координаты
- 6.3. Принцип возможных перемещений
- 6.4. Общее уравнение динамики (принцип Даламбера — Лагранжа)
- 6.5. Уравнения Лагранжа второго рода
- 1. Основные понятия
- 1.1. Введение. Внешние и внутренние силы
- 1.2. Напряжения и деформации в точке
- 1.3. Основные понятия и допущения
- 2. Напряженно-деформированное состояние в точке
- 2.2. Одноосное растяжение и сжатие
- 2.3. Чистый сдвиг
- 3. Центральное растяжение и сжатие
- 3.2. Напряжения и деформации при растяжении или сжатии
- 3.3. Расчеты на прочность при растяжении и сжатии
- 4. Кручение
- 4.2. Напряжения и деформации при кручении
- 4.3. Расчеты на прочность при кручении
- 5. Прямой изгиб
- 5.2. Напряжения и деформации при прямом чистом изгибе
- 5.3. Напряжения и деформации при прямом поперечном изгибе
- 5.4. Расчет на прочность при прямом изгибе
- 6. Сложное сопротивление
- 6.2. Внецентренное растяжение или сжатие
- 6.3. Изгиб с кручением
- 7. Устойчивость сжатых стержней
- 7.2. Формула Эйлера
- 7.3. Влияние способов закрепления концов стержня на величину критической силы
- 7.4. Пределы применимости формулы Эйлера
- 7.5. Расчеты сжатых стержней на устойчивость
- ПРИЛОЖЕНИЯ
- 1. Элементарные функции и их свойства
- 2. Таблица неопределенных интегралов
- 3. Решения обыкновенных дифференциальных уравнений
- 4. Ортогональные криволинейные системы координат
- 5. Некоторые физические постоянные