| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
1. Физические основы механики
Механическим движением называется изменение положения тела по отношению к другим телам. Как видно из определения, механическое движение относительно. Для описания движения необходимо определить систему отсчета, которая включает в себя тело отсчета, жестко связанную с ним систему координат и набор синхронизированных между собой часов. Механика изучает движение модельных объектов — точек и твердых тел. Положение этих объектов определяется конечным числом независимых параметров (т.е. они обладают конечным числом степеней свободы). Кинематика занимается описанием движения без выяснения его причин.
1.1. Кинематика точки
Основные определения. Скорость и ускорение. Материальной точкой называется тело, размерами которого при описании его движения можно пренебречь. Положение точки в момент времени  задается радиусом-вектором
задается радиусом-вектором  проведенным, к этой точке из начала координат (рис. 1).
проведенным, к этой точке из начала координат (рис. 1).
В процессе движения конец радиуса-вектора описывает пространственную кривую — траекторию. В прямоугольной декартовой системе координат положение радиуса-вектора задается тремя его проекциями на оси  — координатами
— координатами  Движение точки полностью определяется заданием закона движения — одной векторной функции
Движение точки полностью определяется заданием закона движения — одной векторной функции  или трех скалярных функций
или трех скалярных функций  Для компактной записи радиуса-вектора (или любого вектора) через его проекции используют единичные орты:
Для компактной записи радиуса-вектора (или любого вектора) через его проекции используют единичные орты:  Путь — длина участка траектории, пройденного точкой за рассматриваемый интервал времени. Путь — величина скалярная, неотрицательная и не убывающая со временем. Перемещением точки называется вектор
Путь — длина участка траектории, пройденного точкой за рассматриваемый интервал времени. Путь — величина скалярная, неотрицательная и не убывающая со временем. Перемещением точки называется вектор  соединяющий начальное положение точки с конечным и равный разности радиусов-векторов в конечный и начальный моменты времени.
соединяющий начальное положение точки с конечным и равный разности радиусов-векторов в конечный и начальный моменты времени.

Рис. 1.
Скорость точки равна производной от радиуса-вектора по времени:  Скорость направлена по касательной к траектории. Средняя (по времени) скорость за конечное время
Скорость направлена по касательной к траектории. Средняя (по времени) скорость за конечное время  определяется как отношение перемещения к интервалу времени:
определяется как отношение перемещения к интервалу времени: 
(Средняя скорость пути равна отношению пройденного пути к интервалу времени.) Движение называют равномерным, если  Равномерное движение происходит по прямой. Равномерным движением по заданной криволинейной траектории называют движение с постоянным модулем скорости. (Пример — равномерное движение по окружности.)
Равномерное движение происходит по прямой. Равномерным движением по заданной криволинейной траектории называют движение с постоянным модулем скорости. (Пример — равномерное движение по окружности.)
Ускорение точки равно производной от скорости по времени:  Ускорение лежит в той же плоскости, что и участок траектории, и направлено «внутрь» траектории (в частном случае, когда траектория является прямой линией, ускорение направлено вдоль этой прямой). Проекцию ускорения на направление скорости называют тангенциальным ускорением и обозначают
Ускорение лежит в той же плоскости, что и участок траектории, и направлено «внутрь» траектории (в частном случае, когда траектория является прямой линией, ускорение направлено вдоль этой прямой). Проекцию ускорения на направление скорости называют тангенциальным ускорением и обозначают  она определяет быстроту изменения модуля скорости и равна производной от модуля скорости:
она определяет быстроту изменения модуля скорости и равна производной от модуля скорости:  Другую компоненту ускорения, перпендикулярную скорости, называют нормальным ускорением (рис. 2) и обозначают
Другую компоненту ускорения, перпендикулярную скорости, называют нормальным ускорением (рис. 2) и обозначают  она характеризует быстроту изменения направления скорости и равна
она характеризует быстроту изменения направления скорости и равна  где
где  — радиус кривизны траектории (т.е. радиус окружности, наиболее близко примыкающей к траектории в данной точке). Среднее ускорение за время
— радиус кривизны траектории (т.е. радиус окружности, наиболее близко примыкающей к траектории в данной точке). Среднее ускорение за время  определяется как
определяется как  Движение называют равноускоренным, если
Движение называют равноускоренным, если  Равноускоренным движением вдоль заданной траектории называют движение
Равноускоренным движением вдоль заданной траектории называют движение 

Рис. 2.
Прямая и обратная задачи кинематики. Задачу определения характеристик движения по известному закону движения называют прямой задачей кинематики.
Пример 1, Пусть закон движения имеет вид:  Найти уравнение траектории, скорость и ускорение.
Найти уравнение траектории, скорость и ускорение.
Решение. Исключая время (с помощью тождества  находим уравнение траектории:
находим уравнение траектории:  (окружность радиуса
(окружность радиуса  ).
).
Дифференцируя исходные выражения по времени, получим

Модуль скорости  и модуль ускорения
и модуль ускорения  не зависят от времени и связаны соотношением
не зависят от времени и связаны соотношением  Ускорение направлено перпендикулярно скорости к центру окружности:
Ускорение направлено перпендикулярно скорости к центру окружности: 
Задачу определения закона движения по известному ускорению  называют обратной задачей кинематики. Для однозначного решения этой задачи нужно знать начальные условия — положение и скорость точки в начальный момент времени.
называют обратной задачей кинематики. Для однозначного решения этой задачи нужно знать начальные условия — положение и скорость точки в начальный момент времени.
Пример 2. Равноускоренное движение. Пусть известны ускорение точки  и ее начальные скорость и положение
и ее начальные скорость и положение  Найти траекторию и закон движения точки.
Найти траекторию и закон движения точки.
Решение. Последовательно интегрируя, находим сначала скорость точки  а затем ее положение
а затем ее положение 
Точка движется в плоскости векторов  по параболе, что видно в системе координат, где ось у направлена по
по параболе, что видно в системе координат, где ось у направлена по  а ось а? — перпендикулярно 3.
а ось а? — перпендикулярно 3.
Во многих случаях задача кинематики не сводится ни к прямой, ни к обратной. В этом случае для определения закона движения приходится решать дифференциальное уравнение. Иногда это уравнение можно решить разделением переменных.
Пример 3. Лодка тормозится силой, пропорциональной квадрату скорости. Найти зависимость скорости движения лодки от времени, если начальная скорость равна 
Решение. Второй закон Ньютона приводит к уравнению  Разделяя переменные, получим:
Разделяя переменные, получим:  Интегрируя левую часть уравнения от
Интегрируя левую часть уравнения от  до
до  а правую — от 0 до
а правую — от 0 до  находим
находим  т.е.
т.е.  Интегрируя далее, можно определить закон движения лодки.
Интегрируя далее, можно определить закон движения лодки.
Движение по окружности. Движение по окружности можно описывать с помощью угловых переменных: угла поворота угловой скорости  и углового ускорения
и углового ускорения  Если угол измерять в радианах, то длина дуги равна
Если угол измерять в радианах, то длина дуги равна  Отсюда следует, что
Отсюда следует, что

Величина  называется центростремительным ускорением.
называется центростремительным ускорением.
Формулы для нормального и тангенциального ускорений можно вывести, если записать скорость в виде  где
где  — единичный вектор, направленный вдоль скорости. Получим
— единичный вектор, направленный вдоль скорости. Получим  и учтем, что
и учтем, что  где
где  единичный вектор, перпендикулярный к скорости и направленный вдоль радиуса. Этот вывод справедлив и для произвольной траектории, если принять соотношение
единичный вектор, перпендикулярный к скорости и направленный вдоль радиуса. Этот вывод справедлив и для произвольной траектории, если принять соотношение  за определение как направления нормали
за определение как направления нормали  так и радиуса кривизны
так и радиуса кривизны 
Относительность движения. Сложение скоростей. Если движение точки рассматривается из двух систем отсчета К и  оси которых остаются все время параллельными друг другу, то между скоростями точки
оси которых остаются все время параллельными друг другу, то между скоростями точки  и
и  относительно этих систем отсчета в каждый момент времени выполняется соотношение
относительно этих систем отсчета в каждый момент времени выполняется соотношение

где  — скорость системы К относительно системы К. Такое же соотношение выполняется и для ускорений:
— скорость системы К относительно системы К. Такое же соотношение выполняется и для ускорений: 
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- 1. Аналитическая геометрия на плоскости
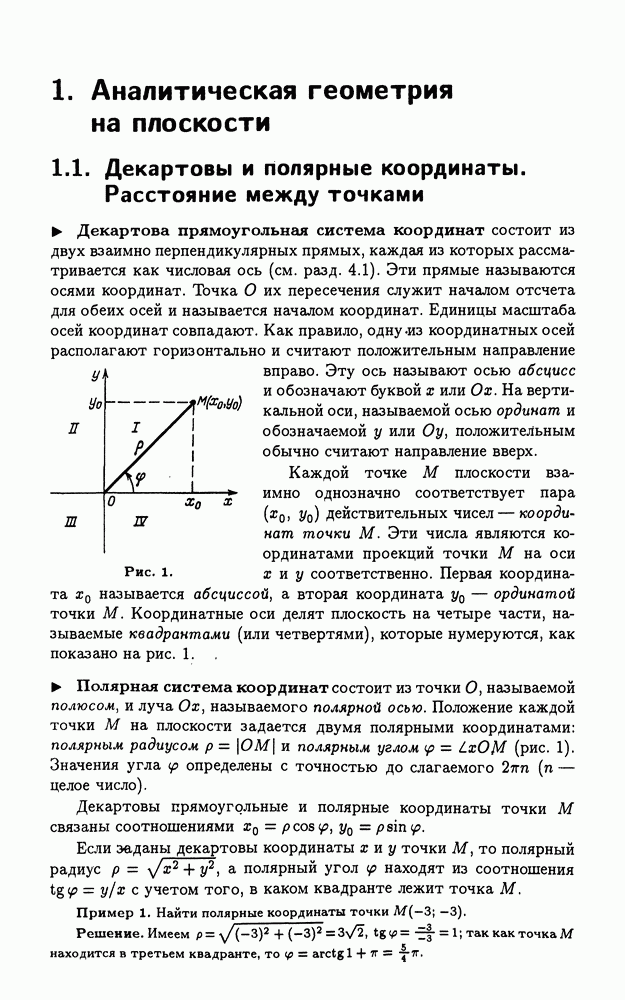
- 1.1. Декартовы и полярные координаты. Расстояние между точками
- 1.2. Деление отрезка в данном отношении. Площадь многоугольника
- 1.3. Различные виды уравнения прямой
- 1.4. Угол между прямыми. Расстояние от точки до прямой
- 1.5. Окружность, эллипс, гипербола и парабола
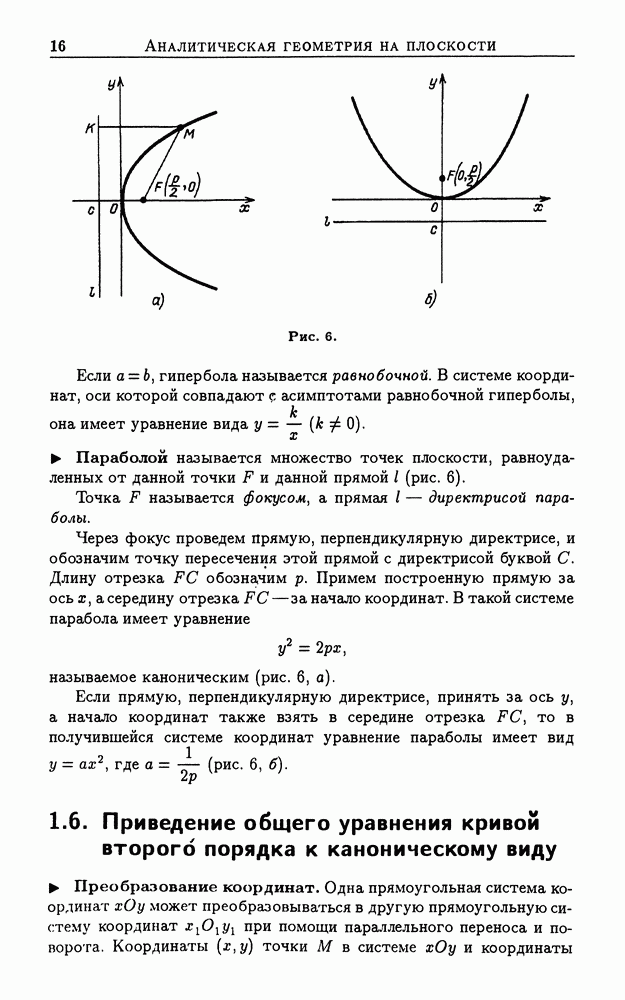
- 1.6. Приведение общего уравнения кривой второго порядка к каноническому виду
- 2. Аналитическая геометрия в пространстве
- 2.2. Векторы
- 2.3. Действия над векторами. Скалярное произведение
- 2.4. Векторное и смешанное произведения
- 2.5. Плоскость в пространстве
- 2.6. Прямая в пространстве
- 2.7. Прямая и плоскость в пространстве
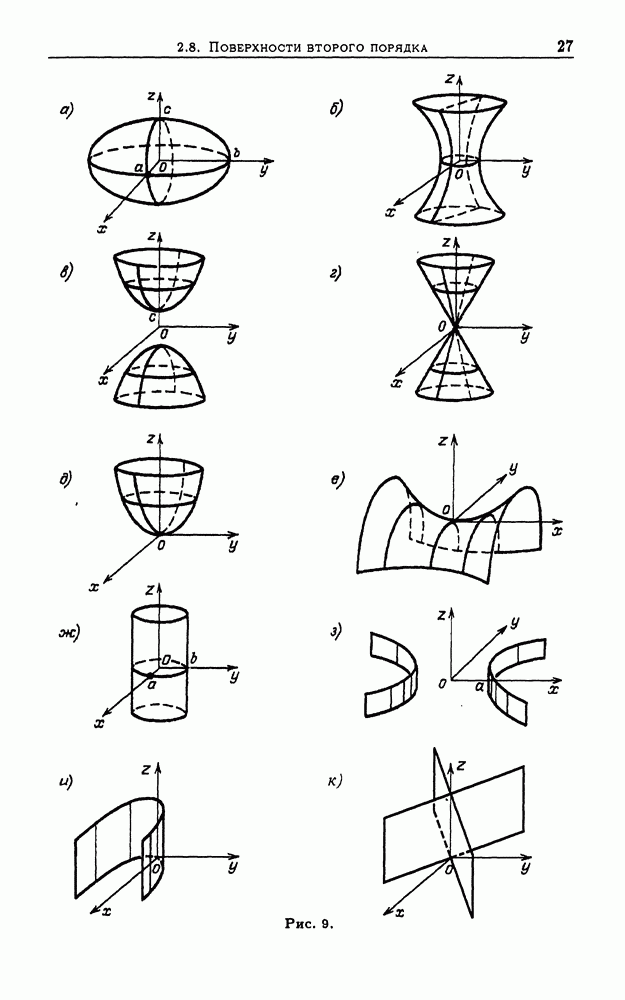
- 2.8. Поверхности второго порядка
- 3. Линейная алгебра
- 3.2. Матрицы
- 3.3. Системы линейных уравнений
- 3.4. Системы n-мерных векторов. Собственные значения и собственные векторы матрицы
- 4. Основные понятия математического анализа
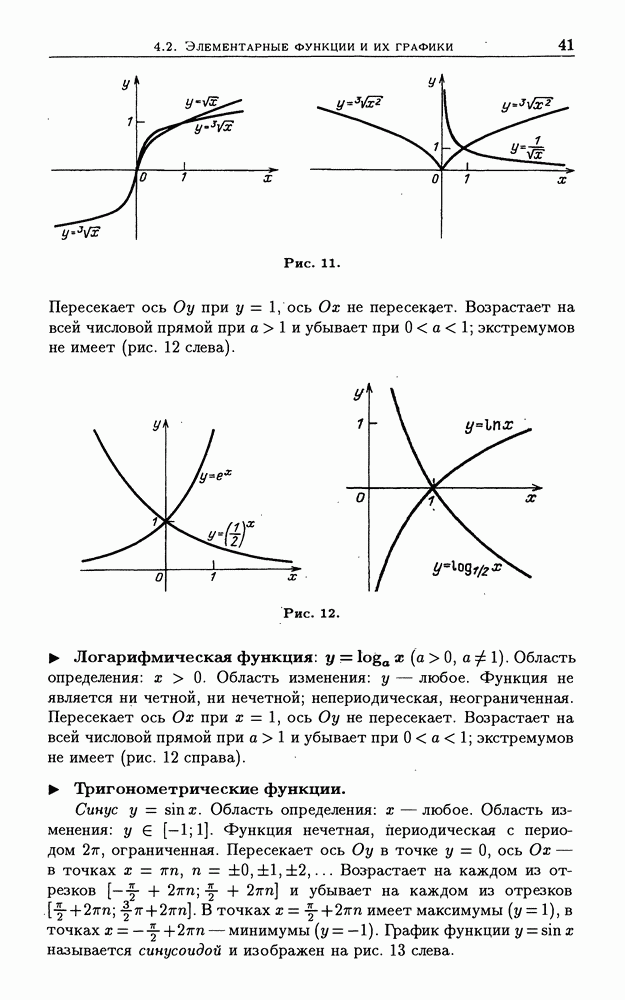
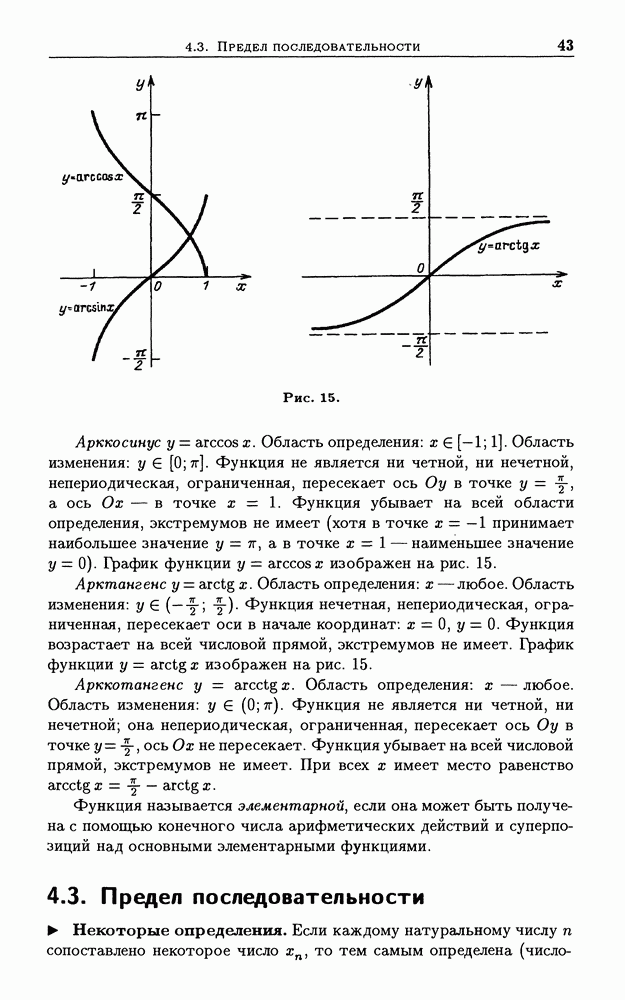
- 4.2. Элементарные функции и их графики
- 4.3. Предел последовательности
- 4.4. Предел функции
- 4.5. Бесконечно малые и бесконечно большие функции
- 4.6. Непрерывность
- 4.7. Асимптоты графика функции
- 5. Дифференциальное исчисление функций одной переменной
- 5.2. Таблица производных и правила дифференцирования
- 5.3. Теоремы о дифференцируемых функциях. Правило Лопиталя
- 5.4. Производные и дифференциалы высших порядков. Формула Тейлора
- 5.5. Экстремумы. Точки перегиба
- 5.6. Общая схема исследования функции и построение графика
- 6. Функции нескольких переменных
- 6.1. Точечные множества. Функции. Предел и непрерывность
- 6.2. Дифференцирование функций нескольких переменных
- 6.3. Производная по направлению. Геометрические приложения
- 6.4. Экстремумы функций нескольких переменных
- 7. Неопределенный интеграл
- 7.1. Первообразная. Неопределенный интеграл и его свойства
- 7.2. Таблица основных интегралов. Примеры интегрирования
- 7.3. Интегрирование по частям. Метод замены переменной
- 7.4. Интегрирование рациональных функций
- 7.5. Интегрирование иррациональных функций
- 7.6. Интегрирование показательных и тригонометрических функций
- 8. Определенный интеграл
- 8.1. Основные определения. Геометрический смысл определенного интеграла
- 8.2. Свойства определенного интеграла
- 8.3. Геометрические и физические приложения определенного интеграла
- 8.4. Несобственные интегралы
- 9. Двойные и тройные интегралы
- 9.1. Определение и свойства двойного интеграла
- 9.2. Вычисление двойного интеграла
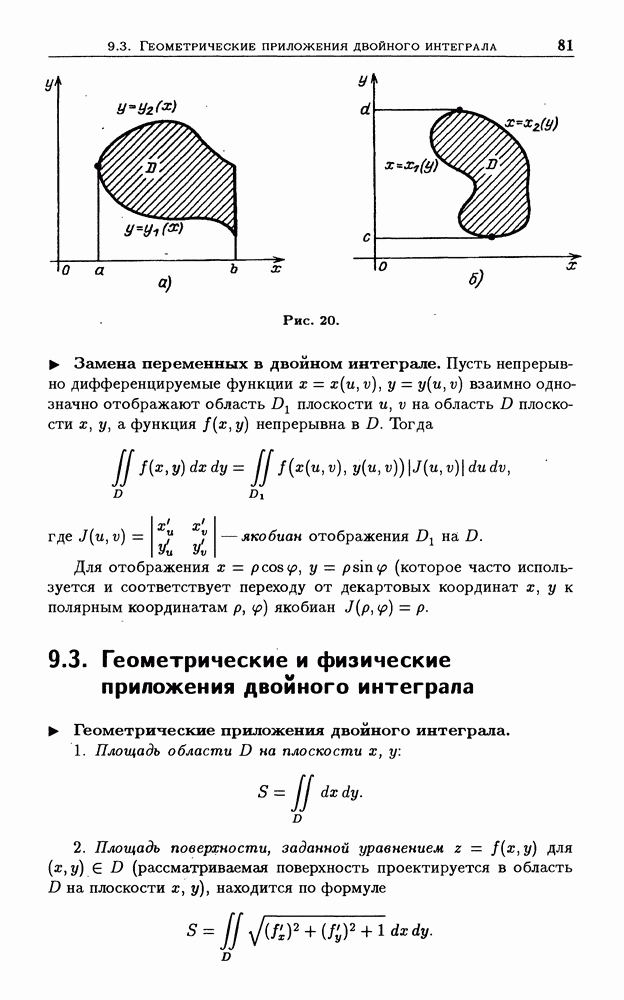
- 9.3. Геометрические и физические приложения двойного интеграла
- 9.4. Определение и свойства тройного интеграла
- 9.5. Вычисление тройного интеграла. Некоторые приложения
- 10. Криволинейные и поверхностные интегралы
- 10.2. Криволинейный интеграл второго рода
- 10.3. Поверхностный интеграл первого рода
- 10.4. Поверхностный интеграл второго рода
- 10.5. Дифференциальные операции и интегральные формулы теории поля
- 11. Ряды
- 11.1. Числовые ряды
- 11.2. Функциональные ряды
- 11.3. Степенные ряды
- 11.4. Ряд Фурье
- 11.5. Интеграл Фурье. Преобразование Фурье
- 12. Обыкновенные дифференциальные уравнения
- 12.2. Дифференциальные уравнения высших порядков
- 12.3. Линейные уравнения n-го порядка
- 12.4. Решение линейных однородных уравнений n-го порядка с постоянными коэффициентами
- 12.5. Линейные неоднородные уравнения n-го порядка
- 12.6. Системы обыкновенных дифференциальных уравнений
- 13. Приближенные вычисления
- 13.1. Метод наименьших квадратов
- 13.2. Приближенное решение алгебраических уравнений
- 13.3. Вычисление определенного интеграла
- 13.4. Численное интегрирование дифференциальных уравнений
- 14. Теория вероятностей
- 14.1. Правила и формулы комбинаторики
- 14.2. Основные понятия теории вероятностей
- 14.3. Условная вероятность. Теоремы и формулы теории вероятностей
- 14.4. Математическое ожидание и дисперсия
- 14.5. Закон больших чисел
- 1. Физические основы механики
- 1.1. Кинематика точки
- 1.2. Кинематика твердого тела
- 1.3. Динамика
- 1.4. Закон сохранения импульса
- 1.5. Закон сохранения энергии
- 1.6. Закон сохранения момента импульса
- 1.7. Задана двух тел и движение в центральном поле
- 1.8. Поле тяготения
- 1.9. Неинерциальные системы отсчета
- 1.10. Динамика твердого тела
- 1.11. Специальная теория относительности
- 2. Молекулярная физика и термодинамика
- 2.2. Первое начало термодинамики
- 2.3. Второе начало термодинамики
- 2.4. Энтропия. Свободная энергия
- 2.5. Кинетическая теория идеального газа
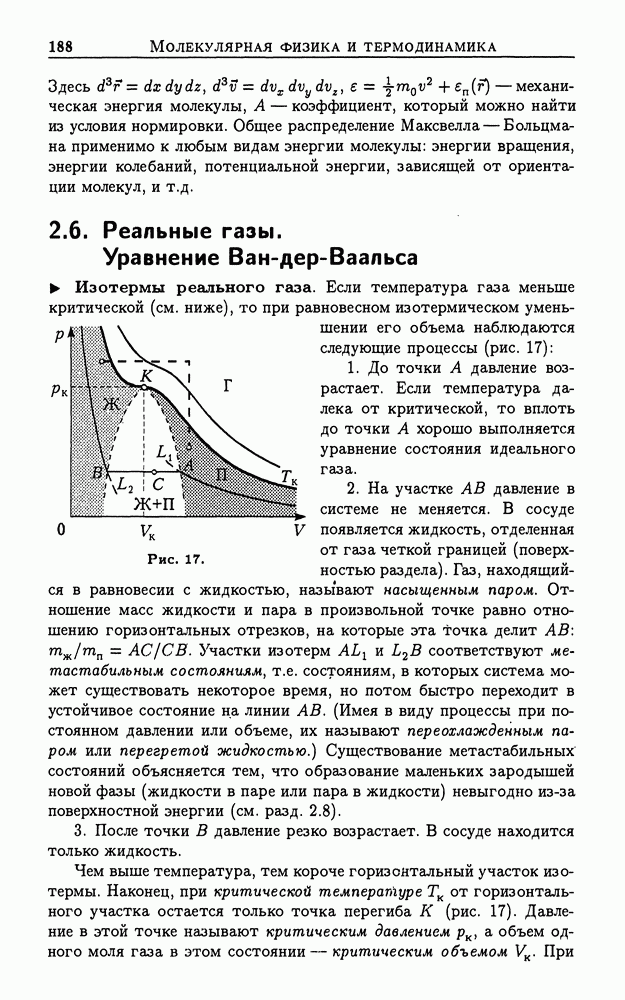
- 2.6. Реальные газы. Уравнение Ван-дер-Ваальса
- 2.7. Равновесие фаз. Фазовые переходы
- 2.8. Поверхностное натяжение
- 2.9. Явления переноса в газах
- 3. Электродинамика
- 3.1. Электрический заряд. Закон Кулона
- 3.2. Электрическое поле. Напряженность поля
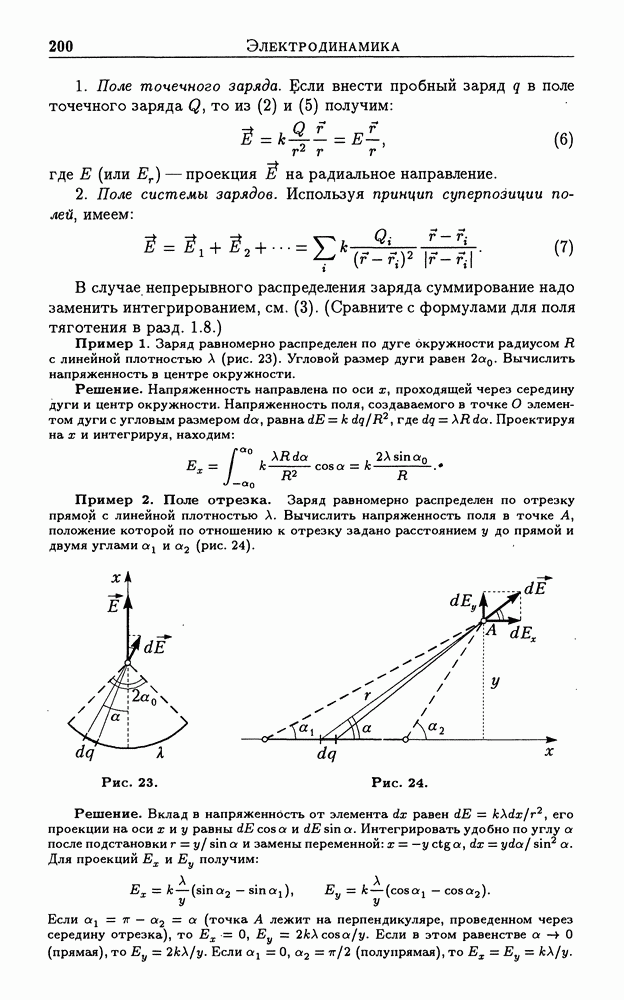
- 3.3. Электростатическое поле. Принцип суперпозиции для напряженности и потенциала
- 3.4. Теорема Гаусса
- 3.5. Электростатика проводников
- 3.6. Электростатика диэлектриков
- 3.7. Конденсаторы
- 3.8. Энергия электростатического поля
- 3.9. Постоянный ток
- 3.10. Магнитное поле. Сила Лоренца и закон Ампера
- 3.11. Вычисление магнитной индукции
- 3.12. Циркуляция и поток вектора магнитной индукции
- 3.13. Магнитное поле в веществе
- 3.14. Электромагнитная индукция
- 3.15. Уравнения Максвелла
- 4. Колебания и волны
- 4.1. Гармонические колебания. Сложение колебаний
- 4.2. Свободные незатухающие колебания
- 4.3. Затухающие и вынужденные колебания
- 4.4. Упругие волны
- 4.5. Электромагнитные волны
- 5. Оптика
- 5.1. Геометрическая оптика. Фотометрия
- 5.2. Интерференция света
- 5.3. Дифракция
- 5.4. Поляризация света. Формулы Френеля
- 5.5. Дисперсия и поглощение света
- 5.6. Тепловое излучение
- 5.7. Световые кванты
- Список литературы
- 1. Кинематика
- 1.1. Кинематика точки
- 1.2. Кинематика твердого тела
- 1.3. Плоскопараллельное движение твердого тела
- 1.4. Произвольное движение твердого тела
- 1.5. Сложное движение точки
- 2. Основные понятия и аксиомы механики
- 2.2. Аксиомы механики
- 3. Статика
- 3.2. Условия уравновешенности систем сил, приложенных к твердому телу
- 3.3. Решение задан статики
- 3.4. Центр параллельных сил. Центр тяжести твердого тела
- 3.5. Распределенные силы
- 3.6. Законы трения (законы Кулона)
- 4. Динамика материальной точки
- 4.2. Первая и вторая задачи динамики
- 5. Общие теоремы динамики механической системы
- 5.2. Теорема о движении центра масс
- 5.3. Теорема об изменении количества движения
- 5.4. Теорема об изменении кинетического момента
- 5.5. Теорема об изменении кинетической энергии
- 6. Принцип Даламбера. Элементы аналитической механики
- 6.2. Классификация механических связей. Обобщенные координаты
- 6.3. Принцип возможных перемещений
- 6.4. Общее уравнение динамики (принцип Даламбера — Лагранжа)
- 6.5. Уравнения Лагранжа второго рода
- 1. Основные понятия
- 1.1. Введение. Внешние и внутренние силы
- 1.2. Напряжения и деформации в точке
- 1.3. Основные понятия и допущения
- 2. Напряженно-деформированное состояние в точке
- 2.2. Одноосное растяжение и сжатие
- 2.3. Чистый сдвиг
- 3. Центральное растяжение и сжатие
- 3.2. Напряжения и деформации при растяжении или сжатии
- 3.3. Расчеты на прочность при растяжении и сжатии
- 4. Кручение
- 4.2. Напряжения и деформации при кручении
- 4.3. Расчеты на прочность при кручении
- 5. Прямой изгиб
- 5.2. Напряжения и деформации при прямом чистом изгибе
- 5.3. Напряжения и деформации при прямом поперечном изгибе
- 5.4. Расчет на прочность при прямом изгибе
- 6. Сложное сопротивление
- 6.2. Внецентренное растяжение или сжатие
- 6.3. Изгиб с кручением
- 7. Устойчивость сжатых стержней
- 7.2. Формула Эйлера
- 7.3. Влияние способов закрепления концов стержня на величину критической силы
- 7.4. Пределы применимости формулы Эйлера
- 7.5. Расчеты сжатых стержней на устойчивость
- ПРИЛОЖЕНИЯ
- 1. Элементарные функции и их свойства
- 2. Таблица неопределенных интегралов
- 3. Решения обыкновенных дифференциальных уравнений
- 4. Ортогональные криволинейные системы координат
- 5. Некоторые физические постоянные