| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
2.9. Явления переноса в газах
Средняя длина свободного пробега. Среднее число столкновений в единицу времени выделенной молекулы с другими молекулами газа:

где  — концентрация молекул,
— концентрация молекул,  — средняя скорость движения молекул, а с — эффективное сечение для упругих соударений молекул. В модели твердых шариков
— средняя скорость движения молекул, а с — эффективное сечение для упругих соударений молекул. В модели твердых шариков  где
где  — диаметр шарика. Множитель
— диаметр шарика. Множитель  учитывает движение встречных молекул; в качественной теории явлений переноса его обычно опускают.
учитывает движение встречных молекул; в качественной теории явлений переноса его обычно опускают.
Для определения числа столкновений траекторию молекулы, имеющую вид ломаной линии, окружают цилиндрической поверхностью радиуса  Движущаяся молекула столкнется с любой неподвижной молекулой, центр которой окажется внутри этого цилиндра. За единицу времени молекула проходит расстояние
Движущаяся молекула столкнется с любой неподвижной молекулой, центр которой окажется внутри этого цилиндра. За единицу времени молекула проходит расстояние  объем цилиндра равен
объем цилиндра равен  число попавших в него молекул равно
число попавших в него молекул равно 
Полное число соударений между молекулами в единице объема в единицу времени равно:

Средняя длина свободного пробега молекулы равна

Эффективное сечение некоторого процесса взаимодействия между сталкивающимися частицами (по отношению к выделенному результату этого взаимодействия) определяют следующим образом. Рассмотрим неподвижную молекулу (мишень) и налетающий на нее пучок молекул интенсивности  (интенсивностъ
(интенсивностъ
пучка — число частиц, проходящих через единичную площадку, перпендикулярную скорости молекул). Эффективным сечением процесса называют отношение числа столкновений в единицу времени, приведших к выделенному результату, к интенсивности пучка:

Ослабление пучка молекул, распространяющихся в газе, на пути  равно
равно

где а — сечение упругого рассеяния молекул,  — число рассеивающих центров на пути
— число рассеивающих центров на пути  (на единицу площади),
(на единицу площади),  Интегрируя, получим зависимость интенсивности пучка от пройденного им расстояния:
Интегрируя, получим зависимость интенсивности пучка от пройденного им расстояния:

т.е. вероятность того, что молекула испытает соударение на интервале  равна
равна  Среднее расстояние, пройденное молекулой до столкновения, равно
Среднее расстояние, пройденное молекулой до столкновения, равно

Качественная модель явлений переноса в газах. Явления вязкости, теплопроводности и диффузии объясняются переносом импульса, энергии, концентрации за счет хаотического теплового движения. Вязкостью называют возникновение силы трения между параллельно движущимися слоями, если скорости слоев различны.
Если скорость направленного движения и параллельна оси х и меняется только в направлении оси у (рис. 22), то между слоями жидкости возникает сила, пропорциональная площади и градиенту скорости и:

где  — коэффициент вязкости (или просто вязкость). Возникновение силы объясняется переносом вдоль оси у импульса
— коэффициент вязкости (или просто вязкость). Возникновение силы объясняется переносом вдоль оси у импульса  молекулами, пересекающими площадку за счет теплового движения.
молекулами, пересекающими площадку за счет теплового движения.
Если в направлении у меняется не скорость направленного движения молекул, а температура газа, то поток теплоты в направлении оси у равен

где  — коэффициент теплопроводности (или просто теплопроводность).
— коэффициент теплопроводности (или просто теплопроводность).

Рис. 22.
Если вдоль оси у меняется концентрация меченых молекул газа  (полная концентрация
(полная концентрация  должна быть постоянной), то поток меченых
должна быть постоянной), то поток меченых
молекул в направлении оси у (самодиффузия) определяется законом Фика:

где  — коэффициент диффузии.
— коэффициент диффузии.
Обозначим за  величину, поток которой вдоль оси у нас интересует. В случае вязкости это — импульс направленного движения молекул:
величину, поток которой вдоль оси у нас интересует. В случае вязкости это — импульс направленного движения молекул:  в случае теплопроводности — средняя энергия теплового движения:
в случае теплопроводности — средняя энергия теплового движения:  — удельная теплоемкость), в случае диффузии:
— удельная теплоемкость), в случае диффузии:  Будем считать, что каждая молекула газа переносит через площадку то значение параметра
Будем считать, что каждая молекула газа переносит через площадку то значение параметра  которое имеют (в среднем) молекулы газа в том месте, где произошло ее последнее соударение. Тогда для потока величины
которое имеют (в среднем) молекулы газа в том месте, где произошло ее последнее соударение. Тогда для потока величины  в направлении оси у можно получить выражение
в направлении оси у можно получить выражение

Для качественной оценки можно считать, что после соударения молекула летит в одном из шести направлений, задаваемых осями координат. С расстояния у прилетят молекулы, испытавшие соударение в цилиндре объемом  полетевшие в направлении —у и не испытавшие более соударений на пути у. С учетом (54), (55), (57) получим
полетевшие в направлении —у и не испытавшие более соударений на пути у. С учетом (54), (55), (57) получим  Интегрируя по у, получим вклад молекул, летящих со стороны положительных у. Вычитая вклад противоположно летящих молекул, приходим к формуле (61).
Интегрируя по у, получим вклад молекул, летящих со стороны положительных у. Вычитая вклад противоположно летящих молекул, приходим к формуле (61).
Формулы для коэффициентов переноса.
1. Подставляя  в формулу (61), получим поток импульса, который равен силе трения (58) для единичной площади. Для вязкости имеем:
в формулу (61), получим поток импульса, который равен силе трения (58) для единичной площади. Для вязкости имеем:

2. Подставляя  в формулу (61) и сравнивая с (59), находим коэффициент теплопроводности:
в формулу (61) и сравнивая с (59), находим коэффициент теплопроводности:

3. Подставляя  в формулу (61) и сравнивая с (60), получим выражение для коэффициента диффузии:
в формулу (61) и сравнивая с (60), получим выражение для коэффициента диффузии:

Из формул (62) — (64) следуют два важных факта:
1) Длина свободного пробега обратно пропорциональна  что видно из уравнения (55); поэтому вязкость и теплопроводность газов не зависят от давления (закон Максвелла). Этот вывод остается верным до тех пор, пока длина свободного пробега мала по сравнению с размерами сосуда.
что видно из уравнения (55); поэтому вязкость и теплопроводность газов не зависят от давления (закон Максвелла). Этот вывод остается верным до тех пор, пока длина свободного пробега мала по сравнению с размерами сосуда.
2) Отношение вязкости и теплопроводности не зависит от температуры.
Если длина пробега становится сравнимой с размерами сосуда (разреженный газ), то вязкость и теплопроводность начинают зависеть от плотности. Например, при вычислении потока теплоты между стенками, расположенными на расстоянии  (ультраразре-женный газ), можно считать, что после удара о стенку, имеющую температуру
(ультраразре-женный газ), можно считать, что после удара о стенку, имеющую температуру  каждая молекула приобретает (в среднем) энергию
каждая молекула приобретает (в среднем) энергию  летит без соударений к противоположной стенке и отдает ей энергию
летит без соударений к противоположной стенке и отдает ей энергию  Из формулы (35) следует, что число попадающих на стенку молекул равно
Из формулы (35) следует, что число попадающих на стенку молекул равно  Отсюда получим:
Отсюда получим: 
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- 1. Аналитическая геометрия на плоскости
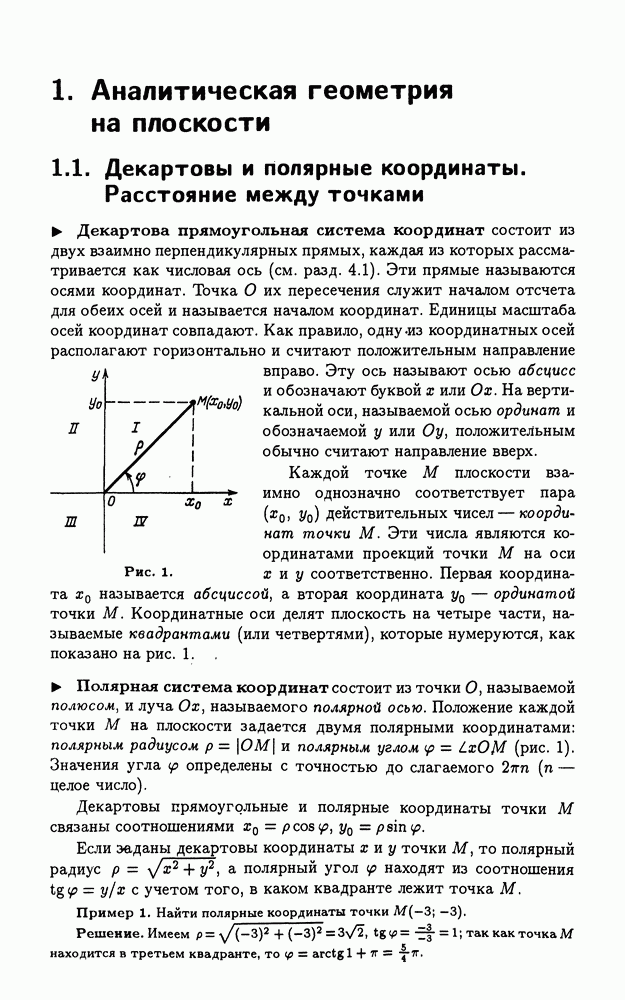
- 1.1. Декартовы и полярные координаты. Расстояние между точками
- 1.2. Деление отрезка в данном отношении. Площадь многоугольника
- 1.3. Различные виды уравнения прямой
- 1.4. Угол между прямыми. Расстояние от точки до прямой
- 1.5. Окружность, эллипс, гипербола и парабола
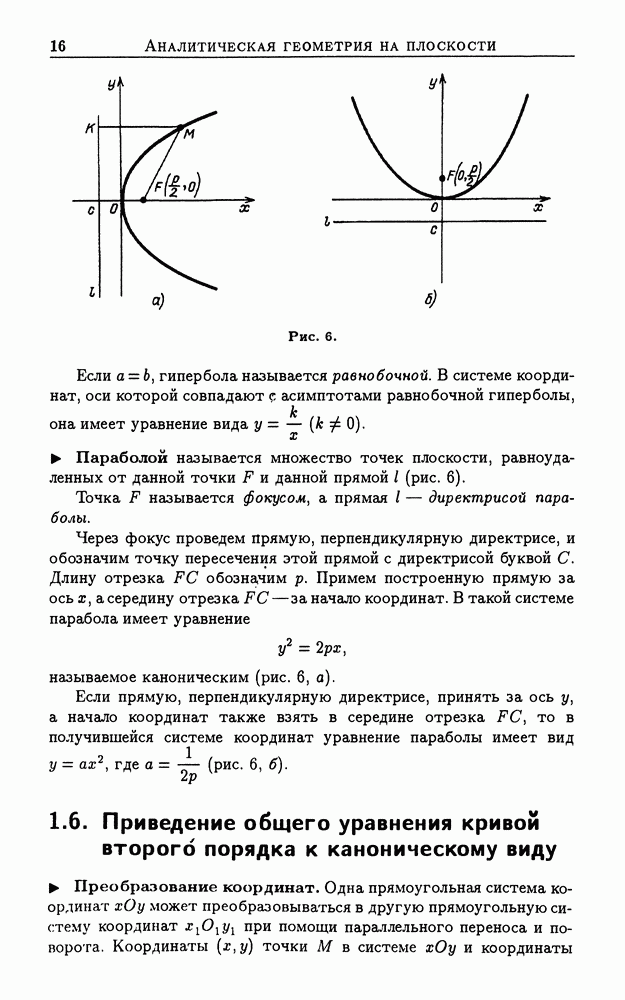
- 1.6. Приведение общего уравнения кривой второго порядка к каноническому виду
- 2. Аналитическая геометрия в пространстве
- 2.2. Векторы
- 2.3. Действия над векторами. Скалярное произведение
- 2.4. Векторное и смешанное произведения
- 2.5. Плоскость в пространстве
- 2.6. Прямая в пространстве
- 2.7. Прямая и плоскость в пространстве
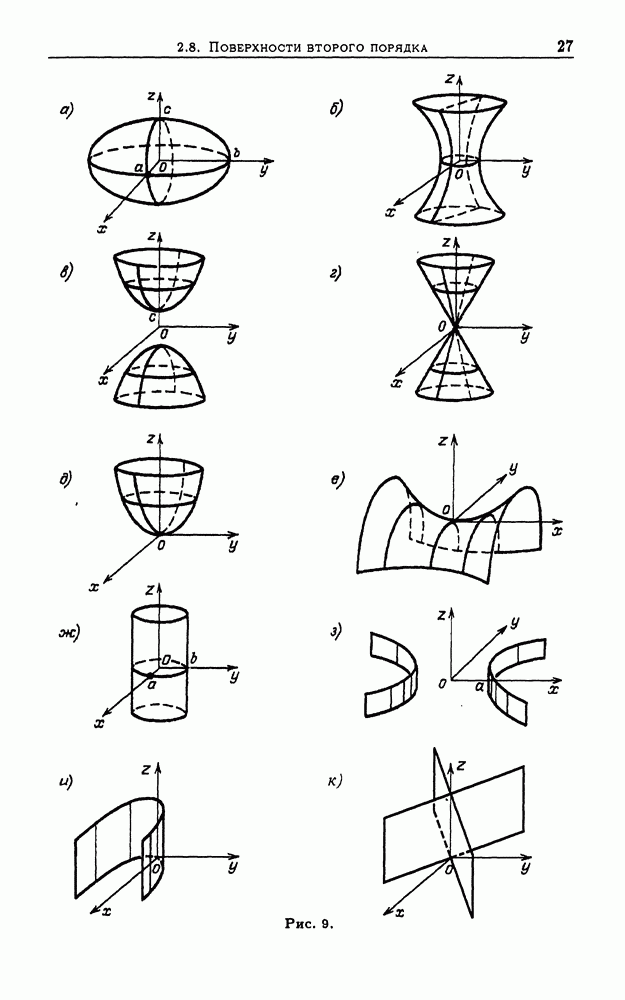
- 2.8. Поверхности второго порядка
- 3. Линейная алгебра
- 3.2. Матрицы
- 3.3. Системы линейных уравнений
- 3.4. Системы n-мерных векторов. Собственные значения и собственные векторы матрицы
- 4. Основные понятия математического анализа
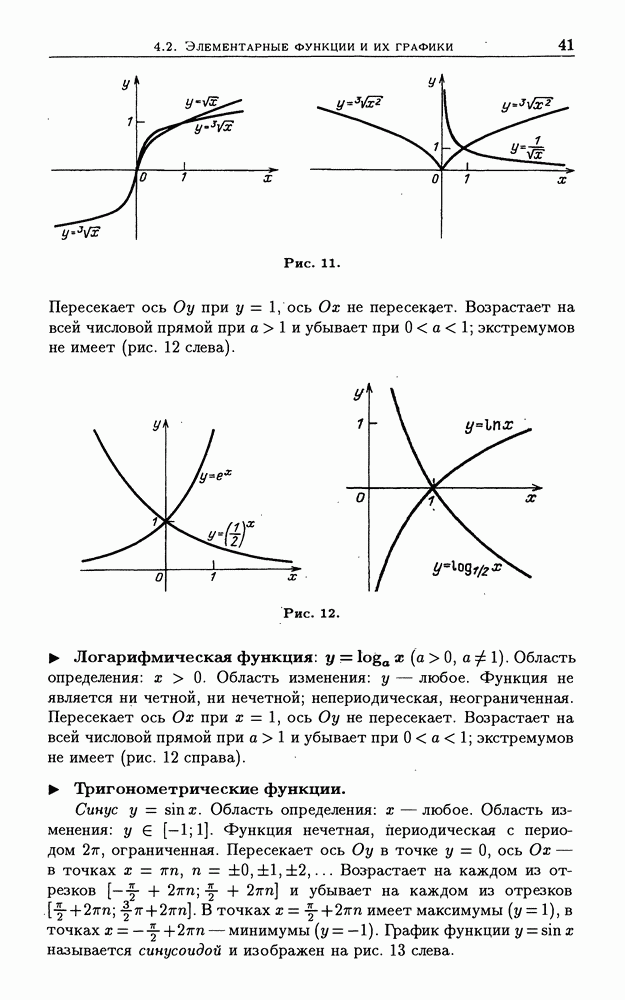
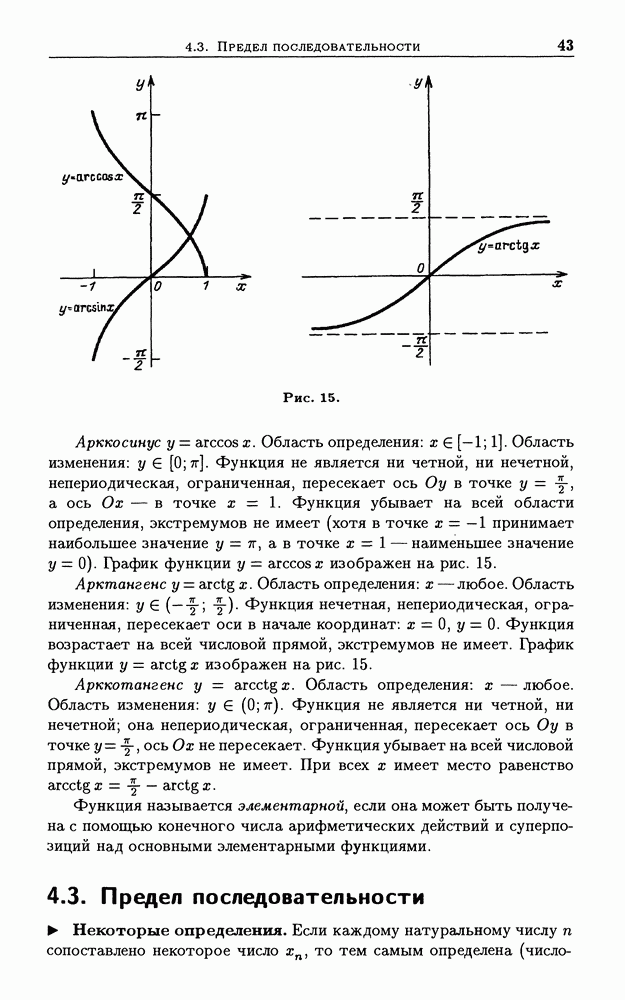
- 4.2. Элементарные функции и их графики
- 4.3. Предел последовательности
- 4.4. Предел функции
- 4.5. Бесконечно малые и бесконечно большие функции
- 4.6. Непрерывность
- 4.7. Асимптоты графика функции
- 5. Дифференциальное исчисление функций одной переменной
- 5.2. Таблица производных и правила дифференцирования
- 5.3. Теоремы о дифференцируемых функциях. Правило Лопиталя
- 5.4. Производные и дифференциалы высших порядков. Формула Тейлора
- 5.5. Экстремумы. Точки перегиба
- 5.6. Общая схема исследования функции и построение графика
- 6. Функции нескольких переменных
- 6.1. Точечные множества. Функции. Предел и непрерывность
- 6.2. Дифференцирование функций нескольких переменных
- 6.3. Производная по направлению. Геометрические приложения
- 6.4. Экстремумы функций нескольких переменных
- 7. Неопределенный интеграл
- 7.1. Первообразная. Неопределенный интеграл и его свойства
- 7.2. Таблица основных интегралов. Примеры интегрирования
- 7.3. Интегрирование по частям. Метод замены переменной
- 7.4. Интегрирование рациональных функций
- 7.5. Интегрирование иррациональных функций
- 7.6. Интегрирование показательных и тригонометрических функций
- 8. Определенный интеграл
- 8.1. Основные определения. Геометрический смысл определенного интеграла
- 8.2. Свойства определенного интеграла
- 8.3. Геометрические и физические приложения определенного интеграла
- 8.4. Несобственные интегралы
- 9. Двойные и тройные интегралы
- 9.1. Определение и свойства двойного интеграла
- 9.2. Вычисление двойного интеграла
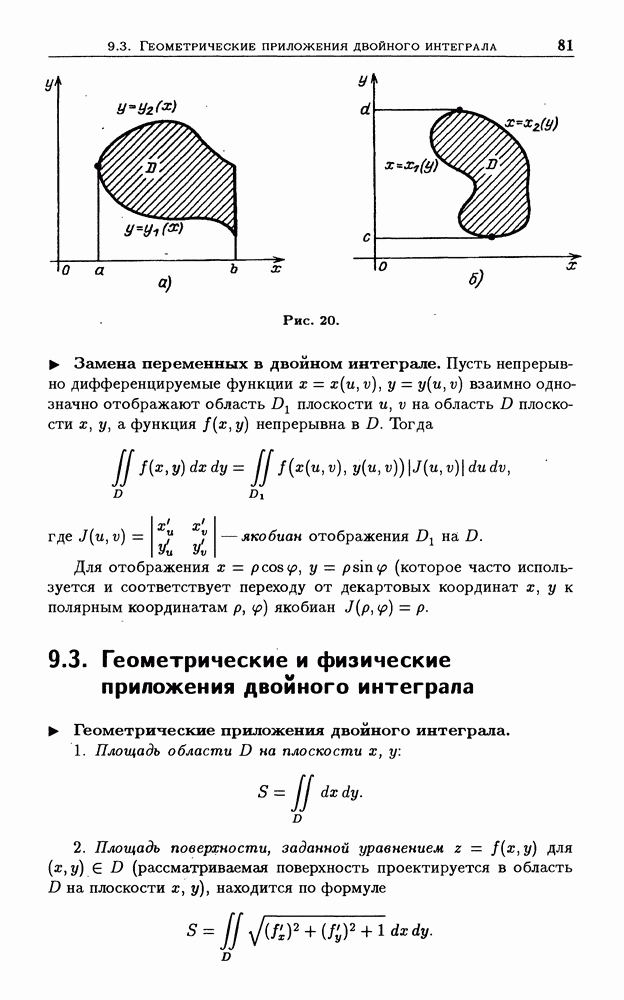
- 9.3. Геометрические и физические приложения двойного интеграла
- 9.4. Определение и свойства тройного интеграла
- 9.5. Вычисление тройного интеграла. Некоторые приложения
- 10. Криволинейные и поверхностные интегралы
- 10.2. Криволинейный интеграл второго рода
- 10.3. Поверхностный интеграл первого рода
- 10.4. Поверхностный интеграл второго рода
- 10.5. Дифференциальные операции и интегральные формулы теории поля
- 11. Ряды
- 11.1. Числовые ряды
- 11.2. Функциональные ряды
- 11.3. Степенные ряды
- 11.4. Ряд Фурье
- 11.5. Интеграл Фурье. Преобразование Фурье
- 12. Обыкновенные дифференциальные уравнения
- 12.2. Дифференциальные уравнения высших порядков
- 12.3. Линейные уравнения n-го порядка
- 12.4. Решение линейных однородных уравнений n-го порядка с постоянными коэффициентами
- 12.5. Линейные неоднородные уравнения n-го порядка
- 12.6. Системы обыкновенных дифференциальных уравнений
- 13. Приближенные вычисления
- 13.1. Метод наименьших квадратов
- 13.2. Приближенное решение алгебраических уравнений
- 13.3. Вычисление определенного интеграла
- 13.4. Численное интегрирование дифференциальных уравнений
- 14. Теория вероятностей
- 14.1. Правила и формулы комбинаторики
- 14.2. Основные понятия теории вероятностей
- 14.3. Условная вероятность. Теоремы и формулы теории вероятностей
- 14.4. Математическое ожидание и дисперсия
- 14.5. Закон больших чисел
- 1. Физические основы механики
- 1.1. Кинематика точки
- 1.2. Кинематика твердого тела
- 1.3. Динамика
- 1.4. Закон сохранения импульса
- 1.5. Закон сохранения энергии
- 1.6. Закон сохранения момента импульса
- 1.7. Задана двух тел и движение в центральном поле
- 1.8. Поле тяготения
- 1.9. Неинерциальные системы отсчета
- 1.10. Динамика твердого тела
- 1.11. Специальная теория относительности
- 2. Молекулярная физика и термодинамика
- 2.2. Первое начало термодинамики
- 2.3. Второе начало термодинамики
- 2.4. Энтропия. Свободная энергия
- 2.5. Кинетическая теория идеального газа
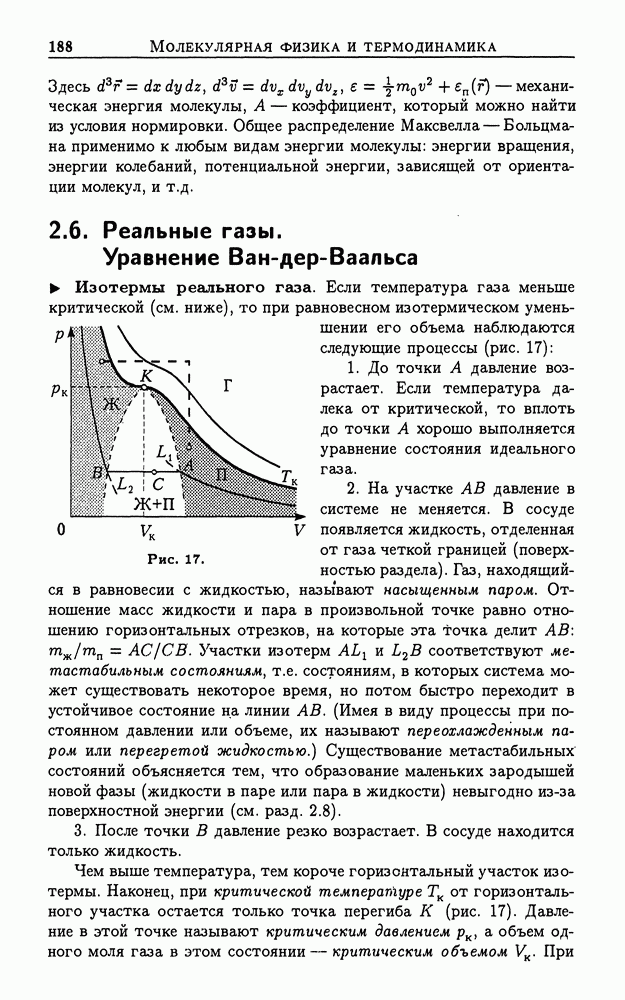
- 2.6. Реальные газы. Уравнение Ван-дер-Ваальса
- 2.7. Равновесие фаз. Фазовые переходы
- 2.8. Поверхностное натяжение
- 2.9. Явления переноса в газах
- 3. Электродинамика
- 3.1. Электрический заряд. Закон Кулона
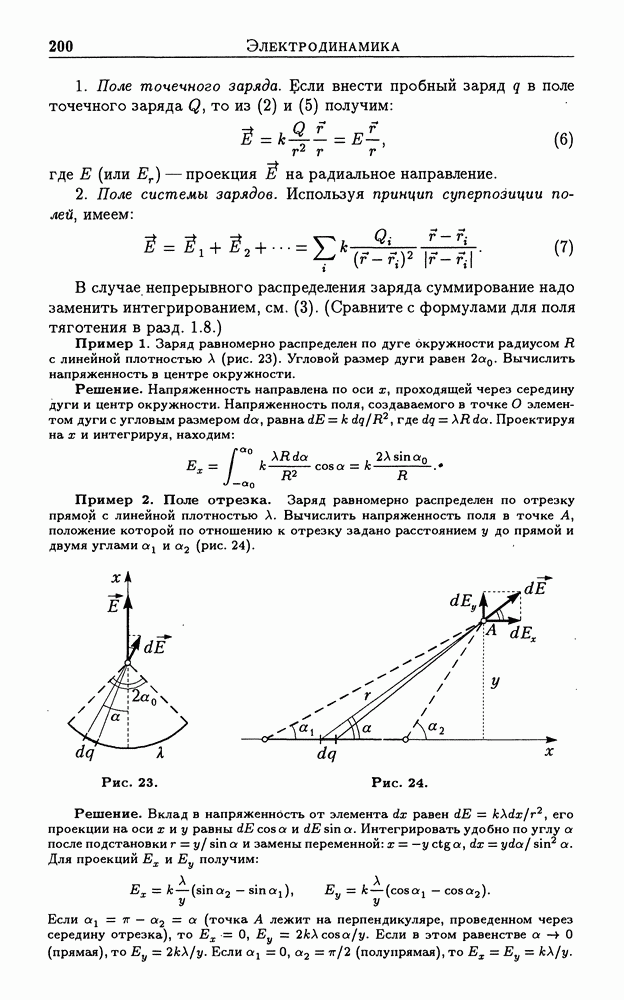
- 3.2. Электрическое поле. Напряженность поля
- 3.3. Электростатическое поле. Принцип суперпозиции для напряженности и потенциала
- 3.4. Теорема Гаусса
- 3.5. Электростатика проводников
- 3.6. Электростатика диэлектриков
- 3.7. Конденсаторы
- 3.8. Энергия электростатического поля
- 3.9. Постоянный ток
- 3.10. Магнитное поле. Сила Лоренца и закон Ампера
- 3.11. Вычисление магнитной индукции
- 3.12. Циркуляция и поток вектора магнитной индукции
- 3.13. Магнитное поле в веществе
- 3.14. Электромагнитная индукция
- 3.15. Уравнения Максвелла
- 4. Колебания и волны
- 4.1. Гармонические колебания. Сложение колебаний
- 4.2. Свободные незатухающие колебания
- 4.3. Затухающие и вынужденные колебания
- 4.4. Упругие волны
- 4.5. Электромагнитные волны
- 5. Оптика
- 5.1. Геометрическая оптика. Фотометрия
- 5.2. Интерференция света
- 5.3. Дифракция
- 5.4. Поляризация света. Формулы Френеля
- 5.5. Дисперсия и поглощение света
- 5.6. Тепловое излучение
- 5.7. Световые кванты
- Список литературы
- 1. Кинематика
- 1.1. Кинематика точки
- 1.2. Кинематика твердого тела
- 1.3. Плоскопараллельное движение твердого тела
- 1.4. Произвольное движение твердого тела
- 1.5. Сложное движение точки
- 2. Основные понятия и аксиомы механики
- 2.2. Аксиомы механики
- 3. Статика
- 3.2. Условия уравновешенности систем сил, приложенных к твердому телу
- 3.3. Решение задан статики
- 3.4. Центр параллельных сил. Центр тяжести твердого тела
- 3.5. Распределенные силы
- 3.6. Законы трения (законы Кулона)
- 4. Динамика материальной точки
- 4.2. Первая и вторая задачи динамики
- 5. Общие теоремы динамики механической системы
- 5.2. Теорема о движении центра масс
- 5.3. Теорема об изменении количества движения
- 5.4. Теорема об изменении кинетического момента
- 5.5. Теорема об изменении кинетической энергии
- 6. Принцип Даламбера. Элементы аналитической механики
- 6.2. Классификация механических связей. Обобщенные координаты
- 6.3. Принцип возможных перемещений
- 6.4. Общее уравнение динамики (принцип Даламбера — Лагранжа)
- 6.5. Уравнения Лагранжа второго рода
- 1. Основные понятия
- 1.1. Введение. Внешние и внутренние силы
- 1.2. Напряжения и деформации в точке
- 1.3. Основные понятия и допущения
- 2. Напряженно-деформированное состояние в точке
- 2.2. Одноосное растяжение и сжатие
- 2.3. Чистый сдвиг
- 3. Центральное растяжение и сжатие
- 3.2. Напряжения и деформации при растяжении или сжатии
- 3.3. Расчеты на прочность при растяжении и сжатии
- 4. Кручение
- 4.2. Напряжения и деформации при кручении
- 4.3. Расчеты на прочность при кручении
- 5. Прямой изгиб
- 5.2. Напряжения и деформации при прямом чистом изгибе
- 5.3. Напряжения и деформации при прямом поперечном изгибе
- 5.4. Расчет на прочность при прямом изгибе
- 6. Сложное сопротивление
- 6.2. Внецентренное растяжение или сжатие
- 6.3. Изгиб с кручением
- 7. Устойчивость сжатых стержней
- 7.2. Формула Эйлера
- 7.3. Влияние способов закрепления концов стержня на величину критической силы
- 7.4. Пределы применимости формулы Эйлера
- 7.5. Расчеты сжатых стержней на устойчивость
- ПРИЛОЖЕНИЯ
- 1. Элементарные функции и их свойства
- 2. Таблица неопределенных интегралов
- 3. Решения обыкновенных дифференциальных уравнений
- 4. Ортогональные криволинейные системы координат
- 5. Некоторые физические постоянные