| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
5. Оптика
5.1. Геометрическая оптика. Фотометрия
Основные законы геометрической оптики. Оптика занимается изучением электромагнитного излучения оптического (светового) диапазона (см. разд. 4.5) явлений, возникающих при его распространении в пространстве и взаимодействии с веществом. Геометрическая оптика отвлекается от волнового характера и от поляризации светового излучения, оперируя понятиями световых лучей, указывающих направление распространения света, и узких световых пучков, образованных световыми лучами.
Основные законы геометрической оптики перечислены ниже.
1. Закон прямолинейного распространения света.  Закон независимости световых пучков. Энергия в каждом пучке распространяется независимо от других пучков; освещенность поверхности, на которую падает несколько пучков, равна сумме освещенностей, создаваемых каждым пучком в отдельности.
Закон независимости световых пучков. Энергия в каждом пучке распространяется независимо от других пучков; освещенность поверхности, на которую падает несколько пучков, равна сумме освещенностей, создаваемых каждым пучком в отдельности.
3. Закон отражения света. Отраженный луч лежит в плоскости падения, образуемой падающим лучом и нормалью к поверхности в точке падейия; угол падения равен углу отражения. Все углы отсчитываются от нормали.
4. Закон преломления света. Преломленный луч лежит в плоскости падения; отношение синуса угла падения к синусу угла преломления  зависит от длины волны, но не зависит от угла падения (закон Снеллиуса):
зависит от длины волны, но не зависит от угла падения (закон Снеллиуса):

Постоянная величина  называется относительным показателем преломления второй среды относительно первой, который равен отношению (абсолютных) показателей преломления каждой из сред (показателей преломления среды относительно вакуума). С точки зрения волновой оптики показатель преломления указывает, во сколько раз фазовая скорость световой волны данной частоты меньше, чем скорость этой волны в вакууме:
называется относительным показателем преломления второй среды относительно первой, который равен отношению (абсолютных) показателей преломления каждой из сред (показателей преломления среды относительно вакуума). С точки зрения волновой оптики показатель преломления указывает, во сколько раз фазовая скорость световой волны данной частоты меньше, чем скорость этой волны в вакууме:

(см. разд. 4.5). Если  то при
то при  , где
, где  апред
апред  наблюдается полное отражение света, т.е. отсутствует преломленный луч. При распространении луча света в среде с постепенно меняющимся вдоль некоторой оси показателем преломления (в слоистой среде) удобно использовать формулу (1) в виде
наблюдается полное отражение света, т.е. отсутствует преломленный луч. При распространении луча света в среде с постепенно меняющимся вдоль некоторой оси показателем преломления (в слоистой среде) удобно использовать формулу (1) в виде  где
где  угол с указанной осью. Видно, что а постепенно меняется, т.е. происходит искривление луча.
угол с указанной осью. Видно, что а постепенно меняется, т.е. происходит искривление луча.
К перечисленным законам геометрической оптики следует добавить принцип обратимости световых пучков.
Законы геометрической оптики действуют тогда, когда оказываются несущественными явления интерференции, дифракции и поляризации. Это происходит в тех случаях, когда амплитуда волны и ее первые пространственные производные мало меняются на длине волны. Эти условия нарушаются на границе тени, вблизи геометрической точки схождения лучей (фокуса), при прохождении света через узкие диафрагмы, при распространении света в средах с резко меняющимся показателем преломления или с большим поглощением. Например, при прохождении света через диафрагму с минимальным размером  пучок света расплывается за счет дифракции на расстоянии
пучок света расплывается за счет дифракции на расстоянии  на расстояниях, малых по сравнению с
на расстояниях, малых по сравнению с  можно пользоваться законами геометрической оптики.
можно пользоваться законами геометрической оптики.
С законами геометрической оптики тесно связаны принцип Гюйгенса (волновое построение Гюйгенса) и принцип Ферма. Принцип Гюйгенса опирается на абстрактно-волновые представления и позволяет построить в каждой точке вспомогательную волновую поверхность, нормаль к которой указывает направление луча света. Для построения волновой поверхности в момент времени  все точки волновой поверхности в момент времени
все точки волновой поверхности в момент времени  рассматриваются как источники вторичных световых волн. Огибающая сферических волновых поверхностей вторичных волн образует новую волновую поверхность основной волны.
рассматриваются как источники вторичных световых волн. Огибающая сферических волновых поверхностей вторичных волн образует новую волновую поверхность основной волны.
Принцип Ферма является одним из примеров вариационных принципов, играющих в физике большую роль. Он утверждает, что время распространения света по истинной траектории является экстремальным (обычно — минимальным или максимальным) по сравнению со всеми воображаемыми близлежащими траекториями. Более точно — это время не меняется (в первом порядке малости) при малом искажении траектории. Время прохождения света через среду с переменным (или кусочно-переменным) показателем преломления удобно выражать через оптическую длину пути 

Это понятие оказывается полезным и при изучении интерференции. Принципы Гюйгенса и Ферма позволяют получить основные законы геометрической оптики, но не позволяют выйти за ее пределы.
Одной из важных задач геометрической оптики является построение изображений, формируемых оптическими системами, и изучение их свойств. Изображением называется точка схождения лучей, прошедших оптическую систему. Система отражающих и преломляющих сферических (и плоских) поверхностей, перпендикулярных к
некоторой оси, формирует изображение точечного источника лучами, падающими под малым углом к оси (параксиальное приближение). Ось системы называют оптической осью; точку схождения параллельного оси пучка лучей — фокусом системы; перпендикулярную оси плоскость, проведенную в фокусе, — фокальной плоскостью. Теоретический предел размеров изображения и разрешающей способности оптических систем определяется дифракцией света. Важное для дальнейшего свойство изображений: оптические длины всех лучей от источника до изображения одинаковы, т.е. оптическая система не изменяет разности хода лучей.
Фотометрия. Излучение в данной точке пространства в данном направлении характеризуется интенсивностью лучистого потока I:

где  — лучистый поток (энергия, переносимая в единицу времени через площадку
— лучистый поток (энергия, переносимая в единицу времени через площадку  лучами, заключенными в телесном угле
лучами, заключенными в телесном угле  угол между выделенным направлением и нормалью к площадке. Произведение
угол между выделенным направлением и нормалью к площадке. Произведение  называется видимой величиной площадки в данном направлении. Объемная плотность лучистой энергии
называется видимой величиной площадки в данном направлении. Объемная плотность лучистой энергии  равна
равна

В случае изотропного излучения  Интенсивность 1 и плотность и можно подвергнуть спектральному разложению по частотам или длинам волн:
Интенсивность 1 и плотность и можно подвергнуть спектральному разложению по частотам или длинам волн:

Приравнивая энергию, заключенную в соответствующих друг другу спектральных интервалах, можно найти связь между различными спектральными представлениями. Например, приравняв  с учетом
с учетом  получим
получим

Аналогично можно произвести разложение по двум взаимно перпендикулярным поляризациям.
Определенные выше энергетические характеристики используют при объективном описании излучения. Фотометрические, или световые характеристики учитывают восприимчивость глаза к световому излучению. Лучистый поток измеряют в ваттах, а соответствующую ему фотометрическую единицу называют световым потоком и измеряют в люменах  Чтобы перейти к световому потоку, надо лучистый поток умножить на световую эффективность
Чтобы перейти к световому потоку, надо лучистый поток умножить на световую эффективность  (измеряется в
(измеряется в  которая для длины волны
которая для длины волны  нм равна
нм равна  а для Других длин волн равна
а для Других длин волн равна  где — кривая видности, или относительной
где — кривая видности, или относительной
спектральной чувствительности глаза  при
при  нм и падает до нуля при приближении к границам видимого диапазона). Для пересчета от произвольного лучистого потока к световому потоку можно использовать формулу
нм и падает до нуля при приближении к границам видимого диапазона). Для пересчета от произвольного лучистого потока к световому потоку можно использовать формулу  Аналогичным образом происходит пересчет от остальных энергетических характеристик к световым и наоборот (например, от интенсивности излучения к интенсивности света).
Аналогичным образом происходит пересчет от остальных энергетических характеристик к световым и наоборот (например, от интенсивности излучения к интенсивности света).
Для характеристики точечного источника используют энергетическую силу источника, определяемую как лучистый поток в данном направлении в расчете на единичный телесный угол:  Световая характеристика - сила света источника — определяется через световой поток. Единица силы света кандела является основной единицей
Световая характеристика - сила света источника — определяется через световой поток. Единица силы света кандела является основной единицей  — кандела
— кандела  где
где  — стерадиан). Если не происходит поглощения или рассеяния излучения, то на расстоянии
— стерадиан). Если не происходит поглощения или рассеяния излучения, то на расстоянии  от источника в том же направлении интенсивность излучения равна
от источника в том же направлении интенсивность излучения равна

Поток лучистой энергии, приходящийся на единицу площади освещаемой поверхности, называется энергетической освещенностью. Соответствующая световая величина называется просто освещенностью и измеряется в люксах  Если излучение точечного источника падает иод углом
Если излучение точечного источника падает иод углом  к нормали, то
к нормали, то

Для протяженных источников, т.е. для излучающей поверхности, вводят энергетическую яркость в данном направлении Вв (световая характеристика яркость). Энергетическая сила источника, соответствующего площадке  равна
равна

где  угол между нормалью к излучающей поверхности и направлением излучения. Источник, у которого
угол между нормалью к излучающей поверхности и направлением излучения. Источник, у которого  не зависит от направления. называется ламбертовским источником. Ламбертовский источник любой формы кажется равномерно ярким (например, диск Луны или Солнца). Энергетическая светимость
не зависит от направления. называется ламбертовским источником. Ламбертовский источник любой формы кажется равномерно ярким (например, диск Луны или Солнца). Энергетическая светимость  (световая характеристика — светимость) определяется как полный лучистый поток в гелем ном угле
(световая характеристика — светимость) определяется как полный лучистый поток в гелем ном угле  в расчете на единицу площади излучающей поверхности
в расчете на единицу площади излучающей поверхности

Для ламбертовского источника 

Рис. 62.

Рис. 63.
Пример. Освещенность, создаваемая светящейся поверхностью  на некотором участке освещаемой поверхности
на некотором участке освещаемой поверхности  равна сумме вкладов от всех участков
равна сумме вкладов от всех участков  Телесный угол, под которым
Телесный угол, под которым  видна от
видна от  равен
равен  (рис. 62). Для светового потока, посылаемого в этот телесный угол, имеем
(рис. 62). Для светового потока, посылаемого в этот телесный угол, имеем  Так как
Так как  равен телесному углу
равен телесному углу  под которым излучающий участок виден от точки освещения, то
под которым излучающий участок виден от точки освещения, то 
Например, при освещении ламбертовским диском маленькой площадки, расположенной на оси диска и ориентированной перпендикулярно оси (рис. 63),  и после интегрирования получим
и после интегрирования получим  где
где  — угол полураствора конуса, под которым диск виден от освещаемой площадки.
— угол полураствора конуса, под которым диск виден от освещаемой площадки.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- 1. Аналитическая геометрия на плоскости
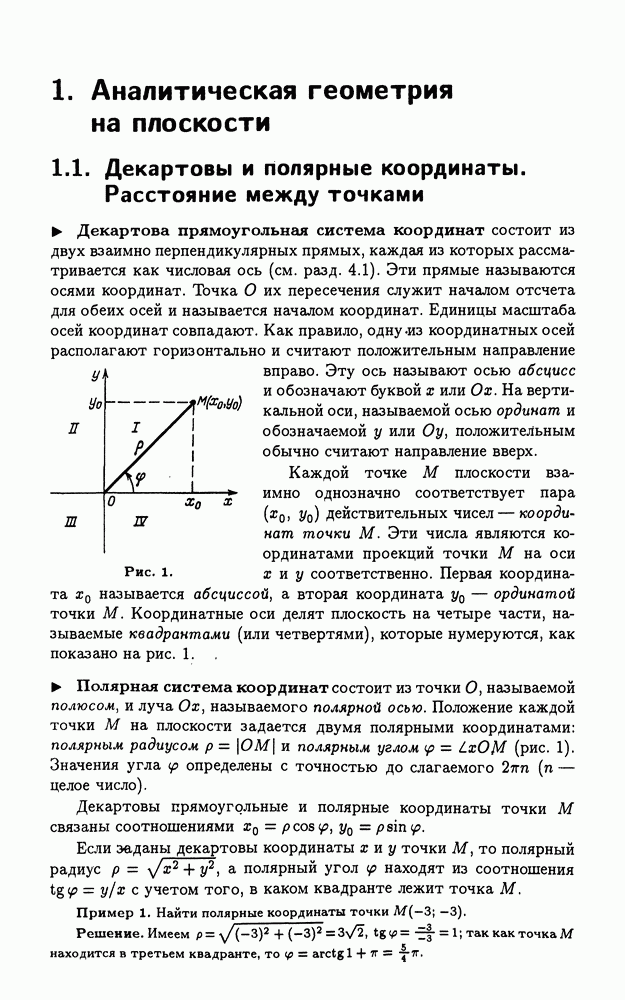
- 1.1. Декартовы и полярные координаты. Расстояние между точками
- 1.2. Деление отрезка в данном отношении. Площадь многоугольника
- 1.3. Различные виды уравнения прямой
- 1.4. Угол между прямыми. Расстояние от точки до прямой
- 1.5. Окружность, эллипс, гипербола и парабола
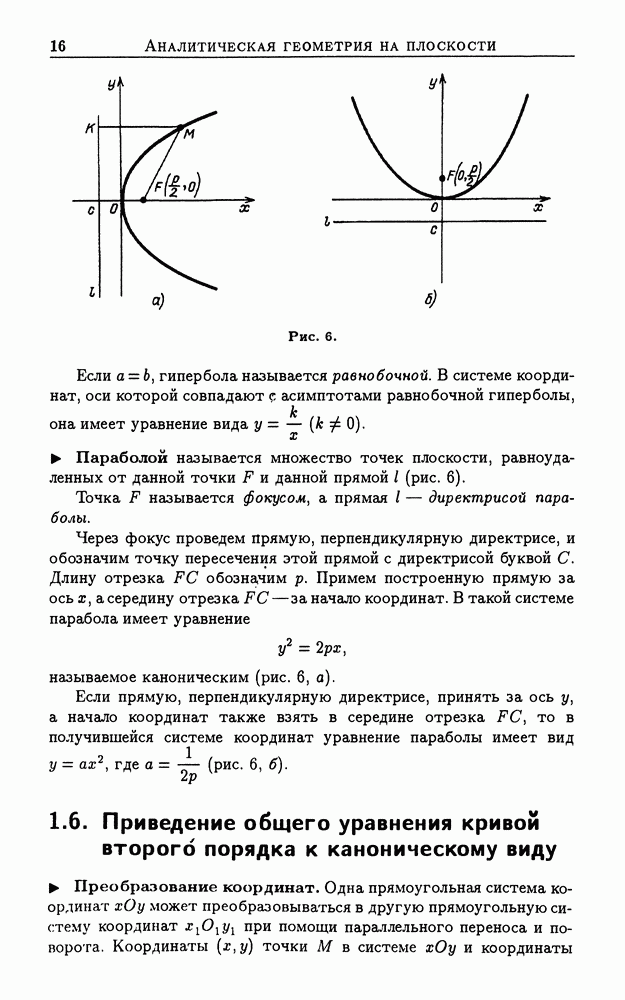
- 1.6. Приведение общего уравнения кривой второго порядка к каноническому виду
- 2. Аналитическая геометрия в пространстве
- 2.2. Векторы
- 2.3. Действия над векторами. Скалярное произведение
- 2.4. Векторное и смешанное произведения
- 2.5. Плоскость в пространстве
- 2.6. Прямая в пространстве
- 2.7. Прямая и плоскость в пространстве
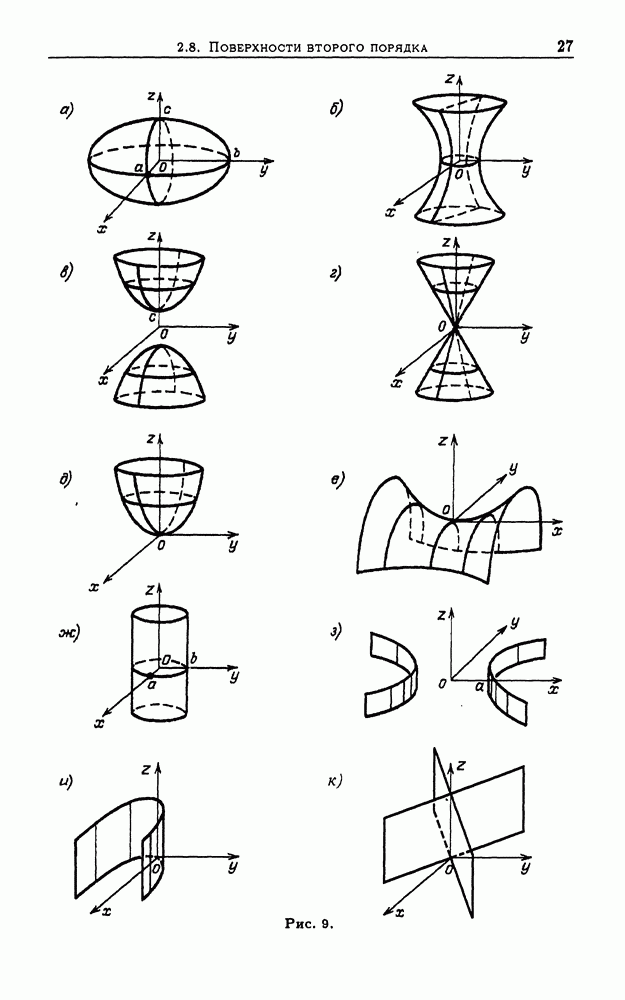
- 2.8. Поверхности второго порядка
- 3. Линейная алгебра
- 3.2. Матрицы
- 3.3. Системы линейных уравнений
- 3.4. Системы n-мерных векторов. Собственные значения и собственные векторы матрицы
- 4. Основные понятия математического анализа
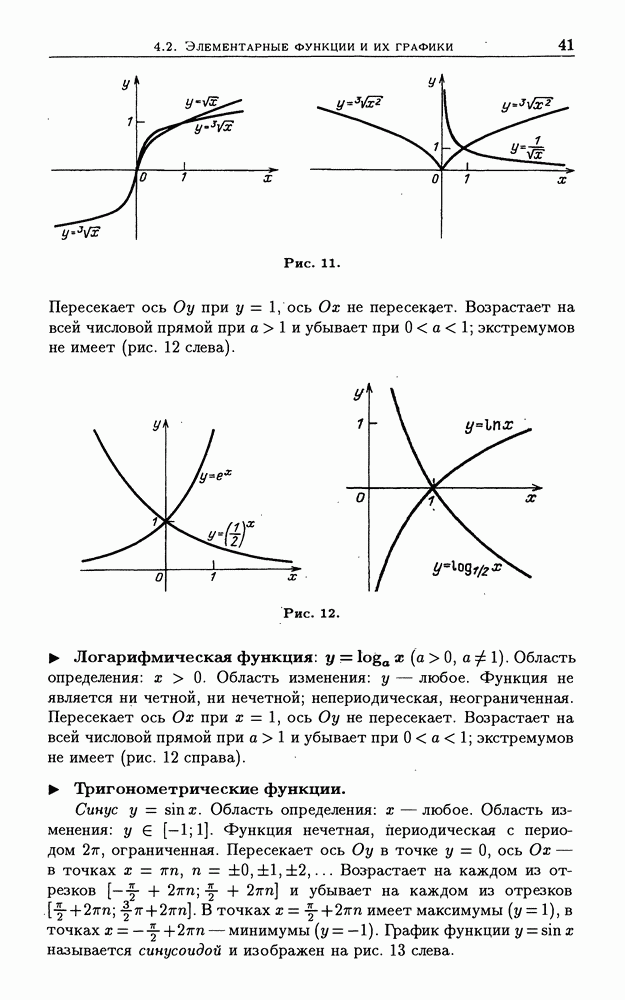
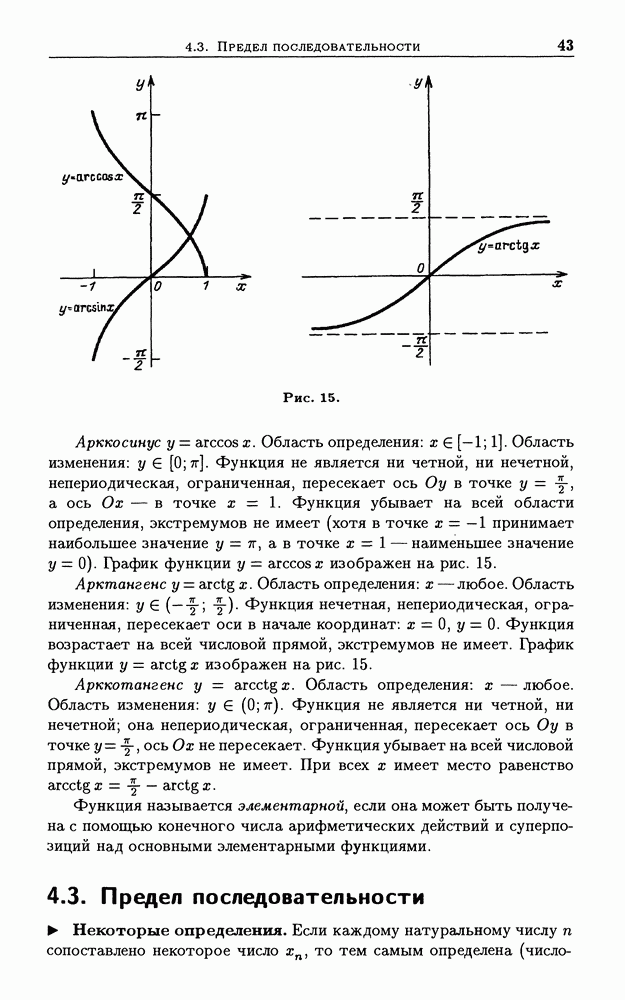
- 4.2. Элементарные функции и их графики
- 4.3. Предел последовательности
- 4.4. Предел функции
- 4.5. Бесконечно малые и бесконечно большие функции
- 4.6. Непрерывность
- 4.7. Асимптоты графика функции
- 5. Дифференциальное исчисление функций одной переменной
- 5.2. Таблица производных и правила дифференцирования
- 5.3. Теоремы о дифференцируемых функциях. Правило Лопиталя
- 5.4. Производные и дифференциалы высших порядков. Формула Тейлора
- 5.5. Экстремумы. Точки перегиба
- 5.6. Общая схема исследования функции и построение графика
- 6. Функции нескольких переменных
- 6.1. Точечные множества. Функции. Предел и непрерывность
- 6.2. Дифференцирование функций нескольких переменных
- 6.3. Производная по направлению. Геометрические приложения
- 6.4. Экстремумы функций нескольких переменных
- 7. Неопределенный интеграл
- 7.1. Первообразная. Неопределенный интеграл и его свойства
- 7.2. Таблица основных интегралов. Примеры интегрирования
- 7.3. Интегрирование по частям. Метод замены переменной
- 7.4. Интегрирование рациональных функций
- 7.5. Интегрирование иррациональных функций
- 7.6. Интегрирование показательных и тригонометрических функций
- 8. Определенный интеграл
- 8.1. Основные определения. Геометрический смысл определенного интеграла
- 8.2. Свойства определенного интеграла
- 8.3. Геометрические и физические приложения определенного интеграла
- 8.4. Несобственные интегралы
- 9. Двойные и тройные интегралы
- 9.1. Определение и свойства двойного интеграла
- 9.2. Вычисление двойного интеграла
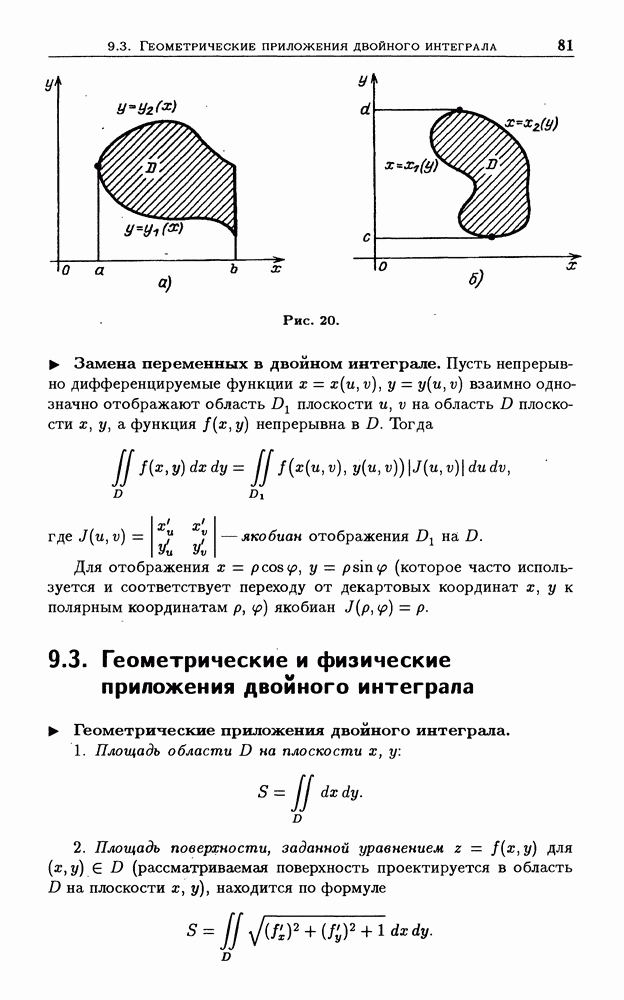
- 9.3. Геометрические и физические приложения двойного интеграла
- 9.4. Определение и свойства тройного интеграла
- 9.5. Вычисление тройного интеграла. Некоторые приложения
- 10. Криволинейные и поверхностные интегралы
- 10.2. Криволинейный интеграл второго рода
- 10.3. Поверхностный интеграл первого рода
- 10.4. Поверхностный интеграл второго рода
- 10.5. Дифференциальные операции и интегральные формулы теории поля
- 11. Ряды
- 11.1. Числовые ряды
- 11.2. Функциональные ряды
- 11.3. Степенные ряды
- 11.4. Ряд Фурье
- 11.5. Интеграл Фурье. Преобразование Фурье
- 12. Обыкновенные дифференциальные уравнения
- 12.2. Дифференциальные уравнения высших порядков
- 12.3. Линейные уравнения n-го порядка
- 12.4. Решение линейных однородных уравнений n-го порядка с постоянными коэффициентами
- 12.5. Линейные неоднородные уравнения n-го порядка
- 12.6. Системы обыкновенных дифференциальных уравнений
- 13. Приближенные вычисления
- 13.1. Метод наименьших квадратов
- 13.2. Приближенное решение алгебраических уравнений
- 13.3. Вычисление определенного интеграла
- 13.4. Численное интегрирование дифференциальных уравнений
- 14. Теория вероятностей
- 14.1. Правила и формулы комбинаторики
- 14.2. Основные понятия теории вероятностей
- 14.3. Условная вероятность. Теоремы и формулы теории вероятностей
- 14.4. Математическое ожидание и дисперсия
- 14.5. Закон больших чисел
- 1. Физические основы механики
- 1.1. Кинематика точки
- 1.2. Кинематика твердого тела
- 1.3. Динамика
- 1.4. Закон сохранения импульса
- 1.5. Закон сохранения энергии
- 1.6. Закон сохранения момента импульса
- 1.7. Задана двух тел и движение в центральном поле
- 1.8. Поле тяготения
- 1.9. Неинерциальные системы отсчета
- 1.10. Динамика твердого тела
- 1.11. Специальная теория относительности
- 2. Молекулярная физика и термодинамика
- 2.2. Первое начало термодинамики
- 2.3. Второе начало термодинамики
- 2.4. Энтропия. Свободная энергия
- 2.5. Кинетическая теория идеального газа
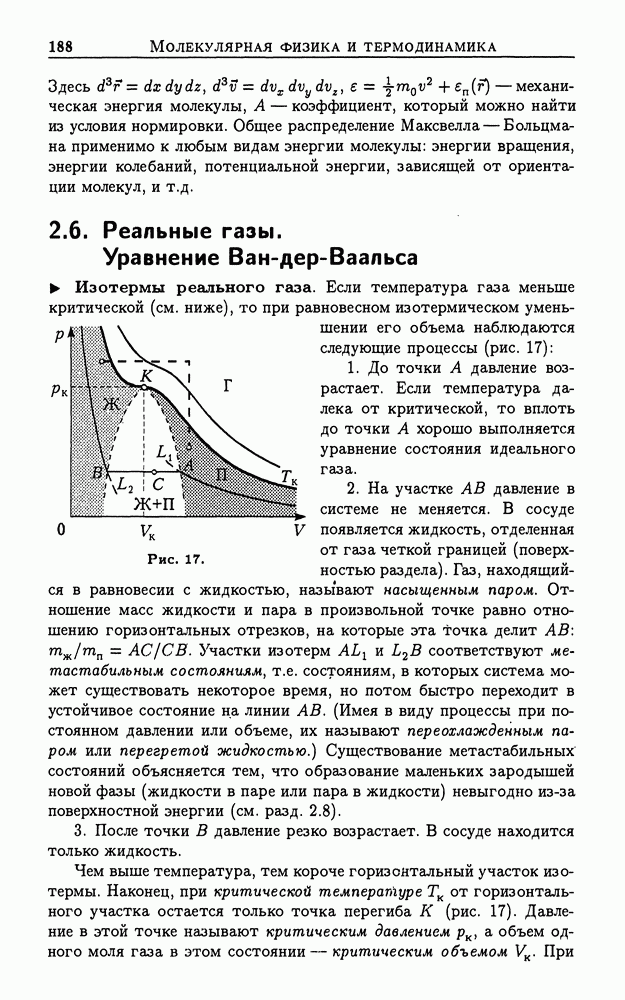
- 2.6. Реальные газы. Уравнение Ван-дер-Ваальса
- 2.7. Равновесие фаз. Фазовые переходы
- 2.8. Поверхностное натяжение
- 2.9. Явления переноса в газах
- 3. Электродинамика
- 3.1. Электрический заряд. Закон Кулона
- 3.2. Электрическое поле. Напряженность поля
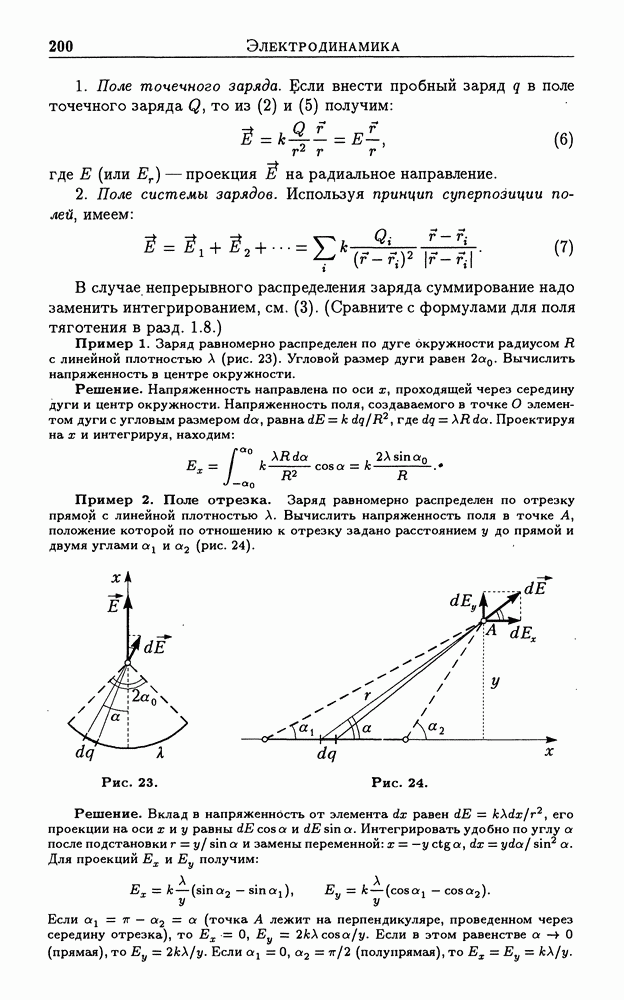
- 3.3. Электростатическое поле. Принцип суперпозиции для напряженности и потенциала
- 3.4. Теорема Гаусса
- 3.5. Электростатика проводников
- 3.6. Электростатика диэлектриков
- 3.7. Конденсаторы
- 3.8. Энергия электростатического поля
- 3.9. Постоянный ток
- 3.10. Магнитное поле. Сила Лоренца и закон Ампера
- 3.11. Вычисление магнитной индукции
- 3.12. Циркуляция и поток вектора магнитной индукции
- 3.13. Магнитное поле в веществе
- 3.14. Электромагнитная индукция
- 3.15. Уравнения Максвелла
- 4. Колебания и волны
- 4.1. Гармонические колебания. Сложение колебаний
- 4.2. Свободные незатухающие колебания
- 4.3. Затухающие и вынужденные колебания
- 4.4. Упругие волны
- 4.5. Электромагнитные волны
- 5. Оптика
- 5.1. Геометрическая оптика. Фотометрия
- 5.2. Интерференция света
- 5.3. Дифракция
- 5.4. Поляризация света. Формулы Френеля
- 5.5. Дисперсия и поглощение света
- 5.6. Тепловое излучение
- 5.7. Световые кванты
- Список литературы
- 1. Кинематика
- 1.1. Кинематика точки
- 1.2. Кинематика твердого тела
- 1.3. Плоскопараллельное движение твердого тела
- 1.4. Произвольное движение твердого тела
- 1.5. Сложное движение точки
- 2. Основные понятия и аксиомы механики
- 2.2. Аксиомы механики
- 3. Статика
- 3.2. Условия уравновешенности систем сил, приложенных к твердому телу
- 3.3. Решение задан статики
- 3.4. Центр параллельных сил. Центр тяжести твердого тела
- 3.5. Распределенные силы
- 3.6. Законы трения (законы Кулона)
- 4. Динамика материальной точки
- 4.2. Первая и вторая задачи динамики
- 5. Общие теоремы динамики механической системы
- 5.2. Теорема о движении центра масс
- 5.3. Теорема об изменении количества движения
- 5.4. Теорема об изменении кинетического момента
- 5.5. Теорема об изменении кинетической энергии
- 6. Принцип Даламбера. Элементы аналитической механики
- 6.2. Классификация механических связей. Обобщенные координаты
- 6.3. Принцип возможных перемещений
- 6.4. Общее уравнение динамики (принцип Даламбера — Лагранжа)
- 6.5. Уравнения Лагранжа второго рода
- 1. Основные понятия
- 1.1. Введение. Внешние и внутренние силы
- 1.2. Напряжения и деформации в точке
- 1.3. Основные понятия и допущения
- 2. Напряженно-деформированное состояние в точке
- 2.2. Одноосное растяжение и сжатие
- 2.3. Чистый сдвиг
- 3. Центральное растяжение и сжатие
- 3.2. Напряжения и деформации при растяжении или сжатии
- 3.3. Расчеты на прочность при растяжении и сжатии
- 4. Кручение
- 4.2. Напряжения и деформации при кручении
- 4.3. Расчеты на прочность при кручении
- 5. Прямой изгиб
- 5.2. Напряжения и деформации при прямом чистом изгибе
- 5.3. Напряжения и деформации при прямом поперечном изгибе
- 5.4. Расчет на прочность при прямом изгибе
- 6. Сложное сопротивление
- 6.2. Внецентренное растяжение или сжатие
- 6.3. Изгиб с кручением
- 7. Устойчивость сжатых стержней
- 7.2. Формула Эйлера
- 7.3. Влияние способов закрепления концов стержня на величину критической силы
- 7.4. Пределы применимости формулы Эйлера
- 7.5. Расчеты сжатых стержней на устойчивость
- ПРИЛОЖЕНИЯ
- 1. Элементарные функции и их свойства
- 2. Таблица неопределенных интегралов
- 3. Решения обыкновенных дифференциальных уравнений
- 4. Ортогональные криволинейные системы координат
- 5. Некоторые физические постоянные