| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
1.5. Закон сохранения энергии
Работа — скалярная величина, являющаяся мерой изменения энергии. Работа внешних сил равна изменению энергии

Определение работы (через интеграл от скалярного произведения):

где  — проекция силы на направление движения точки ее приложения,
— проекция силы на направление движения точки ее приложения,  угол между силой и этим направлением. Работа и энергия измеряются в джоулях
угол между силой и этим направлением. Работа и энергия измеряются в джоулях 
Пример 1. Работа постоянной силы Р

равна скалярному произведению силы на полное перемещение и не зависит от траектории точки приложения.
Пример 2. Работа центральной силы (силы со стороны центрального поля, см. разд. 1.3) равна

(проекция  на радиальное направление равна изменению расстояния
на радиальное направление равна изменению расстояния  до центра). Она зависит только от начального и конечного
до центра). Она зависит только от начального и конечного  расстояний до силового центра и не зависит от траектории.
расстояний до силового центра и не зависит от траектории.
Мощность. Средняя мощность — отношение работы к интервалу времени. Мгновенная механическая мощность равна

Мощность измеряется в ваттах 
Кинетической энергией называется энергия, связанная с движением точки и зависящая от ее скорости. Скорость тела изменяется под действием результирующей силы Р, работа которой равна

Видно, что в соответствии с общим принципом (12) кинетическую энергию надо определить как  Полученное тождество, утверждающее, что изменение кинетической энергии равно работе результирующей силы, называют теоремой о кинетической энергии.
Полученное тождество, утверждающее, что изменение кинетической энергии равно работе результирующей силы, называют теоремой о кинетической энергии.
Кинетическая энергия системы точек определяется как сумма кинетических энергий всех точек системы. Изменение кинетической энергии системы равно работе всех сил, действующих на ее точки. Кинетическая энергия системы равна:

где  — масса системы,
— масса системы,  — скорость ее центра масс,
— скорость ее центра масс,  — кинетическая энергия в системе центра масс (теорема Кёнига).
— кинетическая энергия в системе центра масс (теорема Кёнига).
Консервативные силы. Потенциальное поле. Сила взаимодействия между точками называется консервативной, если работа этой силы зависит только от начального и конечного положения точек, но не зависит от траектории их перемещения. Внешнее стационарное поле называется потенциальным, если работа поля при перемещении точки зависит только от ее начального и конечного положения, но не зависит от ее траектории. (Эквивалентное утверждение — работа поля при перемещении точки по замкнутой траектории равна нулю.) Потенциальное поле — это поле консервативных сил взаимодействия, создаваемое неподвижными внешними источниками. Из примера 1 следует, что однородное поле потенциально (пример — поле тяжести). Из примера 2 следует, что любое центральное поле потенциально. Потенциальным будет также поле, являющееся суперпозицией нескольких центральных полей (создаваемое несколькими источниками). Значит, электростатическое поле и стационарное поле тяготения являются потенциальными. Из примера 2 также следует, что сила упругости, создаваемая легкой пружиной, является консервативной. Система точек, между которыми действуют только консервативные силы, называется консервативной системой.
Потенциальная энергия. Потенциальная энергия характеризует взаимодействие между точками и зависит от их взаимного расположения. Потенциальная энергия точки во внешнем потенциальном поле определяется следующим образом. Сначала определим разность потенциальных энергий для двух положений точки как работу поля по ее переносу из одного положения в другое:

(эта работа не зависит от траектории). Значит, изменение потенциальной энергии  равно работе сил поля, взятой с обратным знаком. Если перемещение частицы в поле осуществляется очень медленно с помощью внешней силы, то работа внешней силы будет равна по величине и противоположна по знаку работе поля, т. е.
равно работе сил поля, взятой с обратным знаком. Если перемещение частицы в поле осуществляется очень медленно с помощью внешней силы, то работа внешней силы будет равна по величине и противоположна по знаку работе поля, т. е.  в соответствии с общим принципом (12). Равенство (15) определяет потенциальную энергию с точностью до константы. Чтобы сделать определение однозначным, надо задать значение потенциальной энергии в какой-то точке пространства (обычно задают точку, в которой потенциальная энергия равна нулю).
в соответствии с общим принципом (12). Равенство (15) определяет потенциальную энергию с точностью до константы. Чтобы сделать определение однозначным, надо задать значение потенциальной энергии в какой-то точке пространства (обычно задают точку, в которой потенциальная энергия равна нулю).
Пример 3. Работа силы тяжести  при перемещении точки массой
при перемещении точки массой  с высоты
с высоты  на высоту
на высоту  равна
равна  -
-  Значит, потенциальная энергия точки в поле тяжести равна
Значит, потенциальная энергия точки в поле тяжести равна  где высота отсчитывается от оговоренного нулевого уровня. Потенциальная энергия системы точек в поле тяжести равна
где высота отсчитывается от оговоренного нулевого уровня. Потенциальная энергия системы точек в поле тяжести равна

где  — масса системы,
— масса системы,  — высота ее центра масс.
— высота ее центра масс.
Пример 4. Работа силы упругости равна  где
где  — начальная и конечная деформация пружины. Значит, потенциальная энергия упругой пружины равна
— начальная и конечная деформация пружины. Значит, потенциальная энергия упругой пружины равна  где за нуль принята энергия недеформированной пружины.
где за нуль принята энергия недеформированной пружины.
Пример 5. Работа сил трения, сопротивления отрицательна как на каждом участке пути, так и вдоль замкнутой траектории. Значит, эти силы не являются консервативными.
Потенциальную энергию консервативного взаимодействия двух частиц можно определить как потенциальную энергию одной частицы в поле другой частицы. Ответ не зависит от того, какую из частиц выбрать в качестве источника поля.
Связь силы с потенциальной энергией. Записав равенство (15) для двух близких точек, лежащих на некоторой оси  получим
получим  Значит, проекция силы на произвольное направление выражается через производную от потенциальной энергии:
Значит, проекция силы на произвольное направление выражается через производную от потенциальной энергии:

(частная производная означает, что  рассматривается как функция одной переменной
рассматривается как функция одной переменной  Вектор силы получается равным градиенту потенциальной энергии:
Вектор силы получается равным градиенту потенциальной энергии:

Для центрального поля формула (16) принимает вид

Механическая энергия системы определяется как сумма ее кинетической энергии, потенциальной энергии взаимодействия между ее частицами и потенциальной энергии во внешнем поле:

Первые две суммы образуют собственную механическую энергию системы.
Изменение механической энергии. Изменение кинетической энергии равно работе всех сил, приложенных к точкам системы (уравнение  Изменение потенциальной энергии равно работе всех консервативных сил (внутренних и внешних, включая работу потенциальных полей), взятой с обратным знаком. Значит, изменение механической энергии равно работе всех неконсервативных сил, как внешних, так и внутренних:
Изменение потенциальной энергии равно работе всех консервативных сил (внутренних и внешних, включая работу потенциальных полей), взятой с обратным знаком. Значит, изменение механической энергии равно работе всех неконсервативных сил, как внешних, так и внутренних:

Закон сохранения механической энергии: механическая энергия замкнутой консервативной системы остается постоянной.
Это утверждение является частным проявлением общего фундаментального принципа сохранения энергии: полная энергия замкнутой системы сохраняется. Полная энергия, кроме механической, включает в себя также различные виды внутренней энергии: тепловую, химическую, ядерную. Общий принцип сохранения энергии выходит далеко за пределы ньютоновской механики, в рамках которой мы получили закон сохранения механической энергии. Этот принцип тесно связан с фундаментальным условием однородности времени (равноправием всех моментов времени), он является основанием всего здания современной физики.
Условие консервативности эквивалентно требованию независимого сохранения двух слагаемых полной энергии: механической и внутренней. Если, напрймер, внутри системы действуют силы трения,
работа которых отрицательна, то механическая энергия уменьшается (уравнение (20)), переходя во внутреннюю (в этом случае говорят, что в системе выделяется тепло). Механическая энергия может также изменяться в том случае, если в системе присутствует какой-нибудь механизм, способный производить работу за счет внутренней энергии (топлива): двигатель внутреннего сгорания, человек.
Пример 6. Упругий удар. При центральном ударе упругих шаров сохраняется и импульс системы, и ее механическая энергия:

Вместо второго уравнения удобно использовать условие, что относительная скорость шаров не меняется по величине, но изменяет свой знак:  Это уравнение можно вывести из первых двух, но оно становится очевидным при переходе в инерциальную систему центра масс (относительная скорость при таком переходе не меняется). В этой системе отсчета полный импульс системы равен нулю, и после удара скорости шаров просто меняются на противоположные (оба закона сохранения при этом выполняются). Решая два линейных уравнения, находим конечные скорости шаров:
Это уравнение можно вывести из первых двух, но оно становится очевидным при переходе в инерциальную систему центра масс (относительная скорость при таком переходе не меняется). В этой системе отсчета полный импульс системы равен нулю, и после удара скорости шаров просто меняются на противоположные (оба закона сохранения при этом выполняются). Решая два линейных уравнения, находим конечные скорости шаров:

При упругом ударе о движущуюся стенку  получим
получим

Пример 7. Неупругий удар. После абсолютно неупругого удара шары движутся поступательно с одинаковой скоростью, т.е. как одно составное тело (вращения не возникнет, если в системе центра масс удар центральный). Скорости сравниваются в результате действия неконсервативных сил, т.е. при неупругом ударе обязательно выделяется тепло. Чтобы убедиться в этом, найдем с помощью закона сохранения импульса конечную скорость шаров:  после чего вычислим уменьшение механической энергии:
после чего вычислим уменьшение механической энергии:

Еще проще получить этот ответ в системе координат, связанной с центром масс, где шары после удара покоятся.
Потенциальные кривые. Устойчивость. Если известна потенциальная энергия одномерного движения в потенциальном поле  (рис. 5), то, опираясь на соотношение (16) между силой и энергией, можно выяснить:
(рис. 5), то, опираясь на соотношение (16) между силой и энергией, можно выяснить:
а) Направление силы  при
при 
б) Точки равновесия  при
при 

Рис. 5.
в) Устойчивость равновесия. В окрестности точки  сила направлена в сторону этой точки, т. е. равновесие устойчиво. В точке
сила направлена в сторону этой точки, т. е. равновесие устойчиво. В точке  равновесие неустойчиво. Устойчивое равновесие соответствует минимуму потенциальной энергии.
равновесие неустойчиво. Устойчивое равновесие соответствует минимуму потенциальной энергии.
г) По значению механической энергии Е можно установить характер движения. Движение может происходить только в области, где  (кинетическая энергия неотрицательна). При
(кинетическая энергия неотрицательна). При  (для рис.
(для рис.  движение финитное, т.е. происходит в ограниченной области
движение финитное, т.е. происходит в ограниченной области  На рис. 5 движение происходит между точками поворота
На рис. 5 движение происходит между точками поворота  При
При  движение либо инфинитно, т.е. точка после отражения от точки поворота
движение либо инфинитно, т.е. точка после отражения от точки поворота  уходит на бесконечность с кинетической энергией
уходит на бесконечность с кинетической энергией  либо заперто потенциальным барьером и движется между точками поворота
либо заперто потенциальным барьером и движется между точками поворота  . В классической механике потенциальный барьер непреодолим; в квантовой механике существует вероятность проникновения сквозь потенциальный барьер (туннельный эффект).
. В классической механике потенциальный барьер непреодолим; в квантовой механике существует вероятность проникновения сквозь потенциальный барьер (туннельный эффект).
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- 1. Аналитическая геометрия на плоскости
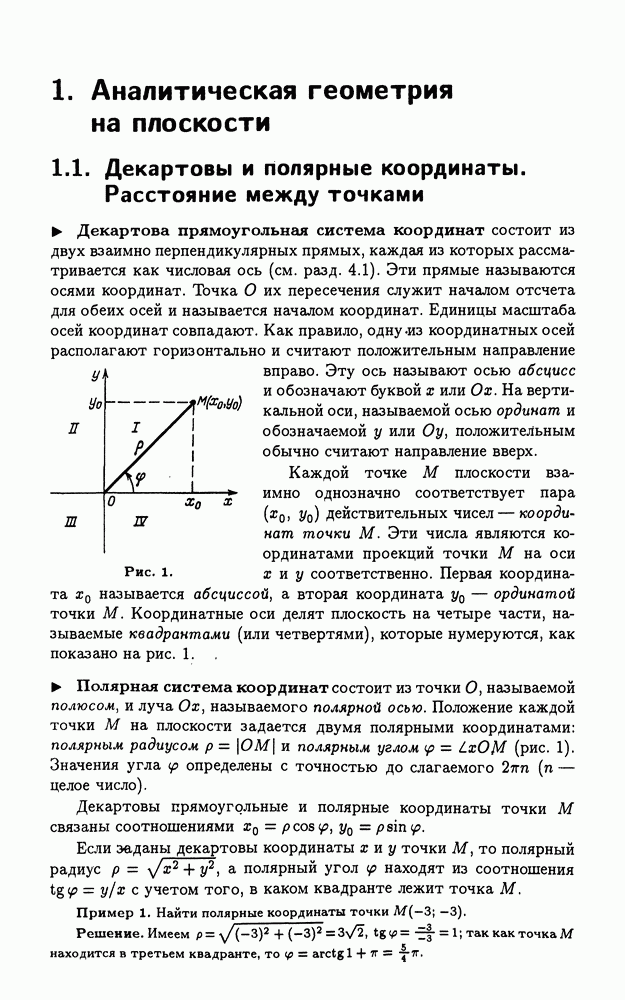
- 1.1. Декартовы и полярные координаты. Расстояние между точками
- 1.2. Деление отрезка в данном отношении. Площадь многоугольника
- 1.3. Различные виды уравнения прямой
- 1.4. Угол между прямыми. Расстояние от точки до прямой
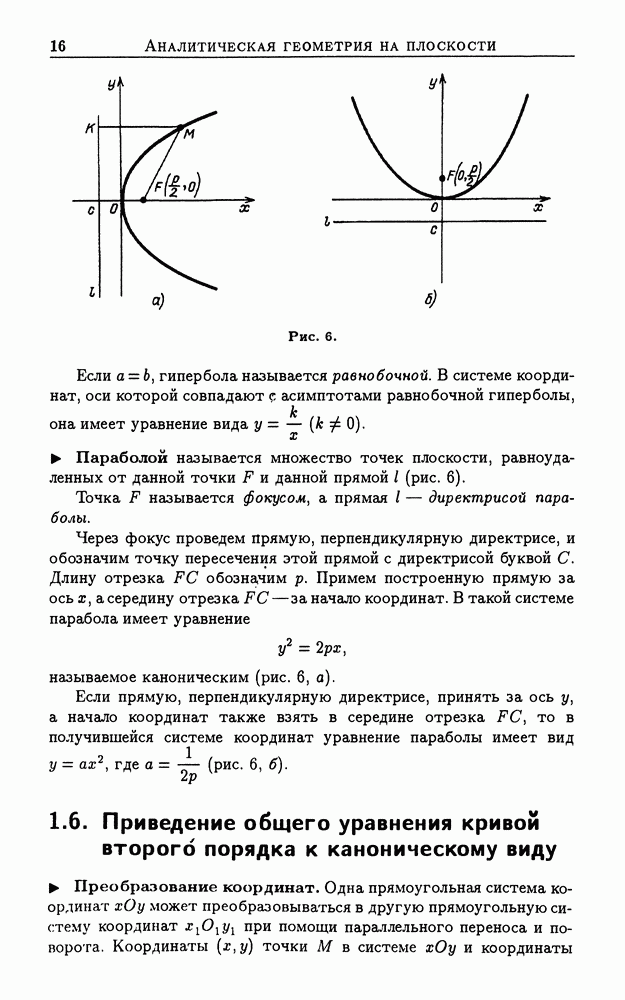
- 1.5. Окружность, эллипс, гипербола и парабола
- 1.6. Приведение общего уравнения кривой второго порядка к каноническому виду
- 2. Аналитическая геометрия в пространстве
- 2.2. Векторы
- 2.3. Действия над векторами. Скалярное произведение
- 2.4. Векторное и смешанное произведения
- 2.5. Плоскость в пространстве
- 2.6. Прямая в пространстве
- 2.7. Прямая и плоскость в пространстве
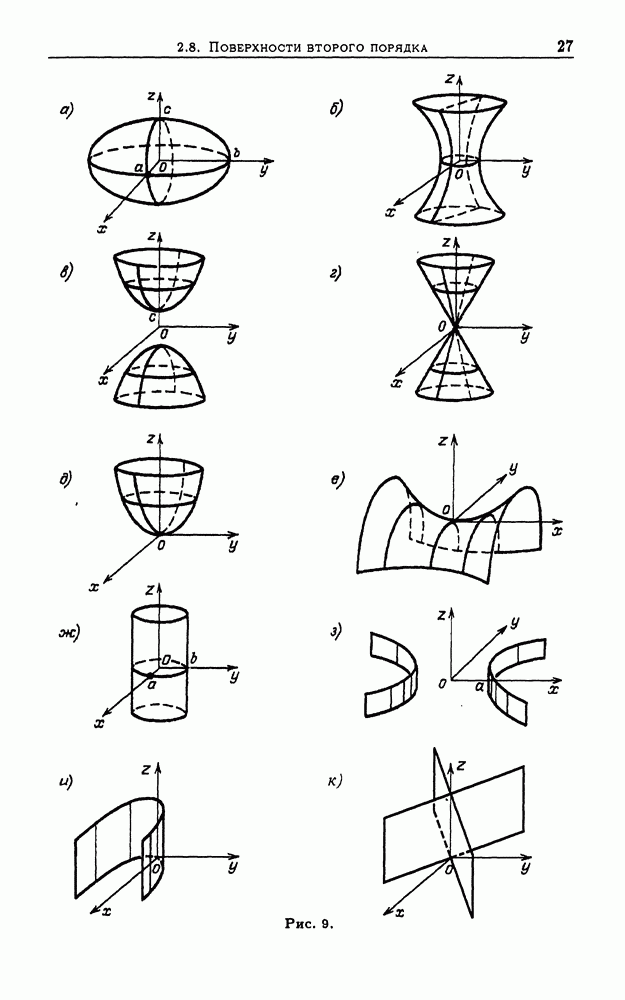
- 2.8. Поверхности второго порядка
- 3. Линейная алгебра
- 3.2. Матрицы
- 3.3. Системы линейных уравнений
- 3.4. Системы n-мерных векторов. Собственные значения и собственные векторы матрицы
- 4. Основные понятия математического анализа
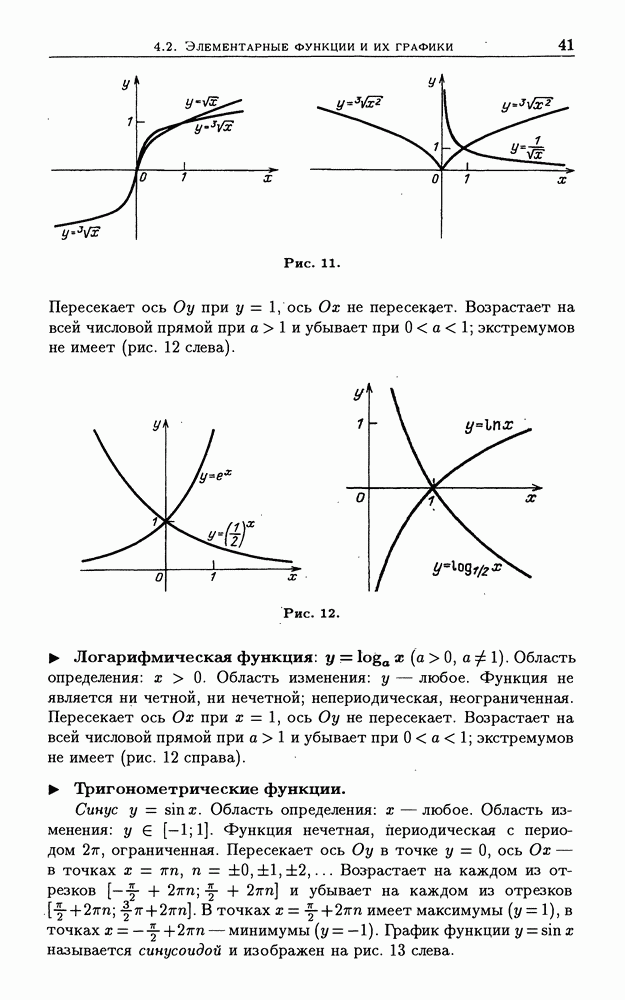
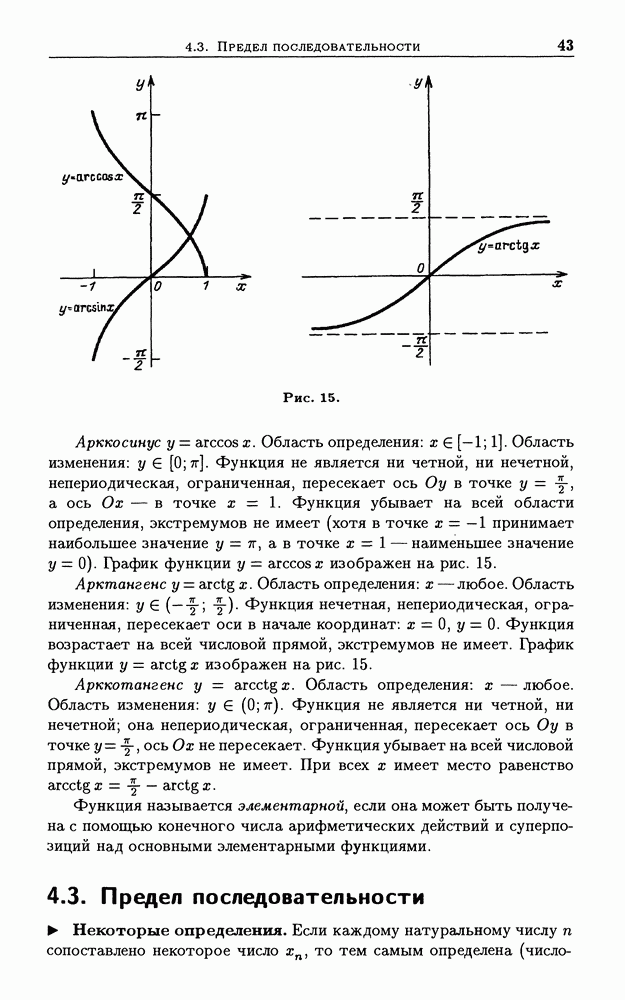
- 4.2. Элементарные функции и их графики
- 4.3. Предел последовательности
- 4.4. Предел функции
- 4.5. Бесконечно малые и бесконечно большие функции
- 4.6. Непрерывность
- 4.7. Асимптоты графика функции
- 5. Дифференциальное исчисление функций одной переменной
- 5.2. Таблица производных и правила дифференцирования
- 5.3. Теоремы о дифференцируемых функциях. Правило Лопиталя
- 5.4. Производные и дифференциалы высших порядков. Формула Тейлора
- 5.5. Экстремумы. Точки перегиба
- 5.6. Общая схема исследования функции и построение графика
- 6. Функции нескольких переменных
- 6.1. Точечные множества. Функции. Предел и непрерывность
- 6.2. Дифференцирование функций нескольких переменных
- 6.3. Производная по направлению. Геометрические приложения
- 6.4. Экстремумы функций нескольких переменных
- 7. Неопределенный интеграл
- 7.1. Первообразная. Неопределенный интеграл и его свойства
- 7.2. Таблица основных интегралов. Примеры интегрирования
- 7.3. Интегрирование по частям. Метод замены переменной
- 7.4. Интегрирование рациональных функций
- 7.5. Интегрирование иррациональных функций
- 7.6. Интегрирование показательных и тригонометрических функций
- 8. Определенный интеграл
- 8.1. Основные определения. Геометрический смысл определенного интеграла
- 8.2. Свойства определенного интеграла
- 8.3. Геометрические и физические приложения определенного интеграла
- 8.4. Несобственные интегралы
- 9. Двойные и тройные интегралы
- 9.1. Определение и свойства двойного интеграла
- 9.2. Вычисление двойного интеграла
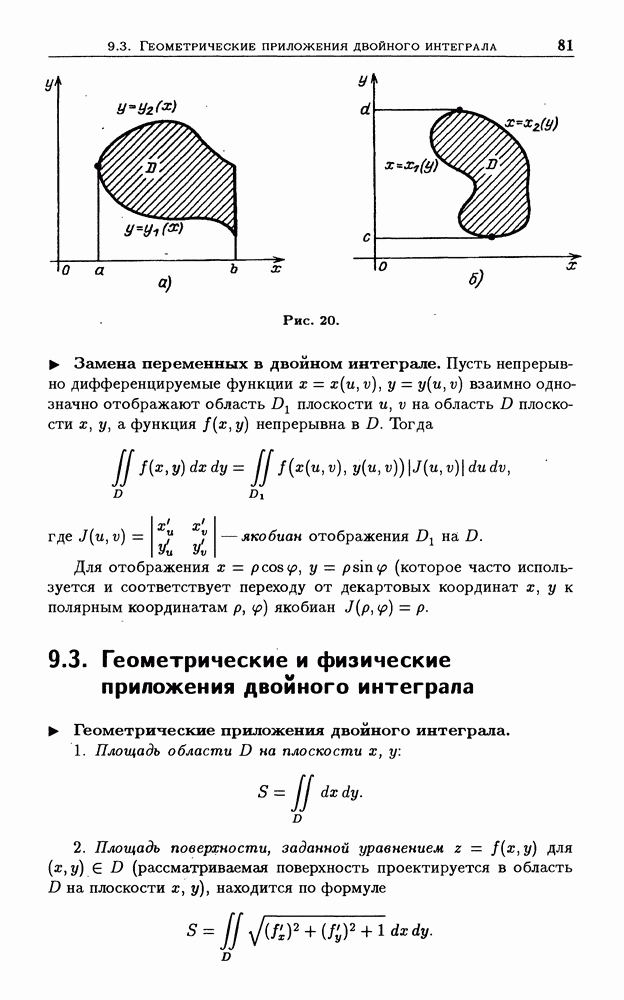
- 9.3. Геометрические и физические приложения двойного интеграла
- 9.4. Определение и свойства тройного интеграла
- 9.5. Вычисление тройного интеграла. Некоторые приложения
- 10. Криволинейные и поверхностные интегралы
- 10.2. Криволинейный интеграл второго рода
- 10.3. Поверхностный интеграл первого рода
- 10.4. Поверхностный интеграл второго рода
- 10.5. Дифференциальные операции и интегральные формулы теории поля
- 11. Ряды
- 11.1. Числовые ряды
- 11.2. Функциональные ряды
- 11.3. Степенные ряды
- 11.4. Ряд Фурье
- 11.5. Интеграл Фурье. Преобразование Фурье
- 12. Обыкновенные дифференциальные уравнения
- 12.2. Дифференциальные уравнения высших порядков
- 12.3. Линейные уравнения n-го порядка
- 12.4. Решение линейных однородных уравнений n-го порядка с постоянными коэффициентами
- 12.5. Линейные неоднородные уравнения n-го порядка
- 12.6. Системы обыкновенных дифференциальных уравнений
- 13. Приближенные вычисления
- 13.1. Метод наименьших квадратов
- 13.2. Приближенное решение алгебраических уравнений
- 13.3. Вычисление определенного интеграла
- 13.4. Численное интегрирование дифференциальных уравнений
- 14. Теория вероятностей
- 14.1. Правила и формулы комбинаторики
- 14.2. Основные понятия теории вероятностей
- 14.3. Условная вероятность. Теоремы и формулы теории вероятностей
- 14.4. Математическое ожидание и дисперсия
- 14.5. Закон больших чисел
- 1. Физические основы механики
- 1.1. Кинематика точки
- 1.2. Кинематика твердого тела
- 1.3. Динамика
- 1.4. Закон сохранения импульса
- 1.5. Закон сохранения энергии
- 1.6. Закон сохранения момента импульса
- 1.7. Задана двух тел и движение в центральном поле
- 1.8. Поле тяготения
- 1.9. Неинерциальные системы отсчета
- 1.10. Динамика твердого тела
- 1.11. Специальная теория относительности
- 2. Молекулярная физика и термодинамика
- 2.2. Первое начало термодинамики
- 2.3. Второе начало термодинамики
- 2.4. Энтропия. Свободная энергия
- 2.5. Кинетическая теория идеального газа
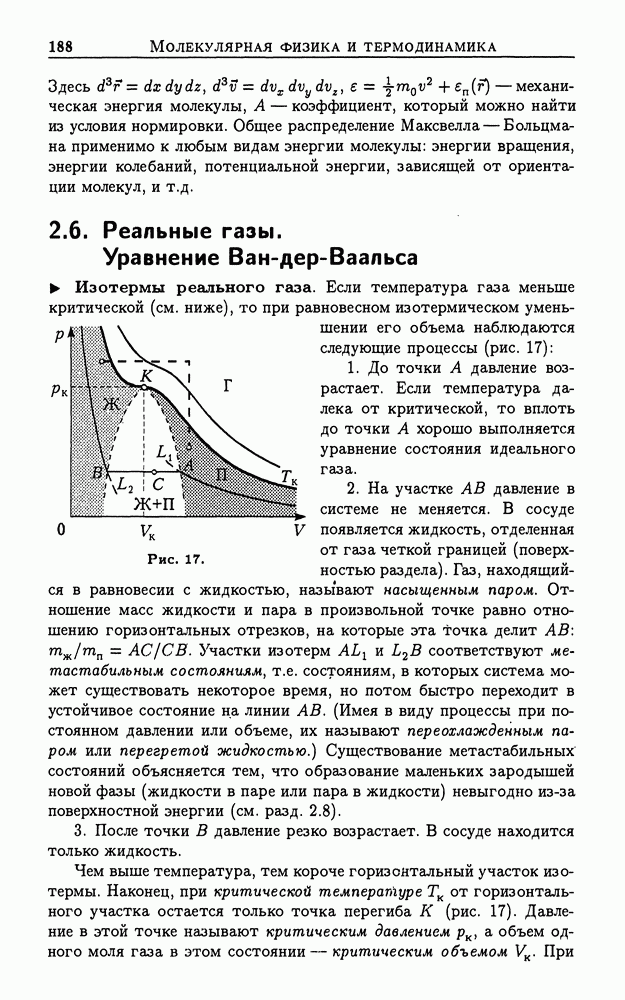
- 2.6. Реальные газы. Уравнение Ван-дер-Ваальса
- 2.7. Равновесие фаз. Фазовые переходы
- 2.8. Поверхностное натяжение
- 2.9. Явления переноса в газах
- 3. Электродинамика
- 3.1. Электрический заряд. Закон Кулона
- 3.2. Электрическое поле. Напряженность поля
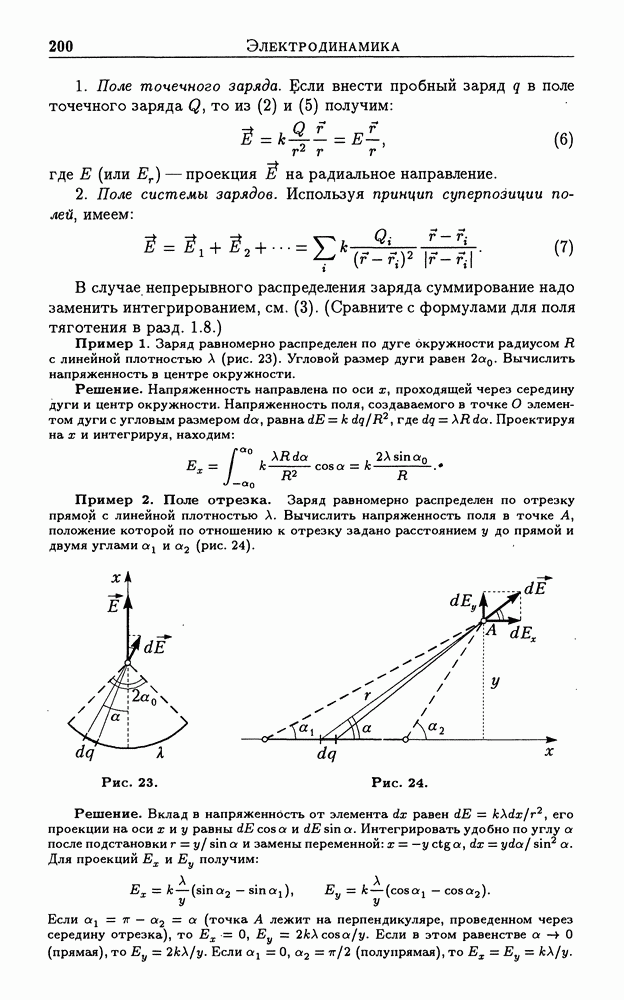
- 3.3. Электростатическое поле. Принцип суперпозиции для напряженности и потенциала
- 3.4. Теорема Гаусса
- 3.5. Электростатика проводников
- 3.6. Электростатика диэлектриков
- 3.7. Конденсаторы
- 3.8. Энергия электростатического поля
- 3.9. Постоянный ток
- 3.10. Магнитное поле. Сила Лоренца и закон Ампера
- 3.11. Вычисление магнитной индукции
- 3.12. Циркуляция и поток вектора магнитной индукции
- 3.13. Магнитное поле в веществе
- 3.14. Электромагнитная индукция
- 3.15. Уравнения Максвелла
- 4. Колебания и волны
- 4.1. Гармонические колебания. Сложение колебаний
- 4.2. Свободные незатухающие колебания
- 4.3. Затухающие и вынужденные колебания
- 4.4. Упругие волны
- 4.5. Электромагнитные волны
- 5. Оптика
- 5.1. Геометрическая оптика. Фотометрия
- 5.2. Интерференция света
- 5.3. Дифракция
- 5.4. Поляризация света. Формулы Френеля
- 5.5. Дисперсия и поглощение света
- 5.6. Тепловое излучение
- 5.7. Световые кванты
- Список литературы
- 1. Кинематика
- 1.1. Кинематика точки
- 1.2. Кинематика твердого тела
- 1.3. Плоскопараллельное движение твердого тела
- 1.4. Произвольное движение твердого тела
- 1.5. Сложное движение точки
- 2. Основные понятия и аксиомы механики
- 2.2. Аксиомы механики
- 3. Статика
- 3.2. Условия уравновешенности систем сил, приложенных к твердому телу
- 3.3. Решение задан статики
- 3.4. Центр параллельных сил. Центр тяжести твердого тела
- 3.5. Распределенные силы
- 3.6. Законы трения (законы Кулона)
- 4. Динамика материальной точки
- 4.2. Первая и вторая задачи динамики
- 5. Общие теоремы динамики механической системы
- 5.2. Теорема о движении центра масс
- 5.3. Теорема об изменении количества движения
- 5.4. Теорема об изменении кинетического момента
- 5.5. Теорема об изменении кинетической энергии
- 6. Принцип Даламбера. Элементы аналитической механики
- 6.2. Классификация механических связей. Обобщенные координаты
- 6.3. Принцип возможных перемещений
- 6.4. Общее уравнение динамики (принцип Даламбера — Лагранжа)
- 6.5. Уравнения Лагранжа второго рода
- 1. Основные понятия
- 1.1. Введение. Внешние и внутренние силы
- 1.2. Напряжения и деформации в точке
- 1.3. Основные понятия и допущения
- 2. Напряженно-деформированное состояние в точке
- 2.2. Одноосное растяжение и сжатие
- 2.3. Чистый сдвиг
- 3. Центральное растяжение и сжатие
- 3.2. Напряжения и деформации при растяжении или сжатии
- 3.3. Расчеты на прочность при растяжении и сжатии
- 4. Кручение
- 4.2. Напряжения и деформации при кручении
- 4.3. Расчеты на прочность при кручении
- 5. Прямой изгиб
- 5.2. Напряжения и деформации при прямом чистом изгибе
- 5.3. Напряжения и деформации при прямом поперечном изгибе
- 5.4. Расчет на прочность при прямом изгибе
- 6. Сложное сопротивление
- 6.2. Внецентренное растяжение или сжатие
- 6.3. Изгиб с кручением
- 7. Устойчивость сжатых стержней
- 7.2. Формула Эйлера
- 7.3. Влияние способов закрепления концов стержня на величину критической силы
- 7.4. Пределы применимости формулы Эйлера
- 7.5. Расчеты сжатых стержней на устойчивость
- ПРИЛОЖЕНИЯ
- 1. Элементарные функции и их свойства
- 2. Таблица неопределенных интегралов
- 3. Решения обыкновенных дифференциальных уравнений
- 4. Ортогональные криволинейные системы координат
- 5. Некоторые физические постоянные