| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2.5. Кинетическая теория идеального газа
Основное уравнений кинетической теории идеального газа. С точки зрения молекулярно-кинетической теории, газ считается идеальным, если можно пренебречь потенциальной энергией взаимодействия его молекул (по сравнению с кинетической энергией) и размерами молекул (по сравнению со средним расстоянием между ними). Давление газа на стенку возникает в результате многочисленных упругих соударений молекул между собой и со стенками сосуда. (Удары можно считать в среднем упругими, так как газ находится со стенкой в тепловом равновесии.) Основное уравнение кинетической теории идеального газа выражает давление через средний квадрат скорости молекул:

где  - концентрация молекул,
- концентрация молекул,  — масса одной молекулы,
— масса одной молекулы,  — ее импульс,
— ее импульс,  — средняя кинетическая энергия поступательного движения молекулы.
— средняя кинетическая энергия поступательного движения молекулы.
Если связь энергии и импульса отличается от классической, то последнее равенство в (33) приобретает иной вид. Для газа фотонов имеем  (см. разд. 1.11). В результате получим
(см. разд. 1.11). В результате получим

Число ударов о стенку. Число молекул  попадающих за время
попадающих за время  на плоский участок поверхности площадью
на плоский участок поверхности площадью  равно
равно

Формулы для вычислений. Формулы для переноса через площадку числа частиц, импульса, энергии и т.д. получают разбиением молекул на удобные группы и вычислением их вклада в вычисляемую величину. Наиболее общий подход — разбиение на группы, имеющие почти одинаковую скорость  Выделим группу молекул, имеющих величину скорости от
Выделим группу молекул, имеющих величину скорости от  до
до  а направление в телесном угле
а направление в телесном угле  Число молекул данной группы в единице объема равно
Число молекул данной группы в единице объема равно 

Рис. 15.
Чтобы найти, сколько молекул данной группы попадает на плоский участок площадью  за время
за время  надо построить на этом участке косой цилиндр (рис. 15), направляющая которого имеет длину
надо построить на этом участке косой цилиндр (рис. 15), направляющая которого имеет длину  и составляет угол
и составляет угол  с осью х. Все молекулы выделенной группы, находящиеся в этом цилиндре (и только
с осью х. Все молекулы выделенной группы, находящиеся в этом цилиндре (и только  попадут на площадку
попадут на площадку  за время
за время  Производя последовательные интегрирования, можно вывести (35) и многие другие формулы, например для проносимой через площадку энергии:
Производя последовательные интегрирования, можно вывести (35) и многие другие формулы, например для проносимой через площадку энергии:

Определение температуры в кинетической теории газов.
В кинетической теории газов доказывается, что если две подсистемы (из одинаковых или разных молекул) могут обмениваться энергией, то в состоянии равновесия оказываются равными средние кинетические энергии поступательного движения их молекул. Исходя из этого, кинетическая теория газов определяет температуру как величину, пропорциональную средней кинетической энергии поступательного движения молекул:

где к — постоянная Больцмана, которая выражается через универсальную газовую постоянную и число Авогадро (см. разд. 2.1):  Коэффициент пропорциональности выбран так, чтобы уравнение состояния идеального газа
Коэффициент пропорциональности выбран так, чтобы уравнение состояния идеального газа

(оно получается из основного уравнения (33) и определения температуры (37)) совпадало с уравнением (2), в котором используется газовая шкала температур.
Средняя квадратичная скорость поступательного движения молекул с учетом (33) и (37) вычисляется по формулам

где  — плотность газа.
— плотность газа.
Внутренняя энергия идеального газа. Важной характеристикой идеального газа является число степеней свободы его молекулы  . У одноатомной молекулы есть только три степени свободы, соответствующих поступательному движению:
. У одноатомной молекулы есть только три степени свободы, соответствующих поступательному движению:  . У жесткой двухатомной молекулы, кроме поступательных, есть еще две вращательные степени свободы (полярные углы, задающие ее направление в пространстве):
. У жесткой двухатомной молекулы, кроме поступательных, есть еще две вращательные степени свободы (полярные углы, задающие ее направление в пространстве):  . У жесткой многоатомной (нелинейной) молекулы — три вращательные степени свободы, поэтому
. У жесткой многоатомной (нелинейной) молекулы — три вращательные степени свободы, поэтому  . В классической статистической физике доказывается теорема о равнораспределении энергии по степеням свободы: на любую степень свободы, которой в выражении для энергии молекулы соответствует член
. В классической статистической физике доказывается теорема о равнораспределении энергии по степеням свободы: на любую степень свободы, которой в выражении для энергии молекулы соответствует член  или
или  приходится средняя энергия
приходится средняя энергия  в расчете на одну молекулу. Формула (37) находится в полном соответствии с утверждением этой теоремы. Средняя энергия одной молекулы и внутренняя энергия всего газа принимают вид:
в расчете на одну молекулу. Формула (37) находится в полном соответствии с утверждением этой теоремы. Средняя энергия одной молекулы и внутренняя энергия всего газа принимают вид:

Физическое число степеней свободы  в случае жестких молекул совпадает с математическим. Однако, когда оказываются возбужденными колебательные степени свободы (при
в случае жестких молекул совпадает с математическим. Однако, когда оказываются возбужденными колебательные степени свободы (при  , то на каждую колебательную степень свободы будет приходиться (с учетом потенциальной энергии колебаний) средняя энергия
, то на каждую колебательную степень свободы будет приходиться (с учетом потенциальной энергии колебаний) средняя энергия  . В результате получим
. В результате получим  где
где  обозначает математическое число колебательных степеней свободы. Для
обозначает математическое число колебательных степеней свободы. Для  -атомной молекулы
-атомной молекулы  (например, для мягкой двухатомной молекулы
(например, для мягкой двухатомной молекулы 
Из (40) получим выражения для теплоемкостей идеального газа и его показателя адиабаты (см. разд. 2.2):

При комнатных температурах измеряемая теплоемкость соответствует модели жестких молекул — колебательные степени свободы оказываются невозбужденными или, как говорят, «замороженными». Однако при повышении температуры до  теплоемкость начинает возрастать, т.е. колебательные степени свободы «размораживаются». Наоборот, при понижении температуры до нескольких десятков кельвинов происходит «вымораживание» вращательных степеней свободы, сопровождающееся соответствующим уменьшением теплоемкостей. Объяснение явлению вымораживания степеней свободы дает квантовая механика: если средняя энергия теплового движения
теплоемкость начинает возрастать, т.е. колебательные степени свободы «размораживаются». Наоборот, при понижении температуры до нескольких десятков кельвинов происходит «вымораживание» вращательных степеней свободы, сопровождающееся соответствующим уменьшением теплоемкостей. Объяснение явлению вымораживания степеней свободы дает квантовая механика: если средняя энергия теплового движения  мала по сравнению с расстоянием до ближайшего дискретного уровня, то данный вид движения не возбуждается.
мала по сравнению с расстоянием до ближайшего дискретного уровня, то данный вид движения не возбуждается.
Смесь идеальных газов. Закон Дальтона: давление смеси двух идеальных газов равно сумме их парциальных давлений:

Внутренняя энергия смеси равна сумме внутренних энергий  Эта формула позволяет ввести: эффективное число степеней свободы:
Эта формула позволяет ввести: эффективное число степеней свободы:  эффективные молярные теплоемкости:
эффективные молярные теплоемкости:  эффективную молярную массу:
эффективную молярную массу: 
Распределение Максвелла. Распределение молекул по скоростям описывается следующими функциями:

Определение любой функции распределения основано на утверждении, что доля молекул, попадающих (в среднем) в очень маленький интервал данной переменной (скорости, проекции скорости, энергии), пропорциональна ширине этого интервала  обозначает физически, а не математически, бесконечно малый интервал — он должен
обозначает физически, а не математически, бесконечно малый интервал — он должен
содержать большое число молекул.) Среднюю долю молекул, обладающих некоторым признаком (например, попадающих в заданный интервал скоростей), можно трактовать как вероятность того, что произвольная молекула обладает данным признаком. Поэтому функцию распределения иногда называют плотностью вероятности:
Перечислим свойства функции распределения (на примере 
1) Доля частиц (вероятность) в конечном интервале

2) Нормированность:

3) Вычисление среднего от любой функции скорости 

Между тремя функциями распределения, определенными в (42), существуют следующие связи:

Функция  является четной функцией, т.е. можно написать:
является четной функцией, т.е. можно написать:  Функция
Функция  зависит только от
зависит только от  Связь между
Связь между  удовлетворяется только функцией
удовлетворяется только функцией  Коэффициенты А и С определяются из двух условий: а) нормировки функции
Коэффициенты А и С определяются из двух условий: а) нормировки функции
б) требования, чтобы  см. (39). Ответ выглядит так:
см. (39). Ответ выглядит так:


Рис. 16.
Обычно именно последнюю формулу называют распределением Максвелла (рис. 16). Функция  достигает максимума при скорости
достигает максимума при скорости  которую называют наиболее вероятной скоростью. Значение функции
которую называют наиболее вероятной скоростью. Значение функции  в этой точке равно
в этой точке равно  Например, при увеличении T в 4 раза максимальная скорость станет в 2 раза больше, а соответствующее значение функции
Например, при увеличении T в 4 раза максимальная скорость станет в 2 раза больше, а соответствующее значение функции  —
—
в 2 раза меньше; напомним, что площадь под кривой  равна единице.
равна единице.
Средняя (или среднеарифметическая) скорость молекул вычисляется в соответствии с правилом (44):

Приведем также распределение молекул по энергиям поступательного движения:

Интегралы для вычислений. Для вычисления средних с распределением Максвелла нужно уметь вычислять интегралы типа  Приведем два первых результата:
Приведем два первых результата:  Дальнейшие интегралы получим дифференцированием по
Дальнейшие интегралы получим дифференцированием по  Например,
Например, 
Распределение Больцмана. Если газ находится во внешнем силовом поле, то концентрация молекул зависит от координат. Из условия механического равновесия газа можно получить:

где  — потенциальная энергия молекулы во внешнем поле (распределение Больцмана). Частным случаем распределения Больцмана является барометрическая формула:
— потенциальная энергия молекулы во внешнем поле (распределение Больцмана). Частным случаем распределения Больцмана является барометрическая формула:

Поясним на примере барометрической формулы, как выводится распределение Больцмана. Условие равновесия в поле тяжести вертикального цилиндра с площадью основания  и высотой
и высотой  имеет вид:
имеет вид:  Отсюда с учетом уравнений
Отсюда с учетом уравнений  получим
получим  Интегрируя, приходим к барометрической формуле.
Интегрируя, приходим к барометрической формуле.
Распределение Максвелла — Больцмана. Оба распределения — Максвелла (45) и Больцмана (46) — содержат выражение  Распределение Максвелла — Больцмана выражает вероятность того, что произвольная молекула из сосуда, содержащего
Распределение Максвелла — Больцмана выражает вероятность того, что произвольная молекула из сосуда, содержащего  молекул, находится в области пространства
молекул, находится в области пространства  и имеет скорость в интервале
и имеет скорость в интервале 

Здесь  механическая энергия молекулы,
механическая энергия молекулы,  — коэффициент, который можно найти из условия нормировки. Общее распределение Максвелла-Больцмана применимо к любым видам энергии молекулы: энергии вращения, энергии колебаний, потенциальной энергии, зависящей от ориентации молекул, и т.д.
— коэффициент, который можно найти из условия нормировки. Общее распределение Максвелла-Больцмана применимо к любым видам энергии молекулы: энергии вращения, энергии колебаний, потенциальной энергии, зависящей от ориентации молекул, и т.д.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- 1. Аналитическая геометрия на плоскости
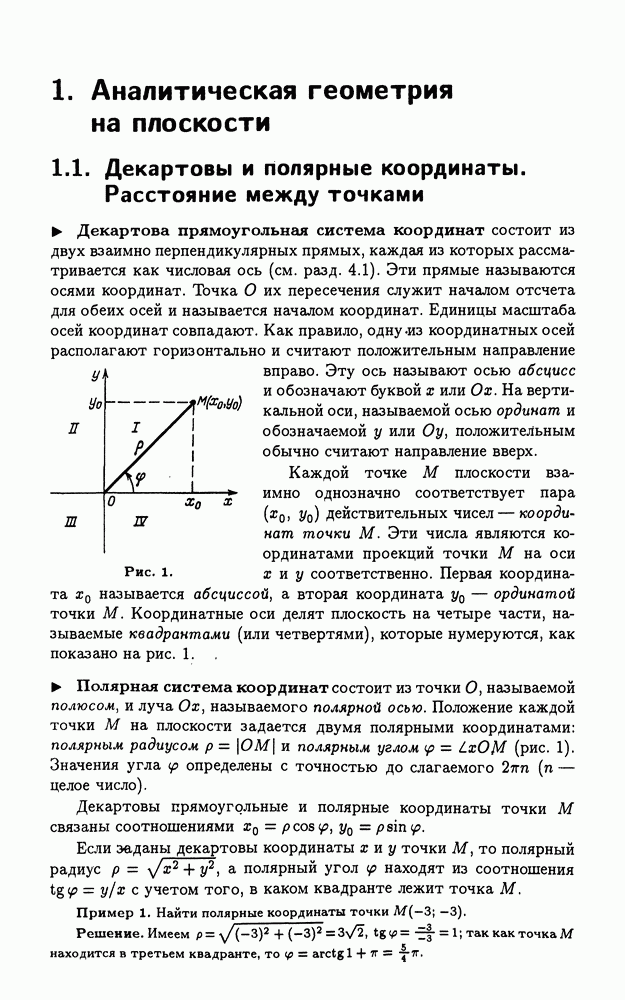
- 1.1. Декартовы и полярные координаты. Расстояние между точками
- 1.2. Деление отрезка в данном отношении. Площадь многоугольника
- 1.3. Различные виды уравнения прямой
- 1.4. Угол между прямыми. Расстояние от точки до прямой
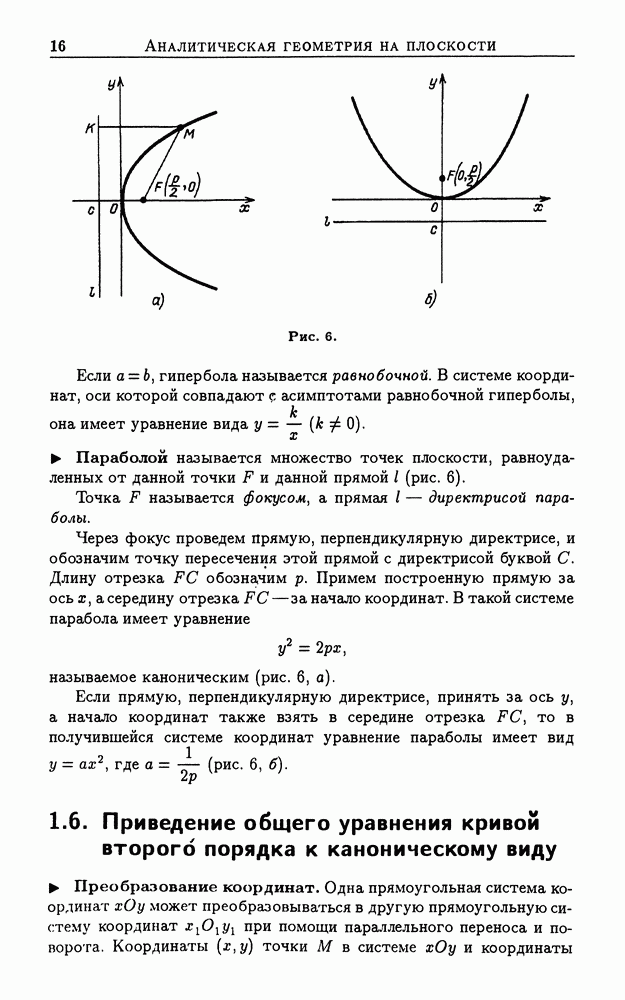
- 1.5. Окружность, эллипс, гипербола и парабола
- 1.6. Приведение общего уравнения кривой второго порядка к каноническому виду
- 2. Аналитическая геометрия в пространстве
- 2.2. Векторы
- 2.3. Действия над векторами. Скалярное произведение
- 2.4. Векторное и смешанное произведения
- 2.5. Плоскость в пространстве
- 2.6. Прямая в пространстве
- 2.7. Прямая и плоскость в пространстве
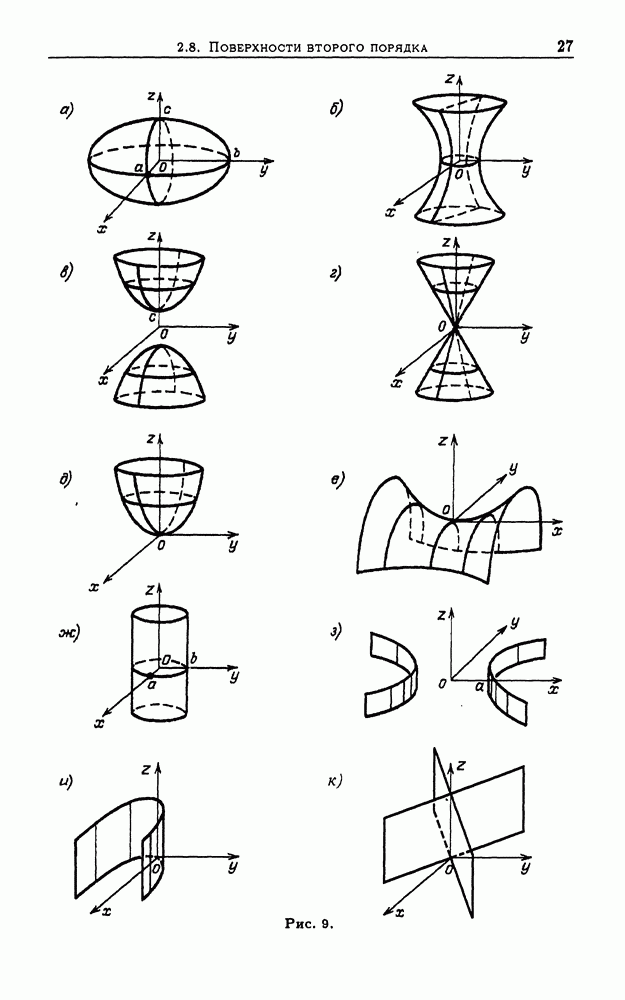
- 2.8. Поверхности второго порядка
- 3. Линейная алгебра
- 3.2. Матрицы
- 3.3. Системы линейных уравнений
- 3.4. Системы n-мерных векторов. Собственные значения и собственные векторы матрицы
- 4. Основные понятия математического анализа
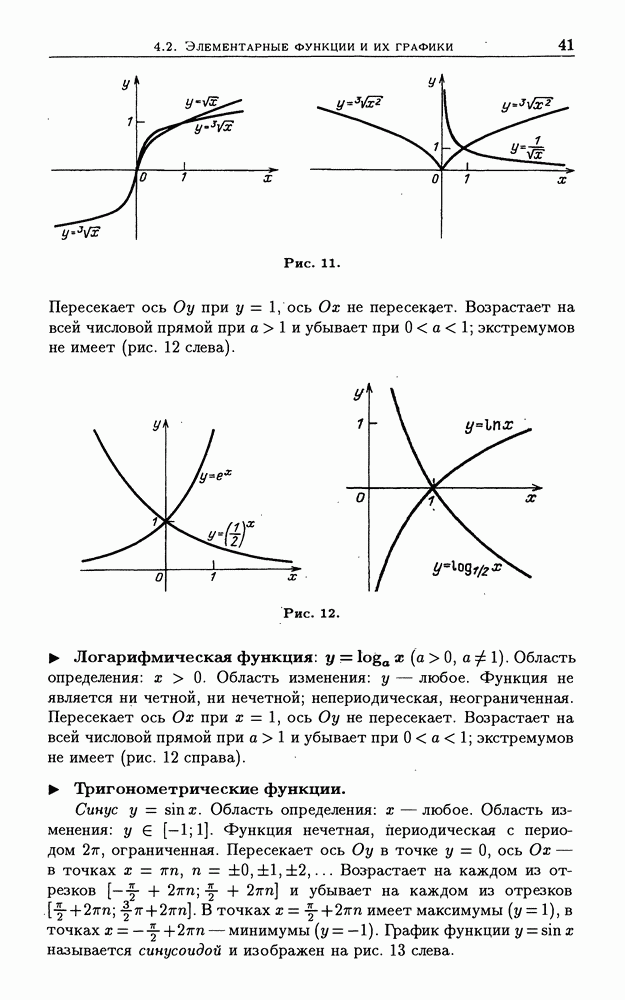
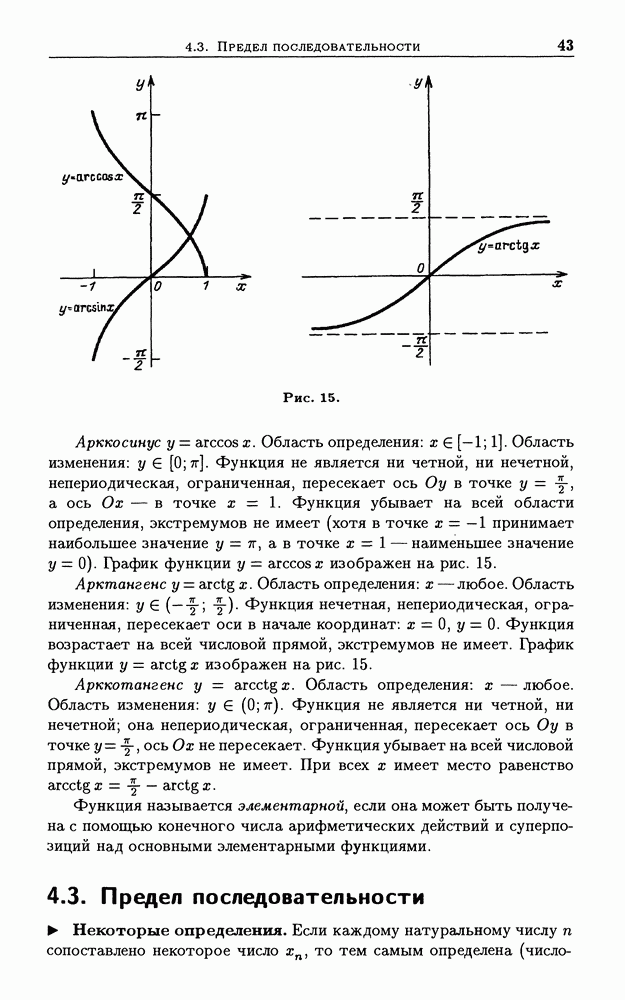
- 4.2. Элементарные функции и их графики
- 4.3. Предел последовательности
- 4.4. Предел функции
- 4.5. Бесконечно малые и бесконечно большие функции
- 4.6. Непрерывность
- 4.7. Асимптоты графика функции
- 5. Дифференциальное исчисление функций одной переменной
- 5.2. Таблица производных и правила дифференцирования
- 5.3. Теоремы о дифференцируемых функциях. Правило Лопиталя
- 5.4. Производные и дифференциалы высших порядков. Формула Тейлора
- 5.5. Экстремумы. Точки перегиба
- 5.6. Общая схема исследования функции и построение графика
- 6. Функции нескольких переменных
- 6.1. Точечные множества. Функции. Предел и непрерывность
- 6.2. Дифференцирование функций нескольких переменных
- 6.3. Производная по направлению. Геометрические приложения
- 6.4. Экстремумы функций нескольких переменных
- 7. Неопределенный интеграл
- 7.1. Первообразная. Неопределенный интеграл и его свойства
- 7.2. Таблица основных интегралов. Примеры интегрирования
- 7.3. Интегрирование по частям. Метод замены переменной
- 7.4. Интегрирование рациональных функций
- 7.5. Интегрирование иррациональных функций
- 7.6. Интегрирование показательных и тригонометрических функций
- 8. Определенный интеграл
- 8.1. Основные определения. Геометрический смысл определенного интеграла
- 8.2. Свойства определенного интеграла
- 8.3. Геометрические и физические приложения определенного интеграла
- 8.4. Несобственные интегралы
- 9. Двойные и тройные интегралы
- 9.1. Определение и свойства двойного интеграла
- 9.2. Вычисление двойного интеграла
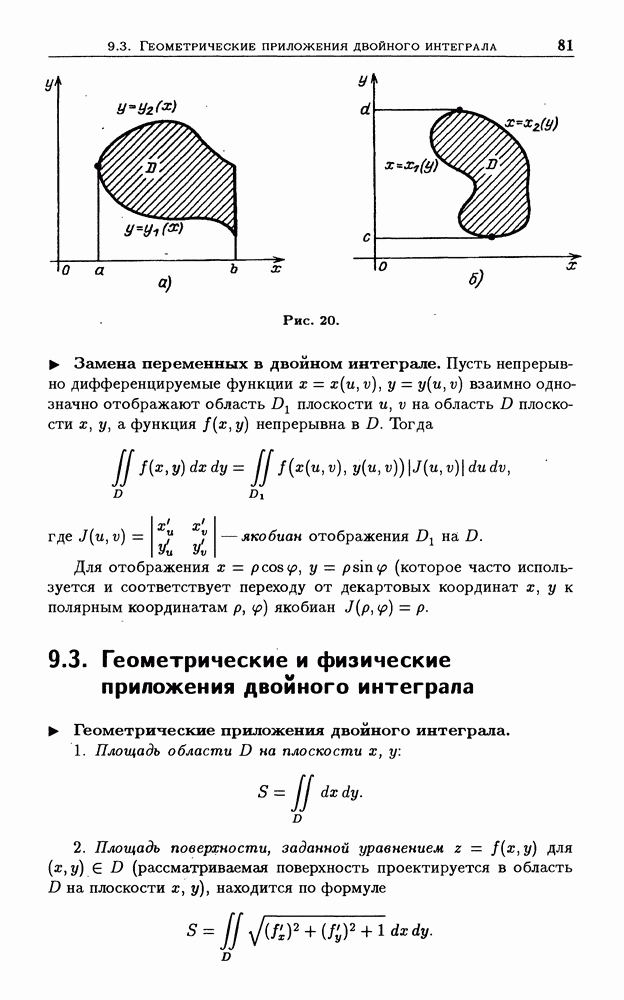
- 9.3. Геометрические и физические приложения двойного интеграла
- 9.4. Определение и свойства тройного интеграла
- 9.5. Вычисление тройного интеграла. Некоторые приложения
- 10. Криволинейные и поверхностные интегралы
- 10.2. Криволинейный интеграл второго рода
- 10.3. Поверхностный интеграл первого рода
- 10.4. Поверхностный интеграл второго рода
- 10.5. Дифференциальные операции и интегральные формулы теории поля
- 11. Ряды
- 11.1. Числовые ряды
- 11.2. Функциональные ряды
- 11.3. Степенные ряды
- 11.4. Ряд Фурье
- 11.5. Интеграл Фурье. Преобразование Фурье
- 12. Обыкновенные дифференциальные уравнения
- 12.2. Дифференциальные уравнения высших порядков
- 12.3. Линейные уравнения n-го порядка
- 12.4. Решение линейных однородных уравнений n-го порядка с постоянными коэффициентами
- 12.5. Линейные неоднородные уравнения n-го порядка
- 12.6. Системы обыкновенных дифференциальных уравнений
- 13. Приближенные вычисления
- 13.1. Метод наименьших квадратов
- 13.2. Приближенное решение алгебраических уравнений
- 13.3. Вычисление определенного интеграла
- 13.4. Численное интегрирование дифференциальных уравнений
- 14. Теория вероятностей
- 14.1. Правила и формулы комбинаторики
- 14.2. Основные понятия теории вероятностей
- 14.3. Условная вероятность. Теоремы и формулы теории вероятностей
- 14.4. Математическое ожидание и дисперсия
- 14.5. Закон больших чисел
- 1. Физические основы механики
- 1.1. Кинематика точки
- 1.2. Кинематика твердого тела
- 1.3. Динамика
- 1.4. Закон сохранения импульса
- 1.5. Закон сохранения энергии
- 1.6. Закон сохранения момента импульса
- 1.7. Задана двух тел и движение в центральном поле
- 1.8. Поле тяготения
- 1.9. Неинерциальные системы отсчета
- 1.10. Динамика твердого тела
- 1.11. Специальная теория относительности
- 2. Молекулярная физика и термодинамика
- 2.2. Первое начало термодинамики
- 2.3. Второе начало термодинамики
- 2.4. Энтропия. Свободная энергия
- 2.5. Кинетическая теория идеального газа
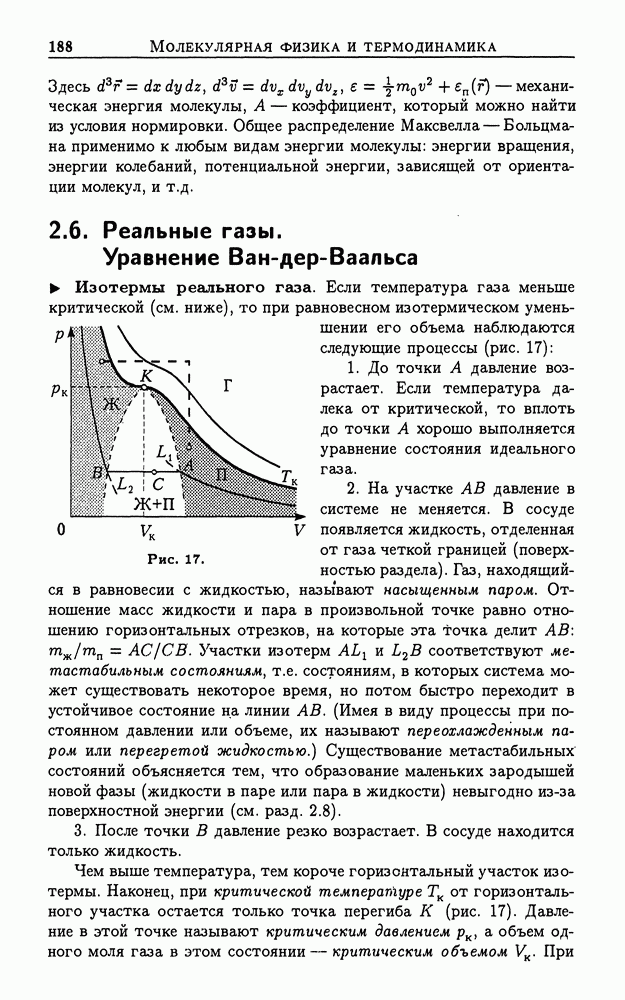
- 2.6. Реальные газы. Уравнение Ван-дер-Ваальса
- 2.7. Равновесие фаз. Фазовые переходы
- 2.8. Поверхностное натяжение
- 2.9. Явления переноса в газах
- 3. Электродинамика
- 3.1. Электрический заряд. Закон Кулона
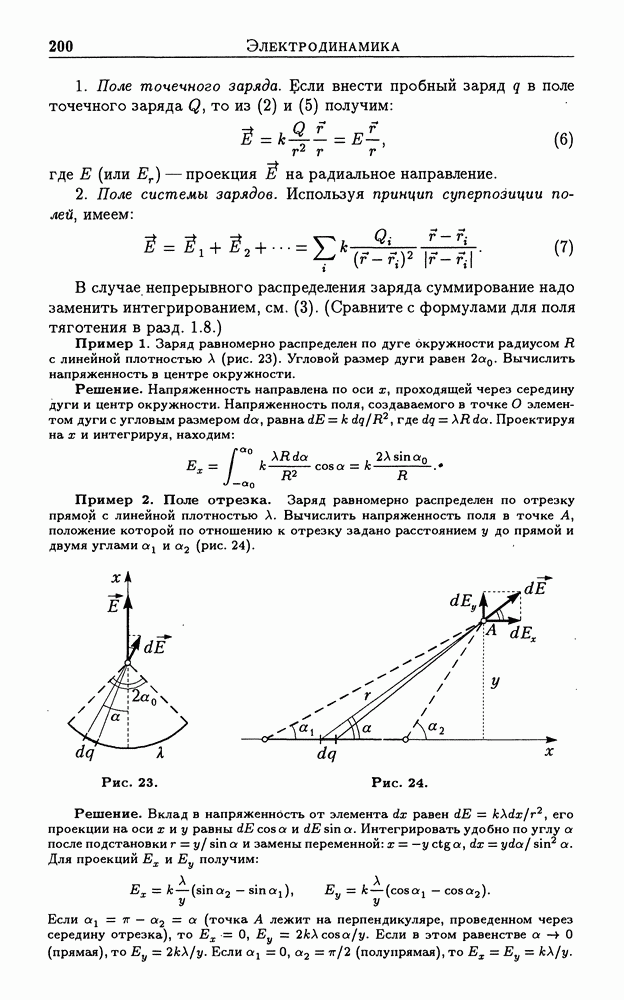
- 3.2. Электрическое поле. Напряженность поля
- 3.3. Электростатическое поле. Принцип суперпозиции для напряженности и потенциала
- 3.4. Теорема Гаусса
- 3.5. Электростатика проводников
- 3.6. Электростатика диэлектриков
- 3.7. Конденсаторы
- 3.8. Энергия электростатического поля
- 3.9. Постоянный ток
- 3.10. Магнитное поле. Сила Лоренца и закон Ампера
- 3.11. Вычисление магнитной индукции
- 3.12. Циркуляция и поток вектора магнитной индукции
- 3.13. Магнитное поле в веществе
- 3.14. Электромагнитная индукция
- 3.15. Уравнения Максвелла
- 4. Колебания и волны
- 4.1. Гармонические колебания. Сложение колебаний
- 4.2. Свободные незатухающие колебания
- 4.3. Затухающие и вынужденные колебания
- 4.4. Упругие волны
- 4.5. Электромагнитные волны
- 5. Оптика
- 5.1. Геометрическая оптика. Фотометрия
- 5.2. Интерференция света
- 5.3. Дифракция
- 5.4. Поляризация света. Формулы Френеля
- 5.5. Дисперсия и поглощение света
- 5.6. Тепловое излучение
- 5.7. Световые кванты
- Список литературы
- 1. Кинематика
- 1.1. Кинематика точки
- 1.2. Кинематика твердого тела
- 1.3. Плоскопараллельное движение твердого тела
- 1.4. Произвольное движение твердого тела
- 1.5. Сложное движение точки
- 2. Основные понятия и аксиомы механики
- 2.2. Аксиомы механики
- 3. Статика
- 3.2. Условия уравновешенности систем сил, приложенных к твердому телу
- 3.3. Решение задан статики
- 3.4. Центр параллельных сил. Центр тяжести твердого тела
- 3.5. Распределенные силы
- 3.6. Законы трения (законы Кулона)
- 4. Динамика материальной точки
- 4.2. Первая и вторая задачи динамики
- 5. Общие теоремы динамики механической системы
- 5.2. Теорема о движении центра масс
- 5.3. Теорема об изменении количества движения
- 5.4. Теорема об изменении кинетического момента
- 5.5. Теорема об изменении кинетической энергии
- 6. Принцип Даламбера. Элементы аналитической механики
- 6.2. Классификация механических связей. Обобщенные координаты
- 6.3. Принцип возможных перемещений
- 6.4. Общее уравнение динамики (принцип Даламбера — Лагранжа)
- 6.5. Уравнения Лагранжа второго рода
- 1. Основные понятия
- 1.1. Введение. Внешние и внутренние силы
- 1.2. Напряжения и деформации в точке
- 1.3. Основные понятия и допущения
- 2. Напряженно-деформированное состояние в точке
- 2.2. Одноосное растяжение и сжатие
- 2.3. Чистый сдвиг
- 3. Центральное растяжение и сжатие
- 3.2. Напряжения и деформации при растяжении или сжатии
- 3.3. Расчеты на прочность при растяжении и сжатии
- 4. Кручение
- 4.2. Напряжения и деформации при кручении
- 4.3. Расчеты на прочность при кручении
- 5. Прямой изгиб
- 5.2. Напряжения и деформации при прямом чистом изгибе
- 5.3. Напряжения и деформации при прямом поперечном изгибе
- 5.4. Расчет на прочность при прямом изгибе
- 6. Сложное сопротивление
- 6.2. Внецентренное растяжение или сжатие
- 6.3. Изгиб с кручением
- 7. Устойчивость сжатых стержней
- 7.2. Формула Эйлера
- 7.3. Влияние способов закрепления концов стержня на величину критической силы
- 7.4. Пределы применимости формулы Эйлера
- 7.5. Расчеты сжатых стержней на устойчивость
- ПРИЛОЖЕНИЯ
- 1. Элементарные функции и их свойства
- 2. Таблица неопределенных интегралов
- 3. Решения обыкновенных дифференциальных уравнений
- 4. Ортогональные криволинейные системы координат
- 5. Некоторые физические постоянные