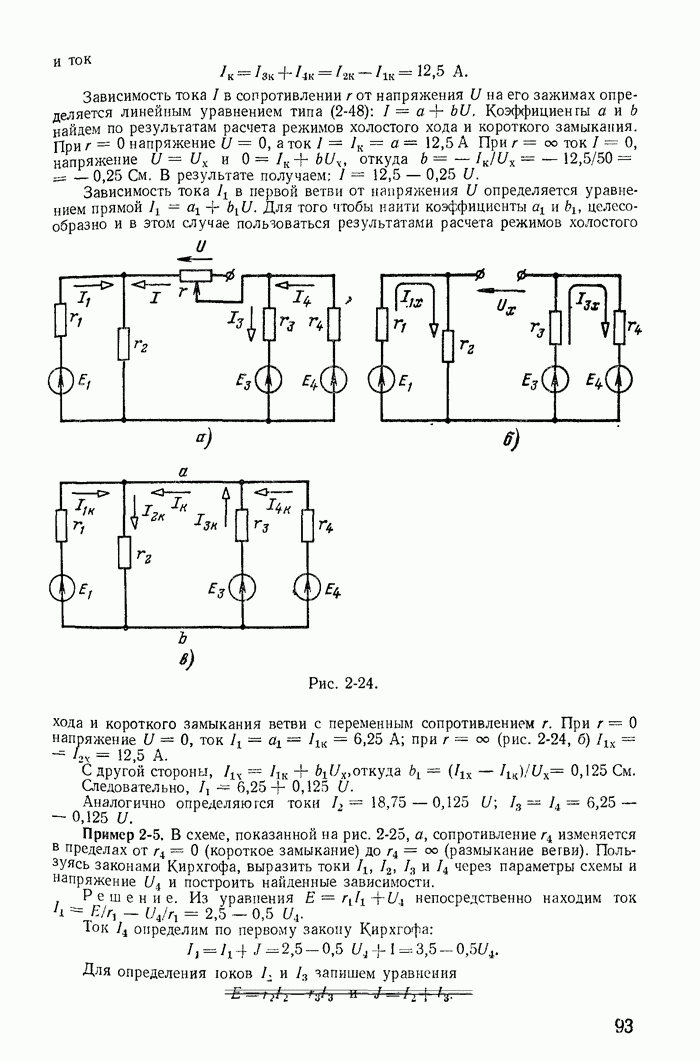
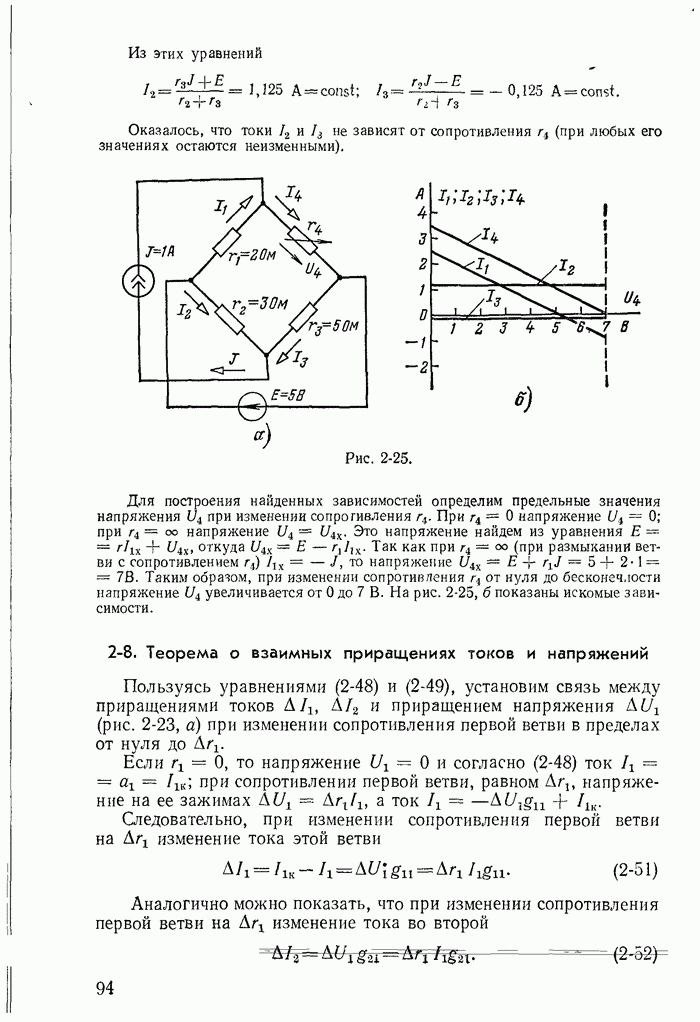
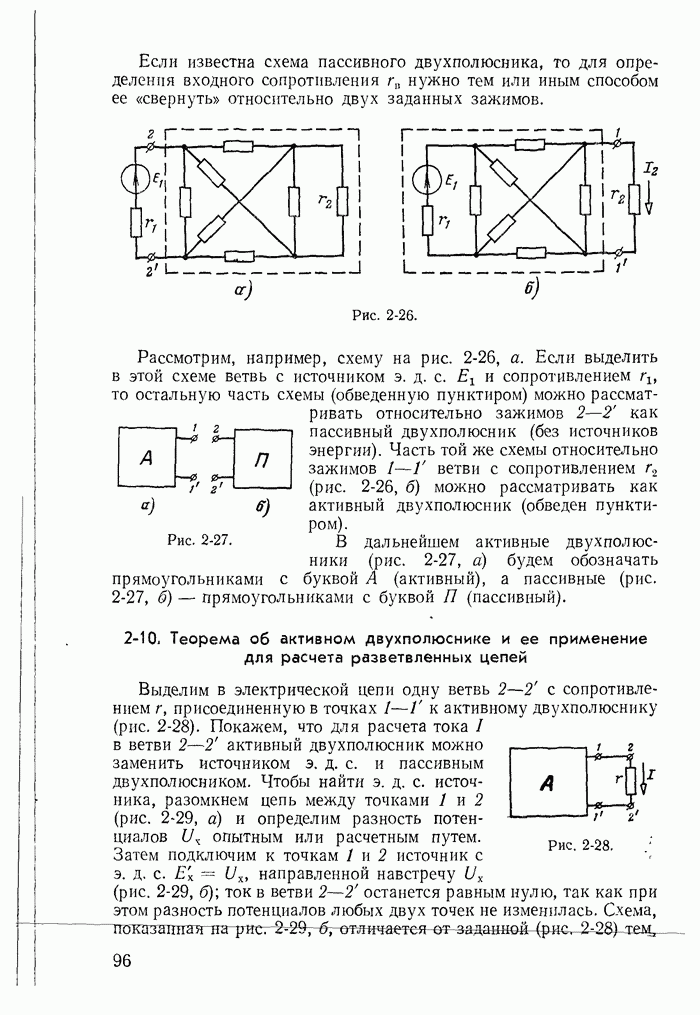
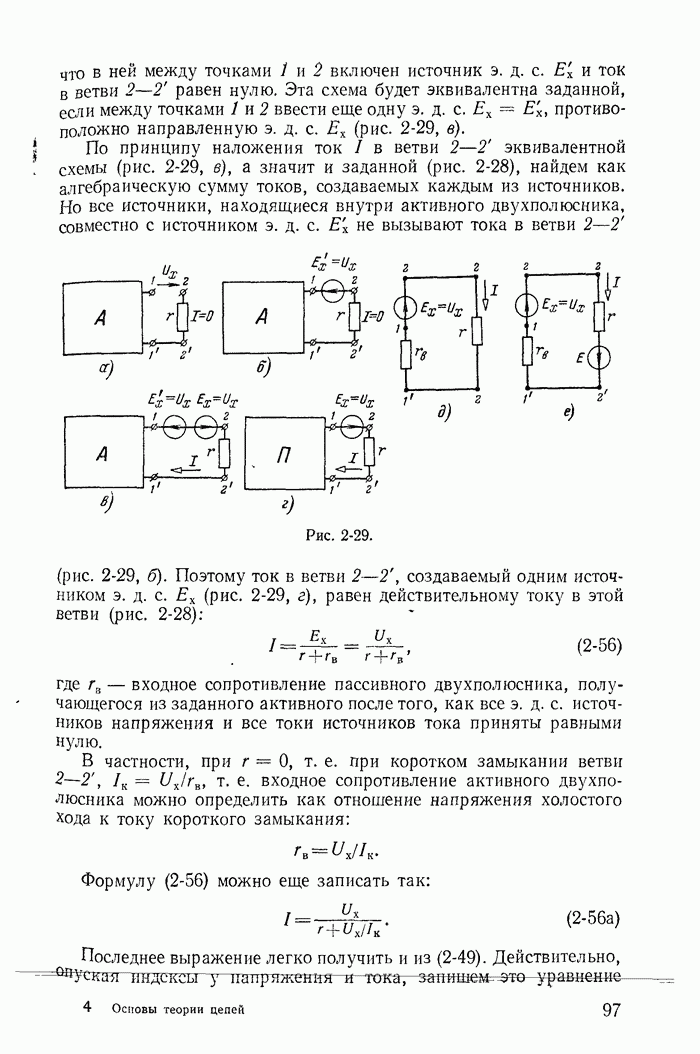
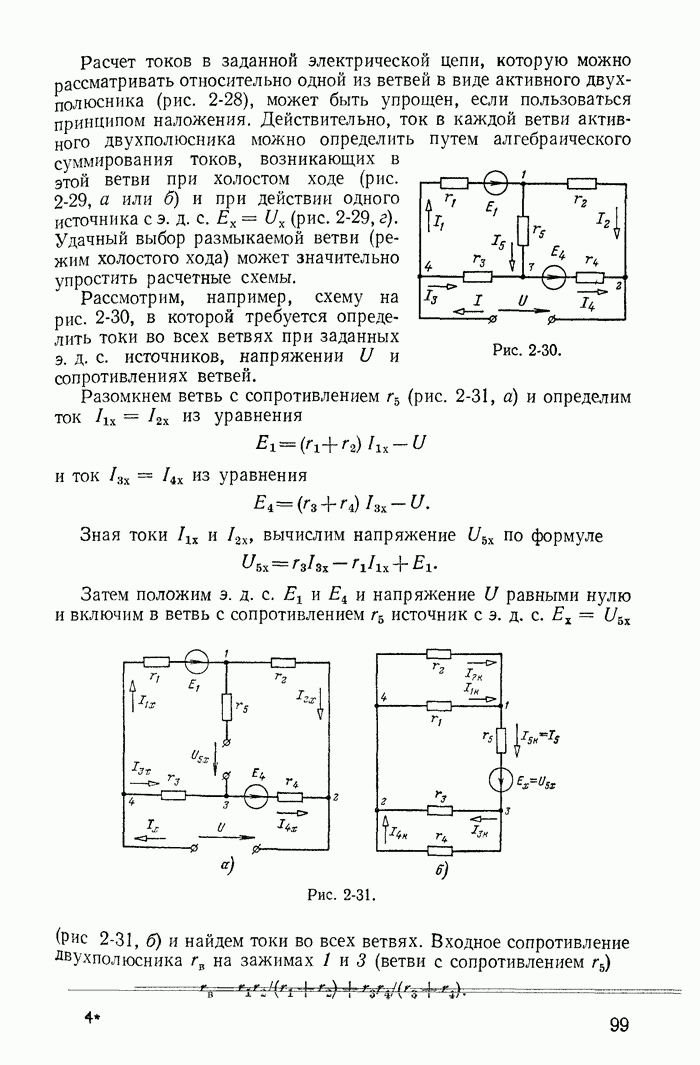
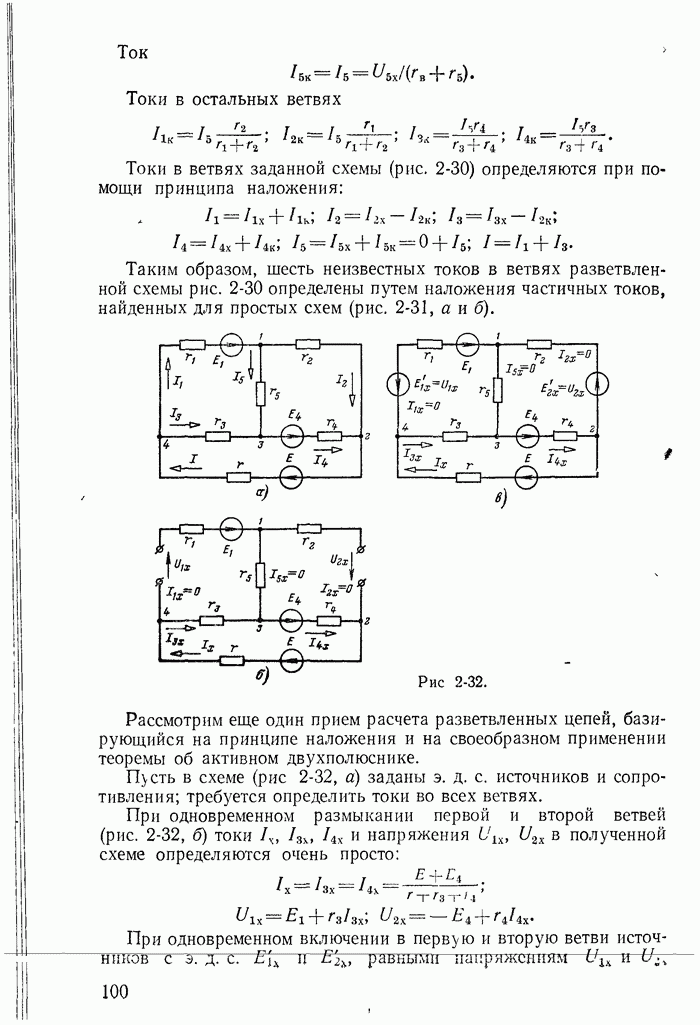
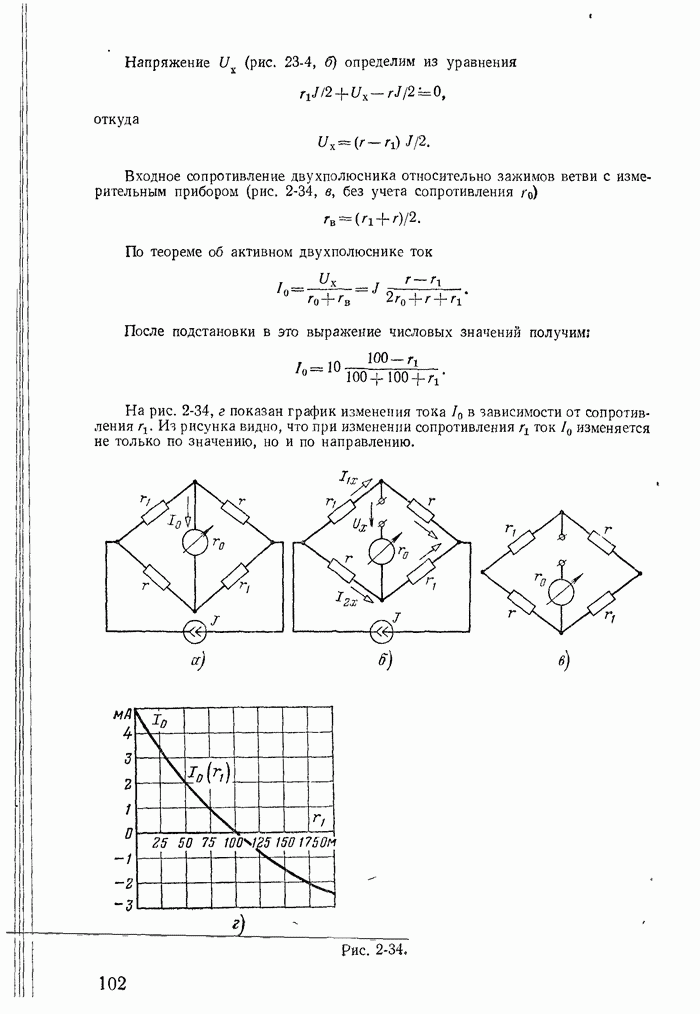
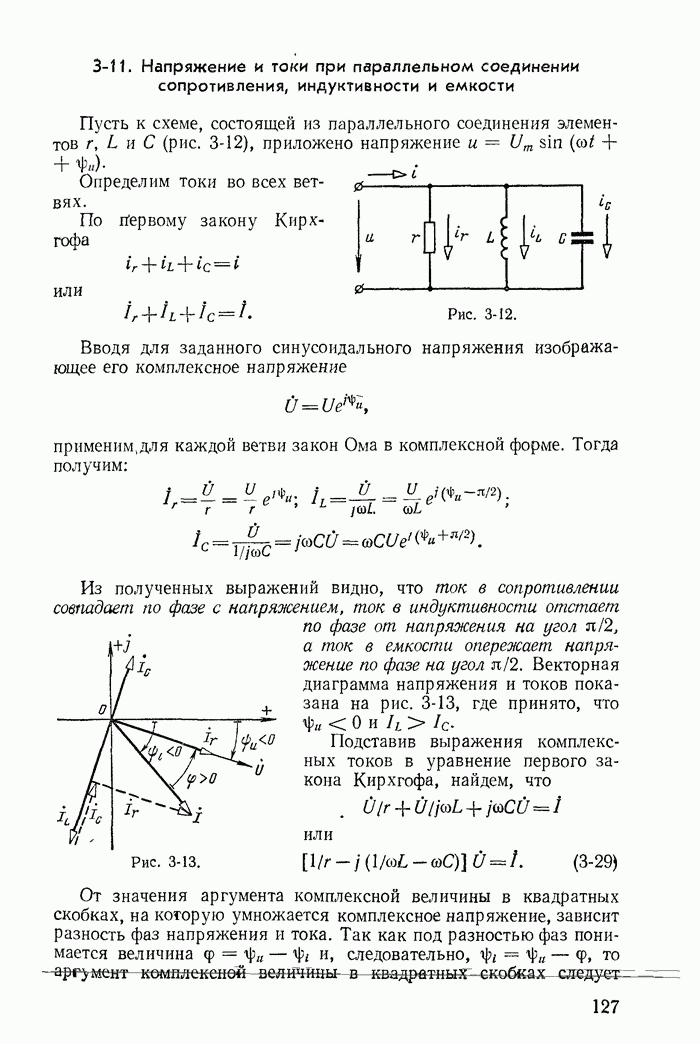
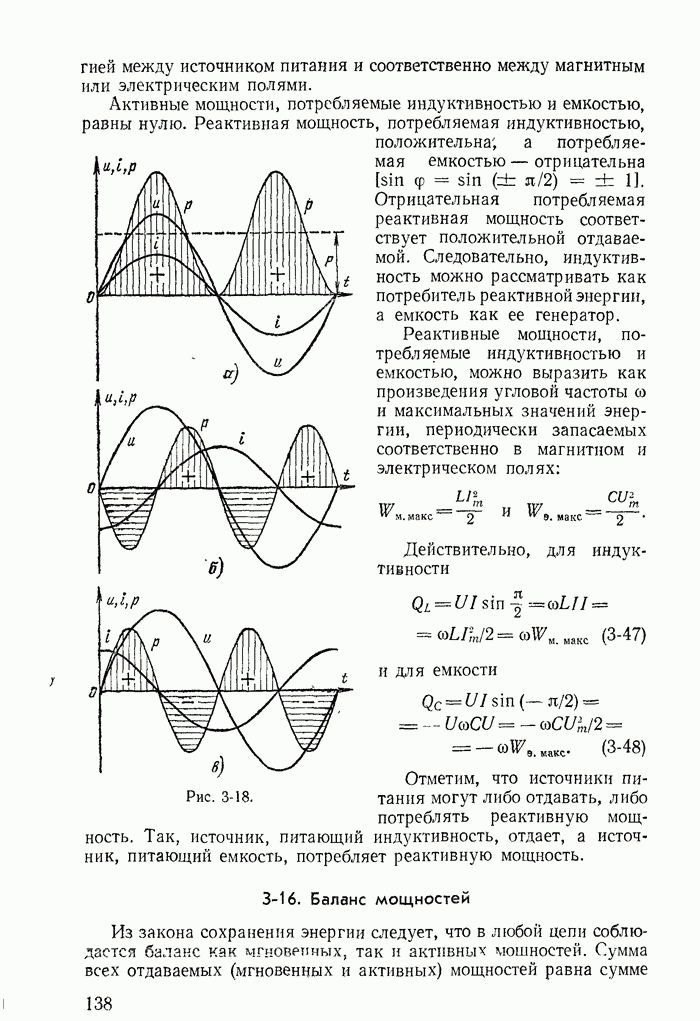
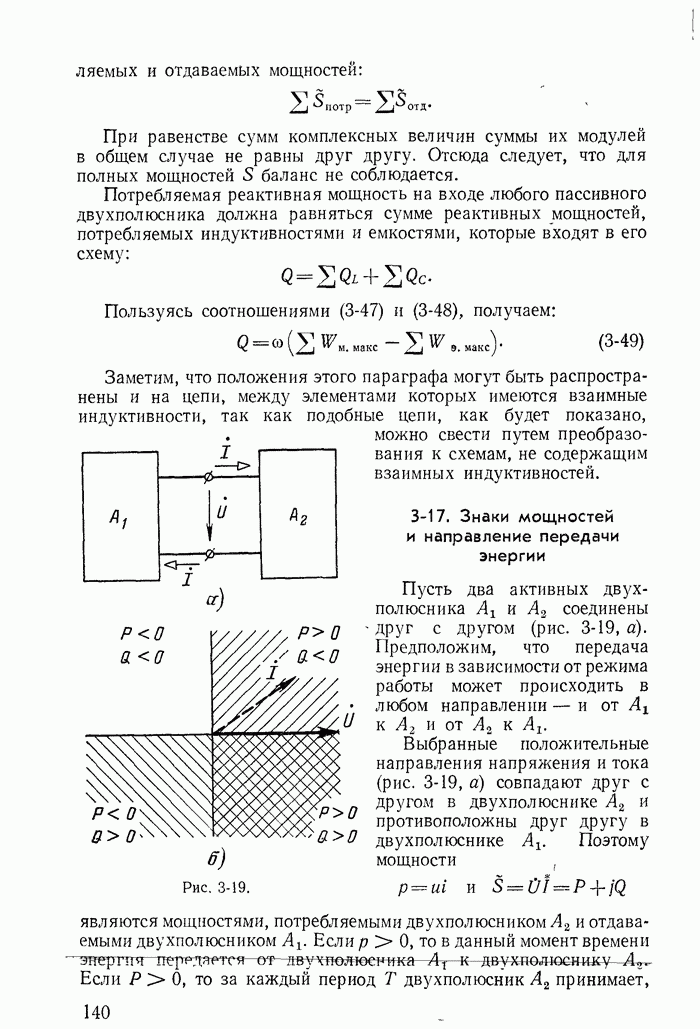
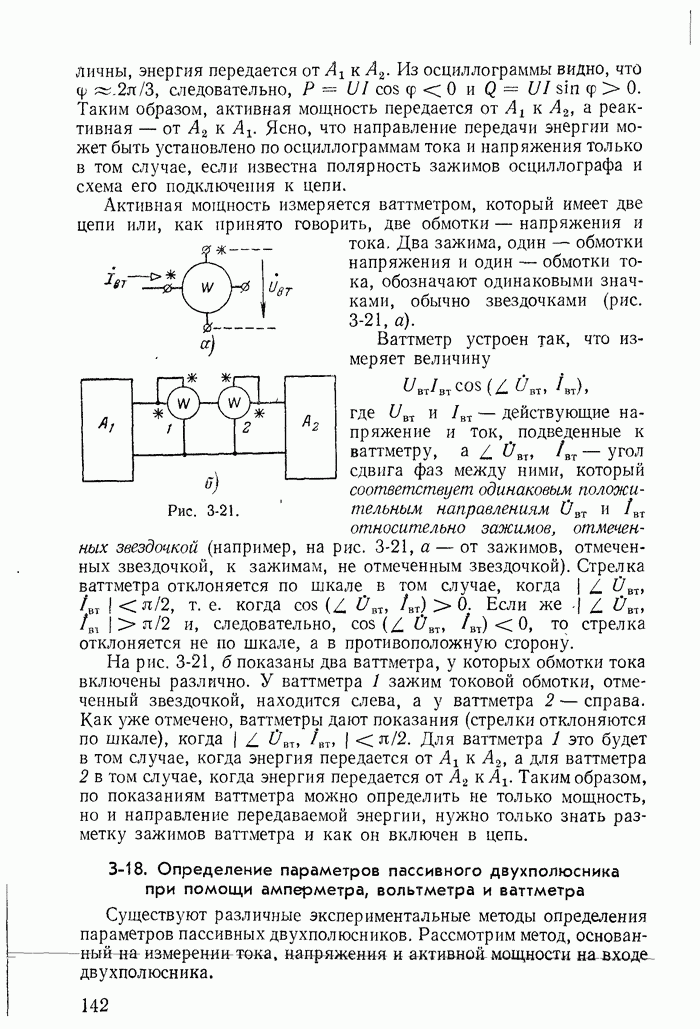
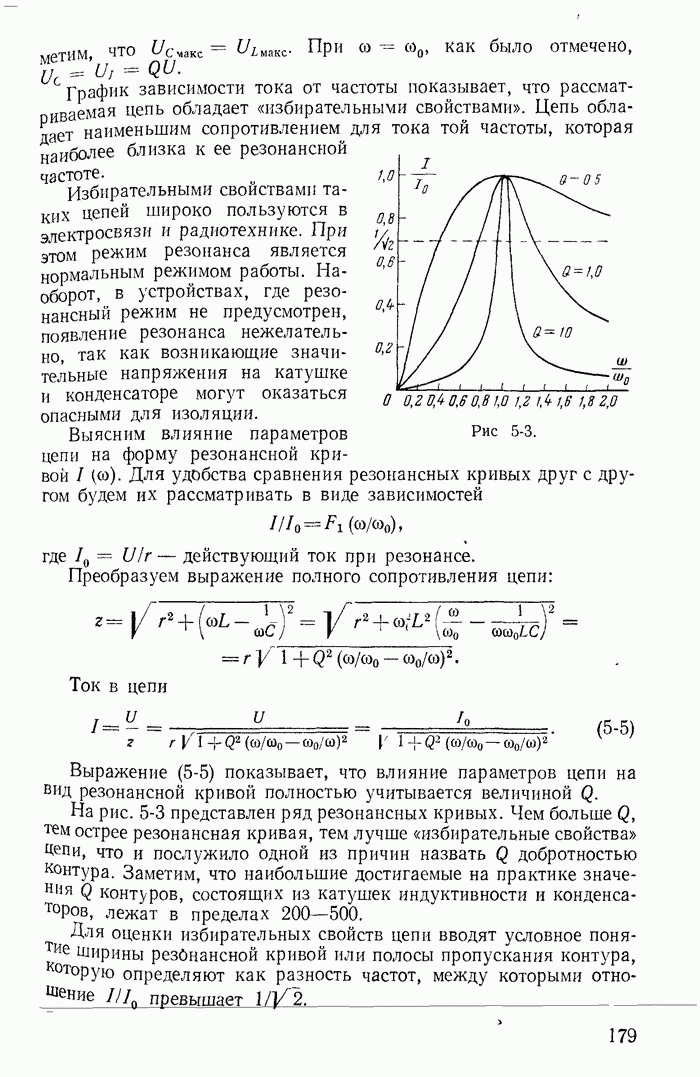
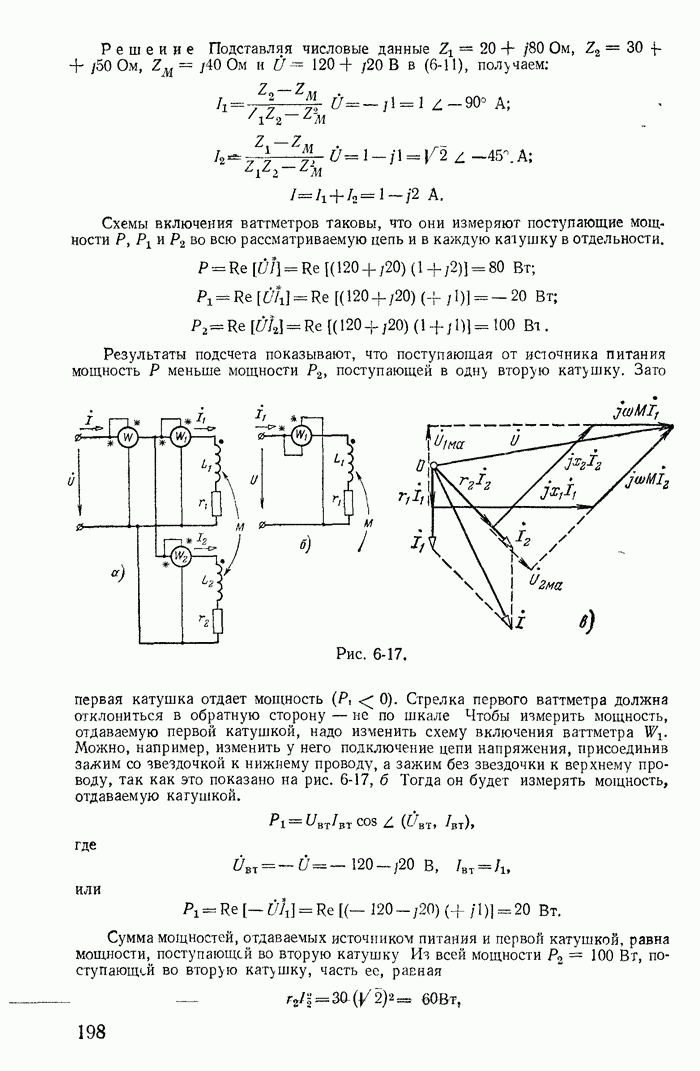
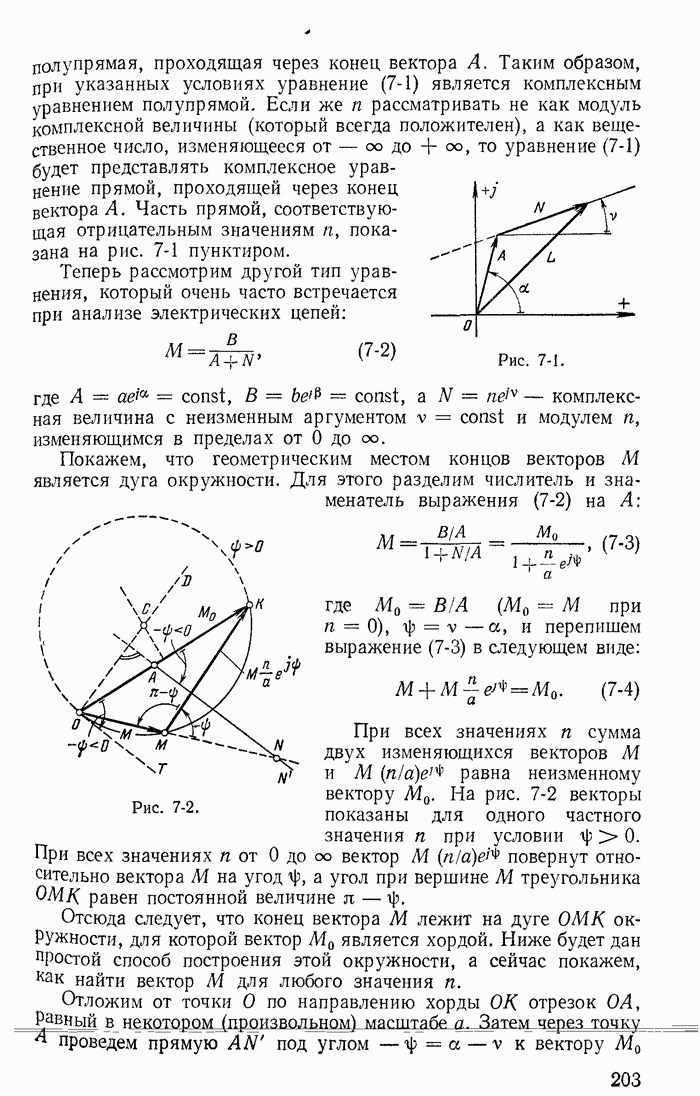
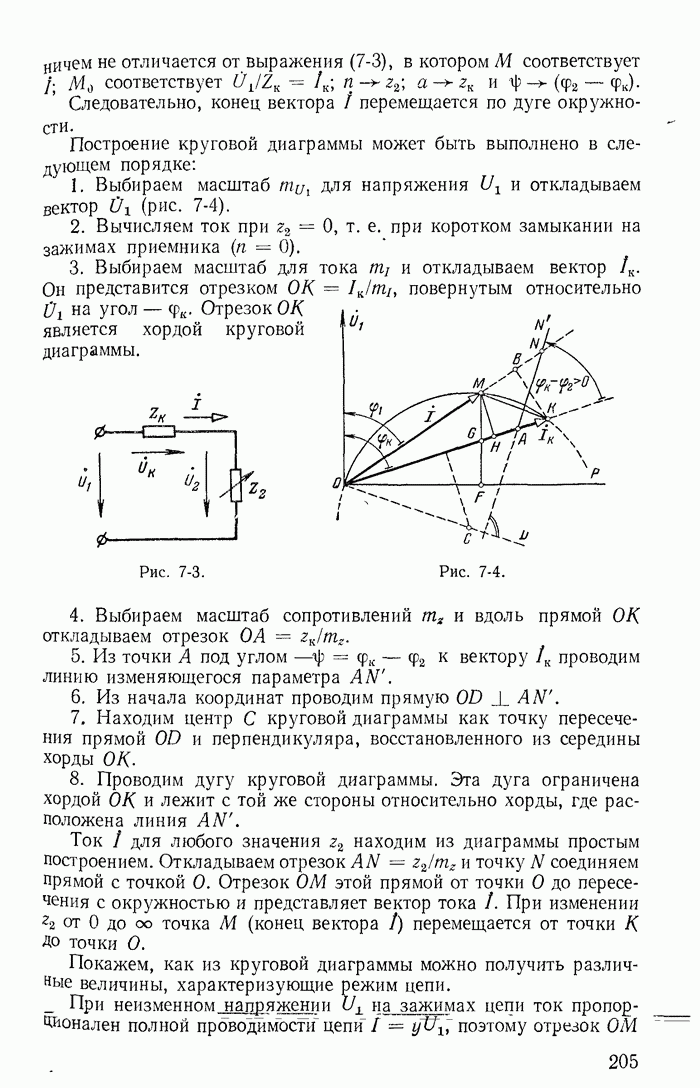
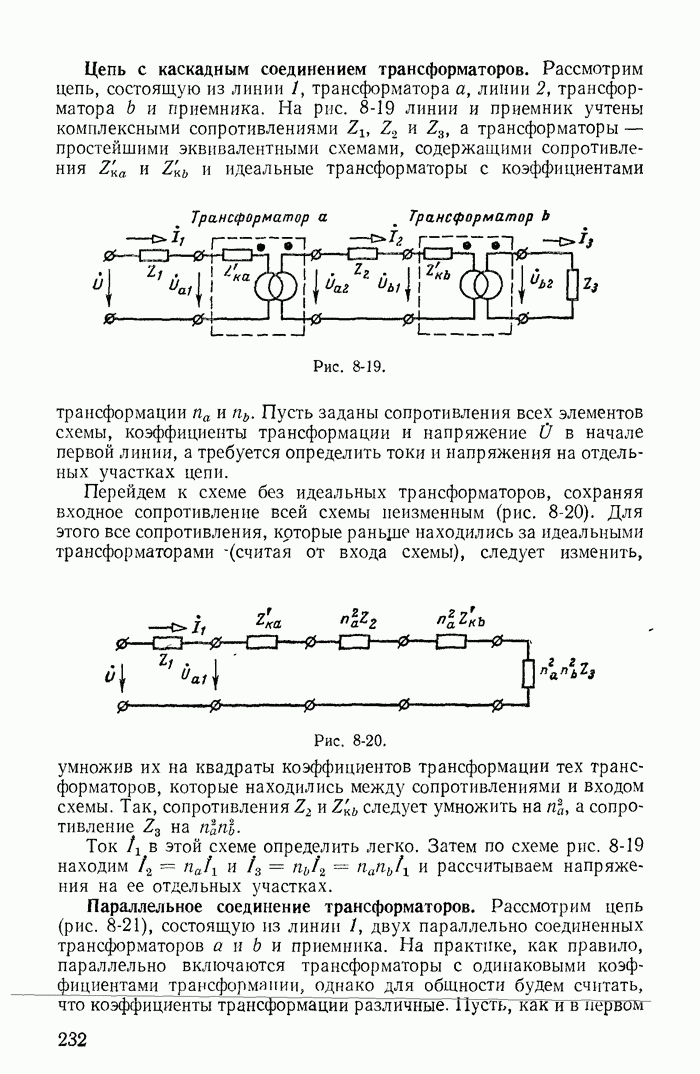
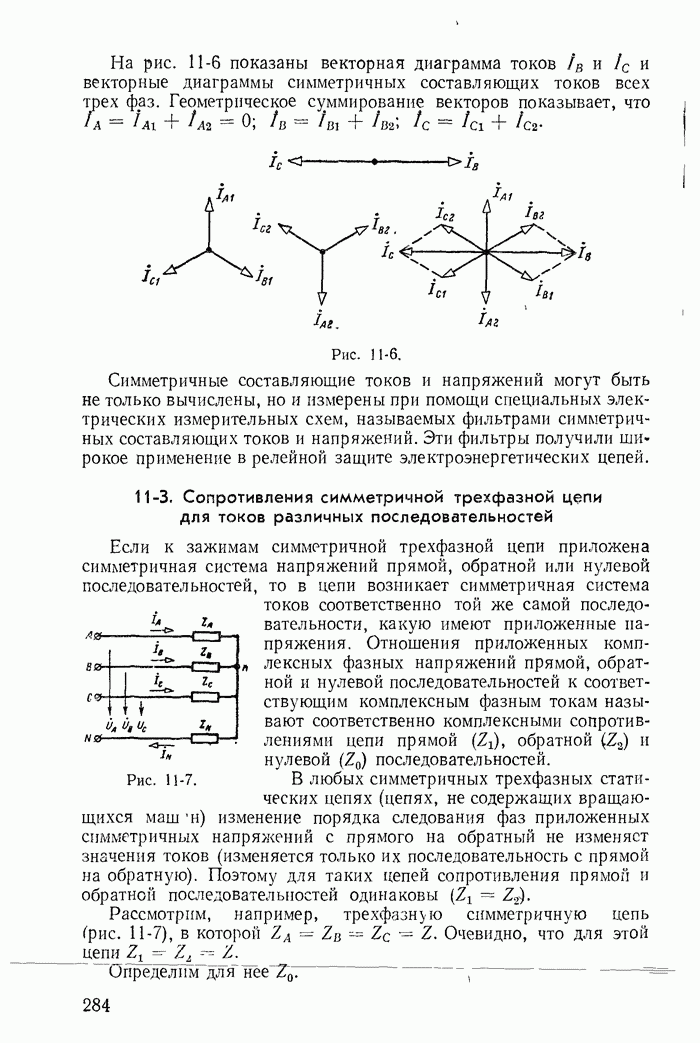
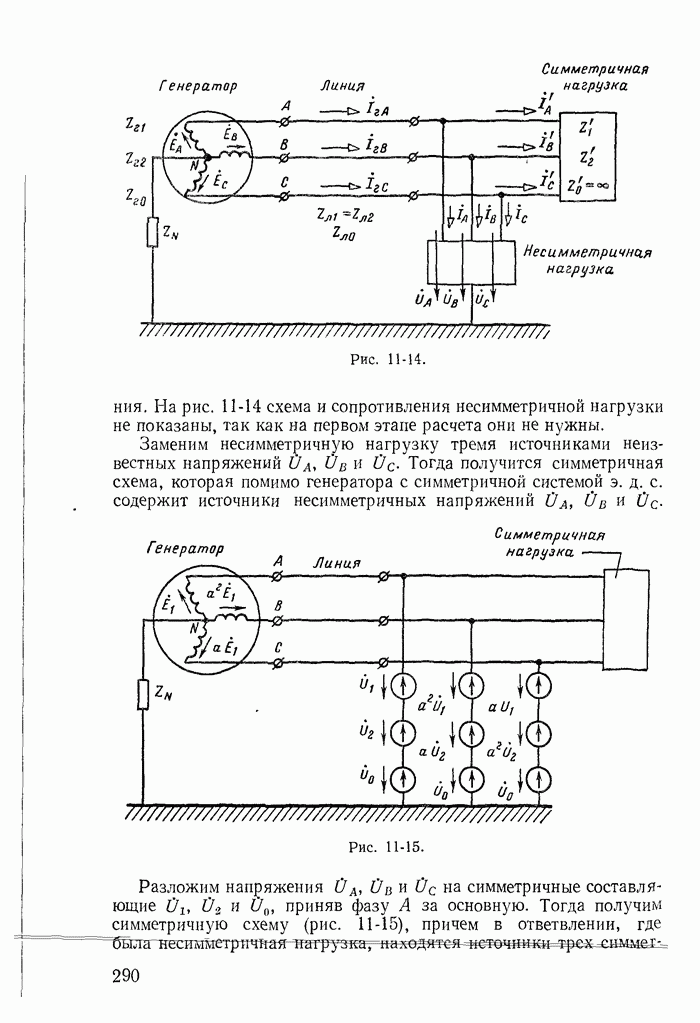
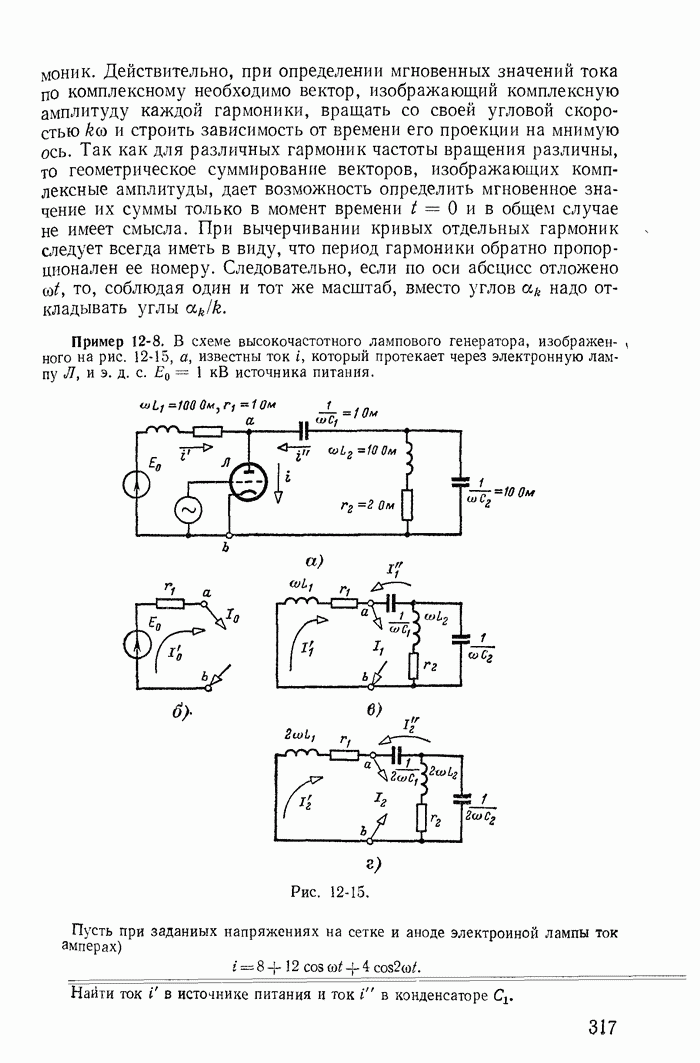
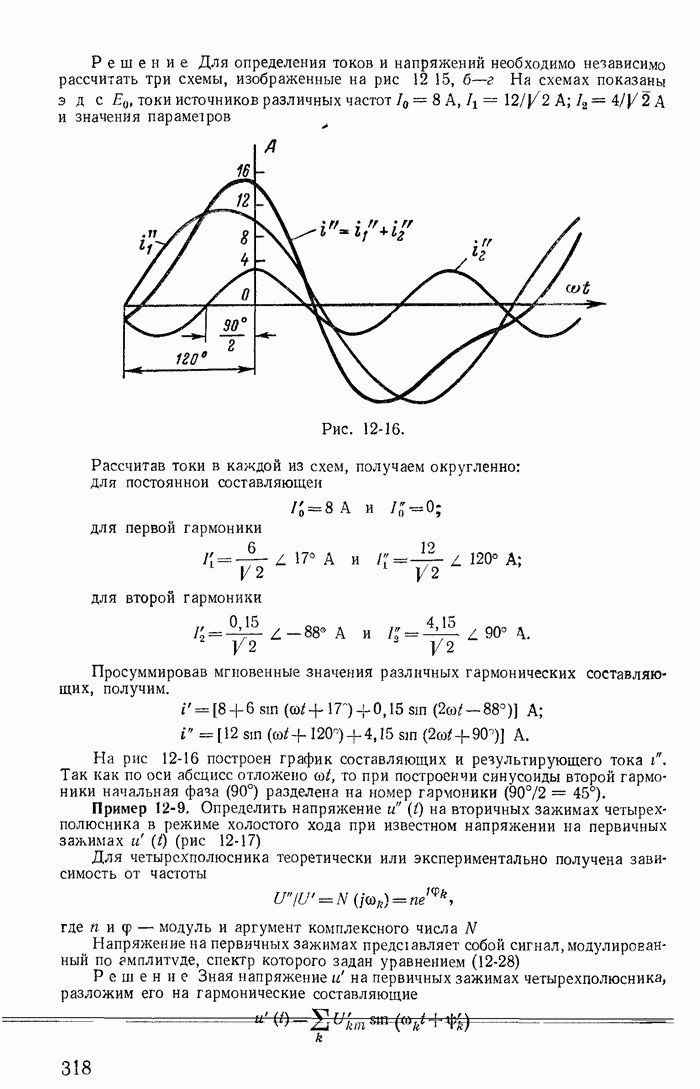
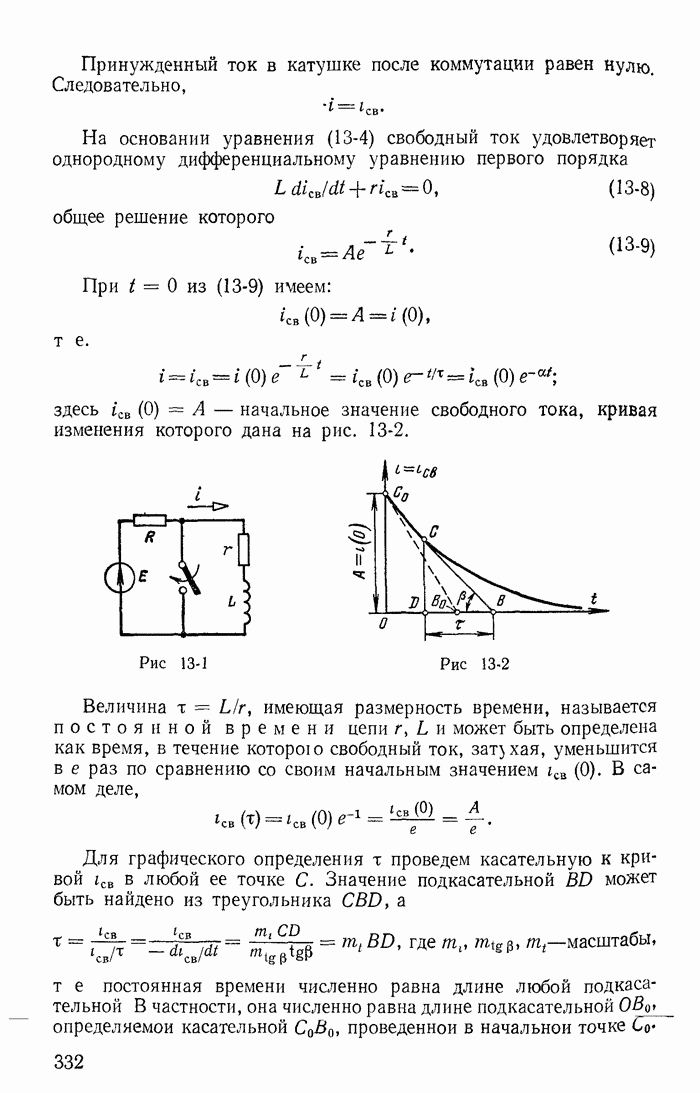
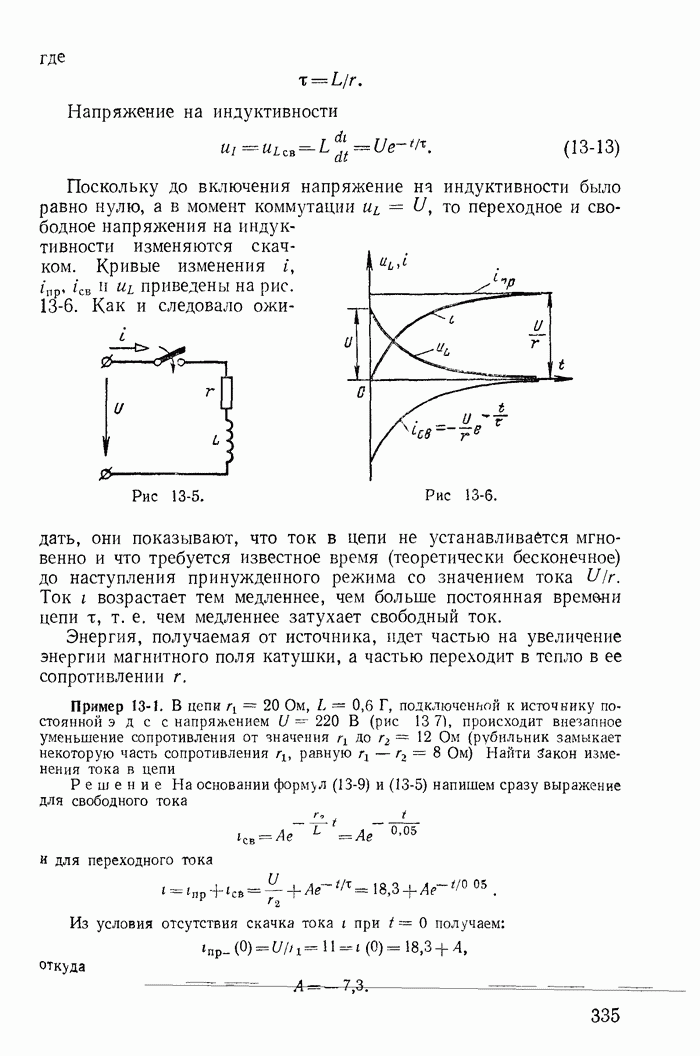
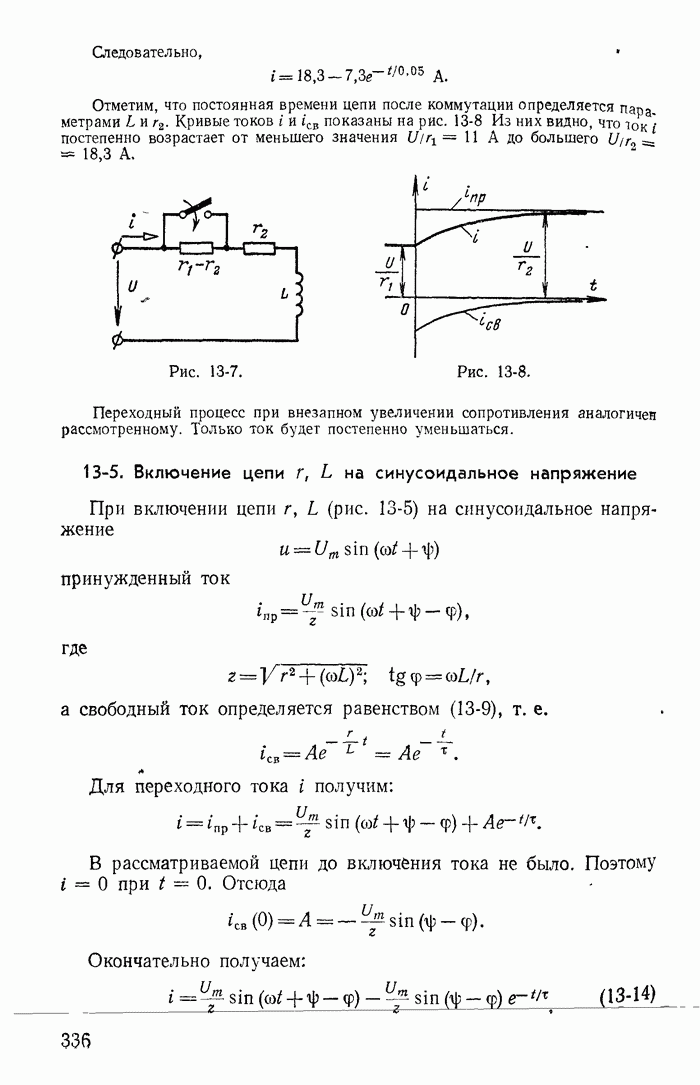
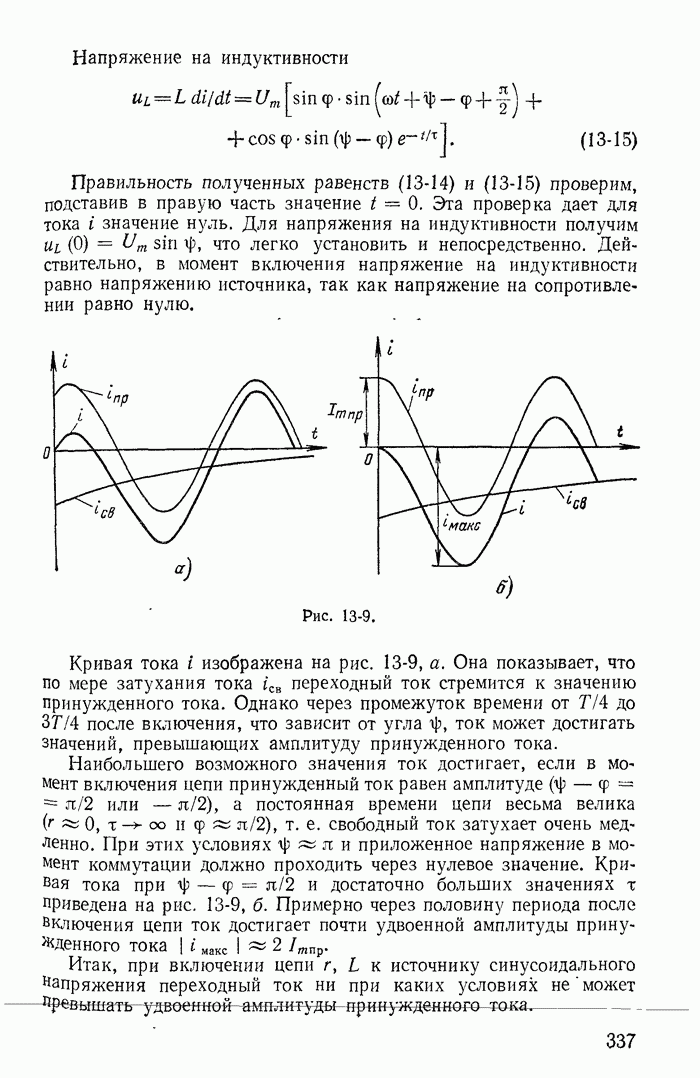
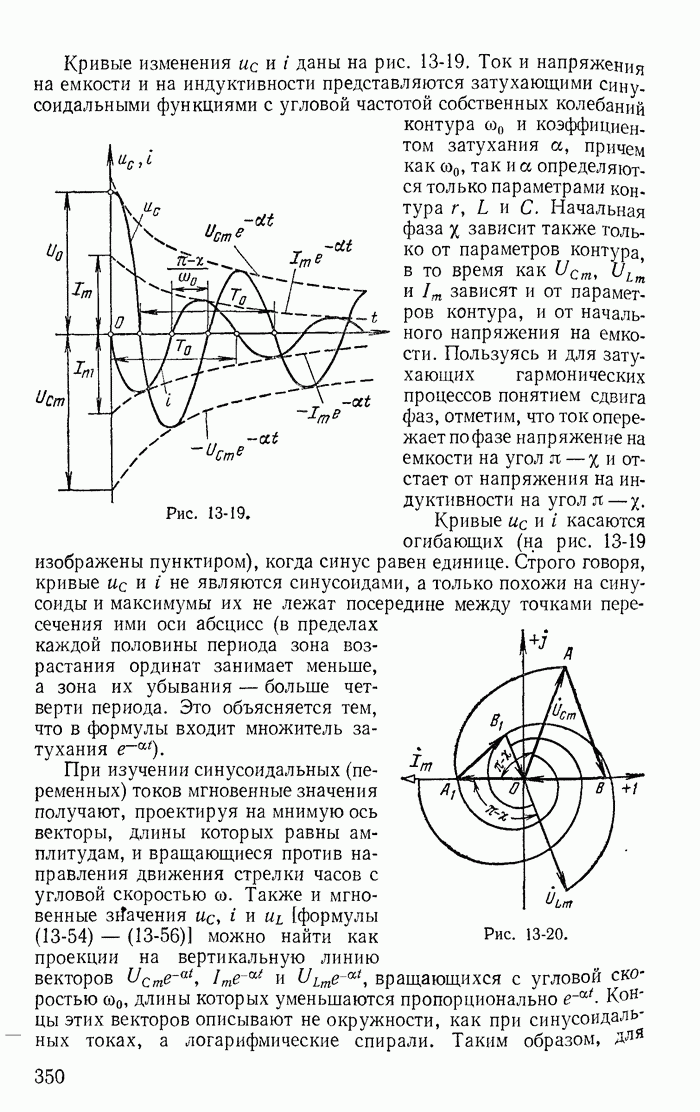
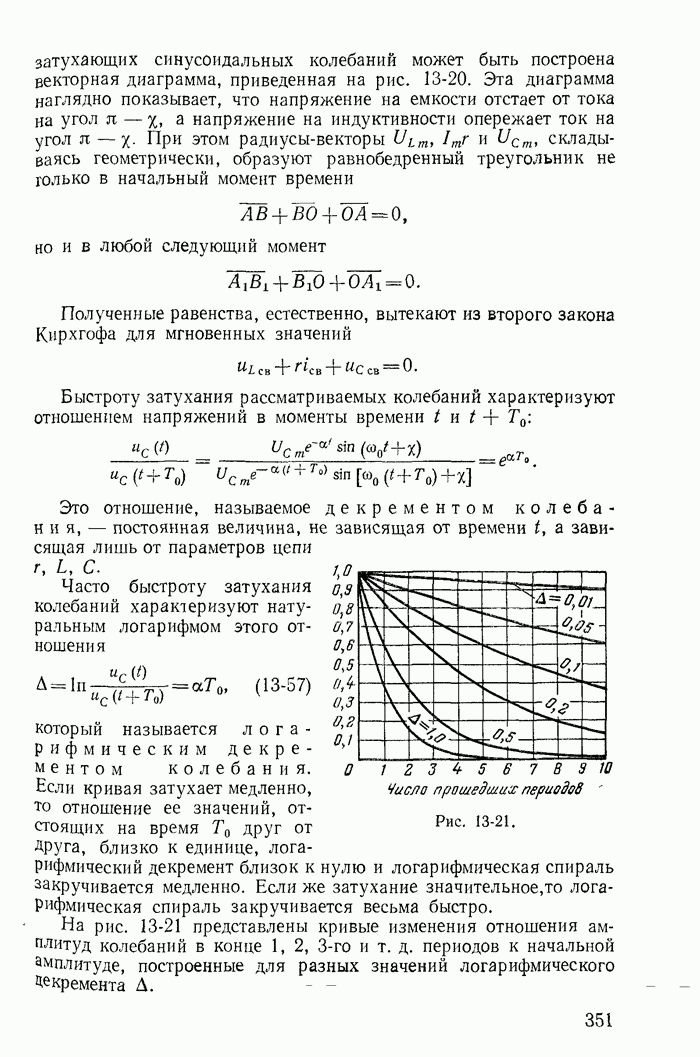
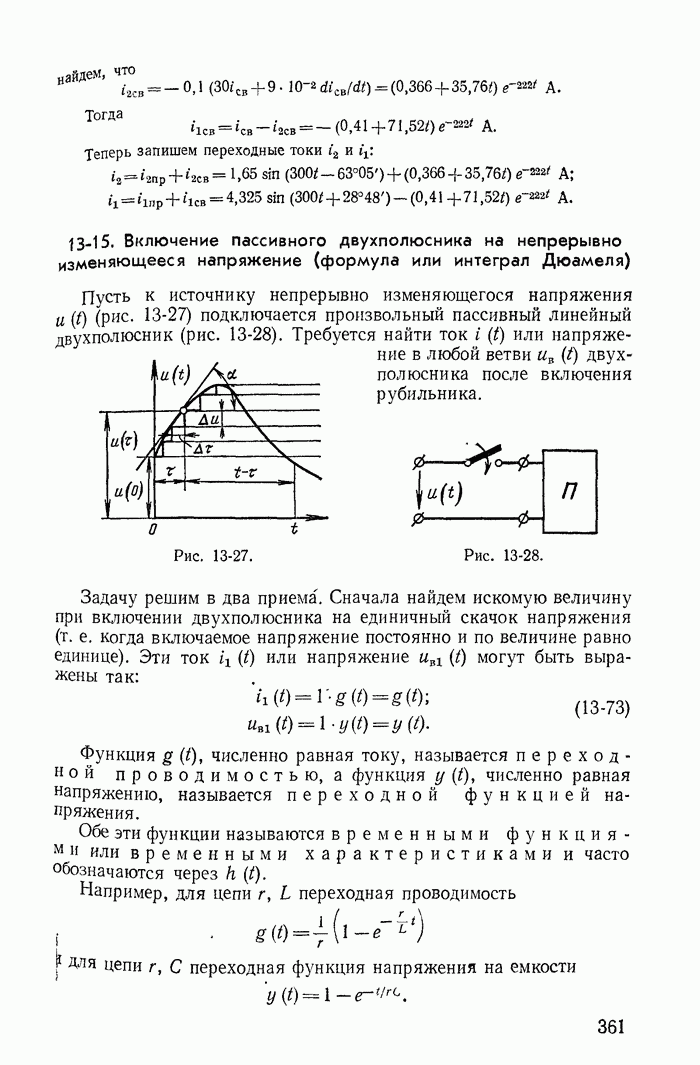
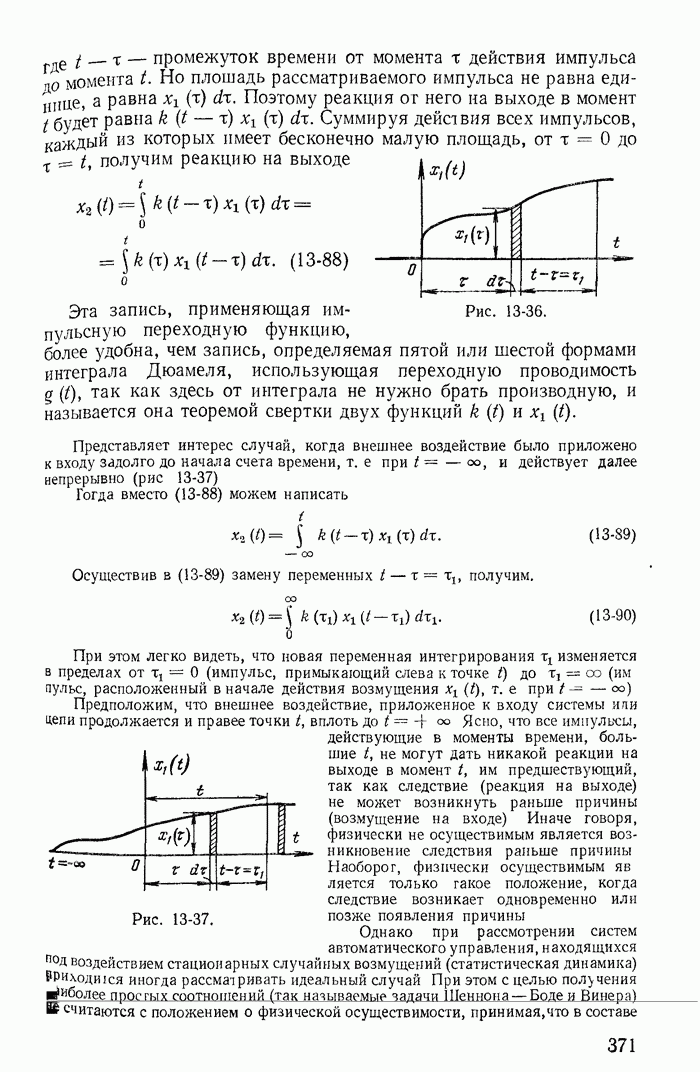
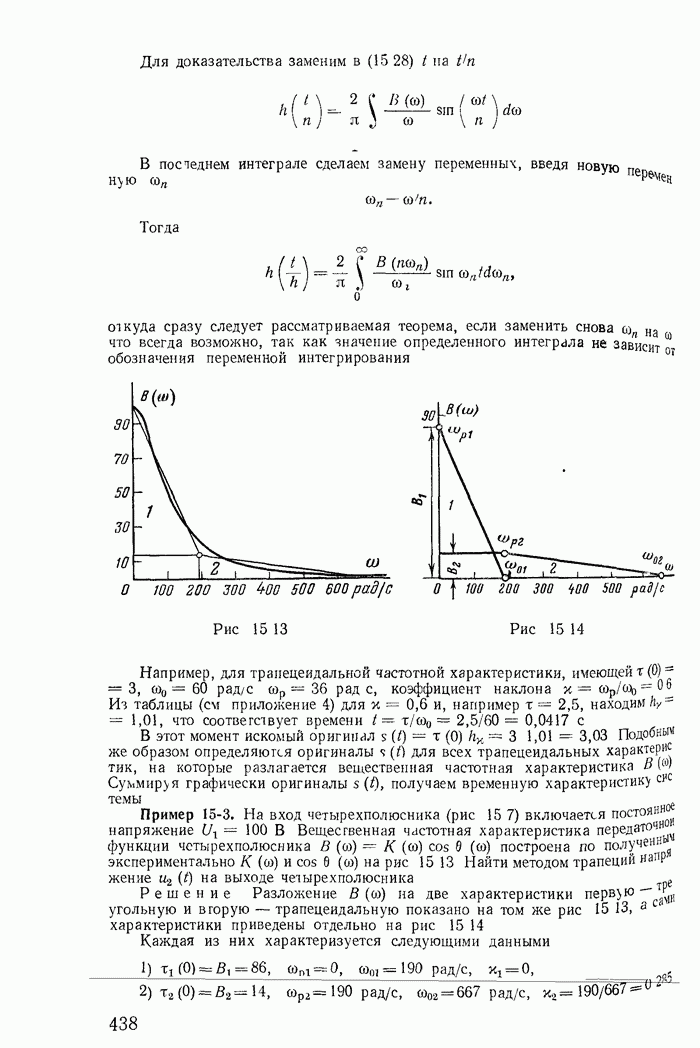
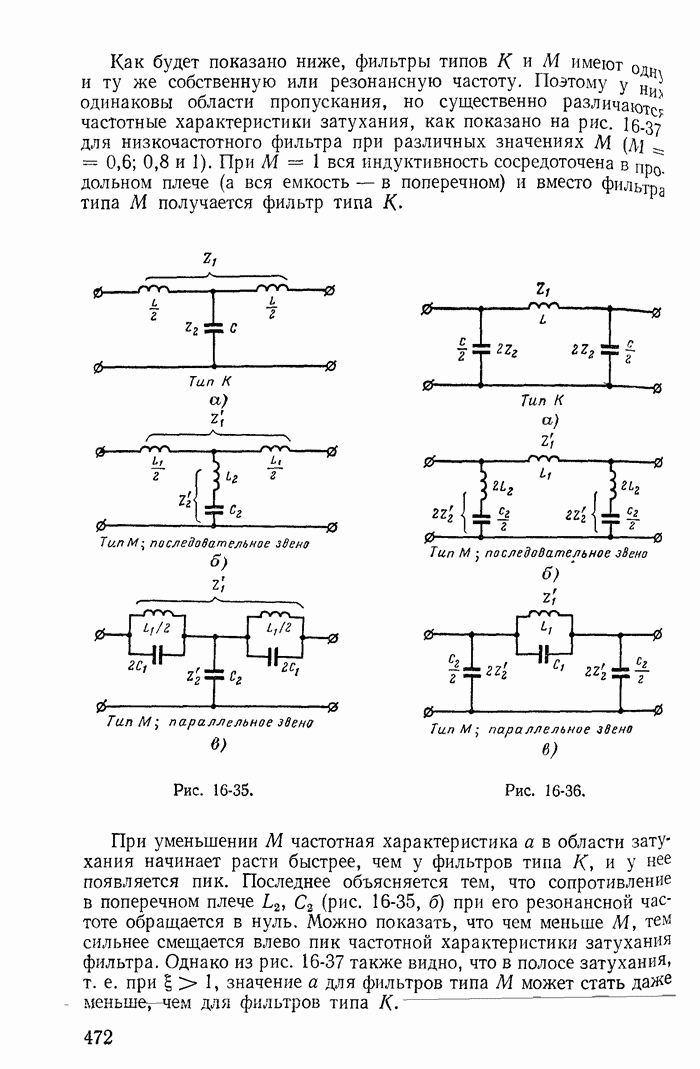
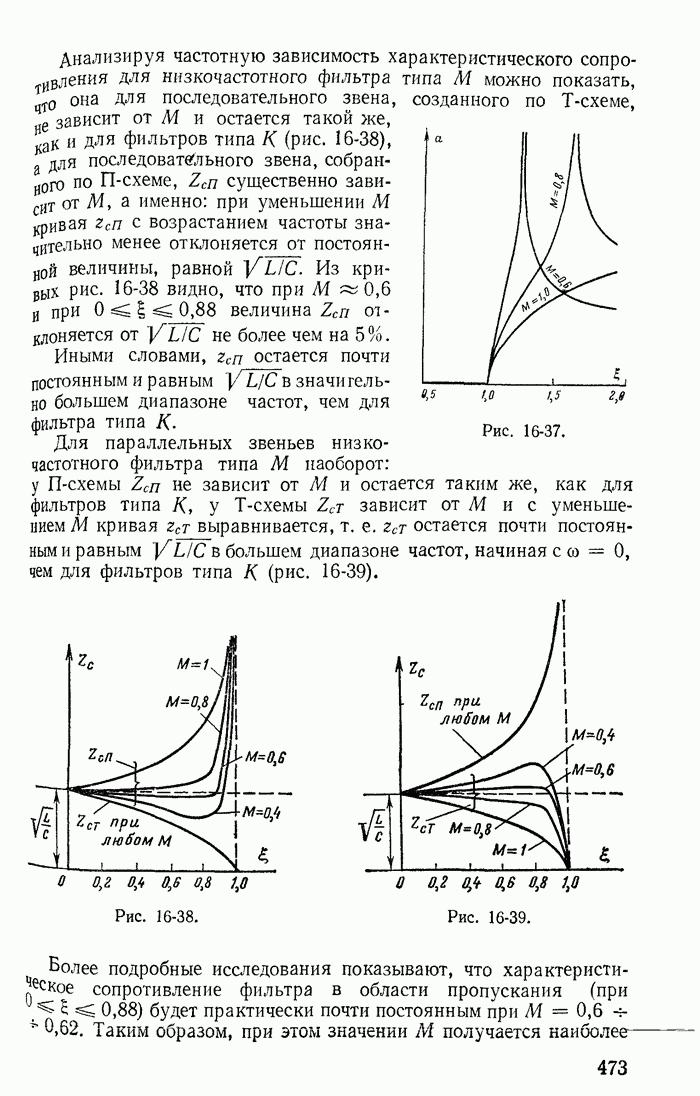
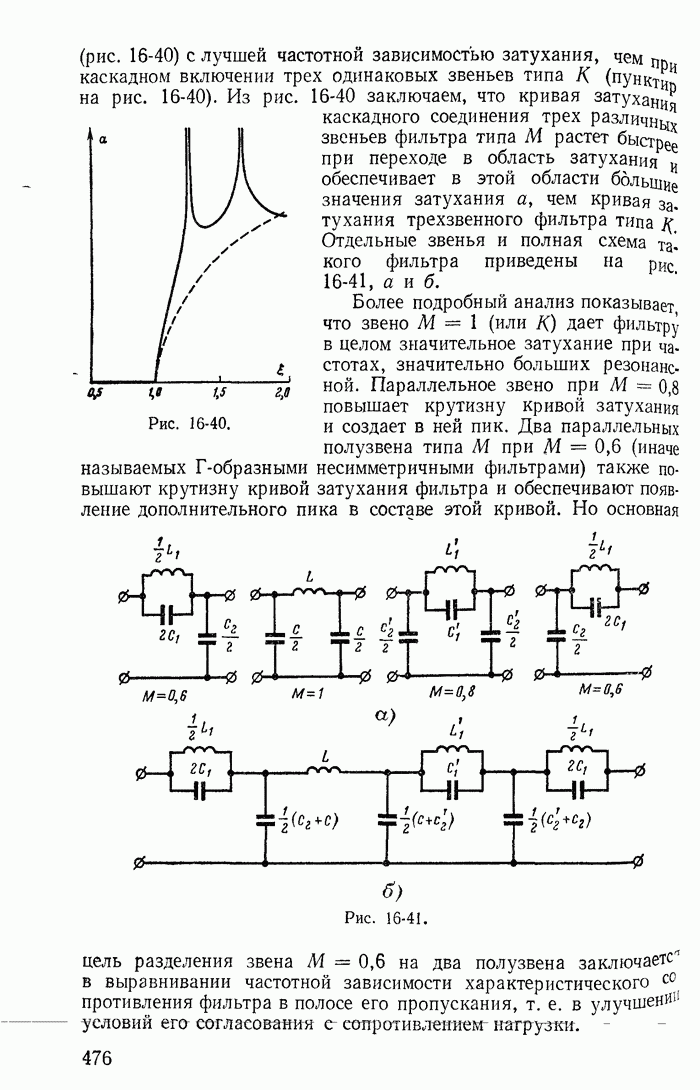
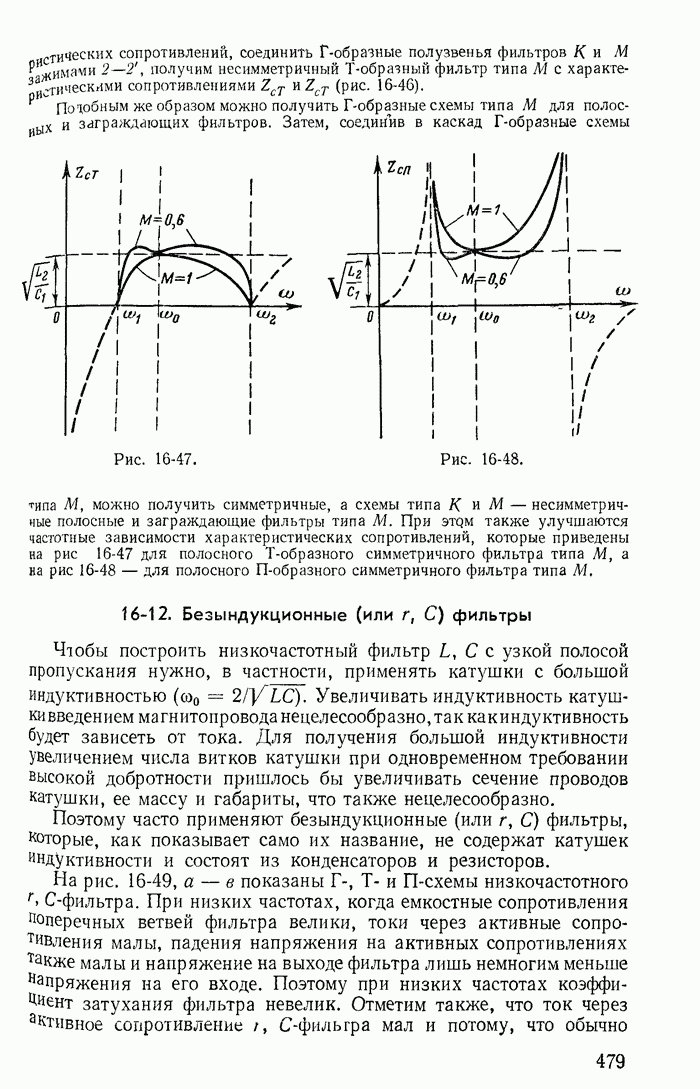
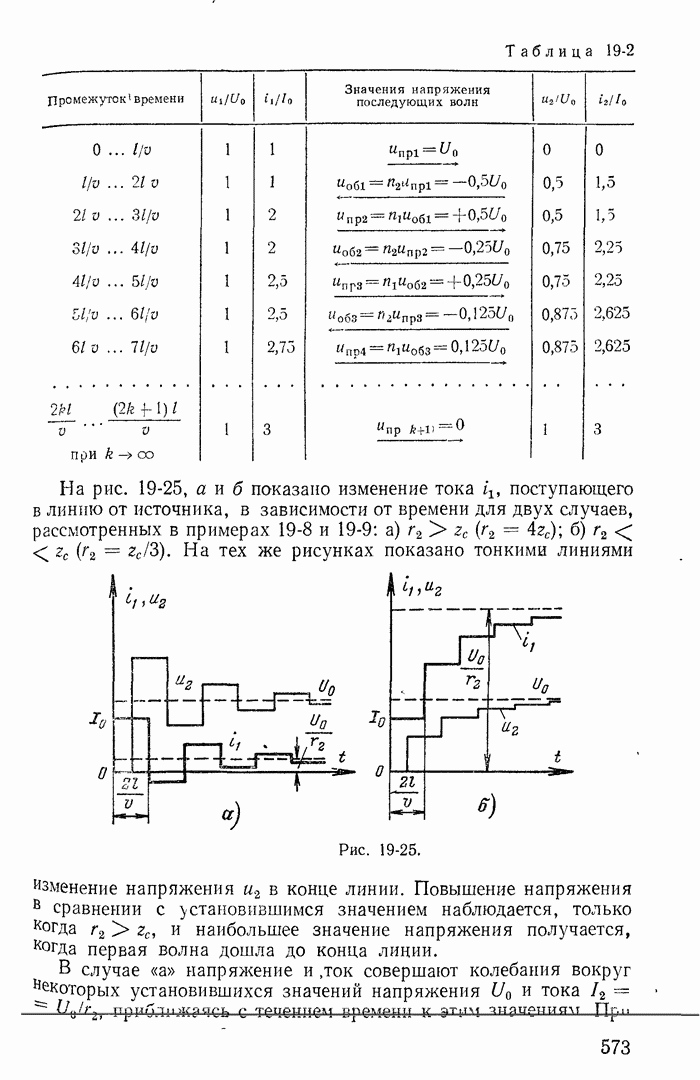
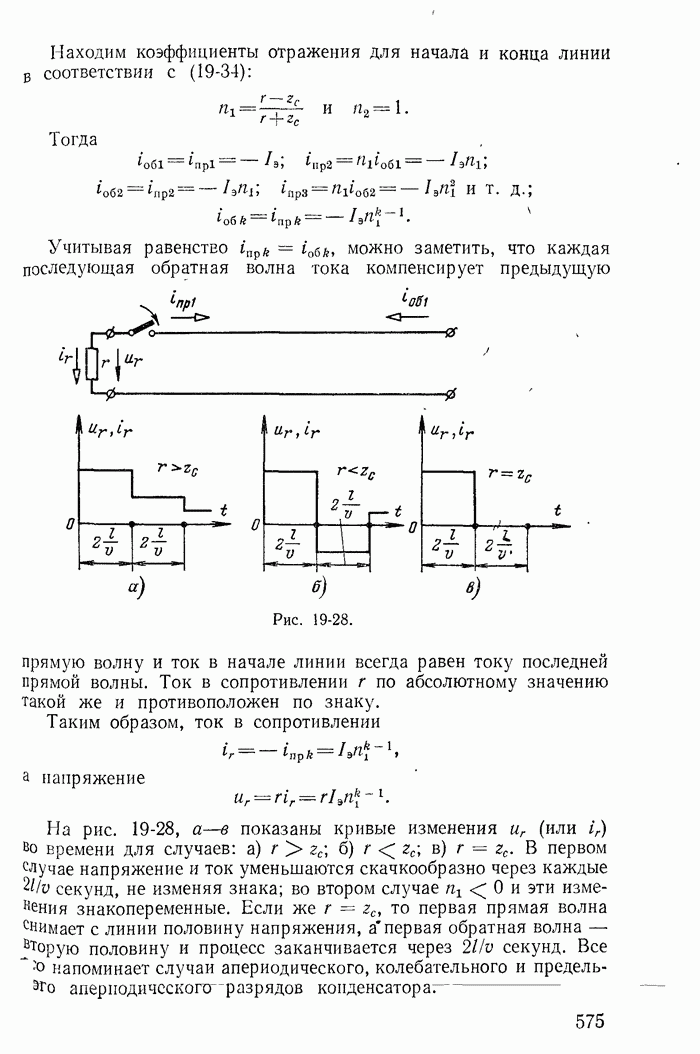
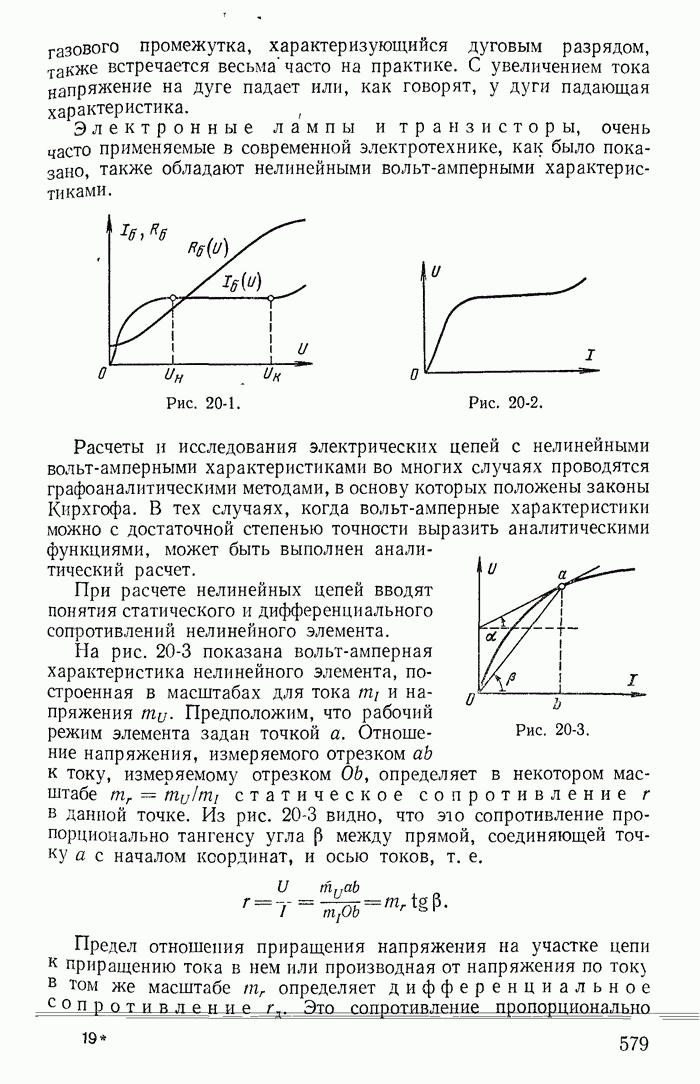
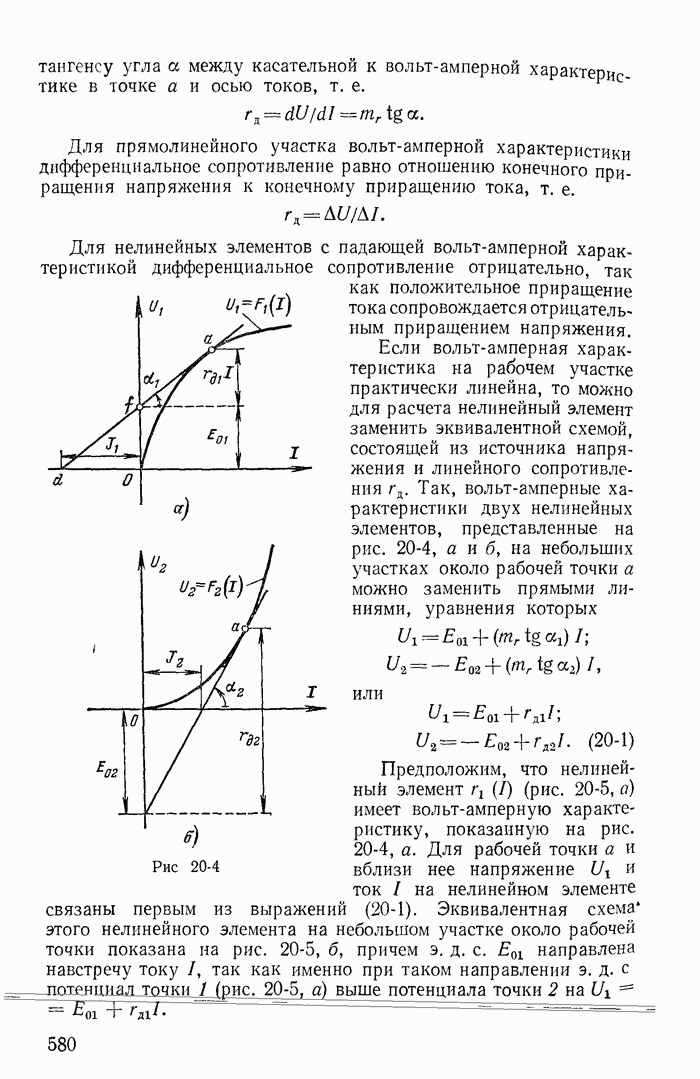
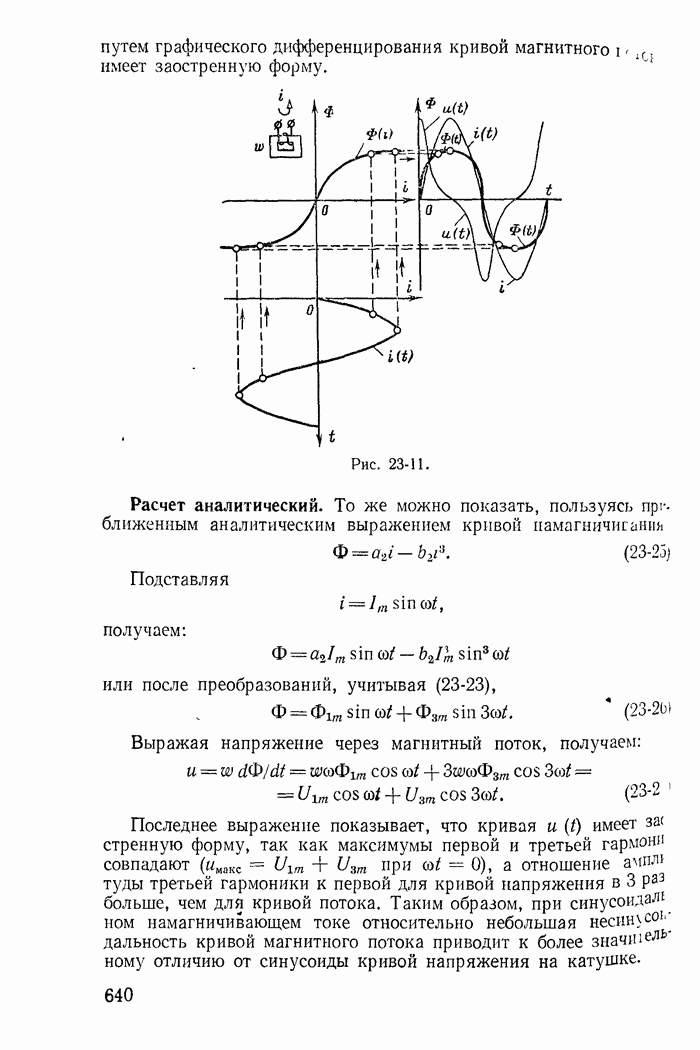
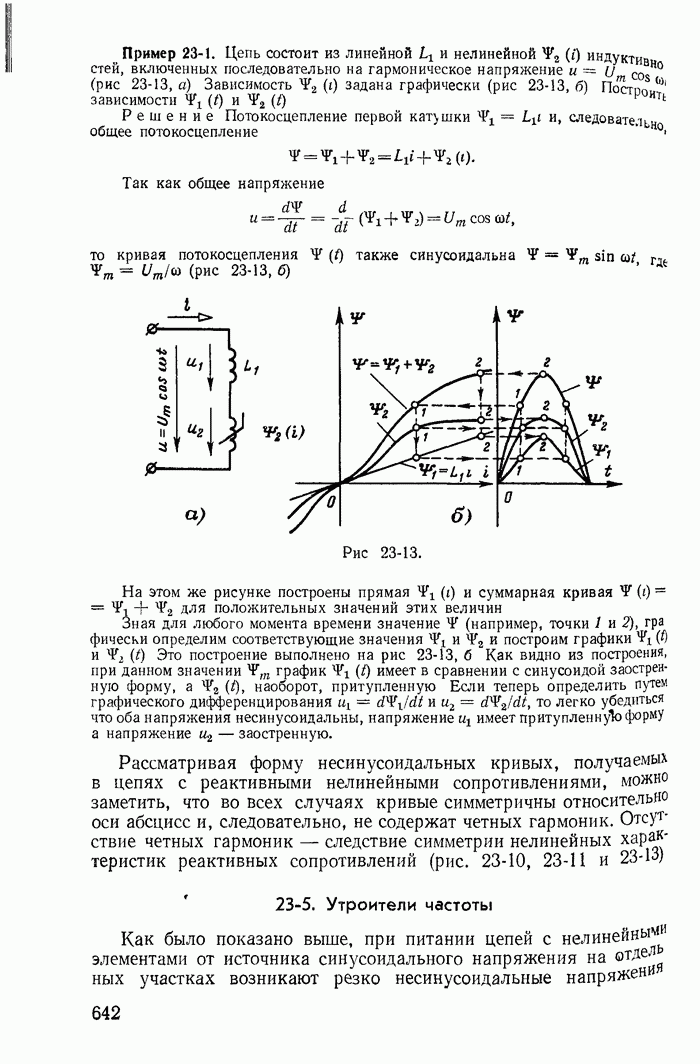
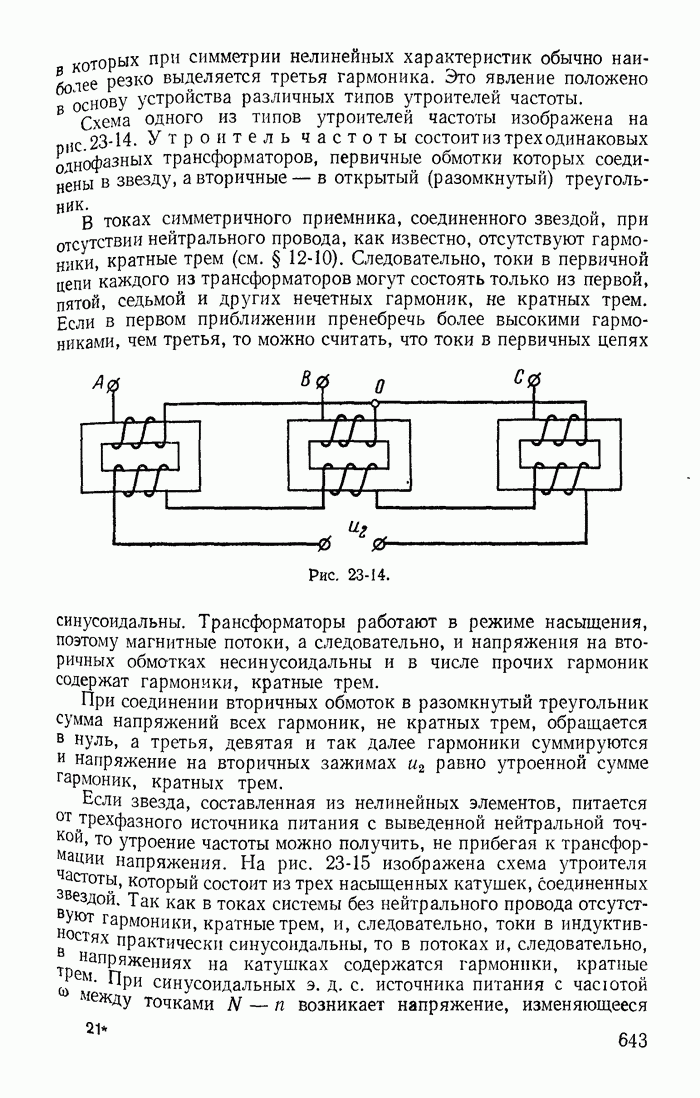
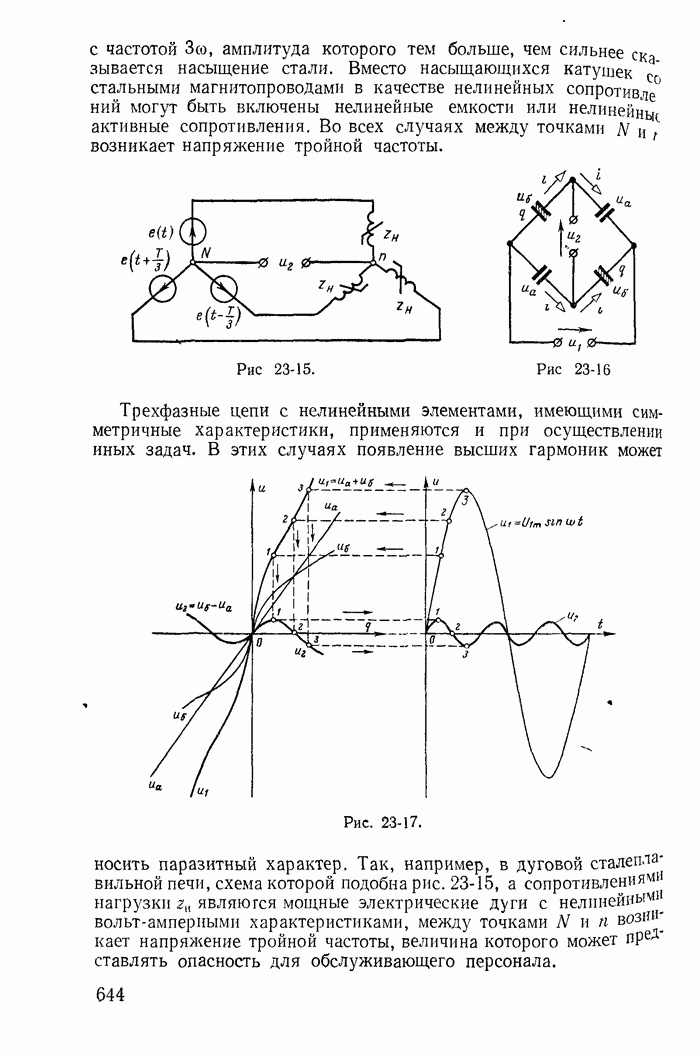
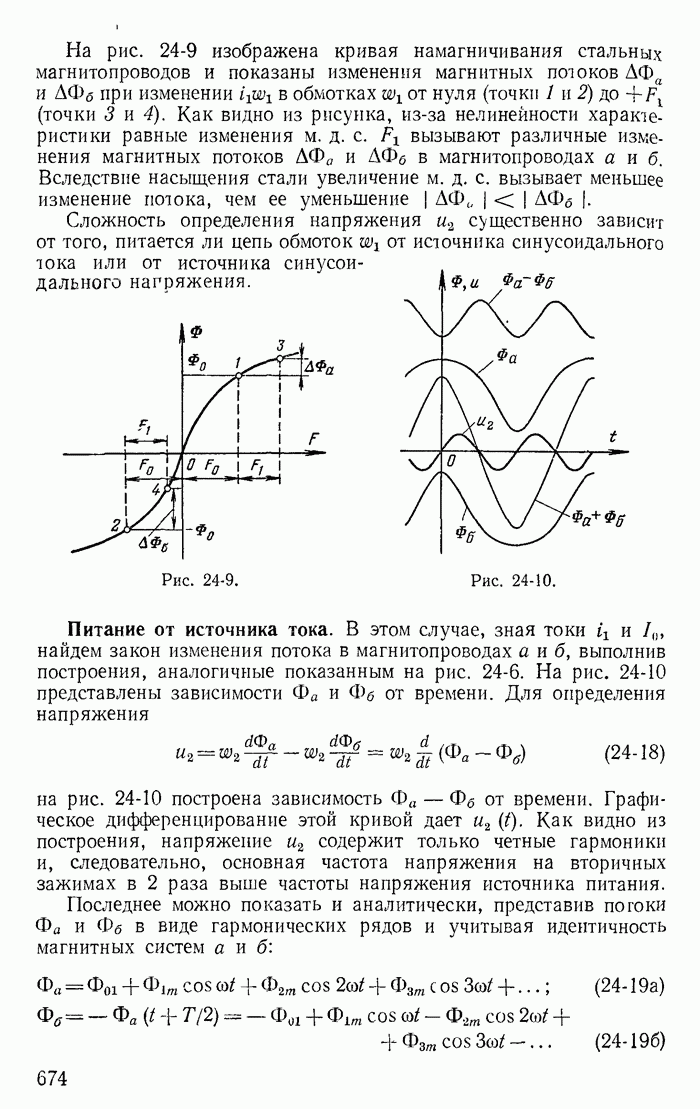
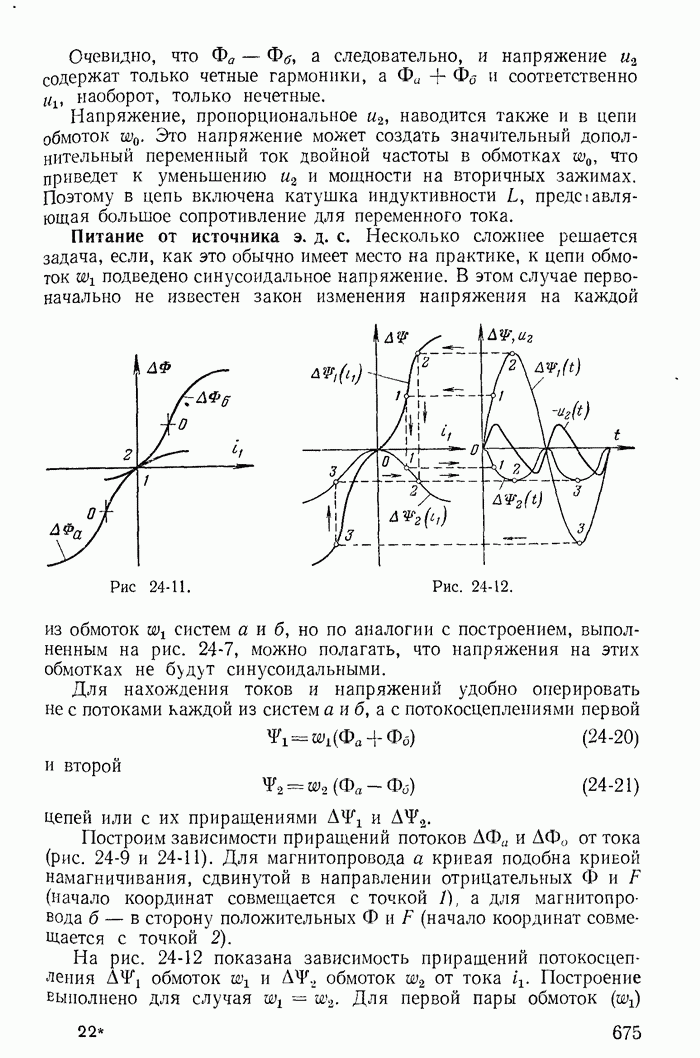
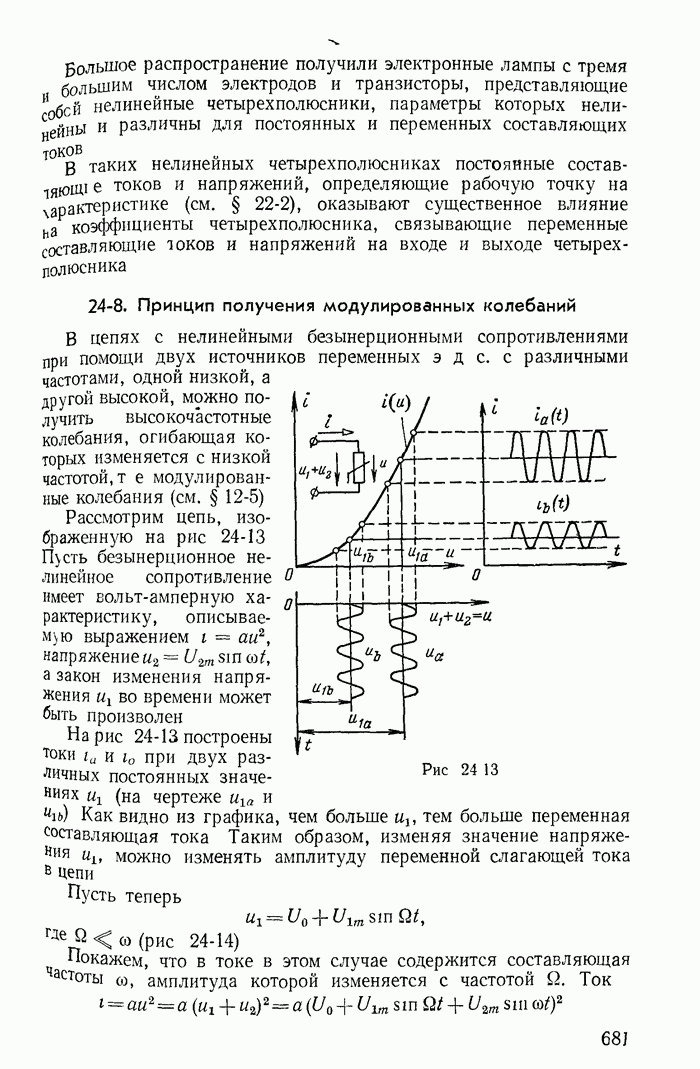
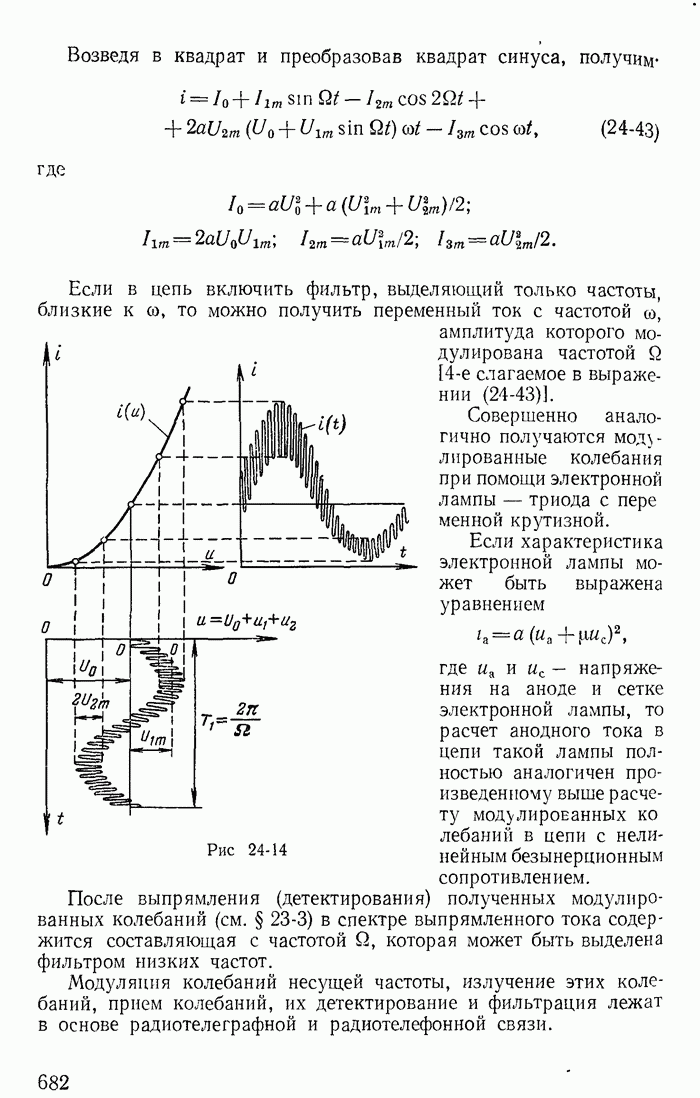
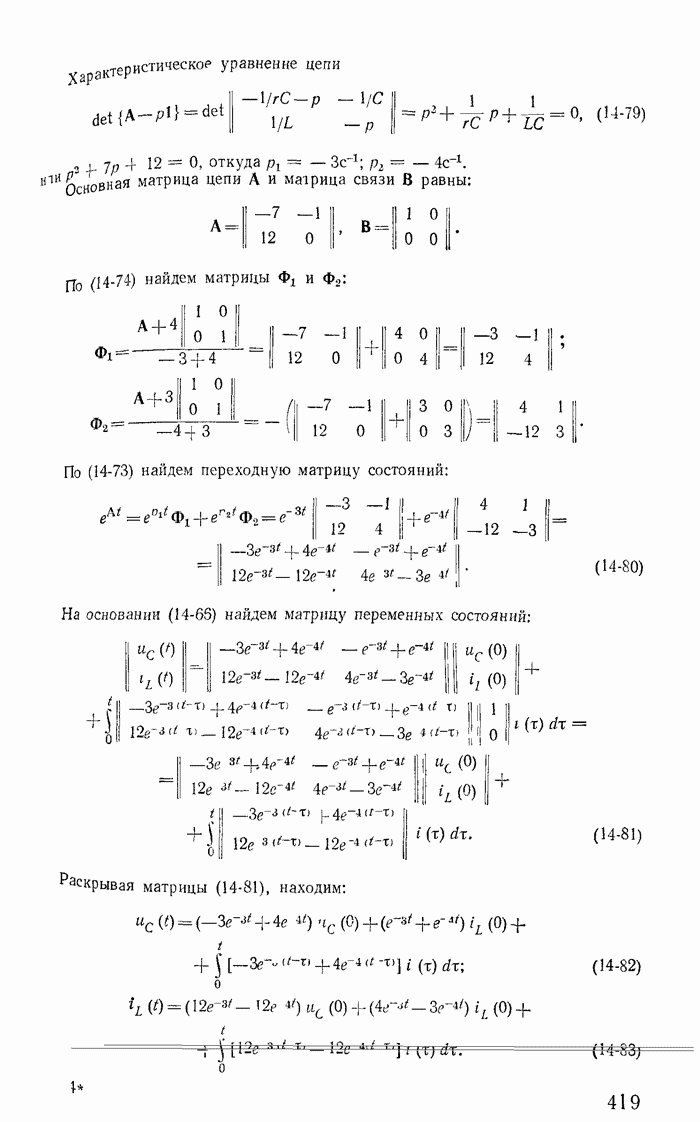| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
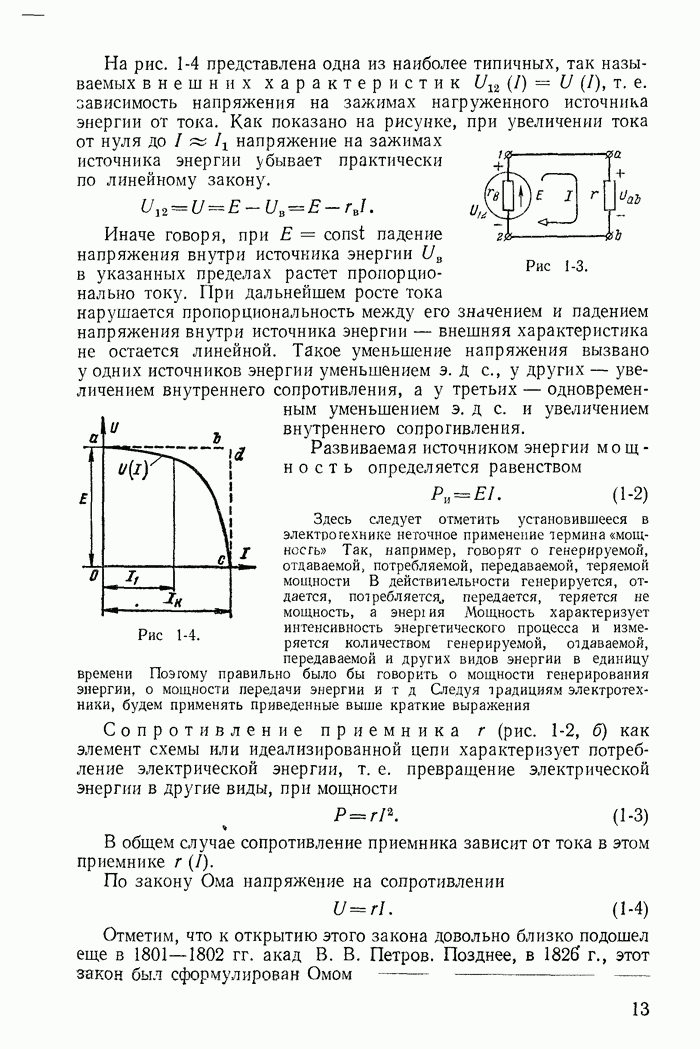
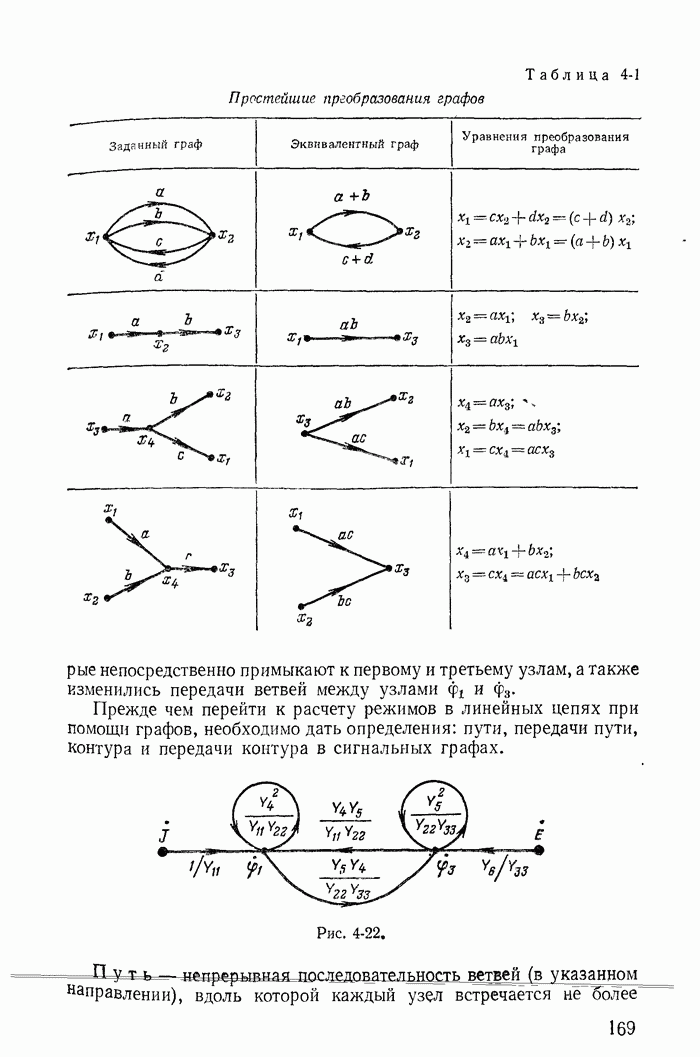
1-8. Метод контурных токов
Для расчета режима сложной электрической цепи можно ограничиться совместным решением лишь  независимых уравнений, составленных на основании второго закона Кирхгофа, воспользовавшись методом контурных токов; здесь в — число ветвей и у - число узлов. При этом закон Кирхгофа, конечно, всегда удовлетворяется.
независимых уравнений, составленных на основании второго закона Кирхгофа, воспользовавшись методом контурных токов; здесь в — число ветвей и у - число узлов. При этом закон Кирхгофа, конечно, всегда удовлетворяется.
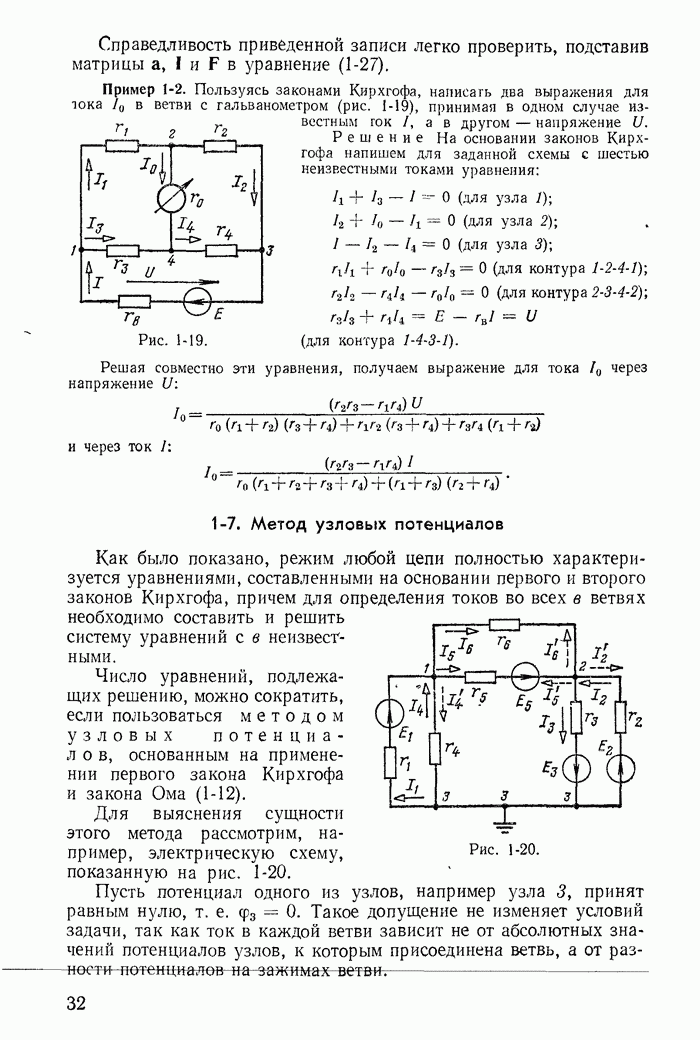
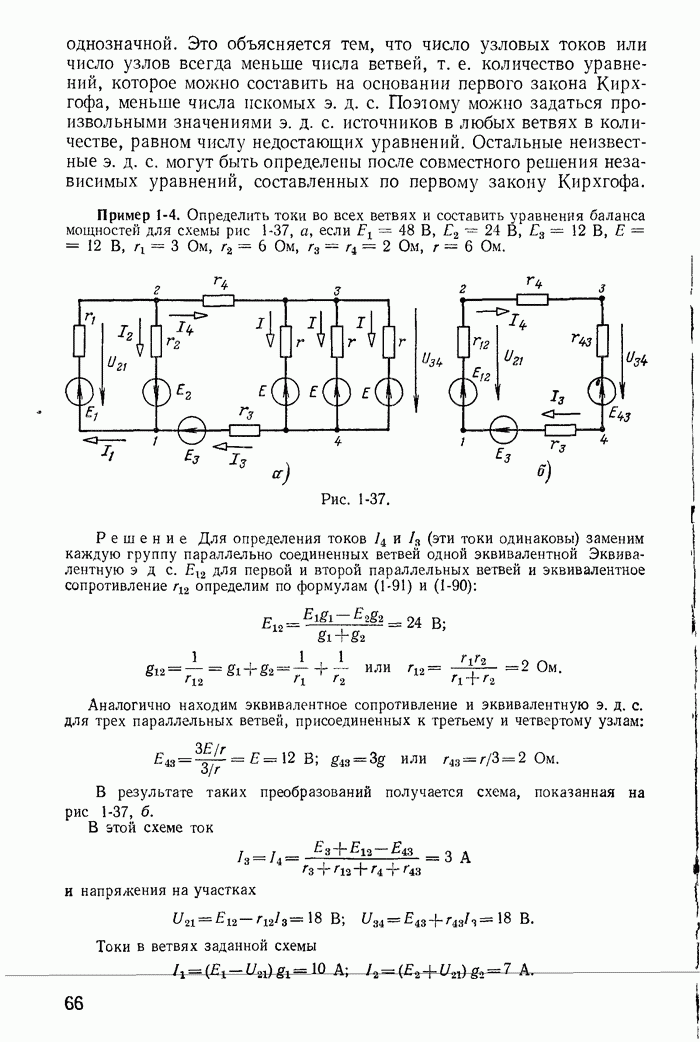
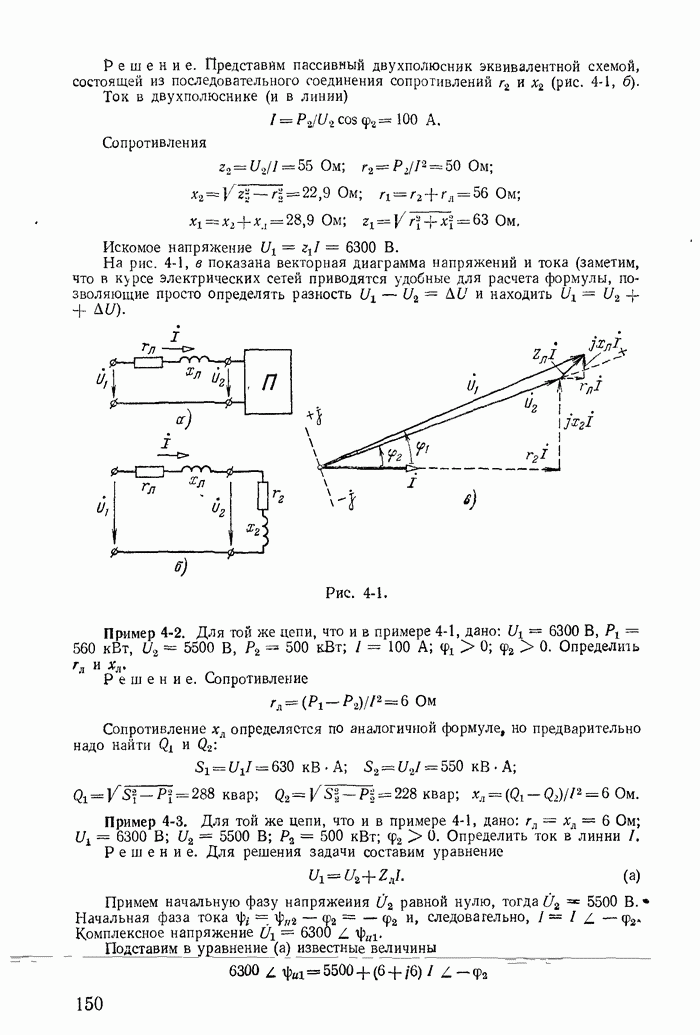
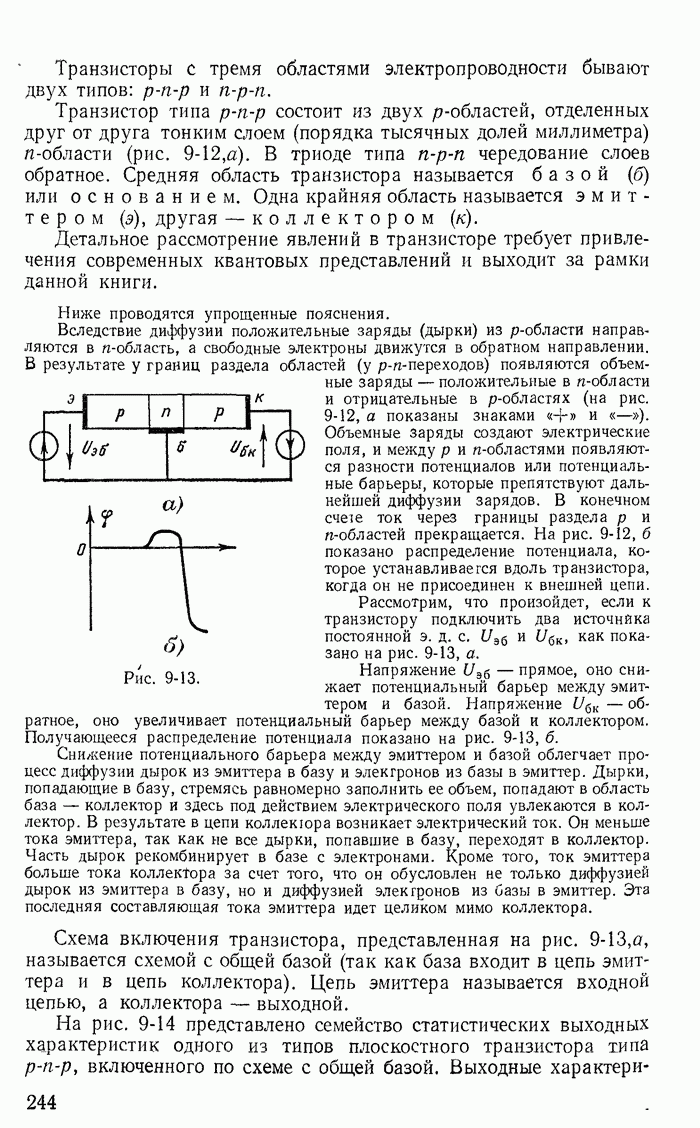
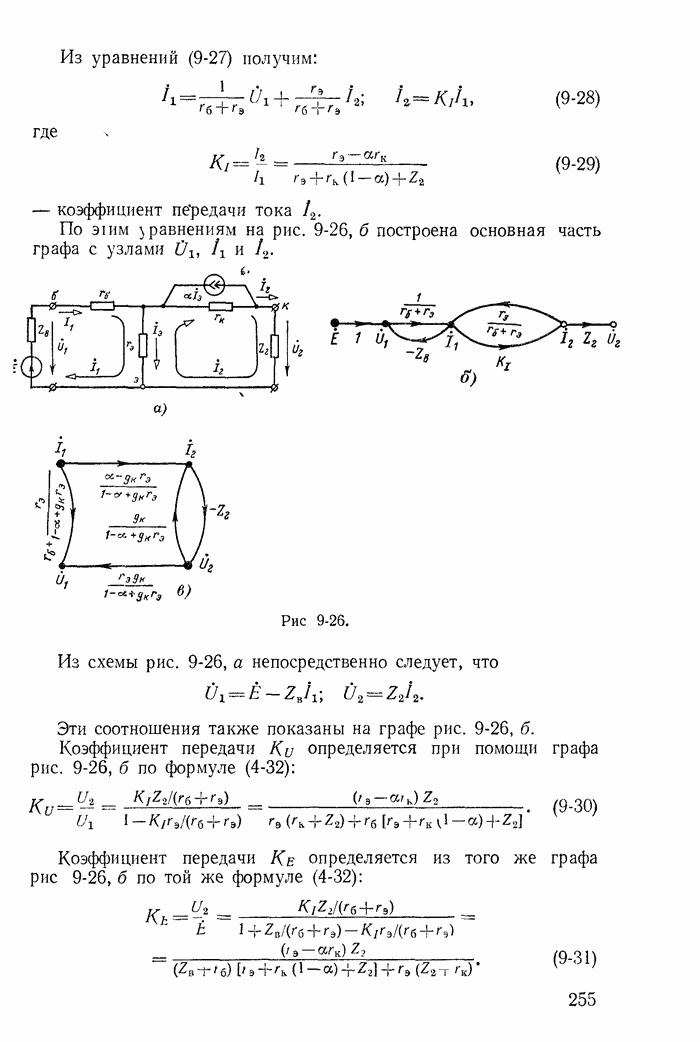
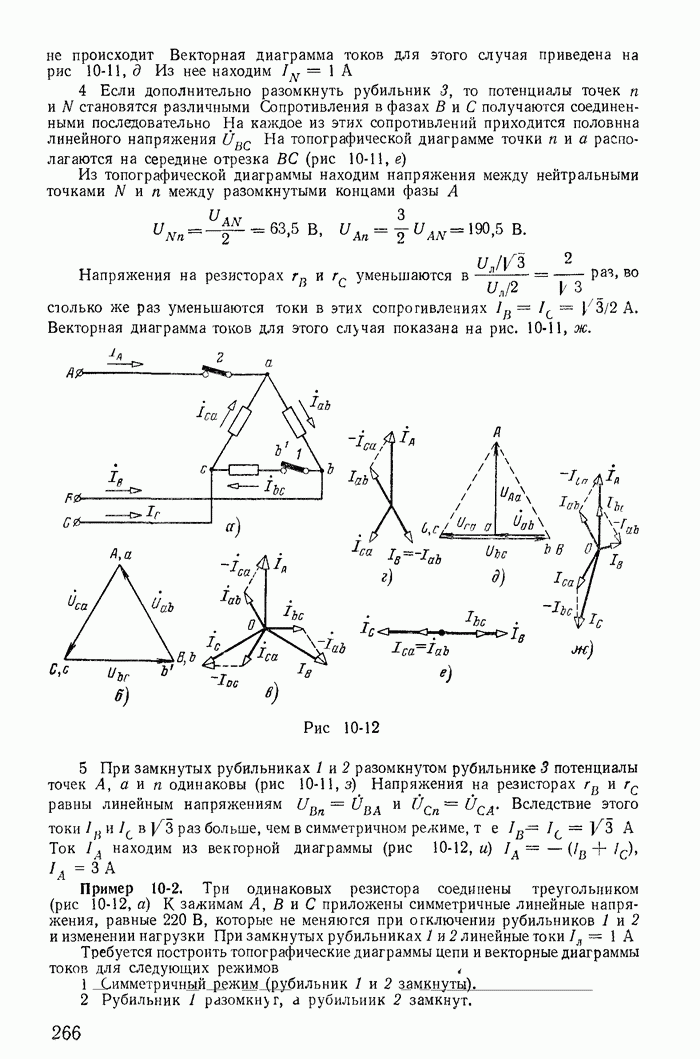
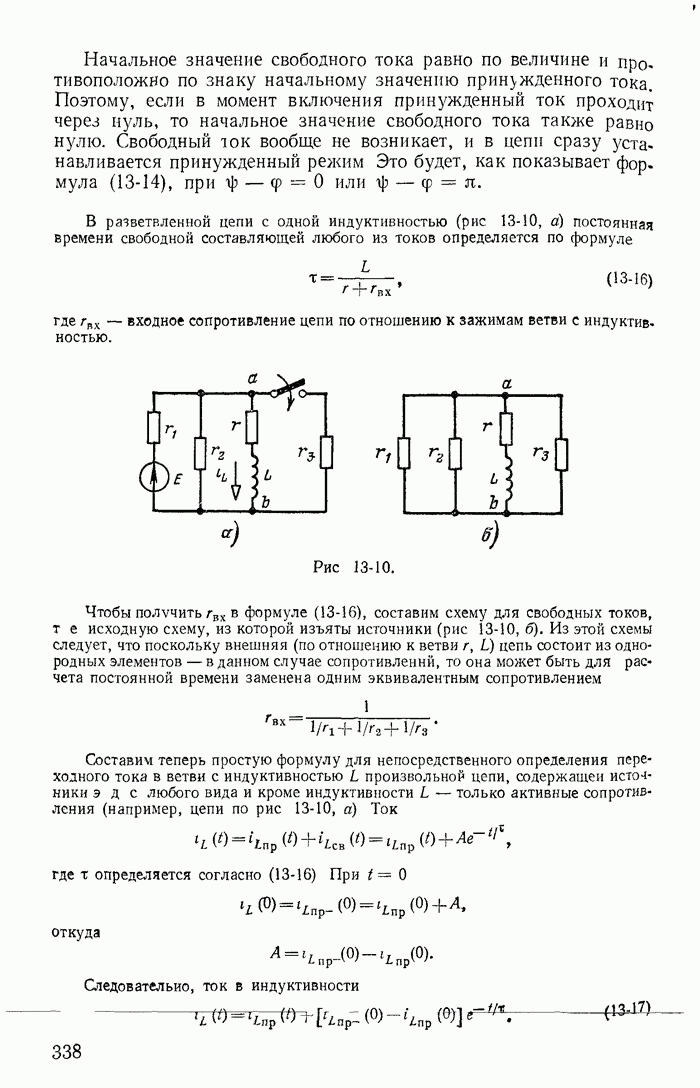
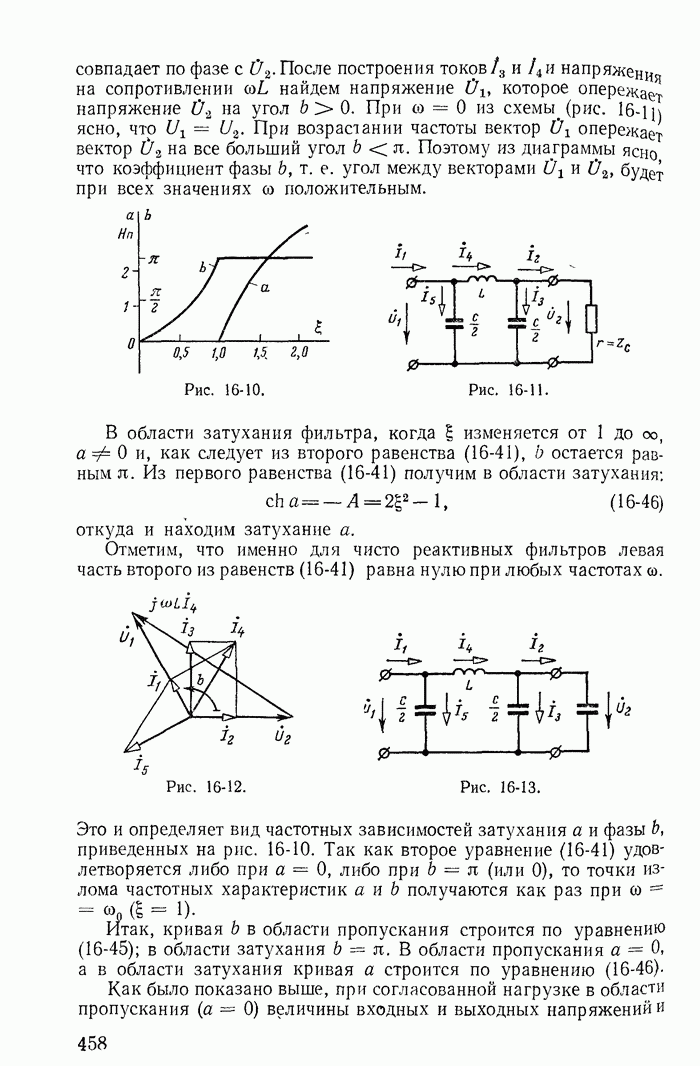
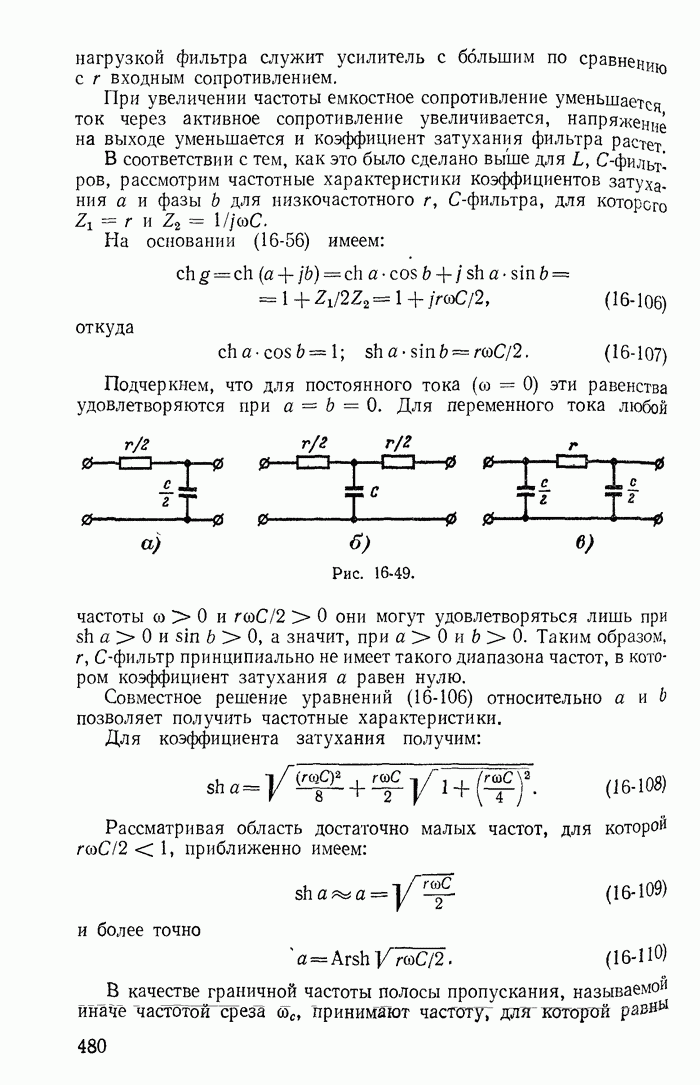
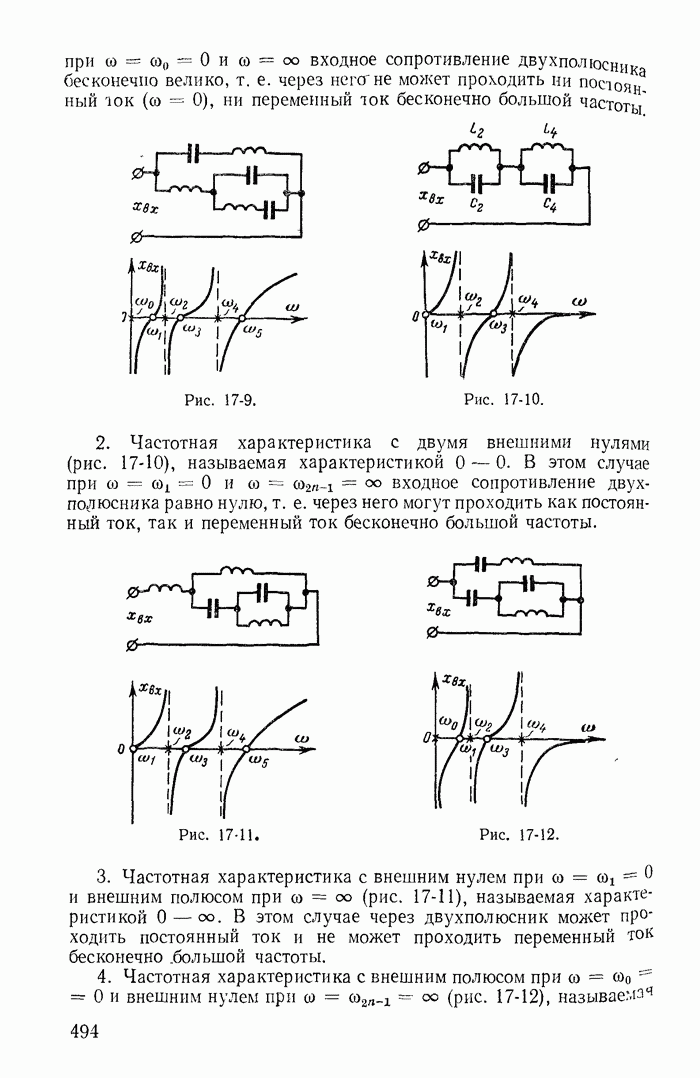
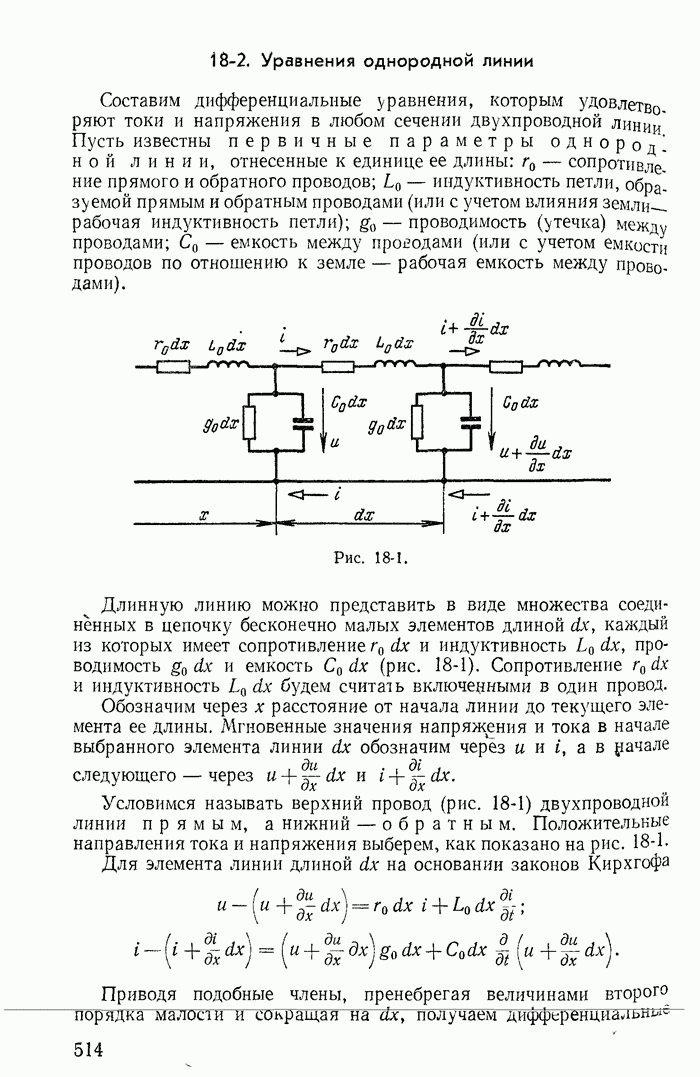
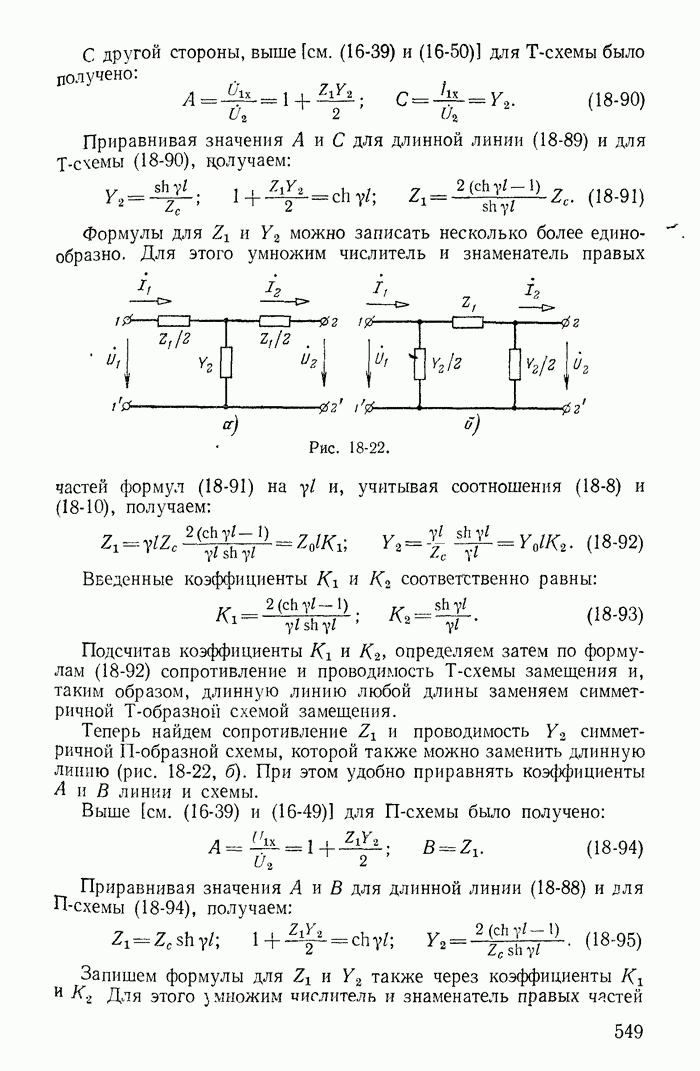
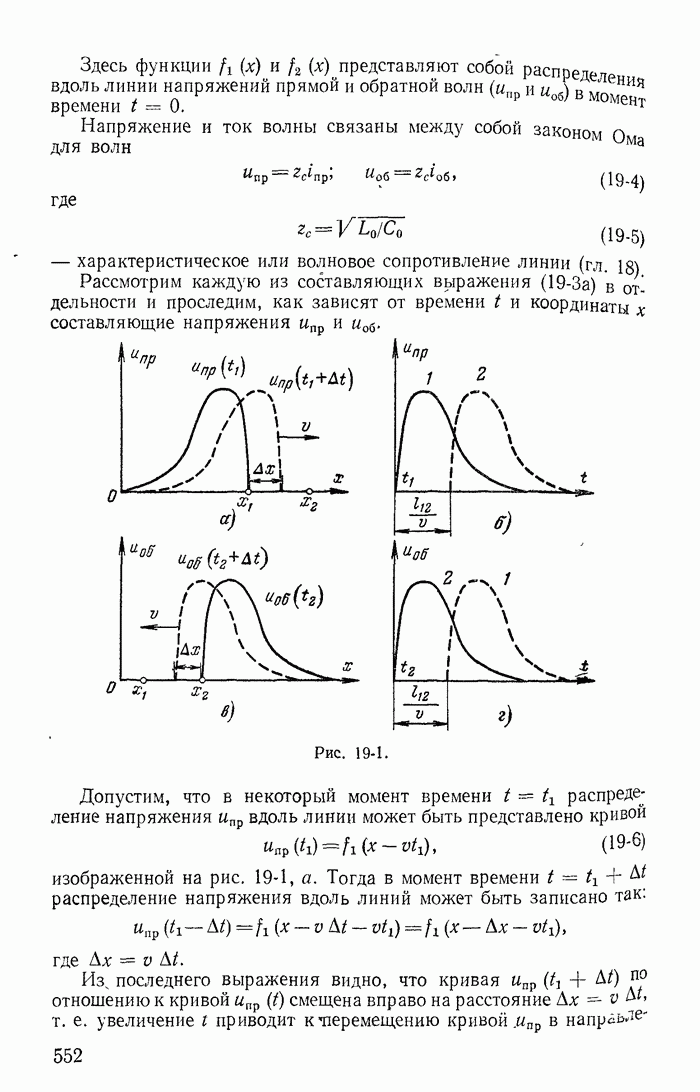
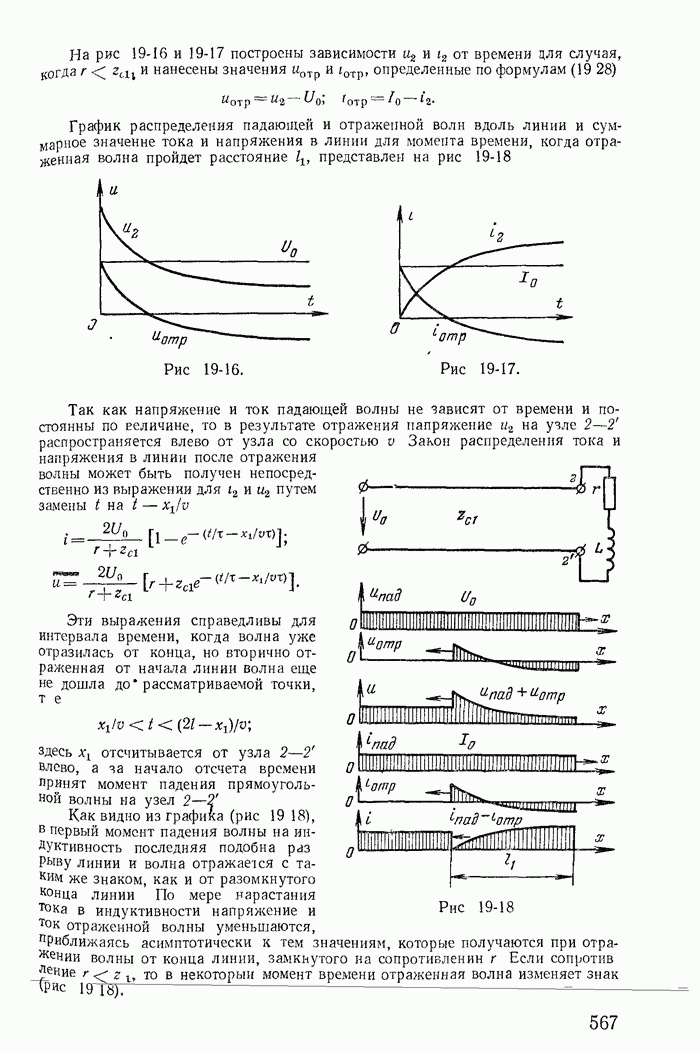
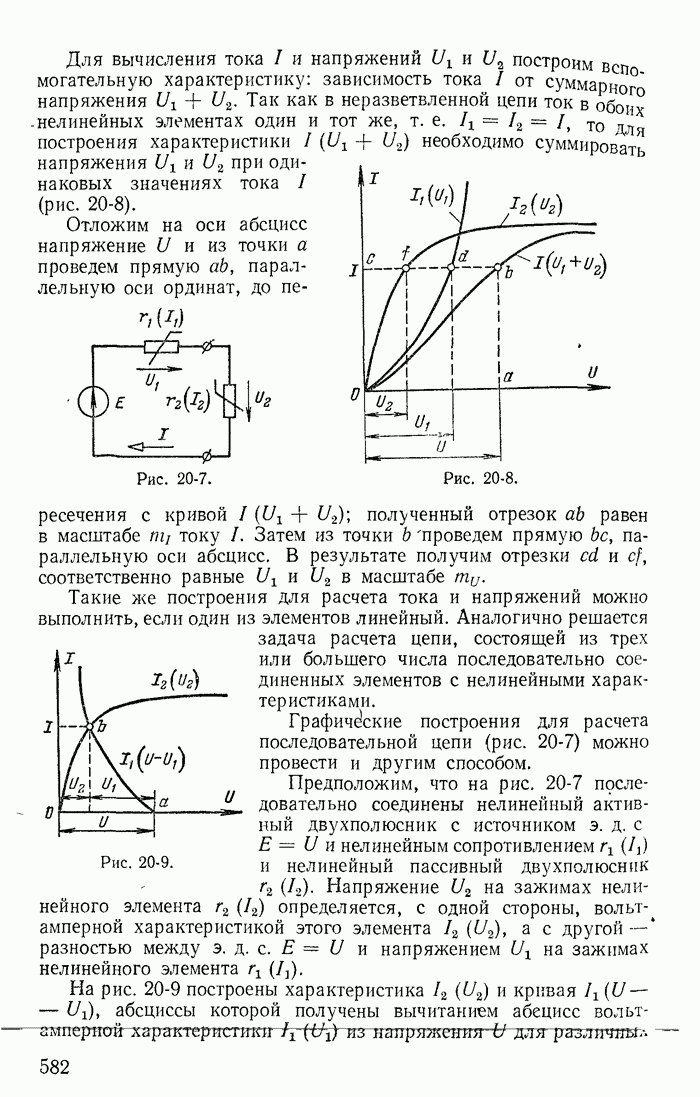
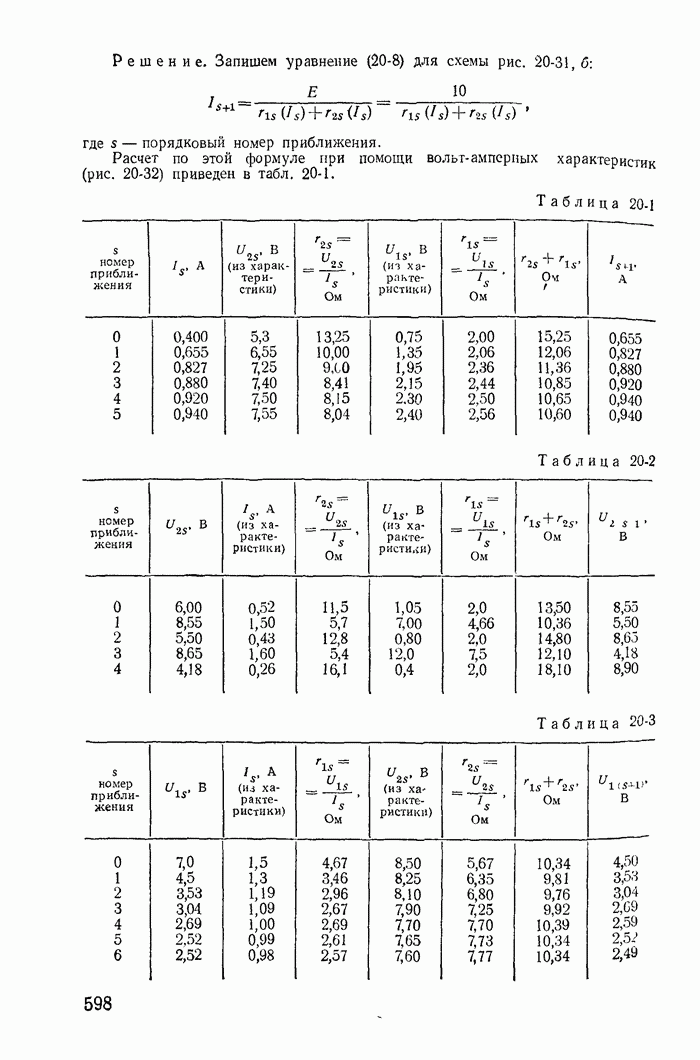
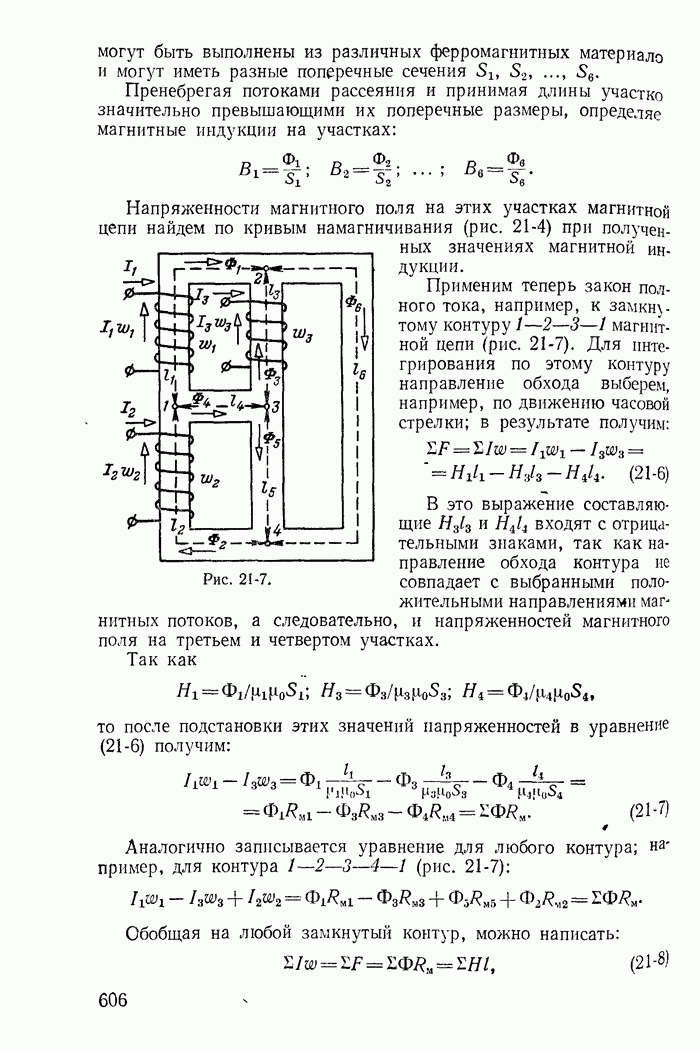
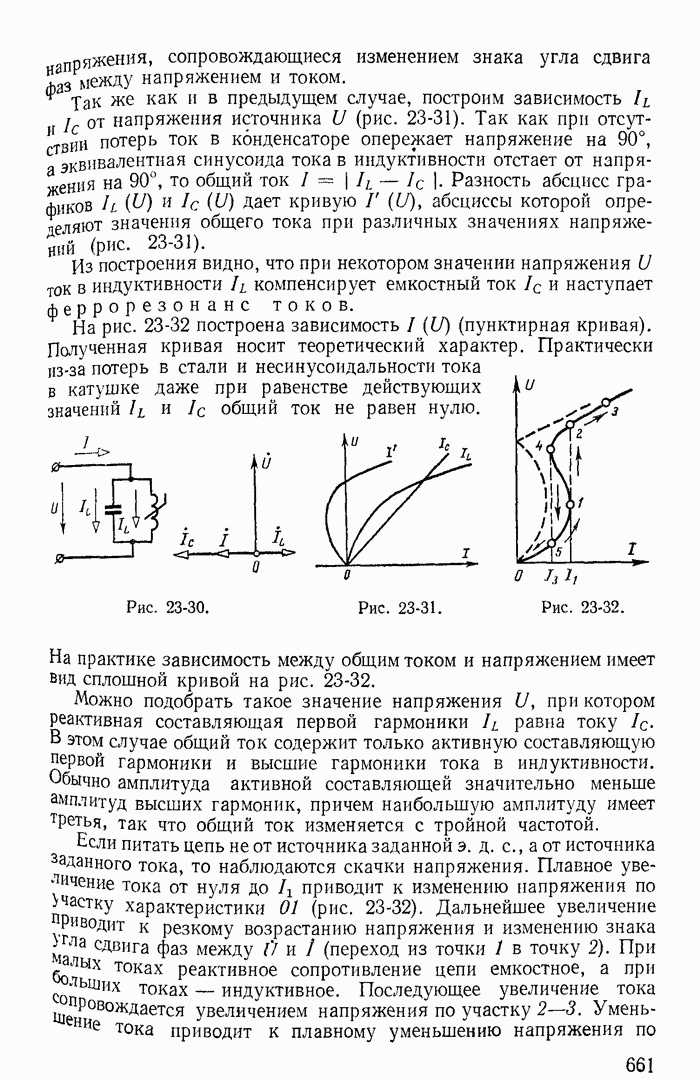
Для иллюстрации применения метода контурных токов рассмотрим схему на рис. 1-27, а с шестью ветвями и четырьмя узлами. Прежде чем составлять уравнения по второму закону Кирхгофа, надо выбрать взаимно независимые контуры так, чтобы одна из ветвей каждого контура входила только в этот контур. Например, в схеме рис. 1-27, а первая, вторая и третья ветви входят соответственно только в контуры 1-2-4-1, 2-3-4-2 и 1-4-3-1.
Для правильного выбора независимых контуров введем еще дополнительные понятия.

Рис. 1-27.
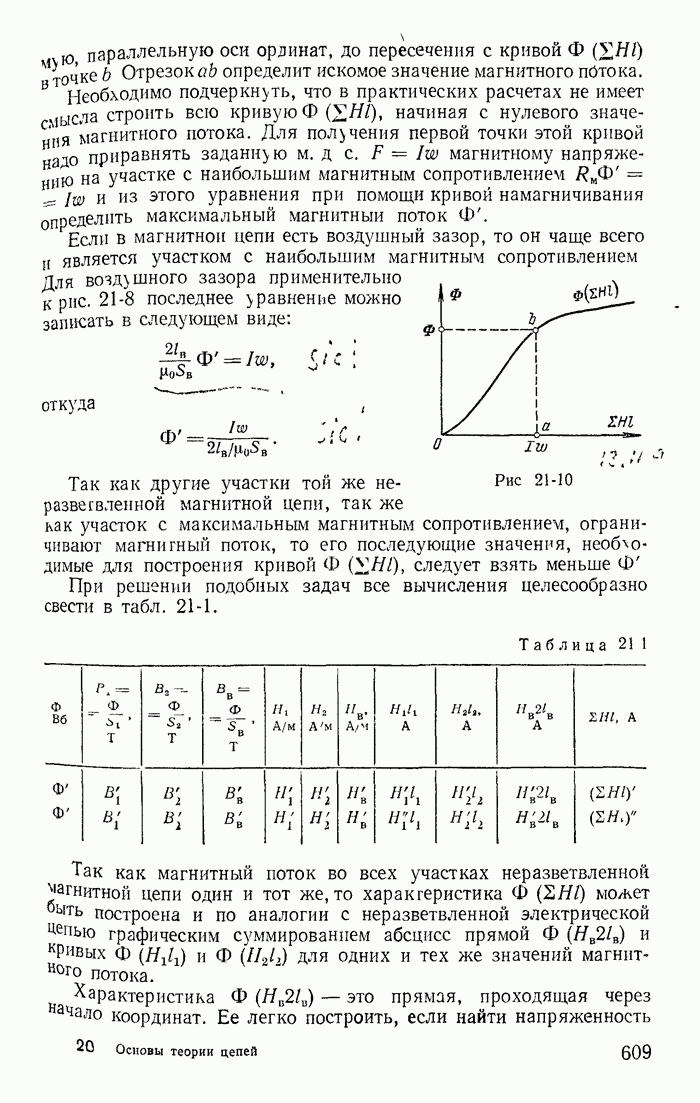
Деревом графа (схемы) называется совокупность ветвей, соединяющих все узлы, но не образующих ни одного контура. Между любыми двумя узлами дерева существует только один путь графа — непрерывная последовательность ветвей между заданными двумя узлами при условии, что каждый узел встречается не более одного раза. Наличие хотя бы двух разных путей между двумя узлами дерева, очевидно, приводит к образованию контура. Если число узлов схемы и ее графа у, то число ветвей дерева равно  , так как из у ветвей можно всегда составить контур. Ветвью связи (связью, главной ветвью или дополнением дерева) называется любая ветвь, не входящая в состав дерева. В дальнейшем будем пользоваться преимущественно термином «ветвь связи». Все ветви схемы, не входящие в состав дерева и называемые ветвями связи, дополняют соответствующее дерево до полной схемы.
, так как из у ветвей можно всегда составить контур. Ветвью связи (связью, главной ветвью или дополнением дерева) называется любая ветвь, не входящая в состав дерева. В дальнейшем будем пользоваться преимущественно термином «ветвь связи». Все ветви схемы, не входящие в состав дерева и называемые ветвями связи, дополняют соответствующее дерево до полной схемы.
Взаимно независимые контуры получатся, если в каждый кон тур войдет одна ветвь связи, действительный ток которой буде равен соответствующему контурному току. Ветви с идеальными источниками э. д. с. и без сопротивлений обычно включают в соствав дерева, а ветви с источниками тока относят к ветвям связи. Ветви с идеальными источниками э. д. с. и сопротивлениями (соединен ными между собой последовательно) могут входить как в соета! ветвей дерева, так и в состав ветвей связи. Например, для схемь рис. 1-27, а ветви с токами  соединяющие узлы 1, 2, 3, 4 выбраны в качестве ветвей дерева; тогда ветви с токами
соединяющие узлы 1, 2, 3, 4 выбраны в качестве ветвей дерева; тогда ветви с токами  будут ветвями связи. На рис. 1-27, б элементы ветвей дерева изображены сплошными линиями, а элементы ветвей связи — пунктирными. Из приведенной схемы видно, что при выбранном дереве токи в ветвях связи
будут ветвями связи. На рис. 1-27, б элементы ветвей дерева изображены сплошными линиями, а элементы ветвей связи — пунктирными. Из приведенной схемы видно, что при выбранном дереве токи в ветвях связи  совпадающие с контурными токами равны действительным токам этих ветвей. Это правило распространяется на любую схему.
совпадающие с контурными токами равны действительным токам этих ветвей. Это правило распространяется на любую схему.
Для схемы рис. 1-27, а по первому закону Кирхгофа

На основании второго закона Кирхгофа

Пользуясь уравнениями (1-51), исключим из уравнений (1-52) токи  всех ветвей дерева, общих для нескольких контуров; в результате получим:
всех ветвей дерева, общих для нескольких контуров; в результате получим:

В соответствии с уравнениями (1-53) можно принять, что каждый из токов  замыкается через соответствующую ветвь связи в одном из контуров (рис. 1-27, а и б) и назвать такие токи контурными. Напряжения на сопротивлениях любого контура равны алгебраической сумме напряжений, обусловленных токами своего и смежных контуров. Например, в контуре из сопротивлений
замыкается через соответствующую ветвь связи в одном из контуров (рис. 1-27, а и б) и назвать такие токи контурными. Напряжения на сопротивлениях любого контура равны алгебраической сумме напряжений, обусловленных токами своего и смежных контуров. Например, в контуре из сопротивлений  разность
разность  равняется сумме трех напряжений: от собственного контурного тока
равняется сумме трех напряжений: от собственного контурного тока  на всех сопротивлениях этого контура и от токов
на всех сопротивлениях этого контура и от токов  соответственно на сопротивлениях
соответственно на сопротивлениях  Действительные токи в ветвях дерева, общих для нескольких контуров, равны алгебраическим суммам контурных токов:
Действительные токи в ветвях дерева, общих для нескольких контуров, равны алгебраическим суммам контурных токов:

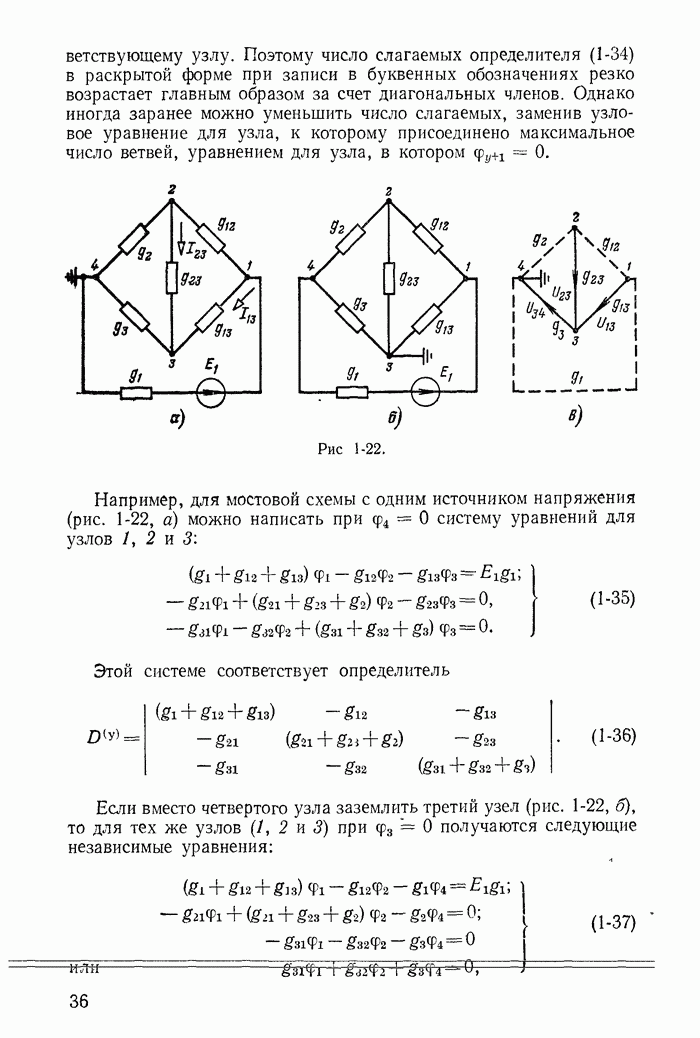
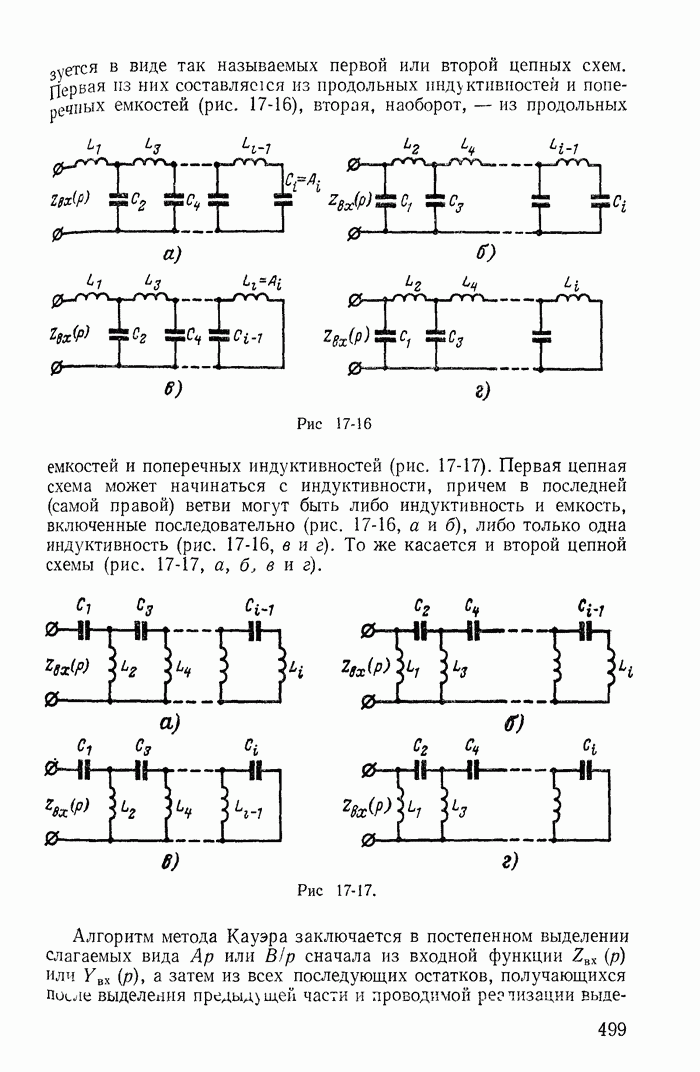
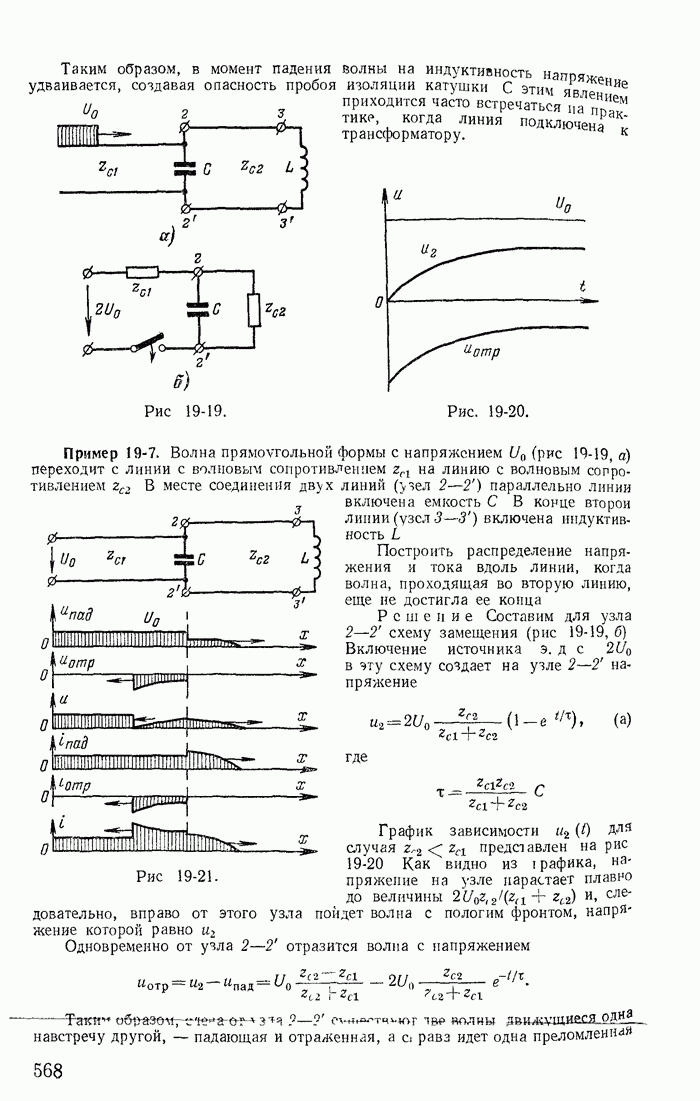
Для этой же схемы можно получить и другие взаимно независимые уравнения. Например, выберем другое дерево из первой, пятой и шестой ветвей (рис. 1-27, в); тогда вторая, третья и четвертая ветви будут ветвями связи, действительные токи в которых совпадают с контурными. Применив в этом случае второй закон Кирхгофа для контуров 2-3-4-2, 3-1-2-4-3 и 2-4-1-2, получим уравнения с контурными токами  замыкающимися через ветви деревьев по ветвям связи. Токи в ветвях дерева однозначно определяются через токи ветвей связи (совпадающие с контурными) по формулам
замыкающимися через ветви деревьев по ветвям связи. Токи в ветвях дерева однозначно определяются через токи ветвей связи (совпадающие с контурными) по формулам

Выражение для тока  получено по первому закону Кирхгофа для действительных токов, примененному к поверхности
получено по первому закону Кирхгофа для действительных токов, примененному к поверхности  след которой показан на рис. 1-27, в пунктиром.
след которой показан на рис. 1-27, в пунктиром.
Таким образом, система взаимно независимых уравнений определяется структурой выбранного дерева и соответствующими ветвями связи.
Ниже будет показано, что мостовая схема рис. 1-27, а имеет 16 деревьев; поэтому для такой схемы можно написать 16 систем независимых уравнений, каждая из которых содержит в качестве неизвестных три тока, замыкающиеся по ветвям связи через ветви выбранного дерева.
Из приведенных примеров следует, что для определения токов в ветвях этим методом нужно ввести в расчет контурные токи и решить совместно систему уравнений, составленных по второму закону Кирхгофа; число этих уравнений меньше числа неизвестных токов ветвей на число узлов схемы без одного (у — 1). При замене токов в ветвях контурными токами первый закон Кирхгофа всегда удовлетворяется, так как каждый контурный ток в одной из ветвей контура направлен к узлу, а в другой — от того же узла. Например, для узла 4 (рис. 1-27, а) по первому закону Кирхгофа для токов ветвей получим:

или для контурных токов

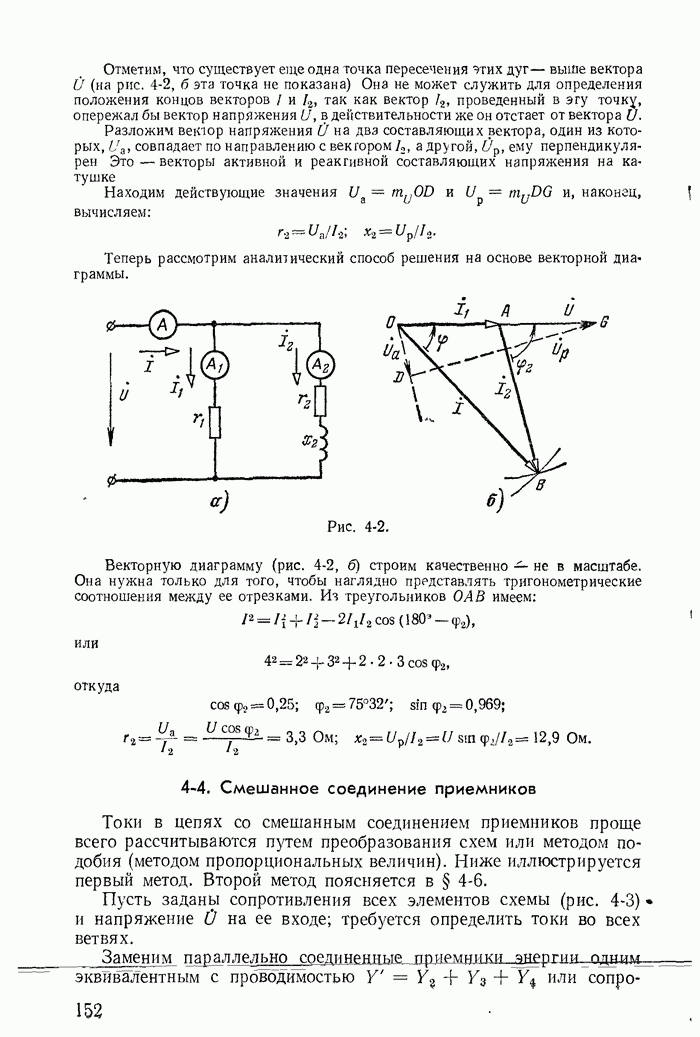
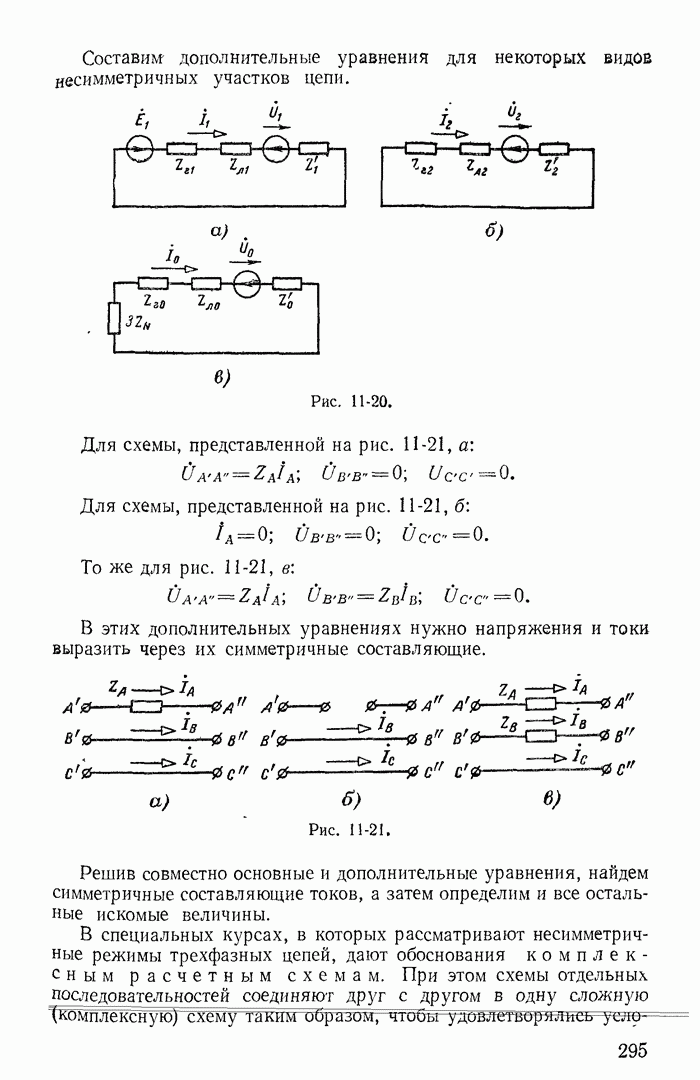
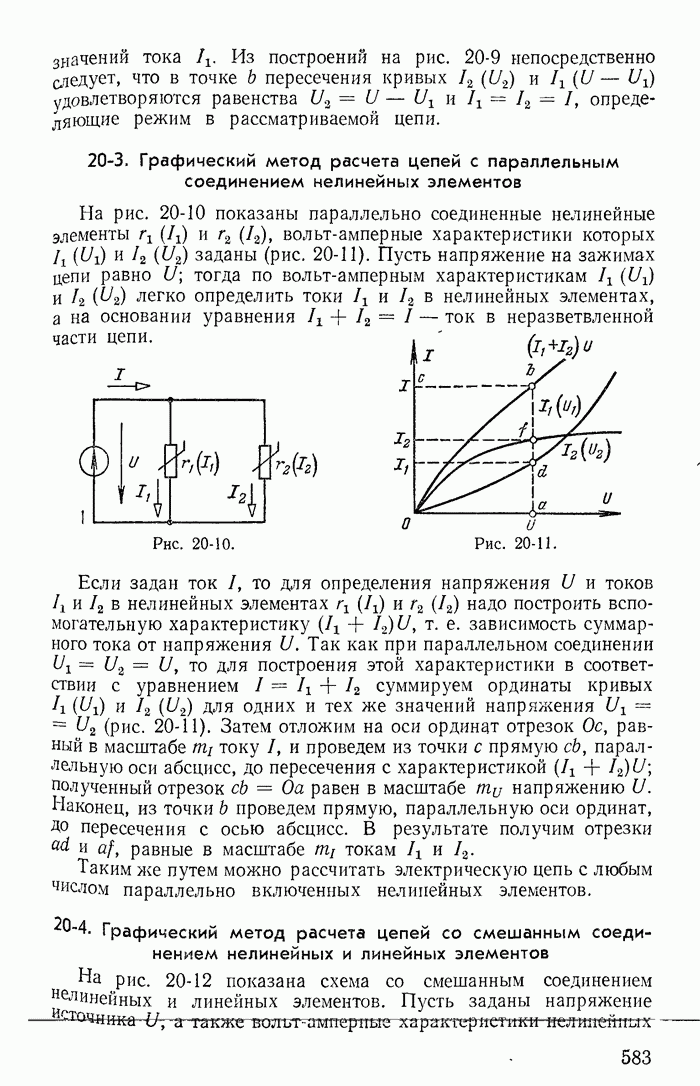
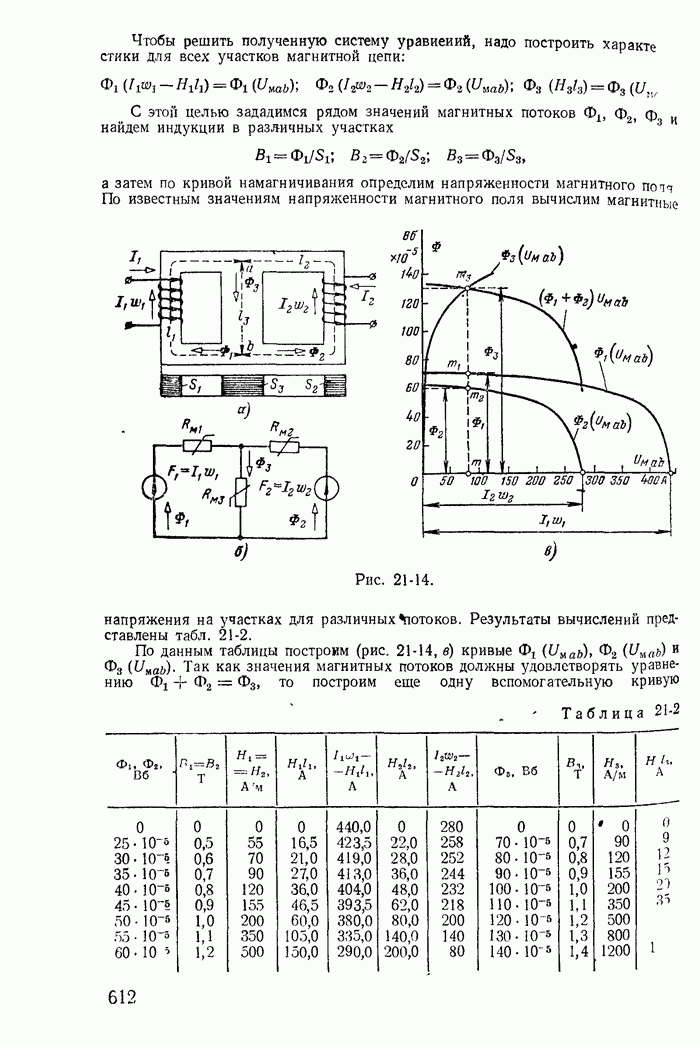
Если схема содержит не только источники э. д. с., но и источники тока, то можно принять ток каждого из источников тока замыкающимся по любым ветвям дерева, составляющим с ветвью источника тока — ветвью связи замкнутый контур. Падение напряжения, вызванное током такого источника на каждом из сопротивлений контура, учитывается при записи левой части уравнений по второму закону Кирхгофа. Однако эти напряжения можно также учесть с обратным знаком в правой части уравнений.
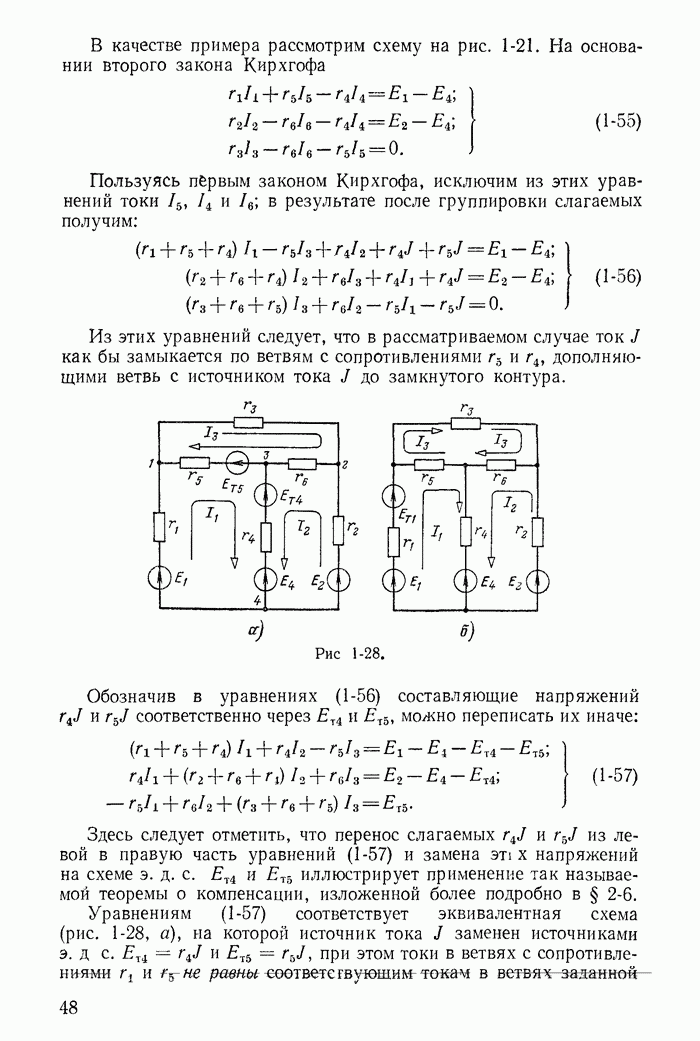
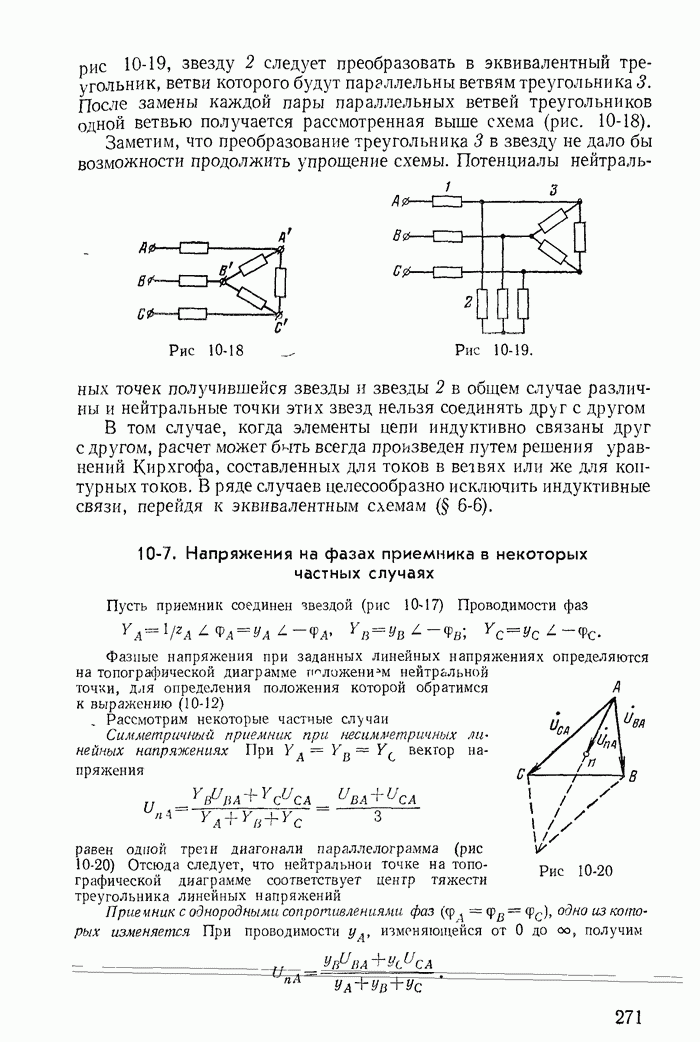
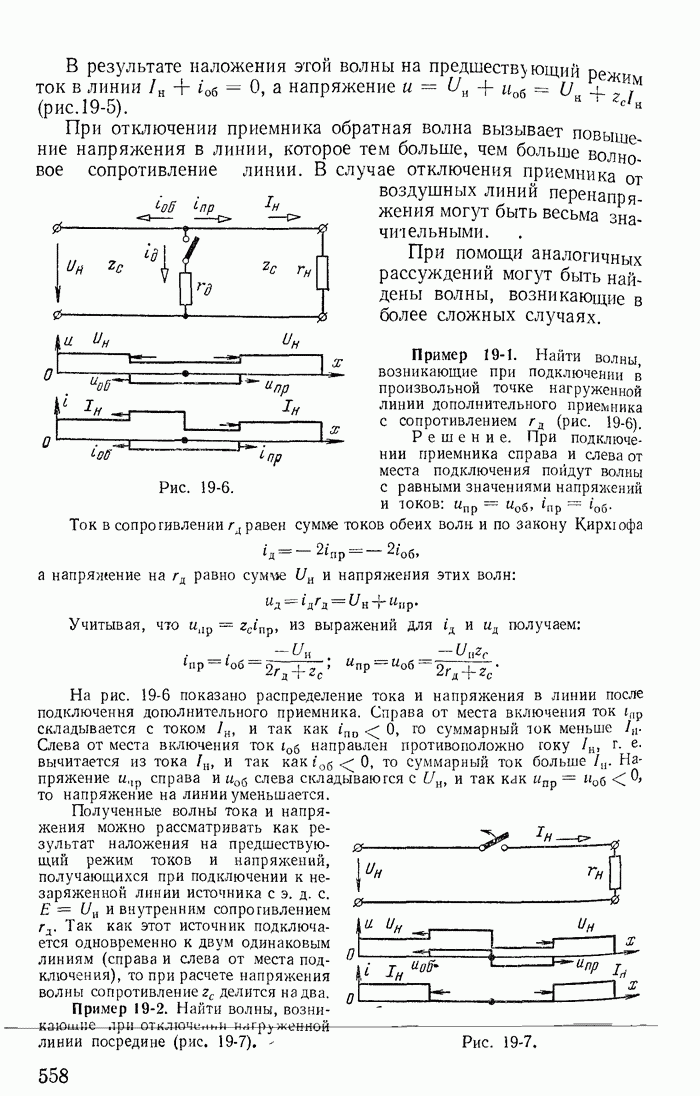
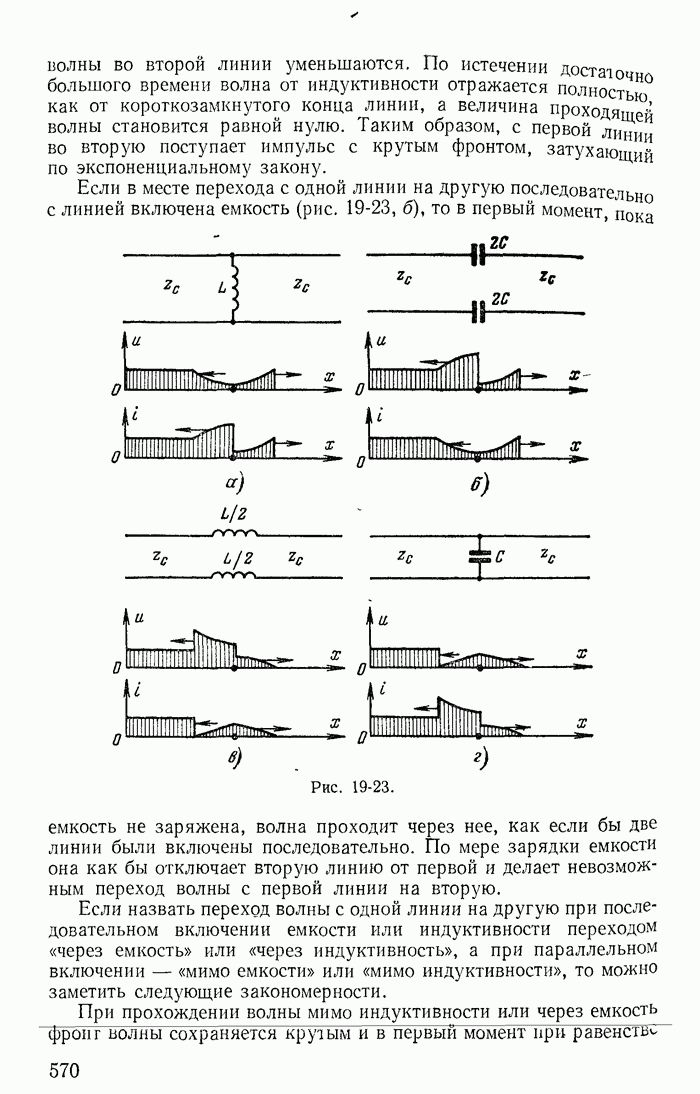
В качестве примера рассмотрим схему на рис. 1-21. На основании второго закона Кирхгофа

Пользуясь первым законом Кирхгофа, исключим из этих уравнений токи  в результате после группировки слагаемых получим:
в результате после группировки слагаемых получим:

Из этих уравнений следует, что в рассматриваемом случае ток J как бы замыкается по ветвям с сопротивлениями  дополняющими ветвь с источником тока J до замкнутого контура.
дополняющими ветвь с источником тока J до замкнутого контура.

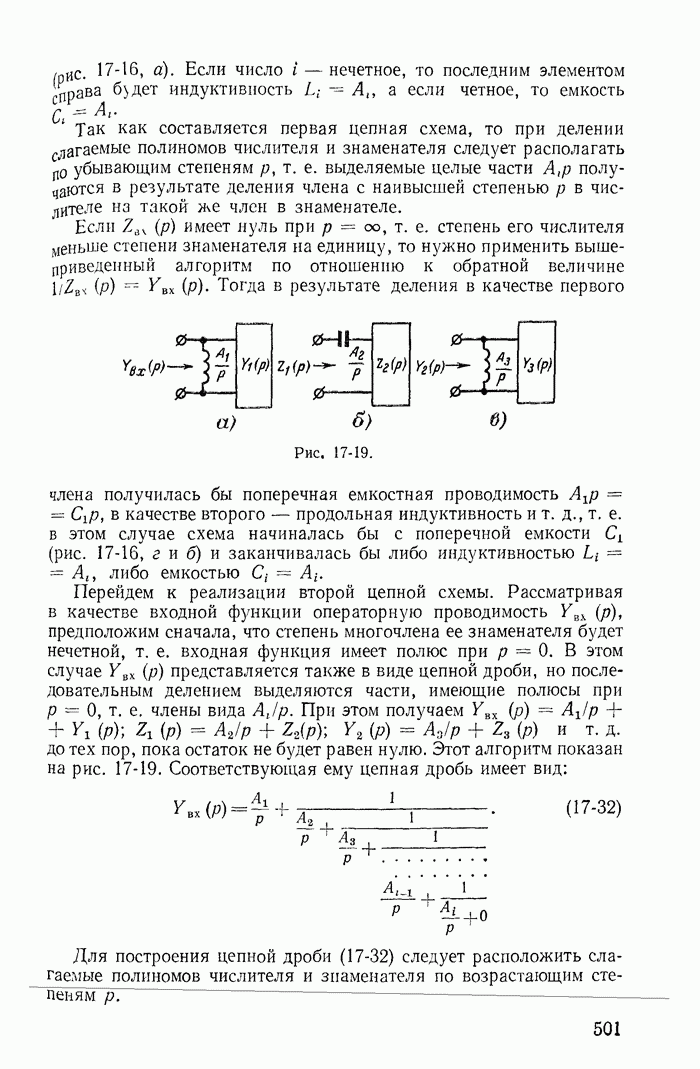
Рис. 1-28.
Обозначив в уравнениях (1-56) составляющие напряжений  соответственно через
соответственно через  можно переписать их иначе:
можно переписать их иначе:

Здесь следует отметить, что перенос слагаемых  из левой в правую часть уравнений (1-57) и замена
из левой в правую часть уравнений (1-57) и замена  напряжений на схеме
напряжений на схеме  иллюстрирует применение так называемой теоремы о компенсации, изложенной более подробно в § 2-6.
иллюстрирует применение так называемой теоремы о компенсации, изложенной более подробно в § 2-6.
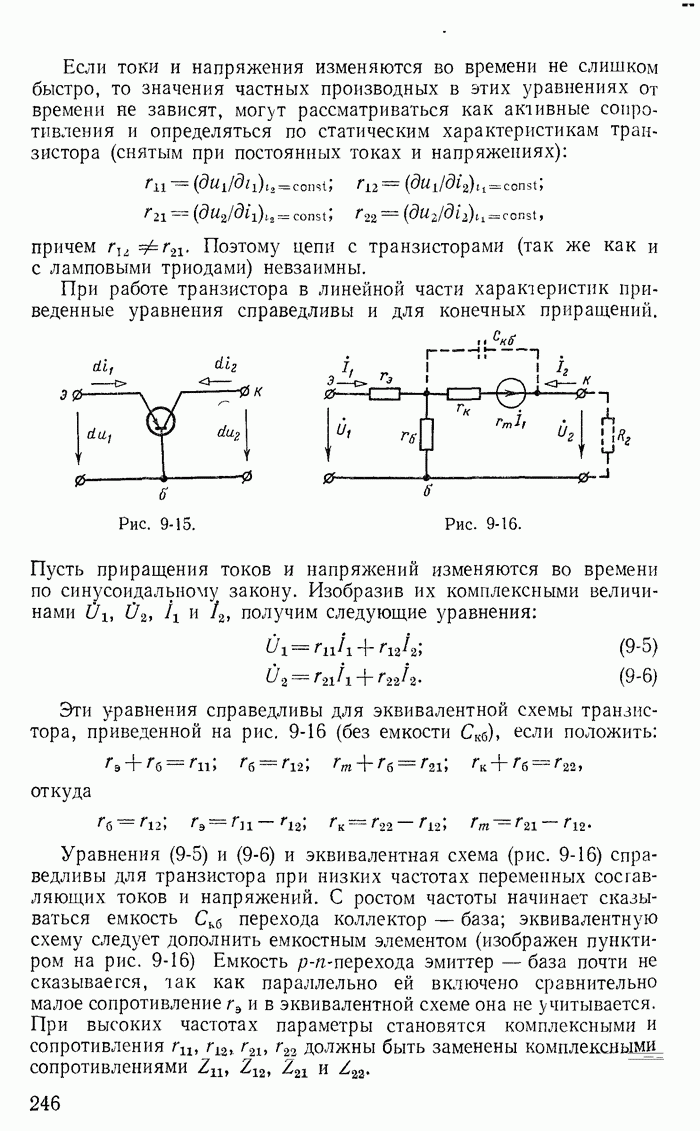
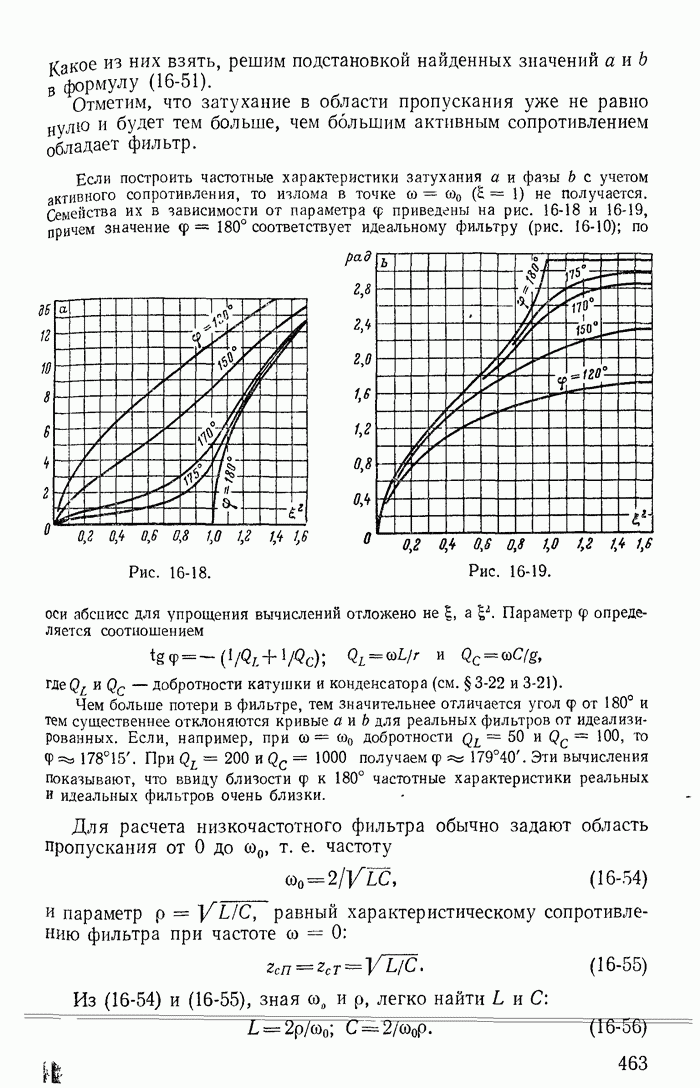
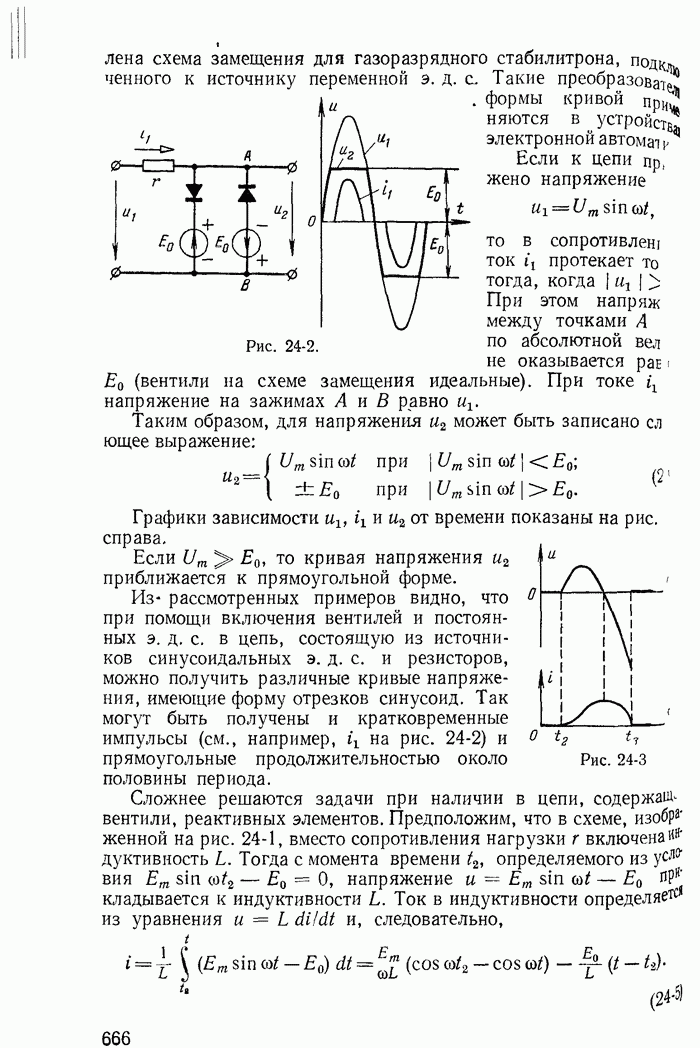
Уравнениям (1-57) соответствует эквивалентная схема (рис. 1-28, а), на которой источник тока J заменен источниками  при этом токи в ветвях с сопротивлениями
при этом токи в ветвях с сопротивлениями  и f не равны соответствующим токам в ветвях заданной
и f не равны соответствующим токам в ветвях заданной
схемы (рис. 1-21) и отличаются от них на ток J источника тока. Иначе говоря, после определения контурных токов  необходимо для вычисления токов
необходимо для вычисления токов  в ветвях заданной схемы (рис. 1-21) записать уравнения по первому закону Кирхгофа именно для заданной схемы:
в ветвях заданной схемы (рис. 1-21) записать уравнения по первому закону Кирхгофа именно для заданной схемы: 
Аналогично можно показать, что если принять ток J замыкающимся по ветви с сопротивлением  то получится новая эквивалентная схема (рис. 1-28, б); контурный ток
то получится новая эквивалентная схема (рис. 1-28, б); контурный ток  в эквивалентной схеме не равен действительному току
в эквивалентной схеме не равен действительному току  в заданной схеме (рис. 1-21) и отличается от него на ток
в заданной схеме (рис. 1-21) и отличается от него на ток 
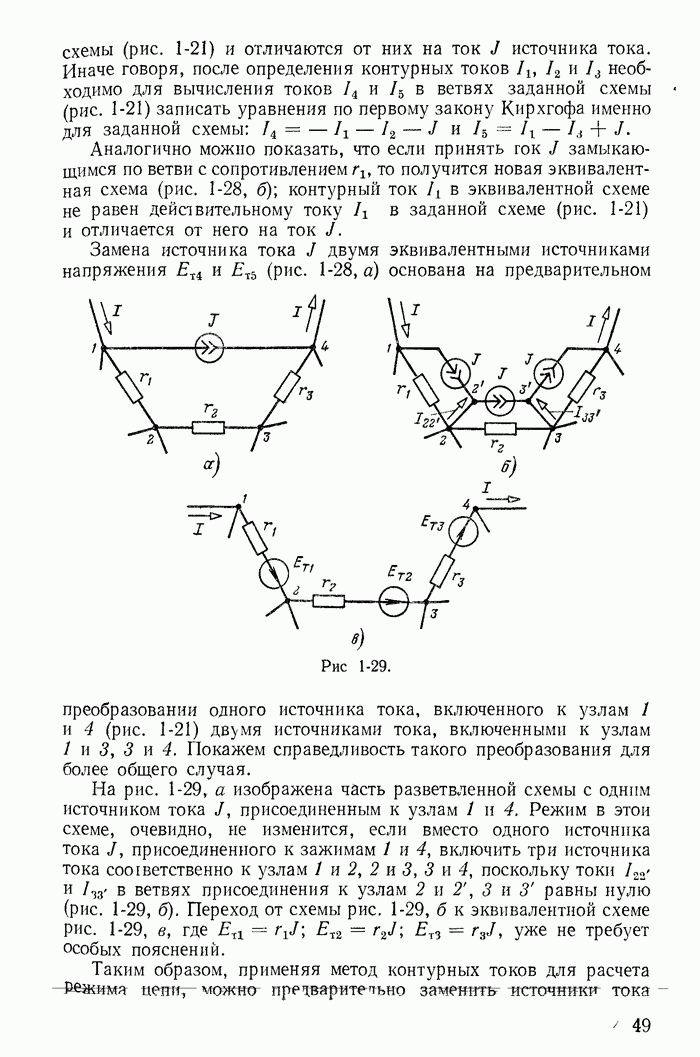
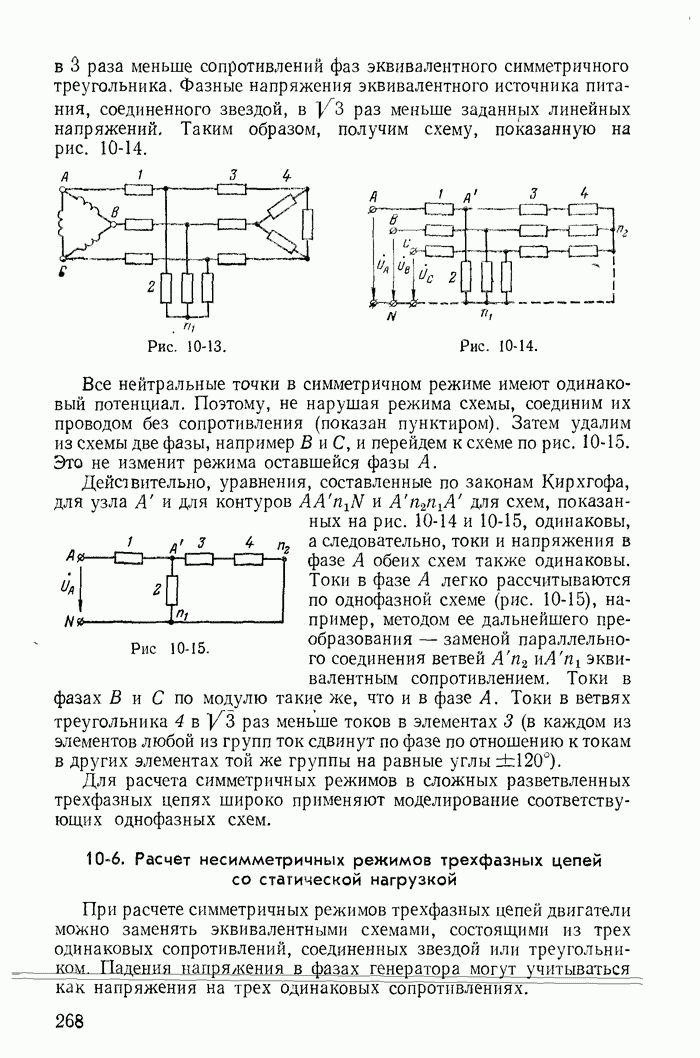
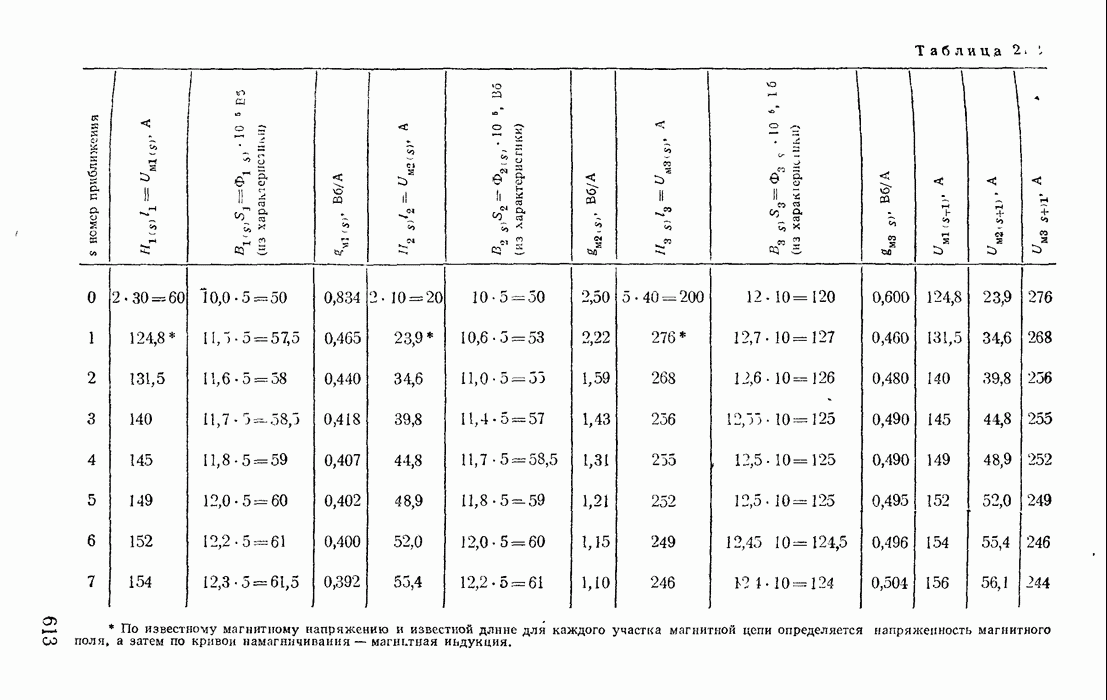
Замена источника тока J двумя эквивалентными источниками напряжения  (рис. 1-28, а) основана на предварительном преобразовании одного источника тока, включенного к узлам 1 и 4 (рис. 1-21) двумя источниками тока, включенными к узлам 1 и 3, 3 и 4.
(рис. 1-28, а) основана на предварительном преобразовании одного источника тока, включенного к узлам 1 и 4 (рис. 1-21) двумя источниками тока, включенными к узлам 1 и 3, 3 и 4.

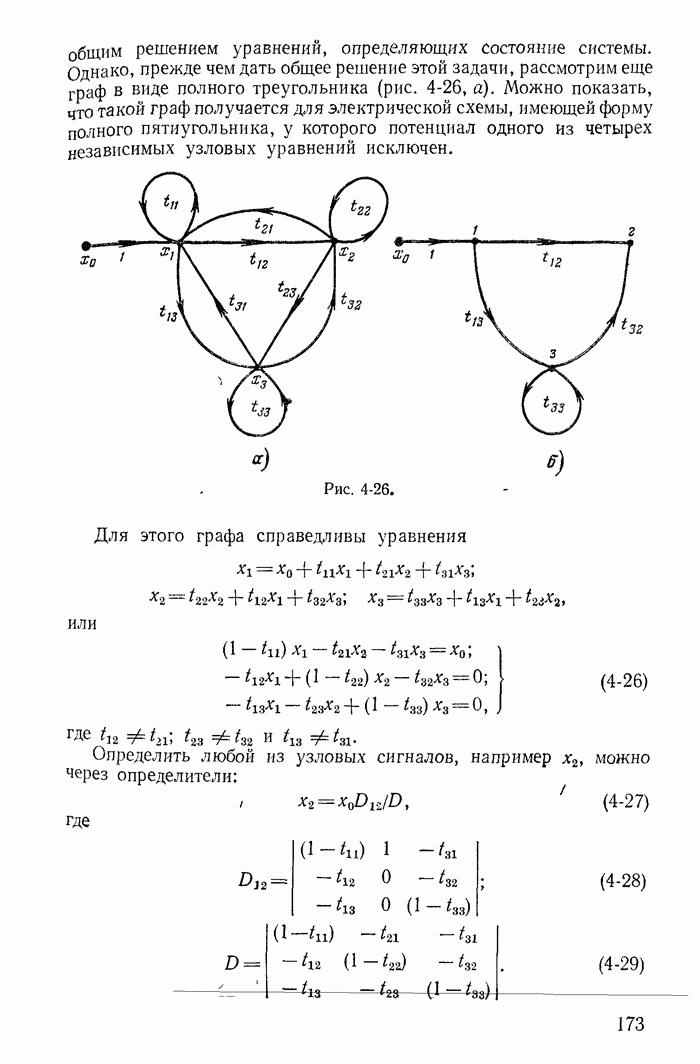
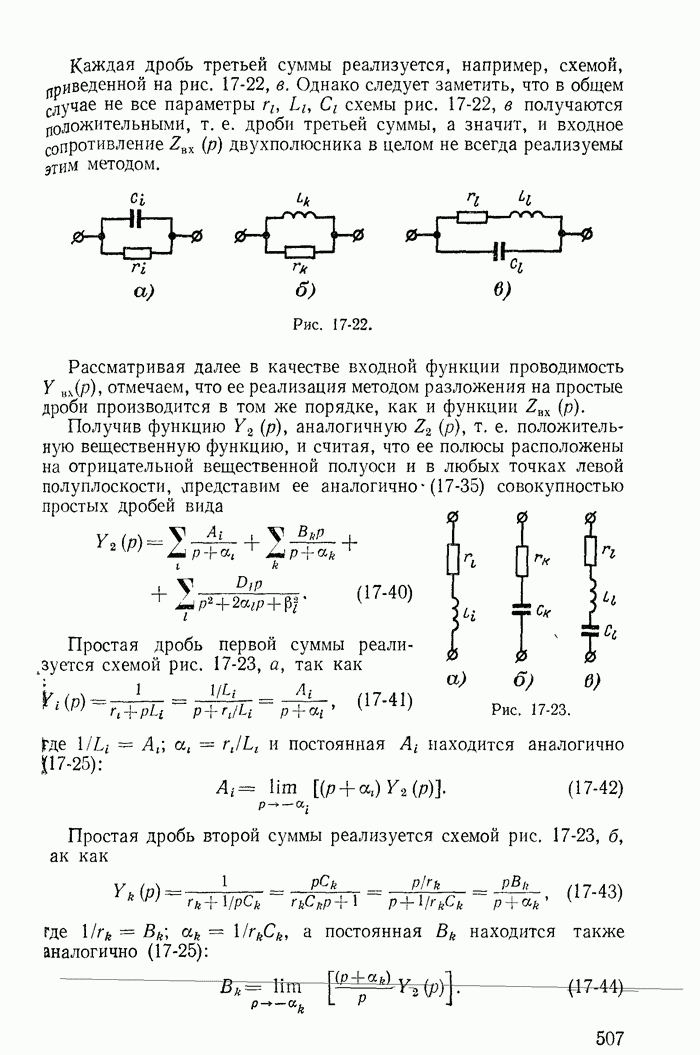
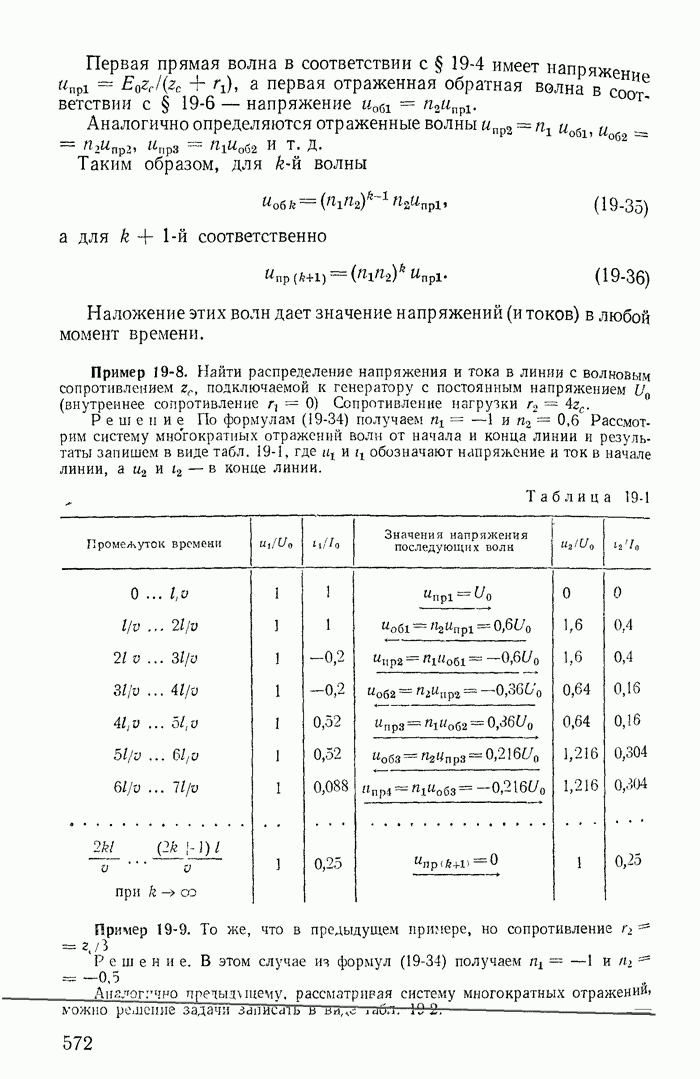
Рис. 1-29.
Покажем справедливость такого преобразования для более общего случая.
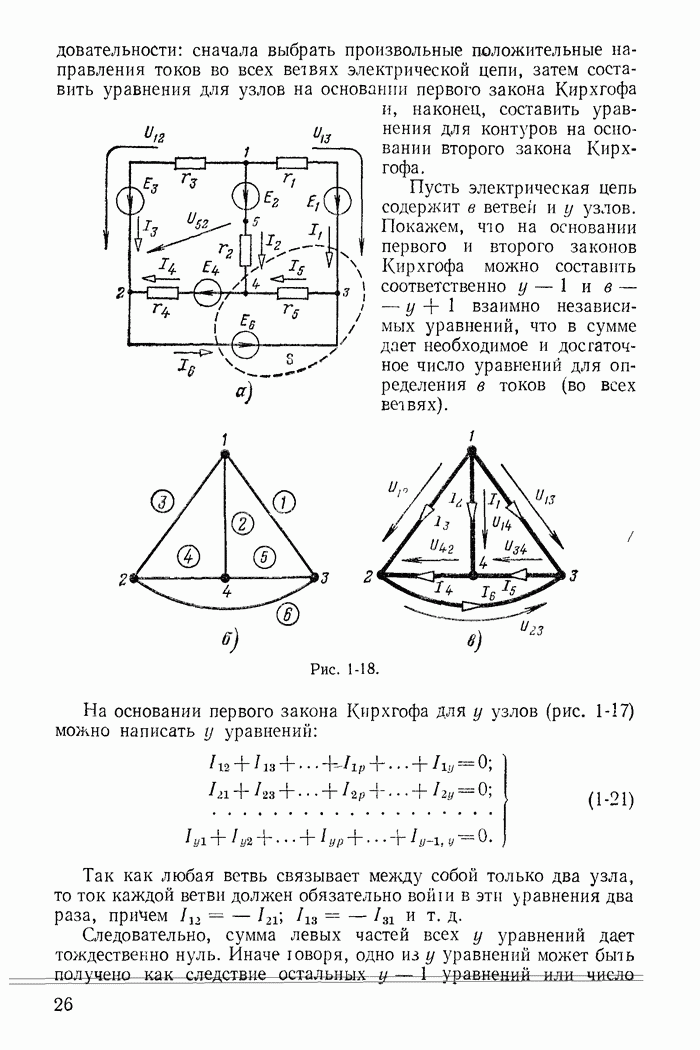
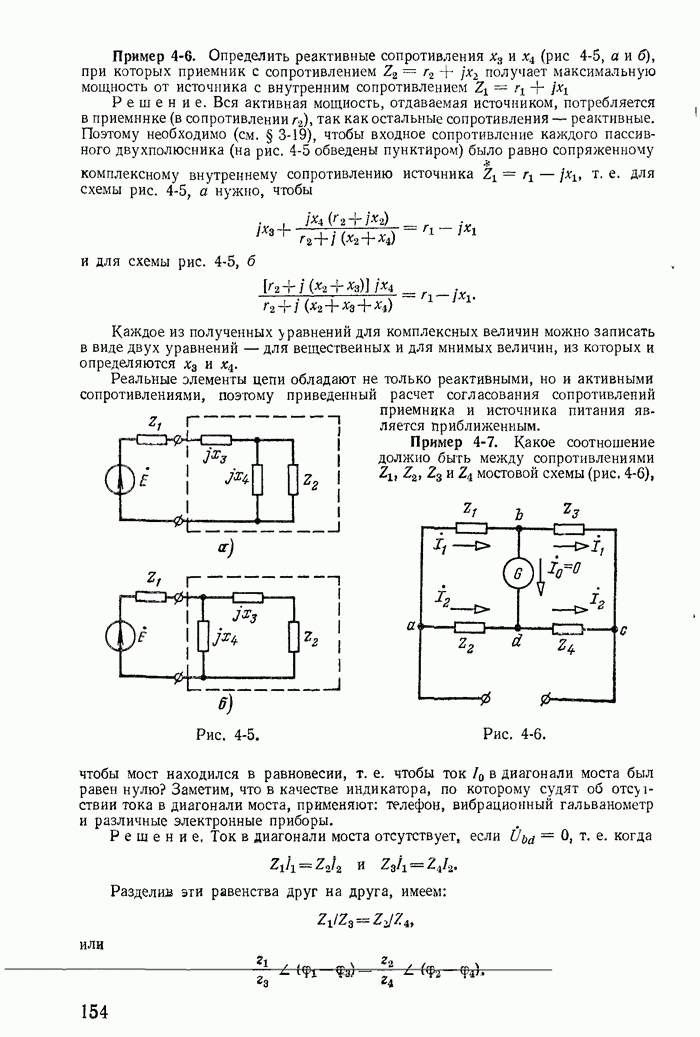
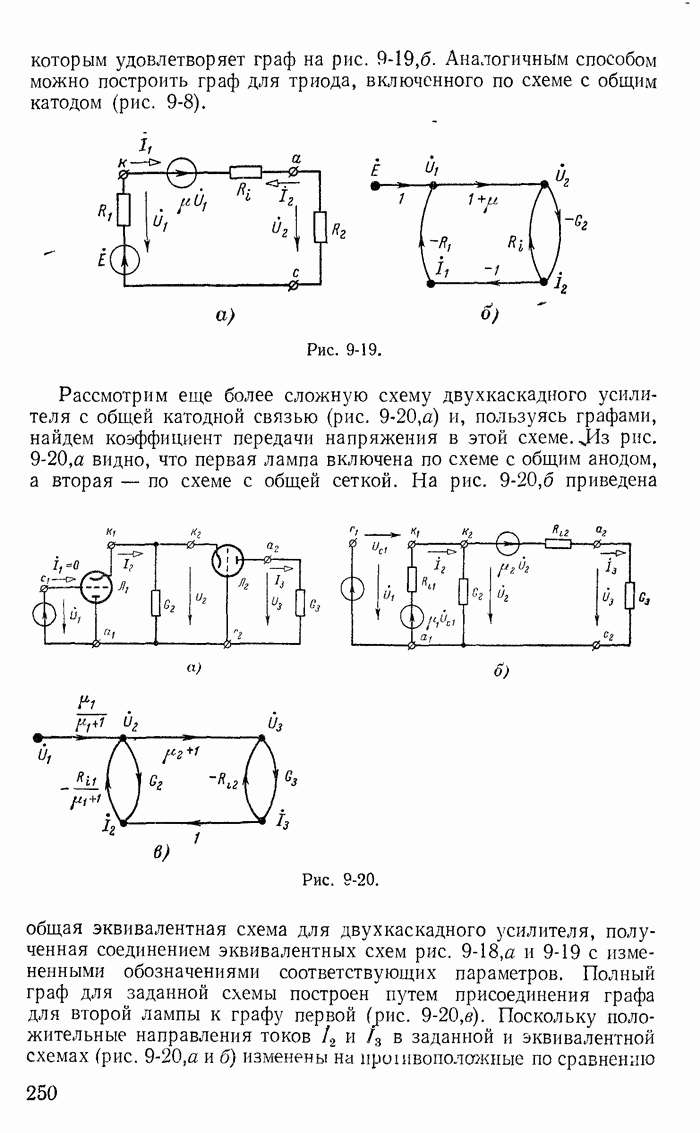
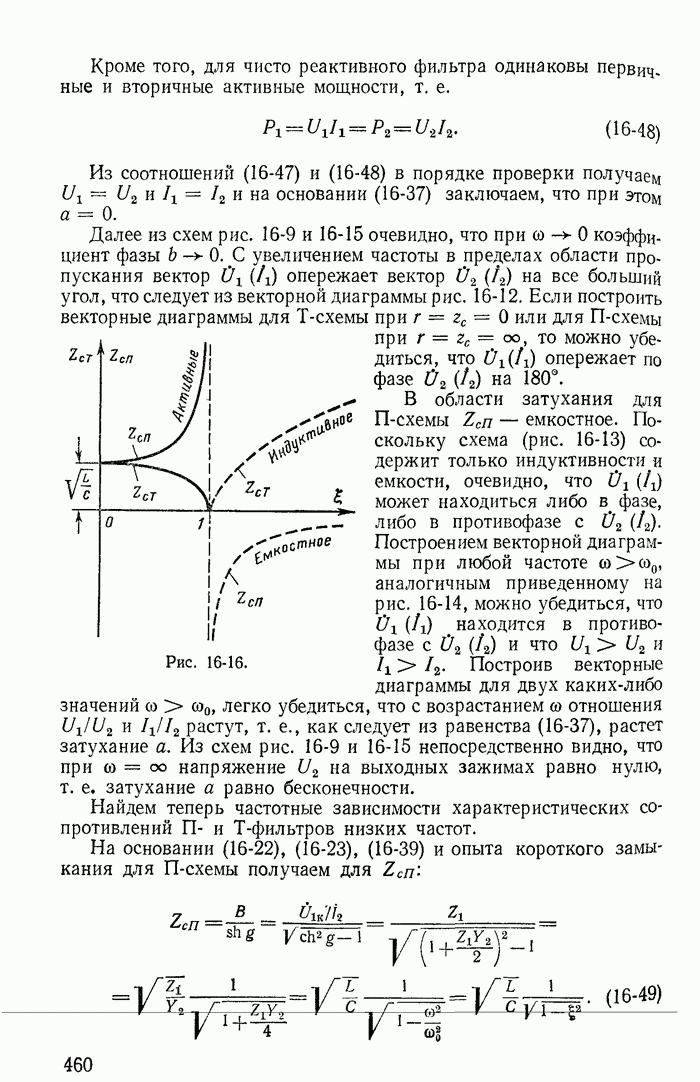
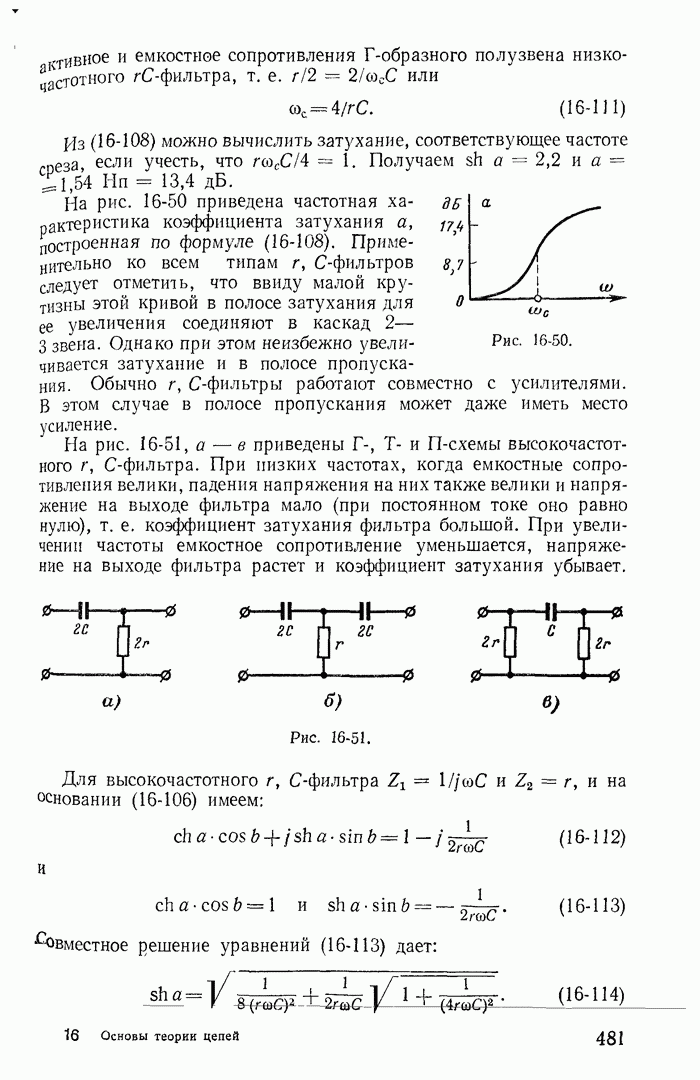
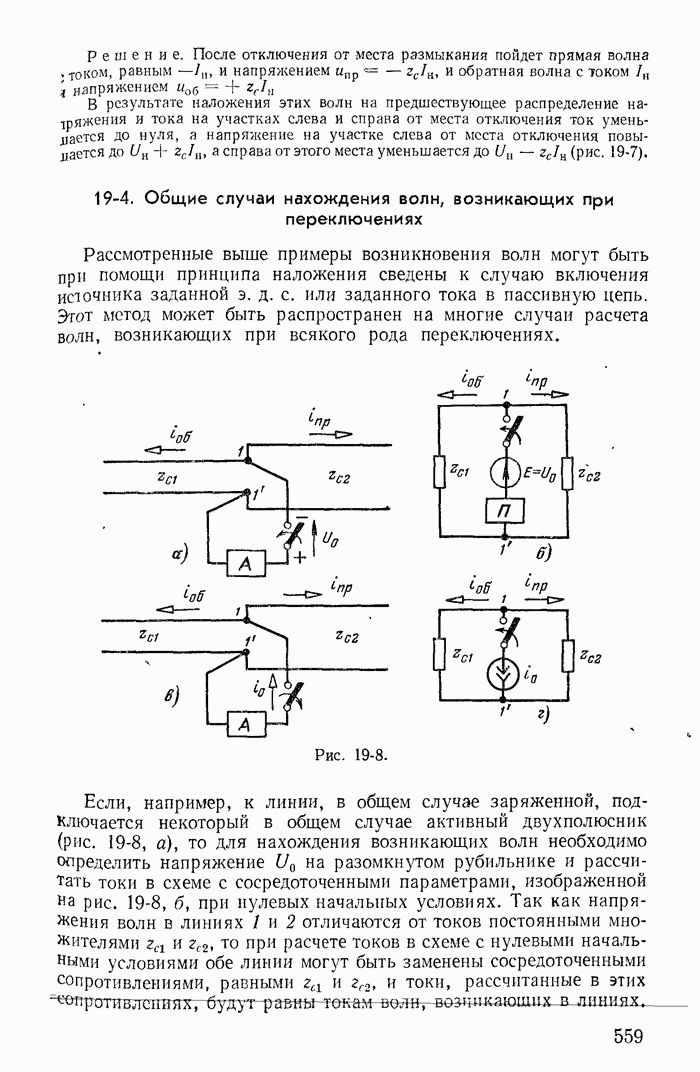
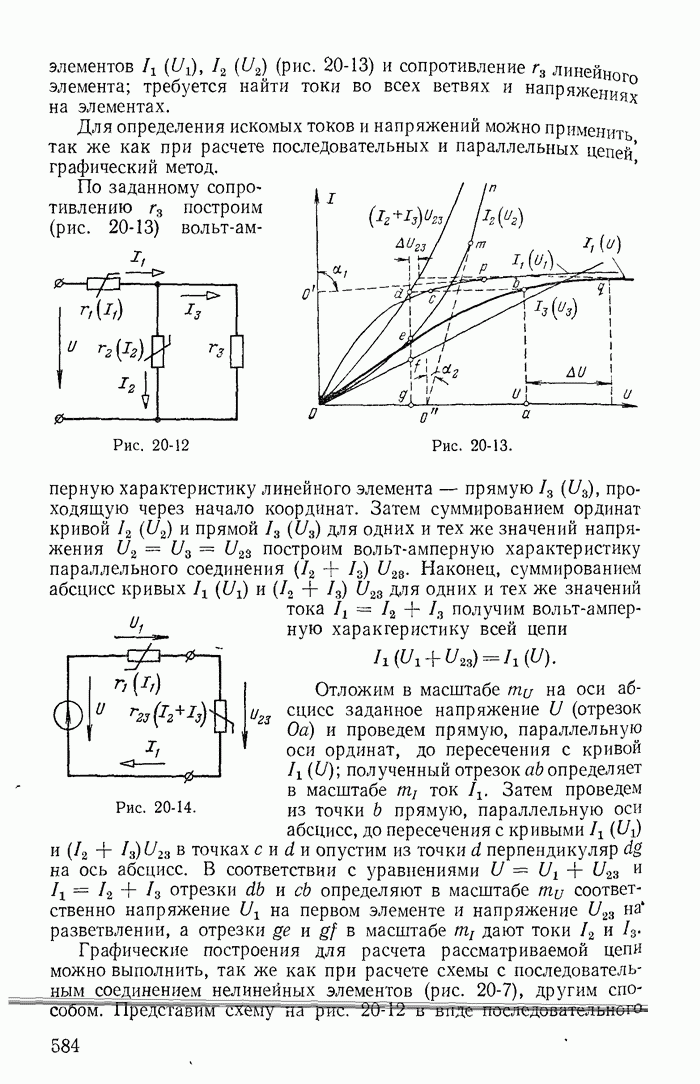
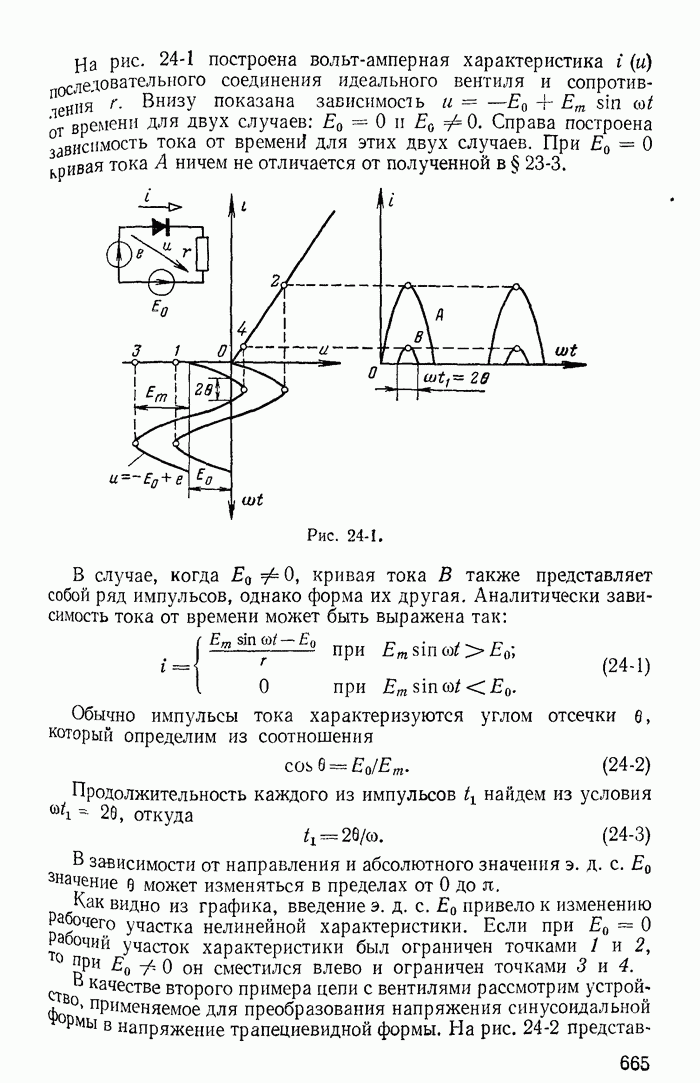
На рис. 1-29, а изображена часть разветвленной схемы с одним источником тока J, присоединенным к узлам 1 и 4. Режим в этой схеме, очевидно, не изменится, если вместо одного источника тока J, присоединенного к зажимам 1 и 4, включить три источника тока соответственно к узлам 1 и 2, 2 и 3, 3 и 4, поскольку токи  в ветвях присоединения к узлам 2 и 2, 3 и 3 равны нулю (рис. 1-29, б). Переход от схемы рис. 1-29, б к эквивалентной схеме рис. 1-29, в, где
в ветвях присоединения к узлам 2 и 2, 3 и 3 равны нулю (рис. 1-29, б). Переход от схемы рис. 1-29, б к эквивалентной схеме рис. 1-29, в, где  уже не требует особых пояснений.
уже не требует особых пояснений.
Таким образом, применяя метод контурных токов для расчета режима цепи, можно предварительно заменить источники тока
эквивалентными источниками э. д. с., а затем ввести контурные токи и на основании второго закона Кирхгофа составить систему уравнений для их определения. Действительные токи в ветвях без эквивалентных источников э. д. с., заменяющих источники тока, определяются по первому закону Кирхгофа суммированием контурных токов; в ветвях заданной схемы, в которых на эквивалентной схеме включены источники э. д. с., учитываются и токи источников тока.
При расчете электрических цепей изложенным методом всегда стремятся к тому, чтобы число контурных токов, замыкающихся через каждую из ветвей, было по возможности минимальным. С этой целью обычно выбирают каждый контур в виде ячейки (на рис. 1-27, а три ячейки с контурными токами  ), руководствуясь указанным выше правилом выбора независимых контуров (дерева и ветвей связи) при составлении уравнений на основании второго закона Кирхгофа.
), руководствуясь указанным выше правилом выбора независимых контуров (дерева и ветвей связи) при составлении уравнений на основании второго закона Кирхгофа.
Положительные направления контурных токов можно выбирать и произвольно, т. е. независимо от положительных направлений токов в ветвях.
Установим теперь более общие, необходимые для дальнейших выводов соотношения между контурными токами, сопротивлениями и э. д. с. цепи произвольной конфигурации. Для схемы, имеющей к независимых контуров, уравнения, аналогичные (1-53), запишутся в виде

В этих уравнениях сопротивление вида  (с двумя одинаковыми индексами) называется собственным сопротивлением контура
(с двумя одинаковыми индексами) называется собственным сопротивлением контура  а сопротивление вида
а сопротивление вида  —
—  (с двумя различными индексами) называется общим сопротивлением контуров
(с двумя различными индексами) называется общим сопротивлением контуров  Правые части уравнений (1-58) называются контурными э. д. с. Каждая из контурных э. д. с. вида
Правые части уравнений (1-58) называются контурными э. д. с. Каждая из контурных э. д. с. вида  равна алгебраической сумме э. д. с. всех источников в ветвях контура
равна алгебраической сумме э. д. с. всех источников в ветвях контура  Положительные знаки в каждом уравнении (1-58) должны быть взяты для токов и э. д. с., положительные направления которых совпадают с произвольно выбранным направлением обхода соответствующего контура.
Положительные знаки в каждом уравнении (1-58) должны быть взяты для токов и э. д. с., положительные направления которых совпадают с произвольно выбранным направлением обхода соответствующего контура.
В более общем случае, огда электрическая цепь содержит как источники э. д. с., так и источники тока, контурное уравнение для  контура записывается в виде
контура записывается в виде

где  обозначает собственное сопротивление контура
обозначает собственное сопротивление контура  — общее сопротивление двух контуров
— общее сопротивление двух контуров 
 — ток источника тока, замыкающийся по сопротивлению
— ток источника тока, замыкающийся по сопротивлению 
Решая систему уравнений (1-58) при помощи определителей относительно любого из токов, например  получаем:
получаем: 

где  — определитель системы уравнений (1-58), т. е.
— определитель системы уравнений (1-58), т. е.

 — алгебраические дополнения определителя
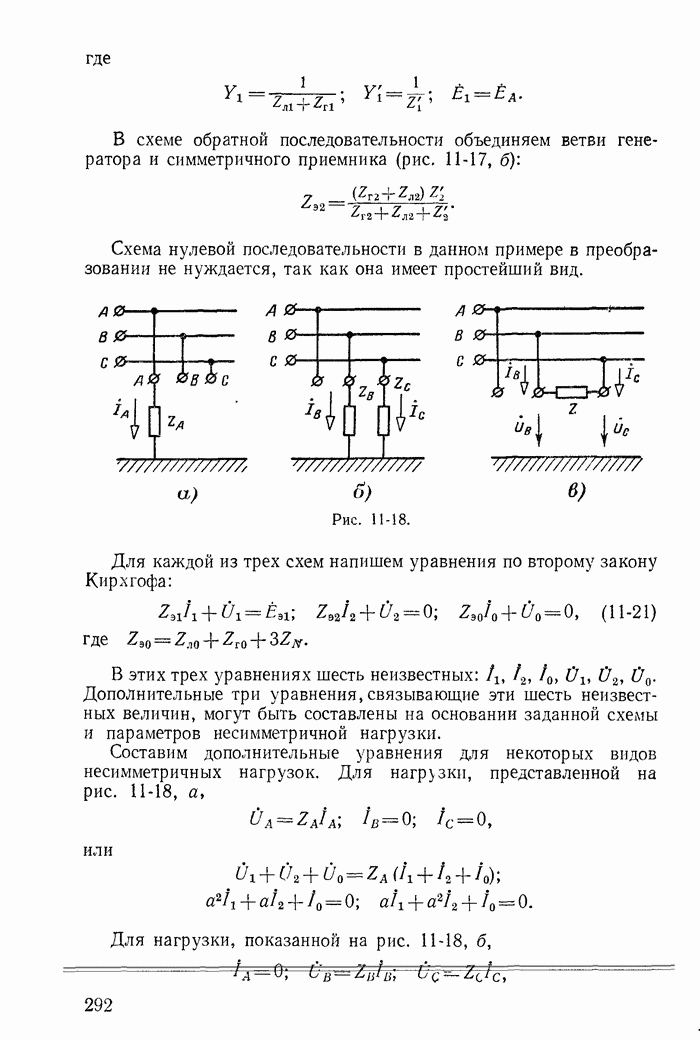
— алгебраические дополнения определителя  причем
причем  получается из
получается из  путем вычеркивания
путем вычеркивания  столбца и
столбца и  строки и умножения полученного определителя на
строки и умножения полученного определителя на  Необходимо отметить, что сопротивления вида
Необходимо отметить, что сопротивления вида  нужно записывать в выражении (1-60) с тем знаком, который стоит перед соответствующим напряжением в уравнениях (1-58).
нужно записывать в выражении (1-60) с тем знаком, который стоит перед соответствующим напряжением в уравнениях (1-58).
Подчеркнем, что при соответствующем выборе контуров получится такая система контурных уравнений, определитель которой имеет аналогично определителю минимальное число слагаемых с отрицательными знаками (которые сокращаются с соответствующими положительными членами).
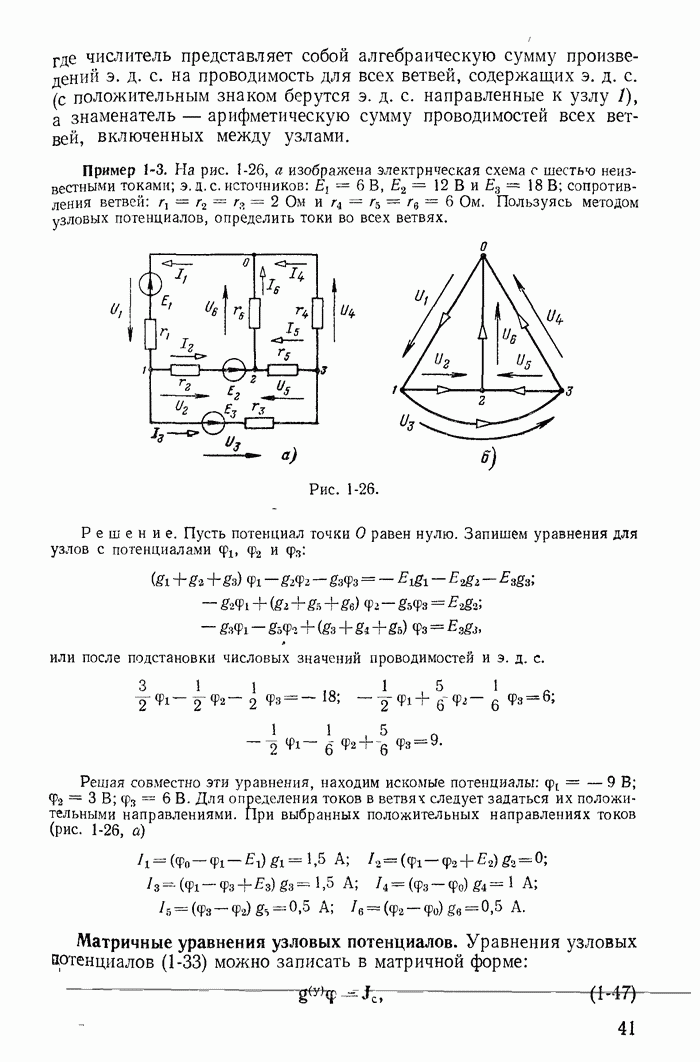
Для иллюстрации отмеченных положений рассмотрим схему на рис. 1-27, а, для которой справедлива, например, следующая система уравнений:

где последнее уравнение получено простым суммированием первых трех; оно справедливо для внешнего контура, проходящего через ветви связи с сопротивлениями  Совместное решение любых трех уравнений системы (1-61) определяет неизвестные контурные токи
Совместное решение любых трех уравнений системы (1-61) определяет неизвестные контурные токи
Покажем, что система из первых трех уравнений дает определитель с большим числом слагаемых (до сокращения), чем система, например, из первых двух и четвертого уравнений. Для первых трех уравнений определитель

Этот определитель после раскрытия имеет 38 слагаемых (до сокращения), из которых 22 попарно равны по абсолютному значению, но по знаку противоположны и сокращаются.
Для первых двух и четвертого уравнений определитель

В этом определителе только два слагаемых равны по абсолютной величине, но противоположны по знаку и сокращаются.
Для решения общей задачи расчета неизвестных токов во всех ветвях линейной электрической цепи можно выбрать один из двух основных методов расчета: узловых потенциалов или контурных токов.
Методом узловых потенциалов целесообразно пользоваться, когда число узлов схемы, уменьшенное на единицу, меньше числа независимых контуров  , а методом контурных токов при
, а методом контурных токов при 
Матричные уравнения контурных токов. Уравнения контурных токов (1-58) с учетом (1-58а) можно записать в матричной форме:

где  — квадратная матрица контурных сопротивлений;
— квадратная матрица контурных сопротивлений;
 — матрица-столбец контурных токов;
— матрица-столбец контурных токов;
 — матрица-столбец контурных э. д. с., учитывающая источники э. д. с. и эквивалентные э. д. с. от источников тока.
— матрица-столбец контурных э. д. с., учитывающая источники э. д. с. и эквивалентные э. д. с. от источников тока.
После умножения уравнения (1-64) слева на  получим:
получим:

Покажем, что матрицу контурных сопротивлений  можно получить непосредственно по схеме при помощи матрицы соединения контурных сопротивлений В:
можно получить непосредственно по схеме при помощи матрицы соединения контурных сопротивлений В:

где  диагональная матрица сопротивлений ветвей;
диагональная матрица сопротивлений ветвей;
 — транспонированная матрица соединения контурных сопротивлений.
— транспонированная матрица соединения контурных сопротивлений.
Матрица соединения контурных сопротивлений В составляется так, что ее строки соответствуют независимым контурам, а столбцы — ветвям. На пересечении строки и столбца записывается ±1 или 0 пробел) в зависимости от того, входит или не входит данная ветвь в соответствующий контур; положительный знак принимается в том случае, если направление ветви совпадает с направлением обхода контура, а отрицательный знак — если не совпадает. При этом направление обхода каждого контура примем совпадающим с положительным направлением соответствующего контурного тока, а направления ветвей — с положительными направлениями токов в ветвях.
Для получения независимых контуров следует сначала выбрать дерево схемы, что в свою очередь определяет вётви связи, а следовательно, и контурные токи.
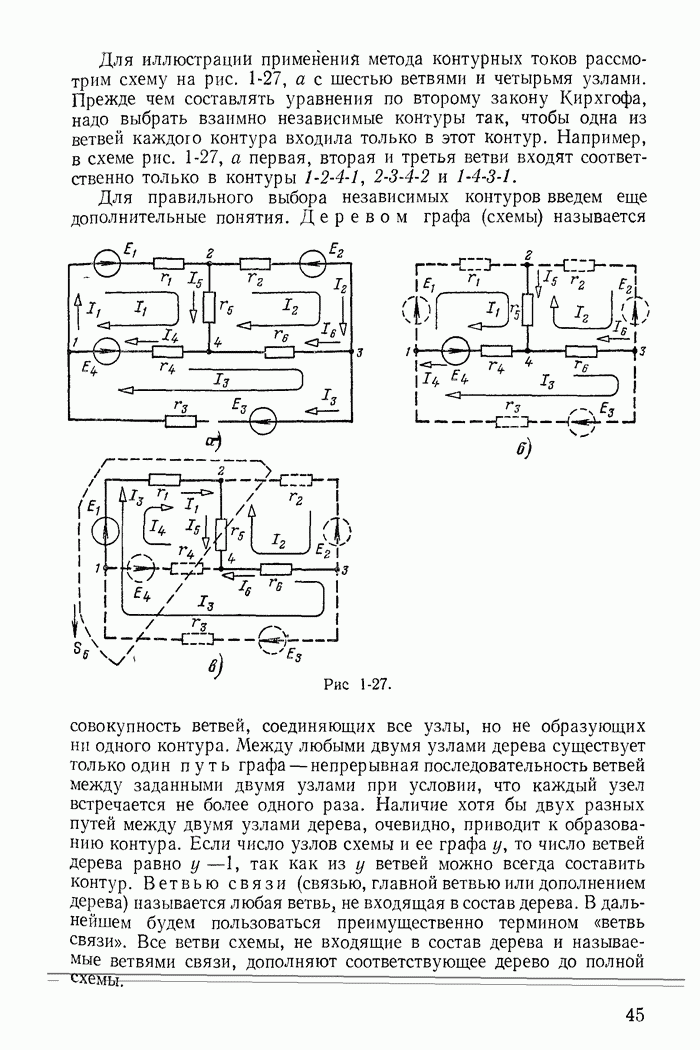
Для иллюстрации рассмотрим схему на рис. 1-27, а с выбранным деревом из четвертой, пятой и шестой ветвей (рис. 1-27, б). В этом случае независимые контуры содержат контурные токи  что соответствует первой, второй и третьей ветвям связи.
что соответствует первой, второй и третьей ветвям связи.
Матрица соединения контурных сопротивлений В состоит из грех строк и шести столбцов:

Диагональная матрица сопротивлений

Произведение матриц В и  равно:
равно:

Квадратная матрица контурных сопротивлений определяется по формуле (1-66):

Матрица-столбец контурных токов

Матрица-столбец контурных э. д. с.

Пользуясь уравнением (1-64), матрицами  , легко получить уравнения (1-53).
, легко получить уравнения (1-53).
Подчеркнем, что матрица токов ветвей  легко определяется через матрицу контурных токов
легко определяется через матрицу контурных токов  по формуле
по формуле

Например, для схемы рис. 1-27, а

Из этого матричного уравнения сразу получаем равенства, определяющие токи ветвей через контурные токи:

В дальнейшем индексы в у токов ветвей и индексы k у контурных токов в алгебраических выражениях, как правило, будем опускать,
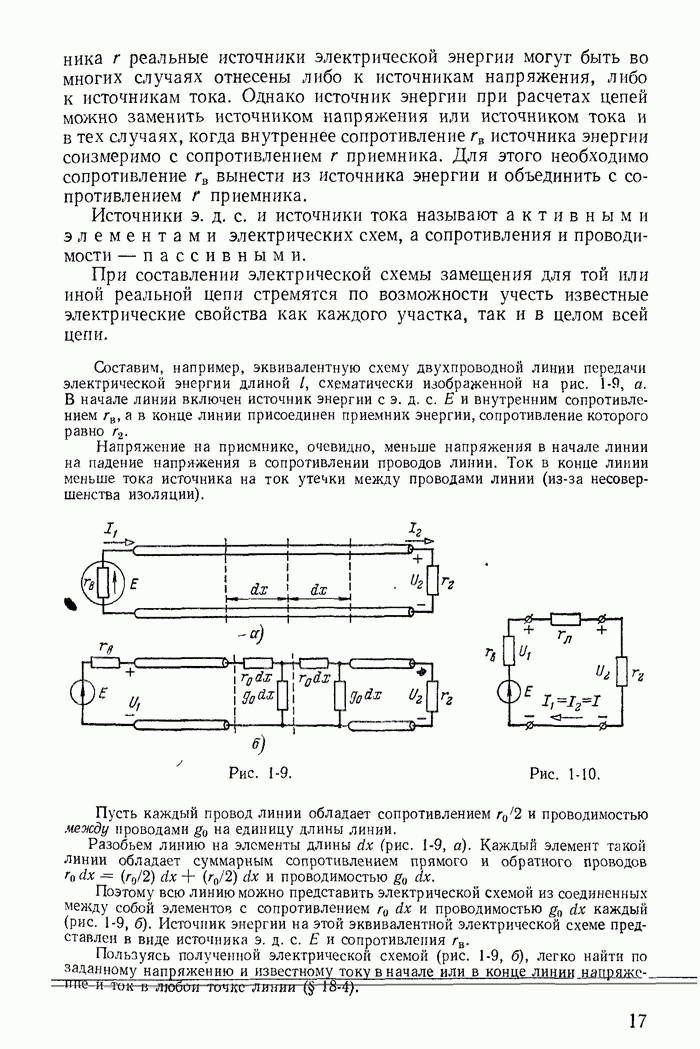
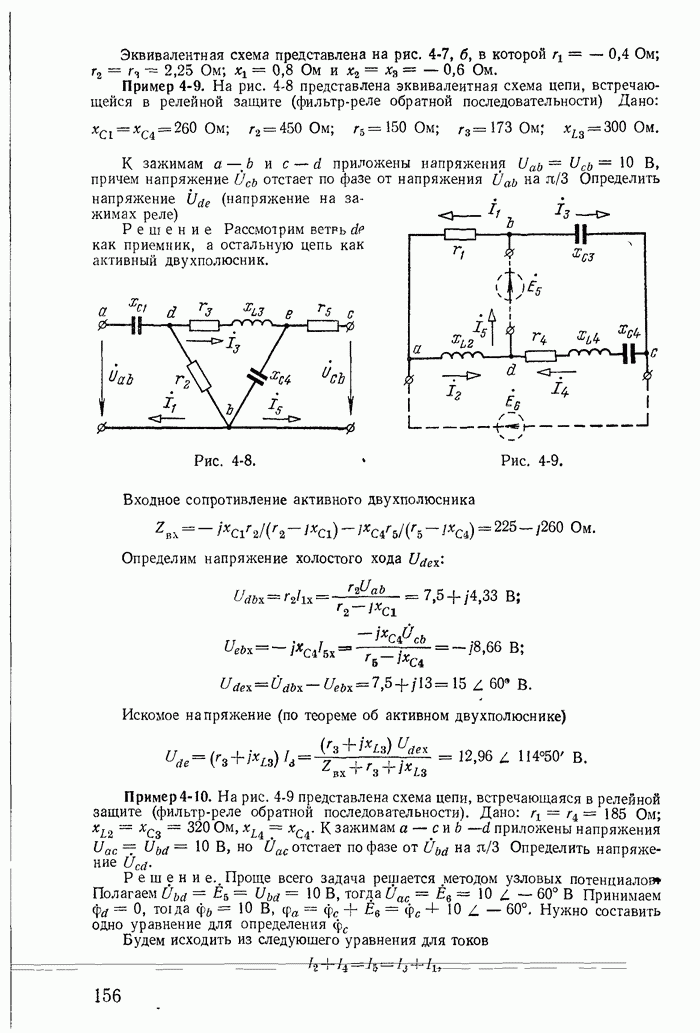
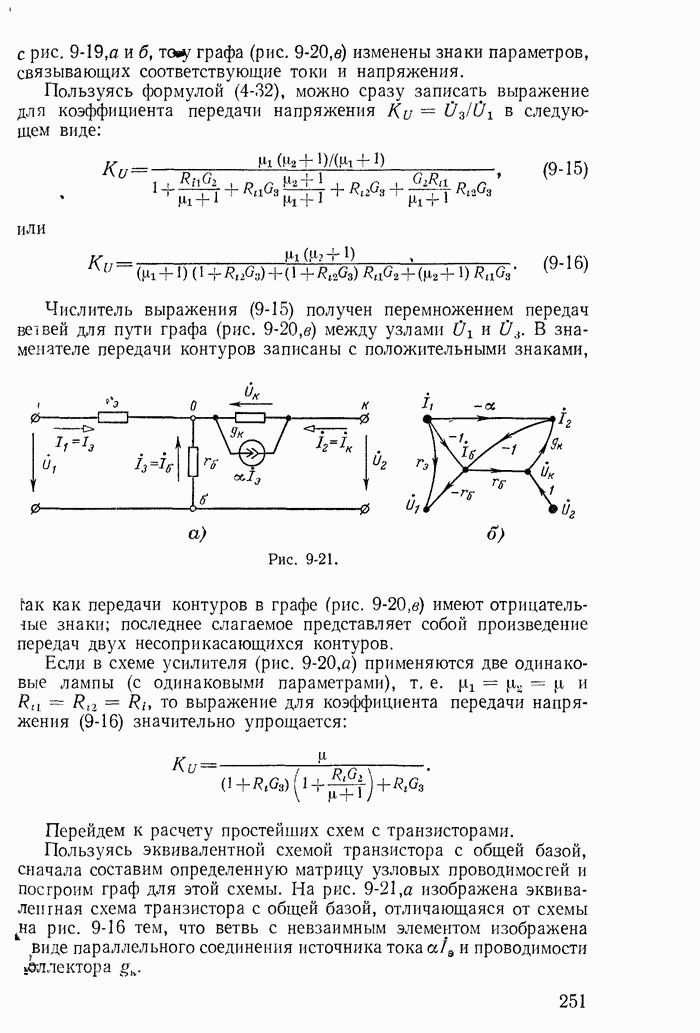
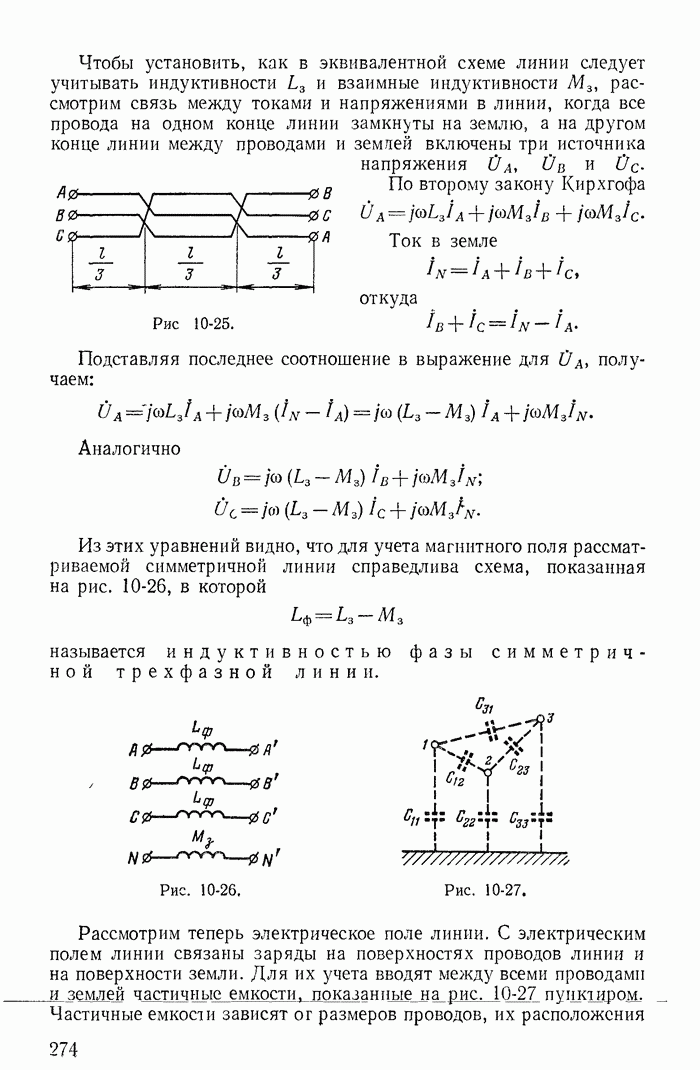
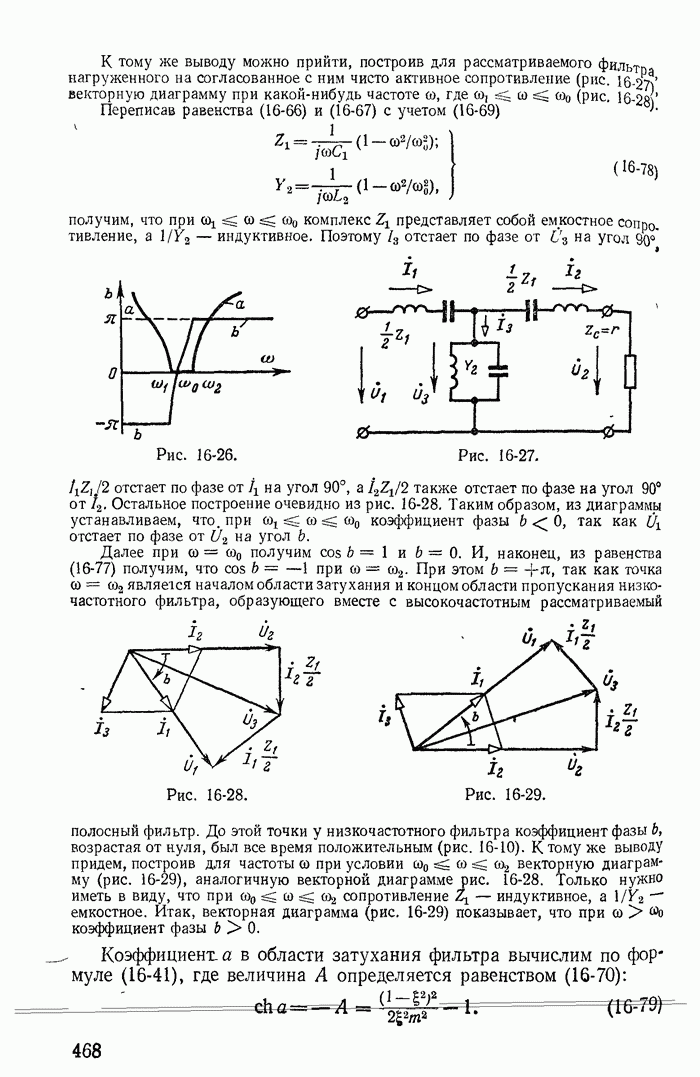
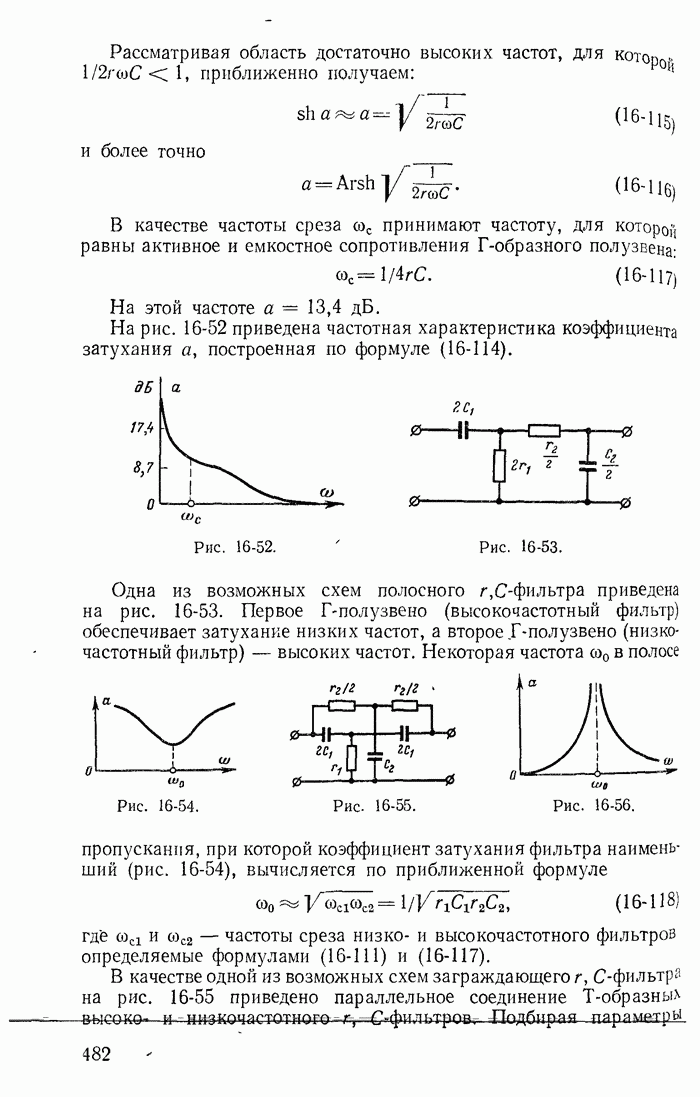
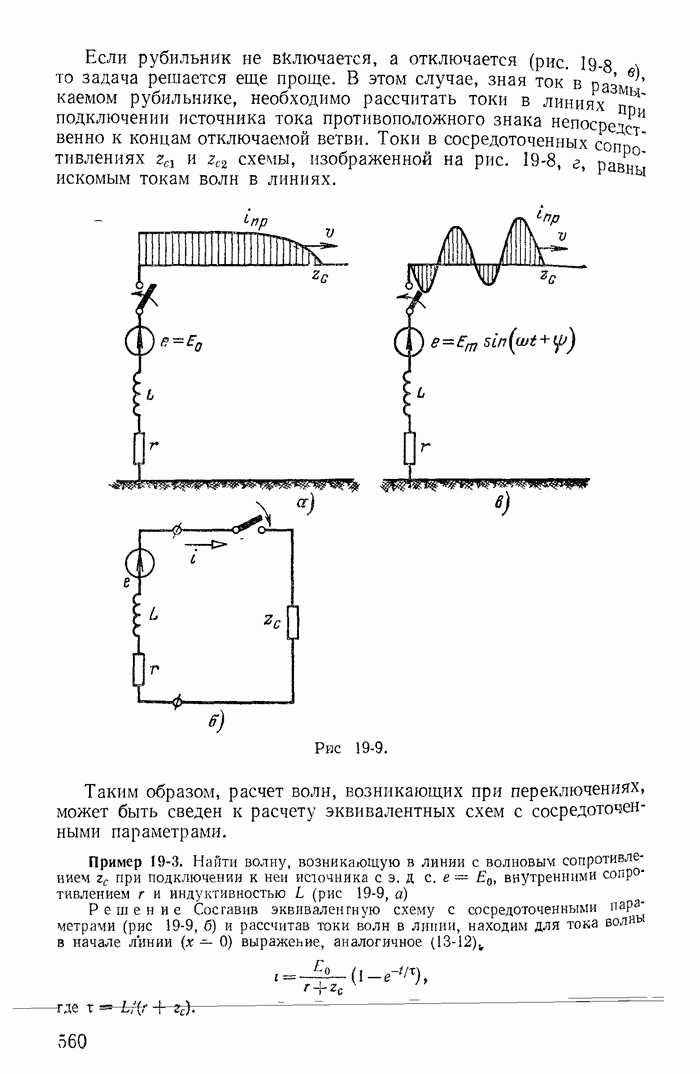
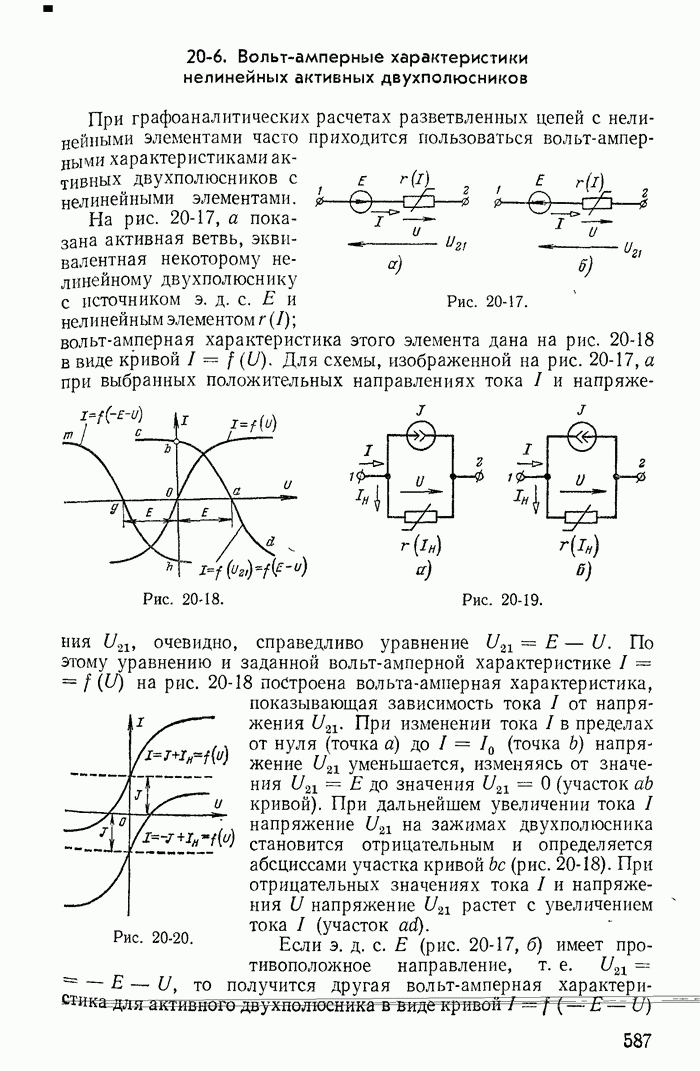
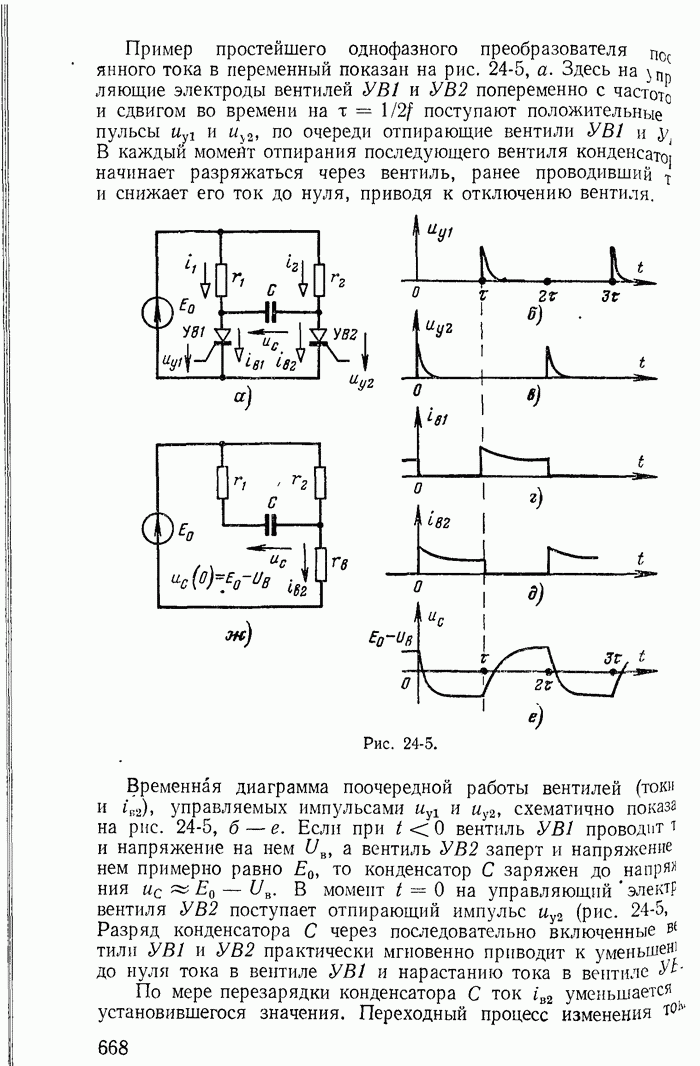
В заключение подчеркнем, что все соотношения между токами ветвей и контурными токами для схем, показанных на рис. 1-27, а-в, легко получить из графов, построенных соответственно для этих схем на рис. 1-30, а-в.

Рис. 1-30.
При этом деревья графа изображены на рис. 1-30, б и в сплошными линиями, а ветви связи — пунктирными.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К ЧЕТВЕРТОМУ ИЗДАНИЮ
- ВВЕДЕНИЕ
- Раздел первый. ЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ С СОСРЕДОТОЧЕННЫМИ ПАРАМЕТРАМИ
- 1-1. Элементы электрических цепей и электрических схем
- 1-2. Эквивалентные схемы для источников энергии
- 1-3. Закон Ома для участка цепи с э. д. с.
- 1-4. Распределение потенциала вдоль неразветвленной электрической цепи
- 1-5. Баланс мощностей для простейшей неразветвленной цепи
- 1-6. Применение законов Кирхгофа для расчета разветвленных цепей
- 1-7. Метод узловых потенциалов
- 1-8. Метод контурных токов
- 1-9. Уравнения состояния цепи в матричной форме
- 1-10. Преобразование линейных электрических схем
- Глава вторая. ОСНОВНЫЕ СВОЙСТВА ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ПРИ ПОСТОЯННЫХ ТОКАХ И НАПРЯЖЕНИЯХ
- 2-2. Свойство взаимности
- 2-3. Входные и взаимные проводимости и сопротивления ветвей; коэффициенты передачи напряжений и токов
- 2-4. Применение топологических методов для расчета цепей
- 2-5. Топологические формулы и правила для определения передачи электрической цепи
- 2-6. Теорема о компенсации
- 2-7. Линейные соотношения между напряжениями и токами
- 2-8. Теорема о взаимных приращениях токов и напряжений
- 2-9. Общие замечания о двухполюсниках
- 2-10. Теорема об активном двухполюснике и ее применение для расчета разветвленных цепей
- 2-11. Передача энергии от активного двухполюсника к пассивному
- Глава третья. ОСНОВНЫЕ ПОНЯТИЯ О ЦЕПЯХ СИНУСОИДАЛЬНОГО ТОКА
- 3-2. Понятие о генераторах переменного тока
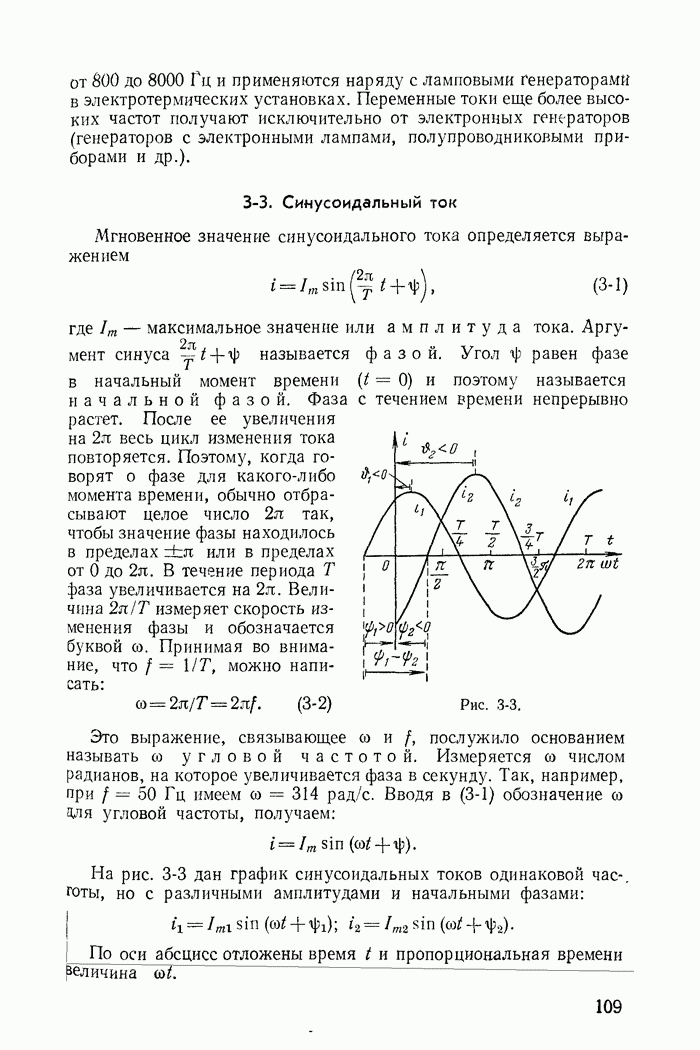
- 3-3. Синусоидальный ток
- 3-4. Действующие ток, э. д. с. и напряжение
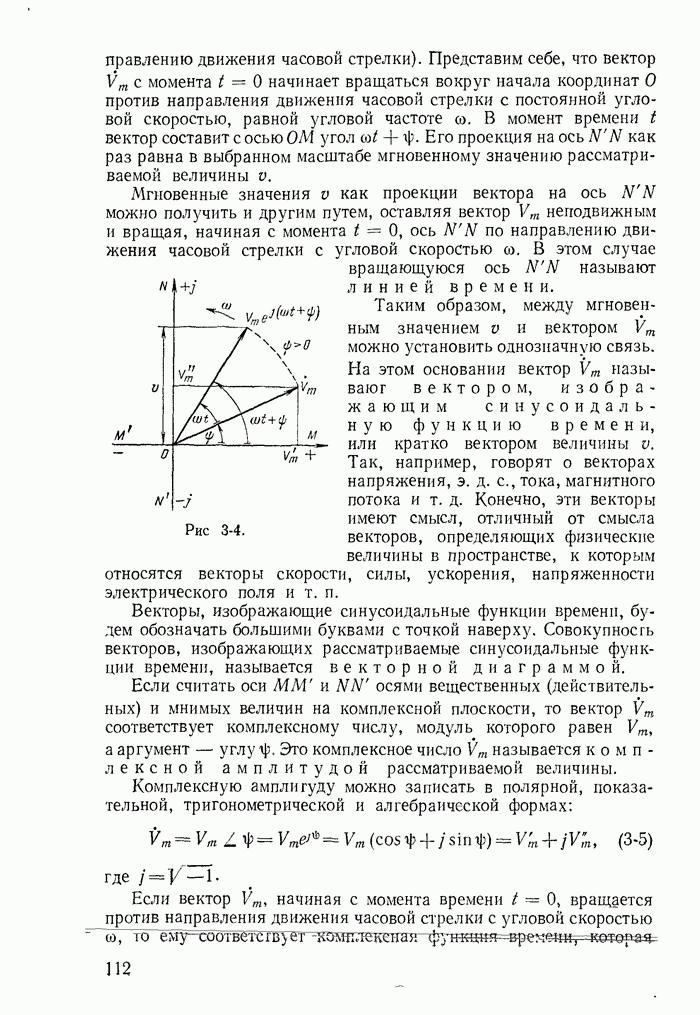
- 3-5. Изображение синусоидальных функций времени векторами и комплексными числами
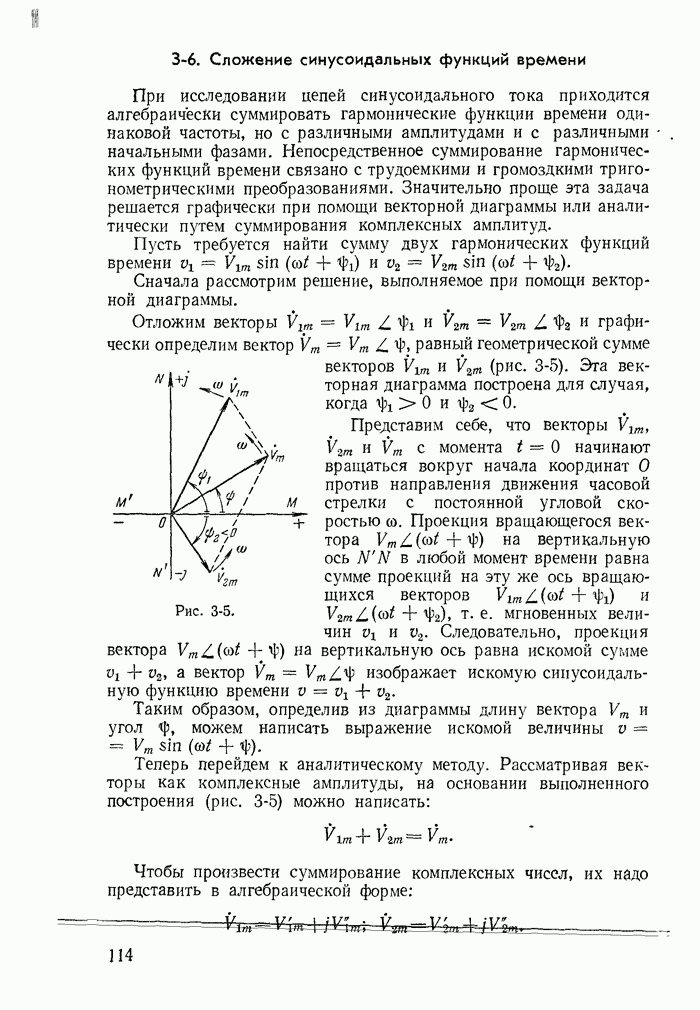
- 3-6. Сложение синусоидальных функций времени
- 3-7. Электрическая цепь и ее схема
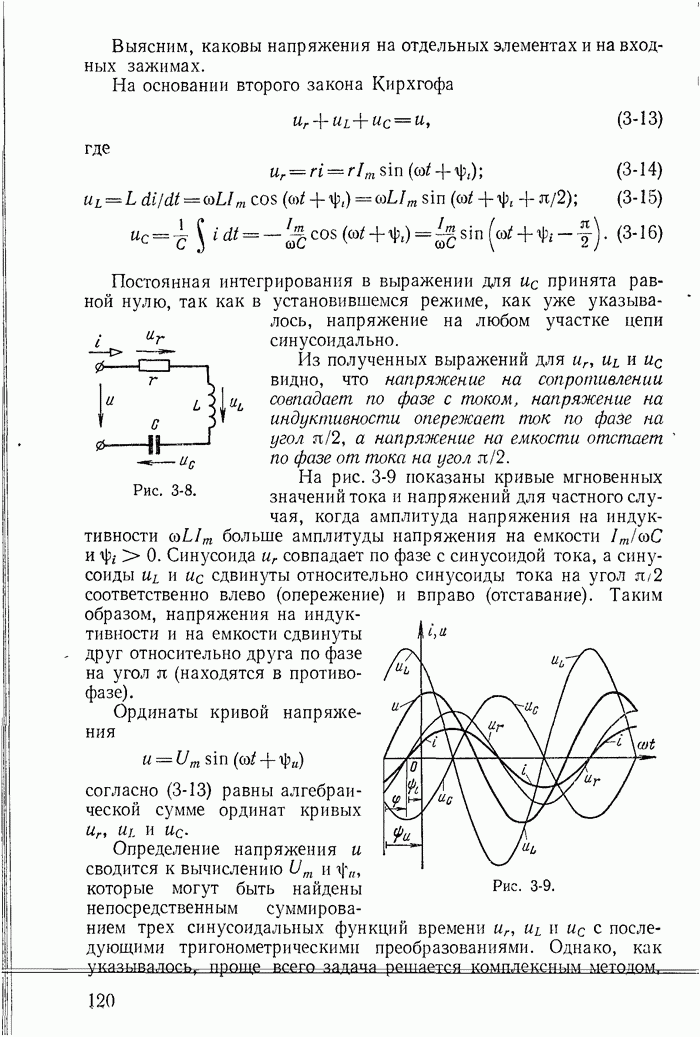
- 3-8. Ток и напряжения при последовательном соединении сопротивления, Индуктивности и емкости
- 3-9. Сопротивления
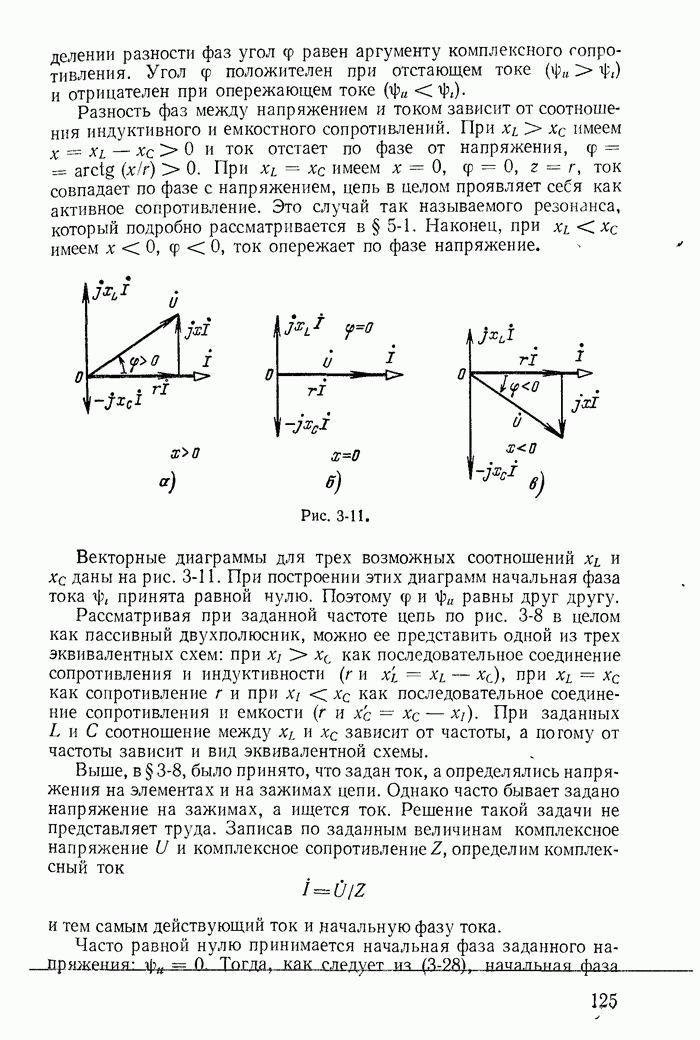
- 3-10. Разность фаз напряжения и тока
- 3-11. Напряжение и токи при параллельном соединении сопротивления, индуктивности и емкости
- 3-12. Проводимости
- 3-13. Пассивный двухполюсник
- 3-14. Мощности
- 3-15. Мощности в сопротивлении, индуктивности и емкости
- 3-16. Баланс мощностей
- 3-17. Знаки мощностей и направление передачи энергии
- 3-18. Определение параметров пассивного двухполюсника при помощи амперметра, вольтметра и ваттметра
- 3-19. Условия передачи максимальной мощности от источника энергии к приемнику
- 3-20. Понятие о поверхностном эффекте и эффекте близости
- 3-21. Параметры и эквивалентные схемы конденсаторов
- 3-22. Параметры и эквивалентные схемы индуктивных катушек и резисторов
- Глава четвертая. РАСЧЕТ ЦЕПЕЙ ПРИ СИНУСОИДАЛЬНЫХ ТОКАХ
- 4-1. О применимости методов расчета цепей постоянного тока к расчетам цепей синусоидального тока
- 4-2. Последовательное соединение приемников
- 4-3. Параллельное соединение приемников
- 4-4. Смешанное соединение приемников
- 4-5. Сложные разветвленные цепи
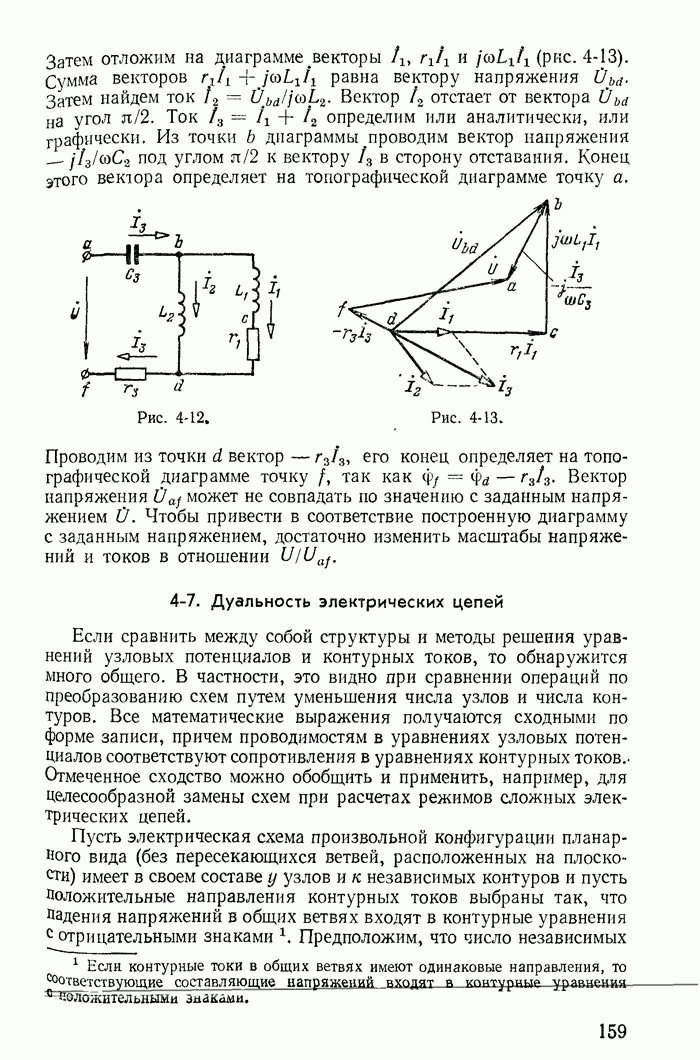
- 4-6. Топографические диаграммы
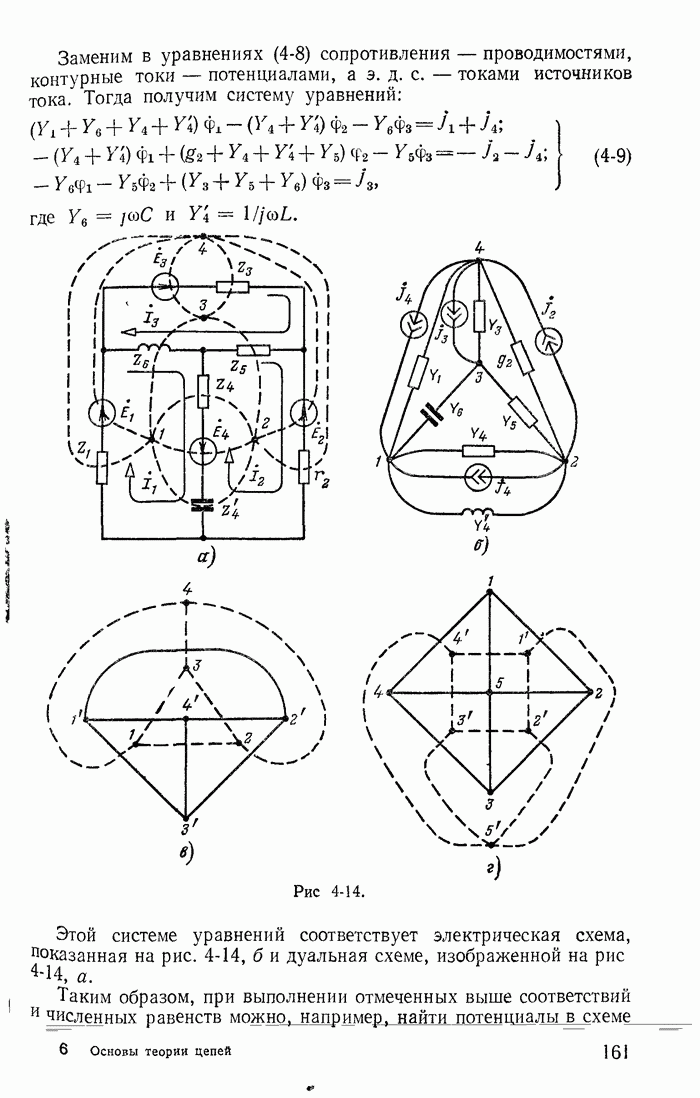
- 4-7. Дуальность электрических цепей
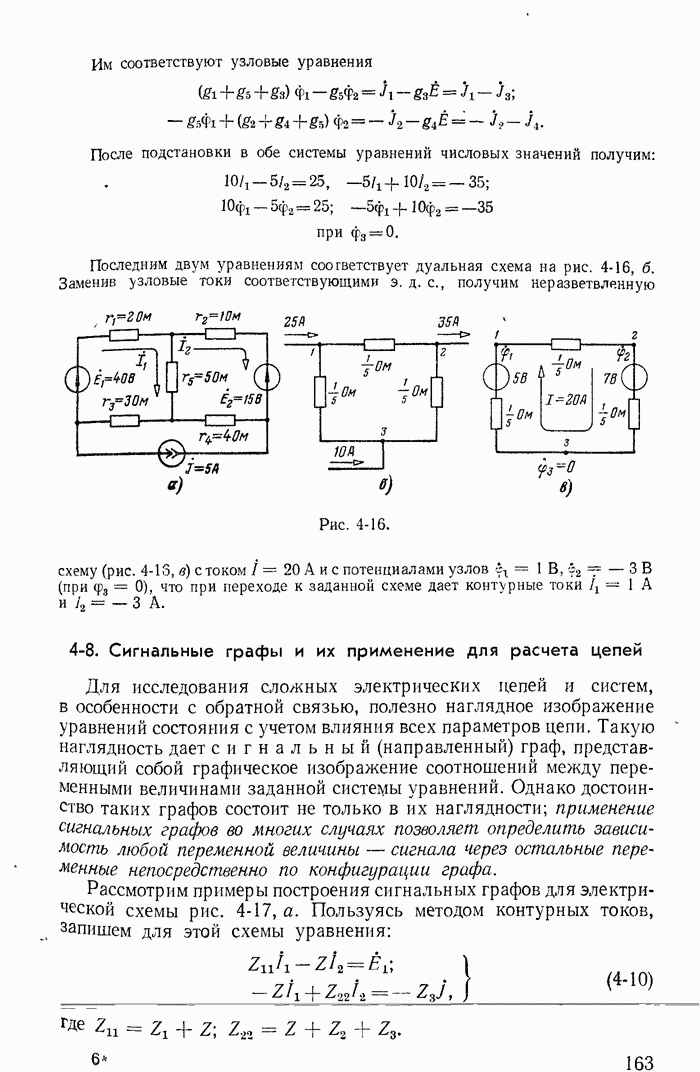
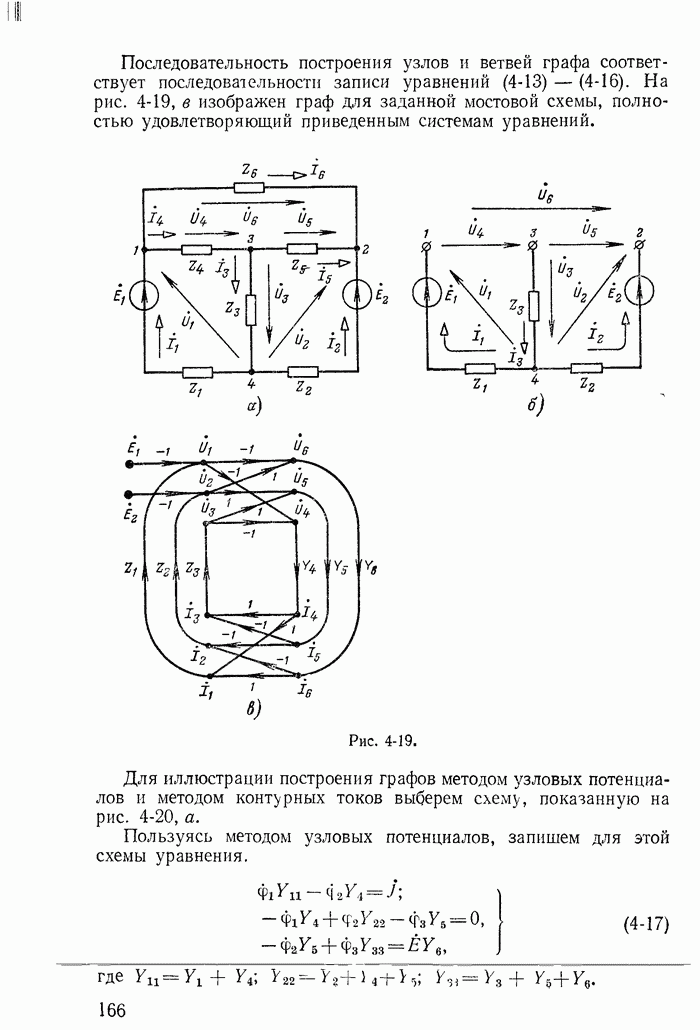
- 4-8. Сигнальные графы и их применение для расчета цепей
- Глава пятая. РЕЗОНАНС В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ
- 5-2. Частотные характеристики неразветвленной цепи
- 5-3. Резонанс в цепи с двумя параллельными ветвями
- 5-4. Частотные характеристики параллельного контура
- 5-5. Понятие о резонансе в сложных цепях
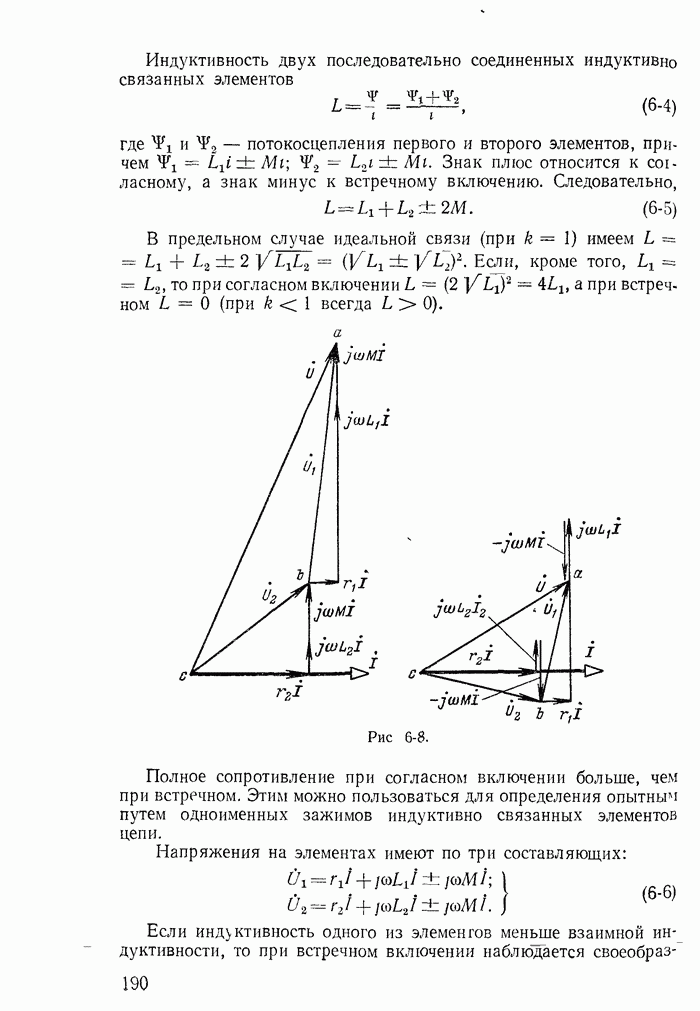
- Глава шестая. ЦЕПИ С ВЗАИМНОЙ ИНДУКТИВНОСТЬЮ
- 6-2. Электродвижущая сила взаимной индукции
- 6-3. Последовательное соединение индуктивно связанных элементов цепи
- 6-4. Параллельное соединение индуктивно связанных элементов цепи
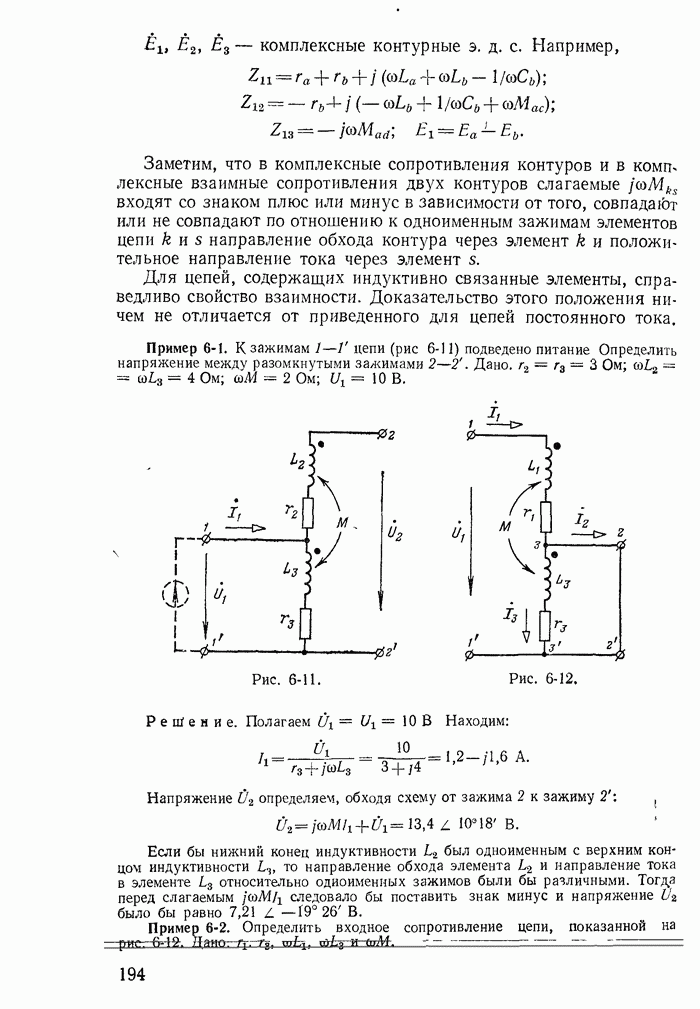
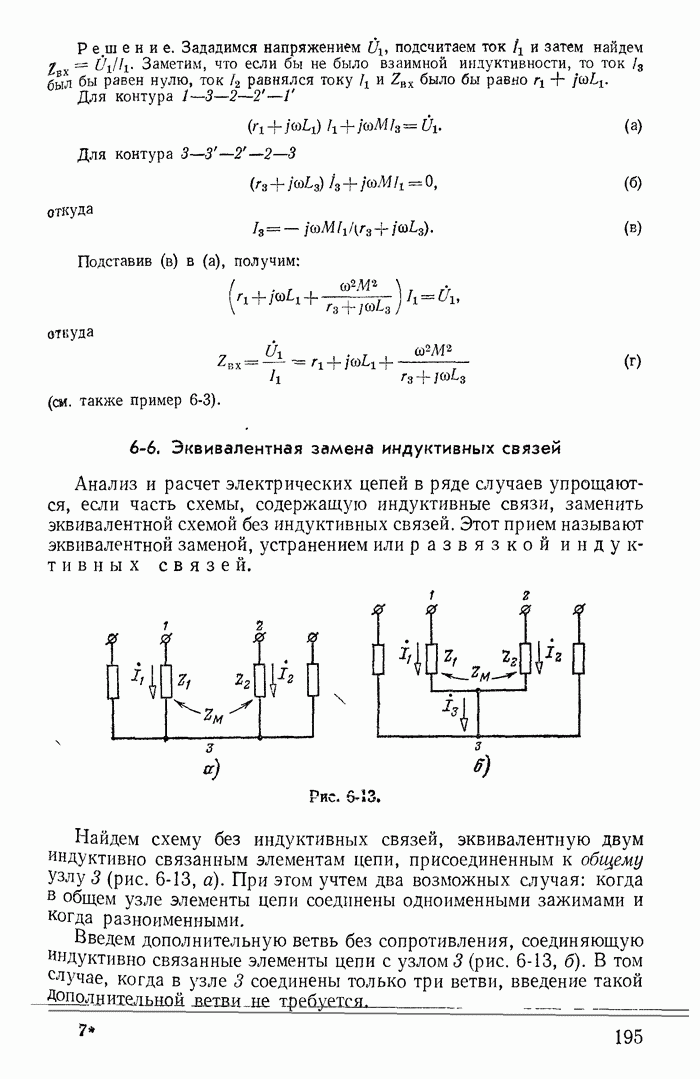
- 6-5. Расчеты разветвленных цепей при наличии взаимной индуктивности
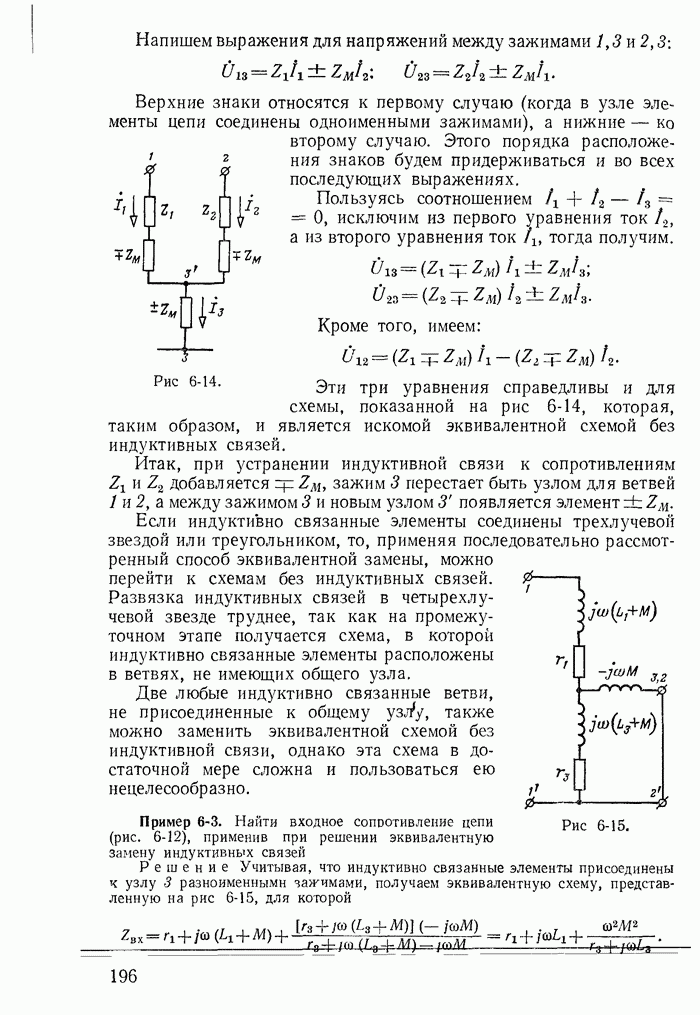
- 6-6. Эквивалентная замена индуктивных связей
- 6-7. Передача энергии между индуктивно связанными элементами цепи
- 6-8. Трансформатор без стального сердечника (воздушный трансформатор)
- Глава седьмая. КРУГОВЫЕ ДИАГРАММЫ
- 7-1. Комплексные уравнения прямой и окружности
- 7-2. Круговые диаграммы для неразветвленной цепи и для активного двухполюсника
- 7-3. Круговые диаграммы для любой разветвленной цепи
- Глава восьмая. МНОГОПОЛЮСНИКИ И ЧЕТЫРЕХПОЛЮСНИКИ ПРИ СИНУСОИДАЛЬНЫХ ТОКАХ И НАПРЯЖЕНИЯХ
- 8-1. Четырехполюсники и их основные уравнения
- 8-2. Определение коэффициентов четырехполюсников
- 8-3. Режим четырехполюсника при нагрузке
- 8-4. Эквивалентные схемы четырехполюсников
- 8-5. Основные уравнения и эквивалентные схемы для активного четырехполюсника
- 8-6. Идеальный трансформатор как четырехполюсник
- 8-7. Эквивалентные схемы с идеальными трансформаторами для четырехполюсника
- 8-8. Эквивалентные схемы трансформатора со стальным магнитопроводом
- 8-9. Расчеты электрических цепей с трансформаторами
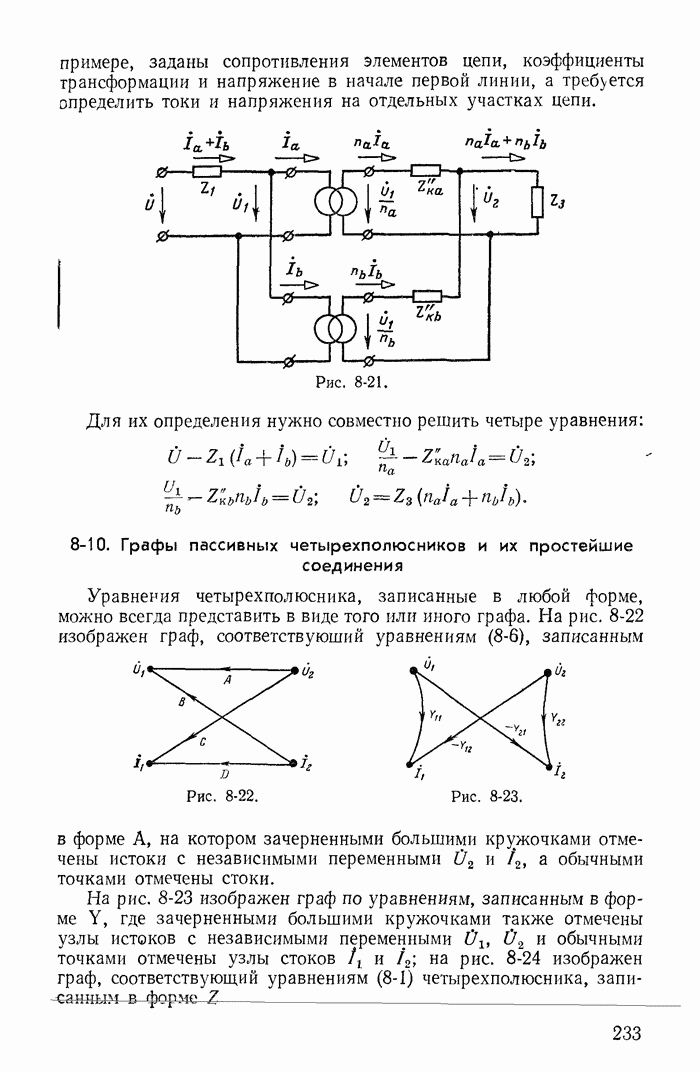
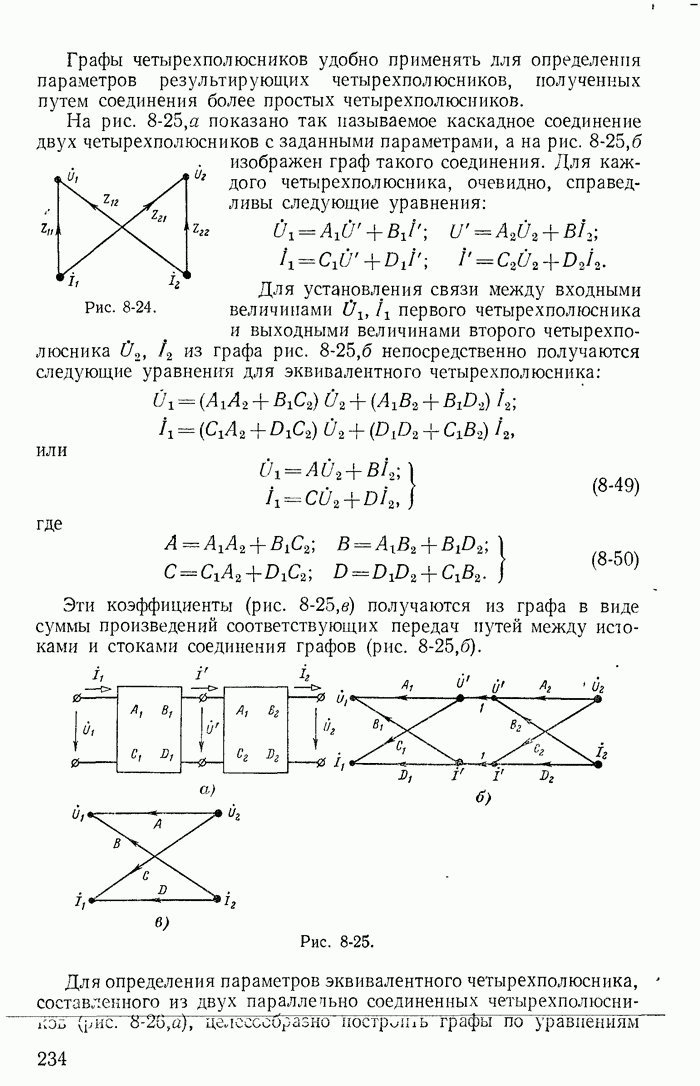
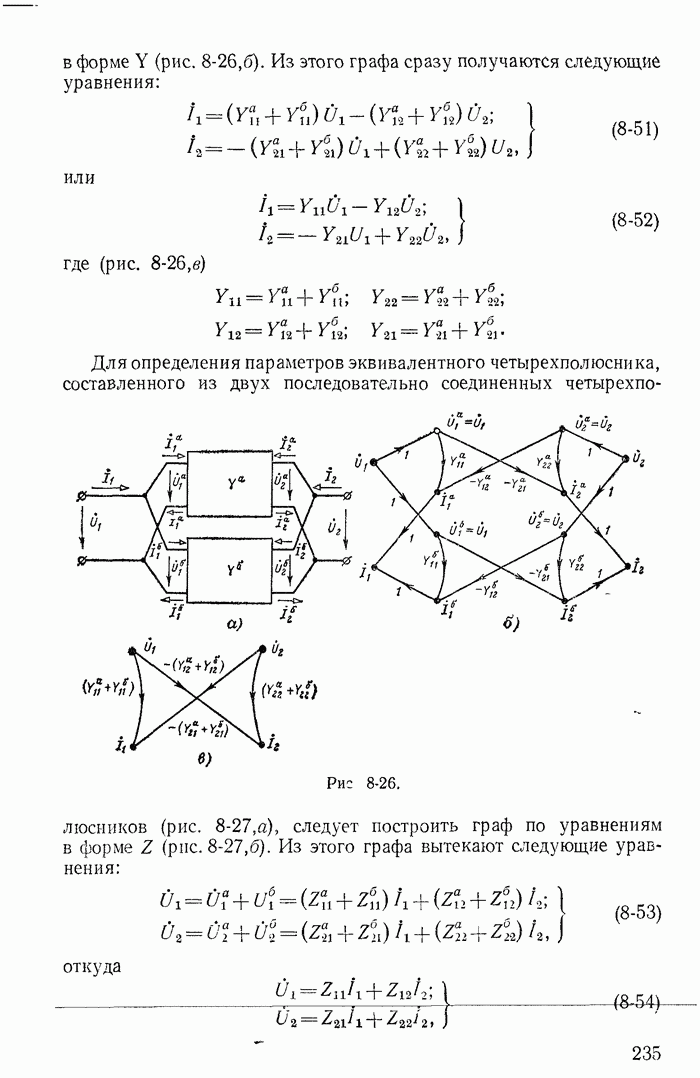
- 8-10. Графы пассивных четырехполюсников и их простейшие соединения
- Глава девятая. ЦЕПИ С ЭЛЕКТРОННЫМИ И ПОЛУПРОВОДНИКОВЫМИ ПРИБОРАМИ В ЛИНЕЙНОМ РЕЖИМЕ
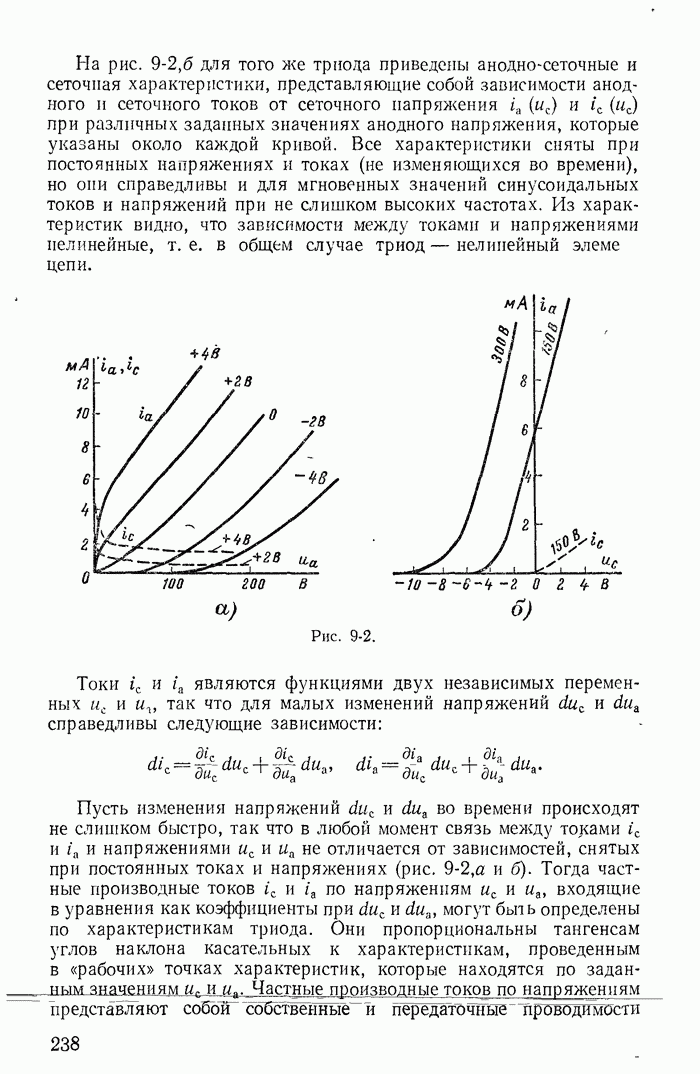
- 9-2. Эквивалентные схемы лампового триода
- 9-3. Транзисторы (полупроводниковые триоды)
- 9-4. Эквивалентные схемы транзисторов
- 9-5. Простейшие электрические цепи с невзаимными элементами и их направленные графы
- Глава десятая. ТРЕХФАЗНЫЕ ЦЕПИ
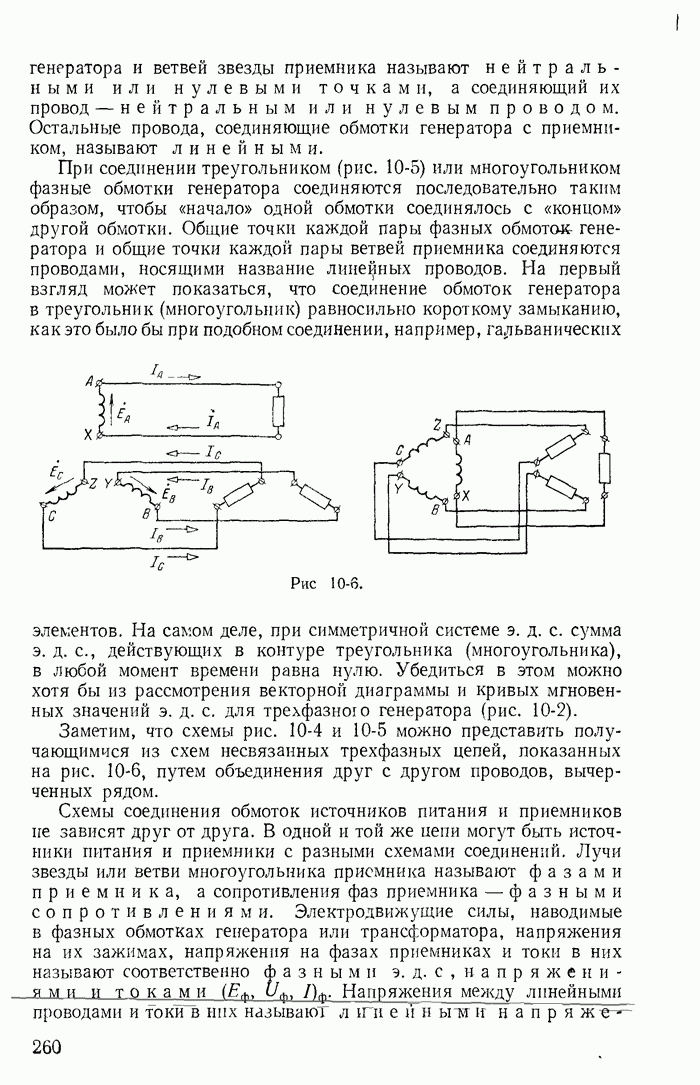
- 10-2. Соединения звездой и многоугольником
- 10-3. Симметричный режим трехфазной цепи
- 10-4. Некоторые свойства трехфазных цепей с различными схемами соединений
- 10-5. Расчет симметричных режимов трехфазных цепей
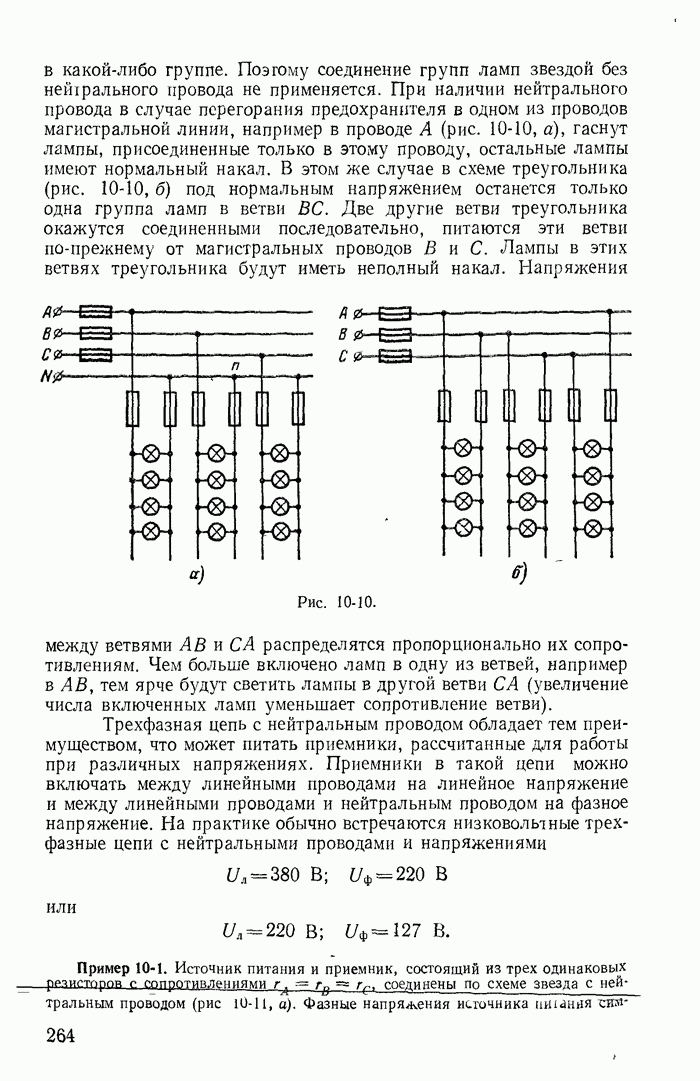
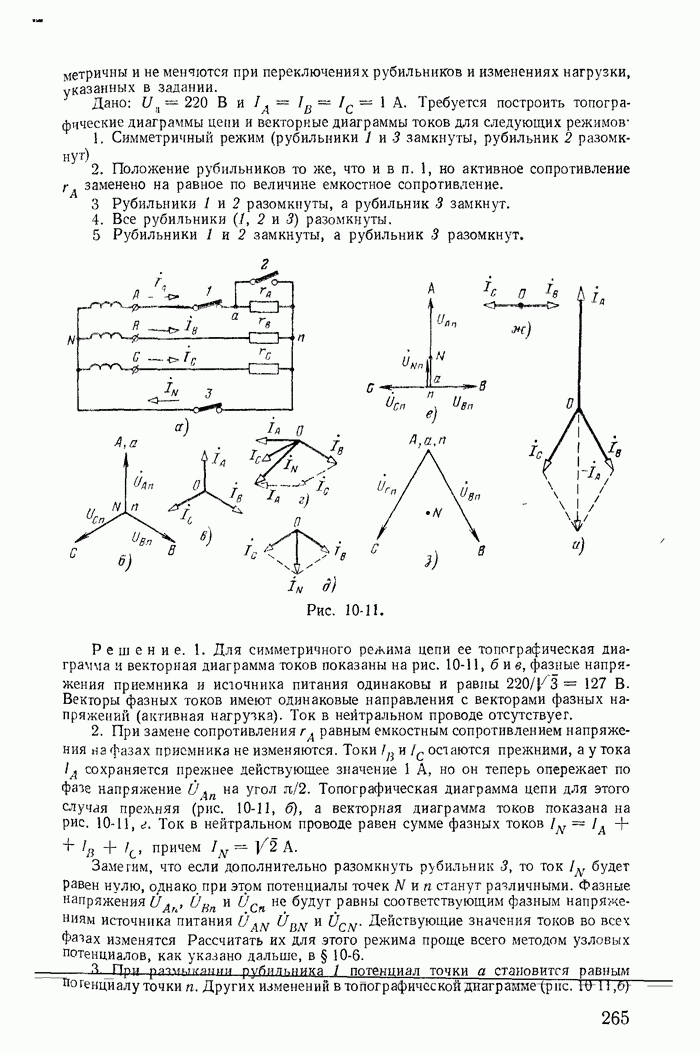
- 10-6. Расчет несимметричных режимов трехфазных цепей со статической нагрузкой
- 10-7. Напряжения на фазах приемника в некоторых частных случаях
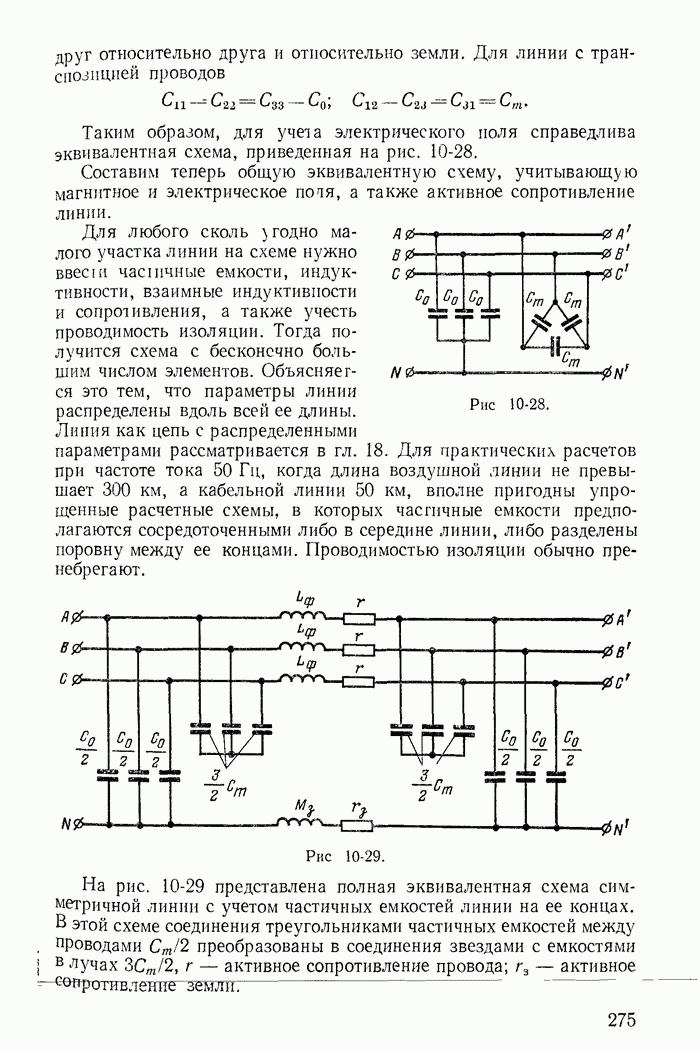
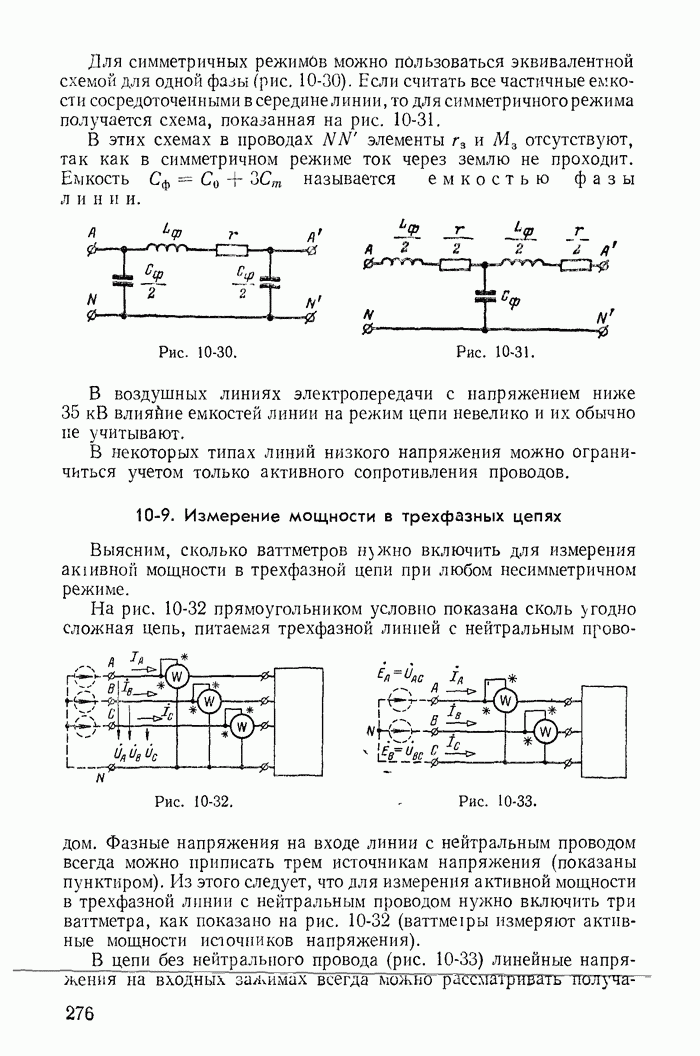
- 10-8. Эквивалентные схемы трехфазных линий
- 10-9. Измерение мощности в трехфазных цепях
- 10-10. Вращающееся магнитное поле
- 10-11. Принципы действия асинхронного и синхронного двигателей
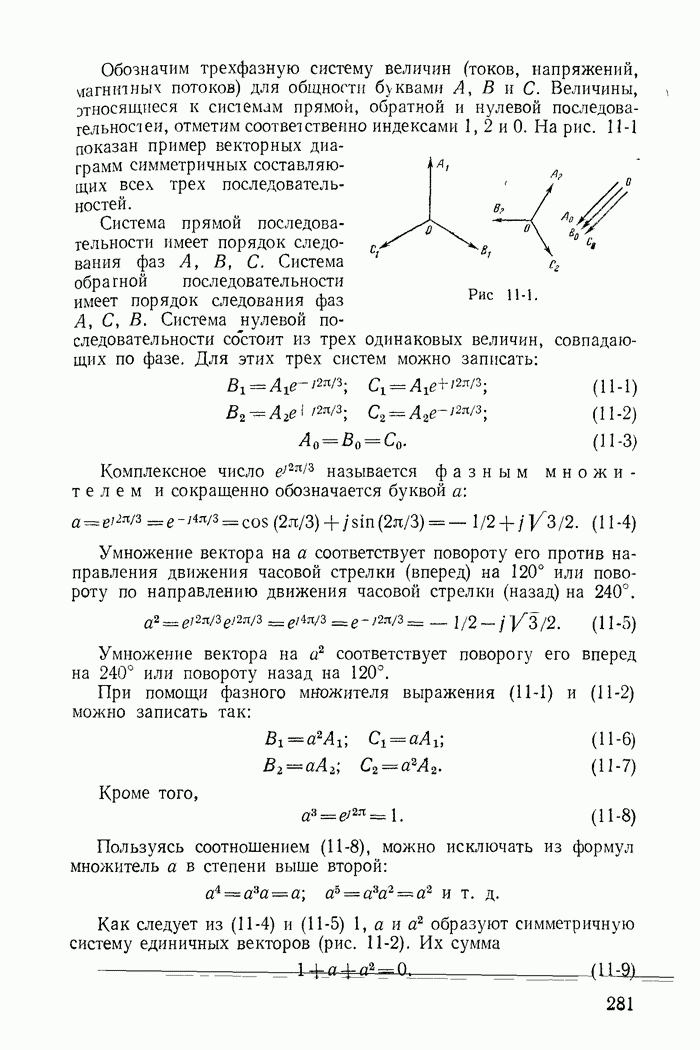
- Глава одиннадцатая. МЕТОД СИММЕТРИЧНЫХ СОСТАВЛЯЮЩИХ
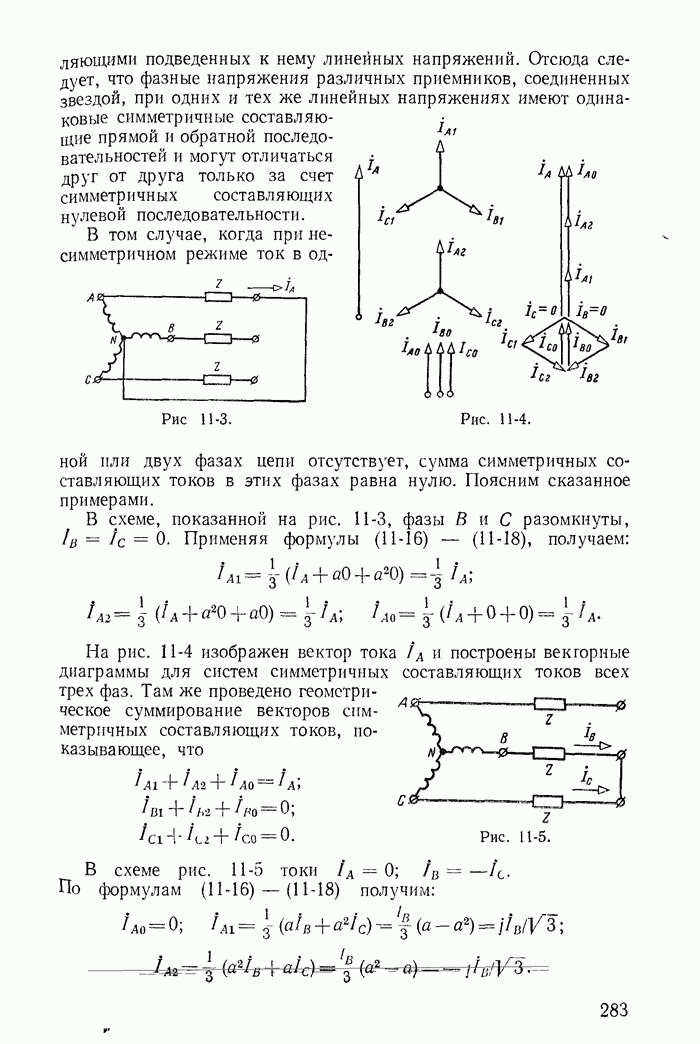
- 11-2. Некоторые свойства трехфазных цепей в отношении симметричных составляющих токов и напряжений
- 11-3. Сопротивления симметричной трехфазной цепи для токов различных последовательностей
- 11-4. Определение токов в симметричной цепи
- 11-5. Симметричные составляющие напряжений и токов в несимметричной трехфазной цепи
- 11-6. Расчет цепи с несимметричной нагрузкой
- 11-7. Расчет цепи с несимметричным участком в линии
- Глава двенадцатая. НЕСИНУСОИДАЛЬНЫЕ ТОКИ
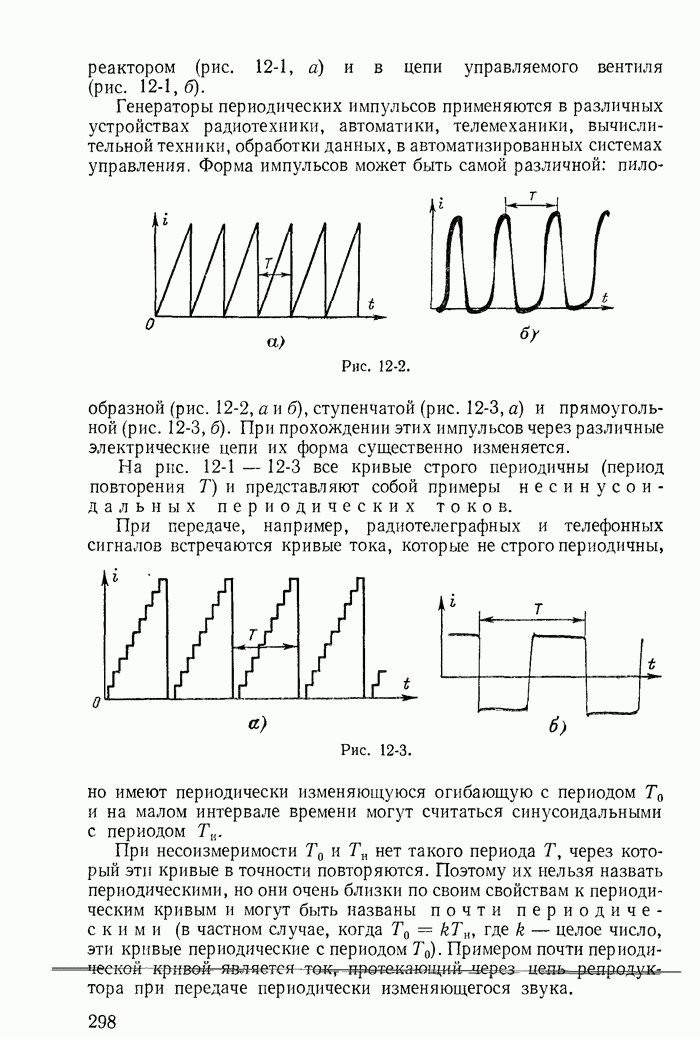
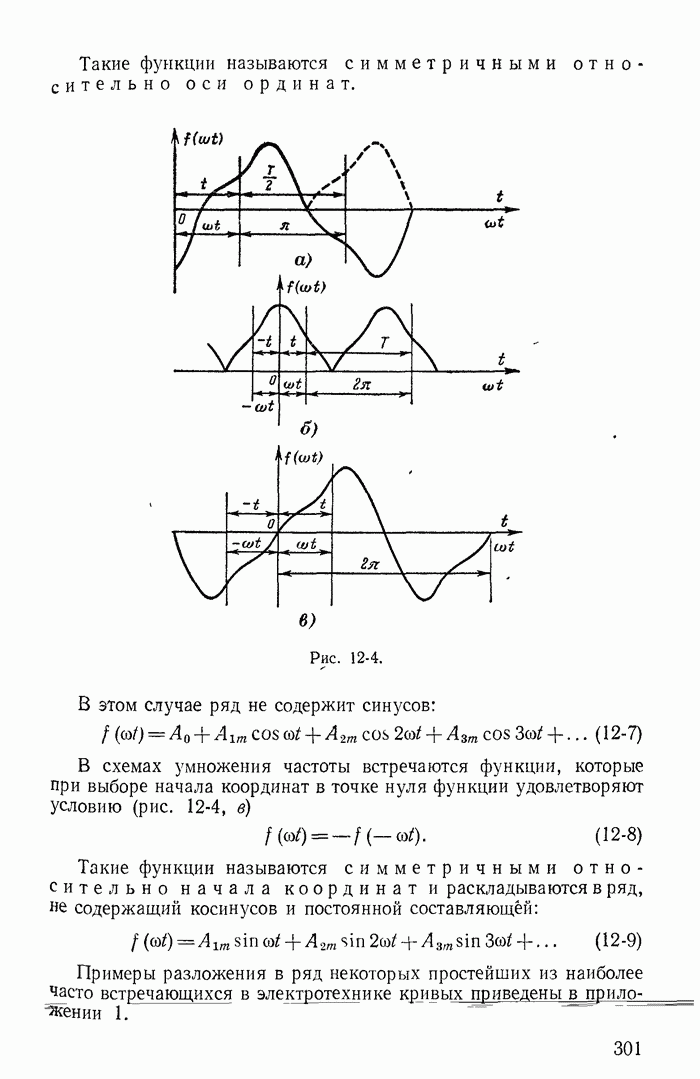
- 12-2. Разложение периодической несинусоидальной кривой в тригонометрический ряд
- 12-3. Максимальные, действующие и средние значения несинусоидальных периодических э. д. с., напряжений и токов
- 12-4. Коэффициенты, характеризующие форму несинусоидальных периодических кривых
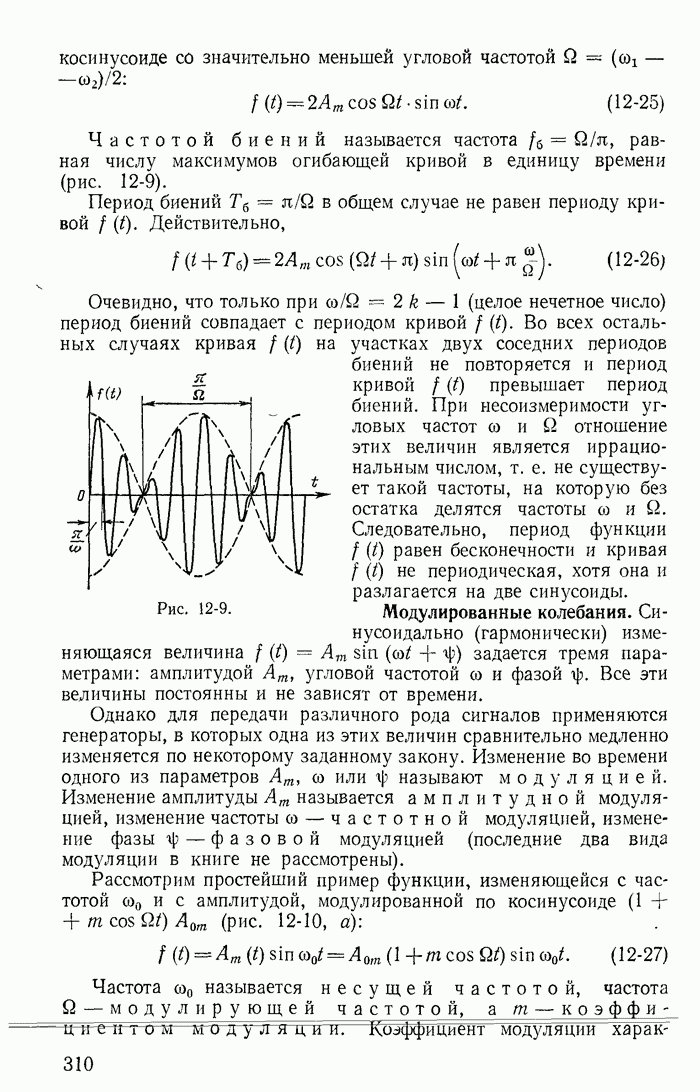
- 12-5. Несинусоидальные кривые с периодической огибающей
- 12-6. Действующие значения э. д. с., напряжений и токов с периодическими огибающими
- 12-7. Расчет цепей с несинусоидальными периодическими э. д. с. и токами
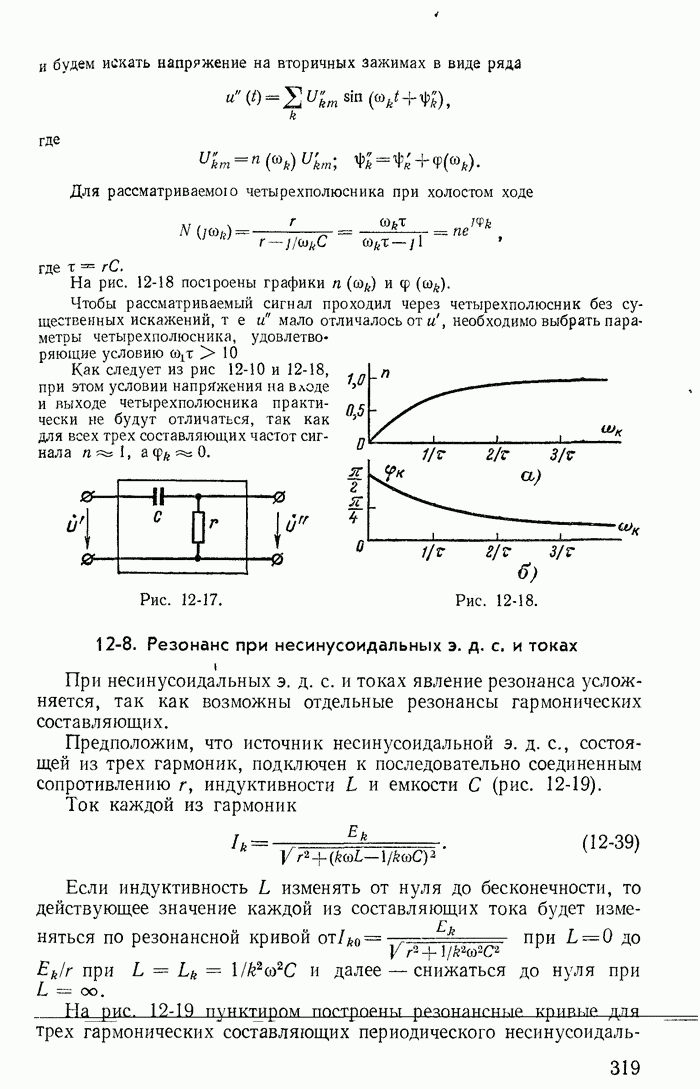
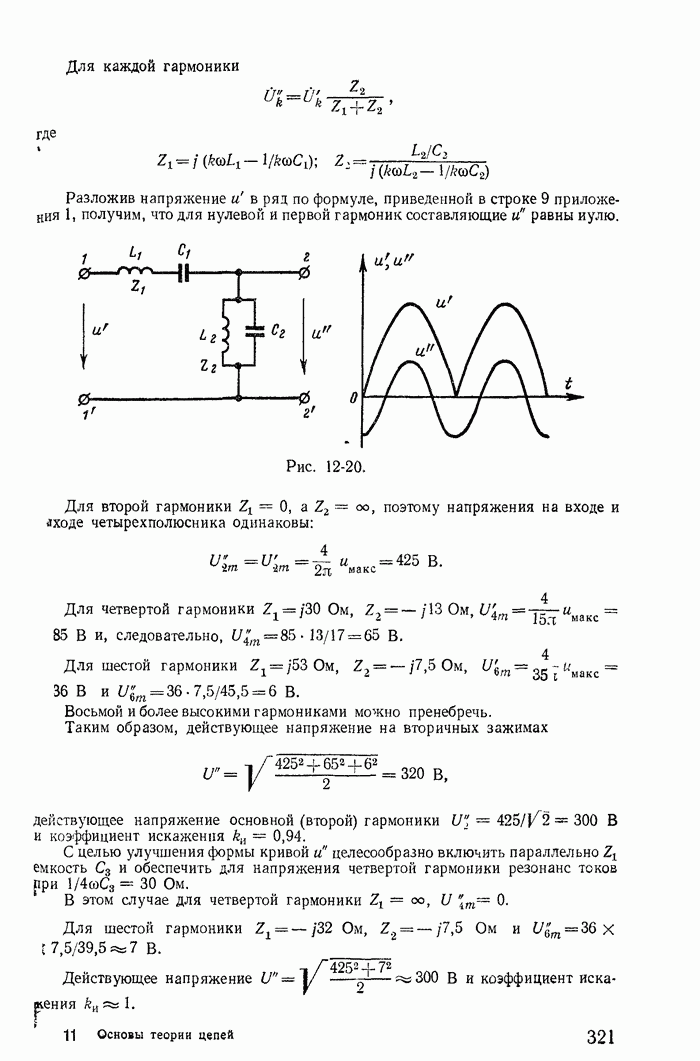
- 12-8. Резонанс при несинусоидальных э. д. с. и токах
- 12-9. Мощность периодических несинусоидальных токов
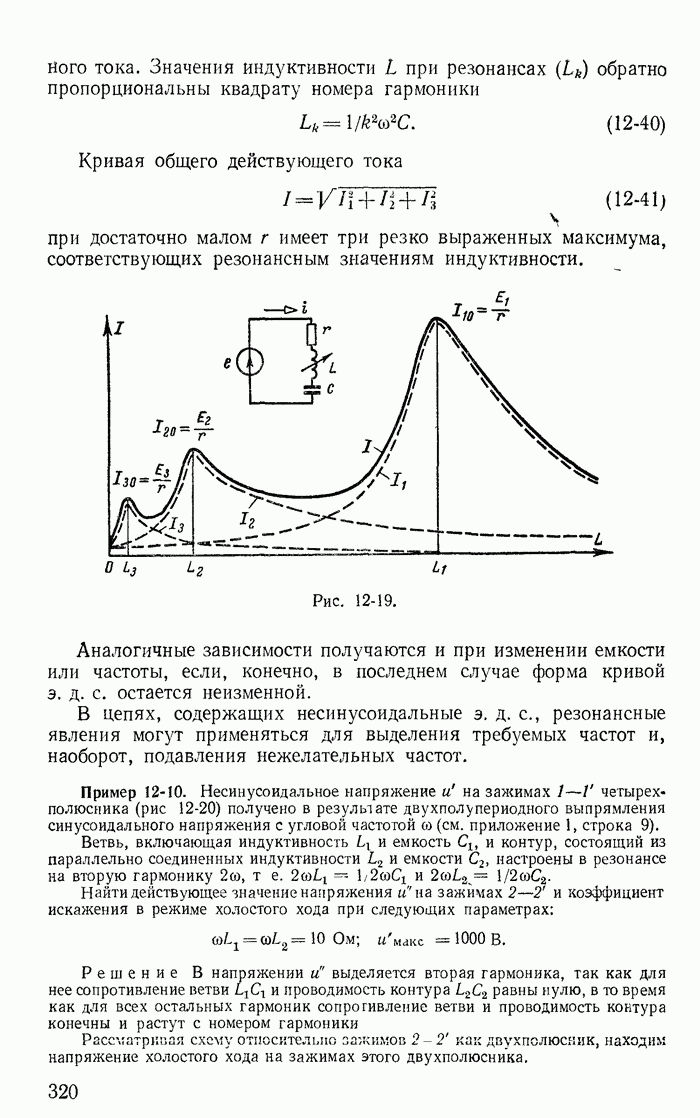
- 12-10. Высшие гармоники в трехфазных цепях
- Глава тринадцатая. КЛАССИЧЕСКИЙ МЕТОД РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ
- 13-2. Переходный, принужденный и свободный процессы
- 13-3. Короткое замыкание цепи r, L
- 13-4. Включение цепи r, L на постоянное напряжение
- 13-5. Включение цепи r, L на синусоидальное напряжение
- 13-6. Короткое замыкание цепи r, С
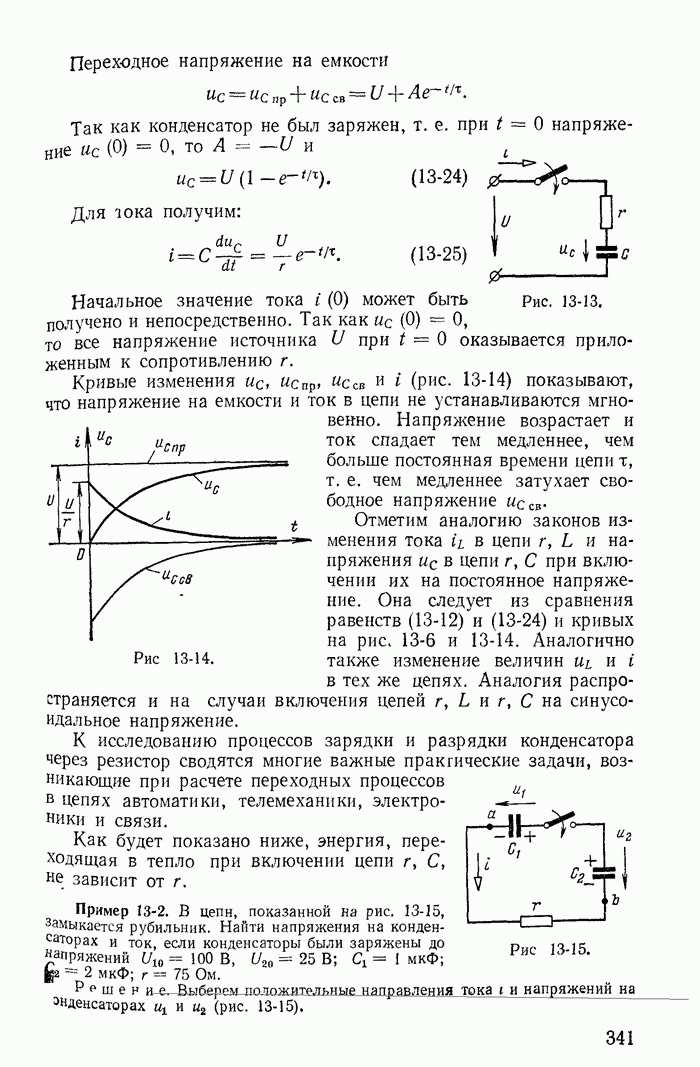
- 13-7. Включение цепи r, С на постоянное напряжение
- 13-8. Включение цепи r, С на синусоидальное напряжение
- 13-9. Переходные процессы в неразветвленной цепи r, С
- 13-10. Апериодический разряд конденсатора
- 13-11. Предельный случай апериодического разряда конденсатора
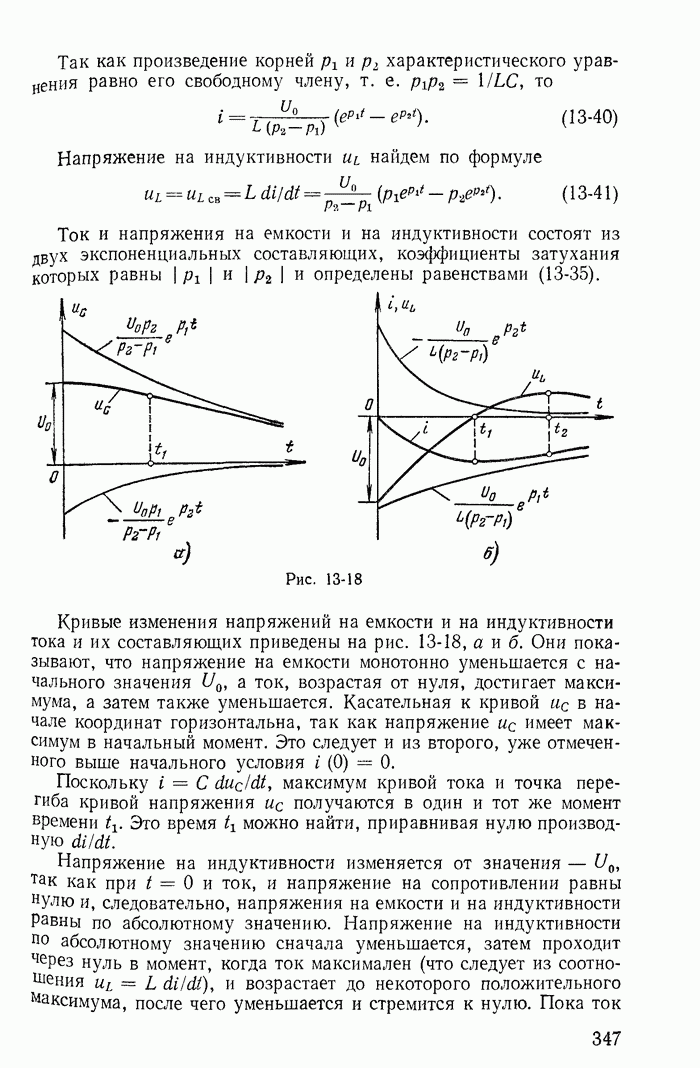
- 13-12. Периодический (колебательный) разряд конденсатора
- 13-13. Включение цепи r, С на постоянное напряжение
- 13-14. Общий случай расчета переходных процессов классическим методом
- 13-15. Включение пассивного двухполюсника на непрерывно изменяющееся напряжение (формула или интеграл Дюамеля)
- 13-16. Включение пассивного двухполюсника на напряжение любой формы
- 13-17. Временная и импульсная переходные характеристики
- 13-18. Запись теоремы свертки при помощи импульсной переходной характеристики
- 13-19. Переходные процессы при скачках токов в индуктивностях и напряжений на конденсаторах
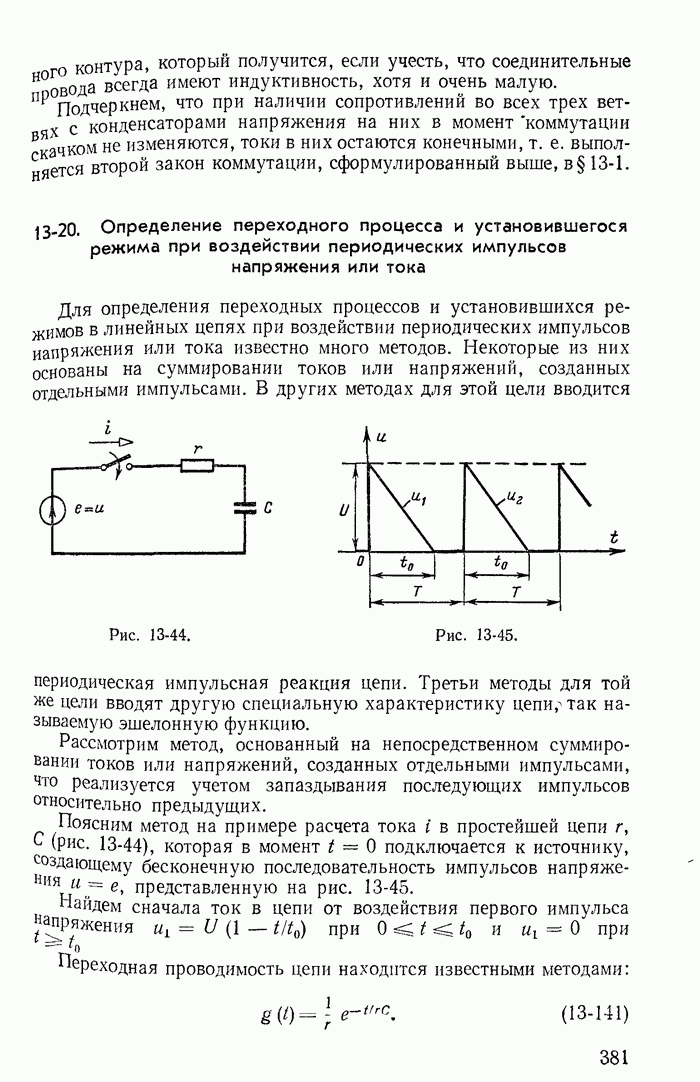
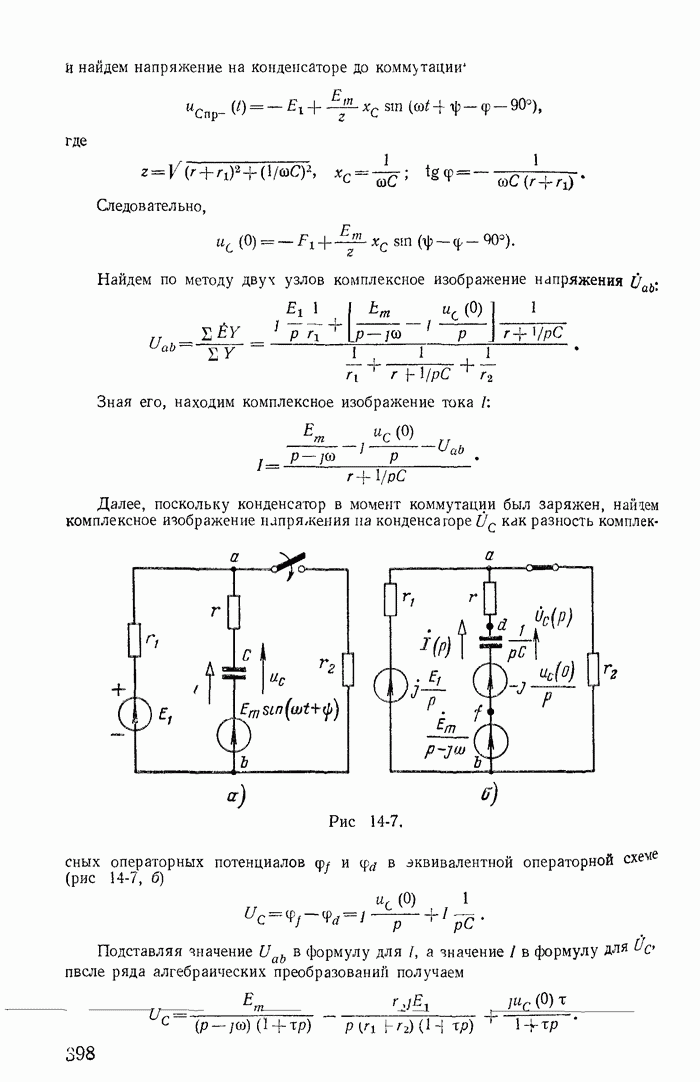
- 13-20. Определение переходного процесса и установившегося режима при воздействии периодических импульсов напряжения или тока
- Глава четырнадцатая. ОПЕРАТОРНЫЙ МЕТОД РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ
- 14-2. Законы Ома и Кирхгофа в операторной форме
- 14-3. Эквивалентные операторные схемы
- 14-4. Переходные процессы в цепях с взаимной индуктивностью
- 14-5. Сведение расчетов переходных процессов к нулевым начальным условиям
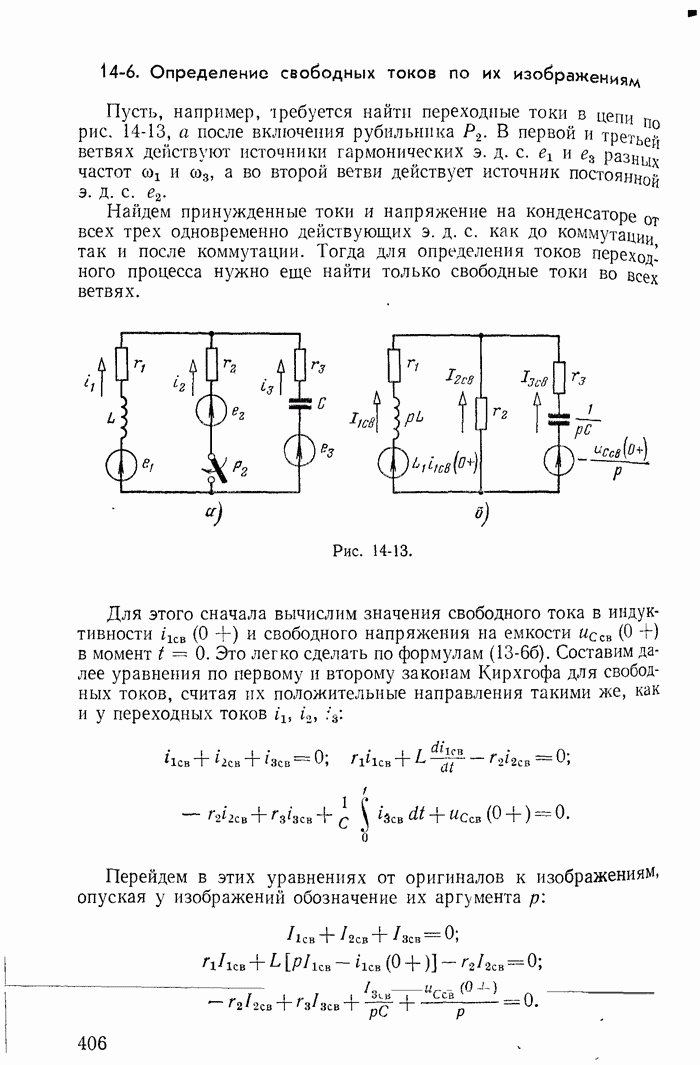
- 14-6. Определение свободных токов по их изображениям
- 14-7. Формулы включения
- 14-8. Расчет переходных процессов методом переменных состояния
- 14-9. Определение принужденного режима цепи при воздействии на нее периодического несинусоидального напряжения
- Глава пятнадцатая. ЧАСТОТНЫЙ МЕТОД РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ
- 15-2. Законы Ома и Кирхгофа и эквивалентные схемы для частотных спектров
- 15-3. Приближенный метод определения оригинала по вещественной частотной характеристике (метод трапеций)
- 15-4. О переходе от преобразований Фурье к преобразованиям Лапласа
- 15-5. Сравнение различных методов расчета переходных процессов в линейных электрических цепях
- Глава шестнадцатая. ЦЕПНЫЕ СХЕМЫ И ЧАСТОТНЫЕ ЭЛЕКТРИЧЕСКИЕ ФИЛЬТРЫ
- 16-2. Характеристическое сопротивление и постоянная передачи симметричного четырехполюсника
- 16-3. Вносимая и рабочая постоянные передачи
- 16-4. Цепные схемы
- 16-5. Частотные электрические фильтры
- 16-6. Низкочастотные фильтры
- 16-8. Полосные фильтры
- 16-11. Г-образный фильтр как пример несимметричного фильтра
- 16-12. Безындукционные (или r, C) фильтры
- Глава семнадцатая. СИНТЕЗ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
- 17-2. Передаточная функция четырехполюсника. Цепи минимальной фазы
- 17-3. Входные функции цепей. Положительные вещественные функции
- 17-4. Реактивные двухполюсники
- 17-5. Частотные характеристики реактивных двухполюсников
- 17-6. Синтез реактивных двухполюсников. Метод Фостера
- 17-7. Синтез реактивных двухполюсников. Метод Кауэра
- 17-8. Синтез двухполюсников с потерями. Метод Фостера
- 17-9. Синтез двухполюсников с потерями. Метод Кауэра
- 17-10. Понятие о синтезе четырехполюсников
- Раздел второй. ЛИНЕЙНЫЕ ЦЕПИ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
- Глава восемнадцатая. ГАРМОНИЧЕСКИЕ ПРОЦЕССЫ В ЦЕПЯХ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
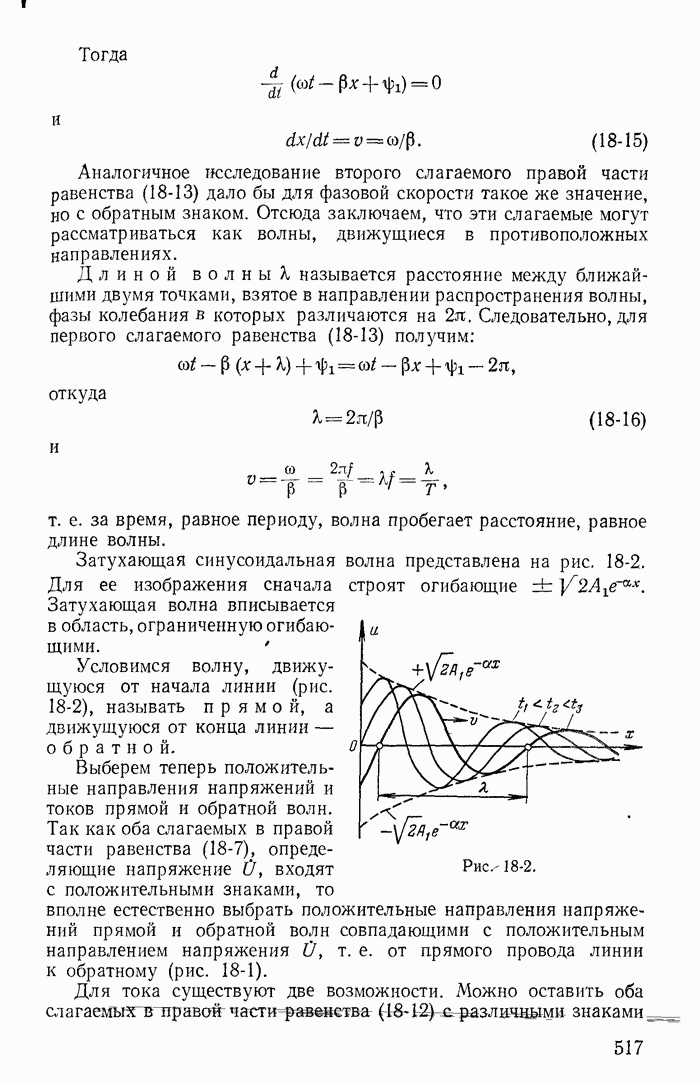
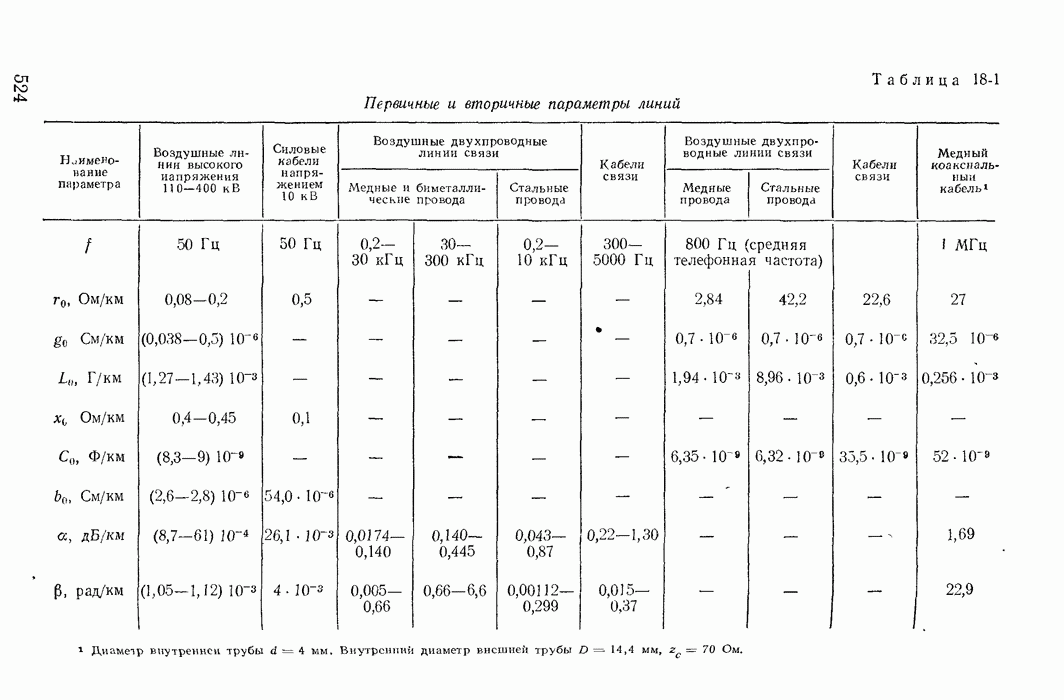
- 18-2. Уравнения однородной линии
- 18-3. Установившийся режим в однородной линии
- 18-4. Уравнения однородной линии с гиперболическими функциями
- 18-5. Характеристики однородной линии
- 18-6. Входное сопротивление линии
- 18-7. Коэффициент отражения волны
- 18-8. Согласованная нагрузка линии
- 18-9. Линия без искажений
- 18-10. Холостой ход, короткое замыкание и нагрузочный режим линии с потерями
- 18-11. Линии без потерь
- 18-12. Стоячие волны
- 18-13. Линия как четырехполюсник
- Глава девятнадцатая. ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЦЕПЯХ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
- 19-2. Общее решение уравнений однородной линии
- 19-3. Возникновение волн с прямоугольным фронтом
- 19-4. Общие случаи нахождения волн, возникающих при переключениях
- 19-5. Отражение волны с прямоугольным фронтом от конца линии
- 19-6. Общий метод определения отраженных волн
- 19-7. Качественное рассмотрение переходных процессов в линиях, содержащих сосредоточенные емкости и индуктивности
- 19-8. Многократные отражения волн с прямоугольным фронтом от активного сопротивления
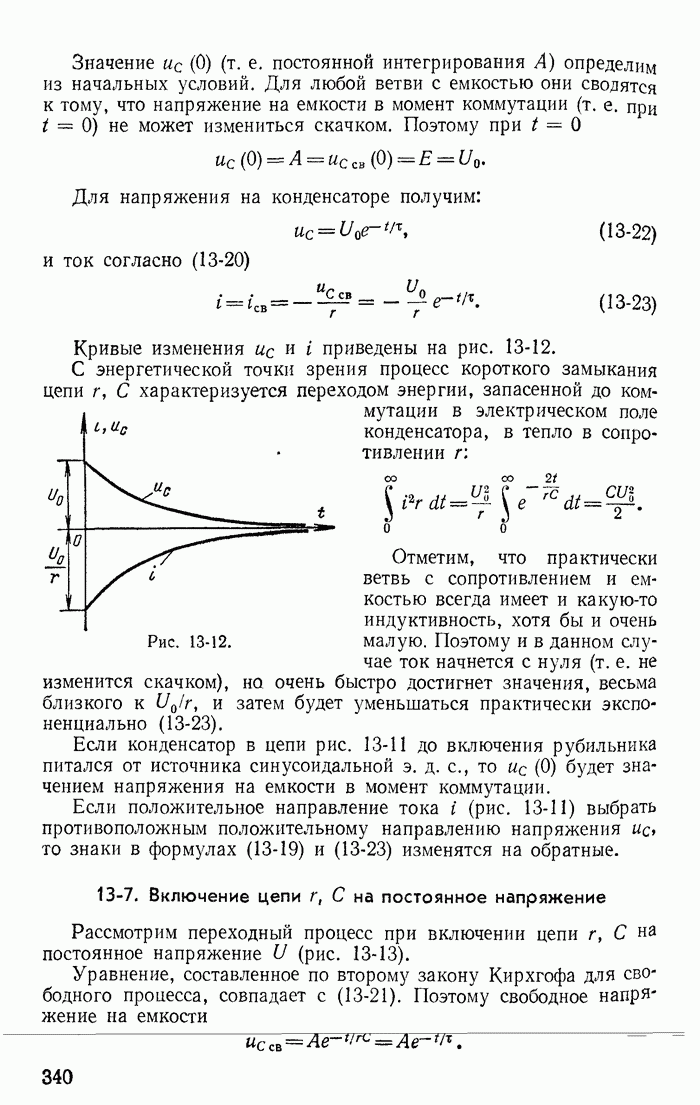
- 19-9. Блуждающие волны
- Раздел III. НЕЛИНЕЙНЫЕ ЦЕПИ
- Глава двадцатая. НЕЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПРИ ПОСТОЯННЫХ ТОКАХ И НАПРЯЖЕНИЯХ
- 20-2. Графический метод расчета неразветвленных цепей с нелинейными элементами
- 20-3. Графический метод расчета цепей с параллельным соединением нелинейных элементов
- 20-4. Графический метод расчета цепей со смешанным соединением нелинейных и линейных элементов
- 20-5. Применение эквивалентных схем с источниками э. д. с. для исследования режима нелинейных цепей
- 20-6. Вольт-амперные характеристики нелинейных активных двухполюсников
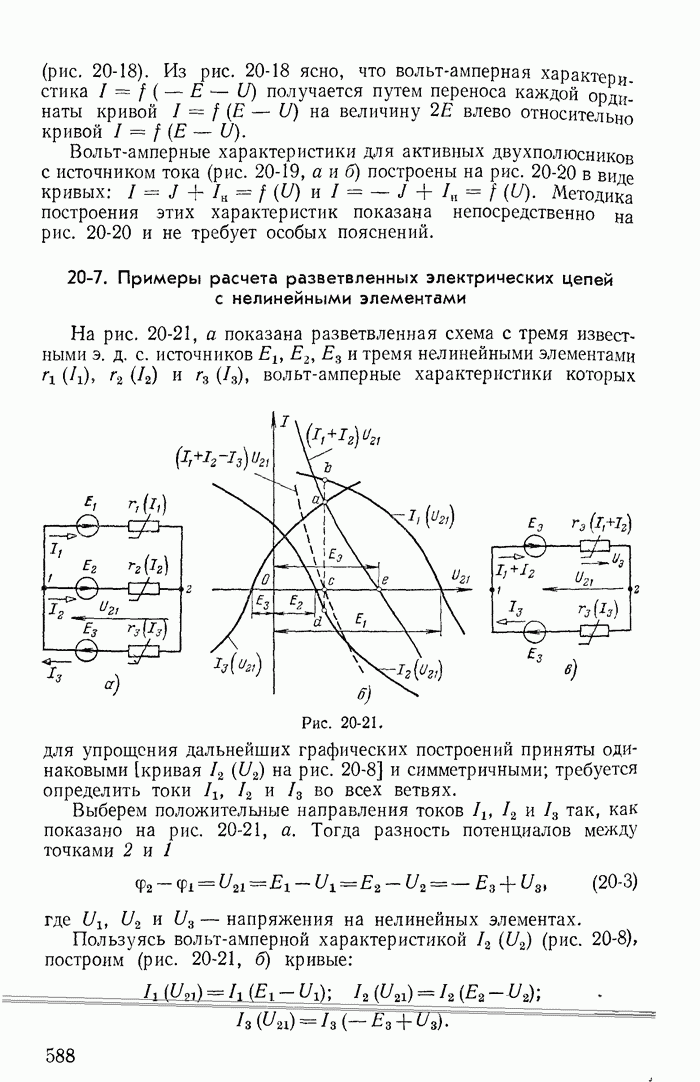
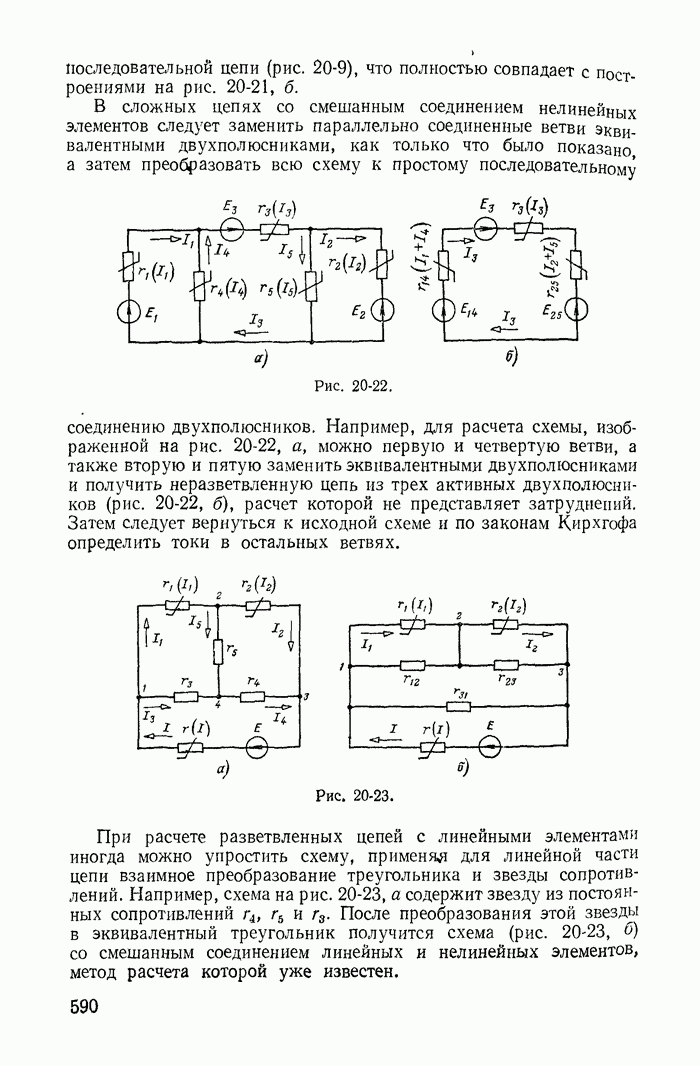
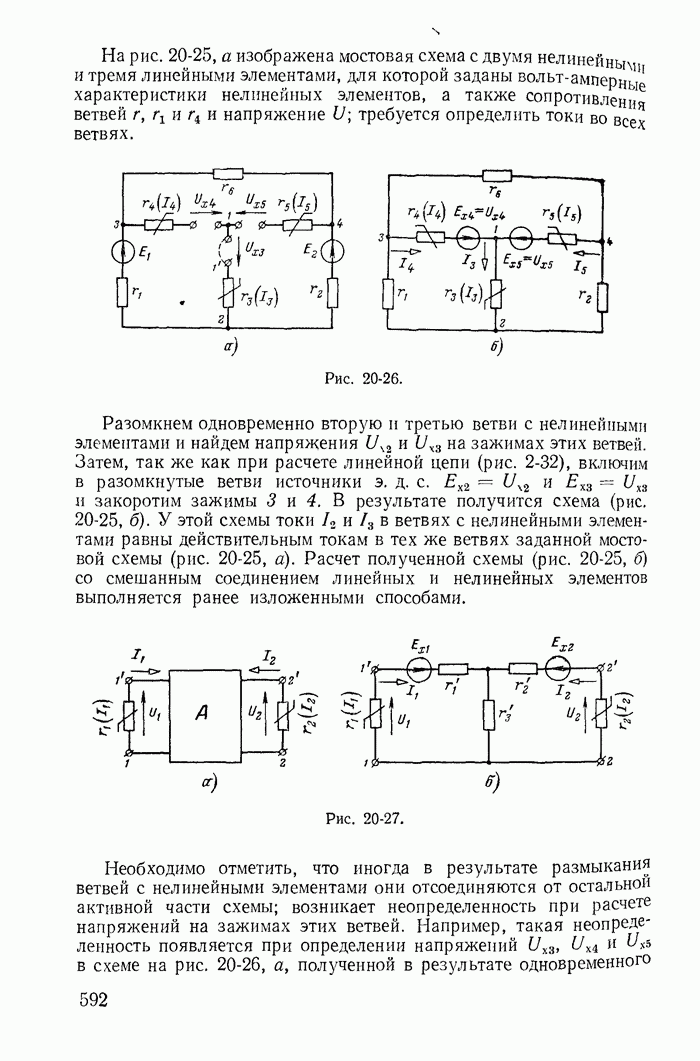
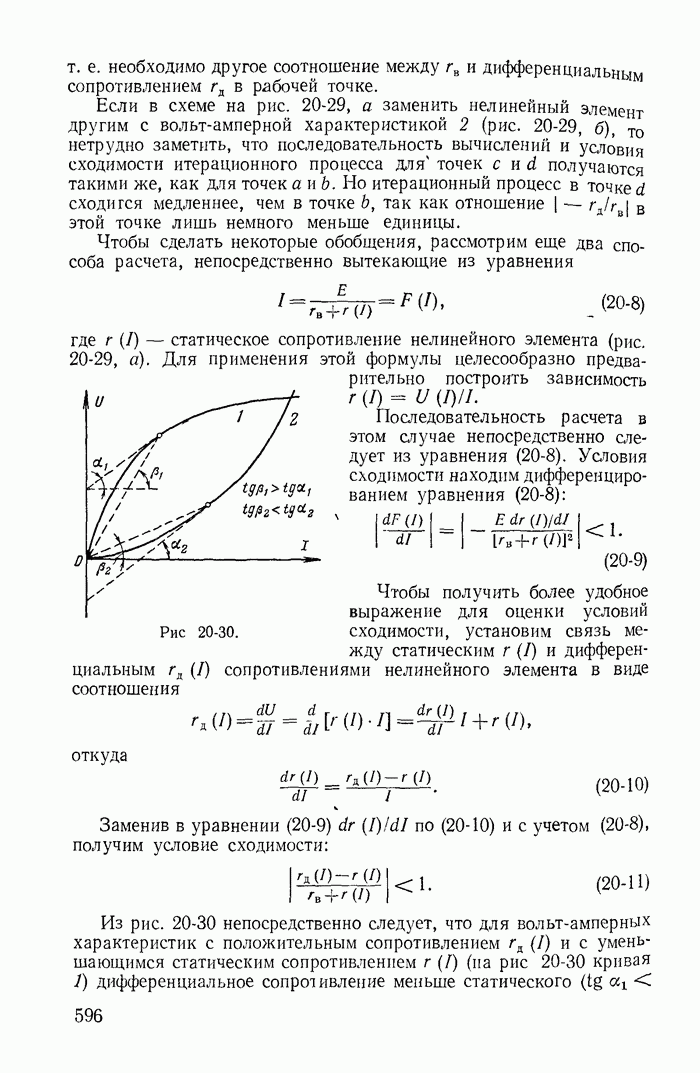
- 20-7. Примеры расчета разветвленных электрических цепей с нелинейными элементами
- 20-8. Применение теории активных двухполюсника, четырехполюсника и шестиполюсника для расчета цепей с линейными и нелинейными элементами
- 20-9. Расчет разветвленных нелинейных цепей итерационным методом (методом последовательных приближений)
- Глава двадцать первая. МАГНИТНЫЕ ЦЕПИ ПРИ ПОСТОЯННЫХ ТОКАХ
- 21-2. Расчет неразветвленных магнитных цепей
- 21-3. Расчет разветвленных магнитных цепей
- 21-4. Расчет магнитной цепи кольцевого постоянного магнита с воздушным зазором
- 21-5. Расчет неразветвленной неоднородной магнитной цепи с постоянным магнитом
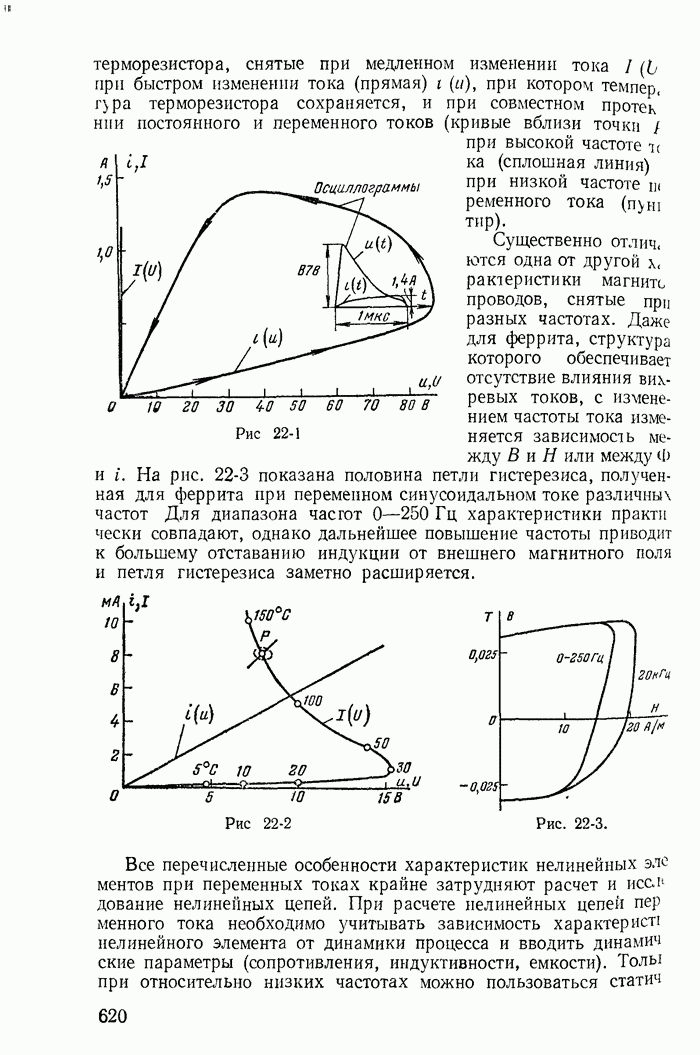
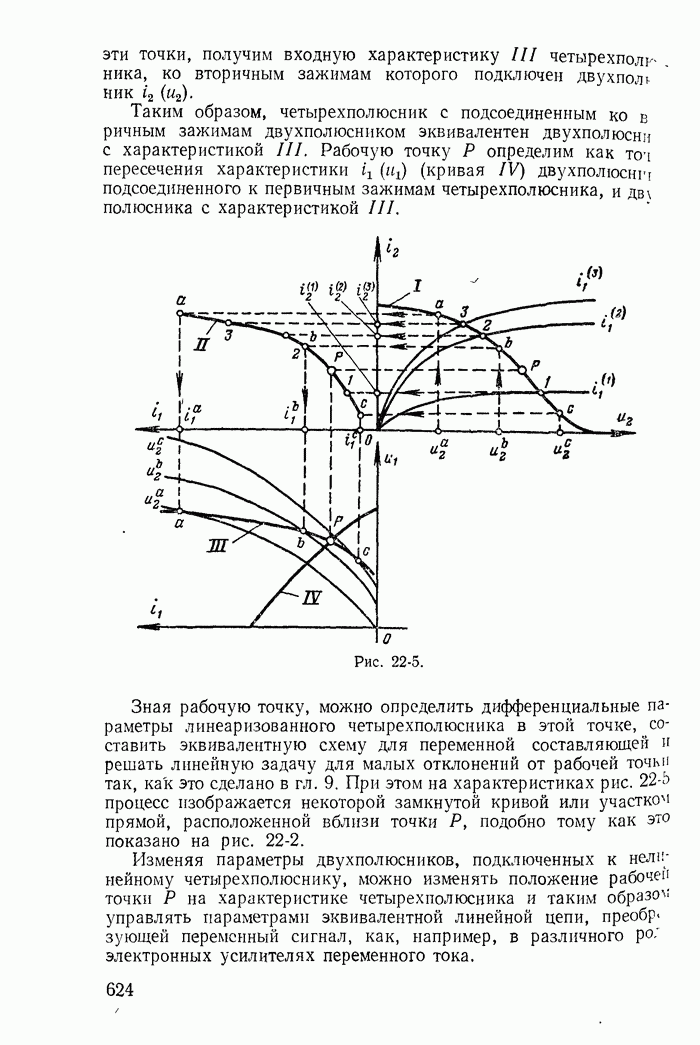
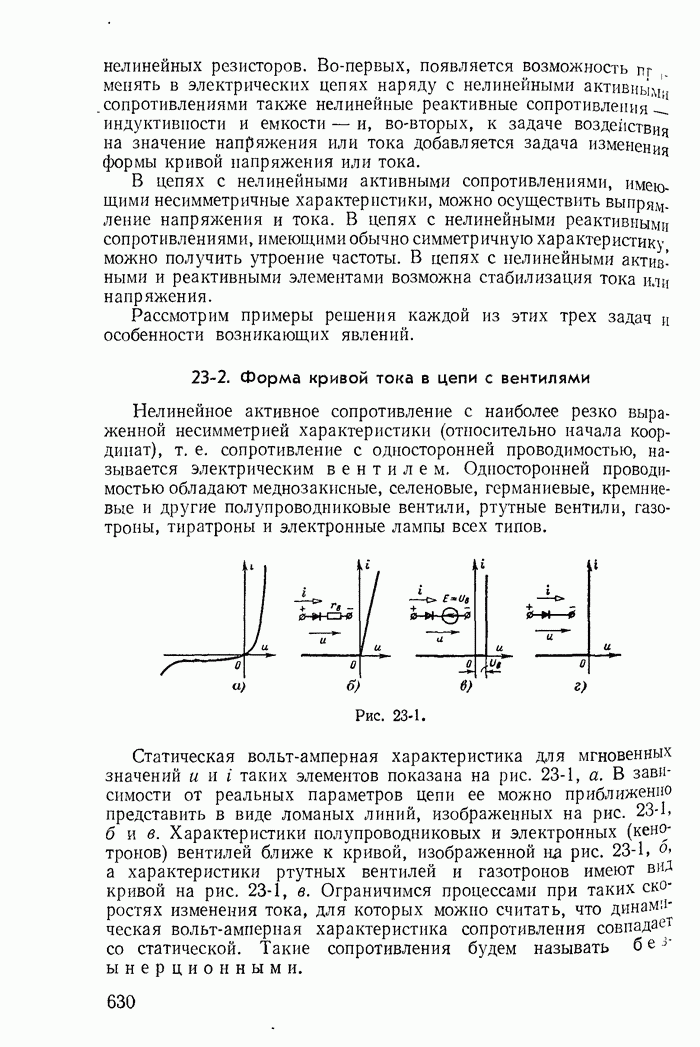
- Глава двадцать вторая. ОБЩАЯ ХАРАКТЕРИСТИКА НЕЛИНЕЙНЫХ ЦЕПЕЙ ПЕРЕМЕННОГО ТОКА И МЕТОДОВ ИХ РАСЧЕТА
- 22-1. Нелинейные двухполюсники и четырехполюсники при переменных токах
- 22-2. Определение рабочих точек на характеристиках нелинейных двухполюсников и четырехполюсников
- 22-3. Явления в нелинейных цепях переменного тока
- 22-4. Методы расчета нелинейных цепей переменного тока
- Глава двадцать третья. НЕЛИНЕЙНЫЕ ЦЕПИ С ИСТОЧНИКАМИ Э. Д. С. И ТОКА ОДИНАКОВОЙ ЧАСТОТЫ
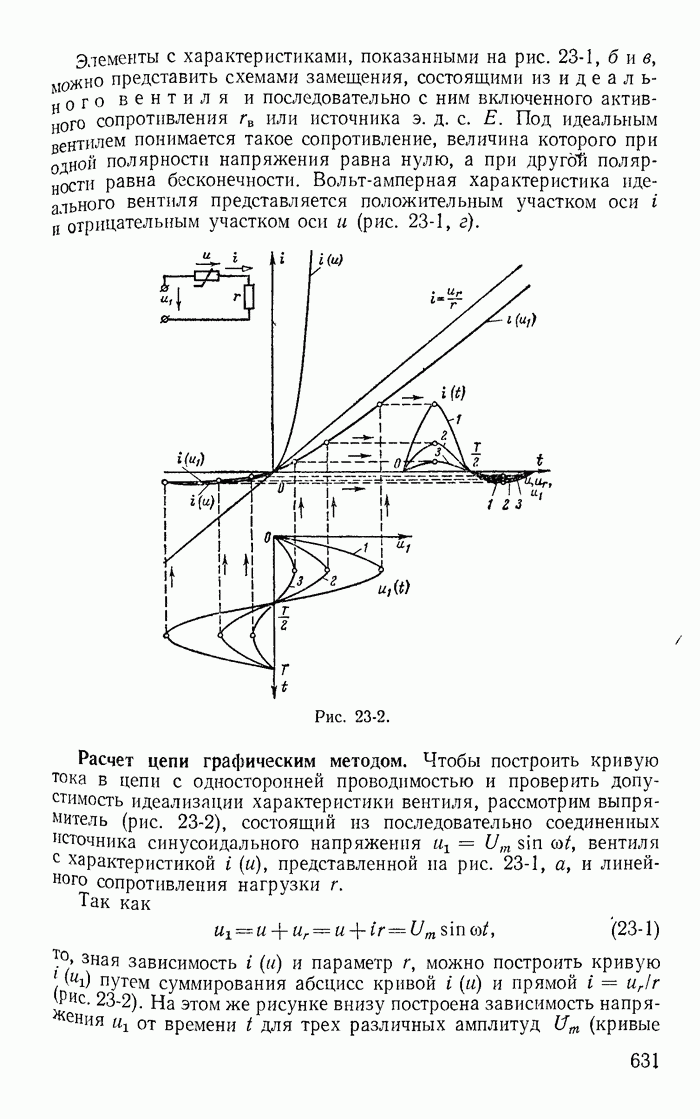
- 23-2. Форма кривой тока в цепи с вентилями
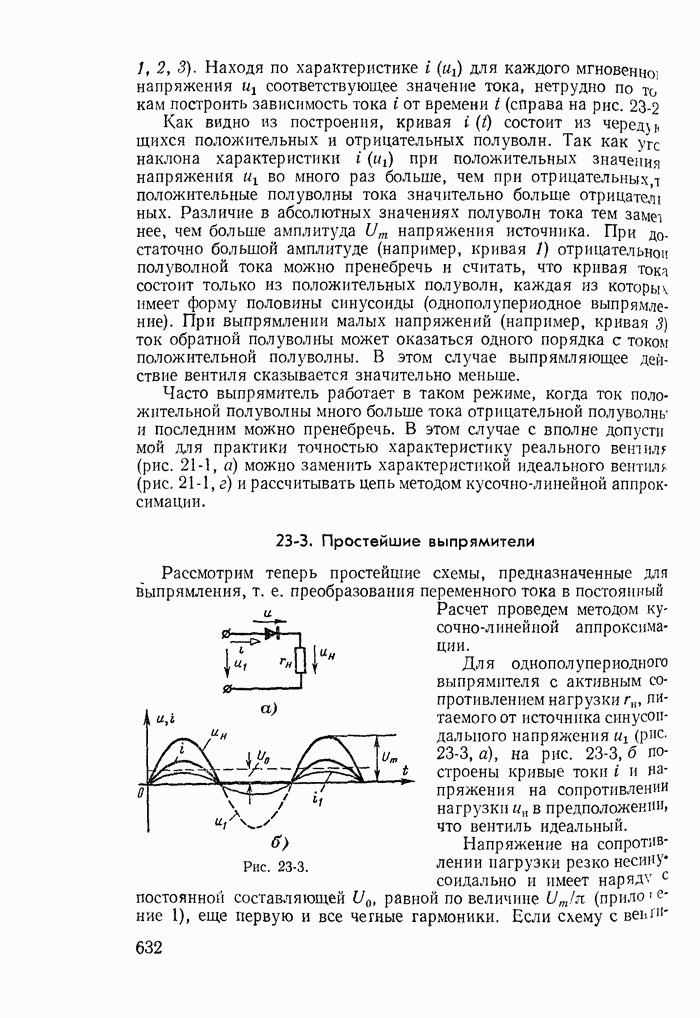
- 23-3. Простейшие выпрямители
- 23-4. Формы кривых тока и напряжения в цепях с нелинейными реактивными сопротивлениями
- 23-5. Утроители частоты
- 23-6. Формы кривых тока и напряжения в цепях с терморезисторами
- 23-7. Замена реальных нелинейных элементов условно-нелинейными
- 23-8. Учет реальных свойств стальных магнитопроводов
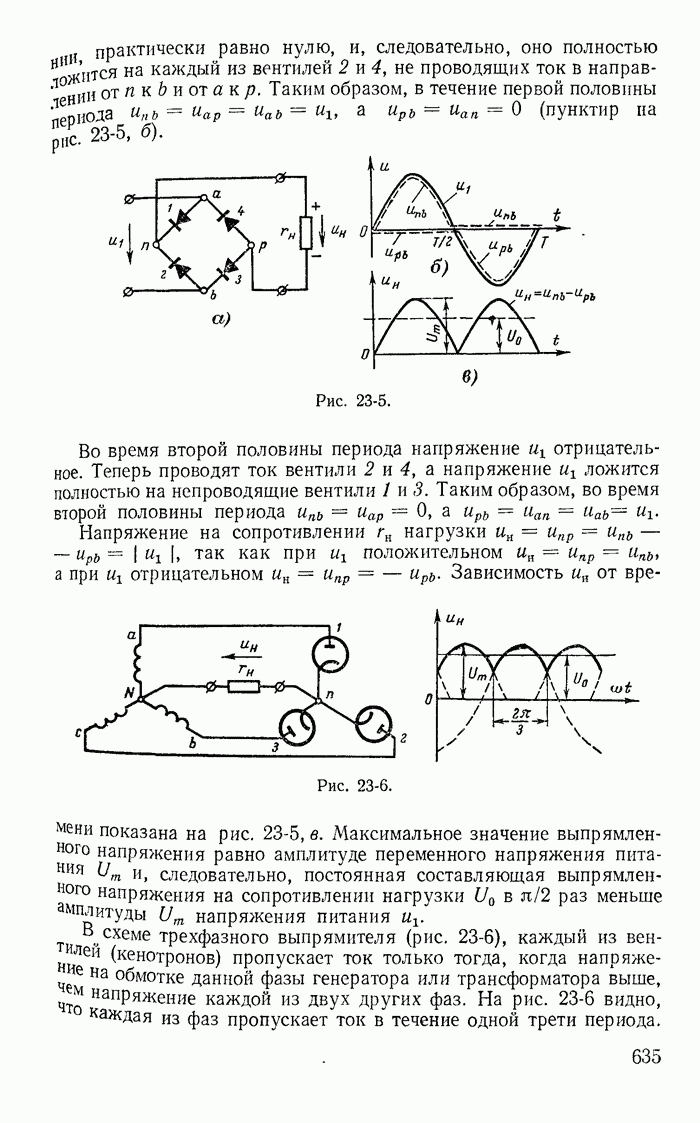
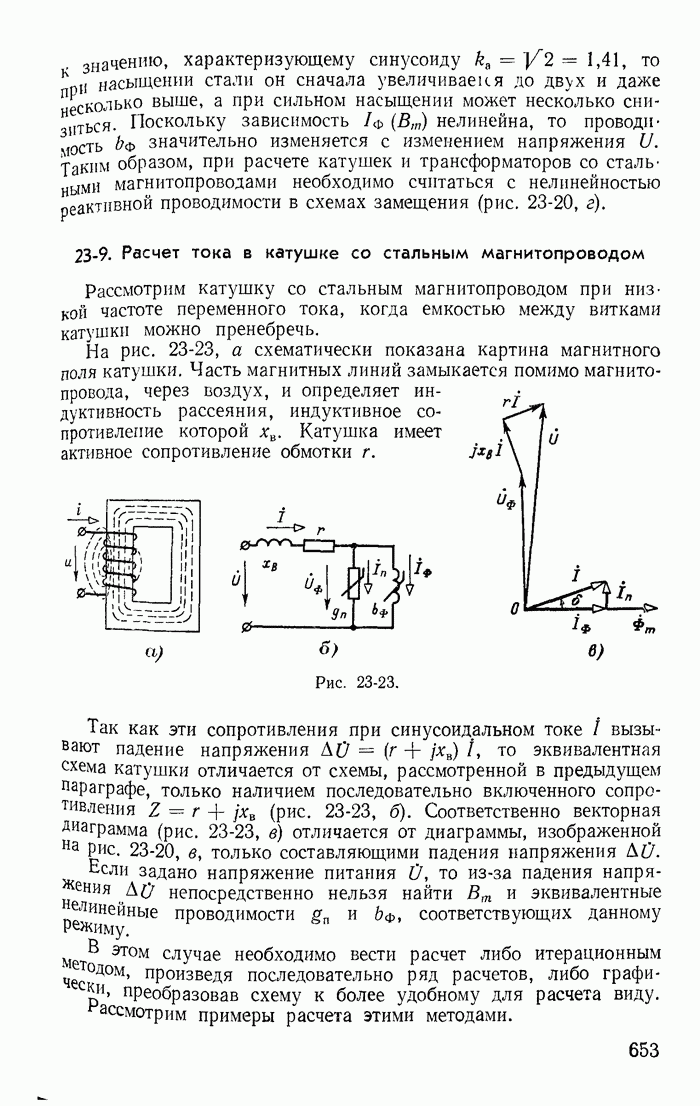
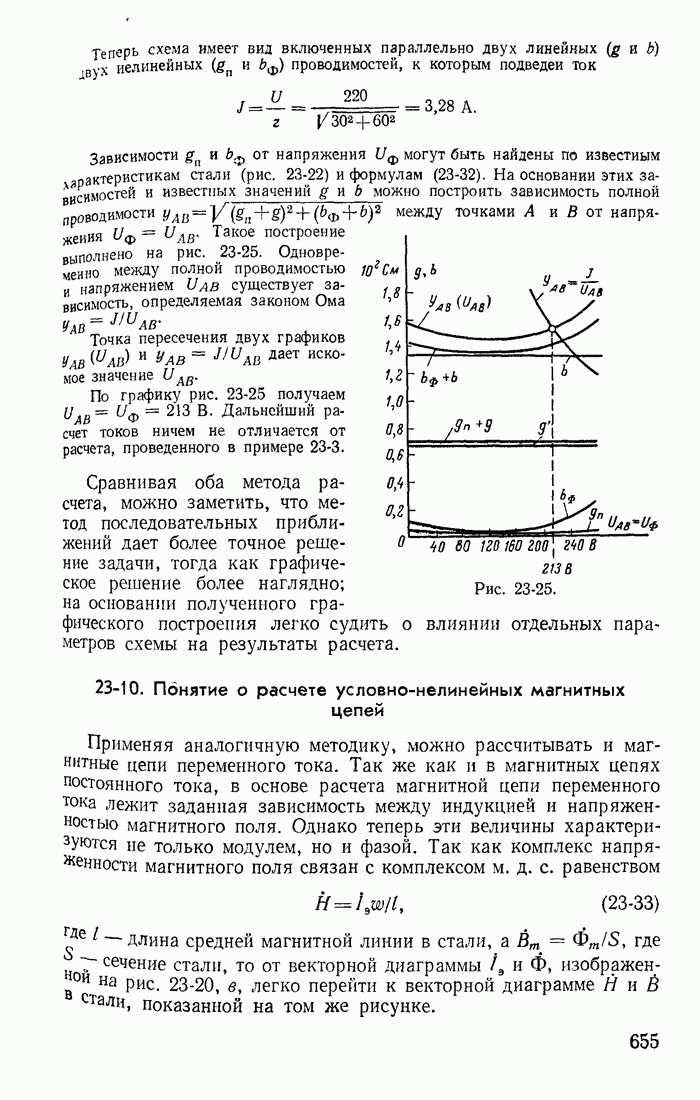
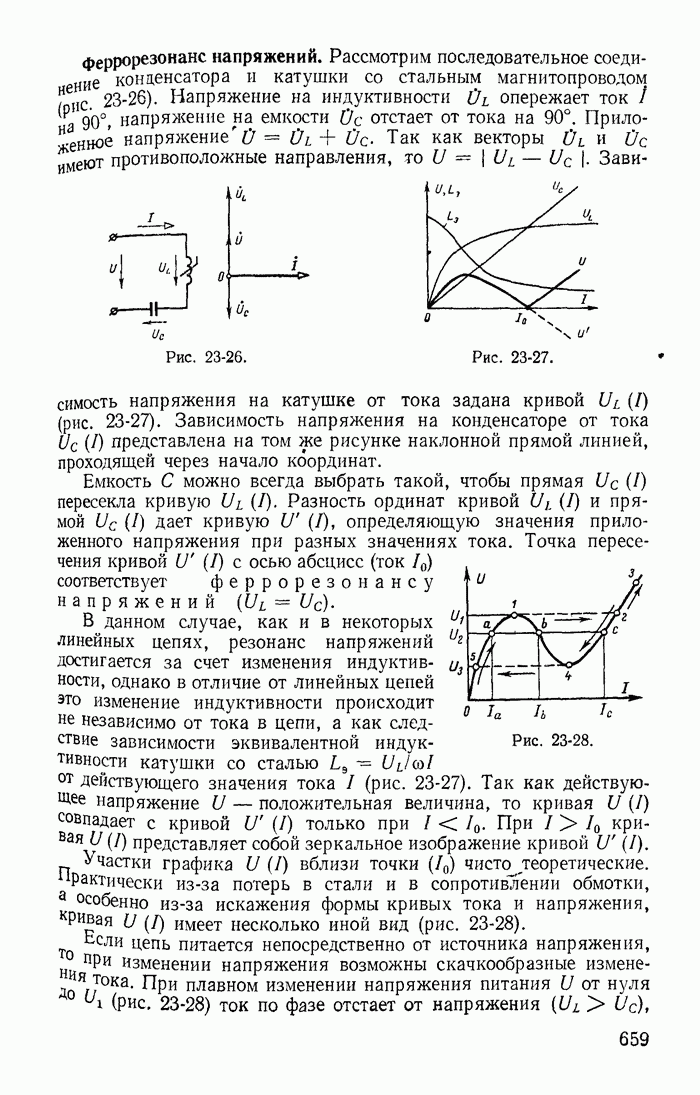
- 23-9. Расчет тока в катушке со стальным магнитопроводом
- 23-10. Понятие о расчете условно-нелинейных магнитных цепей
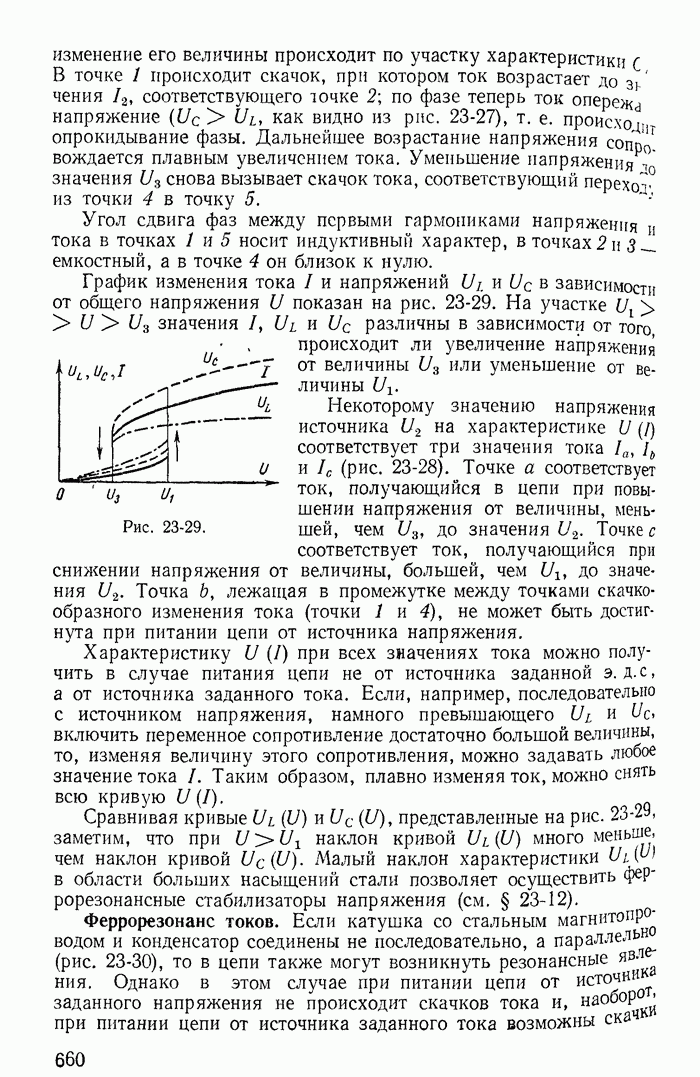
- 23-11. Явление феррорезонанса
- 23-12. Стабилизаторы напряжения
- Глава двадцать четвертая. НЕЛИНЕЙНЫЕ ЦЕПИ С ИСТОЧНИКАМИ Э. Д. С. И ТОКА РАЗЛИЧНЫХ ЧАСТОТ
- 24-1. Общая характеристика нелинейных цепей с источниками э. д. с. различных частот
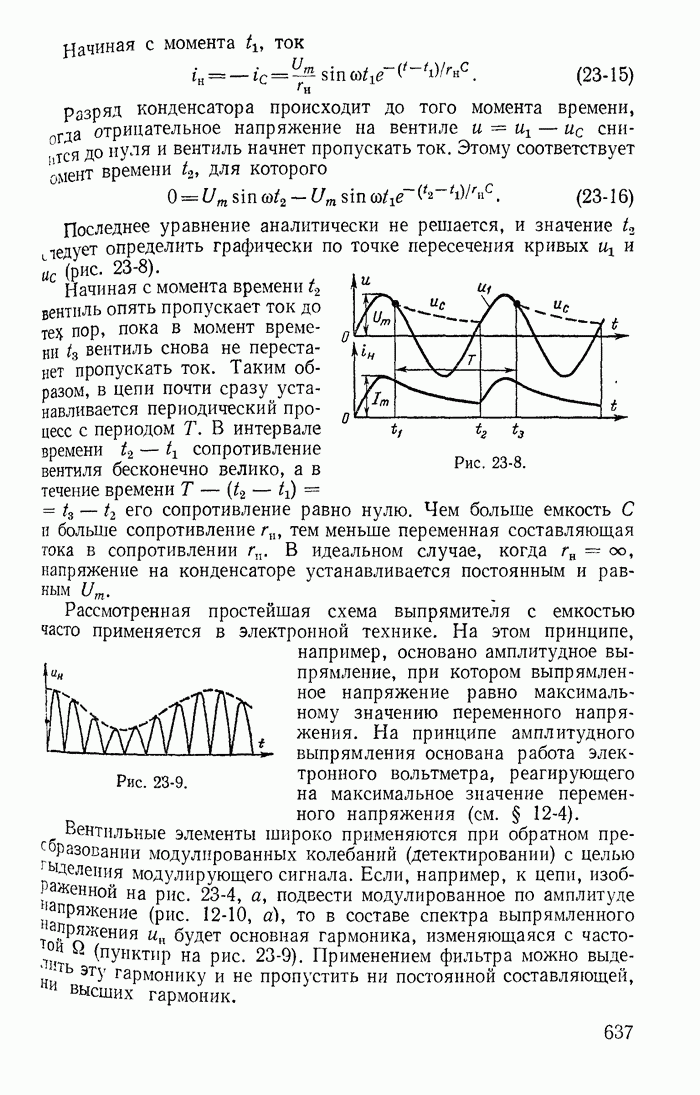
- 24-2. Вентили в цепях с постоянными и переменными э. д. с.
- 24-3. Управляемые вентили в простейших выпрямителях и преобразователях постоянного тока в переменный
- 24-4. Катушки со стальными магнитопроводами в цепях с постоянными и переменными э. д. с.
- 24-5. Удвоитель частоты
- 24-6. Метод гармонического баланса
- 24-7. Влияние постоянной э. д. с. на переменную составляющую тока в цепях с нелинейными безынерционными сопротивлениядли
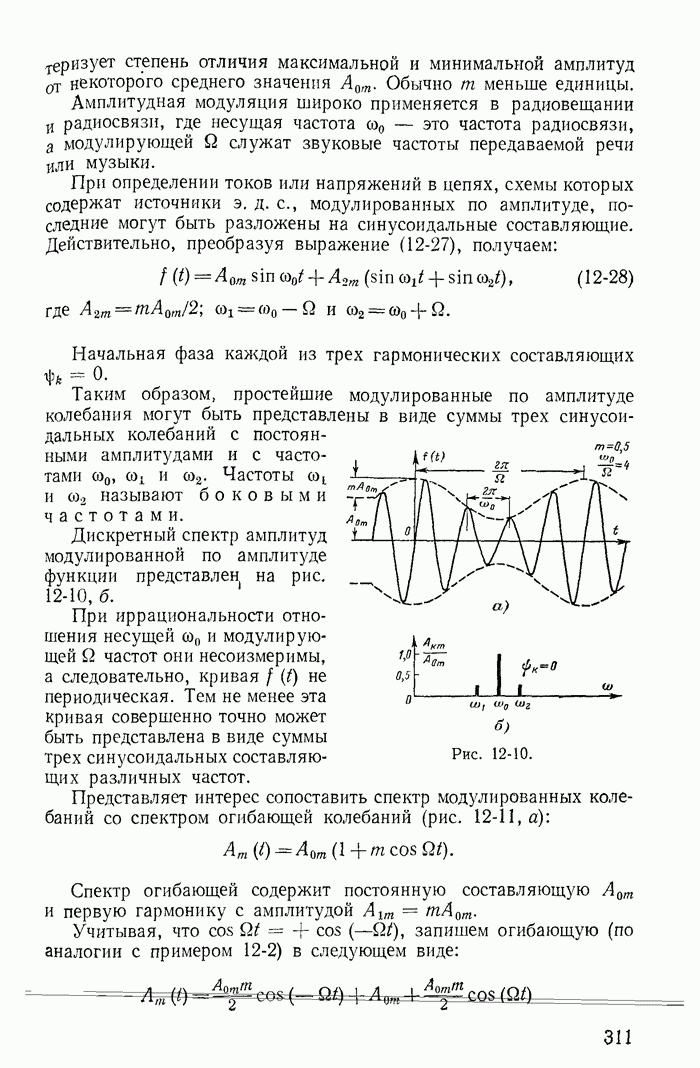
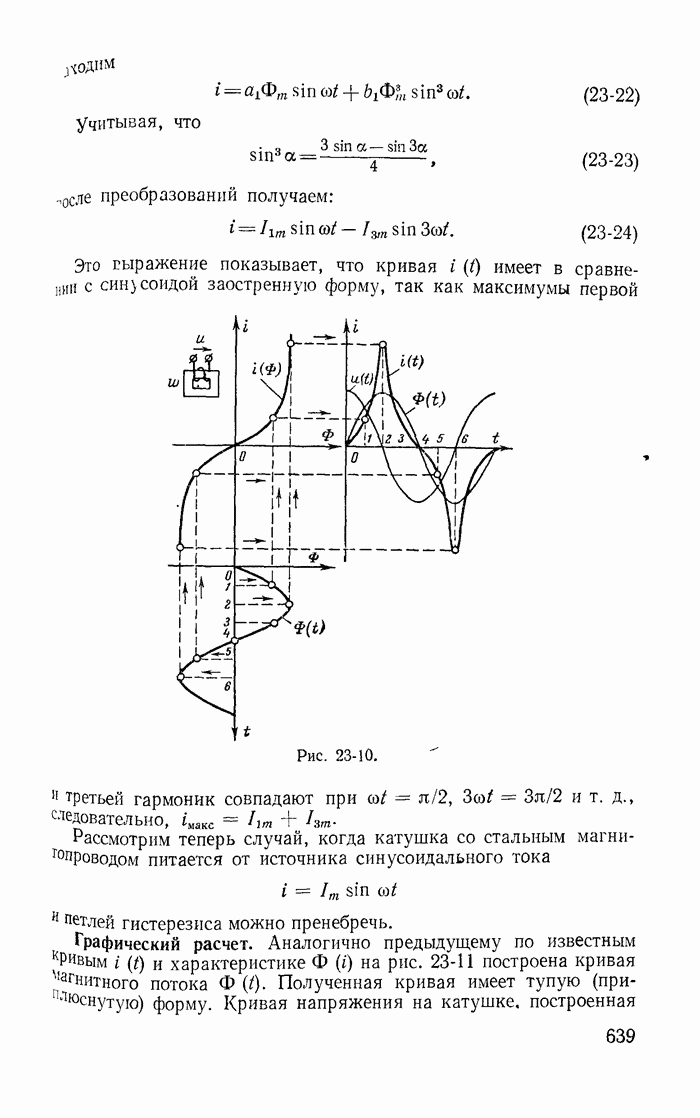
- 24-8. Принцип получения модулированных колебаний
- 24-9. Влияние постоянной составляющей на переменную в цепях с нелинейными индуктивностями
- 24-10. Магнитные усилители мощности
- Глава двадцать пятая. ПЕРЕХОДНЫЕ ПРОЦЕССЫ В НЕЛИНЕЙНЫХ ЦЕПЯХ
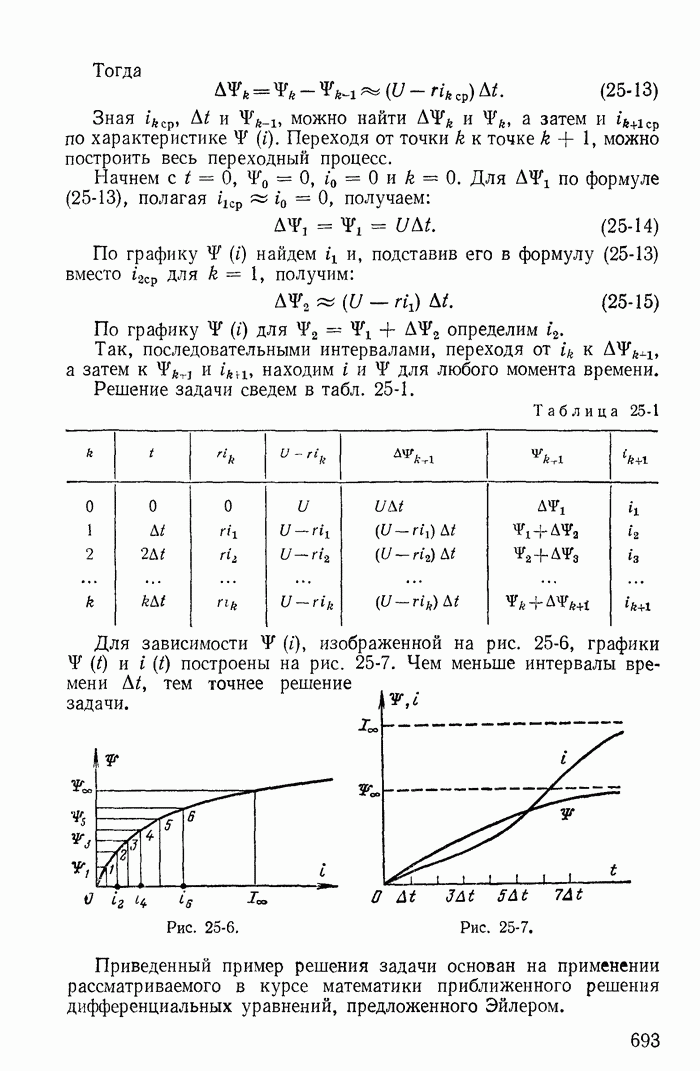
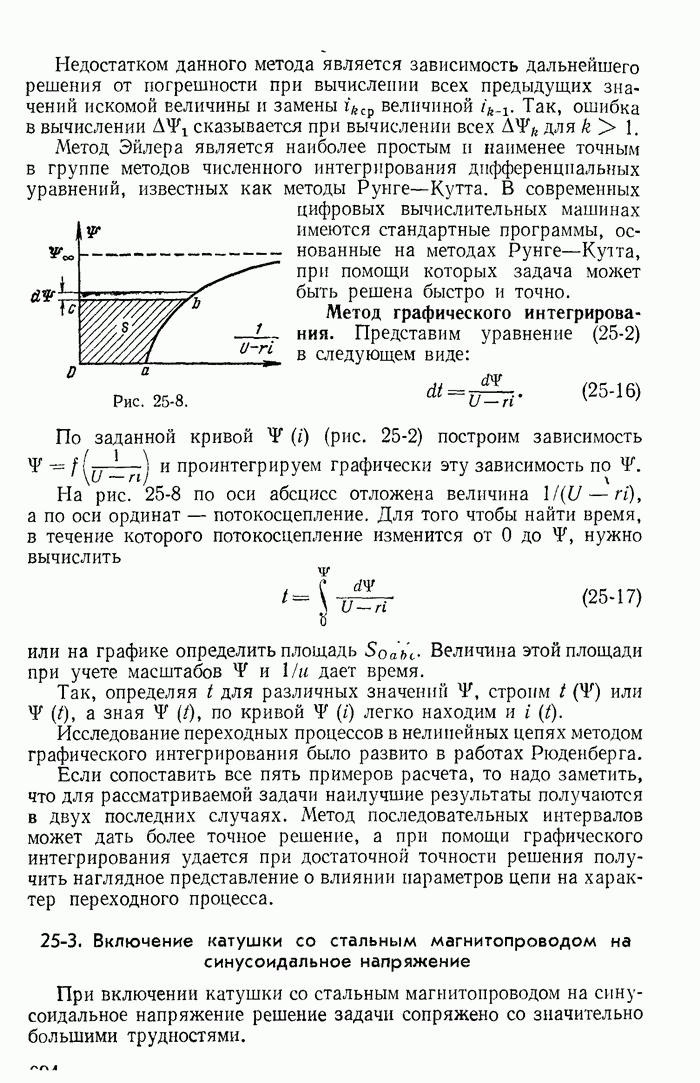
- 25-2. Включение катушки со стальным магнитопроводом на постоянное напряжение
- 25-3. Включение катушки со стальным магнитопроводом на синусоидальное напряжение
- 25-4. Импульсное воздействие в цепях с неоднозначными нелинейностями
- 25-5. Понятие о простейших запоминающих устройствах
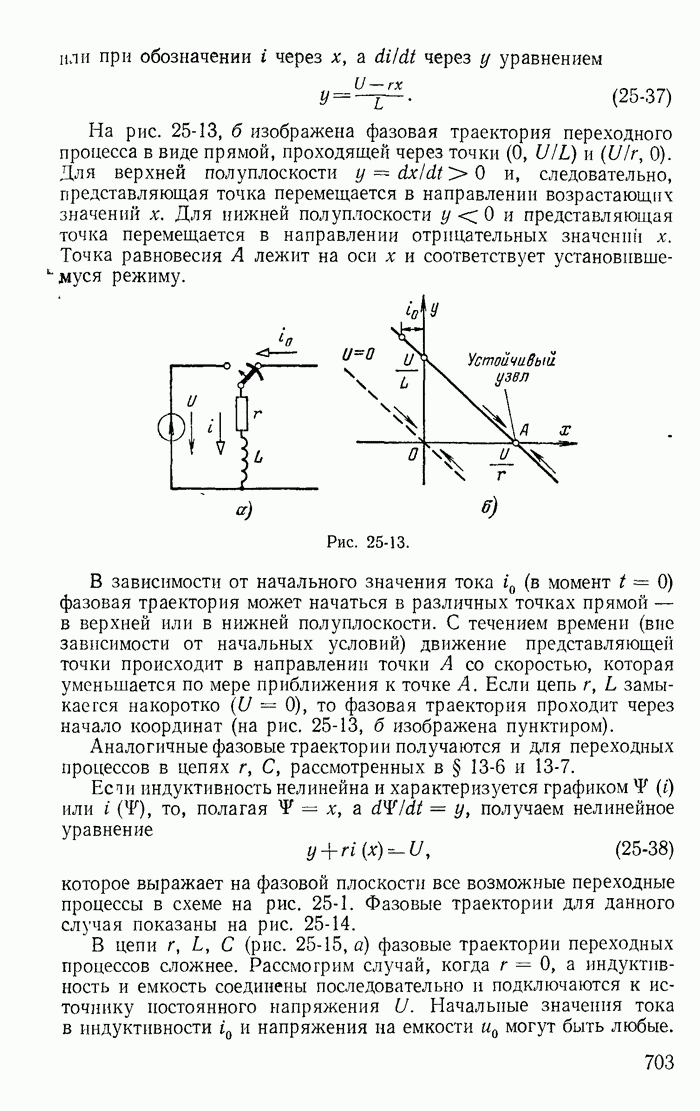
- 25-6. Изображение переходных процессов на фазовой плоскости
- 25-7. Колебательный разряд емкости через нелинейную индуктивность
- Глава двадцать шестая. АВТОКОЛЕБАНИЯ
- 26-1. Нелинейные резисторы со спадающим участком характеристики
- 26-2. Понятие об устойчивости режима в цепи с нелинейными резисторами
- 26-3. Релаксационные колебания в цепи с отрицательным сопротивлением
- 26-4. Близкие к синусоидальным колебания в цепи с отрицательным сопротивлением
- 26-5. Фазовые траектории процессов в цепи с отрицательным сопротивлением
- 26-6. Фазовые траектории процессов в генераторе синусоидальных колебаний
- 26-7. Определение амплитуды автоколебаний методом гармонического баланса
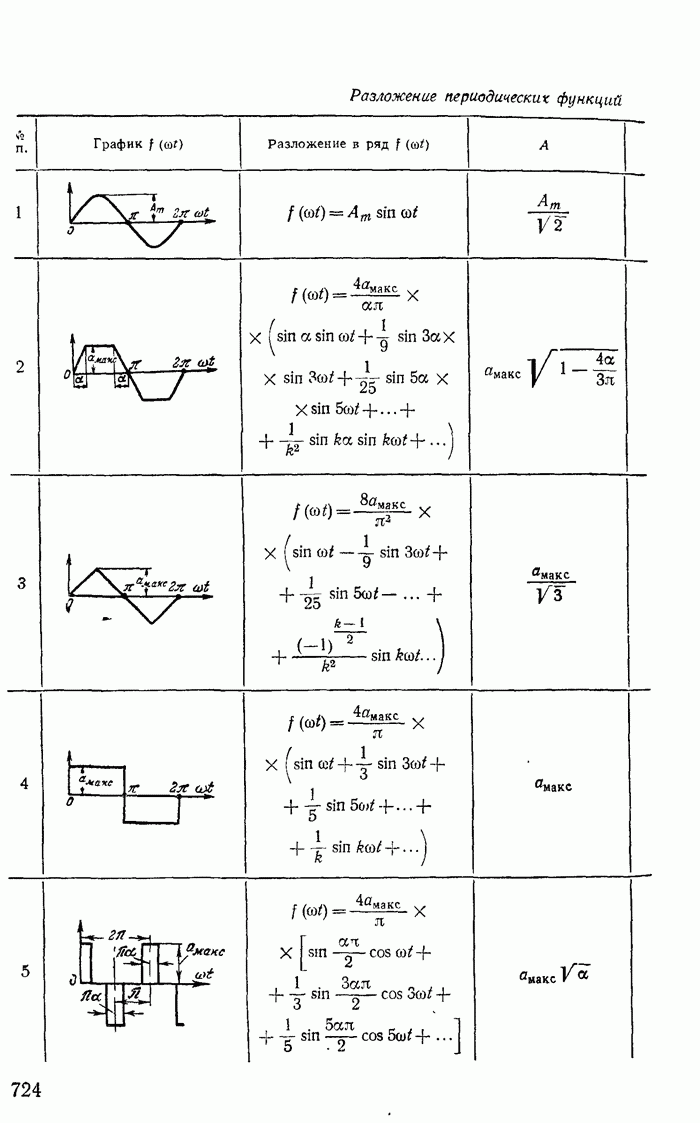
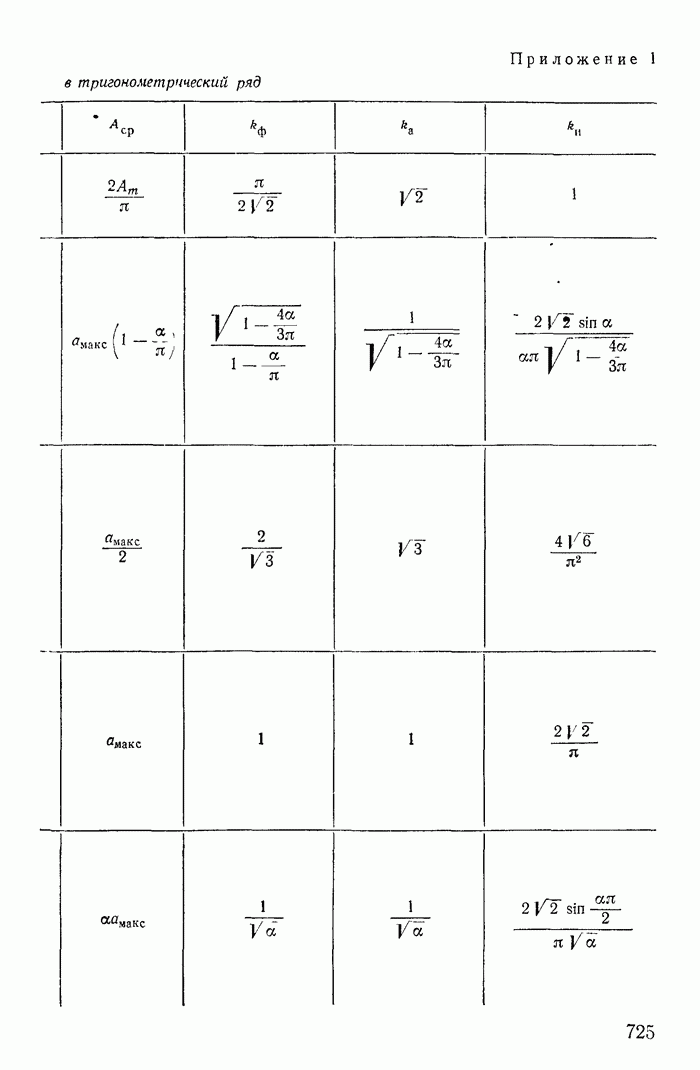
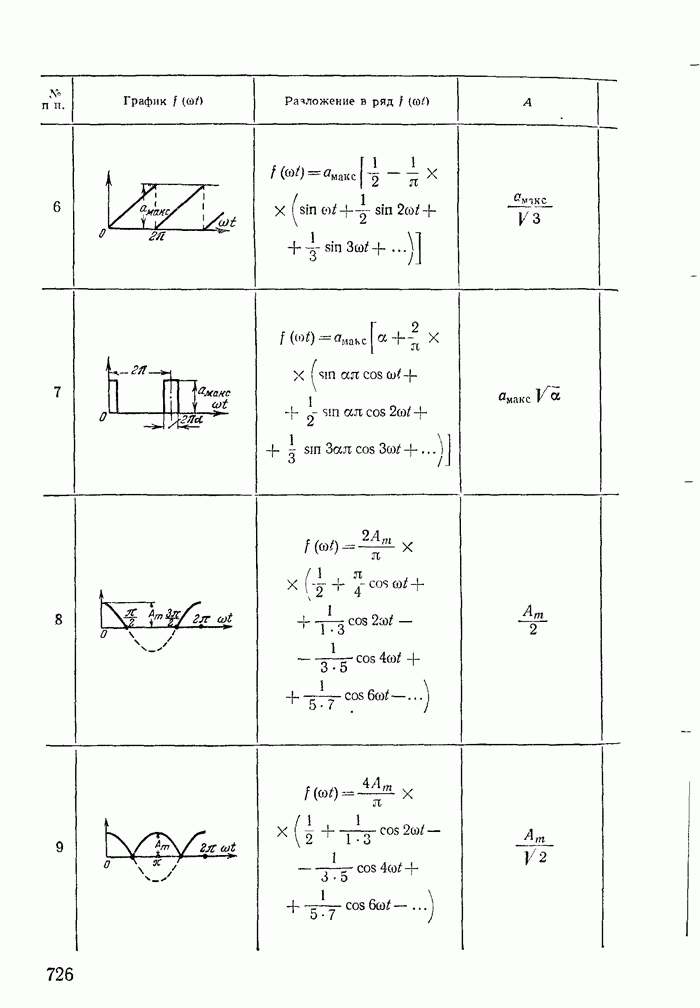
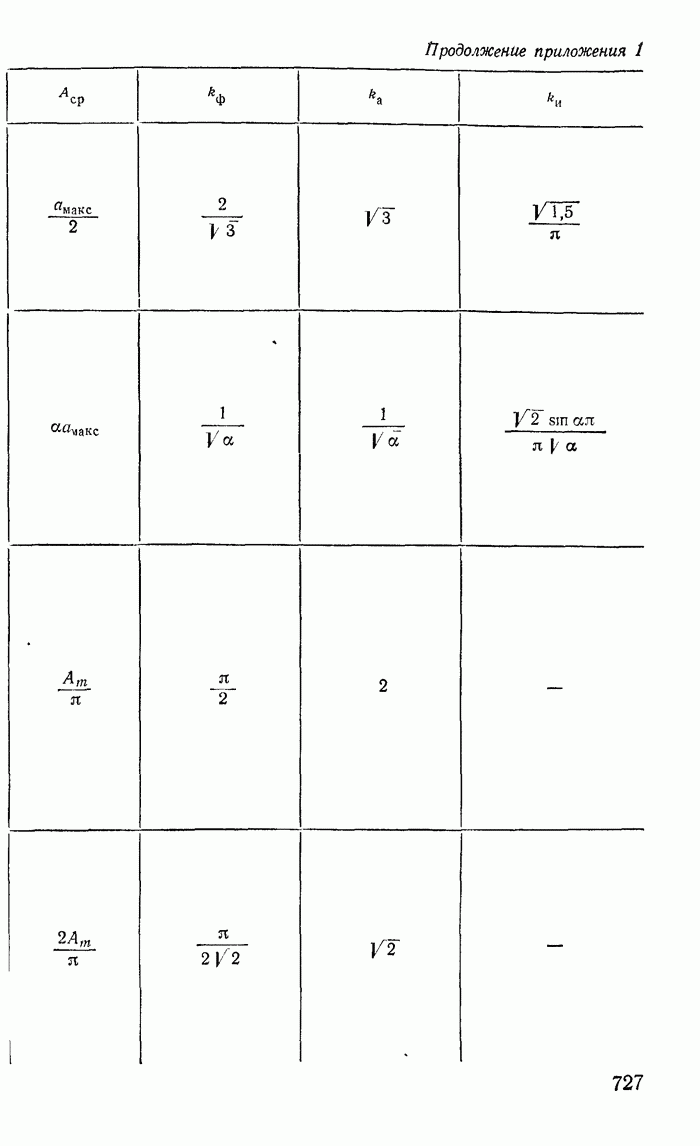
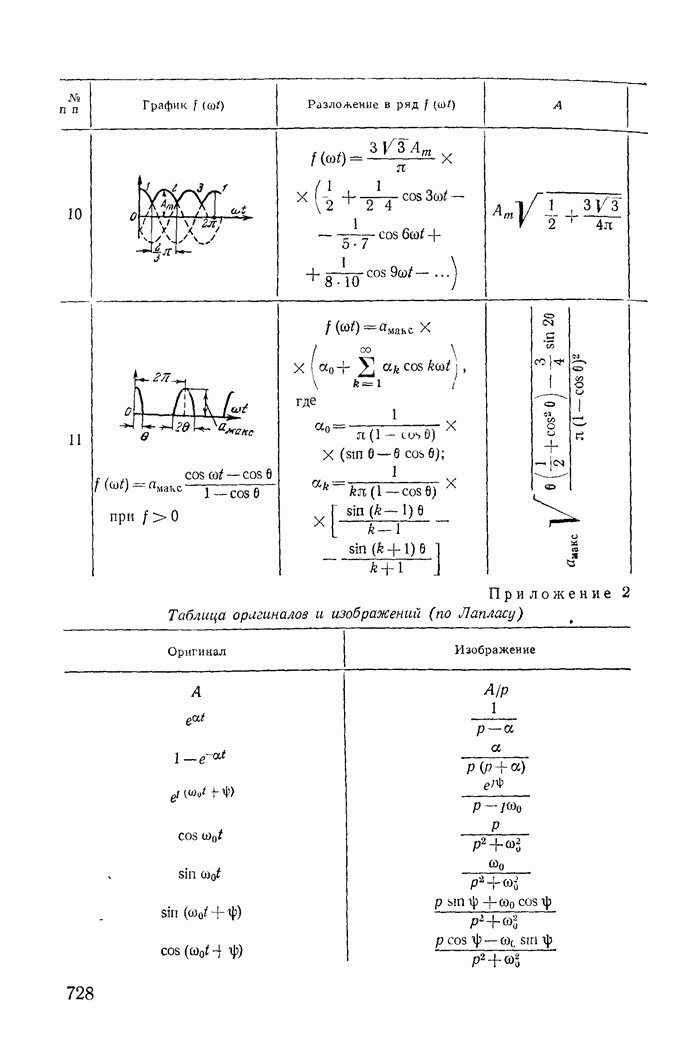
- Приложение 1. Разложение периодических функций в тригонометрический ряд
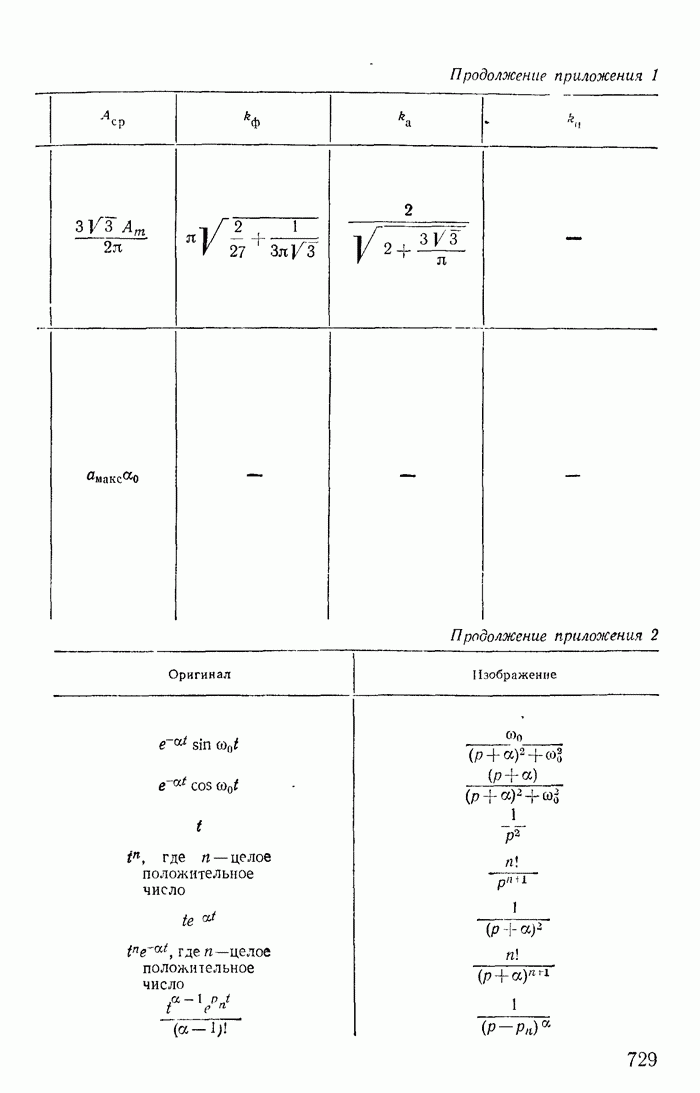
- Приложение 2. Таблица оригиналов и изображений (по Лапласу)
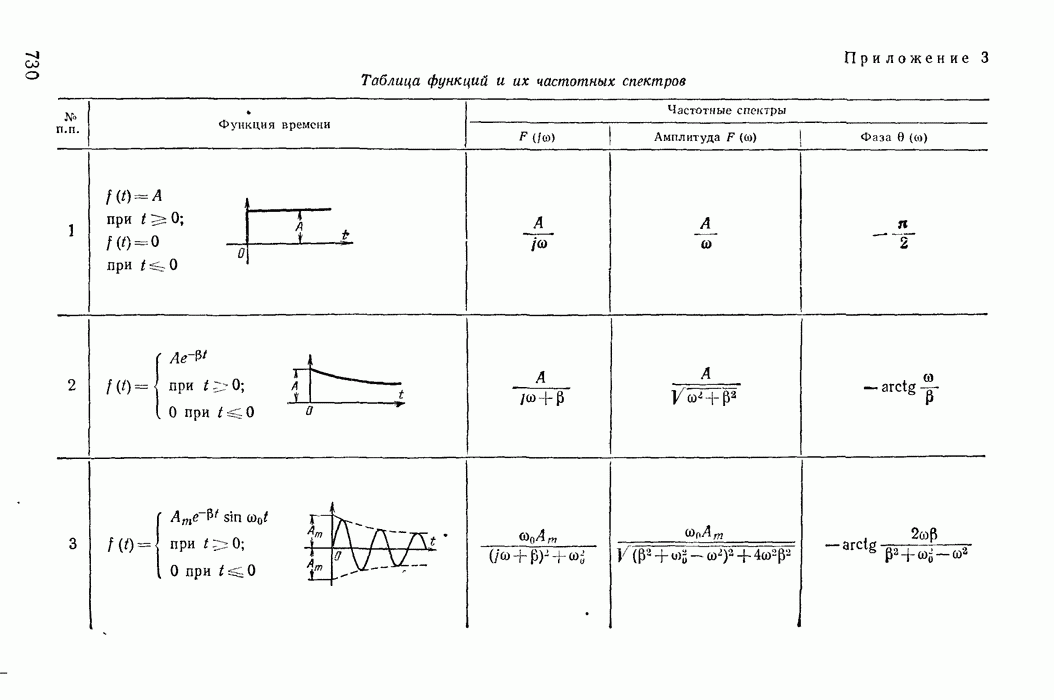
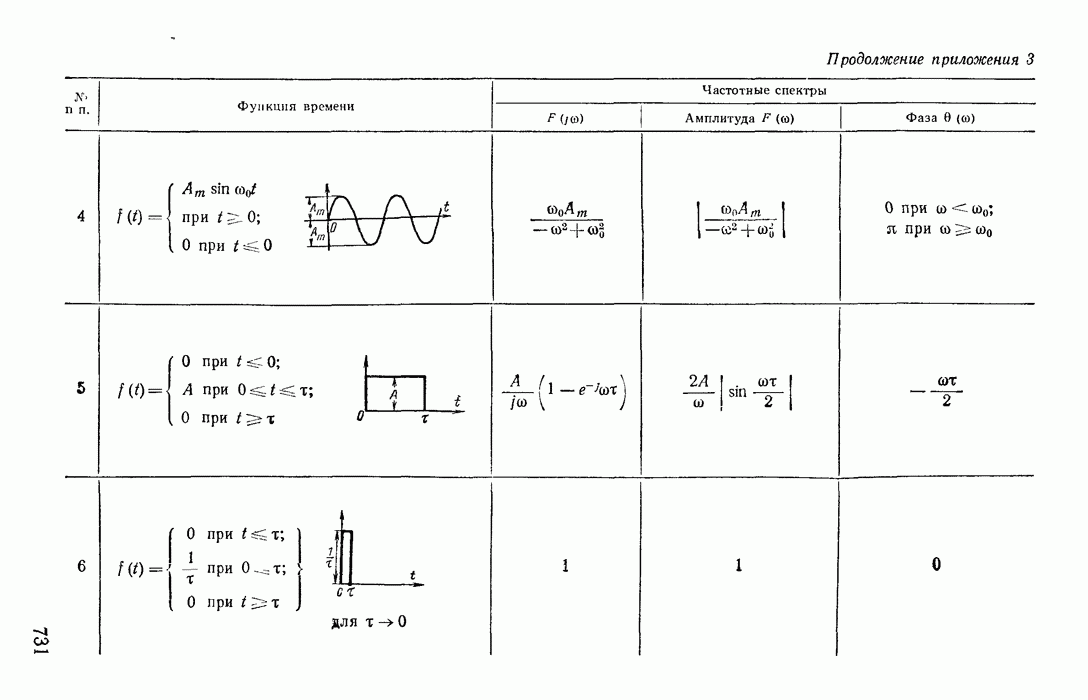
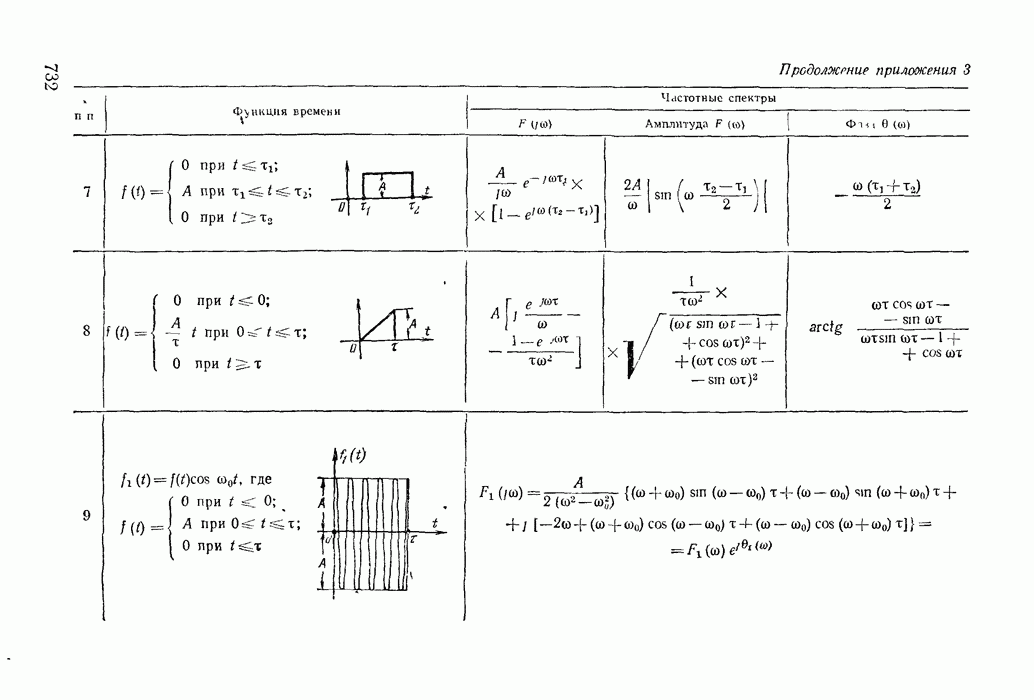
- Приложение 3. Таблица функций и их частных спектров
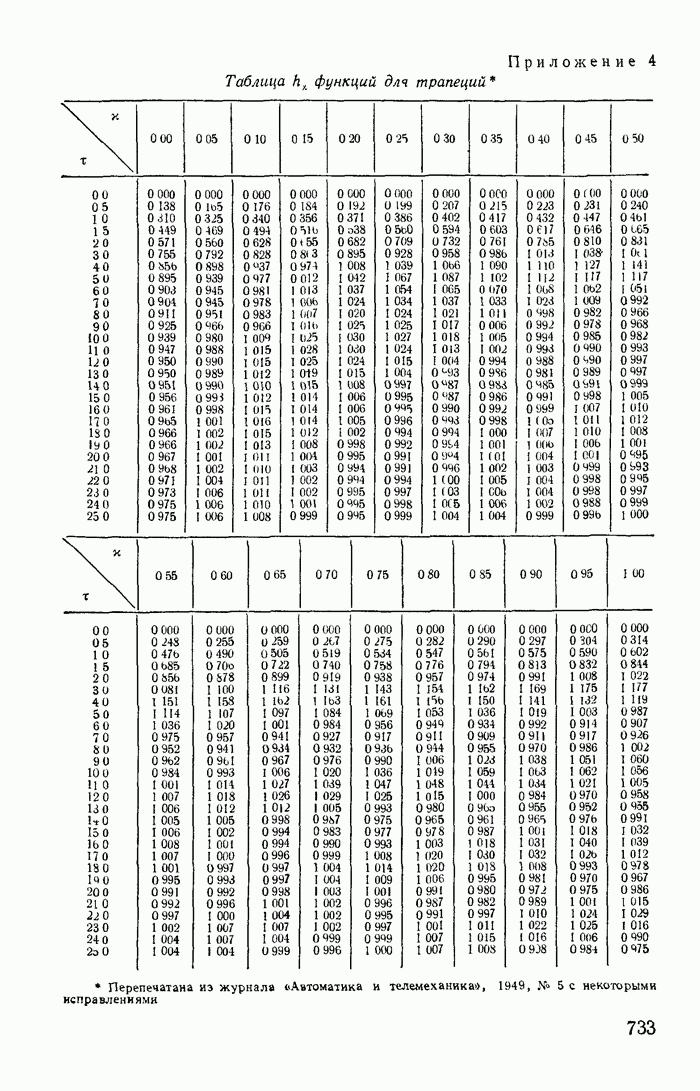
- Приложение 4. Таблица функций для трапеций
- СПИСОК ЛИТЕРАТУРЫ