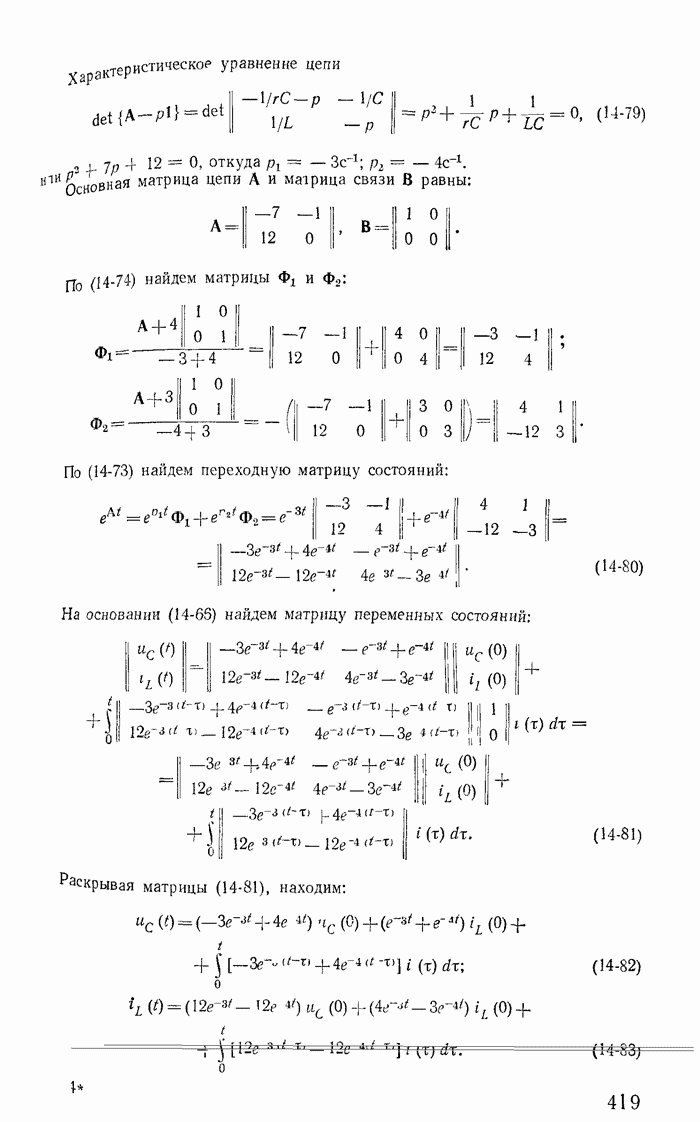| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
23-8. Учет реальных свойств стальных магнитопроводов
Выше в большинстве примеров рассматривались характеристики катушек со сталью без учета потерь в стали, т. е. той части энергии, которая расходуется на нагрев стали, обусловленный гистерезисом и вихревыми потоками
При инженерных расчетах технических устройств, содержащие стальные магнитопроводы и работающих при переменном токе такое допущение недопустимо, так как именно этими явлениями и обусловлены потери энергии, величина которых определяет тепловой режим работы устройств.
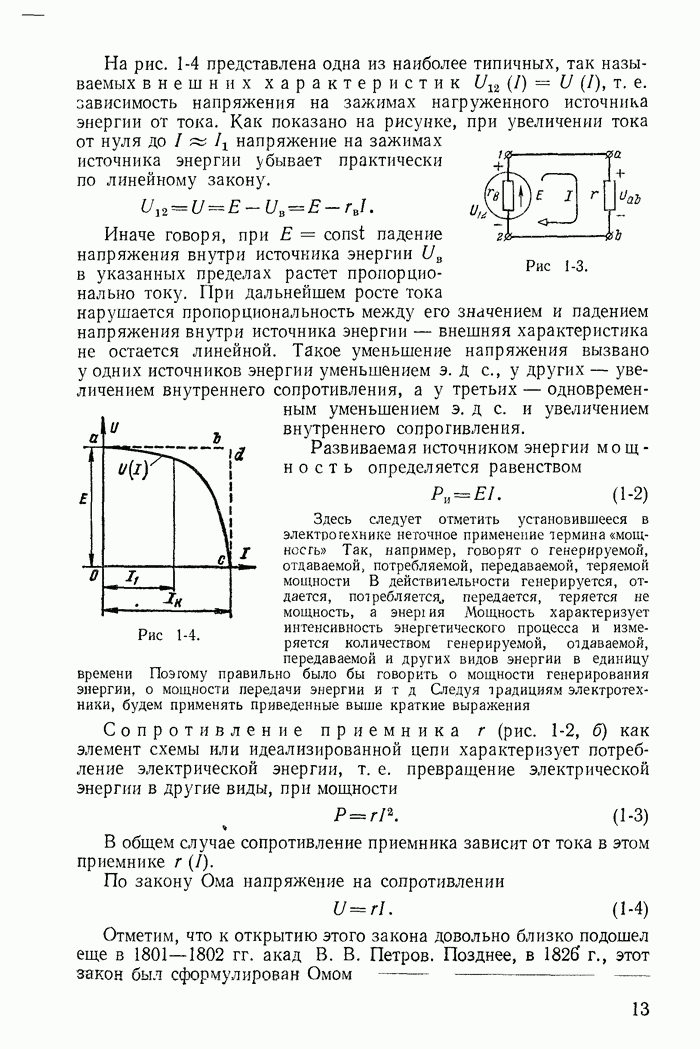
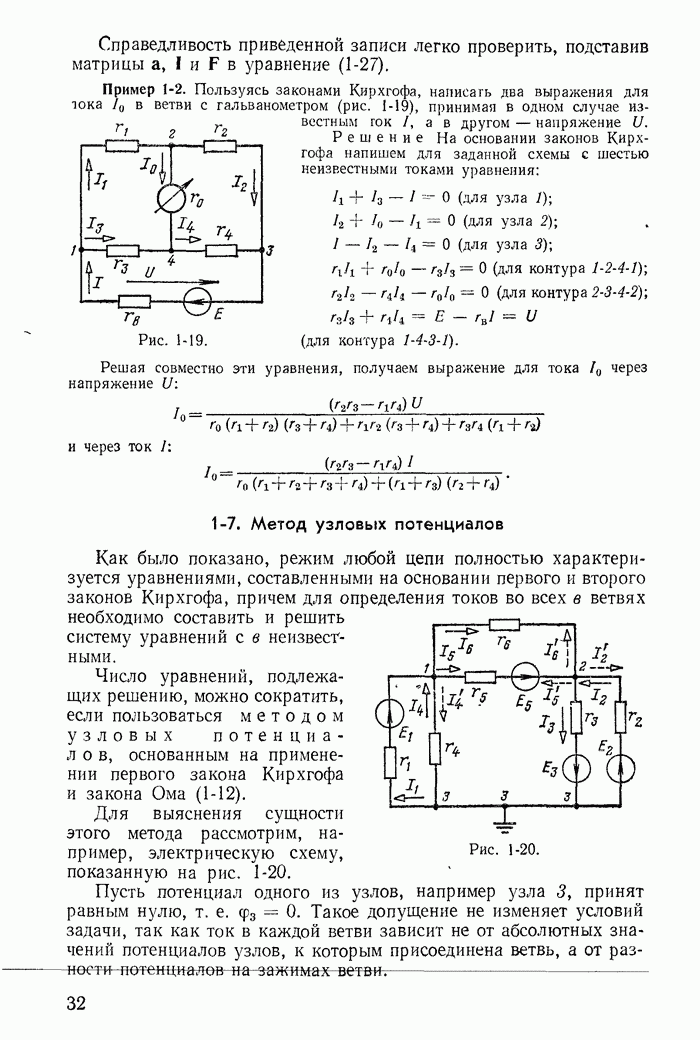
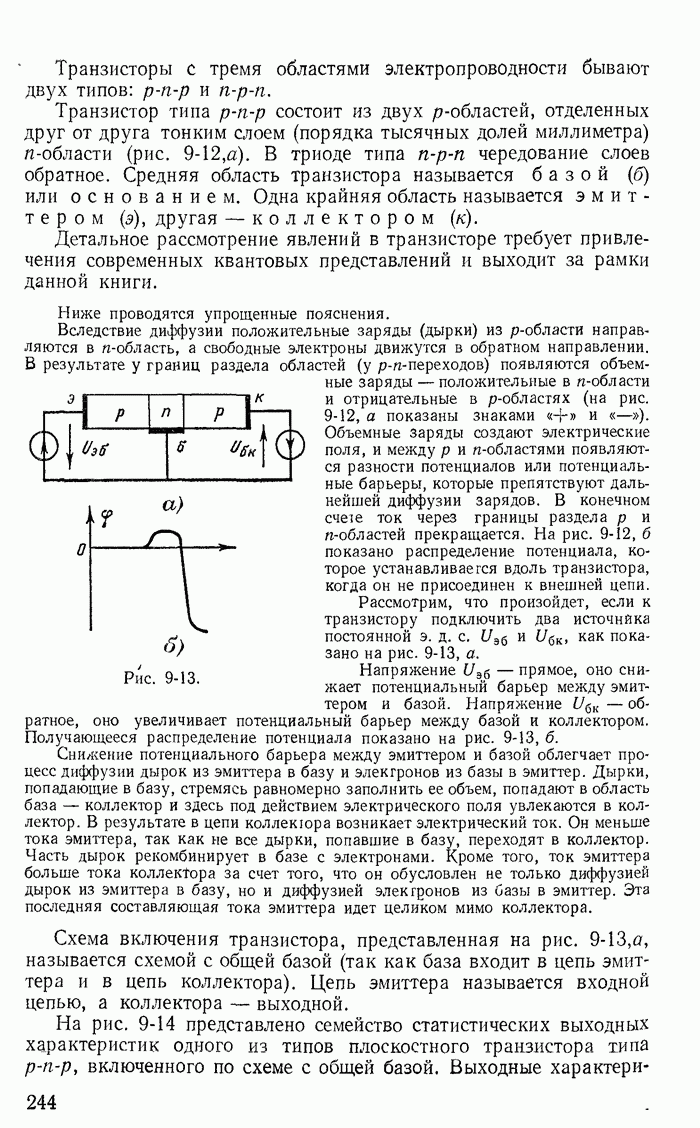
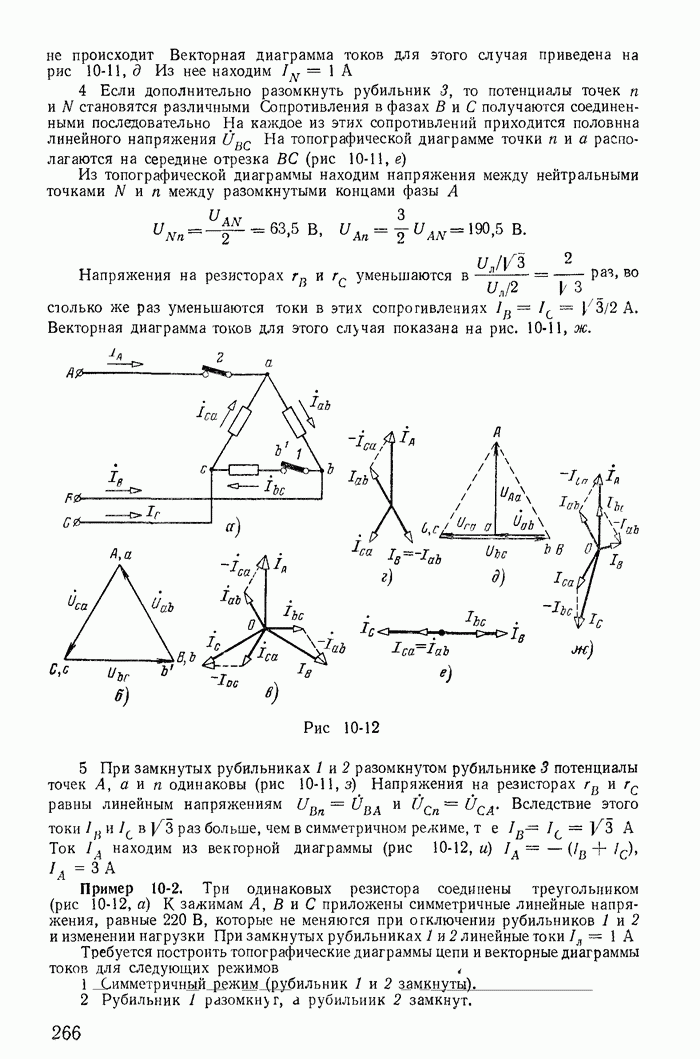
Вихревые токи возникают в стальном магнитопроводе под влиянием электрического поля, наводимого в магнитопроводе переменным магнитным потоком. На рис. 23-19, а распределение вихревых токов в массивном магнитопроводе схематически показано пунктирными линиями.
Кроме потерь энергии вихревое токи производят размагничивающее действие, которое сильнее сказывается в середине магнитопровода и меньше на его поверхности. Это объясняется тем что средние участки магнитопровода охватываются большими вихревыми токами, чем участки, близкие к поверхности магнитопровода. Поэтому распределение магнитного поля по магнитопроводу оказывается неравномерным. Индукция больше на поверхности сердечника и меньше внутри него. Внутренние участки магнитопровода как бы экранируются вихревыми токами.

Рис. 23-19.
Для уменьшения потерь энергии от вихревых токов и их экранирующего действия магнитопровод собирают из отдельных электрически изолированных один от другого листов (рис. 23-19, б). В таком магнитопроводе вихревые токи уменьшатся, так как будут замыкаться по узким вытянутым путям, представляющим большое сопротивление. Кроме того, уменьшится экранирующее действие, так как весь магнитопровод разделен на отдельные листы, находящиеся в одинаковых условиях. Неравномерность распределения магнитного потока в пределах каждого листа при достаточно малой его толщине незначительна. Применяются также магнитопроводы, собранные из электрически изолированных тонких стальных проволок.
Для уменьшения вихревых токов листы и проволоку, из которых собирается магнитная цепь, изготовляют из специальных сортов электротехнической стали, содержащей различные присадки (примеси), снижающие удельную проводимость. Чтобы потери энергии от вихревых токов не были чрезмерно велики, толщину листов берут тем меньше, чем выше частота. При частоте  применяют листы толщиной 0,25-0,5 мм, при звуковых частотах порядка сотен и тысяч герц применяют листы толщиной
применяют листы толщиной 0,25-0,5 мм, при звуковых частотах порядка сотен и тысяч герц применяют листы толщиной  При более высоких частотах применяют сердечники из более тонких лент. Для частот до 30—50 МГц применяют сердечники, выполненные
При более высоких частотах применяют сердечники из более тонких лент. Для частот до 30—50 МГц применяют сердечники, выполненные
из магнитодиэлектриков — ферритов. Магнитодиэлектрики состоят из ферромагнитного порошка с размерами частиц порядка нескольких микрон и связывающего эти частицы диэлектрика.
Расчет распределения магнитного потока в стальных магнитопроводах и подсчет потерь от вихревых токов рассматриваются в теории электромагнитного поля. В том случае, когда можно пренебречь неравномерностью распределения магнитного потока в поперечном сечении листов, из которых собран магнитопровод, для мощности потерь от вихревых токов получается следующая зависимость:

где — коэффициент, зависящий от сорта стали и размеров стальных листов;  — амплитуда магнитной индукции; G — масса рассматриваемой части магнитопровода.
— амплитуда магнитной индукции; G — масса рассматриваемой части магнитопровода.
Периодическое перемагничивание стали сопряжено с потерями энергии, обусловленными гистерезисом. Мощность потере от гистерезиса пропорциональна частоте  и определяется по различным эмпирическим формулам, например
и определяется по различным эмпирическим формулам, например

где  — коэффициент, зависящий от сорта стали;
— коэффициент, зависящий от сорта стали;  при значениях
при значениях  в пределах от 0,1 до 1 Т и
в пределах от 0,1 до 1 Т и  при значениях
при значениях  в пределах от 1 до 1,6 Т.
в пределах от 1 до 1,6 Т.
То обстоятельство, что потери энергии от вихревых токов и от гистерезиса имеют различную зависимость от частоты, позволяет отдельно рассчитать или измерить их, если известны суммарные потери в магнитопроводе для двух (или более) значений частоты, но при одном и том же значении индукции 
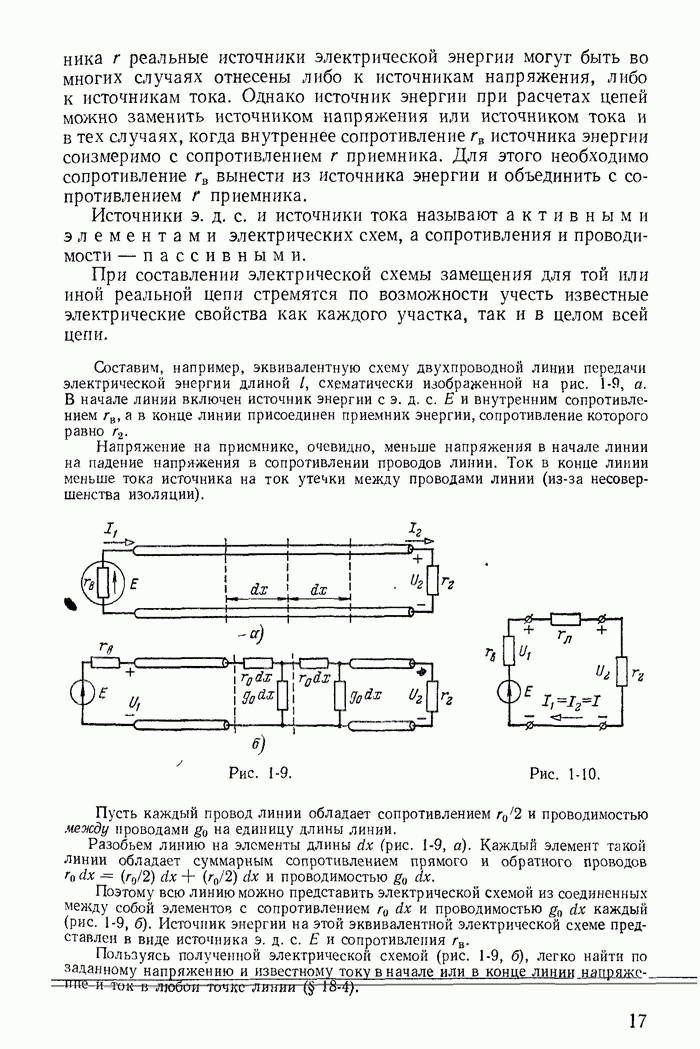
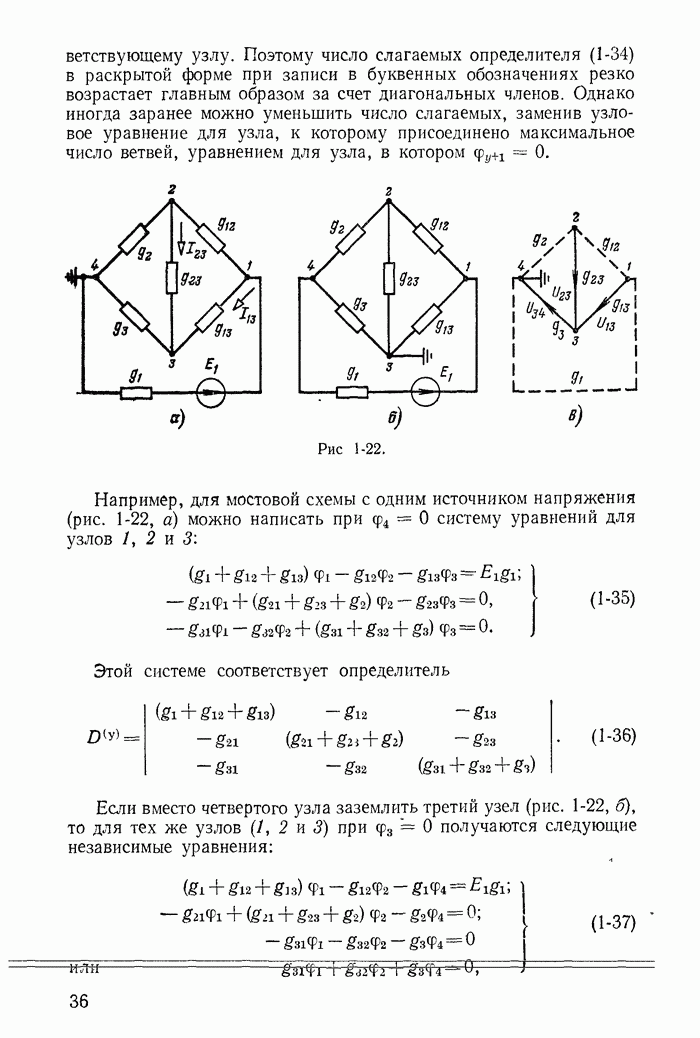
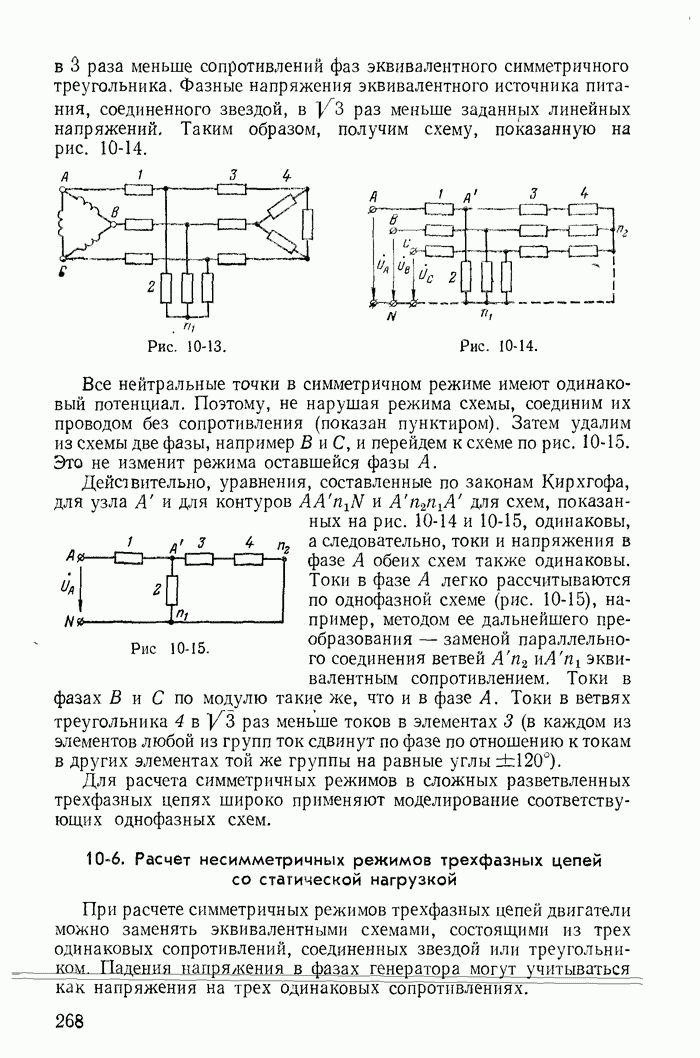
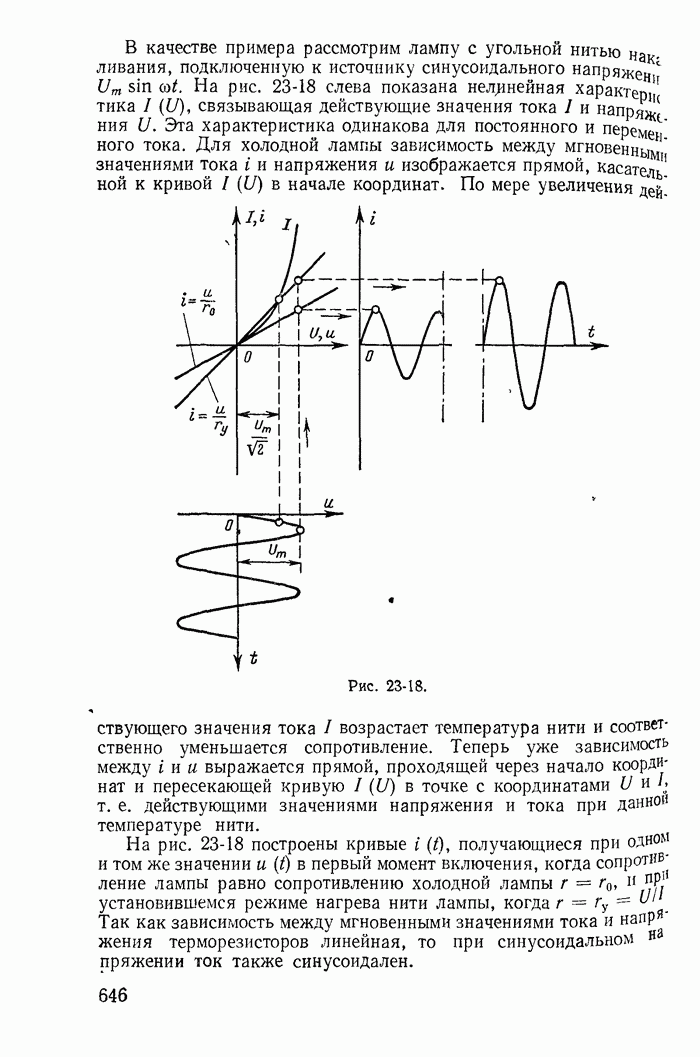
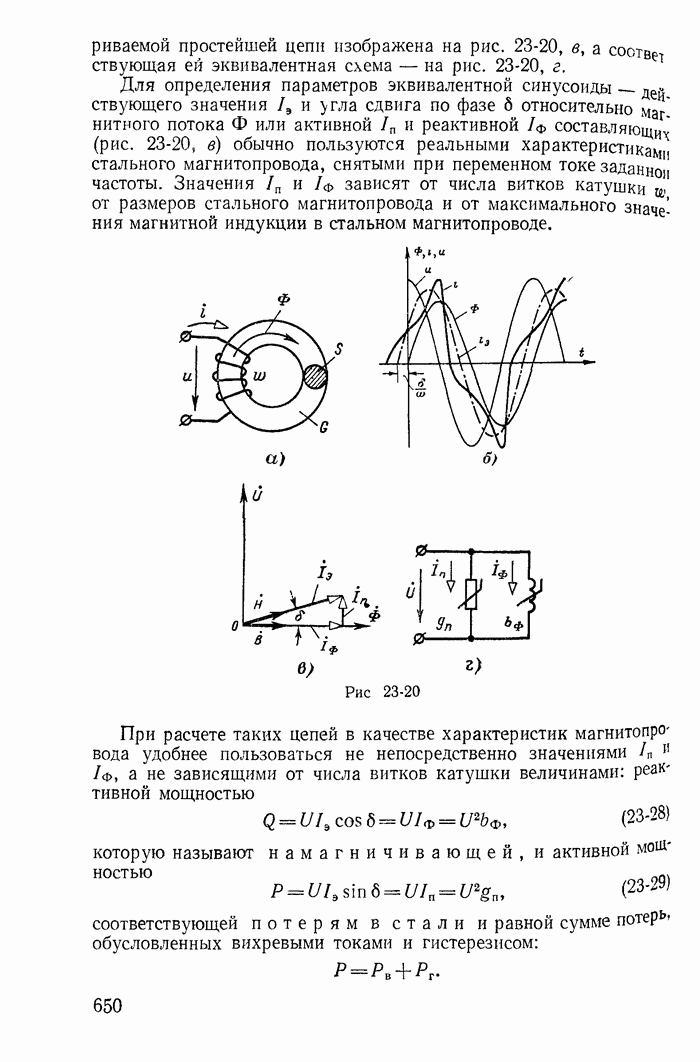
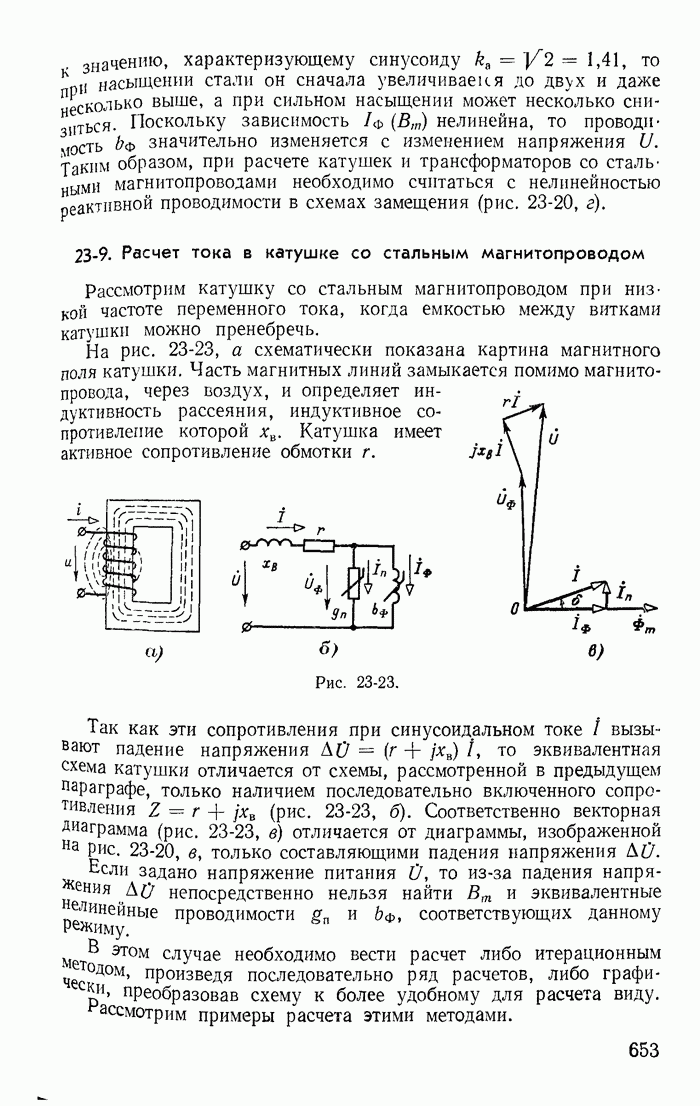
Рассмотрим простейшую магнитную цепь, представленную на рис. 23-20, а, допуская, что активным сопротивлением обмотки и индуктивностью рассеяния, обусловленной частью магнитного потока катушки, замыкающейся через воздух, можно пренебречь. Тогда при синусоидальном напряжении магнитный поток в стальном магнитопроводе синусоидален (23-18), а ток в катушке имеет несинусоидальную форму (рис. 23-20, б).
На практике при расчете катушки со стальным магнитопроводом целесообразно заменить реальный стальной магнитопровод некоторым условно-нелинейным элементом, в котором синусоидальный магнитный поток возникает под действием также синусоиального тока  (рис. 23-20, б), в известной степени эквивалентного иствительному несинусоидальному току i. Условием эквивалентности является, во-первых, равенство действующих значений токов и, во-вторых, равенство потерь, обусловленных токами
(рис. 23-20, б), в известной степени эквивалентного иствительному несинусоидальному току i. Условием эквивалентности является, во-первых, равенство действующих значений токов и, во-вторых, равенство потерь, обусловленных токами  и i. Замена реальной кривой тока эквивалентной синусоидной позволяет при расчете цепи пользоваться комплексным методом и векторными диаграммами. Векторная диаграмма рассматриваемой
и i. Замена реальной кривой тока эквивалентной синусоидной позволяет при расчете цепи пользоваться комплексным методом и векторными диаграммами. Векторная диаграмма рассматриваемой
простейшей цепи изображена на рис. 23-20, в, а соответствующая ей эквивалентная схема — на рис. 23-20, г.
Для определения параметров эквивалентной синусоиды - действующего значения  и угла сдвига по фазе б относительно магнитного потока Ф или активной
и угла сдвига по фазе б относительно магнитного потока Ф или активной  и реактивной
и реактивной  составляющих (рис. 23-20, в) обычно пользуются реальными характеристиками стального магнитопровода, снятыми при переменном токе заданной частоты. Значения
составляющих (рис. 23-20, в) обычно пользуются реальными характеристиками стального магнитопровода, снятыми при переменном токе заданной частоты. Значения  зависят от числа витков катушки
зависят от числа витков катушки  от размеров стального магнитопровода и от максимального значения магнитной индукции в стальном магнитопроводе.
от размеров стального магнитопровода и от максимального значения магнитной индукции в стальном магнитопроводе.

Рис. 23-20
При расчете таких цепей в качестве характеристик магнитопровода удобнее пользоваться не непосредственно значениями  а не зависящими от числа витков катушки величинами: реактивной мощностью
а не зависящими от числа витков катушки величинами: реактивной мощностью
 (23-28)
(23-28)
которую называют намагничивающей, и активной мощностью 

соответствующей потерям в стали и равной сумме потерь обусловленных вихревыми токами и гистерезисом:

Все эти мощности удобнее относить к единице массы стального магнитопровода G и в качестве характеристик стали принимать:

выражающие удельную намагничивающую мощность и удельные потери, обусловленные гистерезисом и вихревыми токами.
Значения  зависят от марки (сорта) стали, способа ее намагничивания (ток или магнитный поток синусоидальные) и особенно от величины максимальной индукции
зависят от марки (сорта) стали, способа ее намагничивания (ток или магнитный поток синусоидальные) и особенно от величины максимальной индукции  . Так как магнитная система обычно рассчитывается для практически синусоидальной формы кривой магнитного потока, то значения
. Так как магнитная система обычно рассчитывается для практически синусоидальной формы кривой магнитного потока, то значения  определяют для синусоидального магнитного потока.
определяют для синусоидального магнитного потока.

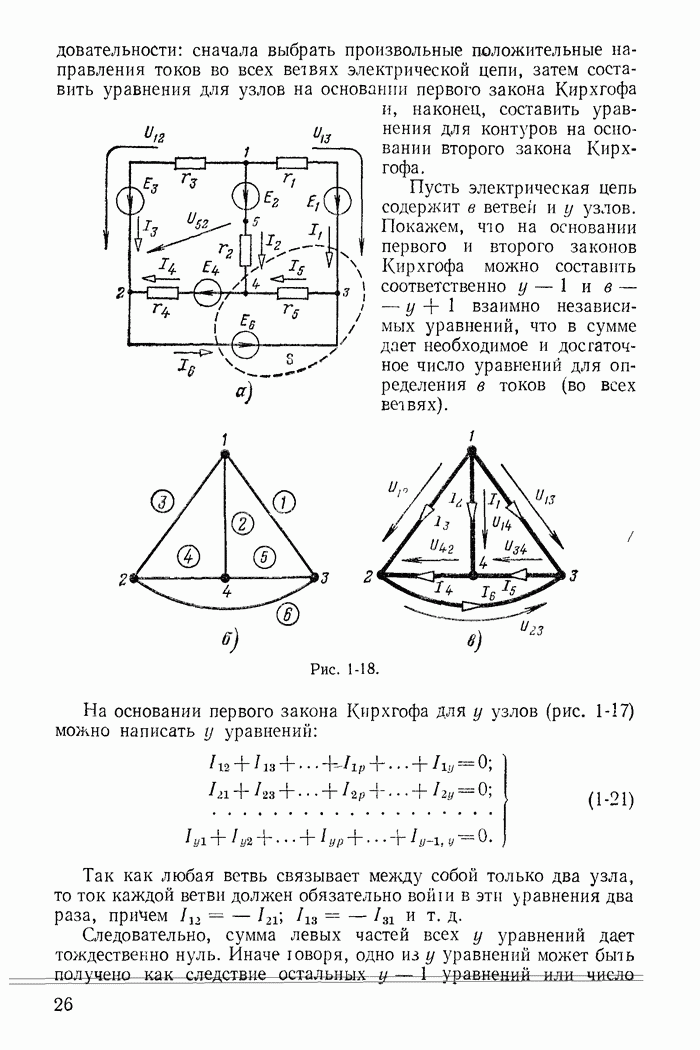
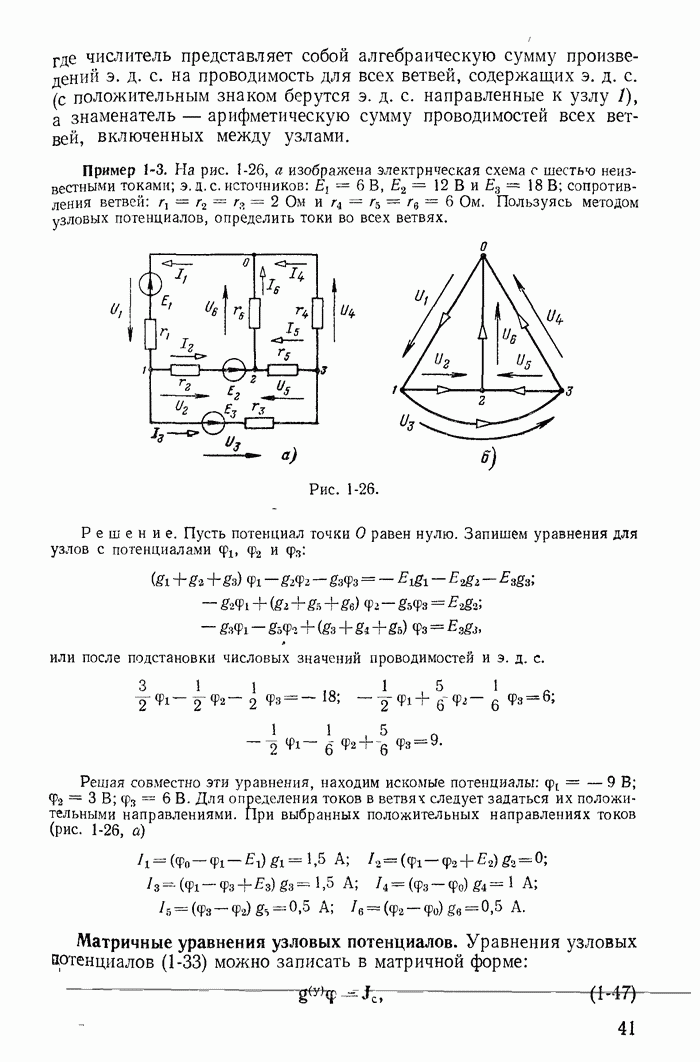
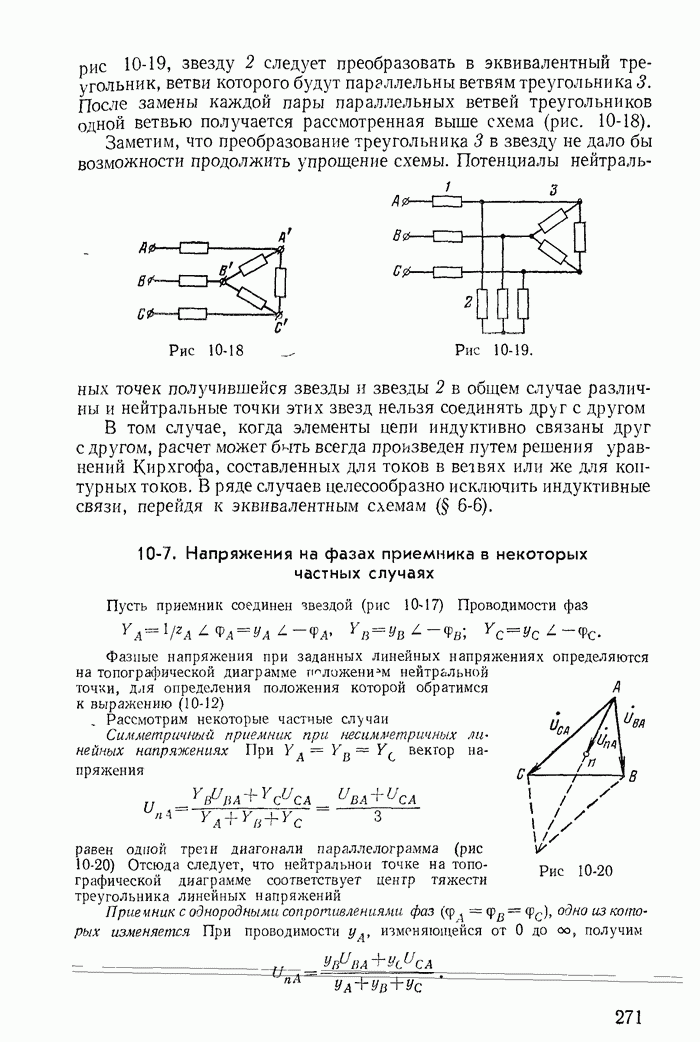
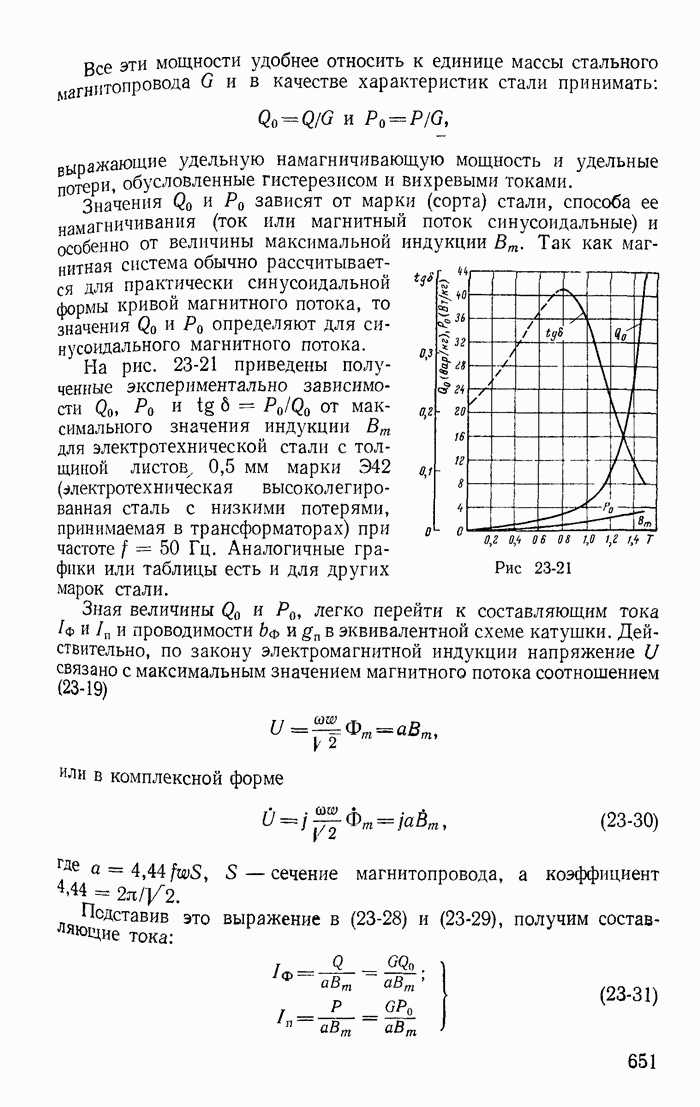
Рис. 23-21
На рис. 23-21 приведены полученные экспериментально зависимости  от максимального значения индукции
от максимального значения индукции  для электротехнической стали с толщиной
для электротехнической стали с толщиной  мм марки
мм марки  (электротехническая высоколегированная сталь с низкими потерями, принимаемая в трансформаторах) при частоте
(электротехническая высоколегированная сталь с низкими потерями, принимаемая в трансформаторах) при частоте  Гц. Аналогичные графики или таблицы есть и для других марок стали.
Гц. Аналогичные графики или таблицы есть и для других марок стали.
Зная величины  легко перейти к составляющим тока
легко перейти к составляющим тока  и проводимости
и проводимости  эквивалентной схеме катушки. Действительно, по закону электромагнитной индукции напряжение U связано с максимальным значением магнитного потока соотношением (23-19)
эквивалентной схеме катушки. Действительно, по закону электромагнитной индукции напряжение U связано с максимальным значением магнитного потока соотношением (23-19)

или в комплексной форме
 (23-30)
(23-30)
где  — сечение магнитопровода, а коэффициент
— сечение магнитопровода, а коэффициент 
Подставив это выражение в (23-28) и (23-29), получим составляющие тока:

или составляющие проводимости в эквивалентной схеме (рис. 23-20, г)

Как видно из полученных выражений, при заданных постоянных значениях частоты  числа витков катушки w, сечения S и массы G стального магнитопровода составляющие тока
числа витков катушки w, сечения S и массы G стального магнитопровода составляющие тока  пропорциональны
пропорциональны  а проводимости
а проводимости  и
и  пропорциональны
пропорциональны 
Таким образом, построив зависимость этих величин от средней по сечению индукции  в свою очередь пропорциональной напряжению U, можно судить о характере нелинейности рассматриваемого элемента.
в свою очередь пропорциональной напряжению U, можно судить о характере нелинейности рассматриваемого элемента.

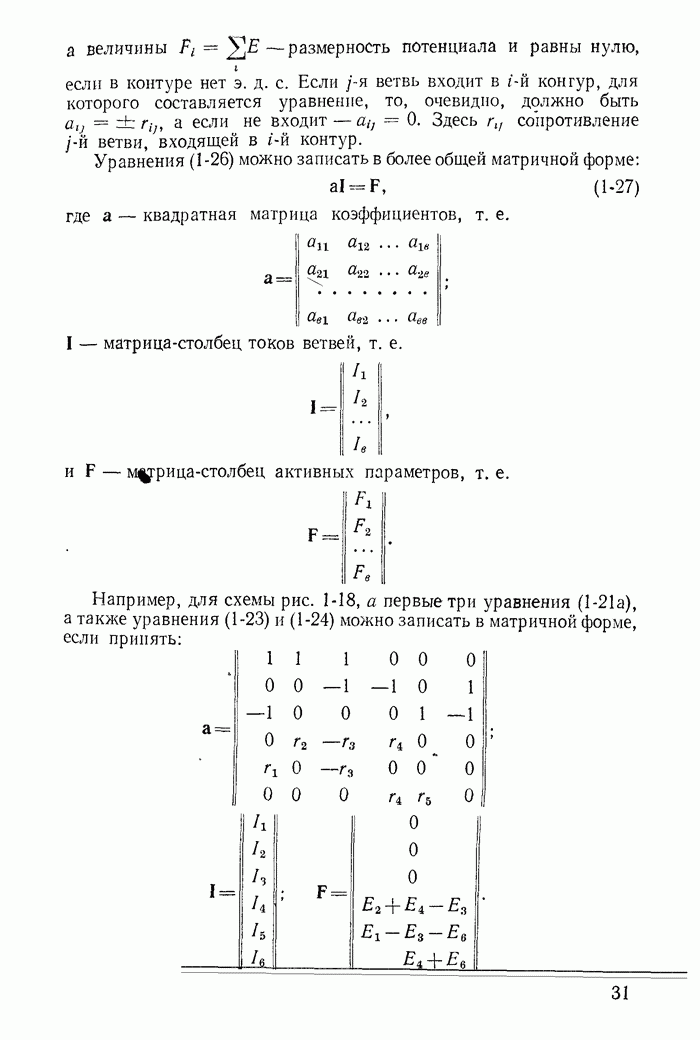
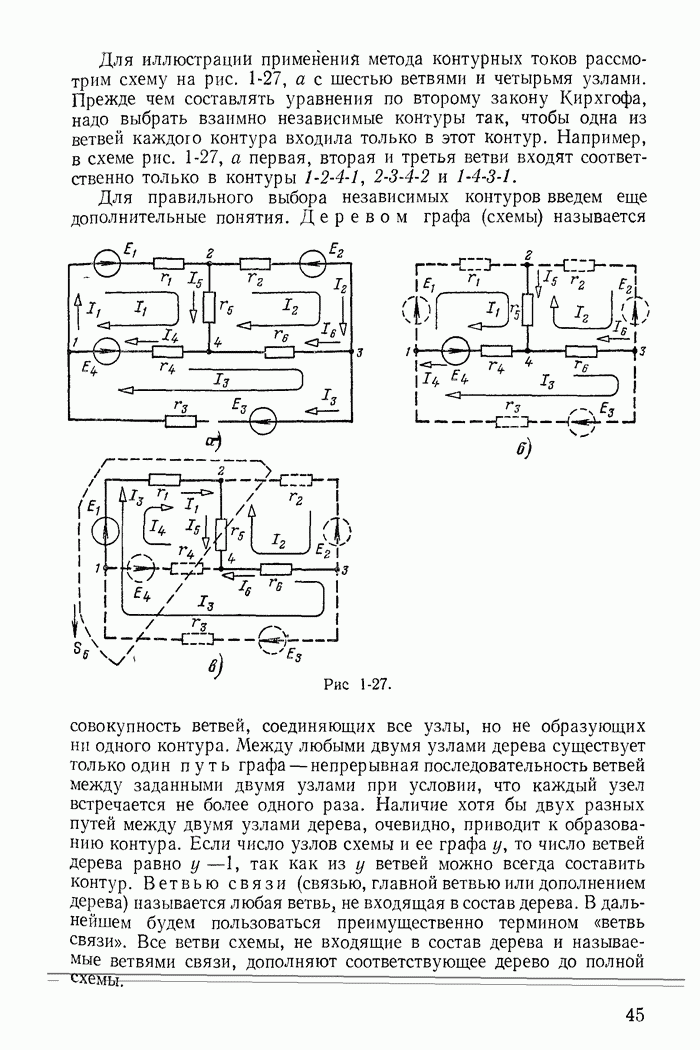
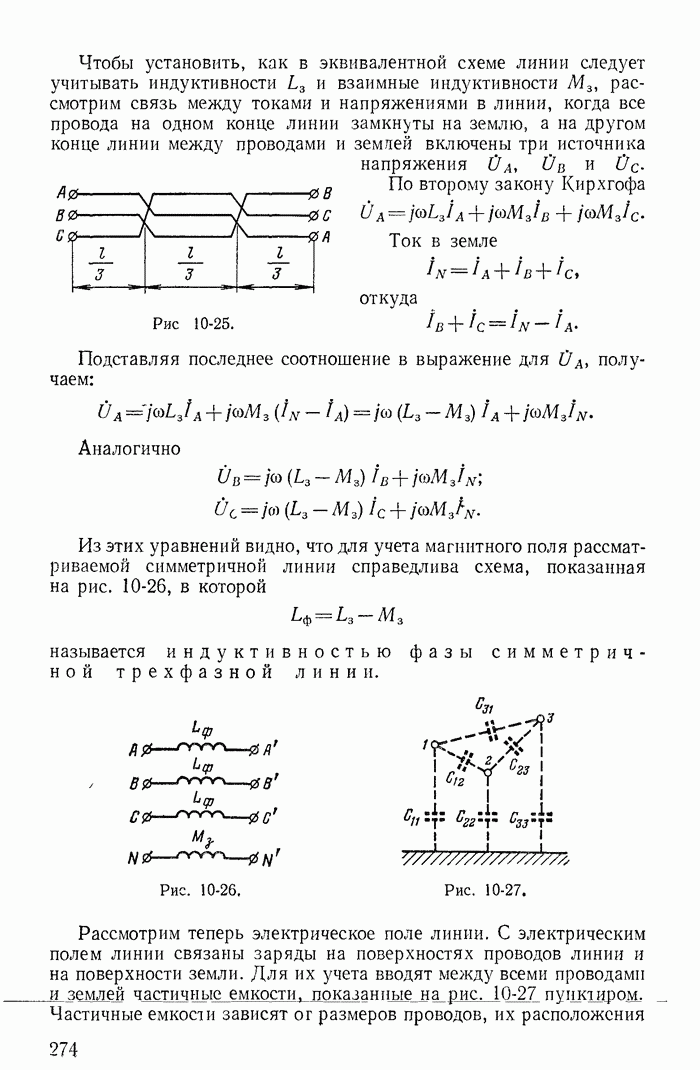
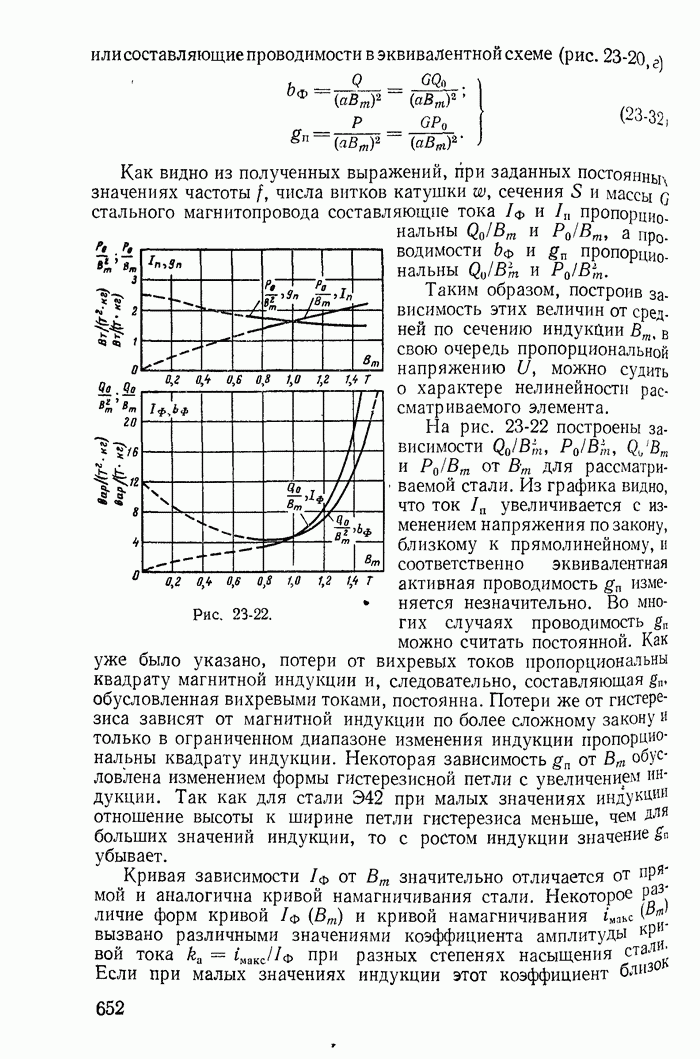
Рис. 23-22.
На рис. 23-22 построены зависимости  от
от  для рассматриваемой стали. Из графика видно, что ток
для рассматриваемой стали. Из графика видно, что ток  увеличивается с изменением напряжения по закону, близкому к прямолинейному, и соответственно эквивалентная активная проводимость
увеличивается с изменением напряжения по закону, близкому к прямолинейному, и соответственно эквивалентная активная проводимость  изменяется незначительно. Во многих случаях проводимость
изменяется незначительно. Во многих случаях проводимость  можно считать постоянной. Как уже было указано, потери от вихревых токов пропорциональны квадрату магнитной индукции и, следовательно, составляющая
можно считать постоянной. Как уже было указано, потери от вихревых токов пропорциональны квадрату магнитной индукции и, следовательно, составляющая  обусловленная вихревыми токами, постоянна. Потери же от гистерезиса зависят от магнитной индукции по более сложному закону и только в ограниченном диапазоне изменения индукции пропорциональны квадрату индукции. Некоторая зависимость
обусловленная вихревыми токами, постоянна. Потери же от гистерезиса зависят от магнитной индукции по более сложному закону и только в ограниченном диапазоне изменения индукции пропорциональны квадрату индукции. Некоторая зависимость  от
от  обусловлена изменением формы гистерезисной петли с увеличением индукции. Так как для стали
обусловлена изменением формы гистерезисной петли с увеличением индукции. Так как для стали  при малых значениях индукции отношение высоты к ширине петли гистерезиса меньше, чем для больших значений индукции, то с ростом индукции значение
при малых значениях индукции отношение высоты к ширине петли гистерезиса меньше, чем для больших значений индукции, то с ростом индукции значение  убывает.
убывает.
Кривая зависимости  от
от  значительно отличается от прямой и аналогична кривой намагничивания стали. Некоторое различие форм кривой
значительно отличается от прямой и аналогична кривой намагничивания стали. Некоторое различие форм кривой  и кривой намагничивания
и кривой намагничивания  вызвано различными значениями коэффициента амплитуды кривой тока
вызвано различными значениями коэффициента амплитуды кривой тока  при разных степенях насыщения стали. Если при малых значениях индукции этот коэффициент близок
при разных степенях насыщения стали. Если при малых значениях индукции этот коэффициент близок
к значению, характеризующему синусоиду  то при насыщении стали он сначала увеличивав к
то при насыщении стали он сначала увеличивав к  до двух и даже несколько выше, а при сильном насыщении может несколько синзиться. Поскольку зависимость
до двух и даже несколько выше, а при сильном насыщении может несколько синзиться. Поскольку зависимость  нелинейна, то проводимость
нелинейна, то проводимость  значительно изменяется с изменением напряжения U. Таким образом, при расчете катушек и трансформаторов со стальными магнитопроводами необходимо считаться с нелинейностью реактивной проводимости в схемах замещения (рис. 23-20, г).
значительно изменяется с изменением напряжения U. Таким образом, при расчете катушек и трансформаторов со стальными магнитопроводами необходимо считаться с нелинейностью реактивной проводимости в схемах замещения (рис. 23-20, г).
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ К ЧЕТВЕРТОМУ ИЗДАНИЮ
- ВВЕДЕНИЕ
- Раздел первый. ЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ С СОСРЕДОТОЧЕННЫМИ ПАРАМЕТРАМИ
- 1-1. Элементы электрических цепей и электрических схем
- 1-2. Эквивалентные схемы для источников энергии
- 1-3. Закон Ома для участка цепи с э. д. с.
- 1-4. Распределение потенциала вдоль неразветвленной электрической цепи
- 1-5. Баланс мощностей для простейшей неразветвленной цепи
- 1-6. Применение законов Кирхгофа для расчета разветвленных цепей
- 1-7. Метод узловых потенциалов
- 1-8. Метод контурных токов
- 1-9. Уравнения состояния цепи в матричной форме
- 1-10. Преобразование линейных электрических схем
- Глава вторая. ОСНОВНЫЕ СВОЙСТВА ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ПРИ ПОСТОЯННЫХ ТОКАХ И НАПРЯЖЕНИЯХ
- 2-2. Свойство взаимности
- 2-3. Входные и взаимные проводимости и сопротивления ветвей; коэффициенты передачи напряжений и токов
- 2-4. Применение топологических методов для расчета цепей
- 2-5. Топологические формулы и правила для определения передачи электрической цепи
- 2-6. Теорема о компенсации
- 2-7. Линейные соотношения между напряжениями и токами
- 2-8. Теорема о взаимных приращениях токов и напряжений
- 2-9. Общие замечания о двухполюсниках
- 2-10. Теорема об активном двухполюснике и ее применение для расчета разветвленных цепей
- 2-11. Передача энергии от активного двухполюсника к пассивному
- Глава третья. ОСНОВНЫЕ ПОНЯТИЯ О ЦЕПЯХ СИНУСОИДАЛЬНОГО ТОКА
- 3-2. Понятие о генераторах переменного тока
- 3-3. Синусоидальный ток
- 3-4. Действующие ток, э. д. с. и напряжение
- 3-5. Изображение синусоидальных функций времени векторами и комплексными числами
- 3-6. Сложение синусоидальных функций времени
- 3-7. Электрическая цепь и ее схема
- 3-8. Ток и напряжения при последовательном соединении сопротивления, Индуктивности и емкости
- 3-9. Сопротивления
- 3-10. Разность фаз напряжения и тока
- 3-11. Напряжение и токи при параллельном соединении сопротивления, индуктивности и емкости
- 3-12. Проводимости
- 3-13. Пассивный двухполюсник
- 3-14. Мощности
- 3-15. Мощности в сопротивлении, индуктивности и емкости
- 3-16. Баланс мощностей
- 3-17. Знаки мощностей и направление передачи энергии
- 3-18. Определение параметров пассивного двухполюсника при помощи амперметра, вольтметра и ваттметра
- 3-19. Условия передачи максимальной мощности от источника энергии к приемнику
- 3-20. Понятие о поверхностном эффекте и эффекте близости
- 3-21. Параметры и эквивалентные схемы конденсаторов
- 3-22. Параметры и эквивалентные схемы индуктивных катушек и резисторов
- Глава четвертая. РАСЧЕТ ЦЕПЕЙ ПРИ СИНУСОИДАЛЬНЫХ ТОКАХ
- 4-1. О применимости методов расчета цепей постоянного тока к расчетам цепей синусоидального тока
- 4-2. Последовательное соединение приемников
- 4-3. Параллельное соединение приемников
- 4-4. Смешанное соединение приемников
- 4-5. Сложные разветвленные цепи
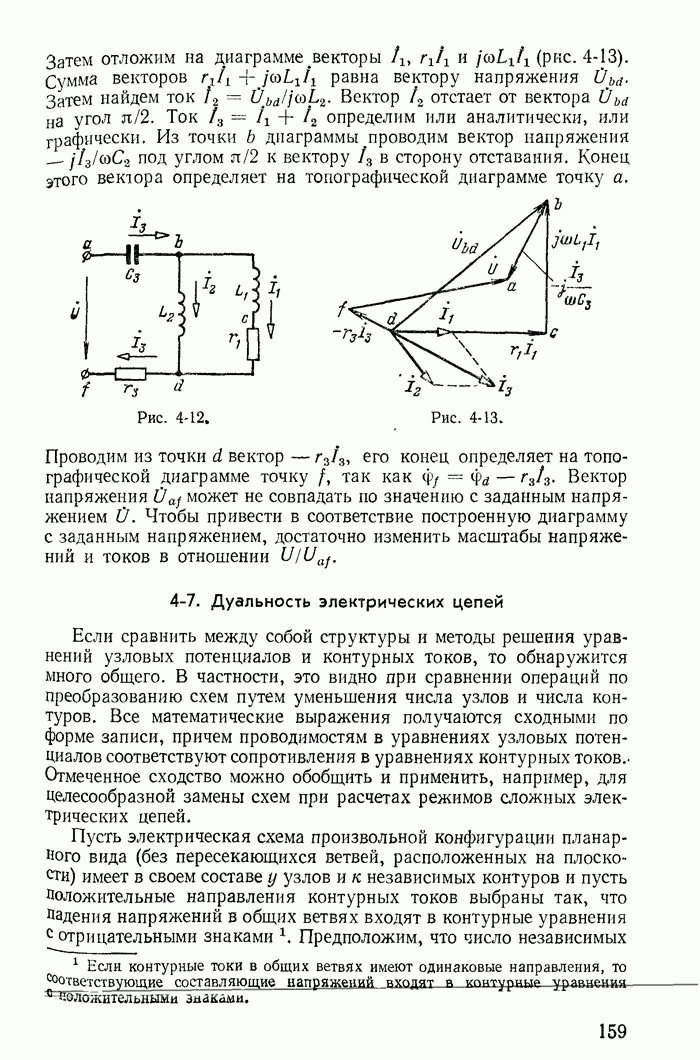
- 4-6. Топографические диаграммы
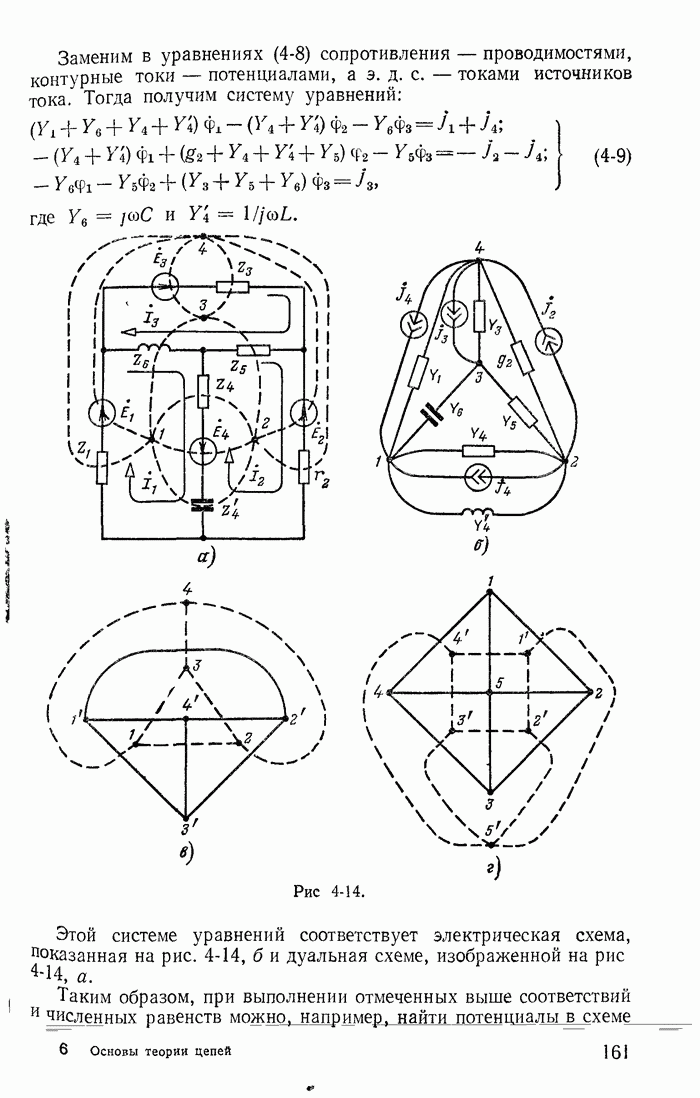
- 4-7. Дуальность электрических цепей
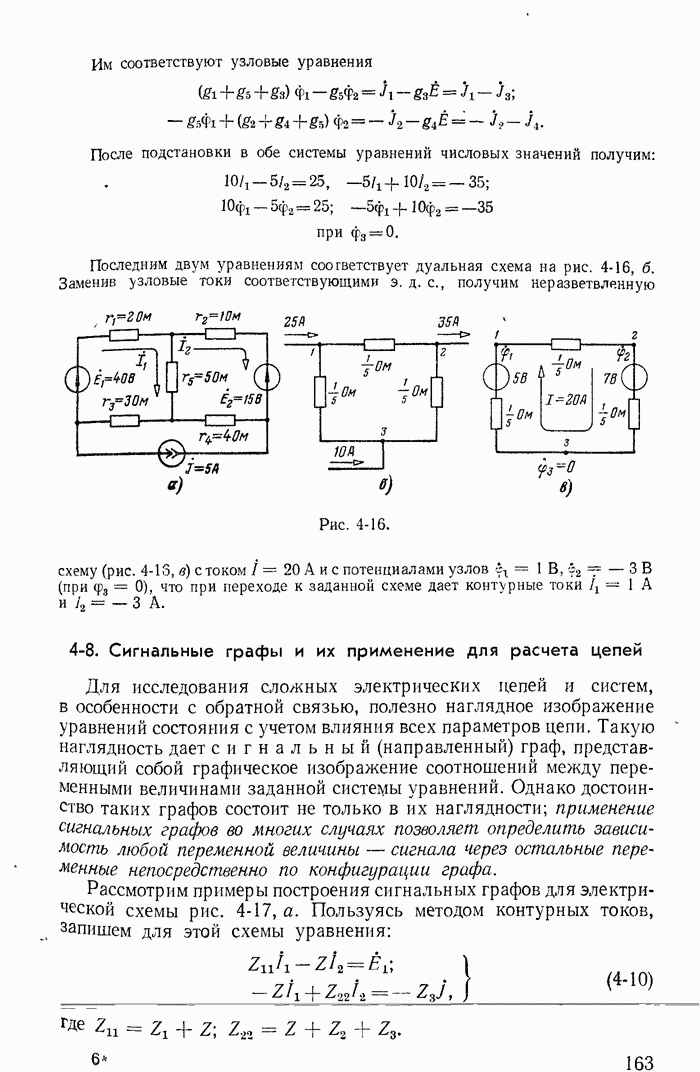
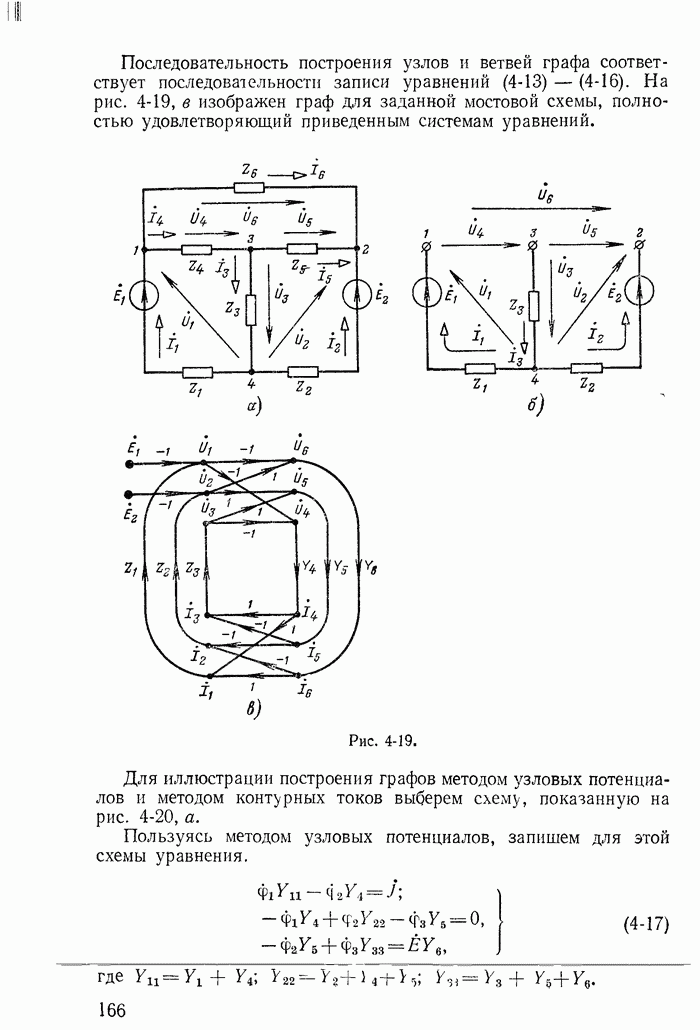
- 4-8. Сигнальные графы и их применение для расчета цепей
- Глава пятая. РЕЗОНАНС В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ
- 5-2. Частотные характеристики неразветвленной цепи
- 5-3. Резонанс в цепи с двумя параллельными ветвями
- 5-4. Частотные характеристики параллельного контура
- 5-5. Понятие о резонансе в сложных цепях
- Глава шестая. ЦЕПИ С ВЗАИМНОЙ ИНДУКТИВНОСТЬЮ
- 6-2. Электродвижущая сила взаимной индукции
- 6-3. Последовательное соединение индуктивно связанных элементов цепи
- 6-4. Параллельное соединение индуктивно связанных элементов цепи
- 6-5. Расчеты разветвленных цепей при наличии взаимной индуктивности
- 6-6. Эквивалентная замена индуктивных связей
- 6-7. Передача энергии между индуктивно связанными элементами цепи
- 6-8. Трансформатор без стального сердечника (воздушный трансформатор)
- Глава седьмая. КРУГОВЫЕ ДИАГРАММЫ
- 7-1. Комплексные уравнения прямой и окружности
- 7-2. Круговые диаграммы для неразветвленной цепи и для активного двухполюсника
- 7-3. Круговые диаграммы для любой разветвленной цепи
- Глава восьмая. МНОГОПОЛЮСНИКИ И ЧЕТЫРЕХПОЛЮСНИКИ ПРИ СИНУСОИДАЛЬНЫХ ТОКАХ И НАПРЯЖЕНИЯХ
- 8-1. Четырехполюсники и их основные уравнения
- 8-2. Определение коэффициентов четырехполюсников
- 8-3. Режим четырехполюсника при нагрузке
- 8-4. Эквивалентные схемы четырехполюсников
- 8-5. Основные уравнения и эквивалентные схемы для активного четырехполюсника
- 8-6. Идеальный трансформатор как четырехполюсник
- 8-7. Эквивалентные схемы с идеальными трансформаторами для четырехполюсника
- 8-8. Эквивалентные схемы трансформатора со стальным магнитопроводом
- 8-9. Расчеты электрических цепей с трансформаторами
- 8-10. Графы пассивных четырехполюсников и их простейшие соединения
- Глава девятая. ЦЕПИ С ЭЛЕКТРОННЫМИ И ПОЛУПРОВОДНИКОВЫМИ ПРИБОРАМИ В ЛИНЕЙНОМ РЕЖИМЕ
- 9-2. Эквивалентные схемы лампового триода
- 9-3. Транзисторы (полупроводниковые триоды)
- 9-4. Эквивалентные схемы транзисторов
- 9-5. Простейшие электрические цепи с невзаимными элементами и их направленные графы
- Глава десятая. ТРЕХФАЗНЫЕ ЦЕПИ
- 10-2. Соединения звездой и многоугольником
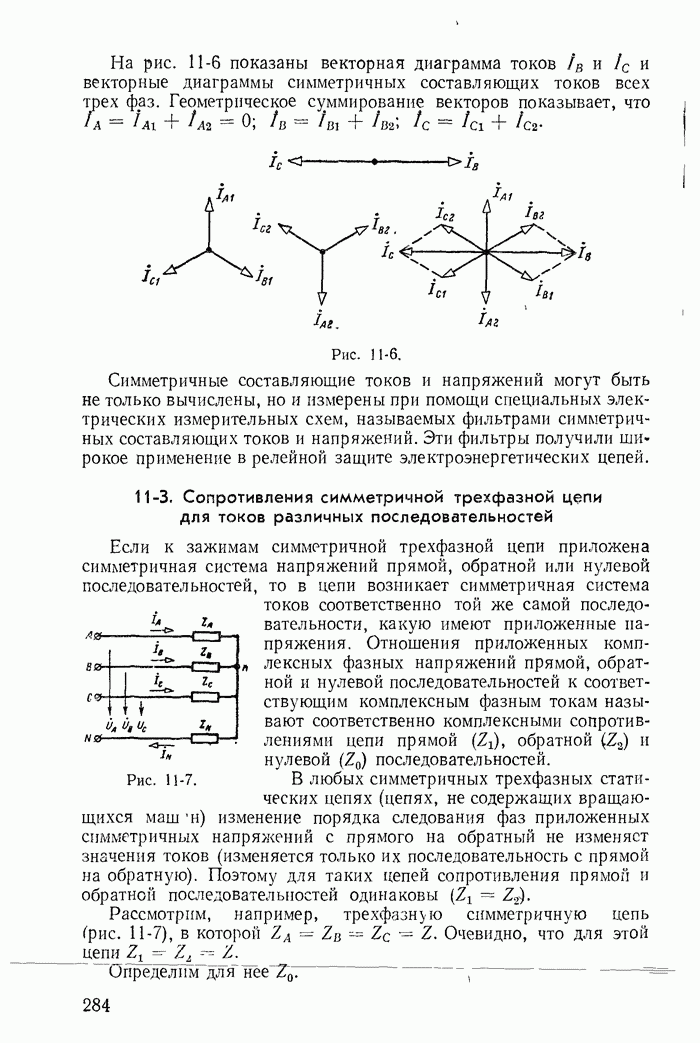
- 10-3. Симметричный режим трехфазной цепи
- 10-4. Некоторые свойства трехфазных цепей с различными схемами соединений
- 10-5. Расчет симметричных режимов трехфазных цепей
- 10-6. Расчет несимметричных режимов трехфазных цепей со статической нагрузкой
- 10-7. Напряжения на фазах приемника в некоторых частных случаях
- 10-8. Эквивалентные схемы трехфазных линий
- 10-9. Измерение мощности в трехфазных цепях
- 10-10. Вращающееся магнитное поле
- 10-11. Принципы действия асинхронного и синхронного двигателей
- Глава одиннадцатая. МЕТОД СИММЕТРИЧНЫХ СОСТАВЛЯЮЩИХ
- 11-2. Некоторые свойства трехфазных цепей в отношении симметричных составляющих токов и напряжений
- 11-3. Сопротивления симметричной трехфазной цепи для токов различных последовательностей
- 11-4. Определение токов в симметричной цепи
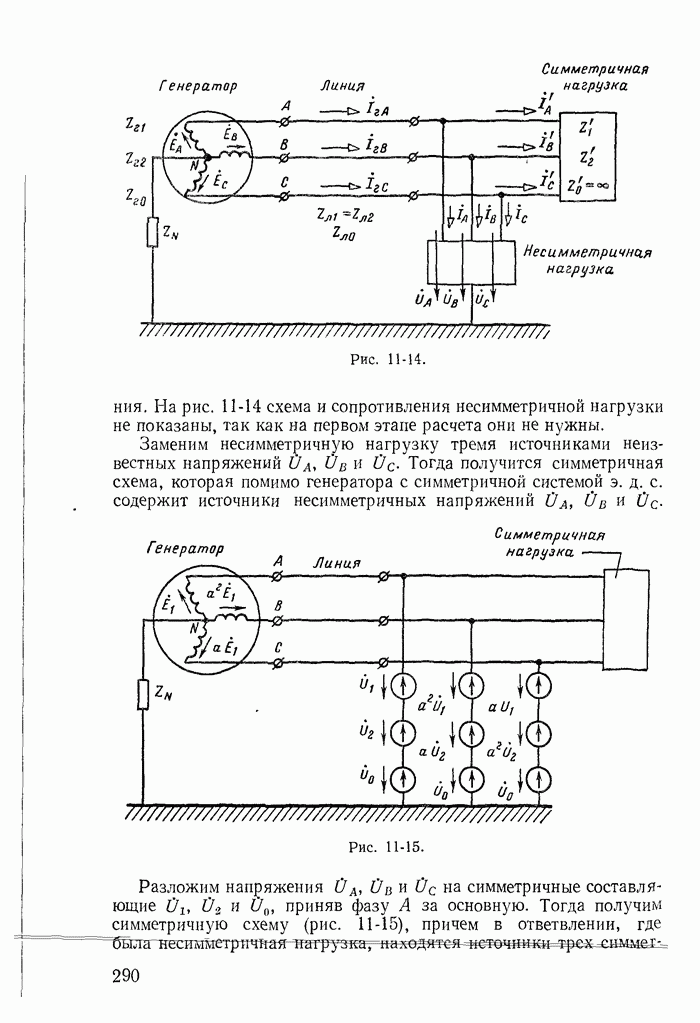
- 11-5. Симметричные составляющие напряжений и токов в несимметричной трехфазной цепи
- 11-6. Расчет цепи с несимметричной нагрузкой
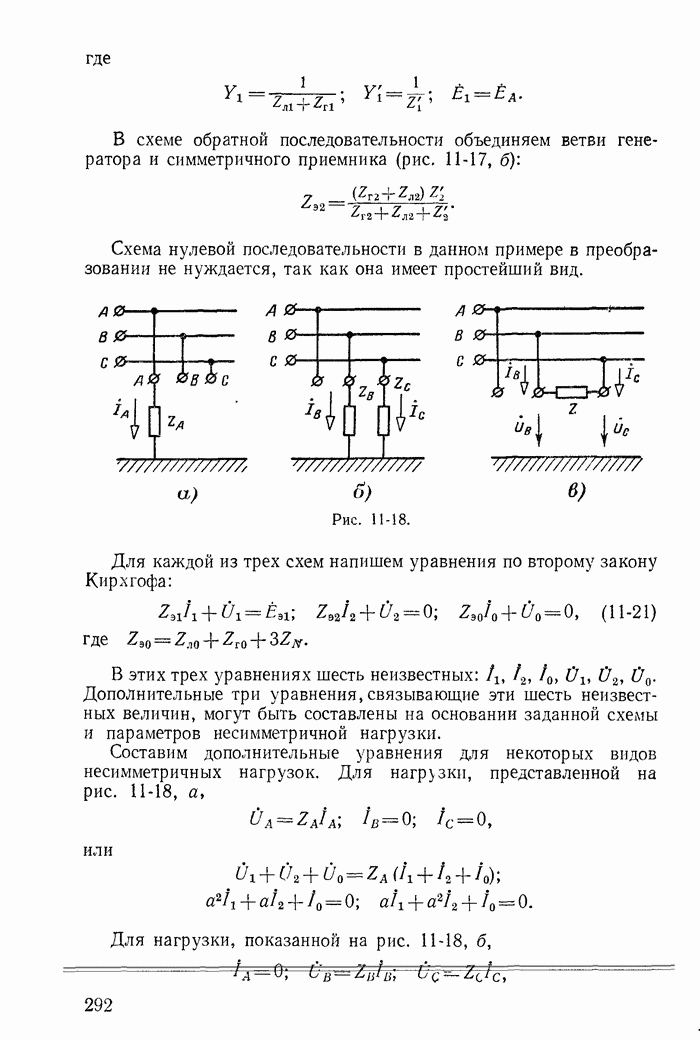
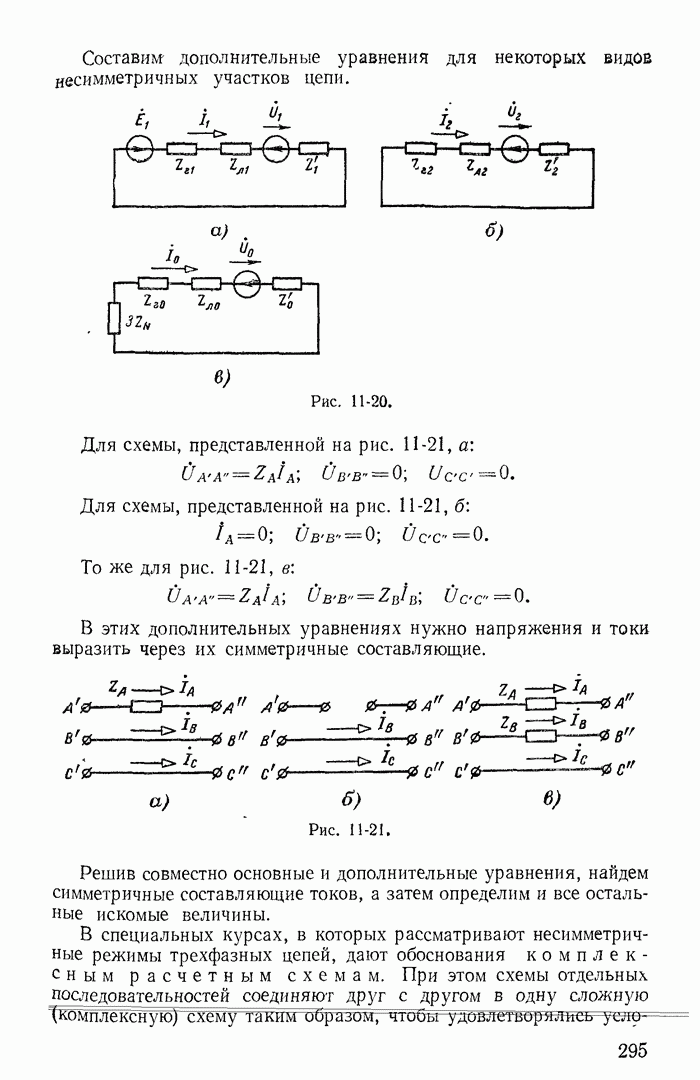
- 11-7. Расчет цепи с несимметричным участком в линии
- Глава двенадцатая. НЕСИНУСОИДАЛЬНЫЕ ТОКИ
- 12-2. Разложение периодической несинусоидальной кривой в тригонометрический ряд
- 12-3. Максимальные, действующие и средние значения несинусоидальных периодических э. д. с., напряжений и токов
- 12-4. Коэффициенты, характеризующие форму несинусоидальных периодических кривых
- 12-5. Несинусоидальные кривые с периодической огибающей
- 12-6. Действующие значения э. д. с., напряжений и токов с периодическими огибающими
- 12-7. Расчет цепей с несинусоидальными периодическими э. д. с. и токами
- 12-8. Резонанс при несинусоидальных э. д. с. и токах
- 12-9. Мощность периодических несинусоидальных токов
- 12-10. Высшие гармоники в трехфазных цепях
- Глава тринадцатая. КЛАССИЧЕСКИЙ МЕТОД РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ
- 13-2. Переходный, принужденный и свободный процессы
- 13-3. Короткое замыкание цепи r, L
- 13-4. Включение цепи r, L на постоянное напряжение
- 13-5. Включение цепи r, L на синусоидальное напряжение
- 13-6. Короткое замыкание цепи r, С
- 13-7. Включение цепи r, С на постоянное напряжение
- 13-8. Включение цепи r, С на синусоидальное напряжение
- 13-9. Переходные процессы в неразветвленной цепи r, С
- 13-10. Апериодический разряд конденсатора
- 13-11. Предельный случай апериодического разряда конденсатора
- 13-12. Периодический (колебательный) разряд конденсатора
- 13-13. Включение цепи r, С на постоянное напряжение
- 13-14. Общий случай расчета переходных процессов классическим методом
- 13-15. Включение пассивного двухполюсника на непрерывно изменяющееся напряжение (формула или интеграл Дюамеля)
- 13-16. Включение пассивного двухполюсника на напряжение любой формы
- 13-17. Временная и импульсная переходные характеристики
- 13-18. Запись теоремы свертки при помощи импульсной переходной характеристики
- 13-19. Переходные процессы при скачках токов в индуктивностях и напряжений на конденсаторах
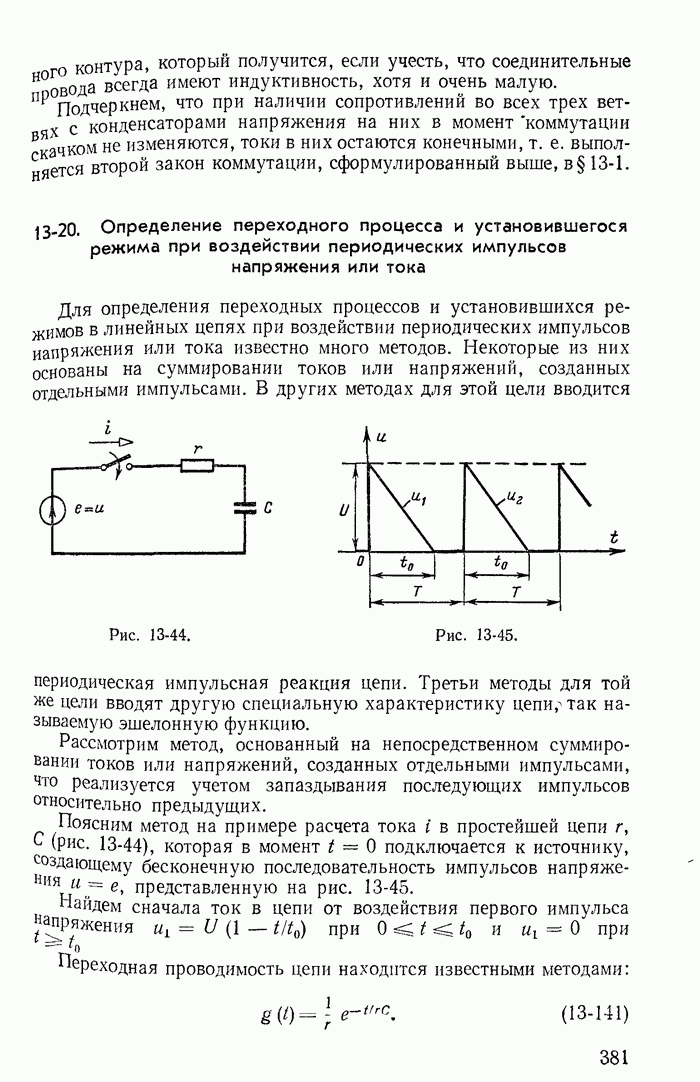
- 13-20. Определение переходного процесса и установившегося режима при воздействии периодических импульсов напряжения или тока
- Глава четырнадцатая. ОПЕРАТОРНЫЙ МЕТОД РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ
- 14-2. Законы Ома и Кирхгофа в операторной форме
- 14-3. Эквивалентные операторные схемы
- 14-4. Переходные процессы в цепях с взаимной индуктивностью
- 14-5. Сведение расчетов переходных процессов к нулевым начальным условиям
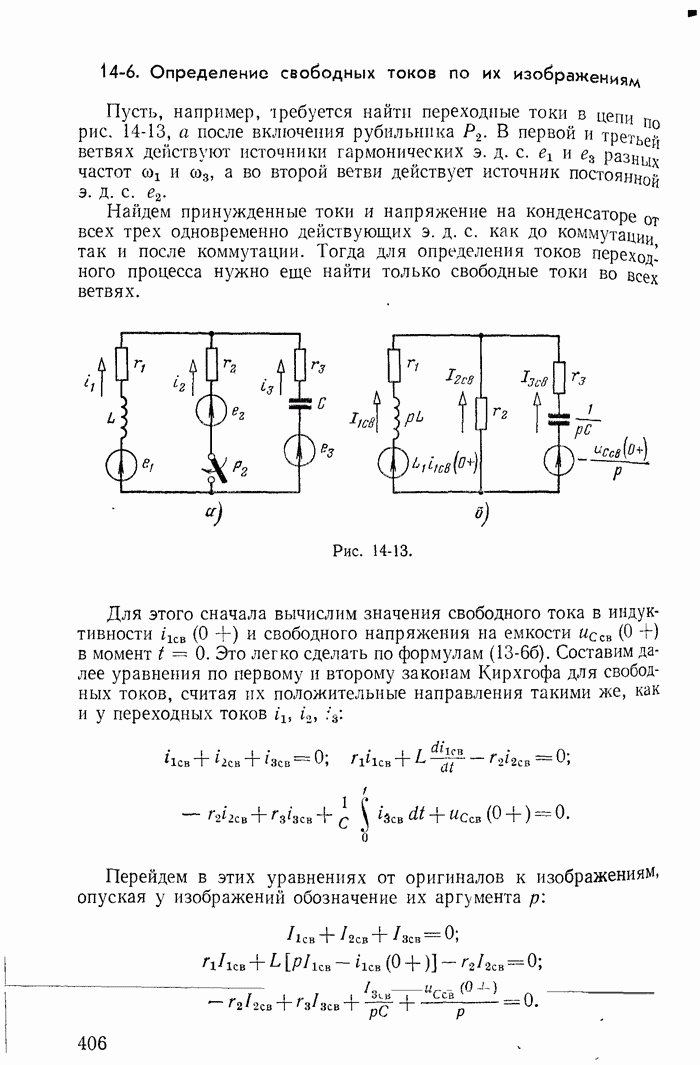
- 14-6. Определение свободных токов по их изображениям
- 14-7. Формулы включения
- 14-8. Расчет переходных процессов методом переменных состояния
- 14-9. Определение принужденного режима цепи при воздействии на нее периодического несинусоидального напряжения
- Глава пятнадцатая. ЧАСТОТНЫЙ МЕТОД РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ
- 15-2. Законы Ома и Кирхгофа и эквивалентные схемы для частотных спектров
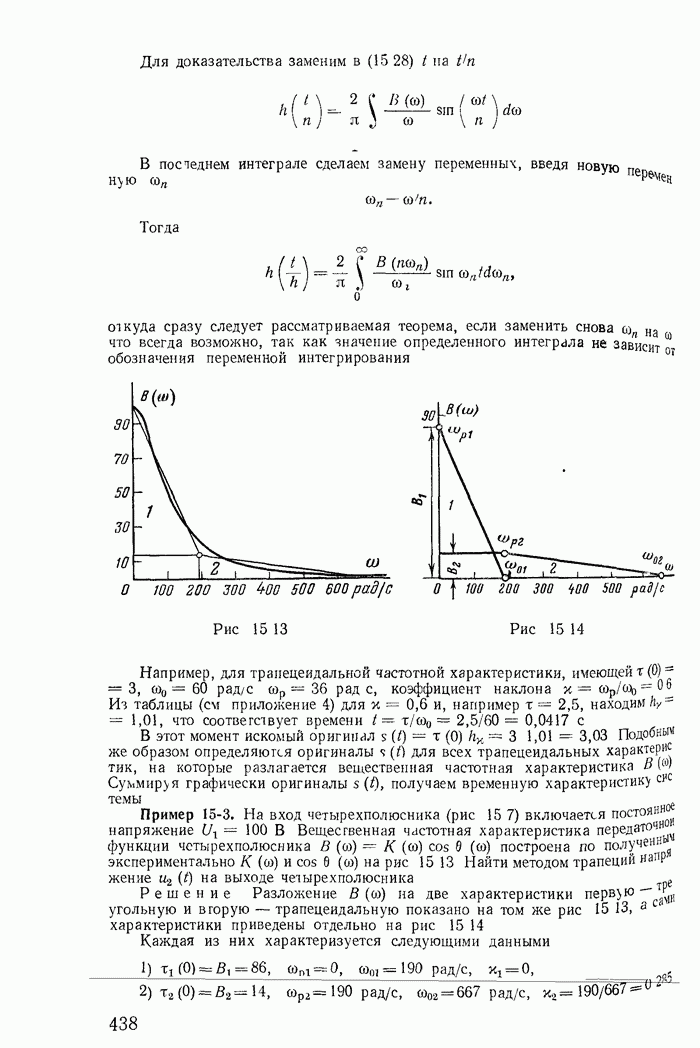
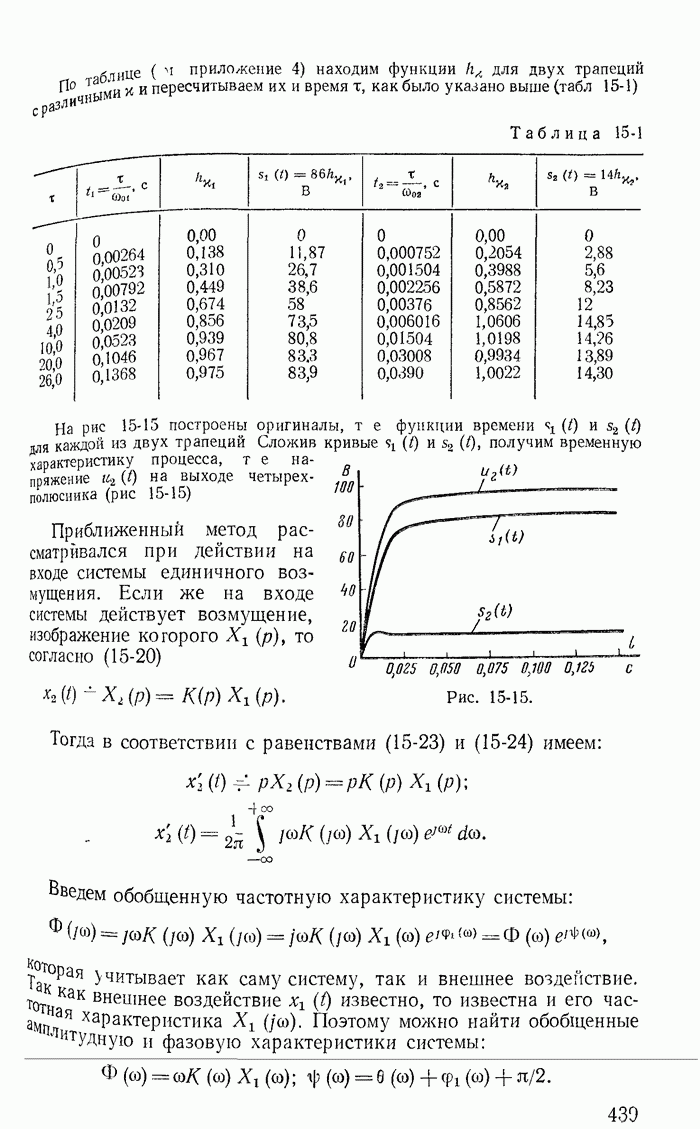
- 15-3. Приближенный метод определения оригинала по вещественной частотной характеристике (метод трапеций)
- 15-4. О переходе от преобразований Фурье к преобразованиям Лапласа
- 15-5. Сравнение различных методов расчета переходных процессов в линейных электрических цепях
- Глава шестнадцатая. ЦЕПНЫЕ СХЕМЫ И ЧАСТОТНЫЕ ЭЛЕКТРИЧЕСКИЕ ФИЛЬТРЫ
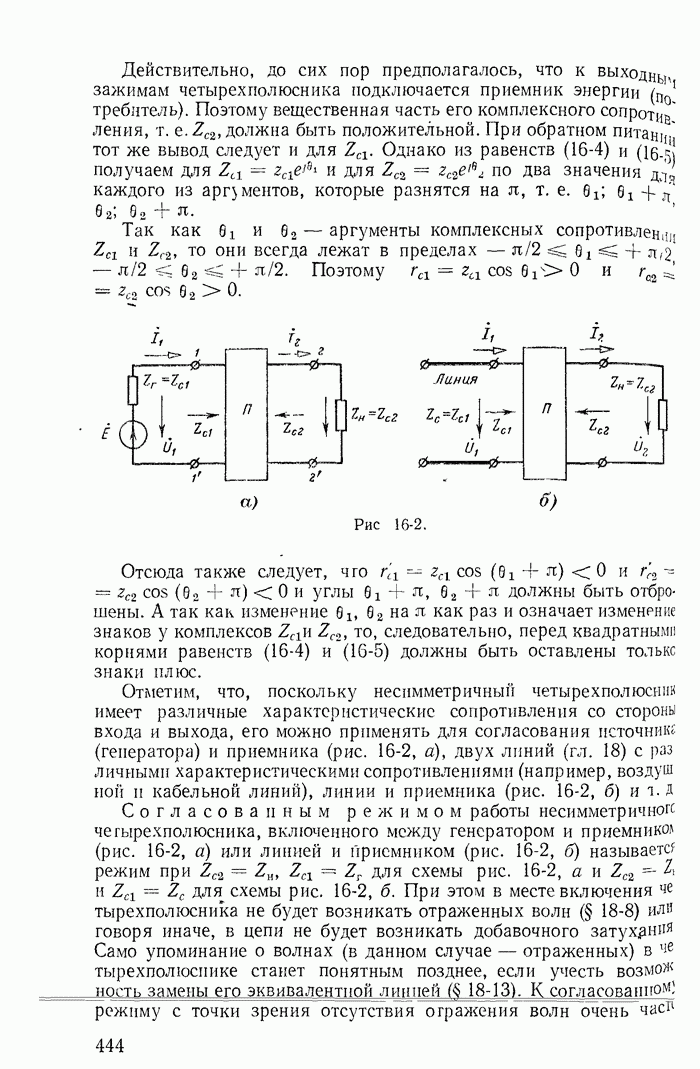
- 16-2. Характеристическое сопротивление и постоянная передачи симметричного четырехполюсника
- 16-3. Вносимая и рабочая постоянные передачи
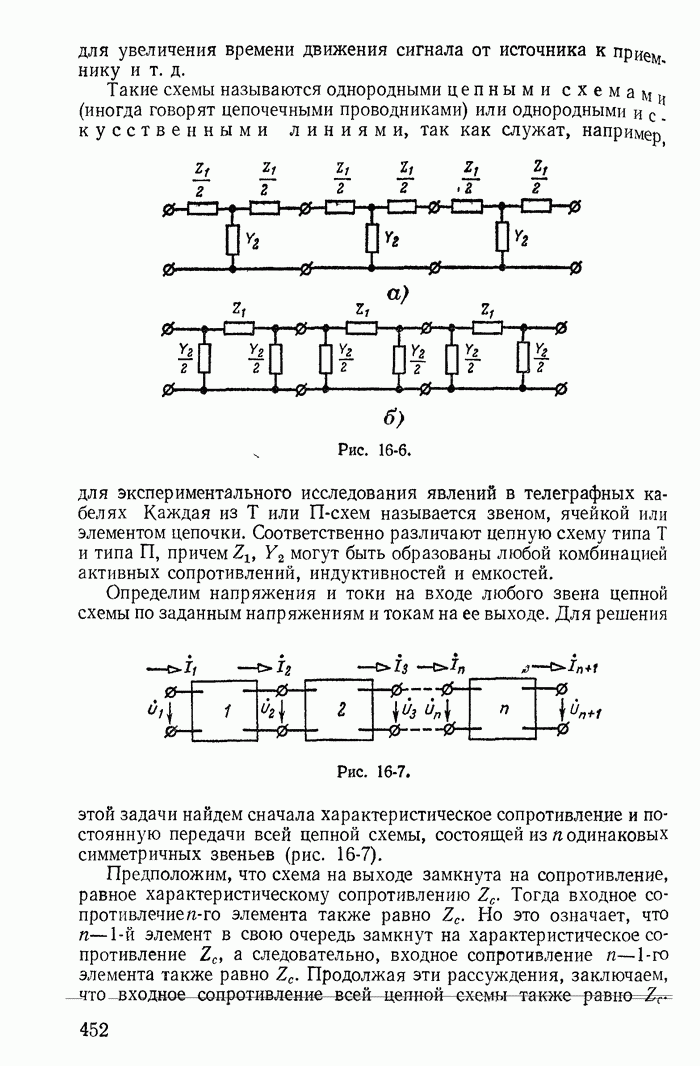
- 16-4. Цепные схемы
- 16-5. Частотные электрические фильтры
- 16-6. Низкочастотные фильтры
- 16-8. Полосные фильтры
- 16-11. Г-образный фильтр как пример несимметричного фильтра
- 16-12. Безындукционные (или r, C) фильтры
- Глава семнадцатая. СИНТЕЗ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
- 17-2. Передаточная функция четырехполюсника. Цепи минимальной фазы
- 17-3. Входные функции цепей. Положительные вещественные функции
- 17-4. Реактивные двухполюсники
- 17-5. Частотные характеристики реактивных двухполюсников
- 17-6. Синтез реактивных двухполюсников. Метод Фостера
- 17-7. Синтез реактивных двухполюсников. Метод Кауэра
- 17-8. Синтез двухполюсников с потерями. Метод Фостера
- 17-9. Синтез двухполюсников с потерями. Метод Кауэра
- 17-10. Понятие о синтезе четырехполюсников
- Раздел второй. ЛИНЕЙНЫЕ ЦЕПИ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
- Глава восемнадцатая. ГАРМОНИЧЕСКИЕ ПРОЦЕССЫ В ЦЕПЯХ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
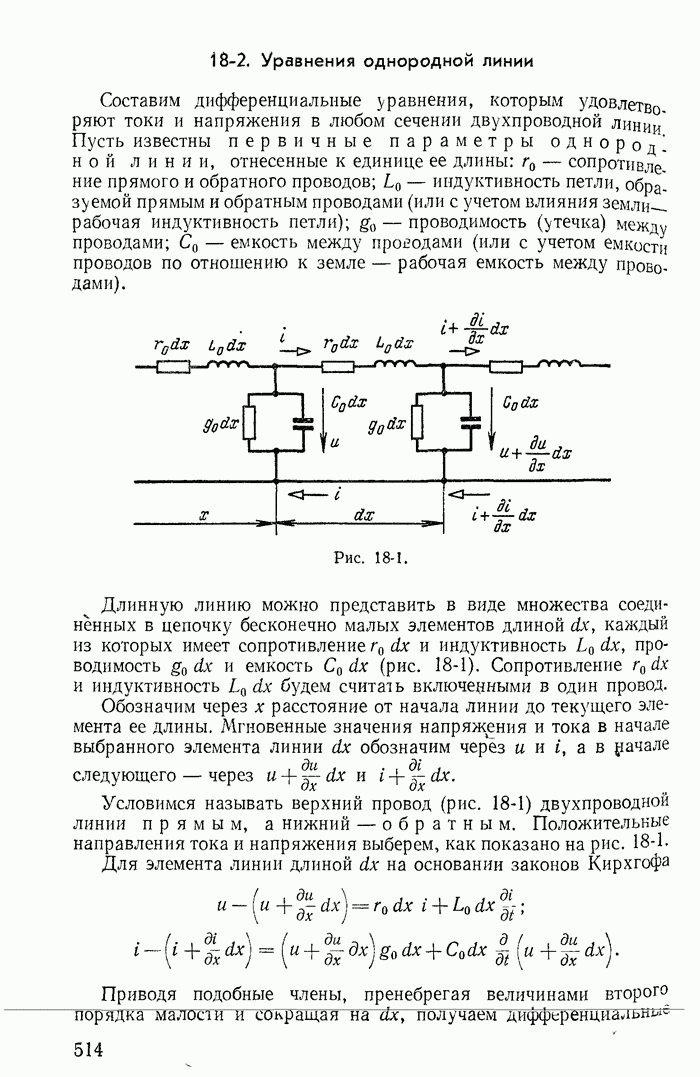
- 18-2. Уравнения однородной линии
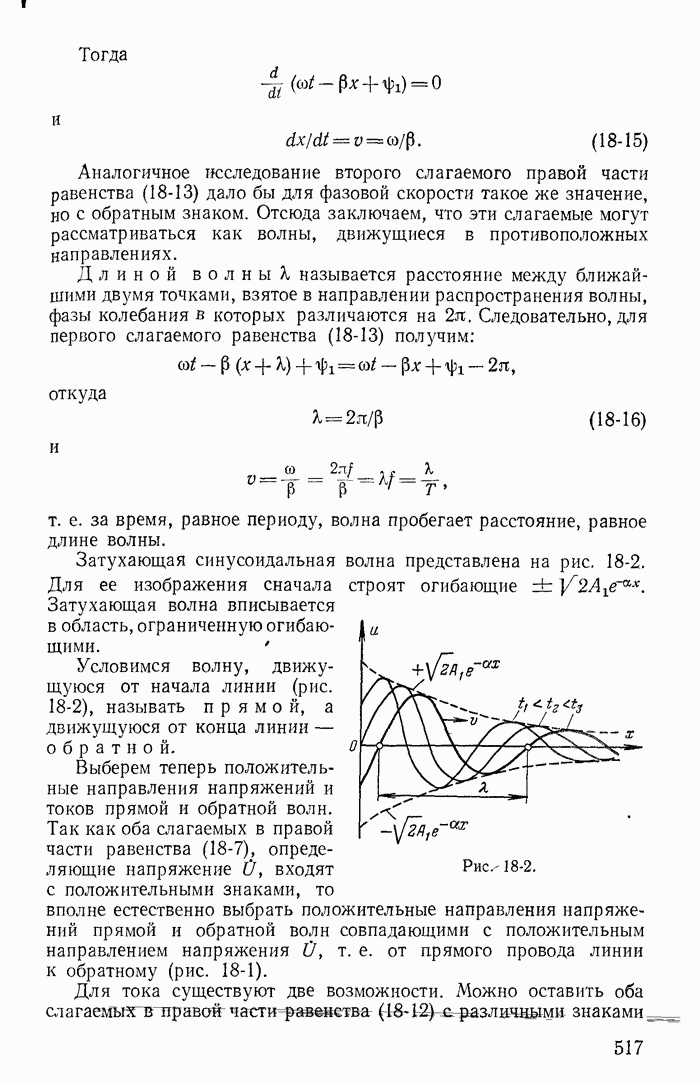
- 18-3. Установившийся режим в однородной линии
- 18-4. Уравнения однородной линии с гиперболическими функциями
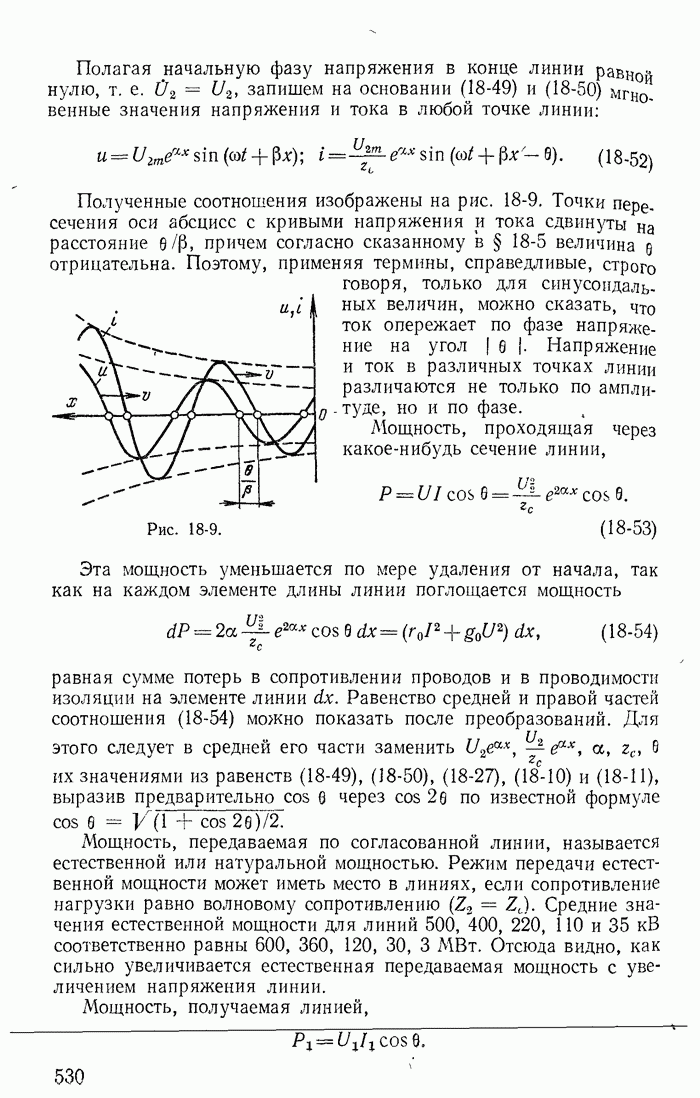
- 18-5. Характеристики однородной линии
- 18-6. Входное сопротивление линии
- 18-7. Коэффициент отражения волны
- 18-8. Согласованная нагрузка линии
- 18-9. Линия без искажений
- 18-10. Холостой ход, короткое замыкание и нагрузочный режим линии с потерями
- 18-11. Линии без потерь
- 18-12. Стоячие волны
- 18-13. Линия как четырехполюсник
- Глава девятнадцатая. ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЦЕПЯХ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
- 19-2. Общее решение уравнений однородной линии
- 19-3. Возникновение волн с прямоугольным фронтом
- 19-4. Общие случаи нахождения волн, возникающих при переключениях
- 19-5. Отражение волны с прямоугольным фронтом от конца линии
- 19-6. Общий метод определения отраженных волн
- 19-7. Качественное рассмотрение переходных процессов в линиях, содержащих сосредоточенные емкости и индуктивности
- 19-8. Многократные отражения волн с прямоугольным фронтом от активного сопротивления
- 19-9. Блуждающие волны
- Раздел III. НЕЛИНЕЙНЫЕ ЦЕПИ
- Глава двадцатая. НЕЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПРИ ПОСТОЯННЫХ ТОКАХ И НАПРЯЖЕНИЯХ
- 20-2. Графический метод расчета неразветвленных цепей с нелинейными элементами
- 20-3. Графический метод расчета цепей с параллельным соединением нелинейных элементов
- 20-4. Графический метод расчета цепей со смешанным соединением нелинейных и линейных элементов
- 20-5. Применение эквивалентных схем с источниками э. д. с. для исследования режима нелинейных цепей
- 20-6. Вольт-амперные характеристики нелинейных активных двухполюсников
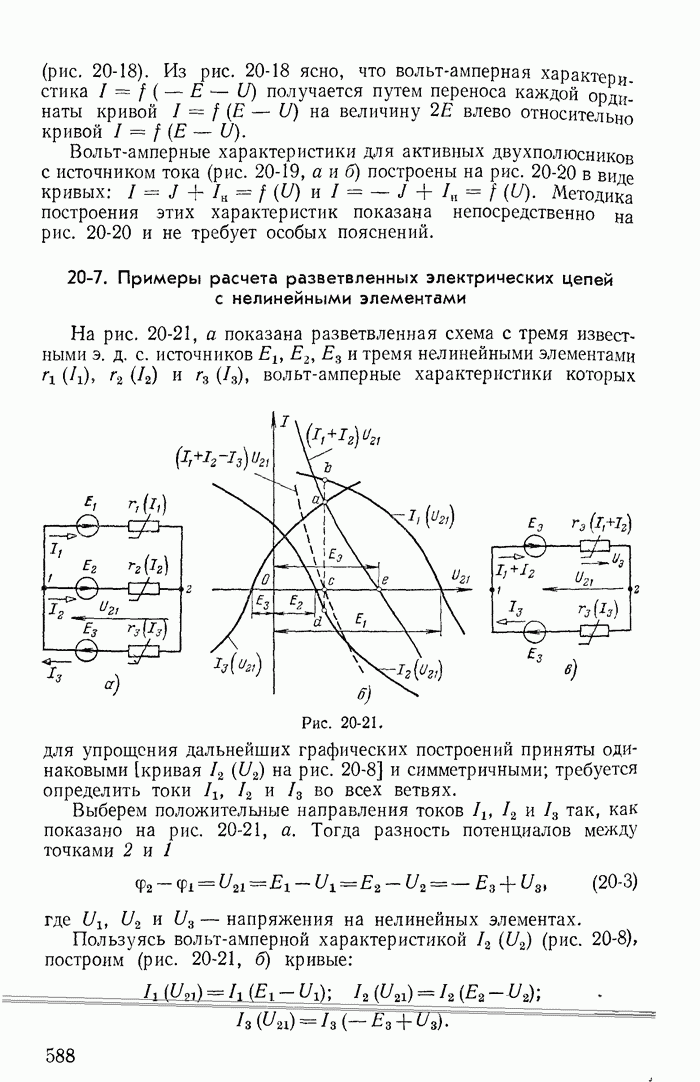
- 20-7. Примеры расчета разветвленных электрических цепей с нелинейными элементами
- 20-8. Применение теории активных двухполюсника, четырехполюсника и шестиполюсника для расчета цепей с линейными и нелинейными элементами
- 20-9. Расчет разветвленных нелинейных цепей итерационным методом (методом последовательных приближений)
- Глава двадцать первая. МАГНИТНЫЕ ЦЕПИ ПРИ ПОСТОЯННЫХ ТОКАХ
- 21-2. Расчет неразветвленных магнитных цепей
- 21-3. Расчет разветвленных магнитных цепей
- 21-4. Расчет магнитной цепи кольцевого постоянного магнита с воздушным зазором
- 21-5. Расчет неразветвленной неоднородной магнитной цепи с постоянным магнитом
- Глава двадцать вторая. ОБЩАЯ ХАРАКТЕРИСТИКА НЕЛИНЕЙНЫХ ЦЕПЕЙ ПЕРЕМЕННОГО ТОКА И МЕТОДОВ ИХ РАСЧЕТА
- 22-1. Нелинейные двухполюсники и четырехполюсники при переменных токах
- 22-2. Определение рабочих точек на характеристиках нелинейных двухполюсников и четырехполюсников
- 22-3. Явления в нелинейных цепях переменного тока
- 22-4. Методы расчета нелинейных цепей переменного тока
- Глава двадцать третья. НЕЛИНЕЙНЫЕ ЦЕПИ С ИСТОЧНИКАМИ Э. Д. С. И ТОКА ОДИНАКОВОЙ ЧАСТОТЫ
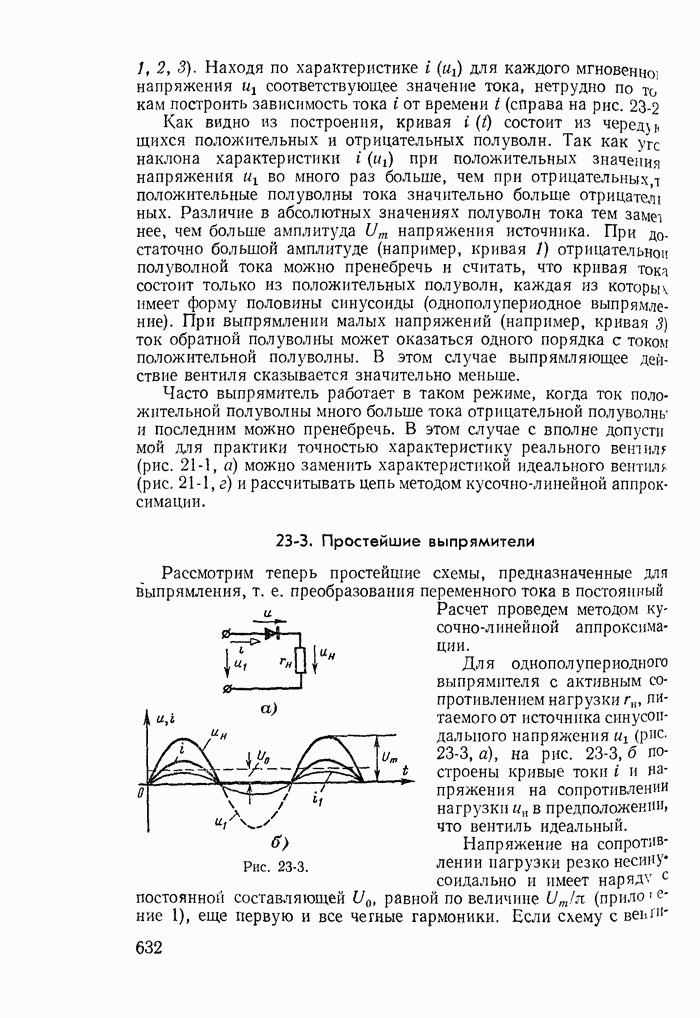
- 23-2. Форма кривой тока в цепи с вентилями
- 23-3. Простейшие выпрямители
- 23-4. Формы кривых тока и напряжения в цепях с нелинейными реактивными сопротивлениями
- 23-5. Утроители частоты
- 23-6. Формы кривых тока и напряжения в цепях с терморезисторами
- 23-7. Замена реальных нелинейных элементов условно-нелинейными
- 23-8. Учет реальных свойств стальных магнитопроводов
- 23-9. Расчет тока в катушке со стальным магнитопроводом
- 23-10. Понятие о расчете условно-нелинейных магнитных цепей
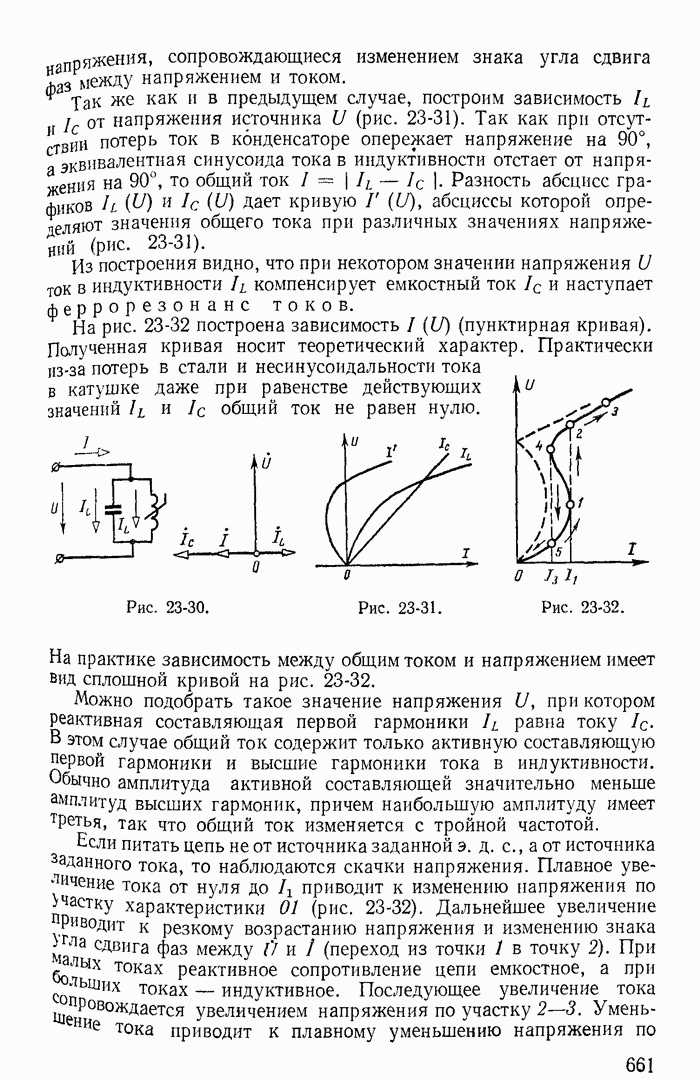
- 23-11. Явление феррорезонанса
- 23-12. Стабилизаторы напряжения
- Глава двадцать четвертая. НЕЛИНЕЙНЫЕ ЦЕПИ С ИСТОЧНИКАМИ Э. Д. С. И ТОКА РАЗЛИЧНЫХ ЧАСТОТ
- 24-1. Общая характеристика нелинейных цепей с источниками э. д. с. различных частот
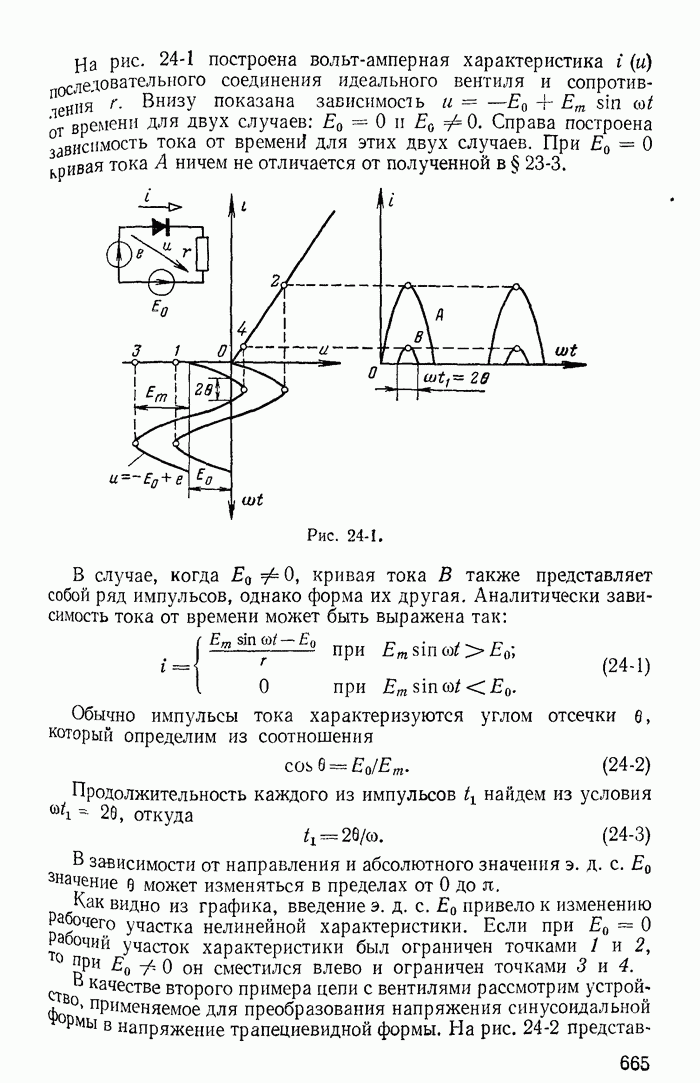
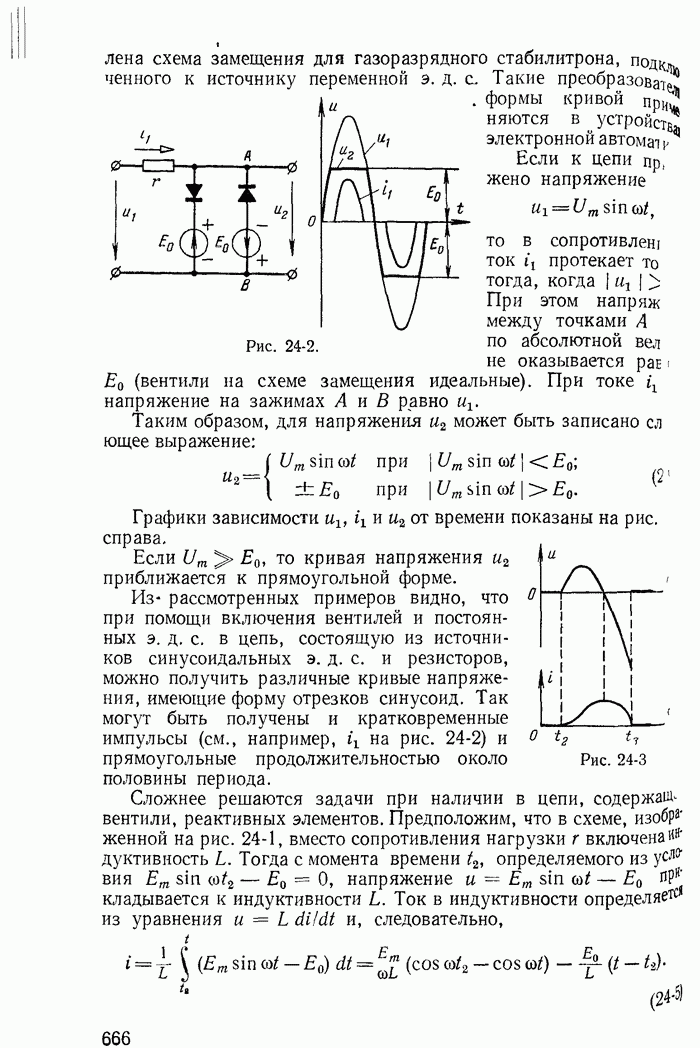
- 24-2. Вентили в цепях с постоянными и переменными э. д. с.
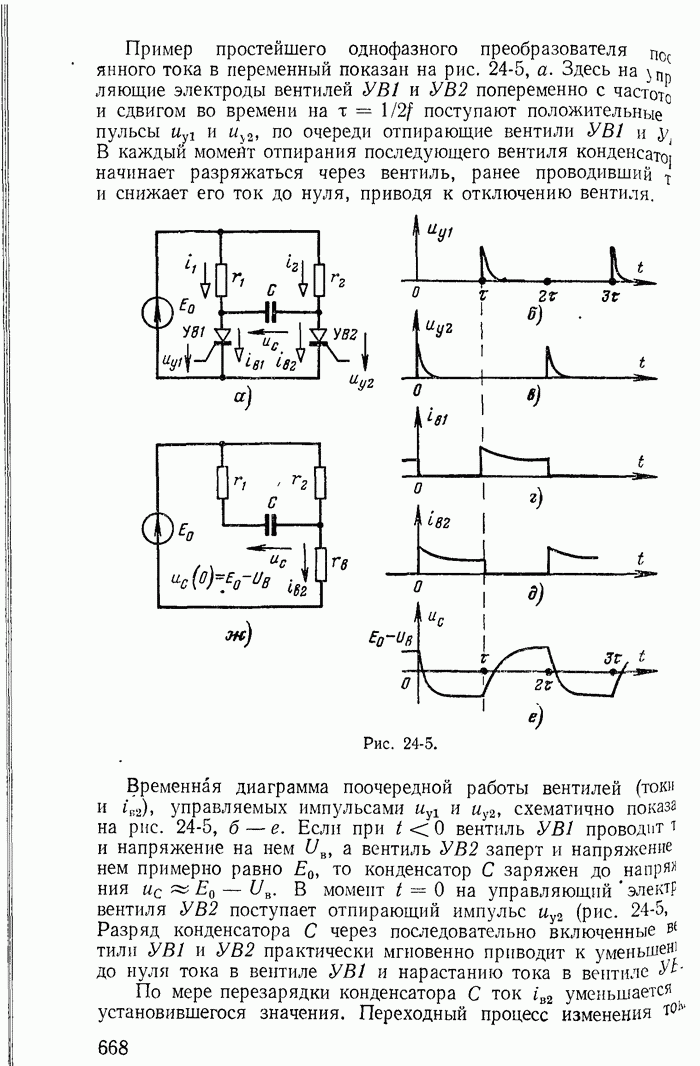
- 24-3. Управляемые вентили в простейших выпрямителях и преобразователях постоянного тока в переменный
- 24-4. Катушки со стальными магнитопроводами в цепях с постоянными и переменными э. д. с.
- 24-5. Удвоитель частоты
- 24-6. Метод гармонического баланса
- 24-7. Влияние постоянной э. д. с. на переменную составляющую тока в цепях с нелинейными безынерционными сопротивлениядли
- 24-8. Принцип получения модулированных колебаний
- 24-9. Влияние постоянной составляющей на переменную в цепях с нелинейными индуктивностями
- 24-10. Магнитные усилители мощности
- Глава двадцать пятая. ПЕРЕХОДНЫЕ ПРОЦЕССЫ В НЕЛИНЕЙНЫХ ЦЕПЯХ
- 25-2. Включение катушки со стальным магнитопроводом на постоянное напряжение
- 25-3. Включение катушки со стальным магнитопроводом на синусоидальное напряжение
- 25-4. Импульсное воздействие в цепях с неоднозначными нелинейностями
- 25-5. Понятие о простейших запоминающих устройствах
- 25-6. Изображение переходных процессов на фазовой плоскости
- 25-7. Колебательный разряд емкости через нелинейную индуктивность
- Глава двадцать шестая. АВТОКОЛЕБАНИЯ
- 26-1. Нелинейные резисторы со спадающим участком характеристики
- 26-2. Понятие об устойчивости режима в цепи с нелинейными резисторами
- 26-3. Релаксационные колебания в цепи с отрицательным сопротивлением
- 26-4. Близкие к синусоидальным колебания в цепи с отрицательным сопротивлением
- 26-5. Фазовые траектории процессов в цепи с отрицательным сопротивлением
- 26-6. Фазовые траектории процессов в генераторе синусоидальных колебаний
- 26-7. Определение амплитуды автоколебаний методом гармонического баланса
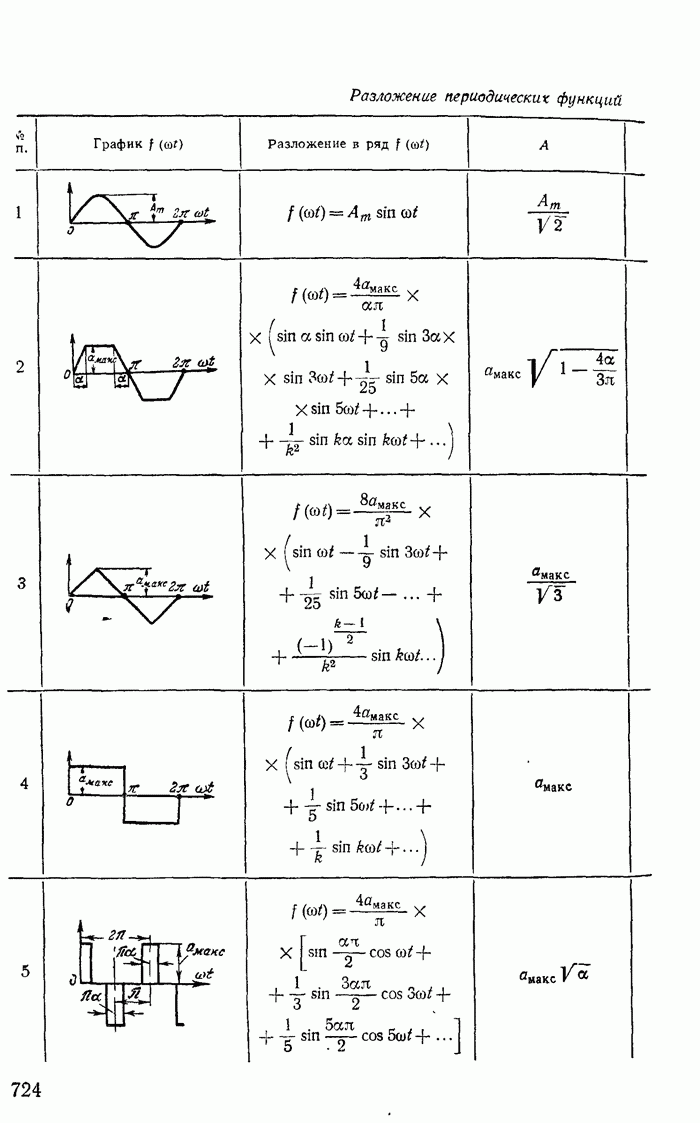
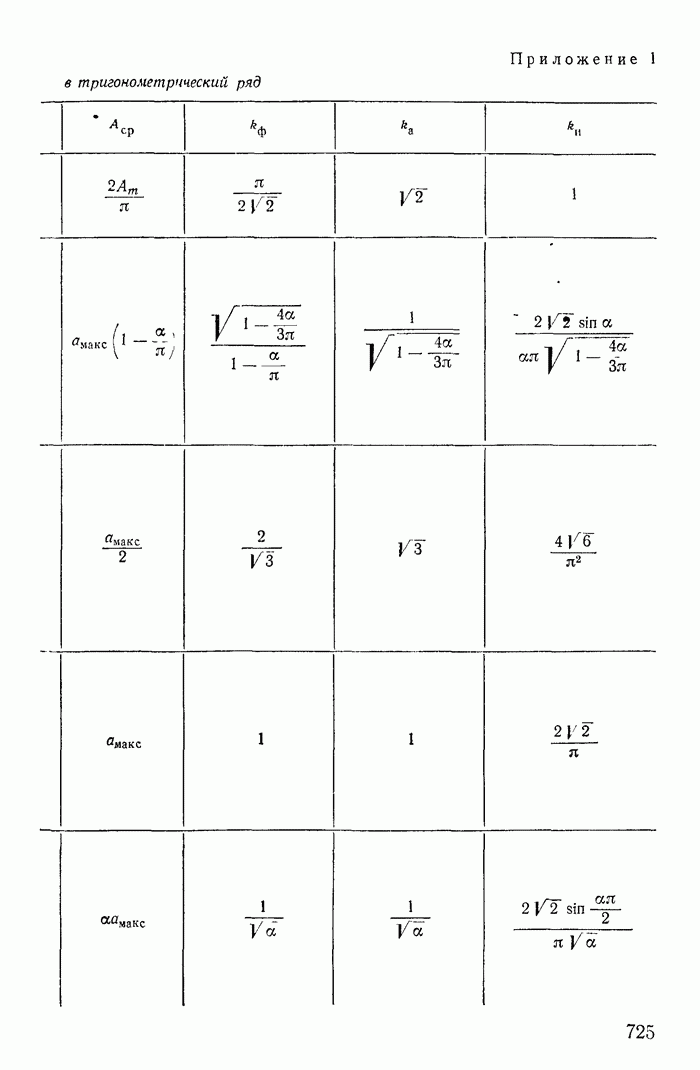
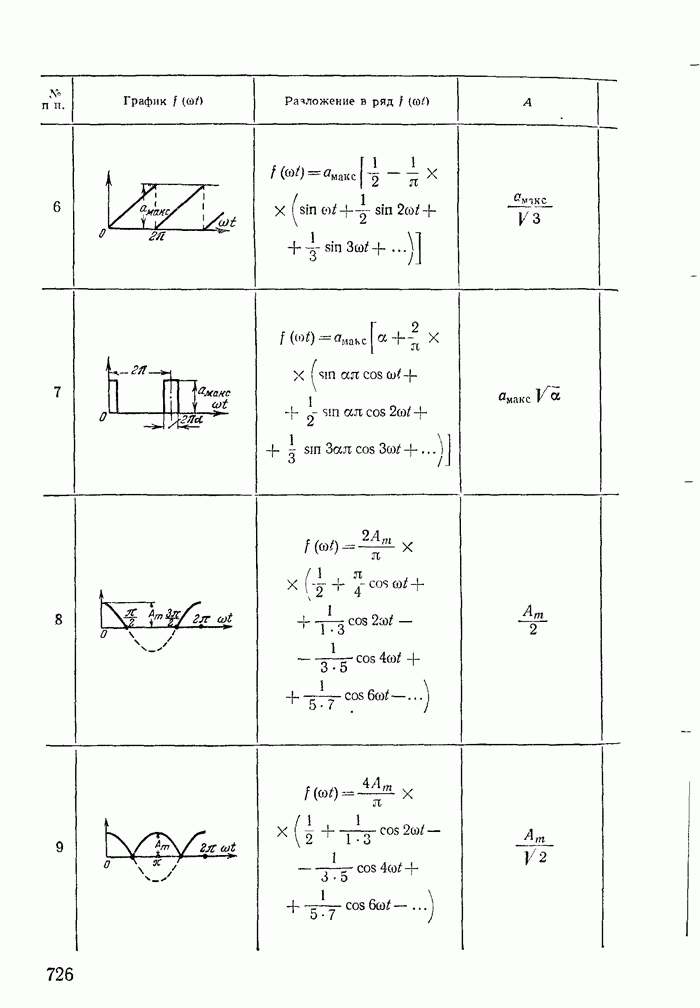
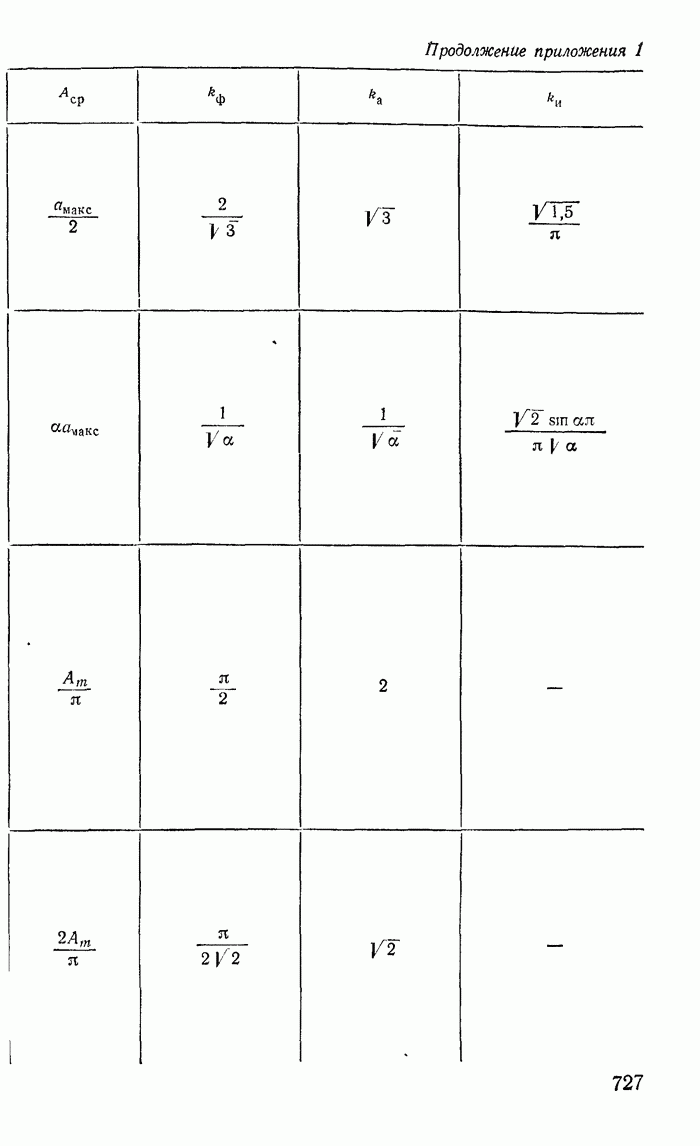
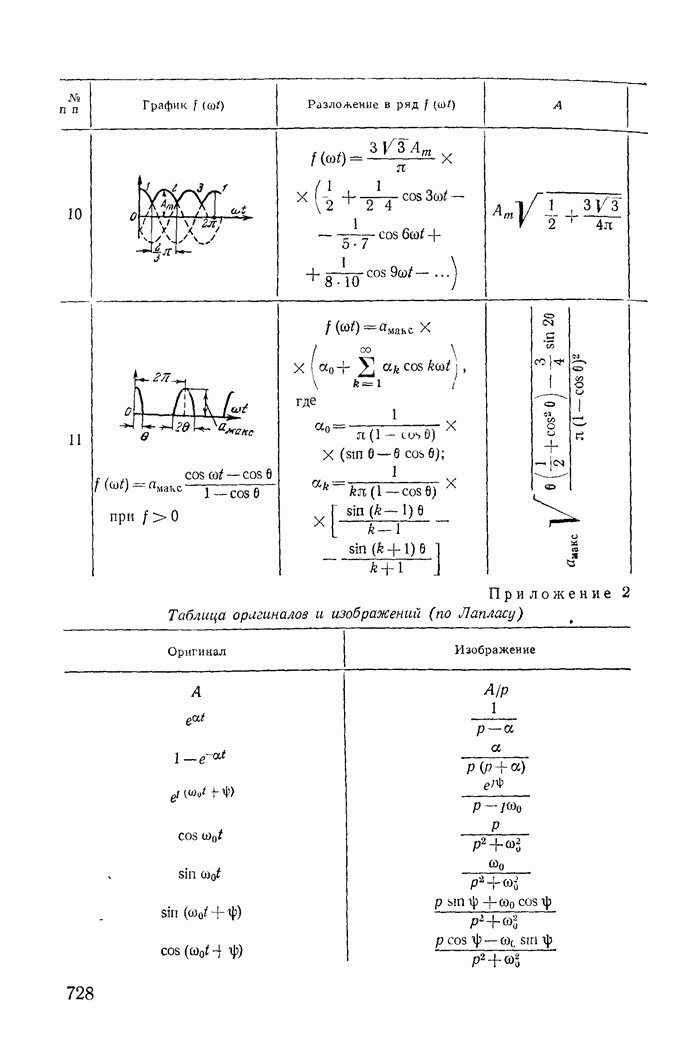
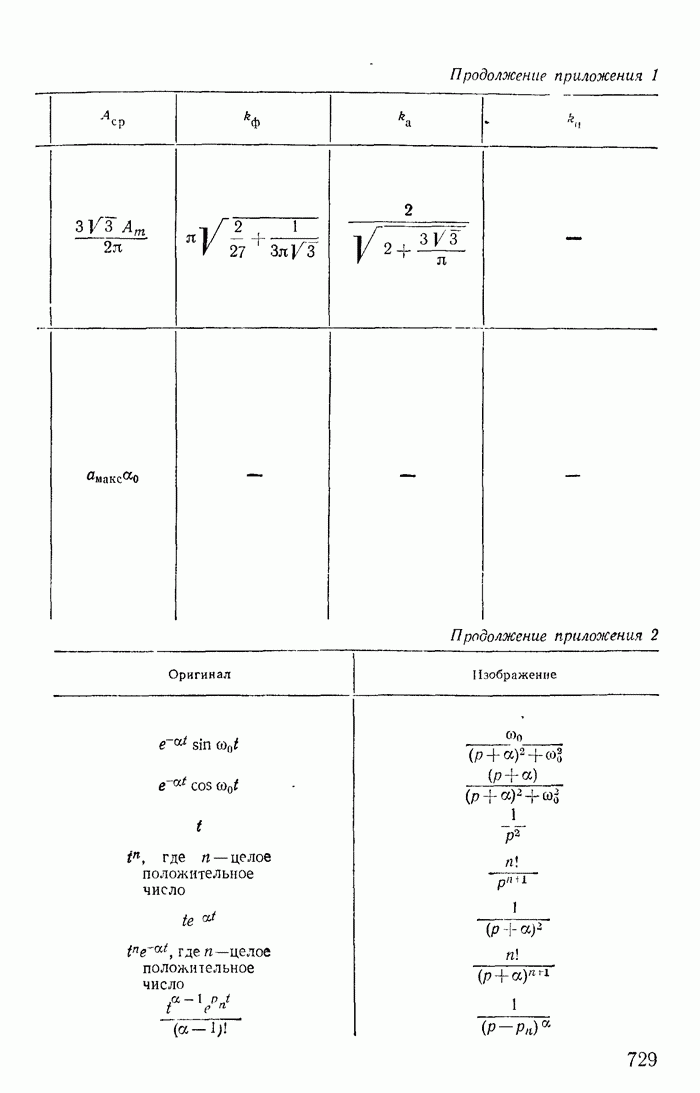
- Приложение 1. Разложение периодических функций в тригонометрический ряд
- Приложение 2. Таблица оригиналов и изображений (по Лапласу)
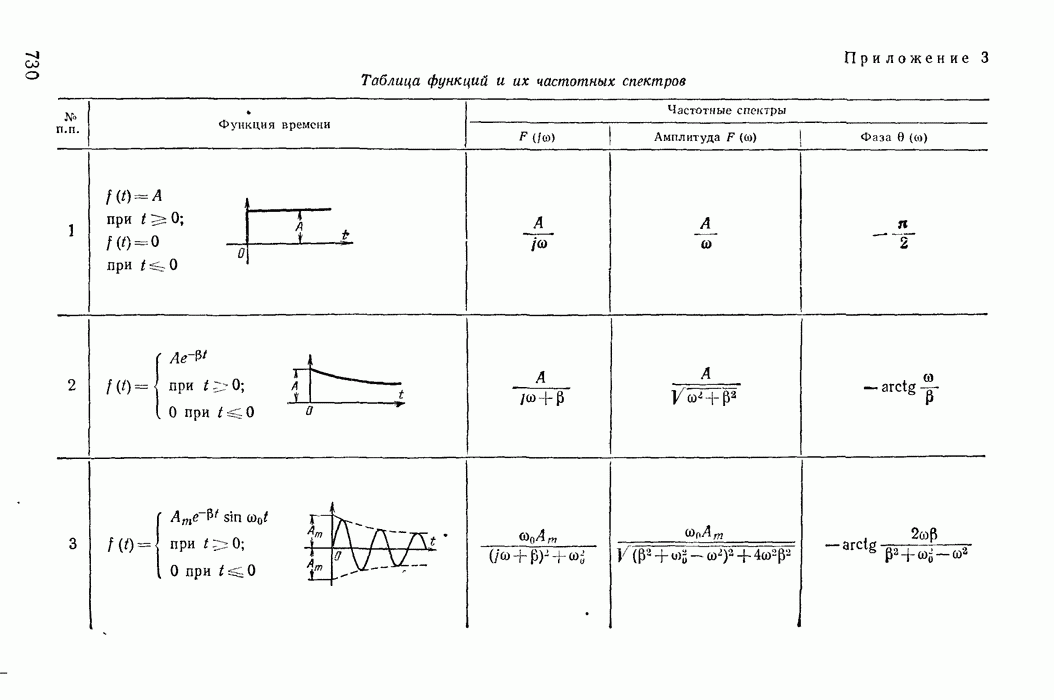
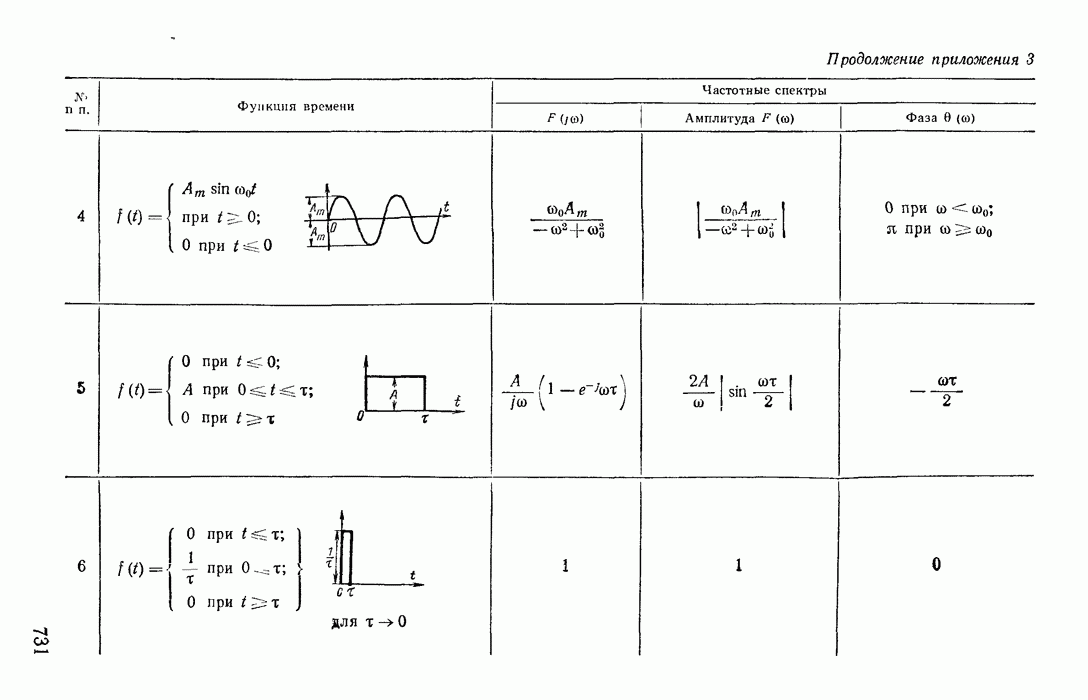
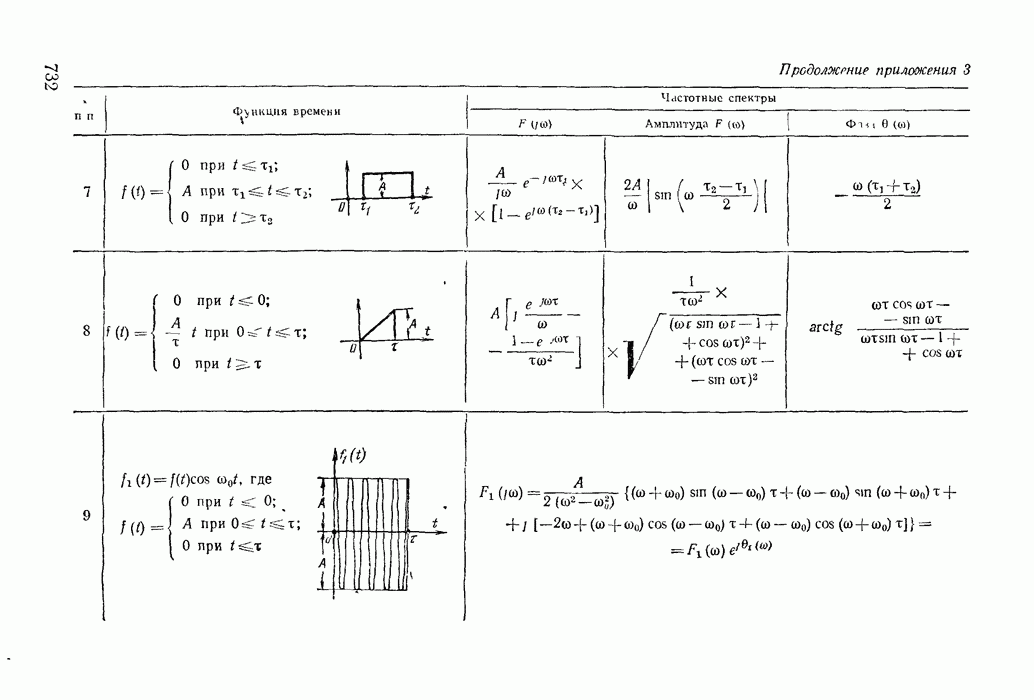
- Приложение 3. Таблица функций и их частных спектров
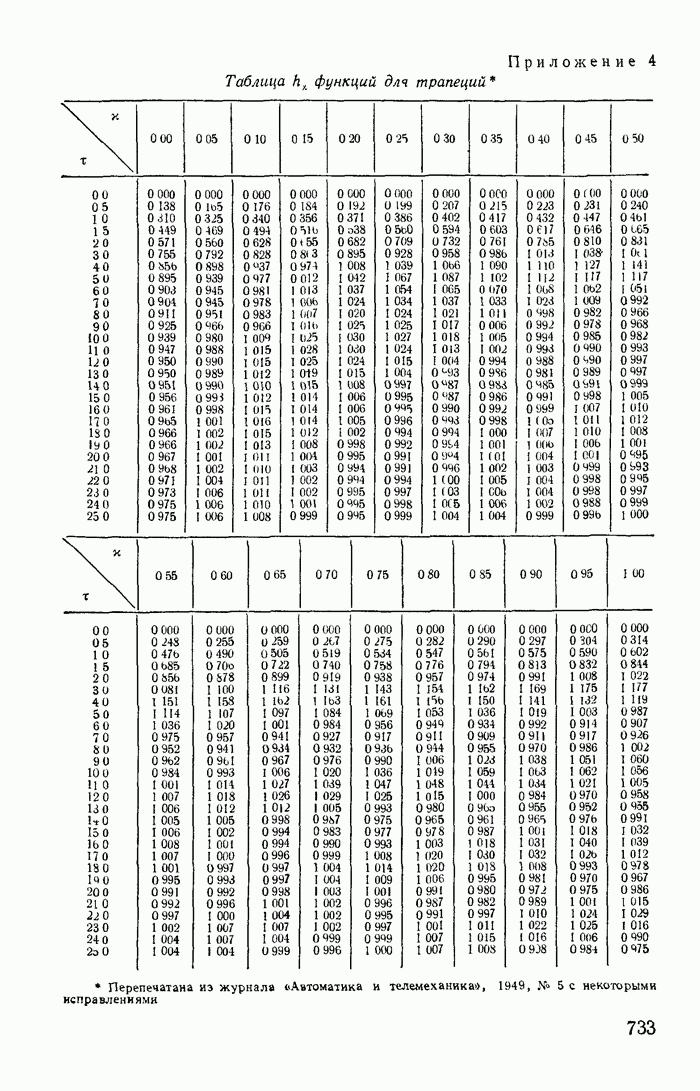
- Приложение 4. Таблица функций для трапеций
- СПИСОК ЛИТЕРАТУРЫ