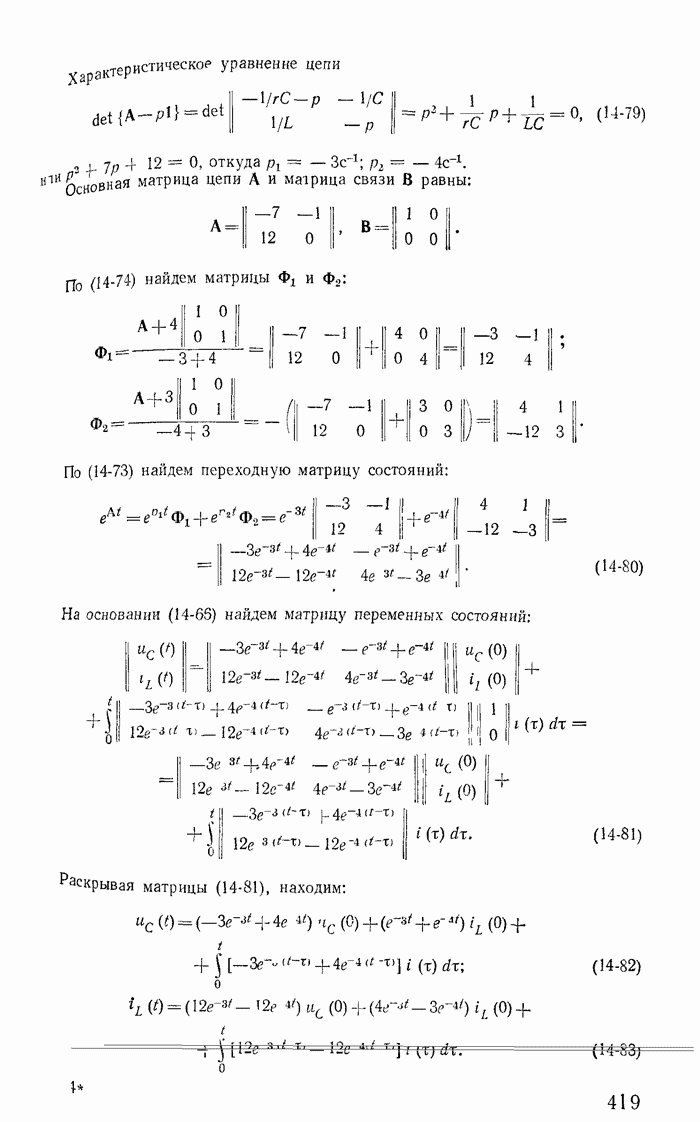| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
14-8. Расчет переходных процессов методом переменных состояния
Метод переменных состояния (называемый иначе методом пространства состояний) основывается на двух уравнениях, записываемых в матричной форме.
Структура первого уравнения определяется тем, что оно связывает матрицу первых производных по времени переменных состояния  с матрицами самих переменных состояния
с матрицами самих переменных состояния  и внешних воздействий и, в качестве которых рассматриваются э. д. с. и токи источников.
и внешних воздействий и, в качестве которых рассматриваются э. д. с. и токи источников.
Второе уравнение по своей структуре является алгебраическим и связывает матрицу выходных величин у с матрицами переменных состояния  и внешних воздействий и.
и внешних воздействий и.
Определяя переменные состояния, отметим следующие их свойства 
1. В качестве переменных состояния в электрических цепях следует выбирать токи  в индуктивностях и напряжения
в индуктивностях и напряжения  на емкостях, причем не во всех индуктивностях и не на всех емкостях, а только для независимых, т. е. таких, которые определяют общий порядок системы дифференциальных уравнений цепи.
на емкостях, причем не во всех индуктивностях и не на всех емкостях, а только для независимых, т. е. таких, которые определяют общий порядок системы дифференциальных уравнений цепи.
2. Дифференциальные уравнения цепи относительно переменных состояния записываются в канонической форме, т. е. представляются решенными относительно первых производных переменных состояния по времени.
Отметим, что только при выборе в качестве переменных состояния токов к в независимых индуктивностях и напряжений  на независимых емкостях первое уравнение метода переменных состояния будет иметь указанную выше структуру.
на независимых емкостях первое уравнение метода переменных состояния будет иметь указанную выше структуру.
Если в качестве переменных состояния выбрать токи  в ветвях с емкостями или токи
в ветвях с емкостями или токи  в ветвях с сопротивлениями, а также напряжения
в ветвях с сопротивлениями, а также напряжения  на индуктивностях или напряжения
на индуктивностях или напряжения  на сопротивлениях то первое уравнение метода переменных состояния также можно представить в канонической форме, т. е. решенным относительно первых производных по времени этих величин. Однако структура их правых частей не будет соответствовать данному выше определению, так как в них будет еще входить матрица первых производных от внешних воздействий
на сопротивлениях то первое уравнение метода переменных состояния также можно представить в канонической форме, т. е. решенным относительно первых производных по времени этих величин. Однако структура их правых частей не будет соответствовать данному выше определению, так как в них будет еще входить матрица первых производных от внешних воздействий 

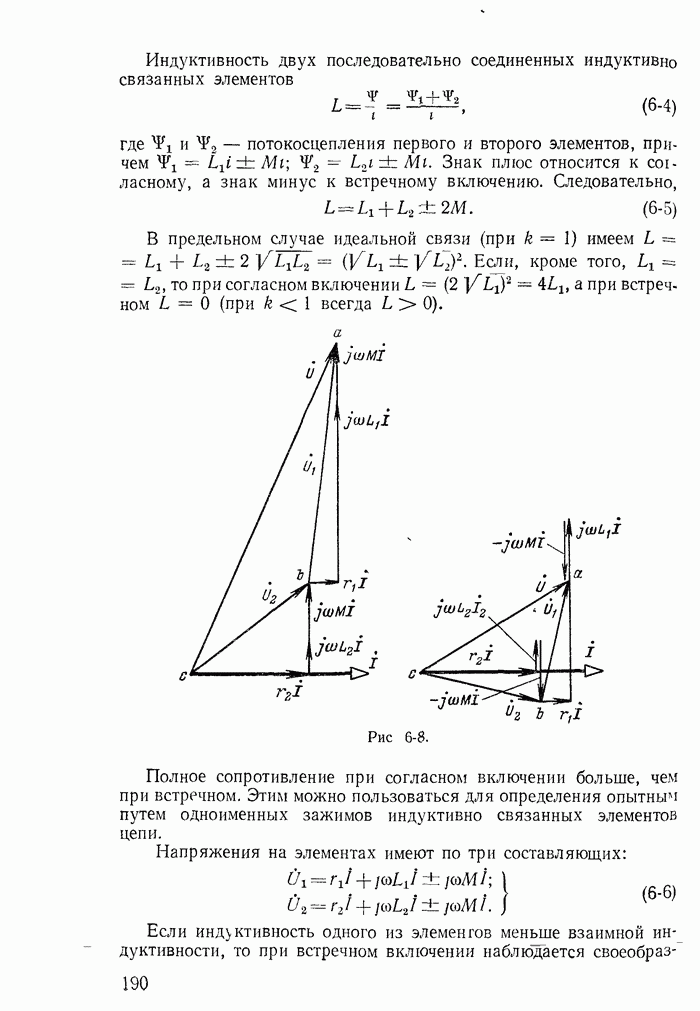
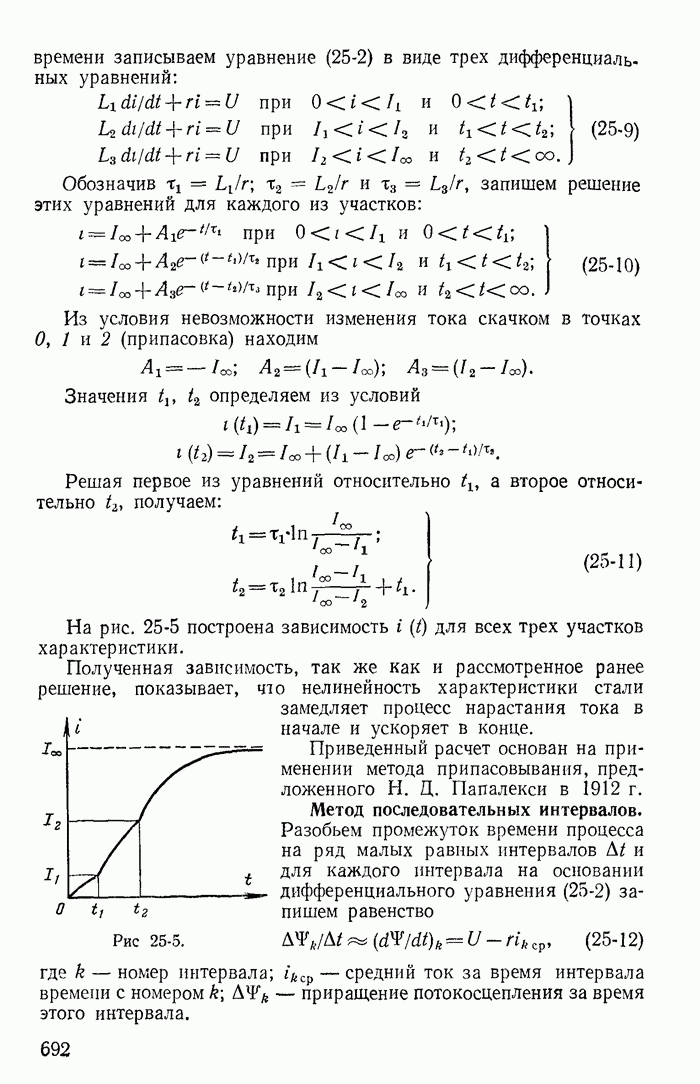
Рис. 14-14.
3. Число переменных состояния равно порядку системы дифференциальных уравнений исследуемой электрической цепи.
4. Выбор в качестве переменных состояния токов  и напряжений
и напряжений  удобен еще и потому, что именно эти величины согласно законам коммутации (§ 13-1) в момент коммутации не изменяются скачком, т. е. одинаковы для моментов времени
удобен еще и потому, что именно эти величины согласно законам коммутации (§ 13-1) в момент коммутации не изменяются скачком, т. е. одинаковы для моментов времени 
5. Переменные состояния  потому так и называются, что в каждый момент времени задают энергетическое состояние электрической цепи, так как последнее определяется суммой выражений
потому так и называются, что в каждый момент времени задают энергетическое состояние электрической цепи, так как последнее определяется суммой выражений 
6. Представление уравнений в канонической форме очень удобно при их решении на аналоговых вычислительных машинах и для программирования при их решении на цифровых вычислительных машинах. Поэтому такое представление имеет очень важное значение при решении этих уравнений с помощью средств современной вычислительной техники.
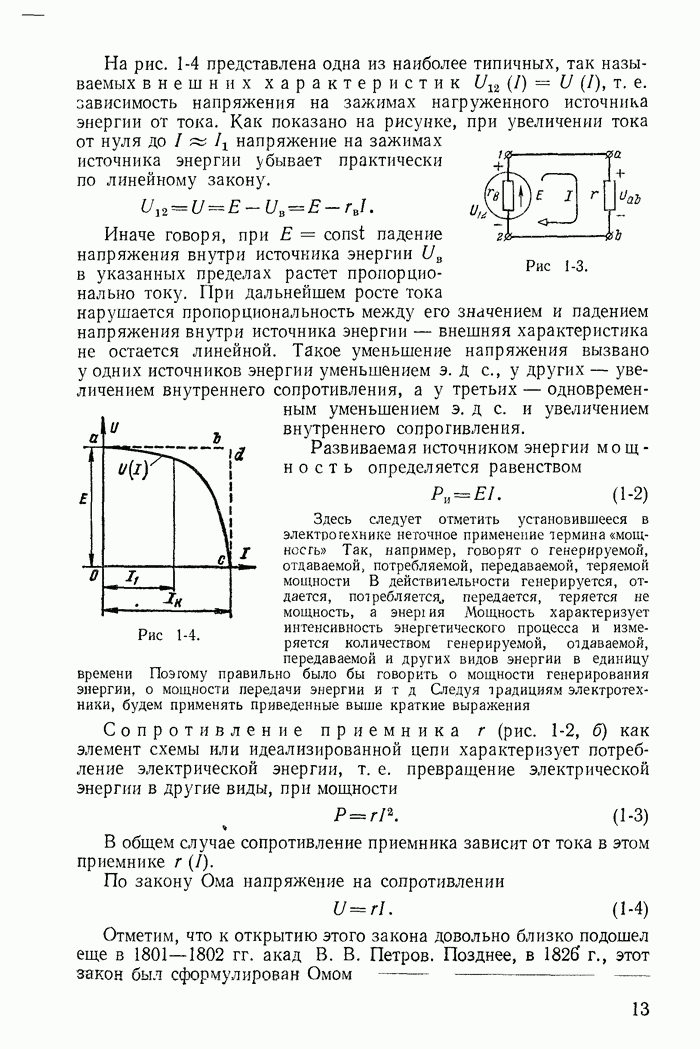
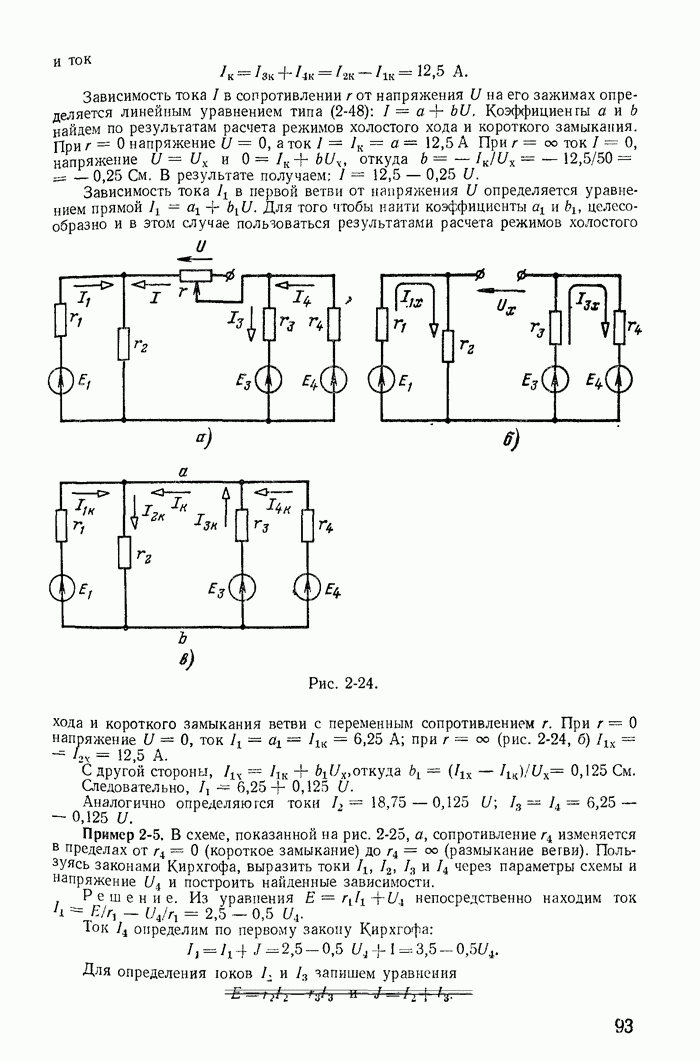
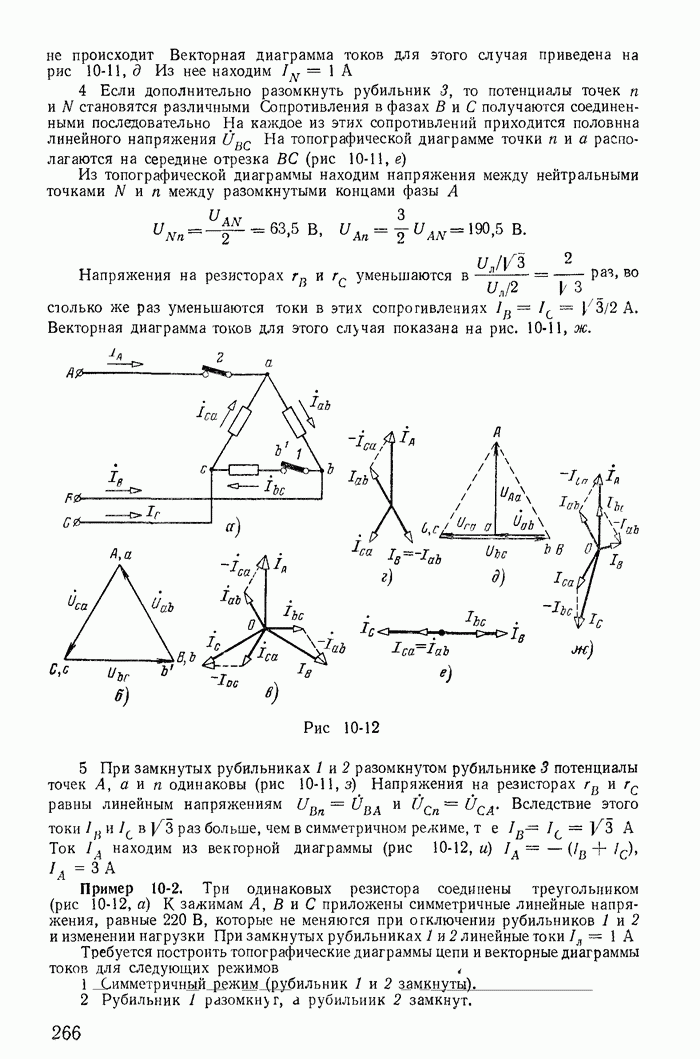
Покажем на примере цепи рис. 14-14, как составляются уравнения по методу переменных состояния.
Сначала получим систему дифференциальных уравнений, соответствующую первому матричному уравнению метода, а затем запишем ее в матричной форме. Алгоритм составления этих уравнений для любой электрической цепи следующий. Сначала записываются урэвнения по законам Кирхгофа или по методу контурных токов; затем выбираются переменные состояния и путем дифференцирования исходных уравнений и исключения других переменных получаются
чаются уравнения метода переменных состояния. Этот алгоритм очень напоминает применяемый в классическом методе расчета пере ходных процессов для получения одного результирующего дифференциального уравнения относительно одного из переменных
В частных случаях, когда в цепи нет емкостных контуров т. е. контуров, все ветви которых содержат емкости, и нет узлов с присоединенными ветвями, в каждой из которых включены индуктивности, может быть указан и другой алгоритм. Не останавливая на нем, отметим лишь, что он основан на замене емкостей источниками э. д. с., индуктивностей — источниками тока и применении метода наложения.
Для цепи рис. 14-14 по законам Кирхгофа
 (14-36)
(14-36)
Определяя  из первого уравнения, подставляя в третье, заменяя
из первого уравнения, подставляя в третье, заменяя  и представляя полученное дифференциальное уравнение в канонической форме относительно
и представляя полученное дифференциальное уравнение в канонической форме относительно  получаем:
получаем: 

Решая второе уравнение (14-36) относительно  , заменяя
, заменяя  согласно первому уравнению (14-36) и подставляя
согласно первому уравнению (14-36) и подставляя  , получаем:
, получаем:
 (14-38)
(14-38)
Складывая почленно (14-38) с умноженным на  уравнением (14-37) и определяя из полученного результата
уравнением (14-37) и определяя из полученного результата  , получаем:
, получаем:

Перепишем уравнения (14-39) и (14-37) в матричной форме:
 (14-4°)
(14-4°)
или

где для рассматриваемой цепи имеем:
 (14-42а)
(14-42а)
В общем случае первое уравнение метода переменных состояния в матричной форме запишется в виде
 (14-43)
(14-43)
Матрицы А и В в линейных цепях зависят только от параметров цепи  , т. е. являются постоянными величинами. При этом А - квадратная матрица порядка
, т. е. являются постоянными величинами. При этом А - квадратная матрица порядка  и называется основной матрицей цепи, матрица В — в общем случае прямоугольная, размера
и называется основной матрицей цепи, матрица В — в общем случае прямоугольная, размера  называется матрицей связи между входом цепи и переменными состояния, матрицы
называется матрицей связи между входом цепи и переменными состояния, матрицы  — матрицы столбцы или векторы переменных состояния (размера
— матрицы столбцы или векторы переменных состояния (размера  и внешних возмущений (размера
и внешних возмущений (размера  )
)
В рассматриваемом примере матрица В получилась квадратной второго порядка, так как число переменных состояния  равно числу внешних возмущении
равно числу внешних возмущении 
Перейдем к составлению второго уравнения метода В качестве  выходных можно выбрать любые из величин. Возьмем, например, в качестве выходных три величины
выходных можно выбрать любые из величин. Возьмем, например, в качестве выходных три величины 
Значения их запишутся через переменные состояния  и внешние возмущения
и внешние возмущения  непосредственно из уравнений (14 36)
непосредственно из уравнений (14 36)
 (14-44)
(14-44)
или в матричнои форме

или сокращенно
 (14-46)
(14-46)
где для рассматриваемой цепи

а в общем случае второе уравнение метода переменных состояния

Матрицы С и D зависят только от параметров цепи  . В общем случае — это прямоугольные матрицы соответственно размеров
. В общем случае — это прямоугольные матрицы соответственно размеров  , причем С называется матрицей связи переменных состояния с выходом цепи,
, причем С называется матрицей связи переменных состояния с выходом цепи,  матрицей непосредственной связи входа и выхода цепи (или системы).
матрицей непосредственной связи входа и выхода цепи (или системы).
Для ряда физических систем D является нулевой матрицей и второй член  в (14-48) обращается в нуль, так как нет непосред. ственной связи между входом и выходом системы.
в (14-48) обращается в нуль, так как нет непосред. ственной связи между входом и выходом системы.
Если в качестве переменных состояния взять, например, ток i и напряжение  и представить дифференциальные уравнения относительно них в канонической форме, то (опуская все промежуточные преобразования) первое из уравнений метода в матричной форме будет иметь вид:
и представить дифференциальные уравнения относительно них в канонической форме, то (опуская все промежуточные преобразования) первое из уравнений метода в матричной форме будет иметь вид:
 (14-49)
(14-49)
где

Таким образом, действительно, первое уравнение метода переменных состояния будет в матричной форме иметь вид (14-43) только при выборе в качестве переменных состояния тока  и напряжения
и напряжения 
Переходя к решению матричного дифференциального уравнения (14-43), прежде всего отметим, что оно особенно упрощается, если квадратная основная матрица А порядка  является диагональной. Тогда все
является диагональной. Тогда все  линейных дифференциальных уравнений (14-43) развязаны, т. е. производные переменных состояния зависят каждая только от своей переменной состояния.
линейных дифференциальных уравнений (14-43) развязаны, т. е. производные переменных состояния зависят каждая только от своей переменной состояния.
Рассмотрим сначала решение линейного неоднородного матричного дифференциального уравнения (14-43) операторным методом Для этого преобразуем его по Лапласу:

где

причем  матрица-столбец начальных значений переменных состояния, т. е.
матрица-столбец начальных значений переменных состояния, т. е.
 (14-53)
(14-53)
которые в момент коммутации не изменяются скачком, заданы и равны их значениям в момент 
Перепишем (14-51):

где  — единичная матрица порядка
— единичная матрица порядка  .
.
Для получения матрицы изображений переменных состояния  умножим слева обе части (14-54) на обратную матрицу
умножим слева обе части (14-54) на обратную матрицу 
 (14-55)
(14-55)
Переходя обратно к оригиналам при помощи обратного преобразования Лапласа, получаем:
 (14-56)
(14-56)
Из операторного метода известно, что
 (14-57)
(14-57)
По аналогии, записывая обратное преобразование Лапласа в матричной форме, будем иметь:
 (14-58)
(14-58)
где  — переходная матрица состояния системы, называемая иначе фундаментальной.
— переходная матрица состояния системы, называемая иначе фундаментальной.
Таким образом, находим оригинал первого слагаемого правой части (14-56)
 (14-59)
(14-59)
Обратная матрица определяется делением присоединенной или взаимной матрицы на определитель основной матрицы:

где уравнение
 (14-61)
(14-61)
представляет собой характеристическое уравнение исследуемой цепи.
Оригинал второго слагаемого правой части (14-56) находится при помощи теоремы свертки в матричной форме

если положить
 (14.64)
(14.64)
и

Тогда на основании (14-62)-(14-64)

и общее решение дифференциального неоднородного матричного уравнения (14-43) на основании (14-56), (14-59) и (14-65) будет иметь вид: 
 (14-66)
(14-66)
Первое слагаемое правой части (14-66) представляет собой значения переменных состояния или реакцию цепи при нулевом входе, т. е.  Иначе говоря, оно представляет первую составляющую свободных процессов в цепи
Иначе говоря, оно представляет первую составляющую свободных процессов в цепи  обусловленную ненулевыми начальными значениями переменных состояния цепи, и поэтому является решением уравнения
обусловленную ненулевыми начальными значениями переменных состояния цепи, и поэтому является решением уравнения  . Второе слагаемое представляет собой составляющую реакции цепи при
. Второе слагаемое представляет собой составляющую реакции цепи при  т. е. при нулевом состоянии цепи.
т. е. при нулевом состоянии цепи.
Нулевым состоянием цепи назовем такое ее состояние, когда начальные значения всех переменных состояния равны нулю. Иначе говоря, второе слагаемое (14-66) представляет собой сумму при принужденной реакции цепи  возникающей под влиянием внешних воздействий
возникающей под влиянием внешних воздействий  и второй составляющей свободных процессов
и второй составляющей свободных процессов 
Равенство (14-66) означает, что реакция цепи равна сумме реакций при нулевом входе и нулевом состоянии.
На основании (14-48) и (14-66) для выходных величин имеем.

Если состояние цепи задано не в момент  , а в момент
, а в момент  , то равенства (14-66) и (14-67) обобщаются:
, то равенства (14-66) и (14-67) обобщаются:
 (14-68)
(14-68)
Пример 14-5. Для разветвленной цепи второго порядка составлены уравнения состояния

при ненулевых начальных условиях  и при единственном имеющем вней источнике э. д. с.
и при единственном имеющем вней источнике э. д. с.

Найти переменные состояния  .
.
Решение. Перепишем уравнения состояния в матричной форме

где

Найдем сначала первые свободные составляющие переменных состояния при нулевом входе Для этого составим матрицу

Для нахождения присоединенной или взаимной матрицы заменим в предыдущей матрице каждый элемент его алгебраическим дополнением Получим матрицу

Транспонируем ее, найдя присоединенную или взаимную матрицу:

Найдем определитель матрицы 

На основании (14-60) обратная матрица будет равна:

Подвергнем ее обратному преобразованию Лапласа с учетом того, что для этого нужно подвергнуть обратному преобразованию Лапласа каждый ее элемент. На основании (14-73) получим переходную матрицу состояния цепи

Например,

Для переходной матрицы состояния системы получим:

Для первых свободных составляющих переменных состояния будем иметь

т. е.

Далее на основании (14-66) найдем сумму принужденных и вторых свободных составляющих переменных состояния:

Суммируя полученные результаты, находим искомые значения переменных состояния:

Так как решение уравнения (14-43) было получено выше и дано формулой (14-66), то для проверки правильности решения (14-66) и вычисления с его помощью матрицы переменных состояния  можно сначала непосредственной подстановкой (14-66) в (14-43) убедиться, что последнее при этом обращается в тождество. Для этого нужно только сначала вычислить
можно сначала непосредственной подстановкой (14-66) в (14-43) убедиться, что последнее при этом обращается в тождество. Для этого нужно только сначала вычислить  дифференцируя (14-66). При этом получаем:
дифференцируя (14-66). При этом получаем:

Теперь нетрудно непосредственно убедиться, что (14-66) действительно является решенпем матричного дифференциального уравненения 
Отметим, что переходная матрица состояния системы ем позволяет найти в пространстве состояний, т. е. в пространстве, число измерений которого равно числу компонент вектора переменных состояния  перемещение, начинающееся из некоторого начального положения (при
перемещение, начинающееся из некоторого начального положения (при  или при
или при  ) причем вектор
) причем вектор  содержит значительную информацию, так как одновременно описывает все переменные состояния, т. е. функции времени
содержит значительную информацию, так как одновременно описывает все переменные состояния, т. е. функции времени  .
.
Для того чтобы непосредственно воспользоваться решением (14-66) и вычислить матричную экспоненциальную функцию  не прибегая к обратному преобразованию Лапласа, следует, например, выполнить ее разложение в ряд:
не прибегая к обратному преобразованию Лапласа, следует, например, выполнить ее разложение в ряд:
 (14-72)
(14-72)
При этом правую часть (14-72) нужно представить в замкнутой форме, чтобы ее вычисление могло быть произведено путем выполнения конечного числа операций, как, например, в формуле (14-70).
Вычисление переходной матрицы состояния может производиться различными методами — методом разложения в бесконечный ряд, методом, основанным на критерии Сильвестра, методом Кэйли — Гамильтона, методом частотной области, методом передаточной функции и др.
Рассмотрим кратко два первых метода. Сначала рассмотрим первый метод (разложение в бесконечный ряд) на числовом примере.
Найдем переходную матрицу состояний по заданной основной матрице А системы

Степени А получим последовательным умножением на А:

На основании (14-72)

Складывая матрицы правой части, получаем:

Далее следует найти в замкнутом виде каждый элемент этой матрицы. Для данного примера нетрудно убедиться в том, что каждый из элементов матрицы можно представить в замкнутом виде как разность двух экспонент:
 (14-73)
(14-73)
что и решает поставленную задачу.
По методу, основанному на критерии Сильвестра,

где
 (14-75)
(14-75)
Здесь  — собственные значения или характеристические числа матрицы А, т. е. простые корни характеристического уравнения цепи (число их равно
— собственные значения или характеристические числа матрицы А, т. е. простые корни характеристического уравнения цепи (число их равно  ).
).

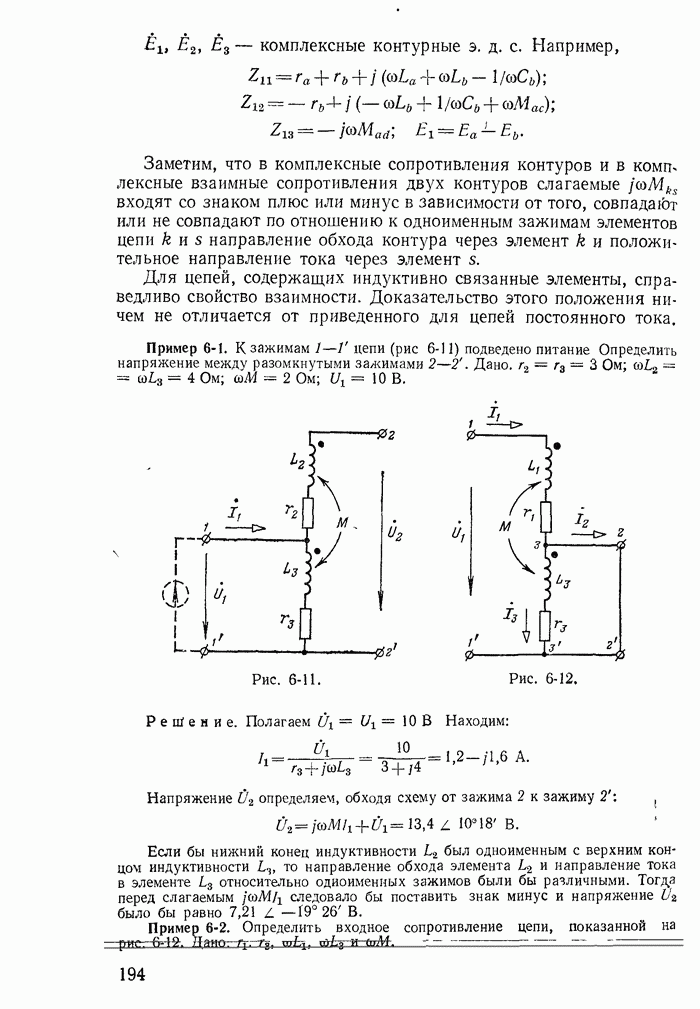
Рис. 14-15.
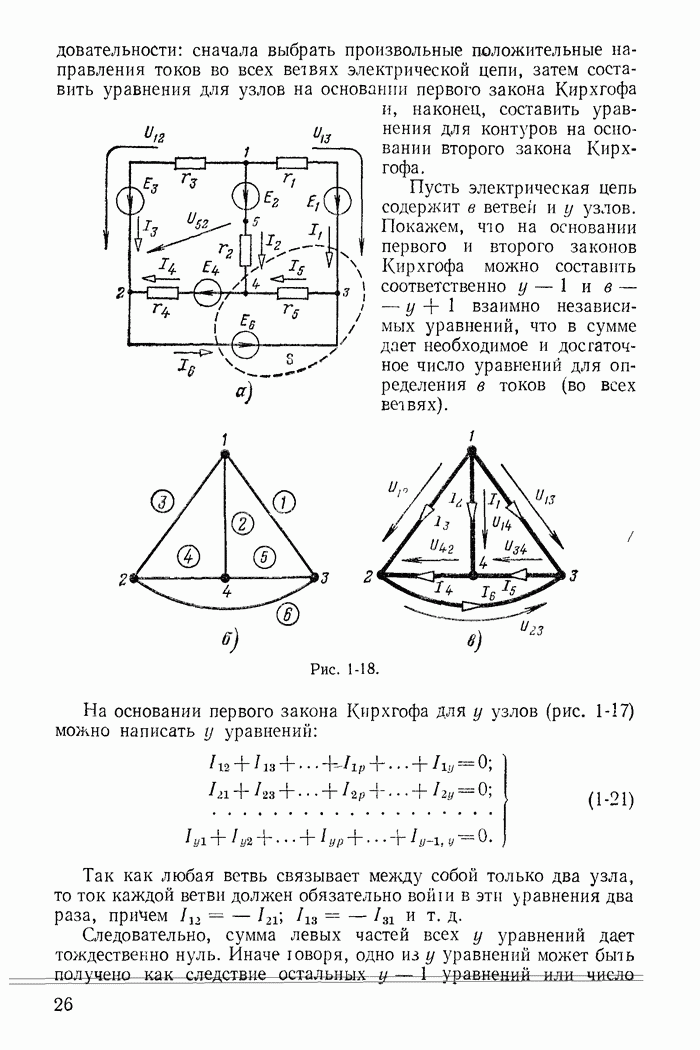
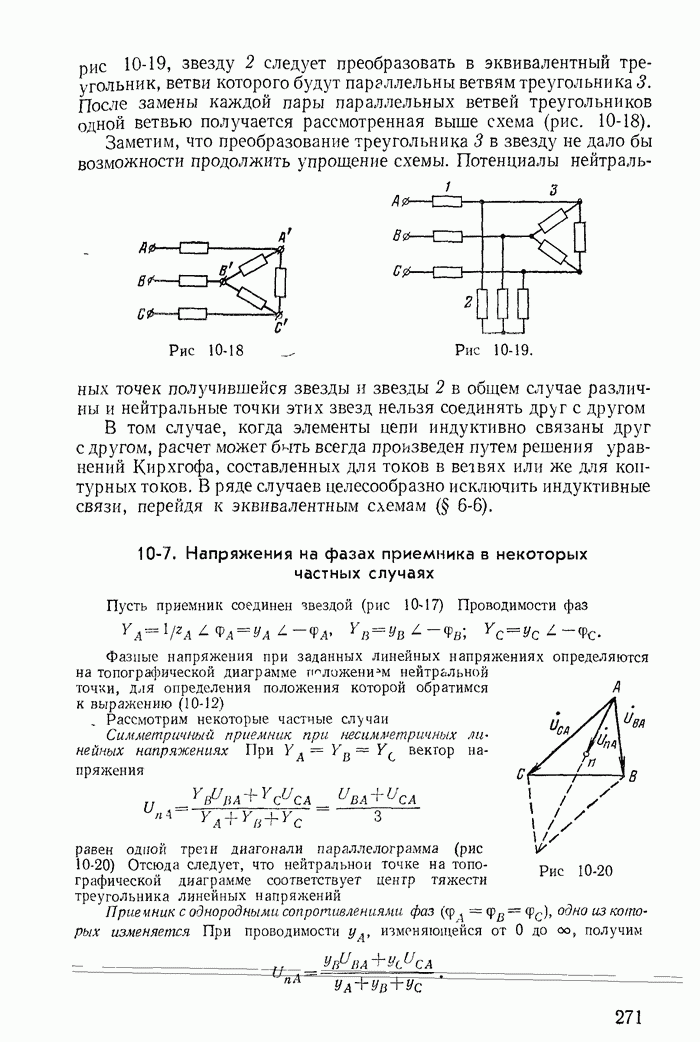
Пример 14-6. Для цепи рис. 14-15 при  рассчитать ток
рассчитать ток  при включении ее к источнику тока
при включении ее к источнику тока  при условии, что в момент включения
при условии, что в момент включения  даны ток в индуктивности
даны ток в индуктивности  и напряжение на конденсаторе
и напряжение на конденсаторе  , что обеспечивается одновременной и мгновенной коммутацией всех трех рубильников цепи.
, что обеспечивается одновременной и мгновенной коммутацией всех трех рубильников цепи.
Решение. В качестве переменных состояния выбираем  а выходной величиной у считаем ток в емкости
а выходной величиной у считаем ток в емкости 
На основании законов Кирхгофа составим уравнения состояния цепи и уравнение для выходной величины.

откуда

В матричной форме

Характеристическое уравненне цепи

или  откуда
откуда 
Основная матрица цепи А и матрица связи В равны:

По (14-74) найдем матрицы 

По (14-73) найдем переходную матрицу состояний:
 (14-80)
(14-80)
На основании (14-63) найдем матрицу переменных состояний:
 (14-81)
(14-81)
Раскрывая матрицы (14-81), находим:
 (14-82)
(14-82)
На основании (14-76), (14-82) и (14-83) наймем выходною величину

Полученные результаты легко проверить непосредственно для установившегося режима, если источник тока  — единичный,
— единичный,  . Непосредственно из схемы рис 14-15 следует, что пои этих условиях ток едичнчного источника тока замкнется через индуктивность, т. е.
. Непосредственно из схемы рис 14-15 следует, что пои этих условиях ток едичнчного источника тока замкнется через индуктивность, т. е.  источник тока будет ею закорочен, т. е.
источник тока будет ею закорочен, т. е.  и ток в конденсаторе будет равен нулю т. е.
и ток в конденсаторе будет равен нулю т. е. 
По формулам (14 83), (14-82) и (14 87) получаем, выполняя интегрирование и полагая 

| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К ЧЕТВЕРТОМУ ИЗДАНИЮ
- ВВЕДЕНИЕ
- Раздел первый. ЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ С СОСРЕДОТОЧЕННЫМИ ПАРАМЕТРАМИ
- 1-1. Элементы электрических цепей и электрических схем
- 1-2. Эквивалентные схемы для источников энергии
- 1-3. Закон Ома для участка цепи с э. д. с.
- 1-4. Распределение потенциала вдоль неразветвленной электрической цепи
- 1-5. Баланс мощностей для простейшей неразветвленной цепи
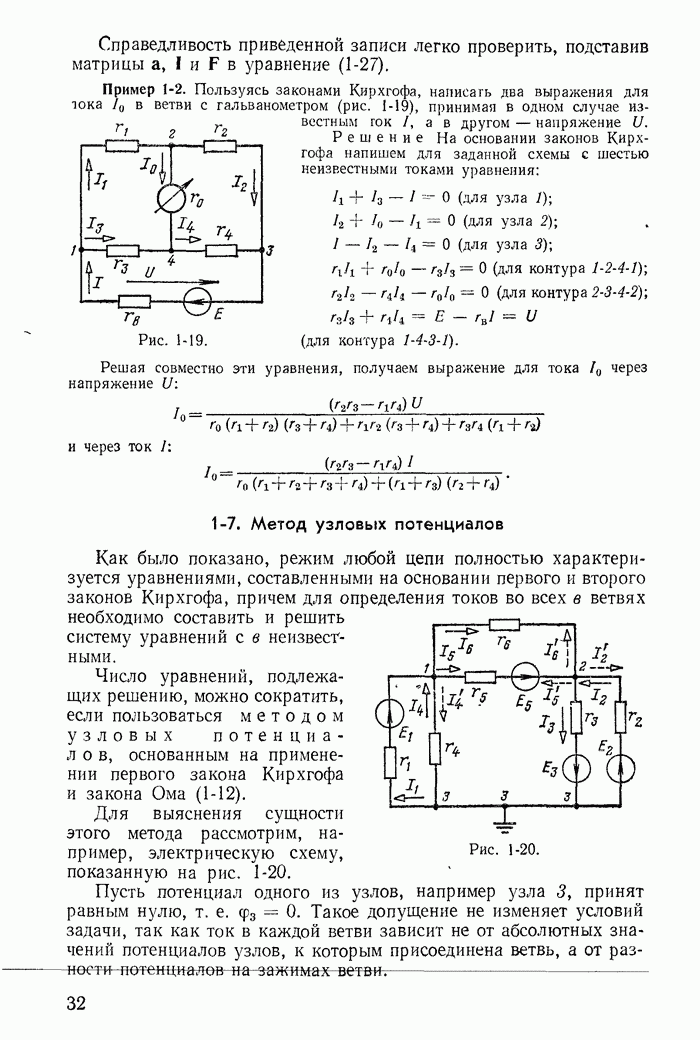
- 1-6. Применение законов Кирхгофа для расчета разветвленных цепей
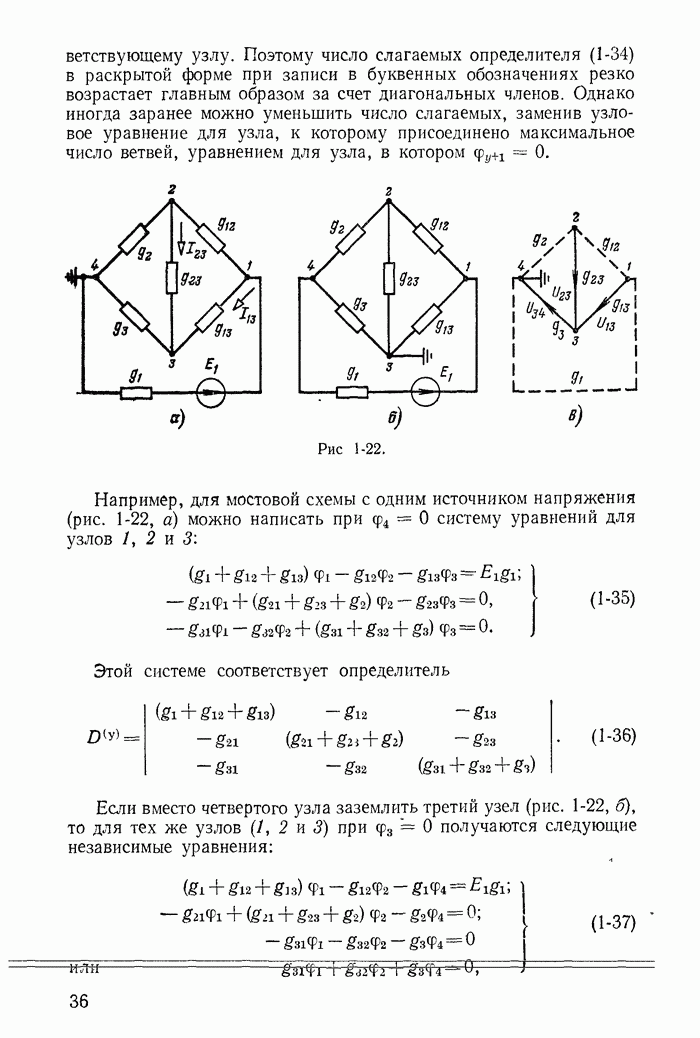
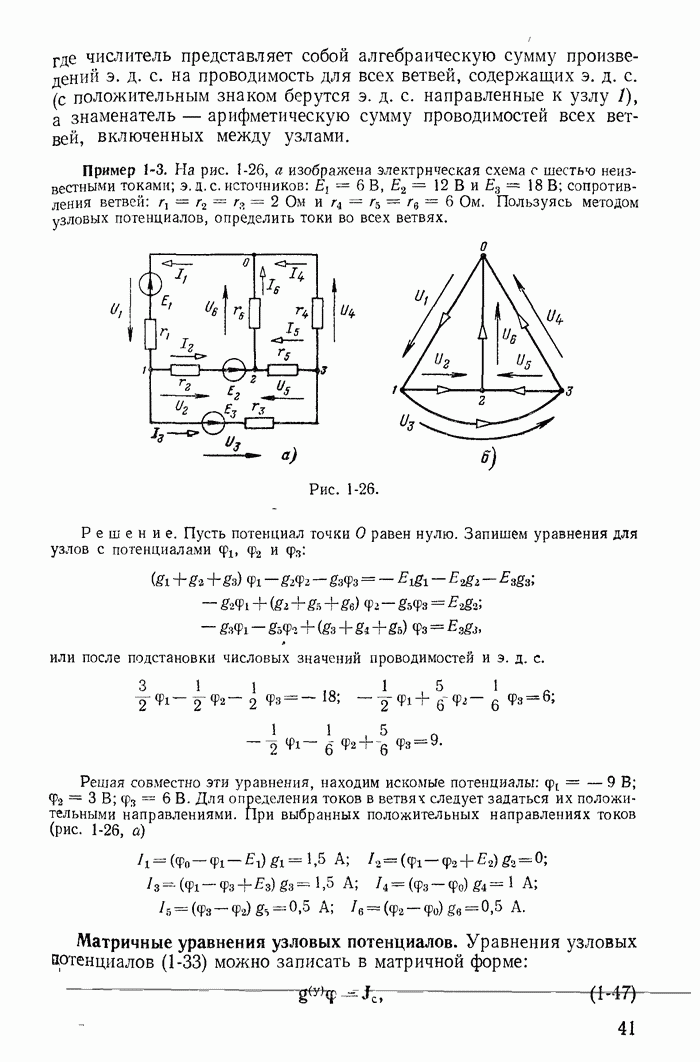
- 1-7. Метод узловых потенциалов
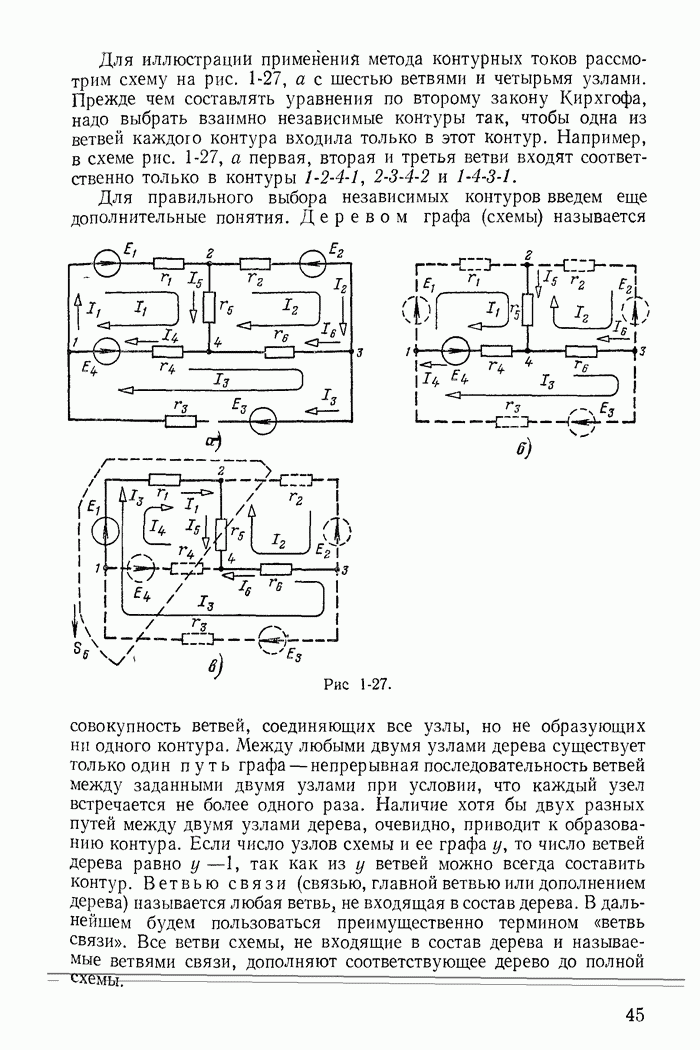
- 1-8. Метод контурных токов
- 1-9. Уравнения состояния цепи в матричной форме
- 1-10. Преобразование линейных электрических схем
- Глава вторая. ОСНОВНЫЕ СВОЙСТВА ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ПРИ ПОСТОЯННЫХ ТОКАХ И НАПРЯЖЕНИЯХ
- 2-2. Свойство взаимности
- 2-3. Входные и взаимные проводимости и сопротивления ветвей; коэффициенты передачи напряжений и токов
- 2-4. Применение топологических методов для расчета цепей
- 2-5. Топологические формулы и правила для определения передачи электрической цепи
- 2-6. Теорема о компенсации
- 2-7. Линейные соотношения между напряжениями и токами
- 2-8. Теорема о взаимных приращениях токов и напряжений
- 2-9. Общие замечания о двухполюсниках
- 2-10. Теорема об активном двухполюснике и ее применение для расчета разветвленных цепей
- 2-11. Передача энергии от активного двухполюсника к пассивному
- Глава третья. ОСНОВНЫЕ ПОНЯТИЯ О ЦЕПЯХ СИНУСОИДАЛЬНОГО ТОКА
- 3-2. Понятие о генераторах переменного тока
- 3-3. Синусоидальный ток
- 3-4. Действующие ток, э. д. с. и напряжение
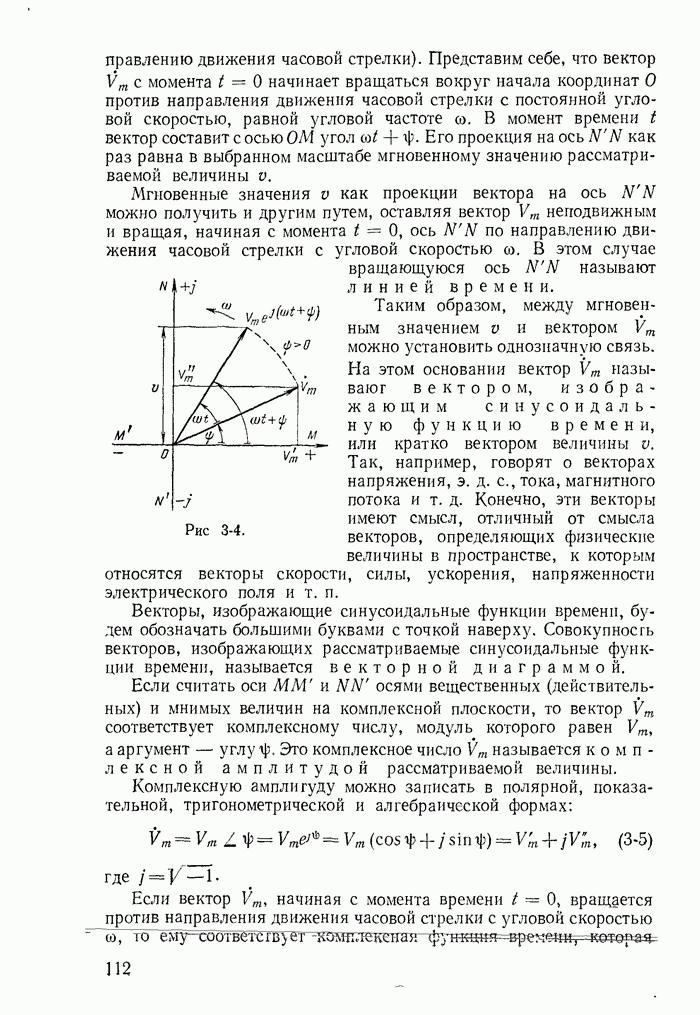
- 3-5. Изображение синусоидальных функций времени векторами и комплексными числами
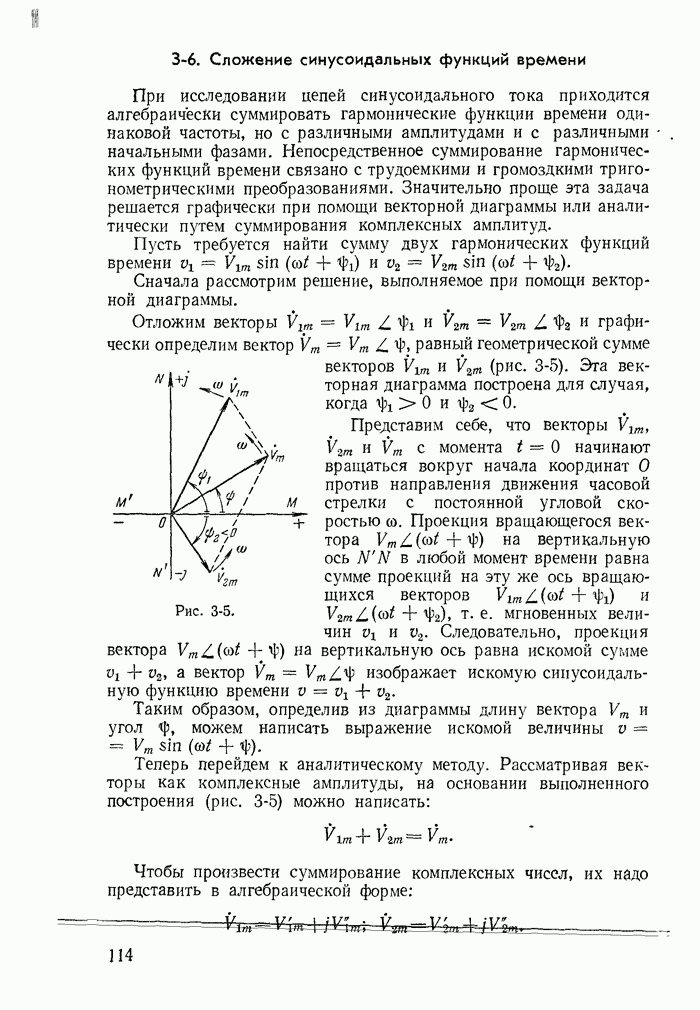
- 3-6. Сложение синусоидальных функций времени
- 3-7. Электрическая цепь и ее схема
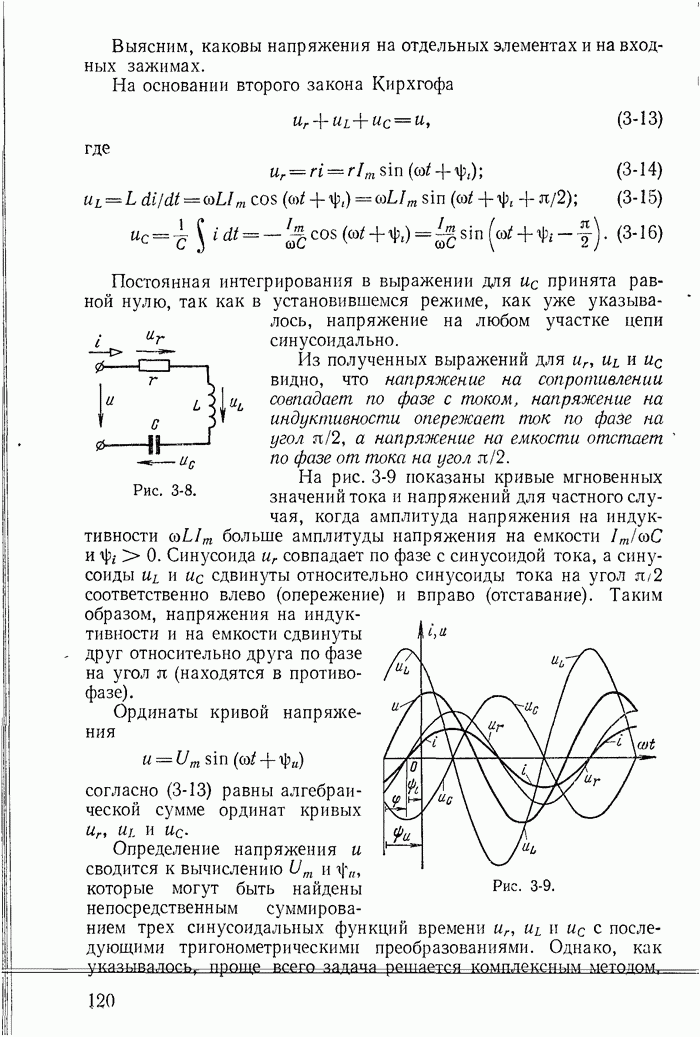
- 3-8. Ток и напряжения при последовательном соединении сопротивления, Индуктивности и емкости
- 3-9. Сопротивления
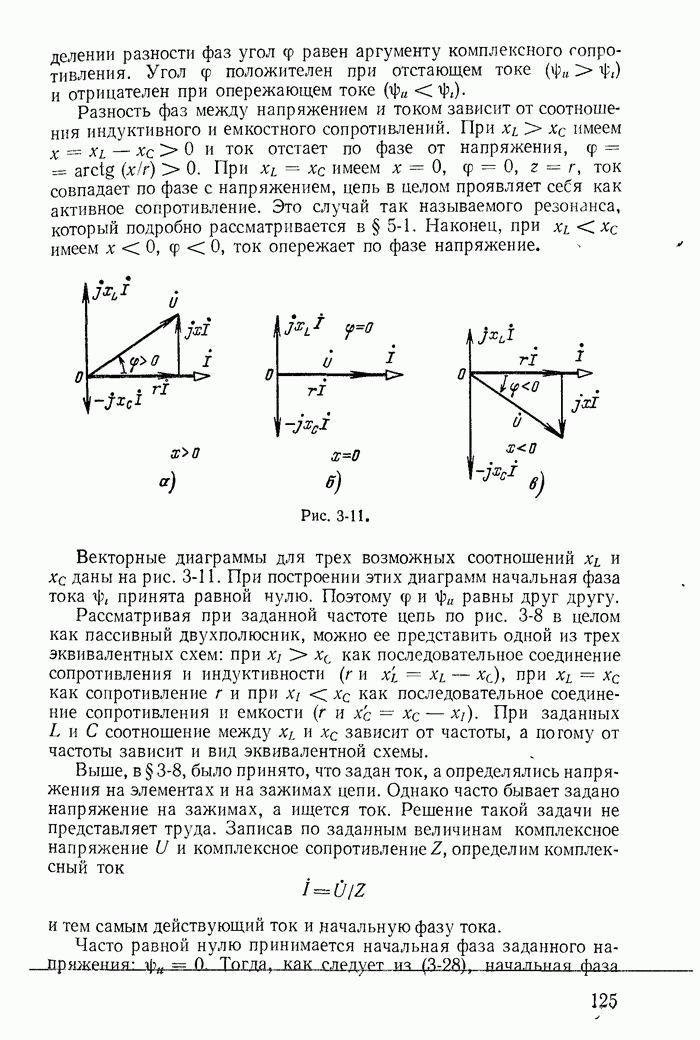
- 3-10. Разность фаз напряжения и тока
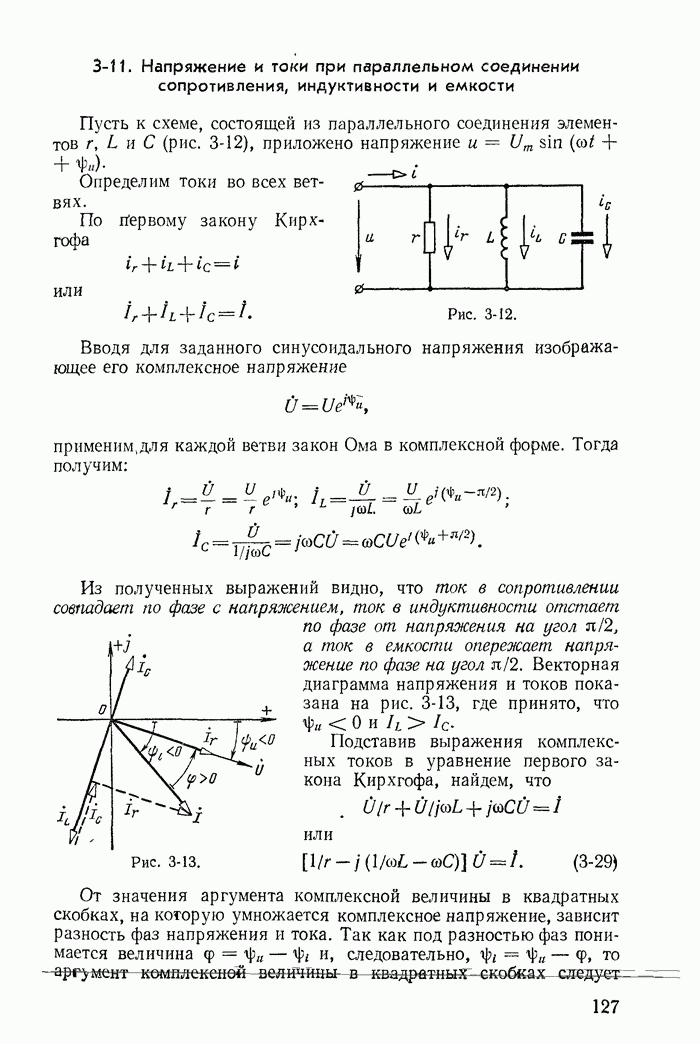
- 3-11. Напряжение и токи при параллельном соединении сопротивления, индуктивности и емкости
- 3-12. Проводимости
- 3-13. Пассивный двухполюсник
- 3-14. Мощности
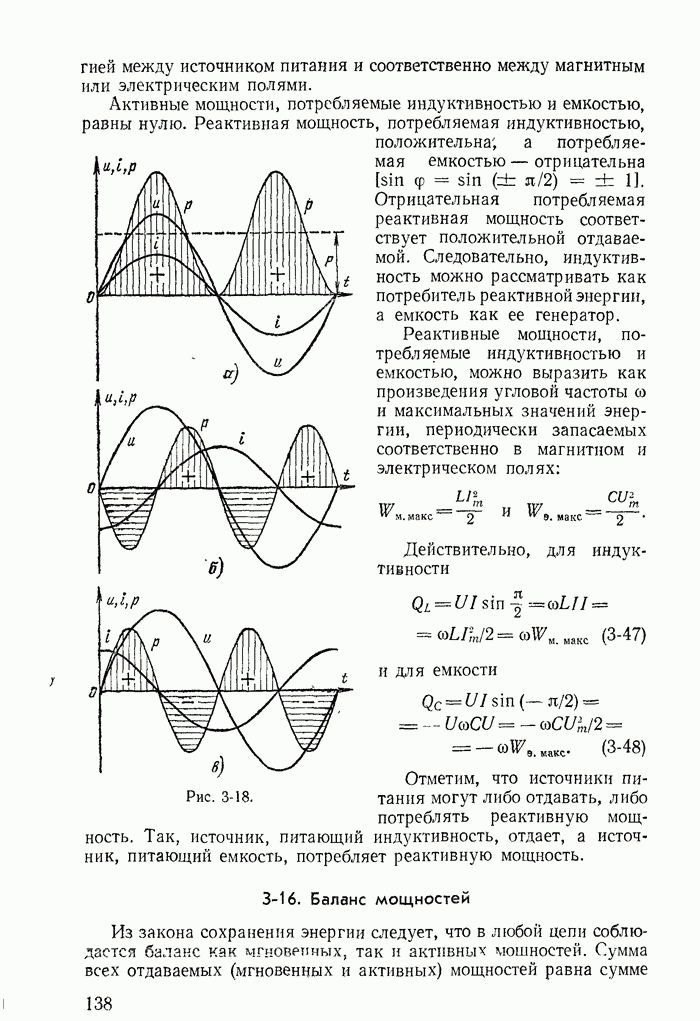
- 3-15. Мощности в сопротивлении, индуктивности и емкости
- 3-16. Баланс мощностей
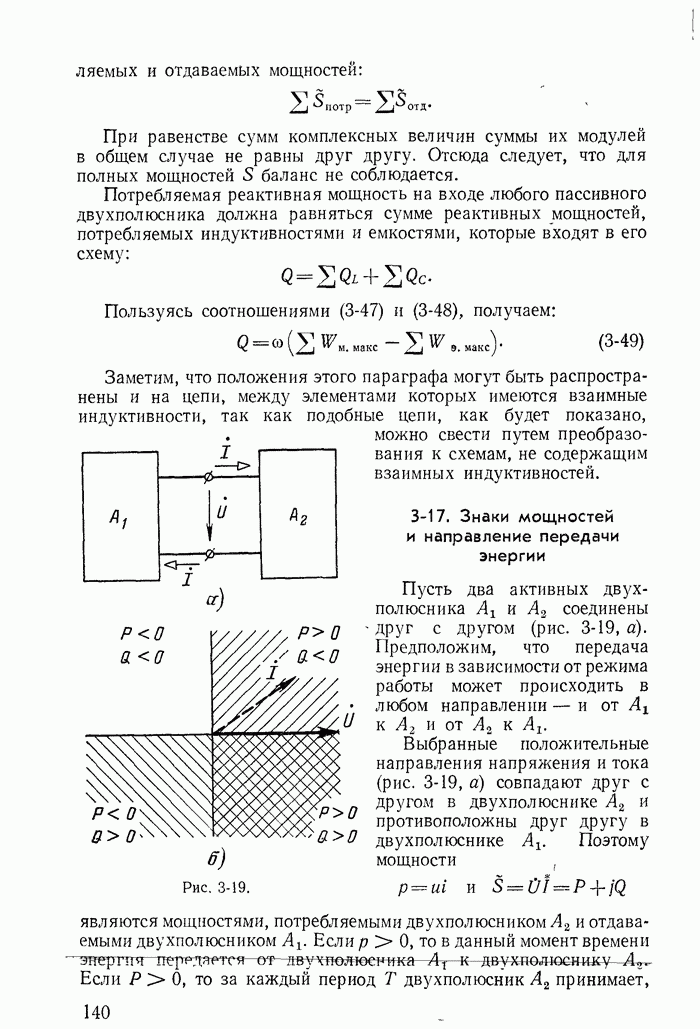
- 3-17. Знаки мощностей и направление передачи энергии
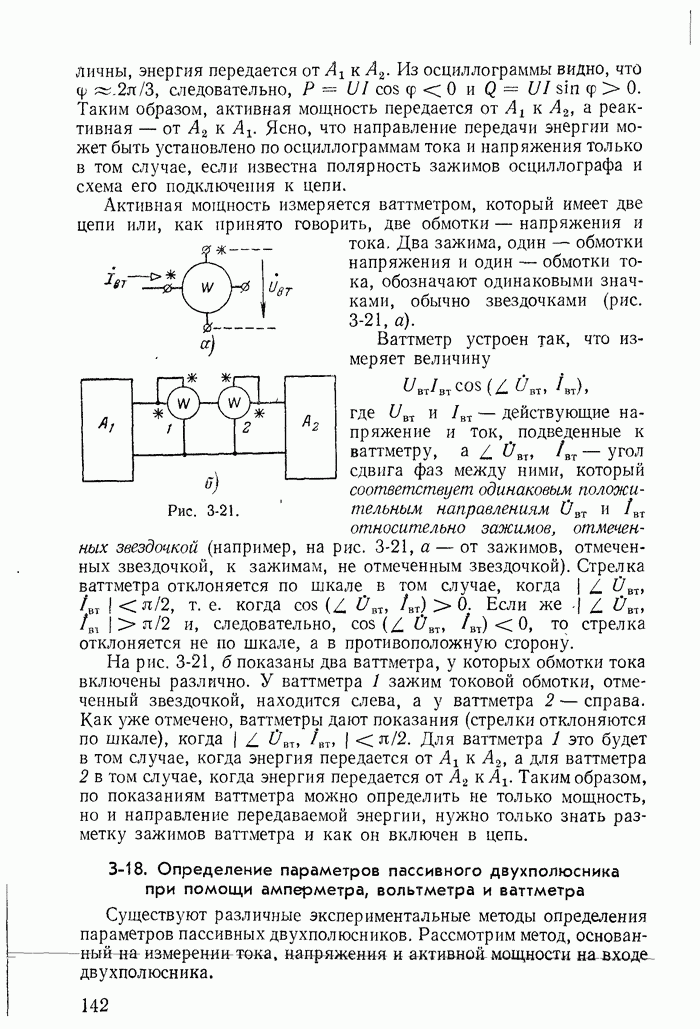
- 3-18. Определение параметров пассивного двухполюсника при помощи амперметра, вольтметра и ваттметра
- 3-19. Условия передачи максимальной мощности от источника энергии к приемнику
- 3-20. Понятие о поверхностном эффекте и эффекте близости
- 3-21. Параметры и эквивалентные схемы конденсаторов
- 3-22. Параметры и эквивалентные схемы индуктивных катушек и резисторов
- Глава четвертая. РАСЧЕТ ЦЕПЕЙ ПРИ СИНУСОИДАЛЬНЫХ ТОКАХ
- 4-1. О применимости методов расчета цепей постоянного тока к расчетам цепей синусоидального тока
- 4-2. Последовательное соединение приемников
- 4-3. Параллельное соединение приемников
- 4-4. Смешанное соединение приемников
- 4-5. Сложные разветвленные цепи
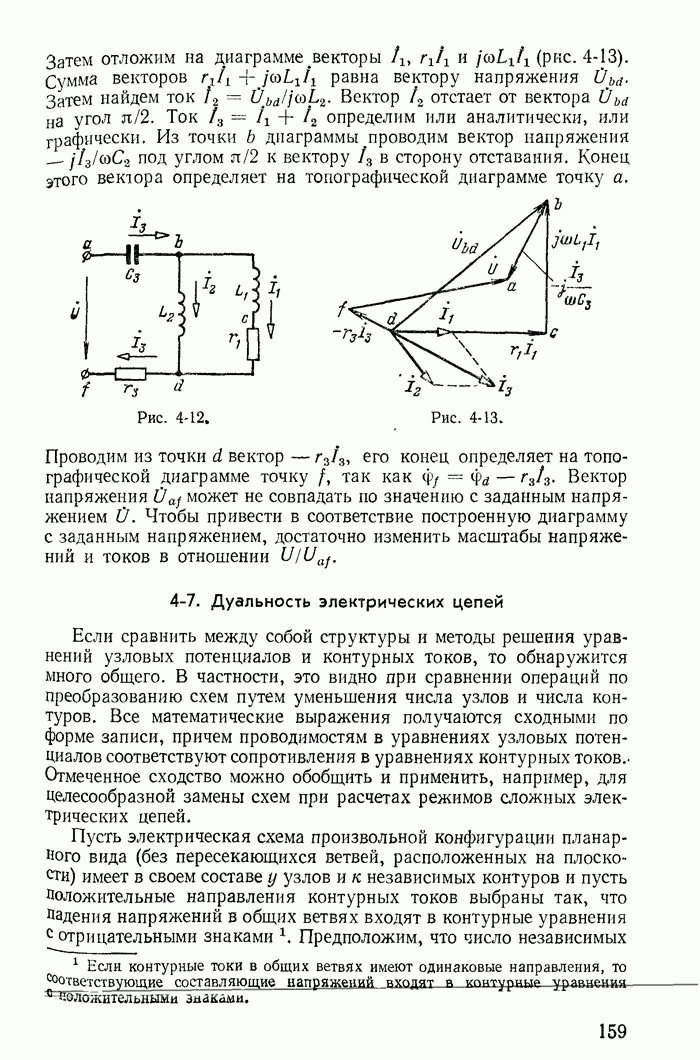
- 4-6. Топографические диаграммы
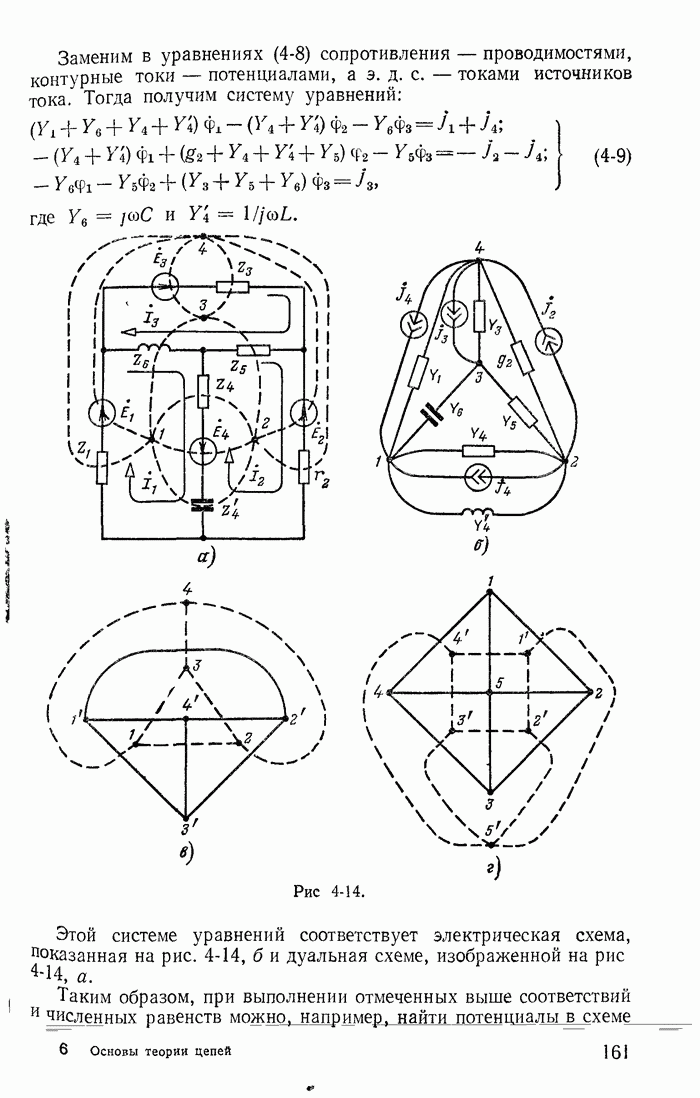
- 4-7. Дуальность электрических цепей
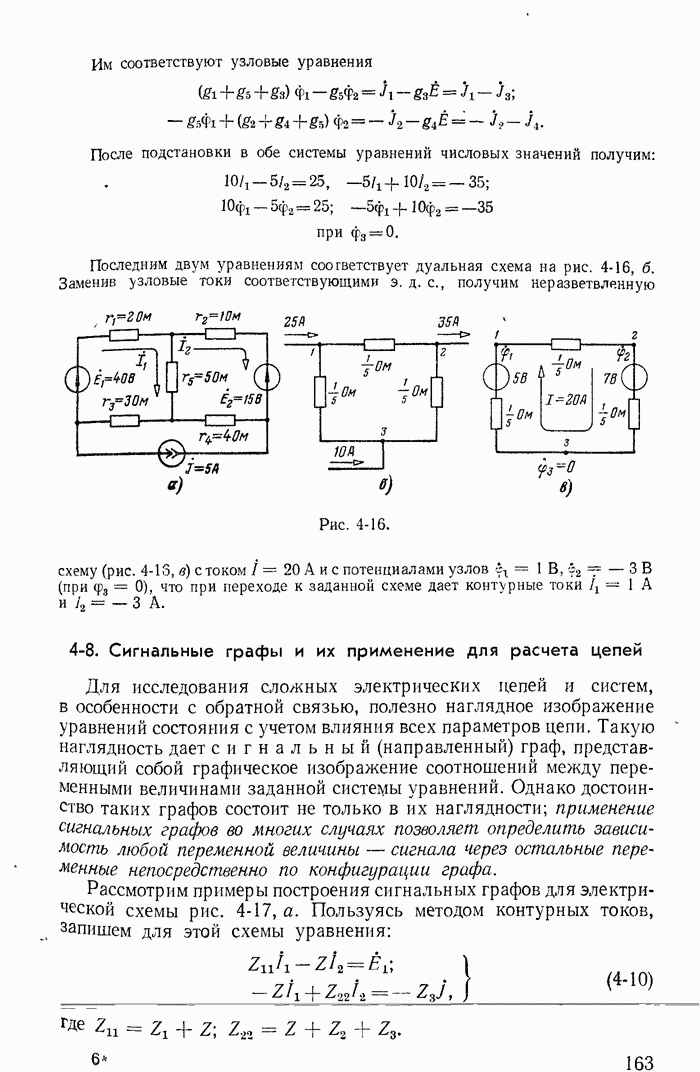
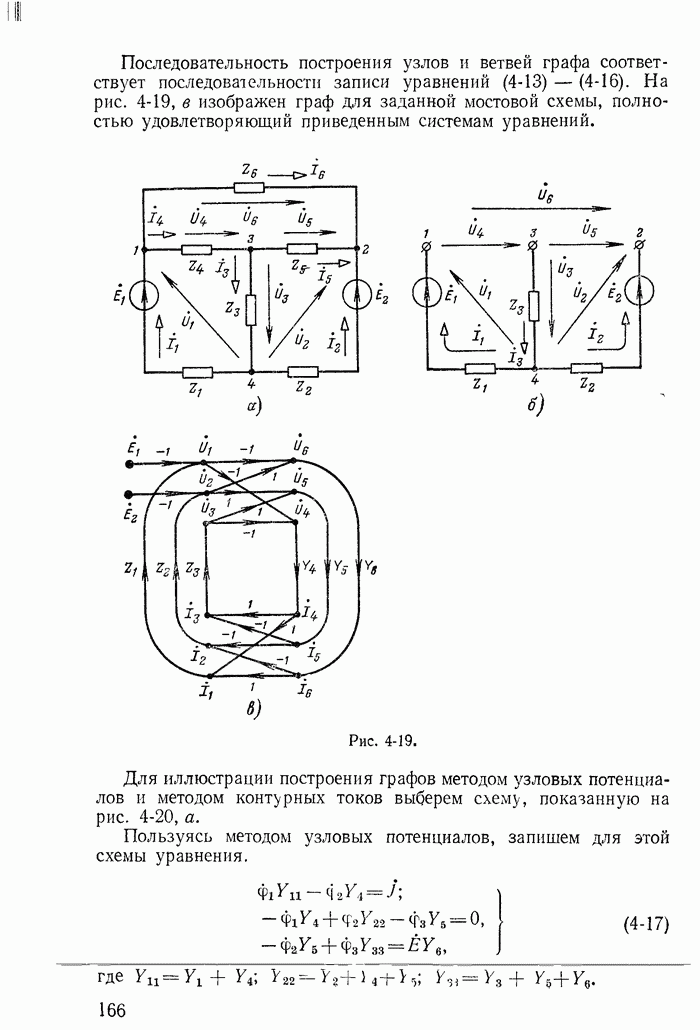
- 4-8. Сигнальные графы и их применение для расчета цепей
- Глава пятая. РЕЗОНАНС В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ
- 5-2. Частотные характеристики неразветвленной цепи
- 5-3. Резонанс в цепи с двумя параллельными ветвями
- 5-4. Частотные характеристики параллельного контура
- 5-5. Понятие о резонансе в сложных цепях
- Глава шестая. ЦЕПИ С ВЗАИМНОЙ ИНДУКТИВНОСТЬЮ
- 6-2. Электродвижущая сила взаимной индукции
- 6-3. Последовательное соединение индуктивно связанных элементов цепи
- 6-4. Параллельное соединение индуктивно связанных элементов цепи
- 6-5. Расчеты разветвленных цепей при наличии взаимной индуктивности
- 6-6. Эквивалентная замена индуктивных связей
- 6-7. Передача энергии между индуктивно связанными элементами цепи
- 6-8. Трансформатор без стального сердечника (воздушный трансформатор)
- Глава седьмая. КРУГОВЫЕ ДИАГРАММЫ
- 7-1. Комплексные уравнения прямой и окружности
- 7-2. Круговые диаграммы для неразветвленной цепи и для активного двухполюсника
- 7-3. Круговые диаграммы для любой разветвленной цепи
- Глава восьмая. МНОГОПОЛЮСНИКИ И ЧЕТЫРЕХПОЛЮСНИКИ ПРИ СИНУСОИДАЛЬНЫХ ТОКАХ И НАПРЯЖЕНИЯХ
- 8-1. Четырехполюсники и их основные уравнения
- 8-2. Определение коэффициентов четырехполюсников
- 8-3. Режим четырехполюсника при нагрузке
- 8-4. Эквивалентные схемы четырехполюсников
- 8-5. Основные уравнения и эквивалентные схемы для активного четырехполюсника
- 8-6. Идеальный трансформатор как четырехполюсник
- 8-7. Эквивалентные схемы с идеальными трансформаторами для четырехполюсника
- 8-8. Эквивалентные схемы трансформатора со стальным магнитопроводом
- 8-9. Расчеты электрических цепей с трансформаторами
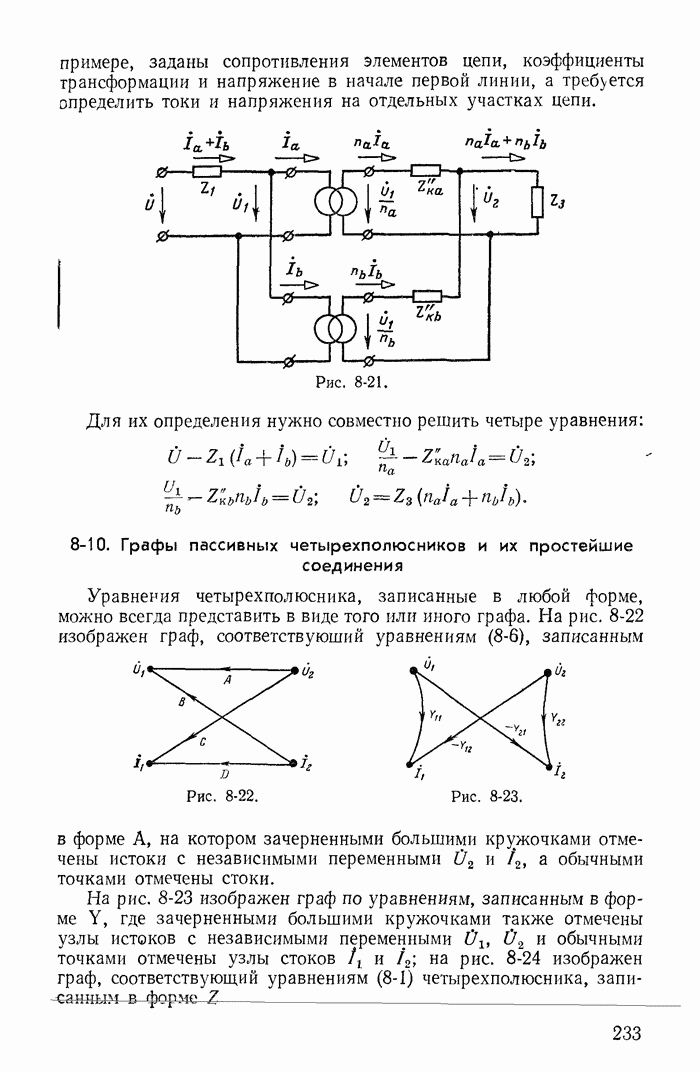
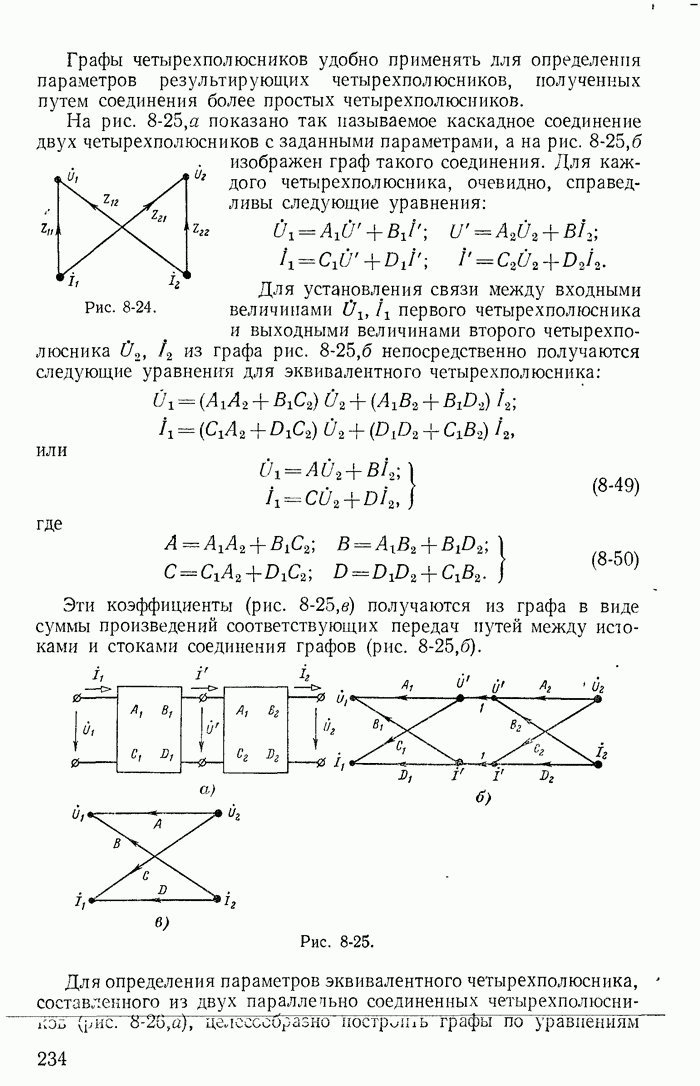
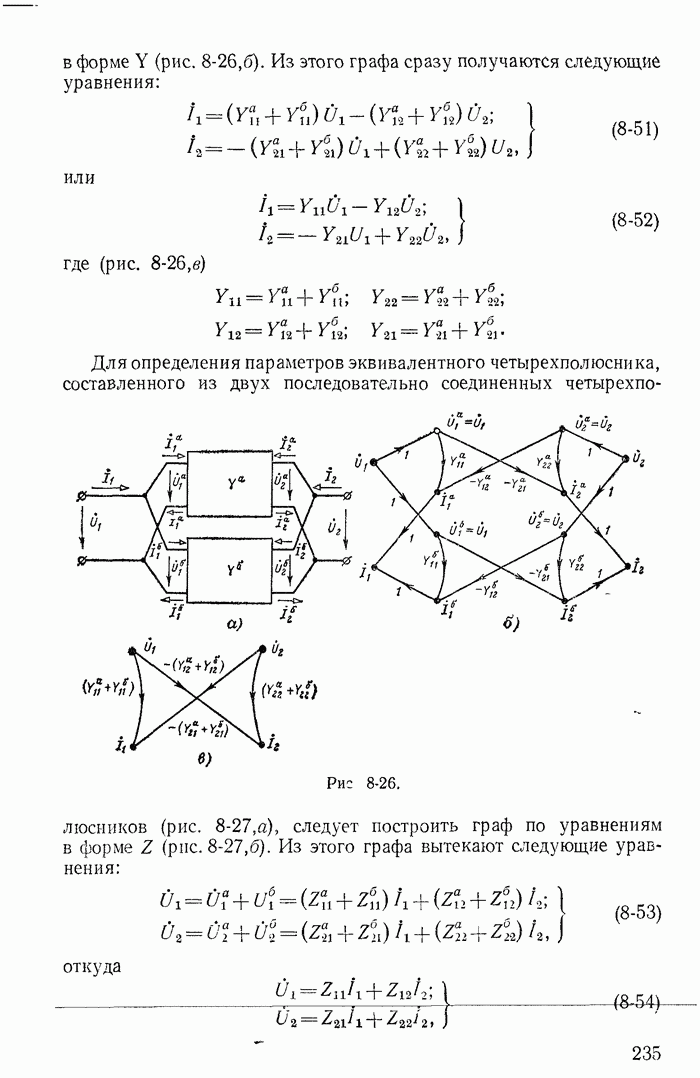
- 8-10. Графы пассивных четырехполюсников и их простейшие соединения
- Глава девятая. ЦЕПИ С ЭЛЕКТРОННЫМИ И ПОЛУПРОВОДНИКОВЫМИ ПРИБОРАМИ В ЛИНЕЙНОМ РЕЖИМЕ
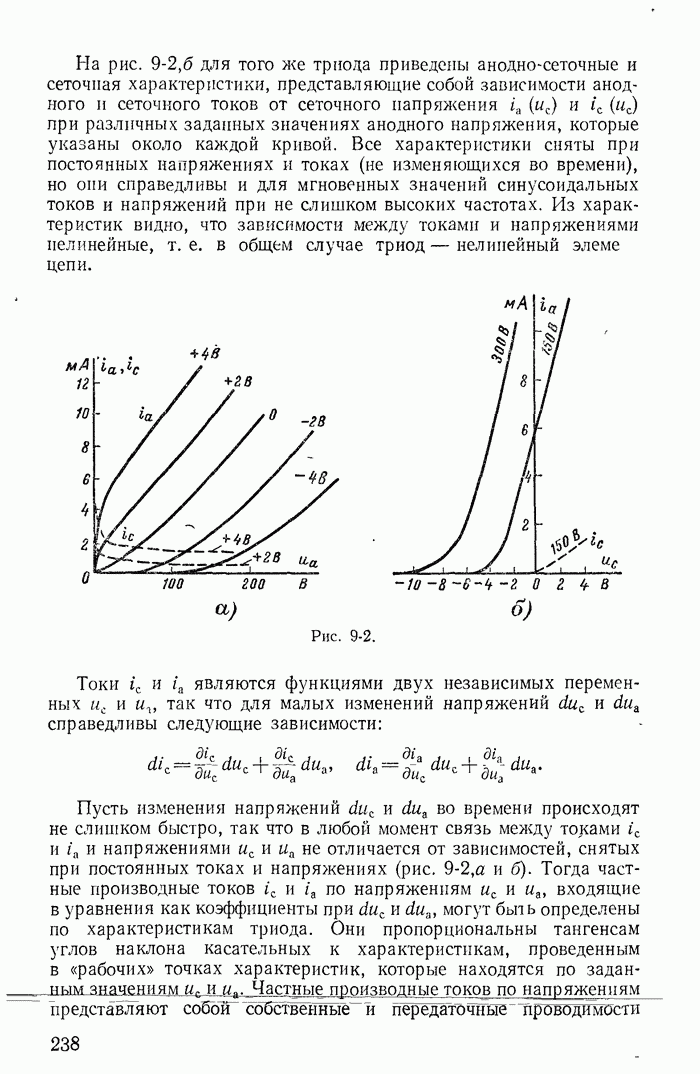
- 9-2. Эквивалентные схемы лампового триода
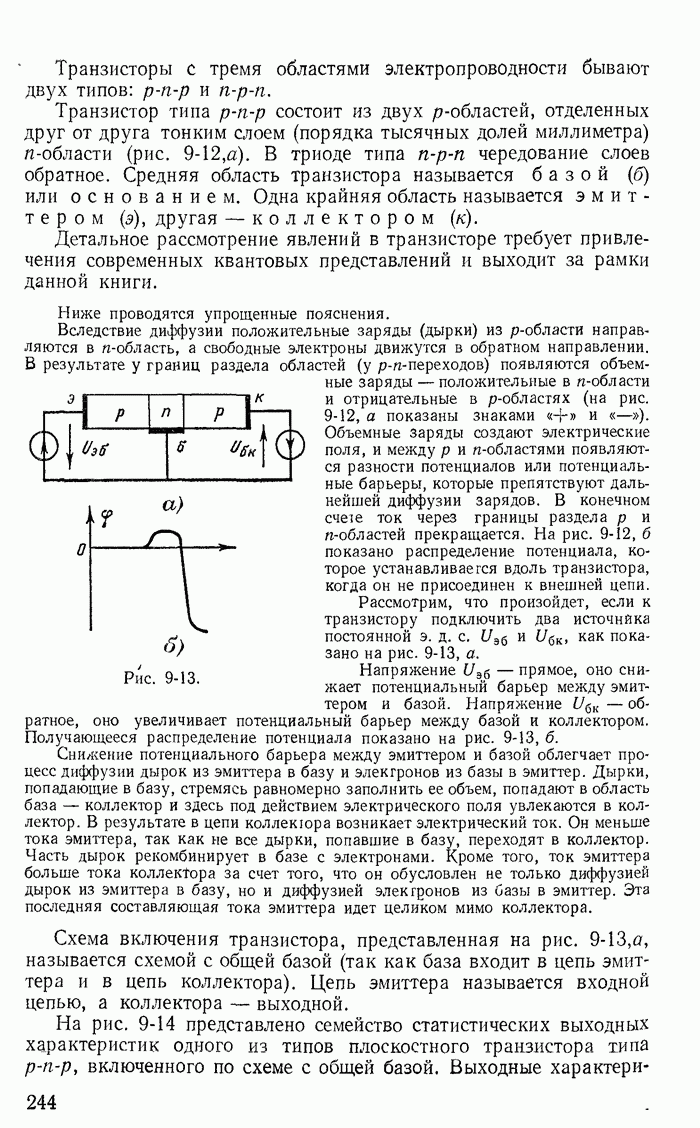
- 9-3. Транзисторы (полупроводниковые триоды)
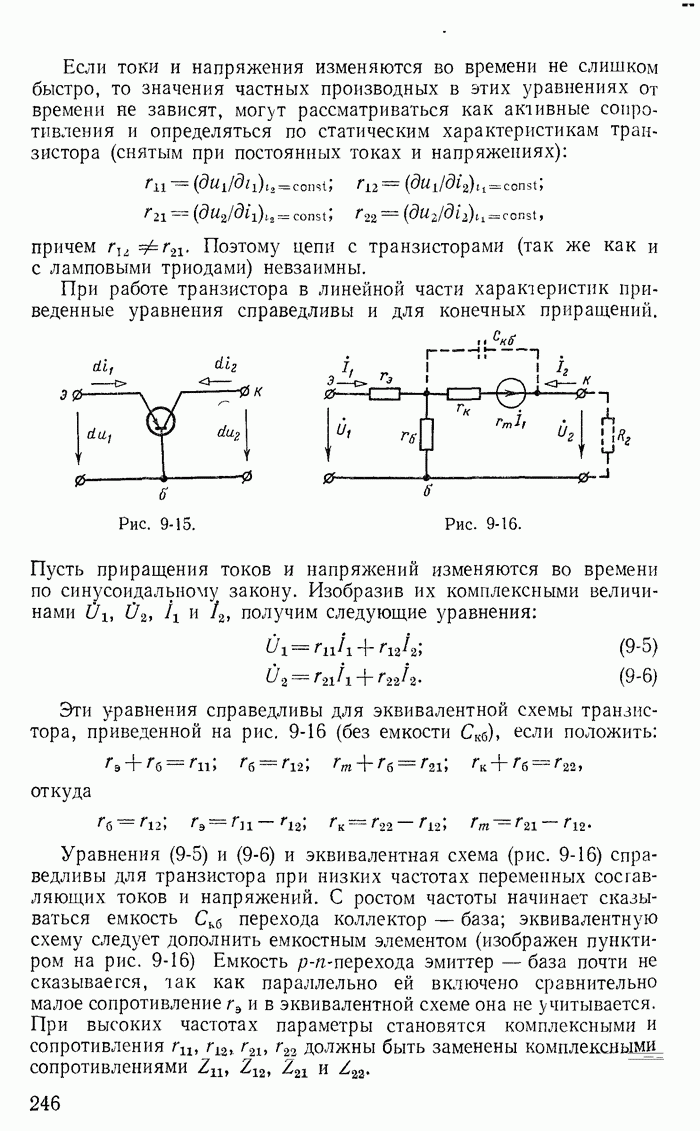
- 9-4. Эквивалентные схемы транзисторов
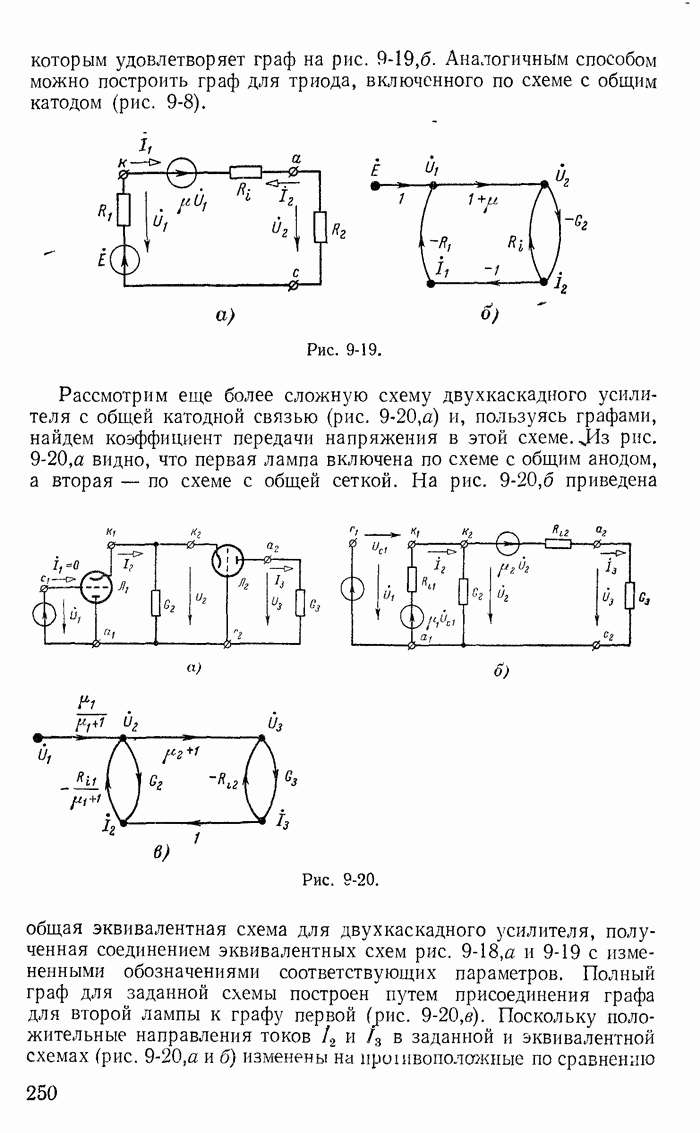
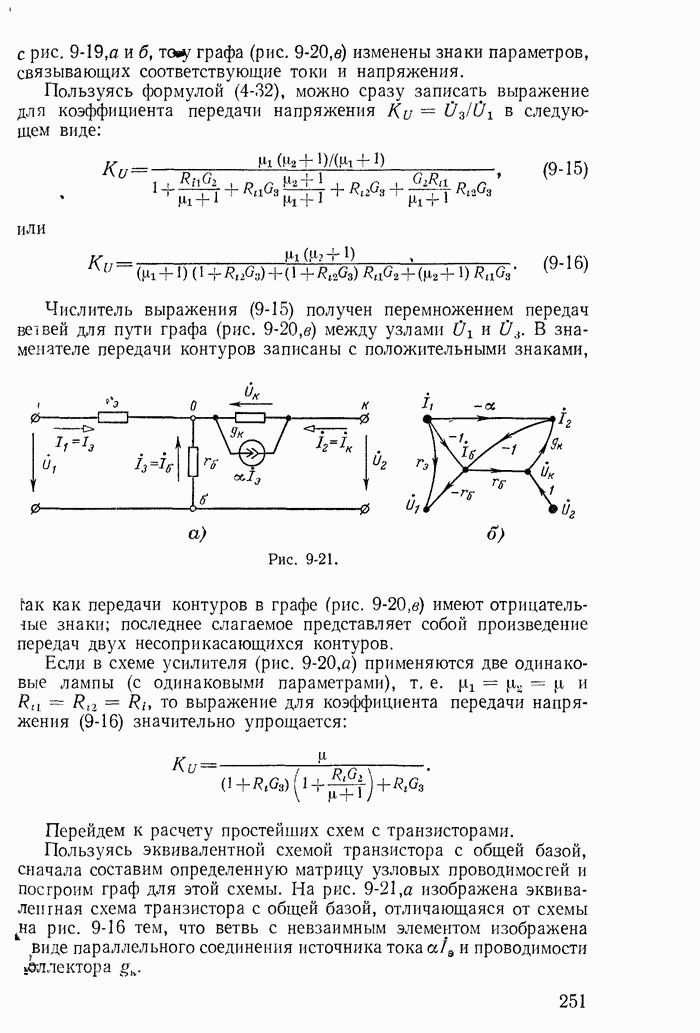
- 9-5. Простейшие электрические цепи с невзаимными элементами и их направленные графы
- Глава десятая. ТРЕХФАЗНЫЕ ЦЕПИ
- 10-2. Соединения звездой и многоугольником
- 10-3. Симметричный режим трехфазной цепи
- 10-4. Некоторые свойства трехфазных цепей с различными схемами соединений
- 10-5. Расчет симметричных режимов трехфазных цепей
- 10-6. Расчет несимметричных режимов трехфазных цепей со статической нагрузкой
- 10-7. Напряжения на фазах приемника в некоторых частных случаях
- 10-8. Эквивалентные схемы трехфазных линий
- 10-9. Измерение мощности в трехфазных цепях
- 10-10. Вращающееся магнитное поле
- 10-11. Принципы действия асинхронного и синхронного двигателей
- Глава одиннадцатая. МЕТОД СИММЕТРИЧНЫХ СОСТАВЛЯЮЩИХ
- 11-2. Некоторые свойства трехфазных цепей в отношении симметричных составляющих токов и напряжений
- 11-3. Сопротивления симметричной трехфазной цепи для токов различных последовательностей
- 11-4. Определение токов в симметричной цепи
- 11-5. Симметричные составляющие напряжений и токов в несимметричной трехфазной цепи
- 11-6. Расчет цепи с несимметричной нагрузкой
- 11-7. Расчет цепи с несимметричным участком в линии
- Глава двенадцатая. НЕСИНУСОИДАЛЬНЫЕ ТОКИ
- 12-2. Разложение периодической несинусоидальной кривой в тригонометрический ряд
- 12-3. Максимальные, действующие и средние значения несинусоидальных периодических э. д. с., напряжений и токов
- 12-4. Коэффициенты, характеризующие форму несинусоидальных периодических кривых
- 12-5. Несинусоидальные кривые с периодической огибающей
- 12-6. Действующие значения э. д. с., напряжений и токов с периодическими огибающими
- 12-7. Расчет цепей с несинусоидальными периодическими э. д. с. и токами
- 12-8. Резонанс при несинусоидальных э. д. с. и токах
- 12-9. Мощность периодических несинусоидальных токов
- 12-10. Высшие гармоники в трехфазных цепях
- Глава тринадцатая. КЛАССИЧЕСКИЙ МЕТОД РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ
- 13-2. Переходный, принужденный и свободный процессы
- 13-3. Короткое замыкание цепи r, L
- 13-4. Включение цепи r, L на постоянное напряжение
- 13-5. Включение цепи r, L на синусоидальное напряжение
- 13-6. Короткое замыкание цепи r, С
- 13-7. Включение цепи r, С на постоянное напряжение
- 13-8. Включение цепи r, С на синусоидальное напряжение
- 13-9. Переходные процессы в неразветвленной цепи r, С
- 13-10. Апериодический разряд конденсатора
- 13-11. Предельный случай апериодического разряда конденсатора
- 13-12. Периодический (колебательный) разряд конденсатора
- 13-13. Включение цепи r, С на постоянное напряжение
- 13-14. Общий случай расчета переходных процессов классическим методом
- 13-15. Включение пассивного двухполюсника на непрерывно изменяющееся напряжение (формула или интеграл Дюамеля)
- 13-16. Включение пассивного двухполюсника на напряжение любой формы
- 13-17. Временная и импульсная переходные характеристики
- 13-18. Запись теоремы свертки при помощи импульсной переходной характеристики
- 13-19. Переходные процессы при скачках токов в индуктивностях и напряжений на конденсаторах
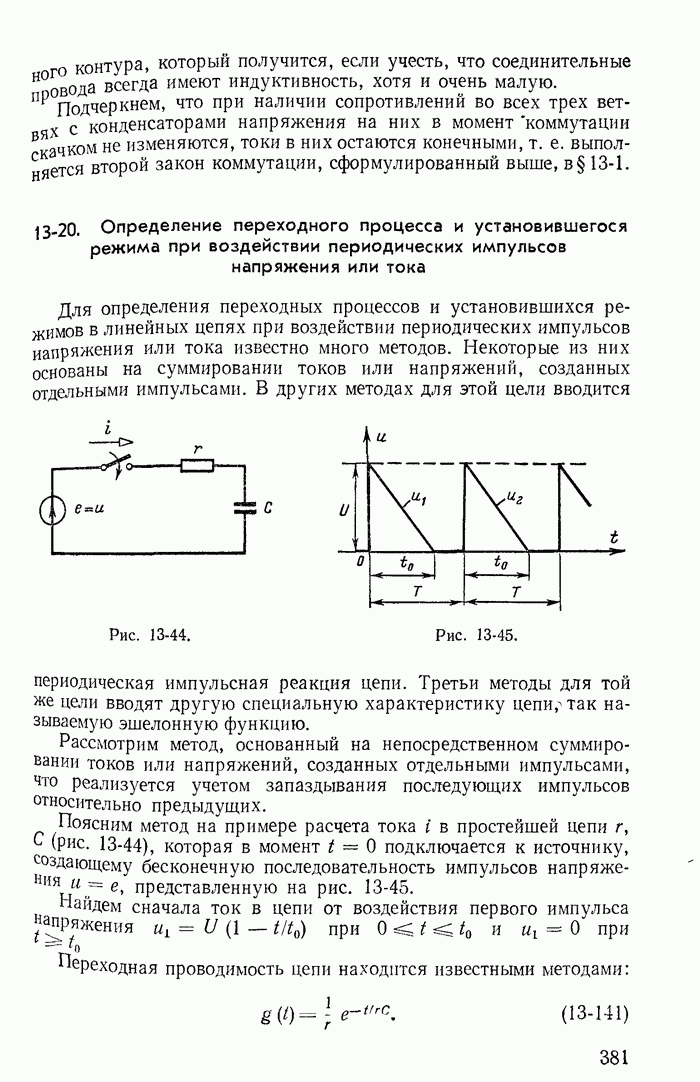
- 13-20. Определение переходного процесса и установившегося режима при воздействии периодических импульсов напряжения или тока
- Глава четырнадцатая. ОПЕРАТОРНЫЙ МЕТОД РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ
- 14-2. Законы Ома и Кирхгофа в операторной форме
- 14-3. Эквивалентные операторные схемы
- 14-4. Переходные процессы в цепях с взаимной индуктивностью
- 14-5. Сведение расчетов переходных процессов к нулевым начальным условиям
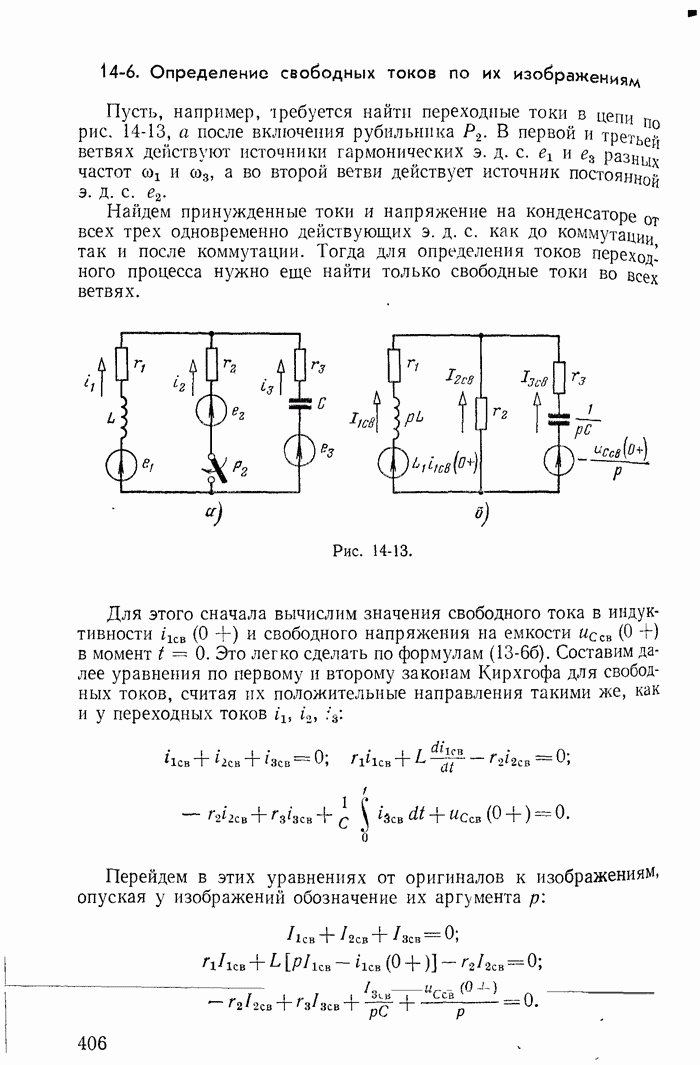
- 14-6. Определение свободных токов по их изображениям
- 14-7. Формулы включения
- 14-8. Расчет переходных процессов методом переменных состояния
- 14-9. Определение принужденного режима цепи при воздействии на нее периодического несинусоидального напряжения
- Глава пятнадцатая. ЧАСТОТНЫЙ МЕТОД РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ
- 15-2. Законы Ома и Кирхгофа и эквивалентные схемы для частотных спектров
- 15-3. Приближенный метод определения оригинала по вещественной частотной характеристике (метод трапеций)
- 15-4. О переходе от преобразований Фурье к преобразованиям Лапласа
- 15-5. Сравнение различных методов расчета переходных процессов в линейных электрических цепях
- Глава шестнадцатая. ЦЕПНЫЕ СХЕМЫ И ЧАСТОТНЫЕ ЭЛЕКТРИЧЕСКИЕ ФИЛЬТРЫ
- 16-2. Характеристическое сопротивление и постоянная передачи симметричного четырехполюсника
- 16-3. Вносимая и рабочая постоянные передачи
- 16-4. Цепные схемы
- 16-5. Частотные электрические фильтры
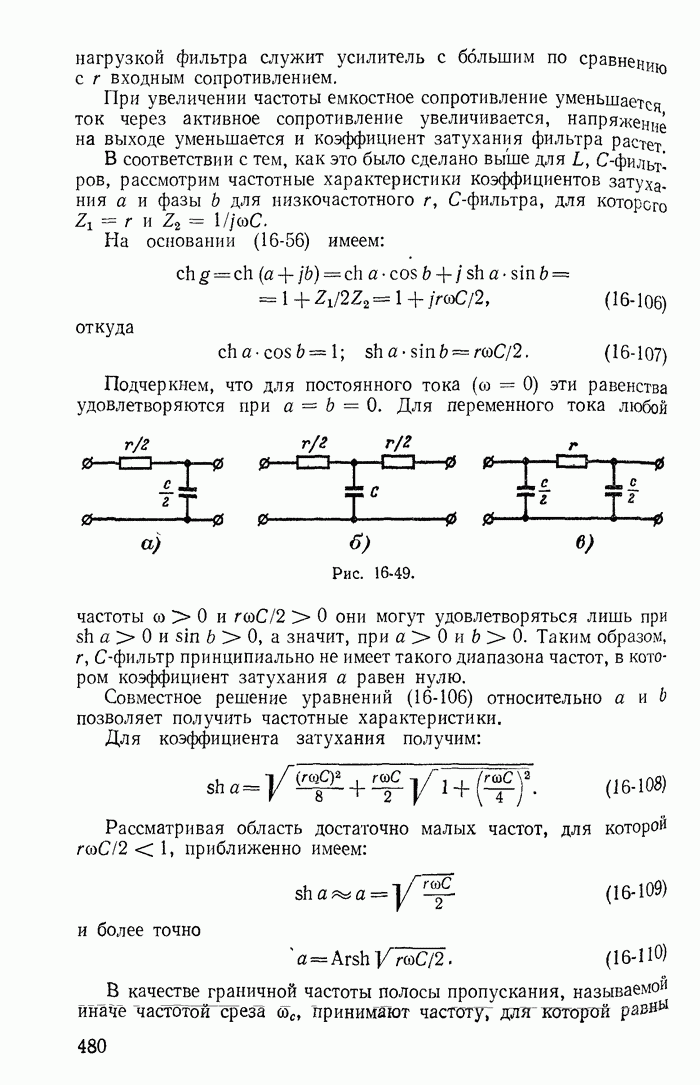
- 16-6. Низкочастотные фильтры
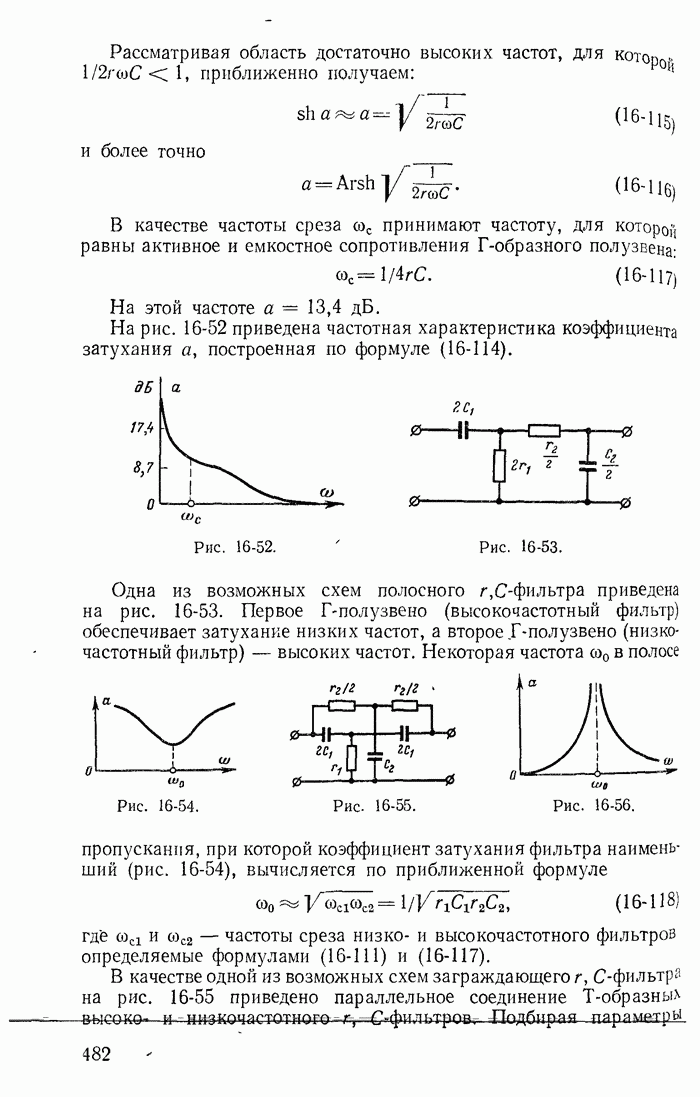
- 16-8. Полосные фильтры
- 16-11. Г-образный фильтр как пример несимметричного фильтра
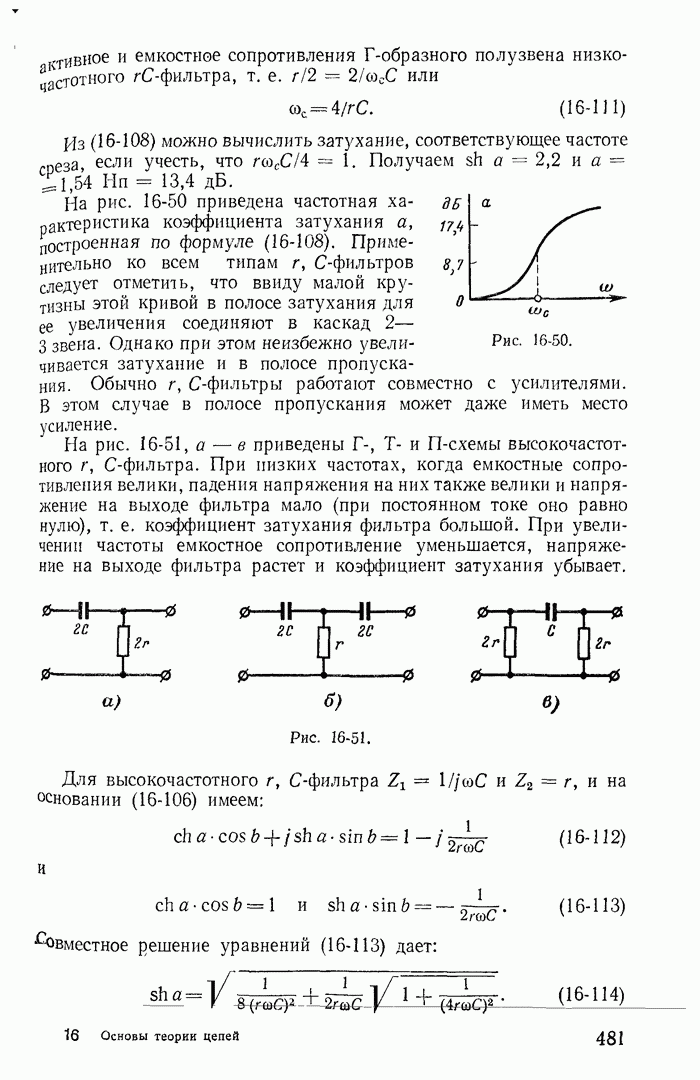
- 16-12. Безындукционные (или r, C) фильтры
- Глава семнадцатая. СИНТЕЗ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
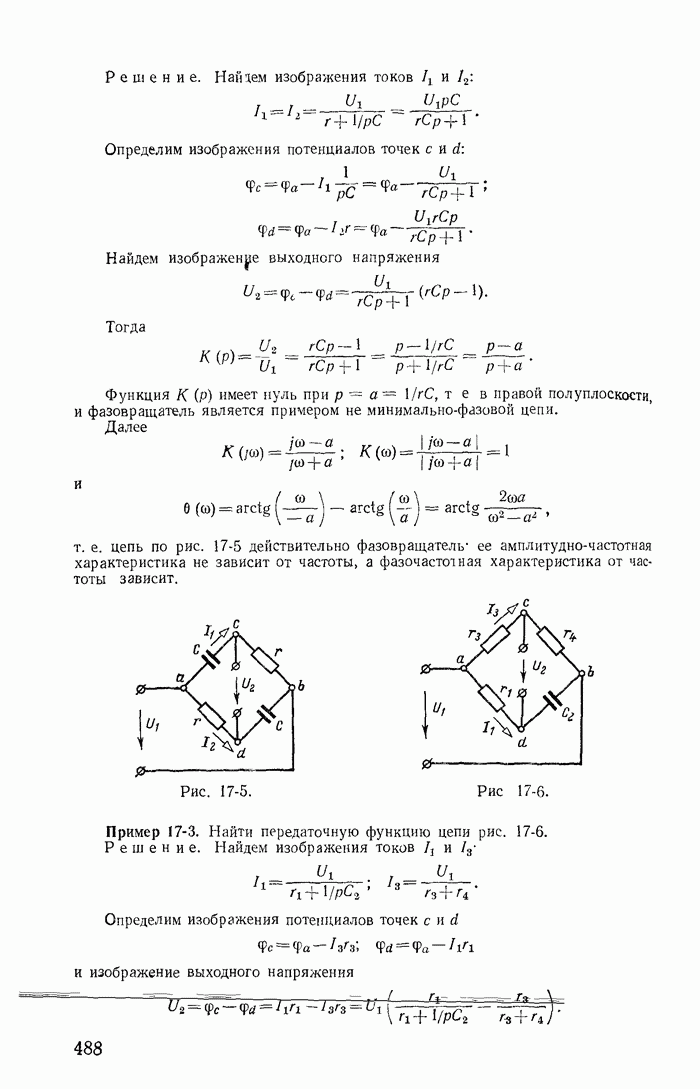
- 17-2. Передаточная функция четырехполюсника. Цепи минимальной фазы
- 17-3. Входные функции цепей. Положительные вещественные функции
- 17-4. Реактивные двухполюсники
- 17-5. Частотные характеристики реактивных двухполюсников
- 17-6. Синтез реактивных двухполюсников. Метод Фостера
- 17-7. Синтез реактивных двухполюсников. Метод Кауэра
- 17-8. Синтез двухполюсников с потерями. Метод Фостера
- 17-9. Синтез двухполюсников с потерями. Метод Кауэра
- 17-10. Понятие о синтезе четырехполюсников
- Раздел второй. ЛИНЕЙНЫЕ ЦЕПИ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
- Глава восемнадцатая. ГАРМОНИЧЕСКИЕ ПРОЦЕССЫ В ЦЕПЯХ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
- 18-2. Уравнения однородной линии
- 18-3. Установившийся режим в однородной линии
- 18-4. Уравнения однородной линии с гиперболическими функциями
- 18-5. Характеристики однородной линии
- 18-6. Входное сопротивление линии
- 18-7. Коэффициент отражения волны
- 18-8. Согласованная нагрузка линии
- 18-9. Линия без искажений
- 18-10. Холостой ход, короткое замыкание и нагрузочный режим линии с потерями
- 18-11. Линии без потерь
- 18-12. Стоячие волны
- 18-13. Линия как четырехполюсник
- Глава девятнадцатая. ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЦЕПЯХ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
- 19-2. Общее решение уравнений однородной линии
- 19-3. Возникновение волн с прямоугольным фронтом
- 19-4. Общие случаи нахождения волн, возникающих при переключениях
- 19-5. Отражение волны с прямоугольным фронтом от конца линии
- 19-6. Общий метод определения отраженных волн
- 19-7. Качественное рассмотрение переходных процессов в линиях, содержащих сосредоточенные емкости и индуктивности
- 19-8. Многократные отражения волн с прямоугольным фронтом от активного сопротивления
- 19-9. Блуждающие волны
- Раздел III. НЕЛИНЕЙНЫЕ ЦЕПИ
- Глава двадцатая. НЕЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПРИ ПОСТОЯННЫХ ТОКАХ И НАПРЯЖЕНИЯХ
- 20-2. Графический метод расчета неразветвленных цепей с нелинейными элементами
- 20-3. Графический метод расчета цепей с параллельным соединением нелинейных элементов
- 20-4. Графический метод расчета цепей со смешанным соединением нелинейных и линейных элементов
- 20-5. Применение эквивалентных схем с источниками э. д. с. для исследования режима нелинейных цепей
- 20-6. Вольт-амперные характеристики нелинейных активных двухполюсников
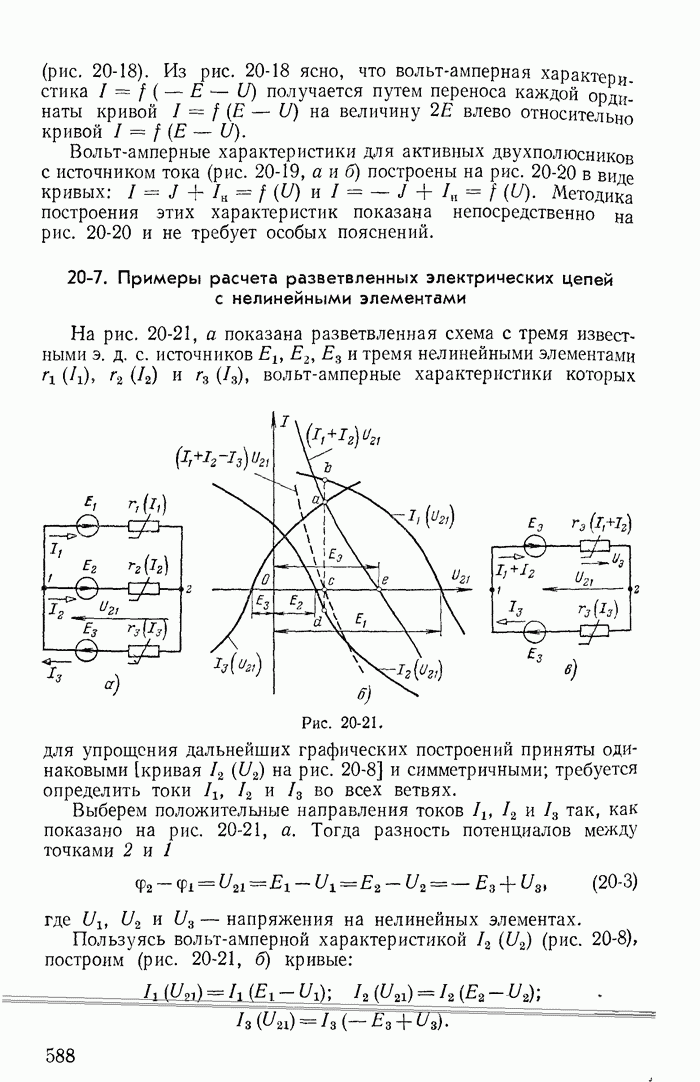
- 20-7. Примеры расчета разветвленных электрических цепей с нелинейными элементами
- 20-8. Применение теории активных двухполюсника, четырехполюсника и шестиполюсника для расчета цепей с линейными и нелинейными элементами
- 20-9. Расчет разветвленных нелинейных цепей итерационным методом (методом последовательных приближений)
- Глава двадцать первая. МАГНИТНЫЕ ЦЕПИ ПРИ ПОСТОЯННЫХ ТОКАХ
- 21-2. Расчет неразветвленных магнитных цепей
- 21-3. Расчет разветвленных магнитных цепей
- 21-4. Расчет магнитной цепи кольцевого постоянного магнита с воздушным зазором
- 21-5. Расчет неразветвленной неоднородной магнитной цепи с постоянным магнитом
- Глава двадцать вторая. ОБЩАЯ ХАРАКТЕРИСТИКА НЕЛИНЕЙНЫХ ЦЕПЕЙ ПЕРЕМЕННОГО ТОКА И МЕТОДОВ ИХ РАСЧЕТА
- 22-1. Нелинейные двухполюсники и четырехполюсники при переменных токах
- 22-2. Определение рабочих точек на характеристиках нелинейных двухполюсников и четырехполюсников
- 22-3. Явления в нелинейных цепях переменного тока
- 22-4. Методы расчета нелинейных цепей переменного тока
- Глава двадцать третья. НЕЛИНЕЙНЫЕ ЦЕПИ С ИСТОЧНИКАМИ Э. Д. С. И ТОКА ОДИНАКОВОЙ ЧАСТОТЫ
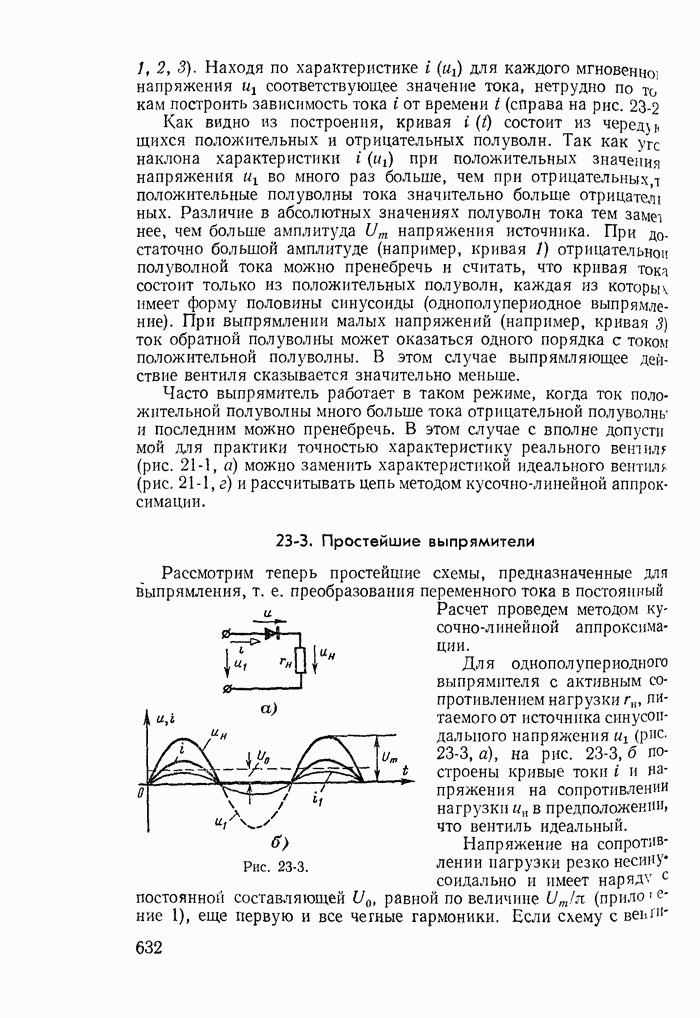
- 23-2. Форма кривой тока в цепи с вентилями
- 23-3. Простейшие выпрямители
- 23-4. Формы кривых тока и напряжения в цепях с нелинейными реактивными сопротивлениями
- 23-5. Утроители частоты
- 23-6. Формы кривых тока и напряжения в цепях с терморезисторами
- 23-7. Замена реальных нелинейных элементов условно-нелинейными
- 23-8. Учет реальных свойств стальных магнитопроводов
- 23-9. Расчет тока в катушке со стальным магнитопроводом
- 23-10. Понятие о расчете условно-нелинейных магнитных цепей
- 23-11. Явление феррорезонанса
- 23-12. Стабилизаторы напряжения
- Глава двадцать четвертая. НЕЛИНЕЙНЫЕ ЦЕПИ С ИСТОЧНИКАМИ Э. Д. С. И ТОКА РАЗЛИЧНЫХ ЧАСТОТ
- 24-1. Общая характеристика нелинейных цепей с источниками э. д. с. различных частот
- 24-2. Вентили в цепях с постоянными и переменными э. д. с.
- 24-3. Управляемые вентили в простейших выпрямителях и преобразователях постоянного тока в переменный
- 24-4. Катушки со стальными магнитопроводами в цепях с постоянными и переменными э. д. с.
- 24-5. Удвоитель частоты
- 24-6. Метод гармонического баланса
- 24-7. Влияние постоянной э. д. с. на переменную составляющую тока в цепях с нелинейными безынерционными сопротивлениядли
- 24-8. Принцип получения модулированных колебаний
- 24-9. Влияние постоянной составляющей на переменную в цепях с нелинейными индуктивностями
- 24-10. Магнитные усилители мощности
- Глава двадцать пятая. ПЕРЕХОДНЫЕ ПРОЦЕССЫ В НЕЛИНЕЙНЫХ ЦЕПЯХ
- 25-2. Включение катушки со стальным магнитопроводом на постоянное напряжение
- 25-3. Включение катушки со стальным магнитопроводом на синусоидальное напряжение
- 25-4. Импульсное воздействие в цепях с неоднозначными нелинейностями
- 25-5. Понятие о простейших запоминающих устройствах
- 25-6. Изображение переходных процессов на фазовой плоскости
- 25-7. Колебательный разряд емкости через нелинейную индуктивность
- Глава двадцать шестая. АВТОКОЛЕБАНИЯ
- 26-1. Нелинейные резисторы со спадающим участком характеристики
- 26-2. Понятие об устойчивости режима в цепи с нелинейными резисторами
- 26-3. Релаксационные колебания в цепи с отрицательным сопротивлением
- 26-4. Близкие к синусоидальным колебания в цепи с отрицательным сопротивлением
- 26-5. Фазовые траектории процессов в цепи с отрицательным сопротивлением
- 26-6. Фазовые траектории процессов в генераторе синусоидальных колебаний
- 26-7. Определение амплитуды автоколебаний методом гармонического баланса
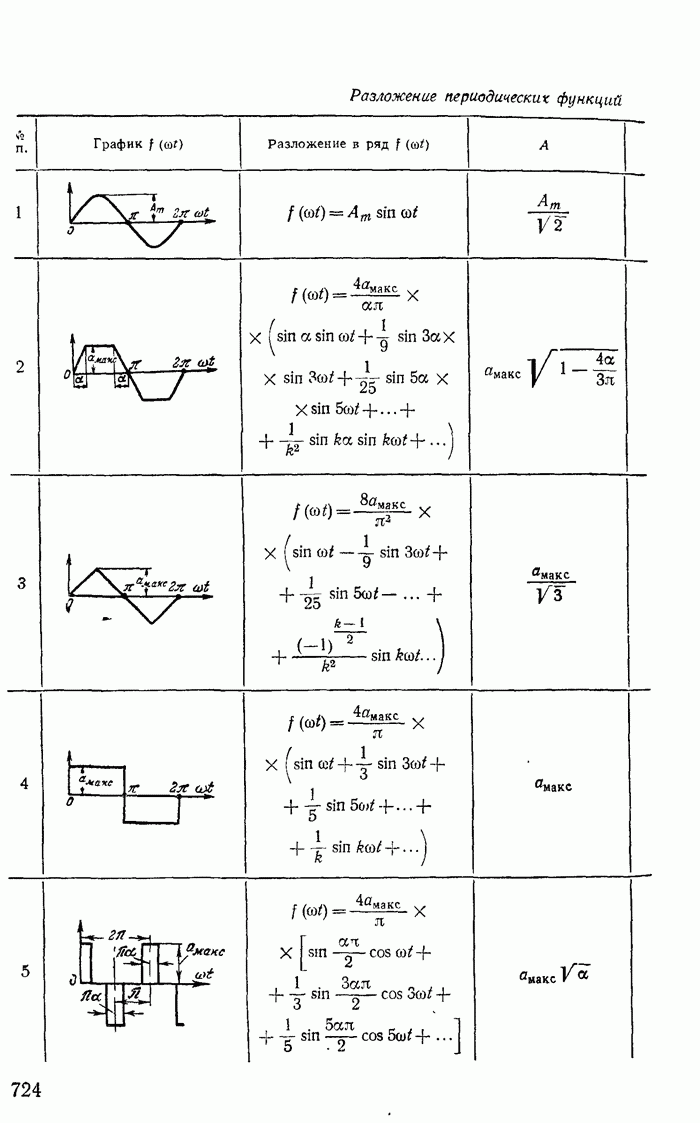
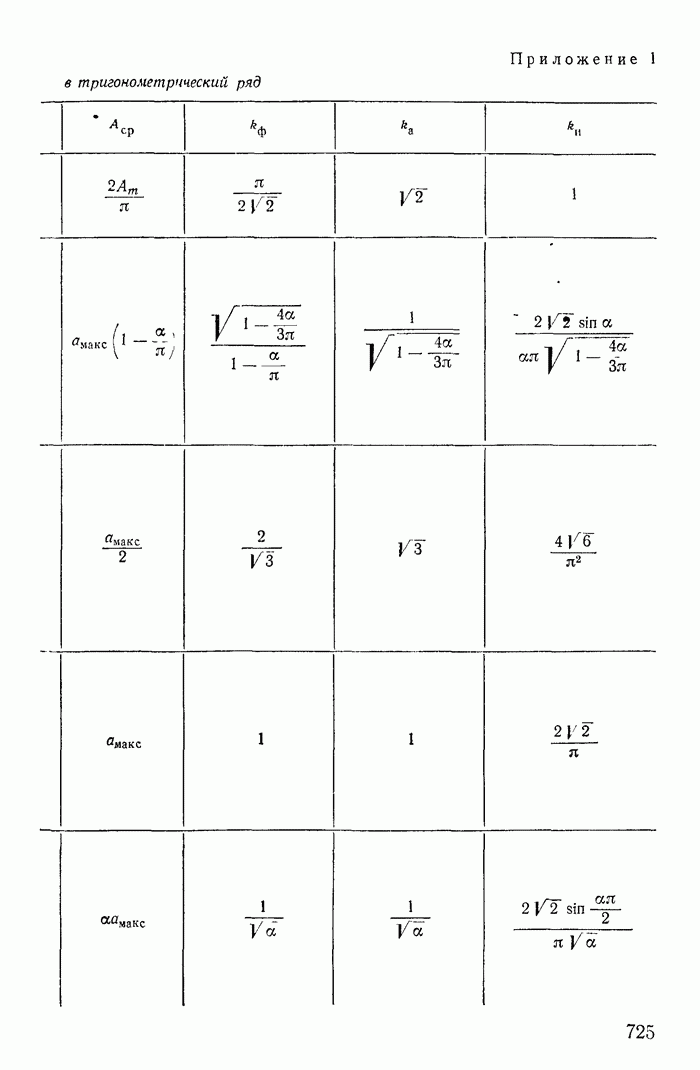
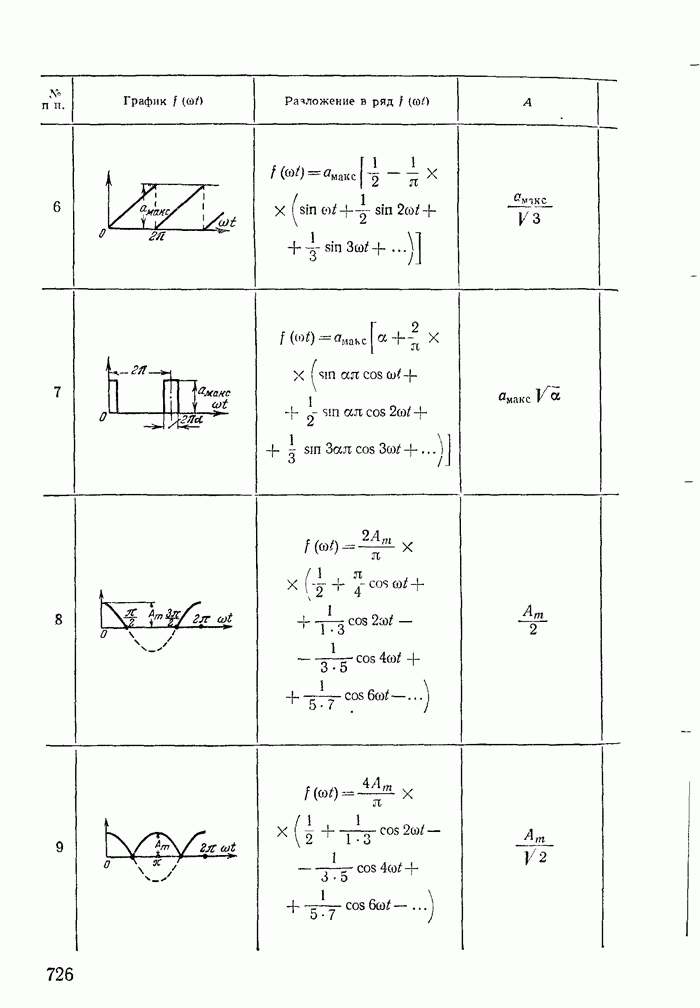
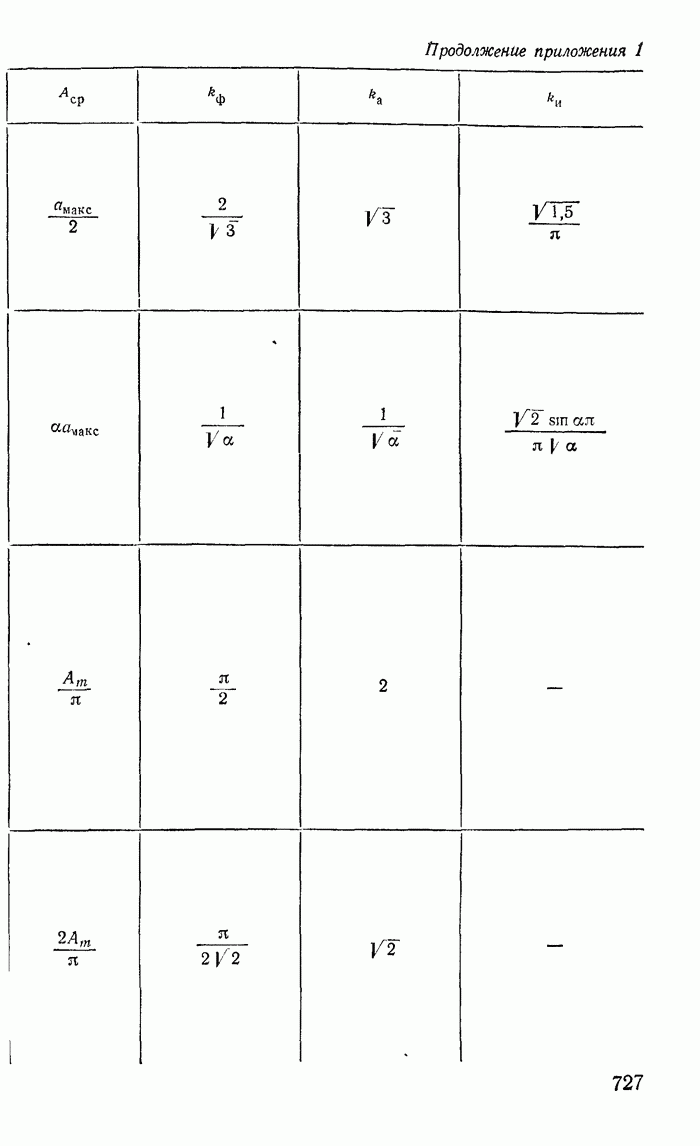
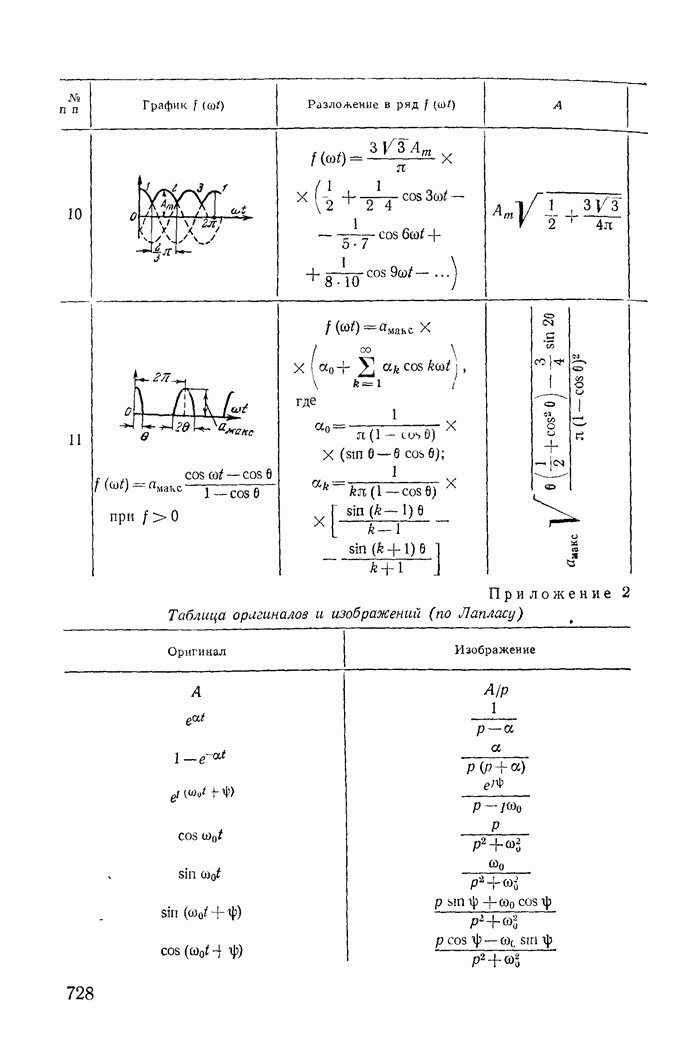
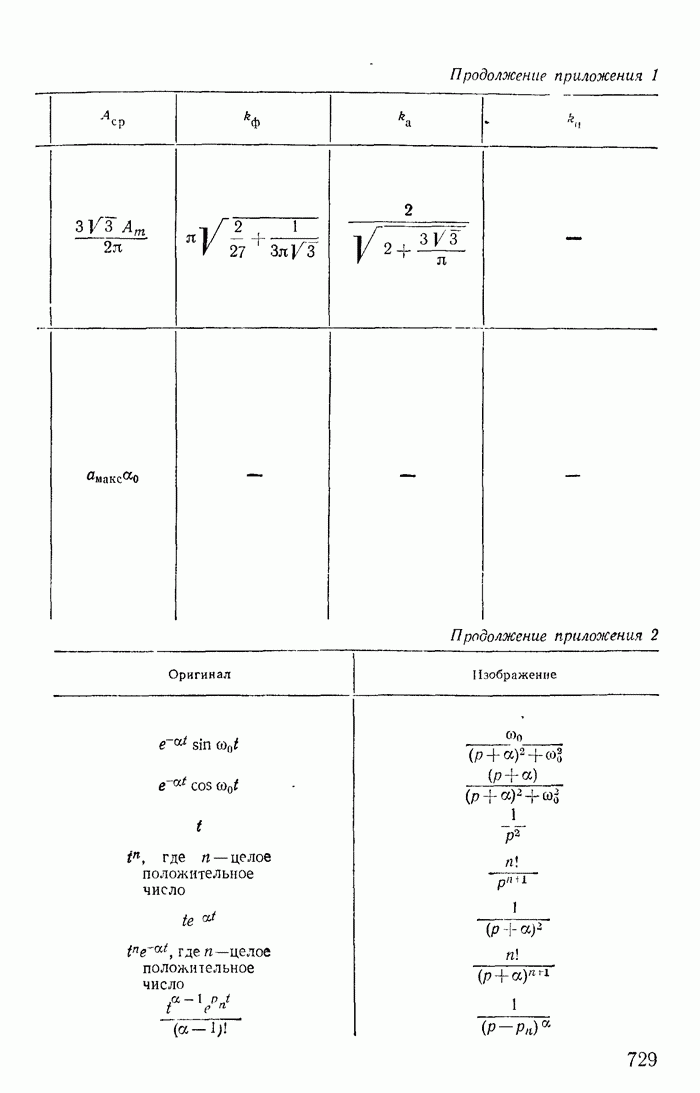
- Приложение 1. Разложение периодических функций в тригонометрический ряд
- Приложение 2. Таблица оригиналов и изображений (по Лапласу)
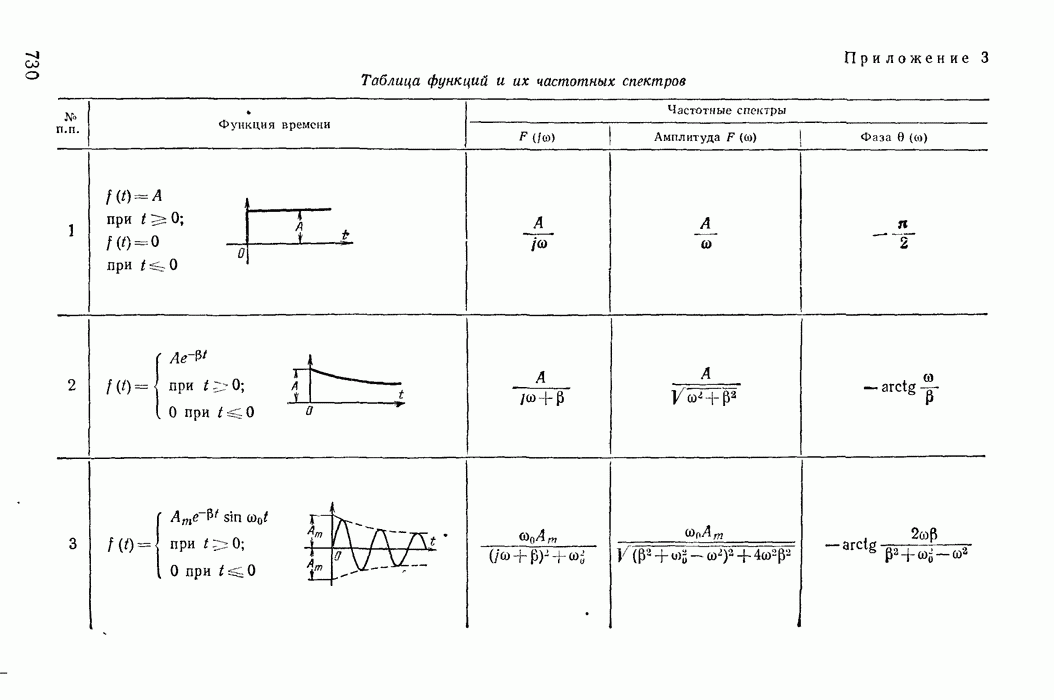
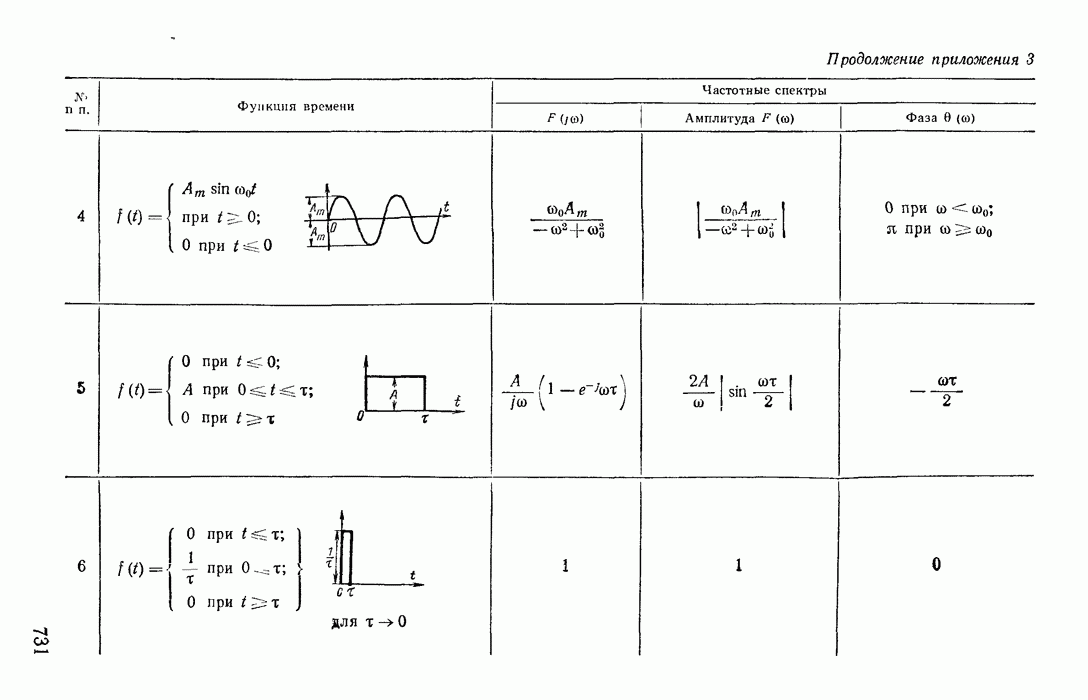
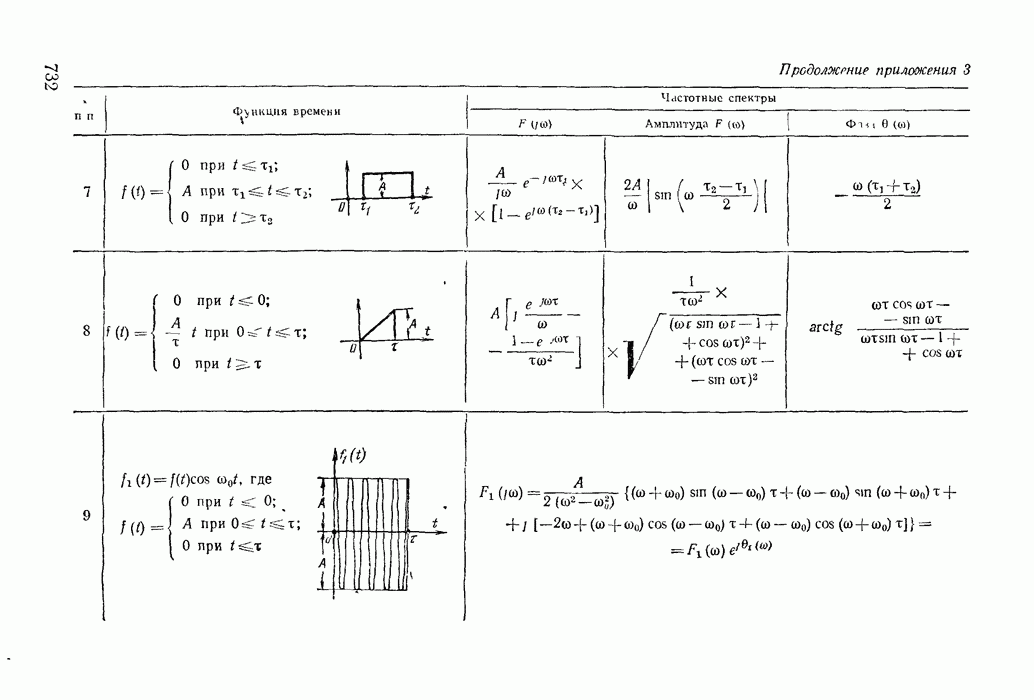
- Приложение 3. Таблица функций и их частных спектров
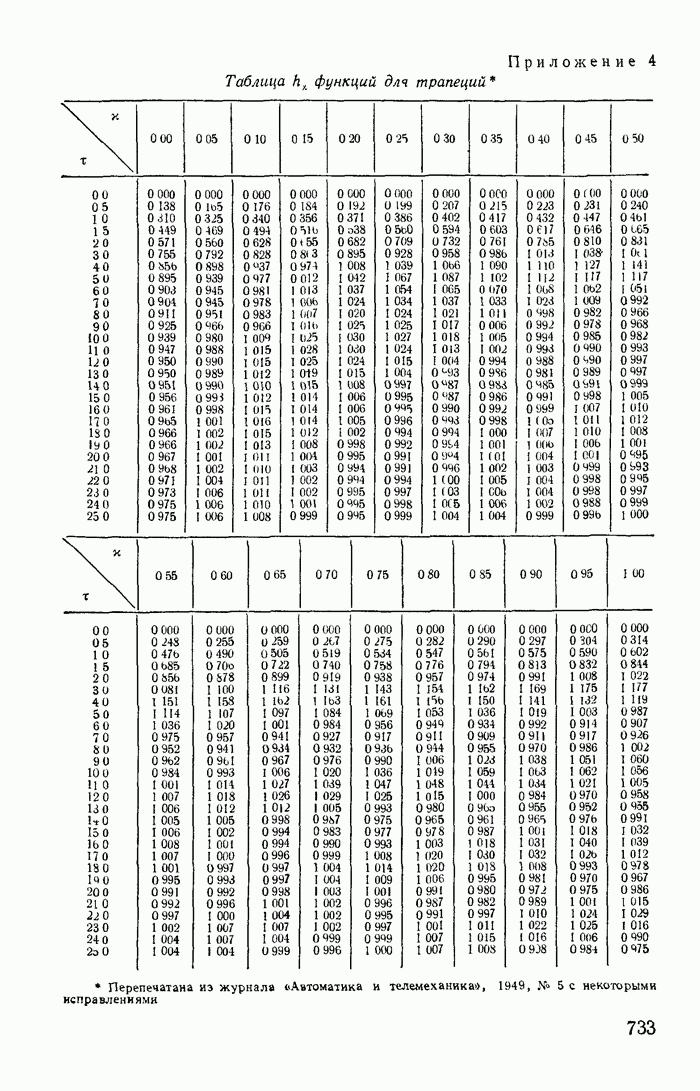
- Приложение 4. Таблица функций для трапеций
- СПИСОК ЛИТЕРАТУРЫ