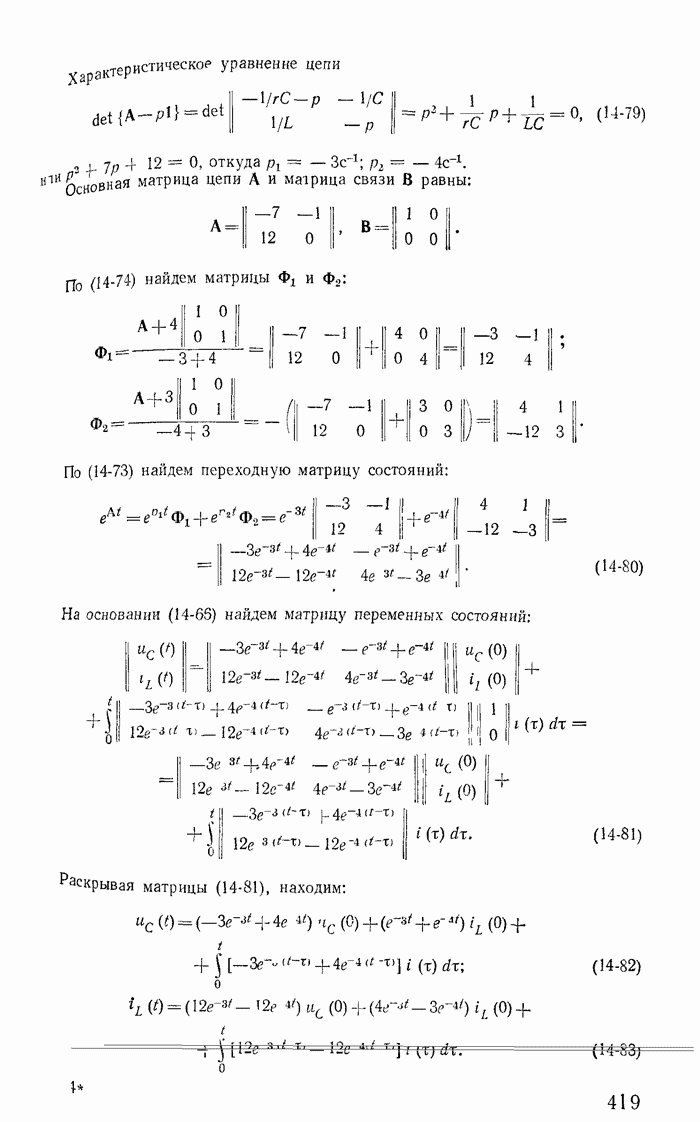| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
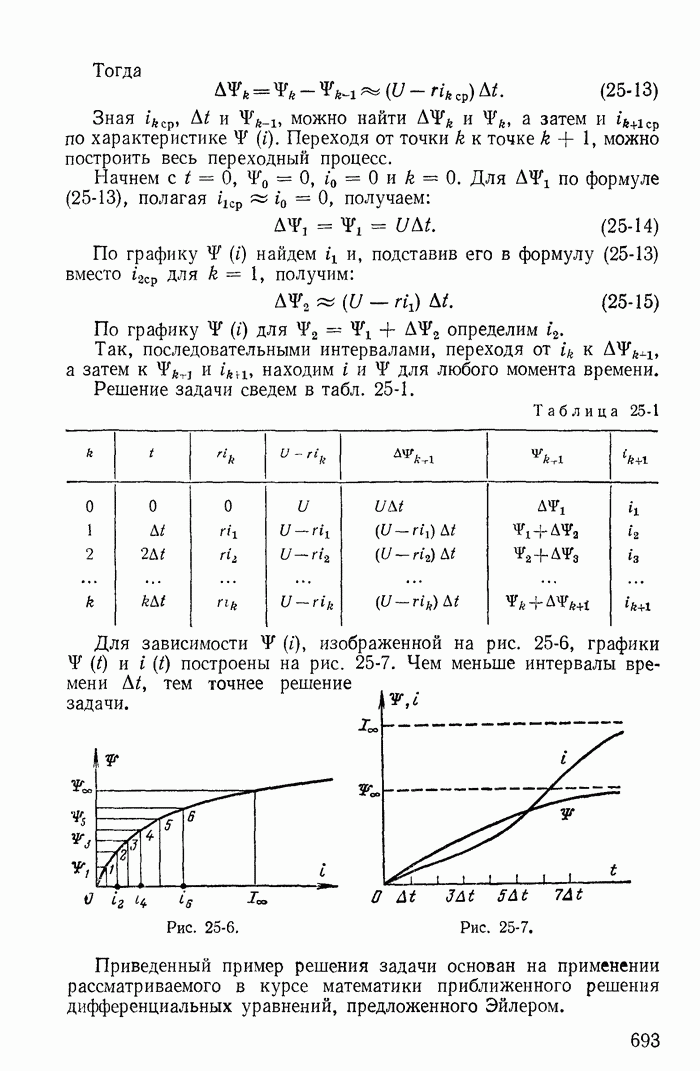
25-6. Изображение переходных процессов на фазовой плоскости
В предыдущих параграфах определялись переходные процессы в нелинейных цепях, описываемых дифференциальным уравнением первого порядка.
С повышением порядка уравнения расчет существенно усложняется. Требуется применение новых методов расчета. Одним из таких методов является изображение переходных процессов в пространстве состояний или в фазовом пространстве.
Переходные процессы можно рассматривать в различных системах координат. До сих пор переходные процессы рассматривались в координатах i и t, Y и t, q и t или и и t. По оси абсцисс откладывалось время, а по оси ординат — исследуемая величина.
Однако те же явления исследуются и в другой системе координат.
Для переходного процесса, описываемого нелинейным дифференциальным уравнением порядка  или
или  нелинейными дифференциальными уравнениями первого порядка, всегда можно выбрать
нелинейными дифференциальными уравнениями первого порядка, всегда можно выбрать  таких переменных, называемых координатами состояния, что система уравнений принимает вид:
таких переменных, называемых координатами состояния, что система уравнений принимает вид:
 (25-34)
(25-34)
Здесь  — координата состояния;
— координата состояния;  — ее производная по времени; и, — внешнее воздействие на электрическую цепь; — некоторая нелинейная функция, в отличие от линейных цепей, где
— ее производная по времени; и, — внешнее воздействие на электрическую цепь; — некоторая нелинейная функция, в отличие от линейных цепей, где  — линейная алгебраическая функция.
— линейная алгебраическая функция.
Решение уравнений (25-34) для этого случая рассматривалось в § 14-8.
Если электрическая цепь не подвержена каким-либо внешним временным воздействиям, то  Для этого случая пространство остояний обычно называется фазовым пространством.
Для этого случая пространство остояний обычно называется фазовым пространством.
Наиболее широкое распространение изображения переходных процессов в фазовом пространстве полечило для систем ьторого порядка. В этом случае переходный процесс изображается на плоскости координат  называемой фазовой плоскостью, некоторой кривой, которая лежит в области, ограниченной по обеим осям координат, а уравнения (25-34) приобретают вид;
называемой фазовой плоскостью, некоторой кривой, которая лежит в области, ограниченной по обеим осям координат, а уравнения (25-34) приобретают вид;
 (25-35)
(25-35)
Исследование переходных процессов в электрических цепях на фазовой плоскости впервые было проведено академиками Л. И. Мандельштамом и И. Д. Папалекси и получило дальнейшее развитие в работах А. А. Андронова, С. Э. Хайкина, А. А. Витта и их учеников.
Изображение процессов на фазовой плоскости может дать представление о характере процесса без решения дифференциального уравнения в конечном виде.
При выборе фазовых координат  для описания переходного процесса возможны различные варианты. Обычно отдается предпочтение такому выбору координат, при котором
для описания переходного процесса возможны различные варианты. Обычно отдается предпочтение такому выбору координат, при котором  . В этом случае обычно обозначают
. В этом случае обычно обозначают  и записывают уравнения (25-35) в виде
и записывают уравнения (25-35) в виде
 (25-36)
(25-36)
Каждому состоянию цепи соответствует точка на фазовой плоскости, которую называют изображающей или представляющей точкой. Всякое изменение состояния цепи на фазовой плоскости изображается некоторой кривой, которую называют фазовой траекторией.
Если процесс описывается уравнениями (25-36), то в верхней полуплоскости  и представляющая точка может перемещаться только направо — в направлении возрастающих значений
и представляющая точка может перемещаться только направо — в направлении возрастающих значений  Для нижней полуплоскости, наоборот,
Для нижней полуплоскости, наоборот,  и представляющая точка может перемещаться только влево. Таким образом, движение представляющей точки происходит только по направлению движения часовой стрелки.
и представляющая точка может перемещаться только влево. Таким образом, движение представляющей точки происходит только по направлению движения часовой стрелки.
Если процесс описывается дифференциальным уравнением первого порядка, то все фазовые траектории лежат на одной кривой и представляющая точка может перемещаться только по этой кривой. Если процесс описывается дифференциальным уравнением второго порядка, то в зависимости от начальных условий представляющая точка может оказаться в любом месте фазовой плоскости.
Рассмотрим фазовые траектории простейших процессов в линейных и нелинейных цепях.
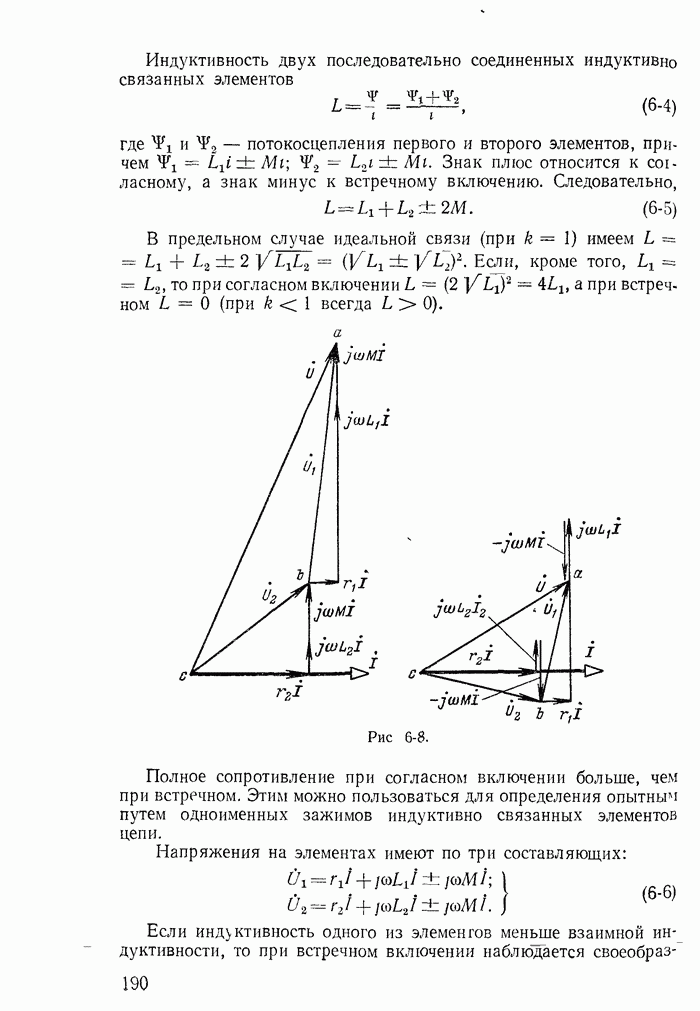
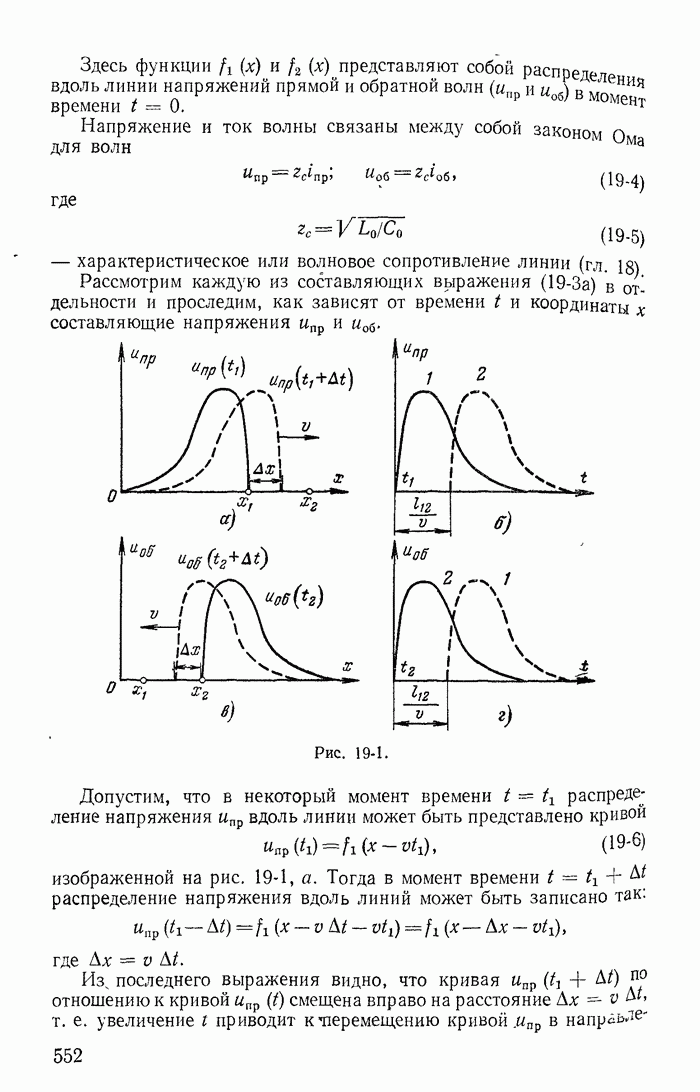
Пусть цепь  с током
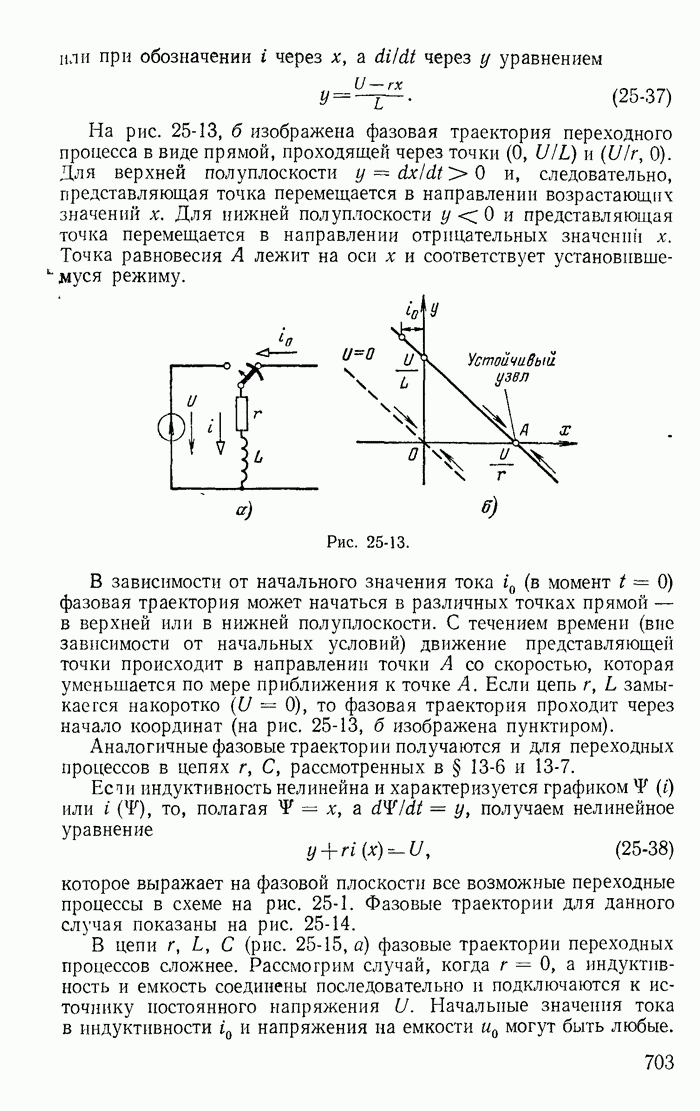
с током  переключается без разрыва тока к источнику постоянной э. д. с. с напряжения U (рис. 25-13, а). Тогда переходный процесс описывается дифференциальным уравнением
переключается без разрыва тока к источнику постоянной э. д. с. с напряжения U (рис. 25-13, а). Тогда переходный процесс описывается дифференциальным уравнением

или при обозначении i через х, a di/dt через у уравнением
 (25-37)
(25-37)
На рис. 25-13, б изображена фазовая траектория переходного процесса в виде прямой, проходящей через точки  Для верхней полуплоскости
Для верхней полуплоскости  и, следовательно, представляющая точка перемещается в направлении возрастающих значений
и, следовательно, представляющая точка перемещается в направлении возрастающих значений  . Для нижней полуплоскости
. Для нижней полуплоскости  и представляющая точка перемещается в направлении отрицательных значении
и представляющая точка перемещается в направлении отрицательных значении  Точка равновесия А лежит на оси
Точка равновесия А лежит на оси  и соответствует установившемуся режиму.
и соответствует установившемуся режиму.

Рис. 25-13.
В зависимости от начального значения тока  (в момент
(в момент  фазовая траектория может начаться в различных точках прямой — в верхней или в нижней полуплоскости. С течением времени (вне зависимости от начальных условий) движение представляющей точки происходит в направлении точки А со скоростью, которая уменьшается по мере приближения к точке А. Если цепь
фазовая траектория может начаться в различных точках прямой — в верхней или в нижней полуплоскости. С течением времени (вне зависимости от начальных условий) движение представляющей точки происходит в направлении точки А со скоростью, которая уменьшается по мере приближения к точке А. Если цепь  замыкается накоротко
замыкается накоротко  то фазовая траектория проходит через начало координат (на рис. 25-13, б изображена пунктиром).
то фазовая траектория проходит через начало координат (на рис. 25-13, б изображена пунктиром).
Аналогичные фазовые траектории получаются и для переходных процессов в цепях  , рассмотренных в § 13-6 и 13-7.
, рассмотренных в § 13-6 и 13-7.
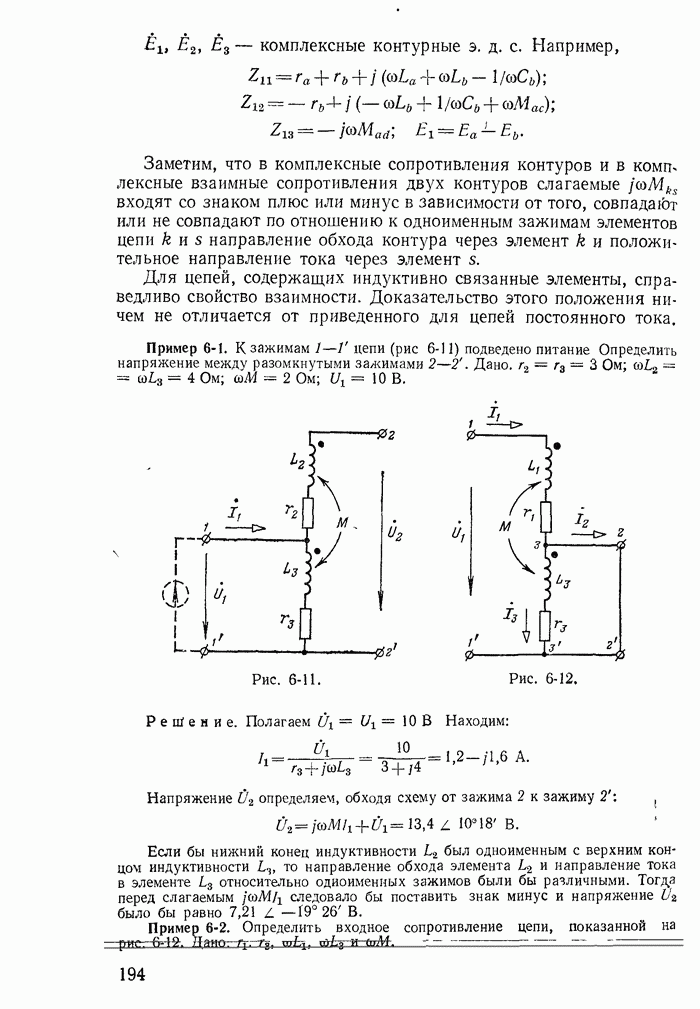
Ести индуктивность нелинейна и характеризуется графиком  или
или  то, полагая
то, полагая  получаем нелинейное уравнение
получаем нелинейное уравнение
 (25-38)
(25-38)
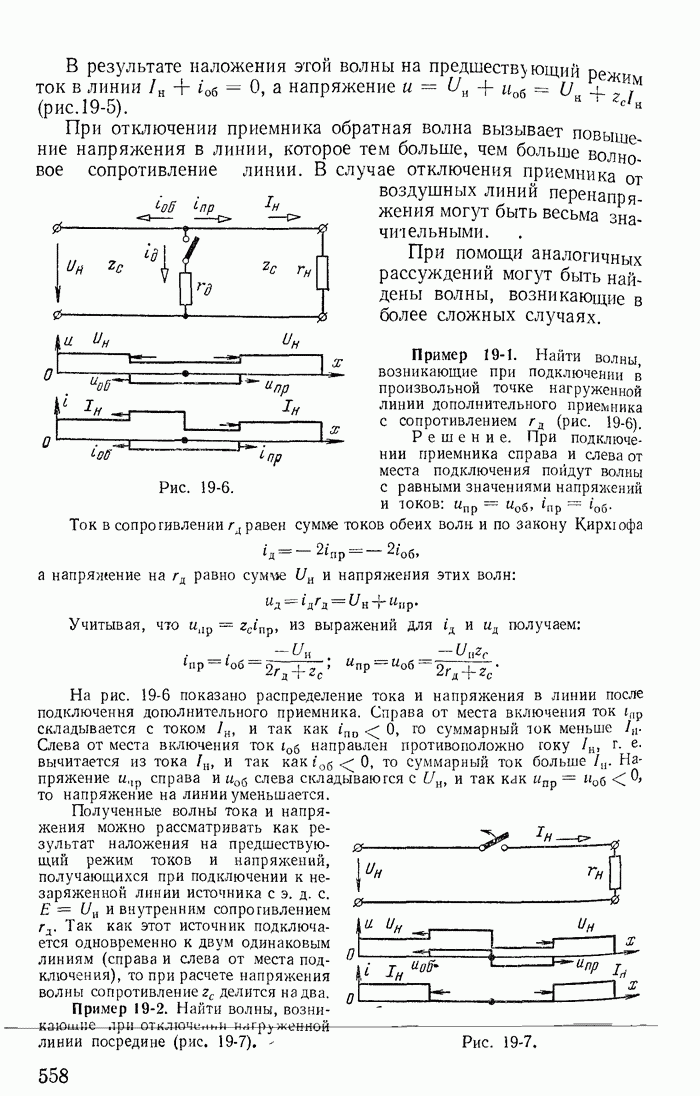
которое выражает на фазовой плоскости все возможные переходные процессы в схеме на рис. 25-1. Фазовые траектории для данного случая показаны на рис. 25-14.
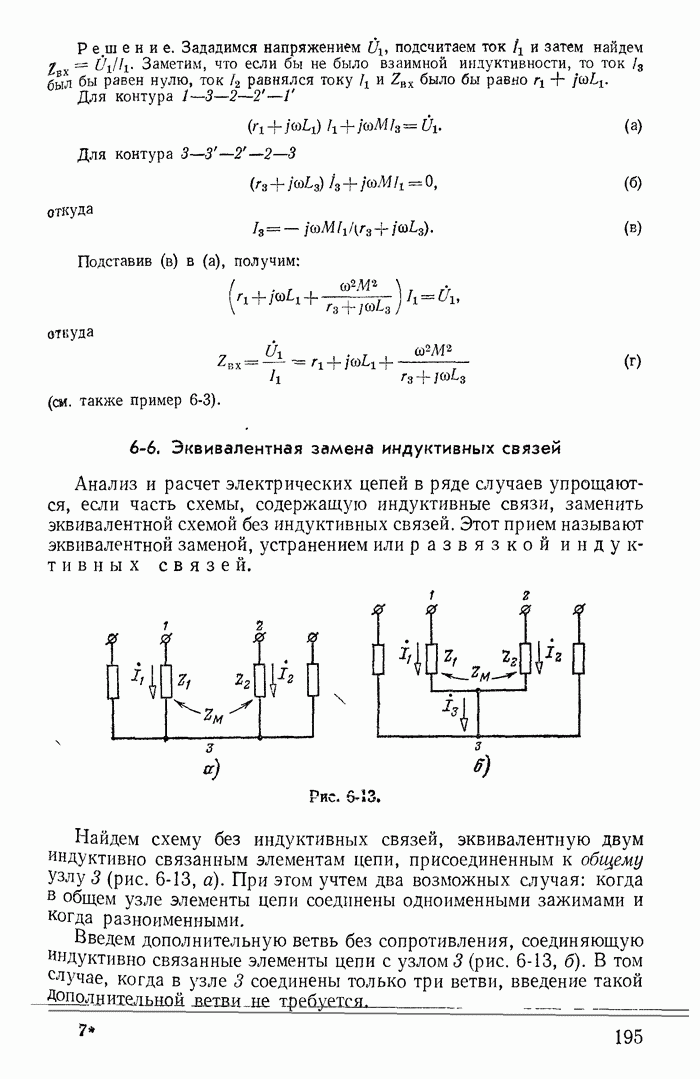
В цепи  (рис. 25-15, а) фазовые траектории переходных процессов сложнее. Рассмотрим случай, когда
(рис. 25-15, а) фазовые траектории переходных процессов сложнее. Рассмотрим случай, когда  а индуктивность и емкость соединены последовательно и подключаются к источнику постоянного напряжения U. Начальные значения тока в индуктивности
а индуктивность и емкость соединены последовательно и подключаются к источнику постоянного напряжения U. Начальные значения тока в индуктивности  и напряжения на емкости
и напряжения на емкости  могут быть любые.
могут быть любые.
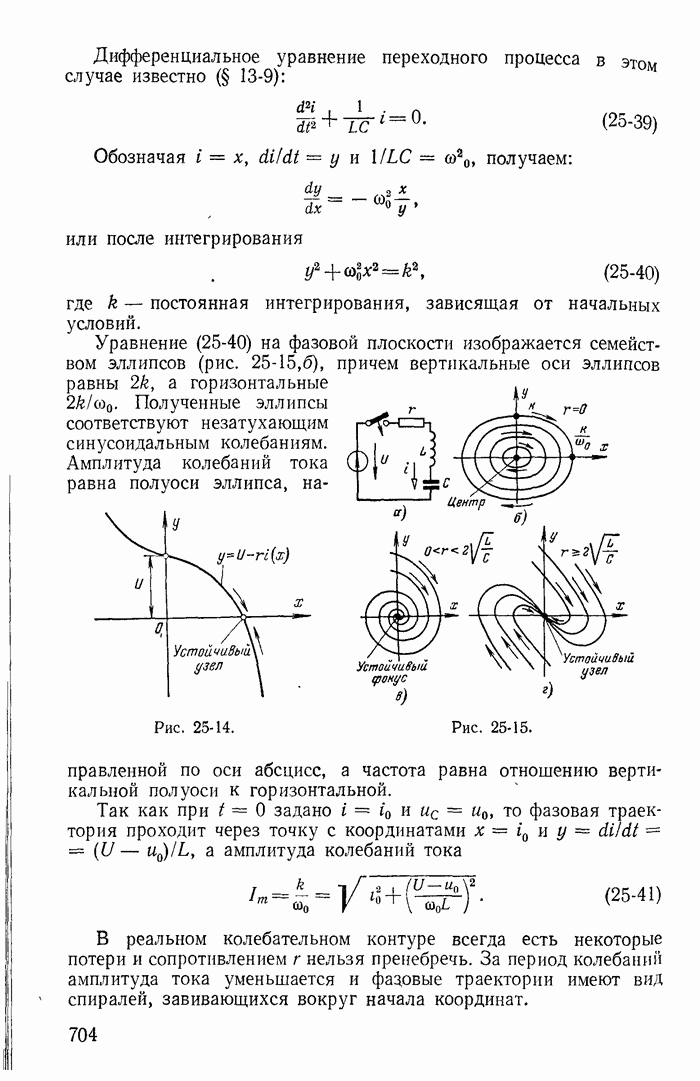
Дифференциальное уравнение переходного процесса в этом случае известно (§ 13-9):

Обозначая  получаем:
получаем:

или после интегрирования
 (25-40)
(25-40)
где k — постоянная интегрирования, зависящая от начальных условий.
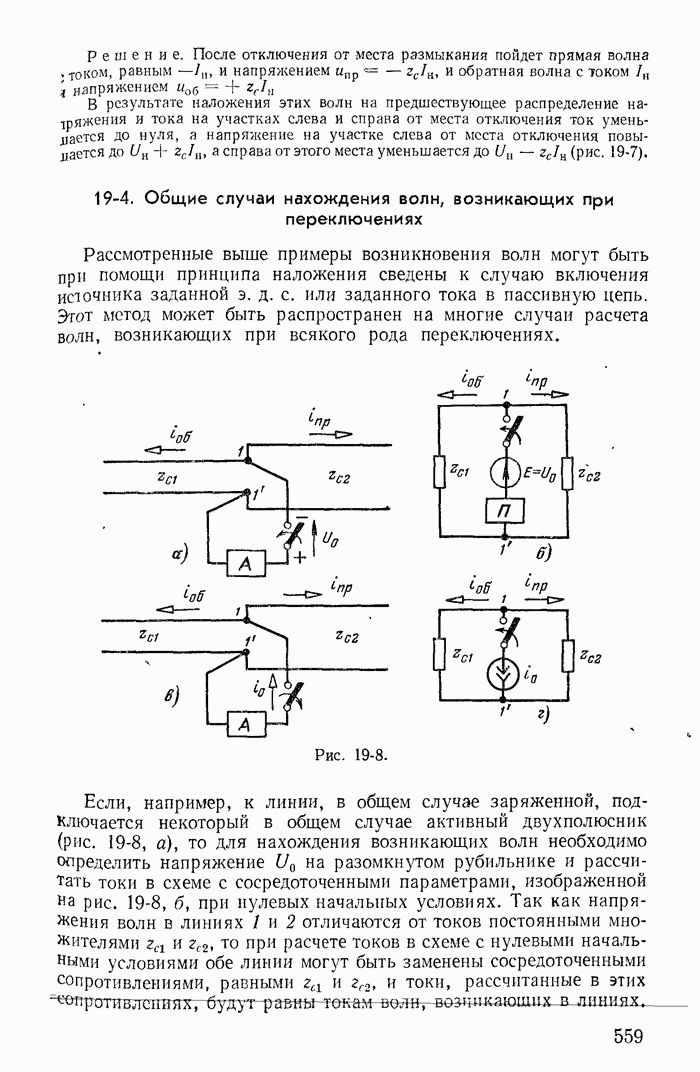
Уравнение (25-40) на фазовой плоскости изображается семейством эллипсов (рис. 25-15, б), причем вертикальные оси эллипсов равны  а горизонтальные
а горизонтальные  . Полученные эллипсы соответствуют незатухающим синусоидальным колебаниям.
. Полученные эллипсы соответствуют незатухающим синусоидальным колебаниям.

Рис. 25-14.

Рис. 25-15.
Амплитуда колебаний тока равна полуоси эллипса, направленной по оси абсцисс, а частота равна отношению вертикальной полуоси к горизонтальной.
Так как при  задано
задано  то фазовая траектория проходит через точку с координатами
то фазовая траектория проходит через точку с координатами  а амплитуда колебаний тока
а амплитуда колебаний тока

В реальном колебательном контуре всегда есть некоторые потери и сопротивлением  нельзя пренебречь. За период колебаний амплитуда тока уменьшается и фазовые траектории имеют вид спиралей, завивающихся вокруг начала координат.
нельзя пренебречь. За период колебаний амплитуда тока уменьшается и фазовые траектории имеют вид спиралей, завивающихся вокруг начала координат.
Так как за один период колебаний  в контуре теряется энергия
в контуре теряется энергия

а общая энергия, запасенная в контуре,  , причем
, причем  , то отношение радиусов двух соседних витков равно:
, то отношение радиусов двух соседних витков равно:
 (25-42)
(25-42)
Полученное выражение справедливо только при  когда при подсчете потерь AW можно пренебречь уменьшением амплитуды колебаний за один период. В общем случае колебательный процесс описывается уравнениями (13-55) и (13-56), которые являются параметрическими уравнениями спирали. Отношение
когда при подсчете потерь AW можно пренебречь уменьшением амплитуды колебаний за один период. В общем случае колебательный процесс описывается уравнениями (13-55) и (13-56), которые являются параметрическими уравнениями спирали. Отношение  представляет собой величину, обратную декременту колебания (см. § 13-12).
представляет собой величину, обратную декременту колебания (см. § 13-12).
По мере увеличения сопротивления шаг спирали увеличивается и при  семейство спиралей вырождается в семейство параболических кривых, проходящих через начало координат.
семейство спиралей вырождается в семейство параболических кривых, проходящих через начало координат.
Фазовые траектории при  изображены на рис. 25-15,б и г.
изображены на рис. 25-15,б и г.
Если сопоставить фазовые траектории для трех различных значений  (рис. 25-15), то можно отметить некоторые общие свойства этих кривых. Все кривые пересекают ось под прямым углом с переменой знака
(рис. 25-15), то можно отметить некоторые общие свойства этих кривых. Все кривые пересекают ось под прямым углом с переменой знака  . Во всех трех рассмотренных случаях имеется только одна точка равновесия, лежащая в начале координат, однако характер равновесия различный.
. Во всех трех рассмотренных случаях имеется только одна точка равновесия, лежащая в начале координат, однако характер равновесия различный.
При  равновесие наименее устойчивое. Достаточно бесконечно малого отклонения от точки равновесия, чтобы начался незатухающий колебательный процесс с бесконечно малой амплитудой колебания. При этом представляющая точка совершает периодические движения по орбите с центром в точке равновесия. Точка равновесия такого типа называется центром.
равновесие наименее устойчивое. Достаточно бесконечно малого отклонения от точки равновесия, чтобы начался незатухающий колебательный процесс с бесконечно малой амплитудой колебания. При этом представляющая точка совершает периодические движения по орбите с центром в точке равновесия. Точка равновесия такого типа называется центром.
При  все процессы, возникающие в цепи, — колебательные затухающие и представляющая точка после любого принужденного отклонения от равновесия возвращается в исходное положение равновесия, совершая при этом несколько оборотов вокруг точки равновесия. Такого рода точка равновесия называется устойчивым фокусом.
все процессы, возникающие в цепи, — колебательные затухающие и представляющая точка после любого принужденного отклонения от равновесия возвращается в исходное положение равновесия, совершая при этом несколько оборотов вокруг точки равновесия. Такого рода точка равновесия называется устойчивым фокусом.
Если  то представляющая точка, возвращаясь апериодически в состояние равновесия, движется по параболе и не совершает более полуоборота вокруг начала координат. Точка равновесия такого типа называется устойчивым узлом.
то представляющая точка, возвращаясь апериодически в состояние равновесия, движется по параболе и не совершает более полуоборота вокруг начала координат. Точка равновесия такого типа называется устойчивым узлом.
При построении фазовых траекторий процессов, описываемых Дифференциальным уравнением второй степени, удобно пользоваться методом изоклин. Изоклиной называется геометрическое
место точек, в которых касательные ко всем интегральным кривым (возможным фазовым траекториям) имеют одинаковый наклон. Если известно семейство изоклин, то фазовые траектории могут быть построены геометрическим путем без дополнительного анализа.
Пример 25-3. Построить фазовые траектории цепи  при
при  (рис 25-15, а) методом изоклин.
(рис 25-15, а) методом изоклин.
Решение. Дифференциальное уравнение цепи (см. § 13-9)

Обозначив  и применив ранее принятые обозначения
и применив ранее принятые обозначения  получаем:
получаем:
 (25-44)
(25-44)
Если  заменить через
заменить через  исключив
исключив  в Уравнении (25-44), получим:
в Уравнении (25-44), получим:

Так как во всех точках изоклин должно выполняться равенство

то уравнением изоклины является

Изоклины представляют собой семейство лучей, проходящих через начало координат. Наклон этих лучей зависит от параметров контура и наклона 0 касательных к интегральным кривым в точках их пересечения с данной изоклиной.
Из последнего уравнения следует, что ось  является изоклиной с
является изоклиной с  а ось у совпадает с изоклиной
а ось у совпадает с изоклиной  Уравнение изоклины
Уравнение изоклины  называемой изоклиной горизонтальных касательных, имеет вид:
называемой изоклиной горизонтальных касательных, имеет вид:  следовательно, она лежит во втором и четвертом квадрантах.
следовательно, она лежит во втором и четвертом квадрантах.
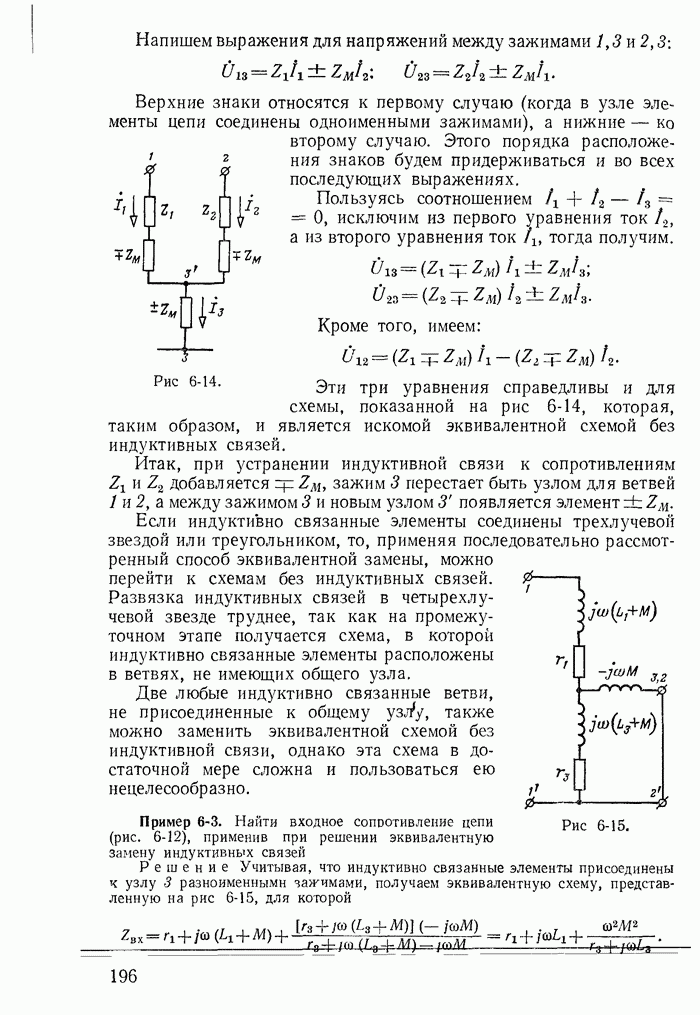
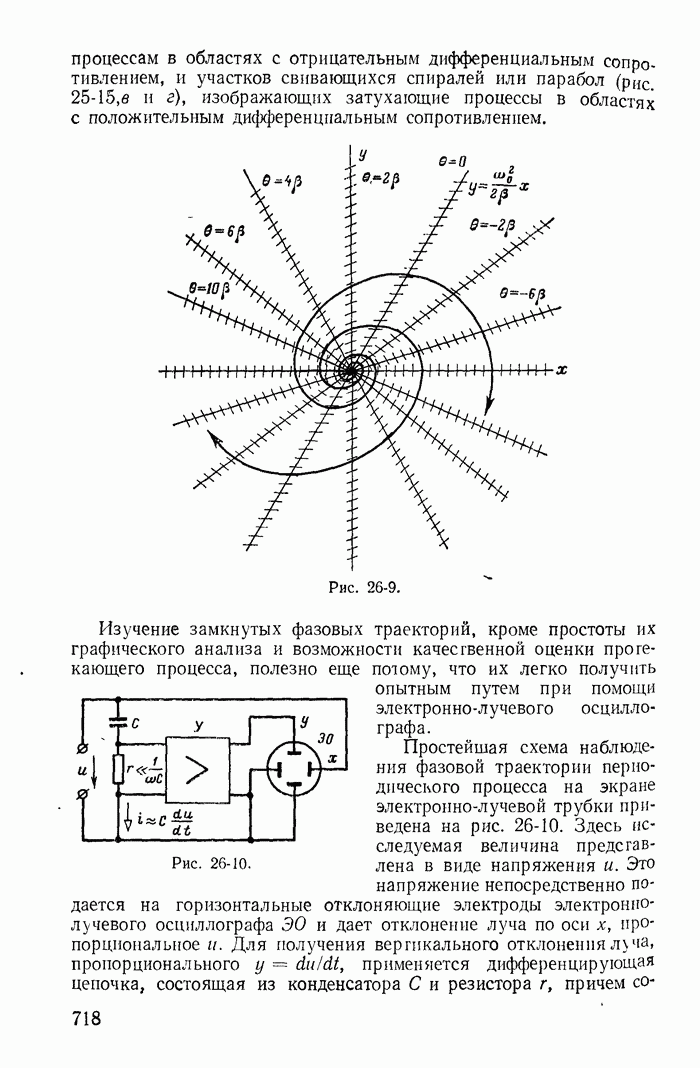
Полагая  где
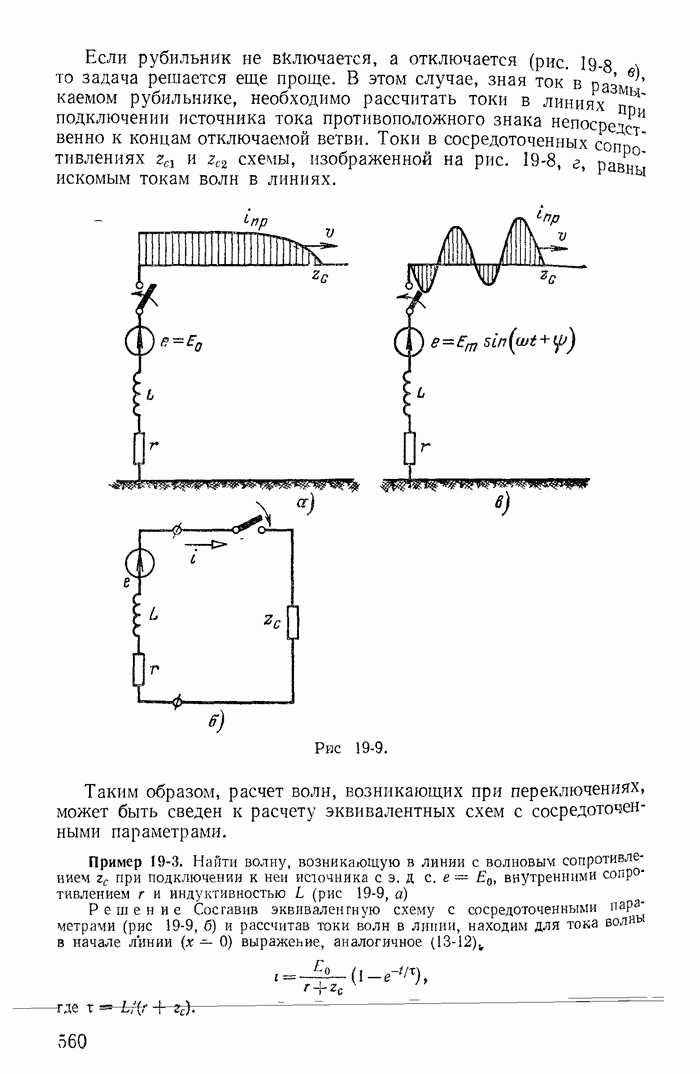
где  — целое число, получим семейство изоклин, представленных на рис. 25-16. Здесь короткими штрихами показан наклон интегральной кривой к изоклинам.
— целое число, получим семейство изоклин, представленных на рис. 25-16. Здесь короткими штрихами показан наклон интегральной кривой к изоклинам.
Проводя интегральные кривые так, чтобы они пересекли каждую изоклину под соответствующим углом, получаем фазовые траекторий переходных процессов. На рис. 25-16 показаны две фазовые траектории для разных начальных условий (точки  ).
).

Рис. 25-16.
Зная фазовые траектории, т. е. имея зависимость
 (23-47)
(23-47)
можно путем графического интегрирования найти соответствующие зависимости (1) в обратном виде:

Затруднение при вычислениях интеграла (2-48) вблизи точек  связанных с обращением подынтегральной функции в бесконечность, можно обойти, заменяя участок фазовой траектории дугой окружности с центром, лежащим на
связанных с обращением подынтегральной функции в бесконечность, можно обойти, заменяя участок фазовой траектории дугой окружности с центром, лежащим на  , и производя аналитическое интегрирование.
, и производя аналитическое интегрирование.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ К ЧЕТВЕРТОМУ ИЗДАНИЮ
- ВВЕДЕНИЕ
- Раздел первый. ЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ С СОСРЕДОТОЧЕННЫМИ ПАРАМЕТРАМИ
- 1-1. Элементы электрических цепей и электрических схем
- 1-2. Эквивалентные схемы для источников энергии
- 1-3. Закон Ома для участка цепи с э. д. с.
- 1-4. Распределение потенциала вдоль неразветвленной электрической цепи
- 1-5. Баланс мощностей для простейшей неразветвленной цепи
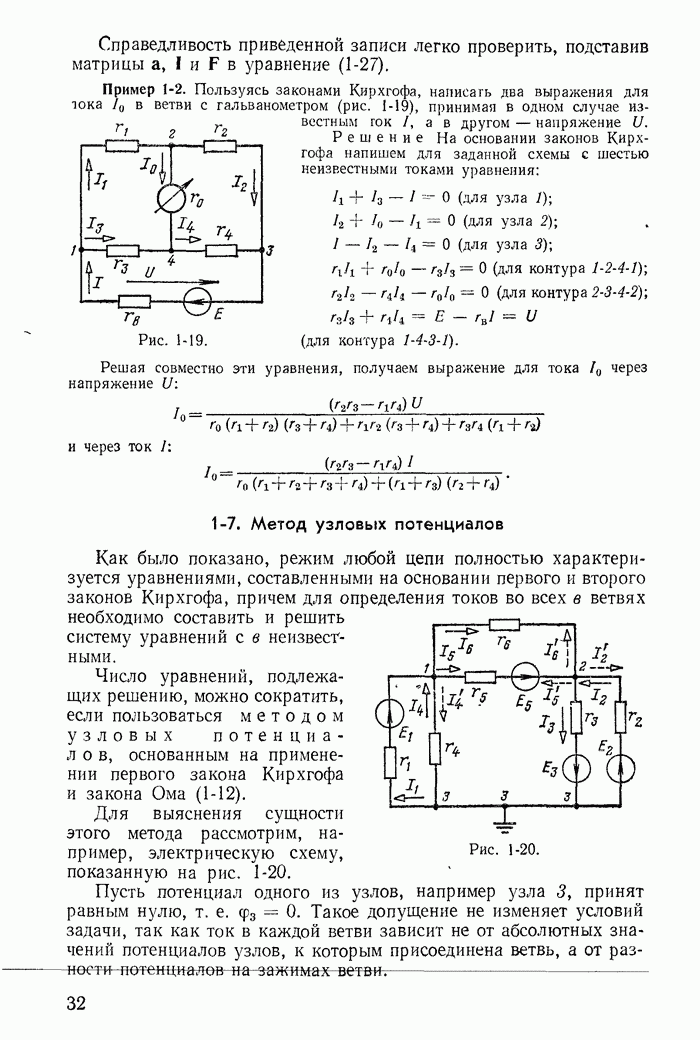
- 1-6. Применение законов Кирхгофа для расчета разветвленных цепей
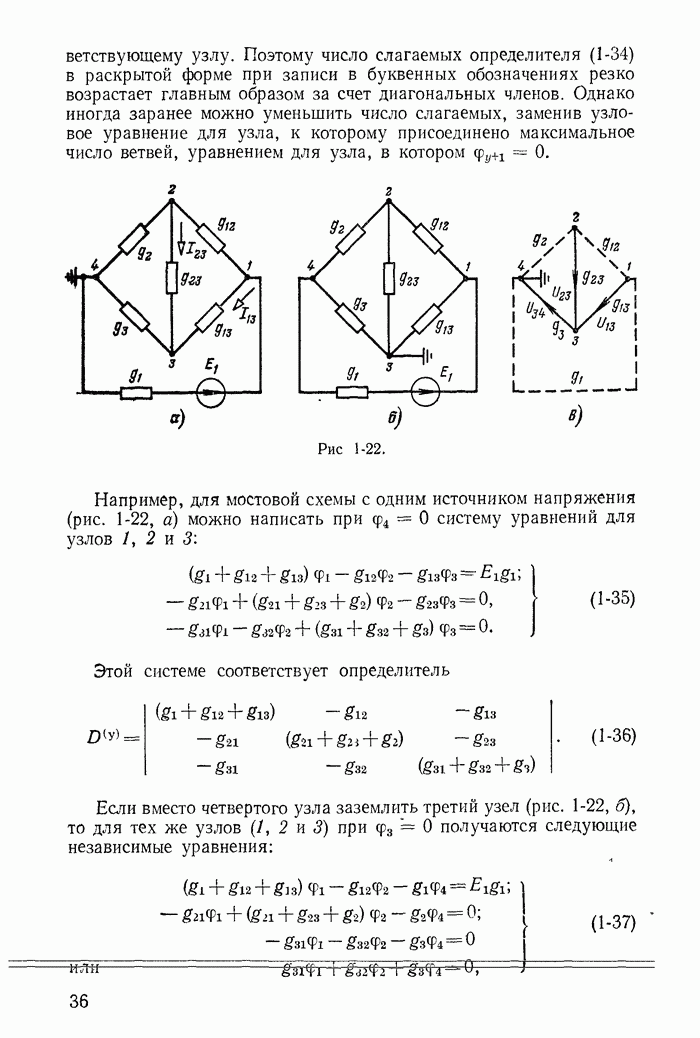
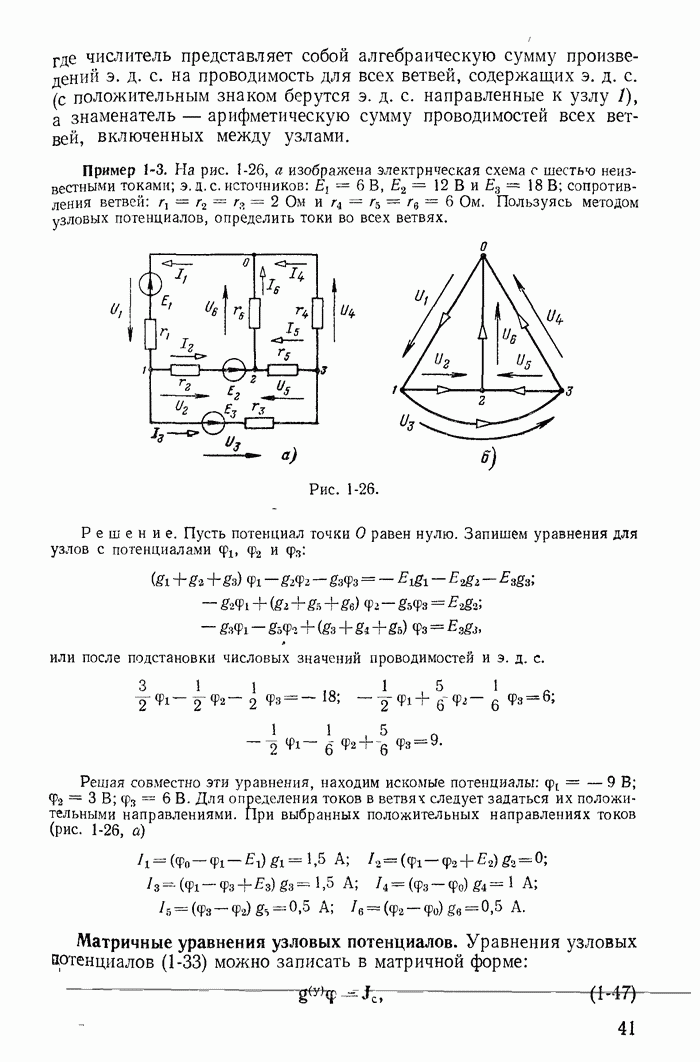
- 1-7. Метод узловых потенциалов
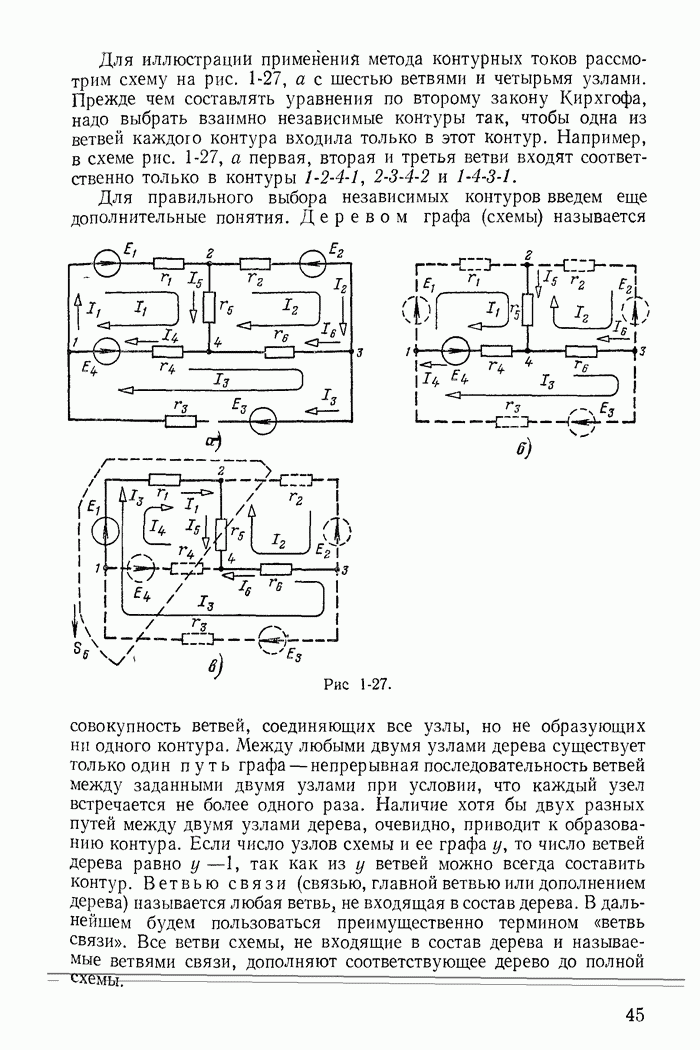
- 1-8. Метод контурных токов
- 1-9. Уравнения состояния цепи в матричной форме
- 1-10. Преобразование линейных электрических схем
- Глава вторая. ОСНОВНЫЕ СВОЙСТВА ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ПРИ ПОСТОЯННЫХ ТОКАХ И НАПРЯЖЕНИЯХ
- 2-2. Свойство взаимности
- 2-3. Входные и взаимные проводимости и сопротивления ветвей; коэффициенты передачи напряжений и токов
- 2-4. Применение топологических методов для расчета цепей
- 2-5. Топологические формулы и правила для определения передачи электрической цепи
- 2-6. Теорема о компенсации
- 2-7. Линейные соотношения между напряжениями и токами
- 2-8. Теорема о взаимных приращениях токов и напряжений
- 2-9. Общие замечания о двухполюсниках
- 2-10. Теорема об активном двухполюснике и ее применение для расчета разветвленных цепей
- 2-11. Передача энергии от активного двухполюсника к пассивному
- Глава третья. ОСНОВНЫЕ ПОНЯТИЯ О ЦЕПЯХ СИНУСОИДАЛЬНОГО ТОКА
- 3-2. Понятие о генераторах переменного тока
- 3-3. Синусоидальный ток
- 3-4. Действующие ток, э. д. с. и напряжение
- 3-5. Изображение синусоидальных функций времени векторами и комплексными числами
- 3-6. Сложение синусоидальных функций времени
- 3-7. Электрическая цепь и ее схема
- 3-8. Ток и напряжения при последовательном соединении сопротивления, Индуктивности и емкости
- 3-9. Сопротивления
- 3-10. Разность фаз напряжения и тока
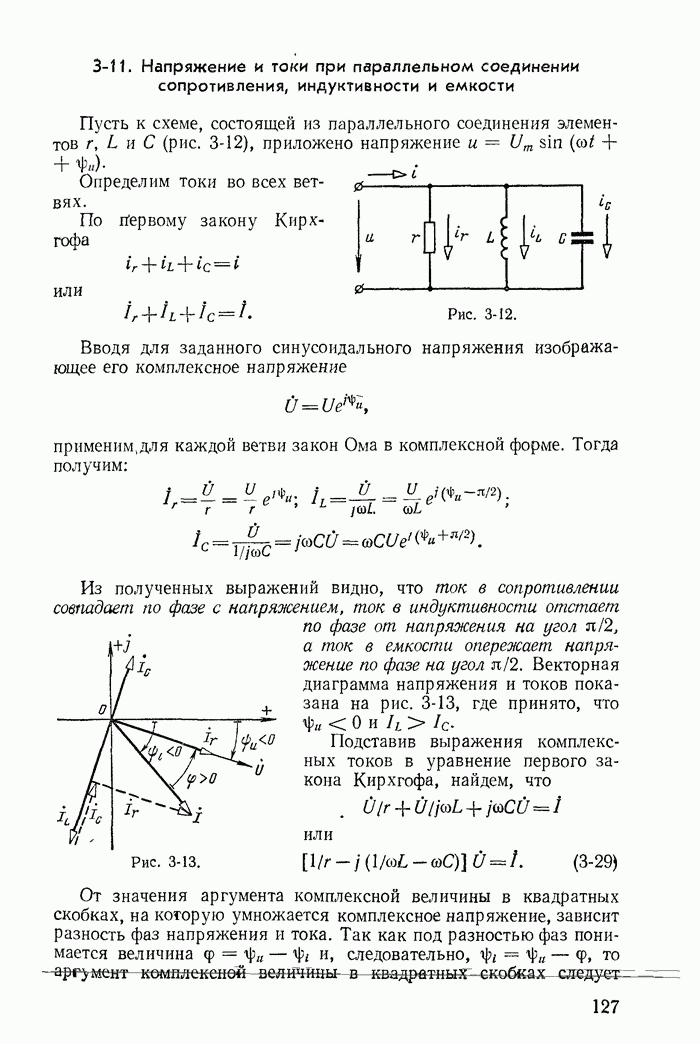
- 3-11. Напряжение и токи при параллельном соединении сопротивления, индуктивности и емкости
- 3-12. Проводимости
- 3-13. Пассивный двухполюсник
- 3-14. Мощности
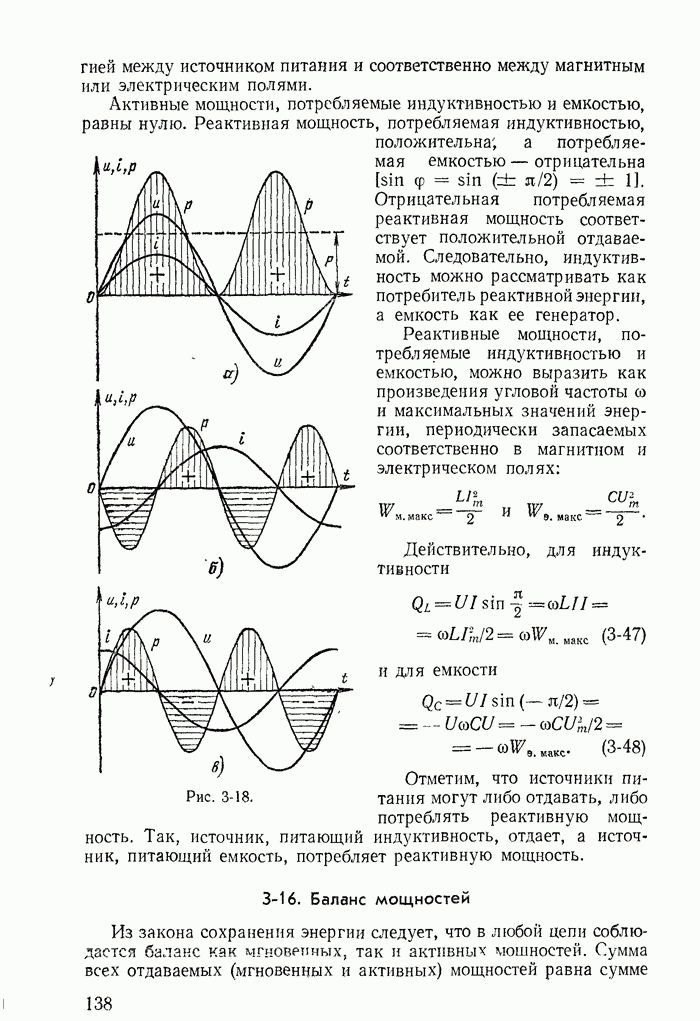
- 3-15. Мощности в сопротивлении, индуктивности и емкости
- 3-16. Баланс мощностей
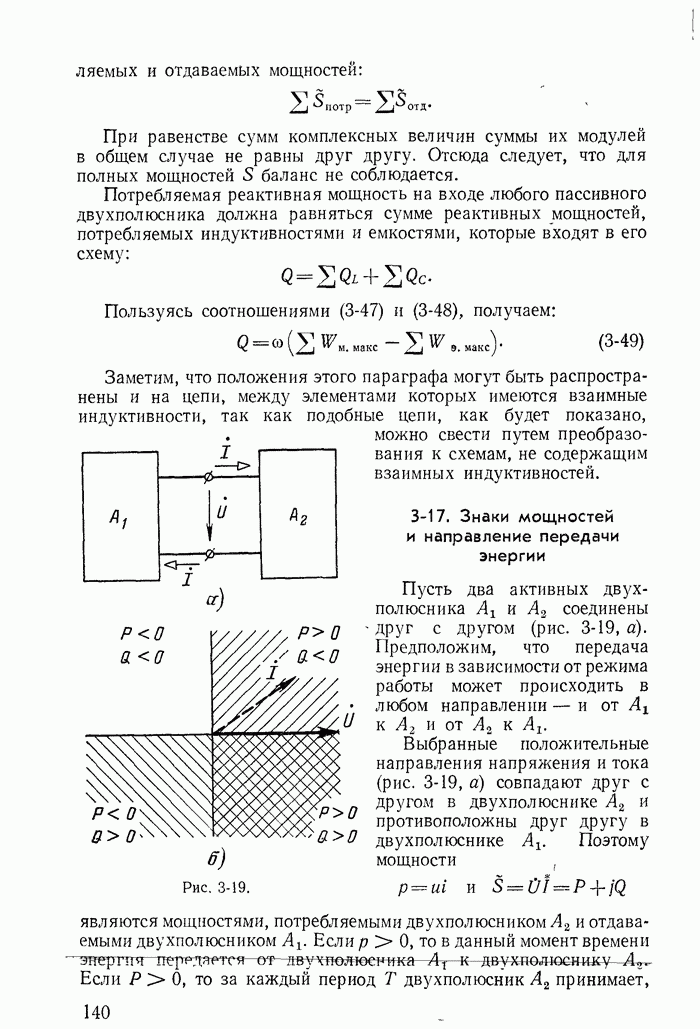
- 3-17. Знаки мощностей и направление передачи энергии
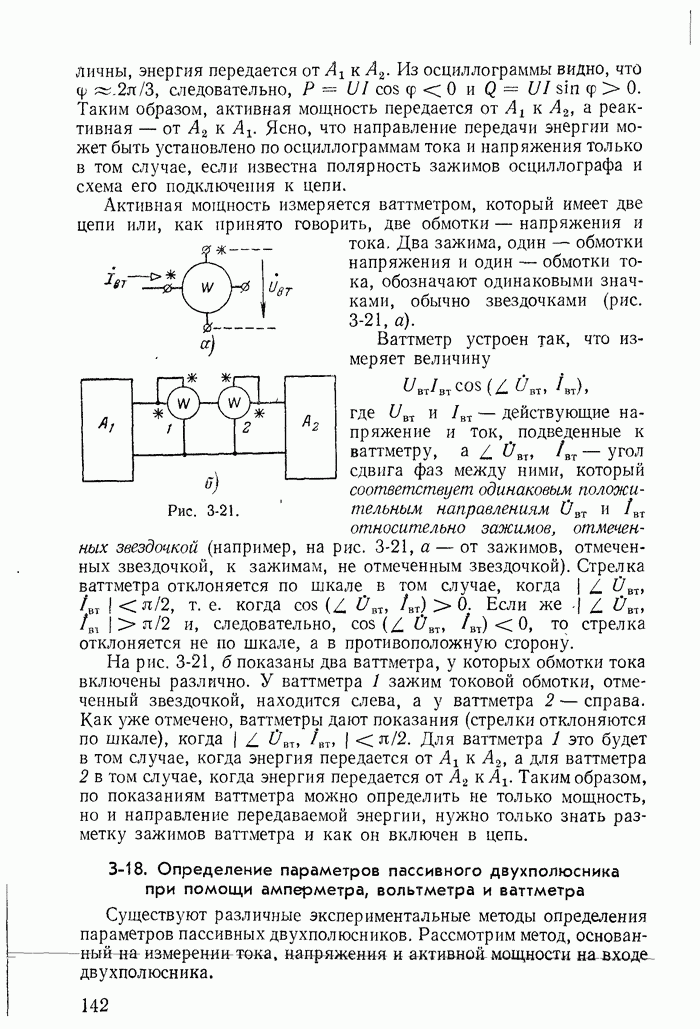
- 3-18. Определение параметров пассивного двухполюсника при помощи амперметра, вольтметра и ваттметра
- 3-19. Условия передачи максимальной мощности от источника энергии к приемнику
- 3-20. Понятие о поверхностном эффекте и эффекте близости
- 3-21. Параметры и эквивалентные схемы конденсаторов
- 3-22. Параметры и эквивалентные схемы индуктивных катушек и резисторов
- Глава четвертая. РАСЧЕТ ЦЕПЕЙ ПРИ СИНУСОИДАЛЬНЫХ ТОКАХ
- 4-1. О применимости методов расчета цепей постоянного тока к расчетам цепей синусоидального тока
- 4-2. Последовательное соединение приемников
- 4-3. Параллельное соединение приемников
- 4-4. Смешанное соединение приемников
- 4-5. Сложные разветвленные цепи
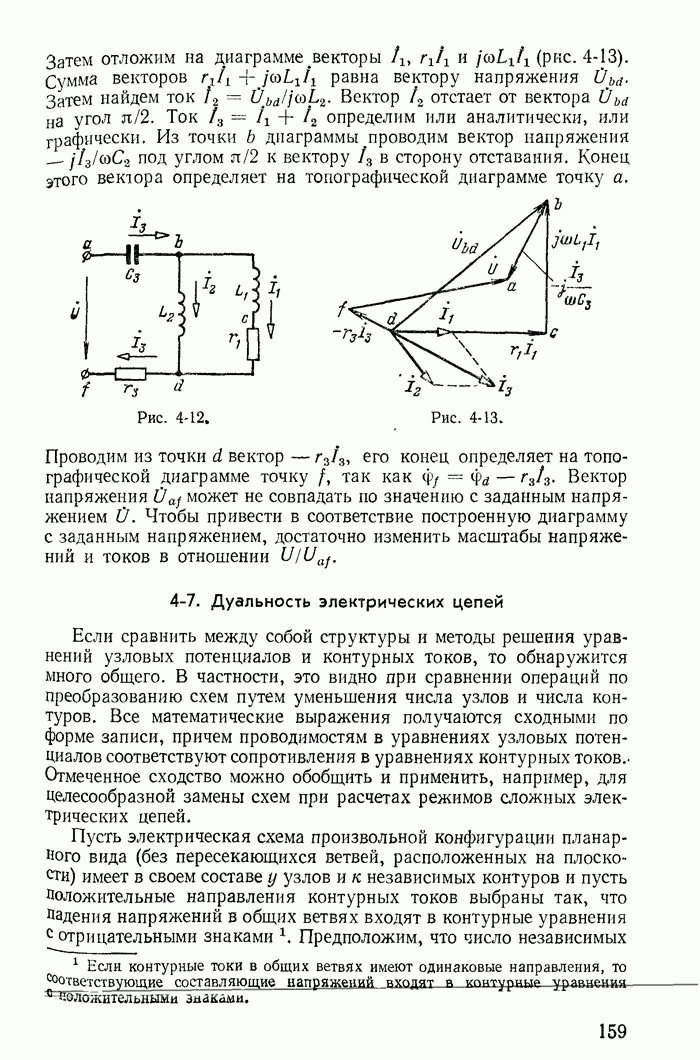
- 4-6. Топографические диаграммы
- 4-7. Дуальность электрических цепей
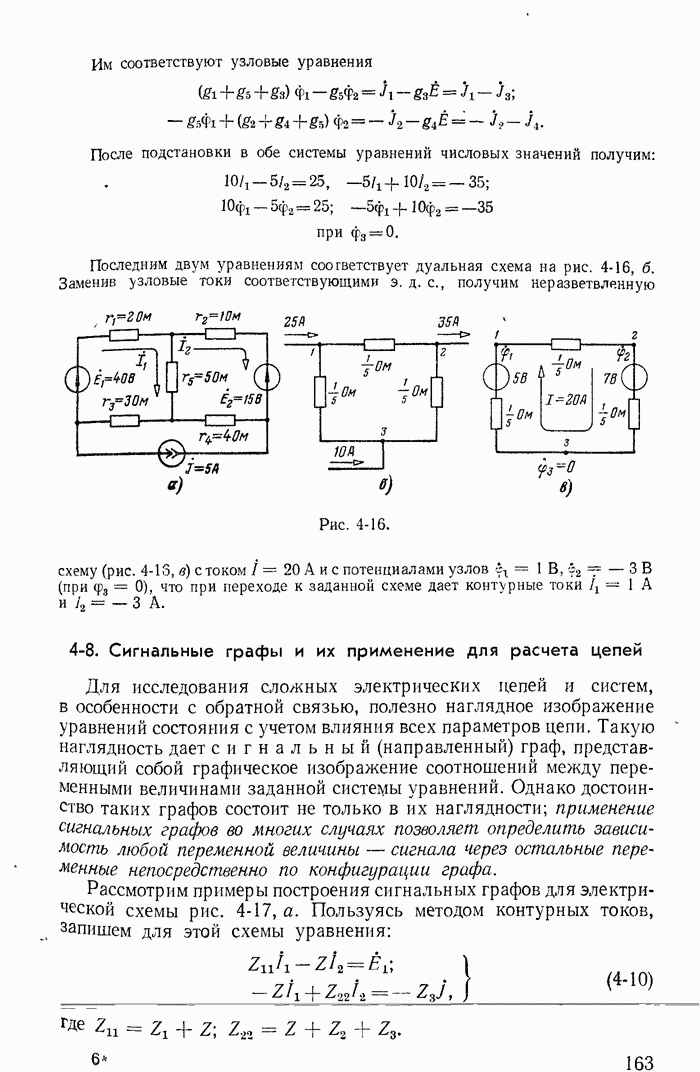
- 4-8. Сигнальные графы и их применение для расчета цепей
- Глава пятая. РЕЗОНАНС В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ
- 5-2. Частотные характеристики неразветвленной цепи
- 5-3. Резонанс в цепи с двумя параллельными ветвями
- 5-4. Частотные характеристики параллельного контура
- 5-5. Понятие о резонансе в сложных цепях
- Глава шестая. ЦЕПИ С ВЗАИМНОЙ ИНДУКТИВНОСТЬЮ
- 6-2. Электродвижущая сила взаимной индукции
- 6-3. Последовательное соединение индуктивно связанных элементов цепи
- 6-4. Параллельное соединение индуктивно связанных элементов цепи
- 6-5. Расчеты разветвленных цепей при наличии взаимной индуктивности
- 6-6. Эквивалентная замена индуктивных связей
- 6-7. Передача энергии между индуктивно связанными элементами цепи
- 6-8. Трансформатор без стального сердечника (воздушный трансформатор)
- Глава седьмая. КРУГОВЫЕ ДИАГРАММЫ
- 7-1. Комплексные уравнения прямой и окружности
- 7-2. Круговые диаграммы для неразветвленной цепи и для активного двухполюсника
- 7-3. Круговые диаграммы для любой разветвленной цепи
- Глава восьмая. МНОГОПОЛЮСНИКИ И ЧЕТЫРЕХПОЛЮСНИКИ ПРИ СИНУСОИДАЛЬНЫХ ТОКАХ И НАПРЯЖЕНИЯХ
- 8-1. Четырехполюсники и их основные уравнения
- 8-2. Определение коэффициентов четырехполюсников
- 8-3. Режим четырехполюсника при нагрузке
- 8-4. Эквивалентные схемы четырехполюсников
- 8-5. Основные уравнения и эквивалентные схемы для активного четырехполюсника
- 8-6. Идеальный трансформатор как четырехполюсник
- 8-7. Эквивалентные схемы с идеальными трансформаторами для четырехполюсника
- 8-8. Эквивалентные схемы трансформатора со стальным магнитопроводом
- 8-9. Расчеты электрических цепей с трансформаторами
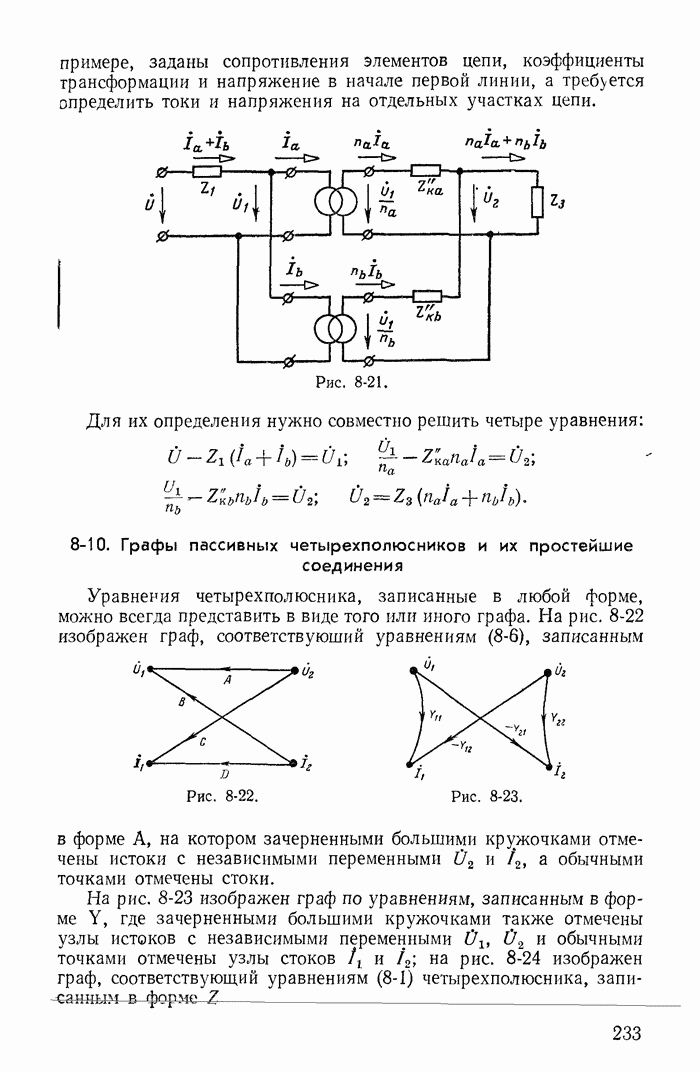
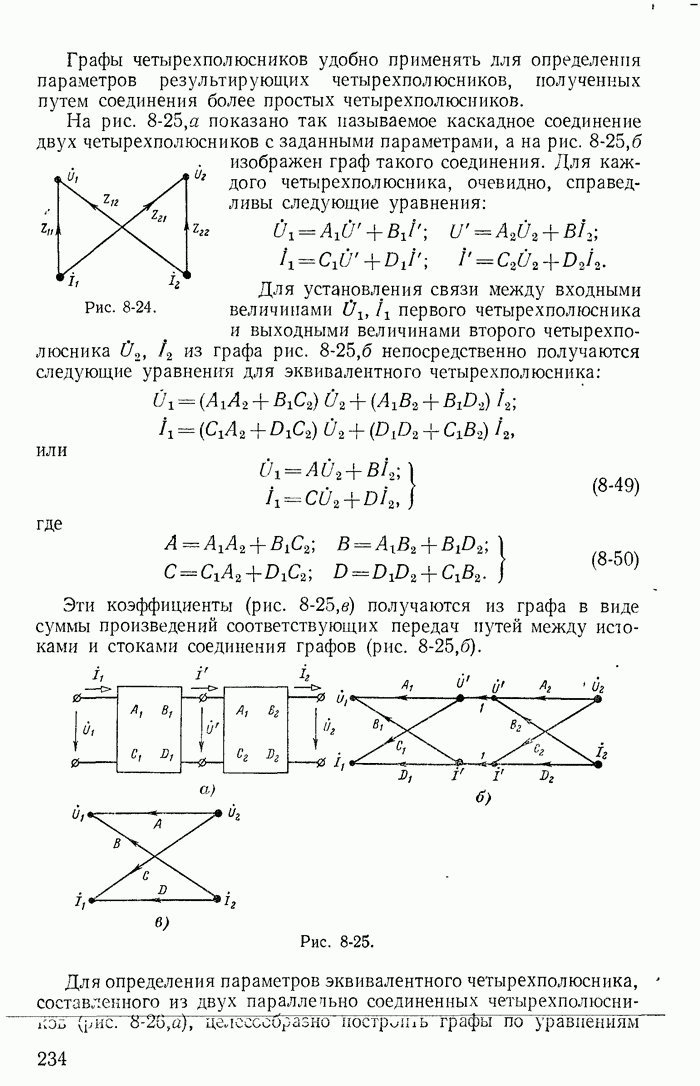
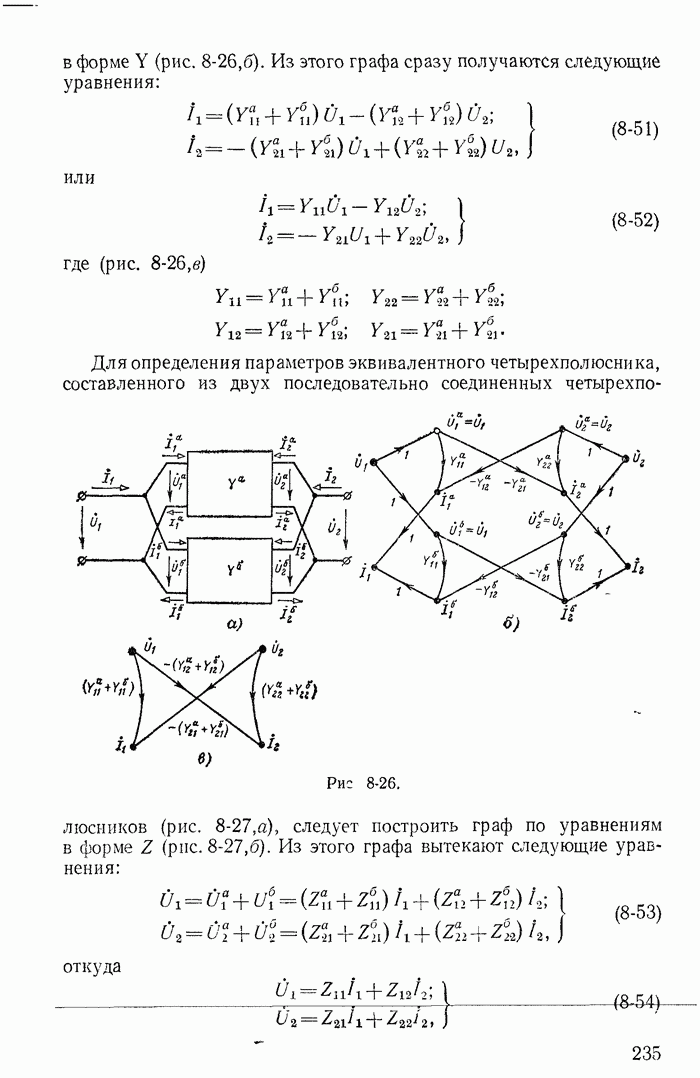
- 8-10. Графы пассивных четырехполюсников и их простейшие соединения
- Глава девятая. ЦЕПИ С ЭЛЕКТРОННЫМИ И ПОЛУПРОВОДНИКОВЫМИ ПРИБОРАМИ В ЛИНЕЙНОМ РЕЖИМЕ
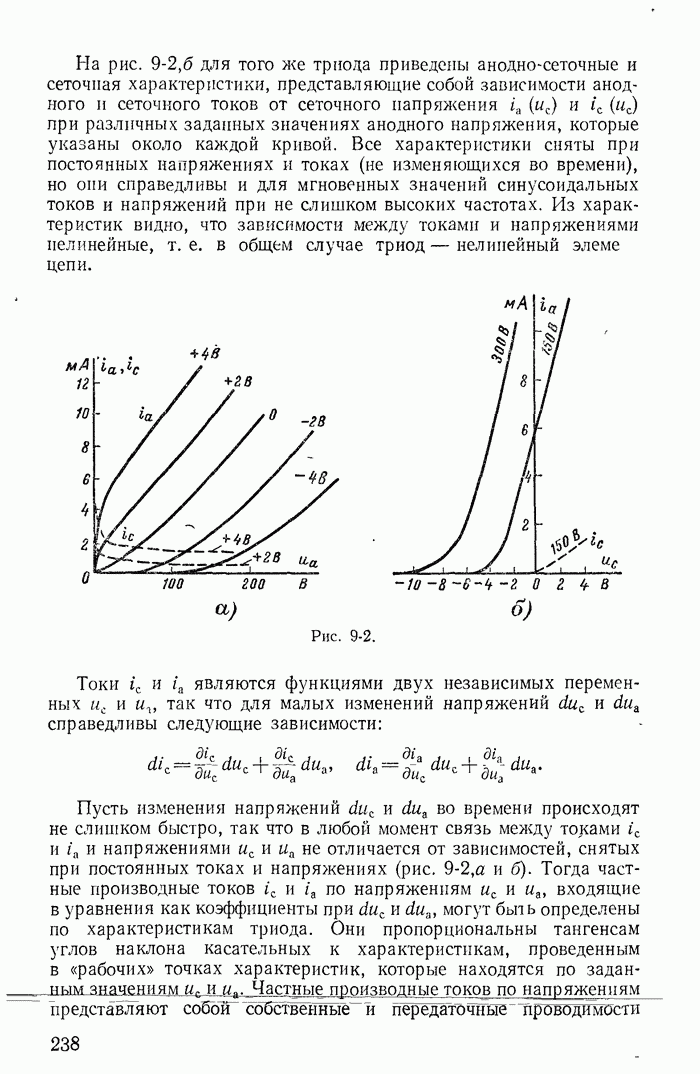
- 9-2. Эквивалентные схемы лампового триода
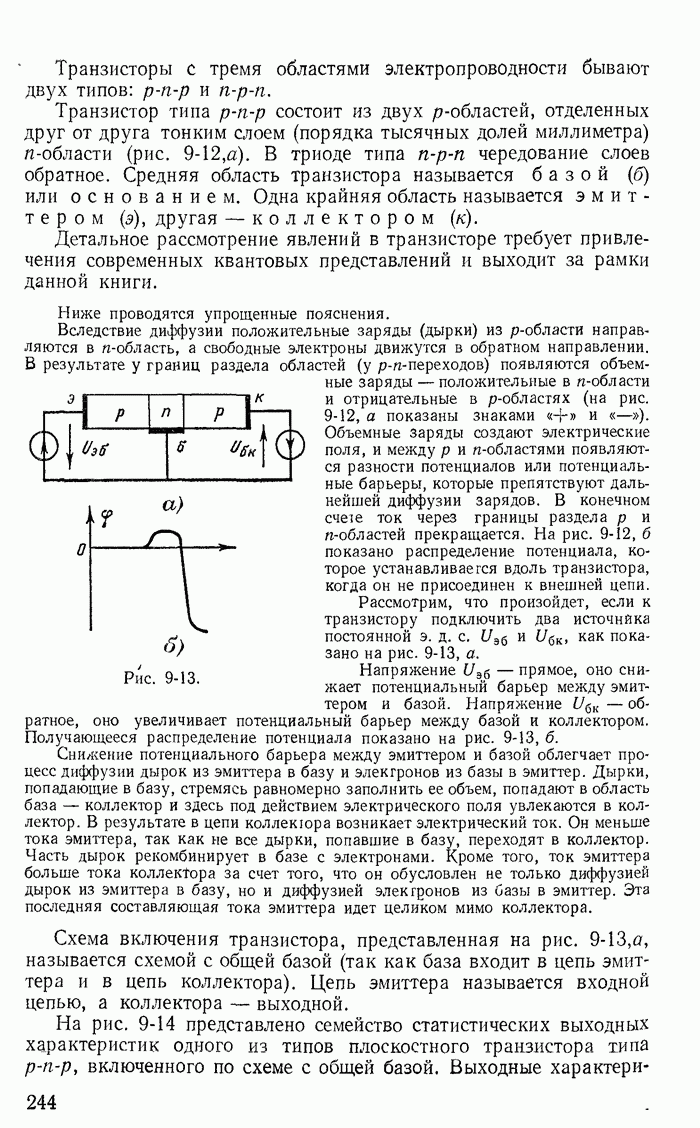
- 9-3. Транзисторы (полупроводниковые триоды)
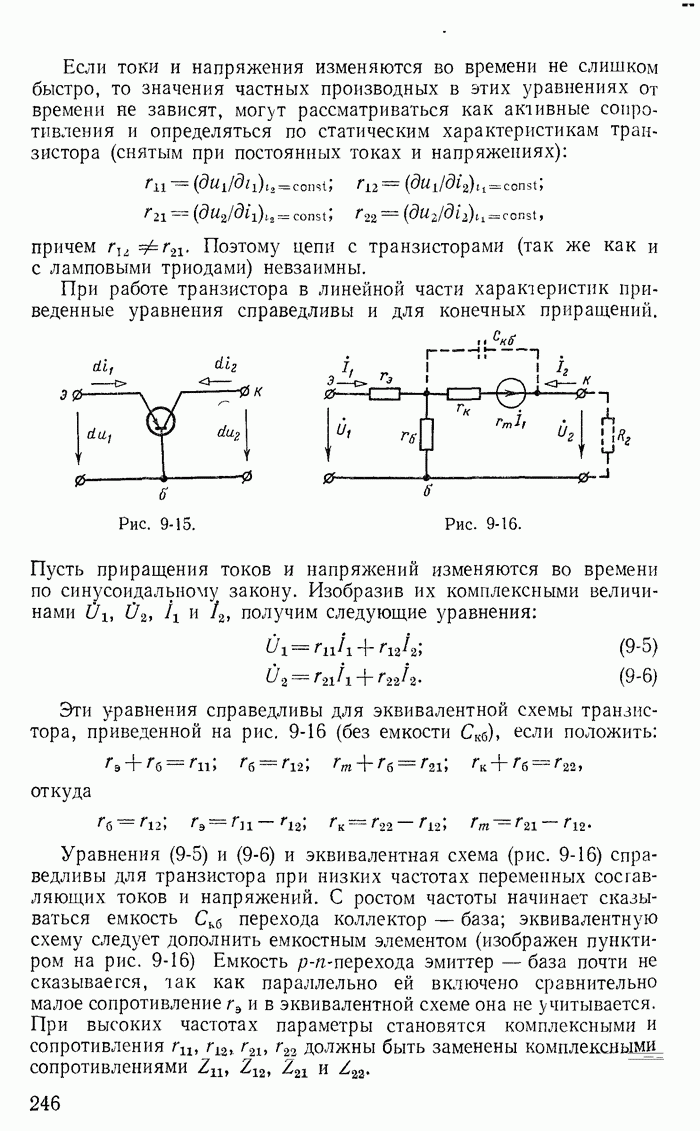
- 9-4. Эквивалентные схемы транзисторов
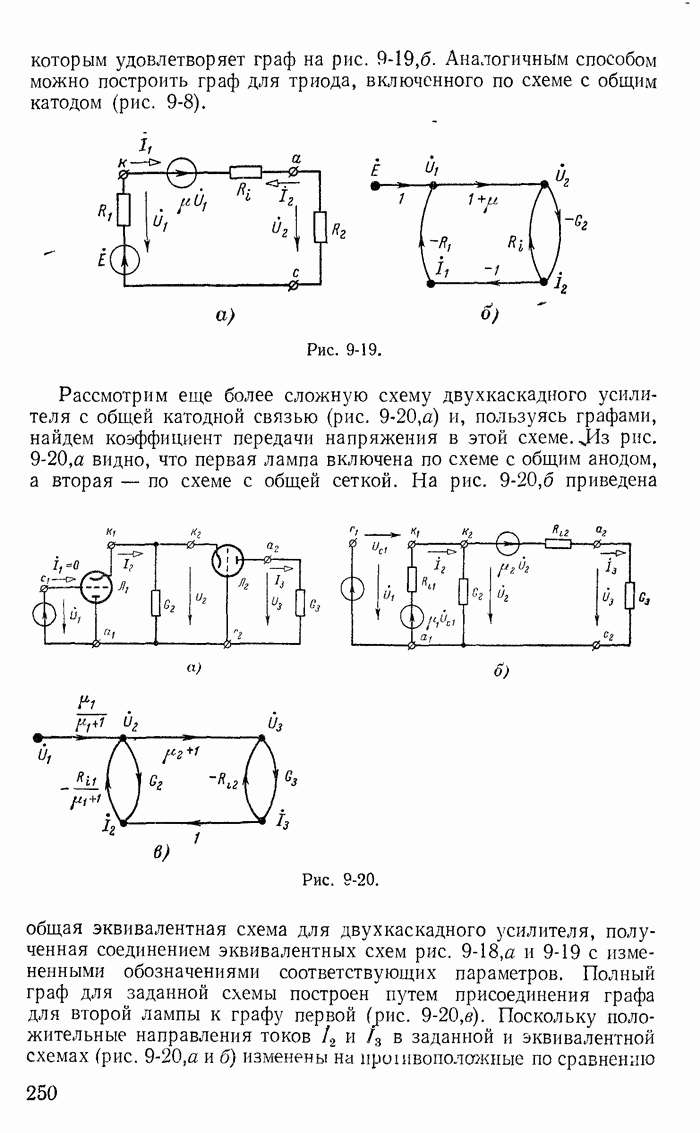
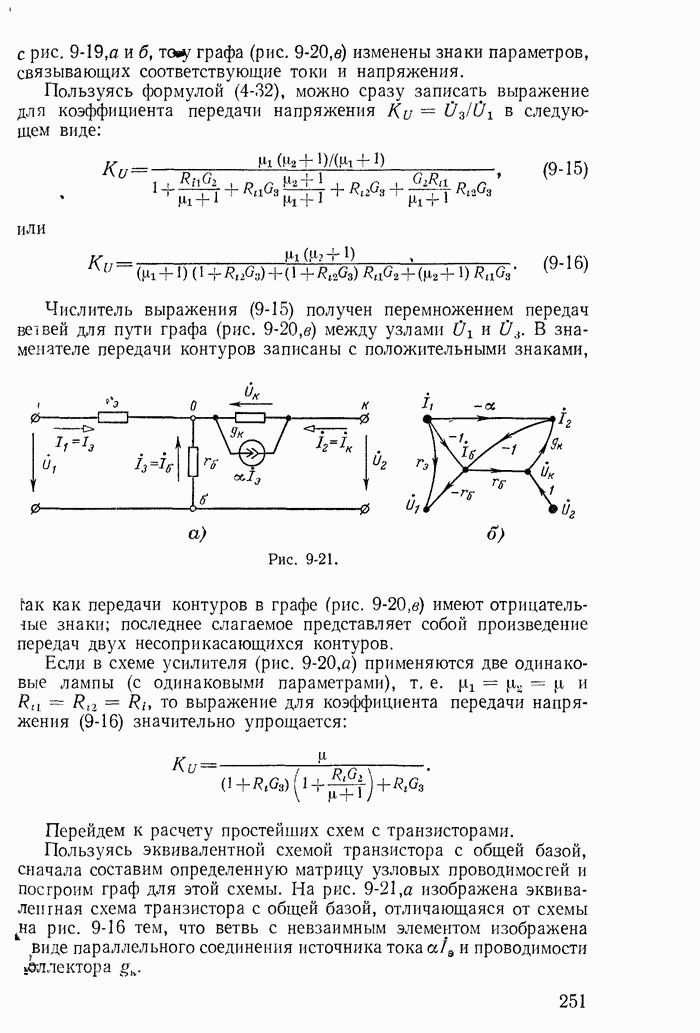
- 9-5. Простейшие электрические цепи с невзаимными элементами и их направленные графы
- Глава десятая. ТРЕХФАЗНЫЕ ЦЕПИ
- 10-2. Соединения звездой и многоугольником
- 10-3. Симметричный режим трехфазной цепи
- 10-4. Некоторые свойства трехфазных цепей с различными схемами соединений
- 10-5. Расчет симметричных режимов трехфазных цепей
- 10-6. Расчет несимметричных режимов трехфазных цепей со статической нагрузкой
- 10-7. Напряжения на фазах приемника в некоторых частных случаях
- 10-8. Эквивалентные схемы трехфазных линий
- 10-9. Измерение мощности в трехфазных цепях
- 10-10. Вращающееся магнитное поле
- 10-11. Принципы действия асинхронного и синхронного двигателей
- Глава одиннадцатая. МЕТОД СИММЕТРИЧНЫХ СОСТАВЛЯЮЩИХ
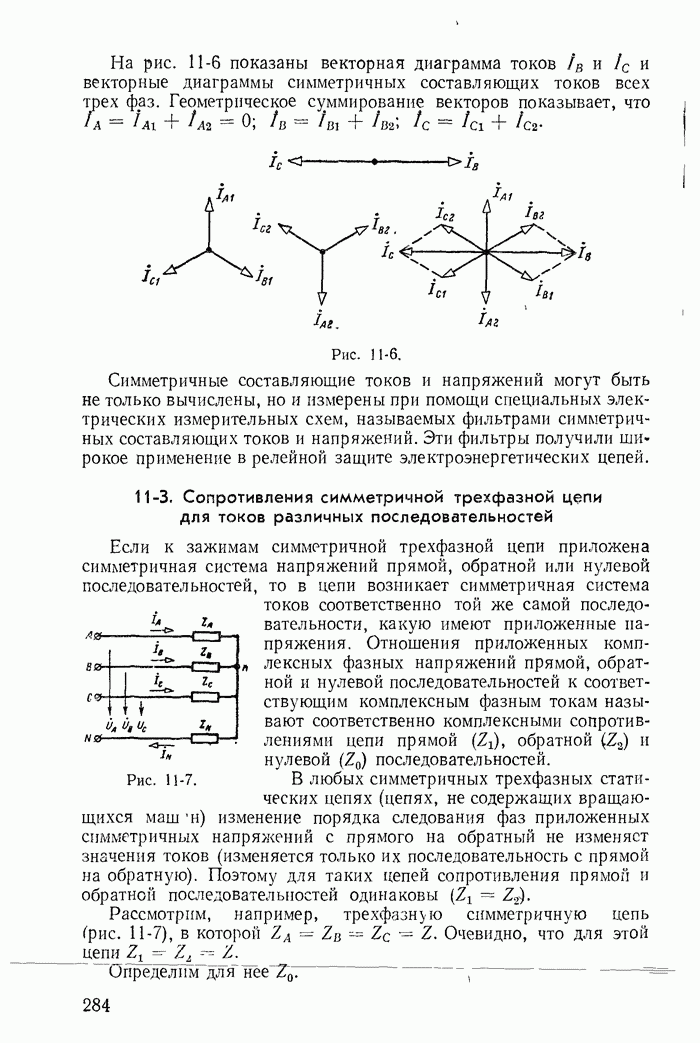
- 11-2. Некоторые свойства трехфазных цепей в отношении симметричных составляющих токов и напряжений
- 11-3. Сопротивления симметричной трехфазной цепи для токов различных последовательностей
- 11-4. Определение токов в симметричной цепи
- 11-5. Симметричные составляющие напряжений и токов в несимметричной трехфазной цепи
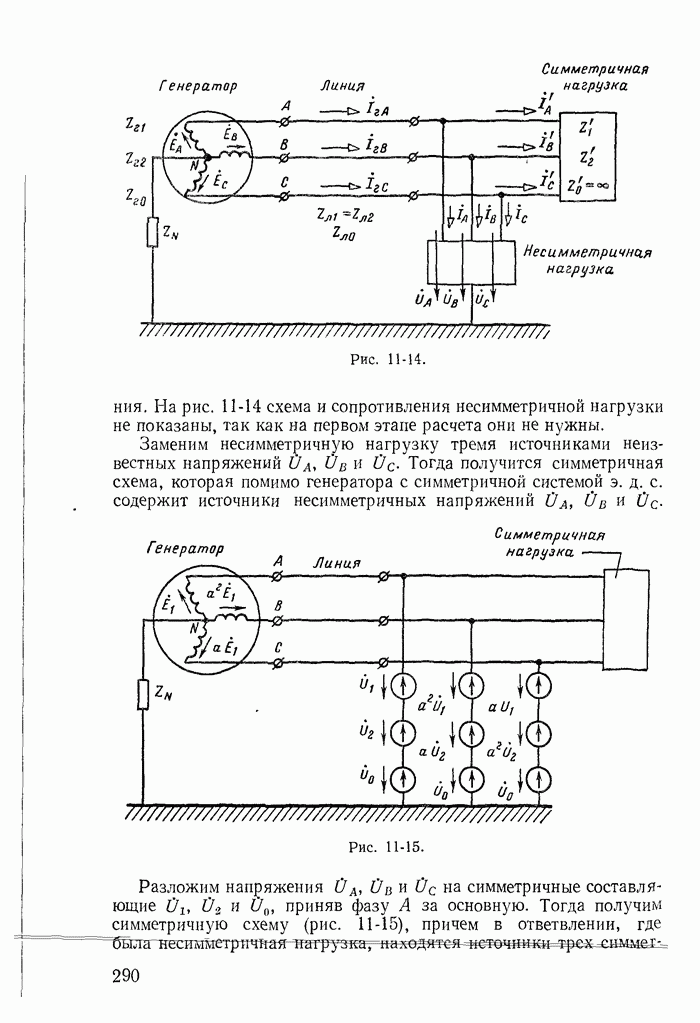
- 11-6. Расчет цепи с несимметричной нагрузкой
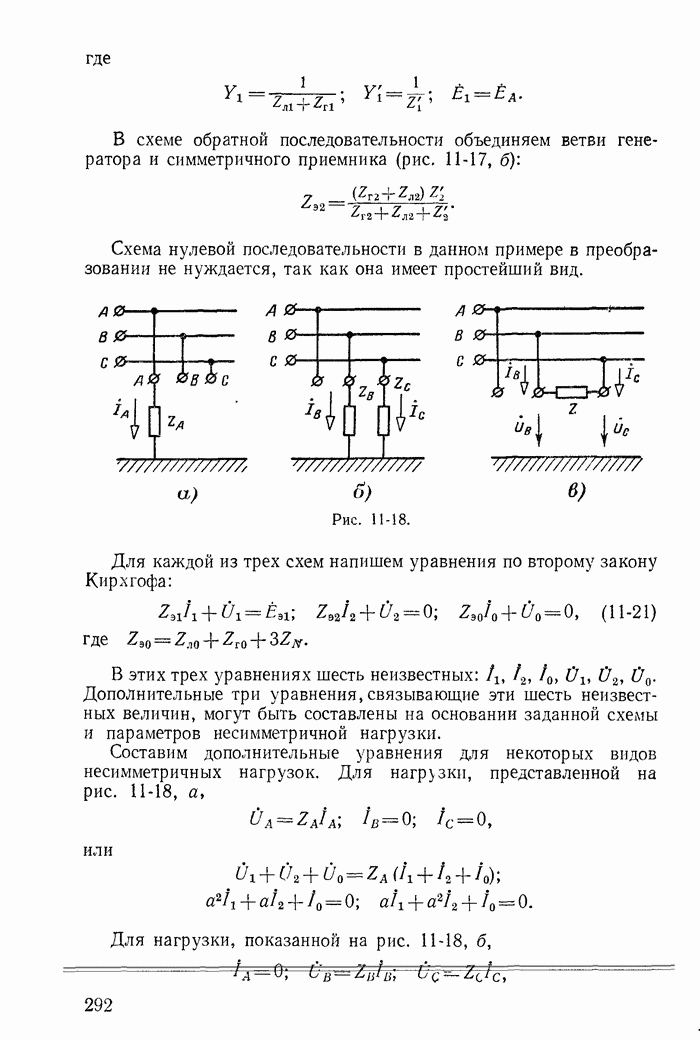
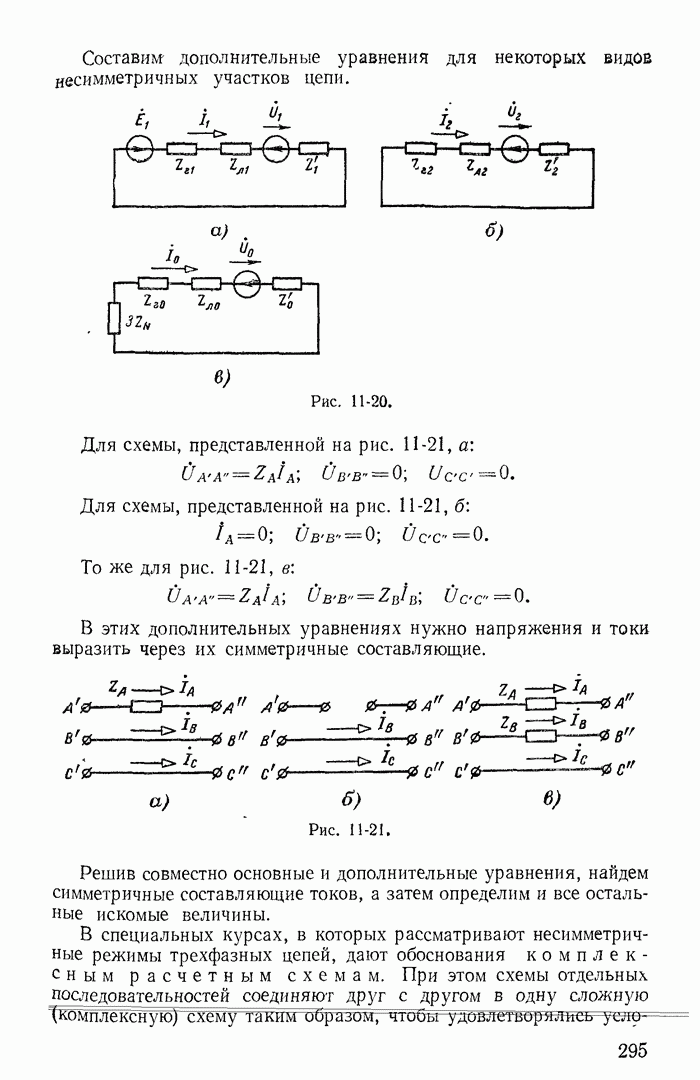
- 11-7. Расчет цепи с несимметричным участком в линии
- Глава двенадцатая. НЕСИНУСОИДАЛЬНЫЕ ТОКИ
- 12-2. Разложение периодической несинусоидальной кривой в тригонометрический ряд
- 12-3. Максимальные, действующие и средние значения несинусоидальных периодических э. д. с., напряжений и токов
- 12-4. Коэффициенты, характеризующие форму несинусоидальных периодических кривых
- 12-5. Несинусоидальные кривые с периодической огибающей
- 12-6. Действующие значения э. д. с., напряжений и токов с периодическими огибающими
- 12-7. Расчет цепей с несинусоидальными периодическими э. д. с. и токами
- 12-8. Резонанс при несинусоидальных э. д. с. и токах
- 12-9. Мощность периодических несинусоидальных токов
- 12-10. Высшие гармоники в трехфазных цепях
- Глава тринадцатая. КЛАССИЧЕСКИЙ МЕТОД РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ
- 13-2. Переходный, принужденный и свободный процессы
- 13-3. Короткое замыкание цепи r, L
- 13-4. Включение цепи r, L на постоянное напряжение
- 13-5. Включение цепи r, L на синусоидальное напряжение
- 13-6. Короткое замыкание цепи r, С
- 13-7. Включение цепи r, С на постоянное напряжение
- 13-8. Включение цепи r, С на синусоидальное напряжение
- 13-9. Переходные процессы в неразветвленной цепи r, С
- 13-10. Апериодический разряд конденсатора
- 13-11. Предельный случай апериодического разряда конденсатора
- 13-12. Периодический (колебательный) разряд конденсатора
- 13-13. Включение цепи r, С на постоянное напряжение
- 13-14. Общий случай расчета переходных процессов классическим методом
- 13-15. Включение пассивного двухполюсника на непрерывно изменяющееся напряжение (формула или интеграл Дюамеля)
- 13-16. Включение пассивного двухполюсника на напряжение любой формы
- 13-17. Временная и импульсная переходные характеристики
- 13-18. Запись теоремы свертки при помощи импульсной переходной характеристики
- 13-19. Переходные процессы при скачках токов в индуктивностях и напряжений на конденсаторах
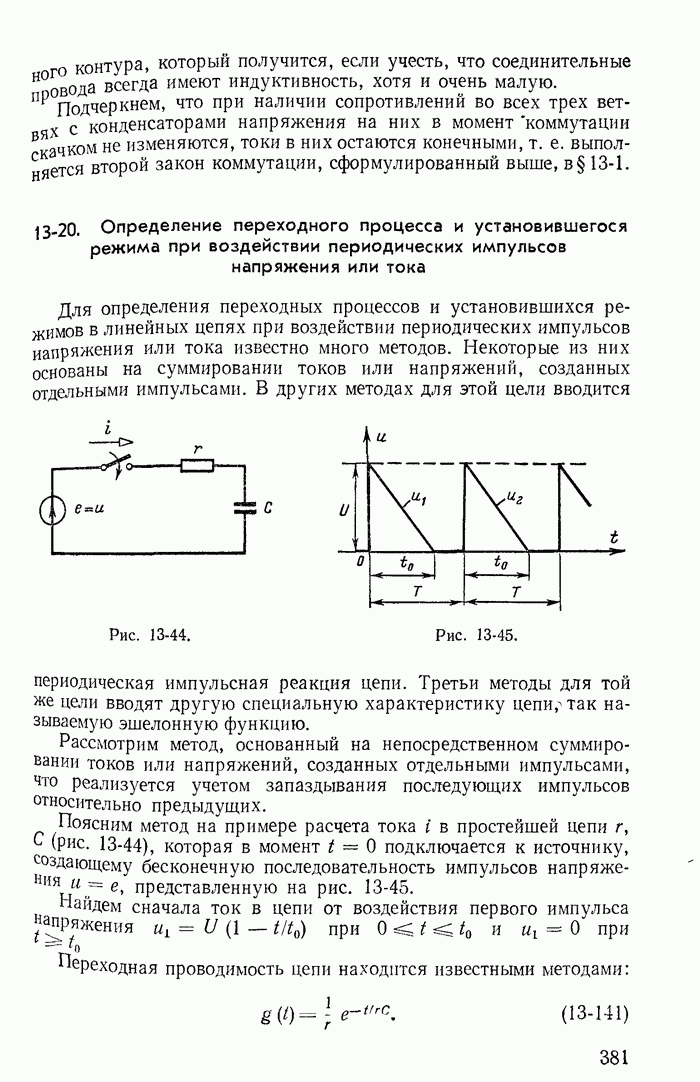
- 13-20. Определение переходного процесса и установившегося режима при воздействии периодических импульсов напряжения или тока
- Глава четырнадцатая. ОПЕРАТОРНЫЙ МЕТОД РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ
- 14-2. Законы Ома и Кирхгофа в операторной форме
- 14-3. Эквивалентные операторные схемы
- 14-4. Переходные процессы в цепях с взаимной индуктивностью
- 14-5. Сведение расчетов переходных процессов к нулевым начальным условиям
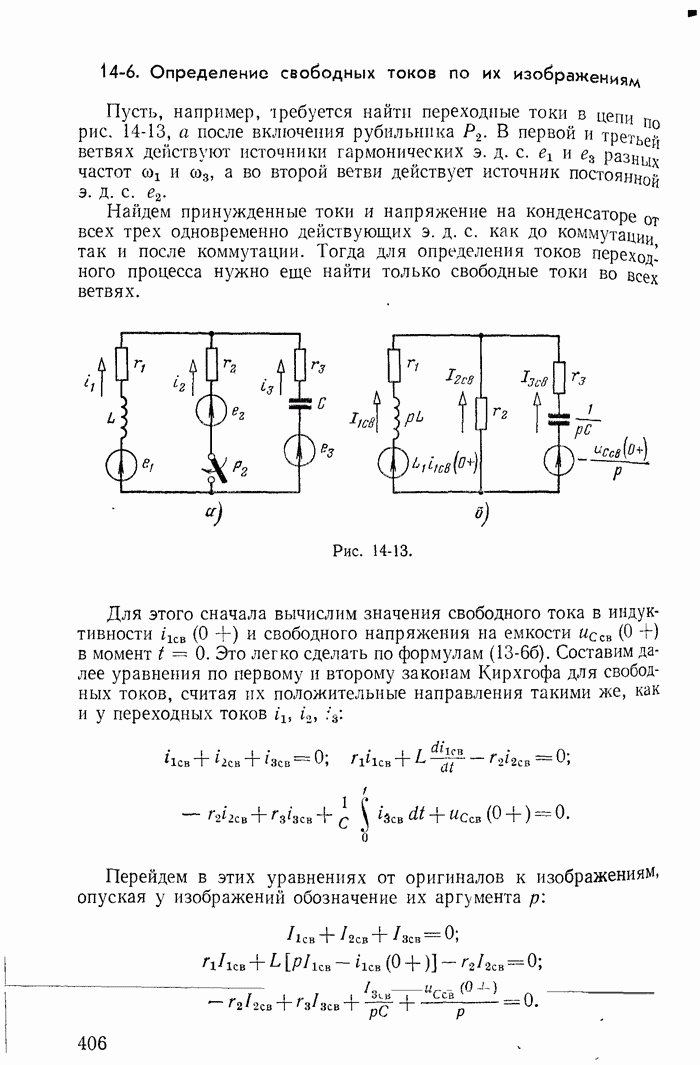
- 14-6. Определение свободных токов по их изображениям
- 14-7. Формулы включения
- 14-8. Расчет переходных процессов методом переменных состояния
- 14-9. Определение принужденного режима цепи при воздействии на нее периодического несинусоидального напряжения
- Глава пятнадцатая. ЧАСТОТНЫЙ МЕТОД РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ
- 15-2. Законы Ома и Кирхгофа и эквивалентные схемы для частотных спектров
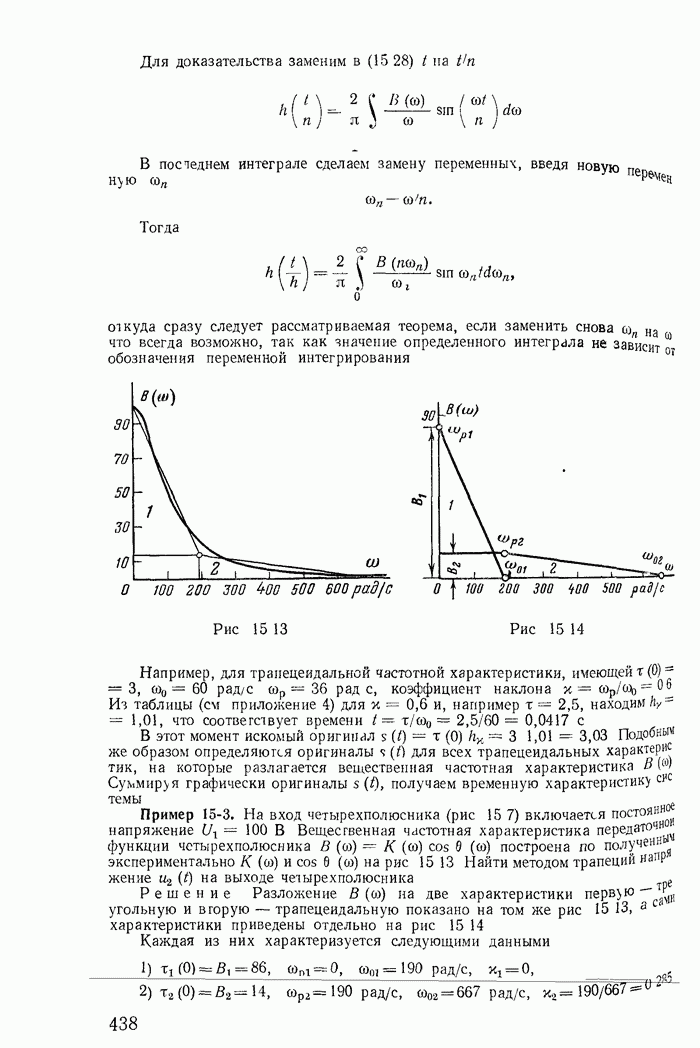
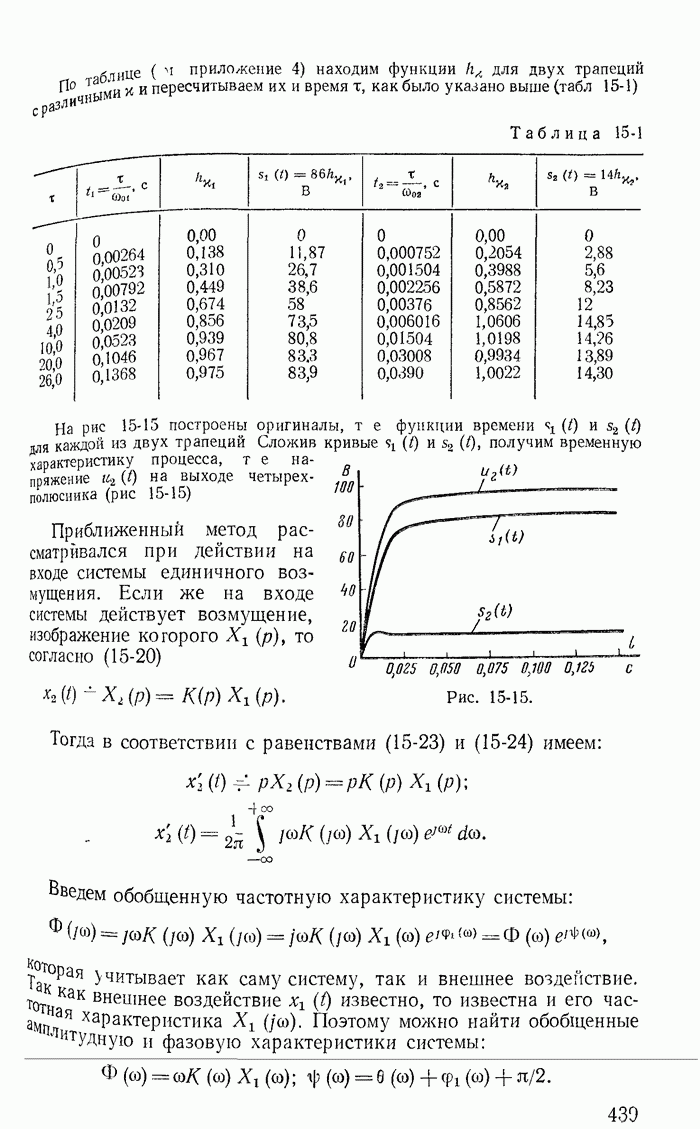
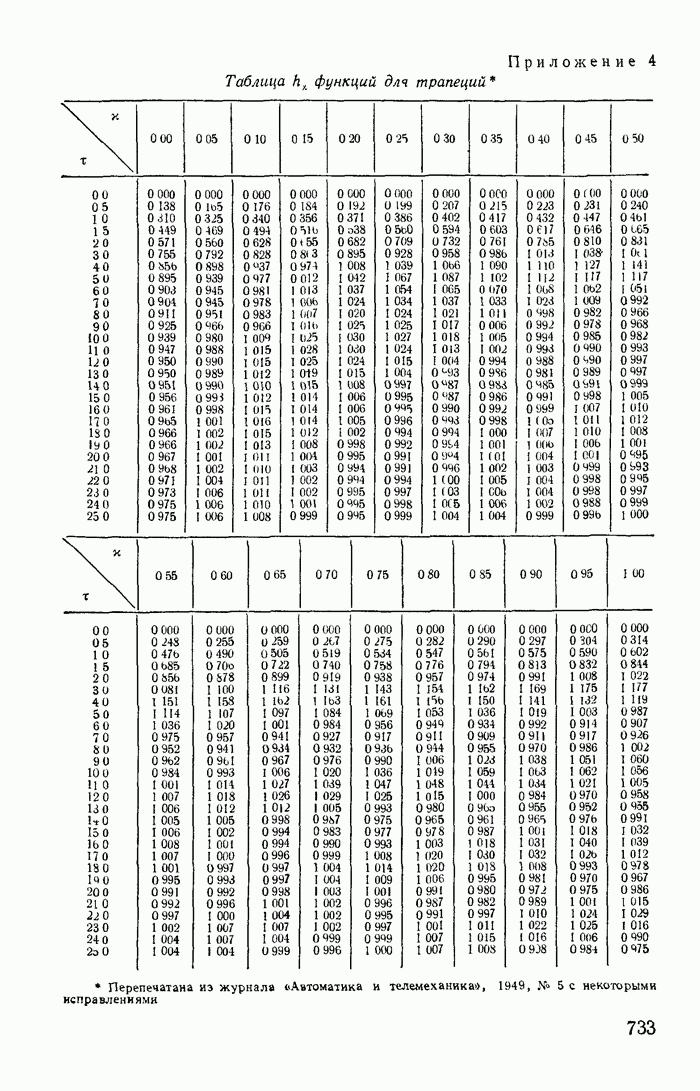
- 15-3. Приближенный метод определения оригинала по вещественной частотной характеристике (метод трапеций)
- 15-4. О переходе от преобразований Фурье к преобразованиям Лапласа
- 15-5. Сравнение различных методов расчета переходных процессов в линейных электрических цепях
- Глава шестнадцатая. ЦЕПНЫЕ СХЕМЫ И ЧАСТОТНЫЕ ЭЛЕКТРИЧЕСКИЕ ФИЛЬТРЫ
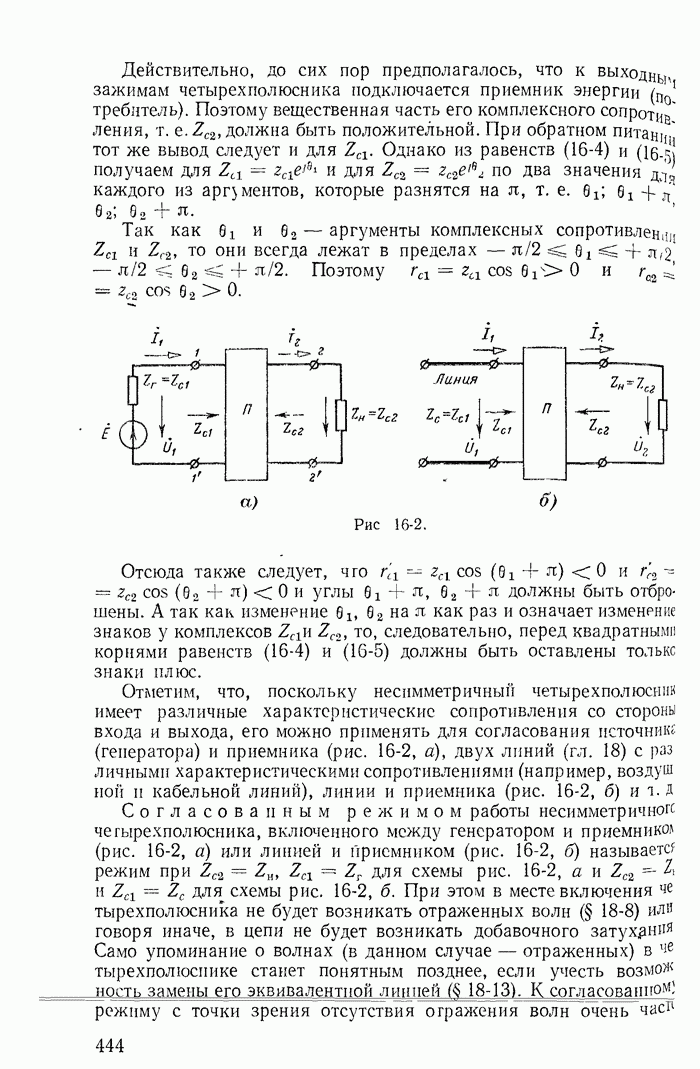
- 16-2. Характеристическое сопротивление и постоянная передачи симметричного четырехполюсника
- 16-3. Вносимая и рабочая постоянные передачи
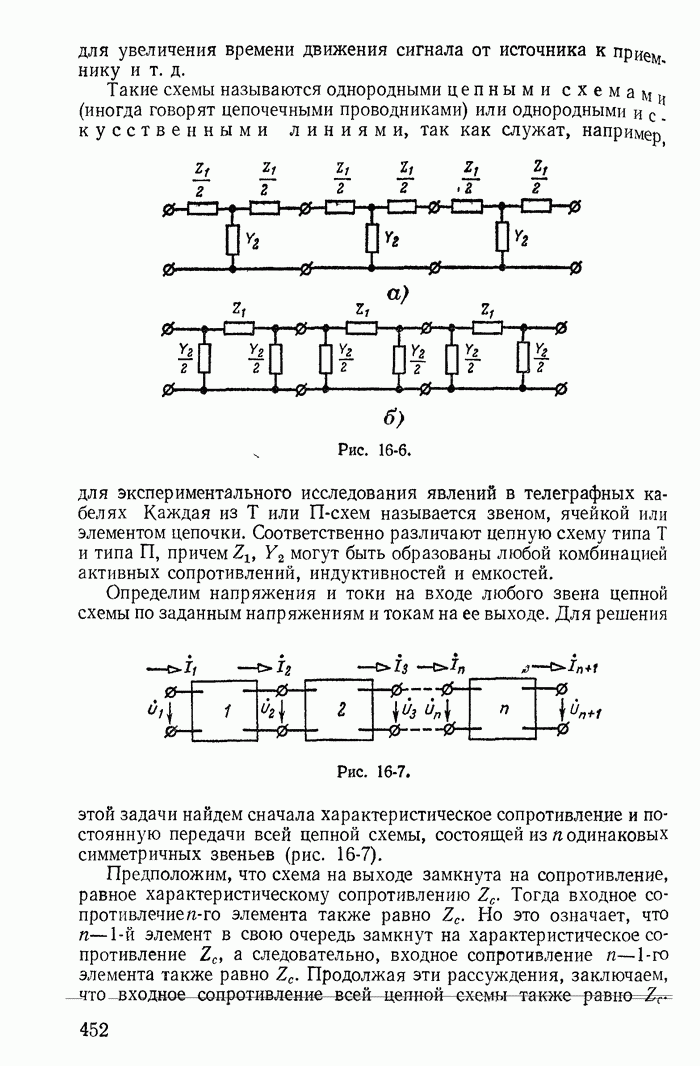
- 16-4. Цепные схемы
- 16-5. Частотные электрические фильтры
- 16-6. Низкочастотные фильтры
- 16-8. Полосные фильтры
- 16-11. Г-образный фильтр как пример несимметричного фильтра
- 16-12. Безындукционные (или r, C) фильтры
- Глава семнадцатая. СИНТЕЗ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
- 17-2. Передаточная функция четырехполюсника. Цепи минимальной фазы
- 17-3. Входные функции цепей. Положительные вещественные функции
- 17-4. Реактивные двухполюсники
- 17-5. Частотные характеристики реактивных двухполюсников
- 17-6. Синтез реактивных двухполюсников. Метод Фостера
- 17-7. Синтез реактивных двухполюсников. Метод Кауэра
- 17-8. Синтез двухполюсников с потерями. Метод Фостера
- 17-9. Синтез двухполюсников с потерями. Метод Кауэра
- 17-10. Понятие о синтезе четырехполюсников
- Раздел второй. ЛИНЕЙНЫЕ ЦЕПИ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
- Глава восемнадцатая. ГАРМОНИЧЕСКИЕ ПРОЦЕССЫ В ЦЕПЯХ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
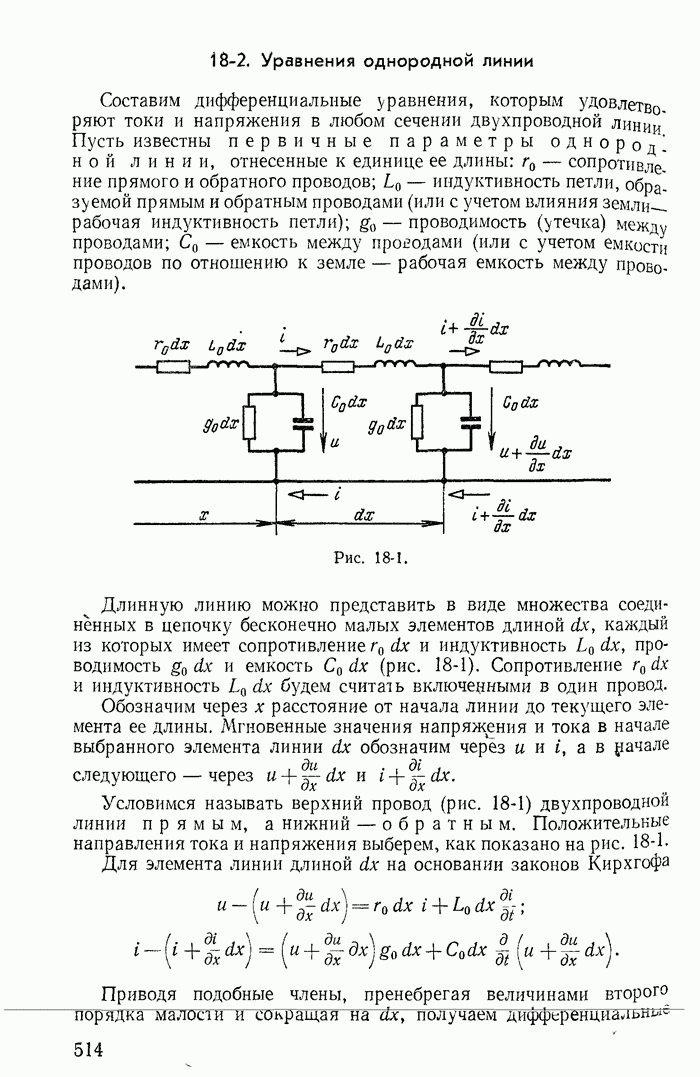
- 18-2. Уравнения однородной линии
- 18-3. Установившийся режим в однородной линии
- 18-4. Уравнения однородной линии с гиперболическими функциями
- 18-5. Характеристики однородной линии
- 18-6. Входное сопротивление линии
- 18-7. Коэффициент отражения волны
- 18-8. Согласованная нагрузка линии
- 18-9. Линия без искажений
- 18-10. Холостой ход, короткое замыкание и нагрузочный режим линии с потерями
- 18-11. Линии без потерь
- 18-12. Стоячие волны
- 18-13. Линия как четырехполюсник
- Глава девятнадцатая. ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЦЕПЯХ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
- 19-2. Общее решение уравнений однородной линии
- 19-3. Возникновение волн с прямоугольным фронтом
- 19-4. Общие случаи нахождения волн, возникающих при переключениях
- 19-5. Отражение волны с прямоугольным фронтом от конца линии
- 19-6. Общий метод определения отраженных волн
- 19-7. Качественное рассмотрение переходных процессов в линиях, содержащих сосредоточенные емкости и индуктивности
- 19-8. Многократные отражения волн с прямоугольным фронтом от активного сопротивления
- 19-9. Блуждающие волны
- Раздел III. НЕЛИНЕЙНЫЕ ЦЕПИ
- Глава двадцатая. НЕЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПРИ ПОСТОЯННЫХ ТОКАХ И НАПРЯЖЕНИЯХ
- 20-2. Графический метод расчета неразветвленных цепей с нелинейными элементами
- 20-3. Графический метод расчета цепей с параллельным соединением нелинейных элементов
- 20-4. Графический метод расчета цепей со смешанным соединением нелинейных и линейных элементов
- 20-5. Применение эквивалентных схем с источниками э. д. с. для исследования режима нелинейных цепей
- 20-6. Вольт-амперные характеристики нелинейных активных двухполюсников
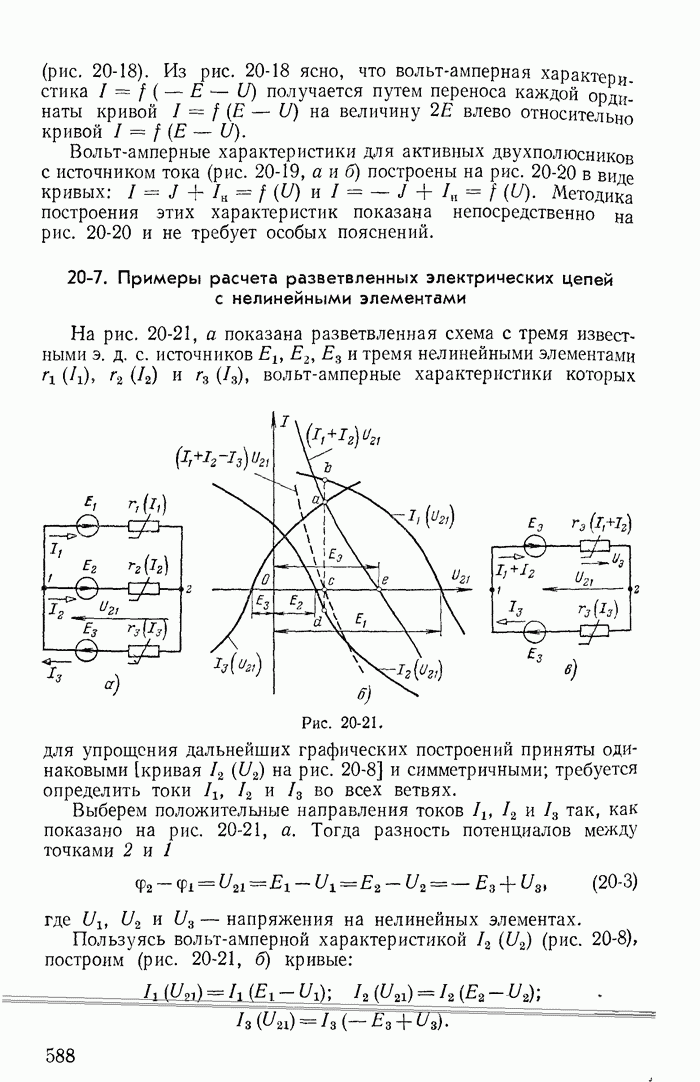
- 20-7. Примеры расчета разветвленных электрических цепей с нелинейными элементами
- 20-8. Применение теории активных двухполюсника, четырехполюсника и шестиполюсника для расчета цепей с линейными и нелинейными элементами
- 20-9. Расчет разветвленных нелинейных цепей итерационным методом (методом последовательных приближений)
- Глава двадцать первая. МАГНИТНЫЕ ЦЕПИ ПРИ ПОСТОЯННЫХ ТОКАХ
- 21-2. Расчет неразветвленных магнитных цепей
- 21-3. Расчет разветвленных магнитных цепей
- 21-4. Расчет магнитной цепи кольцевого постоянного магнита с воздушным зазором
- 21-5. Расчет неразветвленной неоднородной магнитной цепи с постоянным магнитом
- Глава двадцать вторая. ОБЩАЯ ХАРАКТЕРИСТИКА НЕЛИНЕЙНЫХ ЦЕПЕЙ ПЕРЕМЕННОГО ТОКА И МЕТОДОВ ИХ РАСЧЕТА
- 22-1. Нелинейные двухполюсники и четырехполюсники при переменных токах
- 22-2. Определение рабочих точек на характеристиках нелинейных двухполюсников и четырехполюсников
- 22-3. Явления в нелинейных цепях переменного тока
- 22-4. Методы расчета нелинейных цепей переменного тока
- Глава двадцать третья. НЕЛИНЕЙНЫЕ ЦЕПИ С ИСТОЧНИКАМИ Э. Д. С. И ТОКА ОДИНАКОВОЙ ЧАСТОТЫ
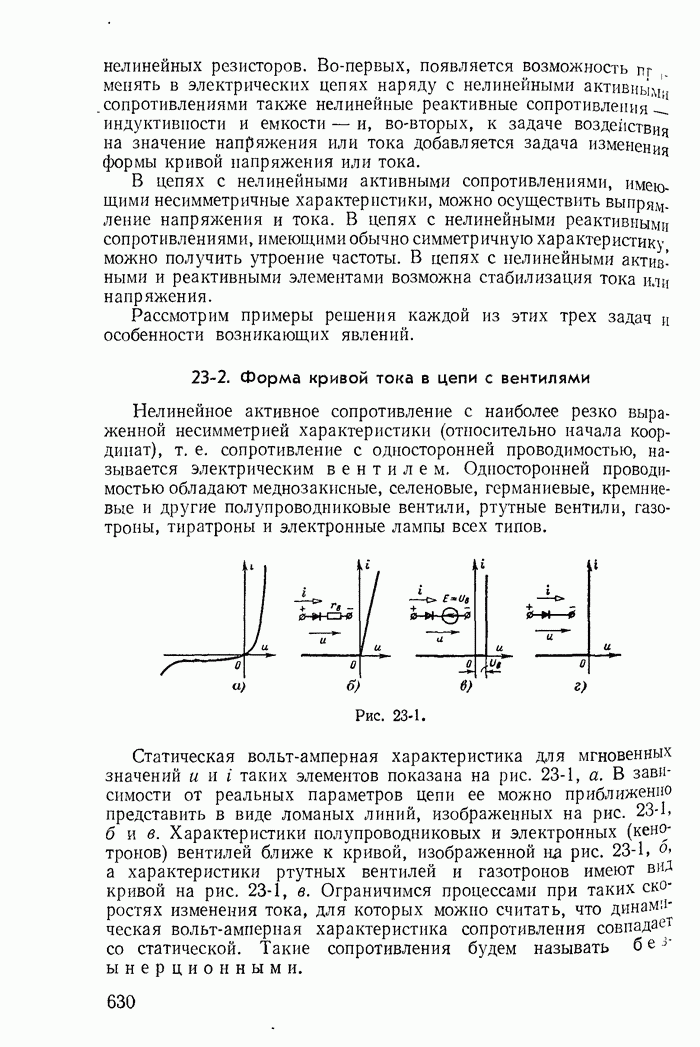
- 23-2. Форма кривой тока в цепи с вентилями
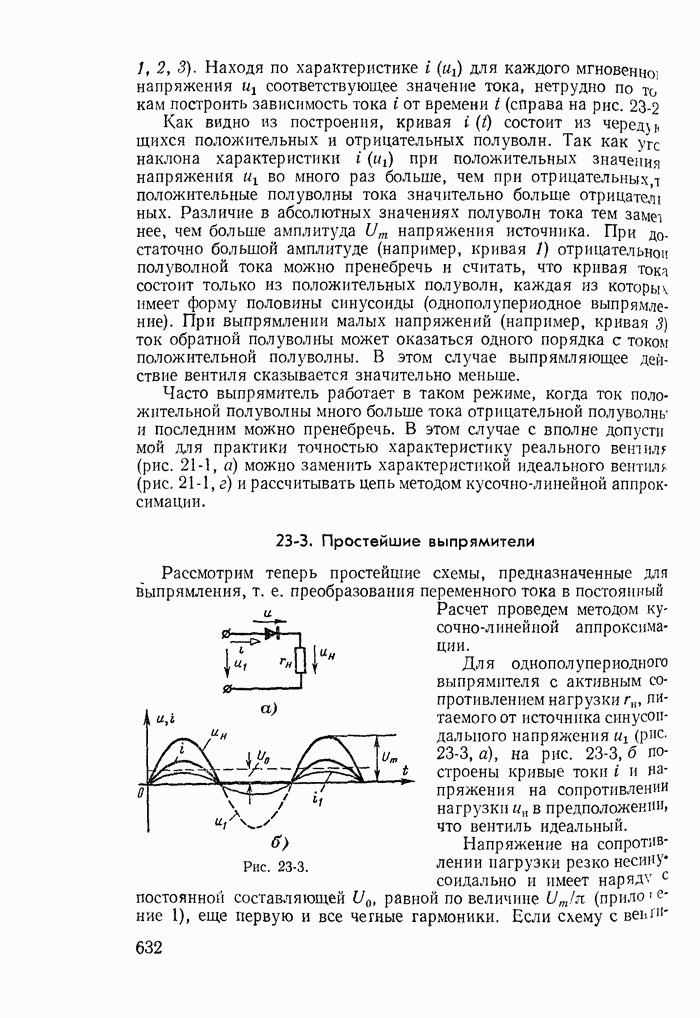
- 23-3. Простейшие выпрямители
- 23-4. Формы кривых тока и напряжения в цепях с нелинейными реактивными сопротивлениями
- 23-5. Утроители частоты
- 23-6. Формы кривых тока и напряжения в цепях с терморезисторами
- 23-7. Замена реальных нелинейных элементов условно-нелинейными
- 23-8. Учет реальных свойств стальных магнитопроводов
- 23-9. Расчет тока в катушке со стальным магнитопроводом
- 23-10. Понятие о расчете условно-нелинейных магнитных цепей
- 23-11. Явление феррорезонанса
- 23-12. Стабилизаторы напряжения
- Глава двадцать четвертая. НЕЛИНЕЙНЫЕ ЦЕПИ С ИСТОЧНИКАМИ Э. Д. С. И ТОКА РАЗЛИЧНЫХ ЧАСТОТ
- 24-1. Общая характеристика нелинейных цепей с источниками э. д. с. различных частот
- 24-2. Вентили в цепях с постоянными и переменными э. д. с.
- 24-3. Управляемые вентили в простейших выпрямителях и преобразователях постоянного тока в переменный
- 24-4. Катушки со стальными магнитопроводами в цепях с постоянными и переменными э. д. с.
- 24-5. Удвоитель частоты
- 24-6. Метод гармонического баланса
- 24-7. Влияние постоянной э. д. с. на переменную составляющую тока в цепях с нелинейными безынерционными сопротивлениядли
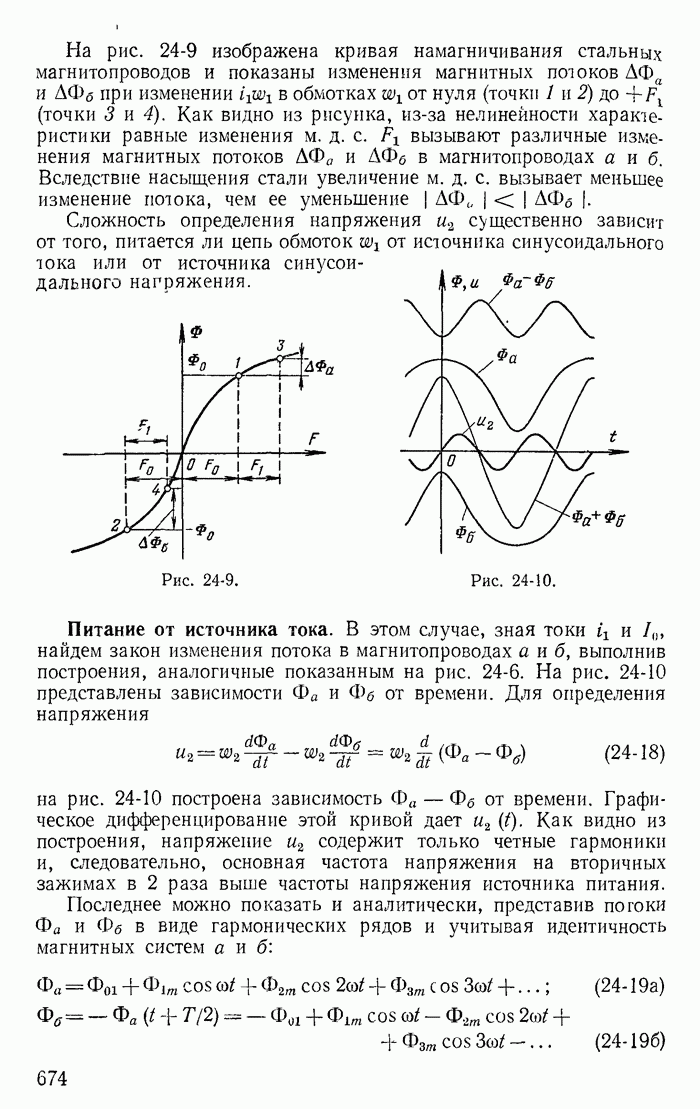
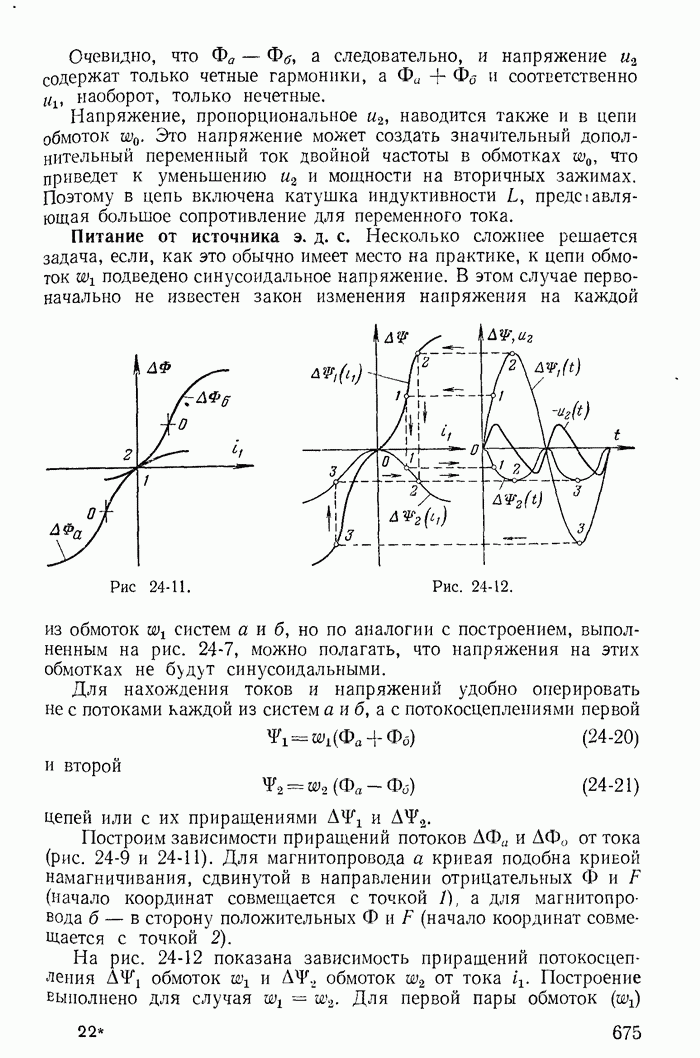
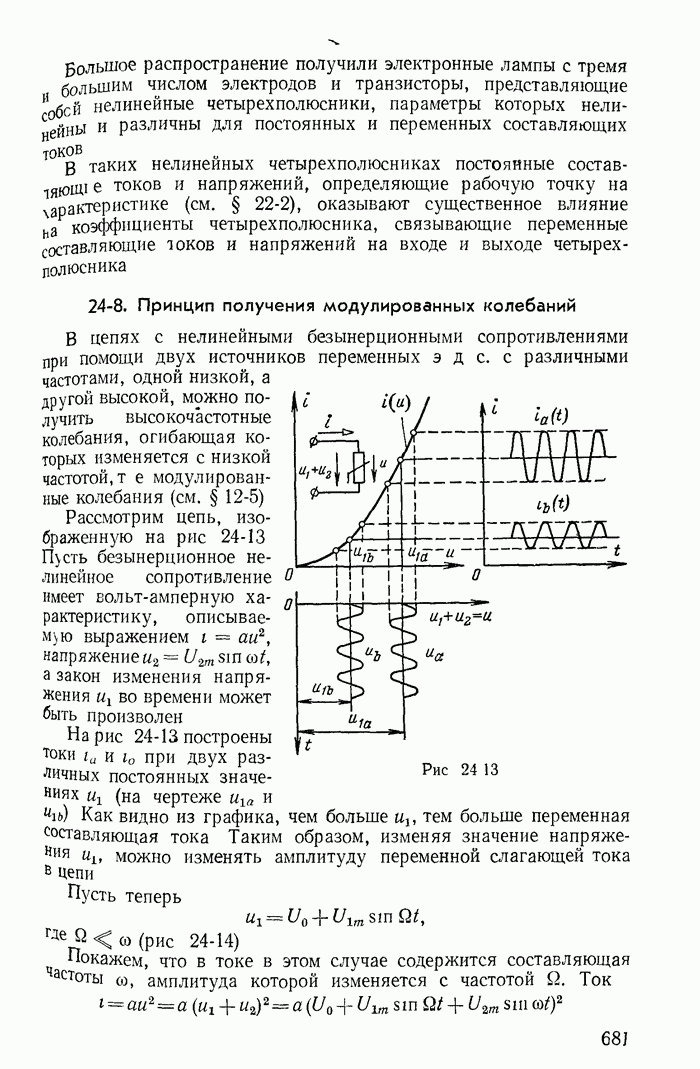
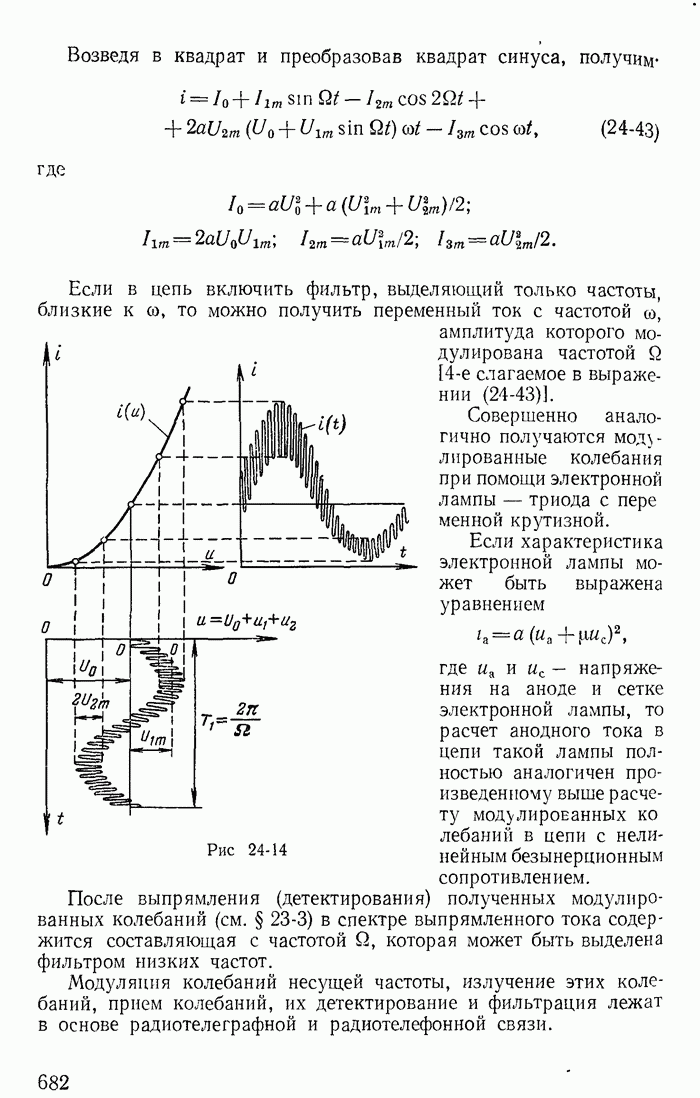
- 24-8. Принцип получения модулированных колебаний
- 24-9. Влияние постоянной составляющей на переменную в цепях с нелинейными индуктивностями
- 24-10. Магнитные усилители мощности
- Глава двадцать пятая. ПЕРЕХОДНЫЕ ПРОЦЕССЫ В НЕЛИНЕЙНЫХ ЦЕПЯХ
- 25-2. Включение катушки со стальным магнитопроводом на постоянное напряжение
- 25-3. Включение катушки со стальным магнитопроводом на синусоидальное напряжение
- 25-4. Импульсное воздействие в цепях с неоднозначными нелинейностями
- 25-5. Понятие о простейших запоминающих устройствах
- 25-6. Изображение переходных процессов на фазовой плоскости
- 25-7. Колебательный разряд емкости через нелинейную индуктивность
- Глава двадцать шестая. АВТОКОЛЕБАНИЯ
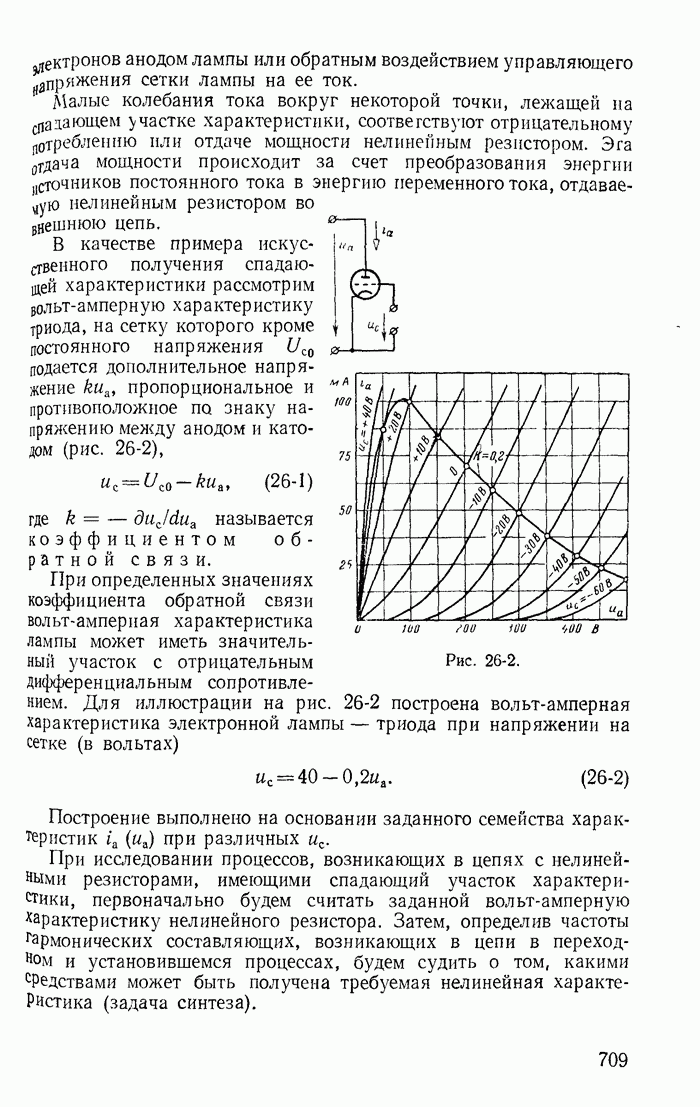
- 26-1. Нелинейные резисторы со спадающим участком характеристики
- 26-2. Понятие об устойчивости режима в цепи с нелинейными резисторами
- 26-3. Релаксационные колебания в цепи с отрицательным сопротивлением
- 26-4. Близкие к синусоидальным колебания в цепи с отрицательным сопротивлением
- 26-5. Фазовые траектории процессов в цепи с отрицательным сопротивлением
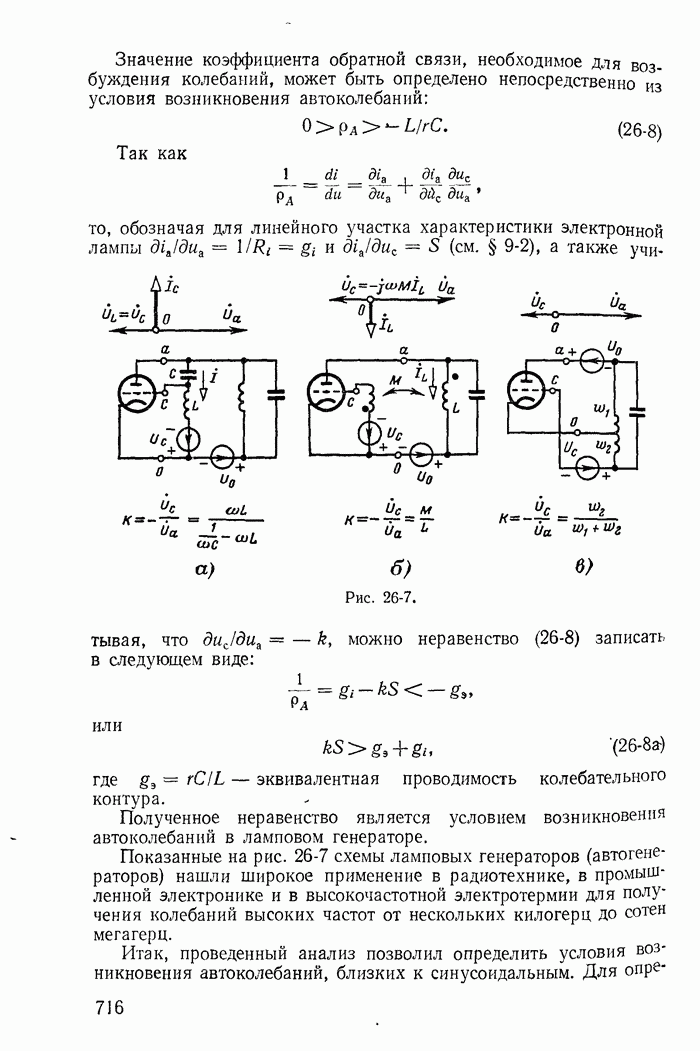
- 26-6. Фазовые траектории процессов в генераторе синусоидальных колебаний
- 26-7. Определение амплитуды автоколебаний методом гармонического баланса
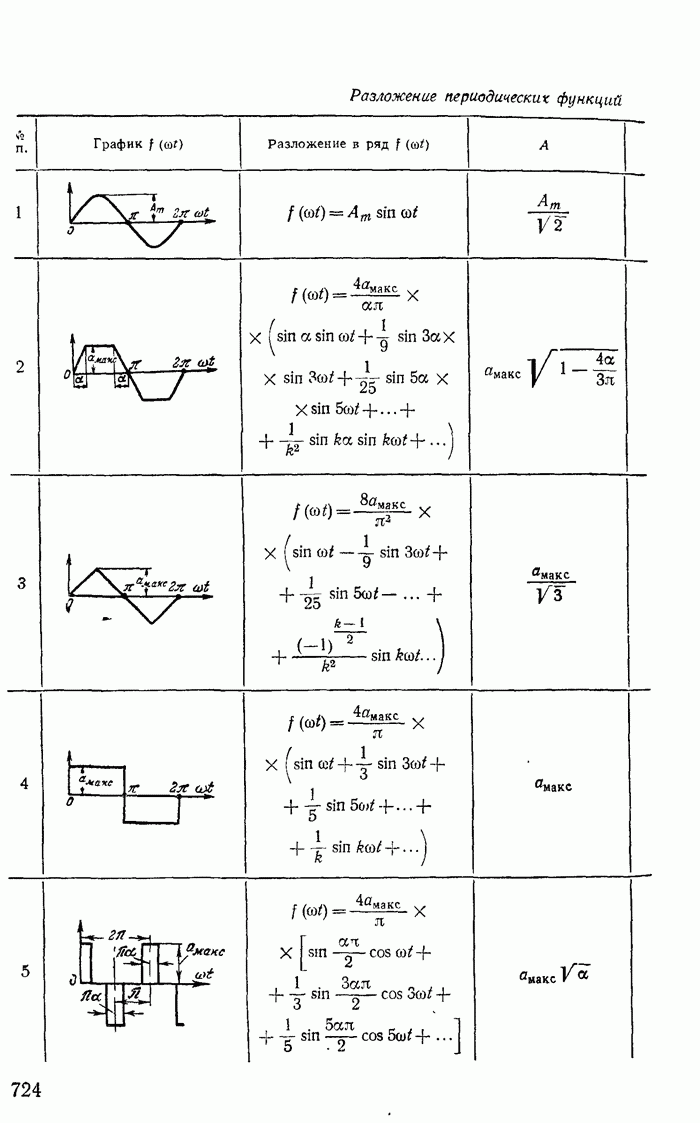
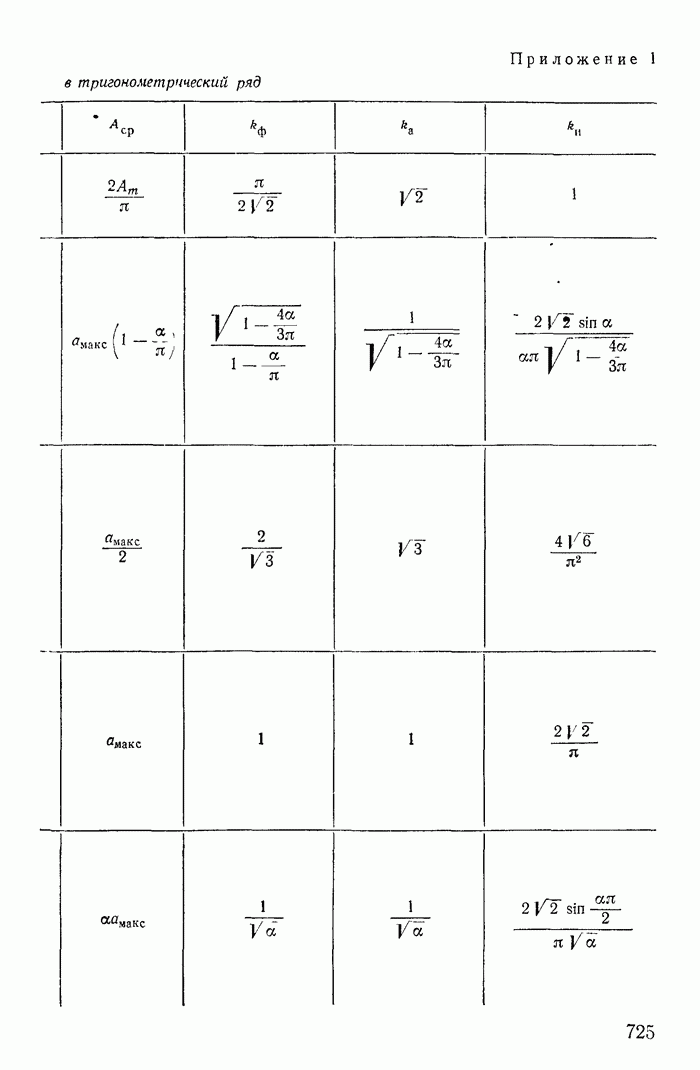
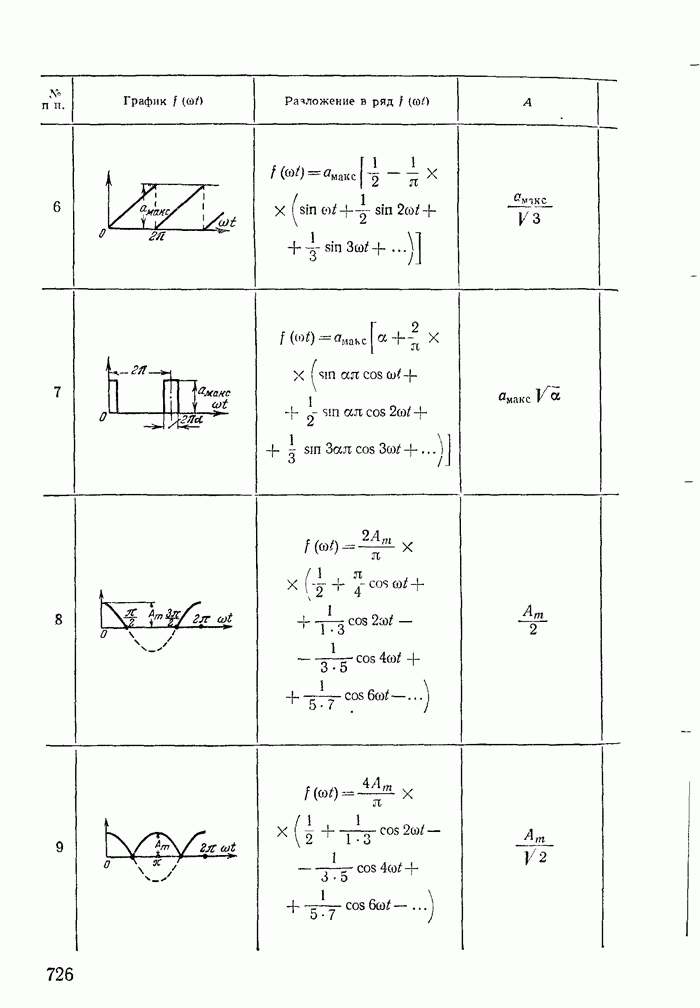
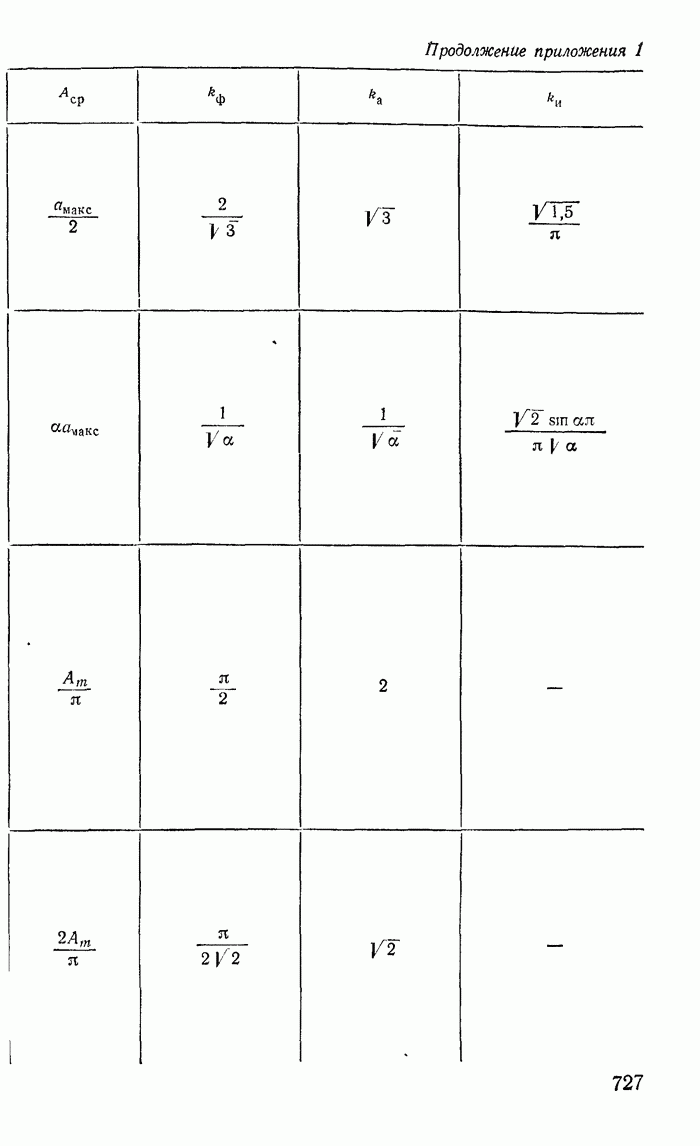
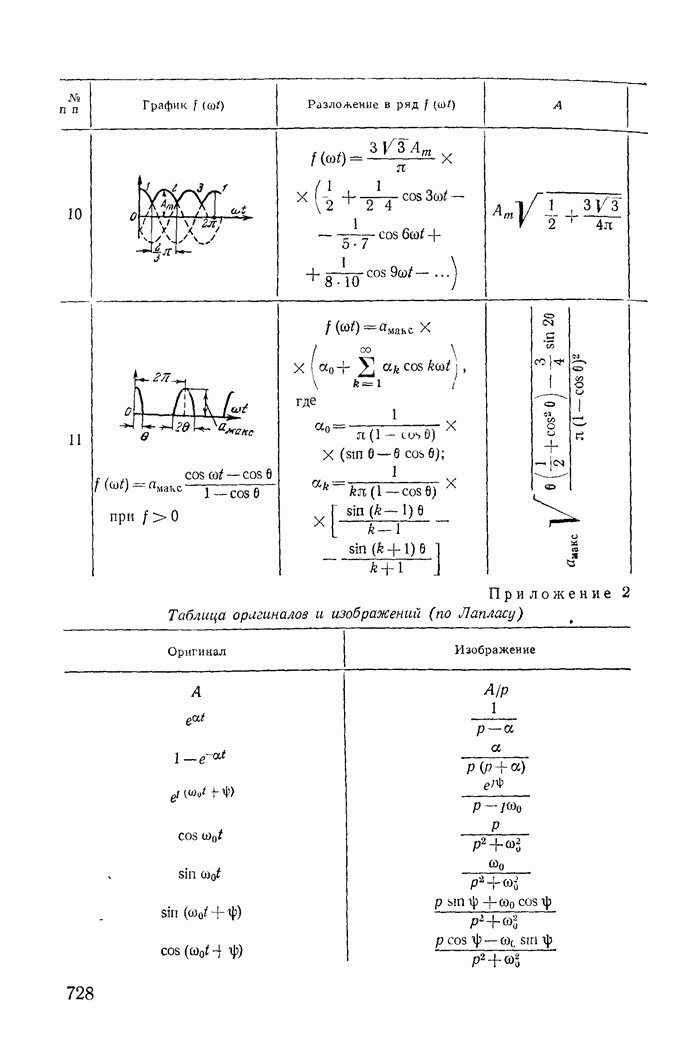
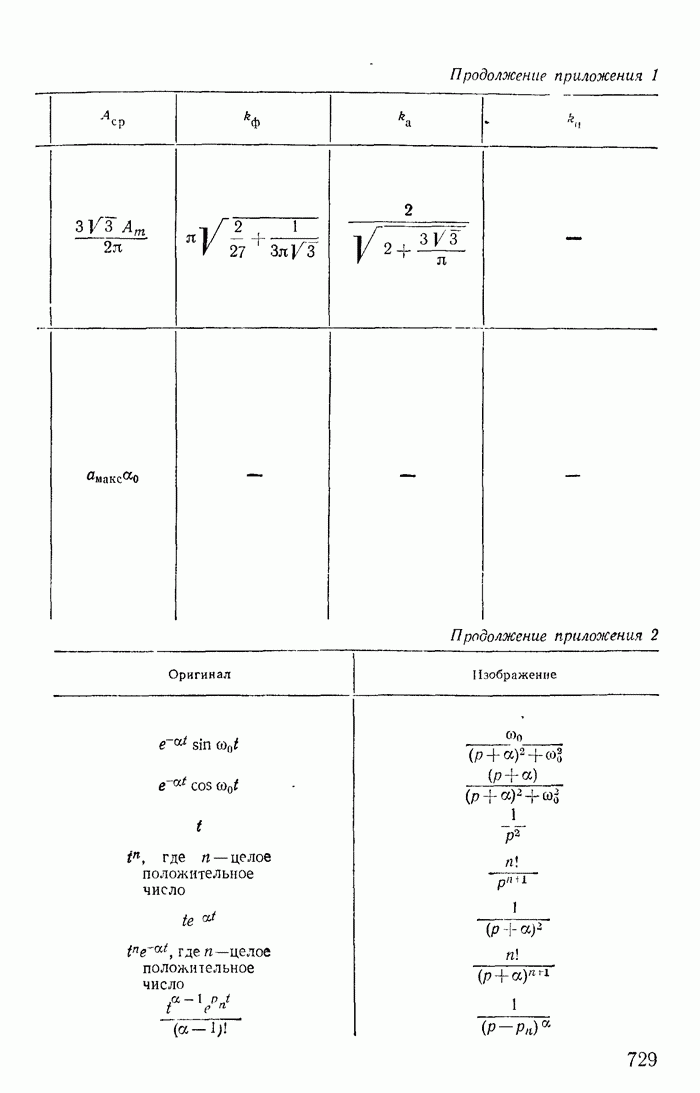
- Приложение 1. Разложение периодических функций в тригонометрический ряд
- Приложение 2. Таблица оригиналов и изображений (по Лапласу)
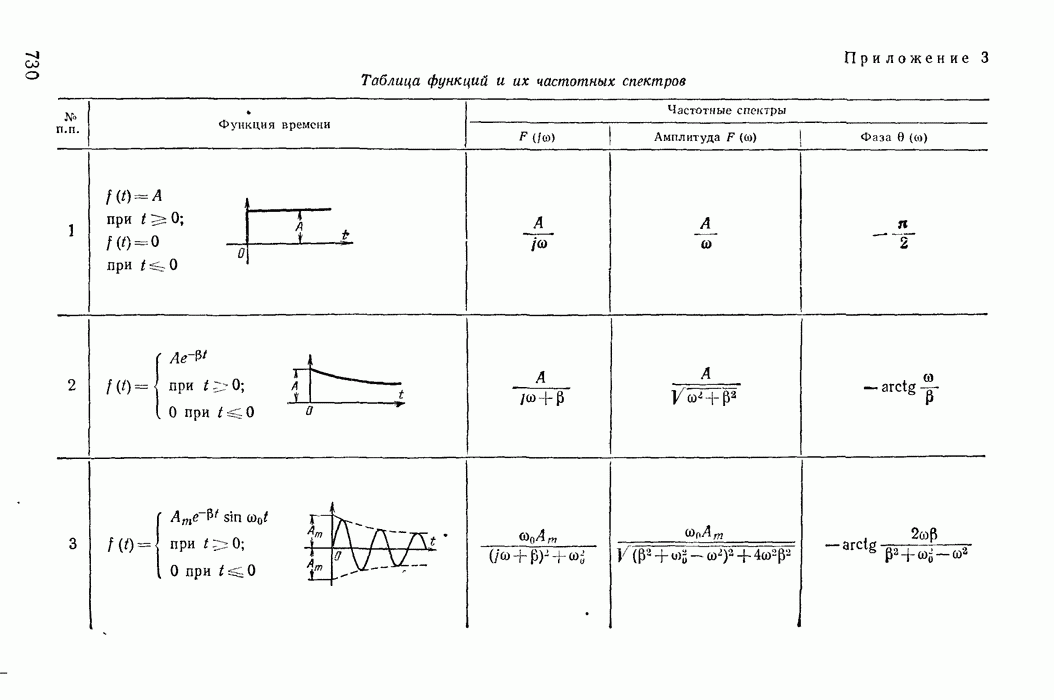
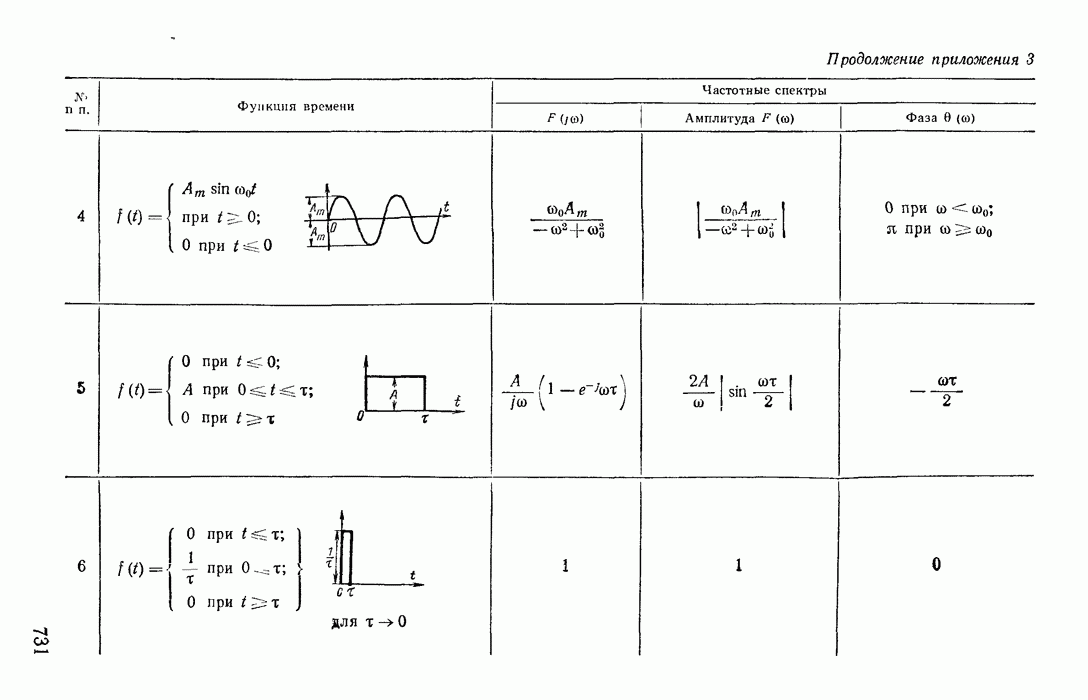
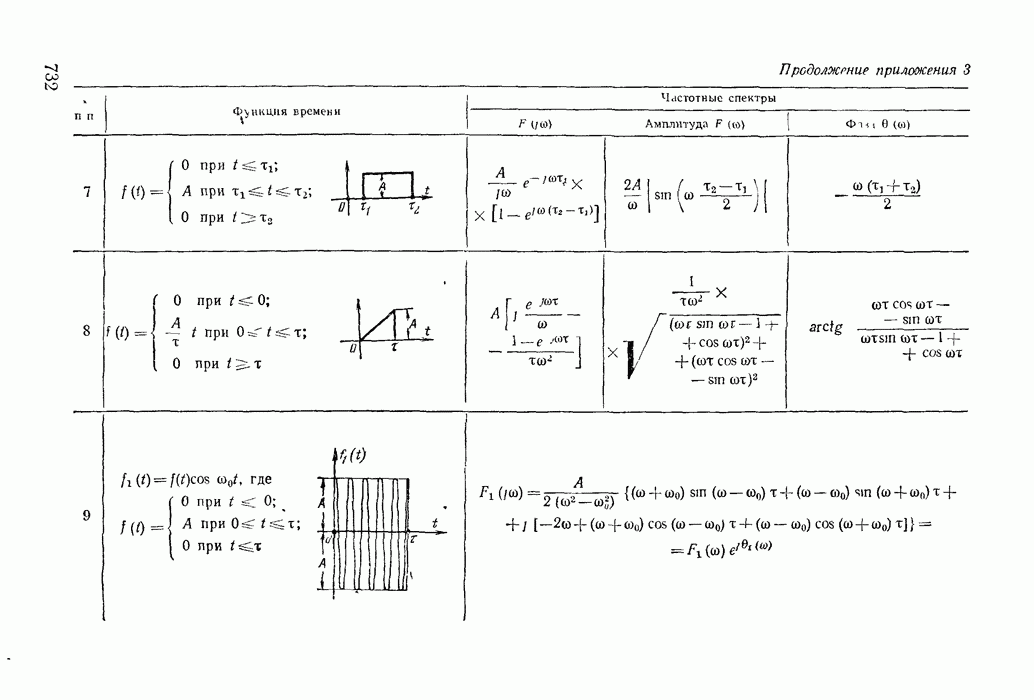
- Приложение 3. Таблица функций и их частных спектров
- Приложение 4. Таблица функций для трапеций
- СПИСОК ЛИТЕРАТУРЫ