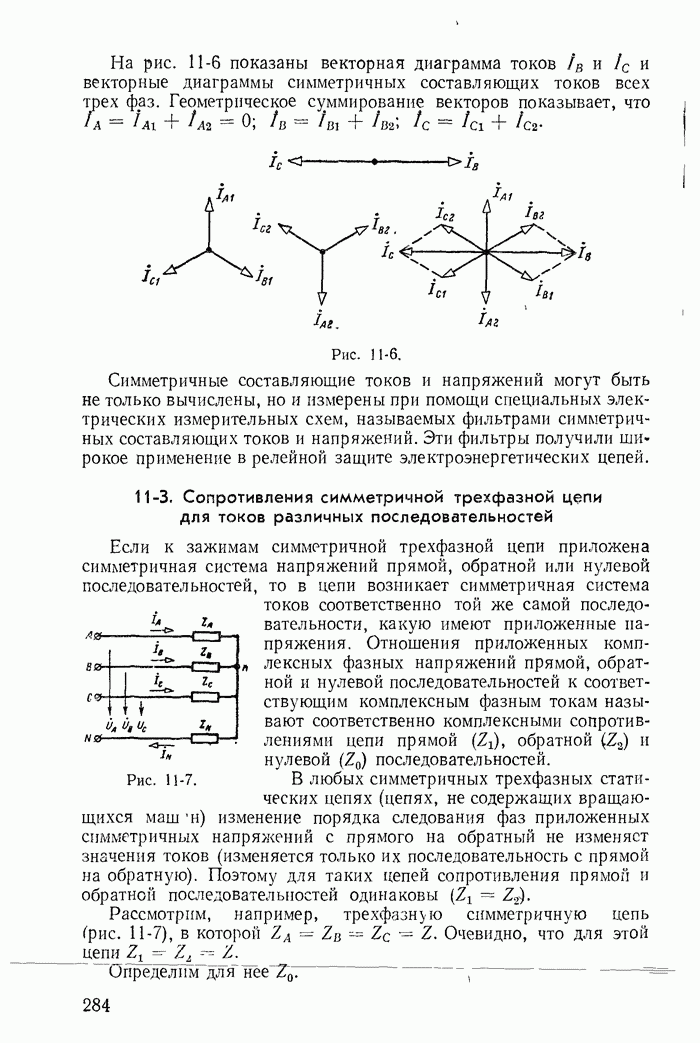
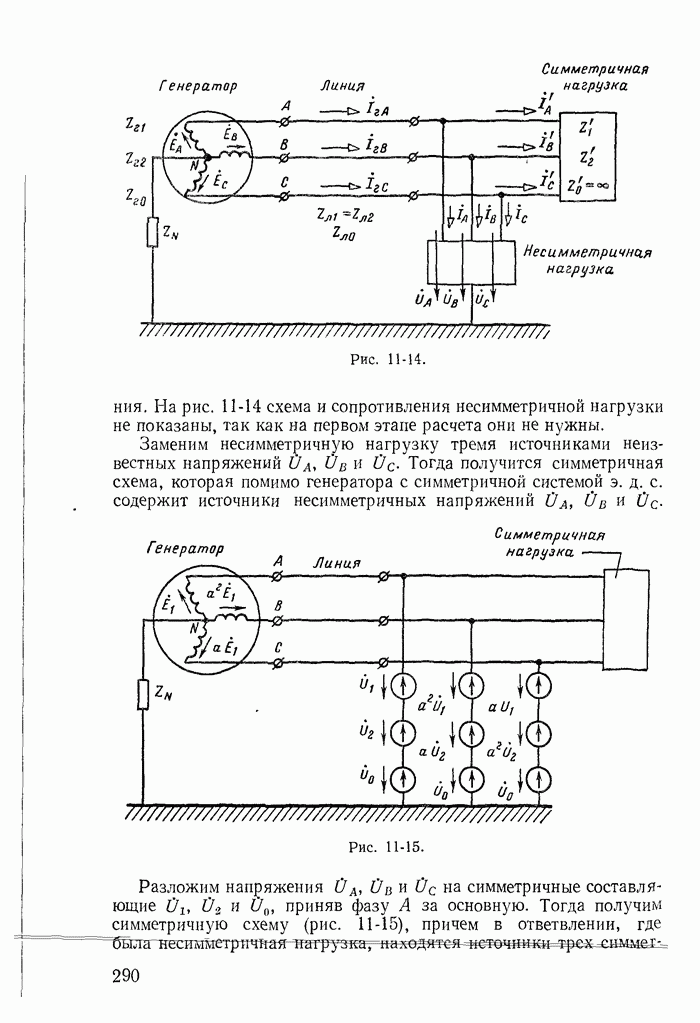
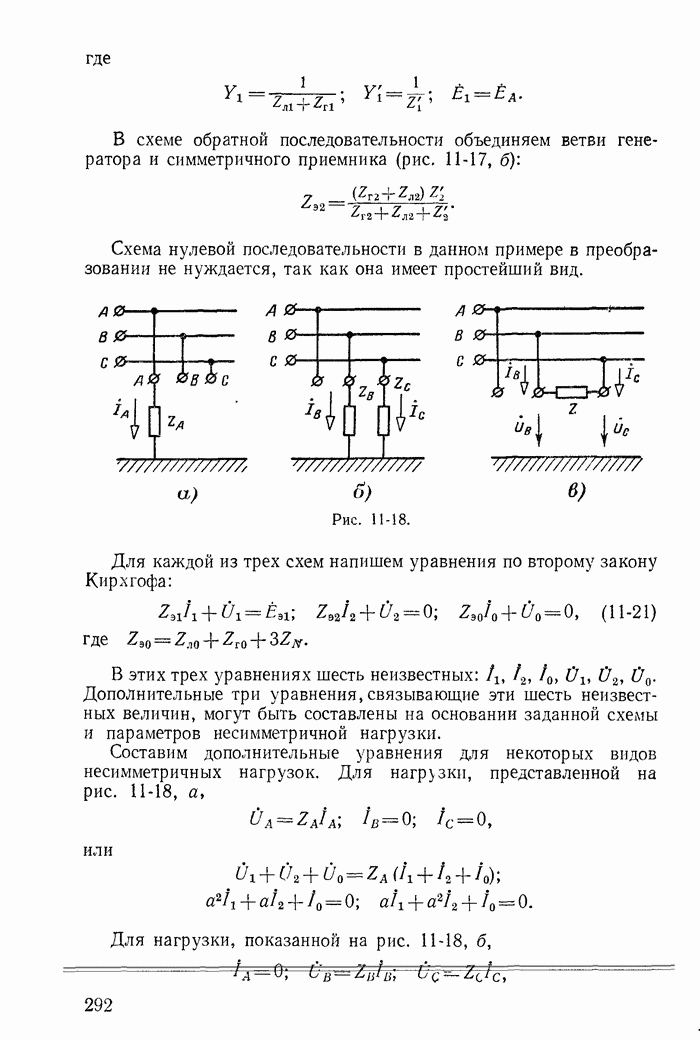
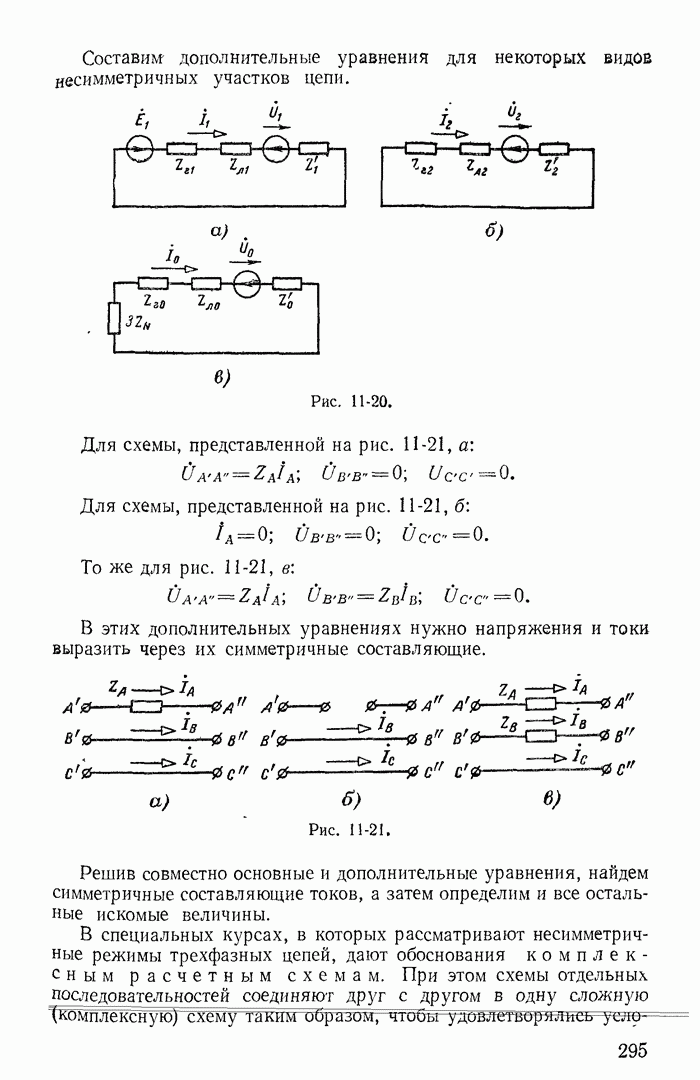
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
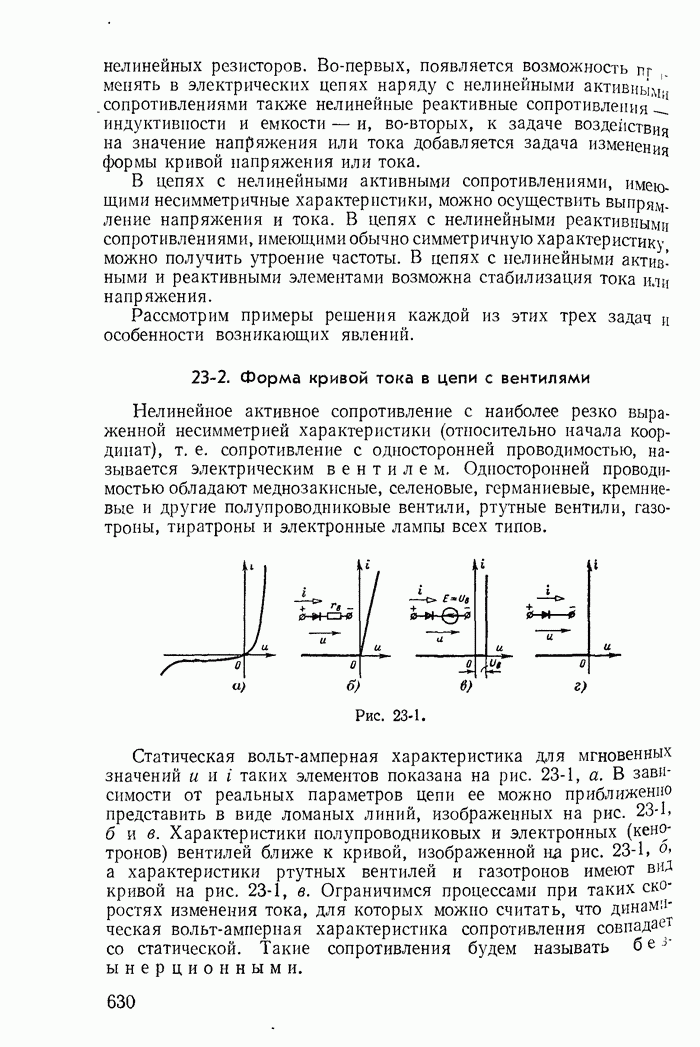
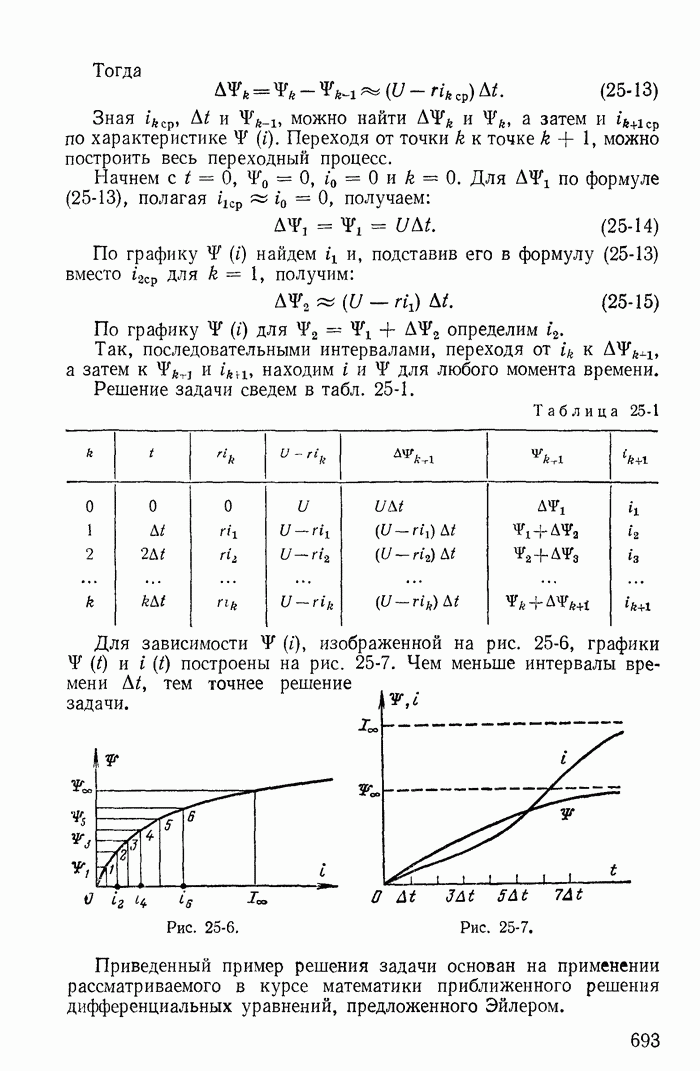
23-3. Простейшие выпрямители
Рассмотрим теперь простейшие схемы, предназначенные для выпрямления, т. е. преобразования переменного тока в постоянный
Расчет проведем методом кусочно-линейной аппроксимации.

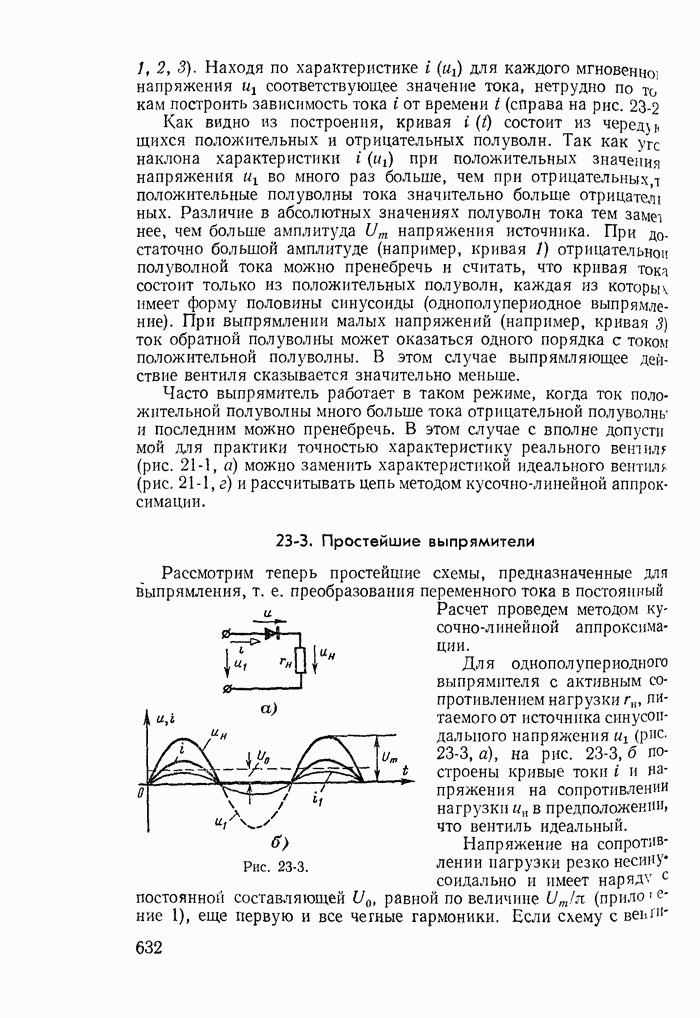
Рис. 23-3.
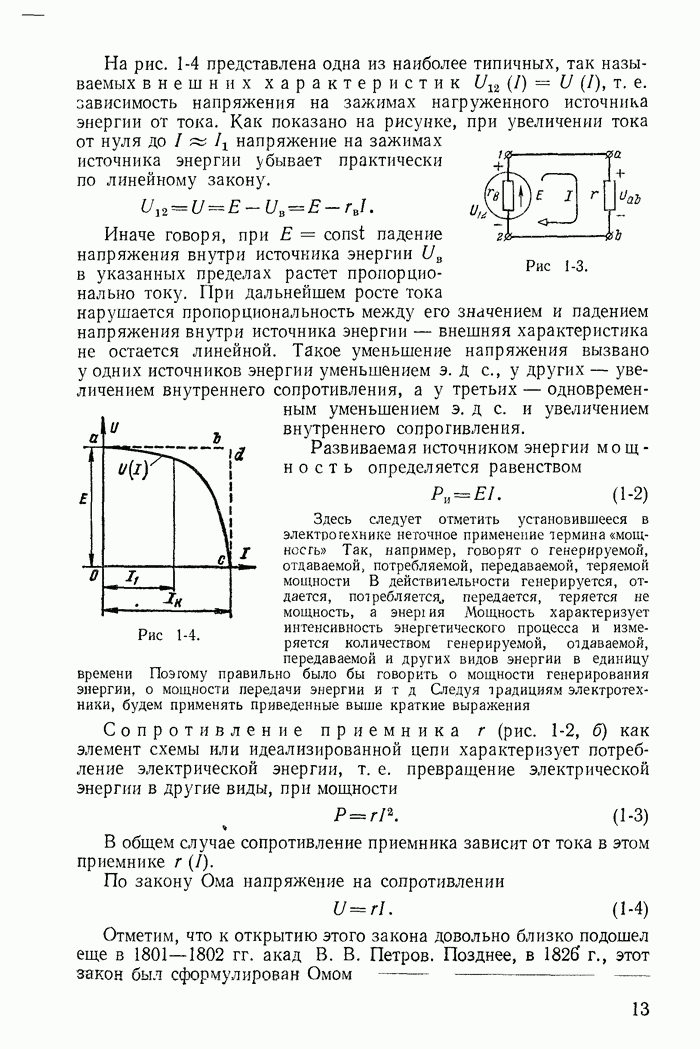
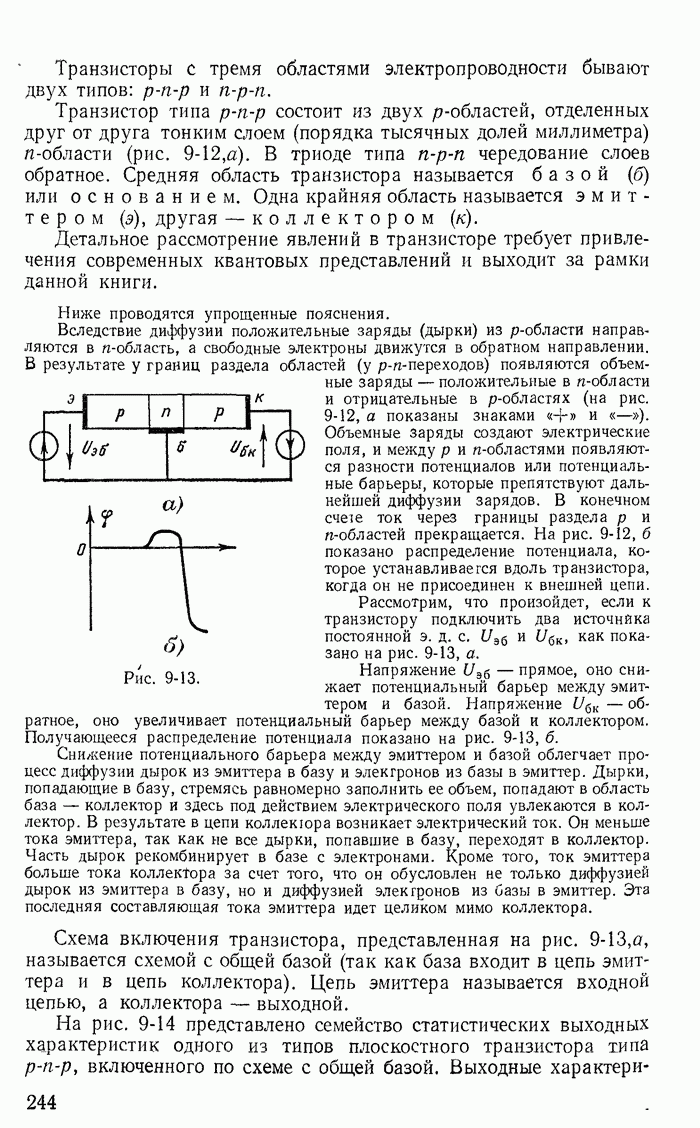
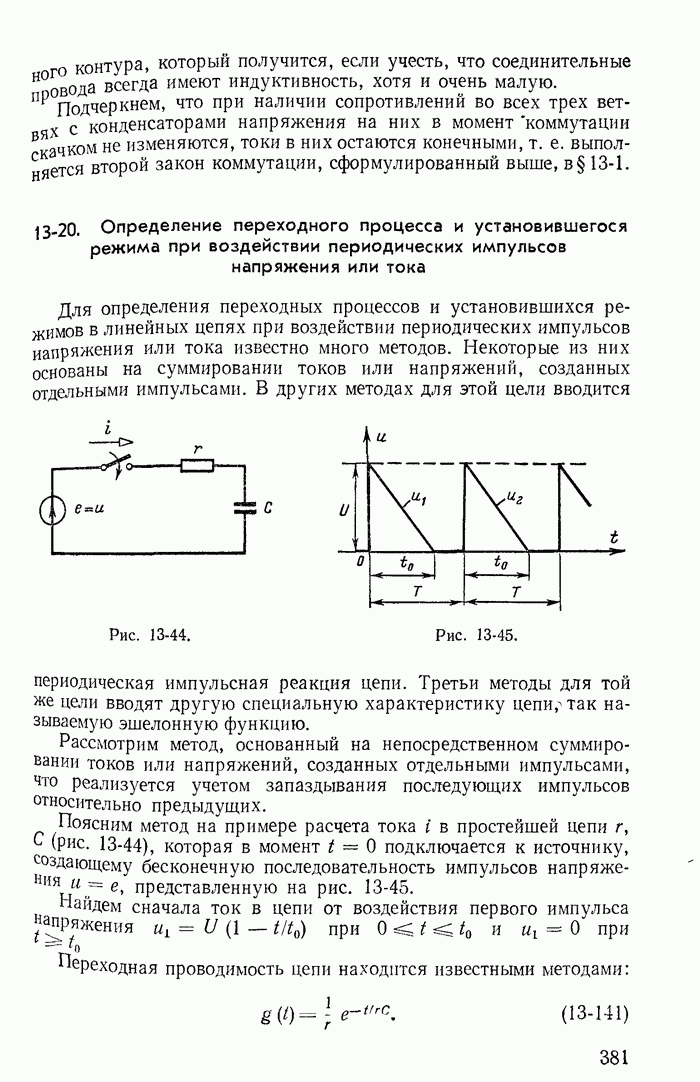
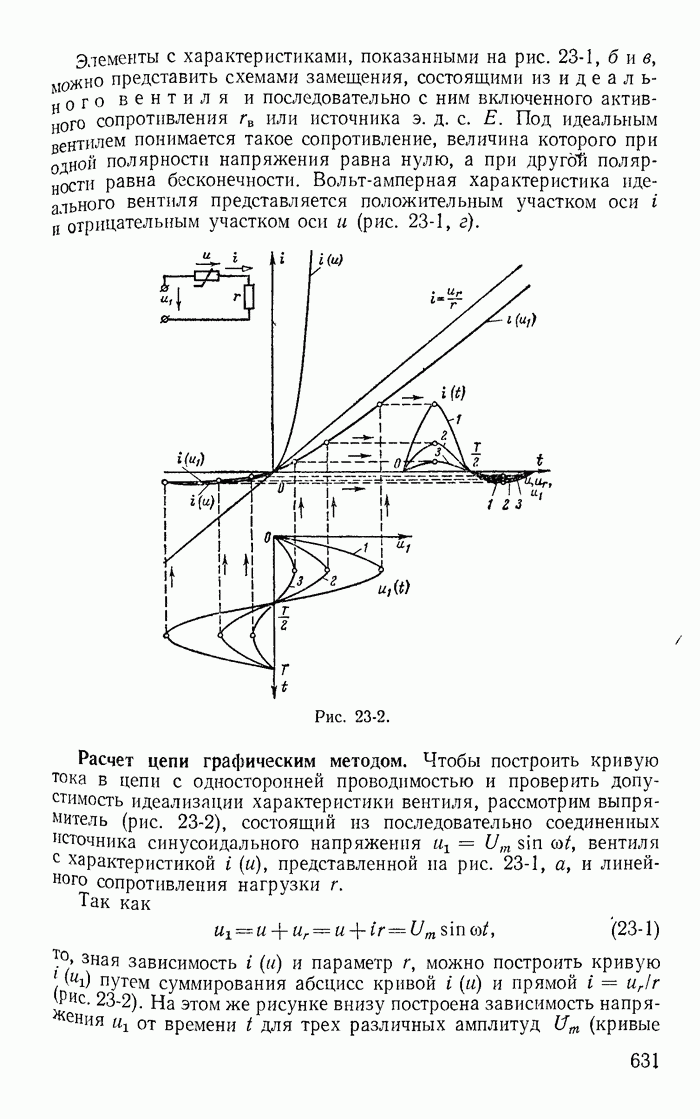
Для однополупериодного выпрямителя с активным сопротивлением нагрузки  питаемого от источника синусоидального напряжения
питаемого от источника синусоидального напряжения  (рис. 23-3, а), на рис. 23-3, б построены кривые токи i и напряжения на сопротивлении нагрузки
(рис. 23-3, а), на рис. 23-3, б построены кривые токи i и напряжения на сопротивлении нагрузки  в предположении, что вентиль идеальный.
в предположении, что вентиль идеальный.
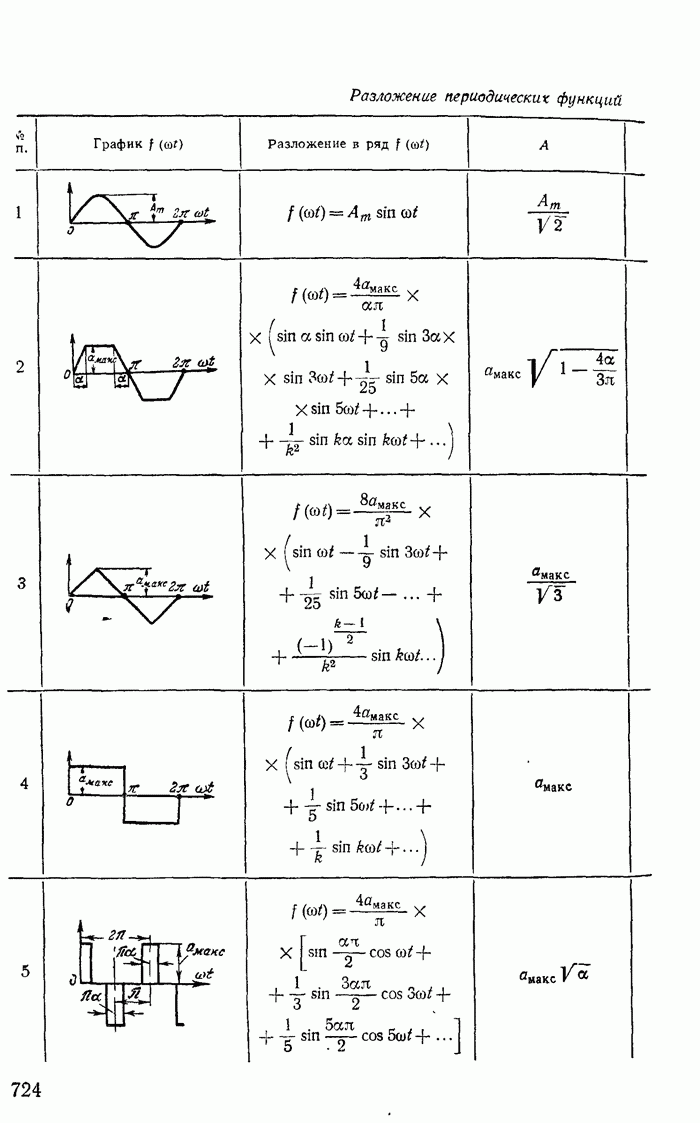
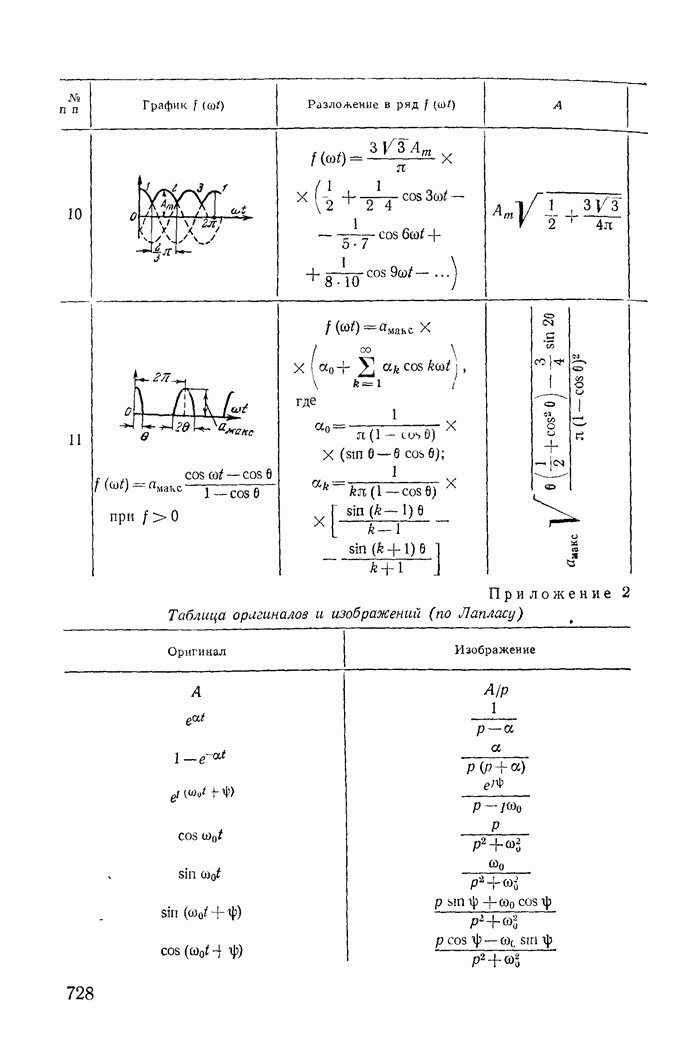
Напряжение на сопротивлении нагрузки резко несинусоидально и имеет наряду с постоянной составляющей  равной по величине
равной по величине  (приложение 1), еще первую и все четные гармоники. Если схему с вентилем
(приложение 1), еще первую и все четные гармоники. Если схему с вентилем
применяют для получения постоянного напряжения, то перед сопротивлением  включается фильтр низкой частоты, пропускающий только постоянную составляющую и не пропускающий все гармоники, начиная с первой
включается фильтр низкой частоты, пропускающий только постоянную составляющую и не пропускающий все гармоники, начиная с первой
Рассмотрим, каковы значения тока, напряжения и мощности источника в цепи (рис 23-3, а) при отсутствии фильтра
Действующее напряжение питания  Действующий ток, как и в цепях синусоидального тока
Действующий ток, как и в цепях синусоидального тока

но интеграл, стоящий под знаком корня, в 2 раза меньше его значения при отсутствии вентиля, когда протекает синусоидальный ток Поэтому

т. е. действующий ток зависит от действующего напряжения источника по линейному закону Действующее напряжение на сопротивлении нагрузки

Активная мощность в сопротивлении нагрузки в 2 раза меньше мощности, выделяемой при отсутствии выпрямителя

Потная мощность источника питания

и, следовательно, коэффициент мощности выпрямителя
 (23-6)
(23-6)
То обстоятельство, что коэффициент мощности не равен единице, объясняется в рассматриваемом случае не наличием реактивных сопротивлений, а искажением формы кривой тока но отношению к форме кривой напряжения источника питания
Для сопротивления нагрузки  действующее напряжение в
действующее напряжение в  раз меньше, чем для источника, и, следовательно,
раз меньше, чем для источника, и, следовательно,

Реактивная мощность источника

так как напряжение содержит только основную гармонику, a первая гармоника тока  (см. приложение 1 и рис. 23-3) совпадает по фазе с напряжением.
(см. приложение 1 и рис. 23-3) совпадает по фазе с напряжением.
На аналогичном принципе построены и более сложные схемы выпрямителей двух, трех и большего числа фаз.
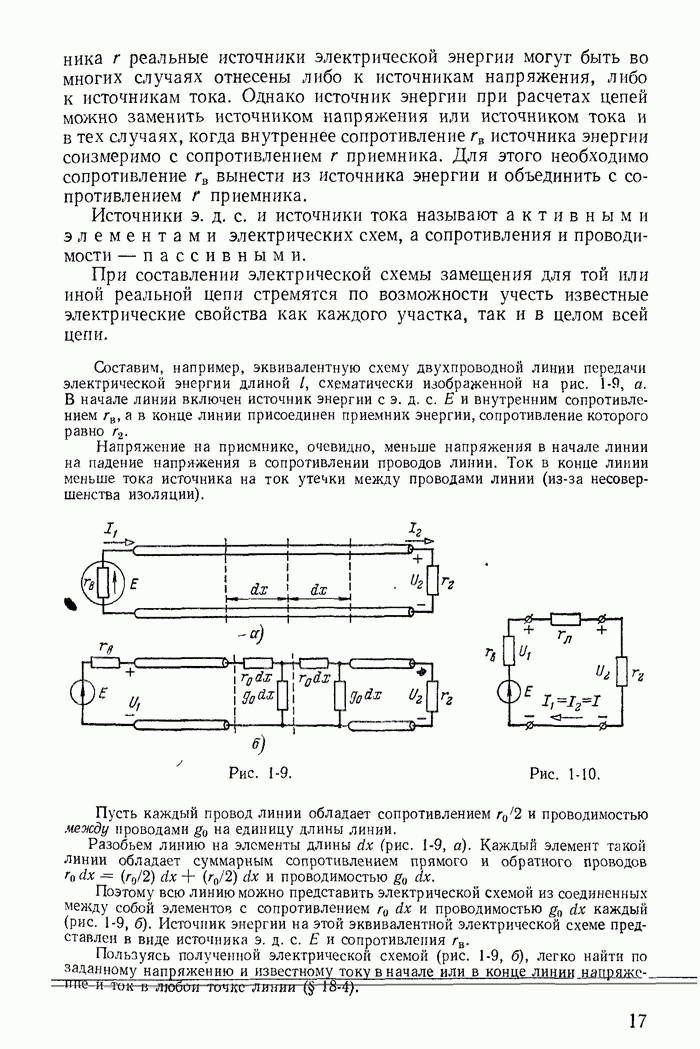
На рис. 23-4, а изображена схема двухполупериодного кенотронного выпрямителя со средней точкой. Токи, проходящие через оба вентиля (кенотрона), в сопротивлении  совпадают по направлению. В течение одного полупериода ток проходит через верхнюю часть вторичной обмотки трансформатора и первый вентиль по пути
совпадают по направлению. В течение одного полупериода ток проходит через верхнюю часть вторичной обмотки трансформатора и первый вентиль по пути  , а в течение другого полупериода — через нижнюю часть обмотки и второй вентиль по пути
, а в течение другого полупериода — через нижнюю часть обмотки и второй вентиль по пути  .
.

Рис. 23-4.
Если принять характеристику вентиля идеальной, то постоянная составляющая напряжения на нагрузке  раз меньше максимального значения напряжения, питающего один вентиль, однако, так же как и в схеме однополупериодного выпрямителя, постоянная составляющая в
раз меньше максимального значения напряжения, питающего один вентиль, однако, так же как и в схеме однополупериодного выпрямителя, постоянная составляющая в  раз меньше амплитуды общего напряжения на вторичной обмотке трансформатора (между зажимами а и b). Выпрямленное напряжение теперь не содержит основной гармоники — частоты питающего напряжения (рис. 23-4, б). Действующее значение выпрямленного напряжения (рис. 23-4, б) равно действующему напряжению одной фазы (между точками а и О или О и b).
раз меньше амплитуды общего напряжения на вторичной обмотке трансформатора (между зажимами а и b). Выпрямленное напряжение теперь не содержит основной гармоники — частоты питающего напряжения (рис. 23-4, б). Действующее значение выпрямленного напряжения (рис. 23-4, б) равно действующему напряжению одной фазы (между точками а и О или О и b).
Фильтр, не пропускающий высшие гармоники, применяемый для сглаживания напряжения  в этом случае должен быть рассчитан на частоты, начиная со второй гармоники и выше.
в этом случае должен быть рассчитан на частоты, начиная со второй гармоники и выше.
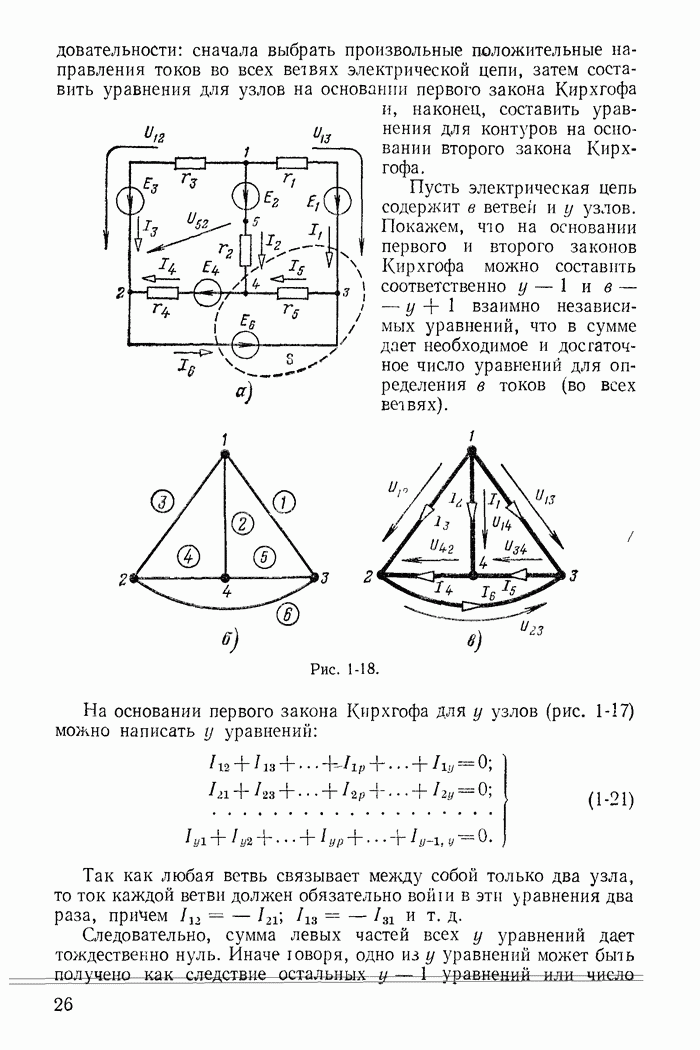
Для двухполупериодного выпрямления широко применяются мостовые схемы. На рис. 23-5, а изображена принципиальная схема мостового выпрямителя. К зажимам  моста, составленного из четырех вентилей, приложено синусоидальное напряжение
моста, составленного из четырех вентилей, приложено синусоидальное напряжение  . В течение первой половины периода (рис. 23-5, б) напряжение
. В течение первой половины периода (рис. 23-5, б) напряжение  положительно, ток протекает через вентиль 1 в направлении а к
положительно, ток протекает через вентиль 1 в направлении а к  , через сопротивление
, через сопротивление  и вентиль 3 в направлении от
и вентиль 3 в направлении от  к b. Напряжение на вентилях 1 и 3, пропускающих ток в этом направлении,
к b. Напряжение на вентилях 1 и 3, пропускающих ток в этом направлении,
практически равно нулю, и, следовательно, оно полностью ложится на каждый из вентилей 2 и 4, не проводящих ток в направлении от  к b и от а к
к b и от а к  . Таким образом, в течение первой половины периода
. Таким образом, в течение первой половины периода  на рис. 23-5, б).
на рис. 23-5, б).

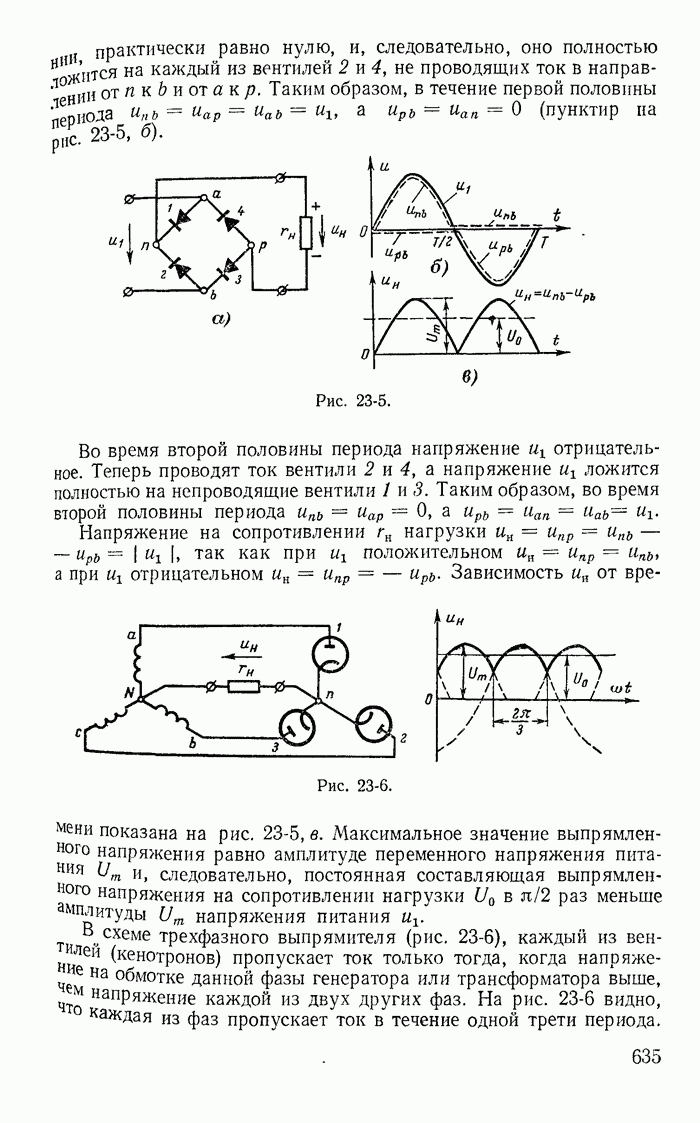
Рис. 23-5.
Во время второй половины периода напряжение  отрицательное. Теперь проводят ток вентили 2 и 4, а напряжение
отрицательное. Теперь проводят ток вентили 2 и 4, а напряжение  ложится полностью на непроводящие вентили 1 и 3. Таким образом, во время второй половины периода
ложится полностью на непроводящие вентили 1 и 3. Таким образом, во время второй половины периода  их.
их.
Напряжение на сопротивлении  нагрузки
нагрузки  , так как при
, так как при  положительном
положительном  , а при отрицательном
, а при отрицательном  Зависимость
Зависимость  от времени показана на рис. 23-5, в.
от времени показана на рис. 23-5, в.

Рис. 23-6.
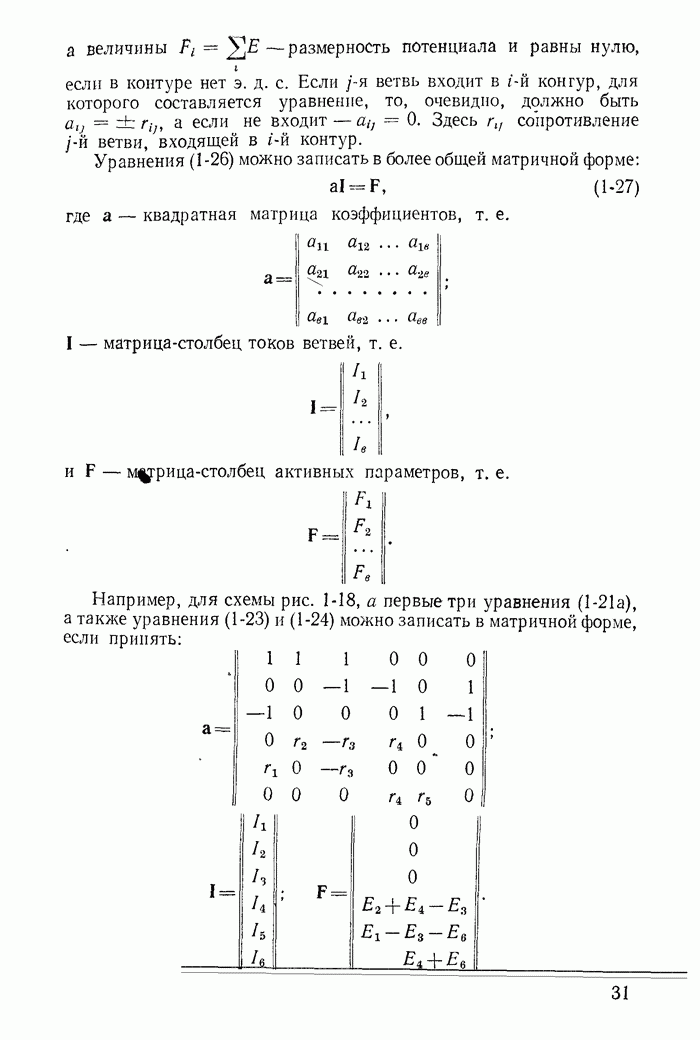
Максимальное значение выпрямленного напряжения равно амплитуде переменного напряжения питания и, следовательно, постоянная составляющая выпрямленного напряжения на сопротивлении нагрузки  раз меньше амплитуды
раз меньше амплитуды  напряжения питания
напряжения питания  схеме трехфазного выпрямителя (рис. 23-6), каждый из вентилей (кенотронов) пропускает ток только тогда, когда напряжение на обмотке данной фазы генератора или трансформатора выше, чем напряжение каждой из двух других фаз. На рис. 23-6 видно, что каждая из фаз пропускает ток в течение одной трети периода.
схеме трехфазного выпрямителя (рис. 23-6), каждый из вентилей (кенотронов) пропускает ток только тогда, когда напряжение на обмотке данной фазы генератора или трансформатора выше, чем напряжение каждой из двух других фаз. На рис. 23-6 видно, что каждая из фаз пропускает ток в течение одной трети периода.
Напряжение на сопротивлении  содержит постоянную состявляющую и высшие гармоники, кратные трем (приложение 1). Постоянная составляющая
содержит постоянную состявляющую и высшие гармоники, кратные трем (приложение 1). Постоянная составляющая  при идеальной характеристике вентиле равна где
при идеальной характеристике вентиле равна где  — амплитуда фазного напряжения. Выпрямленное напряжение содержит еще меньше высших гармоник чем в двух рассмотренных ранее схемах.
— амплитуда фазного напряжения. Выпрямленное напряжение содержит еще меньше высших гармоник чем в двух рассмотренных ранее схемах.

Рис. 23-7
Выше были рассмотрены только простейшие выпрямители, нагруженные на активные сопротивления, на практике при рассмотрении цепей выпрямителями обычно необходим учитывать кроме сопротивления  также индуктивность и емкость фильт
также индуктивность и емкость фильт  . В этих случаях при расчете токо можно пользоваться методами расчета переходных процессов и производить «припасовывание» решений, полученных для каждой из линейных участков характеристики вентиля.
. В этих случаях при расчете токо можно пользоваться методами расчета переходных процессов и производить «припасовывание» решений, полученных для каждой из линейных участков характеристики вентиля.
Рассмотрим включение цепи, представленной на рис. 23-7 при нулевых начальных условиях. Характеристику вентиля приме; идеальной.
Пусть напряжение

и замыкание рубильника происходит при  . Тогда сразу же после включения рубильника в сопротивлении
. Тогда сразу же после включения рубильника в сопротивлении  и в емкости
и в емкости  возникают токи
возникают токи

через вентиль проходит ток

В некоторый момент времени  вентиль перестает пропуская ток
вентиль перестает пропуская ток  так как напряжение на нем становится отрицательным и конденсатор начинает разряжаться на сопротивление нагрузки Для этого момента времени
так как напряжение на нем становится отрицательным и конденсатор начинает разряжаться на сопротивление нагрузки Для этого момента времени

откуда находим:

Начиная с момента  ток
ток
 (23-15)
(23-15)
разряд конденсатора происходит до того момента времени, когда отрицательное напряжение на вентиле  снизится до нуля и вентиль начнет пропускать ток. Этому соответствует момент времени
снизится до нуля и вентиль начнет пропускать ток. Этому соответствует момент времени  для которого
для которого
 (23-16)
(23-16)
Последнее уравнение аналитически не решается, и значение  следует определить графически по точке пересечения кривых их и
следует определить графически по точке пересечения кривых их и  (рис.
(рис. 

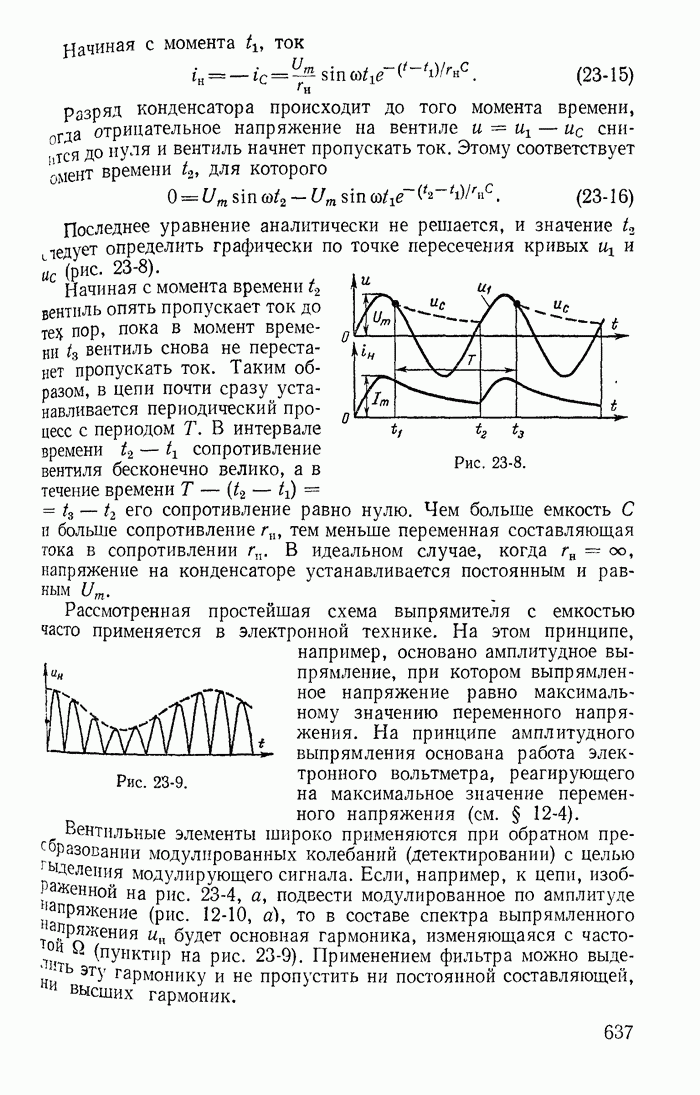
Рис. 23-8.
Начиная с момента времени  вентиль опять пропускает ток до тех пор, пока в момент времени
вентиль опять пропускает ток до тех пор, пока в момент времени  вентиль снова не перестанет пропускать ток. Таким образом, в цепи почти сразу устанавливается периодический процесс с периодом Т. В интервале времени
вентиль снова не перестанет пропускать ток. Таким образом, в цепи почти сразу устанавливается периодический процесс с периодом Т. В интервале времени  сопротивление вентиля бесконечно велико, а в течение времени
сопротивление вентиля бесконечно велико, а в течение времени  его сопротивление равно нулю. Чем больше емкость С и больше сопротивление
его сопротивление равно нулю. Чем больше емкость С и больше сопротивление  тем меньше переменная составляющая тока в сопротивлении
тем меньше переменная составляющая тока в сопротивлении  . В идеальном случае, когда
. В идеальном случае, когда  напряжение на конденсаторе устанавливается постоянным и равным
напряжение на конденсаторе устанавливается постоянным и равным 
Рассмотренная простейшая схема выпрямителя с емкостью часто применяется в электронной технике. На этом принципе, например, основано амплитудное выпрямление, при котором выпрямленное напряжение равно максимальному значению переменного напряжения. На принципе амплитудного выпрямления основана работа электронного вольтметра, реагирующего на максимальное значение переменного напряжения (см. § 12-4).

Рис. 23-9.
Вентильные элементы широко применяются при обратном преобразовании модулированных колебаний (детектировании) с целью выделения модулирующего сигнала. Если, например, к цепи, изображенной на рис. 23-4, а, подвести модулированное по амплитуде напряжение (рис. 12-10, а), то в составе спектра выпрямленного напряжения  будет основная гармоника, изменяющаяся с частотой ВВ (пунктир на рис. 23-9). Применением фильтра можно выделить эту гармонику и не пропустить ни постоянной составляющей, ни высших гармоник.
будет основная гармоника, изменяющаяся с частотой ВВ (пунктир на рис. 23-9). Применением фильтра можно выделить эту гармонику и не пропустить ни постоянной составляющей, ни высших гармоник.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ К ЧЕТВЕРТОМУ ИЗДАНИЮ
- ВВЕДЕНИЕ
- Раздел первый. ЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ С СОСРЕДОТОЧЕННЫМИ ПАРАМЕТРАМИ
- 1-1. Элементы электрических цепей и электрических схем
- 1-2. Эквивалентные схемы для источников энергии
- 1-3. Закон Ома для участка цепи с э. д. с.
- 1-4. Распределение потенциала вдоль неразветвленной электрической цепи
- 1-5. Баланс мощностей для простейшей неразветвленной цепи
- 1-6. Применение законов Кирхгофа для расчета разветвленных цепей
- 1-7. Метод узловых потенциалов
- 1-8. Метод контурных токов
- 1-9. Уравнения состояния цепи в матричной форме
- 1-10. Преобразование линейных электрических схем
- Глава вторая. ОСНОВНЫЕ СВОЙСТВА ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ПРИ ПОСТОЯННЫХ ТОКАХ И НАПРЯЖЕНИЯХ
- 2-2. Свойство взаимности
- 2-3. Входные и взаимные проводимости и сопротивления ветвей; коэффициенты передачи напряжений и токов
- 2-4. Применение топологических методов для расчета цепей
- 2-5. Топологические формулы и правила для определения передачи электрической цепи
- 2-6. Теорема о компенсации
- 2-7. Линейные соотношения между напряжениями и токами
- 2-8. Теорема о взаимных приращениях токов и напряжений
- 2-9. Общие замечания о двухполюсниках
- 2-10. Теорема об активном двухполюснике и ее применение для расчета разветвленных цепей
- 2-11. Передача энергии от активного двухполюсника к пассивному
- Глава третья. ОСНОВНЫЕ ПОНЯТИЯ О ЦЕПЯХ СИНУСОИДАЛЬНОГО ТОКА
- 3-2. Понятие о генераторах переменного тока
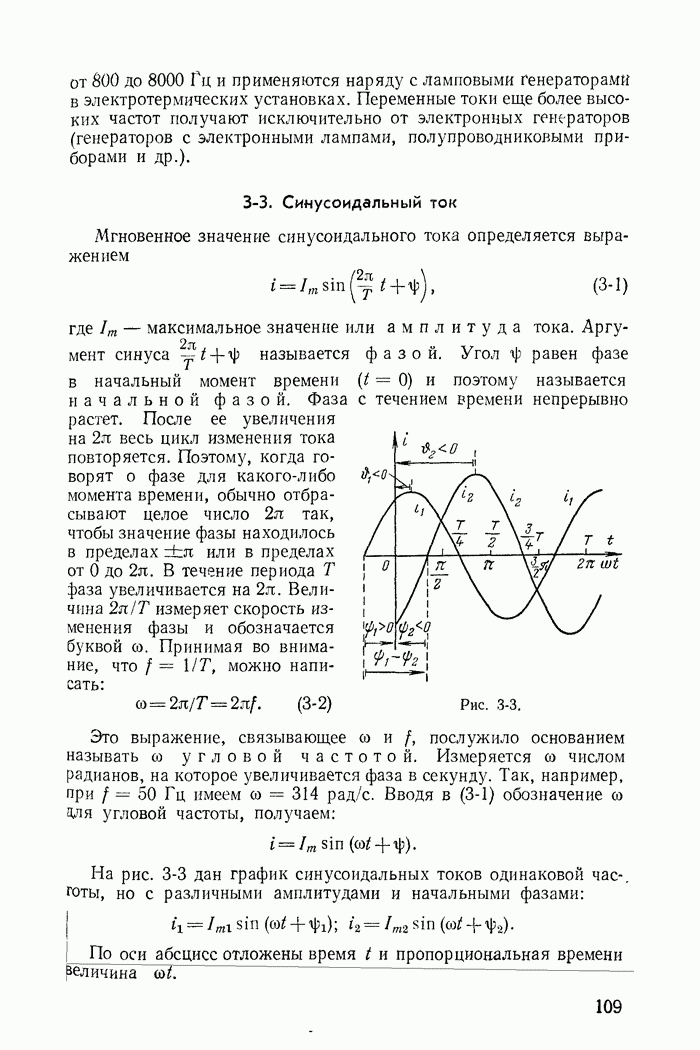
- 3-3. Синусоидальный ток
- 3-4. Действующие ток, э. д. с. и напряжение
- 3-5. Изображение синусоидальных функций времени векторами и комплексными числами
- 3-6. Сложение синусоидальных функций времени
- 3-7. Электрическая цепь и ее схема
- 3-8. Ток и напряжения при последовательном соединении сопротивления, Индуктивности и емкости
- 3-9. Сопротивления
- 3-10. Разность фаз напряжения и тока
- 3-11. Напряжение и токи при параллельном соединении сопротивления, индуктивности и емкости
- 3-12. Проводимости
- 3-13. Пассивный двухполюсник
- 3-14. Мощности
- 3-15. Мощности в сопротивлении, индуктивности и емкости
- 3-16. Баланс мощностей
- 3-17. Знаки мощностей и направление передачи энергии
- 3-18. Определение параметров пассивного двухполюсника при помощи амперметра, вольтметра и ваттметра
- 3-19. Условия передачи максимальной мощности от источника энергии к приемнику
- 3-20. Понятие о поверхностном эффекте и эффекте близости
- 3-21. Параметры и эквивалентные схемы конденсаторов
- 3-22. Параметры и эквивалентные схемы индуктивных катушек и резисторов
- Глава четвертая. РАСЧЕТ ЦЕПЕЙ ПРИ СИНУСОИДАЛЬНЫХ ТОКАХ
- 4-1. О применимости методов расчета цепей постоянного тока к расчетам цепей синусоидального тока
- 4-2. Последовательное соединение приемников
- 4-3. Параллельное соединение приемников
- 4-4. Смешанное соединение приемников
- 4-5. Сложные разветвленные цепи
- 4-6. Топографические диаграммы
- 4-7. Дуальность электрических цепей
- 4-8. Сигнальные графы и их применение для расчета цепей
- Глава пятая. РЕЗОНАНС В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ
- 5-2. Частотные характеристики неразветвленной цепи
- 5-3. Резонанс в цепи с двумя параллельными ветвями
- 5-4. Частотные характеристики параллельного контура
- 5-5. Понятие о резонансе в сложных цепях
- Глава шестая. ЦЕПИ С ВЗАИМНОЙ ИНДУКТИВНОСТЬЮ
- 6-2. Электродвижущая сила взаимной индукции
- 6-3. Последовательное соединение индуктивно связанных элементов цепи
- 6-4. Параллельное соединение индуктивно связанных элементов цепи
- 6-5. Расчеты разветвленных цепей при наличии взаимной индуктивности
- 6-6. Эквивалентная замена индуктивных связей
- 6-7. Передача энергии между индуктивно связанными элементами цепи
- 6-8. Трансформатор без стального сердечника (воздушный трансформатор)
- Глава седьмая. КРУГОВЫЕ ДИАГРАММЫ
- 7-1. Комплексные уравнения прямой и окружности
- 7-2. Круговые диаграммы для неразветвленной цепи и для активного двухполюсника
- 7-3. Круговые диаграммы для любой разветвленной цепи
- Глава восьмая. МНОГОПОЛЮСНИКИ И ЧЕТЫРЕХПОЛЮСНИКИ ПРИ СИНУСОИДАЛЬНЫХ ТОКАХ И НАПРЯЖЕНИЯХ
- 8-1. Четырехполюсники и их основные уравнения
- 8-2. Определение коэффициентов четырехполюсников
- 8-3. Режим четырехполюсника при нагрузке
- 8-4. Эквивалентные схемы четырехполюсников
- 8-5. Основные уравнения и эквивалентные схемы для активного четырехполюсника
- 8-6. Идеальный трансформатор как четырехполюсник
- 8-7. Эквивалентные схемы с идеальными трансформаторами для четырехполюсника
- 8-8. Эквивалентные схемы трансформатора со стальным магнитопроводом
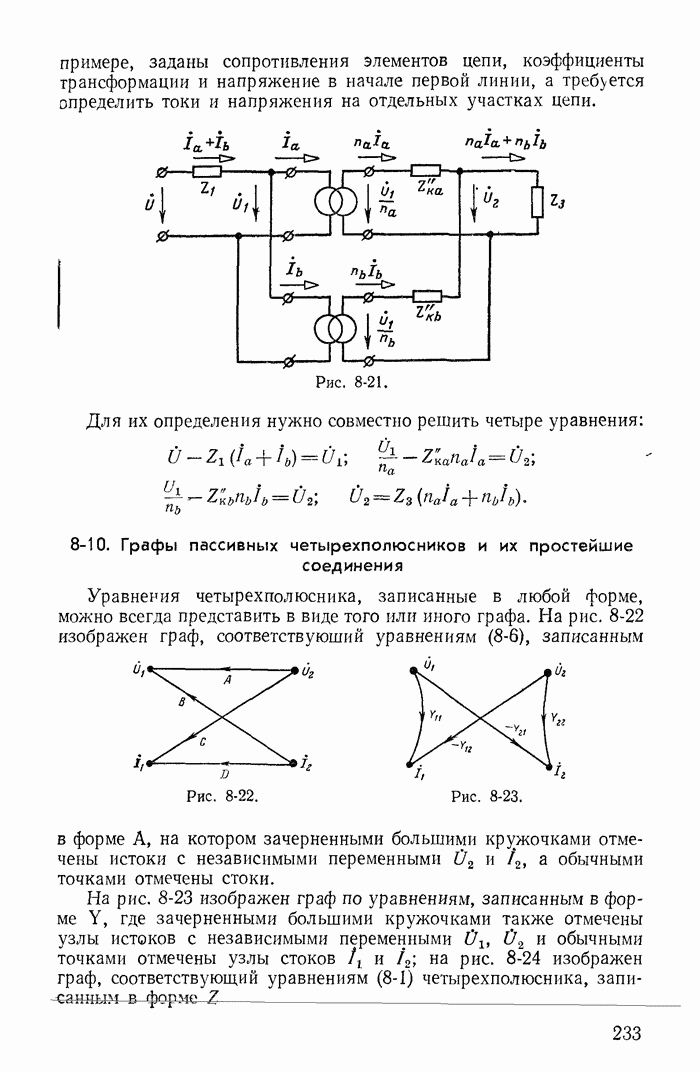
- 8-9. Расчеты электрических цепей с трансформаторами
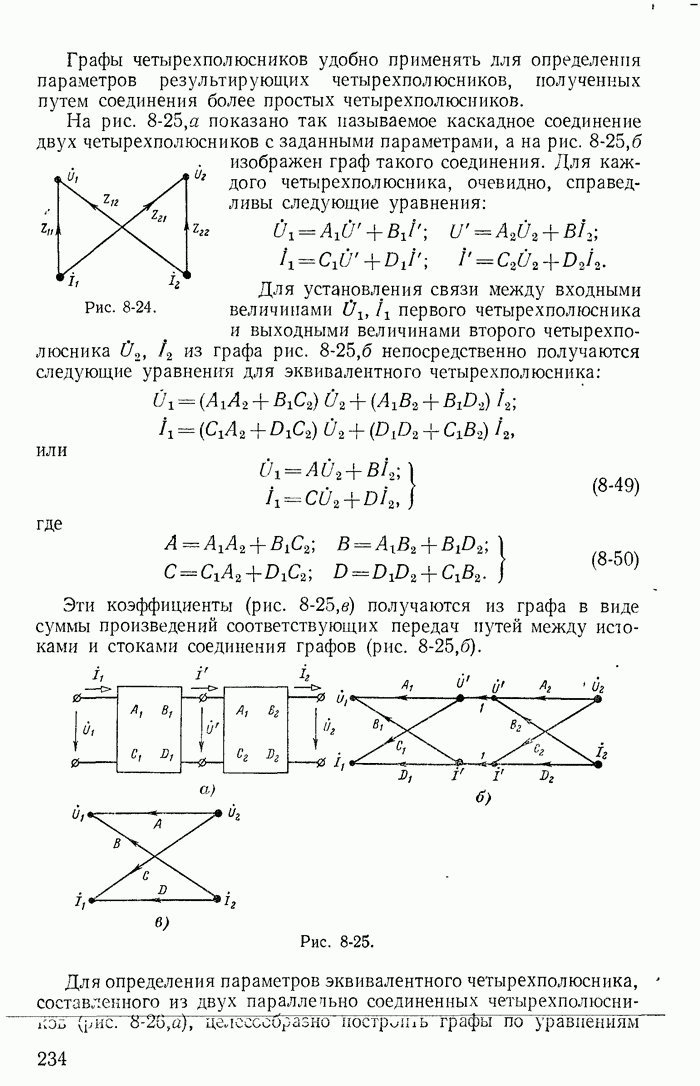
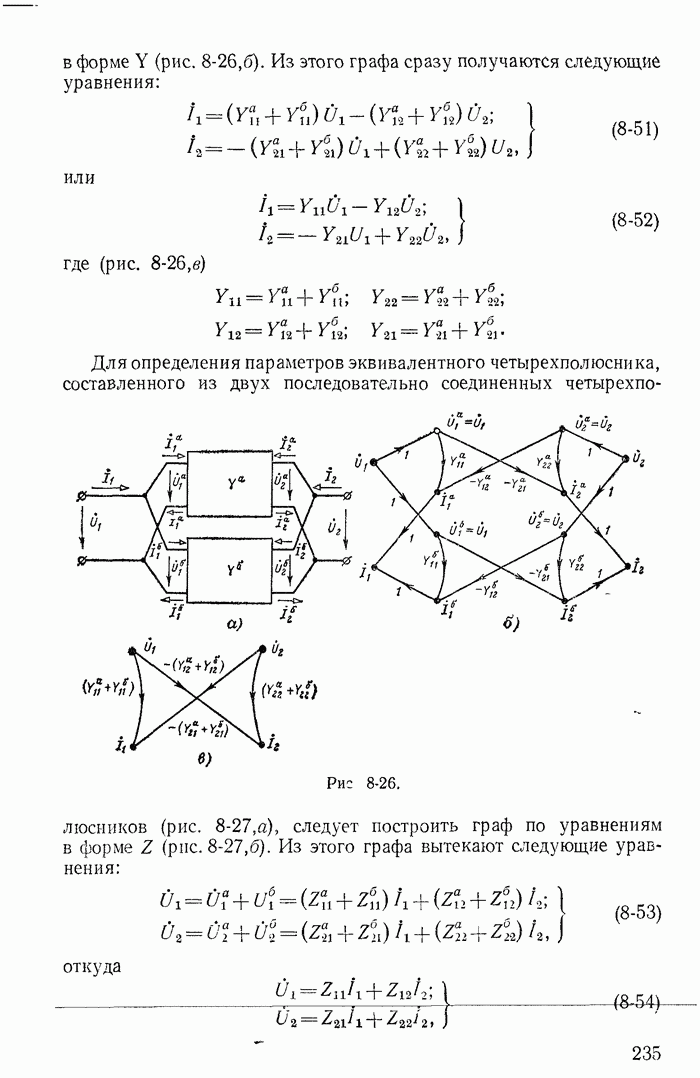
- 8-10. Графы пассивных четырехполюсников и их простейшие соединения
- Глава девятая. ЦЕПИ С ЭЛЕКТРОННЫМИ И ПОЛУПРОВОДНИКОВЫМИ ПРИБОРАМИ В ЛИНЕЙНОМ РЕЖИМЕ
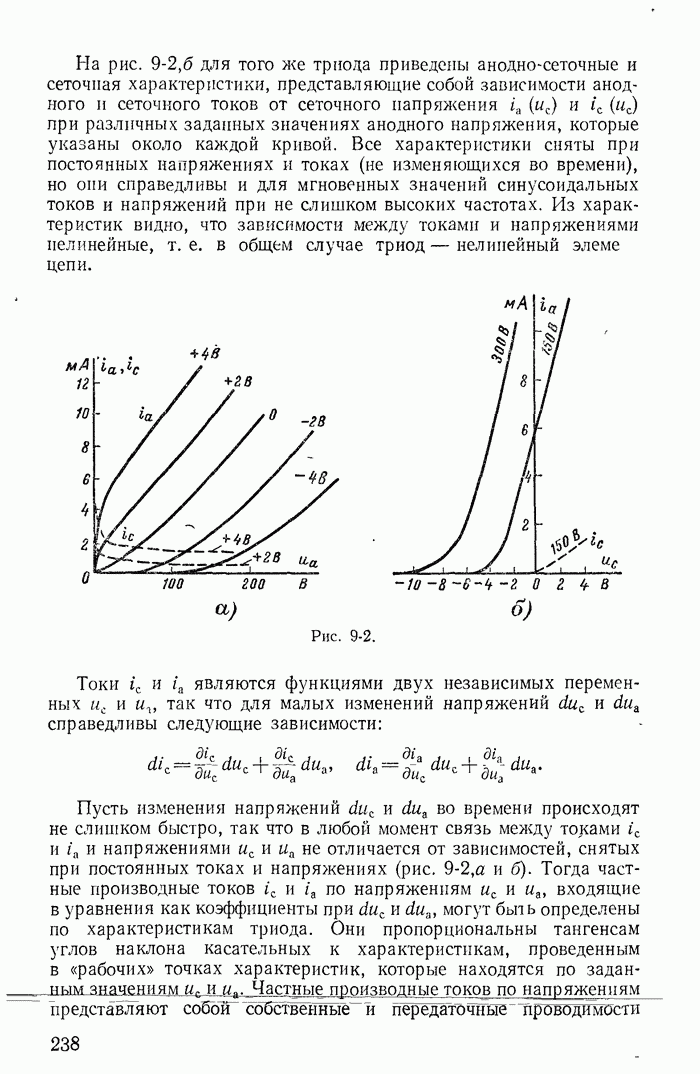
- 9-2. Эквивалентные схемы лампового триода
- 9-3. Транзисторы (полупроводниковые триоды)
- 9-4. Эквивалентные схемы транзисторов
- 9-5. Простейшие электрические цепи с невзаимными элементами и их направленные графы
- Глава десятая. ТРЕХФАЗНЫЕ ЦЕПИ
- 10-2. Соединения звездой и многоугольником
- 10-3. Симметричный режим трехфазной цепи
- 10-4. Некоторые свойства трехфазных цепей с различными схемами соединений
- 10-5. Расчет симметричных режимов трехфазных цепей
- 10-6. Расчет несимметричных режимов трехфазных цепей со статической нагрузкой
- 10-7. Напряжения на фазах приемника в некоторых частных случаях
- 10-8. Эквивалентные схемы трехфазных линий
- 10-9. Измерение мощности в трехфазных цепях
- 10-10. Вращающееся магнитное поле
- 10-11. Принципы действия асинхронного и синхронного двигателей
- Глава одиннадцатая. МЕТОД СИММЕТРИЧНЫХ СОСТАВЛЯЮЩИХ
- 11-2. Некоторые свойства трехфазных цепей в отношении симметричных составляющих токов и напряжений
- 11-3. Сопротивления симметричной трехфазной цепи для токов различных последовательностей
- 11-4. Определение токов в симметричной цепи
- 11-5. Симметричные составляющие напряжений и токов в несимметричной трехфазной цепи
- 11-6. Расчет цепи с несимметричной нагрузкой
- 11-7. Расчет цепи с несимметричным участком в линии
- Глава двенадцатая. НЕСИНУСОИДАЛЬНЫЕ ТОКИ
- 12-2. Разложение периодической несинусоидальной кривой в тригонометрический ряд
- 12-3. Максимальные, действующие и средние значения несинусоидальных периодических э. д. с., напряжений и токов
- 12-4. Коэффициенты, характеризующие форму несинусоидальных периодических кривых
- 12-5. Несинусоидальные кривые с периодической огибающей
- 12-6. Действующие значения э. д. с., напряжений и токов с периодическими огибающими
- 12-7. Расчет цепей с несинусоидальными периодическими э. д. с. и токами
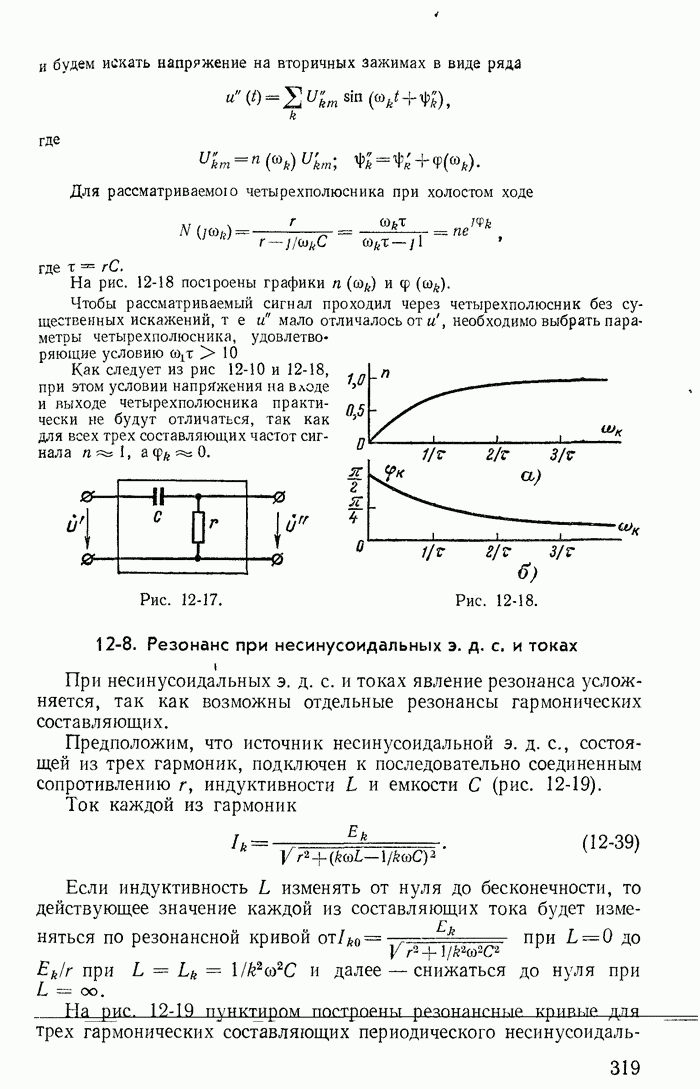
- 12-8. Резонанс при несинусоидальных э. д. с. и токах
- 12-9. Мощность периодических несинусоидальных токов
- 12-10. Высшие гармоники в трехфазных цепях
- Глава тринадцатая. КЛАССИЧЕСКИЙ МЕТОД РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ
- 13-2. Переходный, принужденный и свободный процессы
- 13-3. Короткое замыкание цепи r, L
- 13-4. Включение цепи r, L на постоянное напряжение
- 13-5. Включение цепи r, L на синусоидальное напряжение
- 13-6. Короткое замыкание цепи r, С
- 13-7. Включение цепи r, С на постоянное напряжение
- 13-8. Включение цепи r, С на синусоидальное напряжение
- 13-9. Переходные процессы в неразветвленной цепи r, С
- 13-10. Апериодический разряд конденсатора
- 13-11. Предельный случай апериодического разряда конденсатора
- 13-12. Периодический (колебательный) разряд конденсатора
- 13-13. Включение цепи r, С на постоянное напряжение
- 13-14. Общий случай расчета переходных процессов классическим методом
- 13-15. Включение пассивного двухполюсника на непрерывно изменяющееся напряжение (формула или интеграл Дюамеля)
- 13-16. Включение пассивного двухполюсника на напряжение любой формы
- 13-17. Временная и импульсная переходные характеристики
- 13-18. Запись теоремы свертки при помощи импульсной переходной характеристики
- 13-19. Переходные процессы при скачках токов в индуктивностях и напряжений на конденсаторах
- 13-20. Определение переходного процесса и установившегося режима при воздействии периодических импульсов напряжения или тока
- Глава четырнадцатая. ОПЕРАТОРНЫЙ МЕТОД РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ
- 14-2. Законы Ома и Кирхгофа в операторной форме
- 14-3. Эквивалентные операторные схемы
- 14-4. Переходные процессы в цепях с взаимной индуктивностью
- 14-5. Сведение расчетов переходных процессов к нулевым начальным условиям
- 14-6. Определение свободных токов по их изображениям
- 14-7. Формулы включения
- 14-8. Расчет переходных процессов методом переменных состояния
- 14-9. Определение принужденного режима цепи при воздействии на нее периодического несинусоидального напряжения
- Глава пятнадцатая. ЧАСТОТНЫЙ МЕТОД РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ
- 15-2. Законы Ома и Кирхгофа и эквивалентные схемы для частотных спектров
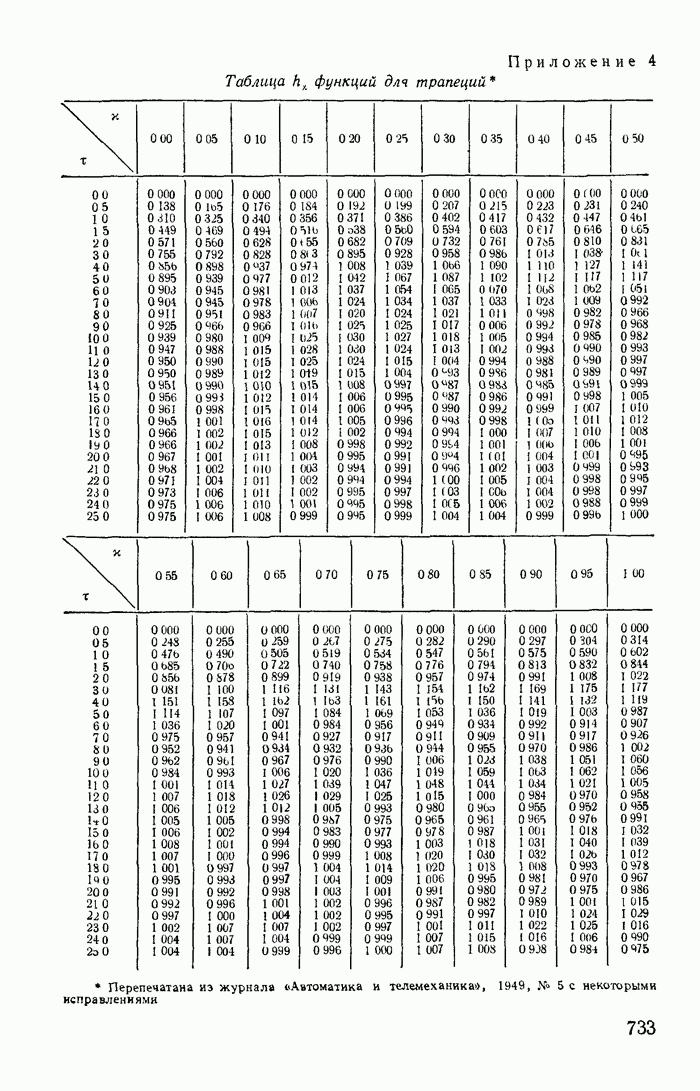
- 15-3. Приближенный метод определения оригинала по вещественной частотной характеристике (метод трапеций)
- 15-4. О переходе от преобразований Фурье к преобразованиям Лапласа
- 15-5. Сравнение различных методов расчета переходных процессов в линейных электрических цепях
- Глава шестнадцатая. ЦЕПНЫЕ СХЕМЫ И ЧАСТОТНЫЕ ЭЛЕКТРИЧЕСКИЕ ФИЛЬТРЫ
- 16-2. Характеристическое сопротивление и постоянная передачи симметричного четырехполюсника
- 16-3. Вносимая и рабочая постоянные передачи
- 16-4. Цепные схемы
- 16-5. Частотные электрические фильтры
- 16-6. Низкочастотные фильтры
- 16-8. Полосные фильтры
- 16-11. Г-образный фильтр как пример несимметричного фильтра
- 16-12. Безындукционные (или r, C) фильтры
- Глава семнадцатая. СИНТЕЗ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
- 17-2. Передаточная функция четырехполюсника. Цепи минимальной фазы
- 17-3. Входные функции цепей. Положительные вещественные функции
- 17-4. Реактивные двухполюсники
- 17-5. Частотные характеристики реактивных двухполюсников
- 17-6. Синтез реактивных двухполюсников. Метод Фостера
- 17-7. Синтез реактивных двухполюсников. Метод Кауэра
- 17-8. Синтез двухполюсников с потерями. Метод Фостера
- 17-9. Синтез двухполюсников с потерями. Метод Кауэра
- 17-10. Понятие о синтезе четырехполюсников
- Раздел второй. ЛИНЕЙНЫЕ ЦЕПИ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
- Глава восемнадцатая. ГАРМОНИЧЕСКИЕ ПРОЦЕССЫ В ЦЕПЯХ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
- 18-2. Уравнения однородной линии
- 18-3. Установившийся режим в однородной линии
- 18-4. Уравнения однородной линии с гиперболическими функциями
- 18-5. Характеристики однородной линии
- 18-6. Входное сопротивление линии
- 18-7. Коэффициент отражения волны
- 18-8. Согласованная нагрузка линии
- 18-9. Линия без искажений
- 18-10. Холостой ход, короткое замыкание и нагрузочный режим линии с потерями
- 18-11. Линии без потерь
- 18-12. Стоячие волны
- 18-13. Линия как четырехполюсник
- Глава девятнадцатая. ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЦЕПЯХ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
- 19-2. Общее решение уравнений однородной линии
- 19-3. Возникновение волн с прямоугольным фронтом
- 19-4. Общие случаи нахождения волн, возникающих при переключениях
- 19-5. Отражение волны с прямоугольным фронтом от конца линии
- 19-6. Общий метод определения отраженных волн
- 19-7. Качественное рассмотрение переходных процессов в линиях, содержащих сосредоточенные емкости и индуктивности
- 19-8. Многократные отражения волн с прямоугольным фронтом от активного сопротивления
- 19-9. Блуждающие волны
- Раздел III. НЕЛИНЕЙНЫЕ ЦЕПИ
- Глава двадцатая. НЕЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПРИ ПОСТОЯННЫХ ТОКАХ И НАПРЯЖЕНИЯХ
- 20-2. Графический метод расчета неразветвленных цепей с нелинейными элементами
- 20-3. Графический метод расчета цепей с параллельным соединением нелинейных элементов
- 20-4. Графический метод расчета цепей со смешанным соединением нелинейных и линейных элементов
- 20-5. Применение эквивалентных схем с источниками э. д. с. для исследования режима нелинейных цепей
- 20-6. Вольт-амперные характеристики нелинейных активных двухполюсников
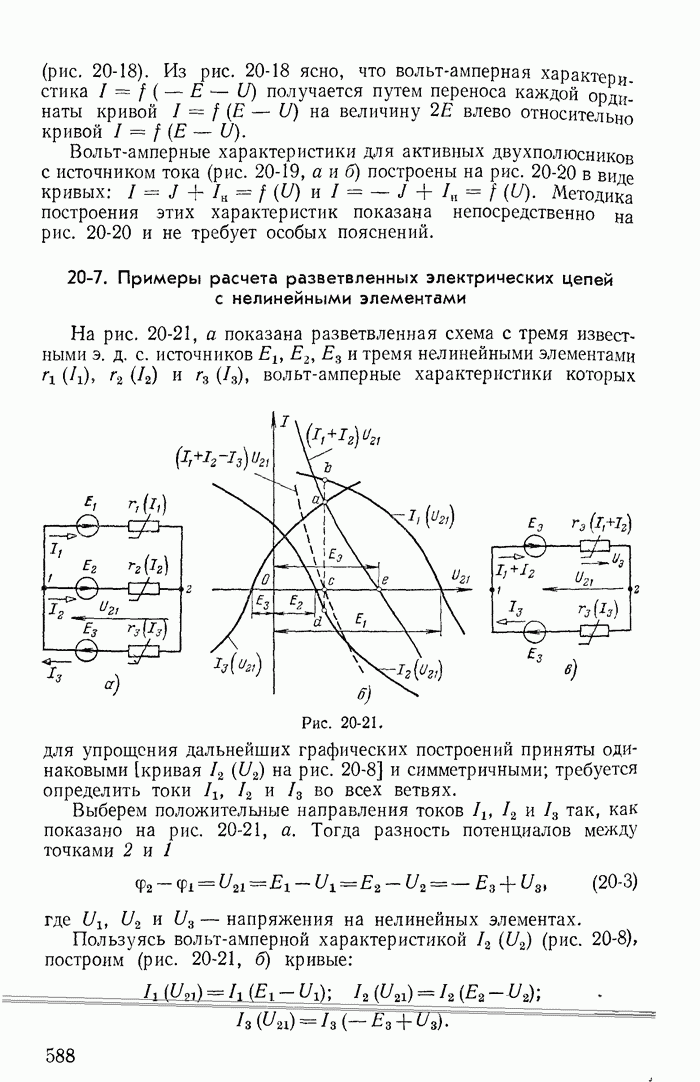
- 20-7. Примеры расчета разветвленных электрических цепей с нелинейными элементами
- 20-8. Применение теории активных двухполюсника, четырехполюсника и шестиполюсника для расчета цепей с линейными и нелинейными элементами
- 20-9. Расчет разветвленных нелинейных цепей итерационным методом (методом последовательных приближений)
- Глава двадцать первая. МАГНИТНЫЕ ЦЕПИ ПРИ ПОСТОЯННЫХ ТОКАХ
- 21-2. Расчет неразветвленных магнитных цепей
- 21-3. Расчет разветвленных магнитных цепей
- 21-4. Расчет магнитной цепи кольцевого постоянного магнита с воздушным зазором
- 21-5. Расчет неразветвленной неоднородной магнитной цепи с постоянным магнитом
- Глава двадцать вторая. ОБЩАЯ ХАРАКТЕРИСТИКА НЕЛИНЕЙНЫХ ЦЕПЕЙ ПЕРЕМЕННОГО ТОКА И МЕТОДОВ ИХ РАСЧЕТА
- 22-1. Нелинейные двухполюсники и четырехполюсники при переменных токах
- 22-2. Определение рабочих точек на характеристиках нелинейных двухполюсников и четырехполюсников
- 22-3. Явления в нелинейных цепях переменного тока
- 22-4. Методы расчета нелинейных цепей переменного тока
- Глава двадцать третья. НЕЛИНЕЙНЫЕ ЦЕПИ С ИСТОЧНИКАМИ Э. Д. С. И ТОКА ОДИНАКОВОЙ ЧАСТОТЫ
- 23-2. Форма кривой тока в цепи с вентилями
- 23-3. Простейшие выпрямители
- 23-4. Формы кривых тока и напряжения в цепях с нелинейными реактивными сопротивлениями
- 23-5. Утроители частоты
- 23-6. Формы кривых тока и напряжения в цепях с терморезисторами
- 23-7. Замена реальных нелинейных элементов условно-нелинейными
- 23-8. Учет реальных свойств стальных магнитопроводов
- 23-9. Расчет тока в катушке со стальным магнитопроводом
- 23-10. Понятие о расчете условно-нелинейных магнитных цепей
- 23-11. Явление феррорезонанса
- 23-12. Стабилизаторы напряжения
- Глава двадцать четвертая. НЕЛИНЕЙНЫЕ ЦЕПИ С ИСТОЧНИКАМИ Э. Д. С. И ТОКА РАЗЛИЧНЫХ ЧАСТОТ
- 24-1. Общая характеристика нелинейных цепей с источниками э. д. с. различных частот
- 24-2. Вентили в цепях с постоянными и переменными э. д. с.
- 24-3. Управляемые вентили в простейших выпрямителях и преобразователях постоянного тока в переменный
- 24-4. Катушки со стальными магнитопроводами в цепях с постоянными и переменными э. д. с.
- 24-5. Удвоитель частоты
- 24-6. Метод гармонического баланса
- 24-7. Влияние постоянной э. д. с. на переменную составляющую тока в цепях с нелинейными безынерционными сопротивлениядли
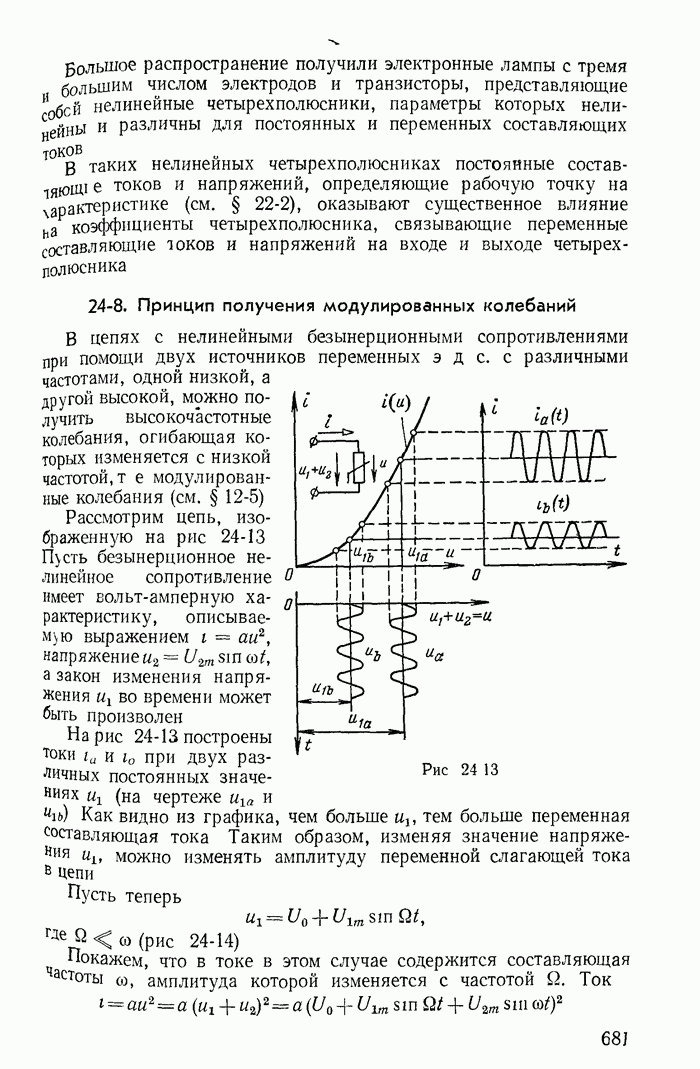
- 24-8. Принцип получения модулированных колебаний
- 24-9. Влияние постоянной составляющей на переменную в цепях с нелинейными индуктивностями
- 24-10. Магнитные усилители мощности
- Глава двадцать пятая. ПЕРЕХОДНЫЕ ПРОЦЕССЫ В НЕЛИНЕЙНЫХ ЦЕПЯХ
- 25-2. Включение катушки со стальным магнитопроводом на постоянное напряжение
- 25-3. Включение катушки со стальным магнитопроводом на синусоидальное напряжение
- 25-4. Импульсное воздействие в цепях с неоднозначными нелинейностями
- 25-5. Понятие о простейших запоминающих устройствах
- 25-6. Изображение переходных процессов на фазовой плоскости
- 25-7. Колебательный разряд емкости через нелинейную индуктивность
- Глава двадцать шестая. АВТОКОЛЕБАНИЯ
- 26-1. Нелинейные резисторы со спадающим участком характеристики
- 26-2. Понятие об устойчивости режима в цепи с нелинейными резисторами
- 26-3. Релаксационные колебания в цепи с отрицательным сопротивлением
- 26-4. Близкие к синусоидальным колебания в цепи с отрицательным сопротивлением
- 26-5. Фазовые траектории процессов в цепи с отрицательным сопротивлением
- 26-6. Фазовые траектории процессов в генераторе синусоидальных колебаний
- 26-7. Определение амплитуды автоколебаний методом гармонического баланса
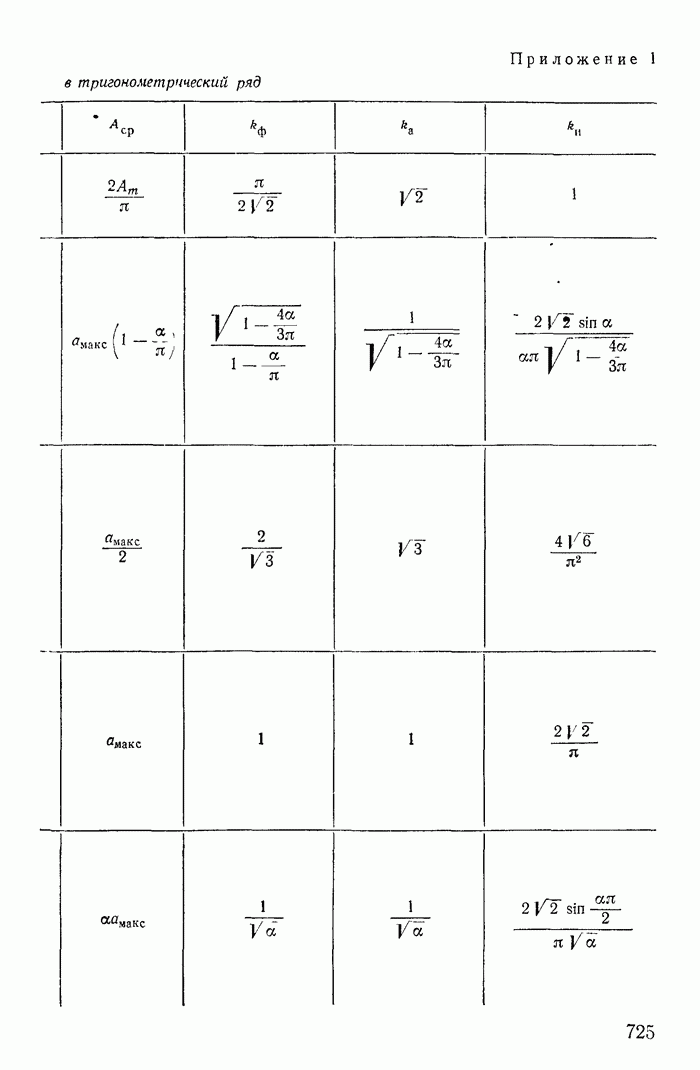
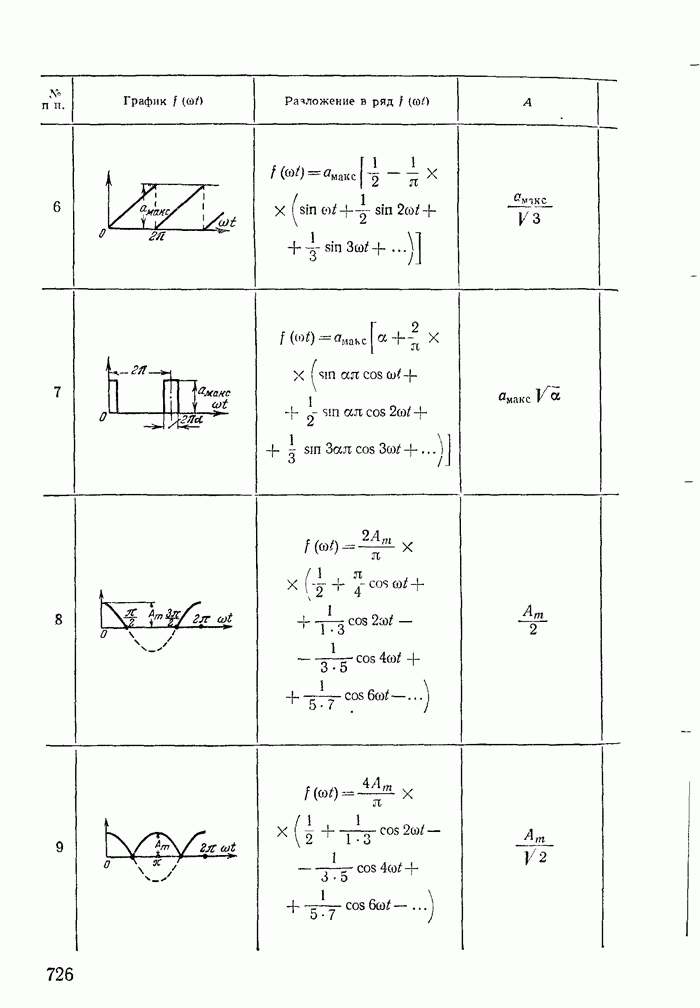
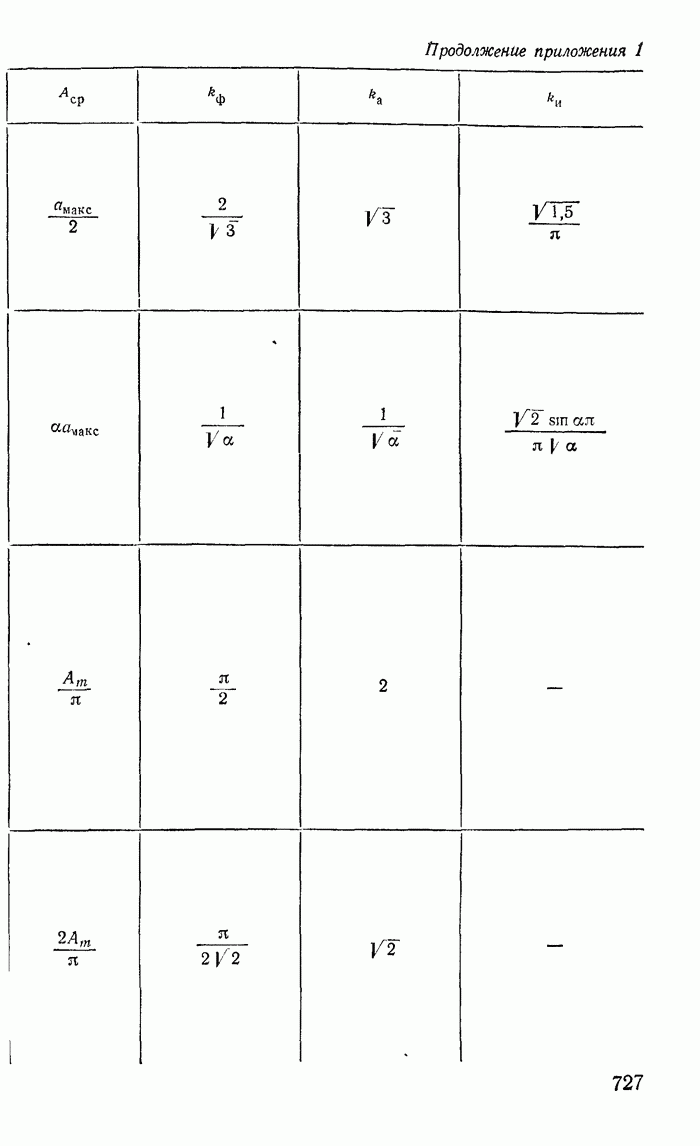
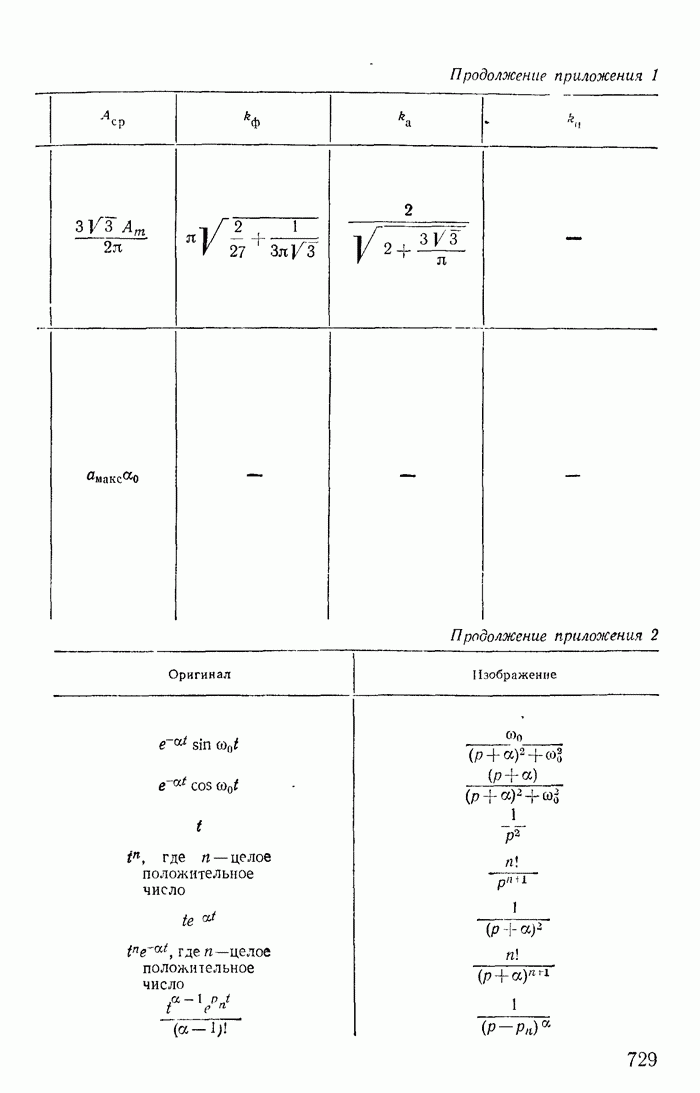
- Приложение 1. Разложение периодических функций в тригонометрический ряд
- Приложение 2. Таблица оригиналов и изображений (по Лапласу)
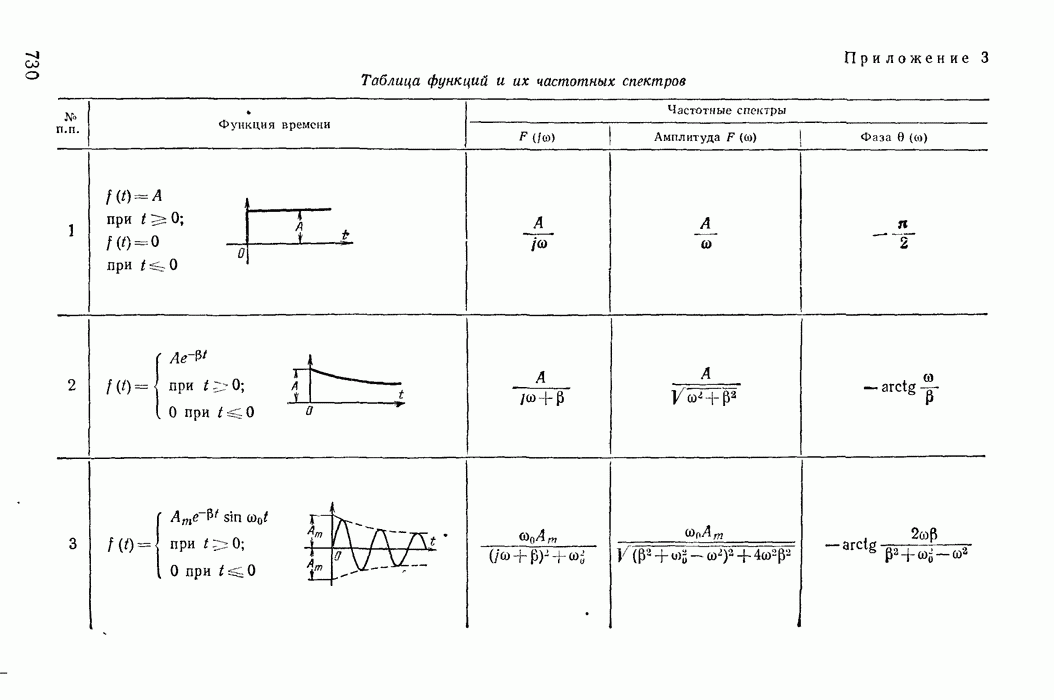
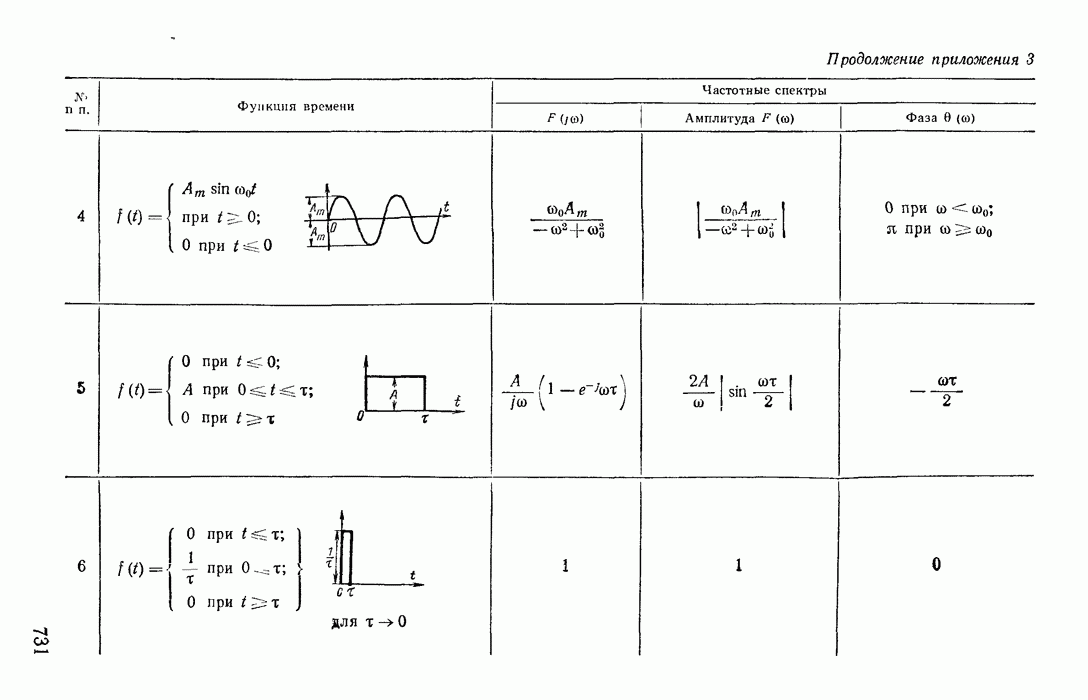
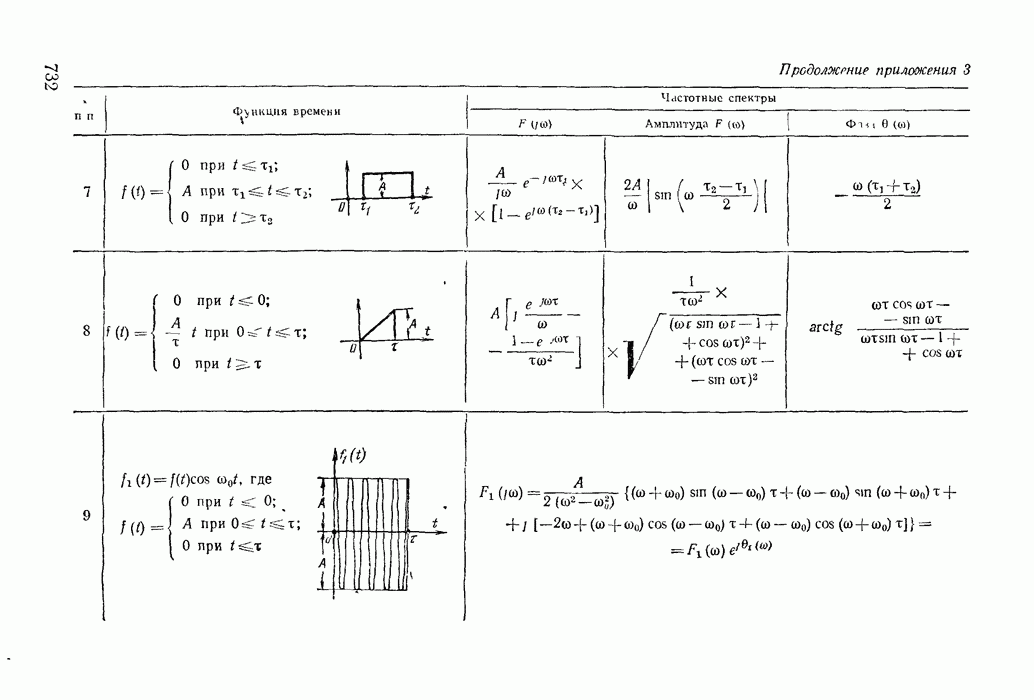
- Приложение 3. Таблица функций и их частных спектров
- Приложение 4. Таблица функций для трапеций
- СПИСОК ЛИТЕРАТУРЫ