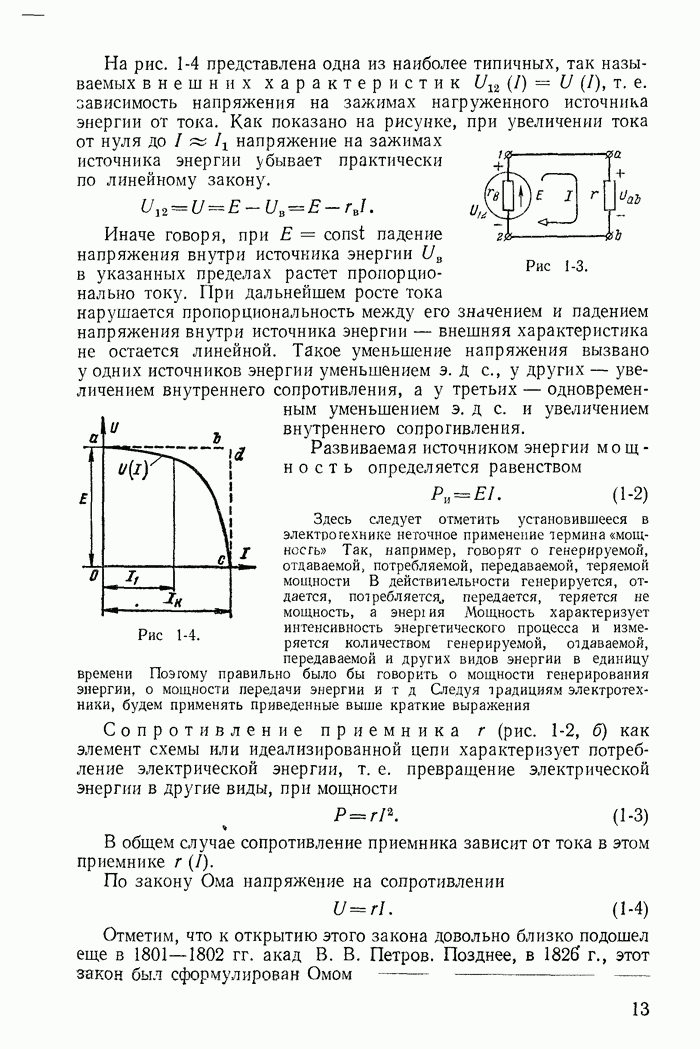
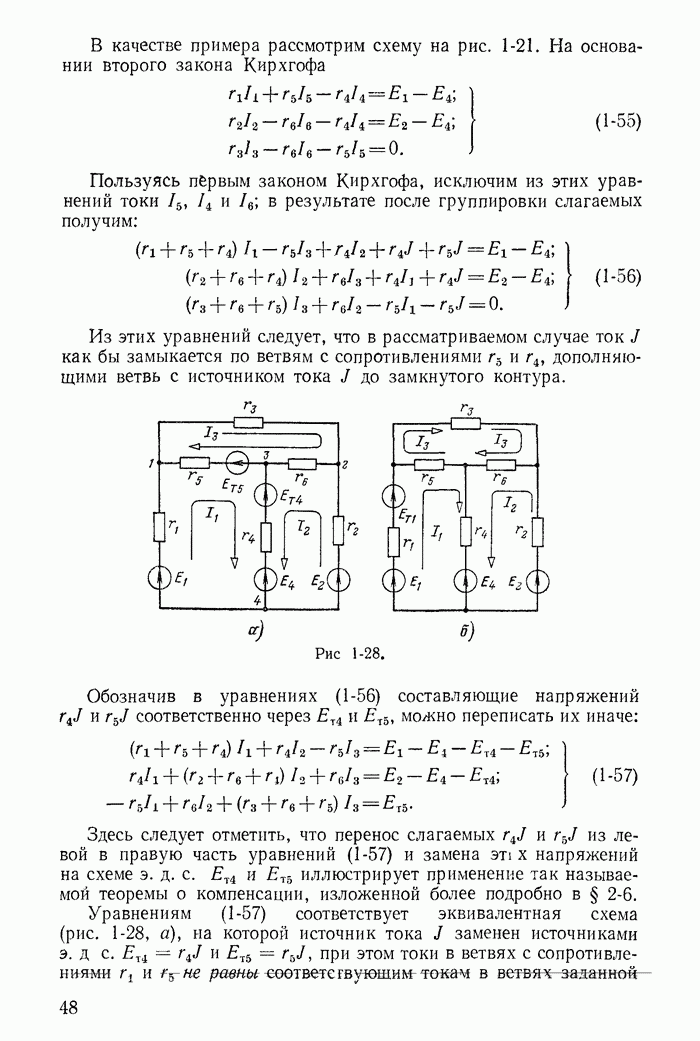
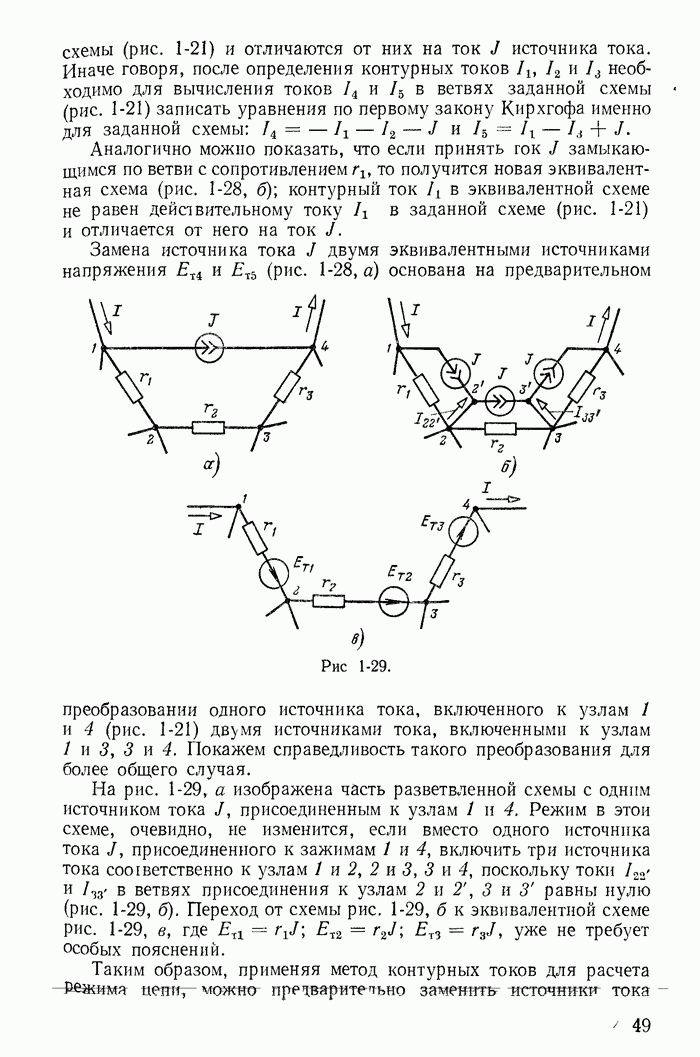
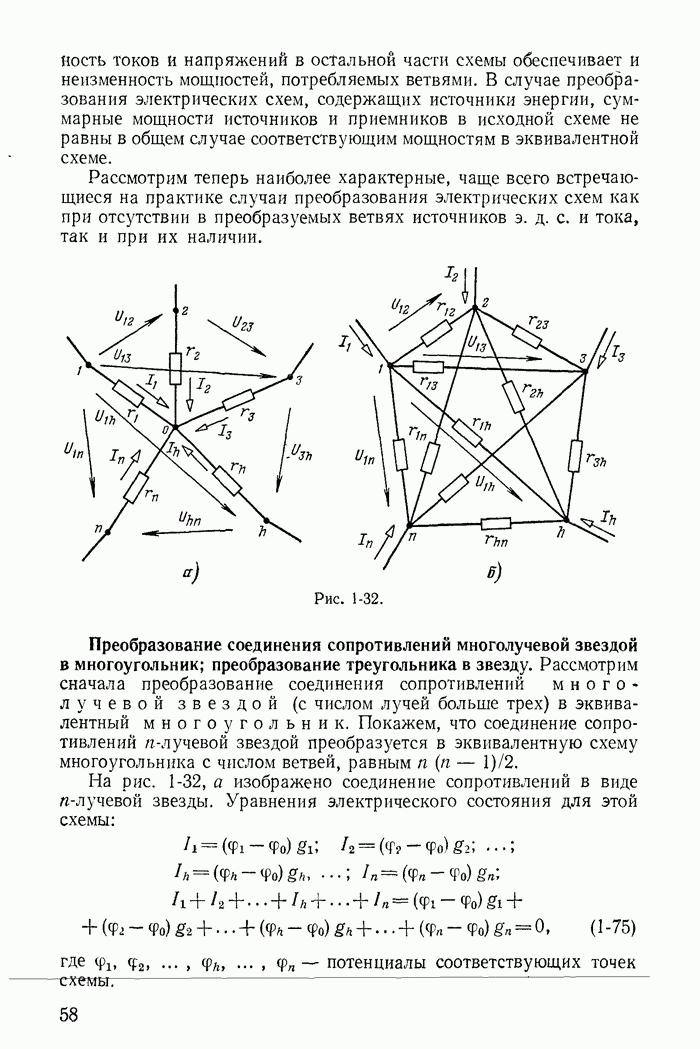
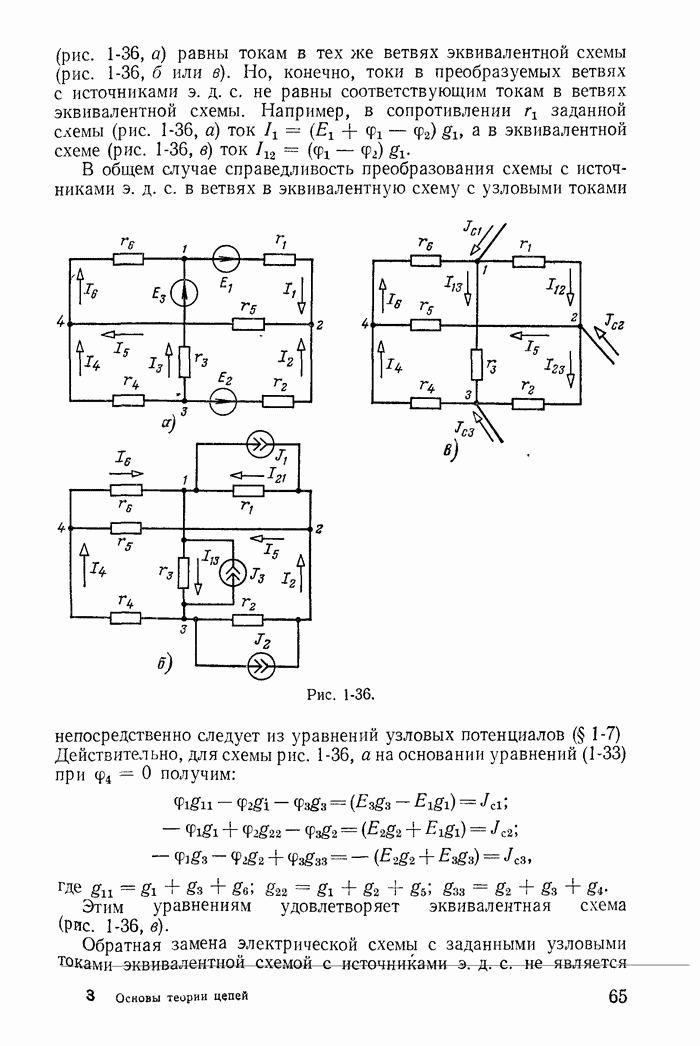
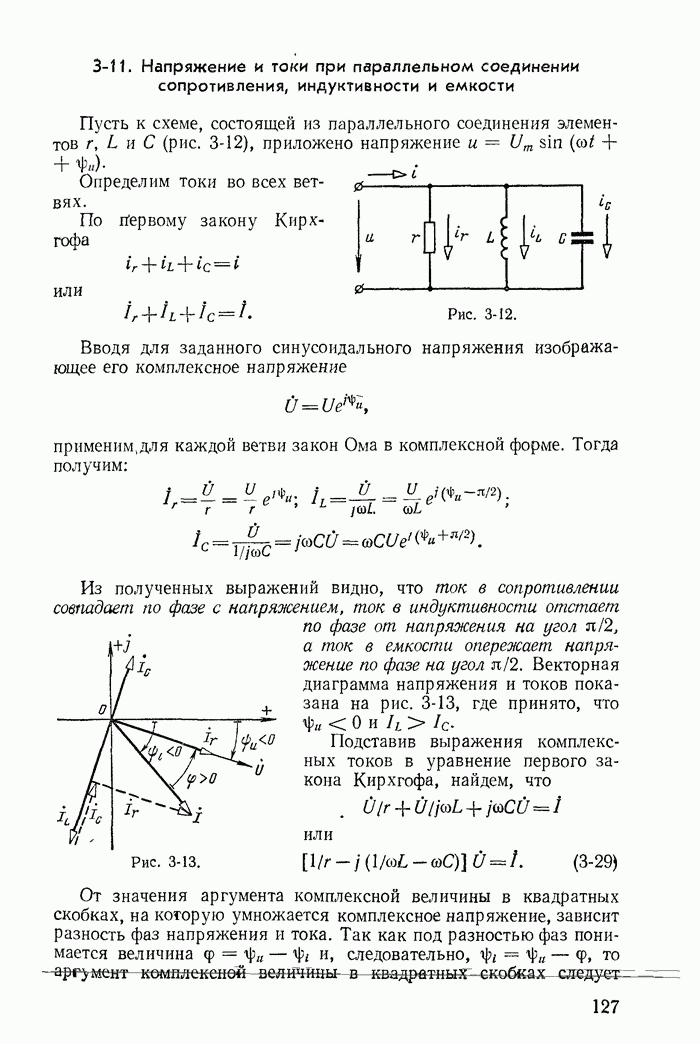
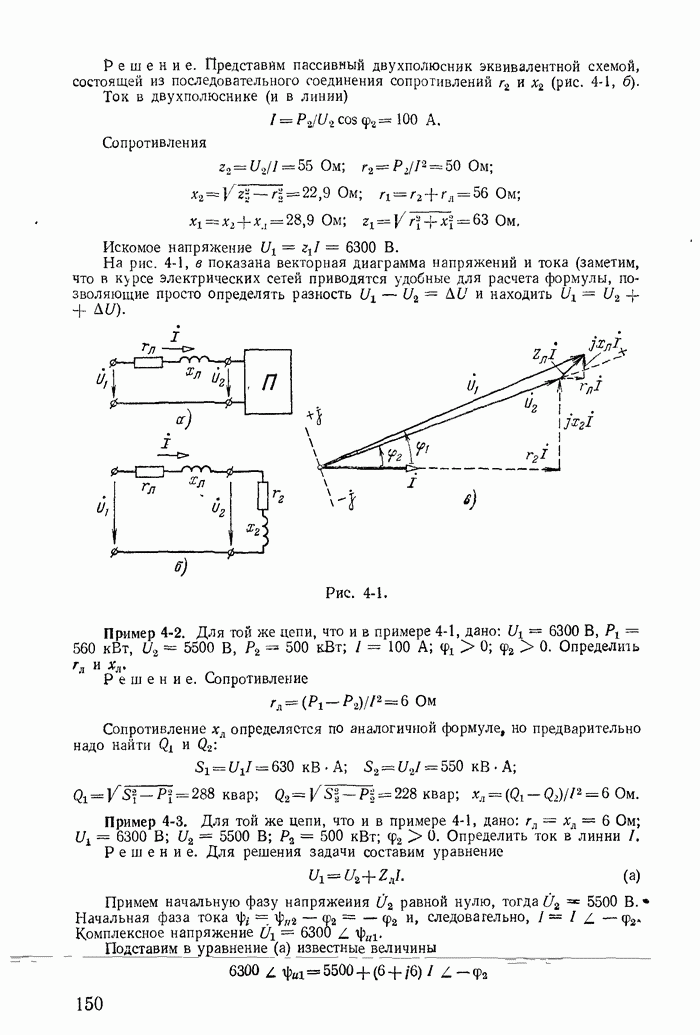
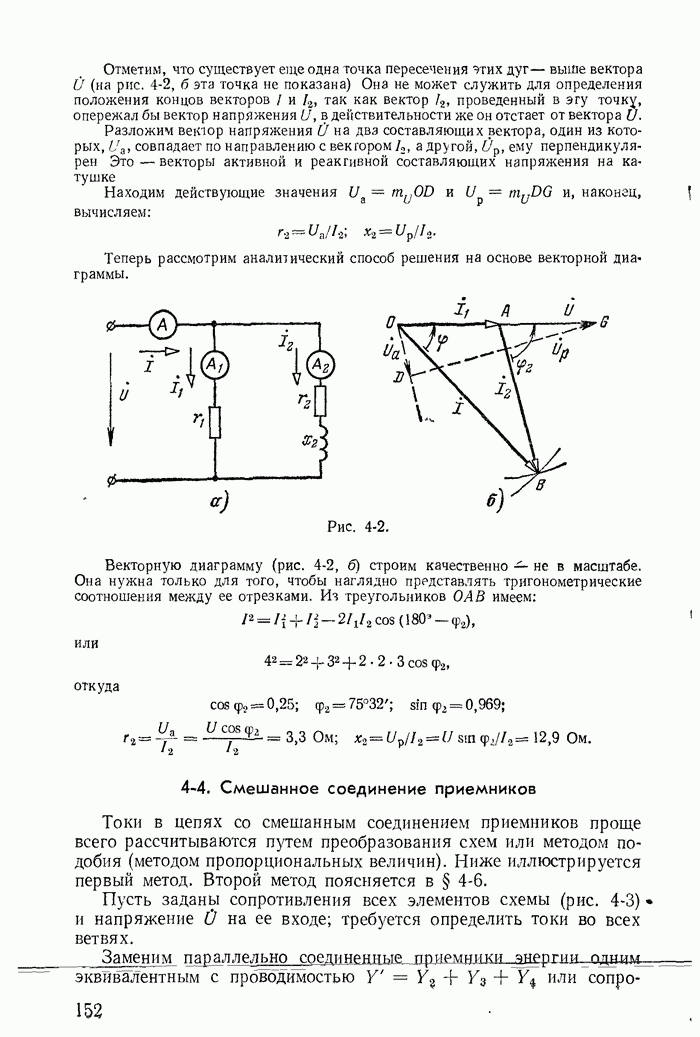
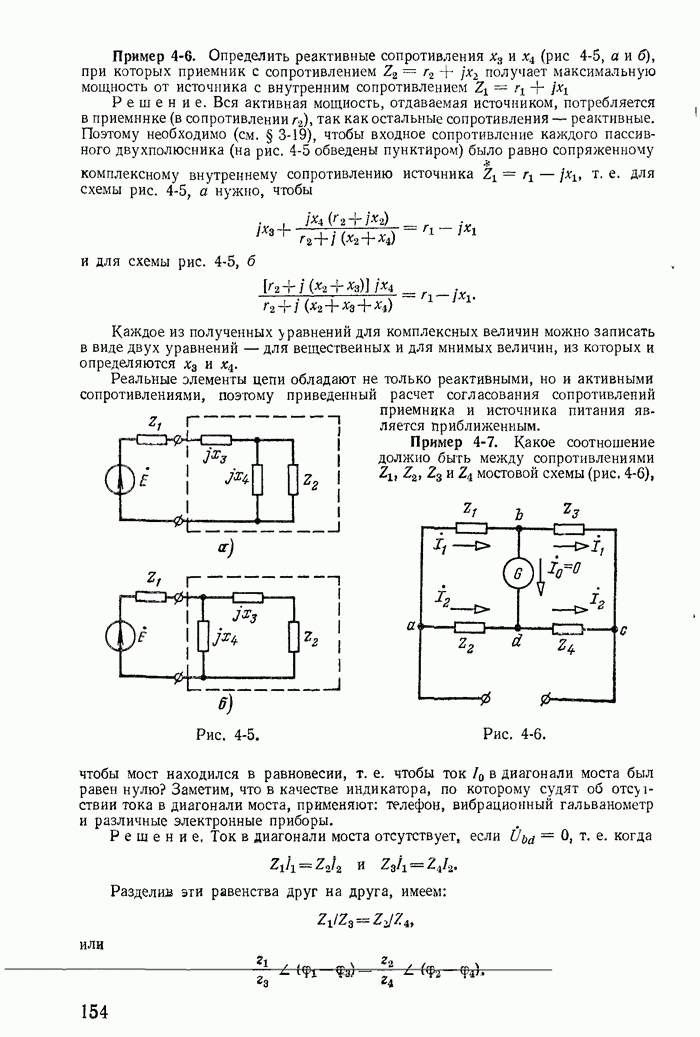
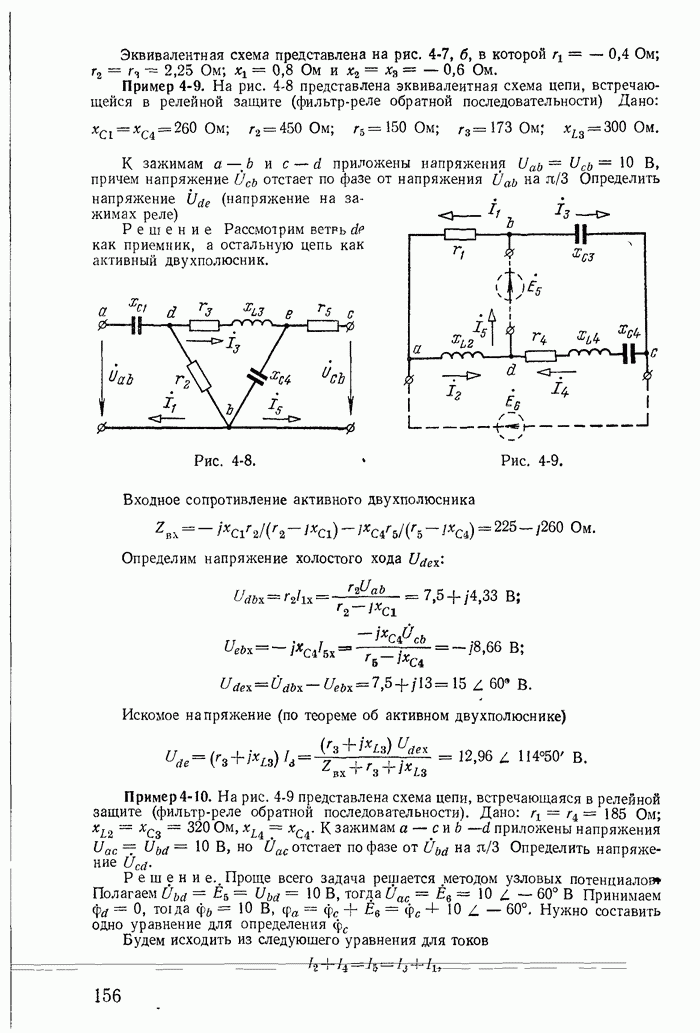
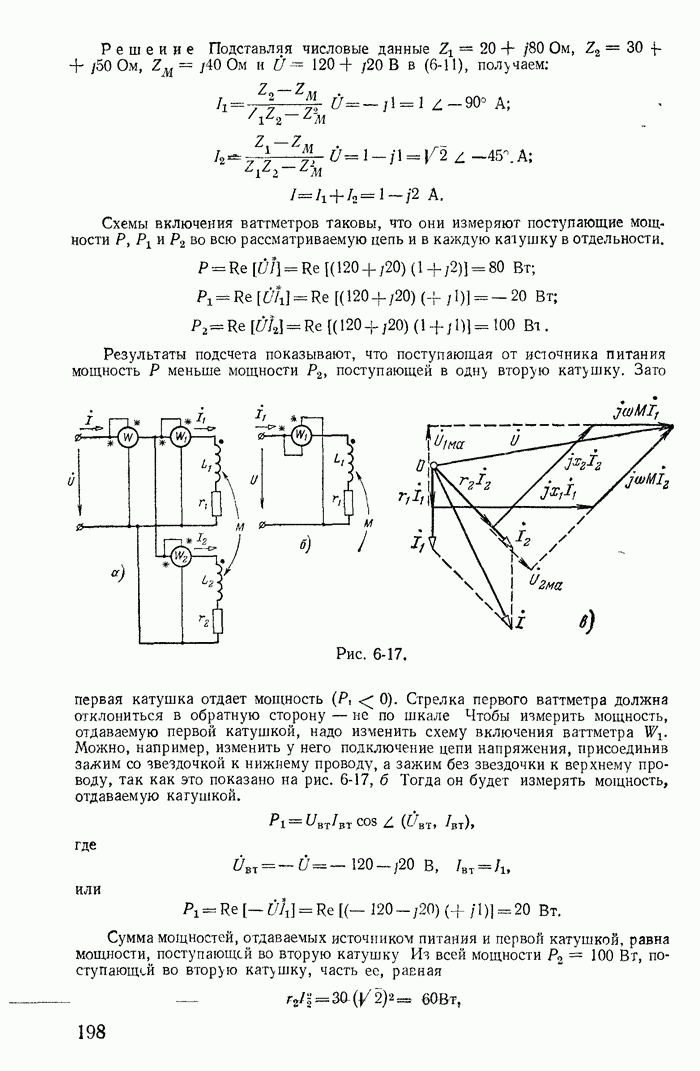
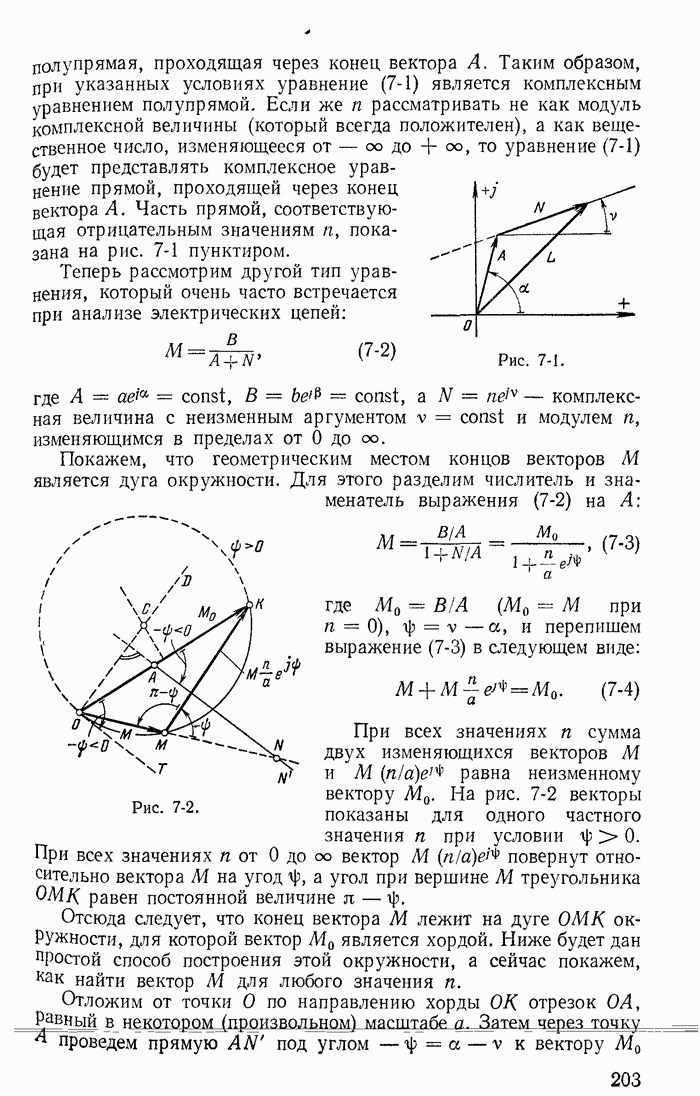
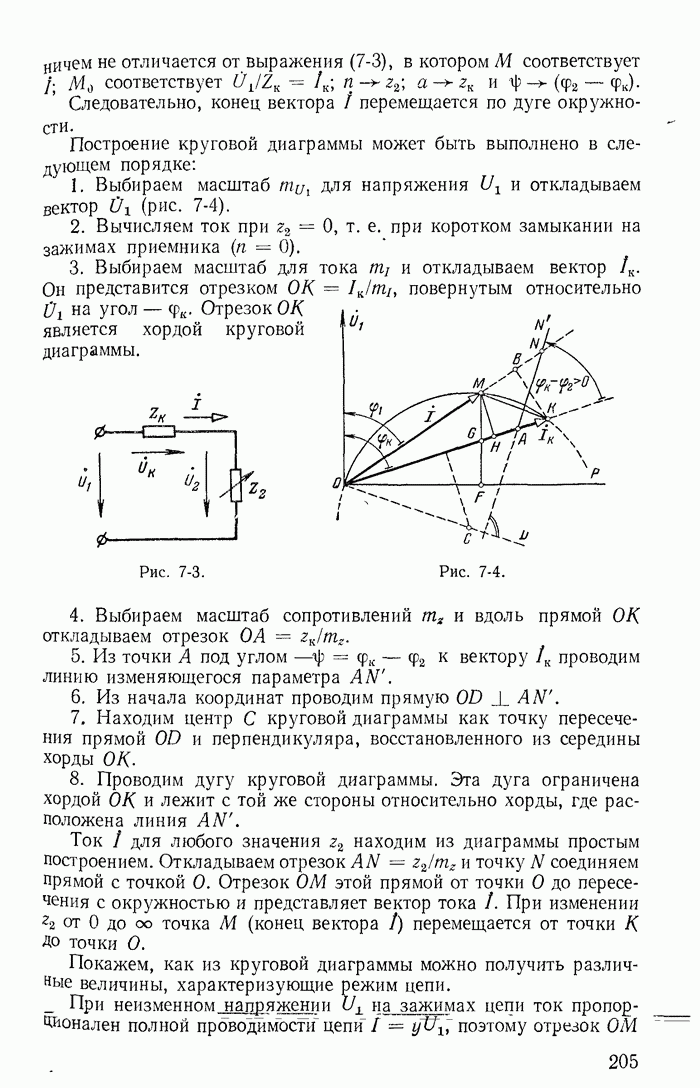
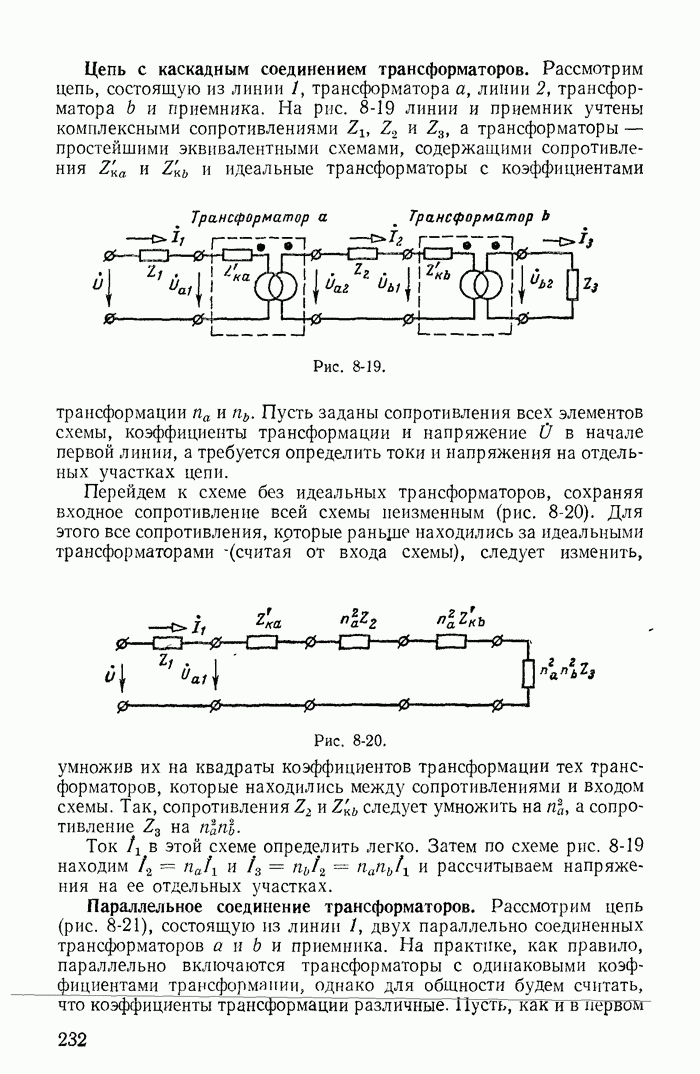
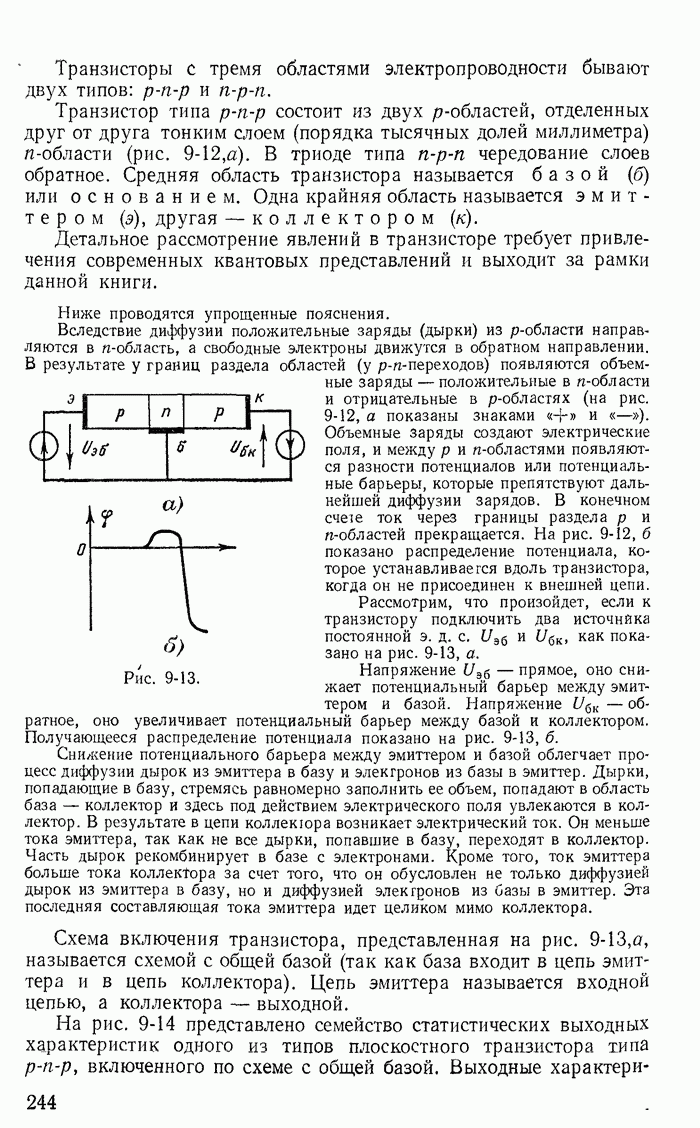
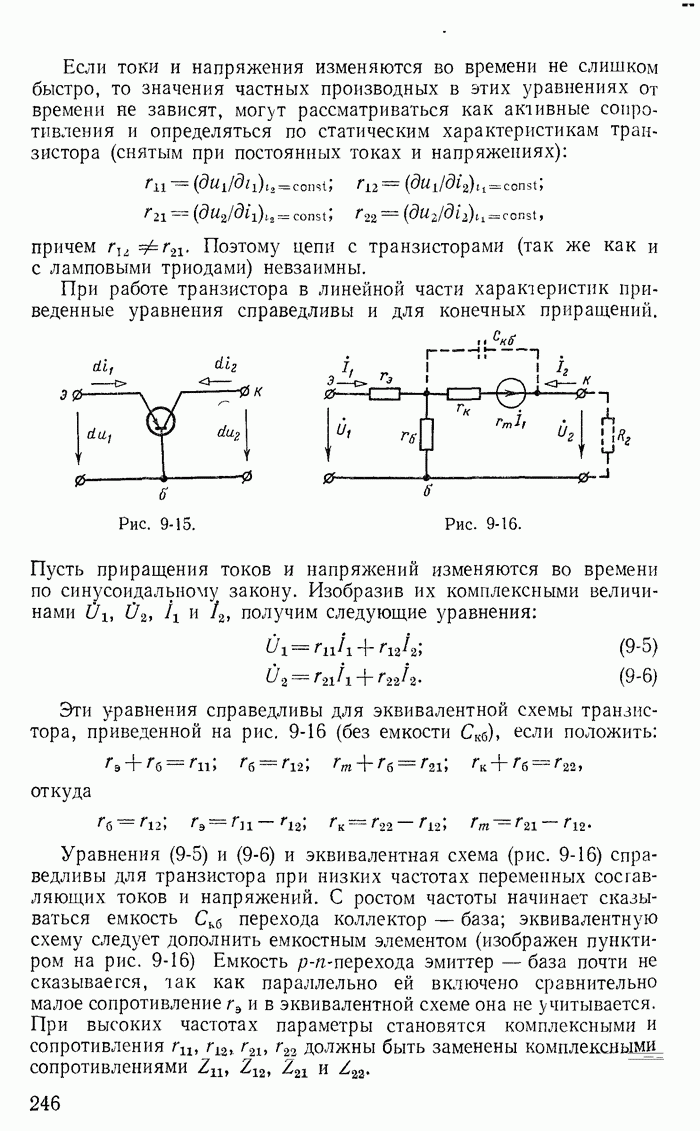
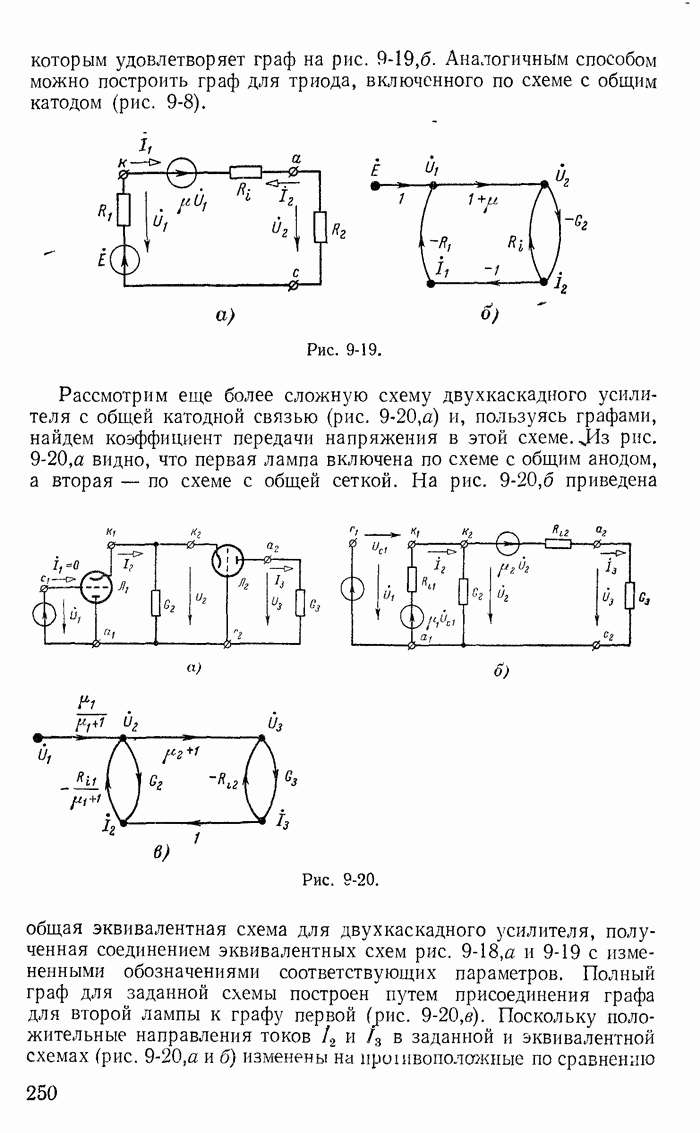
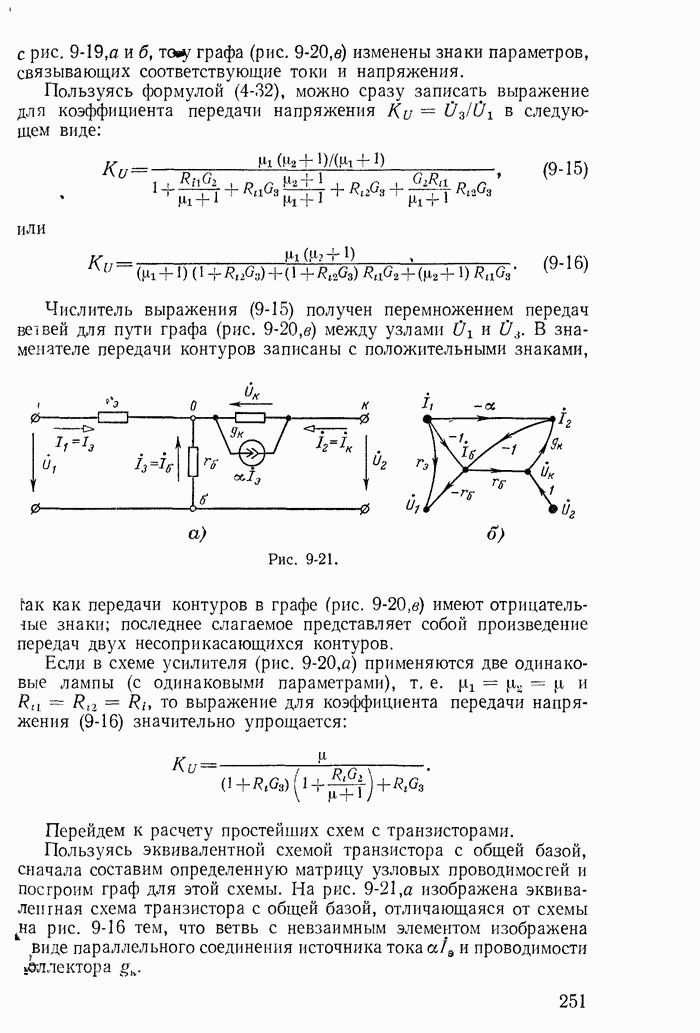
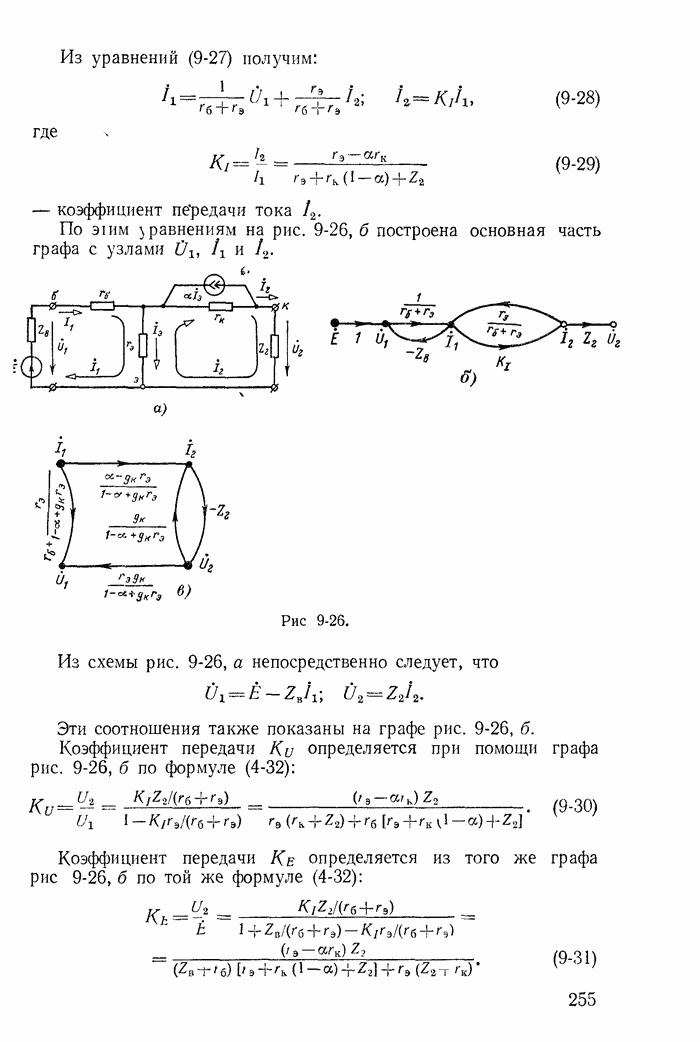
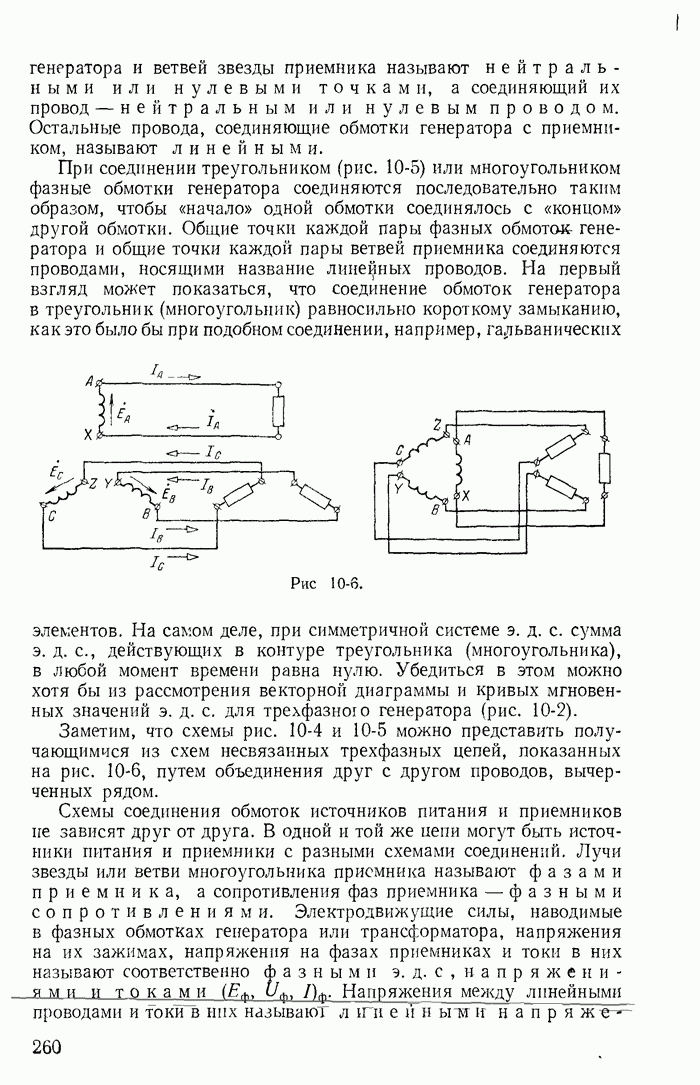
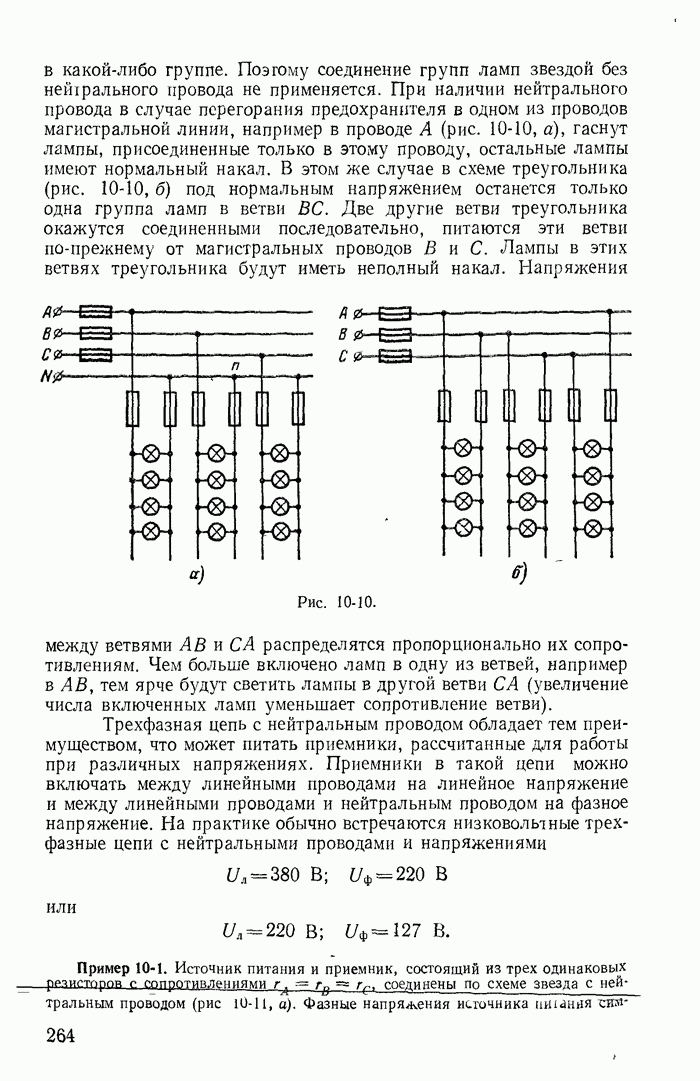
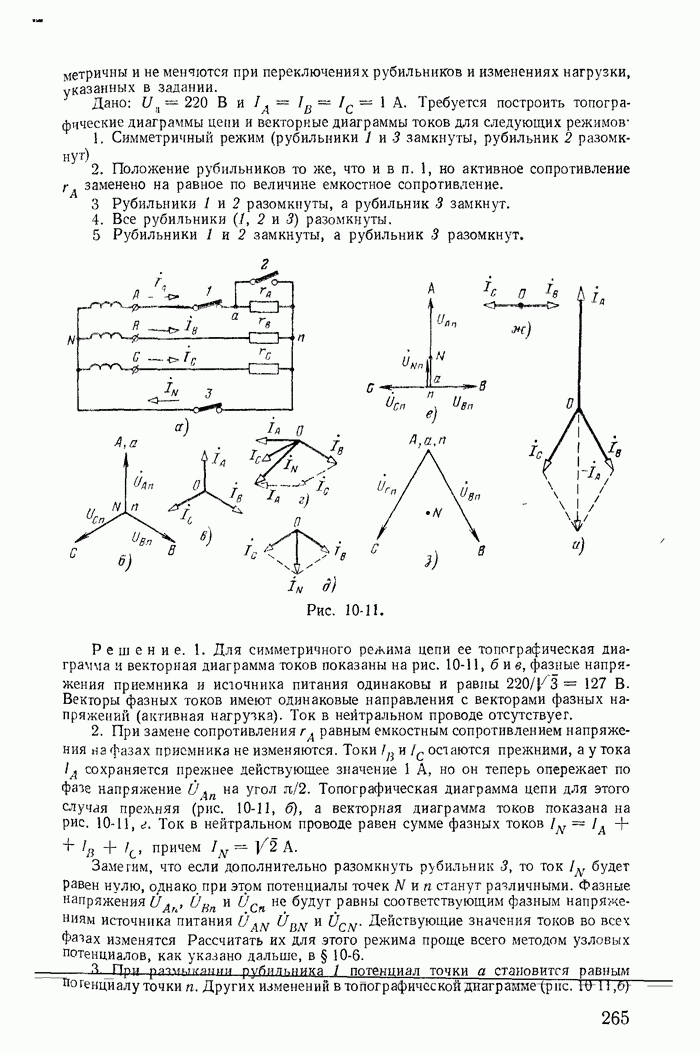
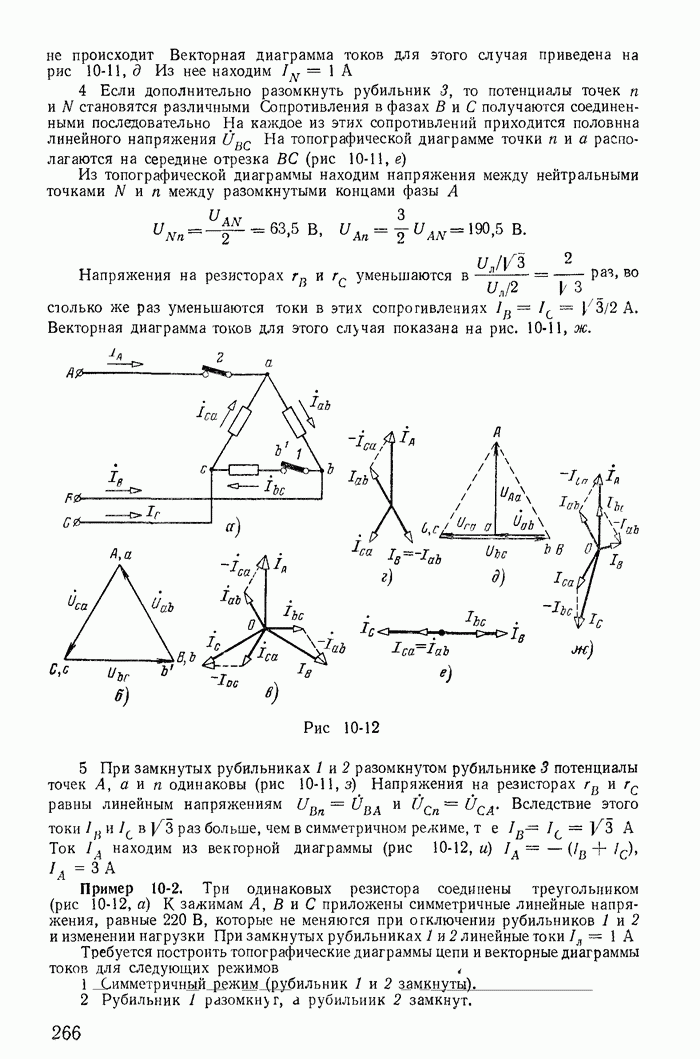
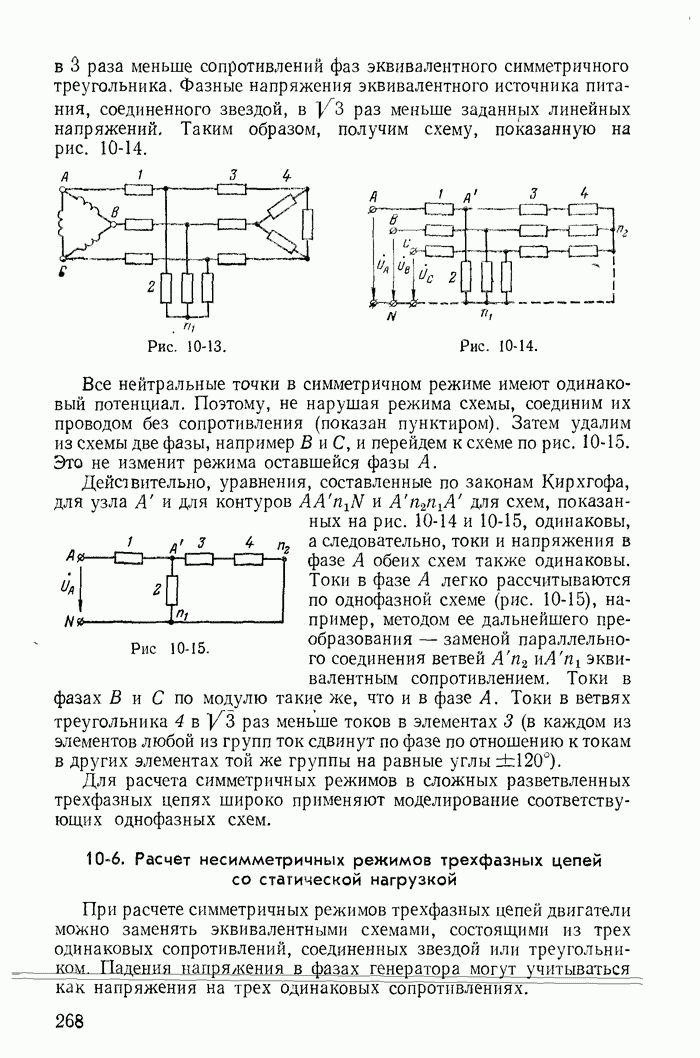
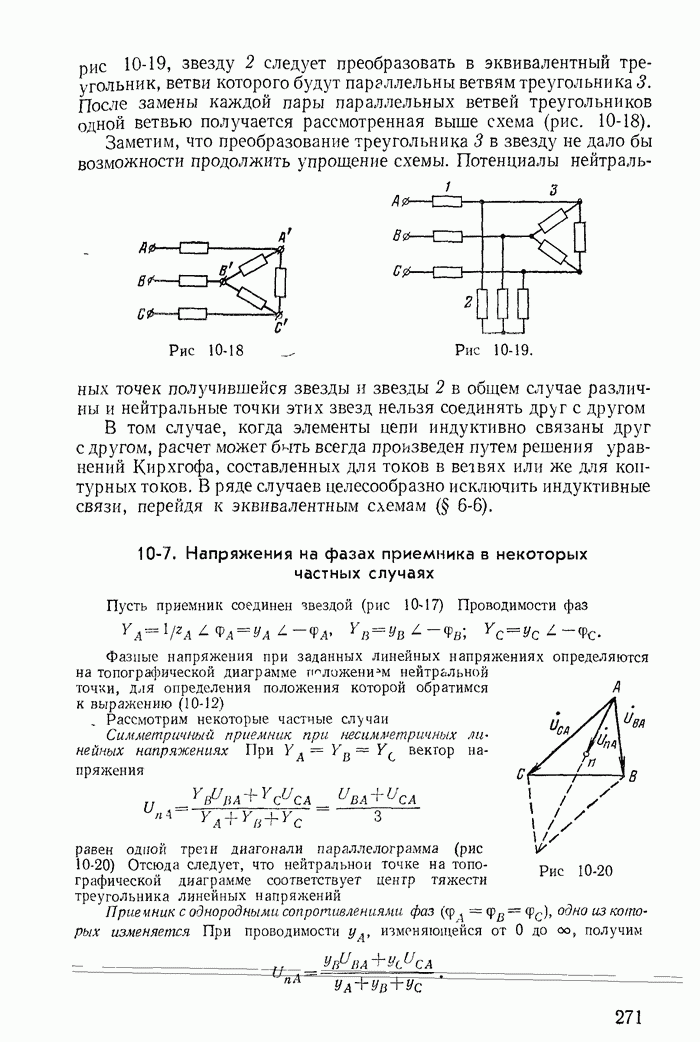
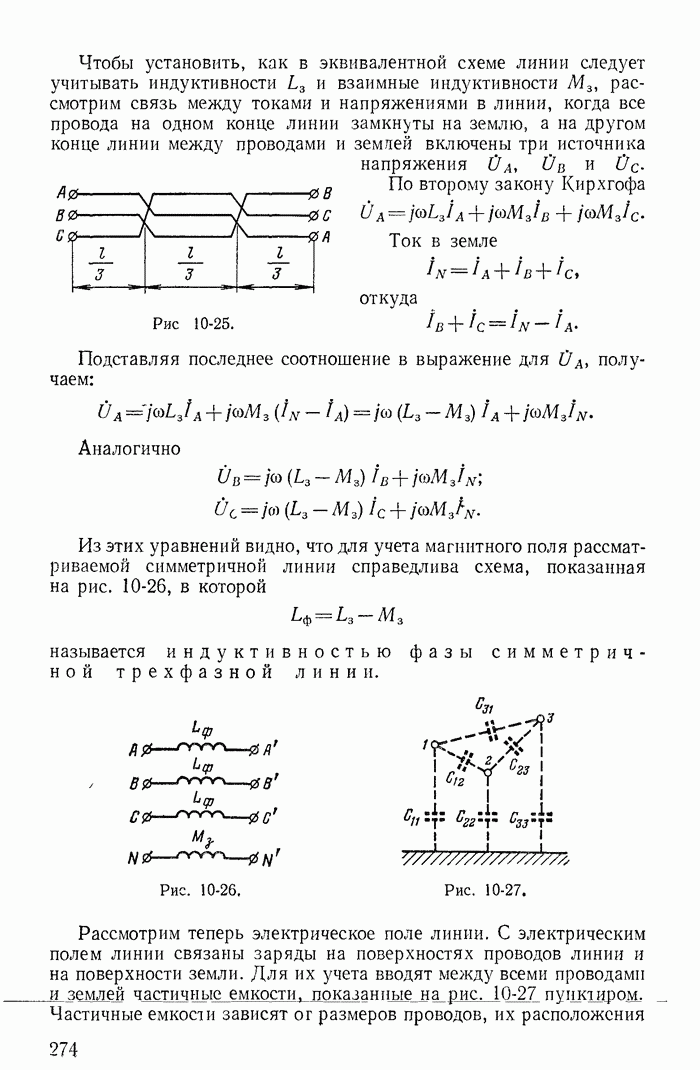
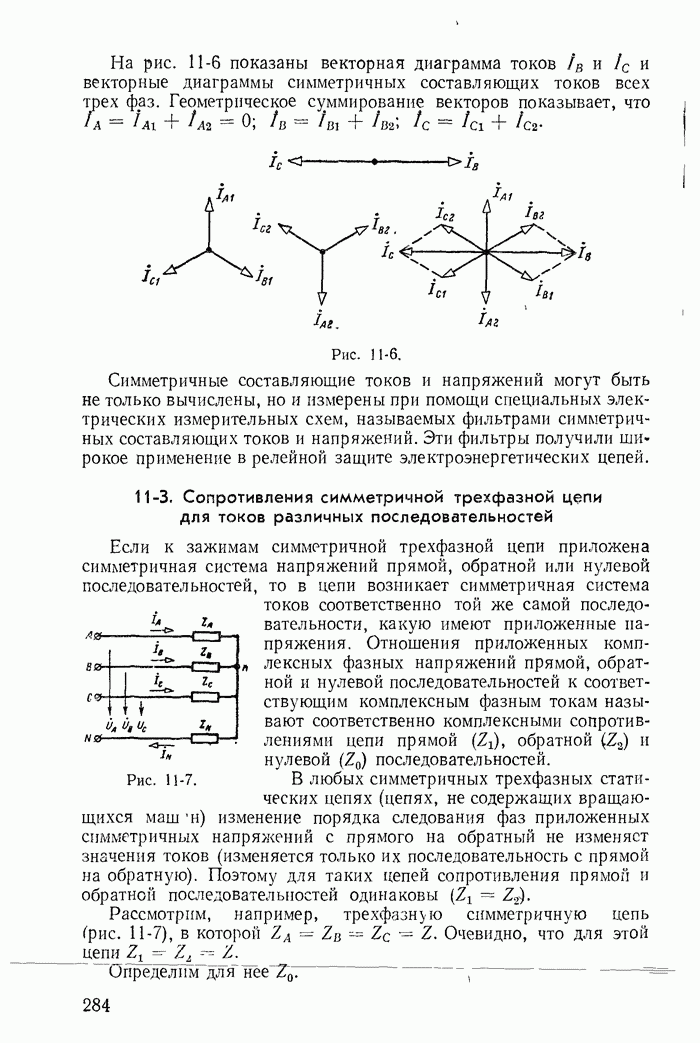
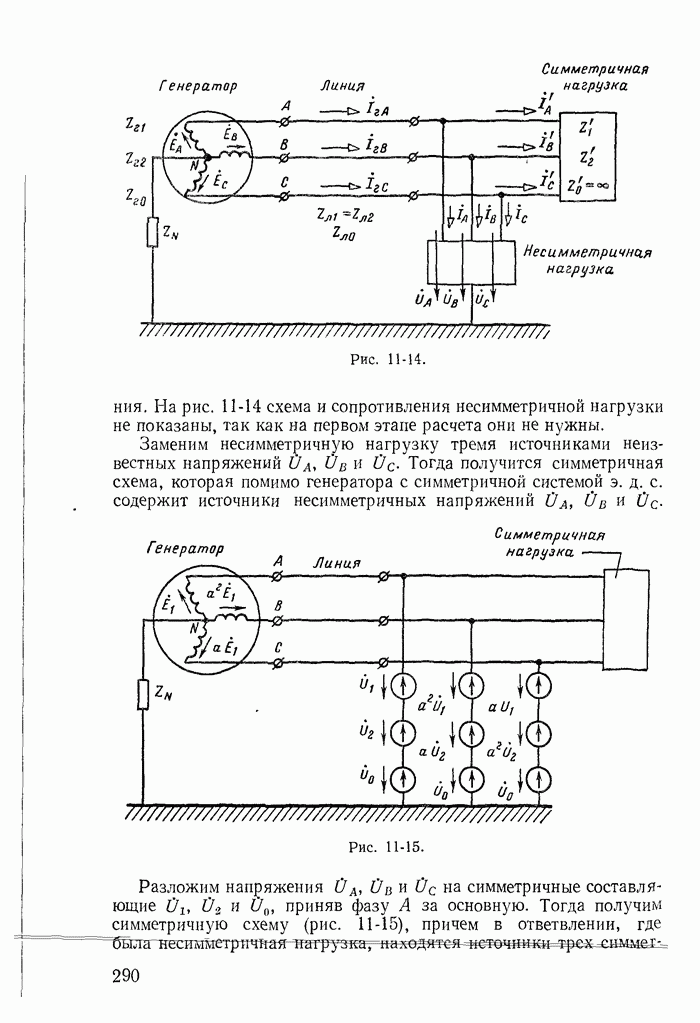
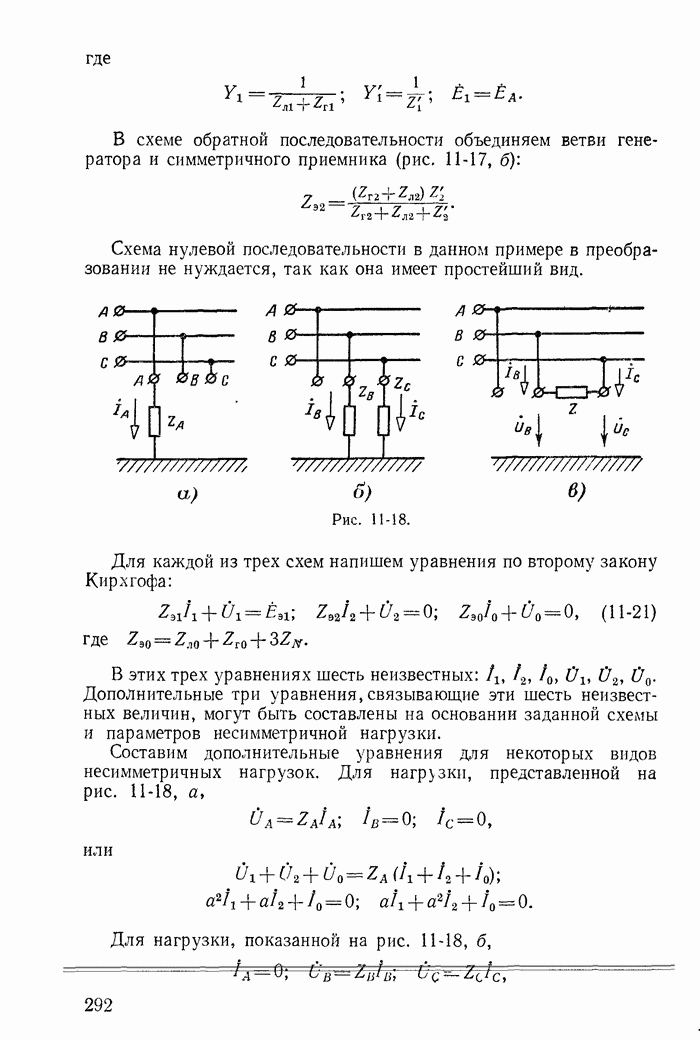
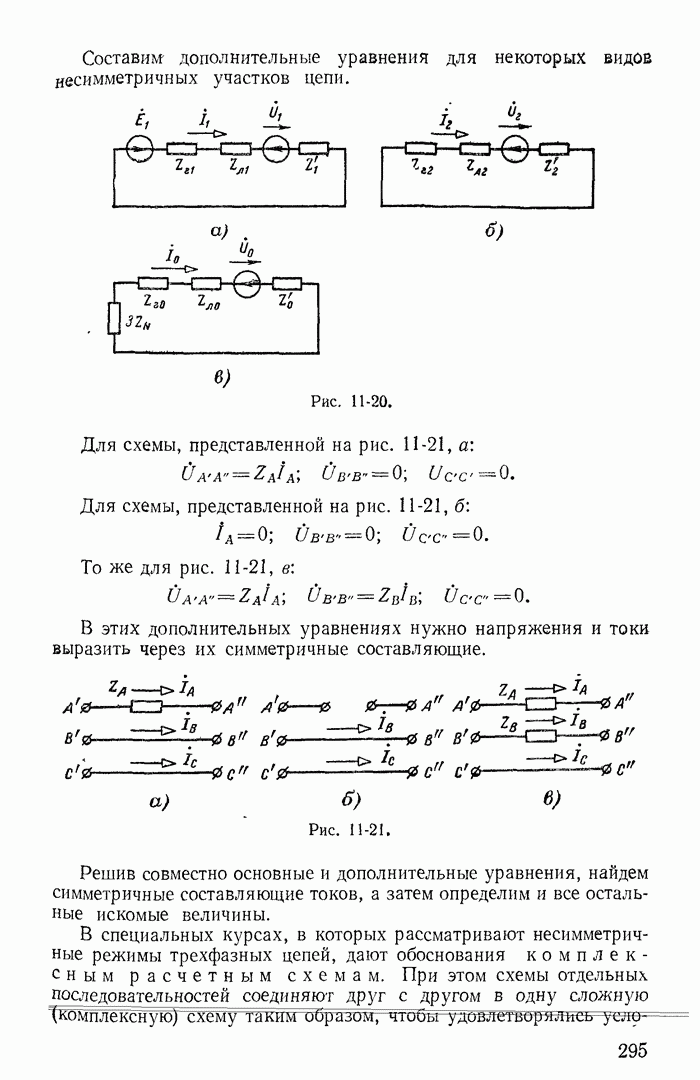
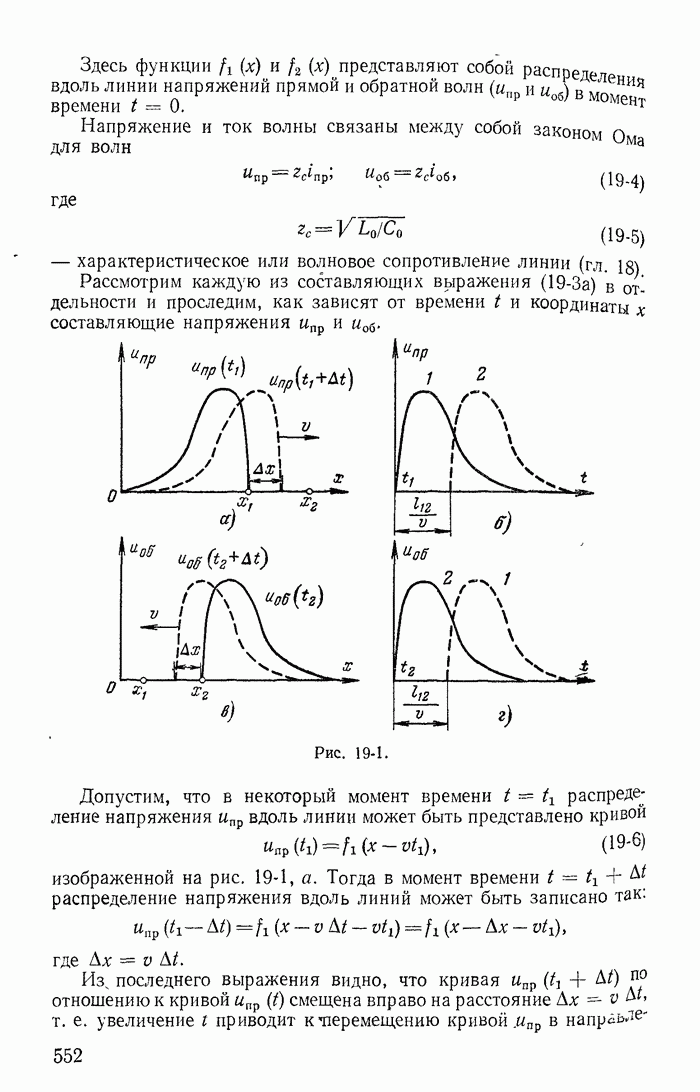
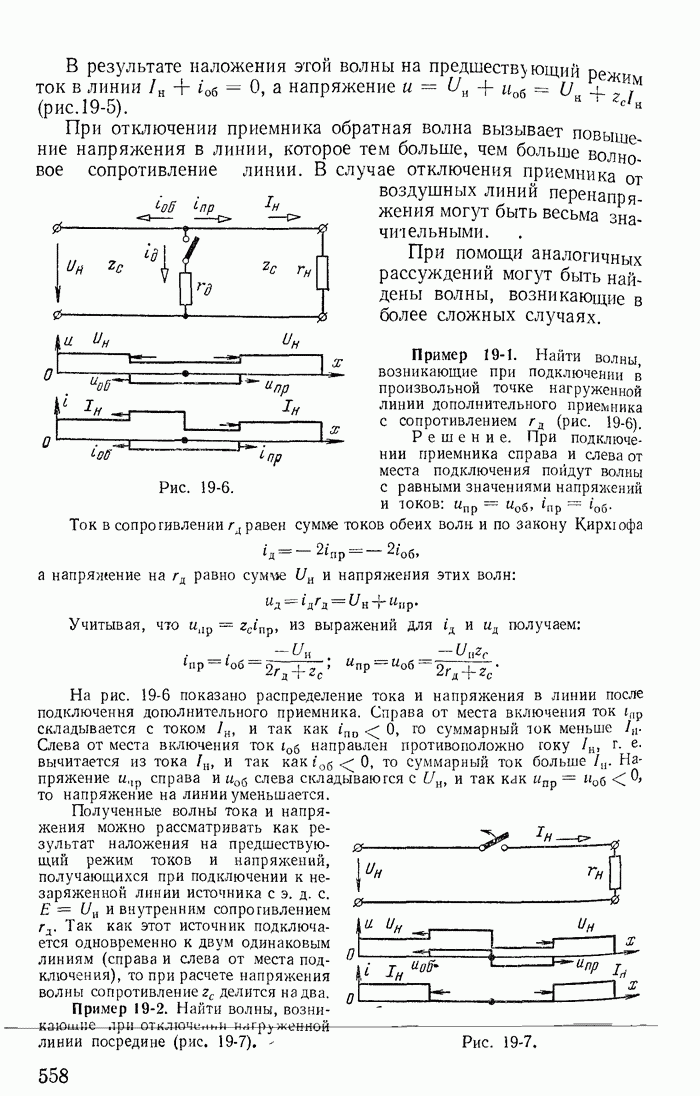
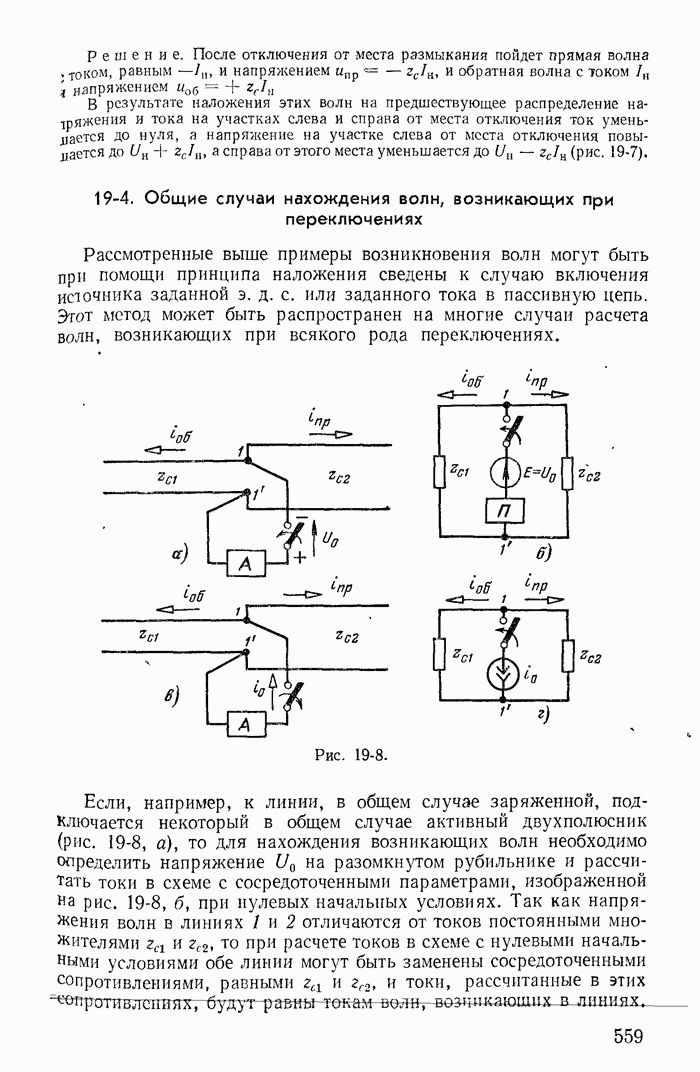
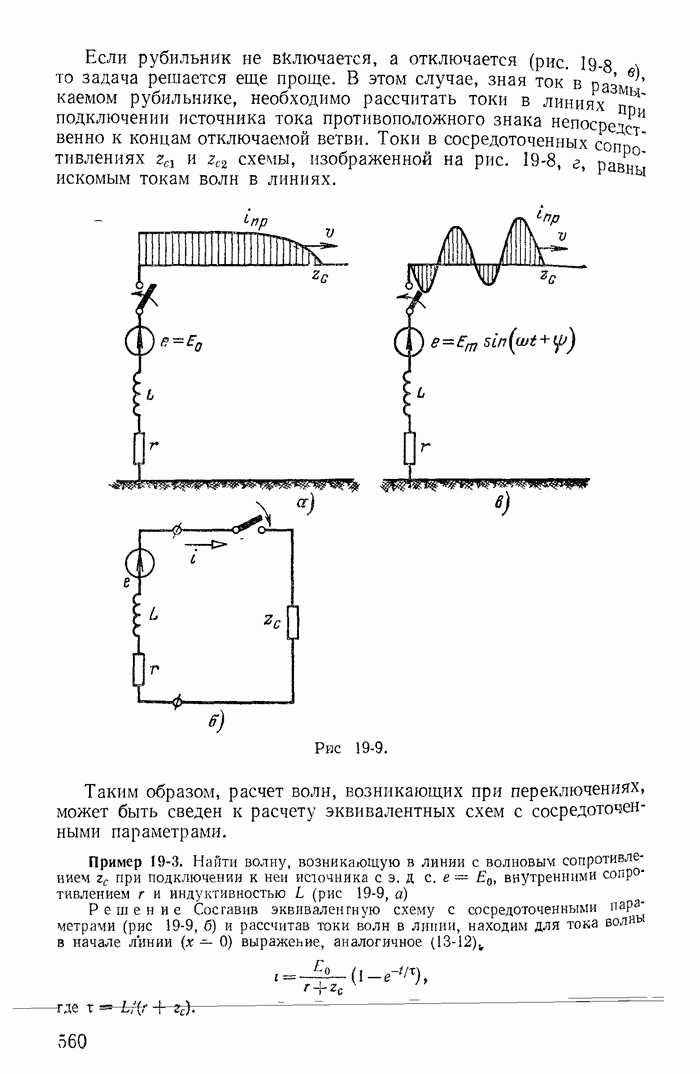
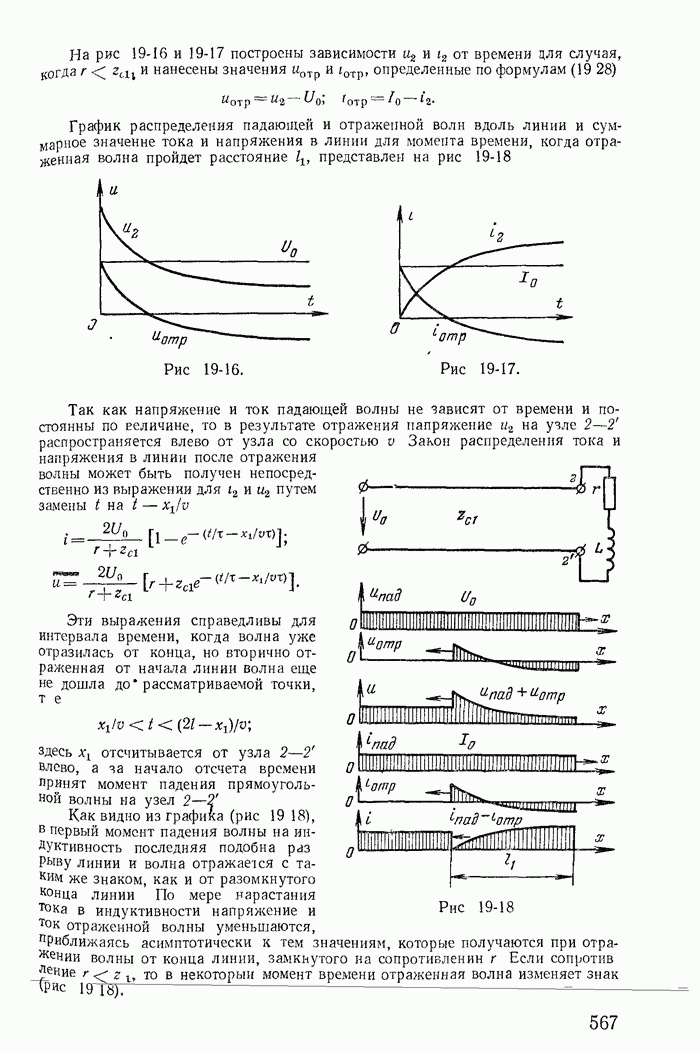
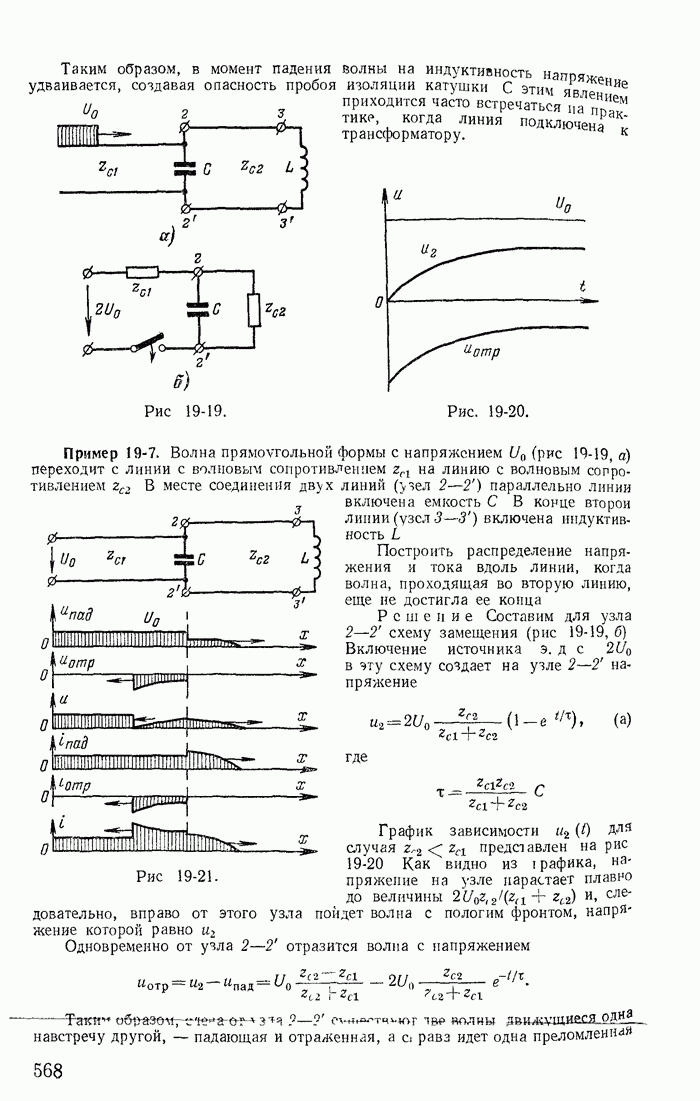
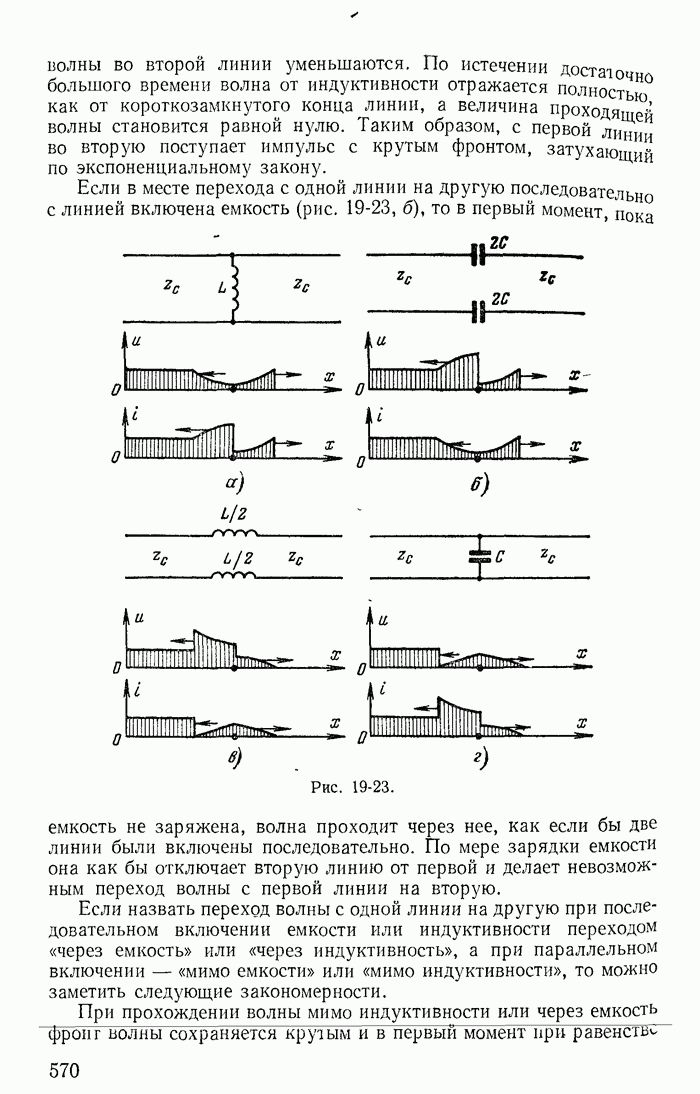
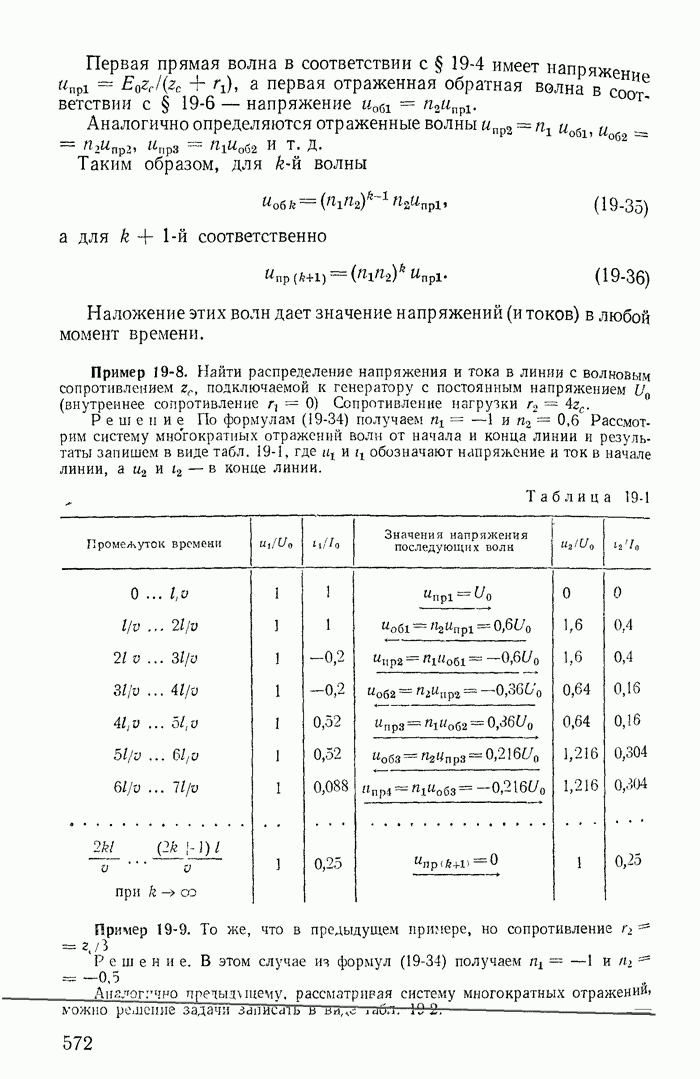
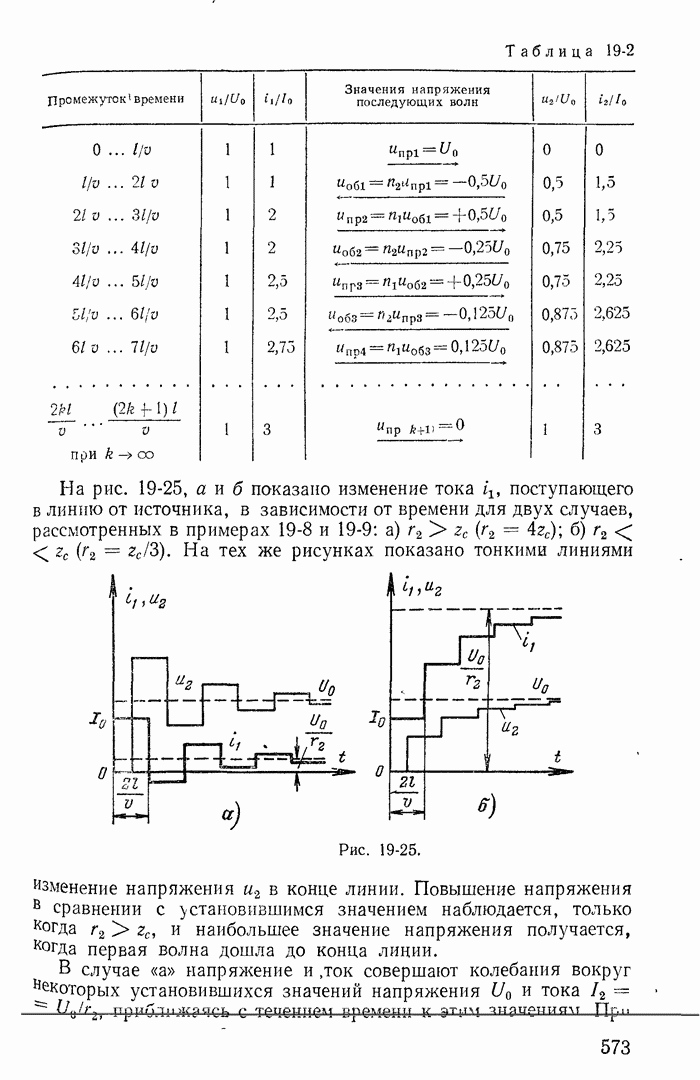
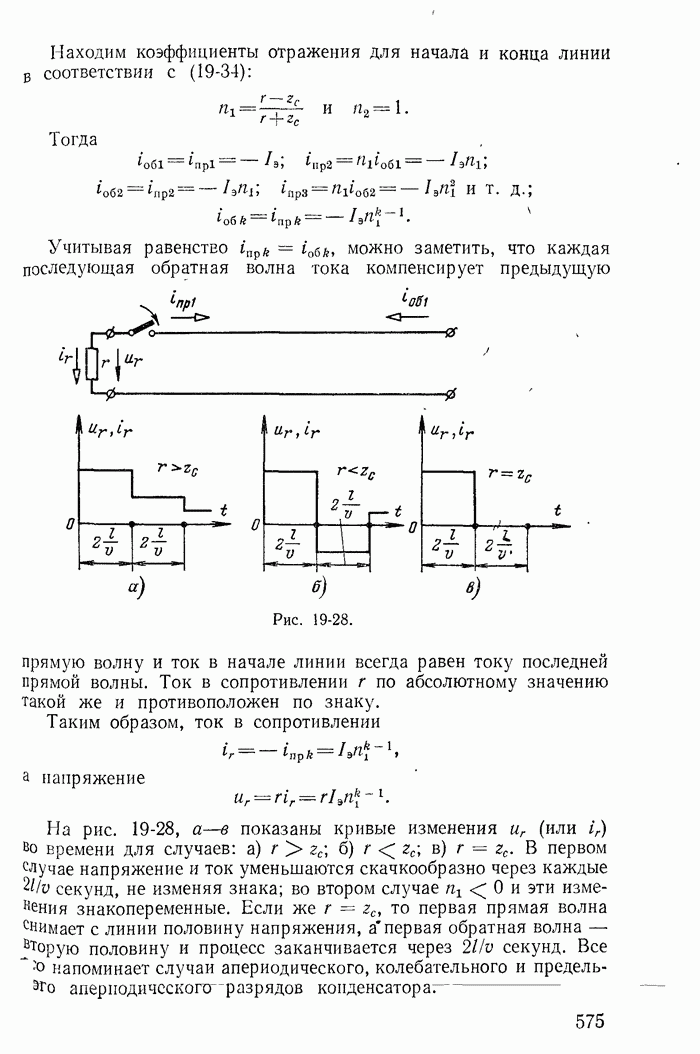
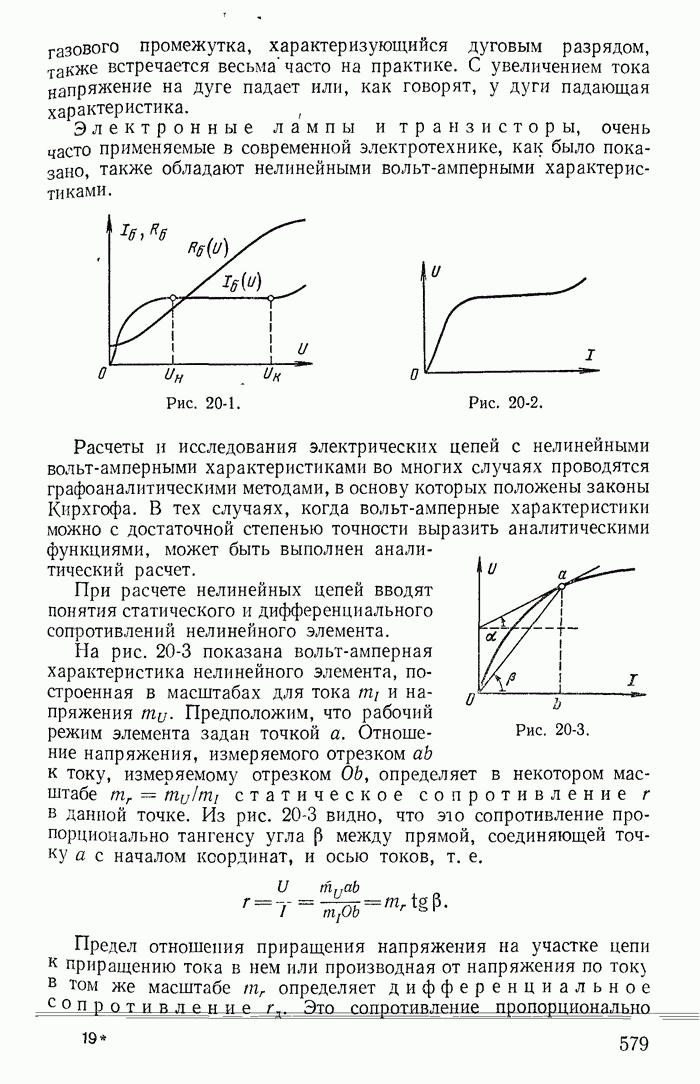
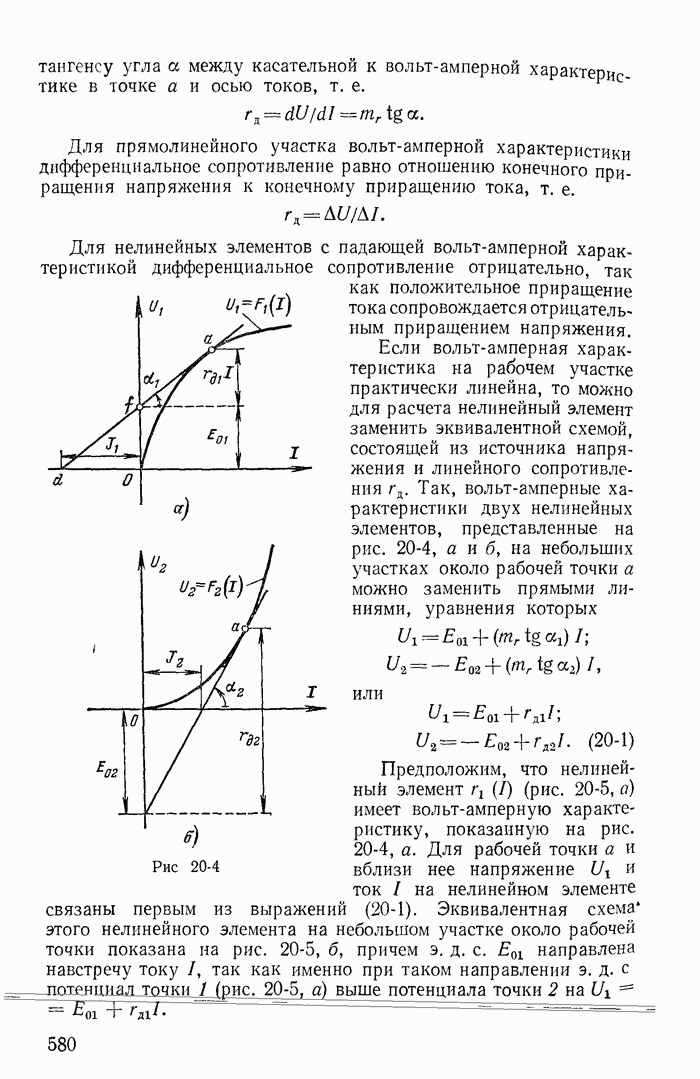
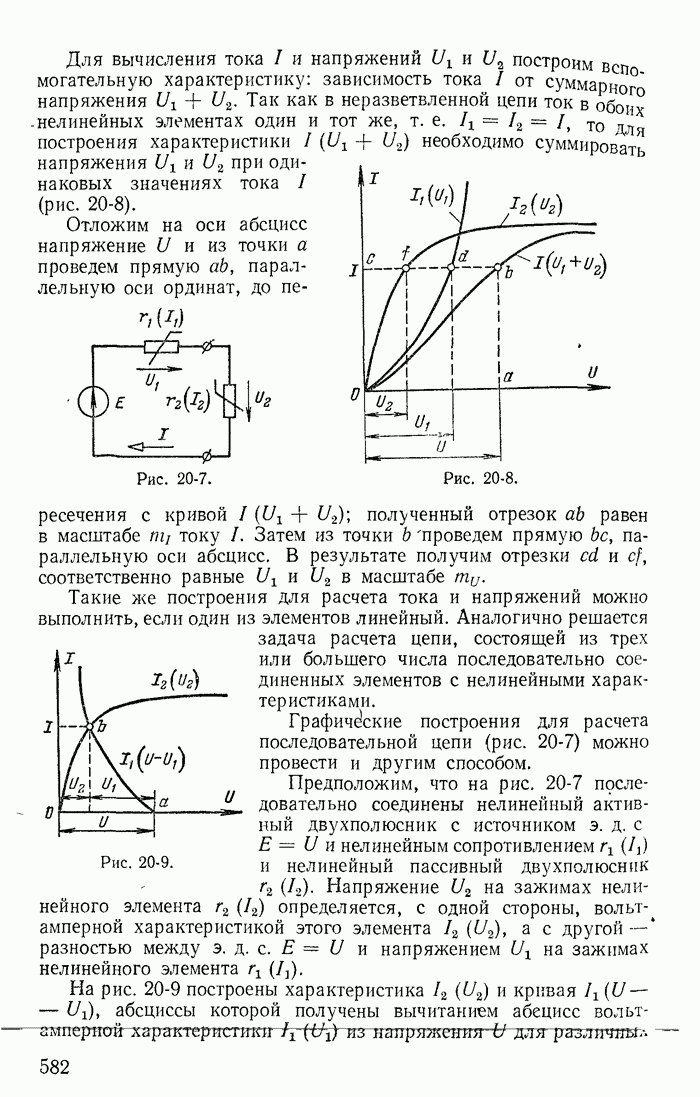
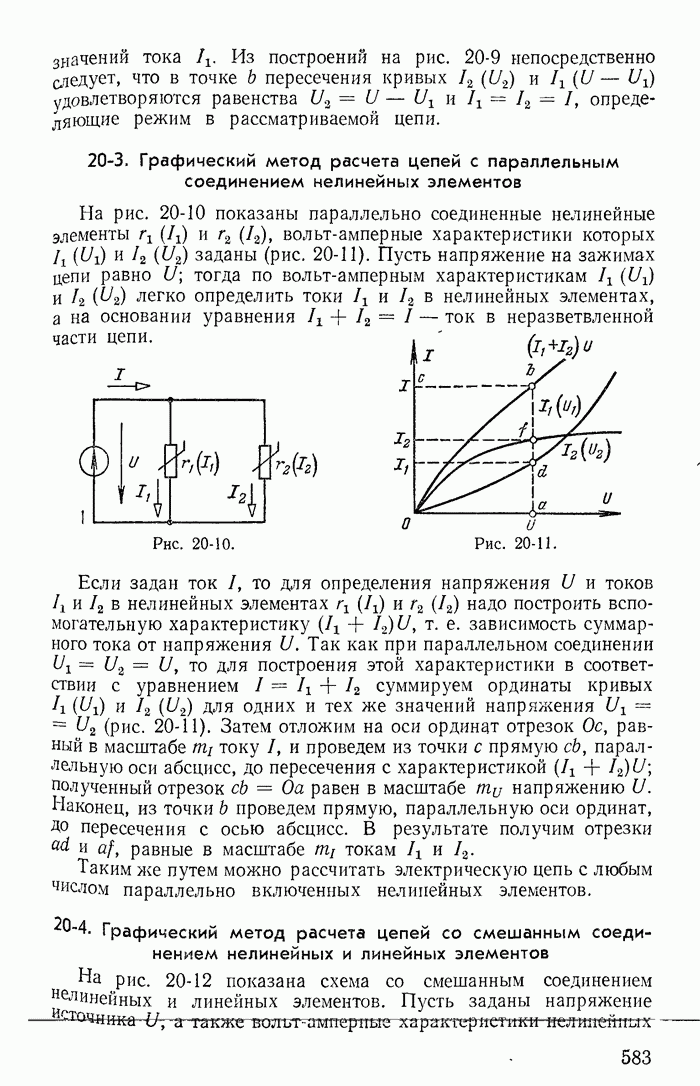
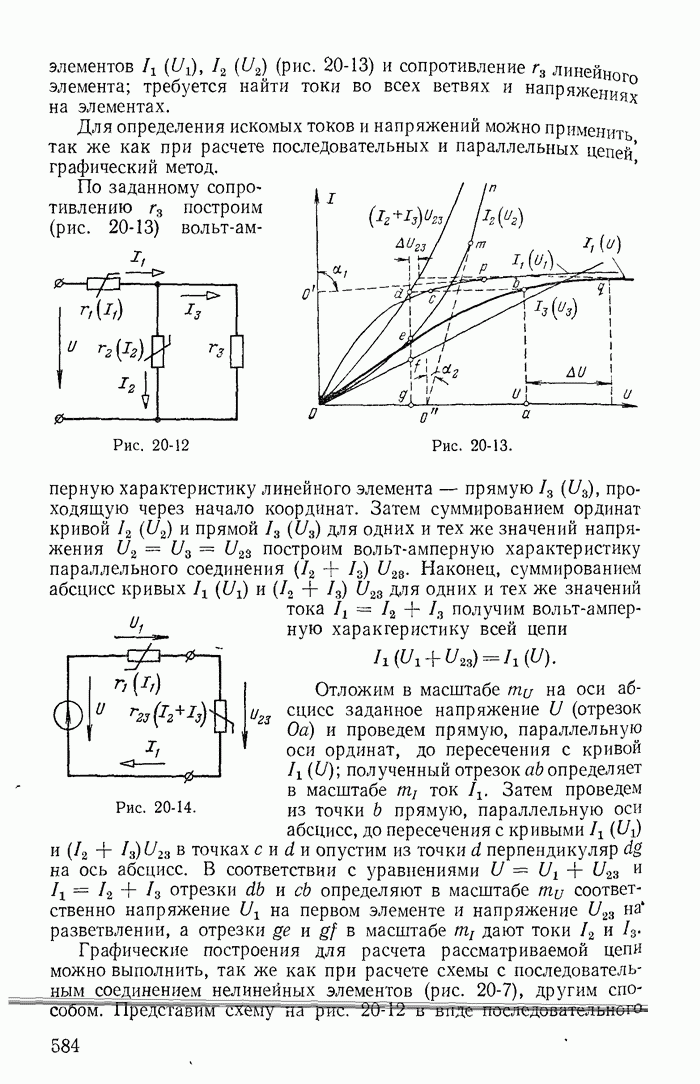
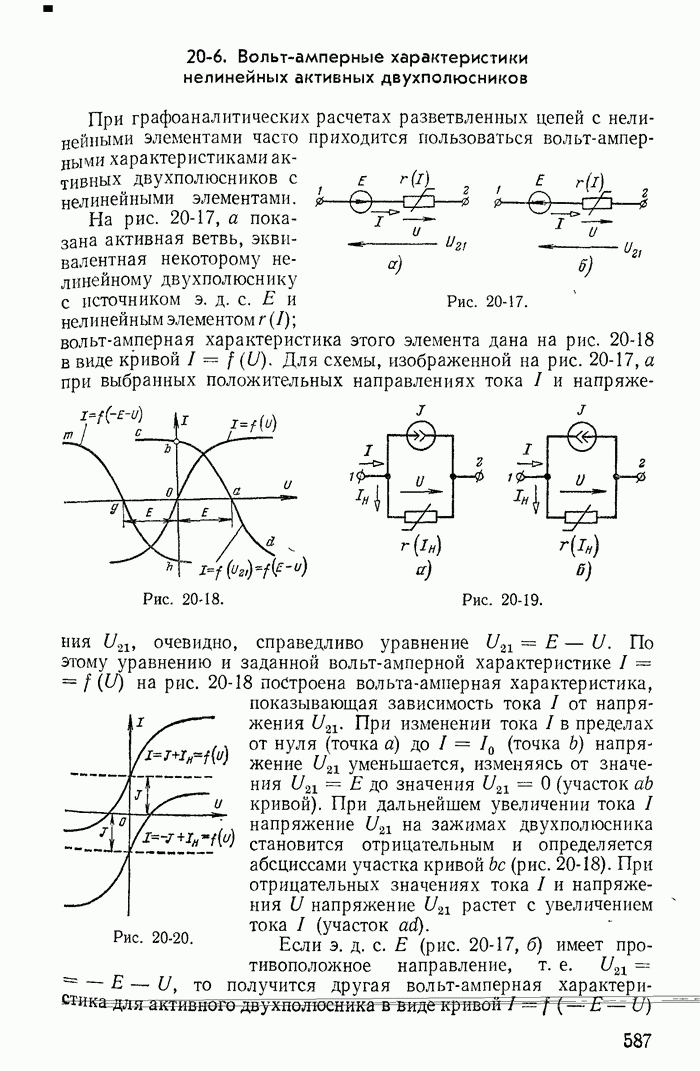
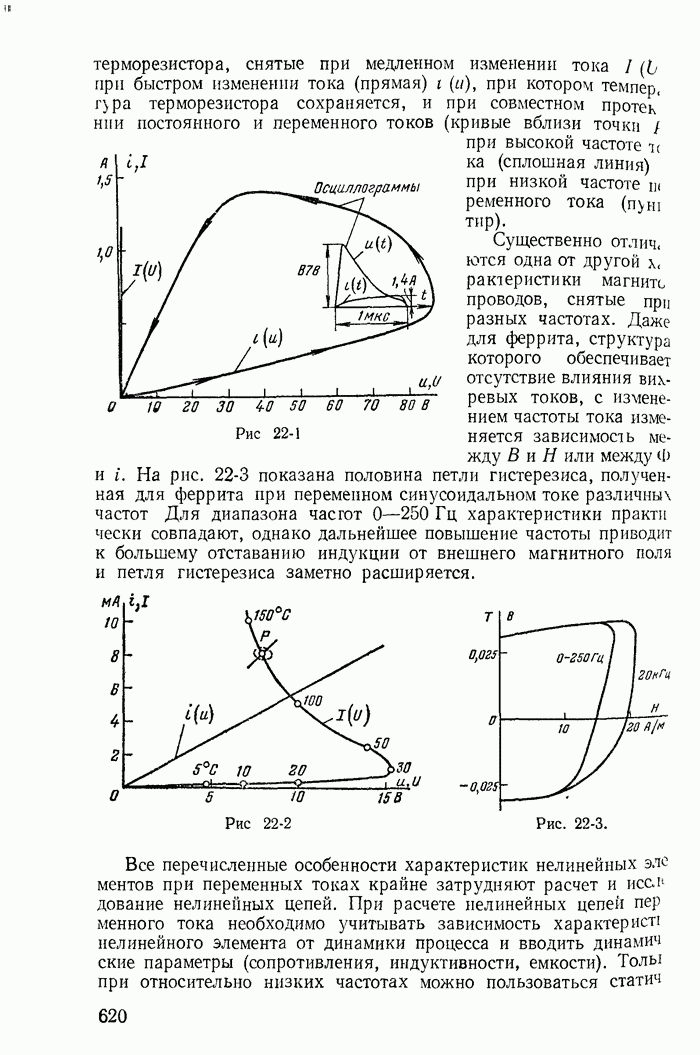
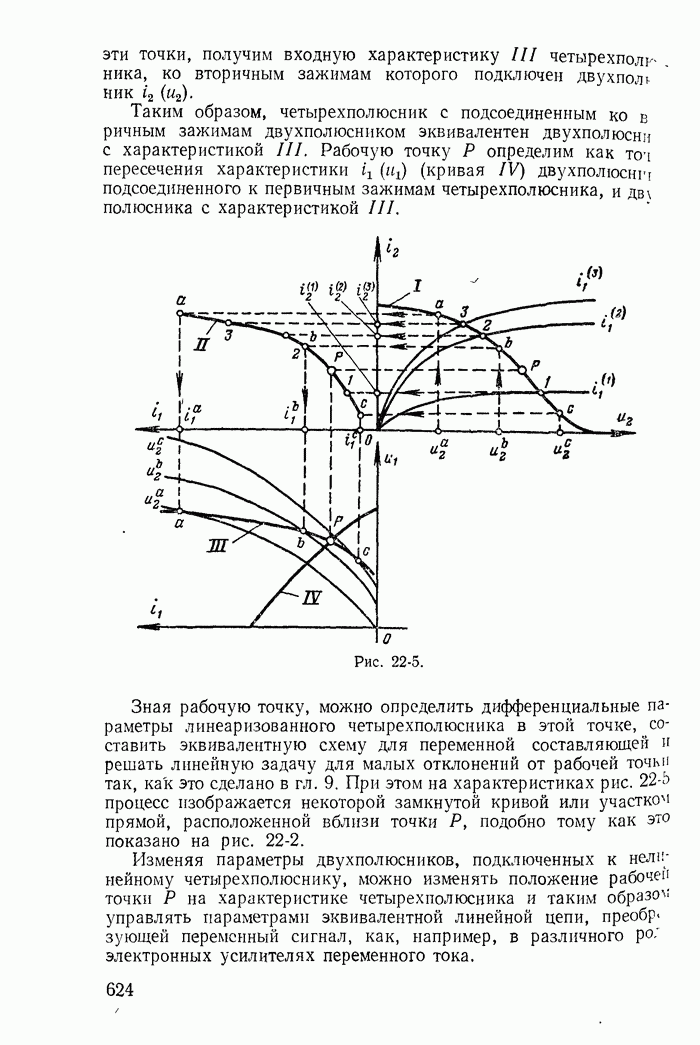
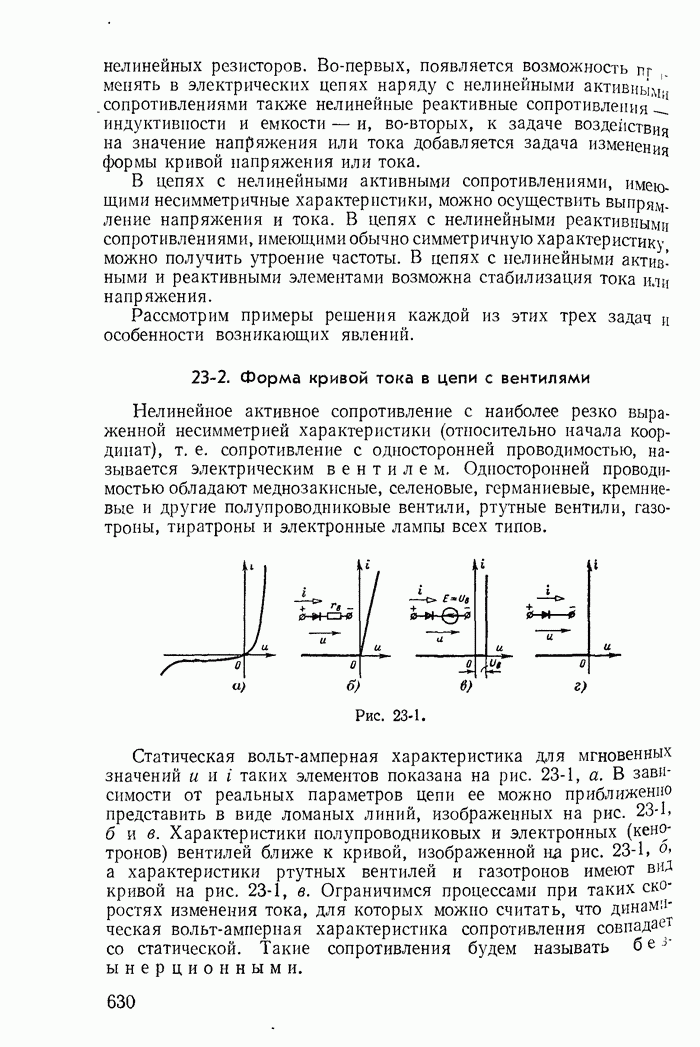
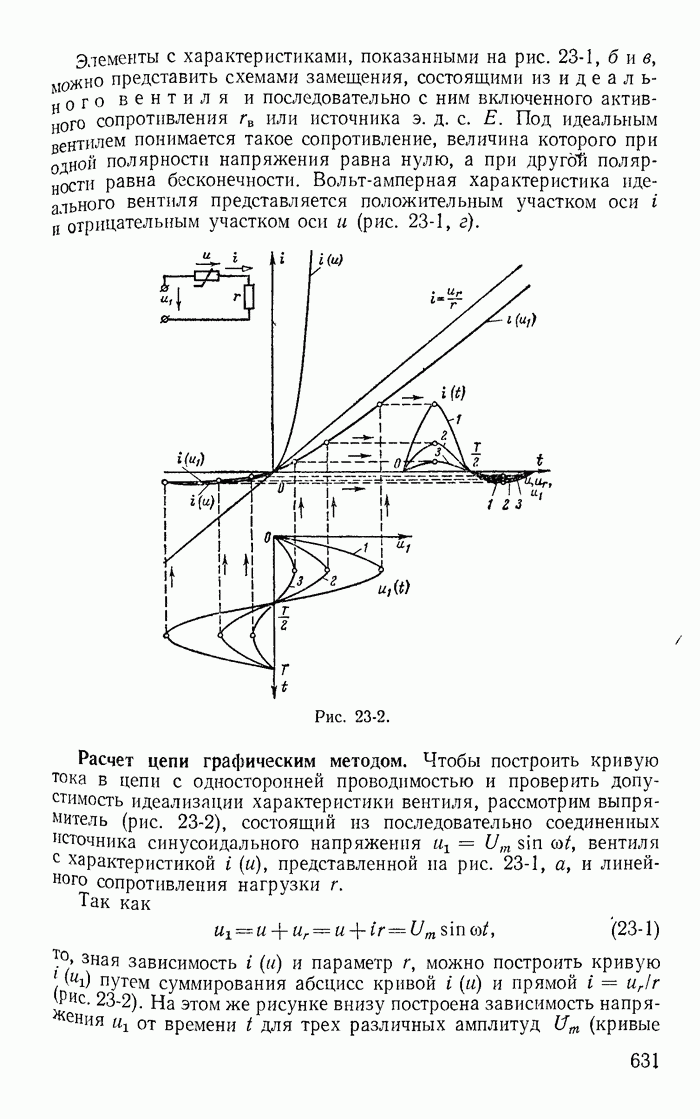
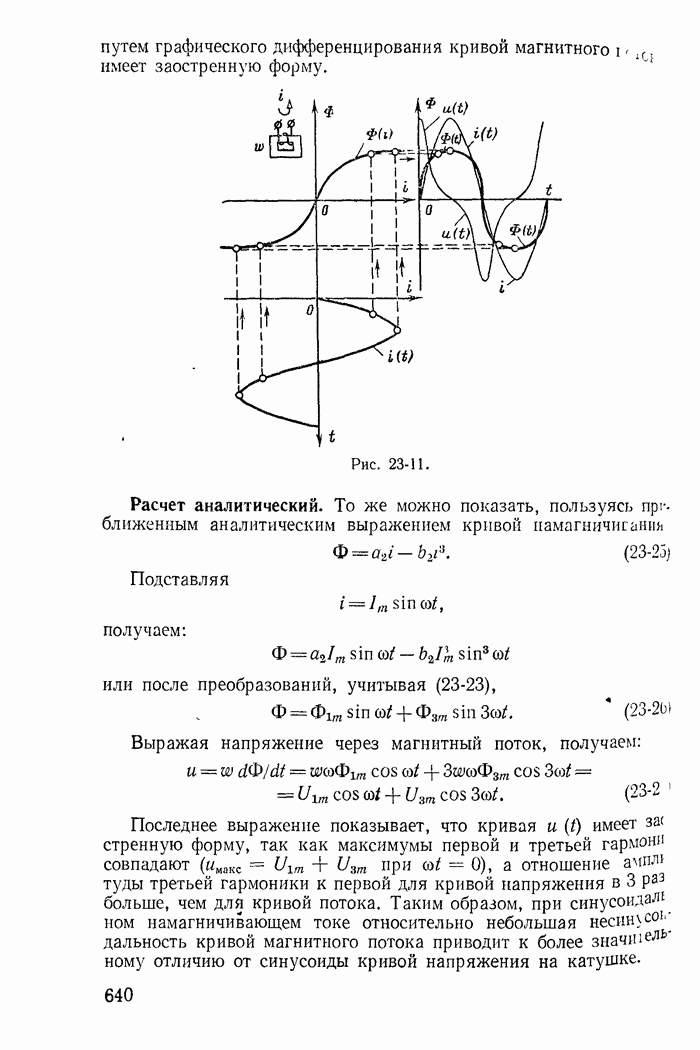
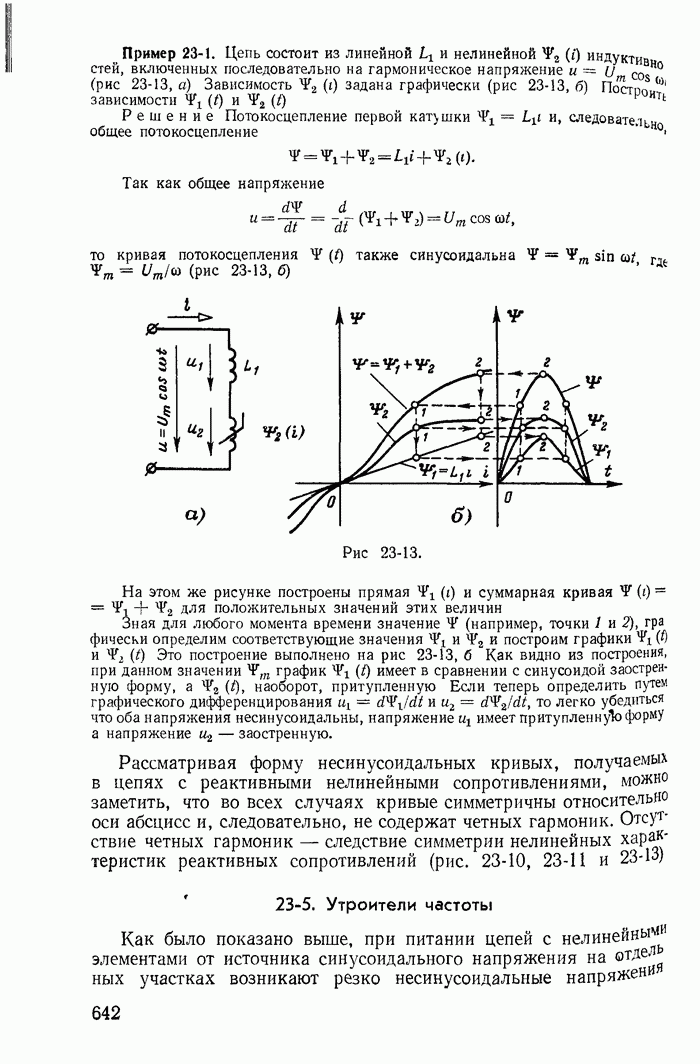
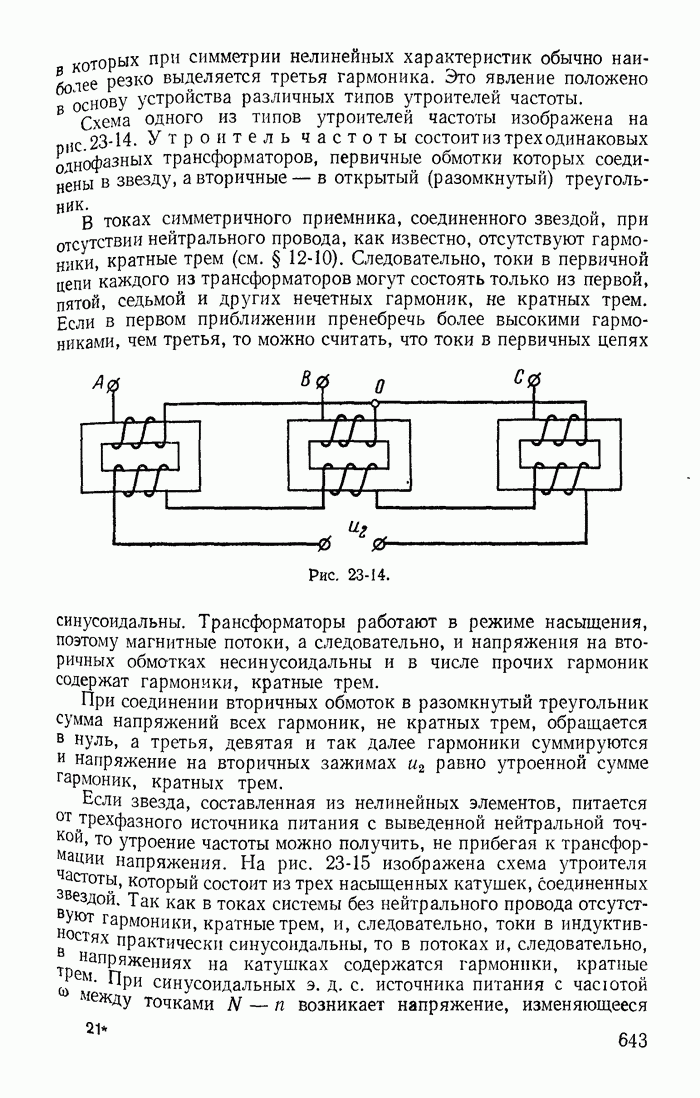
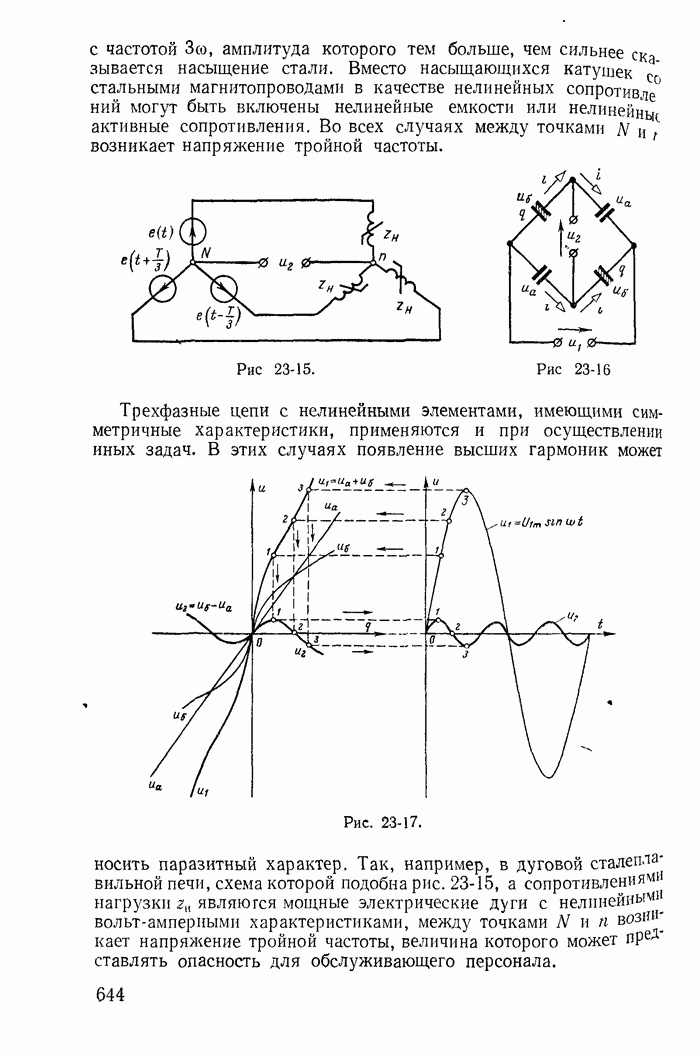
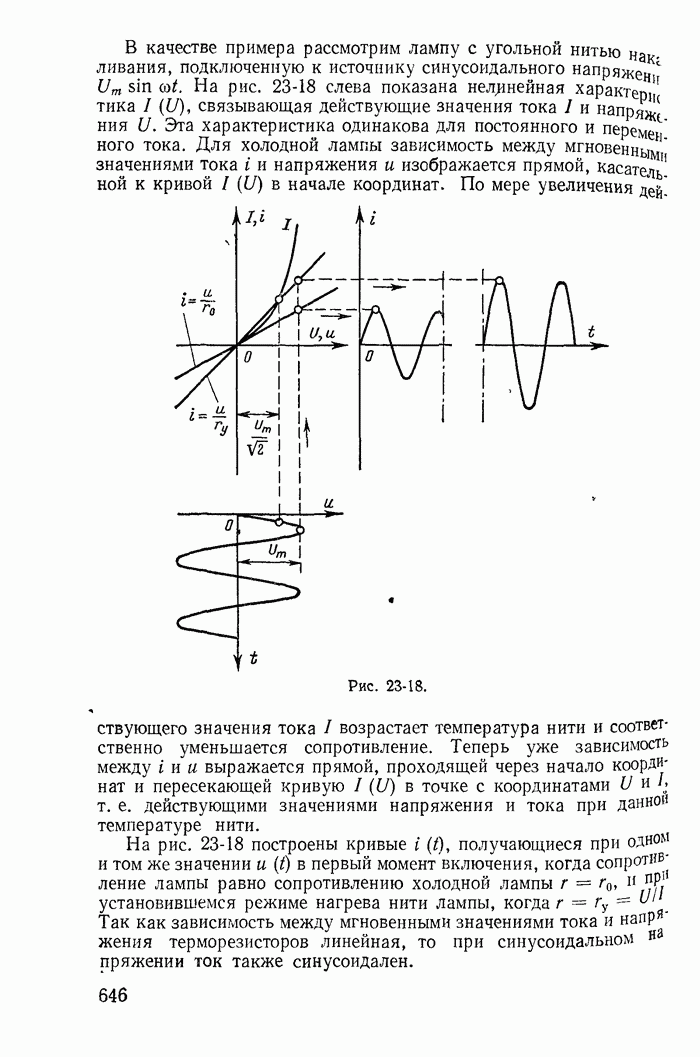
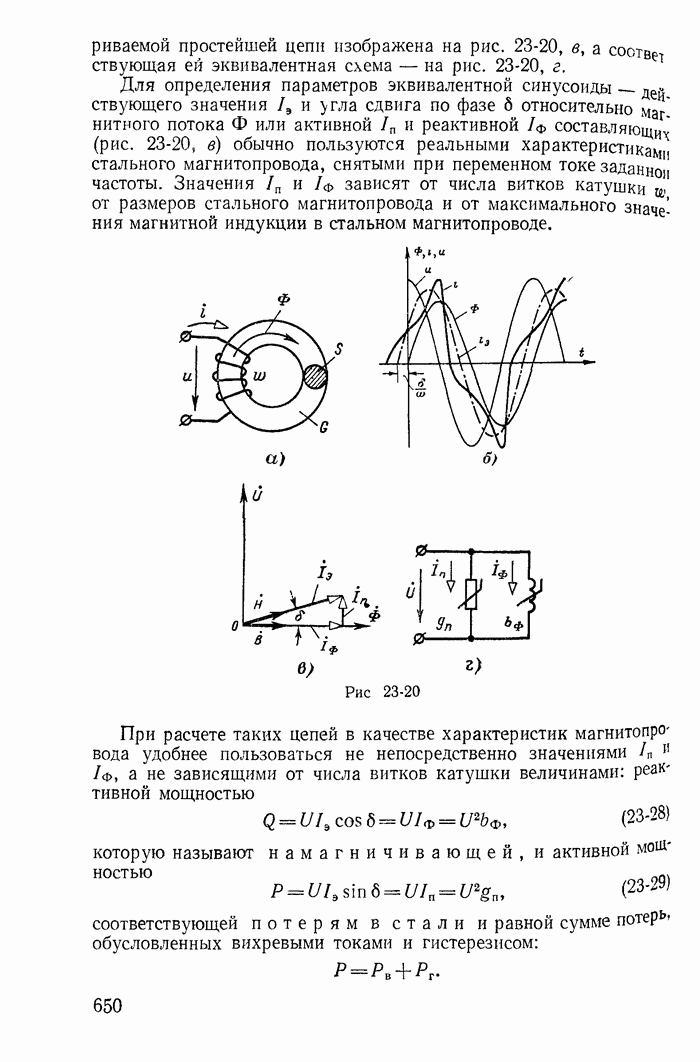
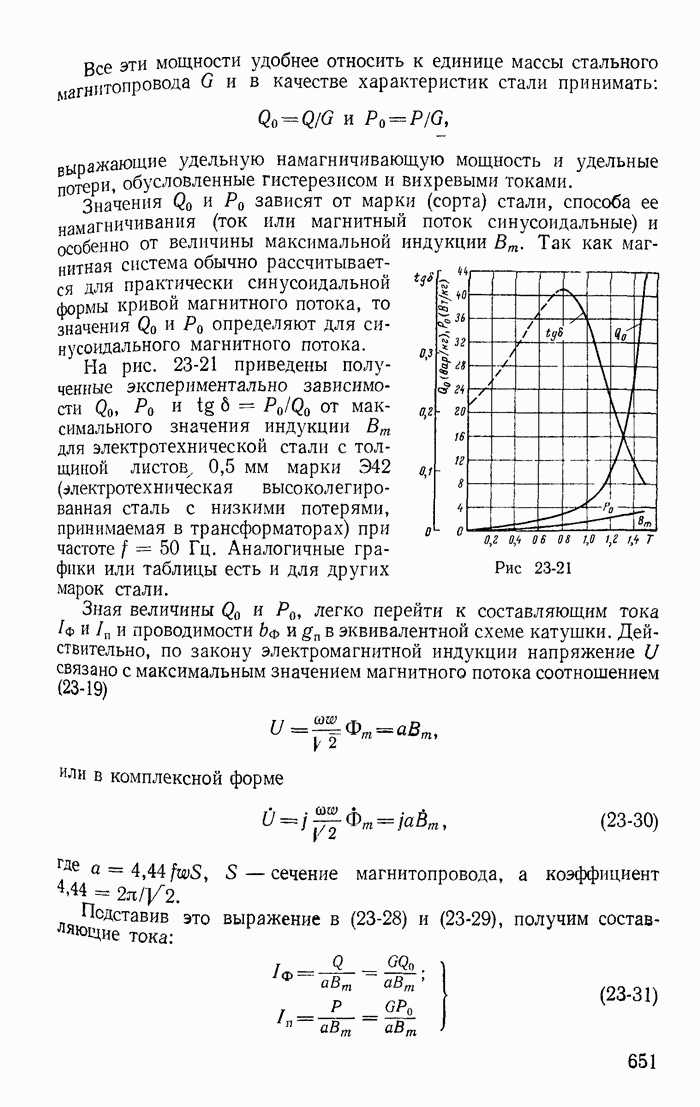
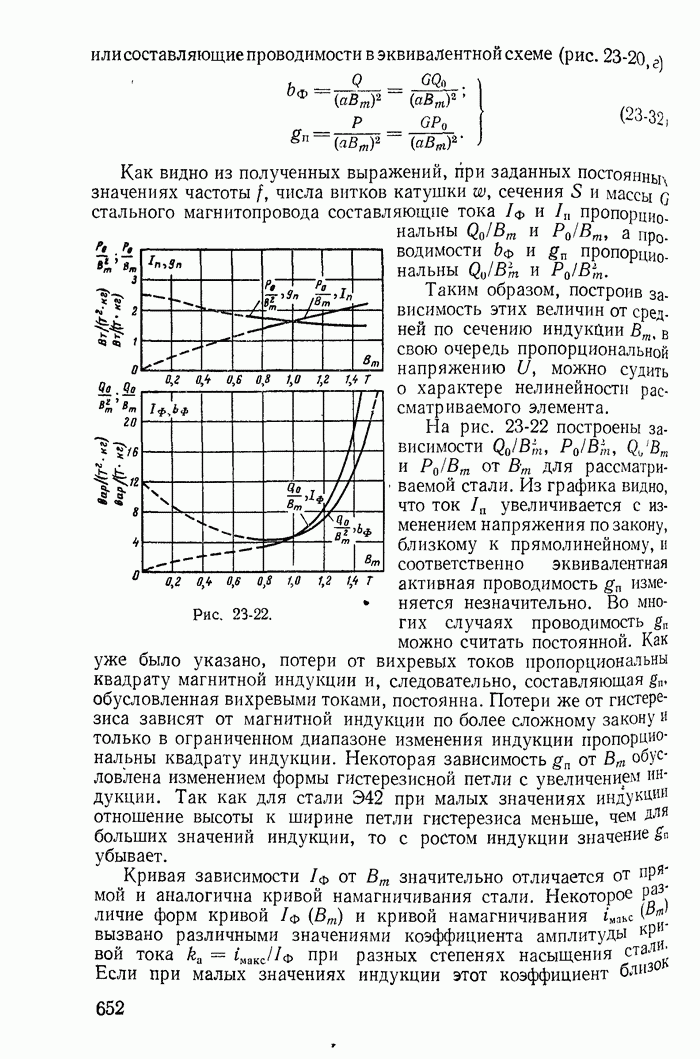
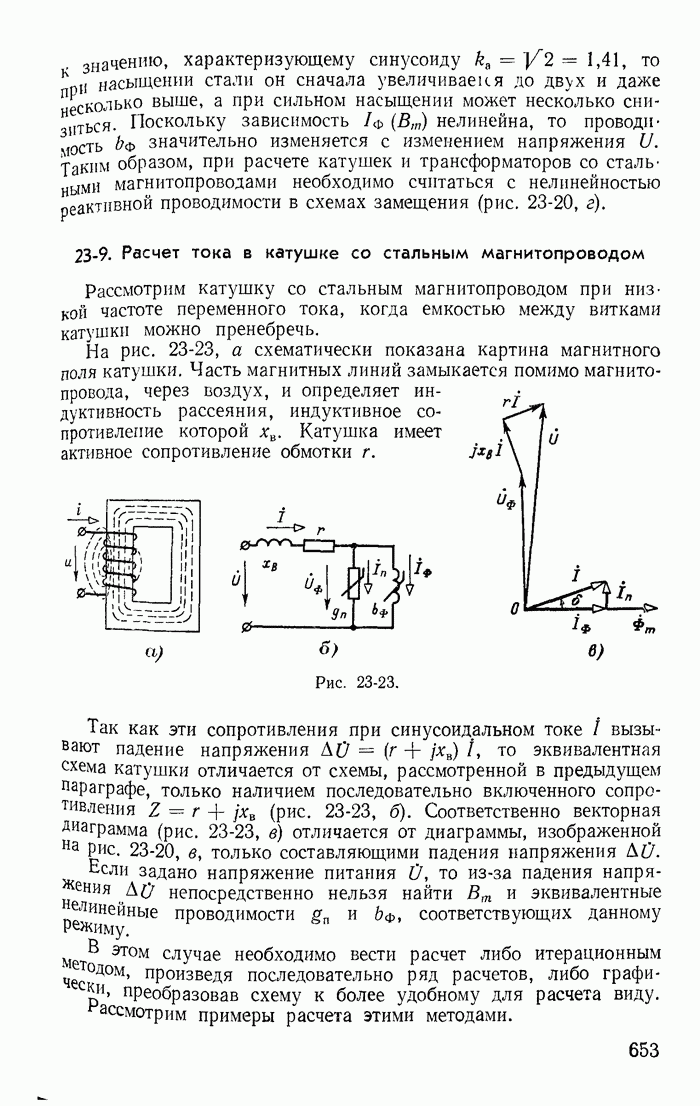
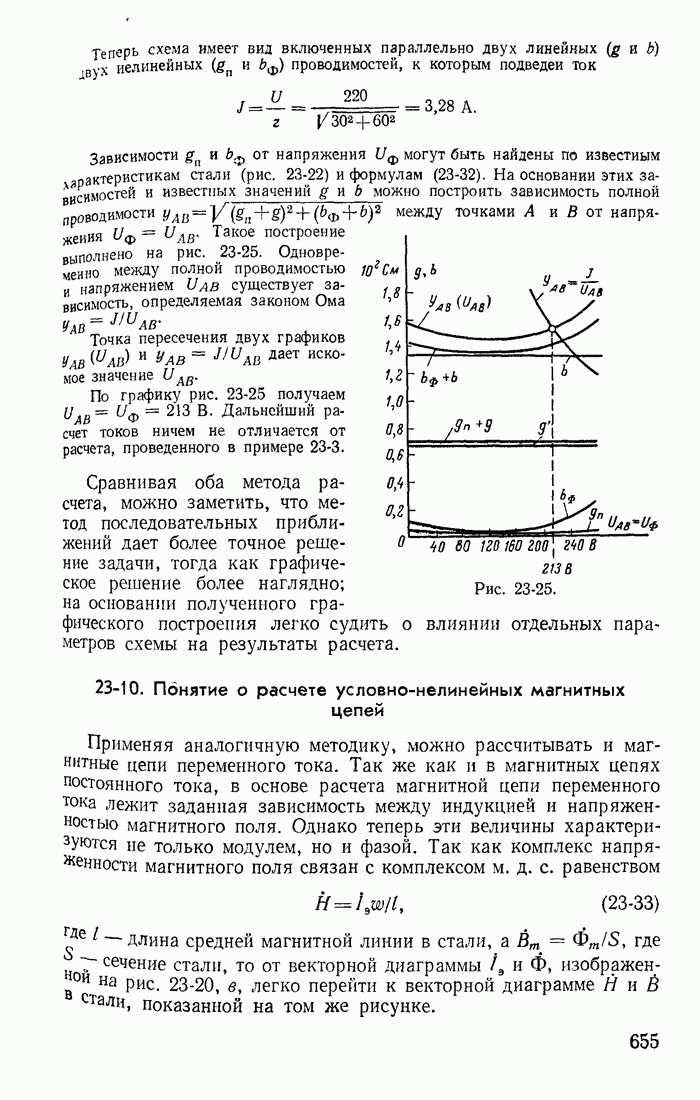
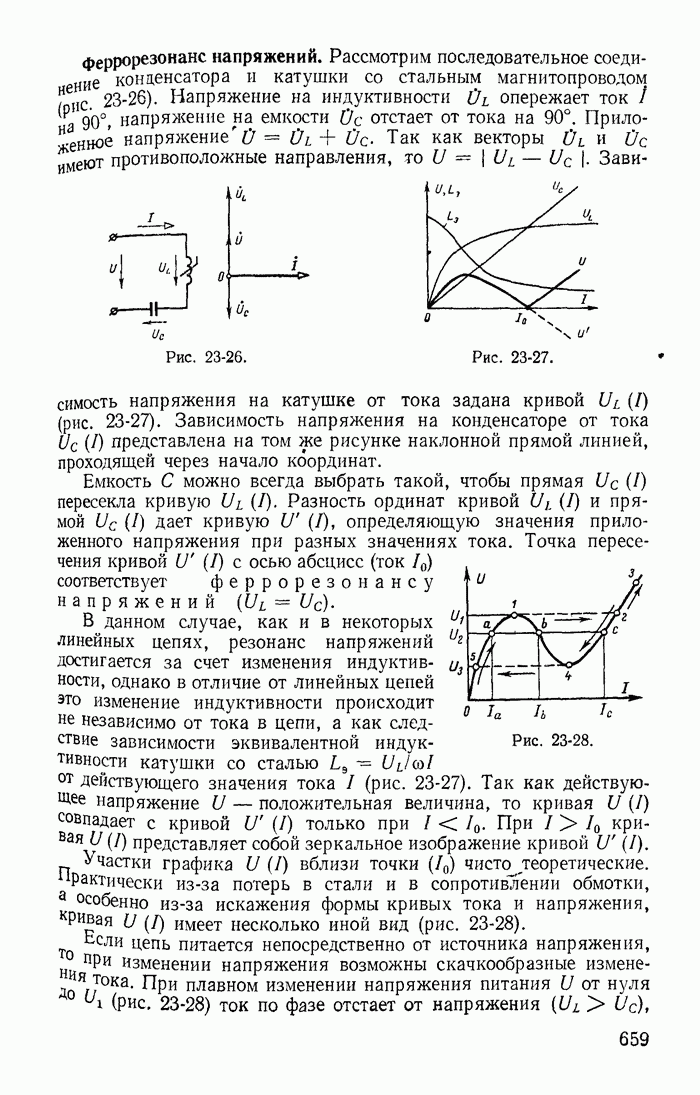
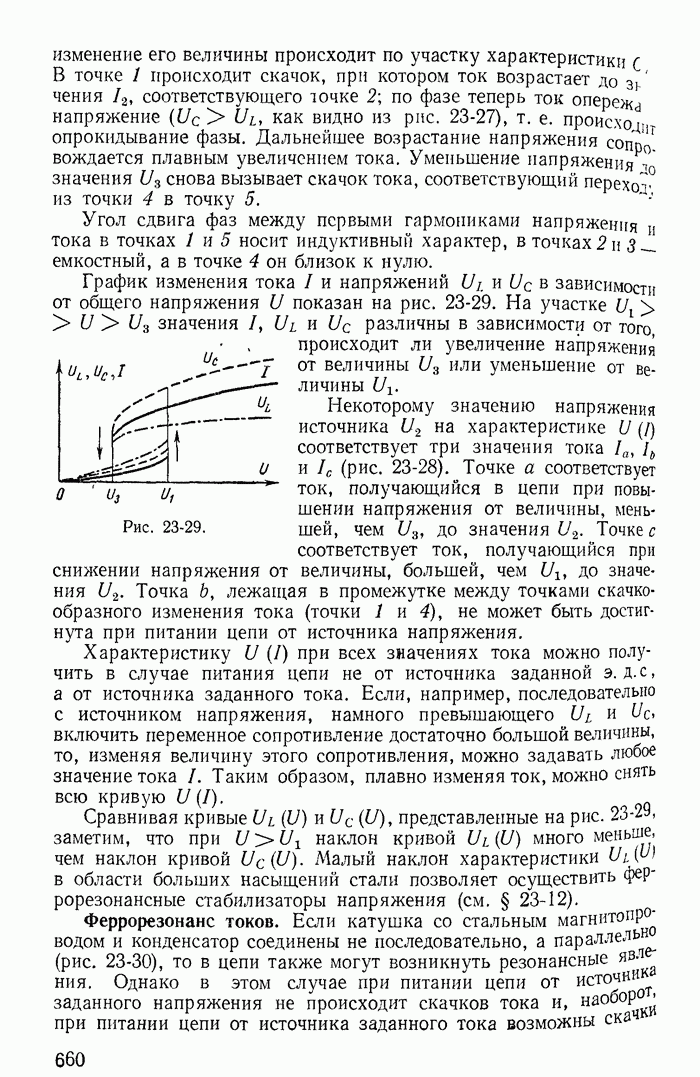
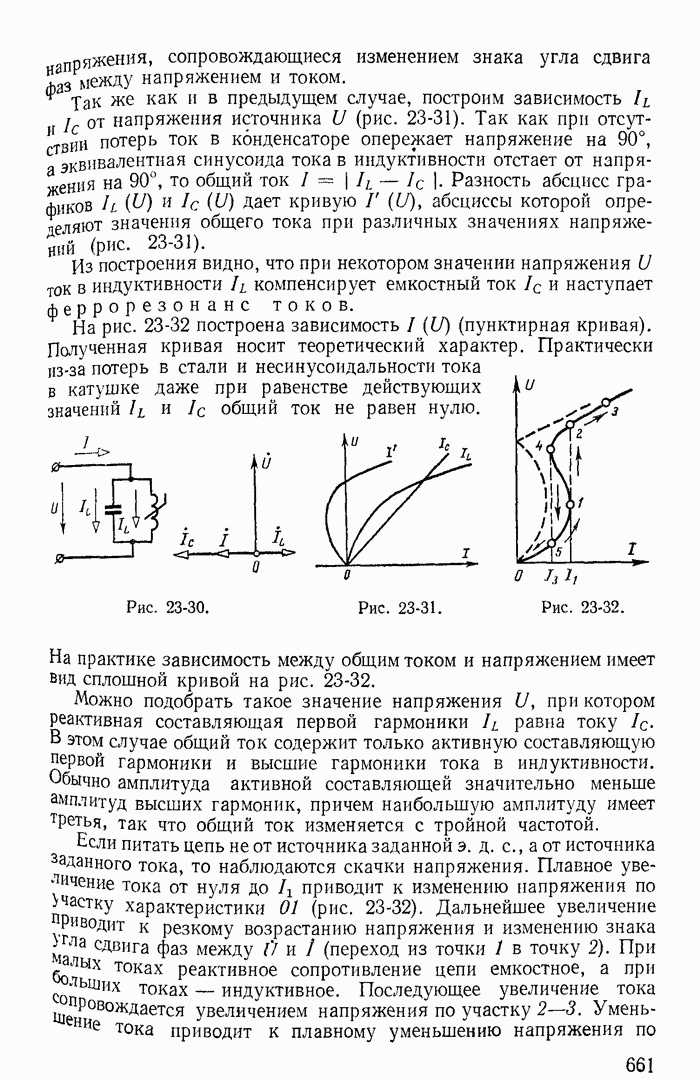
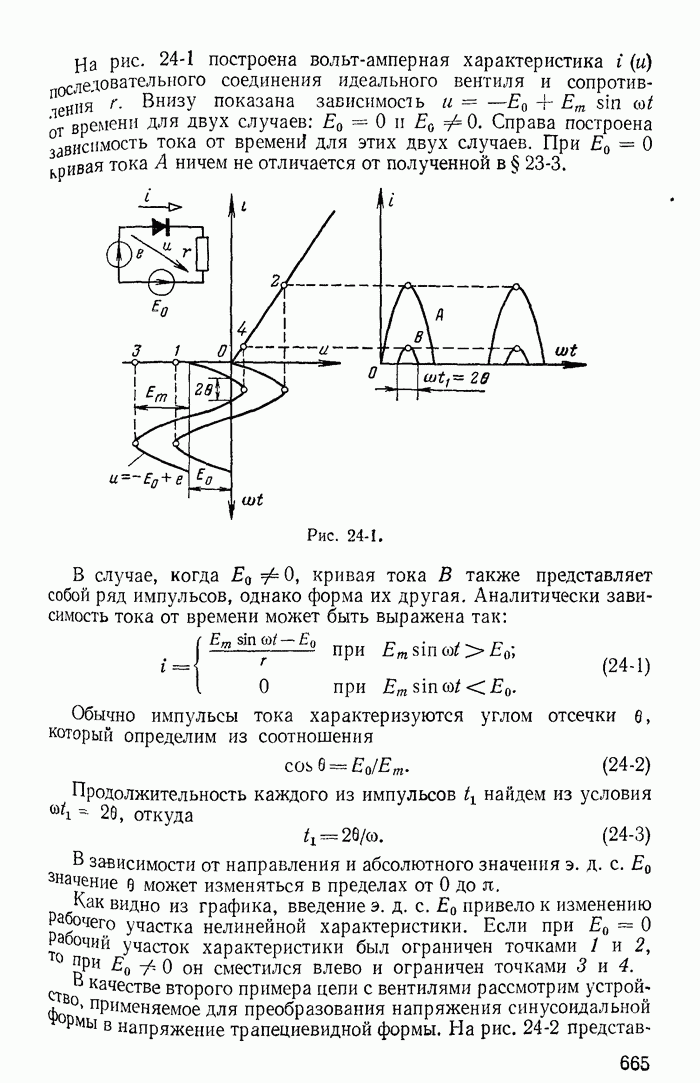
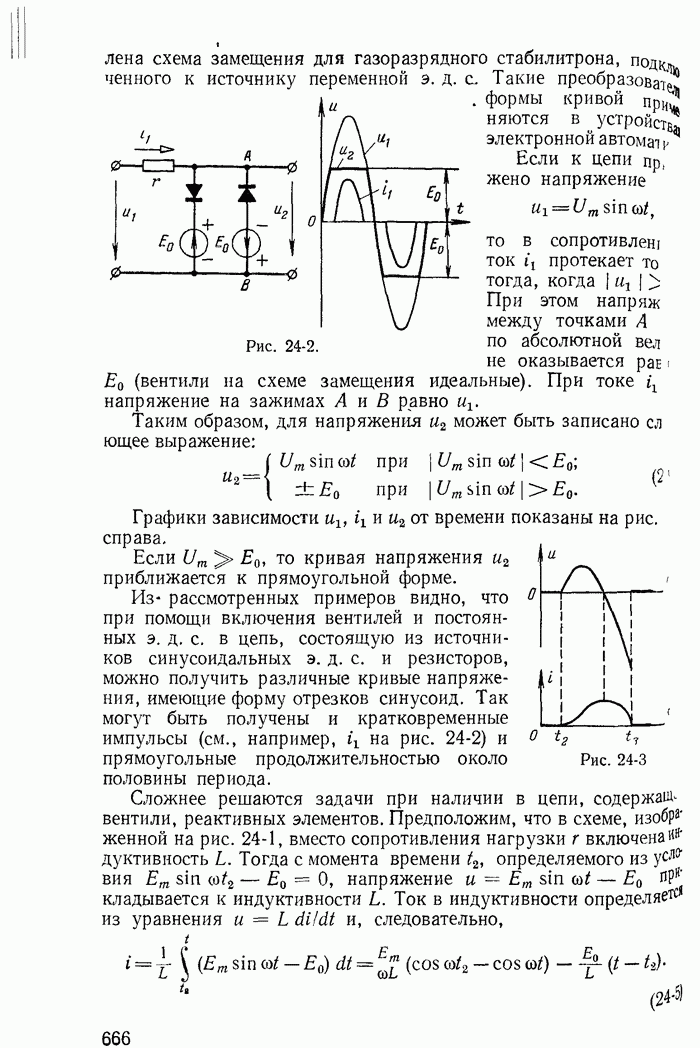
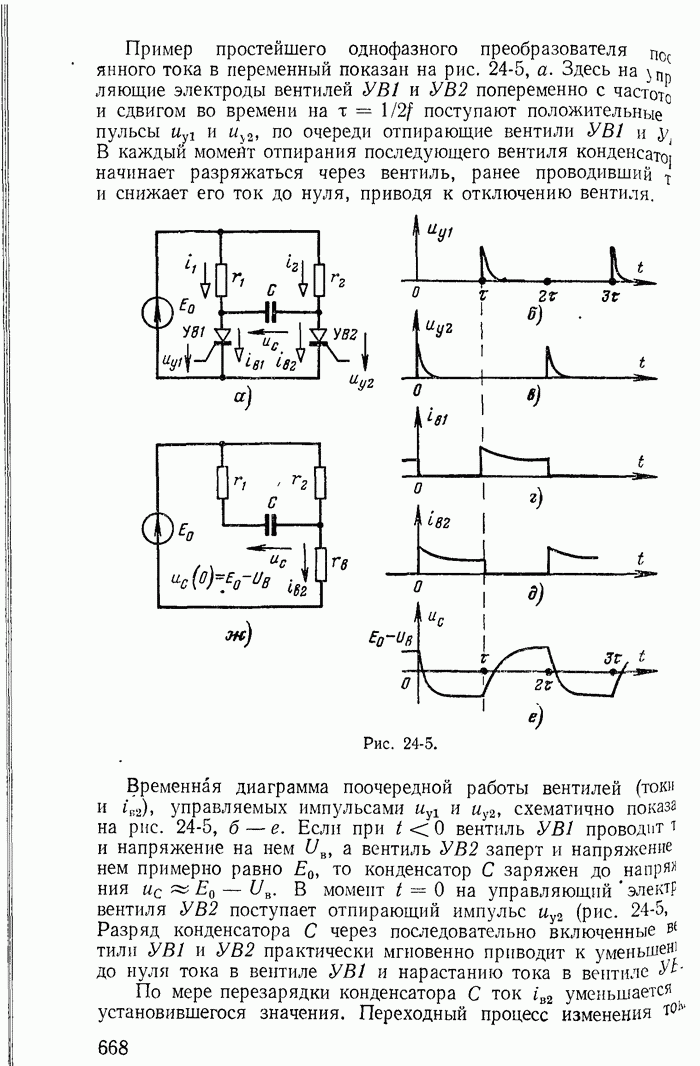
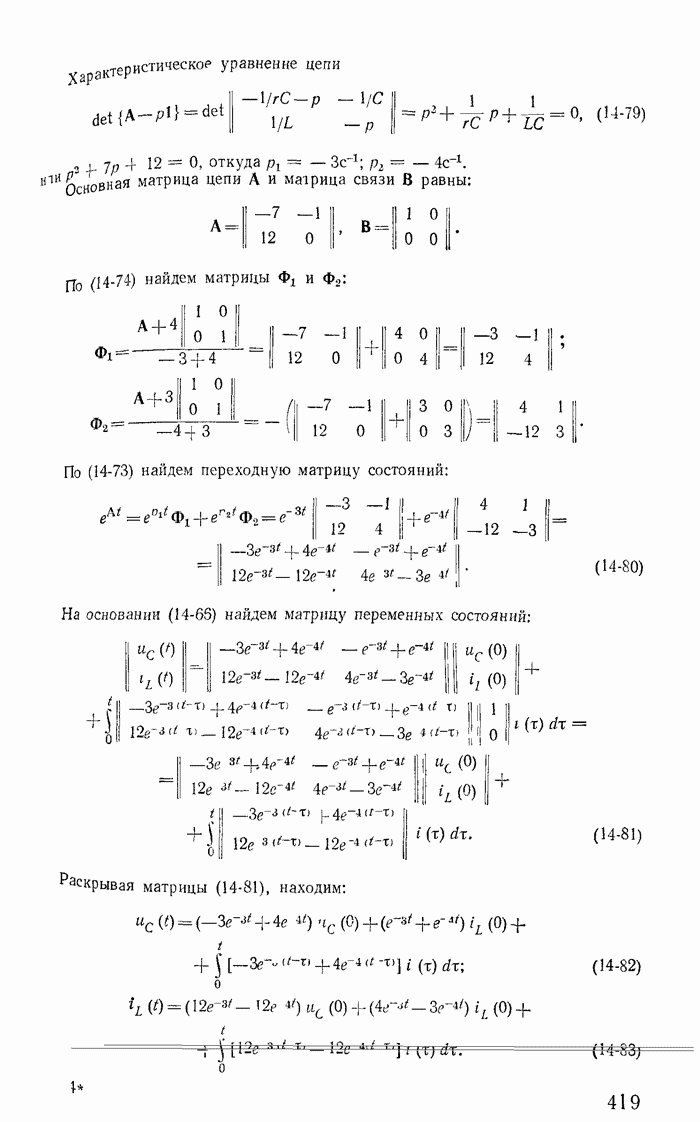| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
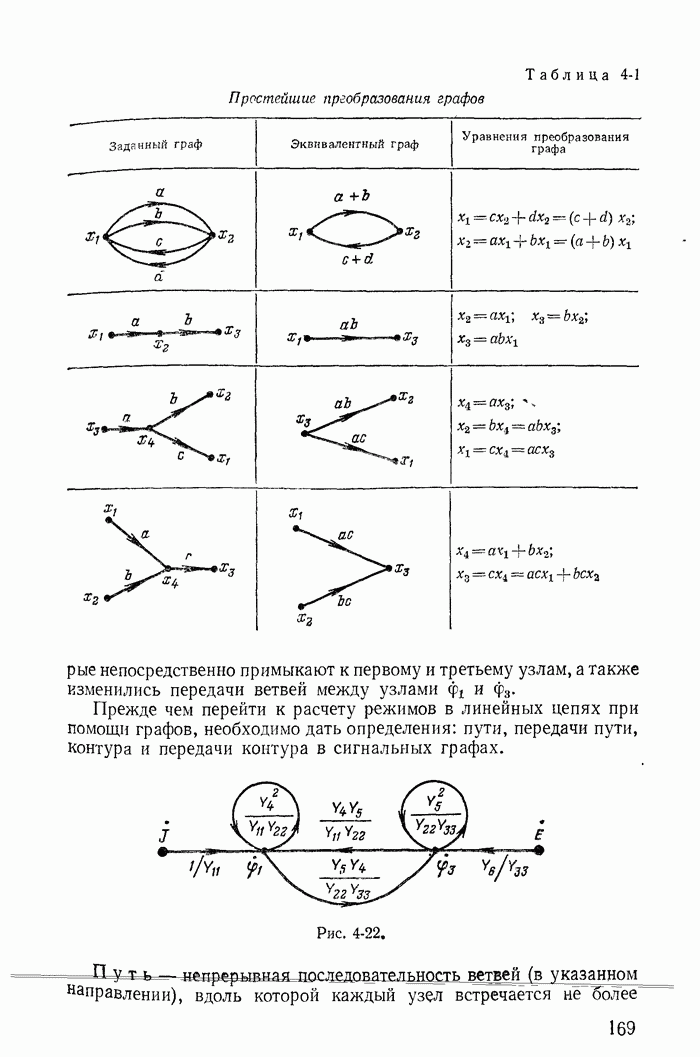
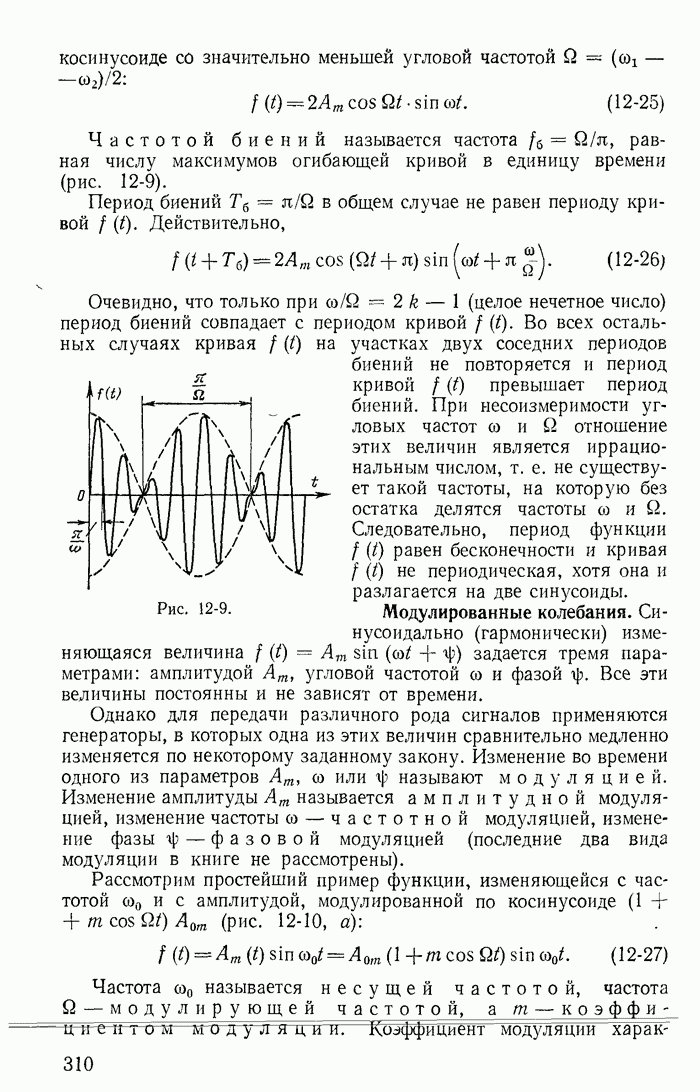
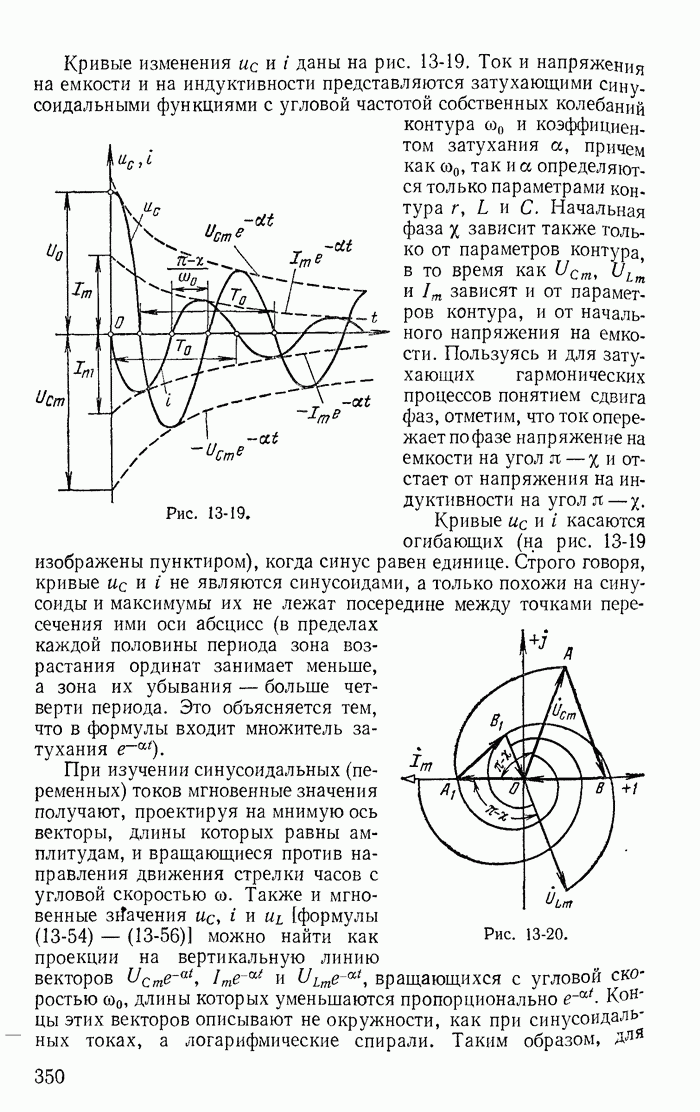
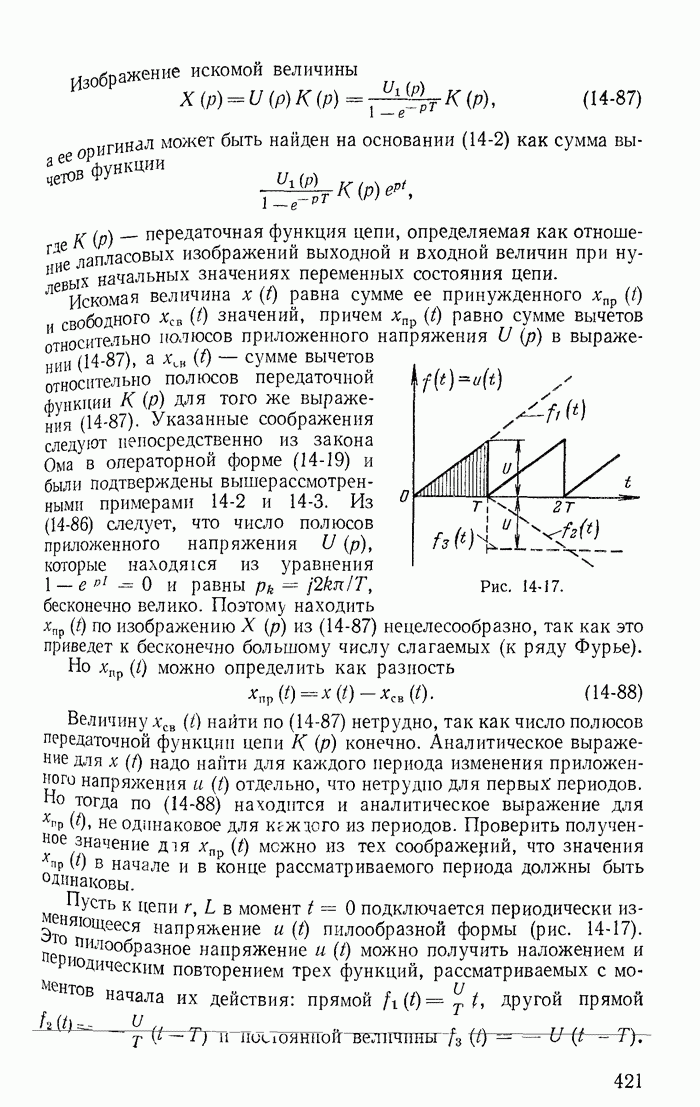
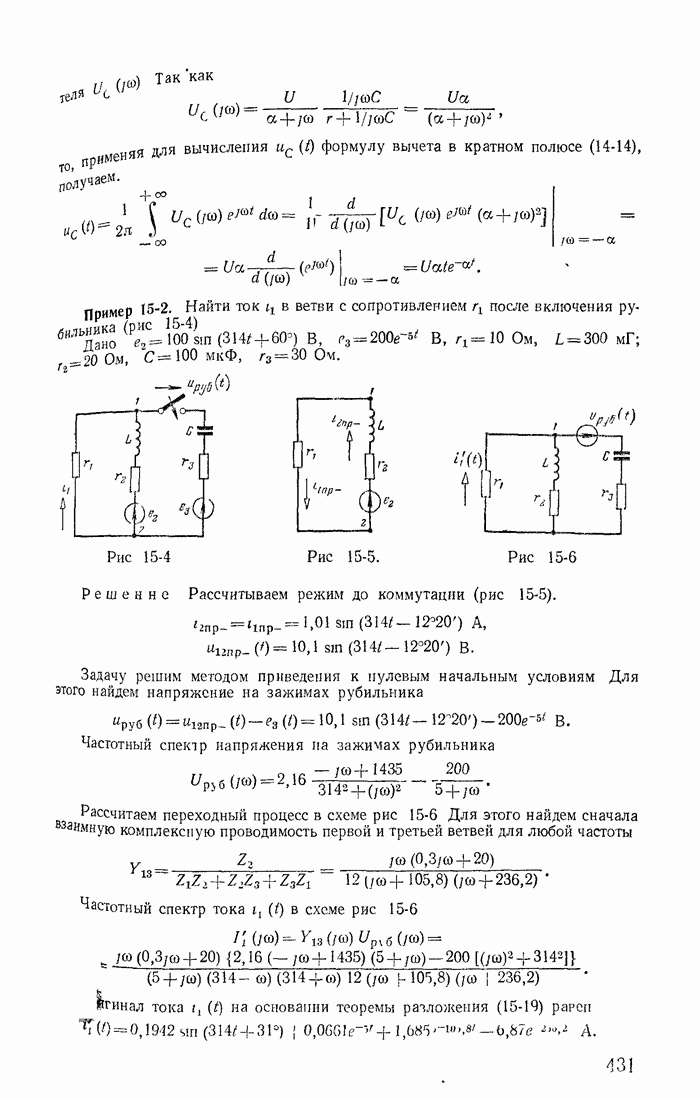
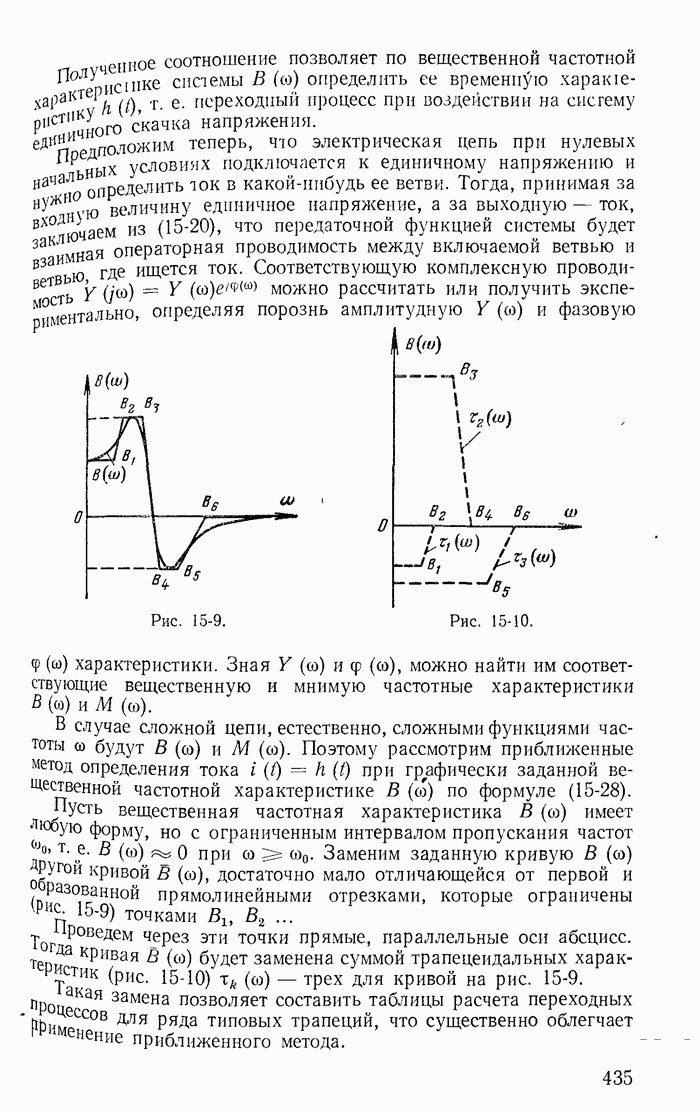
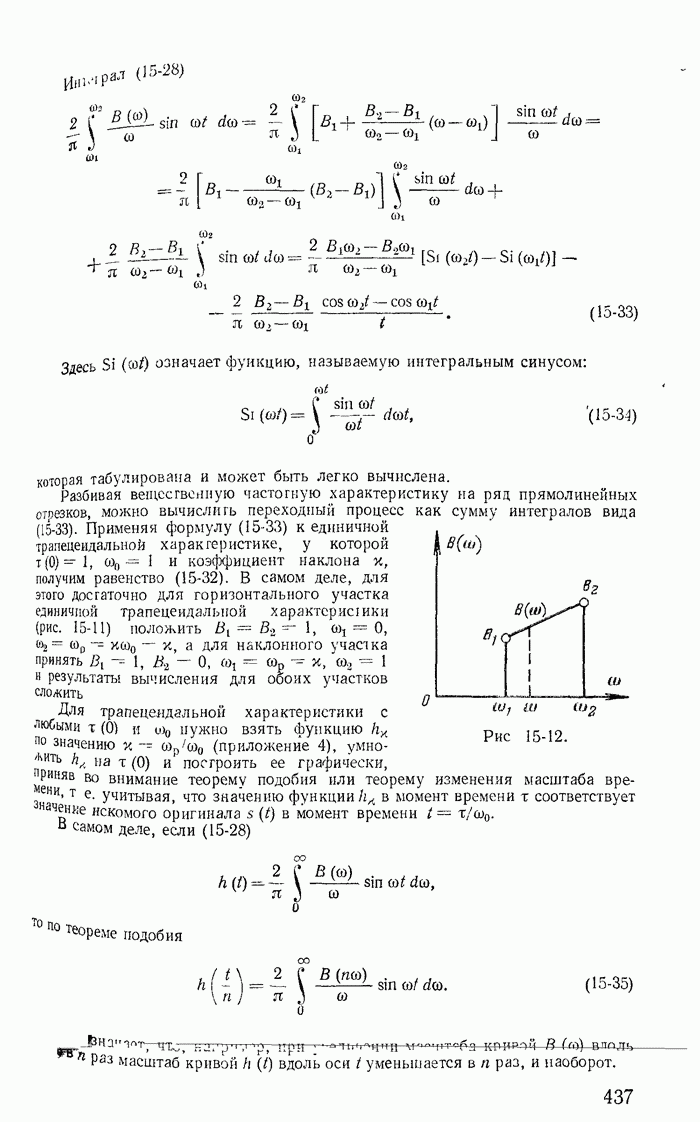
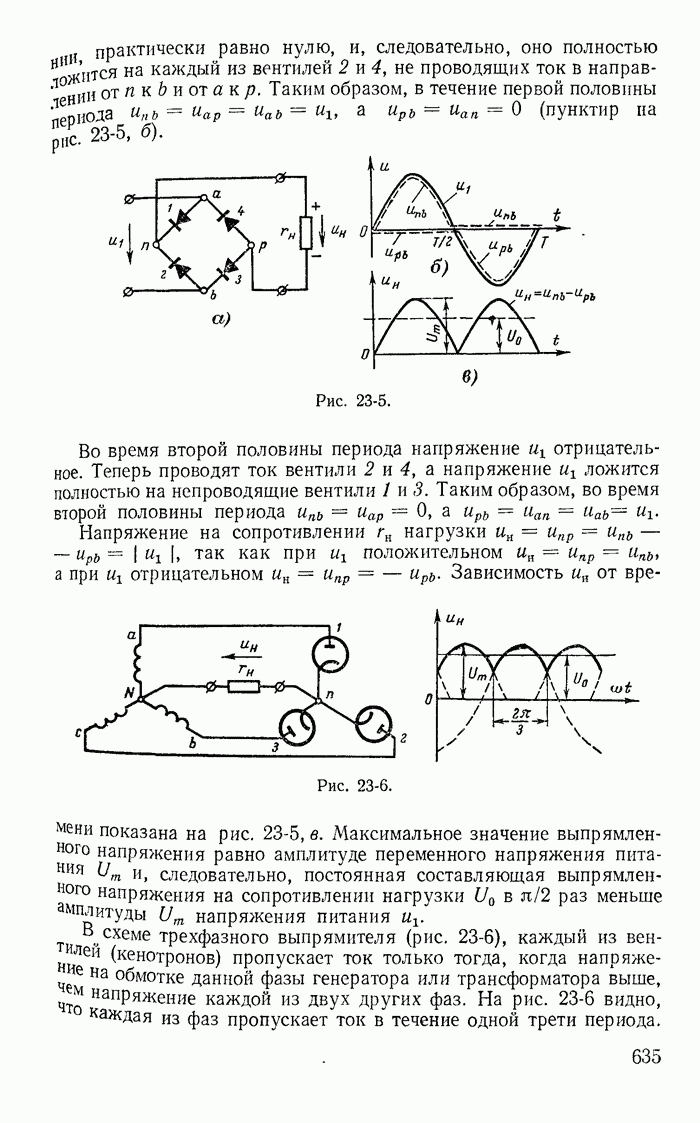
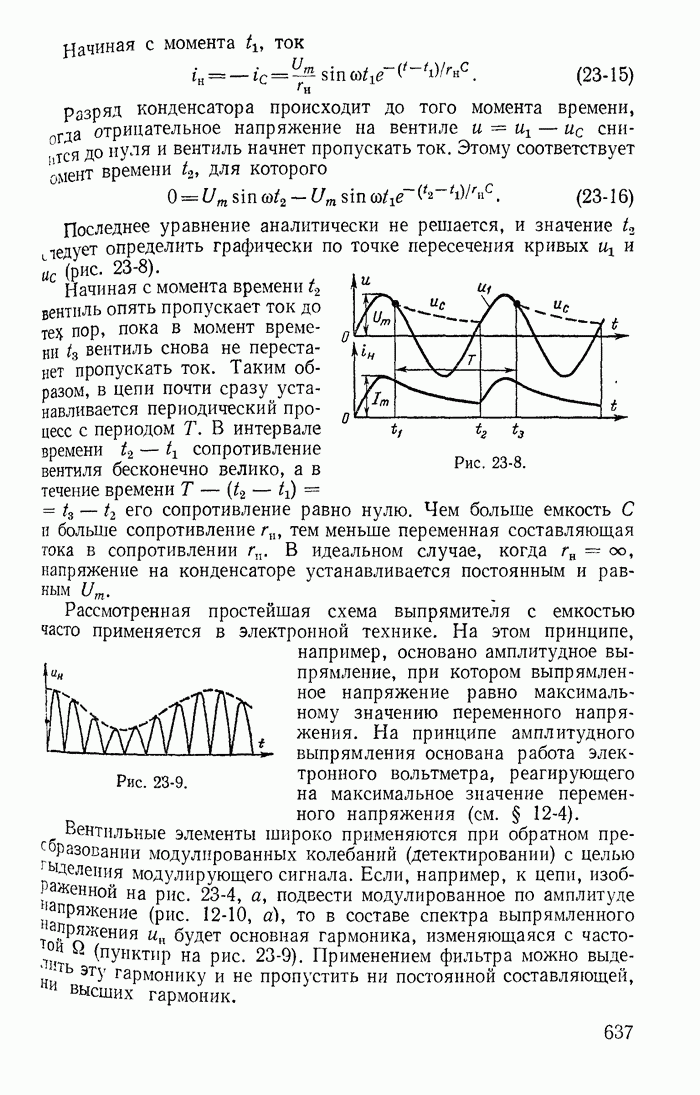
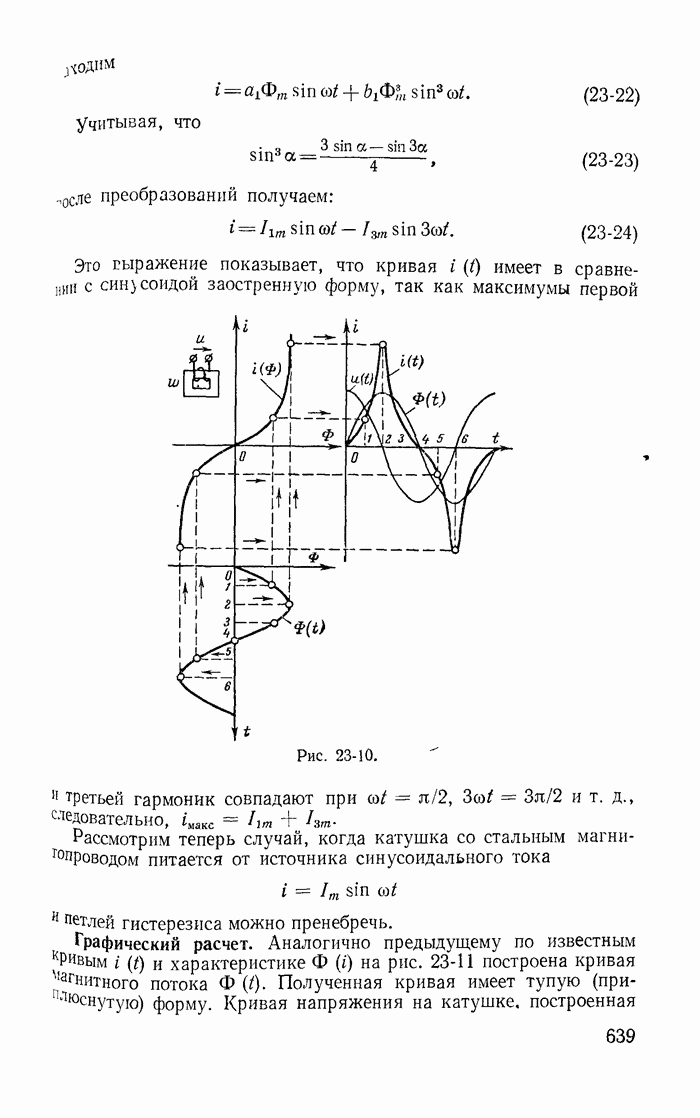
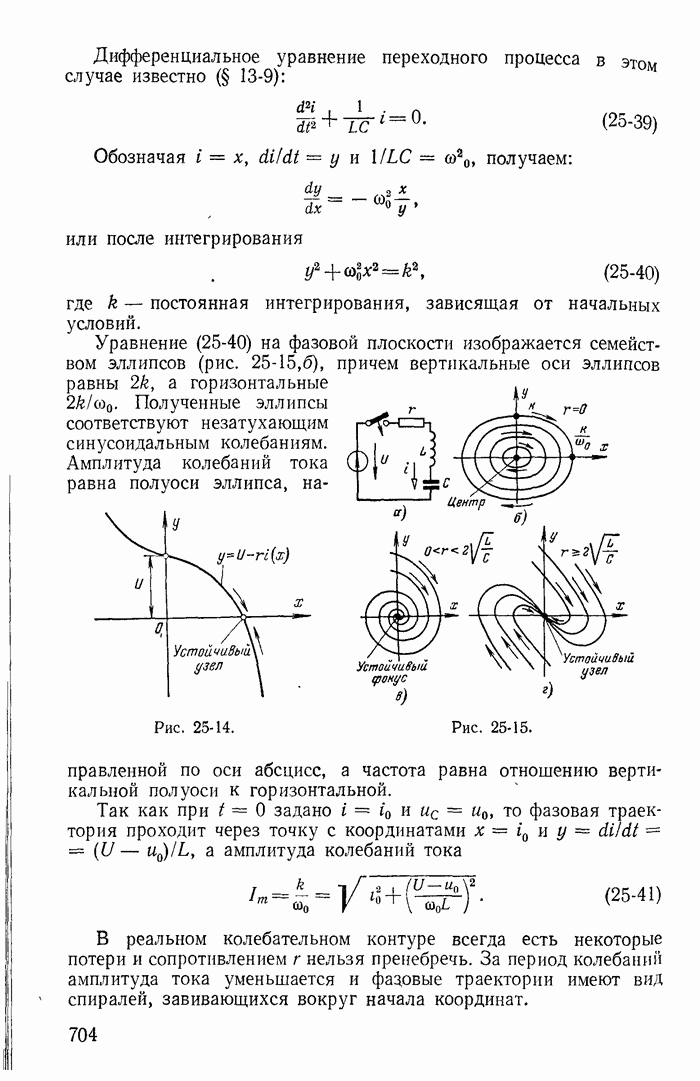
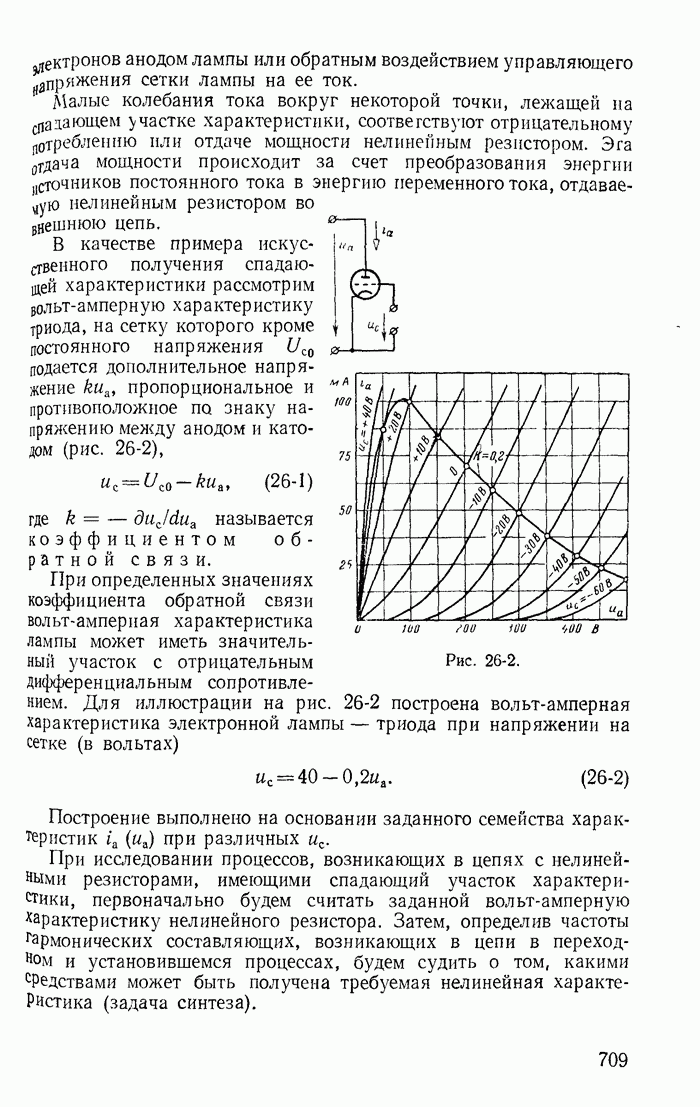
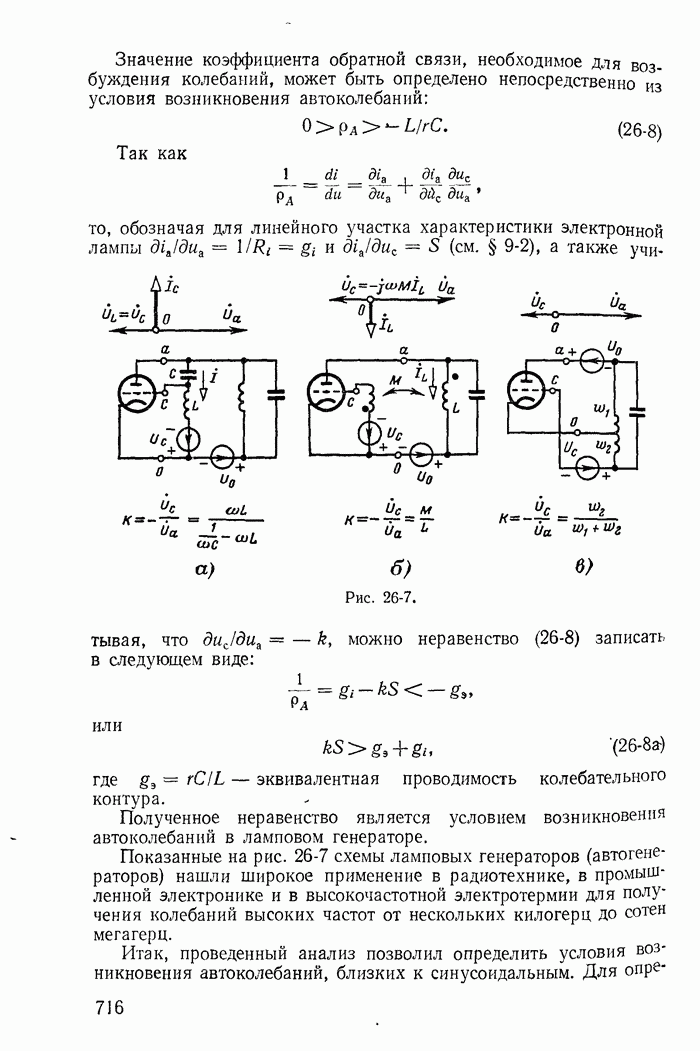
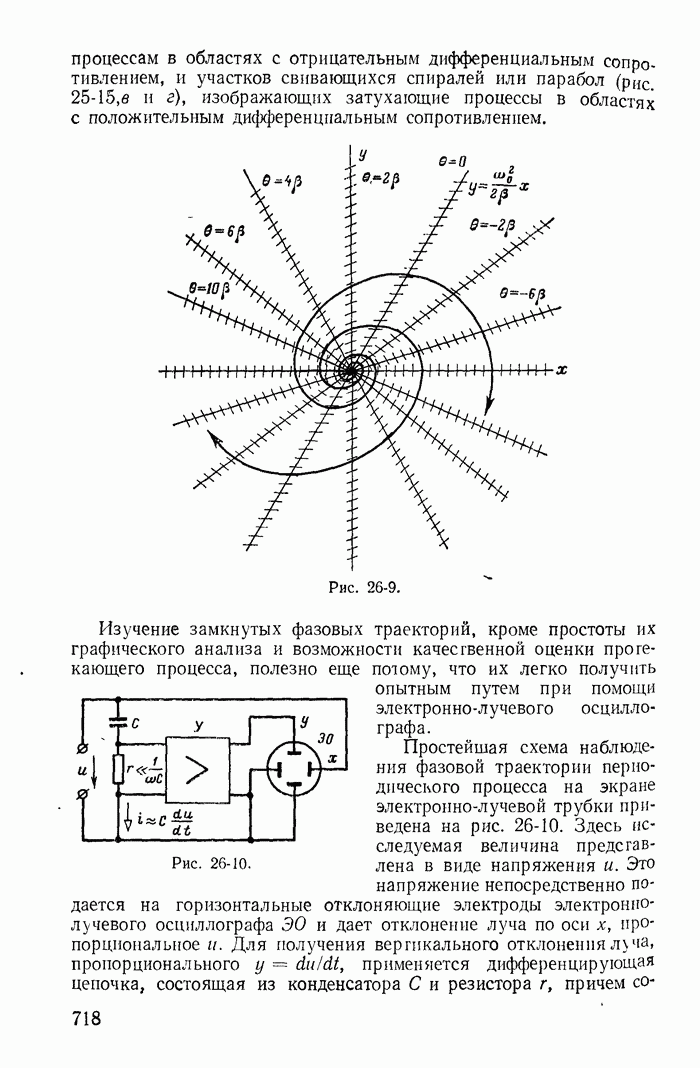
13-19. Переходные процессы при скачках токов в индуктивностях и напряжений на конденсаторах
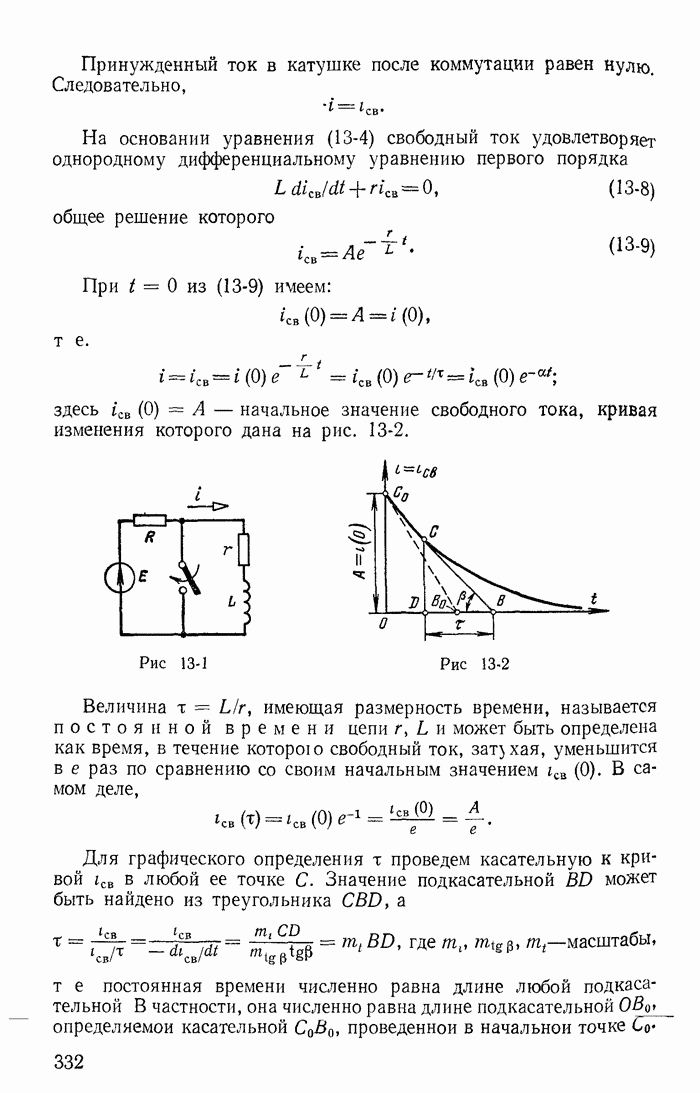
До сих пор рассматривались такие цепи и режимы их работы, для которых удовлетворялись законы коммутации
 (13-91)
(13-91)
где  — момент времени непосредственно перед коммутацией,
— момент времени непосредственно перед коммутацией,  — момент времени сразу после коммутации.
— момент времени сразу после коммутации.
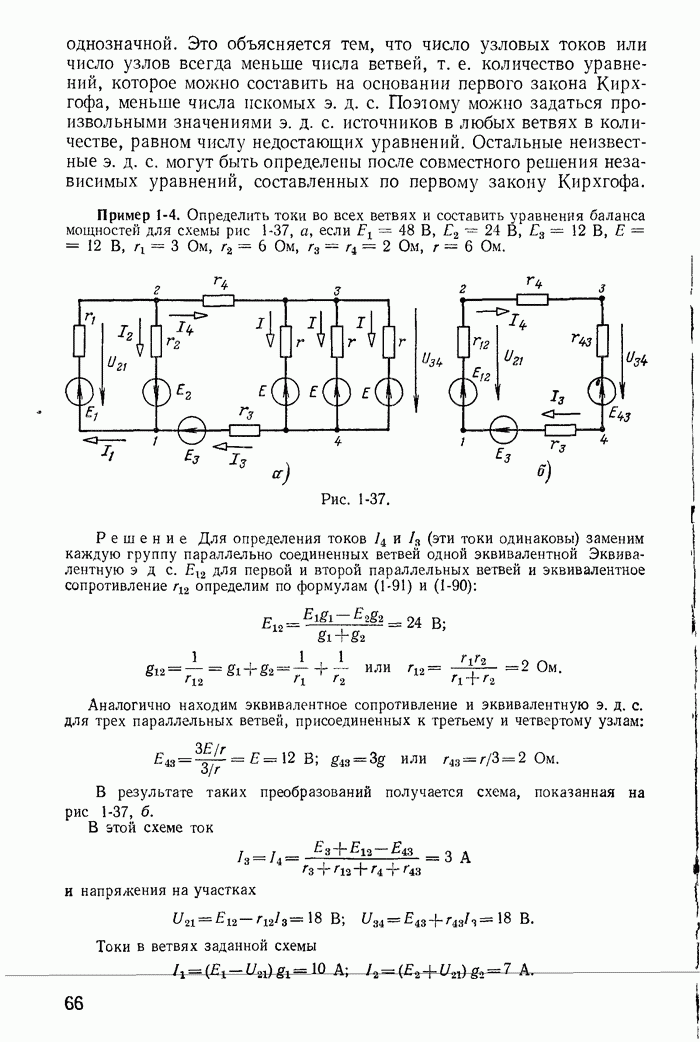
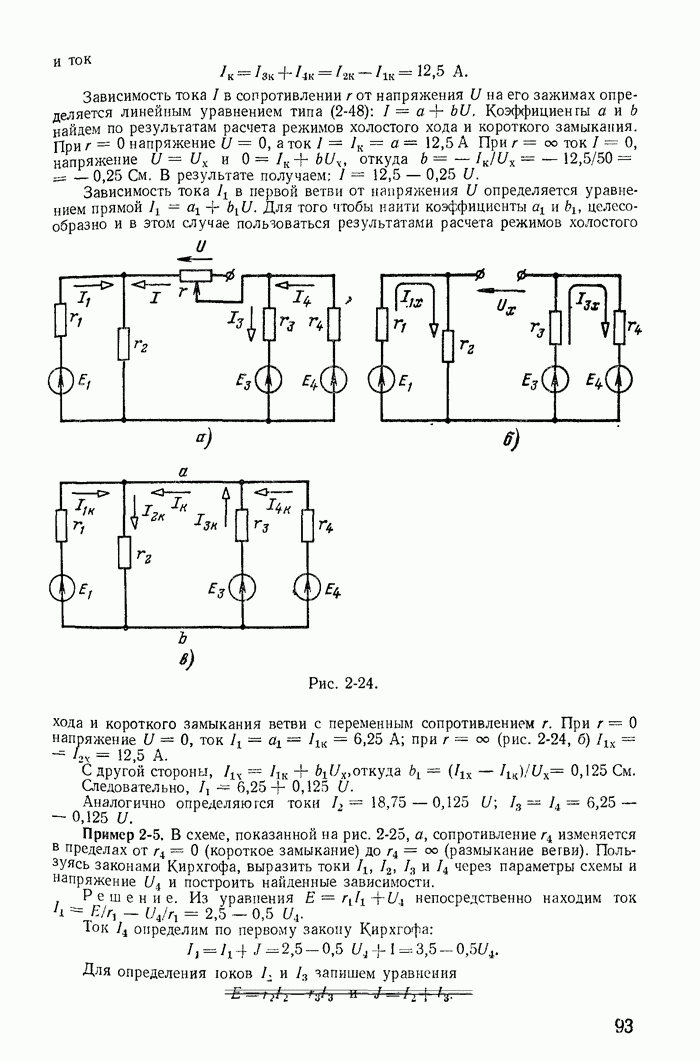
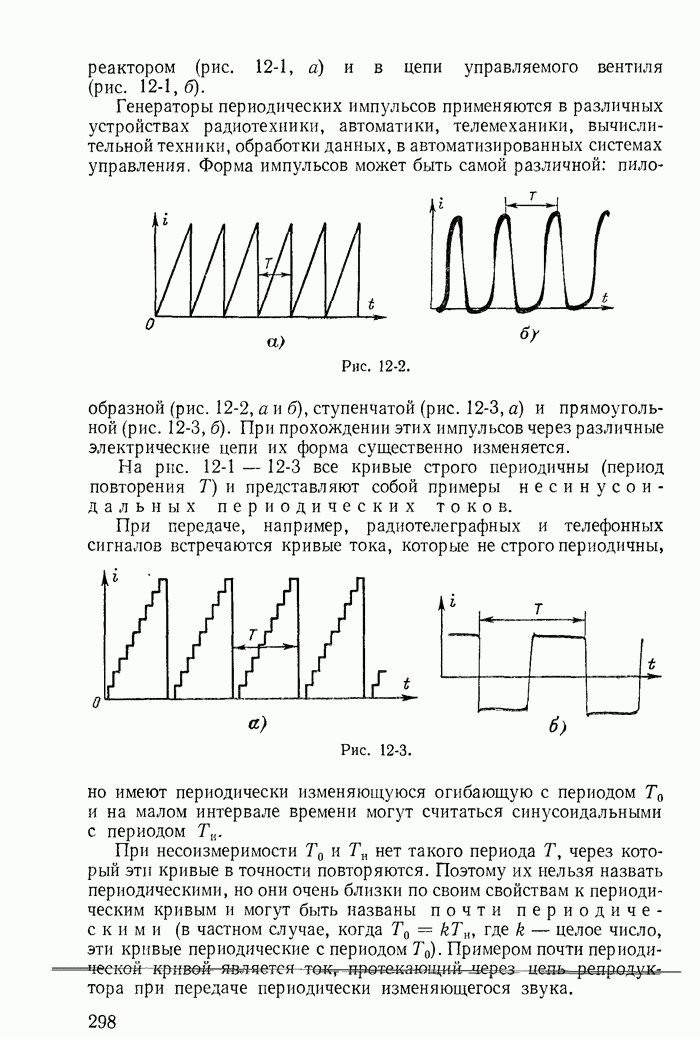
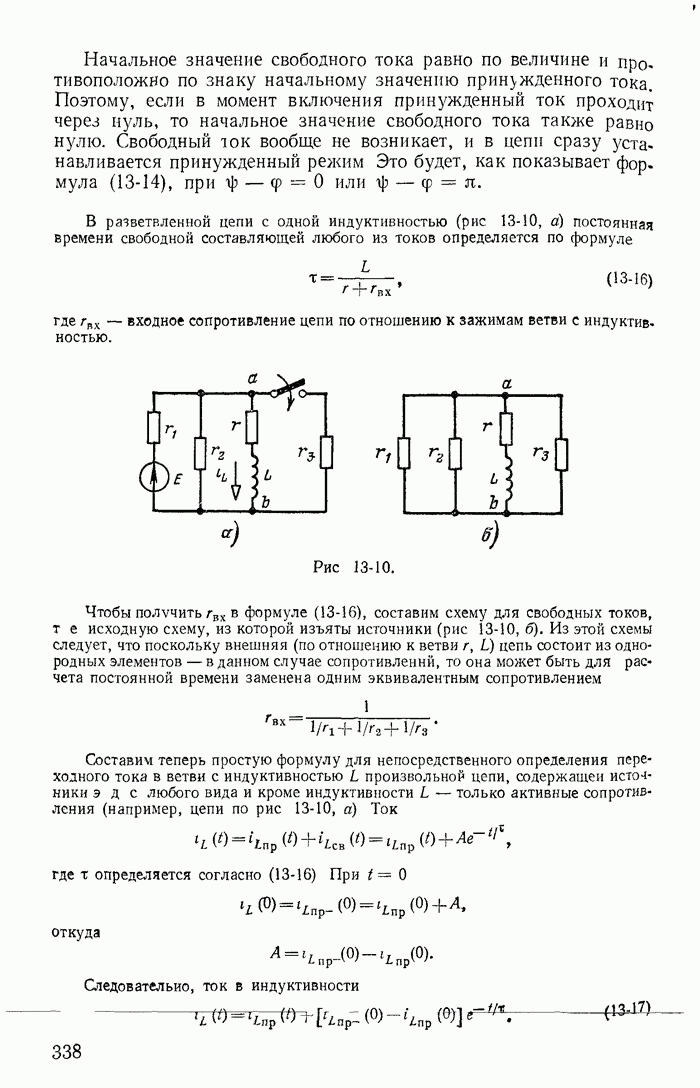
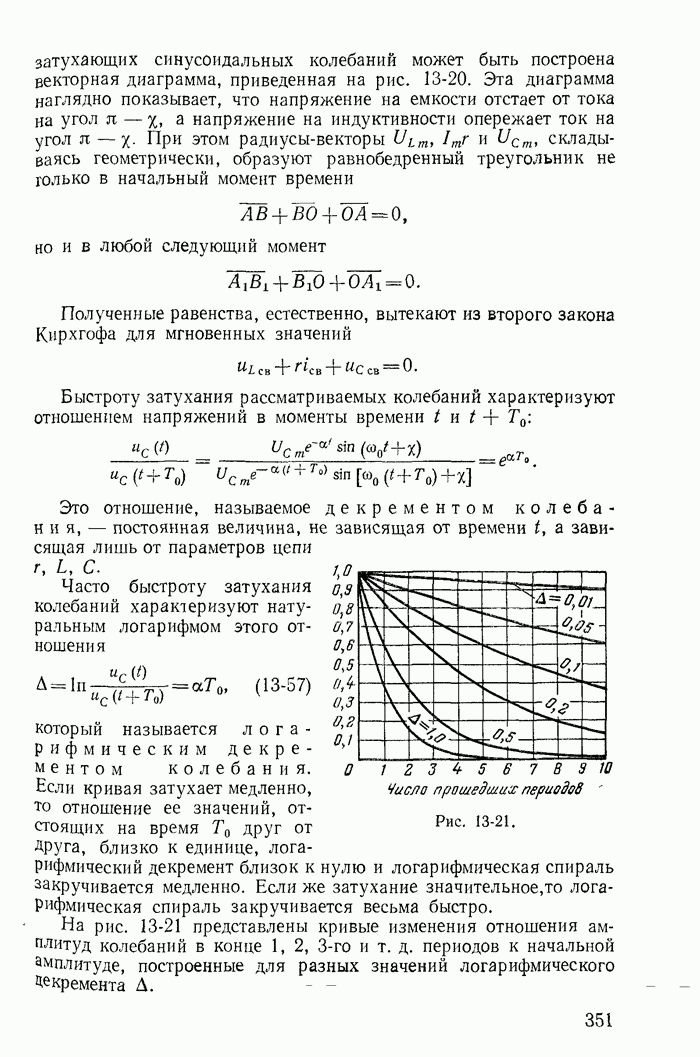
Рассмотрим теперь такие цепи и их режимы, для которых законы коммутации (13-91) не соблюдаются, и прежде всего процессы при отключении ветвей в некоторых цепях с индуктивностями. Например, пусть в цепи, питаемой от источника постоянной э. д. с. с напряжением U (рис. 13-38), мгновенно отключается ветвь с сопротивлением 

Рис. 13-38.
Токи во всех ветвях непосредственно перед коммутацией  легко определяются. После коммутации ток i в контуре, составленном f из первой
легко определяются. После коммутации ток i в контуре, составленном f из первой  и второй
и второй  ветвей, может быть определен из дифференциального уравнения
ветвей, может быть определен из дифференциального уравнения
 (13-92)
(13-92)
решение которого известно:
 (13-93)
(13-93)
где  .
.
Для определения постоянной А нельзя воспользоваться первой из формул (13-91), ибо до отключения ветви с сопротивлением  токи
токи

были различны, а после ее отключения они, очевидно, одинаковы, и, в частности, в первый момент после коммутации  . Значит, токи
. Значит, токи  в момент отключения рубильника
в момент отключения рубильника
должны измениться скачком, что приведет к возникновению бесконечно больших напряжений на индуктивностях. Но так как токи во всех ветвях схемы рис. 13-38 конечны, то для промежутка коммутации  до
до  алгебраическая сумма бесконечно больших напряжений на индуктивностях и напряжений на сопротивлениях должна уравновеситься приложенным напряжением
алгебраическая сумма бесконечно больших напряжений на индуктивностях и напряжений на сопротивлениях должна уравновеситься приложенным напряжением

Интегрируя это равенство за промежуток коммутации, т. е. от  до
до  и учитывая, что ввиду конечности правой части при
и учитывая, что ввиду конечности правой части при  и стремления промежутка интегрирования к нулю интеграл от правой части равен нулю, получим:
и стремления промежутка интегрирования к нулю интеграл от правой части равен нулю, получим:
 (13-94)
(13-94)
Перепишем (13-94) так:
 (13-95)
(13-95)
или

или
 (13-966)
(13-966)
Из равенства (13-966) следует, что потокосцепление контура  составленного из первой и второй катушек (иначе говоря, сумма потокосцеплений с обеими катушками), до и после отключения ветви осталось неизменным:
составленного из первой и второй катушек (иначе говоря, сумма потокосцеплений с обеими катушками), до и после отключения ветви осталось неизменным:

Отсюда находим:
 (13.98)
(13.98)
Далее из (13-93) — постоянную

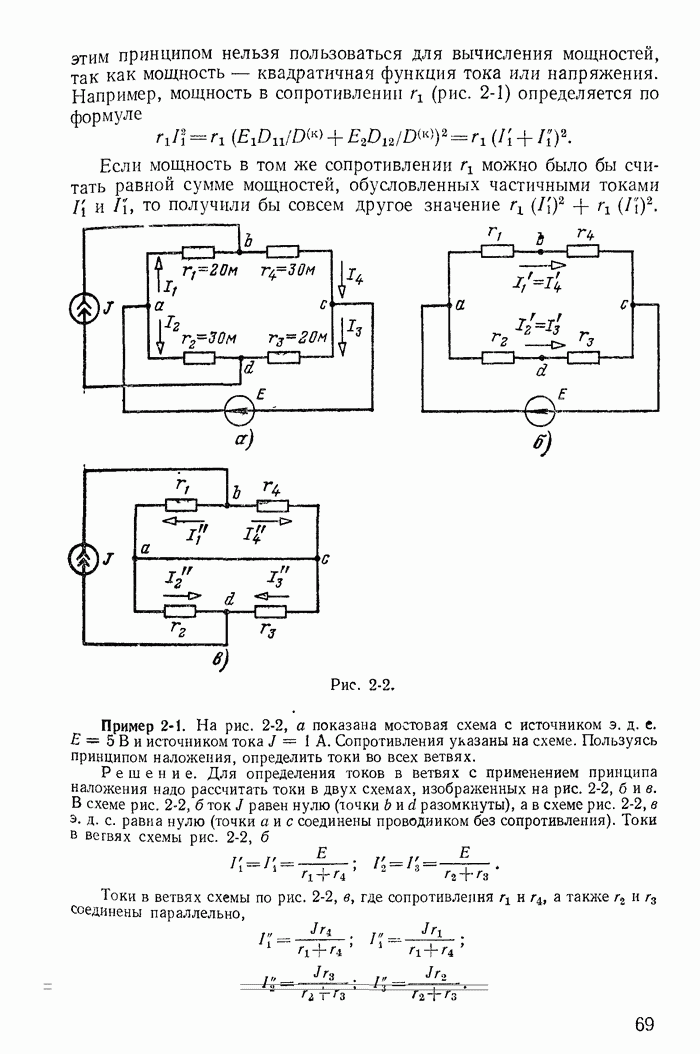
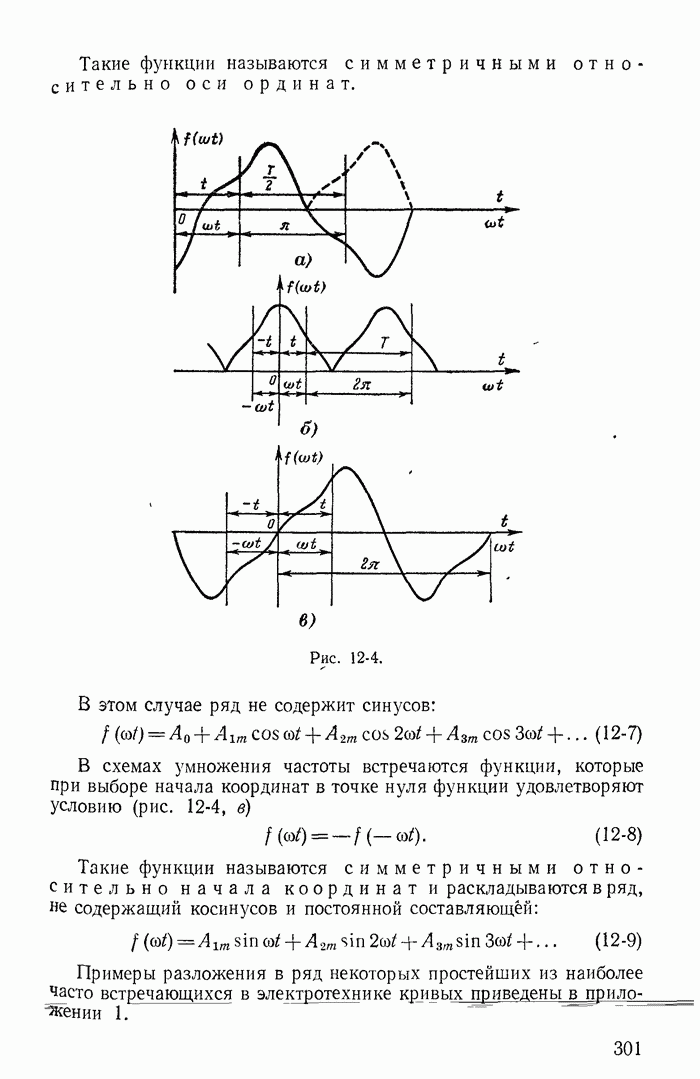
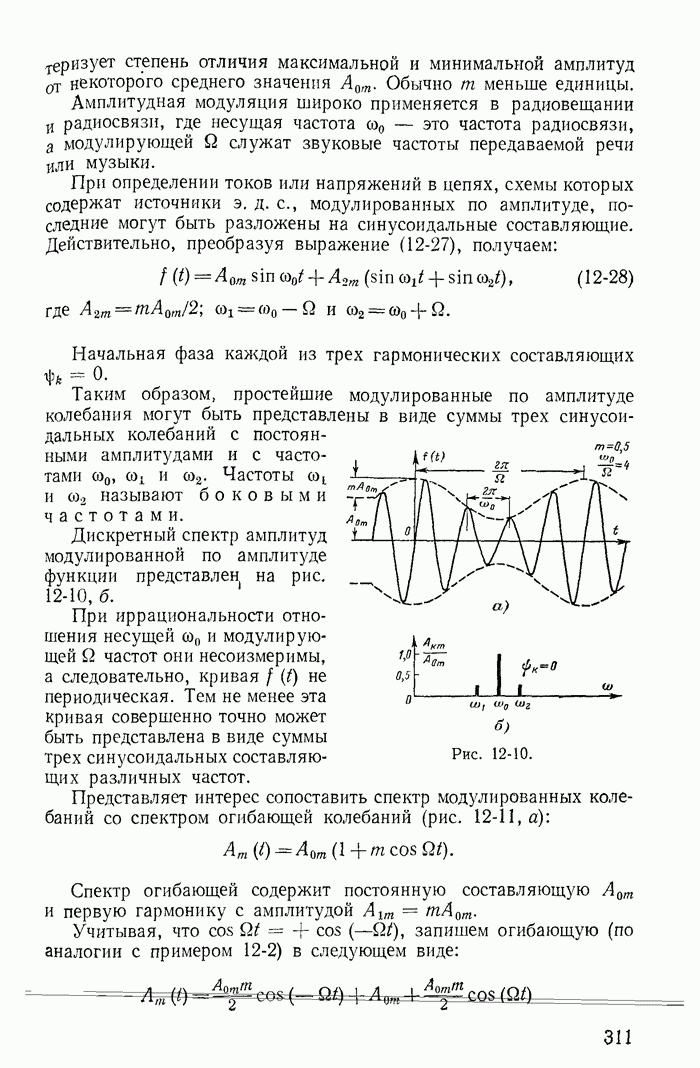
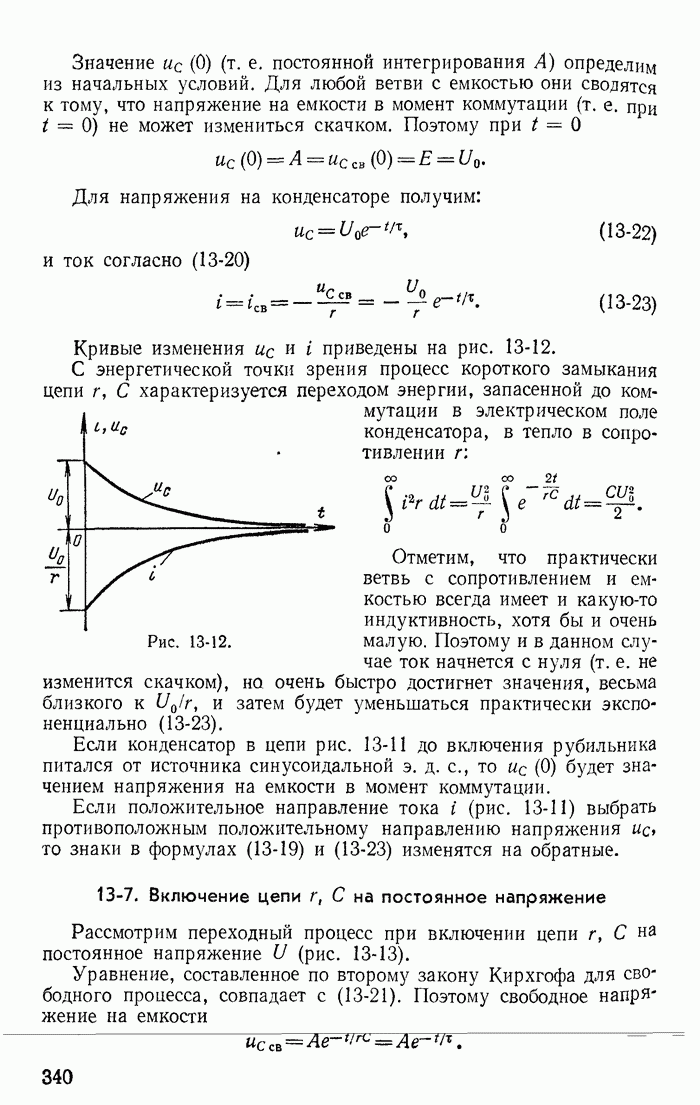
Следует иметь в виду, что бесконечно большие напряжения на катушках  противоположных знаков (рис. 13-39 построен в предположений, что
противоположных знаков (рис. 13-39 построен в предположений, что  ) появились вследствие предположения о том, что коммутация произошла за бесконечно малый промежуток времени Эти импульсы напряжения имеют бесконечно малую длительность. Но
) появились вследствие предположения о том, что коммутация произошла за бесконечно малый промежуток времени Эти импульсы напряжения имеют бесконечно малую длительность. Но
интегралы от этих импульсов (13-94) имеют конечные значения и равны приращениям и  потокосцеплений каждой из катушек. На том же рис. 13-39 показано, что токи в катушках при
потокосцеплений каждой из катушек. На том же рис. 13-39 показано, что токи в катушках при  о изменяются скачком и ток
о изменяются скачком и ток  , протекающий в обеих катушках после отключения ветви с сопротивлением
, протекающий в обеих катушках после отключения ветви с сопротивлением  изменяется в соответствии с постоянной времени
изменяется в соответствии с постоянной времени  и стремится к величине
и стремится к величине 
Подчеркнем, что разность энергий, запасенных в магнитных полях обеих катушек до коммутации,
 (13.100)
(13.100)
и после коммутации
 (13-101)
(13-101)
т. е.

положительна и расходуется на выделение тепла в сопротивлении искры или дуги, которая появится между контактами выключателя, и на возможное здесь излучение.

Рис. 13-39.
При решении задачи была принята идеализация процесса выключения, т. е. мгновенная коммутация. На самом деле она происходит хотя и весьма быстро, но за конечное время  . При этом в сопротивлении возникающей между контактами выключателя электрической искре и расходуется часть энергии AW. Кроме того, катушки
. При этом в сопротивлении возникающей между контактами выключателя электрической искре и расходуется часть энергии AW. Кроме того, катушки  обладают распределенной емкостью между витками и между расходящимися контактами выключателя существует емкость, что приводит к образованию сложного колебательного контура, который может излучать энергию (на высокой частоте), на что расходуется другая часть энергии
обладают распределенной емкостью между витками и между расходящимися контактами выключателя существует емкость, что приводит к образованию сложного колебательного контура, который может излучать энергию (на высокой частоте), на что расходуется другая часть энергии  . Если учесть все эти процессы, то никакие бесконечно большие напряжения на катушках не возникнут и токи в них не будут изменяться скачком, т. е. будут справедливы законы коммутации (13-91), сформулированные выше, в § 13-1.
. Если учесть все эти процессы, то никакие бесконечно большие напряжения на катушках не возникнут и токи в них не будут изменяться скачком, т. е. будут справедливы законы коммутации (13-91), сформулированные выше, в § 13-1.
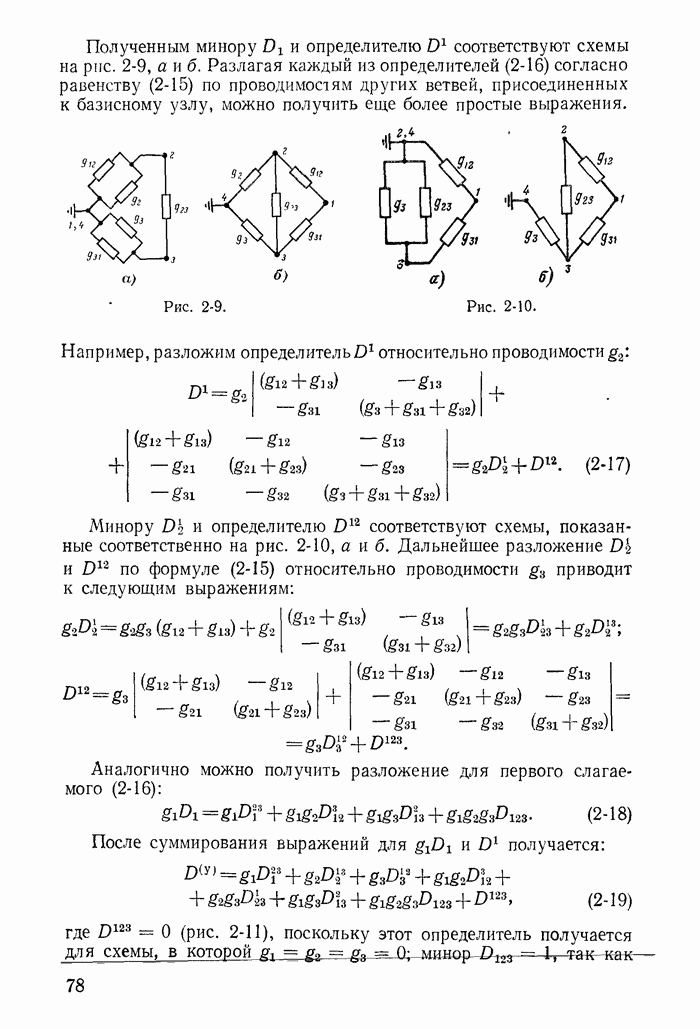
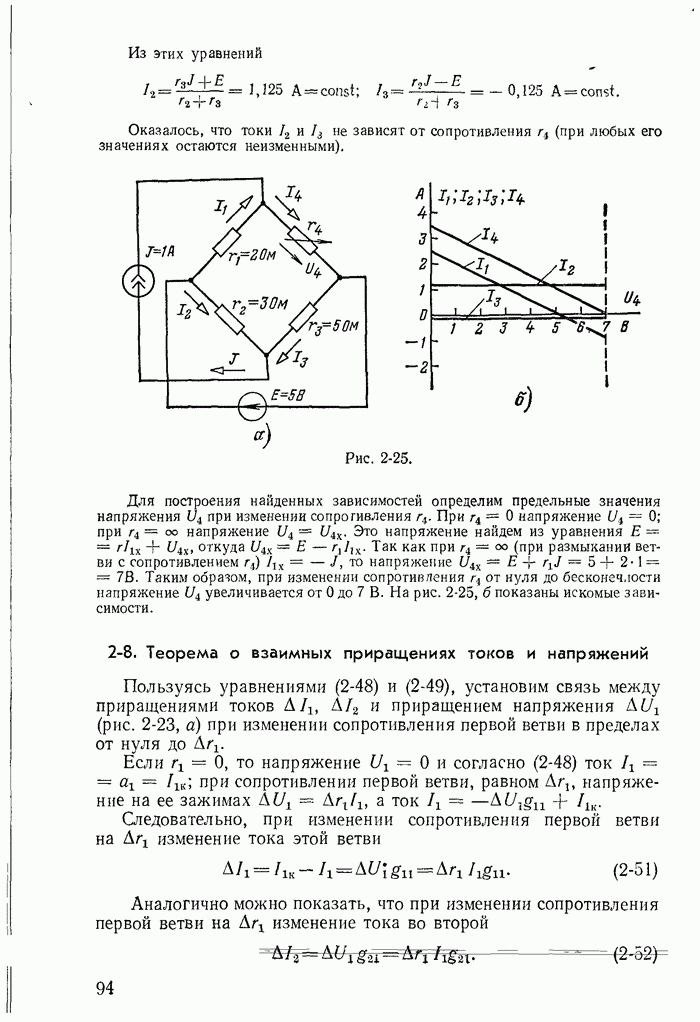
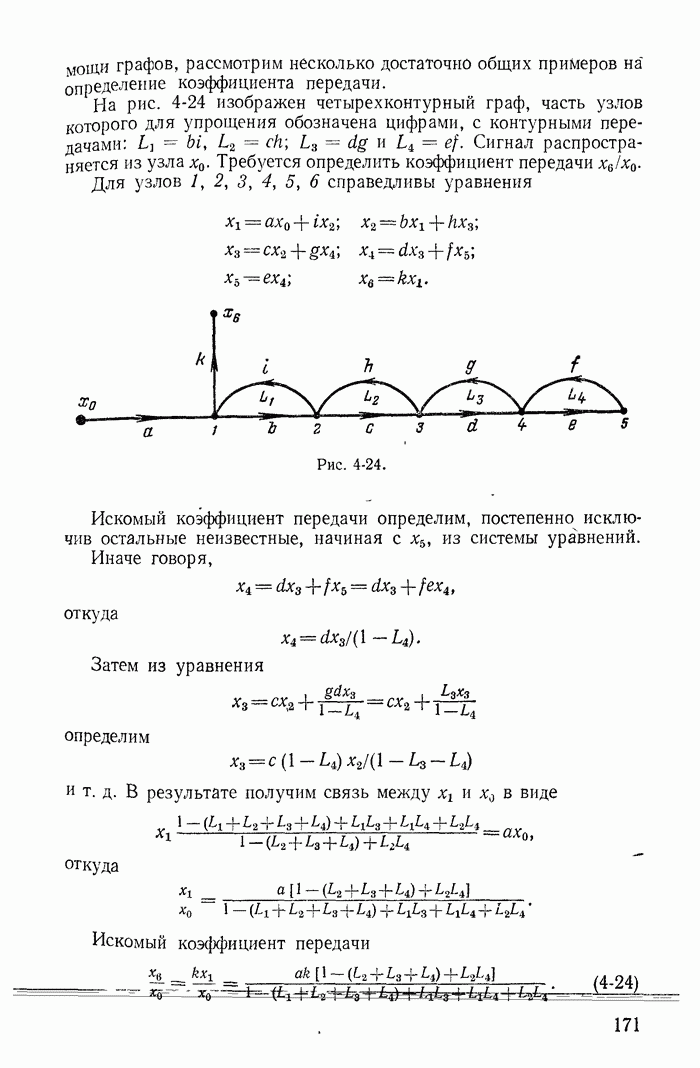
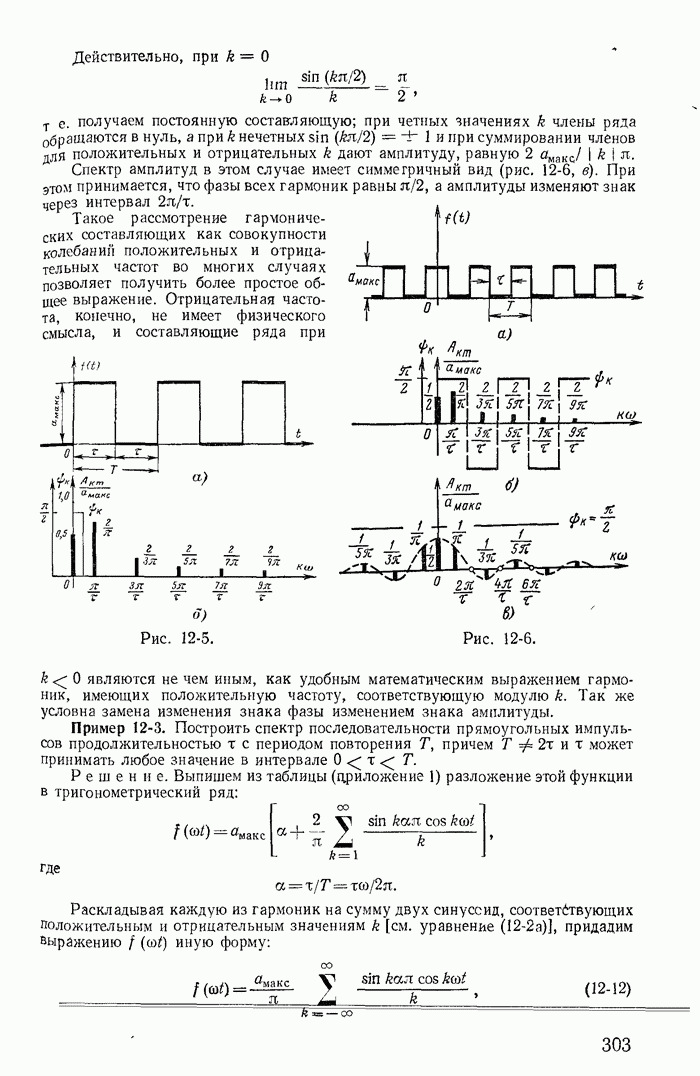
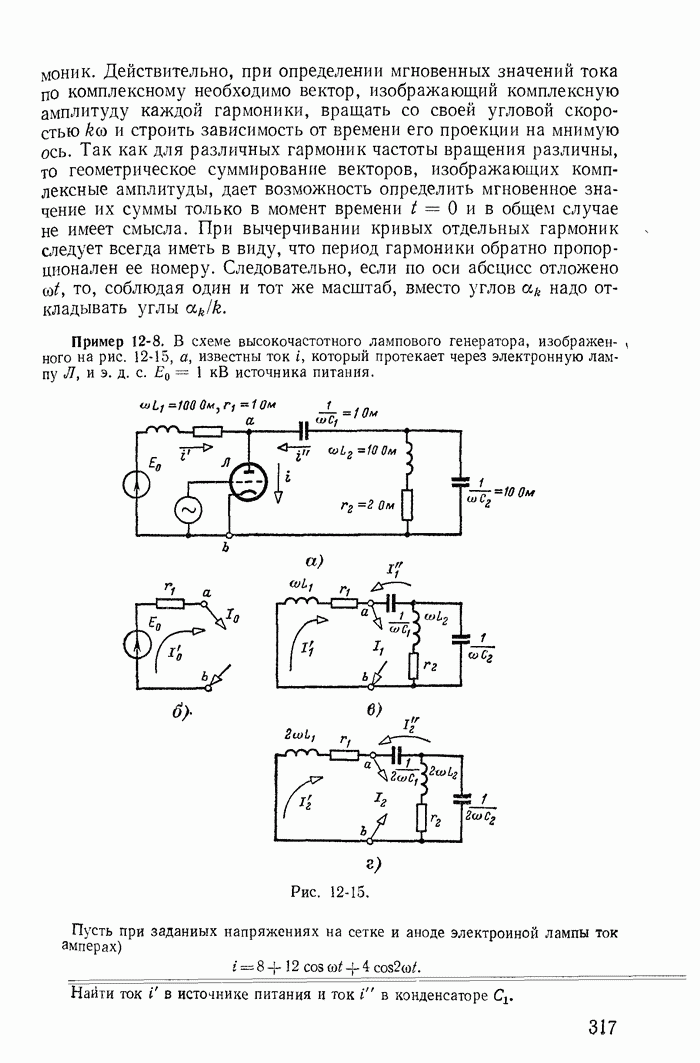
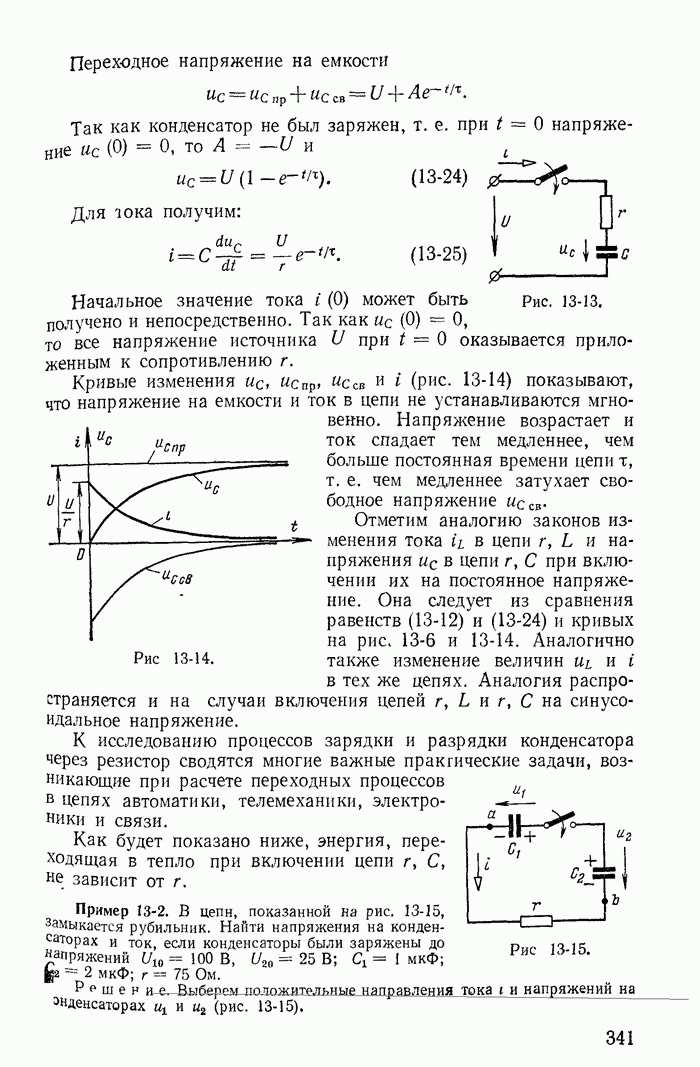
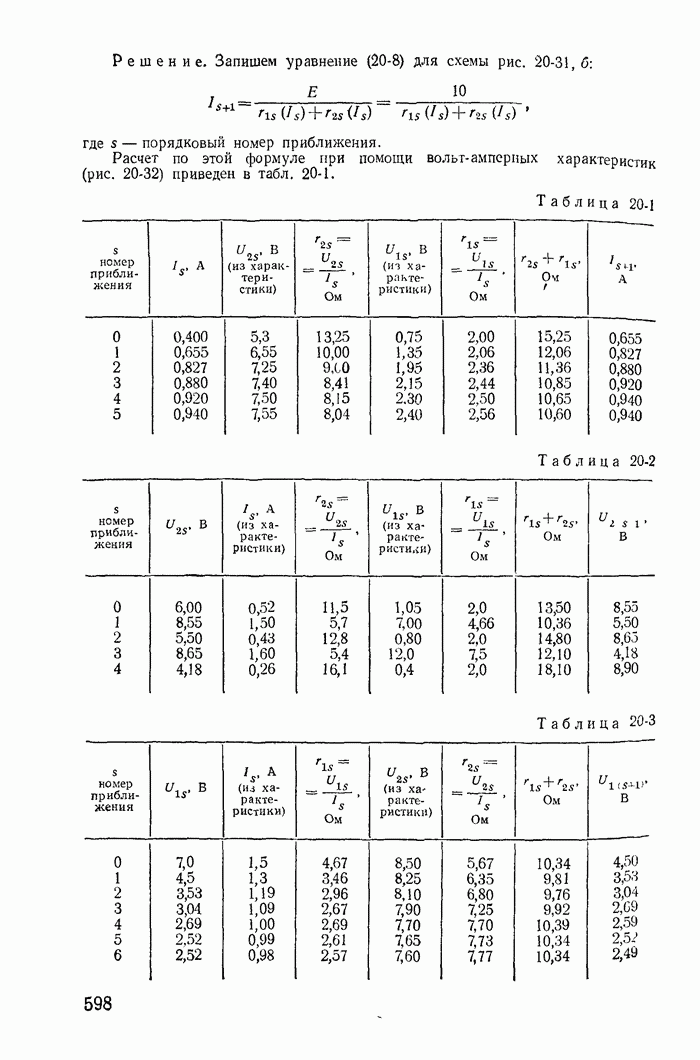
Интересно отметить, что при учете сопротивлений катушек закон коммутации для токов получается из более общего закона о неизменности в момент коммутации потокосцеплений контуров. Покажем это на примере схемы рис. 13-40.
Токи до коммутации:
 (13-103)
(13-103)
Потокосцепления первого контура:
а) до коммутации
 (13-104)
(13-104)
б) в момент коммутации
 (13-105)
(13-105)
Приравнивая их, получаем:
 (13-106)
(13-106)
Потокосцепления второго контура:

Рис. 13-40.
а) до коммутации (полагаем, что в состав второго контура до коммутации входит рубильник, сопротивление которого равно бесконечности, а индуктивность равна нулю)
 (13-107)
(13-107)
б) в момент коммутации
 (13-108)
(13-108)
Приравнивая их, получаем:
 (13-109)
(13-109)
Первый закон Кирхгофа для узла А в момент коммутации
 (13-110)
(13-110)
Решаем совместно уравнения (13-106), (13-109) и (13-110) относительно токов 
 (13-111)
(13-111)
Учитывая (13-103), получаем:
 (13-112)
(13-112)
т. e. именно те же соотношения, которые дал бы закон коммутации 13-91), сформулированный выше, в § 13-1.
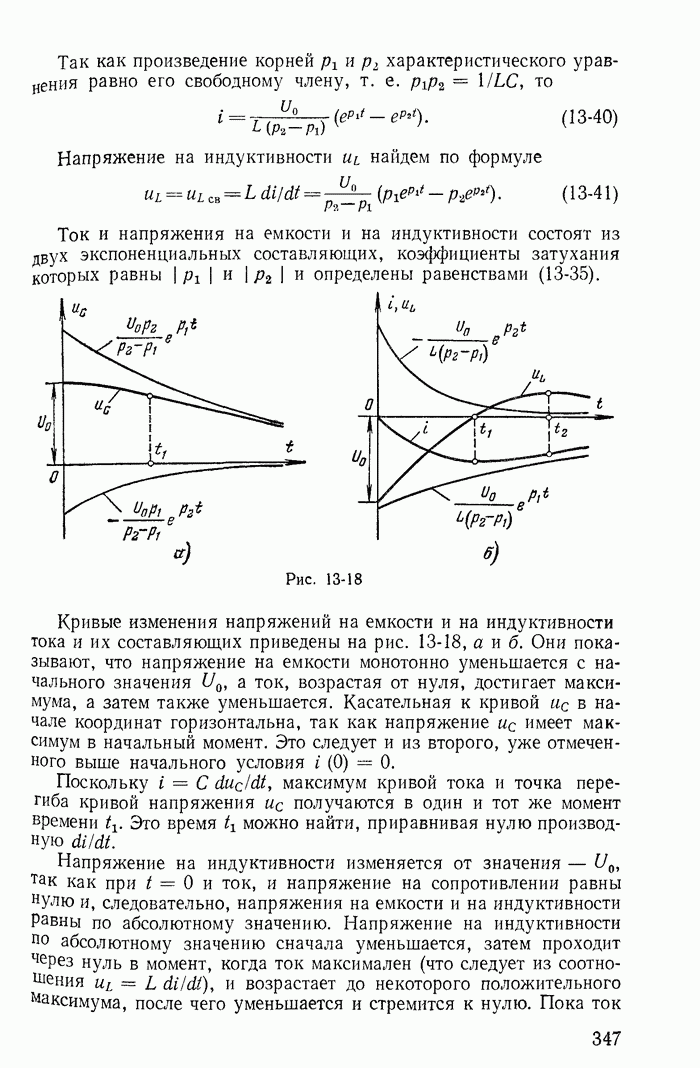
Легко проверить (рекомендуется читателю), что тот же результат получается для схемы рис. 13-41 и для любых схем с ветвями  , при подключении к ним новых ветвей
, при подключении к ним новых ветвей 
Понимая под потокосцеплением контура алгебраическую сумму ]потокосцеплений всех входящих в него катушек, первый закон коммутации будем формулировать как обобщенный закон коммутации:
потокосцепление любого замкнутого контура в момент коммутации,  равно алгебраической сумме потокосцеплений всех входящих в него катушек, которые последние имели непосредственно до коммутации
равно алгебраической сумме потокосцеплений всех входящих в него катушек, которые последние имели непосредственно до коммутации  Некоторые из этих катушек перед комму, тацией могли одного замкнутого контура и не составлять, а образовали его лишь после коммутации.
Некоторые из этих катушек перед комму, тацией могли одного замкнутого контура и не составлять, а образовали его лишь после коммутации.
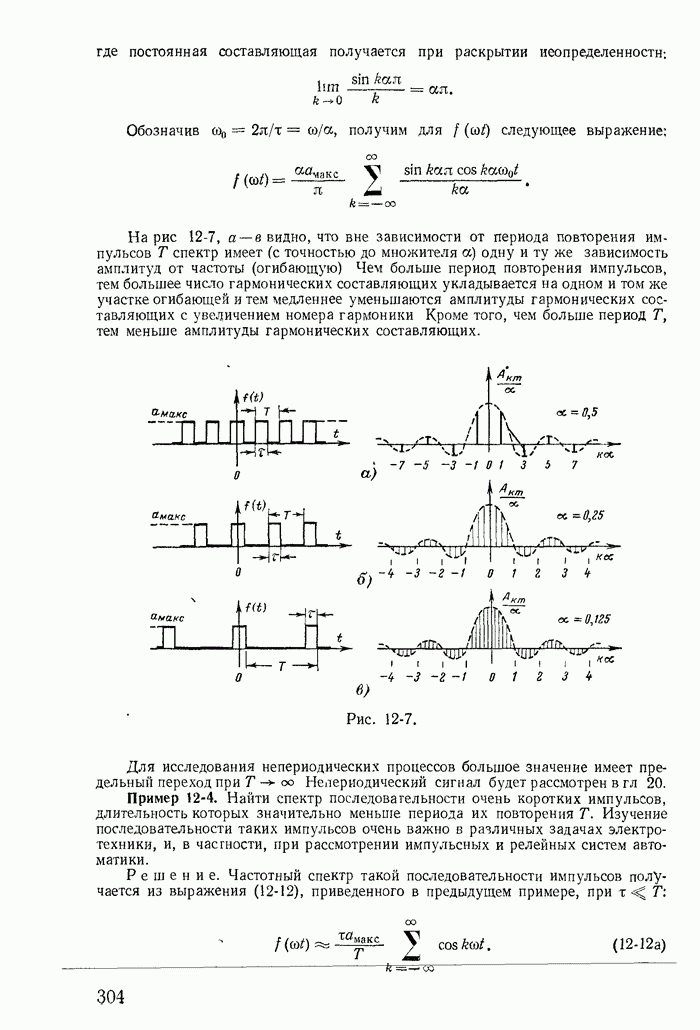
Например, если в рассмотренной выше схеме рис. 13-40 считать что в катушке  до коммутации был ток, то при подключении ее в момент
до коммутации был ток, то при подключении ее в момент  к контуру, образованному катушками
к контуру, образованному катушками  нужно считать, что в этот момент рубильник
нужно считать, что в этот момент рубильник  мгновенно включается, рубильник
мгновенно включается, рубильник  мгновенно отключается (рис. 13-42).
мгновенно отключается (рис. 13-42).

Рис. 13-41.

Рис. 13-42.
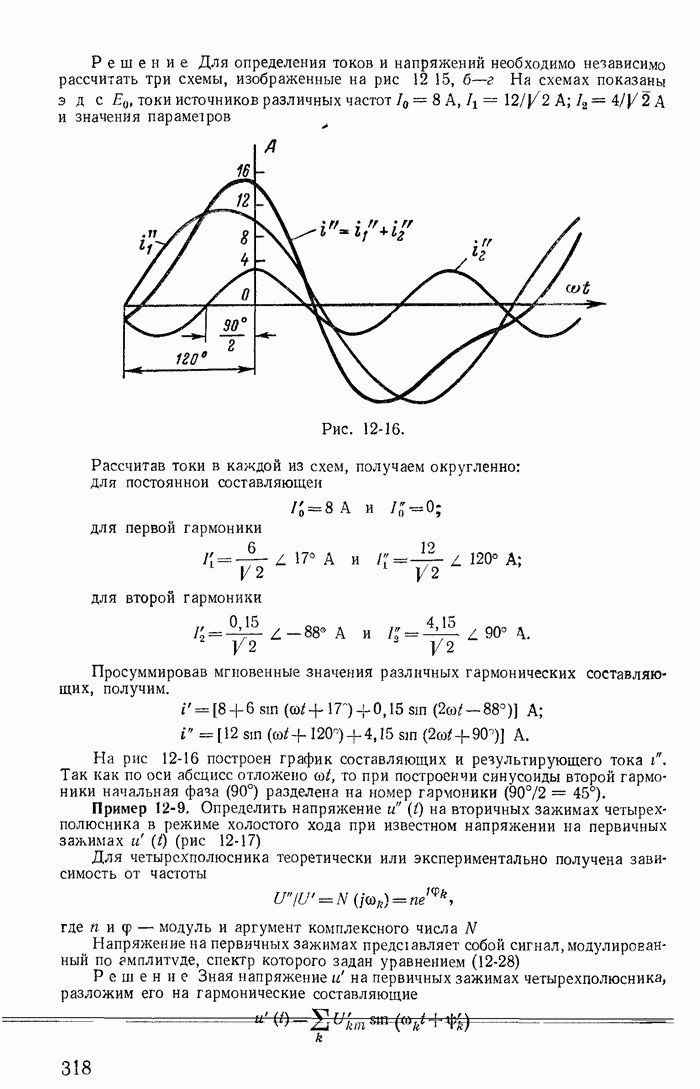
Докажем применительно к рассматриваемой схеме (рис. 13-42) первый обобщенный закон коммутации. Для этого рассмотрим контур 2, образованный катушками  в момент
в момент  , т. е. в момент его образования. Так как второй закон Кирхгофа справедлив для любого момента времени, то имеем:
, т. е. в момент его образования. Так как второй закон Кирхгофа справедлив для любого момента времени, то имеем:

или

Интегрируя последнее равенство от  до
до  на основании сказанного выше получаем:
на основании сказанного выше получаем:

Перенося все токи для момента  в левую часть равенства и учитывая, что
в левую часть равенства и учитывая, что  будем иметь:
будем иметь:

Легко видеть, что левая часть последнего равенства представляет собой результирующее потокосцепление рассматриваемого контура 2 до коммутации, как если бы в этот контур входила катушка r 13, что и доказывает приведенный выше первый обобщенный закон коммутации.
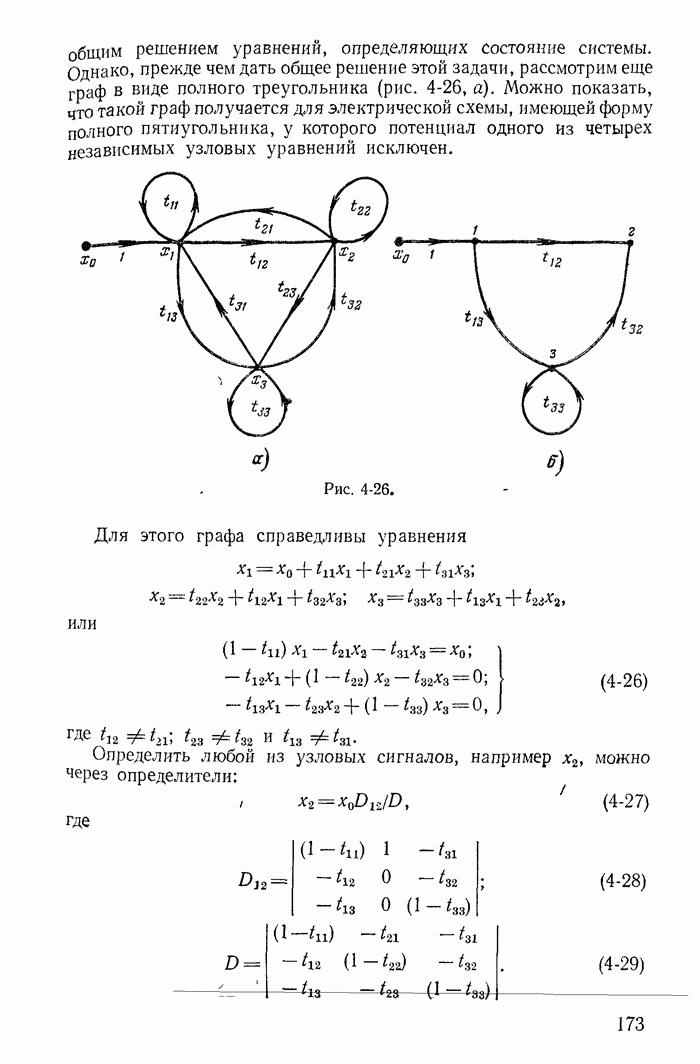
Решим задачу об определении значений токов в катушках в момент коммутации  учитывая в общем случае, что все они связаны взаимными индуктивностями (рис. 13-42).
учитывая в общем случае, что все они связаны взаимными индуктивностями (рис. 13-42).
Запишем потокосцепления  контуров перед коммутацией
контуров перед коммутацией  считая, как обычно,
считая, как обычно,  и понимая под
и понимая под  в соответствии с данным выше определением алгебраическую сумму потокосцеплений катушек 1 и 3, которые непосредственно образуют замкнутый контур 2 после коммутации:
в соответствии с данным выше определением алгебраическую сумму потокосцеплений катушек 1 и 3, которые непосредственно образуют замкнутый контур 2 после коммутации:
 (13-113)
(13-113)
Токи  в случае любых
в случае любых  (постоянных, гармонических и т. д.) находятся из уравнений второго закона Кирхгофа:
(постоянных, гармонических и т. д.) находятся из уравнений второго закона Кирхгофа:
 (13-115)
(13-115)
Далее запишем потокосцепления контуров 1 и 2 в момент коммутации  , учитывая, что для узла А по первому закону Кирхгофа
, учитывая, что для узла А по первому закону Кирхгофа
 (13-117)
(13-117)
Токи  находятся из уравнения
находятся из уравнения  закона Кирхгофа:
закона Кирхгофа:
 (13-119)
(13-119)
Приравнивая потокосцепления
 (13-121)
(13-121)
получаем два уравнения для определения 
Отметим, что значения  которые получаются решением уравнений (13-121), не изменятся, если вместо контура 2 взять контур 3, образованный катушками 2 и 3. Для доказательства запишем потокосцепления третьего контура (рис. 13-42) до и в момент коммутации.
которые получаются решением уравнений (13-121), не изменятся, если вместо контура 2 взять контур 3, образованный катушками 2 и 3. Для доказательства запишем потокосцепления третьего контура (рис. 13-42) до и в момент коммутации.
 (13-122)
(13-122)
Теперь придется для определения  решить совместно два следующих уравнения:
решить совместно два следующих уравнения:
 (13-123)
(13-123)
Легко видеть, что на основании (13-122), (13-117) и (13-118) получаем:
 (13-124)
(13-124)
и соответственно на основании (13-122), (13-113) и (13-114) имеем

так что система уравнений (13-123) приводится к системе уравнений

которая в силу первого из уравнений (13-126) тождественна системе уравнений (13-121), что и доказывает сделанное выше утверждение
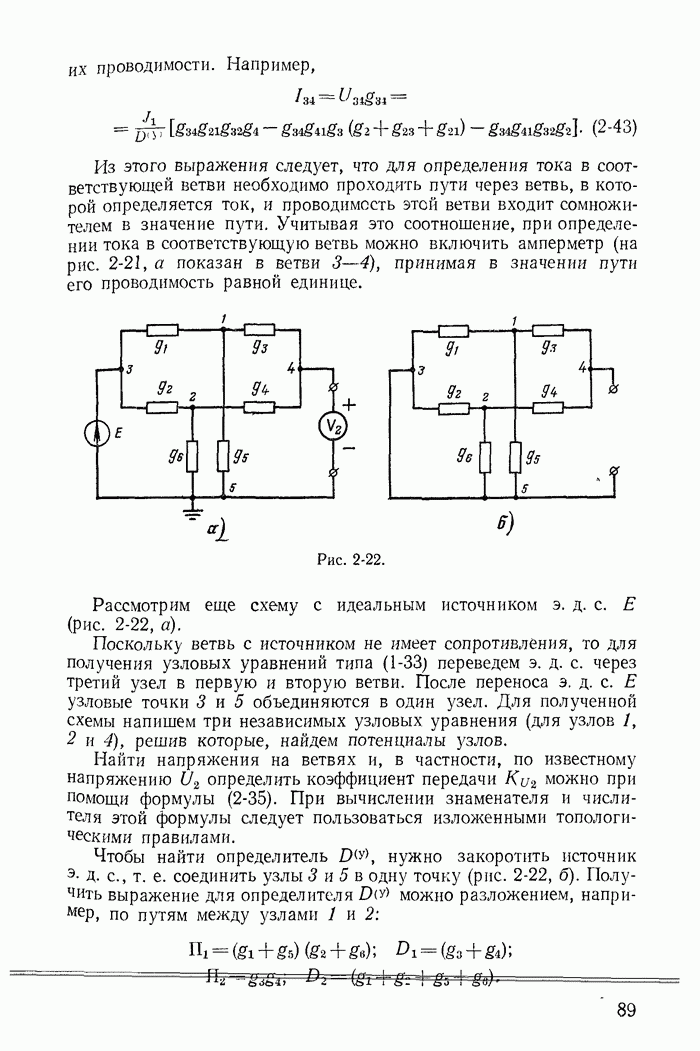
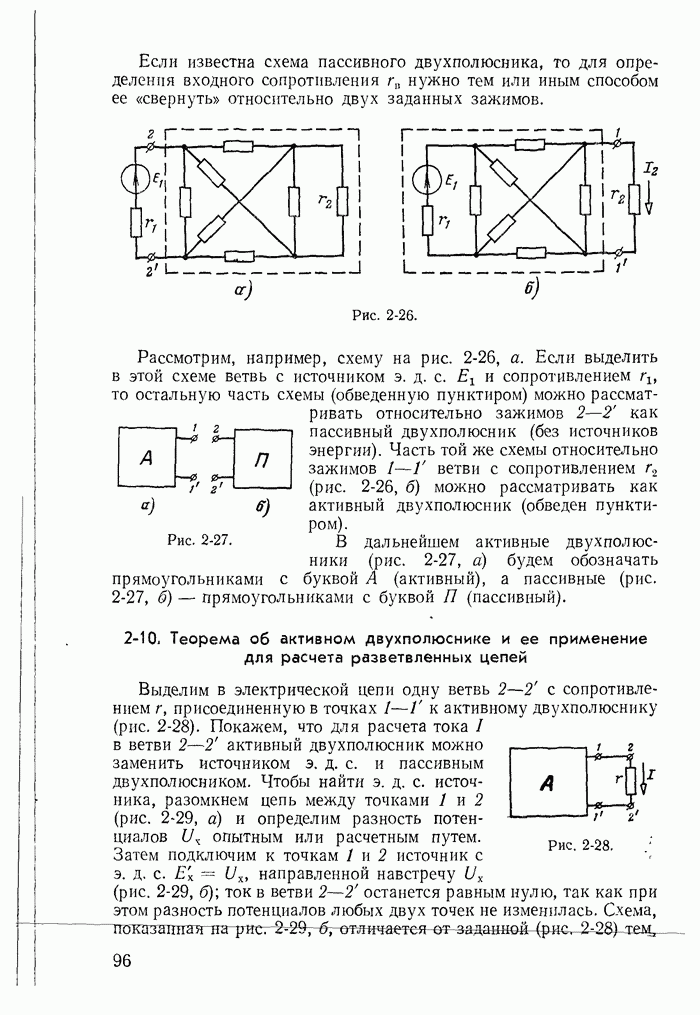
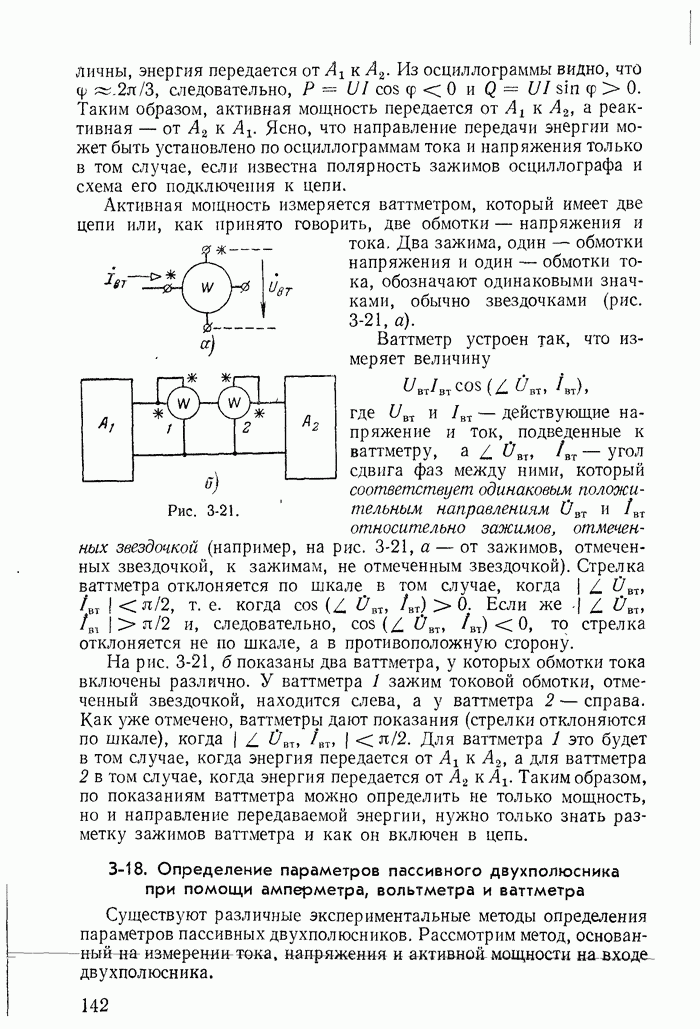
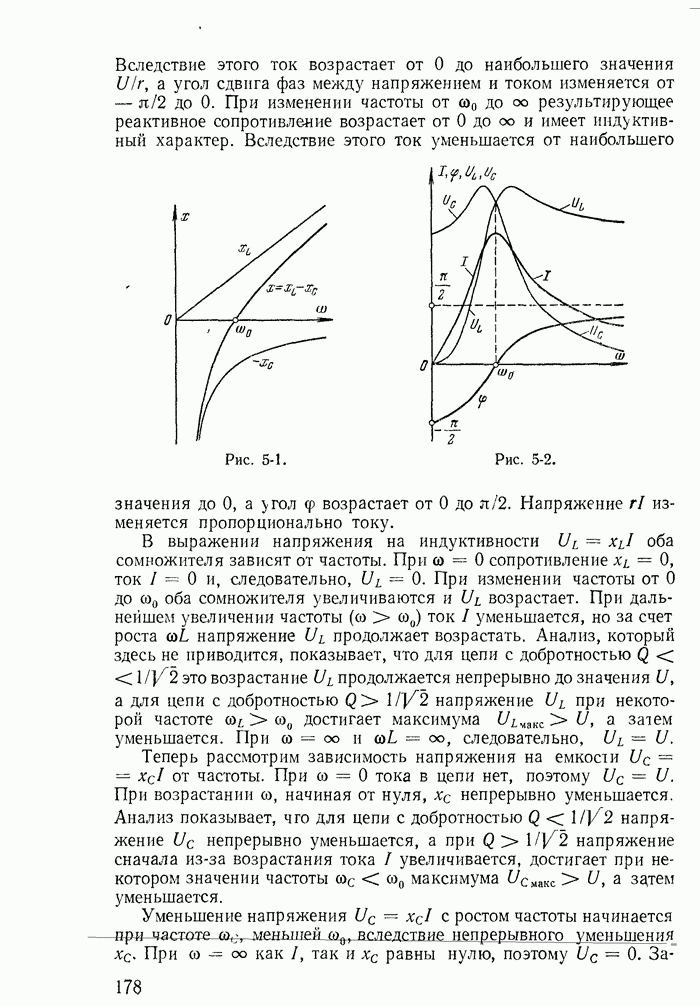
Рассмотрим процессы, возникающие при одновременном включении двух заряженных до разных напряжений конденсаторов  к заряженному до напряжения U конденсатору
к заряженному до напряжения U конденсатору  (рис. 13-43).
(рис. 13-43).
Полагаем, что сопротивления  проводов, соединяющих конденсаторы
проводов, соединяющих конденсаторы  пренебрежимо малы. Поэтому постоянные времени, обусловленные ими, также ничтожны. При этих условиях напряжения на всех трех конденсаторах в момент включения рубильника могут изменяться скачком и через них могут проходить бесконечно большие токи. Все три конденсатора до включения рубильника были заряжены до различных напряжений на
пренебрежимо малы. Поэтому постоянные времени, обусловленные ими, также ничтожны. При этих условиях напряжения на всех трех конденсаторах в момент включения рубильника могут изменяться скачком и через них могут проходить бесконечно большие токи. Все три конденсатора до включения рубильника были заряжены до различных напряжений на  и имели заряды
и имели заряды 

Рис. 13-43.
Токи конденсаторов будут существовать только в течение бесконечно малого промежутка времени от  — до
— до  Так как напряжение источника U и сопротивление последовательного участка цепи
Так как напряжение источника U и сопротивление последовательного участка цепи  конечны, то суммарный ток i должен оставаться конечным и импульсы токов в трех параллельно соединенных конденсаторах должны взаимно уравновешиваться, т. е.
конечны, то суммарный ток i должен оставаться конечным и импульсы токов в трех параллельно соединенных конденсаторах должны взаимно уравновешиваться, т. е.

Интегрируя это равенство по времени от  — до
— до 

или

или
 (13-128)
(13-128)
или
 (13-129)
(13-129)
приходим к равенству
 (13-130)
(13-130)
Отсюда следует, что изменение зарядов на всех параллельно включенных конденсаторах за время коммутации равно нулю, т. е. сумма зарядов конденсаторов перед коммутацией  равна сумме их зарядов непосредственно после коммутации
равна сумме их зарядов непосредственно после коммутации  — закон сохранения заряда. Этот же результат получается и из (13-127),
— закон сохранения заряда. Этот же результат получается и из (13-127),
если учесть, что после коммутации  напряжения на всех параллельно включенных конденсаторах равны:
напряжения на всех параллельно включенных конденсаторах равны:
 (13-131)
(13-131)
На основании (13-128) и (13-131) получаем:
 (13-132)
(13-132)
откуда
 (13-133)
(13-133)
При этом все три конденсатора заменяются одним с емкостью  и напряжение
и напряжение  на нем после коммутации определяется дифференциальным уравнением
на нем после коммутации определяется дифференциальным уравнением
 (13-134)
(13-134)
решение которого известно:
 (13-135)
(13-135)
где

На основании сказанного выше 
Тогда из (13-135) получаем
 (13-136)
(13-136)
и ток

Легко показать, что энергия, запасенная в конденсаторах до коммутации,
 (13-138)
(13-138)
больше энергии электрического поля эквивалентного конденсатора С после коммутации
 (13-139)
(13-139)
а избыток ее
 (13-140)
(13-140)
перейдет в тепло в сопротивлениях контактов рубильника, сопро тивлениях проводов и в энергию излучения сложного колебательного
контура, который получится, если учесть, что соединительные провода всегда имеют индуктивность, хотя и очень малую.
Подчеркнем, что при наличии сопротивлений во всех трех ветвях с конденсаторами напряжения на них в момент коммутации скачком не изменяются, токи в них остаются конечными, т. е. выполняется второй закон коммутации, сформулированный выше, в § 13-1.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ К ЧЕТВЕРТОМУ ИЗДАНИЮ
- ВВЕДЕНИЕ
- Раздел первый. ЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ С СОСРЕДОТОЧЕННЫМИ ПАРАМЕТРАМИ
- 1-1. Элементы электрических цепей и электрических схем
- 1-2. Эквивалентные схемы для источников энергии
- 1-3. Закон Ома для участка цепи с э. д. с.
- 1-4. Распределение потенциала вдоль неразветвленной электрической цепи
- 1-5. Баланс мощностей для простейшей неразветвленной цепи
- 1-6. Применение законов Кирхгофа для расчета разветвленных цепей
- 1-7. Метод узловых потенциалов
- 1-8. Метод контурных токов
- 1-9. Уравнения состояния цепи в матричной форме
- 1-10. Преобразование линейных электрических схем
- Глава вторая. ОСНОВНЫЕ СВОЙСТВА ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ПРИ ПОСТОЯННЫХ ТОКАХ И НАПРЯЖЕНИЯХ
- 2-2. Свойство взаимности
- 2-3. Входные и взаимные проводимости и сопротивления ветвей; коэффициенты передачи напряжений и токов
- 2-4. Применение топологических методов для расчета цепей
- 2-5. Топологические формулы и правила для определения передачи электрической цепи
- 2-6. Теорема о компенсации
- 2-7. Линейные соотношения между напряжениями и токами
- 2-8. Теорема о взаимных приращениях токов и напряжений
- 2-9. Общие замечания о двухполюсниках
- 2-10. Теорема об активном двухполюснике и ее применение для расчета разветвленных цепей
- 2-11. Передача энергии от активного двухполюсника к пассивному
- Глава третья. ОСНОВНЫЕ ПОНЯТИЯ О ЦЕПЯХ СИНУСОИДАЛЬНОГО ТОКА
- 3-2. Понятие о генераторах переменного тока
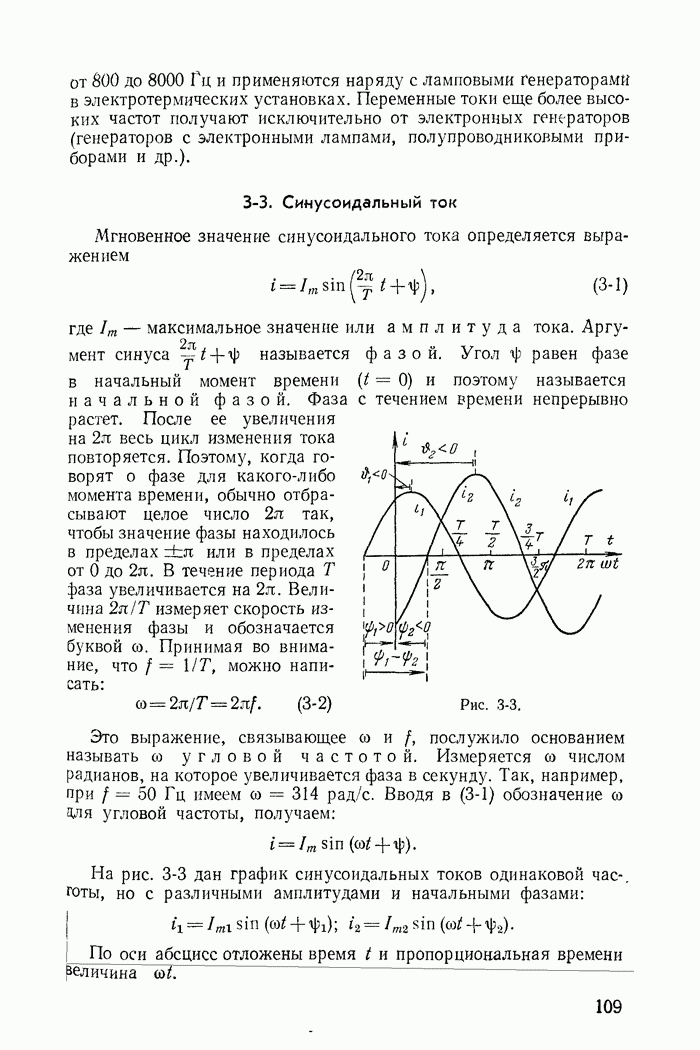
- 3-3. Синусоидальный ток
- 3-4. Действующие ток, э. д. с. и напряжение
- 3-5. Изображение синусоидальных функций времени векторами и комплексными числами
- 3-6. Сложение синусоидальных функций времени
- 3-7. Электрическая цепь и ее схема
- 3-8. Ток и напряжения при последовательном соединении сопротивления, Индуктивности и емкости
- 3-9. Сопротивления
- 3-10. Разность фаз напряжения и тока
- 3-11. Напряжение и токи при параллельном соединении сопротивления, индуктивности и емкости
- 3-12. Проводимости
- 3-13. Пассивный двухполюсник
- 3-14. Мощности
- 3-15. Мощности в сопротивлении, индуктивности и емкости
- 3-16. Баланс мощностей
- 3-17. Знаки мощностей и направление передачи энергии
- 3-18. Определение параметров пассивного двухполюсника при помощи амперметра, вольтметра и ваттметра
- 3-19. Условия передачи максимальной мощности от источника энергии к приемнику
- 3-20. Понятие о поверхностном эффекте и эффекте близости
- 3-21. Параметры и эквивалентные схемы конденсаторов
- 3-22. Параметры и эквивалентные схемы индуктивных катушек и резисторов
- Глава четвертая. РАСЧЕТ ЦЕПЕЙ ПРИ СИНУСОИДАЛЬНЫХ ТОКАХ
- 4-1. О применимости методов расчета цепей постоянного тока к расчетам цепей синусоидального тока
- 4-2. Последовательное соединение приемников
- 4-3. Параллельное соединение приемников
- 4-4. Смешанное соединение приемников
- 4-5. Сложные разветвленные цепи
- 4-6. Топографические диаграммы
- 4-7. Дуальность электрических цепей
- 4-8. Сигнальные графы и их применение для расчета цепей
- Глава пятая. РЕЗОНАНС В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ
- 5-2. Частотные характеристики неразветвленной цепи
- 5-3. Резонанс в цепи с двумя параллельными ветвями
- 5-4. Частотные характеристики параллельного контура
- 5-5. Понятие о резонансе в сложных цепях
- Глава шестая. ЦЕПИ С ВЗАИМНОЙ ИНДУКТИВНОСТЬЮ
- 6-2. Электродвижущая сила взаимной индукции
- 6-3. Последовательное соединение индуктивно связанных элементов цепи
- 6-4. Параллельное соединение индуктивно связанных элементов цепи
- 6-5. Расчеты разветвленных цепей при наличии взаимной индуктивности
- 6-6. Эквивалентная замена индуктивных связей
- 6-7. Передача энергии между индуктивно связанными элементами цепи
- 6-8. Трансформатор без стального сердечника (воздушный трансформатор)
- Глава седьмая. КРУГОВЫЕ ДИАГРАММЫ
- 7-1. Комплексные уравнения прямой и окружности
- 7-2. Круговые диаграммы для неразветвленной цепи и для активного двухполюсника
- 7-3. Круговые диаграммы для любой разветвленной цепи
- Глава восьмая. МНОГОПОЛЮСНИКИ И ЧЕТЫРЕХПОЛЮСНИКИ ПРИ СИНУСОИДАЛЬНЫХ ТОКАХ И НАПРЯЖЕНИЯХ
- 8-1. Четырехполюсники и их основные уравнения
- 8-2. Определение коэффициентов четырехполюсников
- 8-3. Режим четырехполюсника при нагрузке
- 8-4. Эквивалентные схемы четырехполюсников
- 8-5. Основные уравнения и эквивалентные схемы для активного четырехполюсника
- 8-6. Идеальный трансформатор как четырехполюсник
- 8-7. Эквивалентные схемы с идеальными трансформаторами для четырехполюсника
- 8-8. Эквивалентные схемы трансформатора со стальным магнитопроводом
- 8-9. Расчеты электрических цепей с трансформаторами
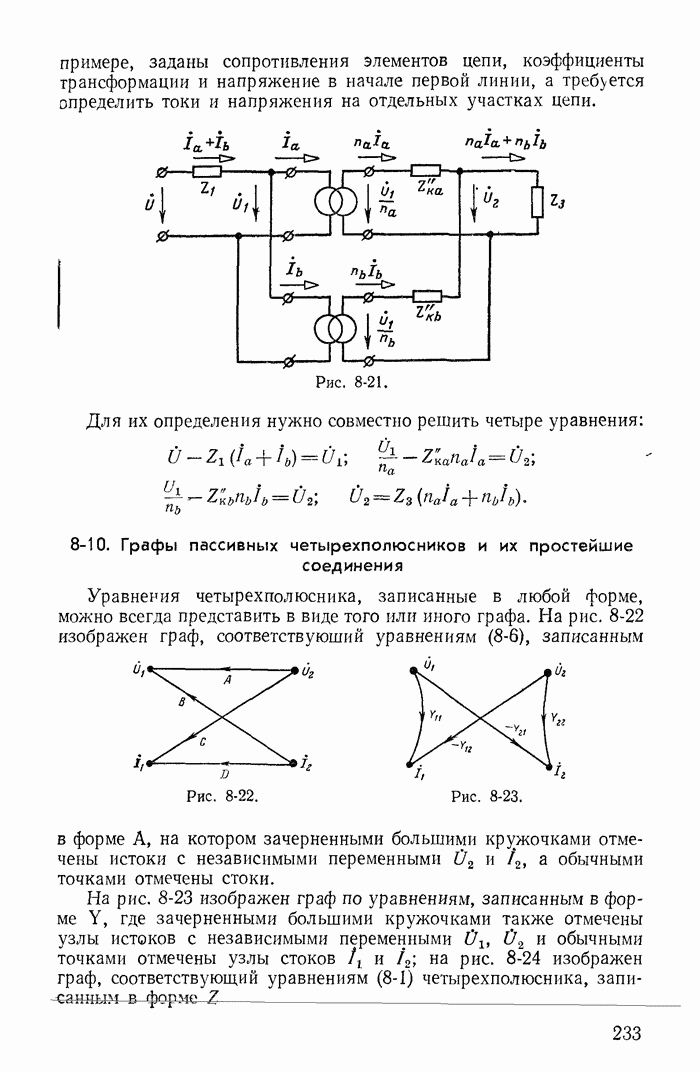
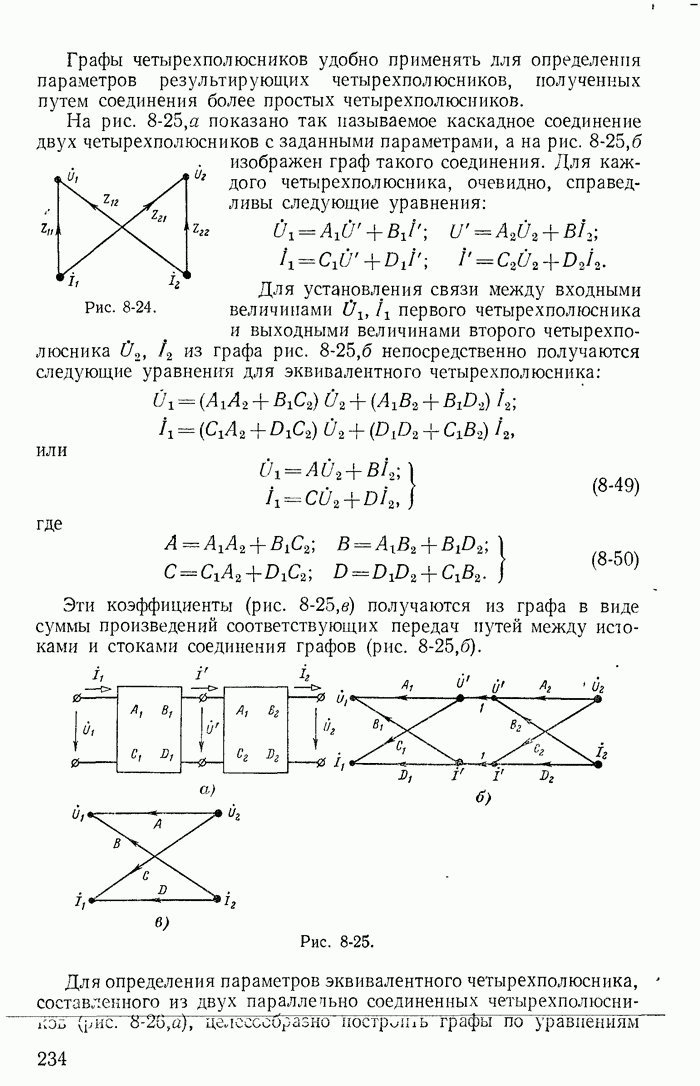
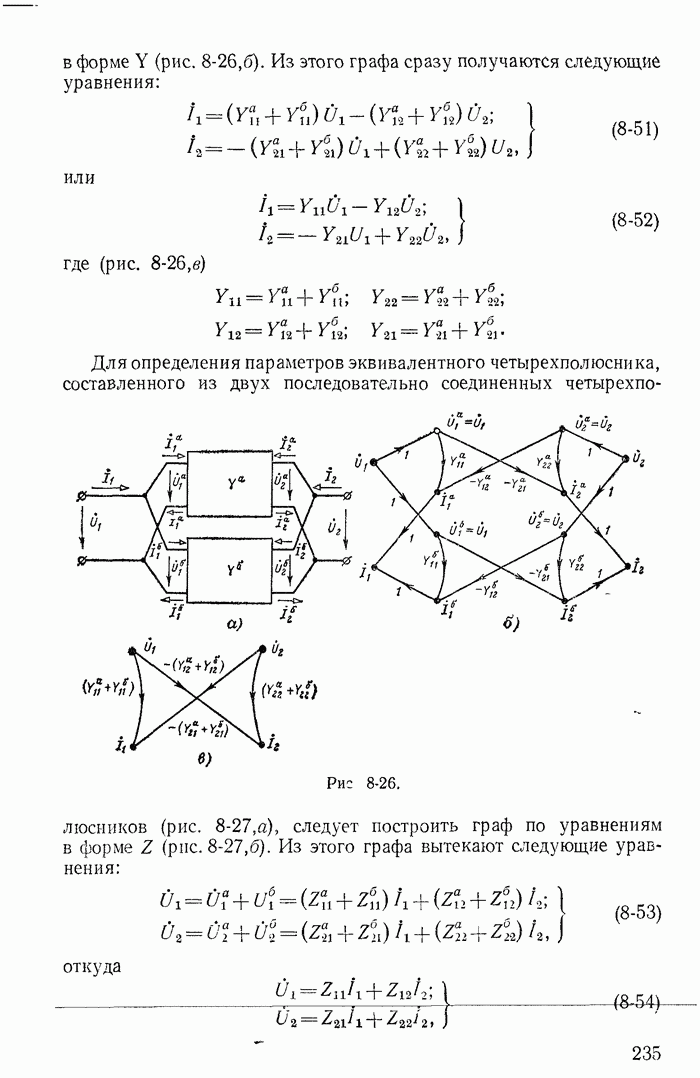
- 8-10. Графы пассивных четырехполюсников и их простейшие соединения
- Глава девятая. ЦЕПИ С ЭЛЕКТРОННЫМИ И ПОЛУПРОВОДНИКОВЫМИ ПРИБОРАМИ В ЛИНЕЙНОМ РЕЖИМЕ
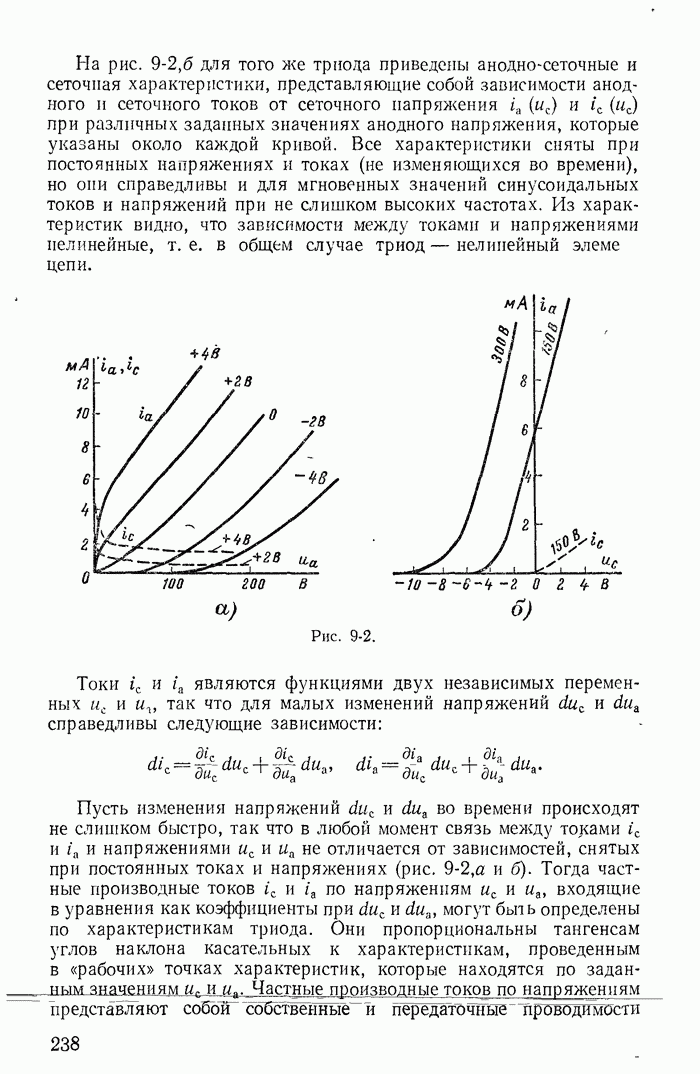
- 9-2. Эквивалентные схемы лампового триода
- 9-3. Транзисторы (полупроводниковые триоды)
- 9-4. Эквивалентные схемы транзисторов
- 9-5. Простейшие электрические цепи с невзаимными элементами и их направленные графы
- Глава десятая. ТРЕХФАЗНЫЕ ЦЕПИ
- 10-2. Соединения звездой и многоугольником
- 10-3. Симметричный режим трехфазной цепи
- 10-4. Некоторые свойства трехфазных цепей с различными схемами соединений
- 10-5. Расчет симметричных режимов трехфазных цепей
- 10-6. Расчет несимметричных режимов трехфазных цепей со статической нагрузкой
- 10-7. Напряжения на фазах приемника в некоторых частных случаях
- 10-8. Эквивалентные схемы трехфазных линий
- 10-9. Измерение мощности в трехфазных цепях
- 10-10. Вращающееся магнитное поле
- 10-11. Принципы действия асинхронного и синхронного двигателей
- Глава одиннадцатая. МЕТОД СИММЕТРИЧНЫХ СОСТАВЛЯЮЩИХ
- 11-2. Некоторые свойства трехфазных цепей в отношении симметричных составляющих токов и напряжений
- 11-3. Сопротивления симметричной трехфазной цепи для токов различных последовательностей
- 11-4. Определение токов в симметричной цепи
- 11-5. Симметричные составляющие напряжений и токов в несимметричной трехфазной цепи
- 11-6. Расчет цепи с несимметричной нагрузкой
- 11-7. Расчет цепи с несимметричным участком в линии
- Глава двенадцатая. НЕСИНУСОИДАЛЬНЫЕ ТОКИ
- 12-2. Разложение периодической несинусоидальной кривой в тригонометрический ряд
- 12-3. Максимальные, действующие и средние значения несинусоидальных периодических э. д. с., напряжений и токов
- 12-4. Коэффициенты, характеризующие форму несинусоидальных периодических кривых
- 12-5. Несинусоидальные кривые с периодической огибающей
- 12-6. Действующие значения э. д. с., напряжений и токов с периодическими огибающими
- 12-7. Расчет цепей с несинусоидальными периодическими э. д. с. и токами
- 12-8. Резонанс при несинусоидальных э. д. с. и токах
- 12-9. Мощность периодических несинусоидальных токов
- 12-10. Высшие гармоники в трехфазных цепях
- Глава тринадцатая. КЛАССИЧЕСКИЙ МЕТОД РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ
- 13-2. Переходный, принужденный и свободный процессы
- 13-3. Короткое замыкание цепи r, L
- 13-4. Включение цепи r, L на постоянное напряжение
- 13-5. Включение цепи r, L на синусоидальное напряжение
- 13-6. Короткое замыкание цепи r, С
- 13-7. Включение цепи r, С на постоянное напряжение
- 13-8. Включение цепи r, С на синусоидальное напряжение
- 13-9. Переходные процессы в неразветвленной цепи r, С
- 13-10. Апериодический разряд конденсатора
- 13-11. Предельный случай апериодического разряда конденсатора
- 13-12. Периодический (колебательный) разряд конденсатора
- 13-13. Включение цепи r, С на постоянное напряжение
- 13-14. Общий случай расчета переходных процессов классическим методом
- 13-15. Включение пассивного двухполюсника на непрерывно изменяющееся напряжение (формула или интеграл Дюамеля)
- 13-16. Включение пассивного двухполюсника на напряжение любой формы
- 13-17. Временная и импульсная переходные характеристики
- 13-18. Запись теоремы свертки при помощи импульсной переходной характеристики
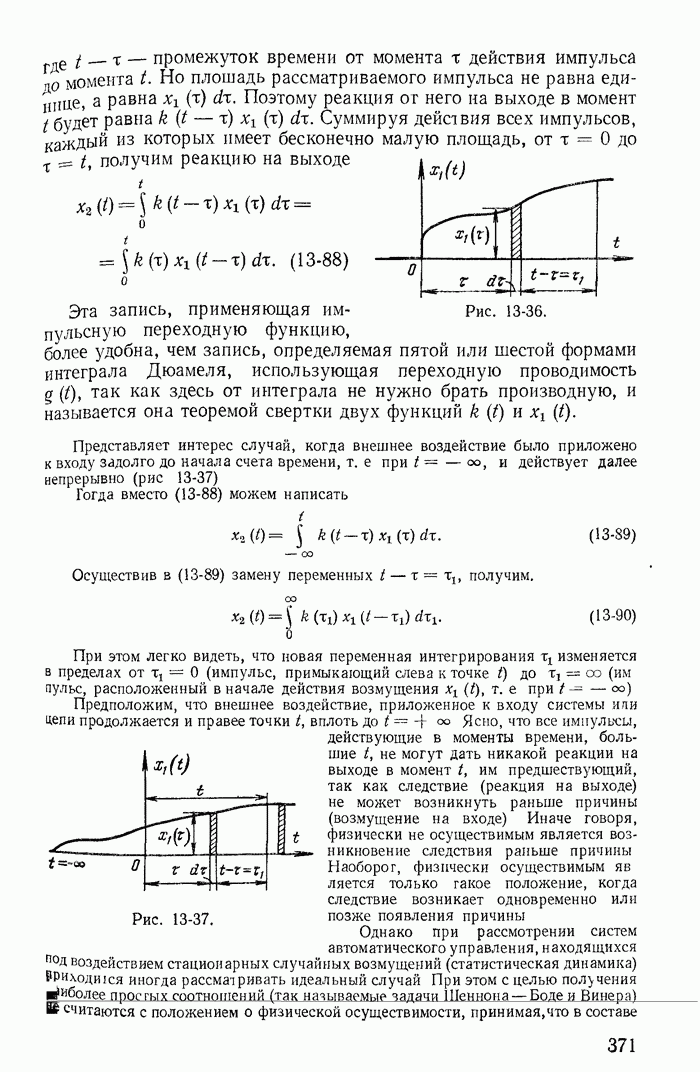
- 13-19. Переходные процессы при скачках токов в индуктивностях и напряжений на конденсаторах
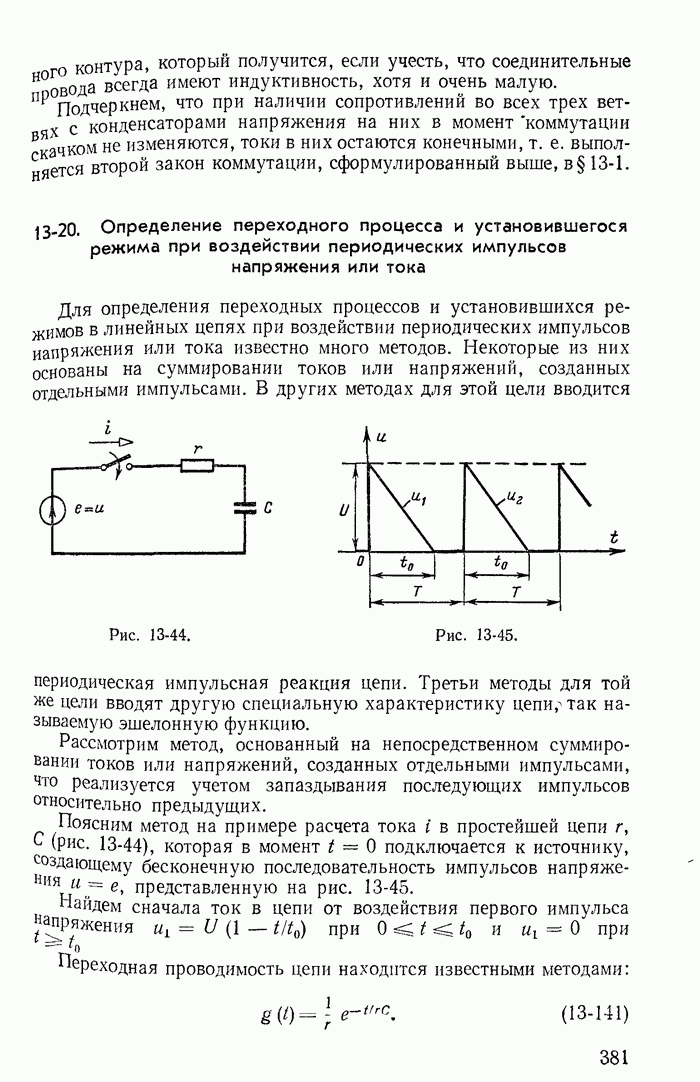
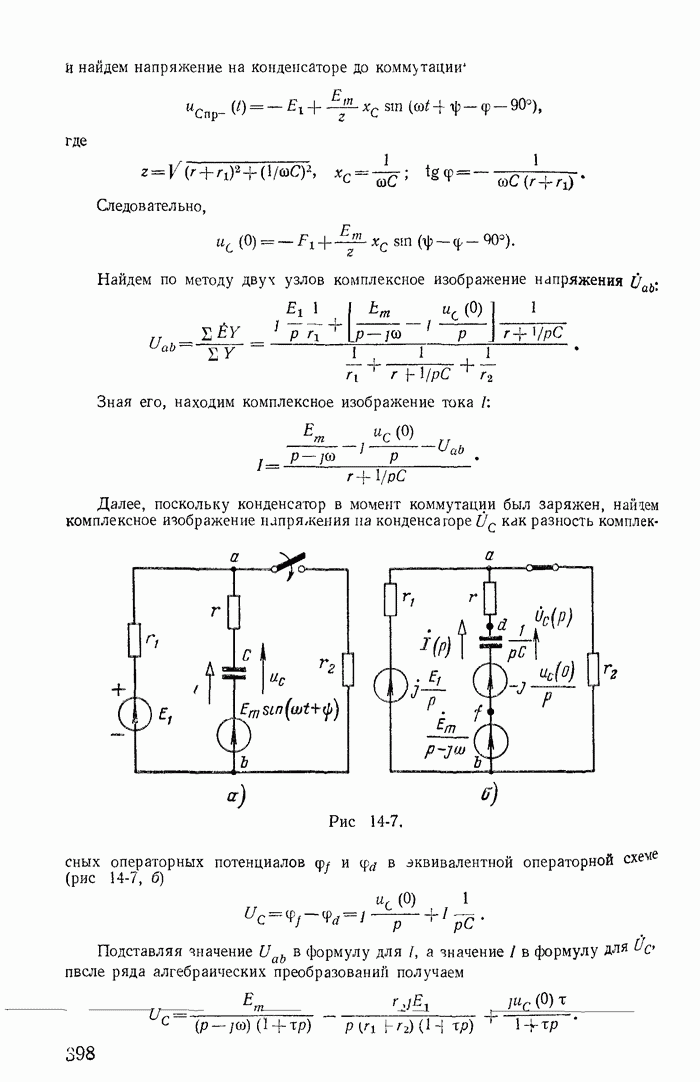
- 13-20. Определение переходного процесса и установившегося режима при воздействии периодических импульсов напряжения или тока
- Глава четырнадцатая. ОПЕРАТОРНЫЙ МЕТОД РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ
- 14-2. Законы Ома и Кирхгофа в операторной форме
- 14-3. Эквивалентные операторные схемы
- 14-4. Переходные процессы в цепях с взаимной индуктивностью
- 14-5. Сведение расчетов переходных процессов к нулевым начальным условиям
- 14-6. Определение свободных токов по их изображениям
- 14-7. Формулы включения
- 14-8. Расчет переходных процессов методом переменных состояния
- 14-9. Определение принужденного режима цепи при воздействии на нее периодического несинусоидального напряжения
- Глава пятнадцатая. ЧАСТОТНЫЙ МЕТОД РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ
- 15-2. Законы Ома и Кирхгофа и эквивалентные схемы для частотных спектров
- 15-3. Приближенный метод определения оригинала по вещественной частотной характеристике (метод трапеций)
- 15-4. О переходе от преобразований Фурье к преобразованиям Лапласа
- 15-5. Сравнение различных методов расчета переходных процессов в линейных электрических цепях
- Глава шестнадцатая. ЦЕПНЫЕ СХЕМЫ И ЧАСТОТНЫЕ ЭЛЕКТРИЧЕСКИЕ ФИЛЬТРЫ
- 16-2. Характеристическое сопротивление и постоянная передачи симметричного четырехполюсника
- 16-3. Вносимая и рабочая постоянные передачи
- 16-4. Цепные схемы
- 16-5. Частотные электрические фильтры
- 16-6. Низкочастотные фильтры
- 16-8. Полосные фильтры
- 16-11. Г-образный фильтр как пример несимметричного фильтра
- 16-12. Безындукционные (или r, C) фильтры
- Глава семнадцатая. СИНТЕЗ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
- 17-2. Передаточная функция четырехполюсника. Цепи минимальной фазы
- 17-3. Входные функции цепей. Положительные вещественные функции
- 17-4. Реактивные двухполюсники
- 17-5. Частотные характеристики реактивных двухполюсников
- 17-6. Синтез реактивных двухполюсников. Метод Фостера
- 17-7. Синтез реактивных двухполюсников. Метод Кауэра
- 17-8. Синтез двухполюсников с потерями. Метод Фостера
- 17-9. Синтез двухполюсников с потерями. Метод Кауэра
- 17-10. Понятие о синтезе четырехполюсников
- Раздел второй. ЛИНЕЙНЫЕ ЦЕПИ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
- Глава восемнадцатая. ГАРМОНИЧЕСКИЕ ПРОЦЕССЫ В ЦЕПЯХ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
- 18-2. Уравнения однородной линии
- 18-3. Установившийся режим в однородной линии
- 18-4. Уравнения однородной линии с гиперболическими функциями
- 18-5. Характеристики однородной линии
- 18-6. Входное сопротивление линии
- 18-7. Коэффициент отражения волны
- 18-8. Согласованная нагрузка линии
- 18-9. Линия без искажений
- 18-10. Холостой ход, короткое замыкание и нагрузочный режим линии с потерями
- 18-11. Линии без потерь
- 18-12. Стоячие волны
- 18-13. Линия как четырехполюсник
- Глава девятнадцатая. ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЦЕПЯХ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
- 19-2. Общее решение уравнений однородной линии
- 19-3. Возникновение волн с прямоугольным фронтом
- 19-4. Общие случаи нахождения волн, возникающих при переключениях
- 19-5. Отражение волны с прямоугольным фронтом от конца линии
- 19-6. Общий метод определения отраженных волн
- 19-7. Качественное рассмотрение переходных процессов в линиях, содержащих сосредоточенные емкости и индуктивности
- 19-8. Многократные отражения волн с прямоугольным фронтом от активного сопротивления
- 19-9. Блуждающие волны
- Раздел III. НЕЛИНЕЙНЫЕ ЦЕПИ
- Глава двадцатая. НЕЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПРИ ПОСТОЯННЫХ ТОКАХ И НАПРЯЖЕНИЯХ
- 20-2. Графический метод расчета неразветвленных цепей с нелинейными элементами
- 20-3. Графический метод расчета цепей с параллельным соединением нелинейных элементов
- 20-4. Графический метод расчета цепей со смешанным соединением нелинейных и линейных элементов
- 20-5. Применение эквивалентных схем с источниками э. д. с. для исследования режима нелинейных цепей
- 20-6. Вольт-амперные характеристики нелинейных активных двухполюсников
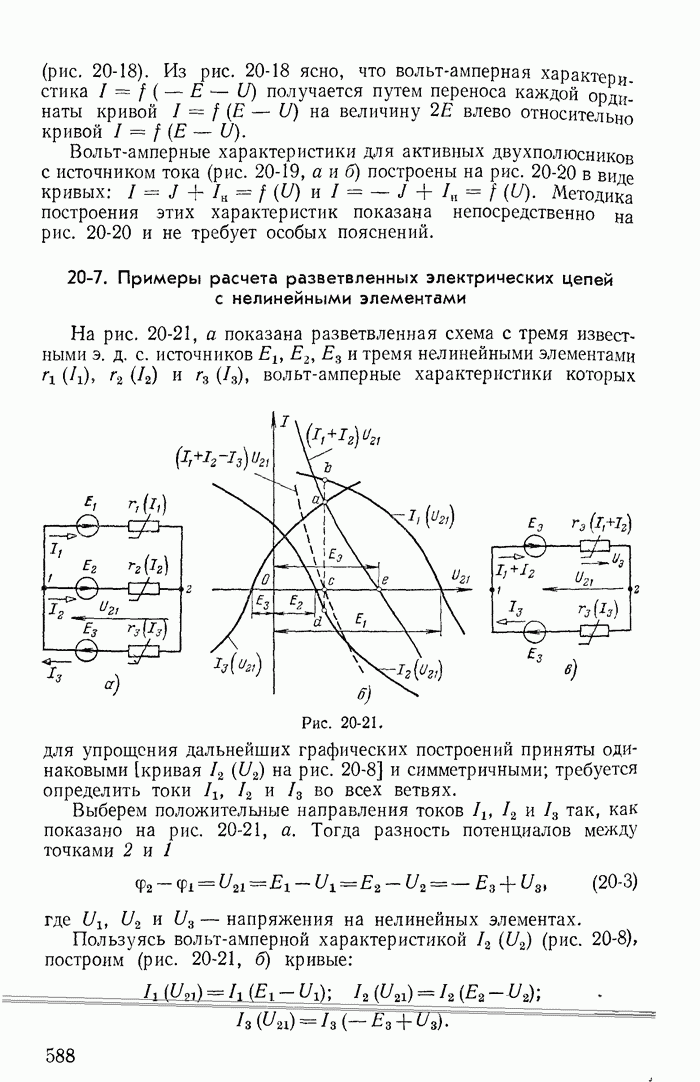
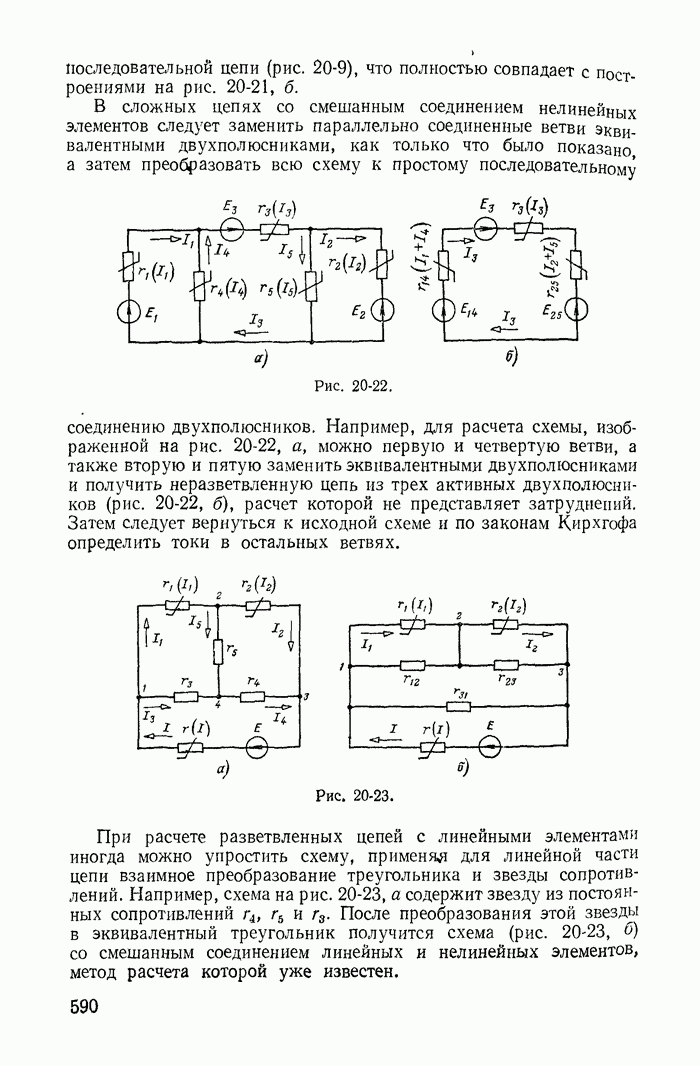
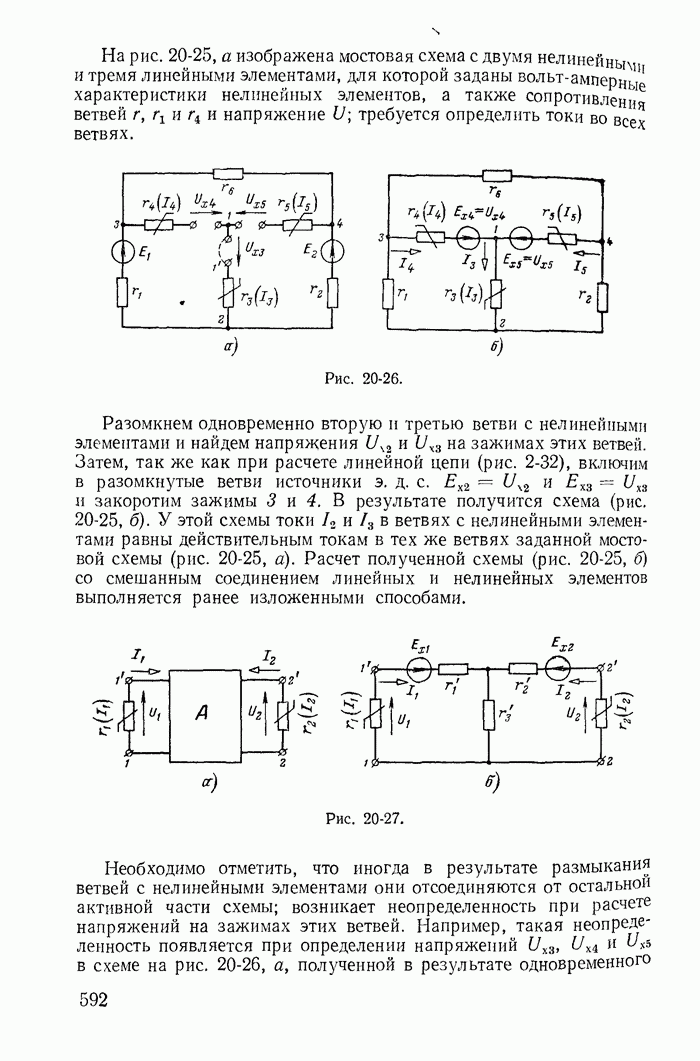
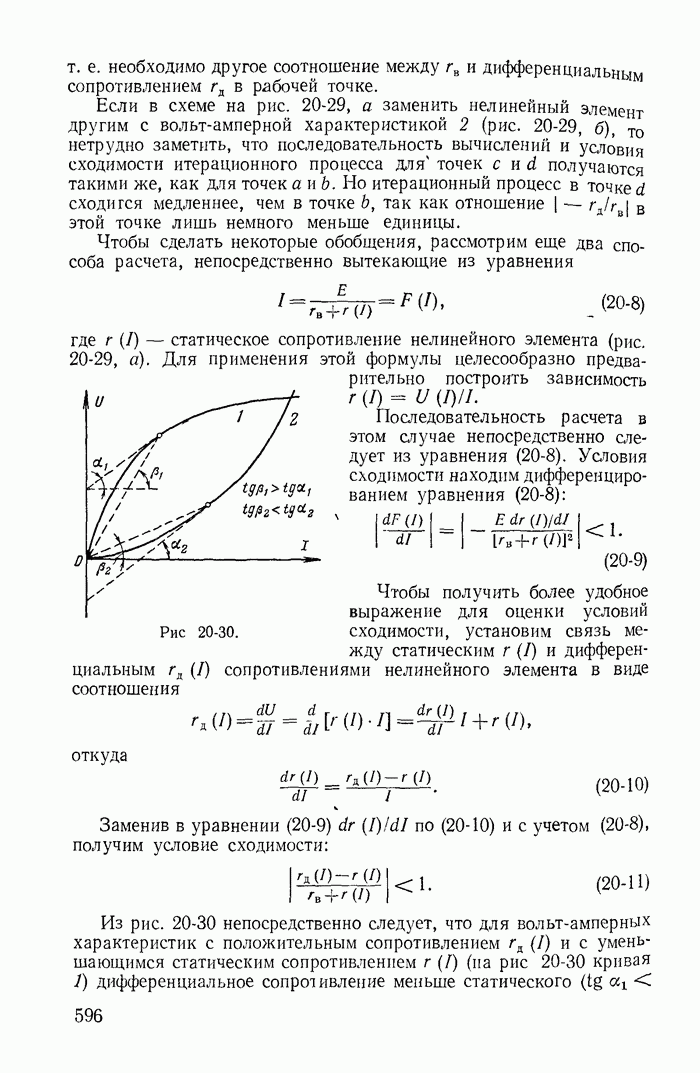
- 20-7. Примеры расчета разветвленных электрических цепей с нелинейными элементами
- 20-8. Применение теории активных двухполюсника, четырехполюсника и шестиполюсника для расчета цепей с линейными и нелинейными элементами
- 20-9. Расчет разветвленных нелинейных цепей итерационным методом (методом последовательных приближений)
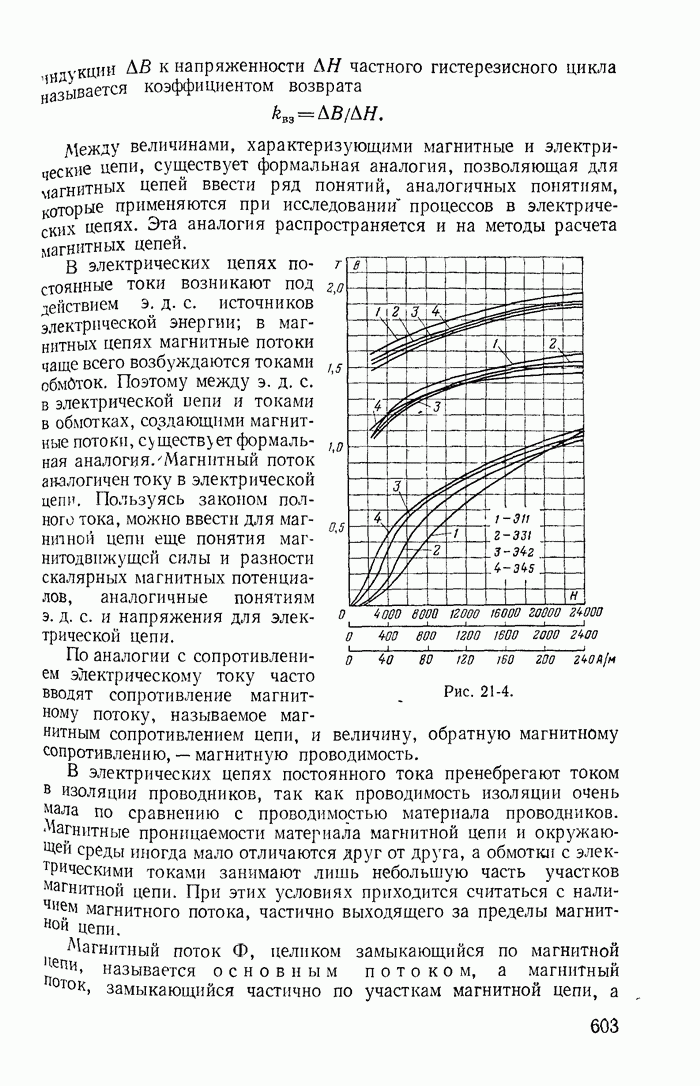
- Глава двадцать первая. МАГНИТНЫЕ ЦЕПИ ПРИ ПОСТОЯННЫХ ТОКАХ
- 21-2. Расчет неразветвленных магнитных цепей
- 21-3. Расчет разветвленных магнитных цепей
- 21-4. Расчет магнитной цепи кольцевого постоянного магнита с воздушным зазором
- 21-5. Расчет неразветвленной неоднородной магнитной цепи с постоянным магнитом
- Глава двадцать вторая. ОБЩАЯ ХАРАКТЕРИСТИКА НЕЛИНЕЙНЫХ ЦЕПЕЙ ПЕРЕМЕННОГО ТОКА И МЕТОДОВ ИХ РАСЧЕТА
- 22-1. Нелинейные двухполюсники и четырехполюсники при переменных токах
- 22-2. Определение рабочих точек на характеристиках нелинейных двухполюсников и четырехполюсников
- 22-3. Явления в нелинейных цепях переменного тока
- 22-4. Методы расчета нелинейных цепей переменного тока
- Глава двадцать третья. НЕЛИНЕЙНЫЕ ЦЕПИ С ИСТОЧНИКАМИ Э. Д. С. И ТОКА ОДИНАКОВОЙ ЧАСТОТЫ
- 23-2. Форма кривой тока в цепи с вентилями
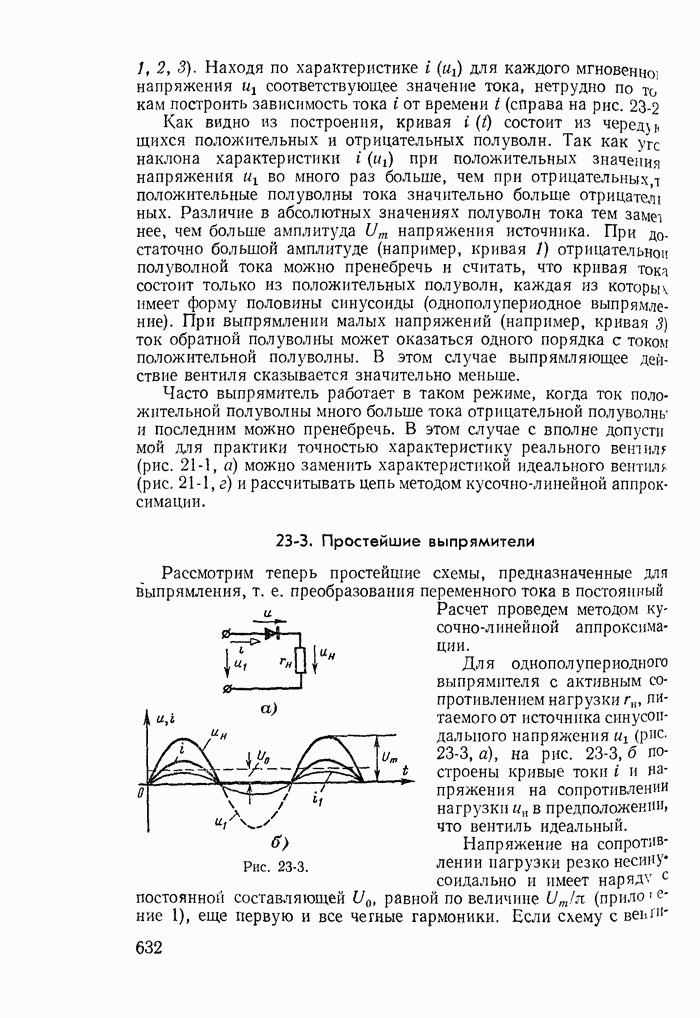
- 23-3. Простейшие выпрямители
- 23-4. Формы кривых тока и напряжения в цепях с нелинейными реактивными сопротивлениями
- 23-5. Утроители частоты
- 23-6. Формы кривых тока и напряжения в цепях с терморезисторами
- 23-7. Замена реальных нелинейных элементов условно-нелинейными
- 23-8. Учет реальных свойств стальных магнитопроводов
- 23-9. Расчет тока в катушке со стальным магнитопроводом
- 23-10. Понятие о расчете условно-нелинейных магнитных цепей
- 23-11. Явление феррорезонанса
- 23-12. Стабилизаторы напряжения
- Глава двадцать четвертая. НЕЛИНЕЙНЫЕ ЦЕПИ С ИСТОЧНИКАМИ Э. Д. С. И ТОКА РАЗЛИЧНЫХ ЧАСТОТ
- 24-1. Общая характеристика нелинейных цепей с источниками э. д. с. различных частот
- 24-2. Вентили в цепях с постоянными и переменными э. д. с.
- 24-3. Управляемые вентили в простейших выпрямителях и преобразователях постоянного тока в переменный
- 24-4. Катушки со стальными магнитопроводами в цепях с постоянными и переменными э. д. с.
- 24-5. Удвоитель частоты
- 24-6. Метод гармонического баланса
- 24-7. Влияние постоянной э. д. с. на переменную составляющую тока в цепях с нелинейными безынерционными сопротивлениядли
- 24-8. Принцип получения модулированных колебаний
- 24-9. Влияние постоянной составляющей на переменную в цепях с нелинейными индуктивностями
- 24-10. Магнитные усилители мощности
- Глава двадцать пятая. ПЕРЕХОДНЫЕ ПРОЦЕССЫ В НЕЛИНЕЙНЫХ ЦЕПЯХ
- 25-2. Включение катушки со стальным магнитопроводом на постоянное напряжение
- 25-3. Включение катушки со стальным магнитопроводом на синусоидальное напряжение
- 25-4. Импульсное воздействие в цепях с неоднозначными нелинейностями
- 25-5. Понятие о простейших запоминающих устройствах
- 25-6. Изображение переходных процессов на фазовой плоскости
- 25-7. Колебательный разряд емкости через нелинейную индуктивность
- Глава двадцать шестая. АВТОКОЛЕБАНИЯ
- 26-1. Нелинейные резисторы со спадающим участком характеристики
- 26-2. Понятие об устойчивости режима в цепи с нелинейными резисторами
- 26-3. Релаксационные колебания в цепи с отрицательным сопротивлением
- 26-4. Близкие к синусоидальным колебания в цепи с отрицательным сопротивлением
- 26-5. Фазовые траектории процессов в цепи с отрицательным сопротивлением
- 26-6. Фазовые траектории процессов в генераторе синусоидальных колебаний
- 26-7. Определение амплитуды автоколебаний методом гармонического баланса
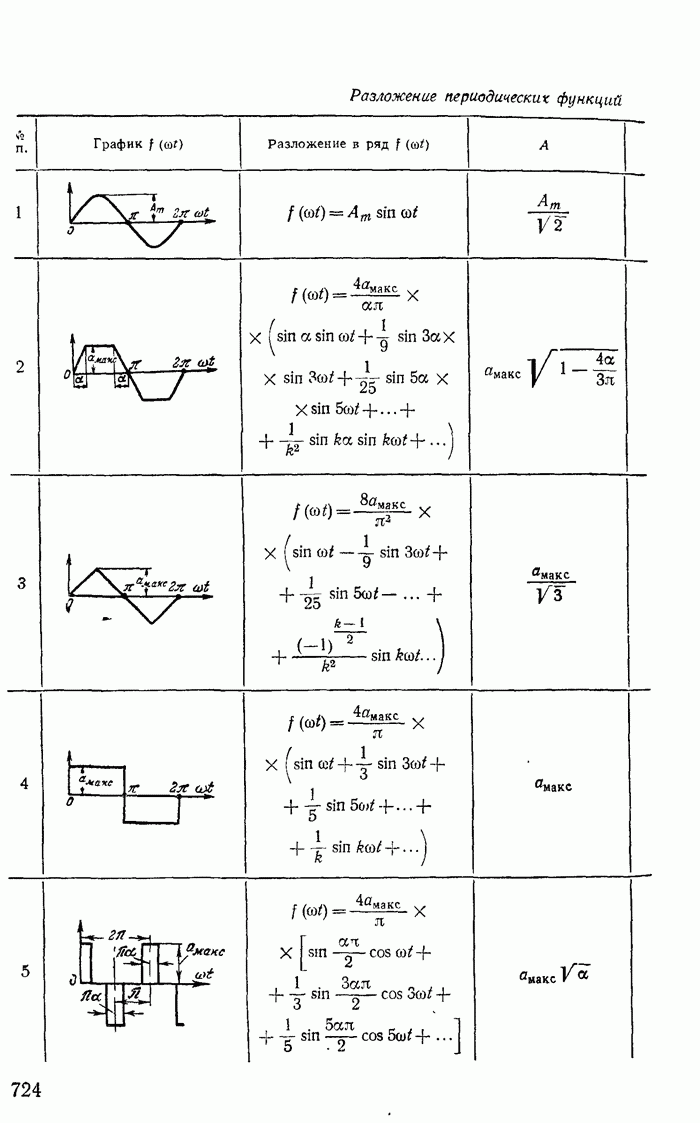
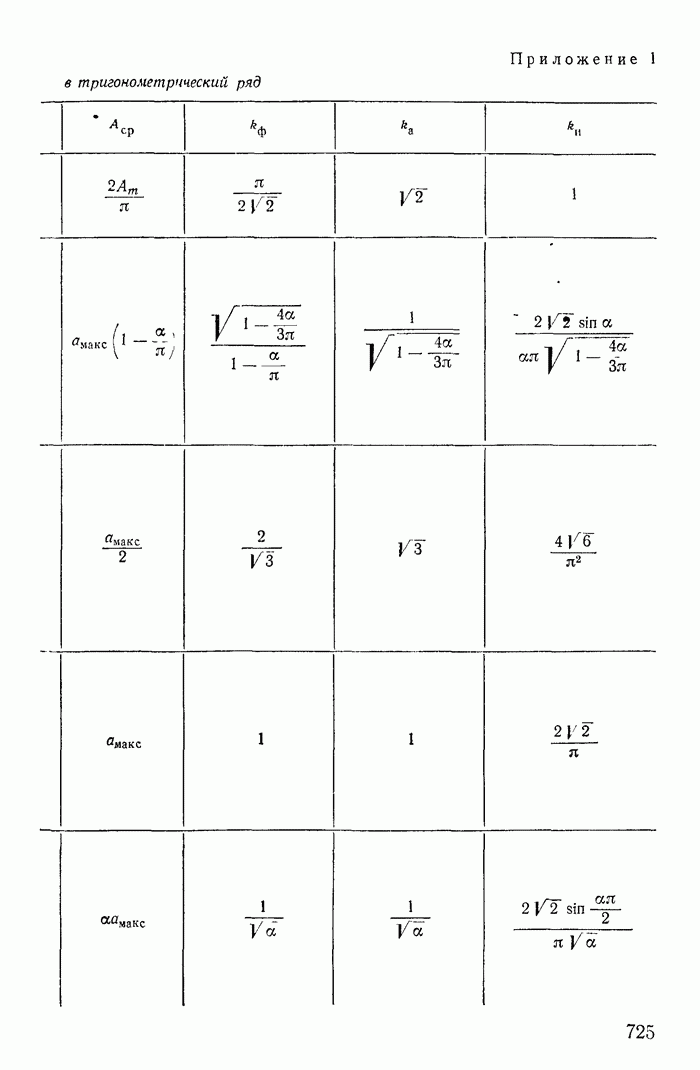
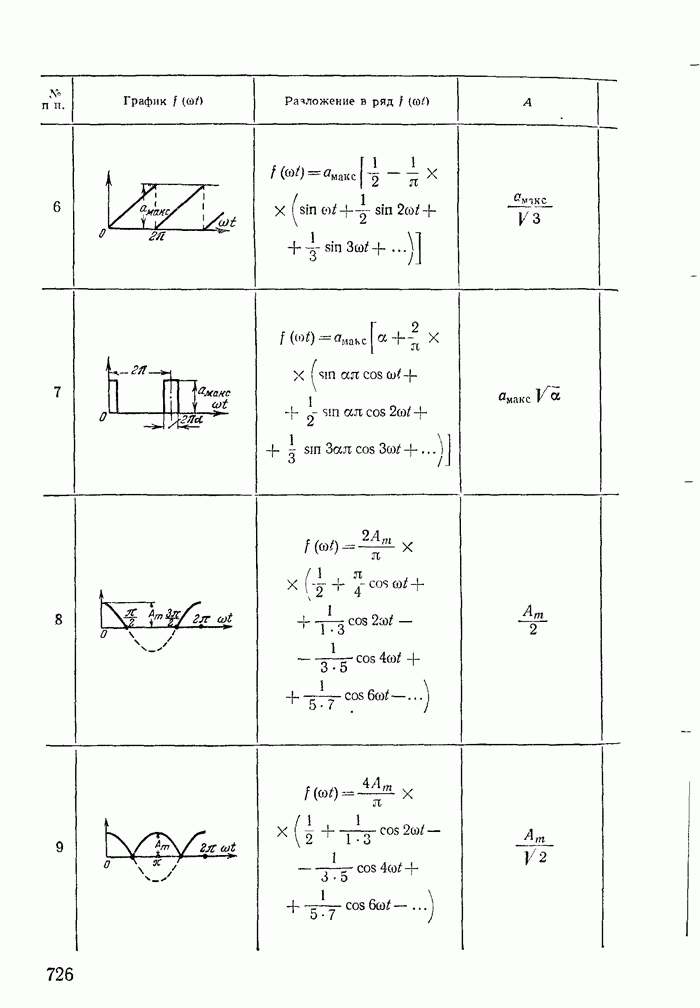
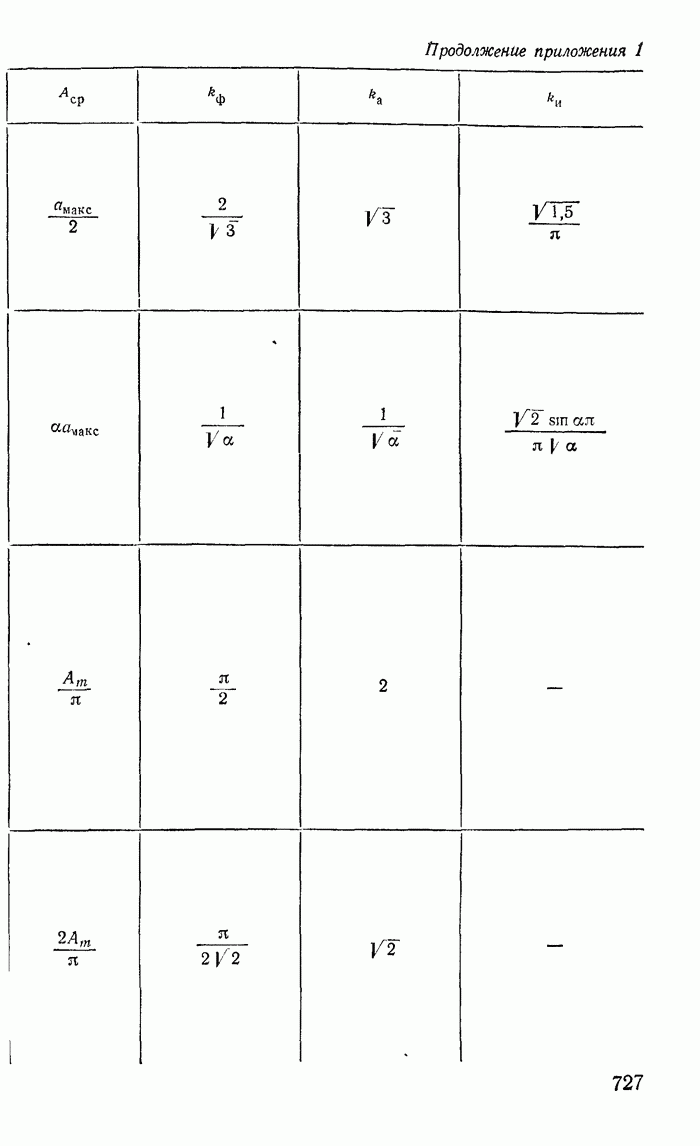
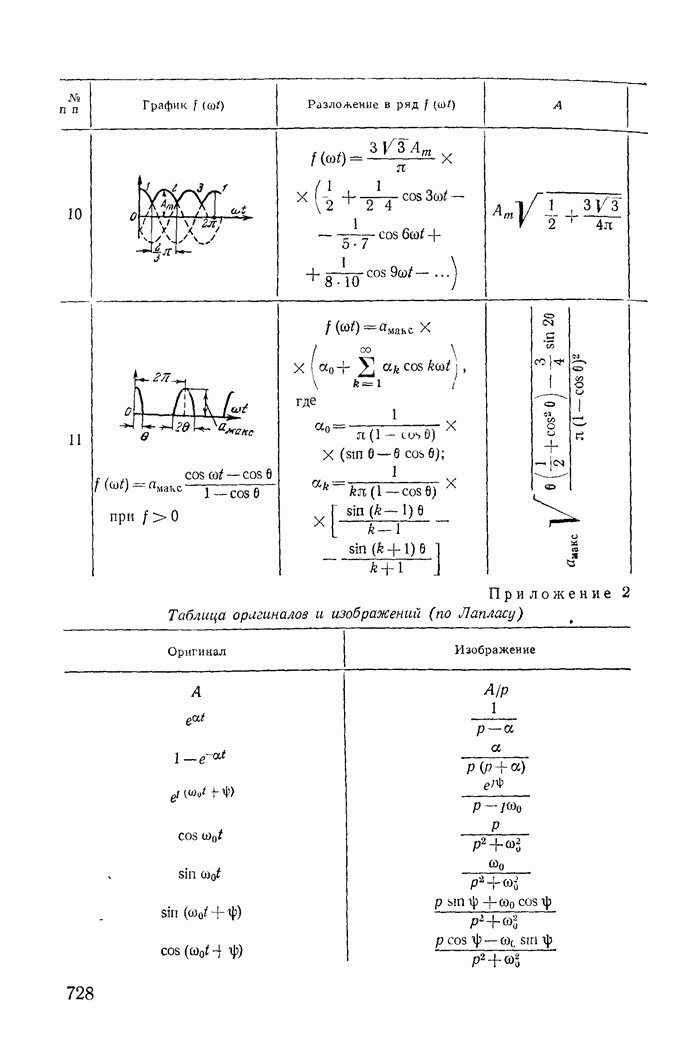
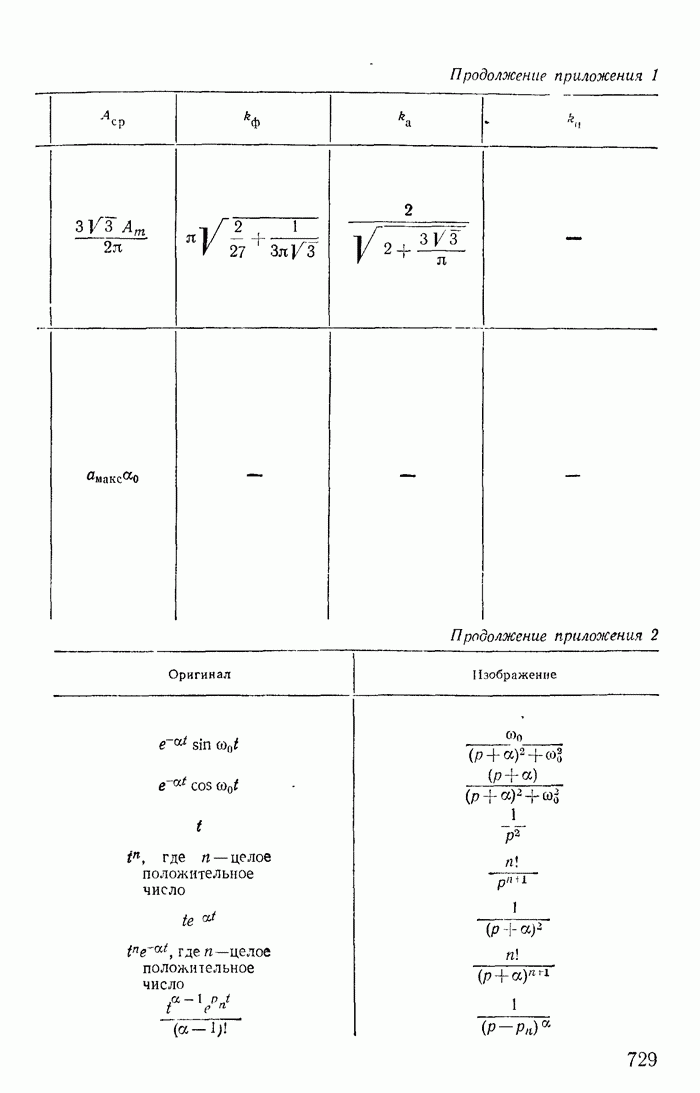
- Приложение 1. Разложение периодических функций в тригонометрический ряд
- Приложение 2. Таблица оригиналов и изображений (по Лапласу)
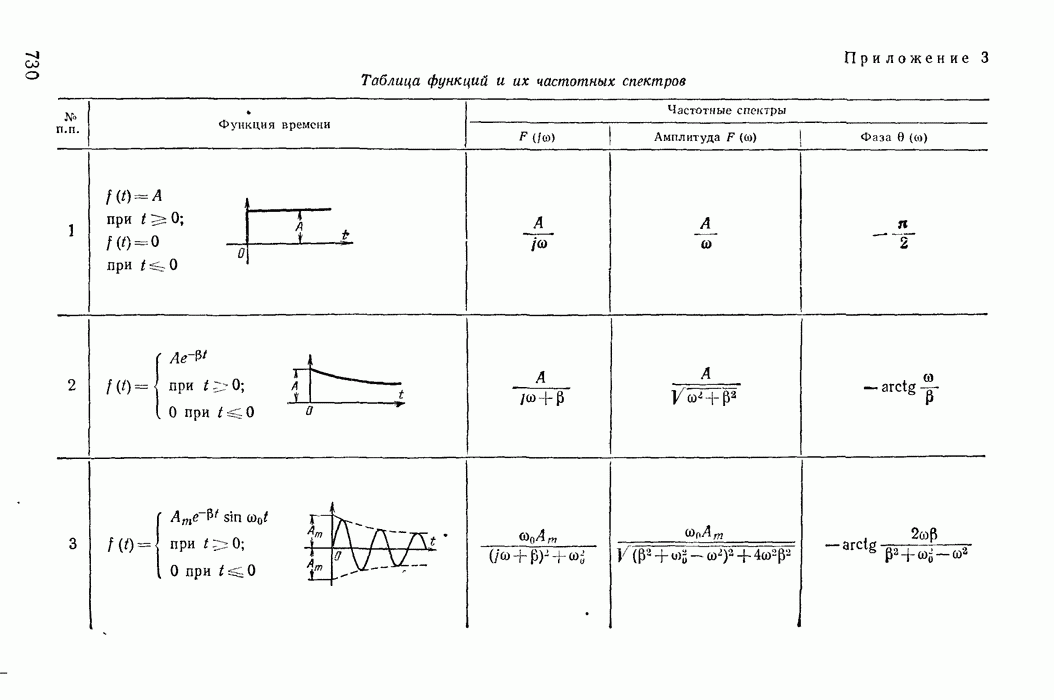
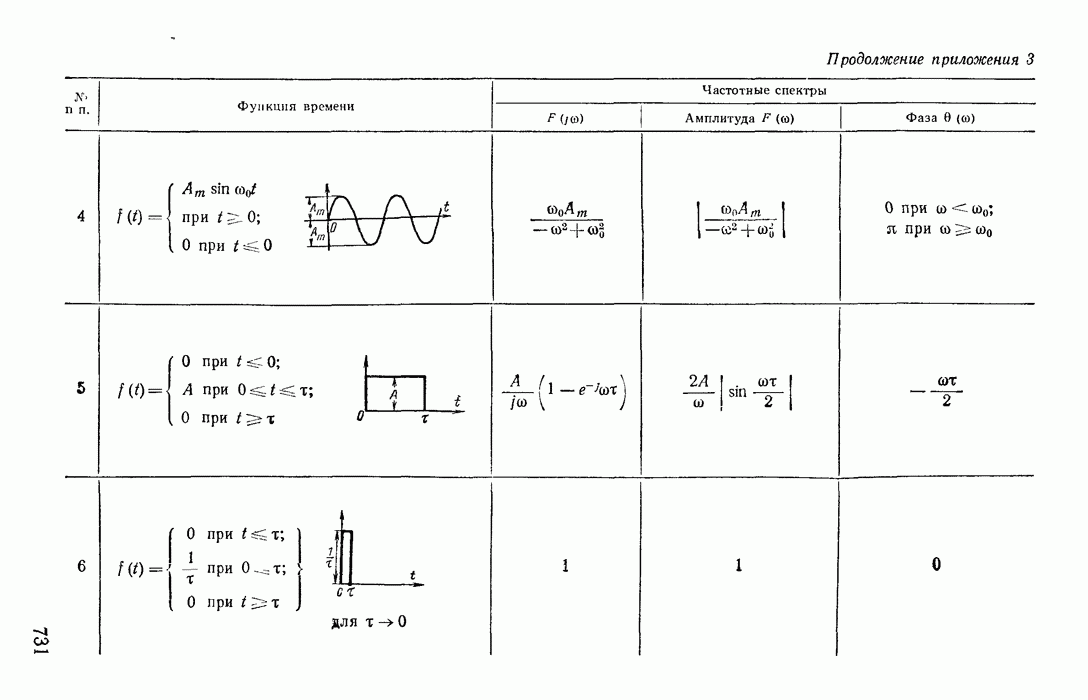
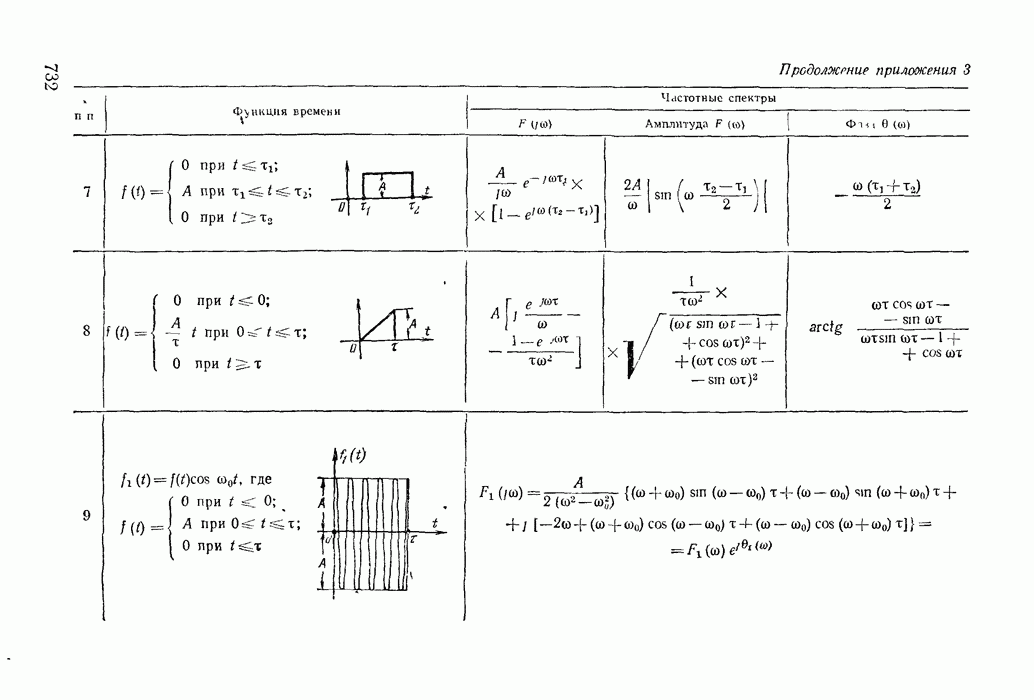
- Приложение 3. Таблица функций и их частных спектров
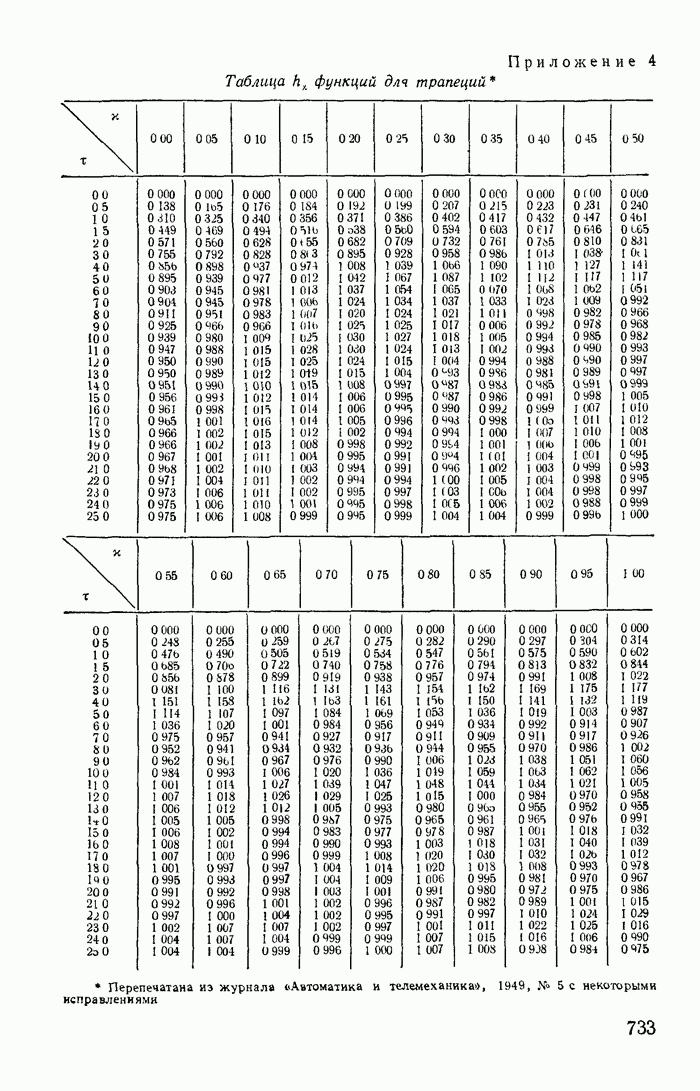
- Приложение 4. Таблица функций для трапеций
- СПИСОК ЛИТЕРАТУРЫ