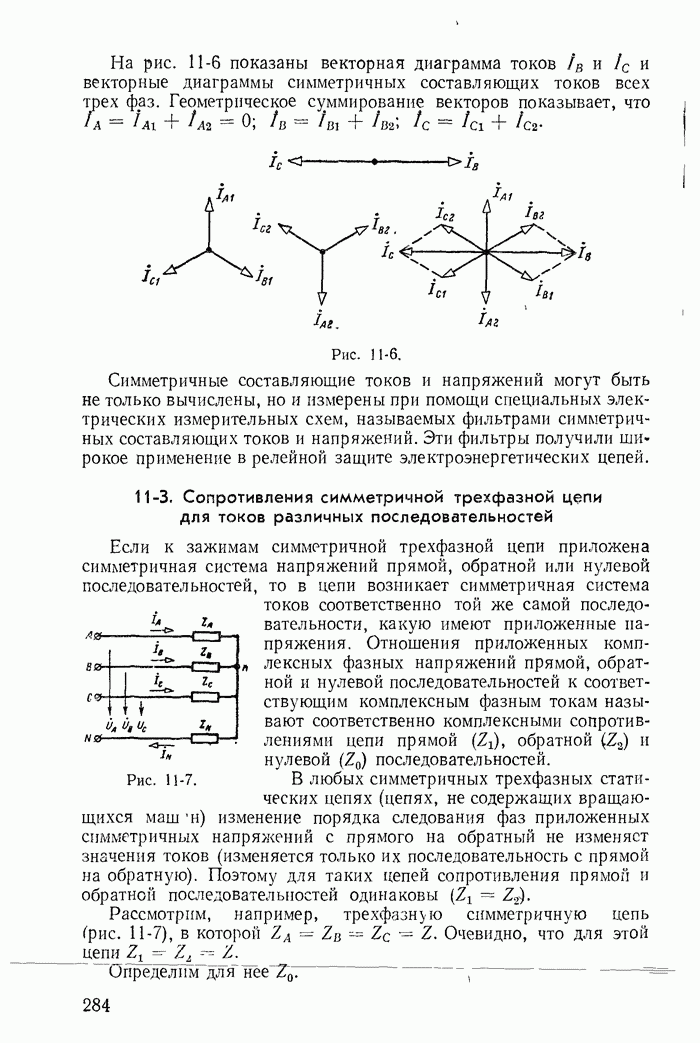
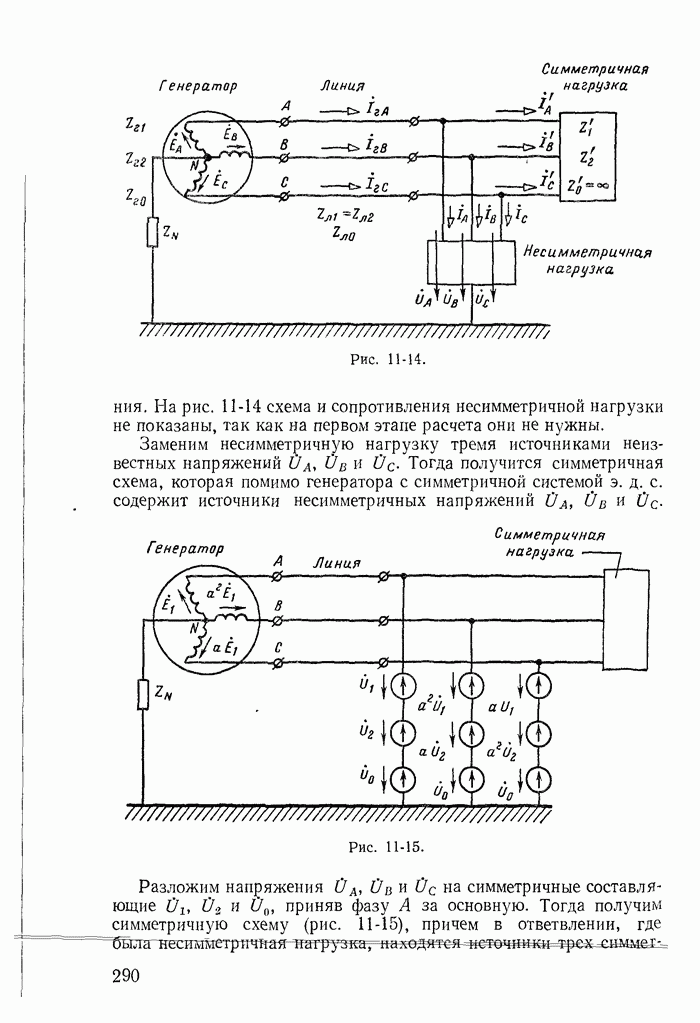
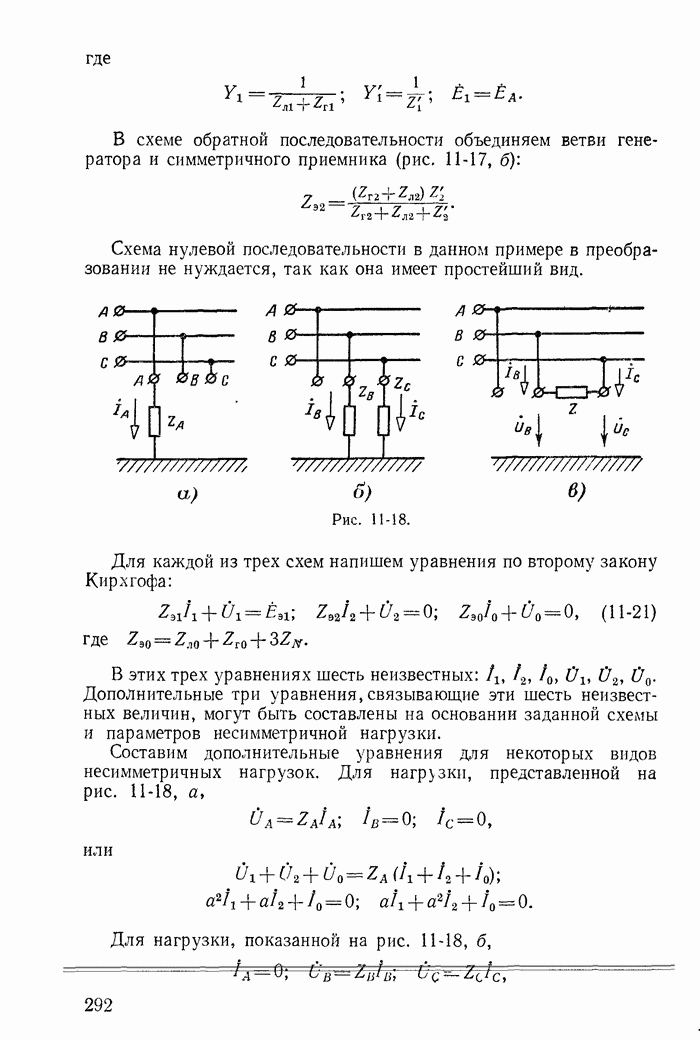
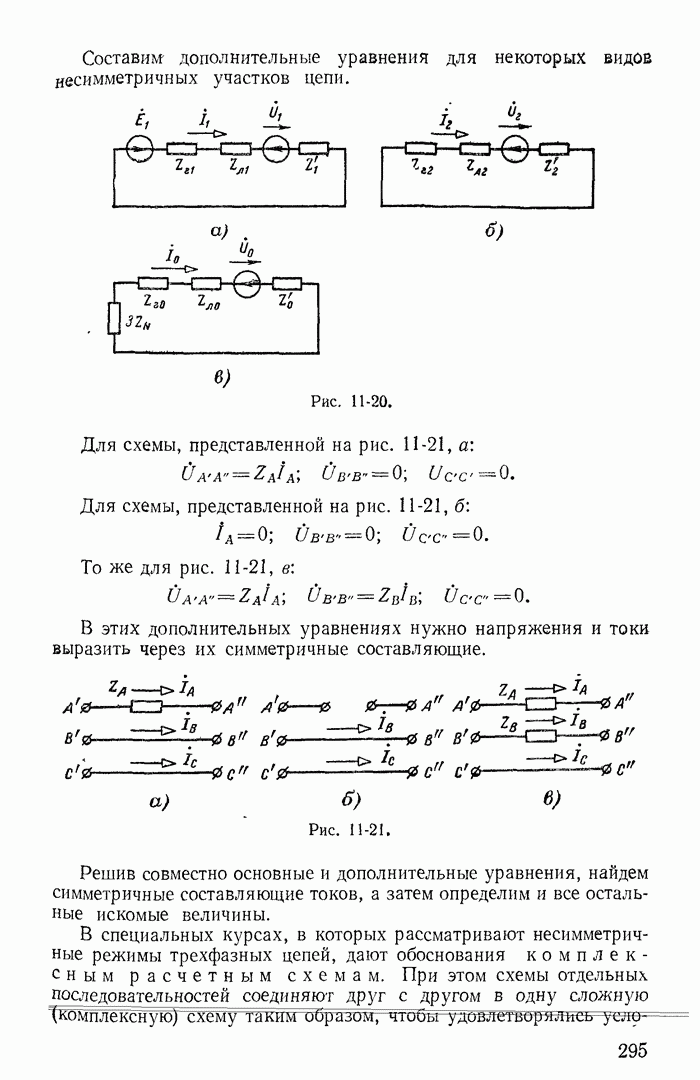
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
18-11. Линии без потерь
Если положить равными нулю сопротивление проводов линии  и проводимость утечки между проводами
и проводимость утечки между проводами  то получим так называемую линию без потерь.
то получим так называемую линию без потерь.
Для коротких высокочастотных линий, применяемых в радиотехнике, часто с достаточно большой точностью можно пренебречь сопротивлением  и утечкой
и утечкой  по сравнению с
по сравнению с  Поэтому в радиотехнике очень часто рассматривают двухпроводные воздушные линии и коаксиальные кабели как линии без потерь. Вообще же говоря, линию без потерь следует рассматривать как идеализацию действительной линии.
Поэтому в радиотехнике очень часто рассматривают двухпроводные воздушные линии и коаксиальные кабели как линии без потерь. Вообще же говоря, линию без потерь следует рассматривать как идеализацию действительной линии.
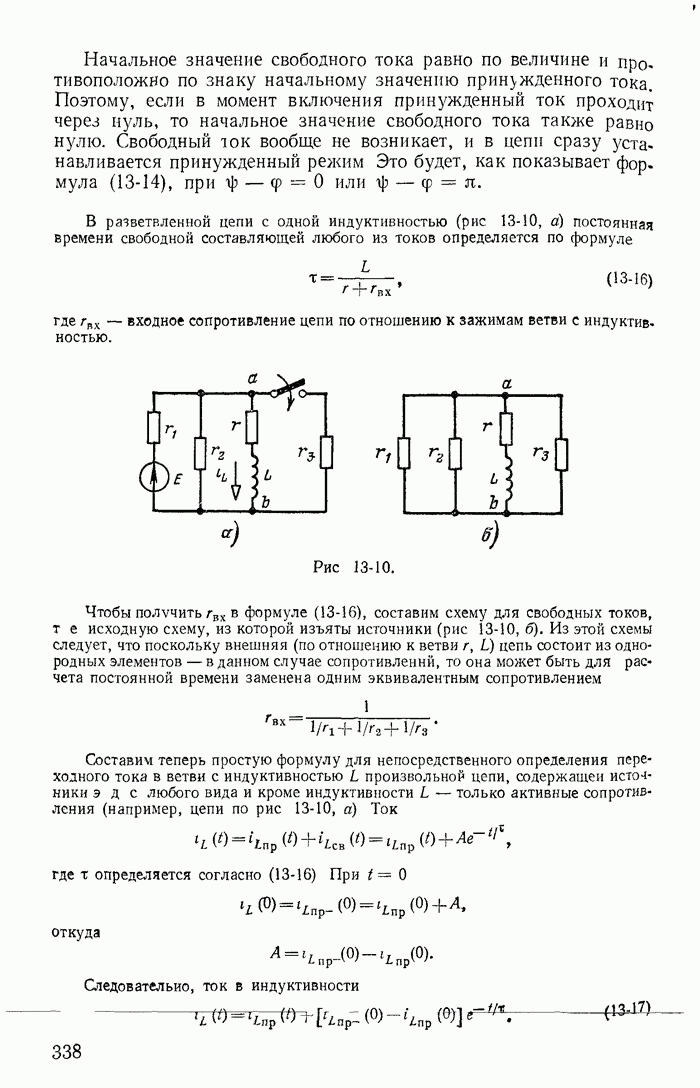
Из соотношений (18-8), (18-10), (18-15) и (18-16) для такой линии получим:
 (18-64)
(18-64)
т. e. у линии без потерь затухание равно нулю, а волновое сопротивление активное и не зависит от частоты. Точно так же и фазовая скорость в линиях без потерь не зависит от частоты. Заметим, что  для линии без потерь такие же, как и для неискажающей линии с потерями.
для линии без потерь такие же, как и для неискажающей линии с потерями.
Преобразуем формулу (18-66) для фазовой скорости к другому виду. Это преобразование проведем, например, для двухпроводной линии. Емкость единицы длины двухпроводной линии, 
 (18-68)
(18-68)
а индуктивность той же линии, 
 (18-69)
(18-69)
здесь  — радиус провода,
— радиус провода,  расстояние между осями проводов.
расстояние между осями проводов.
Подставляя значения [0 и  в формулу (18-66) для v, получаем:
в формулу (18-66) для v, получаем:
 (18-70)
(18-70)
где  - абсолютные диэлектрическая и магнитная проницаемости среды между проводами.
- абсолютные диэлектрическая и магнитная проницаемости среды между проводами.
Но, как известно, скорость света в вакууме
 (18-71)
(18-71)
и для фазовой скорости можно записав:

Для воздушных линий  и фазовая скорость совпадает со скоростью света. Для кабельных линий
и фазовая скорость совпадает со скоростью света. Для кабельных линий 
Аргумент волнового сопротивления линии без потерь  т. е. токи прямой и обратной волн совпадают по фазе с напряжениями.
т. е. токи прямой и обратной волн совпадают по фазе с напряжениями.
Уравнения длинной линии с гиперболическими функциями от комплексного аргумента (18-21) и (18-24) для линии без потерь переходят в уравнения с круговыми функциями от вещественного аргумента. Если заданы напряжение  и ток
и ток  в начале линии, то получим:
в начале линии, то получим:

Если заданы напряжение и ток  в конце линии, то имеем:
в конце линии, то имеем:

Входное сопротивление линии согласно (18-31) и (18-64) — (18-67)
 (18-75)
(18-75)
Переходя в уравнениях (18-74) к мгновенным значениям при  получаем:
получаем:
 (18-766)
(18-766)
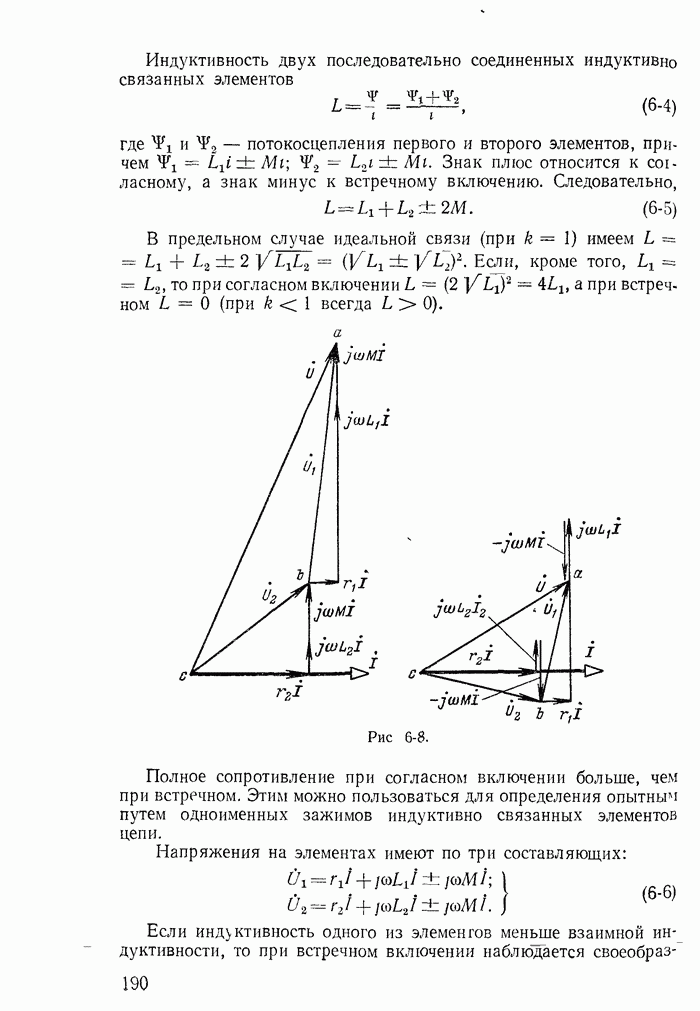
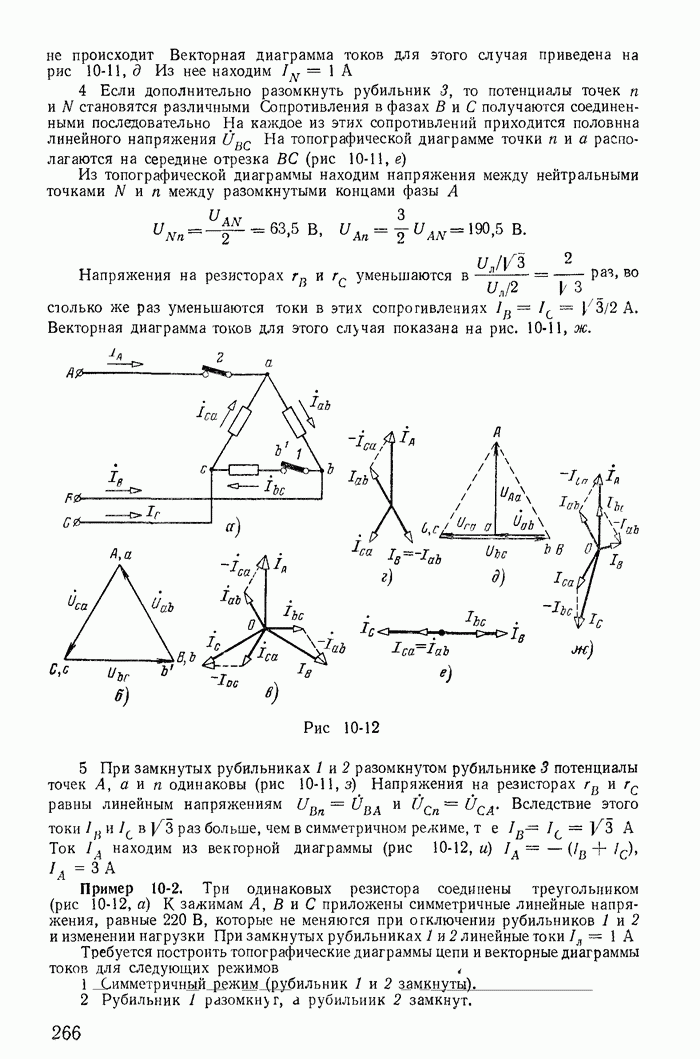
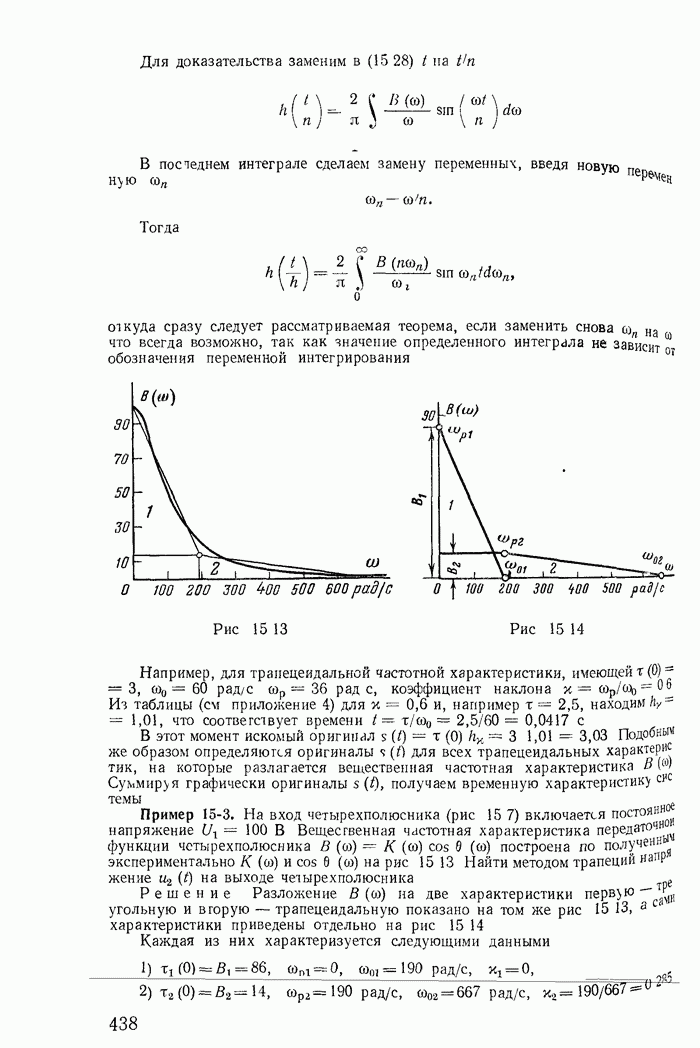
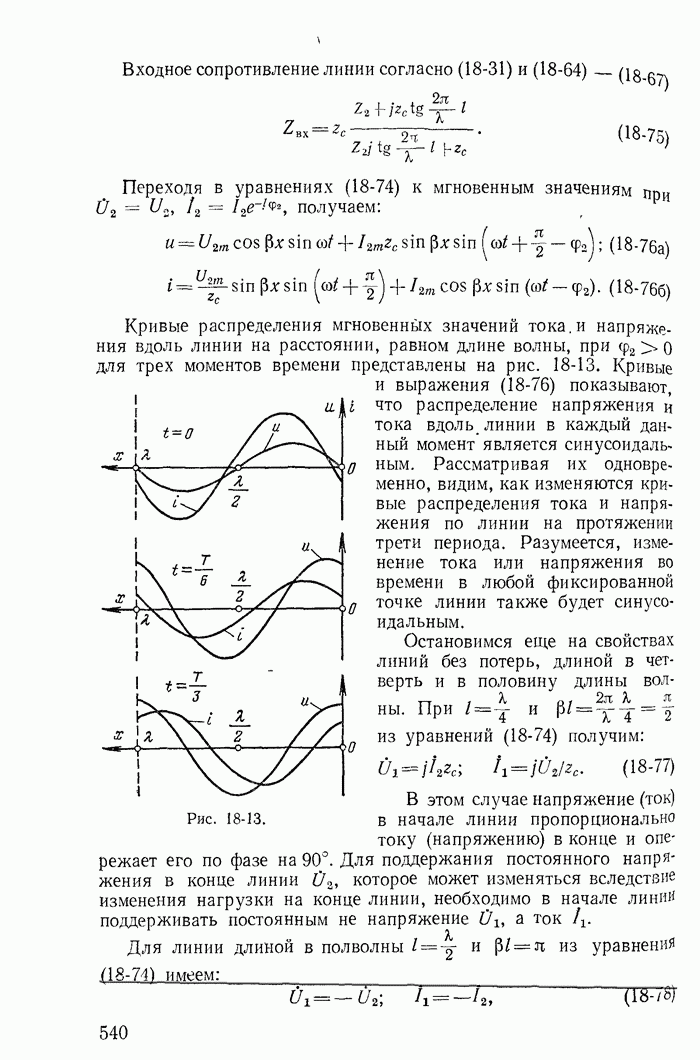
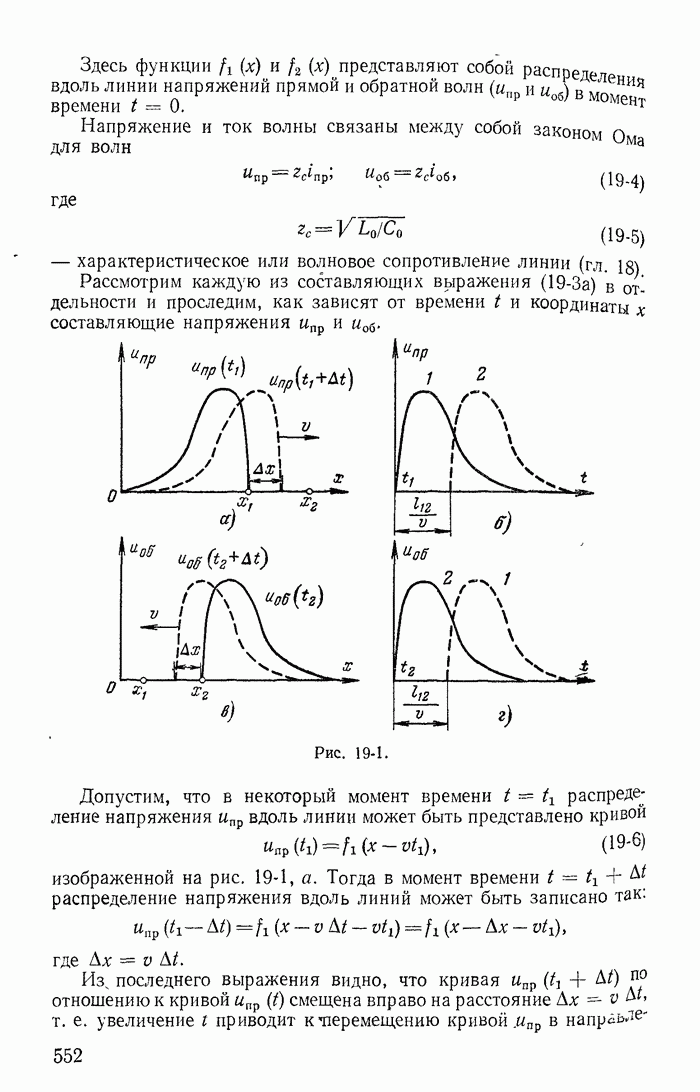
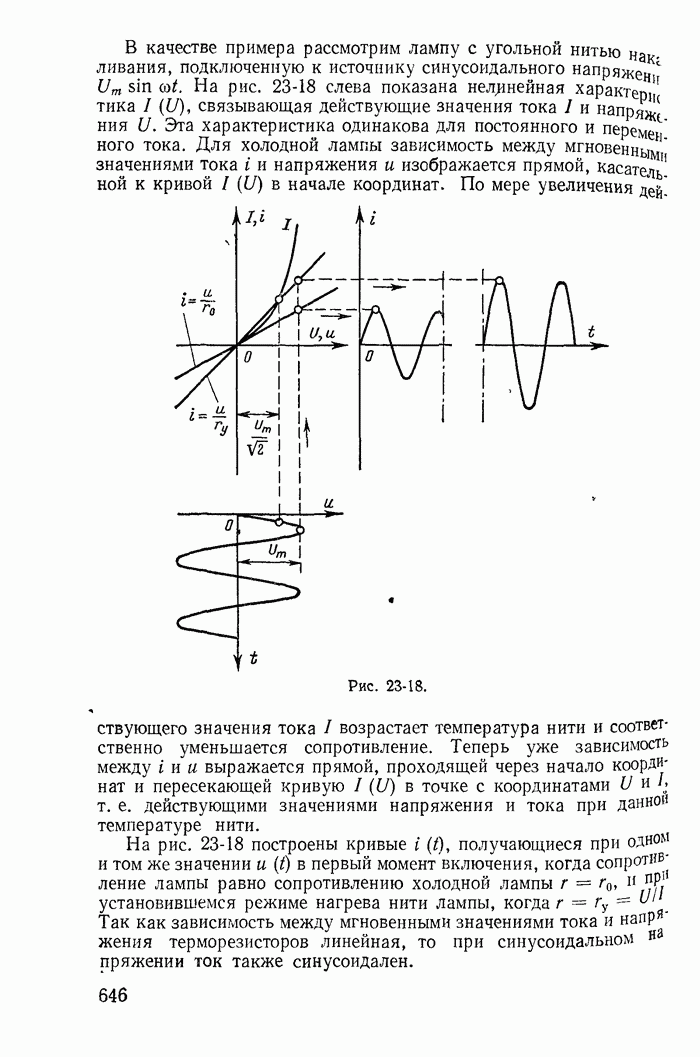
Кривые распределения мгновенных значений тока и напряжения вдоль линии на расстоянии, равном длине волны, при  для трех моментов времени представлены на рис. 18-13. Кривые и выражения (18-76) показывают, что распределение напряжения и тока вдоль линии в каждый данный момент является синусоидальным. Рассматривая их одновременно, видим, как изменяются кривые распределения тока и напряжения по линии на протяжении трети периода. Разумеется, изменение тока или напряжения во времени в любой фиксированной точке линии также будет синусоидальным.
для трех моментов времени представлены на рис. 18-13. Кривые и выражения (18-76) показывают, что распределение напряжения и тока вдоль линии в каждый данный момент является синусоидальным. Рассматривая их одновременно, видим, как изменяются кривые распределения тока и напряжения по линии на протяжении трети периода. Разумеется, изменение тока или напряжения во времени в любой фиксированной точке линии также будет синусоидальным.

Рис. 18-13.
Остановимся еще на свойствах линий без потерь, длиной в четверть и в половину длины волны. При  из уравнений (18-74) получим:
из уравнений (18-74) получим:
 (18-77)
(18-77)
В этом случае напряжение (ток) в начале линии пропорционально току (напряжению) в конце и опережает его по фазе на 90°. Для поддержания постоянного напряжения в конце линии  которое может изменяться вследствие изменения нагрузки на конце линии, необходимо в начале линий поддерживать постоянным не напряжение
которое может изменяться вследствие изменения нагрузки на конце линии, необходимо в начале линий поддерживать постоянным не напряжение  а ток
а ток  .
.
Для линии длиной в полволны  уравнения (18-74) имеем:
уравнения (18-74) имеем:

т. e. напряжение и ток в начале линии равны по величине и противоположны по фазе напряжению и току в конце линии. Если не считать поворота векторов на 180°, питание приемника от источника энергии происходит таким образом, как будто бы самой линии передачи нет.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ К ЧЕТВЕРТОМУ ИЗДАНИЮ
- ВВЕДЕНИЕ
- Раздел первый. ЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ С СОСРЕДОТОЧЕННЫМИ ПАРАМЕТРАМИ
- 1-1. Элементы электрических цепей и электрических схем
- 1-2. Эквивалентные схемы для источников энергии
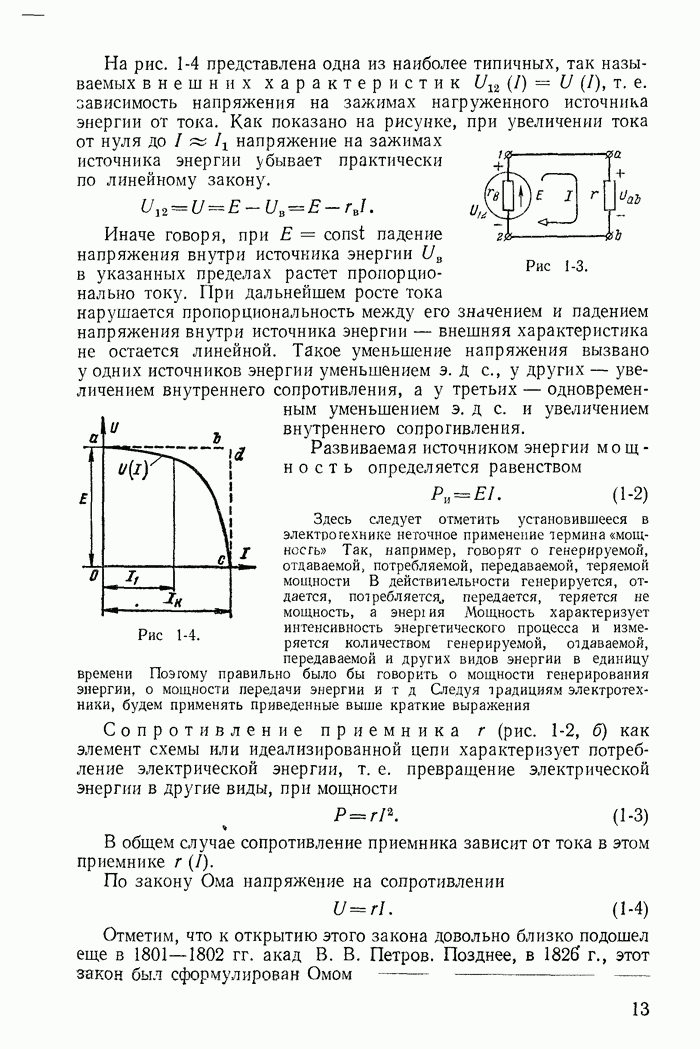
- 1-3. Закон Ома для участка цепи с э. д. с.
- 1-4. Распределение потенциала вдоль неразветвленной электрической цепи
- 1-5. Баланс мощностей для простейшей неразветвленной цепи
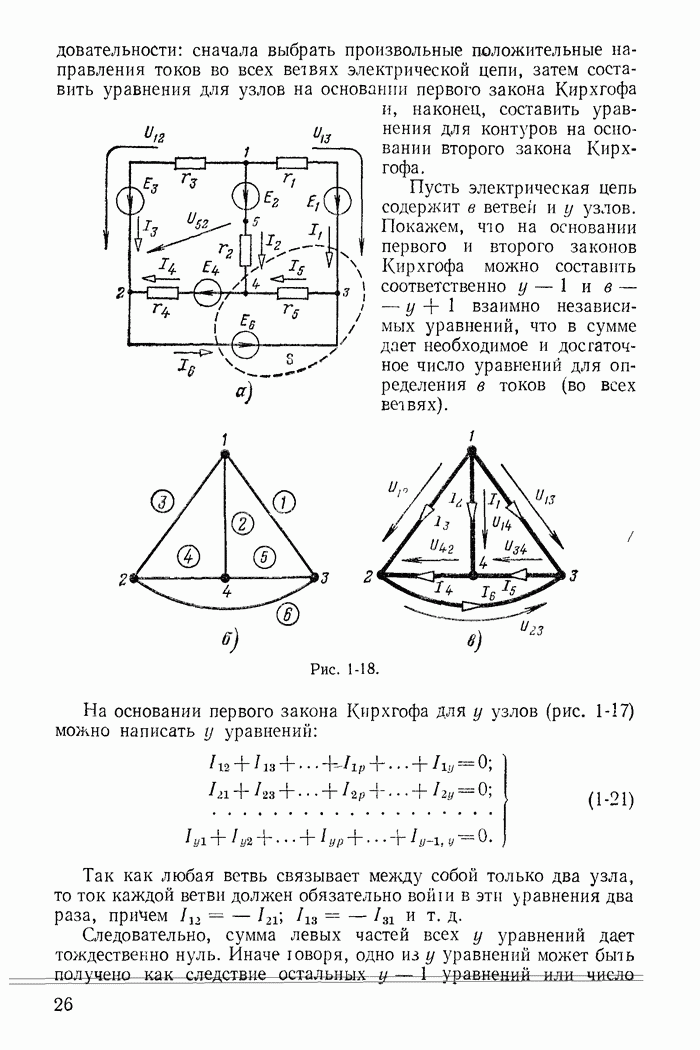
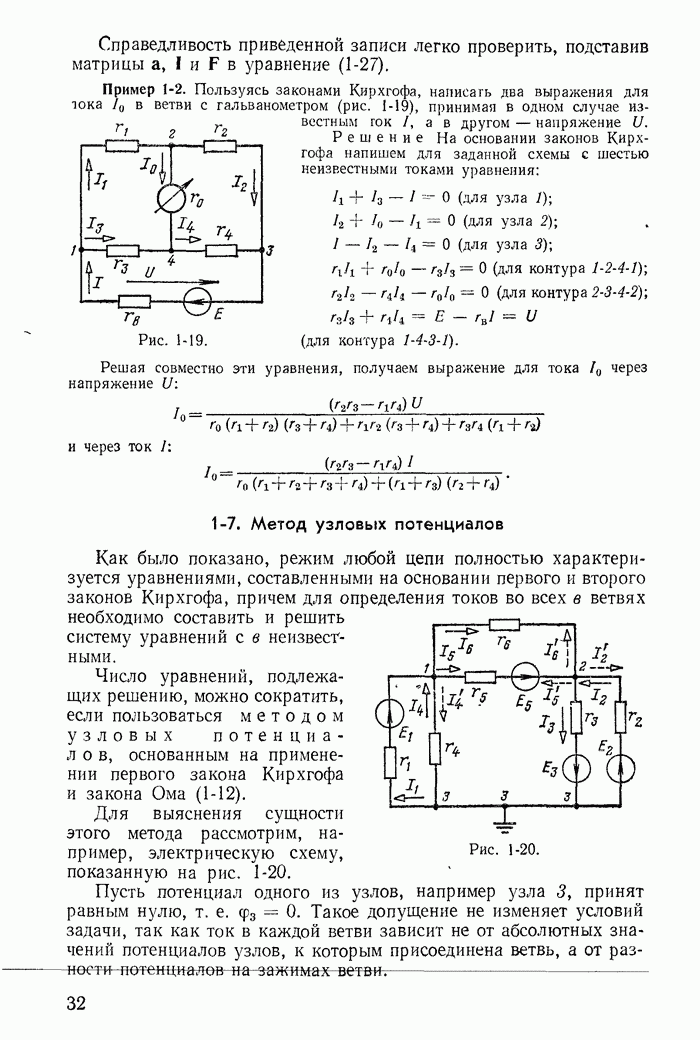
- 1-6. Применение законов Кирхгофа для расчета разветвленных цепей
- 1-7. Метод узловых потенциалов
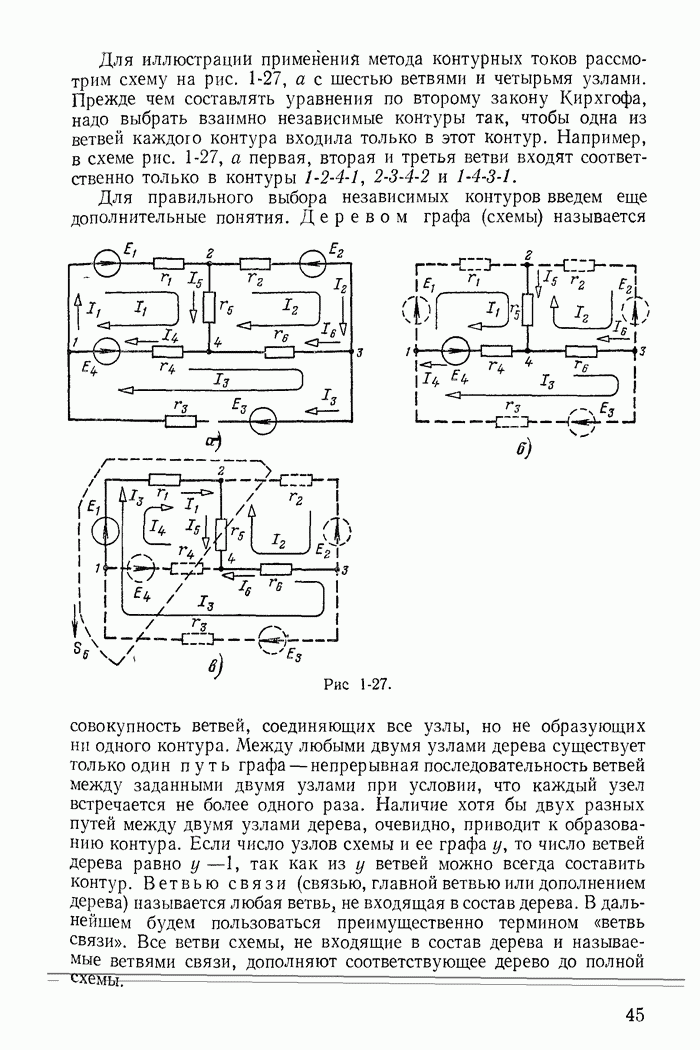
- 1-8. Метод контурных токов
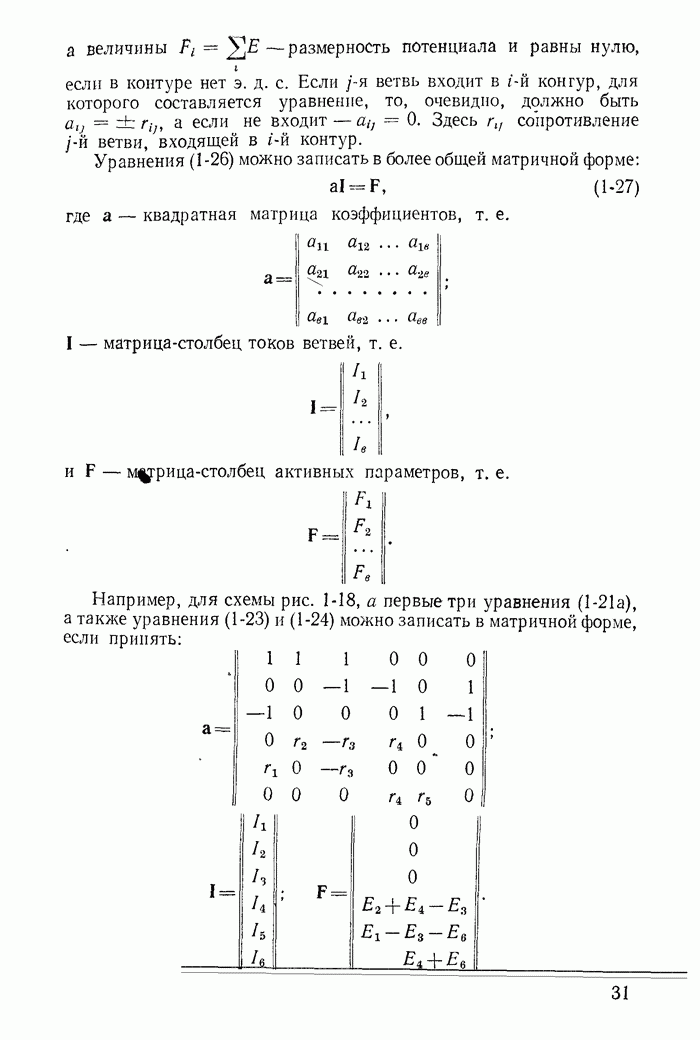
- 1-9. Уравнения состояния цепи в матричной форме
- 1-10. Преобразование линейных электрических схем
- Глава вторая. ОСНОВНЫЕ СВОЙСТВА ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ПРИ ПОСТОЯННЫХ ТОКАХ И НАПРЯЖЕНИЯХ
- 2-2. Свойство взаимности
- 2-3. Входные и взаимные проводимости и сопротивления ветвей; коэффициенты передачи напряжений и токов
- 2-4. Применение топологических методов для расчета цепей
- 2-5. Топологические формулы и правила для определения передачи электрической цепи
- 2-6. Теорема о компенсации
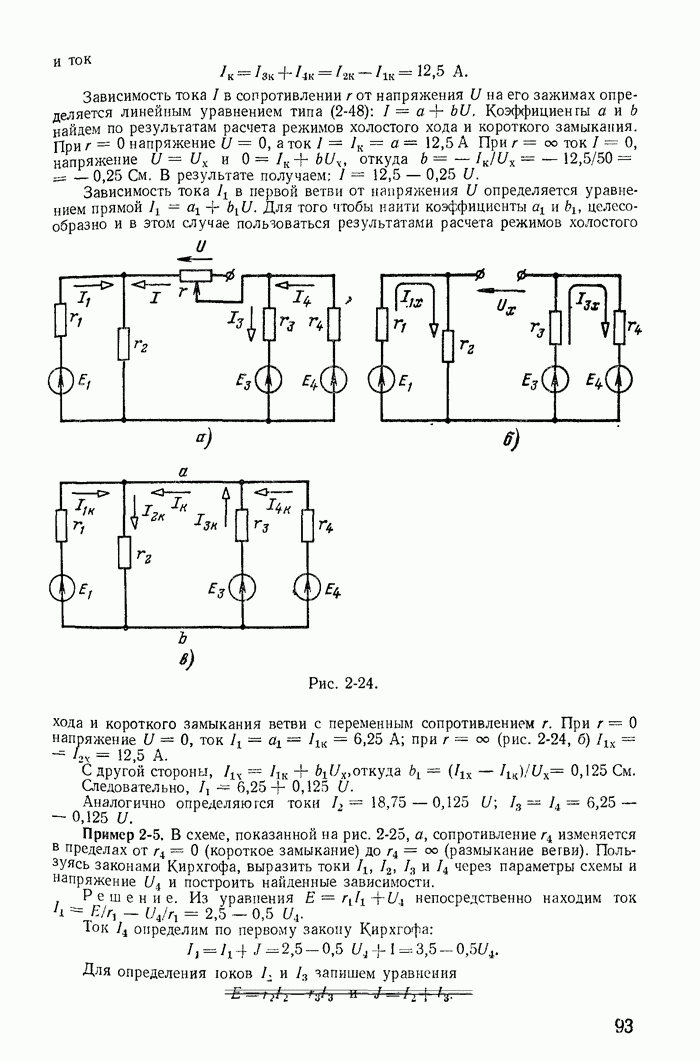
- 2-7. Линейные соотношения между напряжениями и токами
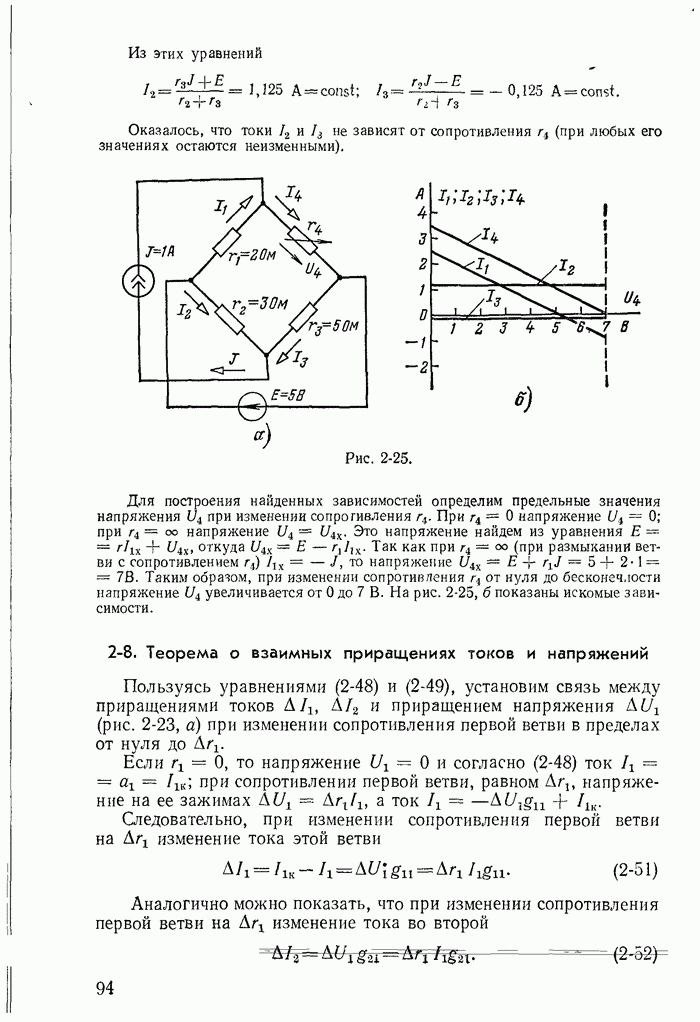
- 2-8. Теорема о взаимных приращениях токов и напряжений
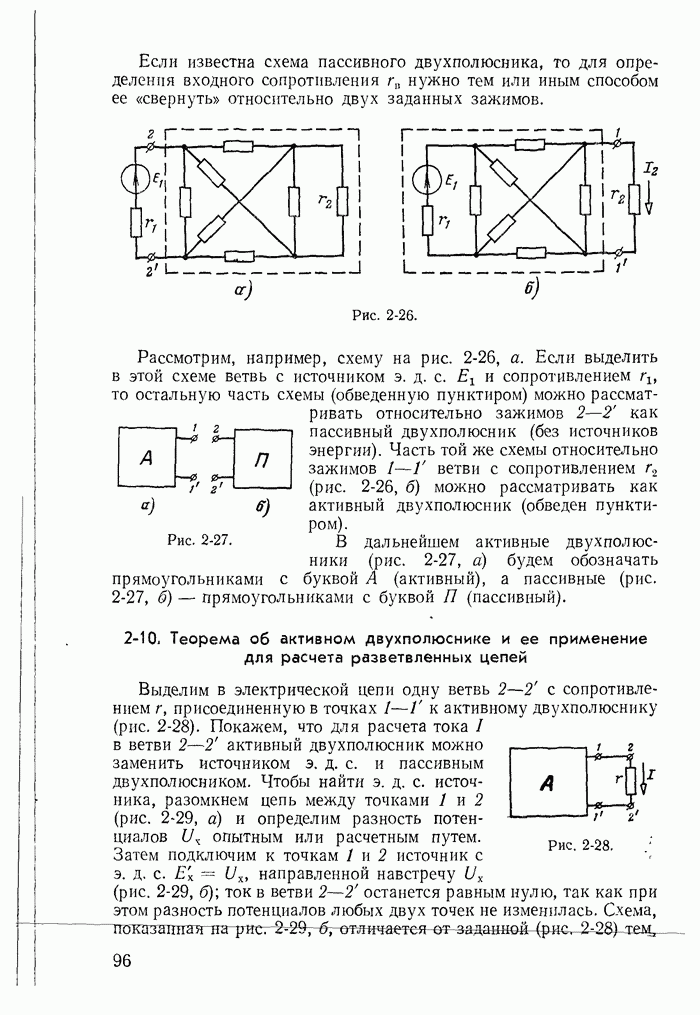
- 2-9. Общие замечания о двухполюсниках
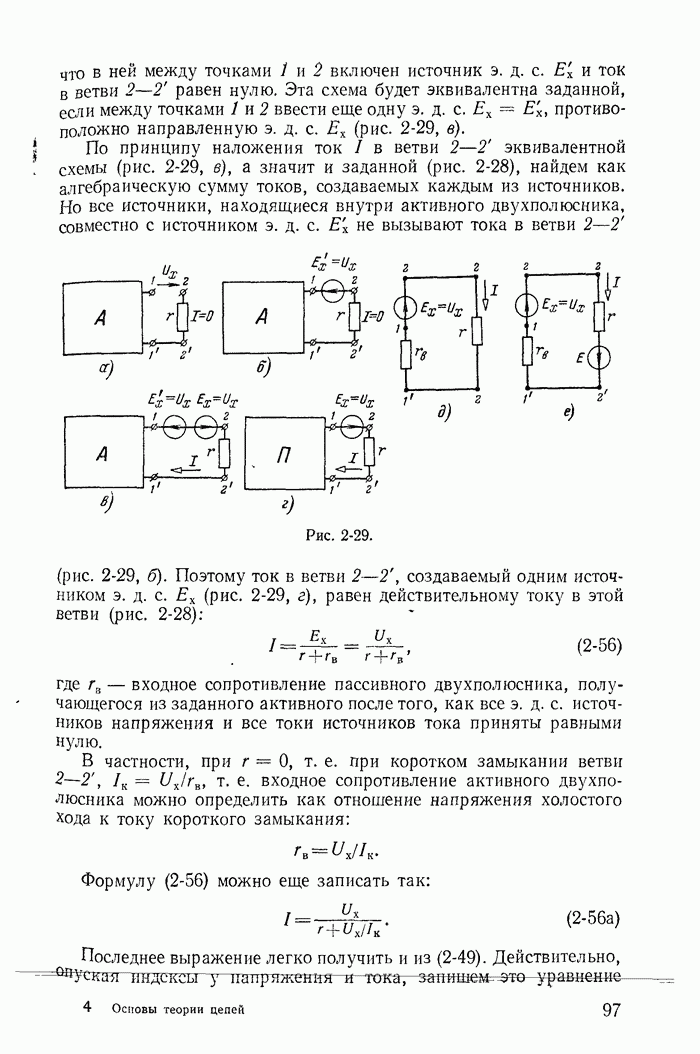
- 2-10. Теорема об активном двухполюснике и ее применение для расчета разветвленных цепей
- 2-11. Передача энергии от активного двухполюсника к пассивному
- Глава третья. ОСНОВНЫЕ ПОНЯТИЯ О ЦЕПЯХ СИНУСОИДАЛЬНОГО ТОКА
- 3-2. Понятие о генераторах переменного тока
- 3-3. Синусоидальный ток
- 3-4. Действующие ток, э. д. с. и напряжение
- 3-5. Изображение синусоидальных функций времени векторами и комплексными числами
- 3-6. Сложение синусоидальных функций времени
- 3-7. Электрическая цепь и ее схема
- 3-8. Ток и напряжения при последовательном соединении сопротивления, Индуктивности и емкости
- 3-9. Сопротивления
- 3-10. Разность фаз напряжения и тока
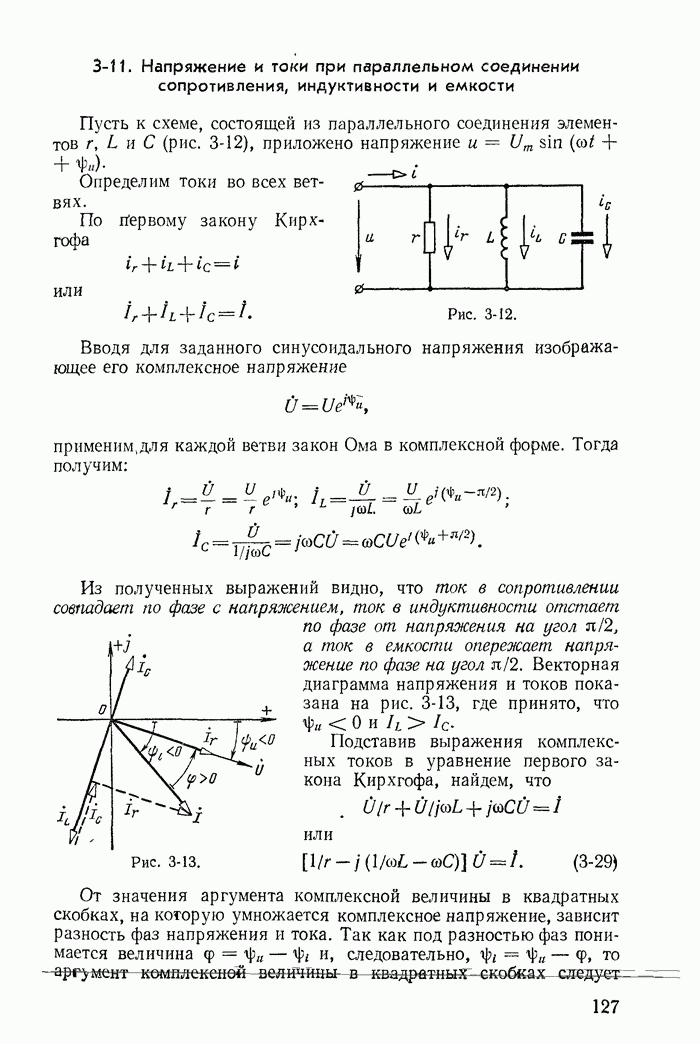
- 3-11. Напряжение и токи при параллельном соединении сопротивления, индуктивности и емкости
- 3-12. Проводимости
- 3-13. Пассивный двухполюсник
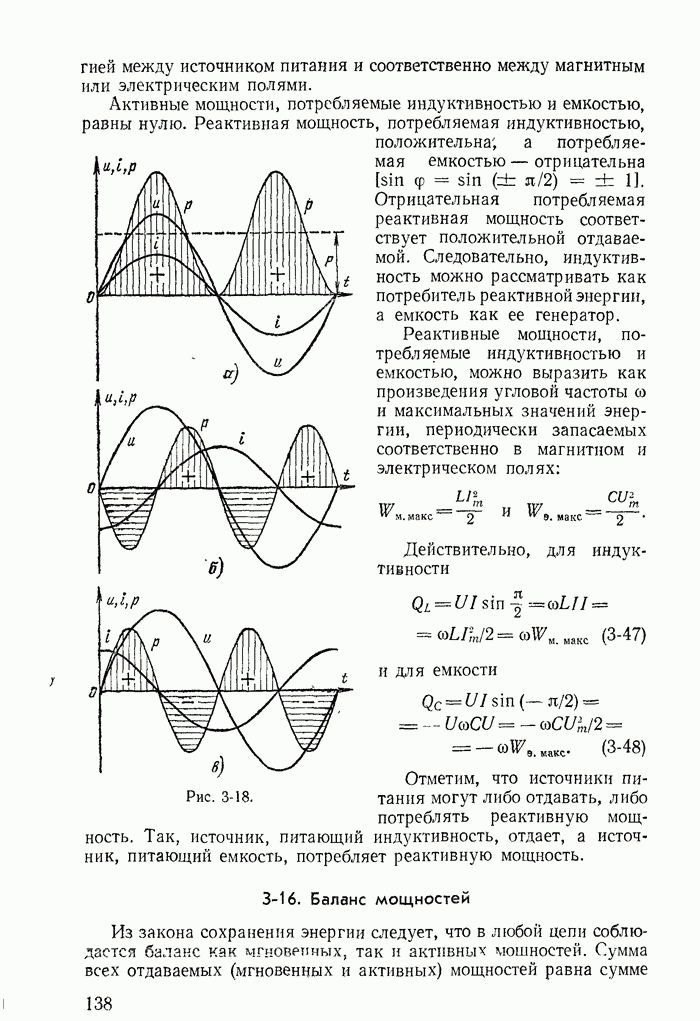
- 3-14. Мощности
- 3-15. Мощности в сопротивлении, индуктивности и емкости
- 3-16. Баланс мощностей
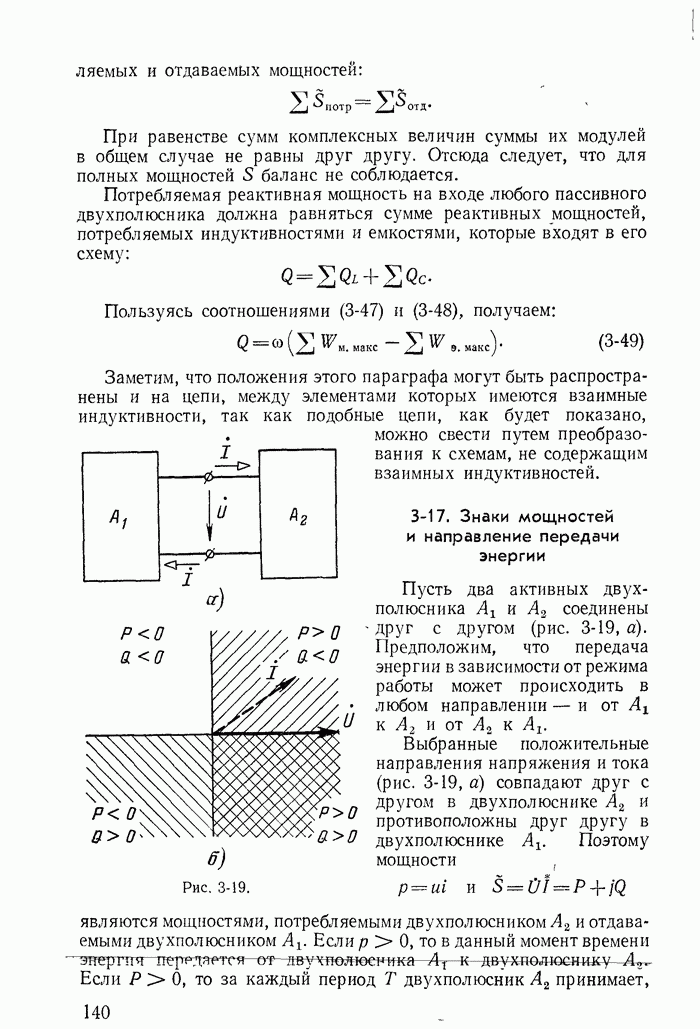
- 3-17. Знаки мощностей и направление передачи энергии
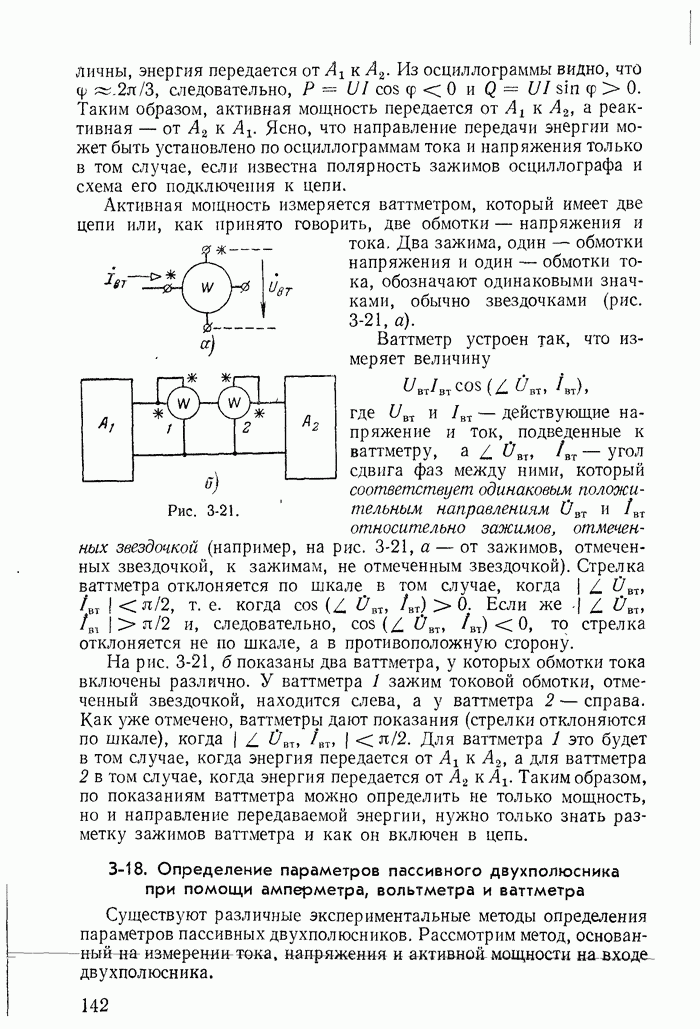
- 3-18. Определение параметров пассивного двухполюсника при помощи амперметра, вольтметра и ваттметра
- 3-19. Условия передачи максимальной мощности от источника энергии к приемнику
- 3-20. Понятие о поверхностном эффекте и эффекте близости
- 3-21. Параметры и эквивалентные схемы конденсаторов
- 3-22. Параметры и эквивалентные схемы индуктивных катушек и резисторов
- Глава четвертая. РАСЧЕТ ЦЕПЕЙ ПРИ СИНУСОИДАЛЬНЫХ ТОКАХ
- 4-1. О применимости методов расчета цепей постоянного тока к расчетам цепей синусоидального тока
- 4-2. Последовательное соединение приемников
- 4-3. Параллельное соединение приемников
- 4-4. Смешанное соединение приемников
- 4-5. Сложные разветвленные цепи
- 4-6. Топографические диаграммы
- 4-7. Дуальность электрических цепей
- 4-8. Сигнальные графы и их применение для расчета цепей
- Глава пятая. РЕЗОНАНС В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ
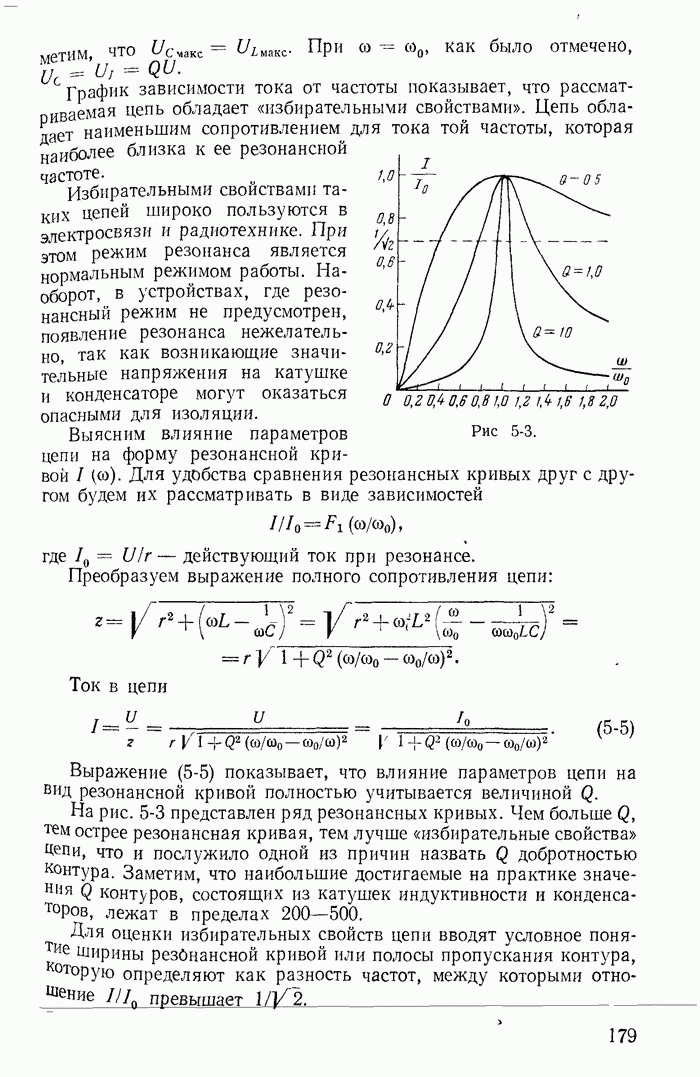
- 5-2. Частотные характеристики неразветвленной цепи
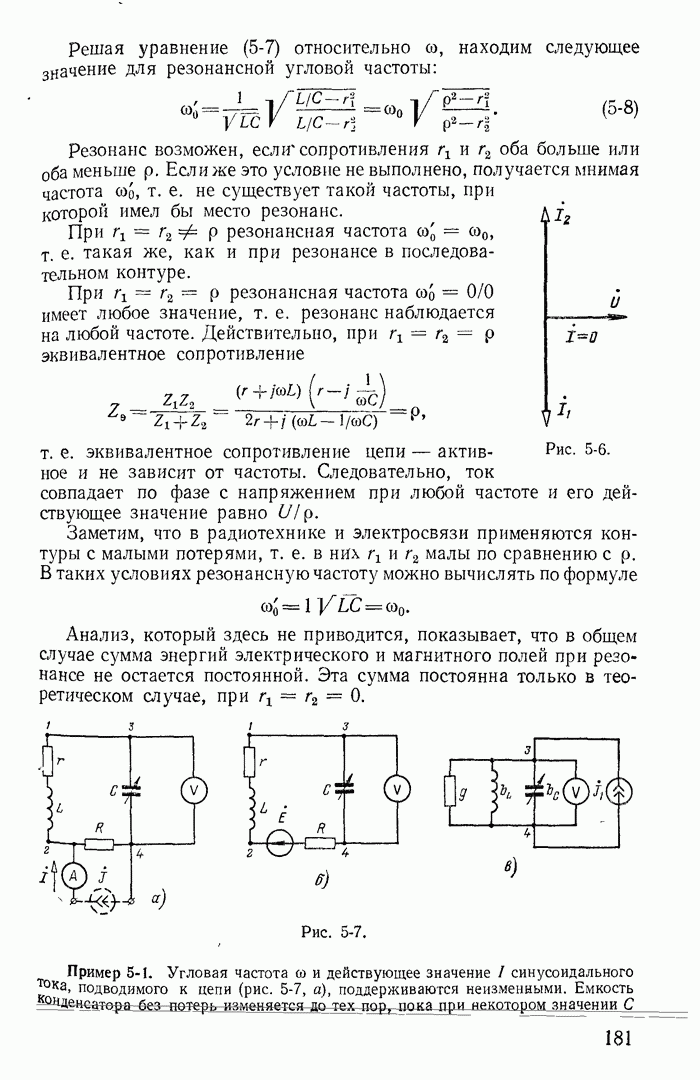
- 5-3. Резонанс в цепи с двумя параллельными ветвями
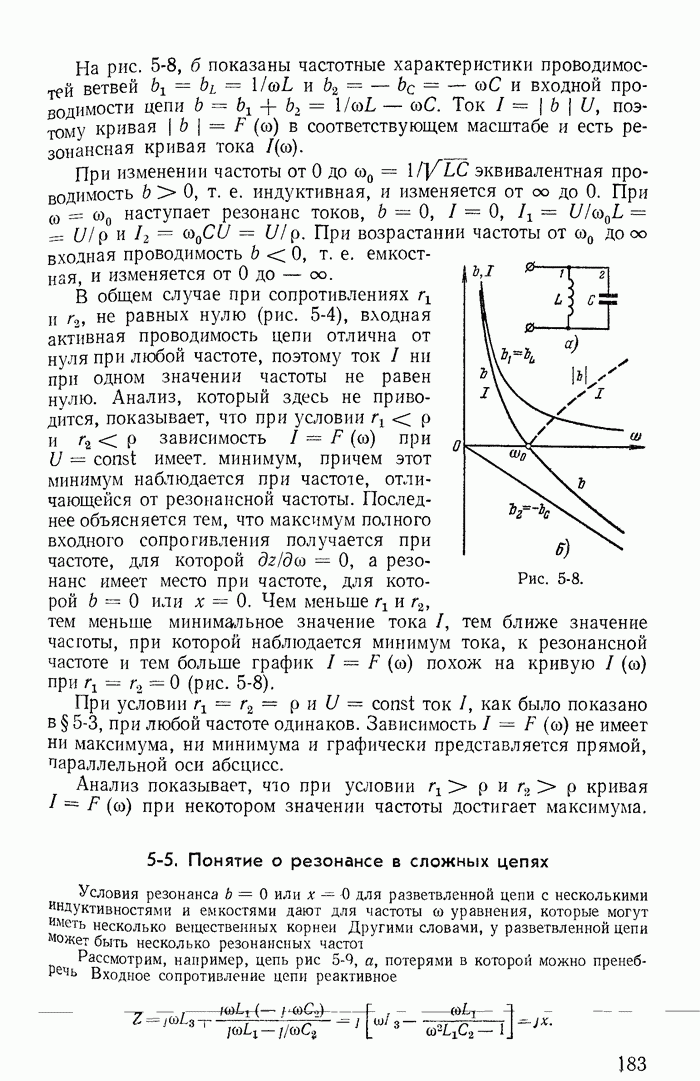
- 5-4. Частотные характеристики параллельного контура
- 5-5. Понятие о резонансе в сложных цепях
- Глава шестая. ЦЕПИ С ВЗАИМНОЙ ИНДУКТИВНОСТЬЮ
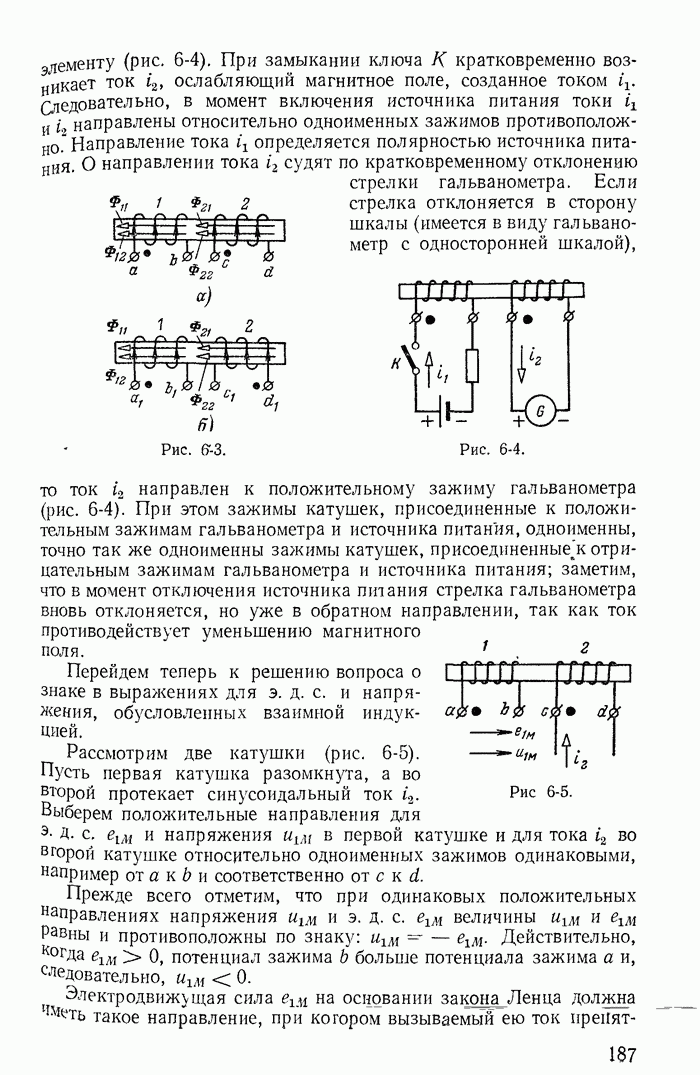
- 6-2. Электродвижущая сила взаимной индукции
- 6-3. Последовательное соединение индуктивно связанных элементов цепи
- 6-4. Параллельное соединение индуктивно связанных элементов цепи
- 6-5. Расчеты разветвленных цепей при наличии взаимной индуктивности
- 6-6. Эквивалентная замена индуктивных связей
- 6-7. Передача энергии между индуктивно связанными элементами цепи
- 6-8. Трансформатор без стального сердечника (воздушный трансформатор)
- Глава седьмая. КРУГОВЫЕ ДИАГРАММЫ
- 7-1. Комплексные уравнения прямой и окружности
- 7-2. Круговые диаграммы для неразветвленной цепи и для активного двухполюсника
- 7-3. Круговые диаграммы для любой разветвленной цепи
- Глава восьмая. МНОГОПОЛЮСНИКИ И ЧЕТЫРЕХПОЛЮСНИКИ ПРИ СИНУСОИДАЛЬНЫХ ТОКАХ И НАПРЯЖЕНИЯХ
- 8-1. Четырехполюсники и их основные уравнения
- 8-2. Определение коэффициентов четырехполюсников
- 8-3. Режим четырехполюсника при нагрузке
- 8-4. Эквивалентные схемы четырехполюсников
- 8-5. Основные уравнения и эквивалентные схемы для активного четырехполюсника
- 8-6. Идеальный трансформатор как четырехполюсник
- 8-7. Эквивалентные схемы с идеальными трансформаторами для четырехполюсника
- 8-8. Эквивалентные схемы трансформатора со стальным магнитопроводом
- 8-9. Расчеты электрических цепей с трансформаторами
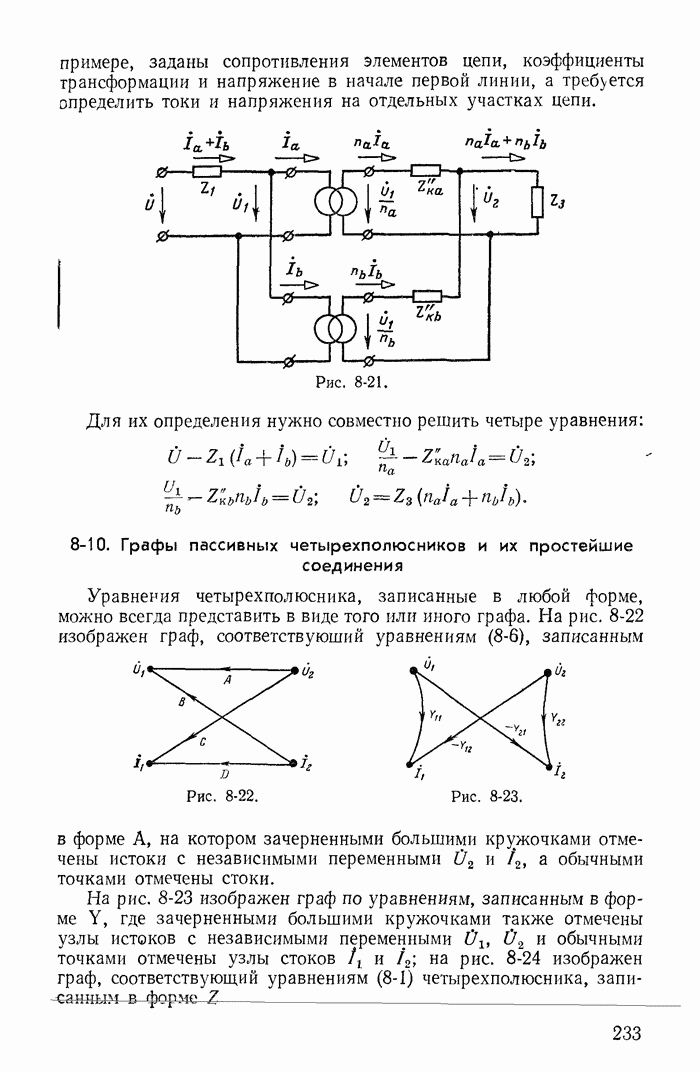
- 8-10. Графы пассивных четырехполюсников и их простейшие соединения
- Глава девятая. ЦЕПИ С ЭЛЕКТРОННЫМИ И ПОЛУПРОВОДНИКОВЫМИ ПРИБОРАМИ В ЛИНЕЙНОМ РЕЖИМЕ
- 9-2. Эквивалентные схемы лампового триода
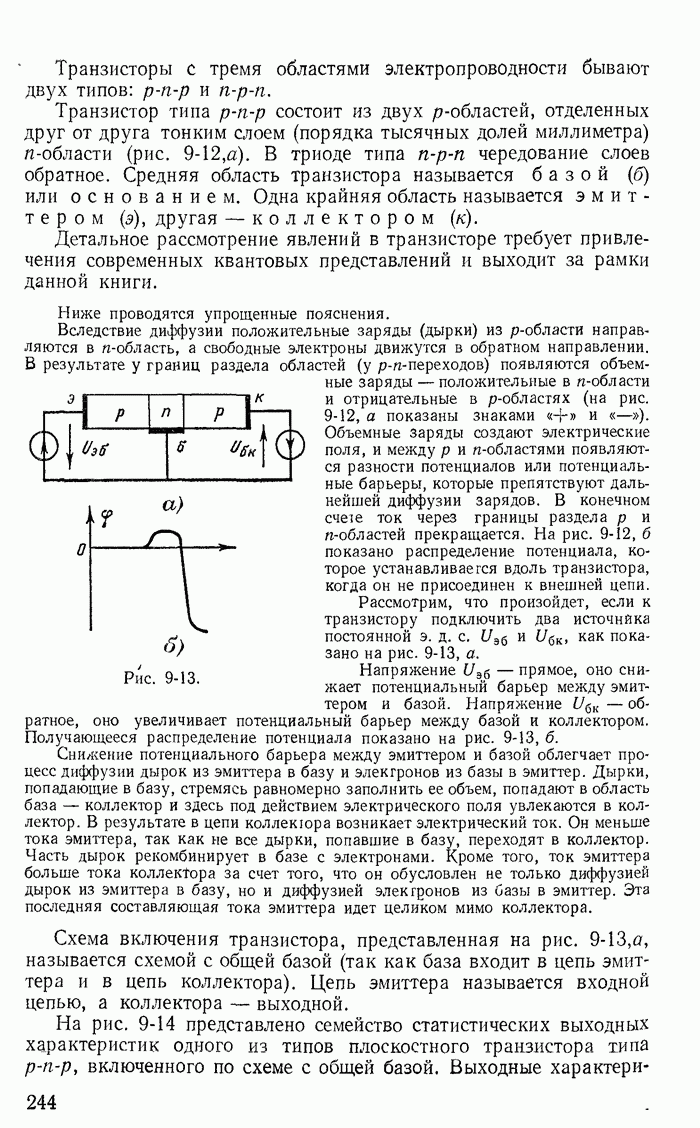
- 9-3. Транзисторы (полупроводниковые триоды)
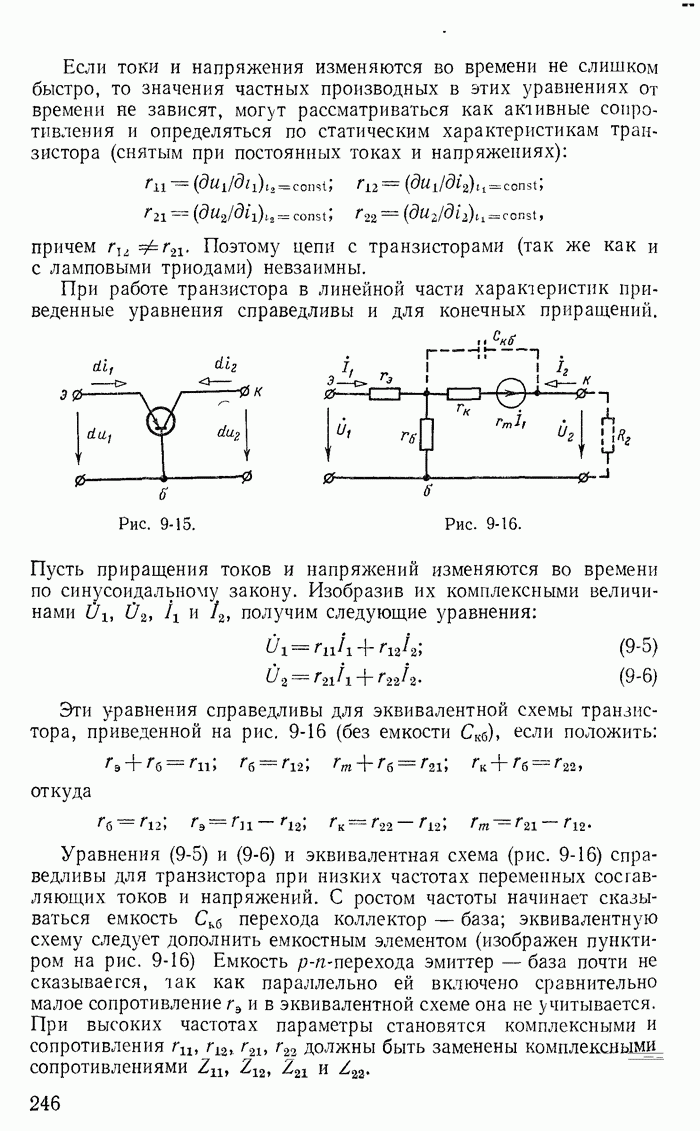
- 9-4. Эквивалентные схемы транзисторов
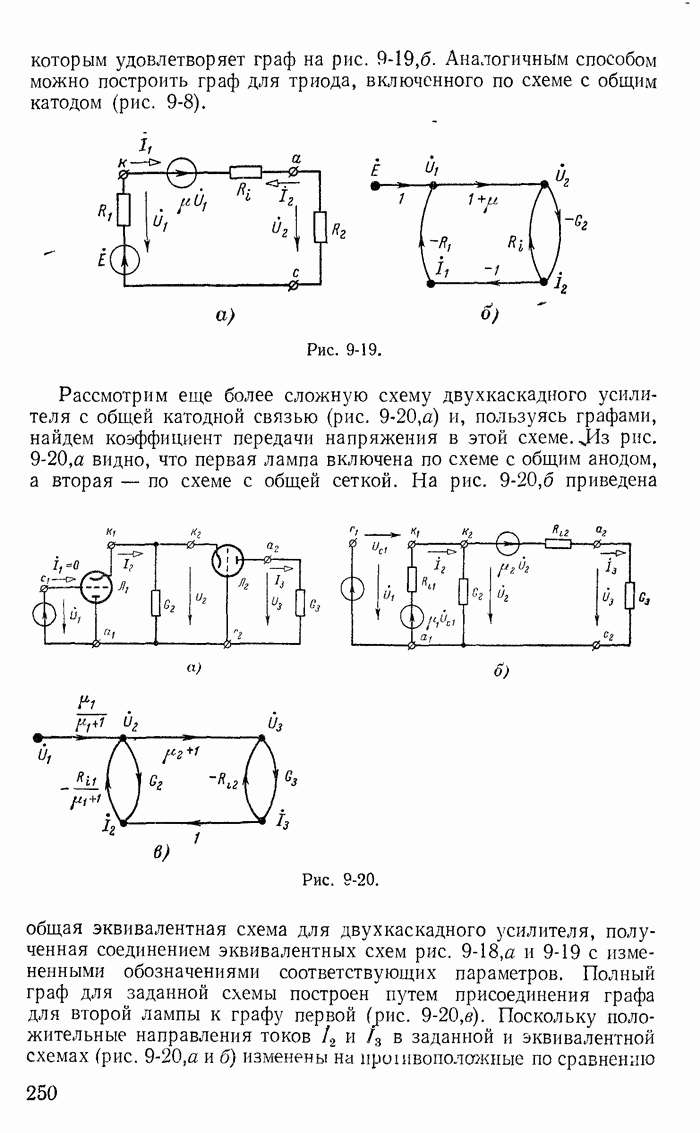
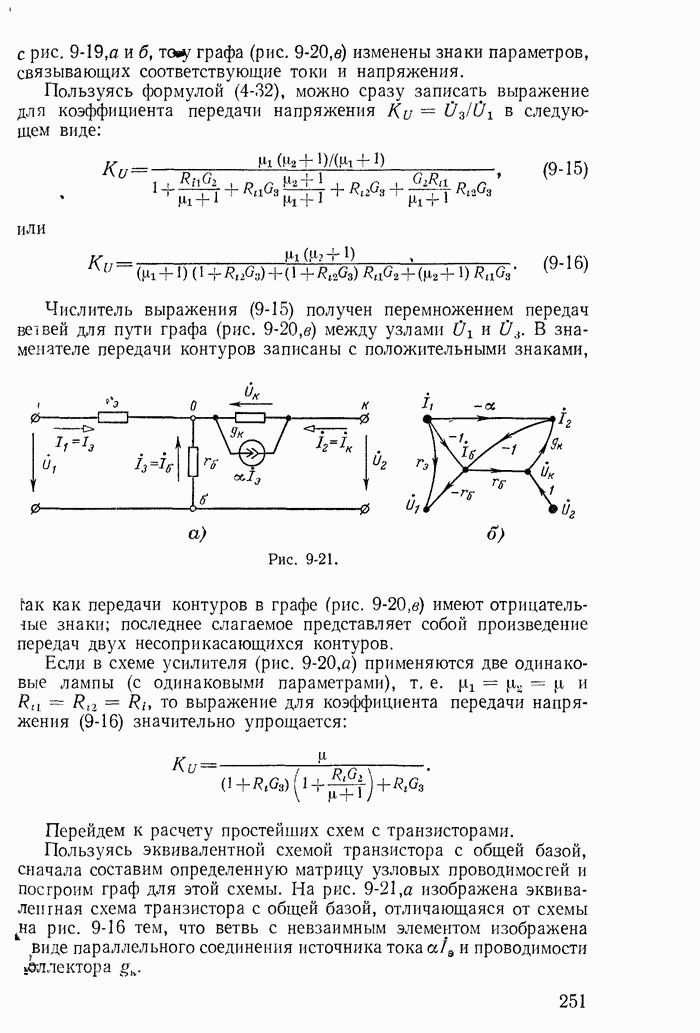
- 9-5. Простейшие электрические цепи с невзаимными элементами и их направленные графы
- Глава десятая. ТРЕХФАЗНЫЕ ЦЕПИ
- 10-2. Соединения звездой и многоугольником
- 10-3. Симметричный режим трехфазной цепи
- 10-4. Некоторые свойства трехфазных цепей с различными схемами соединений
- 10-5. Расчет симметричных режимов трехфазных цепей
- 10-6. Расчет несимметричных режимов трехфазных цепей со статической нагрузкой
- 10-7. Напряжения на фазах приемника в некоторых частных случаях
- 10-8. Эквивалентные схемы трехфазных линий
- 10-9. Измерение мощности в трехфазных цепях
- 10-10. Вращающееся магнитное поле
- 10-11. Принципы действия асинхронного и синхронного двигателей
- Глава одиннадцатая. МЕТОД СИММЕТРИЧНЫХ СОСТАВЛЯЮЩИХ
- 11-2. Некоторые свойства трехфазных цепей в отношении симметричных составляющих токов и напряжений
- 11-3. Сопротивления симметричной трехфазной цепи для токов различных последовательностей
- 11-4. Определение токов в симметричной цепи
- 11-5. Симметричные составляющие напряжений и токов в несимметричной трехфазной цепи
- 11-6. Расчет цепи с несимметричной нагрузкой
- 11-7. Расчет цепи с несимметричным участком в линии
- Глава двенадцатая. НЕСИНУСОИДАЛЬНЫЕ ТОКИ
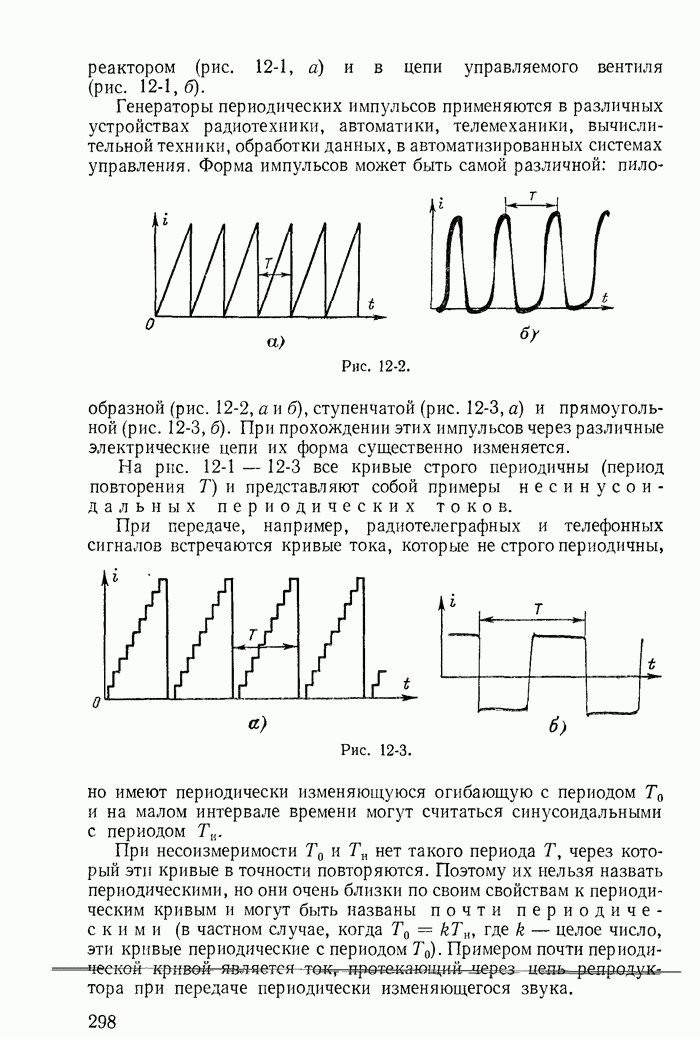
- 12-2. Разложение периодической несинусоидальной кривой в тригонометрический ряд
- 12-3. Максимальные, действующие и средние значения несинусоидальных периодических э. д. с., напряжений и токов
- 12-4. Коэффициенты, характеризующие форму несинусоидальных периодических кривых
- 12-5. Несинусоидальные кривые с периодической огибающей
- 12-6. Действующие значения э. д. с., напряжений и токов с периодическими огибающими
- 12-7. Расчет цепей с несинусоидальными периодическими э. д. с. и токами
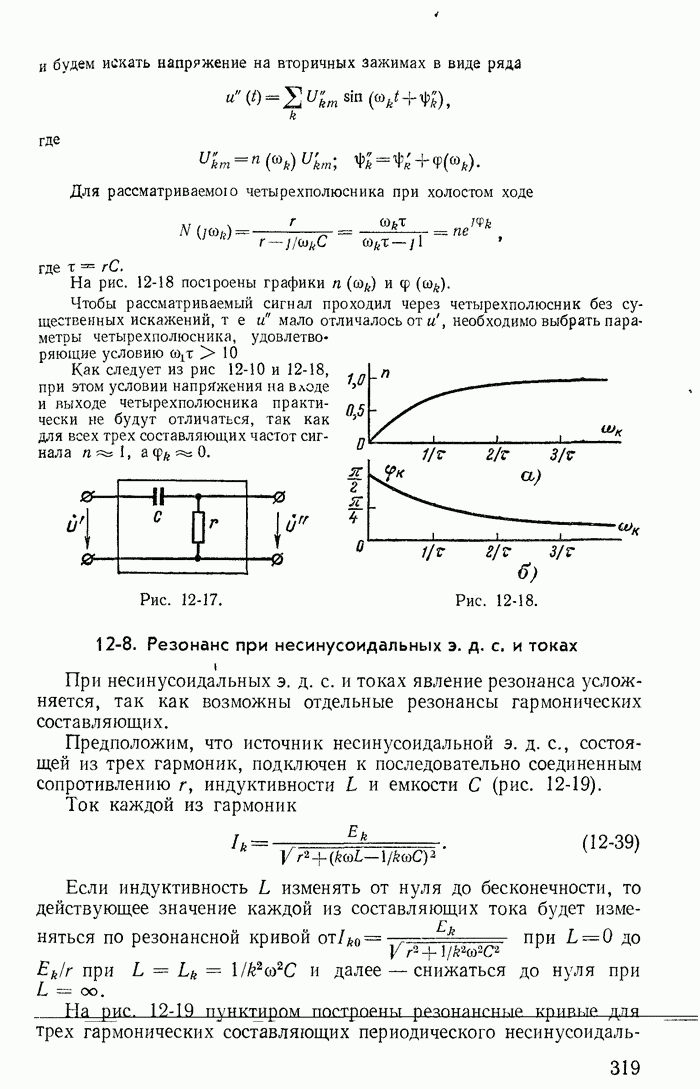
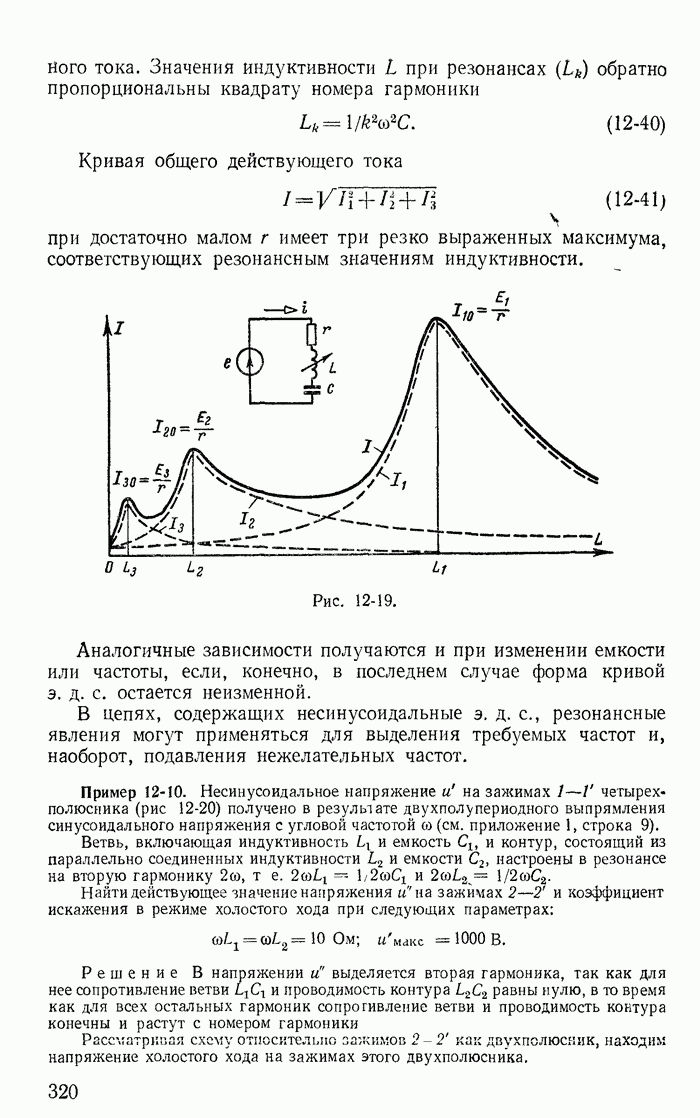
- 12-8. Резонанс при несинусоидальных э. д. с. и токах
- 12-9. Мощность периодических несинусоидальных токов
- 12-10. Высшие гармоники в трехфазных цепях
- Глава тринадцатая. КЛАССИЧЕСКИЙ МЕТОД РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ
- 13-2. Переходный, принужденный и свободный процессы
- 13-3. Короткое замыкание цепи r, L
- 13-4. Включение цепи r, L на постоянное напряжение
- 13-5. Включение цепи r, L на синусоидальное напряжение
- 13-6. Короткое замыкание цепи r, С
- 13-7. Включение цепи r, С на постоянное напряжение
- 13-8. Включение цепи r, С на синусоидальное напряжение
- 13-9. Переходные процессы в неразветвленной цепи r, С
- 13-10. Апериодический разряд конденсатора
- 13-11. Предельный случай апериодического разряда конденсатора
- 13-12. Периодический (колебательный) разряд конденсатора
- 13-13. Включение цепи r, С на постоянное напряжение
- 13-14. Общий случай расчета переходных процессов классическим методом
- 13-15. Включение пассивного двухполюсника на непрерывно изменяющееся напряжение (формула или интеграл Дюамеля)
- 13-16. Включение пассивного двухполюсника на напряжение любой формы
- 13-17. Временная и импульсная переходные характеристики
- 13-18. Запись теоремы свертки при помощи импульсной переходной характеристики
- 13-19. Переходные процессы при скачках токов в индуктивностях и напряжений на конденсаторах
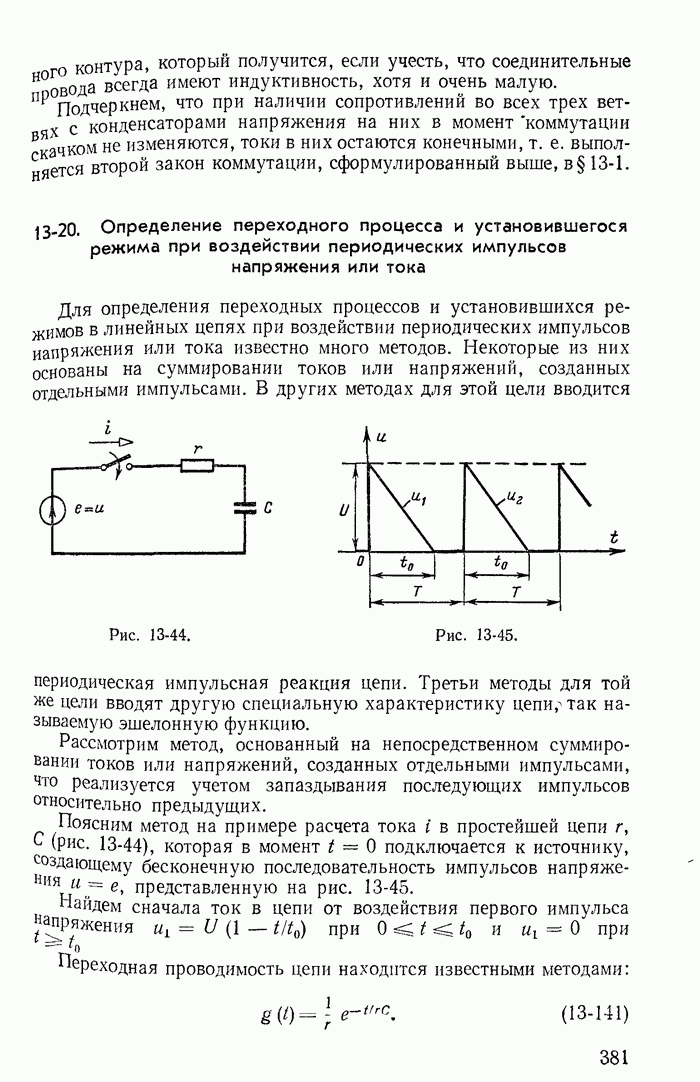
- 13-20. Определение переходного процесса и установившегося режима при воздействии периодических импульсов напряжения или тока
- Глава четырнадцатая. ОПЕРАТОРНЫЙ МЕТОД РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ
- 14-2. Законы Ома и Кирхгофа в операторной форме
- 14-3. Эквивалентные операторные схемы
- 14-4. Переходные процессы в цепях с взаимной индуктивностью
- 14-5. Сведение расчетов переходных процессов к нулевым начальным условиям
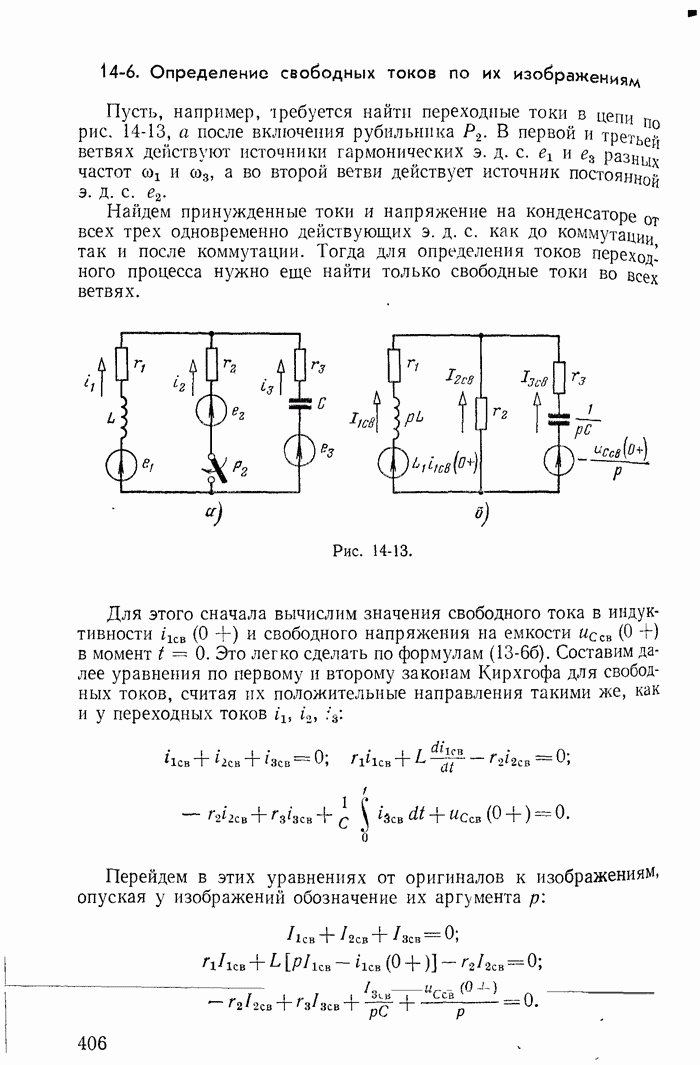
- 14-6. Определение свободных токов по их изображениям
- 14-7. Формулы включения
- 14-8. Расчет переходных процессов методом переменных состояния
- 14-9. Определение принужденного режима цепи при воздействии на нее периодического несинусоидального напряжения
- Глава пятнадцатая. ЧАСТОТНЫЙ МЕТОД РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ
- 15-2. Законы Ома и Кирхгофа и эквивалентные схемы для частотных спектров
- 15-3. Приближенный метод определения оригинала по вещественной частотной характеристике (метод трапеций)
- 15-4. О переходе от преобразований Фурье к преобразованиям Лапласа
- 15-5. Сравнение различных методов расчета переходных процессов в линейных электрических цепях
- Глава шестнадцатая. ЦЕПНЫЕ СХЕМЫ И ЧАСТОТНЫЕ ЭЛЕКТРИЧЕСКИЕ ФИЛЬТРЫ
- 16-2. Характеристическое сопротивление и постоянная передачи симметричного четырехполюсника
- 16-3. Вносимая и рабочая постоянные передачи
- 16-4. Цепные схемы
- 16-5. Частотные электрические фильтры
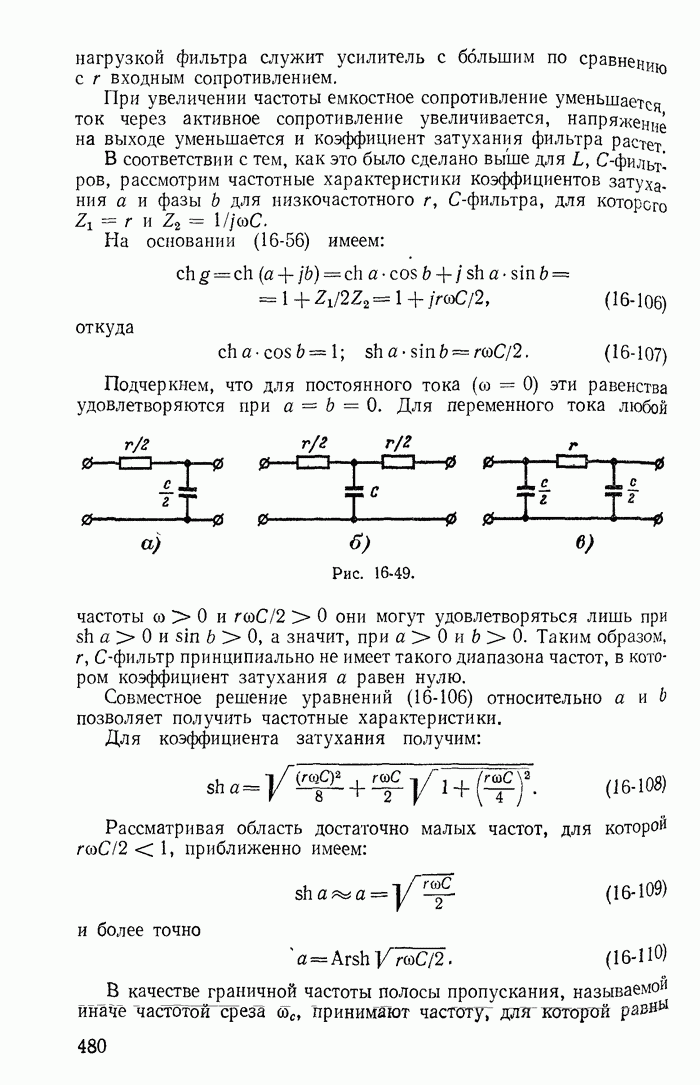
- 16-6. Низкочастотные фильтры
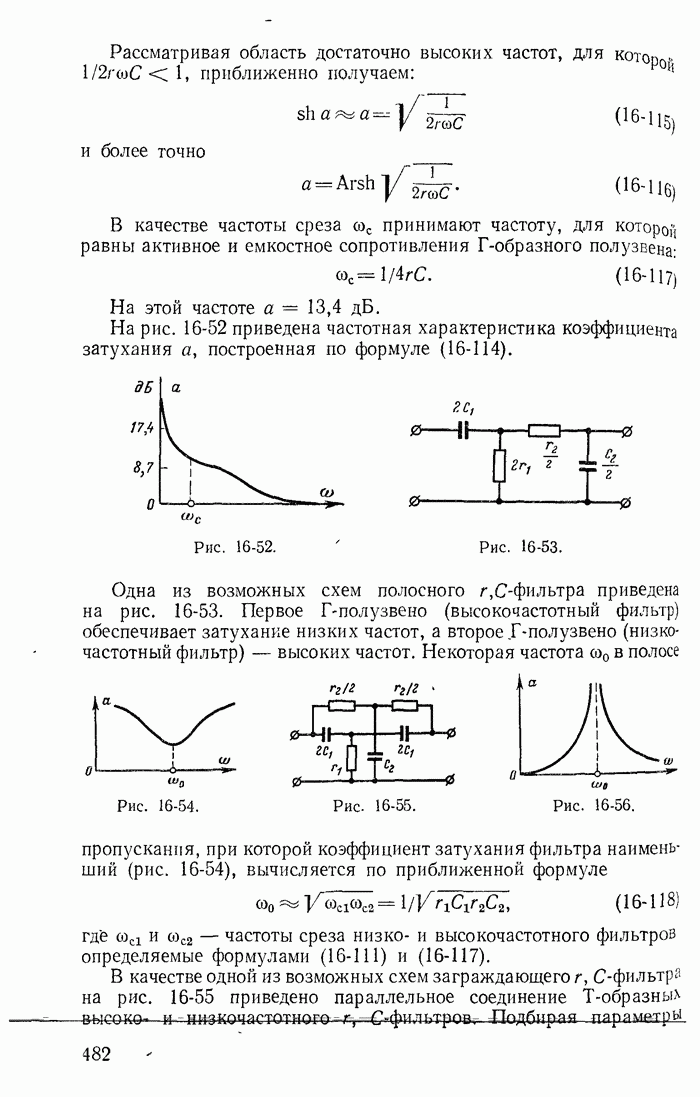
- 16-8. Полосные фильтры
- 16-11. Г-образный фильтр как пример несимметричного фильтра
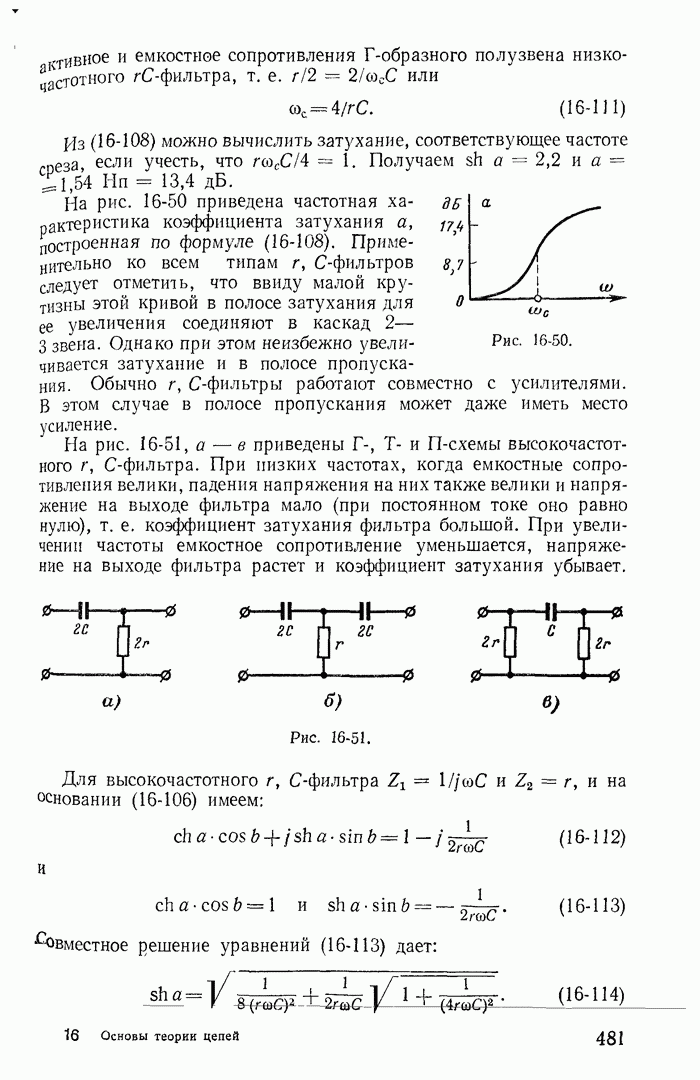
- 16-12. Безындукционные (или r, C) фильтры
- Глава семнадцатая. СИНТЕЗ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
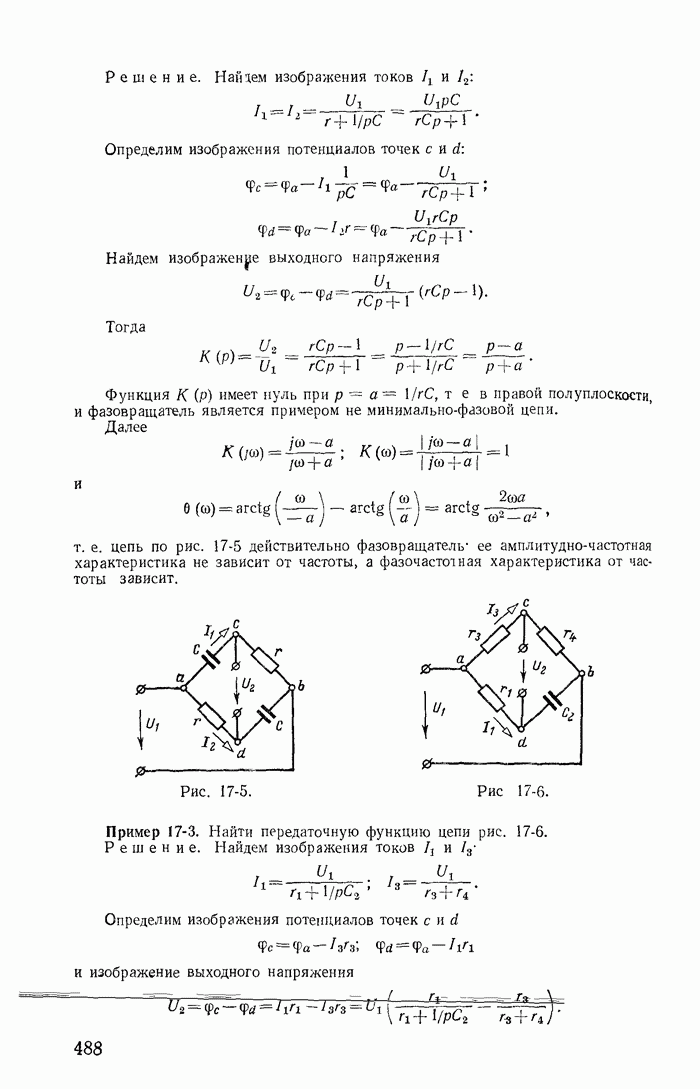
- 17-2. Передаточная функция четырехполюсника. Цепи минимальной фазы
- 17-3. Входные функции цепей. Положительные вещественные функции
- 17-4. Реактивные двухполюсники
- 17-5. Частотные характеристики реактивных двухполюсников
- 17-6. Синтез реактивных двухполюсников. Метод Фостера
- 17-7. Синтез реактивных двухполюсников. Метод Кауэра
- 17-8. Синтез двухполюсников с потерями. Метод Фостера
- 17-9. Синтез двухполюсников с потерями. Метод Кауэра
- 17-10. Понятие о синтезе четырехполюсников
- Раздел второй. ЛИНЕЙНЫЕ ЦЕПИ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
- Глава восемнадцатая. ГАРМОНИЧЕСКИЕ ПРОЦЕССЫ В ЦЕПЯХ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
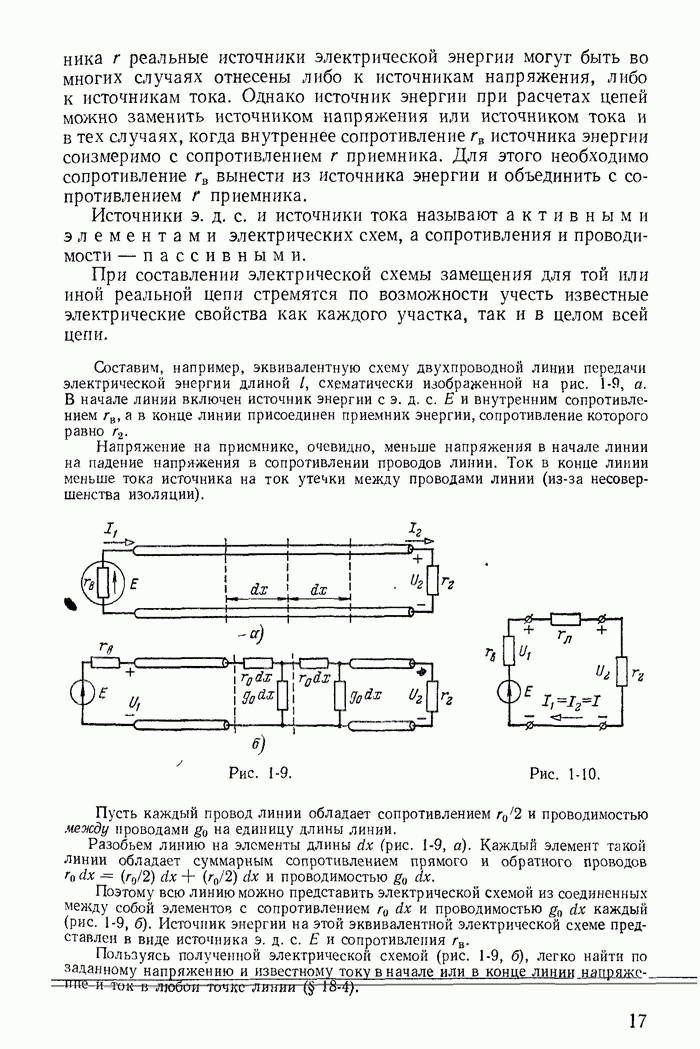
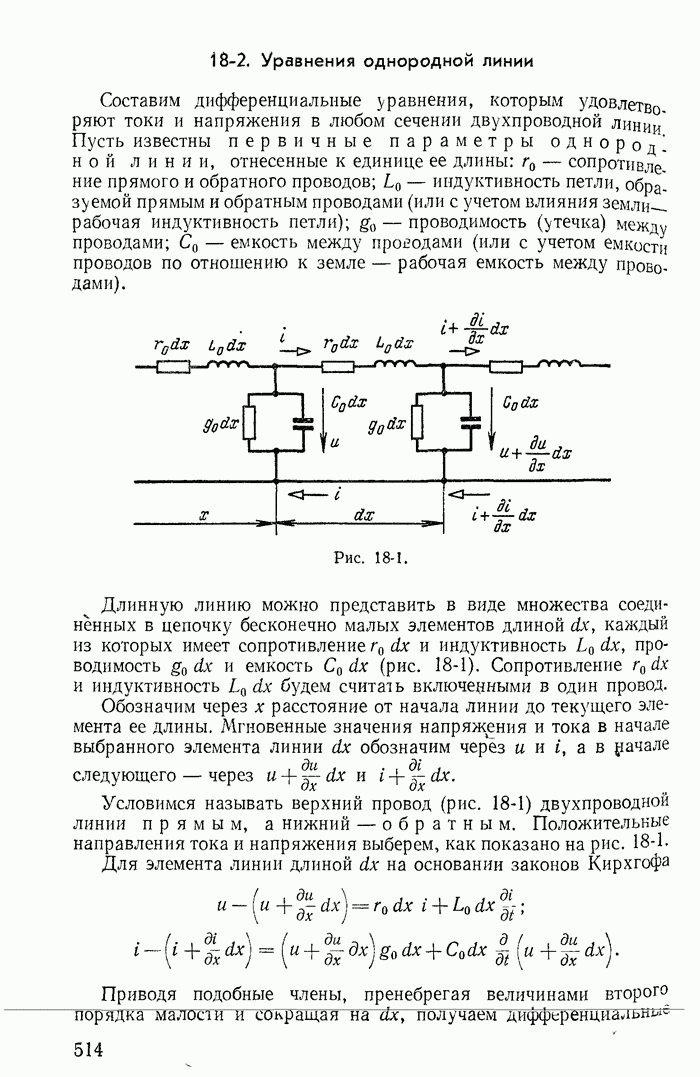
- 18-2. Уравнения однородной линии
- 18-3. Установившийся режим в однородной линии
- 18-4. Уравнения однородной линии с гиперболическими функциями
- 18-5. Характеристики однородной линии
- 18-6. Входное сопротивление линии
- 18-7. Коэффициент отражения волны
- 18-8. Согласованная нагрузка линии
- 18-9. Линия без искажений
- 18-10. Холостой ход, короткое замыкание и нагрузочный режим линии с потерями
- 18-11. Линии без потерь
- 18-12. Стоячие волны
- 18-13. Линия как четырехполюсник
- Глава девятнадцатая. ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЦЕПЯХ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
- 19-2. Общее решение уравнений однородной линии
- 19-3. Возникновение волн с прямоугольным фронтом
- 19-4. Общие случаи нахождения волн, возникающих при переключениях
- 19-5. Отражение волны с прямоугольным фронтом от конца линии
- 19-6. Общий метод определения отраженных волн
- 19-7. Качественное рассмотрение переходных процессов в линиях, содержащих сосредоточенные емкости и индуктивности
- 19-8. Многократные отражения волн с прямоугольным фронтом от активного сопротивления
- 19-9. Блуждающие волны
- Раздел III. НЕЛИНЕЙНЫЕ ЦЕПИ
- Глава двадцатая. НЕЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПРИ ПОСТОЯННЫХ ТОКАХ И НАПРЯЖЕНИЯХ
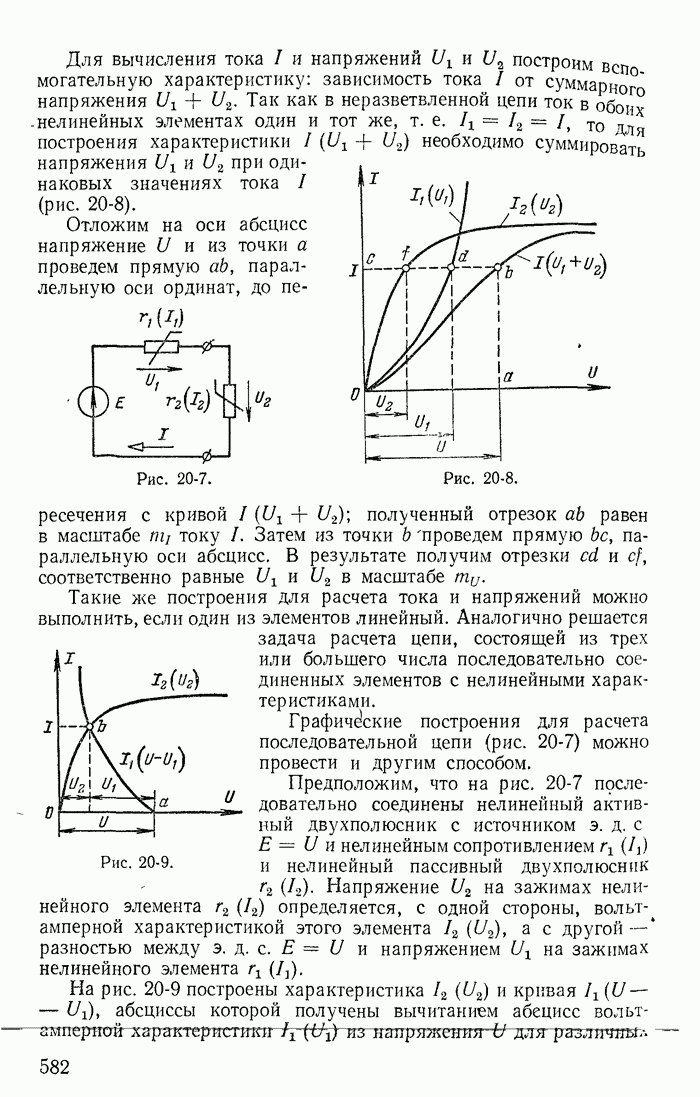
- 20-2. Графический метод расчета неразветвленных цепей с нелинейными элементами
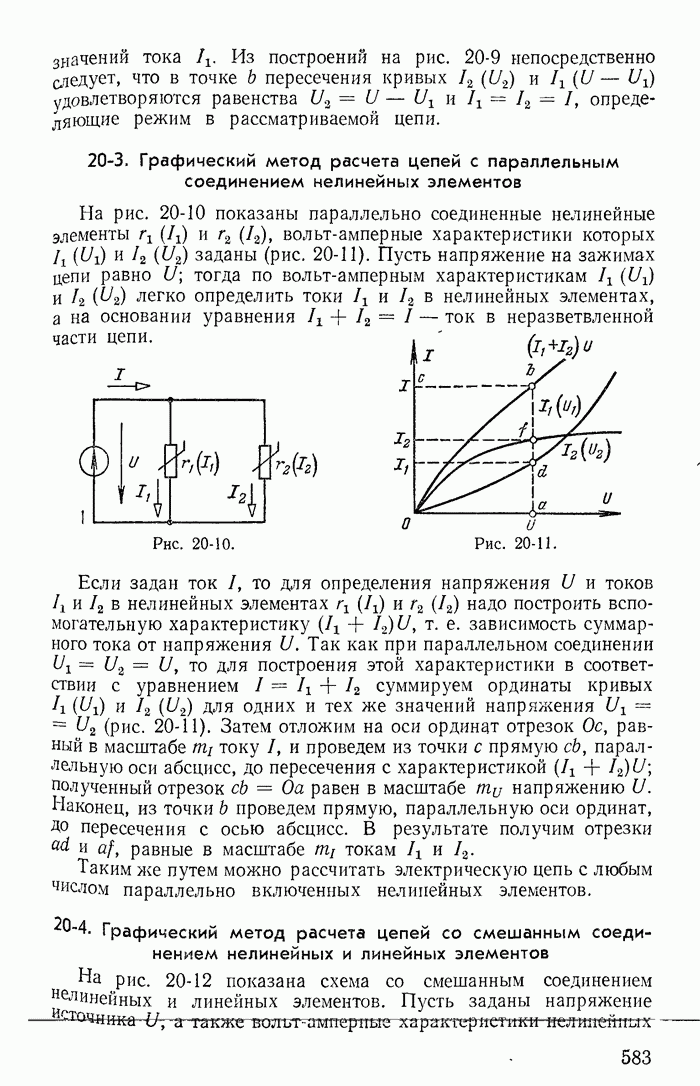
- 20-3. Графический метод расчета цепей с параллельным соединением нелинейных элементов
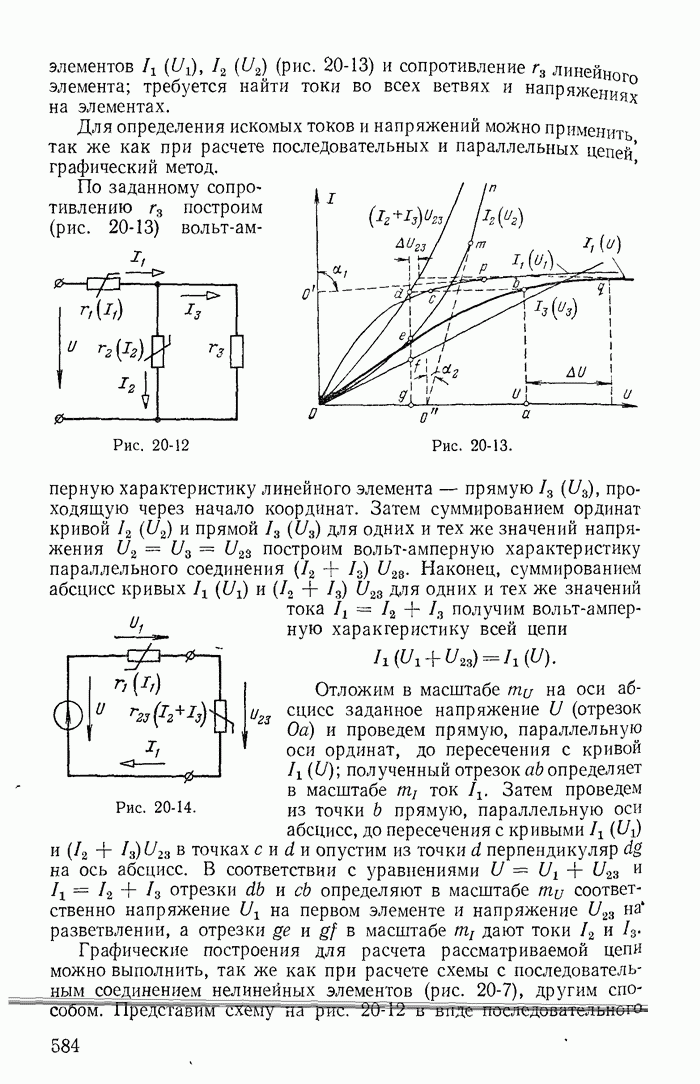
- 20-4. Графический метод расчета цепей со смешанным соединением нелинейных и линейных элементов
- 20-5. Применение эквивалентных схем с источниками э. д. с. для исследования режима нелинейных цепей
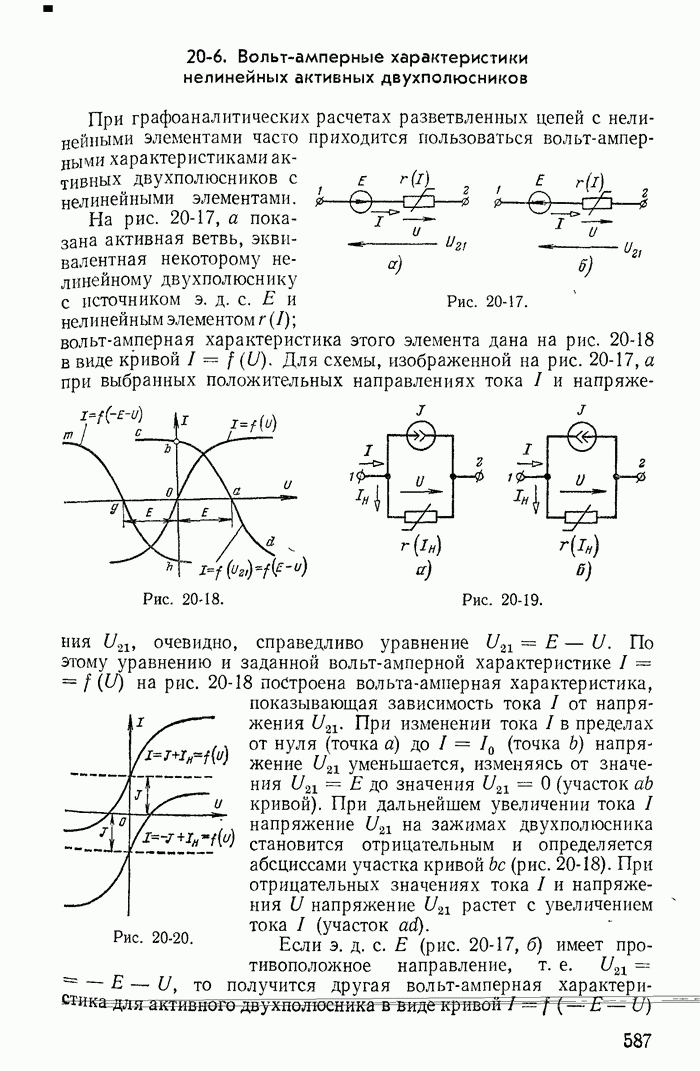
- 20-6. Вольт-амперные характеристики нелинейных активных двухполюсников
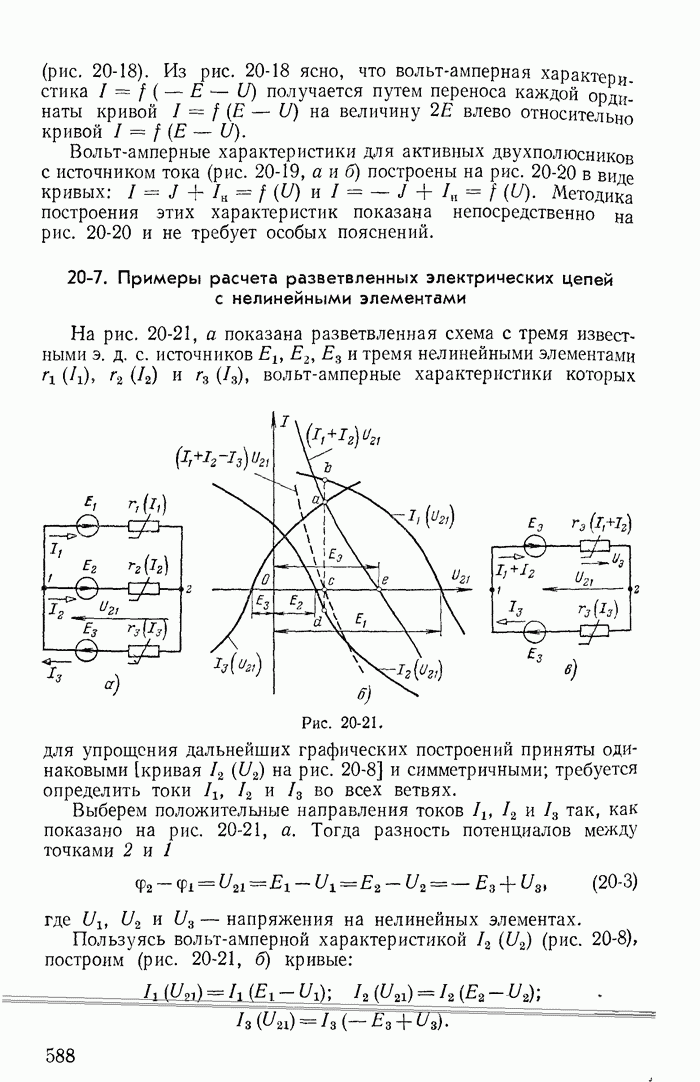
- 20-7. Примеры расчета разветвленных электрических цепей с нелинейными элементами
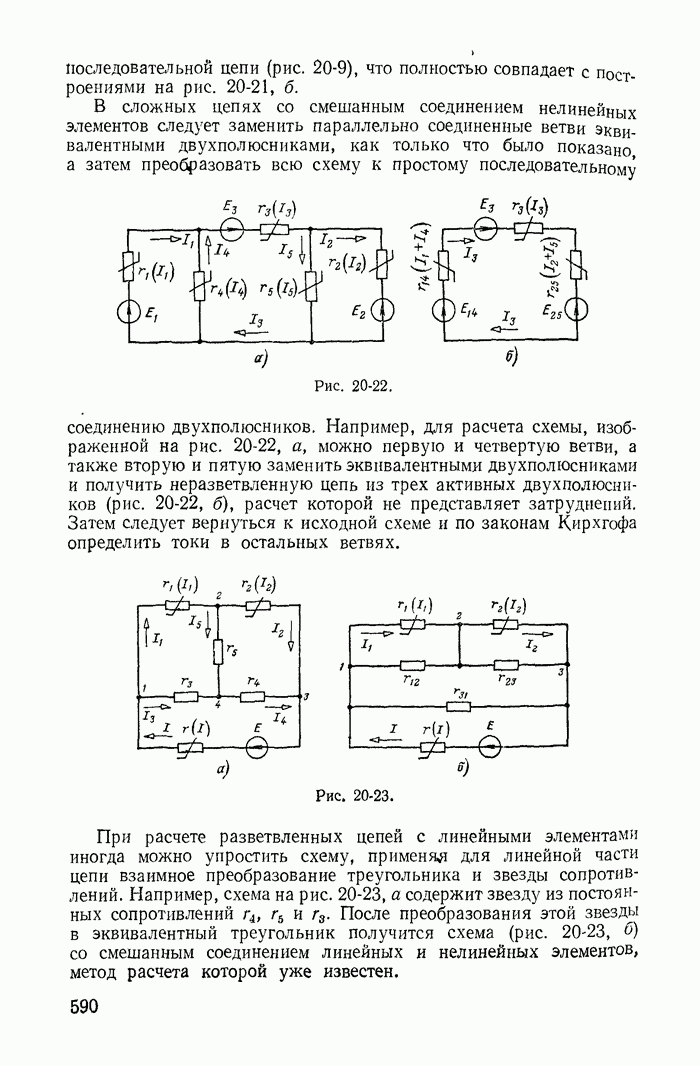
- 20-8. Применение теории активных двухполюсника, четырехполюсника и шестиполюсника для расчета цепей с линейными и нелинейными элементами
- 20-9. Расчет разветвленных нелинейных цепей итерационным методом (методом последовательных приближений)
- Глава двадцать первая. МАГНИТНЫЕ ЦЕПИ ПРИ ПОСТОЯННЫХ ТОКАХ
- 21-2. Расчет неразветвленных магнитных цепей
- 21-3. Расчет разветвленных магнитных цепей
- 21-4. Расчет магнитной цепи кольцевого постоянного магнита с воздушным зазором
- 21-5. Расчет неразветвленной неоднородной магнитной цепи с постоянным магнитом
- Глава двадцать вторая. ОБЩАЯ ХАРАКТЕРИСТИКА НЕЛИНЕЙНЫХ ЦЕПЕЙ ПЕРЕМЕННОГО ТОКА И МЕТОДОВ ИХ РАСЧЕТА
- 22-1. Нелинейные двухполюсники и четырехполюсники при переменных токах
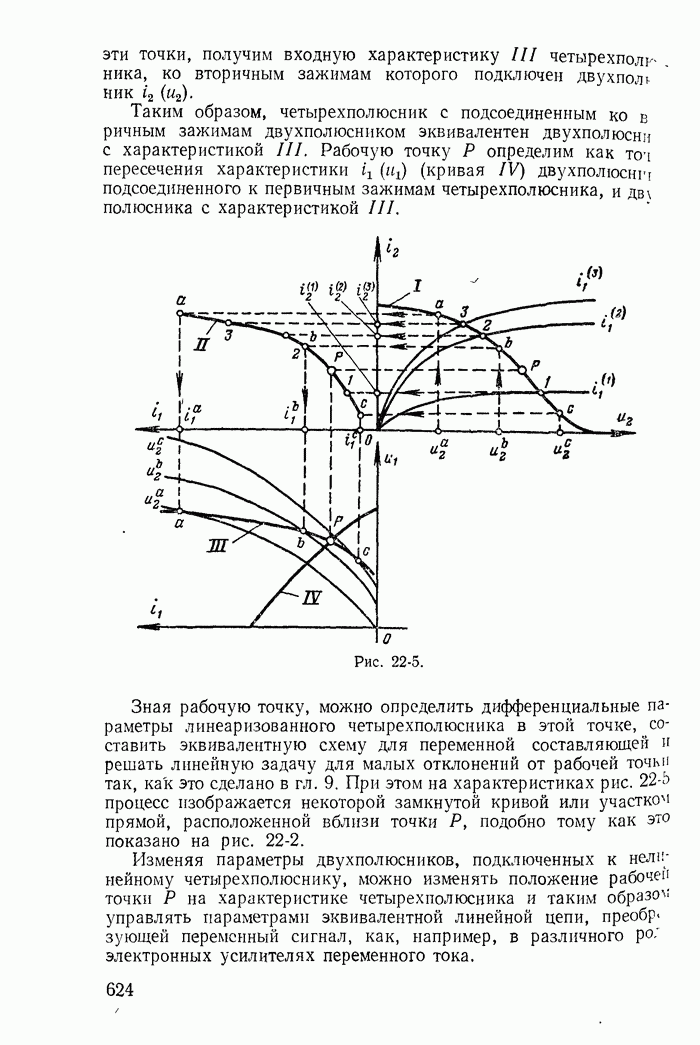
- 22-2. Определение рабочих точек на характеристиках нелинейных двухполюсников и четырехполюсников
- 22-3. Явления в нелинейных цепях переменного тока
- 22-4. Методы расчета нелинейных цепей переменного тока
- Глава двадцать третья. НЕЛИНЕЙНЫЕ ЦЕПИ С ИСТОЧНИКАМИ Э. Д. С. И ТОКА ОДИНАКОВОЙ ЧАСТОТЫ
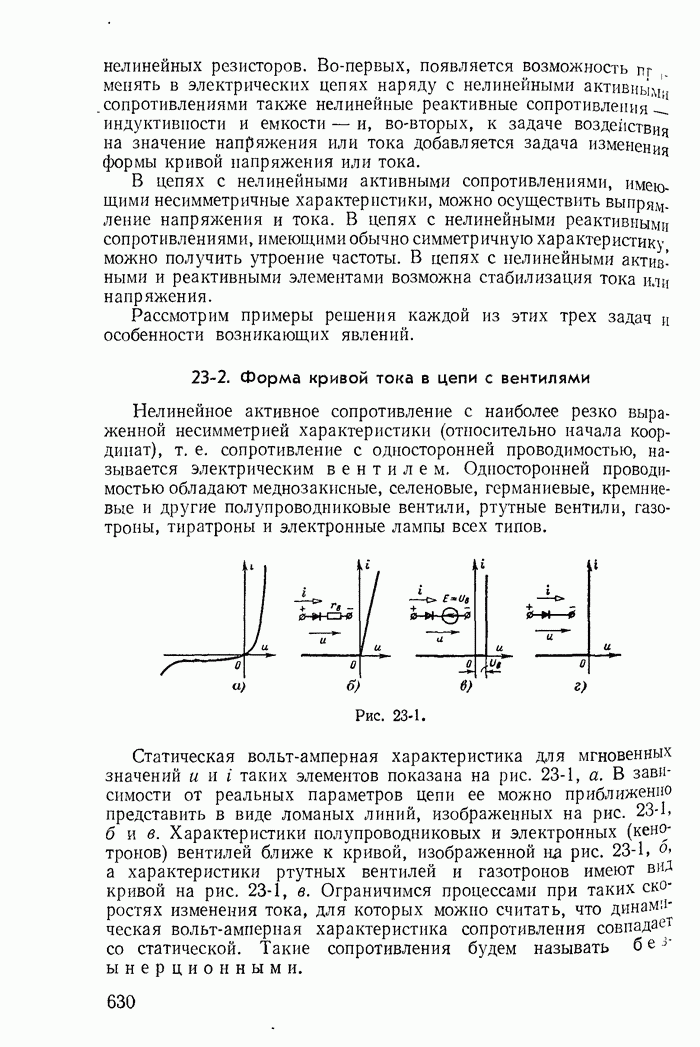
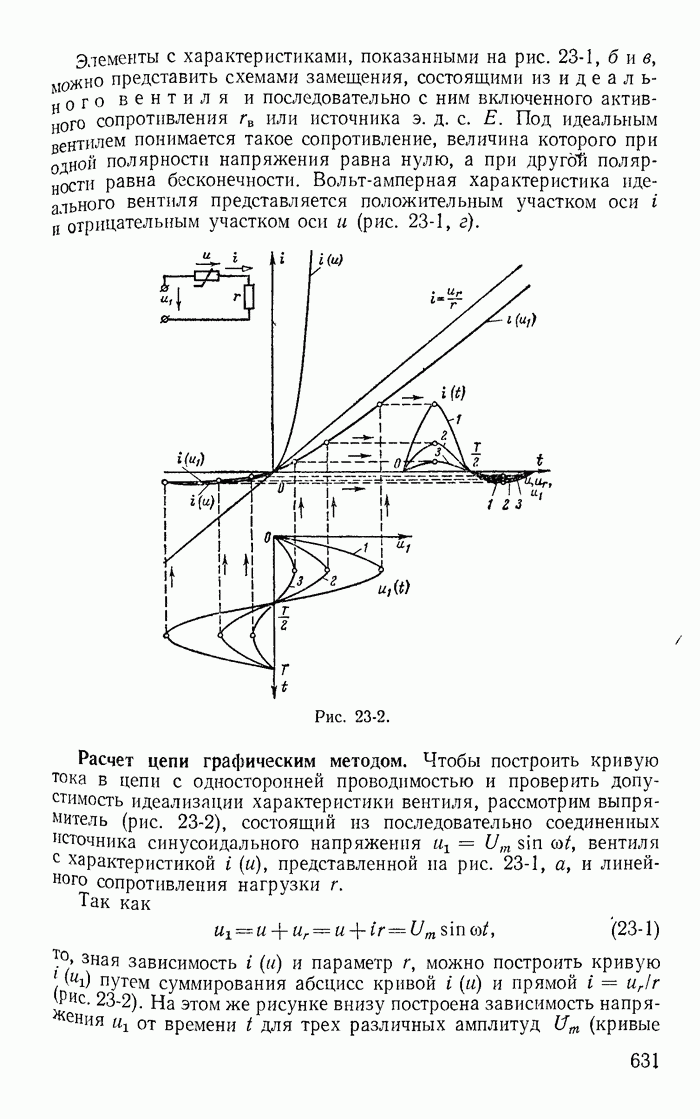
- 23-2. Форма кривой тока в цепи с вентилями
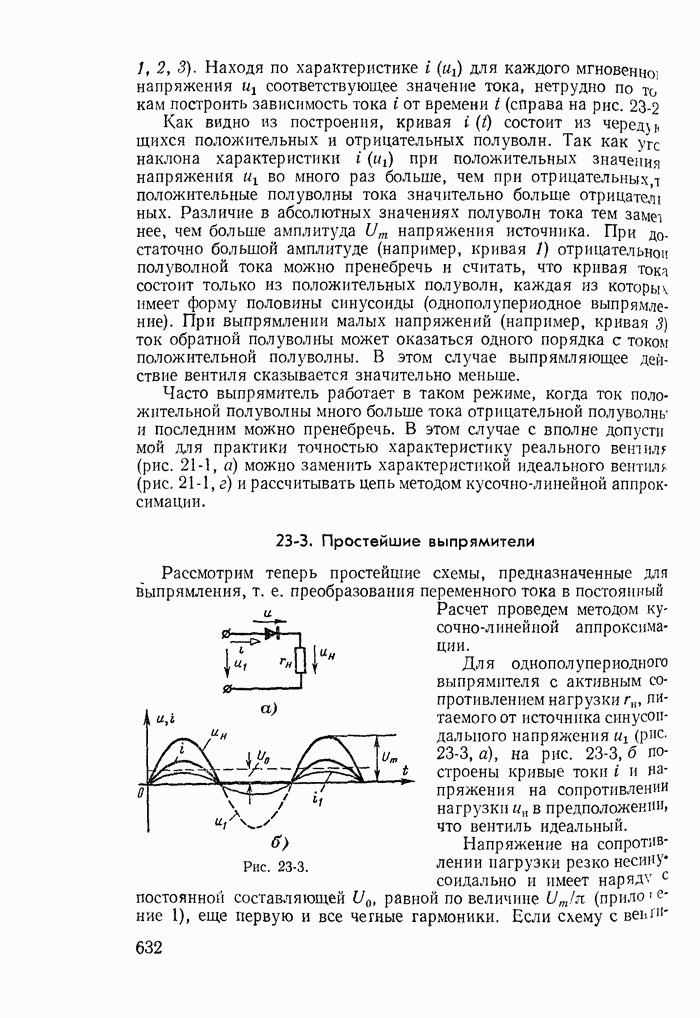
- 23-3. Простейшие выпрямители
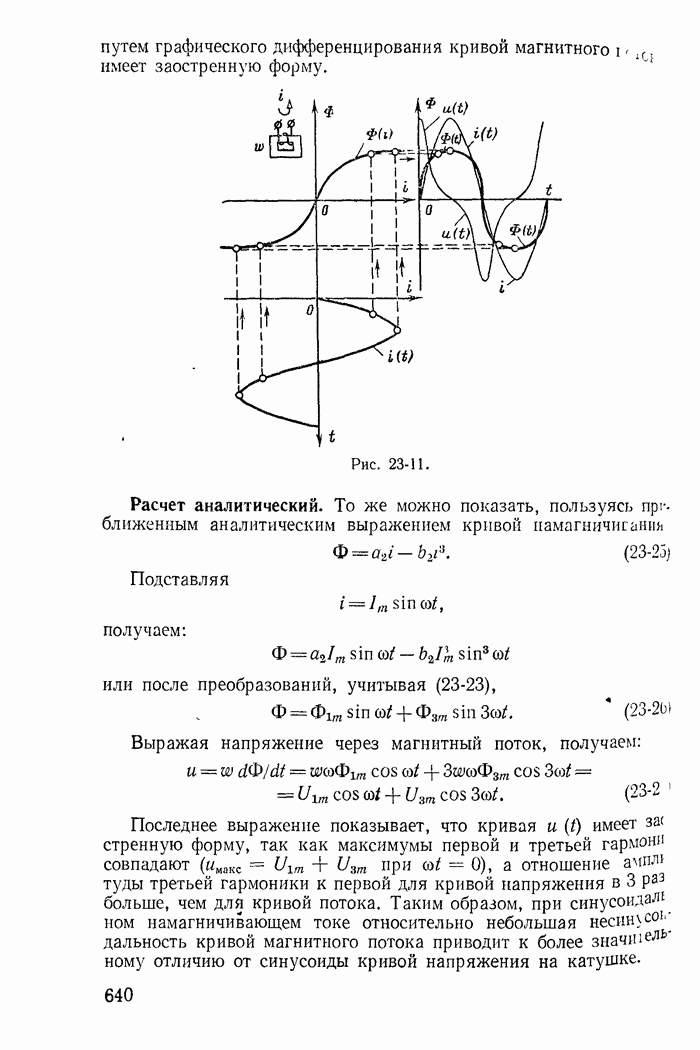
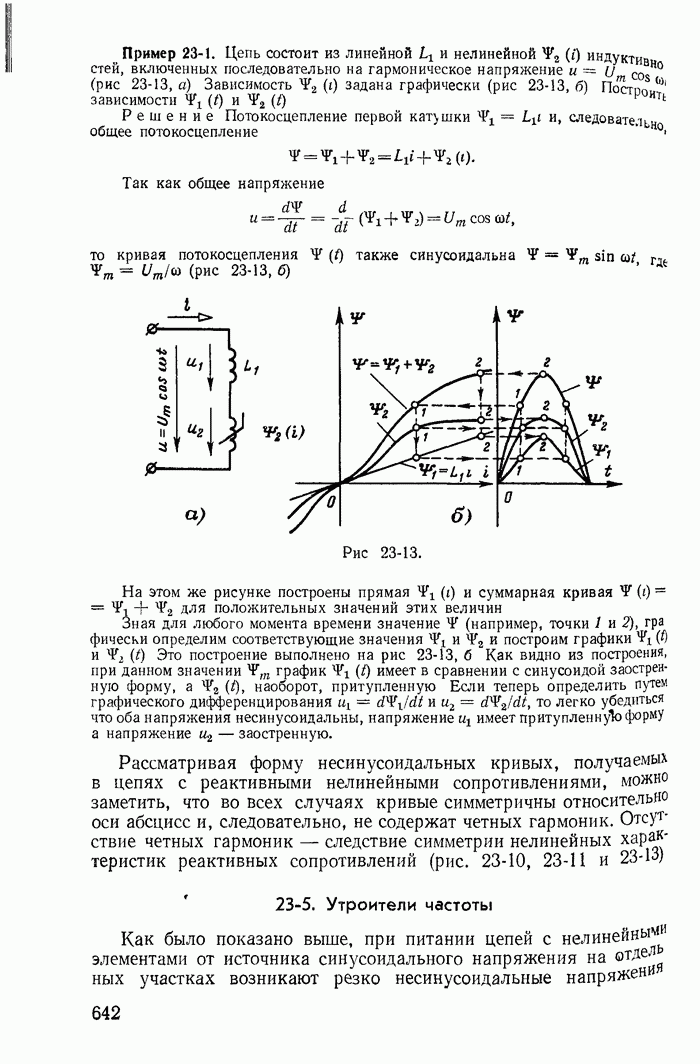
- 23-4. Формы кривых тока и напряжения в цепях с нелинейными реактивными сопротивлениями
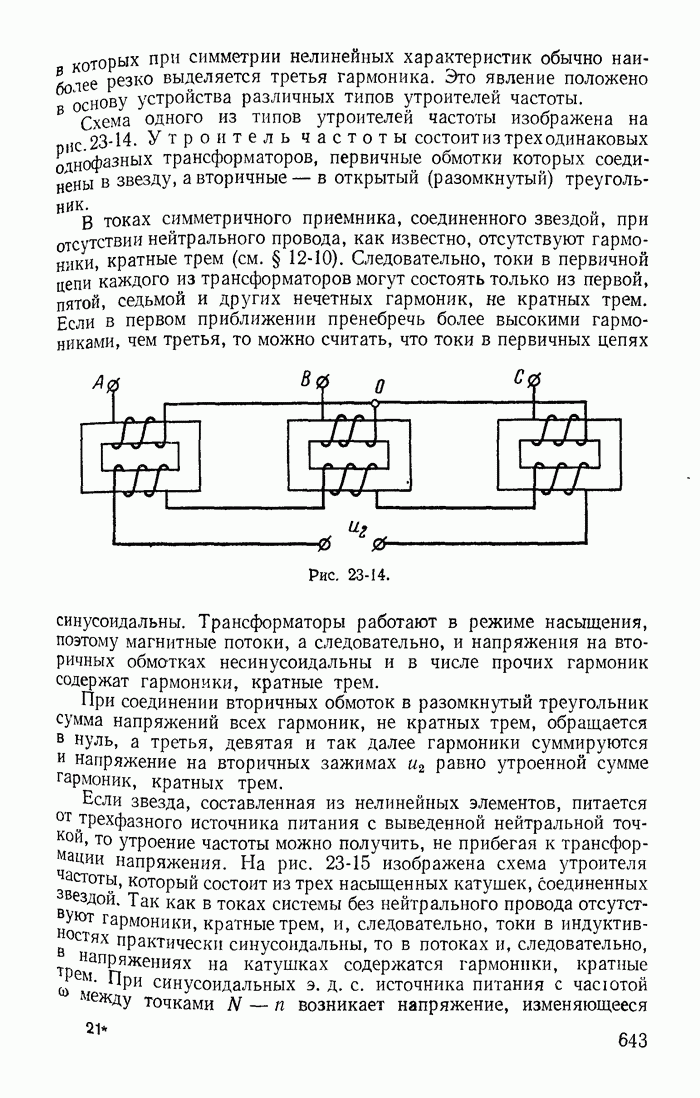
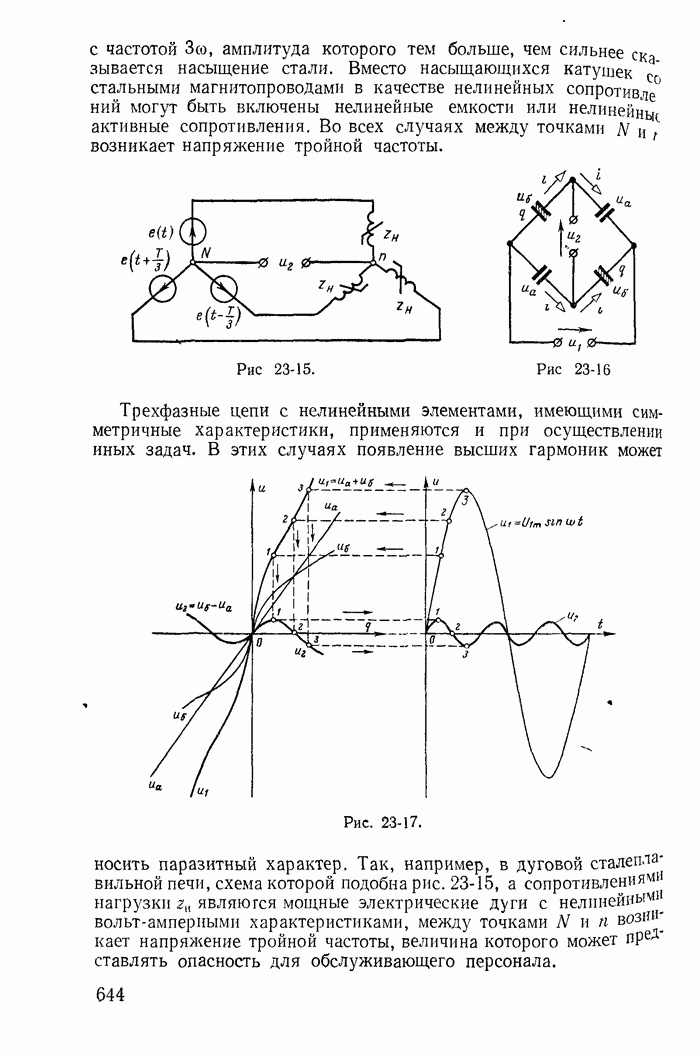
- 23-5. Утроители частоты
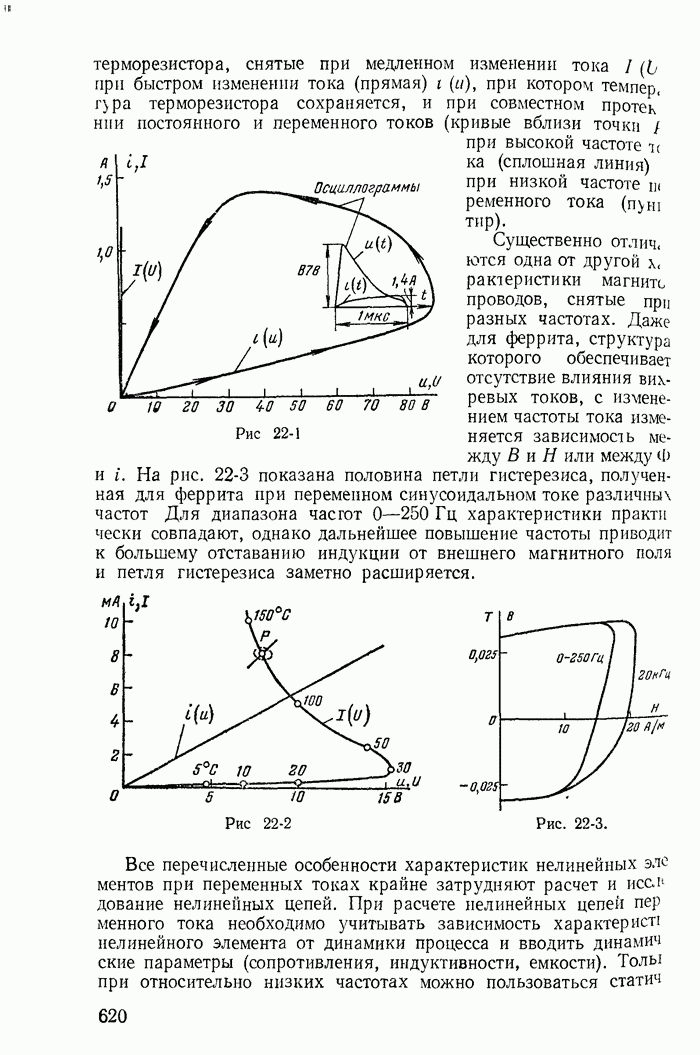
- 23-6. Формы кривых тока и напряжения в цепях с терморезисторами
- 23-7. Замена реальных нелинейных элементов условно-нелинейными
- 23-8. Учет реальных свойств стальных магнитопроводов
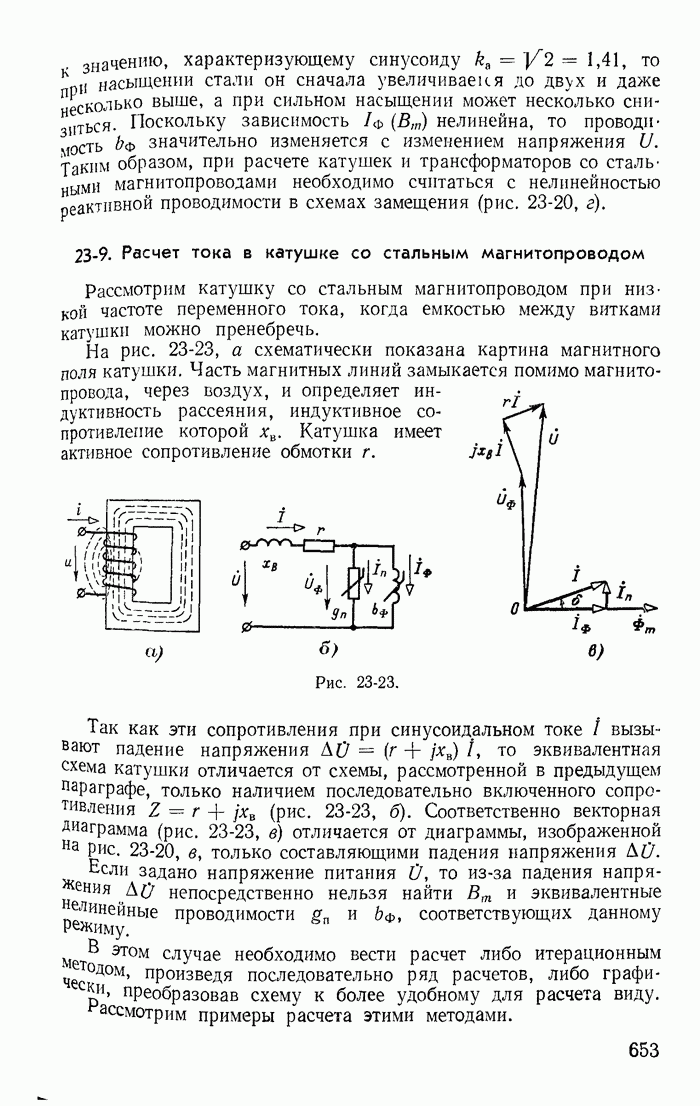
- 23-9. Расчет тока в катушке со стальным магнитопроводом
- 23-10. Понятие о расчете условно-нелинейных магнитных цепей
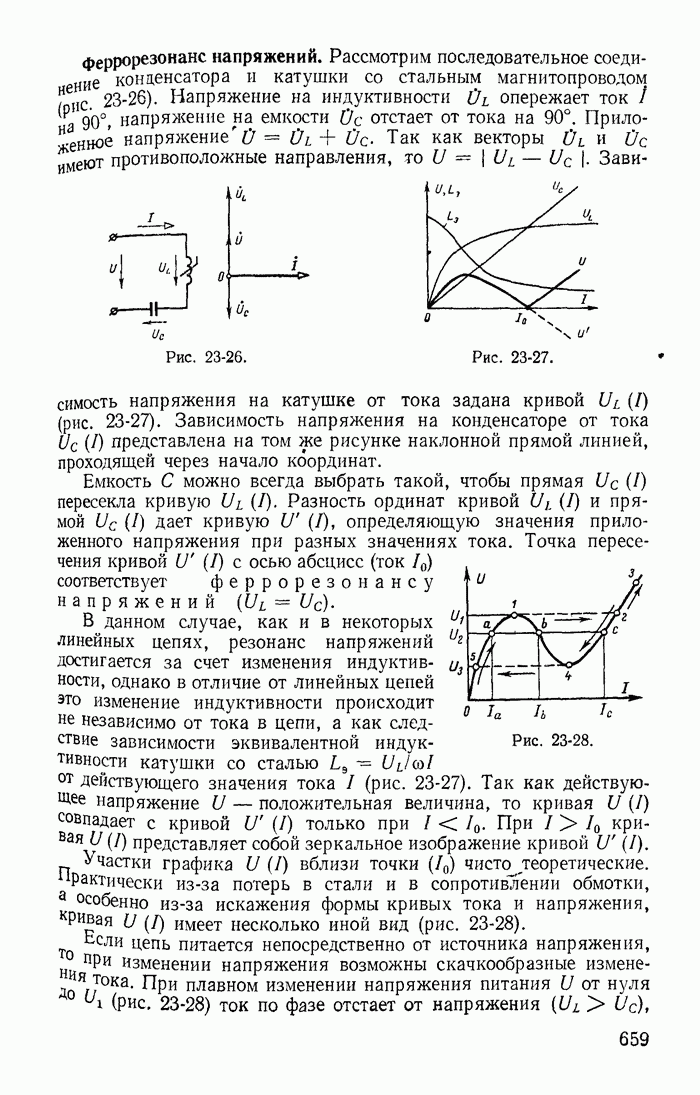
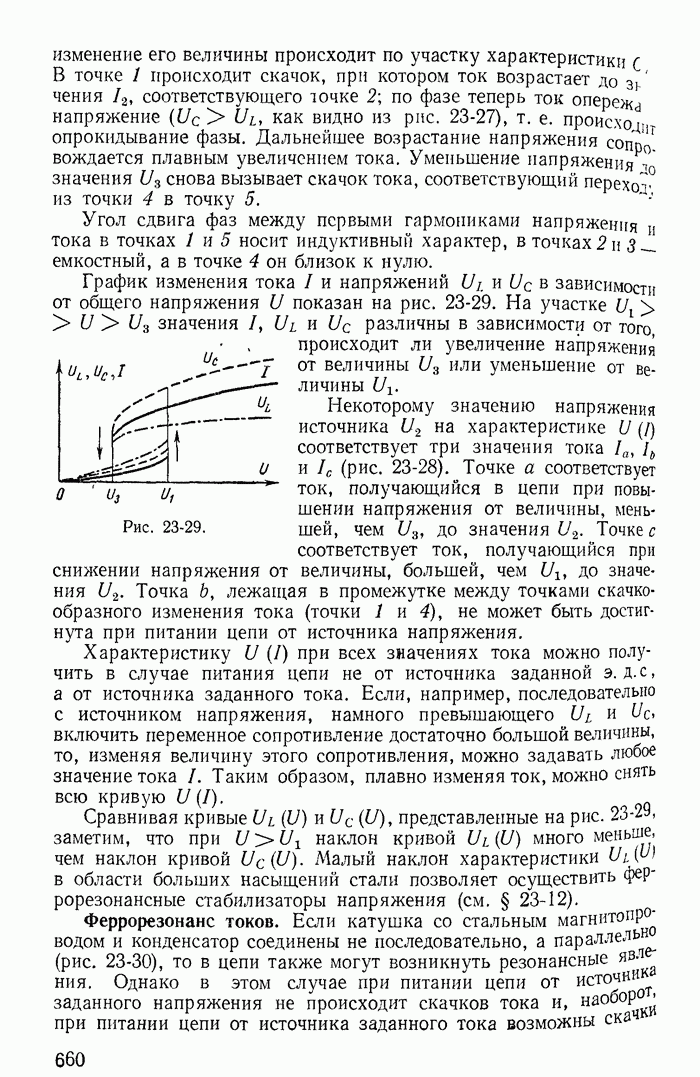
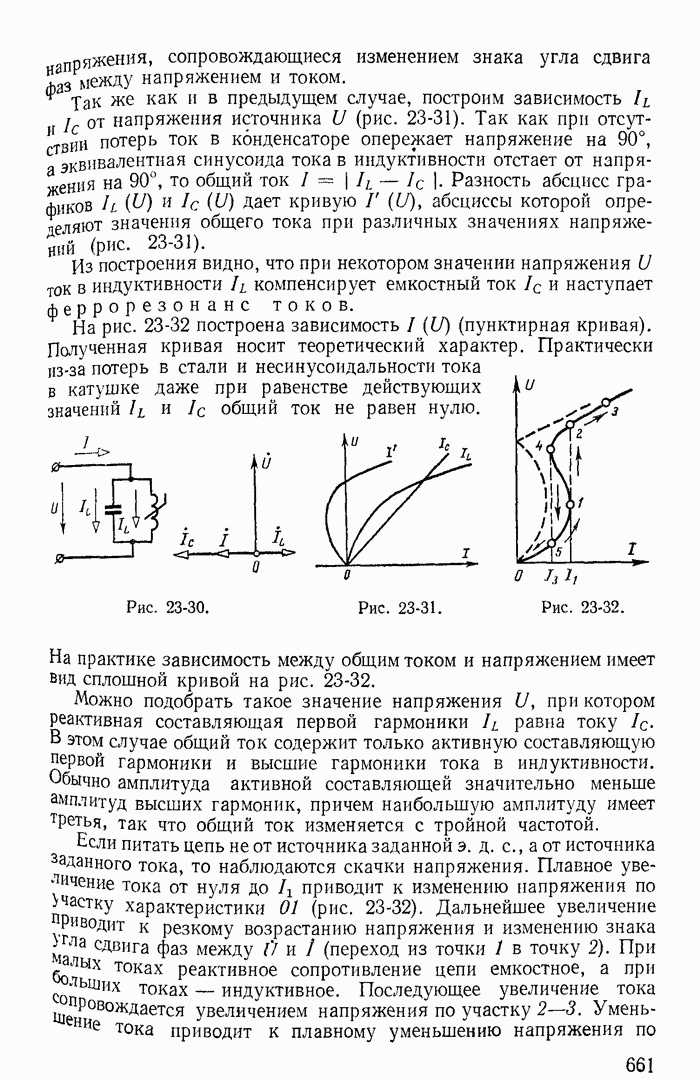
- 23-11. Явление феррорезонанса
- 23-12. Стабилизаторы напряжения
- Глава двадцать четвертая. НЕЛИНЕЙНЫЕ ЦЕПИ С ИСТОЧНИКАМИ Э. Д. С. И ТОКА РАЗЛИЧНЫХ ЧАСТОТ
- 24-1. Общая характеристика нелинейных цепей с источниками э. д. с. различных частот
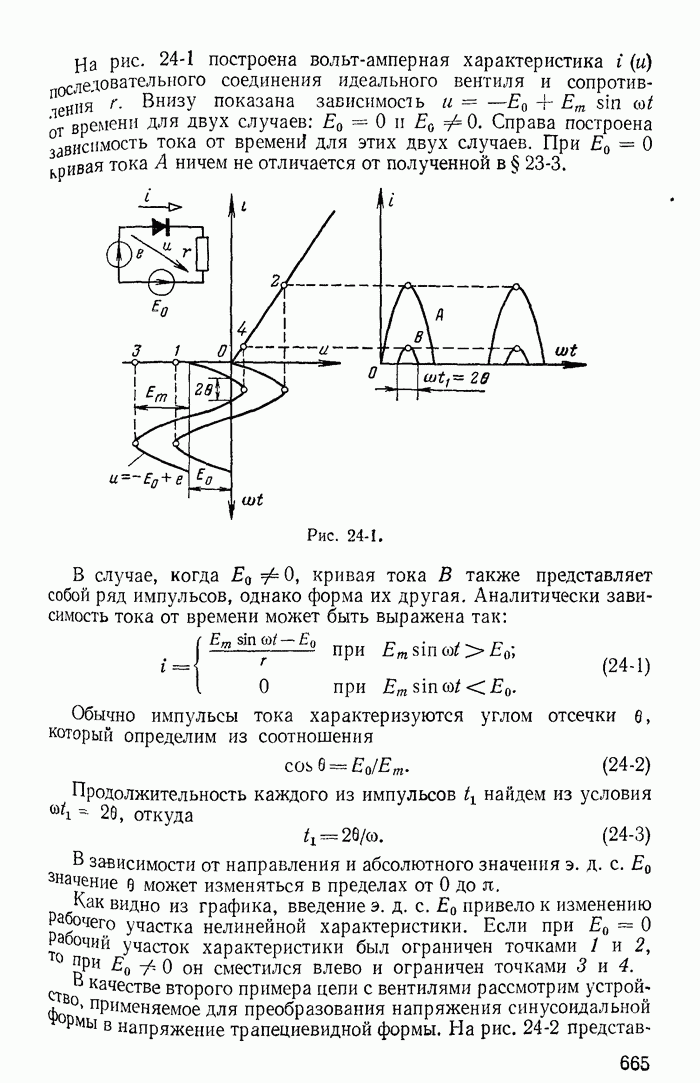
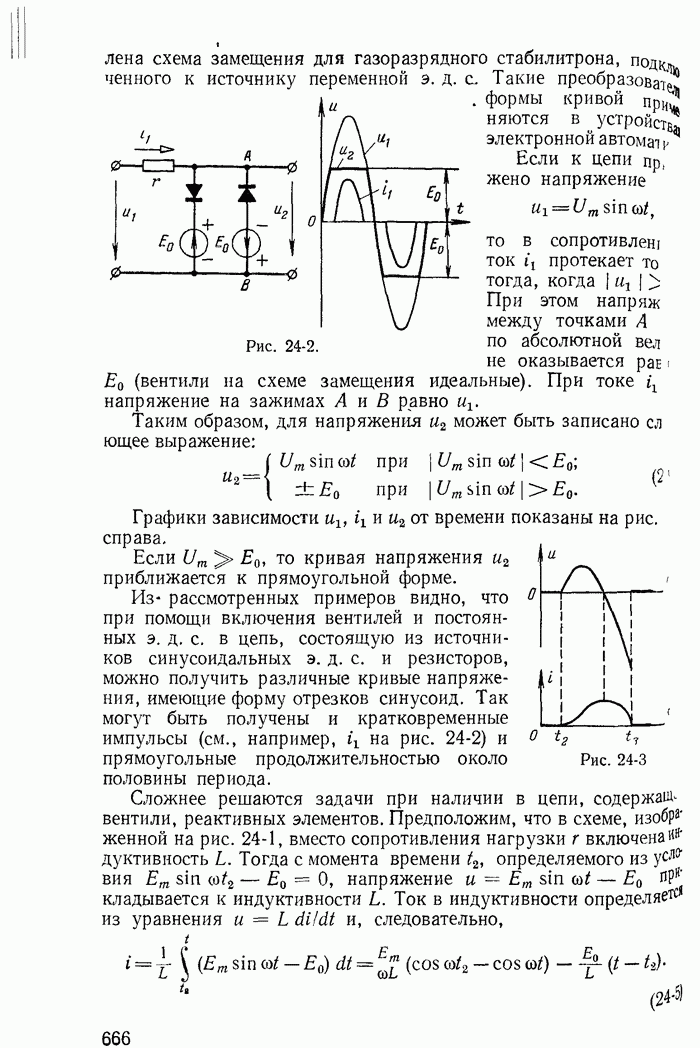
- 24-2. Вентили в цепях с постоянными и переменными э. д. с.
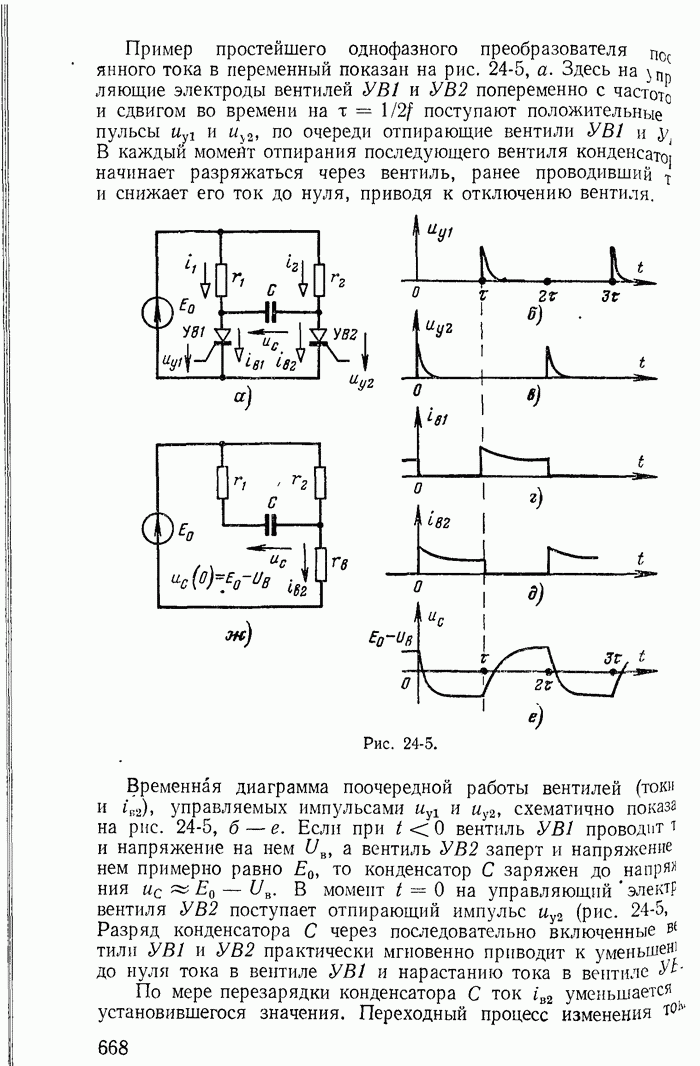
- 24-3. Управляемые вентили в простейших выпрямителях и преобразователях постоянного тока в переменный
- 24-4. Катушки со стальными магнитопроводами в цепях с постоянными и переменными э. д. с.
- 24-5. Удвоитель частоты
- 24-6. Метод гармонического баланса
- 24-7. Влияние постоянной э. д. с. на переменную составляющую тока в цепях с нелинейными безынерционными сопротивлениядли
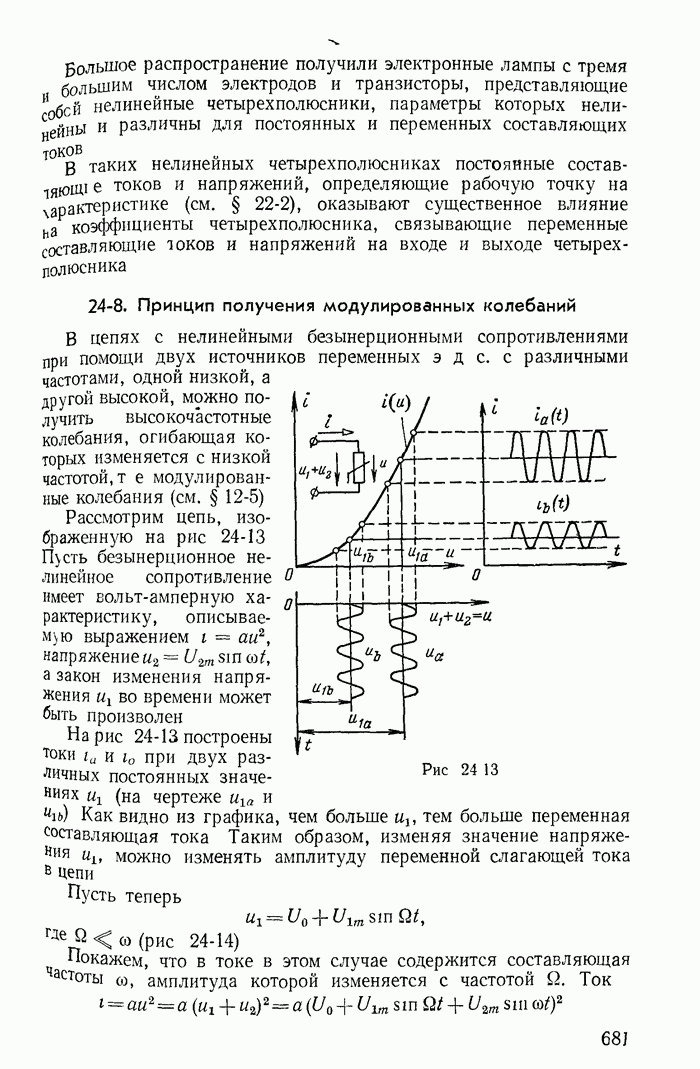
- 24-8. Принцип получения модулированных колебаний
- 24-9. Влияние постоянной составляющей на переменную в цепях с нелинейными индуктивностями
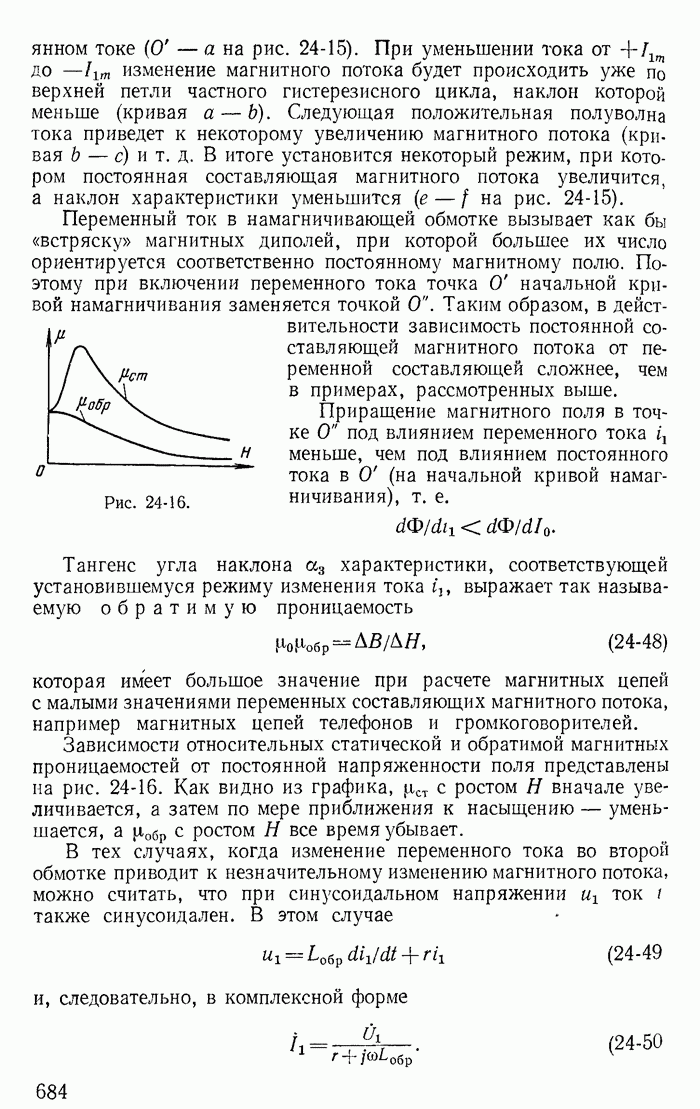
- 24-10. Магнитные усилители мощности
- Глава двадцать пятая. ПЕРЕХОДНЫЕ ПРОЦЕССЫ В НЕЛИНЕЙНЫХ ЦЕПЯХ
- 25-2. Включение катушки со стальным магнитопроводом на постоянное напряжение
- 25-3. Включение катушки со стальным магнитопроводом на синусоидальное напряжение
- 25-4. Импульсное воздействие в цепях с неоднозначными нелинейностями
- 25-5. Понятие о простейших запоминающих устройствах
- 25-6. Изображение переходных процессов на фазовой плоскости
- 25-7. Колебательный разряд емкости через нелинейную индуктивность
- Глава двадцать шестая. АВТОКОЛЕБАНИЯ
- 26-1. Нелинейные резисторы со спадающим участком характеристики
- 26-2. Понятие об устойчивости режима в цепи с нелинейными резисторами
- 26-3. Релаксационные колебания в цепи с отрицательным сопротивлением
- 26-4. Близкие к синусоидальным колебания в цепи с отрицательным сопротивлением
- 26-5. Фазовые траектории процессов в цепи с отрицательным сопротивлением
- 26-6. Фазовые траектории процессов в генераторе синусоидальных колебаний
- 26-7. Определение амплитуды автоколебаний методом гармонического баланса
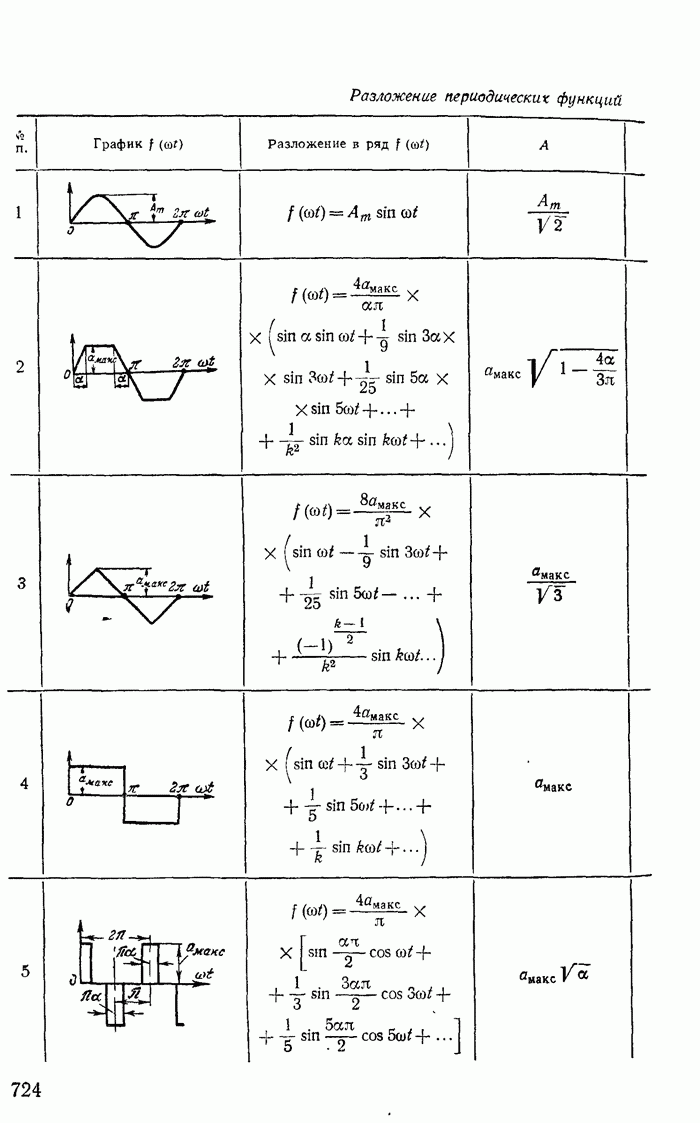
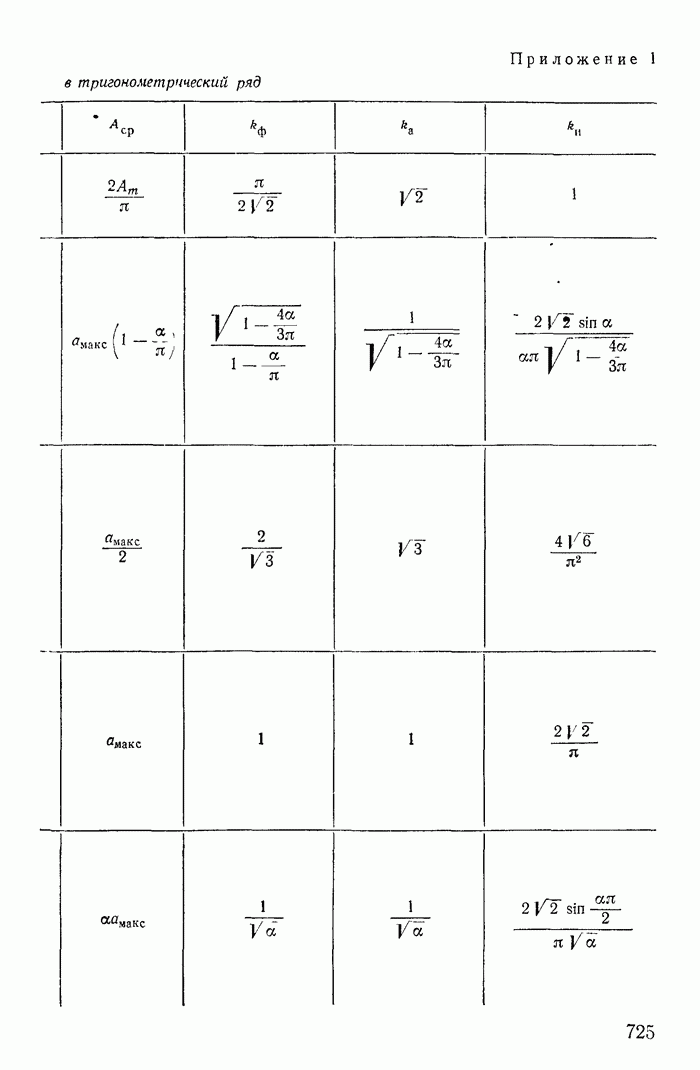
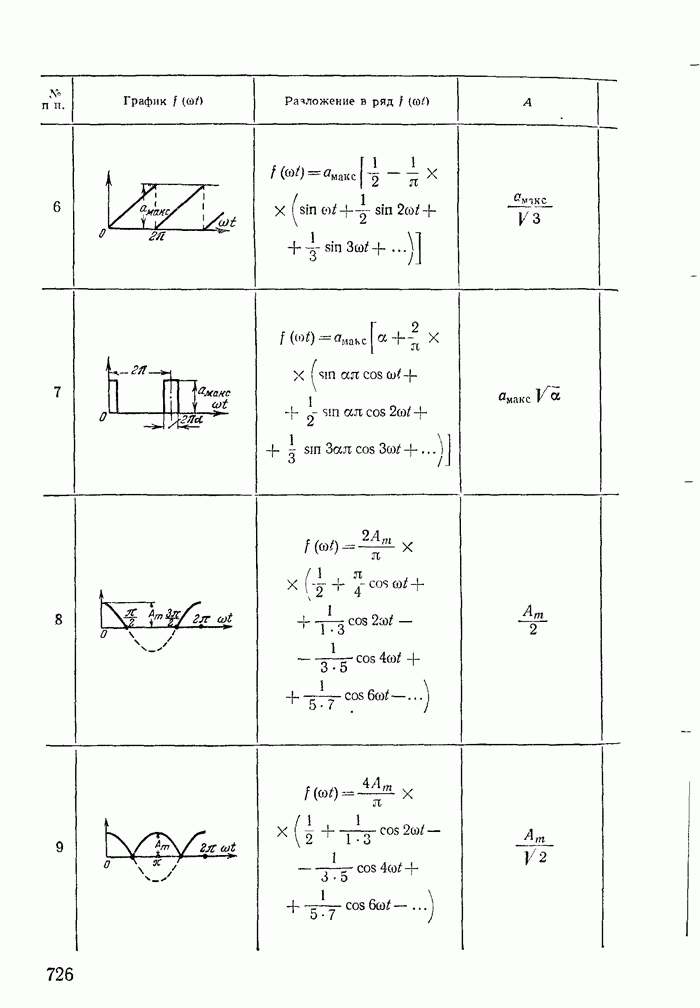
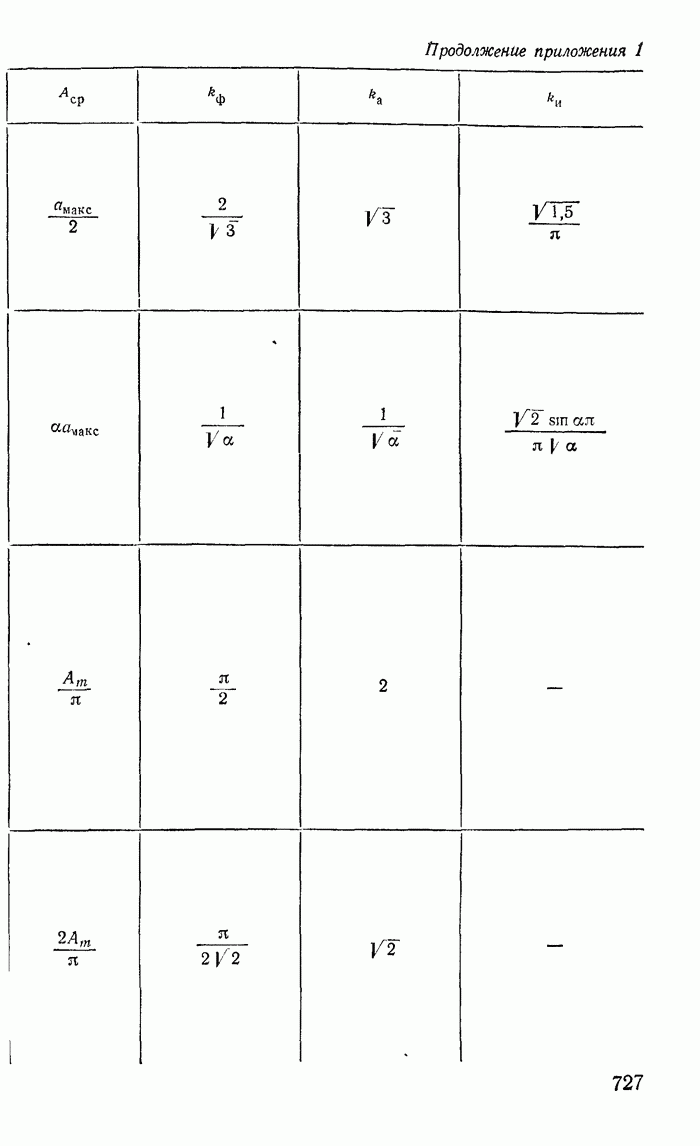
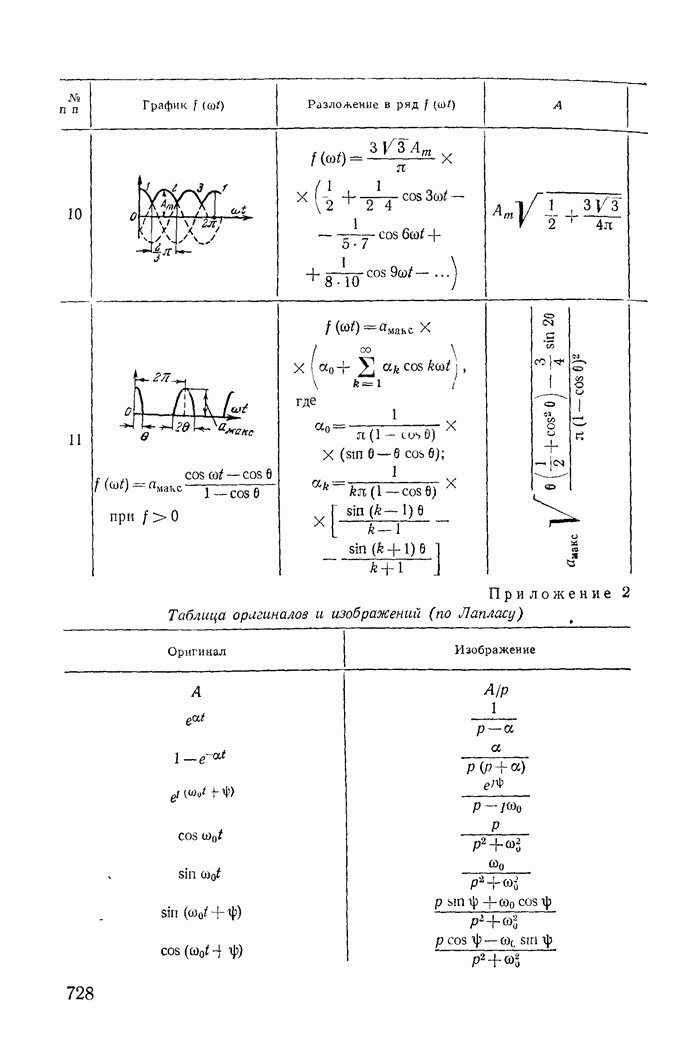
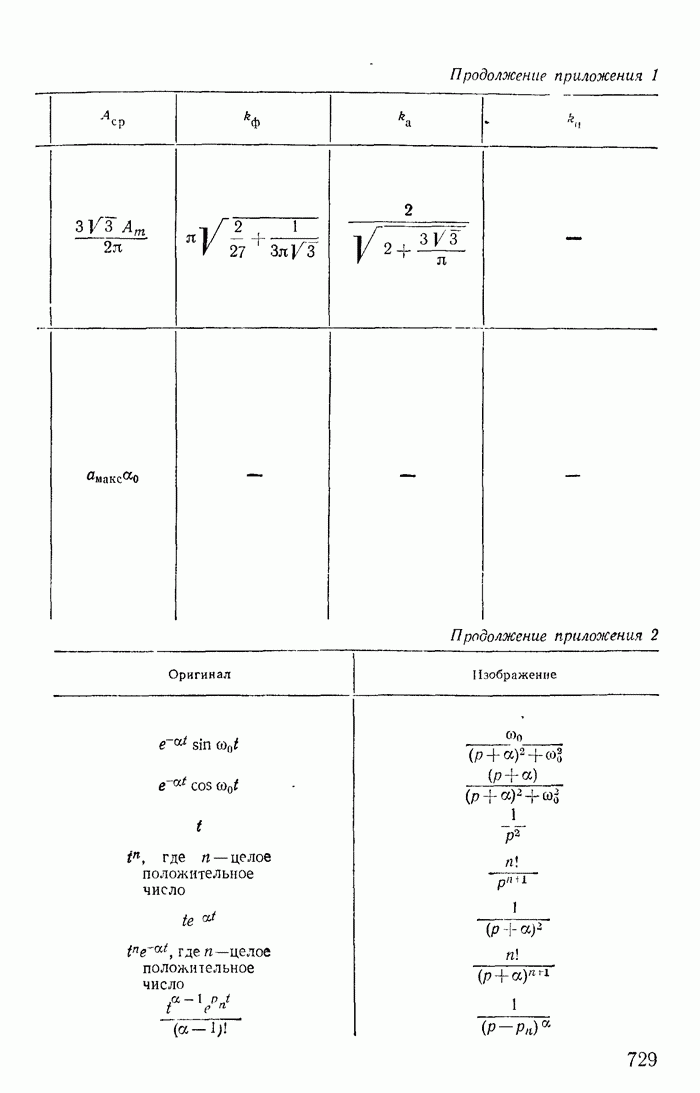
- Приложение 1. Разложение периодических функций в тригонометрический ряд
- Приложение 2. Таблица оригиналов и изображений (по Лапласу)
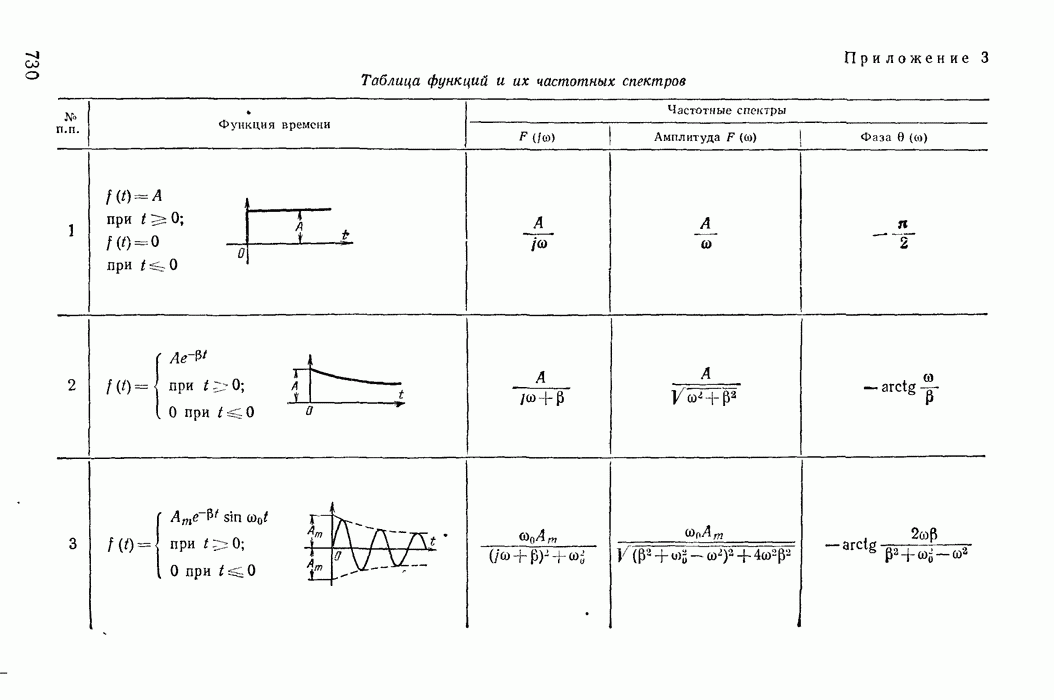
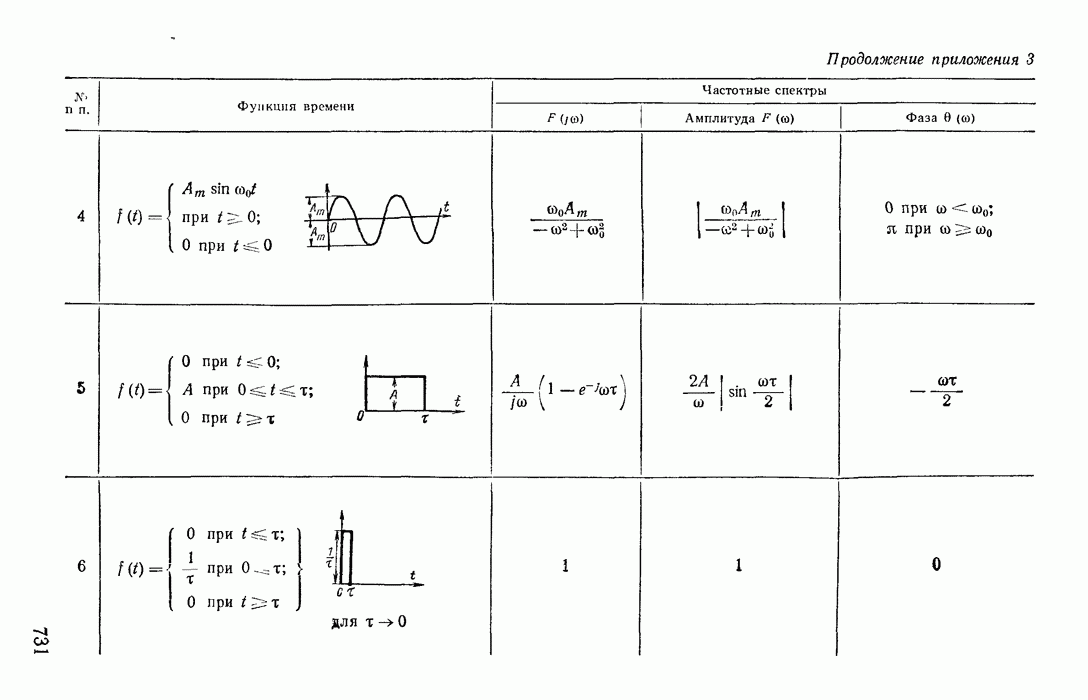
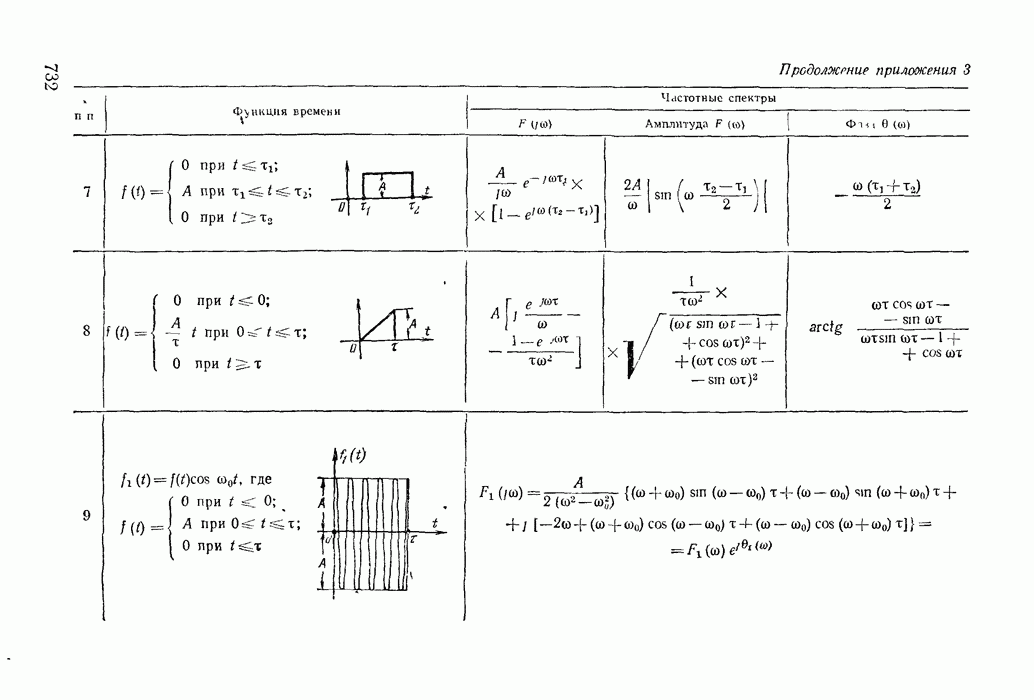
- Приложение 3. Таблица функций и их частных спектров
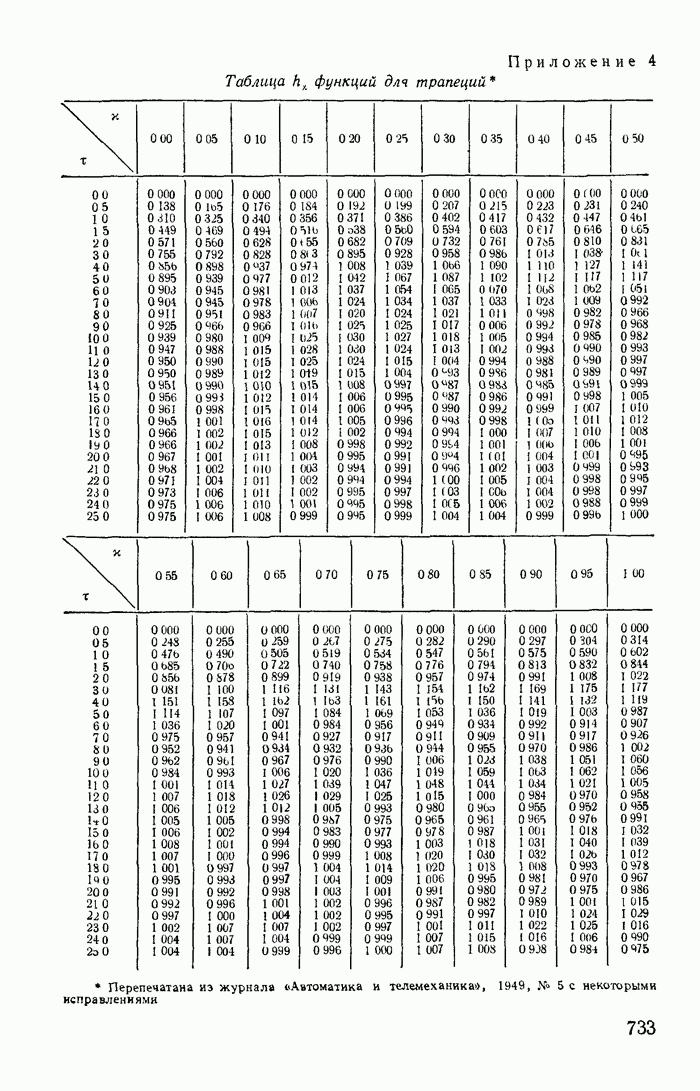
- Приложение 4. Таблица функций для трапеций
- СПИСОК ЛИТЕРАТУРЫ