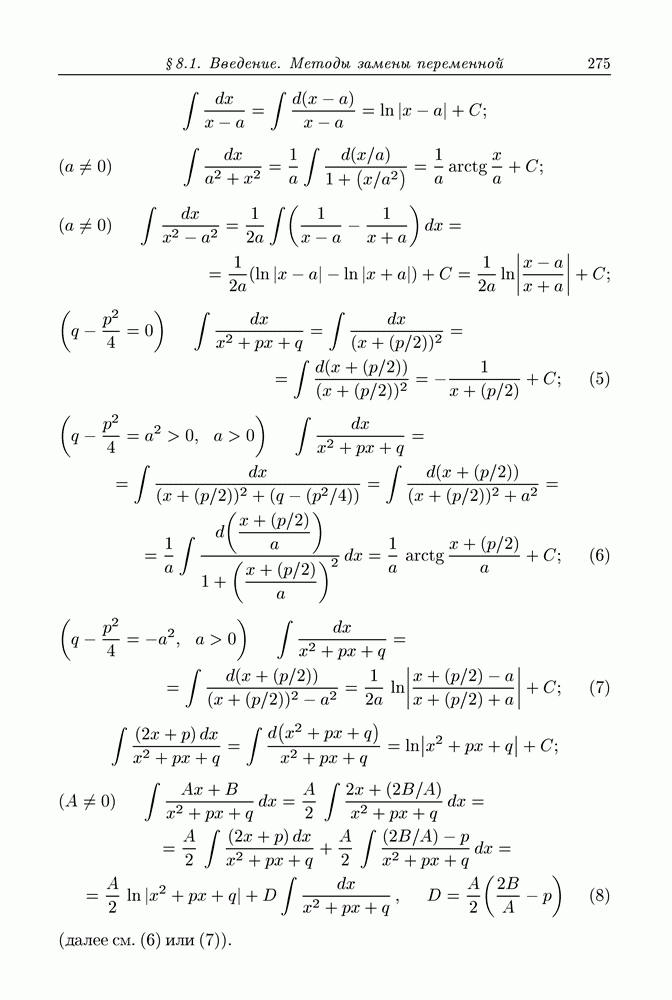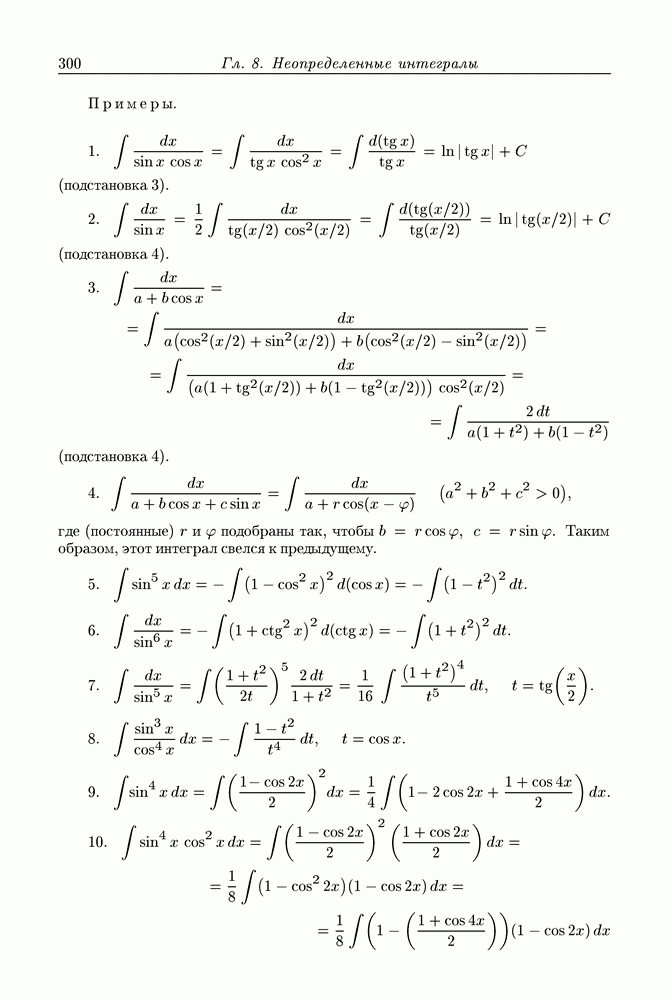| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 2.3. Основная лемма. Определение арифметических действий
Пусть каждому неотрицательному целому числу (индексу)  в силу некоторого закона приведено в соответствие число
в силу некоторого закона приведено в соответствие число  Совокупность
Совокупность

называется последовательностью (чисел). Отдельные числа  последовательности (1) называются ее элементами. Элементы
последовательности (1) называются ее элементами. Элементы  при
при  считаются отличными как элементы данной последовательности, хотя как числа они могут быть равны между собой, т.е. может быть
считаются отличными как элементы данной последовательности, хотя как числа они могут быть равны между собой, т.е. может быть  Последовательность называется неубывающей (невозрастающей), если
Последовательность называется неубывающей (невозрастающей), если  Для всех
Для всех 
Будем говорить, что последовательность (1) ограничена сверху (числом  если существует целое число
если существует целое число  такое, что
такое, что  для всех
для всех 
Если числа  последовательности (1) целые, то будем говорить, что она стабилизируется к числу если найдется такое ко, что
последовательности (1) целые, то будем говорить, что она стабилизируется к числу если найдется такое ко, что  для всех
для всех 
Очевидно, что если последовательность целых чисел не убывает и ограничена сверху числом  то она стабилизируется к некоторому целому числу
то она стабилизируется к некоторому целому числу 
Рассмотрим теперь последовательность неотрицательных десятичных дробей

Правые части в (2) образуют таблицу (бесконечную матрицу).
Будем говорить, что последовательность (2) стабилизируется к числу  и писать
и писать

если  столбец таблицы (2) стабилизируется к каково бы ни было
столбец таблицы (2) стабилизируется к каково бы ни было  При этом, очевидно, автоматически оказывается, что
При этом, очевидно, автоматически оказывается, что  целое неотрицательное, а
целое неотрицательное, а  цифры.
цифры.
Замечание. Последовательность чисел  где
где

не стабилизируется. Из § 3.1, где вводится понятие предела, будет ясно, что данная последовательность имеет предел, равный  Итак, последовательность десятичных дробей может иметь предел и в то же время не стабилизироваться. Однако из того, что
Итак, последовательность десятичных дробей может иметь предел и в то же время не стабилизироваться. Однако из того, что  следует, что
следует, что  (см. § 3.1).
(см. § 3.1).
Для произвольного числа  введем его
введем его  срезку
срезку  представляющую собой конечную десятичную дробь. Мы считаем, что операции с конечными десятичными дробями читателю известны из курса арифметики. Очевидно,
представляющую собой конечную десятичную дробь. Мы считаем, что операции с конечными десятичными дробями читателю известны из курса арифметики. Очевидно,

и еще

потому что

Лемма 1. Если неубывающая последовательность (2) десятичных дробей, не имеющих периода 9, ограничена сверху числом  то она стабилизируется к некоторому числу
то она стабилизируется к некоторому числу  , удовлетворяющему неравенствам
, удовлетворяющему неравенствам

Доказательство. Считаем, что исходные дроби  не имеют периода 9, но все же может оказаться, что дробь
не имеют периода 9, но все же может оказаться, что дробь  имеет период 9. Столбцы матрицы (2) с номерами, не большими к, стабилизируются соответственно к
имеет период 9. Столбцы матрицы (2) с номерами, не большими к, стабилизируются соответственно к

В самом деле, в условиях леммы целые числа  не убывают и ограничены сверху числом
не убывают и ограничены сверху числом  поэтому они стабилизируются к некоторому целому неотрицательному числу 70 Пусть теперь для любого к установлено, что столбцы матрицы (2) с номерами, не большими к, стабилизируются соответственно к
поэтому они стабилизируются к некоторому целому неотрицательному числу 70 Пусть теперь для любого к установлено, что столбцы матрицы (2) с номерами, не большими к, стабилизируются соответственно к  и верны неравенства (5). Тогда это утверждение верно для к
и верны неравенства (5). Тогда это утверждение верно для к 
В самом деле, раз десятичные разложения чисел  для
для  при достаточно большом
при достаточно большом  имеют вид
имеют вид

 не убывает, то цифры
не убывает, то цифры  не убывают и, следовательно, стабилизируются при
не убывают и, следовательно, стабилизируются при  где
где  достаточно велико, к некоторой цифре
достаточно велико, к некоторой цифре  При этом
При этом  и мы доказали (5) для любого к и тот факт, что
и мы доказали (5) для любого к и тот факт, что  где
где 
Отметим, что  для любого к, поэтому
для любого к, поэтому  , т.е. выполняется (4). В самом деле, если, например,
, т.е. выполняется (4). В самом деле, если, например,  для любого k, то цифры одинаковых разрядов равны между собой и
для любого k, то цифры одинаковых разрядов равны между собой и 
Если  для некоторого
для некоторого  то а
то а  т.е. а
т.е. а  Аналогично доказывается, что
Аналогично доказывается, что 
Лемма 1 имеет фундаментальный характер. Она служит основой для доказательства свойства V действительных чисел (см. ниже). На ее основе также даются теоретические определения арифметических действий над бесконечными десятичными дробями.
Сумма, произведение, разность и частное чисел  определяем следующим образом:
определяем следующим образом:


Выражения слева в (6)-(9) не убывают при возрастании  благодаря этому и ограниченности их сверху они на основании доказанной леммы стабилизируются к определенным числам, которые обозначаются соответственно через а
благодаря этому и ограниченности их сверху они на основании доказанной леммы стабилизируются к определенным числам, которые обозначаются соответственно через а  Надо иметь в виду, что
Надо иметь в виду, что  не убывает при возрастании
не убывает при возрастании  не возрастает; кроме того, верны неравенства
не возрастает; кроме того, верны неравенства

(где s такое, что  показывающие, что левые их части ограничены. Положим еще (пока для
показывающие, что левые их части ограничены. Положим еще (пока для  )
)

Мы определили для неотрицательных чисел  их сумму, разность, произведение и частное, предполагая в случае разности, что а
их сумму, разность, произведение и частное, предполагая в случае разности, что а  случае частного, что
случае частного, что  Эти определения распространяются обычными способами на числа
Эти определения распространяются обычными способами на числа  произвольных знаков. Например, если
произвольных знаков. Например, если  то полагаем
то полагаем

Если же  числа разных знаков и
числа разных знаков и  то полагаем
то полагаем

где выбирается знак, одинаковый со знаком  . В частности,
. В частности, 
Подобные правила можно было бы привести для остальных арифметических действий — они хорошо известны.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- Глава 1. ВВЕДЕНИЕ
- § 1.2. Множество. Интервал, отрезок
- § 1.3. Функция
- § 1.4. Понятие непрерывности функции
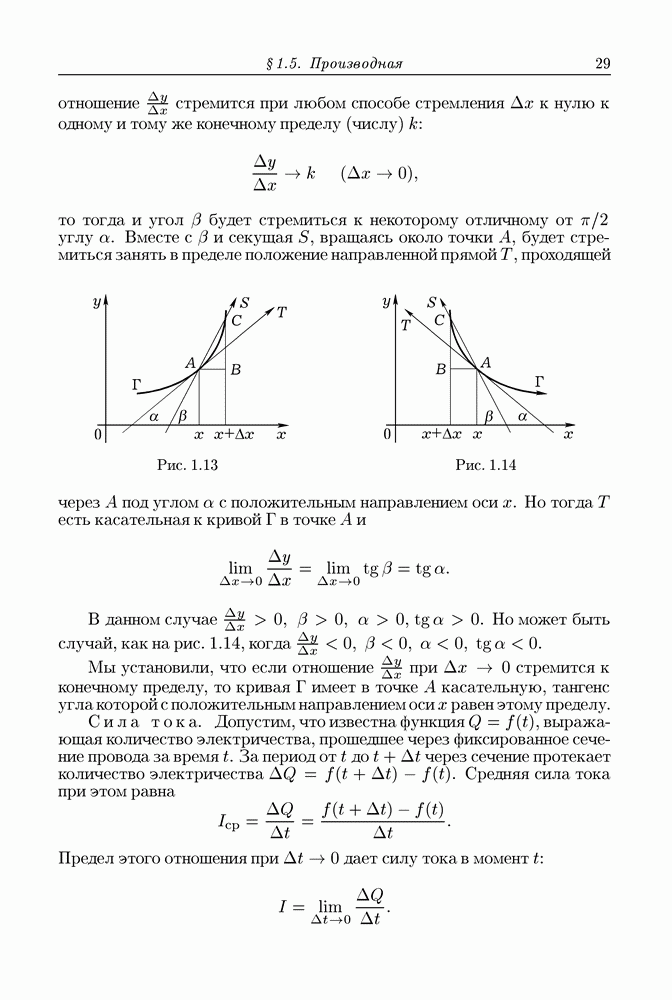
- § 1.5. Производная
- § 1.6. Первообразная. Неопределенный интеграл
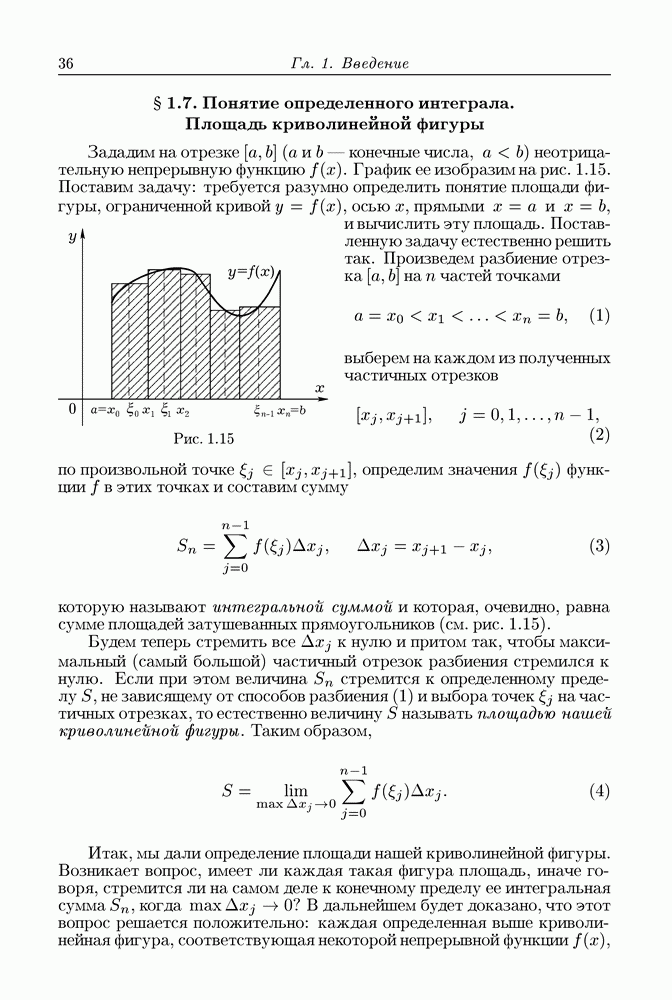
- § 1.7. Понятие определенного интеграла. Площадь криволинейной фигуры
- Глава 2. ДЕЙСТВИТЕЛЬНОЕ ЧИСЛО
- § 2.1. Рациональные и иррациональные числа
- § 2.2. Определение неравенства
- § 2.3. Основная лемма. Определение арифметических действий
- § 2.4. Основные свойства действительных чисел
- § 2.5. Изоморфизм различных представлений действительных чисел. Физические величины
- § 2.6. Неравенства для абсолютных величин
- § 2.7. Точные верхняя и нижняя грани множества
- § 2.8. Символика математической логики
- Глава 3. ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ
- § 3.1. Понятие предела последовательности
- § 3.2. Арифметические действия с пределами
- § 3.3. Бесконечно малая и бесконечно большая величины
- § 3.4. Существование предела у монотонной ограниченной последовательности
- § 3.5. Число е
- § 3.6. Леммы о вложенных отрезках, существовании точных граней множества и сечения во множестве действительных чисел
- § 3.7. Теорема Больцано-Вейерштрасса. Верхний и нижний пределы
- § 3.8. Критерий Коши существования предела
- § 3.9. Счетное множество. Счетность множества рациональных чисел. Несчетность множества действительных чисел
- Глава 4. ПРЕДЕЛ ФУНКЦИИ
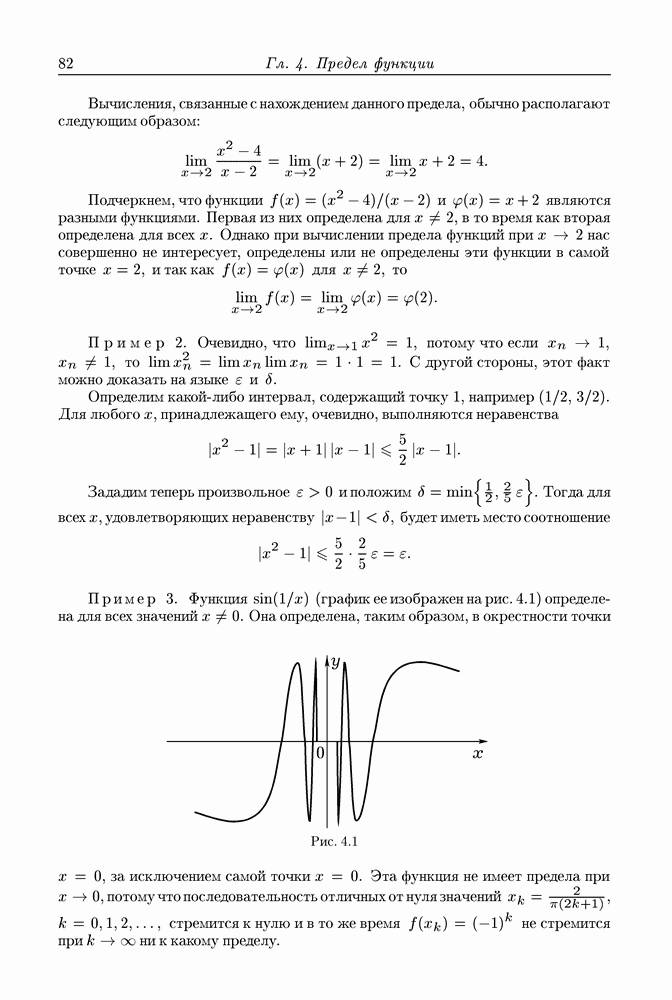
- § 4.1. Понятие предела функции
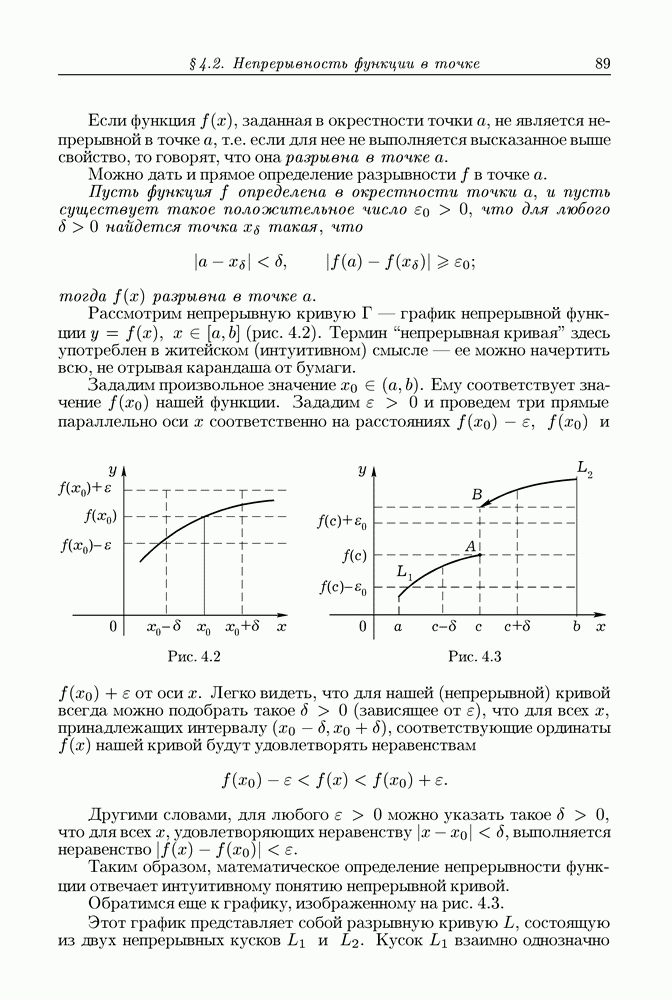
- § 4.2. Непрерывность функции в точке
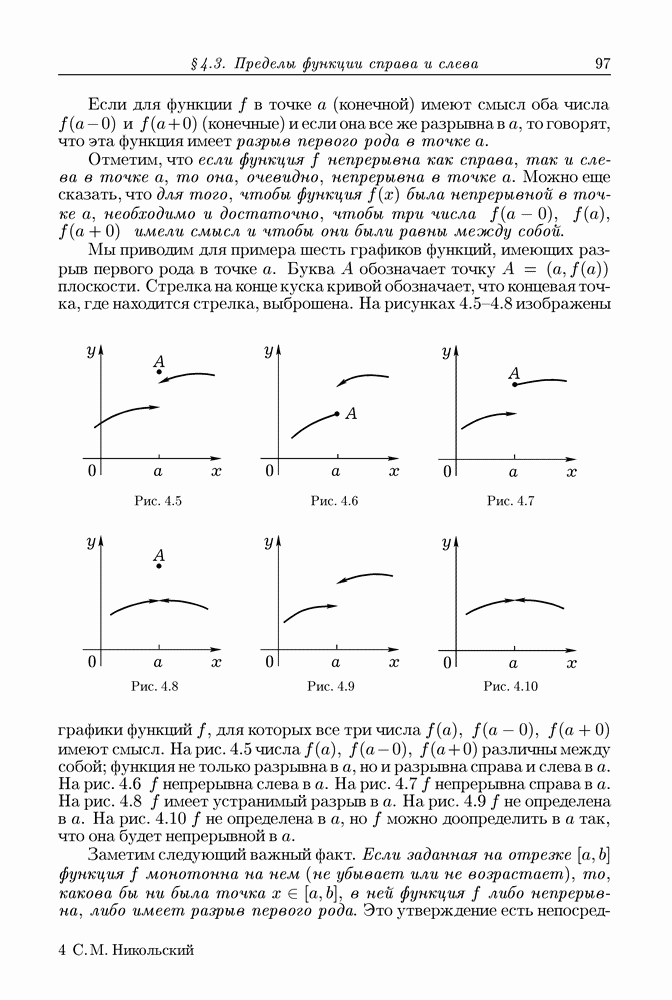
- § 4.3. Пределы функции справа и слева. Монотонная функция
- § 4.4. Функции, непрерывные на отрезке
- § 4.5. Обратная функция
- § 4.6. Показательная и логарифмическая функции
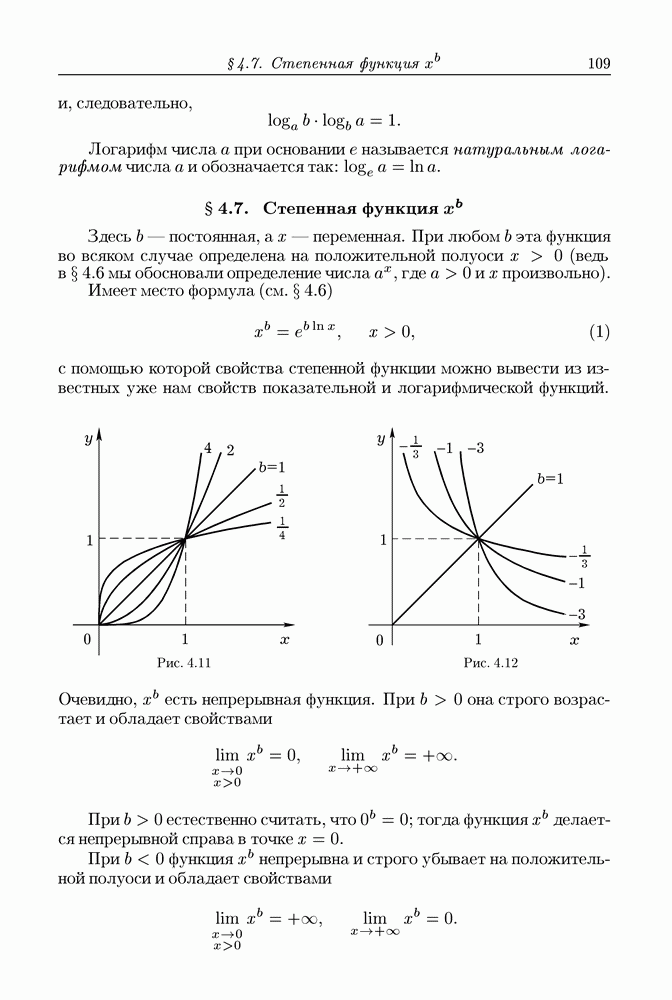
- § 4.7. Степенная функция x^b
- § 4.8. Еще о числе е
- § 4.9. lim sin oo/oo
- § 4.10. Порядок переменной, эквивалентность (асимптотика)
- Глава 5. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ДЛЯ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ
- § 5.1. Производная
- § 5.2. Дифференциал функции
- § 5.3. Производная функции от функции
- § 5.4. Производная обратной функции
- § 5.6. Производные и дифференциалы высшего порядка
- § 5.7. Возрастание и убывание функции на интервале и в точке. Локальный экстремум
- § 5.8. Теоремы о среднем значении. Критерии возрастания и убывания функции на интервале. Достаточные критерии локальных экстремумов
- § 5.9. Формула Тейлора
- § 5.10. Формулы Тейлора для важнейших элементарных функций
- § 5.11. Ряд Тейлора
- § 5.12. Выпуклость кривой в точке. Точка перегиба
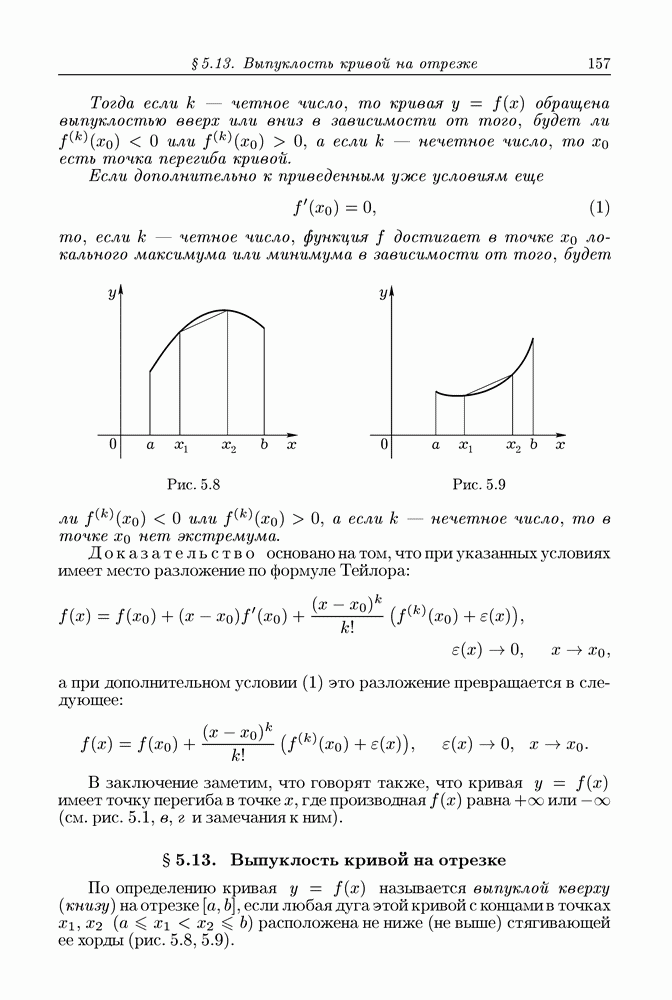
- § 5.13. Выпуклость кривой на отрезке
- § 5.14. Раскрытие неопределенностей
- § 5.15. Асимптота
- § 5.16. Схема построения графика функции
- § 5.17. Кусочно непрерывные и кусочно гладкие функции
- Глава 6. n-МЕРНОЕ ПРОСТРАНСТВО. ГЕОМЕТРИЯ КРИВОЙ
- § 6.1. n-мерное пространство. Линейное множество
- § 6.2. Евклидово n-мерное пространство. Пространство со скалярным произведением
- § 6.3. Линейное нормированное пространство
- § 6.4. Вектор-функция в n-мерном евклидовом пространстве
- § 6.5. Непрерывная кривая. Гладкая кривая
- § 6.6. Геометрический смысл производной вектор-функции
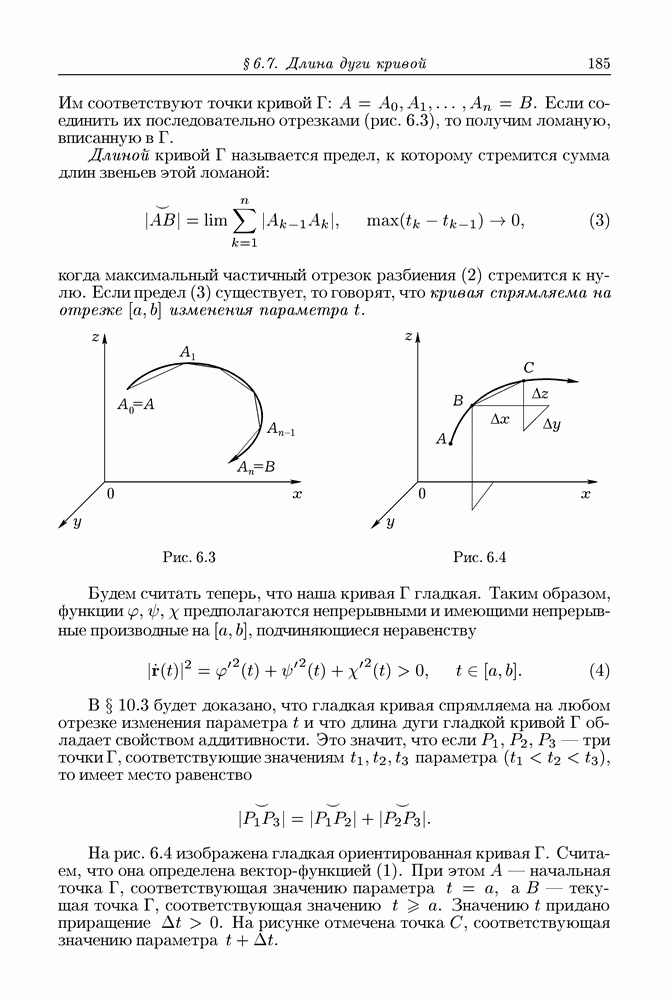
- § 6.7. Длина дуги кривой
- § 6.8. Касательная
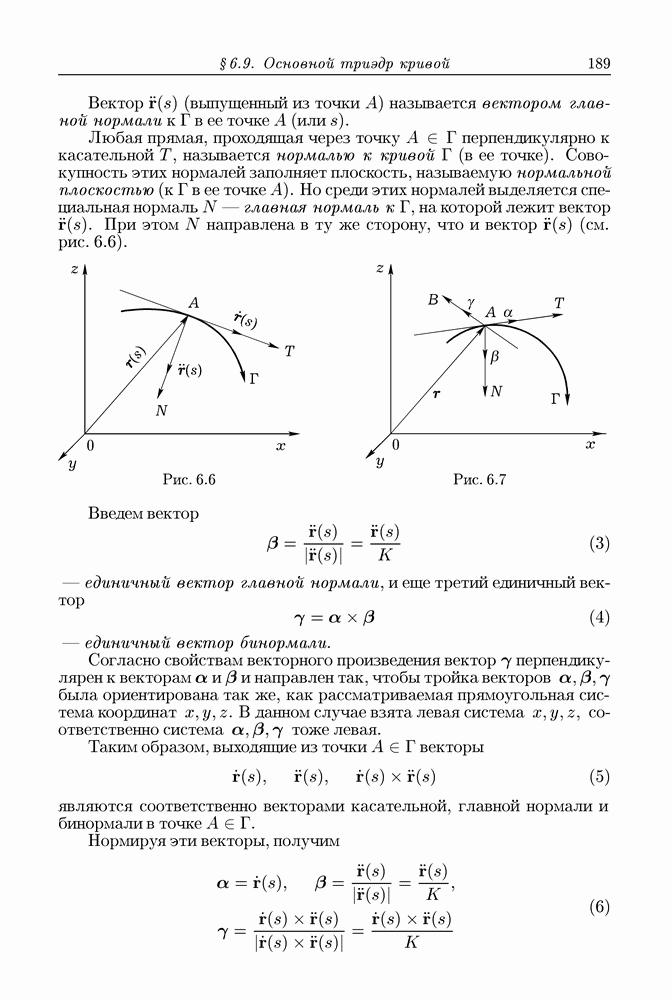
- § 6.9. Основной триэдр кривой
- § 6.10. Соприкасающаяся плоскость
- § 6.11. Кривизна и радиус кривизны кривой
- § 6.12. Эволюта
- § 6.13. Формулы Френе. Свойства эволюты
- Глава 7. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ
- § 7.1. Открытое множество
- § 7.2. Предел функции
- § 7.3. Непрерывная функция
- § 7.4. Частные производные и производная по направлению
- § 7.5. Дифференцируемая функция. Касательная плоскость
- § 7.6. Производная сложной функции. Производная по направлению. Градиент
- § 7.7. Независимость от порядка дифференцирования
- § 7.8. Дифференциал функции. Дифференциал высшего порядка
- § 7.9. Теорема Больцано-Вейерштрасса
- § 7.10. Замкнутые и открытые множества
- § 7.11. Функции на множестве. Свойства непрерывных функций на замкнутом ограниченном множестве
- § 7.12. Лемма о вложенных прямоугольниках и лемма Бореля
- § 7.13. Формула Тейлора
- § 7.14. локальный (абсолютный) экстремум функции
- § 7.15. Теоремы существования неявной функции
- § 7.16. Теорема существования решения системы уравнений
- § 7.17. Отображения
- § 7.18. Гладкая поверхность
- § 7.19. Дифференциалы неявных функций. Линеаризация
- § 7.20. Локальный относительный экстремум
- § 7.21. Замена переменных в частных производных
- § 7.22. Система зависимых функций
- Глава 8. НЕОПРЕДЕЛЕННЫЕ ИНТЕГРАЛЫ. АЛГЕБРА МНОГОЧЛЕНОВ
- § 8.1. Введение. Методы замены переменной и интегрирования по частям
- § 8.2. Комплексные числа
- § 8.3. Комплексные функции
- § 8.4. Многочлены
- § 8.5. Разложение рациональной функции на простейшие дроби
- § 8.6. Интегрирование рациональных дробей
- § 8.7. Интегрирование алгебраических иррациональностей
- § 8.8. Подстановки Эйлера
- § 8.9. Биномиальные дифференциалы. Теорема Чебышева
- § 8.10. Интегрирование тригонометрических выражений
- § 8.11. Тригонометрические подстановки
- § 8.12. Несколько важных интегралов, не выражаемых в элементарных функциях
- Глава 9. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ РИМАНА
- § 9.2. Ограниченность интегрируемой функции
- § 9.3. Суммы Дарбу
- § 9.4. Основная теорема
- § 9.5. Теоремы о существовании интеграла от непрерывной и монотонной функции на [a, b]
- § 9.6. Аддитивные и однородные свойства интеграла
- § 9.7. Неравенства и теорема о среднем
- § 9.8. Интеграл как функция верхнего предела. Теорема Ньютона-Лейбница
- § 9.9. Вторая теорема о среднем
- § 9.10. Видоизменение функции
- § 9.11. Несобственные интегралы
- § 9.12. Несобственные интегралы от неотрицательных функций
- § 9.13. Интегрирование по частям
- § 9.14. Несобственный интеграл и ряд
- § 9.15. Несобственные интегралы с особенностями в нескольких точках
- § 9.16. Формула Тейлора с остатком в интегральной форме
- § 9.17. Формулы Валлиса и Стирлинга
- Глава 10. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ ИНТЕГРАЛОВ. ПРИБЛИЖЕННЫЕ МЕТОДЫ
- § 10.1. Площадь в полярных координатах
- § 10.2. Объем тела вращения
- § 10.3. Длина дуги гладкой кривой
- § 10.4. Площадь поверхности тела вращения
- § 10.5. Интерполяционный многочлен Лагранжа
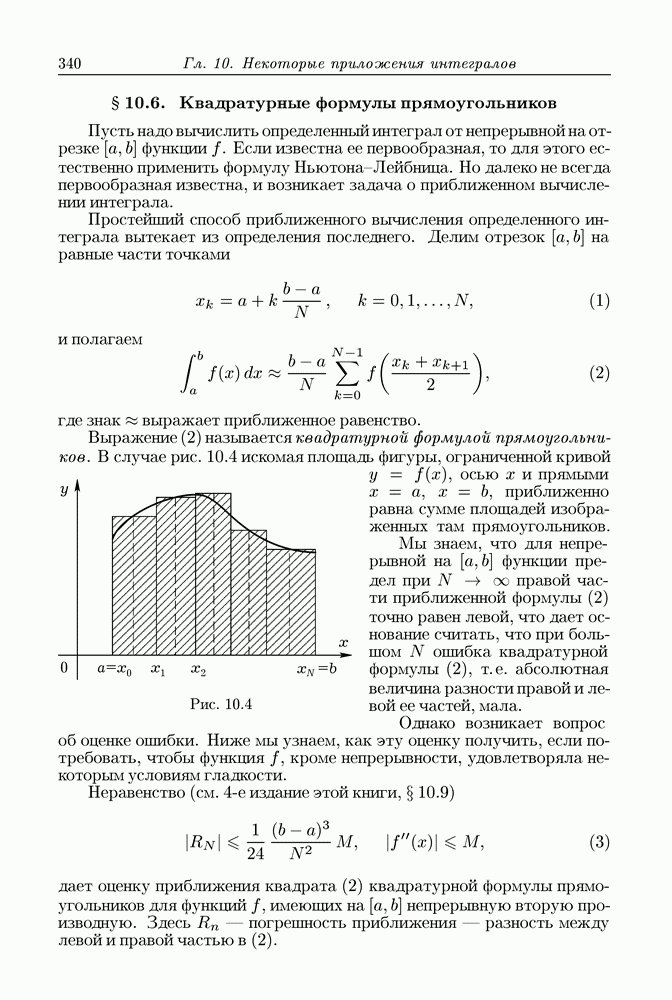
- § 10.6. Квадратурные формулы прямоугольников
- § 10.7. Формула Симпсона
- Глава 11. РЯДЫ
- § 11.1. Понятие ряда
- § 11.2. Действия с рядами
- § 11.3. Ряды с неотрицательными членами
- § 11.4. Ряд Лейбница
- § 11.5. Абсолютно сходящиеся ряды
- § 11.6. Условно и безусловно сходящиеся ряды с действительными членами
- § 11.7. Последовательности и ряды функций. Равномерная сходимость
- § 11.8. Интегрирование и дифференцирование равномерно сходящихся рядов на отрезке
- § 11.9. Кратные ряды. Перемножение абсолютно сходящихся рядов
- § 11.10. Суммирование рядов и последовательностей методом средних арифметических
- § 11.11. Степенные ряды
- § 11.12. Дифференцирование и интегрирование степенных рядов
- § 11.13. Степенные ряды функций e^z, cos z, sinz комплексной переменной
- Глава 12. КРАТНЫЕ ИНТЕГРАЛЫ
- § 12.2. Мера Жордана
- § 12.3. Важные примеры квадрируемых по Жордану множеств
- § 12.4. Еще один критерий измеримости множества. Полярные координаты
- § 12.5. Другие случаи измеримости
- § 12.6. Понятие кратного интеграла
- § 12.7. Верхняя и нижняя интегральные суммы. Основная теорема
- § 12.8. Интегрируемость непрерывной функции на замкнутом измеримом множестве. Другие критерии
- § 12.9. Свойства кратных интегралов
- § 12.10. Сведение кратного интеграла к интегрированию по отдельным переменным
- § 12.11. Непрерывность интеграла по параметру
- § 12.12. Геометрическая интерпретация знака определителя
- § 12.13. Замена переменных в кратном интеграле. Простейший случай
- § 12.14. Замена переменных в кратном интеграле
- § 12.15. Доказательство леммы 1 § 12.14
- § 12.16. Полярные координаты в плоскости
- § 12.17. Полярные и цилиндрические координаты в пространстве
- § 12.18. Гладкая поверхность
- § 12.19. Площадь поверхности
- Глава 13. ТЕОРИЯ ПОЛЯ. ДИФФЕРЕНЦИРОВАНИЕ И ИНТЕГРИРОВАНИЕ ПО ПАРАМЕТРУ. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
- § 13.1. Криволинейный интеграл первого рода
- § 13.2. Криволинейный интеграл второго рода
- § 13.3. Поле потенциала
- § 13.4. Ориентация плоской области
- § 13.5. Формула Грина. Выражение площади через криволинейный интеграл
- § 13.6. Интеграл по поверхности первого рода
- § 13.7. Ориентация поверхностей
- § 13.8. Интеграл по ориентированной плоской области
- § 13.9. Поток вектора через ориентированную поверхность
- § 13.10. Дивергенция. Теорема Гаусса-Остроградского
- § 13.11. Ротор вектора. Формула Стокса
- § 13.12. Дифференцирование интеграла по параметру
- § 13.13. Несобственный интеграл
- § 13.14. Равномерная сходимость несобственного интеграла
- § 13.15. Равномерно сходящийся интеграл для неограниченной области
- Глава 14. ЛИНЕЙНЫЕ НОРМИРОВАННЫЕ ПРОСТРАНСТВА. ОРТОГОНАЛЬНЫЕ СИСТЕМЫ
- § 14.2. Пространство L'(L)
- § 14.3. Пространство L2 (L2)
- § 14.4. Пространство …
- § 14.5. Полнота системы элементов в банаховом пространстве
- § 14.6. Ортогональная система в пространстве со скалярным произведением
- § 14.7. Ортогонализация системы
- § 14.8. Полнота системы функций в …
- Глава 15. РЯДЫ ФУРЬЕ. ПРИБЛИЖЕНИЕ ФУНКЦИЙ ПОЛИНОМАМИ
- § 15.2. Сумма Дирихле
- § 15.3. Формулы для остатка ряда Фурье
- § 15.4. Теоремы об осцилляции
- § 15.5. Критерий сходимости рядов Фурье. Полнота тригонометрической системы функций
- § 15.6. Комплексная форма записи ряда Фурье
- § 15.7. Дифференцирование и интегрирование рядов Фурье
- § 15.8. Оценка остатка ряда Фурье
- § 15.9. Алгебраические многочлены. Многочлены Чебышева
- § 15.10. Теорема Вейерштрасса
- § 15.11. Многочлены Лежандра
- Глава 16. ИНТЕГРАЛ ФУРЬЕ. ОБОБЩЕННЫЕ ФУНКЦИИ
- § 16.1. Понятие интеграла Фурье
- § 16.2. Сходимость простого интеграла Фурье к порождающей его функции
- § 16.3. Преобразование Фурье. Повторный интеграл Фурье. Косинус- и синус-преобразования Фурье
- § 16.4. Производная преобразования Фурье
- § 16.5. Обобщенные функции в смысле D
- § 16.6. Пространство S
- § 16.7. Пространство S обобщенных функций