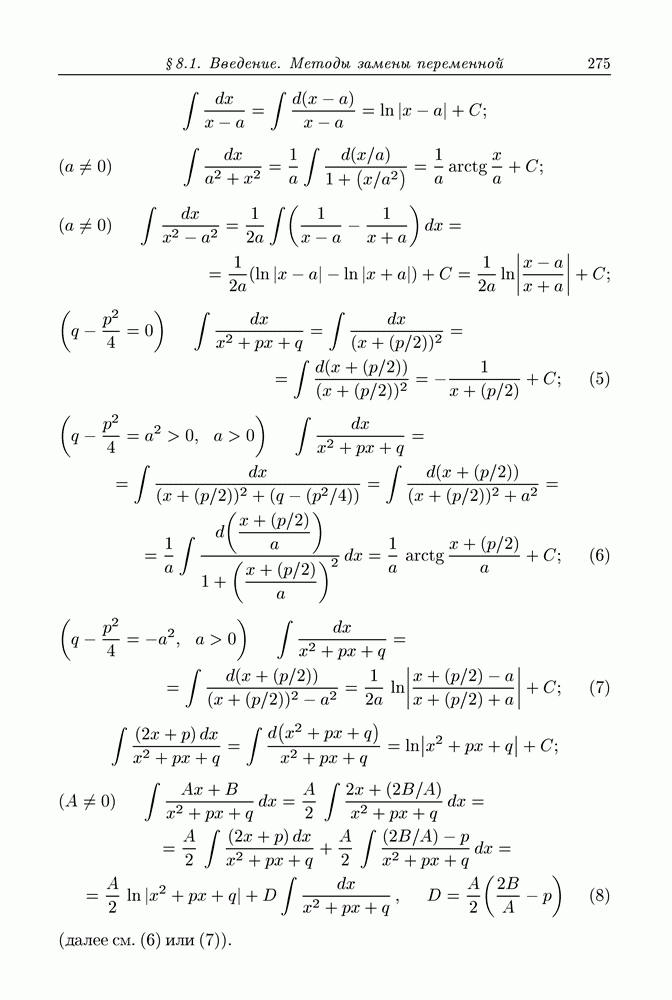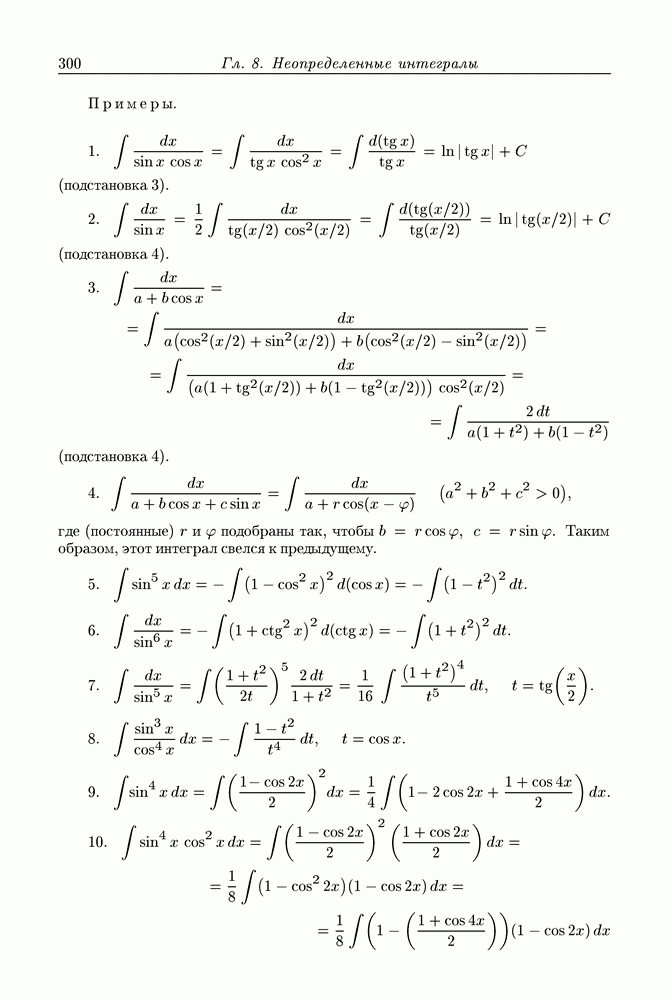| << Предыдущий параграф | Следующий параграф >> |
Пред.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
353
354
355
356
357
358
359
360
361
362
363
364
365
366
367
368
369
370
371
372
373
374
375
376
377
378
379
380
381
382
383
384
385
386
387
388
389
390
391
392
393
394
395
396
397
398
399
400
401
402
403
404
405
406
407
408
409
410
411
412
413
414
415
416
417
418
419
420
421
422
423
424
425
426
427
428
429
430
431
432
433
434
435
436
437
438
439
440
441
442
443
444
445
446
447
448
449
450
451
452
453
454
455
456
457
458
459
460
461
462
463
464
465
466
467
468
469
470
471
472
473
474
475
476
477
478
479
480
481
482
483
484
485
486
487
488
489
490
491
492
493
494
495
496
497
498
499
500
501
502
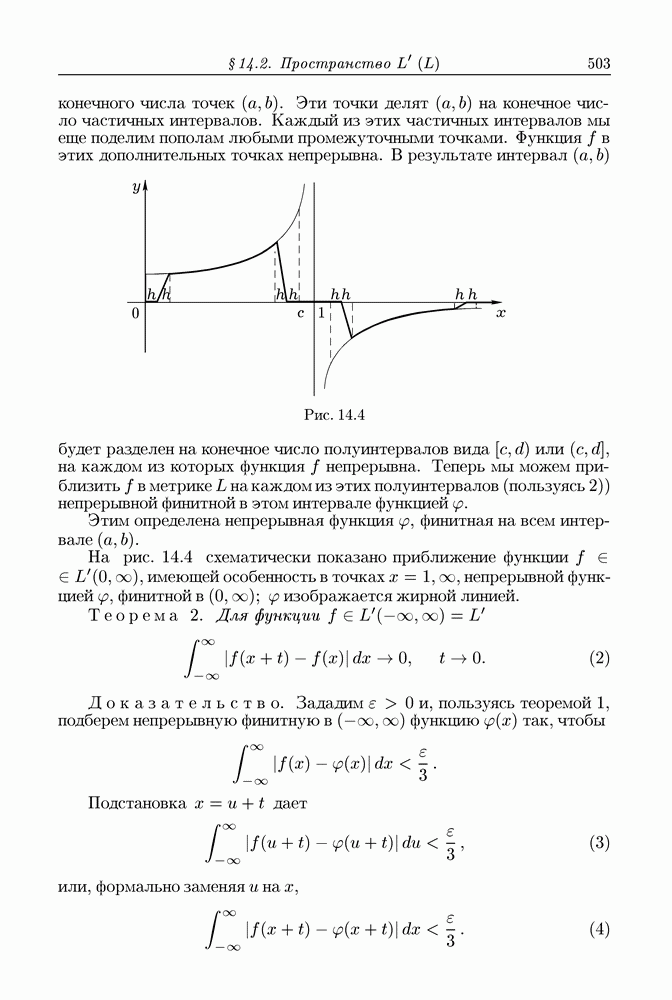
503
504
505
506
507
508
509
510
511
512
513
514
515
516
517
518
519
520
521
522
523
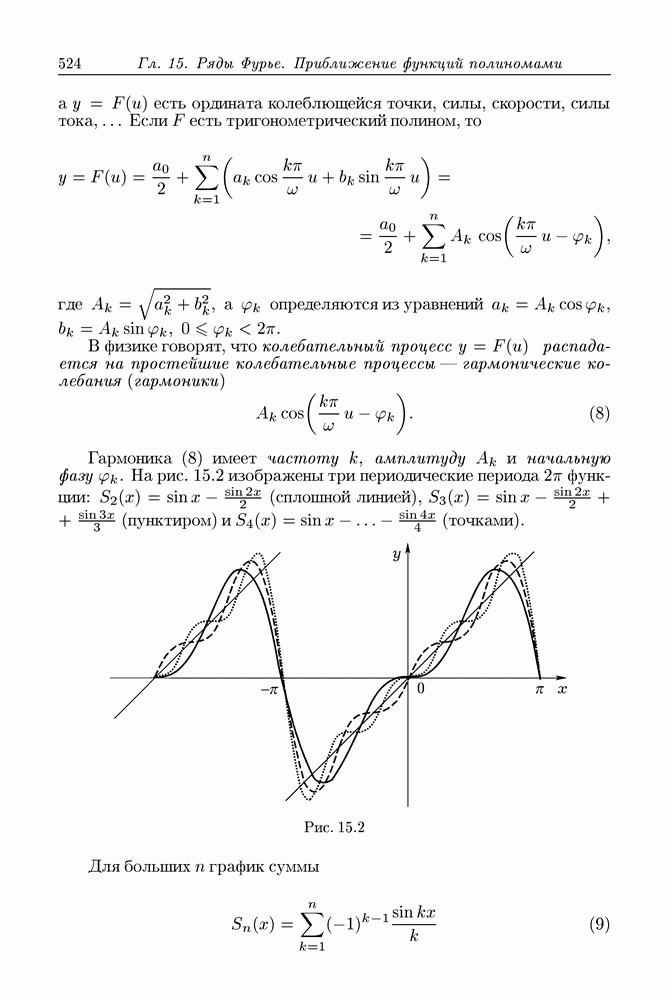
524
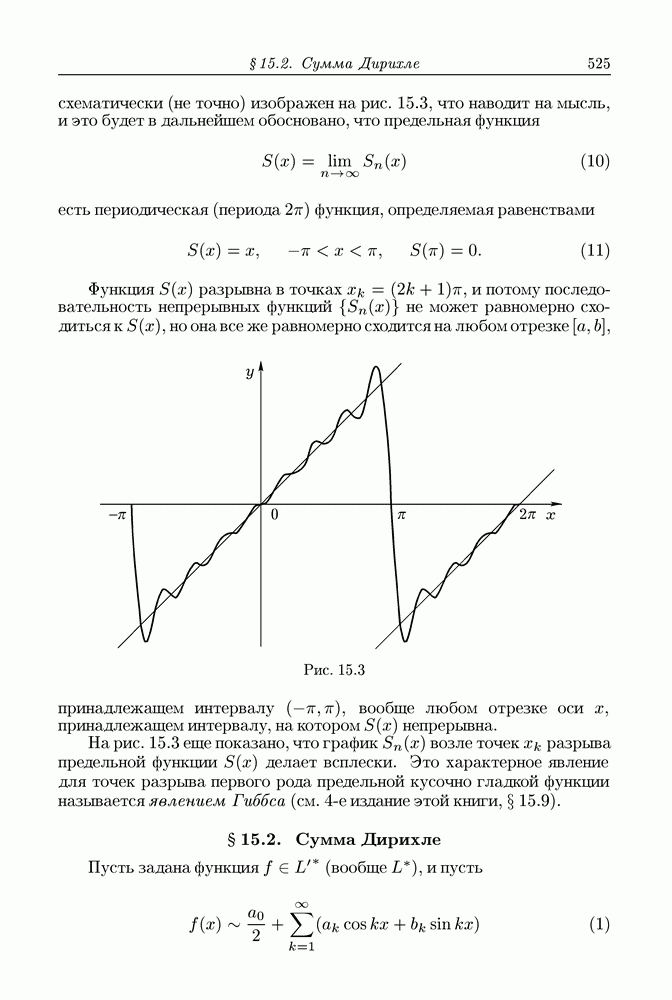
525
526
527
528
529
530
531
532
533
534
535
536
537
538
539
540
541
542
543
544
545
546
547
548
549
550
551
552
553
554
555
556
557
558
559
560
561
562
563
564
565
566
567
568
569
570
571
572
573
574
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 4.6. Показательная и логарифмическая функции
Функция  Зададим положительное число
Зададим положительное число  Если
Если  натуральное число, то число
натуральное число, то число  определяется как произведение
определяется как произведение  а из
а из  сомножителей, каждый из которых равен а, а число
сомножителей, каждый из которых равен а, а число  как арифметическое значение корня
как арифметическое значение корня  степени из а.
степени из а.
Если теперь  (
( целые) есть рациональная дробь, то по определению полагают
целые) есть рациональная дробь, то по определению полагают

Доказательство второго равенства в этой цепи и того факта, что это определение приводит к тому же числу, если дробь  будет записана в форме
будет записана в форме  где
где  произвольное натуральное число, известно читателю из элементарной алгебры.
произвольное натуральное число, известно читателю из элементарной алгебры.
Обозначим через  множество всех рациональных чисел. Функция
множество всех рациональных чисел. Функция  определена пока на этом множестве. В курсе элементарной математики доказывается на основании только аксиом числа I-IV групп, что имеет место свойство:
определена пока на этом множестве. В курсе элементарной математики доказывается на основании только аксиом числа I-IV групп, что имеет место свойство:

каковы бы ни были  Там доказывается также неравенство
Там доказывается также неравенство 
Но функцию  можно доопределить на всех иррациональных точках так, что определенная таким образом на всей действительной оси
можно доопределить на всех иррациональных точках так, что определенная таким образом на всей действительной оси  продолженная функция, которую естественно обозначить снова через
продолженная функция, которую естественно обозначить снова через  будет непрерывной всюду на
будет непрерывной всюду на  Больше
Больше
того, для продолженной функции свойство (2) выполняется уже для всех 
Начнем с того, что докажем вспомогательное неравенство (Бернулли).
Если  натуральное число,
натуральное число,  где
где  Поэтому, учитывая формулу бинома Ньютона, получим
Поэтому, учитывая формулу бинома Ньютона, получим

Если теперь  есть произвольное положительное рациональное число, удовлетворяющее неравенствам
есть произвольное положительное рациональное число, удовлетворяющее неравенствам  то можно подобрать такое натуральное число
то можно подобрать такое натуральное число  что
что  Поэтому при
Поэтому при 

На основании этого неравенства, называемого неравенством Бернулли, получим

Зададим произвольное положительное рациональное число с и введем новое множество  состоящее из всех
состоящее из всех  которые удовлетворяют неравенству
которые удовлетворяют неравенству  Из (3) следует:
Из (3) следует:

где, таким образом,  есть константа, не зависящая от рассматриваемых х, у, но зависящая от с.
есть константа, не зависящая от рассматриваемых х, у, но зависящая от с.
Следовательно,

Пусть  тогда
тогда

и, следовательно, имеет место

Так как с может быть любым числом, то мы доказали (6) для любых 
Пусть теперь  — любое иррациональное число
— любое иррациональное число  . На основании критерия Коши существования предела для любого
. На основании критерия Коши существования предела для любого  найдется такое
найдется такое  что
что

Это показывает в силу (5), что имеет место неравенство

т.е. условие Коши для последовательности чисел  Но тогда существует предел этой последовательности, который обозначим через
Но тогда существует предел этой последовательности, который обозначим через 

Найденный предел не зависит от выбранной нами последовательности  Ведь если
Ведь если  другая последовательность, для которой
другая последовательность, для которой  то
то

Итак, функция  определена для любых х. Для рациональных х посредством формулы (1) и для иррациональных х формулой (7).
определена для любых х. Для рациональных х посредством формулы (1) и для иррациональных х формулой (7).
Пусть теперь  любые действительные числа,
любые действительные числа,  Тогда
Тогда

Перейдем в полученном неравенстве к пределу при  Так как
Так как  и функция
и функция  непрерывна, то получим
непрерывна, то получим

при  Из неравенства (9) непосредственно следует, что функция
Из неравенства (9) непосредственно следует, что функция  непрерывна для любого
непрерывна для любого  следовательно, и для любого
следовательно, и для любого  потому что с можно считать произвольным. Имеют место свойства:
потому что с можно считать произвольным. Имеют место свойства:

Чтобы доказать эти свойства, будем исходить из того, что для рациональных  они известны из школьного курса элементарной алгебры.
они известны из школьного курса элементарной алгебры.
Пусть  постоянные рациональные числа такие, что
постоянные рациональные числа такие, что  и пусть
и пусть  переменные такие, что
переменные такие, что  возрастая, и
возрастая, и  убывая. Тогда
убывая. Тогда  а после перехода к пределу
а после перехода к пределу  и мы получили (11) и (10), потому что
и мы получили (11) и (10), потому что  Свойства (12) следуют из того, что это верно в случае, когда
Свойства (12) следуют из того, что это верно в случае, когда  или
или  пробегая рациональные значения, и из доказанной уже монотонности (см. (11)). Наконец, (13) следует из равенства
пробегая рациональные значения, и из доказанной уже монотонности (см. (11)). Наконец, (13) следует из равенства  после перехода в нем к пределу.
после перехода в нем к пределу.
До сих пор мы считали  Если
Если  то полагаем 1
то полагаем 1

В этом случае свойство (13) функции  и ее непрерывность сохраняются, но теперь уже функция будет строго убывать. Наконец, полагаем
и ее непрерывность сохраняются, но теперь уже функция будет строго убывать. Наконец, полагаем

Отметим еще, что при натуральном 

поэтому для рационального числа 

Далее, если у — произвольное число  , где
, где  рациональные, то
рациональные, то

и мы доказали, что 
Функция  Пусть для определенности
Пусть для определенности  Тогда
Тогда  есть функция, непрерывная и строго возрастающая на всей действительной оси. При этом
есть функция, непрерывная и строго возрастающая на всей действительной оси. При этом

Таким образом, функция  отображает действительную ось
отображает действительную ось  на открытую полуось
на открытую полуось  и обратная к ней функция по теореме 2 § 4.5
и обратная к ней функция по теореме 2 § 4.5
однозначна, строго возрастает и непрерывна на  Эта функция называется логарифмом у при основании
Эта функция называется логарифмом у при основании  и обозначается так:
и обозначается так:

Из сказанного следует, что (мы заменяем у на  )
)

При  рассуждения аналогичны. Функция
рассуждения аналогичны. Функция  также отображает действительную ось
также отображает действительную ось  на полуось
на полуось  но строго убывая. Обратная функция
но строго убывая. Обратная функция  определенная на
определенная на  также будет строго убывать, и теперь
также будет строго убывать, и теперь

Имеют место тождества 

Отсюда на основании свойств функции х при  имеем
имеем

Если в этом равенстве заменить х на  то получим
то получим

Далее,

поэтому

Наконец, отметим, что для положительных не равных 1 чисел а и b имеет место

и, следовательно,

Логарифм числа а при основании  называется натуральным логарифмом числа а и обозначается так:
называется натуральным логарифмом числа а и обозначается так: 
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- Глава 1. ВВЕДЕНИЕ
- § 1.2. Множество. Интервал, отрезок
- § 1.3. Функция
- § 1.4. Понятие непрерывности функции
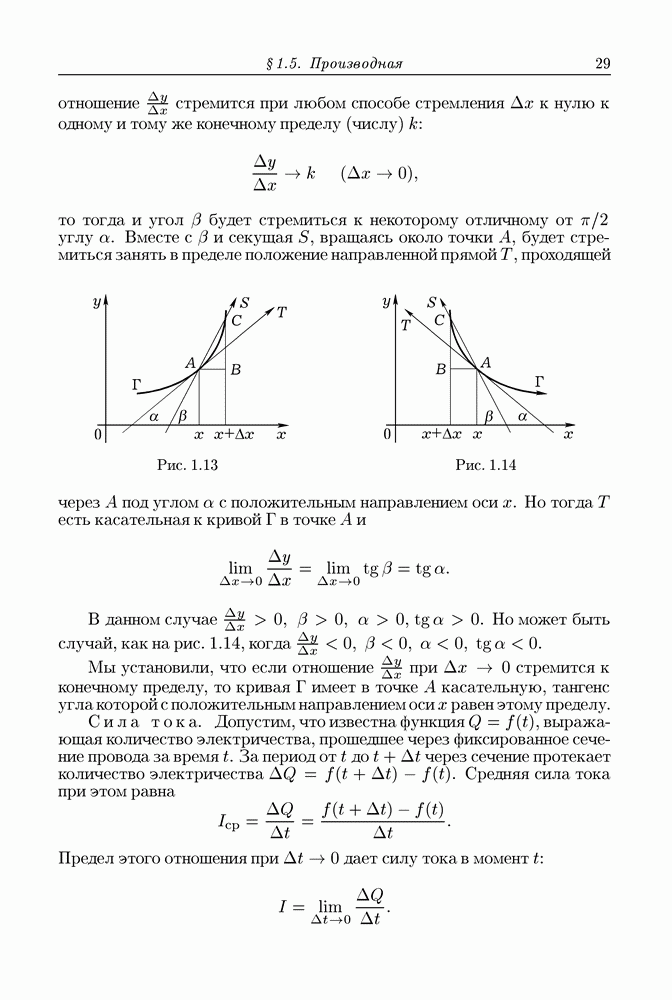
- § 1.5. Производная
- § 1.6. Первообразная. Неопределенный интеграл
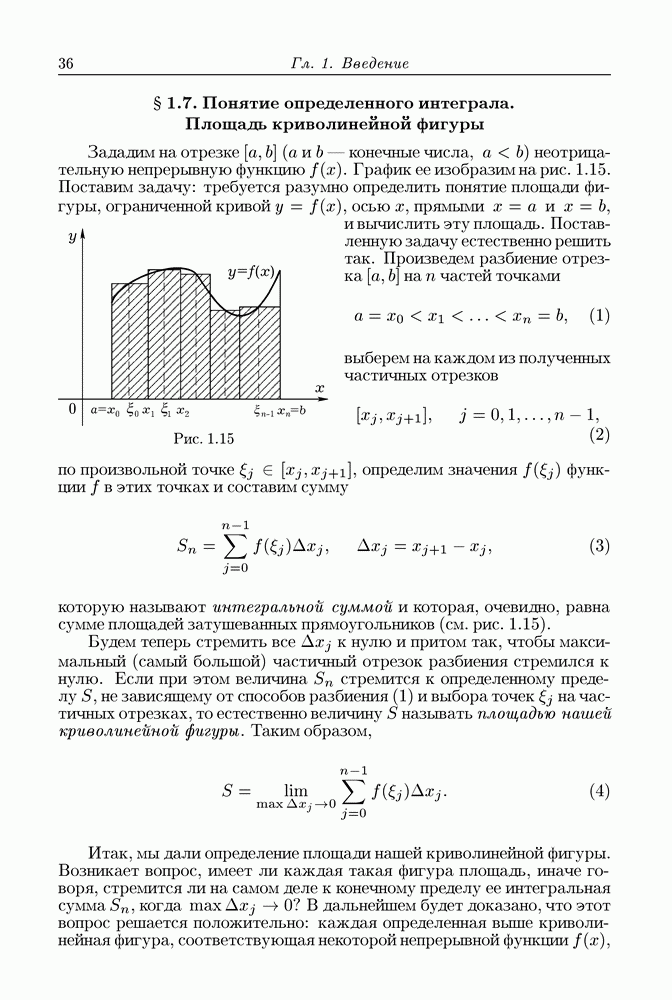
- § 1.7. Понятие определенного интеграла. Площадь криволинейной фигуры
- Глава 2. ДЕЙСТВИТЕЛЬНОЕ ЧИСЛО
- § 2.1. Рациональные и иррациональные числа
- § 2.2. Определение неравенства
- § 2.3. Основная лемма. Определение арифметических действий
- § 2.4. Основные свойства действительных чисел
- § 2.5. Изоморфизм различных представлений действительных чисел. Физические величины
- § 2.6. Неравенства для абсолютных величин
- § 2.7. Точные верхняя и нижняя грани множества
- § 2.8. Символика математической логики
- Глава 3. ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ
- § 3.1. Понятие предела последовательности
- § 3.2. Арифметические действия с пределами
- § 3.3. Бесконечно малая и бесконечно большая величины
- § 3.4. Существование предела у монотонной ограниченной последовательности
- § 3.5. Число е
- § 3.6. Леммы о вложенных отрезках, существовании точных граней множества и сечения во множестве действительных чисел
- § 3.7. Теорема Больцано-Вейерштрасса. Верхний и нижний пределы
- § 3.8. Критерий Коши существования предела
- § 3.9. Счетное множество. Счетность множества рациональных чисел. Несчетность множества действительных чисел
- Глава 4. ПРЕДЕЛ ФУНКЦИИ
- § 4.1. Понятие предела функции
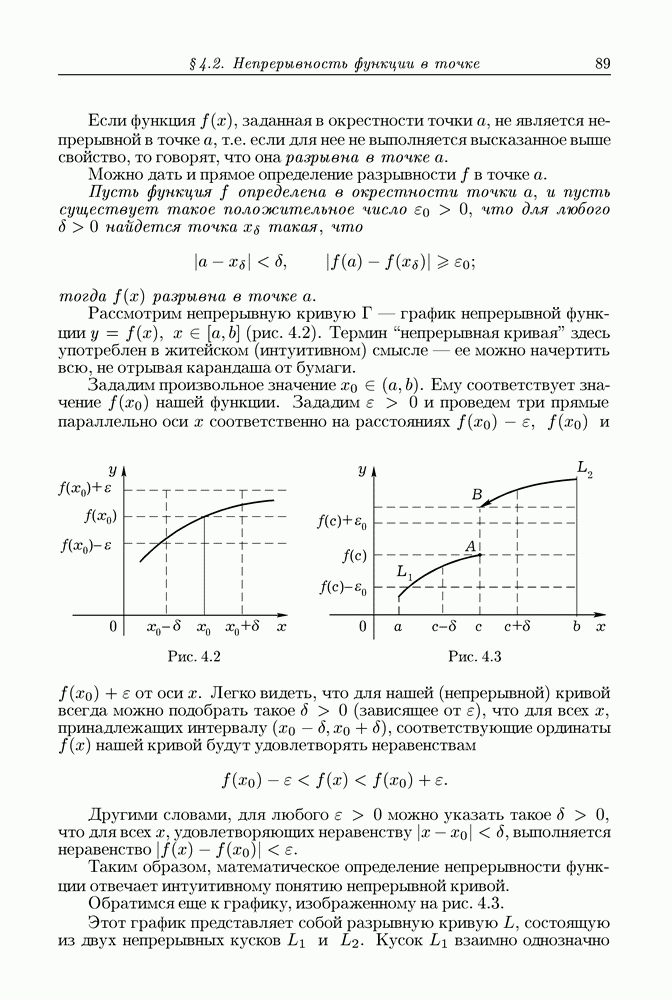
- § 4.2. Непрерывность функции в точке
- § 4.3. Пределы функции справа и слева. Монотонная функция
- § 4.4. Функции, непрерывные на отрезке
- § 4.5. Обратная функция
- § 4.6. Показательная и логарифмическая функции
- § 4.7. Степенная функция x^b
- § 4.8. Еще о числе е
- § 4.9. lim sin oo/oo
- § 4.10. Порядок переменной, эквивалентность (асимптотика)
- Глава 5. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ДЛЯ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ
- § 5.1. Производная
- § 5.2. Дифференциал функции
- § 5.3. Производная функции от функции
- § 5.4. Производная обратной функции
- § 5.6. Производные и дифференциалы высшего порядка
- § 5.7. Возрастание и убывание функции на интервале и в точке. Локальный экстремум
- § 5.8. Теоремы о среднем значении. Критерии возрастания и убывания функции на интервале. Достаточные критерии локальных экстремумов
- § 5.9. Формула Тейлора
- § 5.10. Формулы Тейлора для важнейших элементарных функций
- § 5.11. Ряд Тейлора
- § 5.12. Выпуклость кривой в точке. Точка перегиба
- § 5.13. Выпуклость кривой на отрезке
- § 5.14. Раскрытие неопределенностей
- § 5.15. Асимптота
- § 5.16. Схема построения графика функции
- § 5.17. Кусочно непрерывные и кусочно гладкие функции
- Глава 6. n-МЕРНОЕ ПРОСТРАНСТВО. ГЕОМЕТРИЯ КРИВОЙ
- § 6.1. n-мерное пространство. Линейное множество
- § 6.2. Евклидово n-мерное пространство. Пространство со скалярным произведением
- § 6.3. Линейное нормированное пространство
- § 6.4. Вектор-функция в n-мерном евклидовом пространстве
- § 6.5. Непрерывная кривая. Гладкая кривая
- § 6.6. Геометрический смысл производной вектор-функции
- § 6.7. Длина дуги кривой
- § 6.8. Касательная
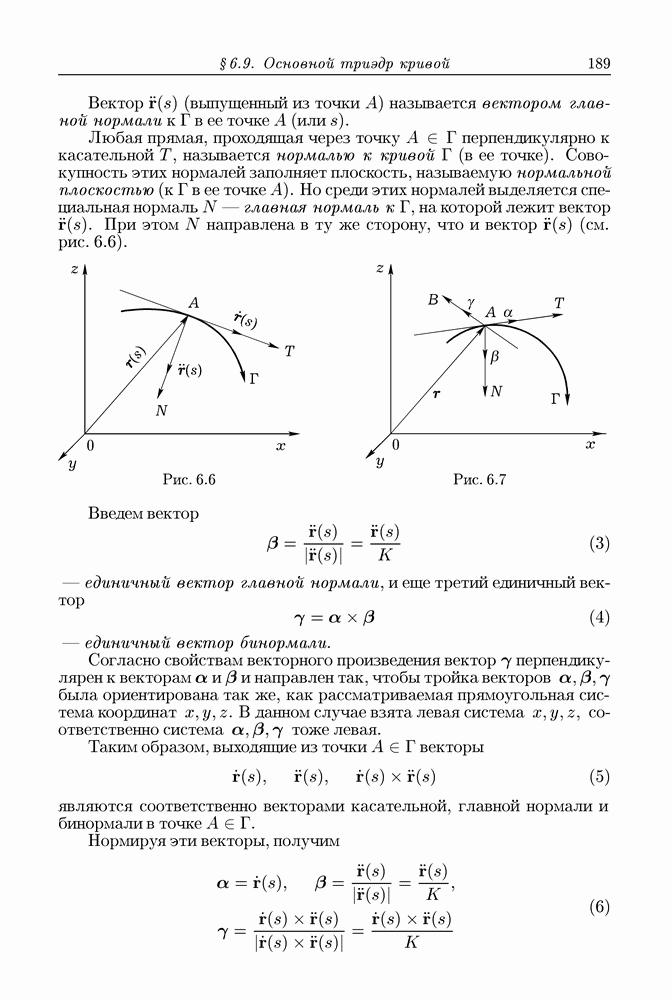
- § 6.9. Основной триэдр кривой
- § 6.10. Соприкасающаяся плоскость
- § 6.11. Кривизна и радиус кривизны кривой
- § 6.12. Эволюта
- § 6.13. Формулы Френе. Свойства эволюты
- Глава 7. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ
- § 7.1. Открытое множество
- § 7.2. Предел функции
- § 7.3. Непрерывная функция
- § 7.4. Частные производные и производная по направлению
- § 7.5. Дифференцируемая функция. Касательная плоскость
- § 7.6. Производная сложной функции. Производная по направлению. Градиент
- § 7.7. Независимость от порядка дифференцирования
- § 7.8. Дифференциал функции. Дифференциал высшего порядка
- § 7.9. Теорема Больцано-Вейерштрасса
- § 7.10. Замкнутые и открытые множества
- § 7.11. Функции на множестве. Свойства непрерывных функций на замкнутом ограниченном множестве
- § 7.12. Лемма о вложенных прямоугольниках и лемма Бореля
- § 7.13. Формула Тейлора
- § 7.14. локальный (абсолютный) экстремум функции
- § 7.15. Теоремы существования неявной функции
- § 7.16. Теорема существования решения системы уравнений
- § 7.17. Отображения
- § 7.18. Гладкая поверхность
- § 7.19. Дифференциалы неявных функций. Линеаризация
- § 7.20. Локальный относительный экстремум
- § 7.21. Замена переменных в частных производных
- § 7.22. Система зависимых функций
- Глава 8. НЕОПРЕДЕЛЕННЫЕ ИНТЕГРАЛЫ. АЛГЕБРА МНОГОЧЛЕНОВ
- § 8.1. Введение. Методы замены переменной и интегрирования по частям
- § 8.2. Комплексные числа
- § 8.3. Комплексные функции
- § 8.4. Многочлены
- § 8.5. Разложение рациональной функции на простейшие дроби
- § 8.6. Интегрирование рациональных дробей
- § 8.7. Интегрирование алгебраических иррациональностей
- § 8.8. Подстановки Эйлера
- § 8.9. Биномиальные дифференциалы. Теорема Чебышева
- § 8.10. Интегрирование тригонометрических выражений
- § 8.11. Тригонометрические подстановки
- § 8.12. Несколько важных интегралов, не выражаемых в элементарных функциях
- Глава 9. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ РИМАНА
- § 9.2. Ограниченность интегрируемой функции
- § 9.3. Суммы Дарбу
- § 9.4. Основная теорема
- § 9.5. Теоремы о существовании интеграла от непрерывной и монотонной функции на [a, b]
- § 9.6. Аддитивные и однородные свойства интеграла
- § 9.7. Неравенства и теорема о среднем
- § 9.8. Интеграл как функция верхнего предела. Теорема Ньютона-Лейбница
- § 9.9. Вторая теорема о среднем
- § 9.10. Видоизменение функции
- § 9.11. Несобственные интегралы
- § 9.12. Несобственные интегралы от неотрицательных функций
- § 9.13. Интегрирование по частям
- § 9.14. Несобственный интеграл и ряд
- § 9.15. Несобственные интегралы с особенностями в нескольких точках
- § 9.16. Формула Тейлора с остатком в интегральной форме
- § 9.17. Формулы Валлиса и Стирлинга
- Глава 10. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ ИНТЕГРАЛОВ. ПРИБЛИЖЕННЫЕ МЕТОДЫ
- § 10.1. Площадь в полярных координатах
- § 10.2. Объем тела вращения
- § 10.3. Длина дуги гладкой кривой
- § 10.4. Площадь поверхности тела вращения
- § 10.5. Интерполяционный многочлен Лагранжа
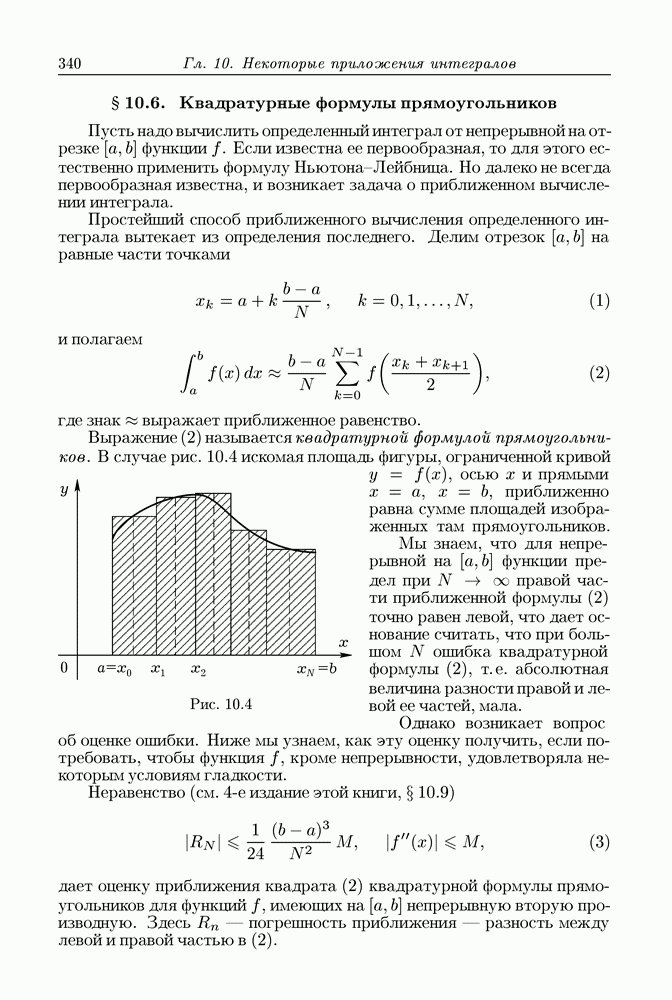
- § 10.6. Квадратурные формулы прямоугольников
- § 10.7. Формула Симпсона
- Глава 11. РЯДЫ
- § 11.1. Понятие ряда
- § 11.2. Действия с рядами
- § 11.3. Ряды с неотрицательными членами
- § 11.4. Ряд Лейбница
- § 11.5. Абсолютно сходящиеся ряды
- § 11.6. Условно и безусловно сходящиеся ряды с действительными членами
- § 11.7. Последовательности и ряды функций. Равномерная сходимость
- § 11.8. Интегрирование и дифференцирование равномерно сходящихся рядов на отрезке
- § 11.9. Кратные ряды. Перемножение абсолютно сходящихся рядов
- § 11.10. Суммирование рядов и последовательностей методом средних арифметических
- § 11.11. Степенные ряды
- § 11.12. Дифференцирование и интегрирование степенных рядов
- § 11.13. Степенные ряды функций e^z, cos z, sinz комплексной переменной
- Глава 12. КРАТНЫЕ ИНТЕГРАЛЫ
- § 12.2. Мера Жордана
- § 12.3. Важные примеры квадрируемых по Жордану множеств
- § 12.4. Еще один критерий измеримости множества. Полярные координаты
- § 12.5. Другие случаи измеримости
- § 12.6. Понятие кратного интеграла
- § 12.7. Верхняя и нижняя интегральные суммы. Основная теорема
- § 12.8. Интегрируемость непрерывной функции на замкнутом измеримом множестве. Другие критерии
- § 12.9. Свойства кратных интегралов
- § 12.10. Сведение кратного интеграла к интегрированию по отдельным переменным
- § 12.11. Непрерывность интеграла по параметру
- § 12.12. Геометрическая интерпретация знака определителя
- § 12.13. Замена переменных в кратном интеграле. Простейший случай
- § 12.14. Замена переменных в кратном интеграле
- § 12.15. Доказательство леммы 1 § 12.14
- § 12.16. Полярные координаты в плоскости
- § 12.17. Полярные и цилиндрические координаты в пространстве
- § 12.18. Гладкая поверхность
- § 12.19. Площадь поверхности
- Глава 13. ТЕОРИЯ ПОЛЯ. ДИФФЕРЕНЦИРОВАНИЕ И ИНТЕГРИРОВАНИЕ ПО ПАРАМЕТРУ. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
- § 13.1. Криволинейный интеграл первого рода
- § 13.2. Криволинейный интеграл второго рода
- § 13.3. Поле потенциала
- § 13.4. Ориентация плоской области
- § 13.5. Формула Грина. Выражение площади через криволинейный интеграл
- § 13.6. Интеграл по поверхности первого рода
- § 13.7. Ориентация поверхностей
- § 13.8. Интеграл по ориентированной плоской области
- § 13.9. Поток вектора через ориентированную поверхность
- § 13.10. Дивергенция. Теорема Гаусса-Остроградского
- § 13.11. Ротор вектора. Формула Стокса
- § 13.12. Дифференцирование интеграла по параметру
- § 13.13. Несобственный интеграл
- § 13.14. Равномерная сходимость несобственного интеграла
- § 13.15. Равномерно сходящийся интеграл для неограниченной области
- Глава 14. ЛИНЕЙНЫЕ НОРМИРОВАННЫЕ ПРОСТРАНСТВА. ОРТОГОНАЛЬНЫЕ СИСТЕМЫ
- § 14.2. Пространство L'(L)
- § 14.3. Пространство L2 (L2)
- § 14.4. Пространство …
- § 14.5. Полнота системы элементов в банаховом пространстве
- § 14.6. Ортогональная система в пространстве со скалярным произведением
- § 14.7. Ортогонализация системы
- § 14.8. Полнота системы функций в …
- Глава 15. РЯДЫ ФУРЬЕ. ПРИБЛИЖЕНИЕ ФУНКЦИЙ ПОЛИНОМАМИ
- § 15.2. Сумма Дирихле
- § 15.3. Формулы для остатка ряда Фурье
- § 15.4. Теоремы об осцилляции
- § 15.5. Критерий сходимости рядов Фурье. Полнота тригонометрической системы функций
- § 15.6. Комплексная форма записи ряда Фурье
- § 15.7. Дифференцирование и интегрирование рядов Фурье
- § 15.8. Оценка остатка ряда Фурье
- § 15.9. Алгебраические многочлены. Многочлены Чебышева
- § 15.10. Теорема Вейерштрасса
- § 15.11. Многочлены Лежандра
- Глава 16. ИНТЕГРАЛ ФУРЬЕ. ОБОБЩЕННЫЕ ФУНКЦИИ
- § 16.1. Понятие интеграла Фурье
- § 16.2. Сходимость простого интеграла Фурье к порождающей его функции
- § 16.3. Преобразование Фурье. Повторный интеграл Фурье. Косинус- и синус-преобразования Фурье
- § 16.4. Производная преобразования Фурье
- § 16.5. Обобщенные функции в смысле D
- § 16.6. Пространство S
- § 16.7. Пространство S обобщенных функций