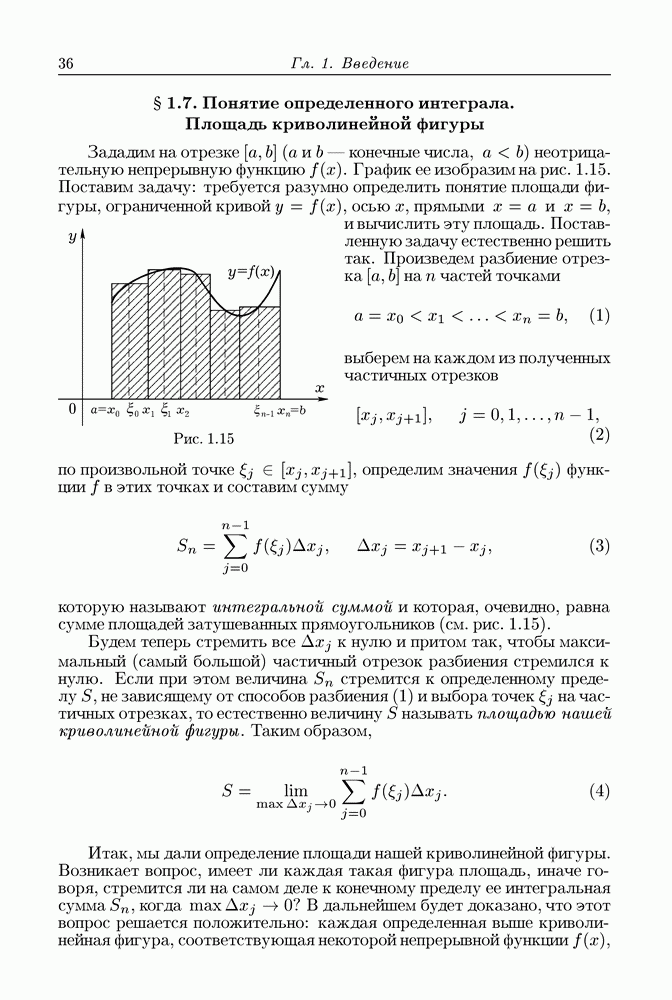
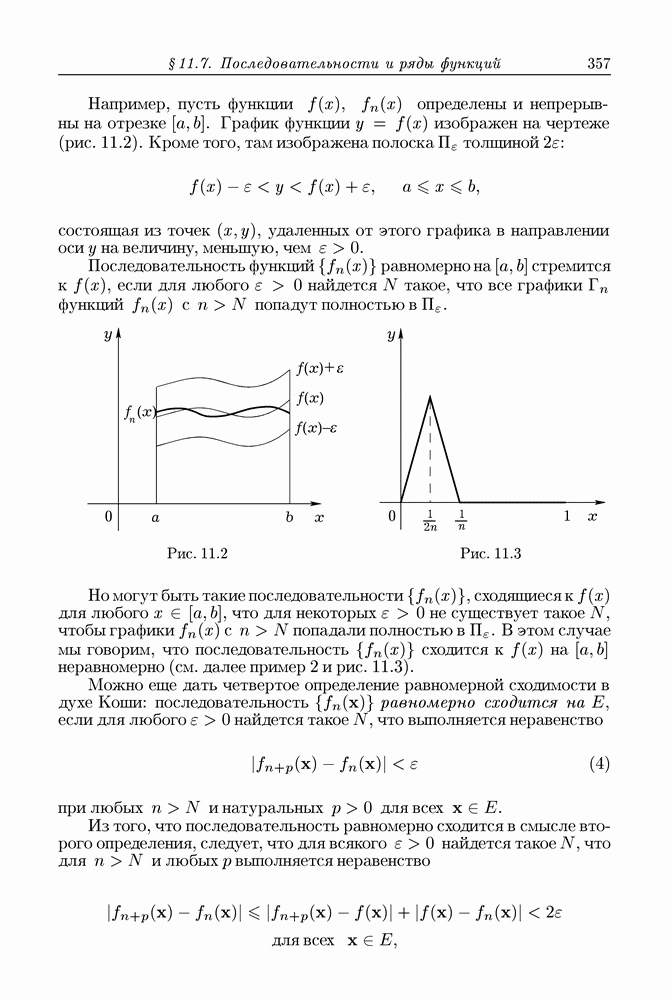
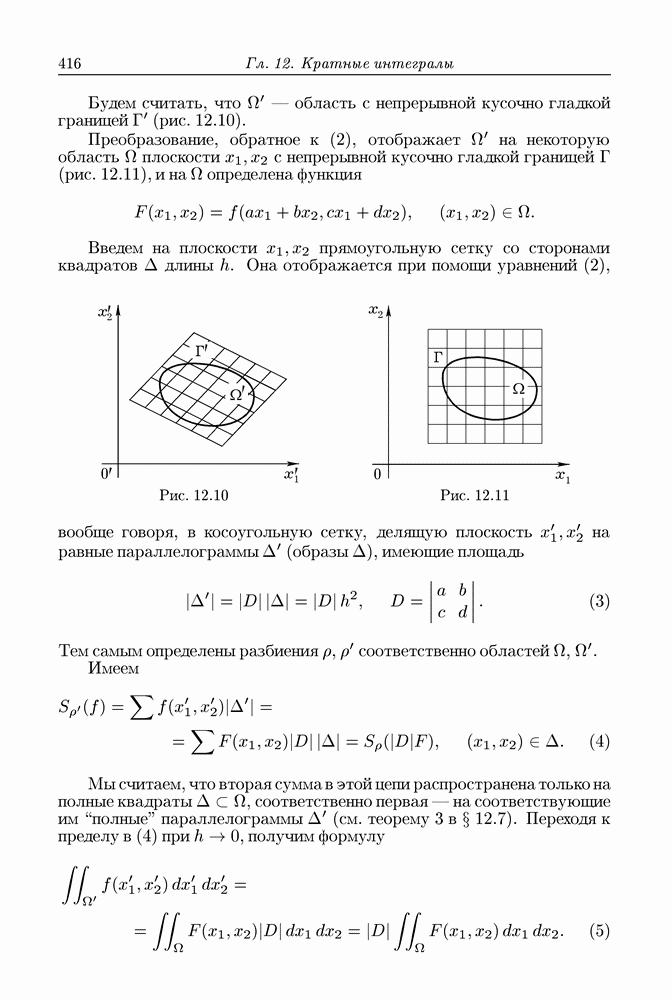
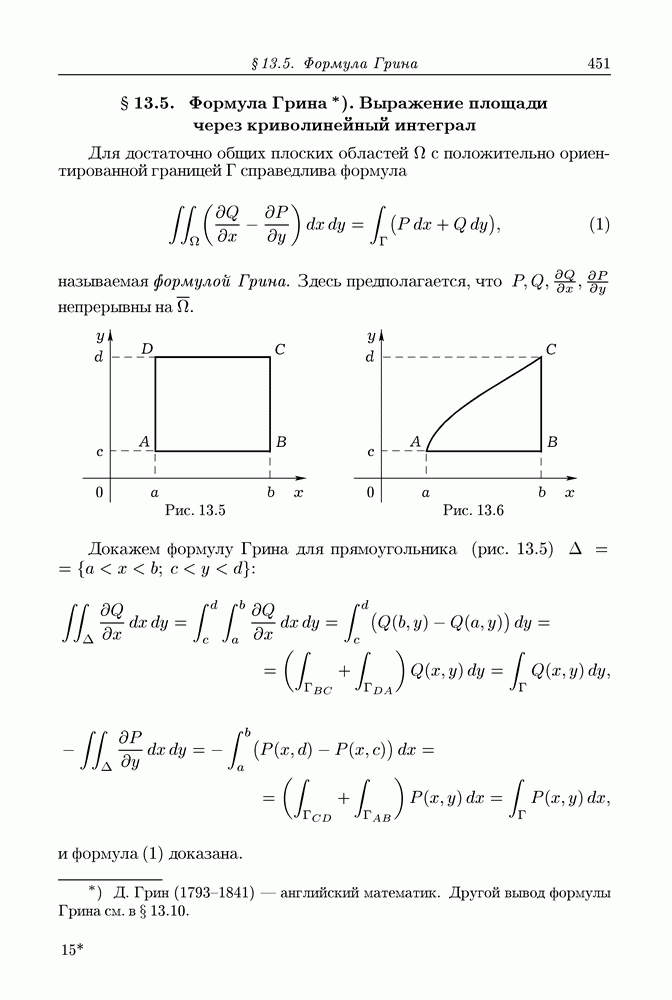
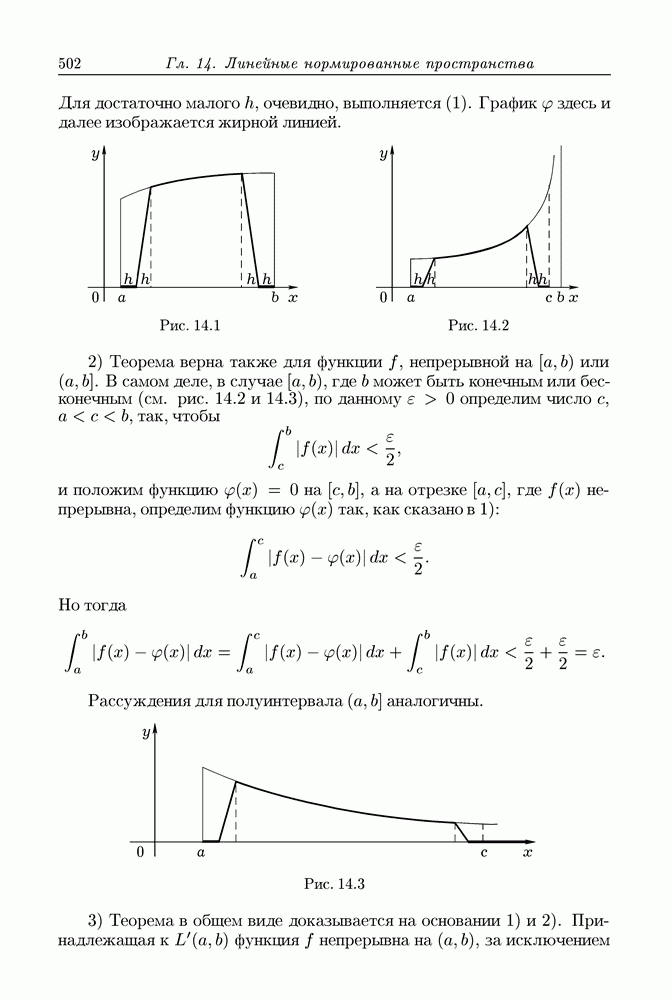
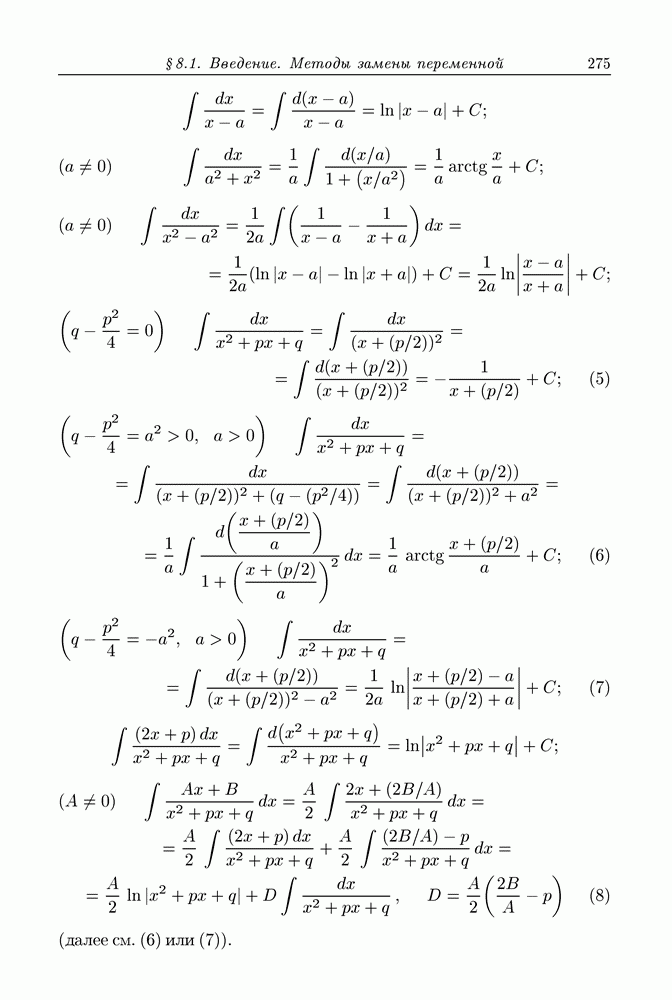| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 13.10. Дивергенция. Теорема Гаусса-Остроградского
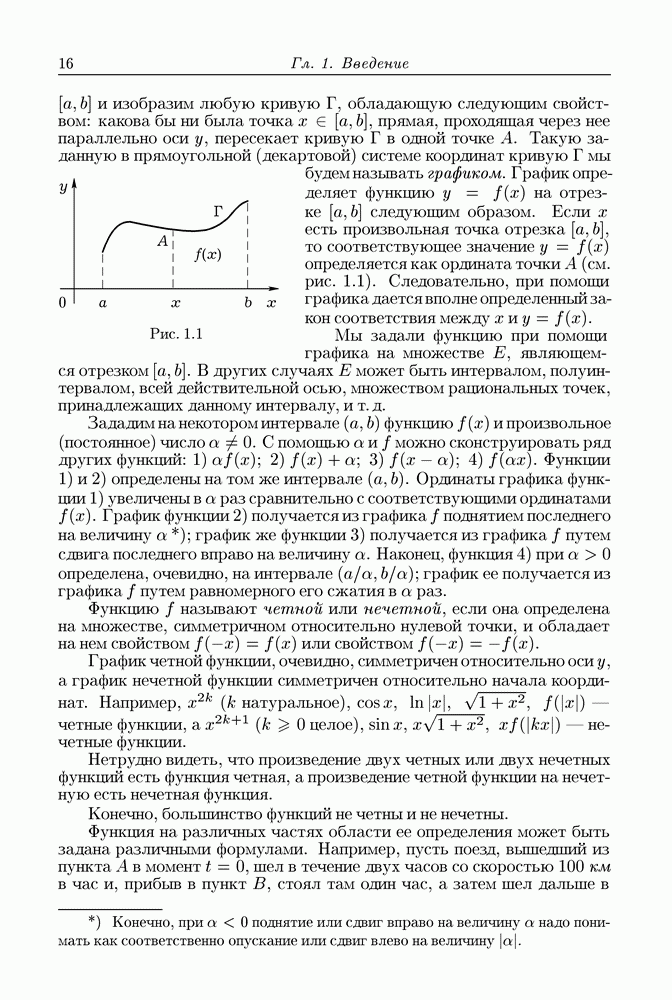
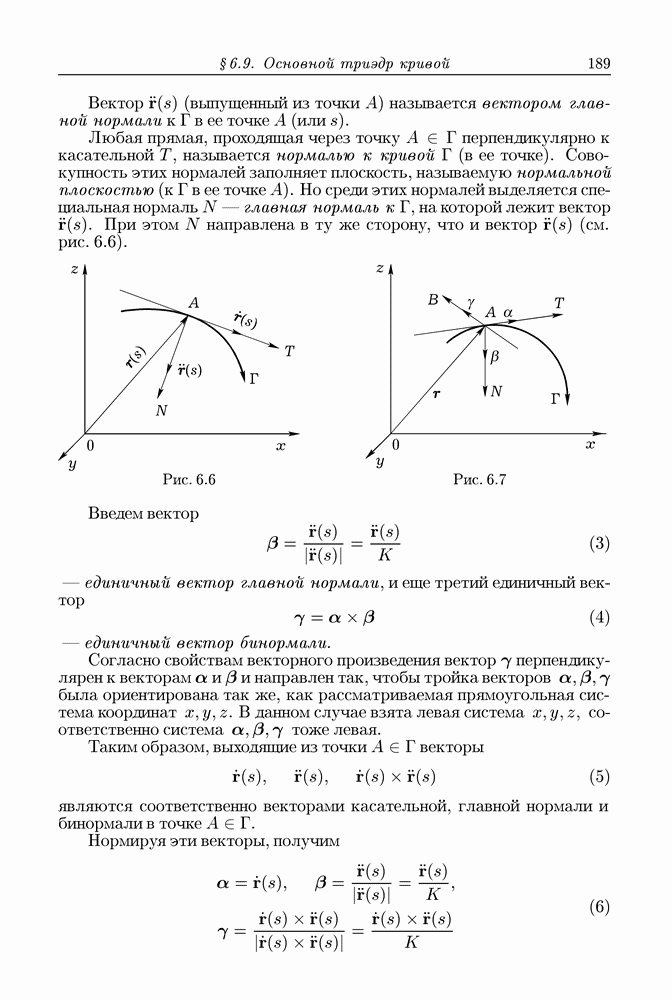
Пусть  есть пространство, где задана прямоугольная система координат
есть пространство, где задана прямоугольная система координат  область с кусочно гладкой границей
область с кусочно гладкой границей  и на
и на  определено поле вектора
определено поле вектора

Мы будем предполагать, что  непрерывны на
непрерывны на  откуда следует, что для вектора а имеет смысл непрерывная функция
откуда следует, что для вектора а имеет смысл непрерывная функция

называемая дивергенцией вектора  .
.
Будем считать, что поверхность  ориентирована при помощи единичной нормали
ориентирована при помощи единичной нормали  направленной во внешность
направленной во внешность  Целью нашей будет доказательство равенства
Целью нашей будет доказательство равенства

при некоторых дополнительных условиях, налагаемых на  Это равенство называют формулой Гаусса-Остроградского по имени математиков, ее доказавших.
Это равенство называют формулой Гаусса-Остроградского по имени математиков, ее доказавших.
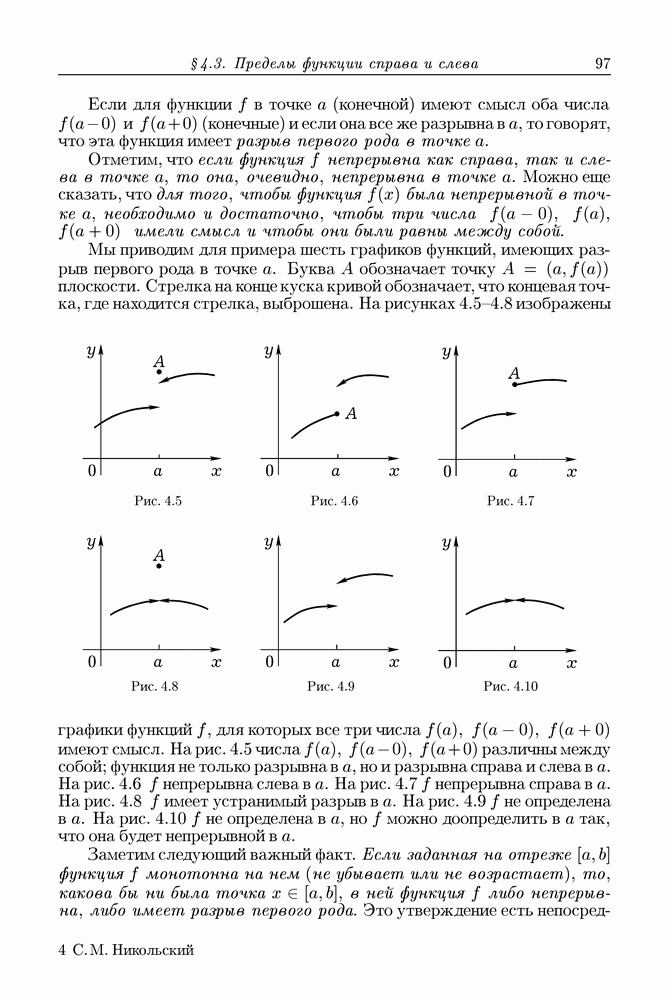
Формула Гаусса-Остроградского говорит, что объемный интеграл от дивергенции вектора по области  равен потоку вектора через границу этой области, ориентированную в направлении ее внешней нормали.
равен потоку вектора через границу этой области, ориентированную в направлении ее внешней нормали.

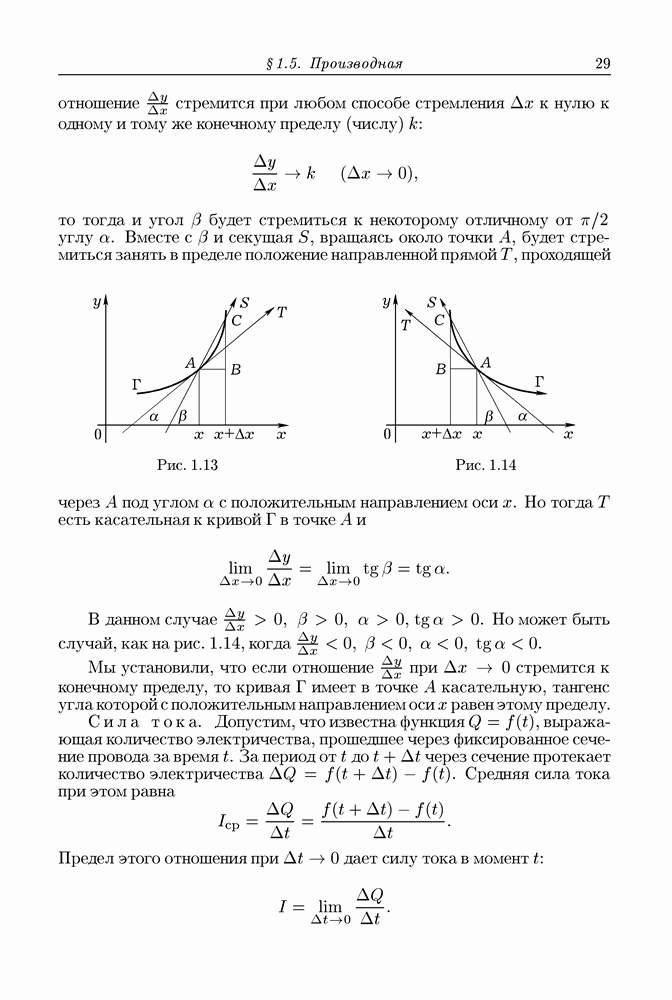
Рис. 13.20
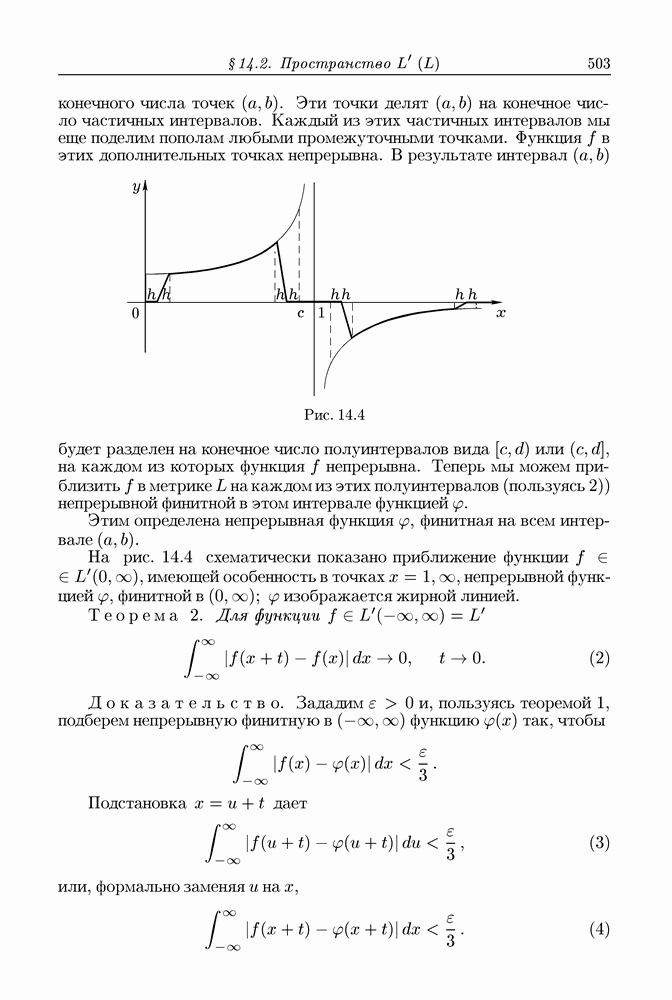
Начнем с того, что рассмотрим область  изображенную на рис. 13.20, которую мы будем называть элементарной
изображенную на рис. 13.20, которую мы будем называть элементарной  -областью. Сверху и снизу
-областью. Сверху и снизу  ограничена поверхностями
ограничена поверхностями  (с кусочно гладкими краями), определяемыми соответственно уравнениями
(с кусочно гладкими краями), определяемыми соответственно уравнениями

где  — плоская область с (кусочно гладкой) границей
— плоская область с (кусочно гладкой) границей  непрерывны на
непрерывны на  имеют непрерывные частные производные на открытом множестве
имеют непрерывные частные производные на открытом множестве  . С боков
. С боков  ограничена цилиндрической поверхностью
ограничена цилиндрической поверхностью  с направляющей
с направляющей  и образующей, параллельной оси
и образующей, параллельной оси 
Пусть  есть граница
есть граница  ориентированная при помощи внешней к
ориентированная при помощи внешней к  нормали. Тем самым нижний и верхний куски
нормали. Тем самым нижний и верхний куски  так же как боковая повехность
так же как боковая повехность  области
области  соответственно ориентированы. Для области
соответственно ориентированы. Для области  имеют место равенства (пояснения ниже)
имеют место равенства (пояснения ниже)


Нормаль  образует с осью
образует с осью  соответственно тупой и острый углы, поэтому проекции
соответственно тупой и острый углы, поэтому проекции  кусков
кусков  на плоскость
на плоскость  ориентированы: первая отрицательно, а вторая положительно. Это обосновывает переход от третьего члена цепи (4) к четвертому. К сумме, составляющей четвертый член, можно формально добавить интеграл
ориентированы: первая отрицательно, а вторая положительно. Это обосновывает переход от третьего члена цепи (4) к четвертому. К сумме, составляющей четвертый член, можно формально добавить интеграл

равный нулю, потому что  вдоль
вдоль  Но тогда полученная сумма трех интегралов равна интегралу, стоящему в качестве последнего члена цепи (4) (потоку вектора
Но тогда полученная сумма трех интегралов равна интегралу, стоящему в качестве последнего члена цепи (4) (потоку вектора  ) через
) через  . В формуле (3) звездочка при
. В формуле (3) звездочка при  опущена.
опущена.
Этим мы доказали теорему Гаусса-Остроградского для элементарной  -области и вектора
-области и вектора 
Назовем теперь область  -областью, если ее замыкание
-областью, если ее замыкание  можно разрезать на конечное число замыканий элементарных областей:
можно разрезать на конечное число замыканий элементарных областей:

так, что нижний и верхний куски границы  суть части ориентированной границы
суть части ориентированной границы  области
области  и докажем, что для
и докажем, что для  и вектора
и вектора  тоже справедлива теорема Гаусса-Остроградского.
тоже справедлива теорема Гаусса-Остроградского.
В самом деле, обозначим соответственно через  нижние и верхние куски границ
нижние и верхние куски границ  и через
и через  боковые куски
боковые куски  Тогда (пояснения ниже)
Тогда (пояснения ниже)

потому что интегралы по  очевидно, равны нулю, а куски к и к либо составляют в совокупности поверхность
очевидно, равны нулю, а куски к и к либо составляют в совокупности поверхность  либо, если это не так, множество
либо, если это не так, множество

есть часть  нормаль в любой точке которой перпендикулярна оси
нормаль в любой точке которой перпендикулярна оси  Но тогда интеграл по а равен нулю.
Но тогда интеграл по а равен нулю.
По аналогии можно ввести понятия  -области и
-области и  -области. Например,
-области. Например,  -область обладает тем свойством, что ее замыкание можно разрезать на конечное число замыканий элементарных
-область обладает тем свойством, что ее замыкание можно разрезать на конечное число замыканий элементарных  -областей. Элементарная же
-областей. Элементарная же  -область определяется так же, как элементарная
-область определяется так же, как элементарная  -область, только роль
-область, только роль  теперь играет х. По аналогии доказывается, что для
теперь играет х. По аналогии доказывается, что для  -области
-области  имеет место равенство
имеет место равенство

т. е. формула Гаусса-Остроградского для вектора  , а для
, а для  -области
-области  формула
формула

Если теперь  есть одновременно
есть одновременно  и
и  -область, то для нее, очевидно, верна теорема Гаусса-Остроградского для произвольного непрерывно дифференцируемого на
-область, то для нее, очевидно, верна теорема Гаусса-Остроградского для произвольного непрерывно дифференцируемого на  вектора
вектора  т.е. верно равенство
т.е. верно равенство

где интеграл справа есть интеграл по поверхности  ориентированной внешней нормалью к
ориентированной внешней нормалью к 
Если в формуле Гаусса-Остроградского положить  то получим выражение для объема области
то получим выражение для объема области 

через интеграл по ее ориентированной (внешней нормалью) границе 
Области, с которыми приходится обычно иметь дело, являются одновременно  и
и  -областями.
-областями.
Пример 1. Шар  есть
есть  -область, даже элементарная
-область, даже элементарная  -область, потому что вся его внутренность ограничена двумя лежащими друг над другом гладкими на
-область, потому что вся его внутренность ограничена двумя лежащими друг над другом гладкими на  поверхностями
поверхностями  непрерывными на замкнутом круге
непрерывными на замкнутом круге  имеющем гладкую границу. Очевидно, шар есть также
имеющем гладкую границу. Очевидно, шар есть также  и
и  -область.
-область.
Пример 2. Возьмем тор  полученный вращением заданного в плоскости
полученный вращением заданного в плоскости  круга
круга  вокруг оси у. Чтобы убедиться в том, что
вокруг оси у. Чтобы убедиться в том, что  есть
есть  -область, достаточно поверхность
-область, достаточно поверхность  разделить на две части плоскостью
разделить на две части плоскостью  . Далее, плоскости
. Далее, плоскости  рассекают
рассекают  на четыре элементарные
на четыре элементарные  -области, а плоскости
-области, а плоскости  на четыре элементарные
на четыре элементарные  -области.
-области.
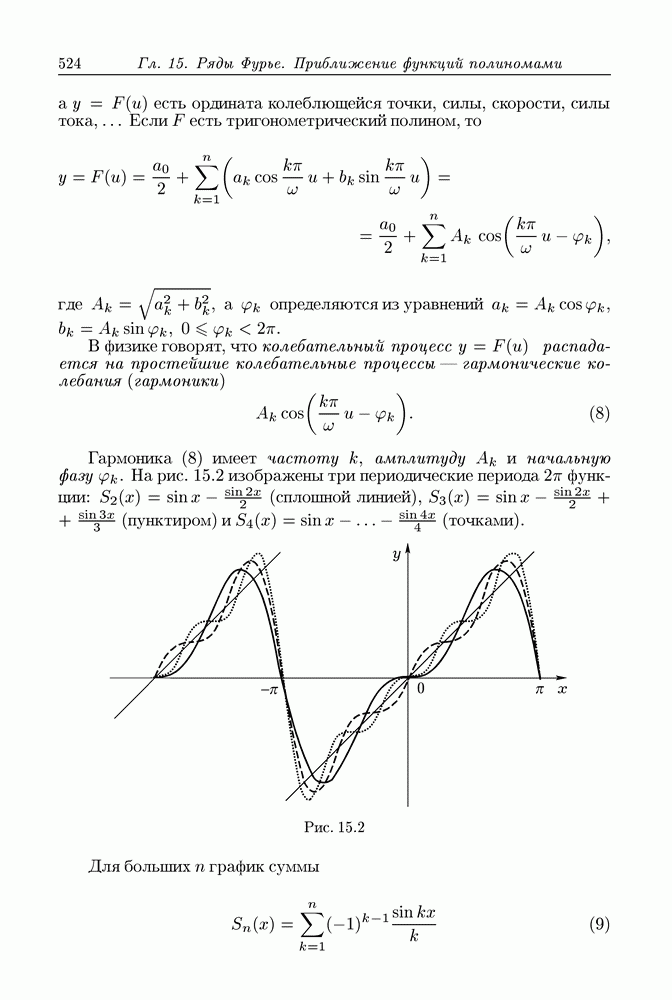
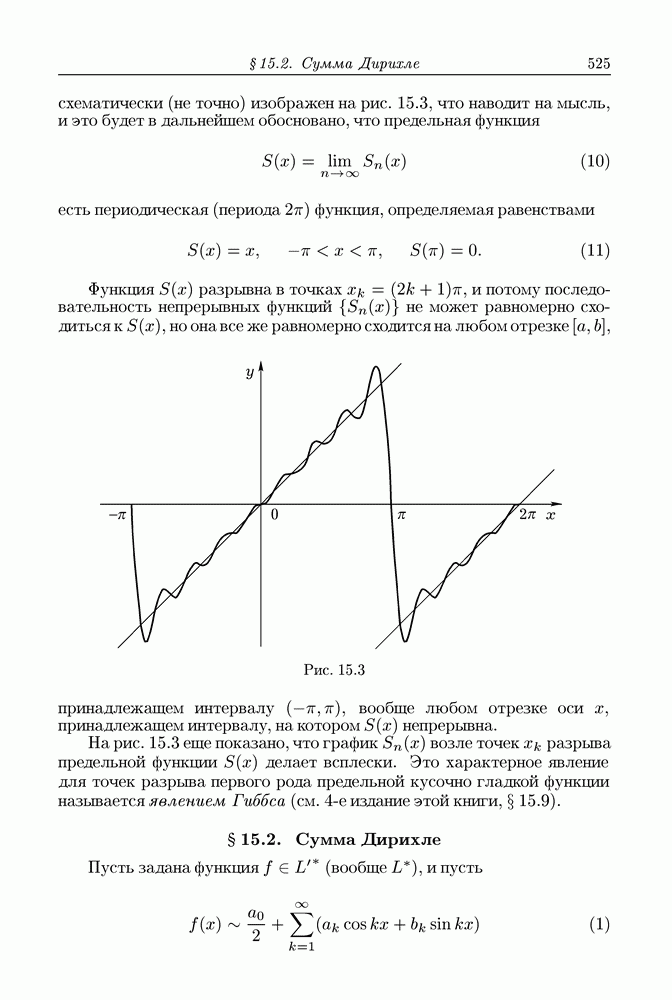
Формула Гаусса-Остроградского преобразует объемный интеграл в интеграл по поверхности. В следующем параграфе доказывается формула Стокса, при помощи которой при определенных условиях интеграл по поверхности преобразуется в криволинейный интеграл.
Чтобы выяснить физическое значение понятия дивергенции, будем считать, что в  имеет место стационарное течение жидкости, скорость которой в произвольной точке
имеет место стационарное течение жидкости, скорость которой в произвольной точке  равна
равна  Зададим произвольную, но фиксированную точку
Зададим произвольную, но фиксированную точку  и окружим ее шаром
и окружим ее шаром  радиуса
радиуса  Пусть
Пусть  есть его граница (шаровая поверхность), ориентированная посредством внешней нормали. Тогда на основании формулы Гаусса-Остроградского
есть его граница (шаровая поверхность), ориентированная посредством внешней нормали. Тогда на основании формулы Гаусса-Остроградского

Левая часть этого равенства выражает количество жидкости, вытекающей из  (вовне
(вовне  ) за единицу времени.
) за единицу времени.
Применяя к правой его части теорему о среднем, получим

где  есть объем
есть объем  скорость жидкости в некоторой точке из
скорость жидкости в некоторой точке из  Разделив обе части полученного равенства на
Разделив обе части полученного равенства на  и перейдя к пределу при
и перейдя к пределу при  получим в силу непрерывности
получим в силу непрерывности  что существует предел, равный дивергенции а:
что существует предел, равный дивергенции а:

в точке  Таким образом,
Таким образом,  представляет собой производительность источников, непрерывно распределенных по
представляет собой производительность источников, непрерывно распределенных по  в точке
в точке  Если в точке А (или всюду на
Если в точке А (или всюду на  то это значит, что в А (или всюду на
то это значит, что в А (или всюду на  ) производительность источников равна нулю. Если
) производительность источников равна нулю. Если  то это означает, что на самом деле в соответствующей точке имеет место сток.
то это означает, что на самом деле в соответствующей точке имеет место сток.
Из физических соображений ясно, что  а есть инвариант относительно любых преобразований прямоугольных координат. Но это заключение можно сделать и на основании математических соображений, если учесть, что поток вектора через поверхность
а есть инвариант относительно любых преобразований прямоугольных координат. Но это заключение можно сделать и на основании математических соображений, если учесть, что поток вектора через поверхность  есть инвариант.
есть инвариант.
Этим доказано, что если одно и то же поле вектора определяется в двух прямоугольных системах координат  соответственно функциями
соответственно функциями

то в одной и той же точке

Конечно, это утверждение можно доказать непосредственно, не прибегая к теореме Гаусса-Остроградского.
Дивергенцию а можно рассматривать еще как (символическое) скалярное произведение оператора V Гамильтона на вектор а:

С этой точки зрения указанную инвариантность можно доказать следующим образом: V и а — векторы, а скалярное произведение двух векторов инвариантно относительно преобразований прямоугольных координат, поэтому этим свойством обладает и дивергенция 
Формулу Гаусса-Остроградского можно записать в плоском случае, когда  есть область в плоскости х,у и а
есть область в плоскости х,у и а  определенное на ней поле. Если
определенное на ней поле. Если  есть внешняя нормаль к кусочно гладкому контуру
есть внешняя нормаль к кусочно гладкому контуру  области
области  то имеет место равенство
то имеет место равенство

где  дифференциал дуги
дифференциал дуги  .
.
Если считать, что направление  касательной в точке контура
касательной в точке контура  совпадает с положительным направлением обхода по
совпадает с положительным направлением обхода по  вдоль которого исчисляется также длина дуги контура
вдоль которого исчисляется также длина дуги контура  то
то

Поэтому 

Если в этой формуле заменить соответственно  на
на  то мы придем к формуле Грина, которая уже была получена в § 13.5.
то мы придем к формуле Грина, которая уже была получена в § 13.5.
Пусть  есть ограниченная область с гладкой дважды непрерывно дифференцируемой границей
есть ограниченная область с гладкой дважды непрерывно дифференцируемой границей  — часть ограниченная поверхностью
— часть ограниченная поверхностью  точки которой отстоят от
точки которой отстоят от  по направлению нормали к
по направлению нормали к  на расстоянии
на расстоянии  (см. § 7.25). Пусть еще задано поле вектора
(см. § 7.25). Пусть еще задано поле вектора  , непрерывного на
, непрерывного на  и имеющего непрерывные частные производные на
и имеющего непрерывные частные производные на  . Вблизи границы
. Вблизи границы  последние могут быть неограниченными. Будем считать, что область
последние могут быть неограниченными. Будем считать, что область  при достаточно малом
при достаточно малом  удовлетворяет требованиям, которые предъявляются к областям, чтобы для них была верна теорема Гаусса-Остроградского.
удовлетворяет требованиям, которые предъявляются к областям, чтобы для них была верна теорема Гаусса-Остроградского.
В этом случае формула Гаусса-Остроградского 

остается верной, если ее левую часть понимать в следующем несобственном смысле:

Доказательство см. в 4-ом издании этой книги, § 13.10.
Вектор а называется соленоидалъным в области  если
если

Для того чтобы вектор а был соленоидальным в  необходимо и достаточно, чтобы поток вектора а через любую замкнутую ориентированную поверхность
необходимо и достаточно, чтобы поток вектора а через любую замкнутую ориентированную поверхность  был равен нулю.
был равен нулю.
Необходимость следует из теоремы Гаусса-Остроградского, примененной к области  внутренней к
внутренней к 
Достаточность следует из формулы (7), где интеграл справа равен нулю для любого  что влечет (10).
что влечет (10).
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1. ВВЕДЕНИЕ
- § 1.2. Множество. Интервал, отрезок
- § 1.3. Функция
- § 1.4. Понятие непрерывности функции
- § 1.5. Производная
- § 1.6. Первообразная. Неопределенный интеграл
- § 1.7. Понятие определенного интеграла. Площадь криволинейной фигуры
- Глава 2. ДЕЙСТВИТЕЛЬНОЕ ЧИСЛО
- § 2.1. Рациональные и иррациональные числа
- § 2.2. Определение неравенства
- § 2.3. Основная лемма. Определение арифметических действий
- § 2.4. Основные свойства действительных чисел
- § 2.5. Изоморфизм различных представлений действительных чисел. Физические величины
- § 2.6. Неравенства для абсолютных величин
- § 2.7. Точные верхняя и нижняя грани множества
- § 2.8. Символика математической логики
- Глава 3. ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ
- § 3.1. Понятие предела последовательности
- § 3.2. Арифметические действия с пределами
- § 3.3. Бесконечно малая и бесконечно большая величины
- § 3.4. Существование предела у монотонной ограниченной последовательности
- § 3.5. Число е
- § 3.6. Леммы о вложенных отрезках, существовании точных граней множества и сечения во множестве действительных чисел
- § 3.7. Теорема Больцано-Вейерштрасса. Верхний и нижний пределы
- § 3.8. Критерий Коши существования предела
- § 3.9. Счетное множество. Счетность множества рациональных чисел. Несчетность множества действительных чисел
- Глава 4. ПРЕДЕЛ ФУНКЦИИ
- § 4.1. Понятие предела функции
- § 4.2. Непрерывность функции в точке
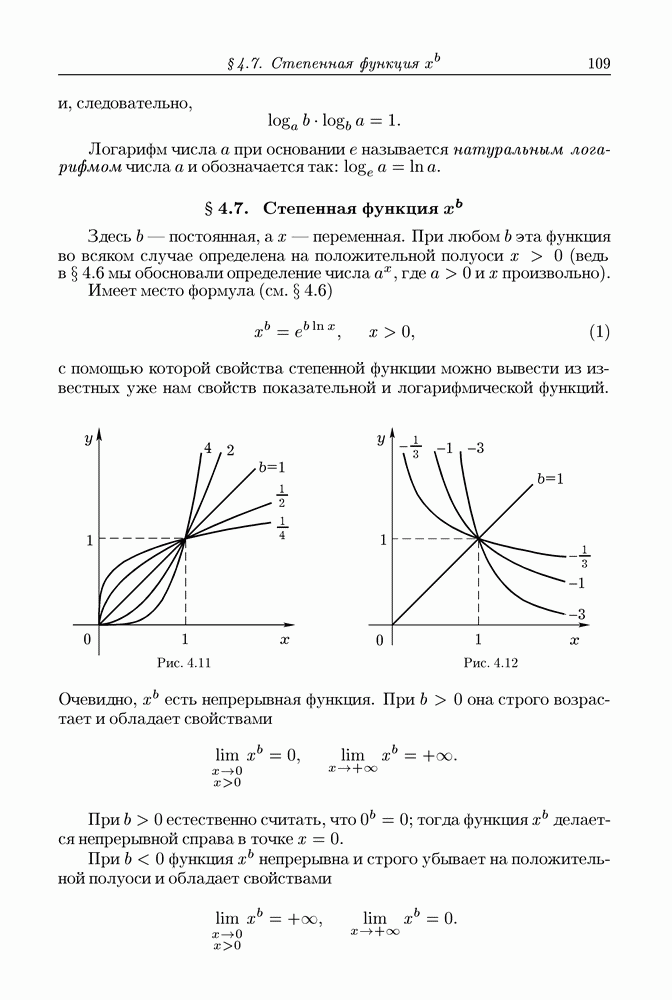
- § 4.3. Пределы функции справа и слева. Монотонная функция
- § 4.4. Функции, непрерывные на отрезке
- § 4.5. Обратная функция
- § 4.6. Показательная и логарифмическая функции
- § 4.7. Степенная функция x^b
- § 4.8. Еще о числе е
- § 4.9. lim sin oo/oo
- § 4.10. Порядок переменной, эквивалентность (асимптотика)
- Глава 5. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ДЛЯ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ
- § 5.1. Производная
- § 5.2. Дифференциал функции
- § 5.3. Производная функции от функции
- § 5.4. Производная обратной функции
- § 5.6. Производные и дифференциалы высшего порядка
- § 5.7. Возрастание и убывание функции на интервале и в точке. Локальный экстремум
- § 5.8. Теоремы о среднем значении. Критерии возрастания и убывания функции на интервале. Достаточные критерии локальных экстремумов
- § 5.9. Формула Тейлора
- § 5.10. Формулы Тейлора для важнейших элементарных функций
- § 5.11. Ряд Тейлора
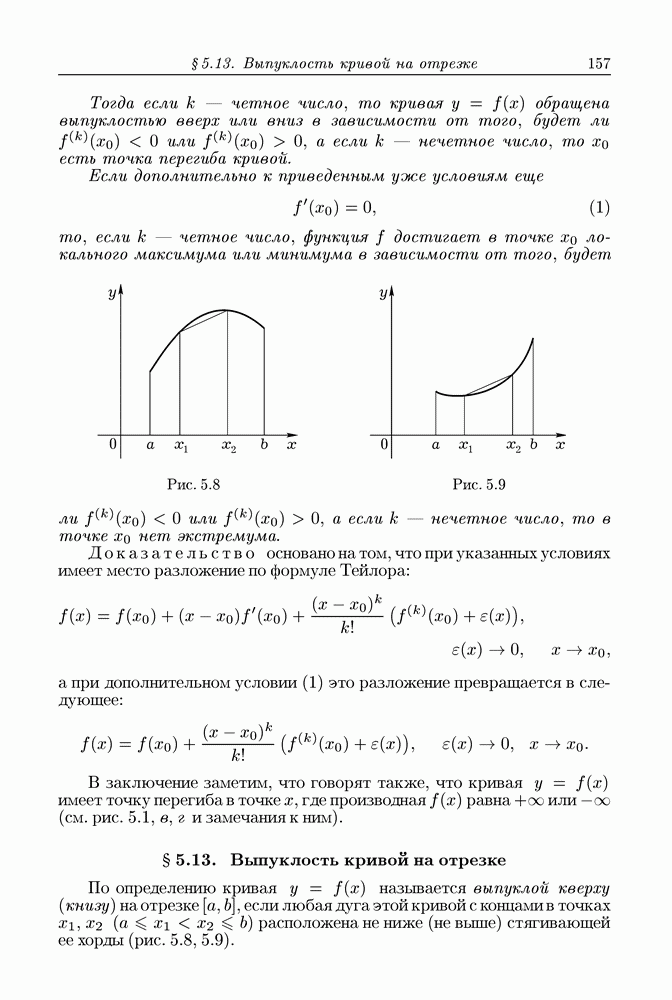
- § 5.12. Выпуклость кривой в точке. Точка перегиба
- § 5.13. Выпуклость кривой на отрезке
- § 5.14. Раскрытие неопределенностей
- § 5.15. Асимптота
- § 5.16. Схема построения графика функции
- § 5.17. Кусочно непрерывные и кусочно гладкие функции
- Глава 6. n-МЕРНОЕ ПРОСТРАНСТВО. ГЕОМЕТРИЯ КРИВОЙ
- § 6.1. n-мерное пространство. Линейное множество
- § 6.2. Евклидово n-мерное пространство. Пространство со скалярным произведением
- § 6.3. Линейное нормированное пространство
- § 6.4. Вектор-функция в n-мерном евклидовом пространстве
- § 6.5. Непрерывная кривая. Гладкая кривая
- § 6.6. Геометрический смысл производной вектор-функции
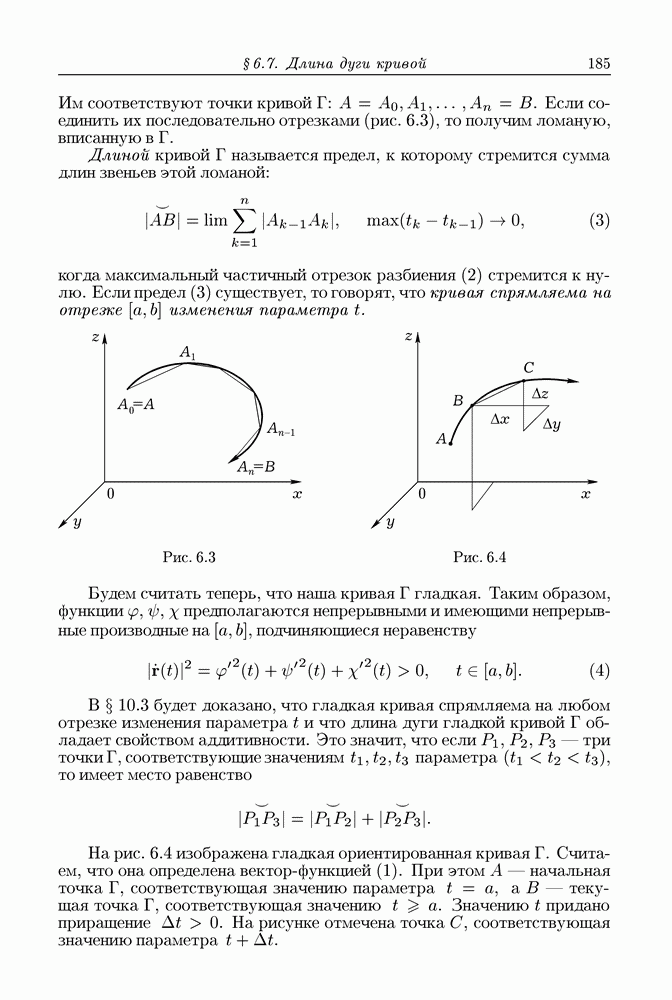
- § 6.7. Длина дуги кривой
- § 6.8. Касательная
- § 6.9. Основной триэдр кривой
- § 6.10. Соприкасающаяся плоскость
- § 6.11. Кривизна и радиус кривизны кривой
- § 6.12. Эволюта
- § 6.13. Формулы Френе. Свойства эволюты
- Глава 7. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ
- § 7.1. Открытое множество
- § 7.2. Предел функции
- § 7.3. Непрерывная функция
- § 7.4. Частные производные и производная по направлению
- § 7.5. Дифференцируемая функция. Касательная плоскость
- § 7.6. Производная сложной функции. Производная по направлению. Градиент
- § 7.7. Независимость от порядка дифференцирования
- § 7.8. Дифференциал функции. Дифференциал высшего порядка
- § 7.9. Теорема Больцано-Вейерштрасса
- § 7.10. Замкнутые и открытые множества
- § 7.11. Функции на множестве. Свойства непрерывных функций на замкнутом ограниченном множестве
- § 7.12. Лемма о вложенных прямоугольниках и лемма Бореля
- § 7.13. Формула Тейлора
- § 7.14. локальный (абсолютный) экстремум функции
- § 7.15. Теоремы существования неявной функции
- § 7.16. Теорема существования решения системы уравнений
- § 7.17. Отображения
- § 7.18. Гладкая поверхность
- § 7.19. Дифференциалы неявных функций. Линеаризация
- § 7.20. Локальный относительный экстремум
- § 7.21. Замена переменных в частных производных
- § 7.22. Система зависимых функций
- Глава 8. НЕОПРЕДЕЛЕННЫЕ ИНТЕГРАЛЫ. АЛГЕБРА МНОГОЧЛЕНОВ
- § 8.1. Введение. Методы замены переменной и интегрирования по частям
- § 8.2. Комплексные числа
- § 8.3. Комплексные функции
- § 8.4. Многочлены
- § 8.5. Разложение рациональной функции на простейшие дроби
- § 8.6. Интегрирование рациональных дробей
- § 8.7. Интегрирование алгебраических иррациональностей
- § 8.8. Подстановки Эйлера
- § 8.9. Биномиальные дифференциалы. Теорема Чебышева
- § 8.10. Интегрирование тригонометрических выражений
- § 8.11. Тригонометрические подстановки
- § 8.12. Несколько важных интегралов, не выражаемых в элементарных функциях
- Глава 9. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ РИМАНА
- § 9.2. Ограниченность интегрируемой функции
- § 9.3. Суммы Дарбу
- § 9.4. Основная теорема
- § 9.5. Теоремы о существовании интеграла от непрерывной и монотонной функции на [a, b]
- § 9.6. Аддитивные и однородные свойства интеграла
- § 9.7. Неравенства и теорема о среднем
- § 9.8. Интеграл как функция верхнего предела. Теорема Ньютона-Лейбница
- § 9.9. Вторая теорема о среднем
- § 9.10. Видоизменение функции
- § 9.11. Несобственные интегралы
- § 9.12. Несобственные интегралы от неотрицательных функций
- § 9.13. Интегрирование по частям
- § 9.14. Несобственный интеграл и ряд
- § 9.15. Несобственные интегралы с особенностями в нескольких точках
- § 9.16. Формула Тейлора с остатком в интегральной форме
- § 9.17. Формулы Валлиса и Стирлинга
- Глава 10. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ ИНТЕГРАЛОВ. ПРИБЛИЖЕННЫЕ МЕТОДЫ
- § 10.1. Площадь в полярных координатах
- § 10.2. Объем тела вращения
- § 10.3. Длина дуги гладкой кривой
- § 10.4. Площадь поверхности тела вращения
- § 10.5. Интерполяционный многочлен Лагранжа
- § 10.6. Квадратурные формулы прямоугольников
- § 10.7. Формула Симпсона
- Глава 11. РЯДЫ
- § 11.1. Понятие ряда
- § 11.2. Действия с рядами
- § 11.3. Ряды с неотрицательными членами
- § 11.4. Ряд Лейбница
- § 11.5. Абсолютно сходящиеся ряды
- § 11.6. Условно и безусловно сходящиеся ряды с действительными членами
- § 11.7. Последовательности и ряды функций. Равномерная сходимость
- § 11.8. Интегрирование и дифференцирование равномерно сходящихся рядов на отрезке
- § 11.9. Кратные ряды. Перемножение абсолютно сходящихся рядов
- § 11.10. Суммирование рядов и последовательностей методом средних арифметических
- § 11.11. Степенные ряды
- § 11.12. Дифференцирование и интегрирование степенных рядов
- § 11.13. Степенные ряды функций e^z, cos z, sinz комплексной переменной
- Глава 12. КРАТНЫЕ ИНТЕГРАЛЫ
- § 12.2. Мера Жордана
- § 12.3. Важные примеры квадрируемых по Жордану множеств
- § 12.4. Еще один критерий измеримости множества. Полярные координаты
- § 12.5. Другие случаи измеримости
- § 12.6. Понятие кратного интеграла
- § 12.7. Верхняя и нижняя интегральные суммы. Основная теорема
- § 12.8. Интегрируемость непрерывной функции на замкнутом измеримом множестве. Другие критерии
- § 12.9. Свойства кратных интегралов
- § 12.10. Сведение кратного интеграла к интегрированию по отдельным переменным
- § 12.11. Непрерывность интеграла по параметру
- § 12.12. Геометрическая интерпретация знака определителя
- § 12.13. Замена переменных в кратном интеграле. Простейший случай
- § 12.14. Замена переменных в кратном интеграле
- § 12.15. Доказательство леммы 1 § 12.14
- § 12.16. Полярные координаты в плоскости
- § 12.17. Полярные и цилиндрические координаты в пространстве
- § 12.18. Гладкая поверхность
- § 12.19. Площадь поверхности
- Глава 13. ТЕОРИЯ ПОЛЯ. ДИФФЕРЕНЦИРОВАНИЕ И ИНТЕГРИРОВАНИЕ ПО ПАРАМЕТРУ. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
- § 13.1. Криволинейный интеграл первого рода
- § 13.2. Криволинейный интеграл второго рода
- § 13.3. Поле потенциала
- § 13.4. Ориентация плоской области
- § 13.5. Формула Грина. Выражение площади через криволинейный интеграл
- § 13.6. Интеграл по поверхности первого рода
- § 13.7. Ориентация поверхностей
- § 13.8. Интеграл по ориентированной плоской области
- § 13.9. Поток вектора через ориентированную поверхность
- § 13.10. Дивергенция. Теорема Гаусса-Остроградского
- § 13.11. Ротор вектора. Формула Стокса
- § 13.12. Дифференцирование интеграла по параметру
- § 13.13. Несобственный интеграл
- § 13.14. Равномерная сходимость несобственного интеграла
- § 13.15. Равномерно сходящийся интеграл для неограниченной области
- Глава 14. ЛИНЕЙНЫЕ НОРМИРОВАННЫЕ ПРОСТРАНСТВА. ОРТОГОНАЛЬНЫЕ СИСТЕМЫ
- § 14.2. Пространство L'(L)
- § 14.3. Пространство L2 (L2)
- § 14.4. Пространство …
- § 14.5. Полнота системы элементов в банаховом пространстве
- § 14.6. Ортогональная система в пространстве со скалярным произведением
- § 14.7. Ортогонализация системы
- § 14.8. Полнота системы функций в …
- Глава 15. РЯДЫ ФУРЬЕ. ПРИБЛИЖЕНИЕ ФУНКЦИЙ ПОЛИНОМАМИ
- § 15.2. Сумма Дирихле
- § 15.3. Формулы для остатка ряда Фурье
- § 15.4. Теоремы об осцилляции
- § 15.5. Критерий сходимости рядов Фурье. Полнота тригонометрической системы функций
- § 15.6. Комплексная форма записи ряда Фурье
- § 15.7. Дифференцирование и интегрирование рядов Фурье
- § 15.8. Оценка остатка ряда Фурье
- § 15.9. Алгебраические многочлены. Многочлены Чебышева
- § 15.10. Теорема Вейерштрасса
- § 15.11. Многочлены Лежандра
- Глава 16. ИНТЕГРАЛ ФУРЬЕ. ОБОБЩЕННЫЕ ФУНКЦИИ
- § 16.1. Понятие интеграла Фурье
- § 16.2. Сходимость простого интеграла Фурье к порождающей его функции
- § 16.3. Преобразование Фурье. Повторный интеграл Фурье. Косинус- и синус-преобразования Фурье
- § 16.4. Производная преобразования Фурье
- § 16.5. Обобщенные функции в смысле D
- § 16.6. Пространство S
- § 16.7. Пространство S обобщенных функций