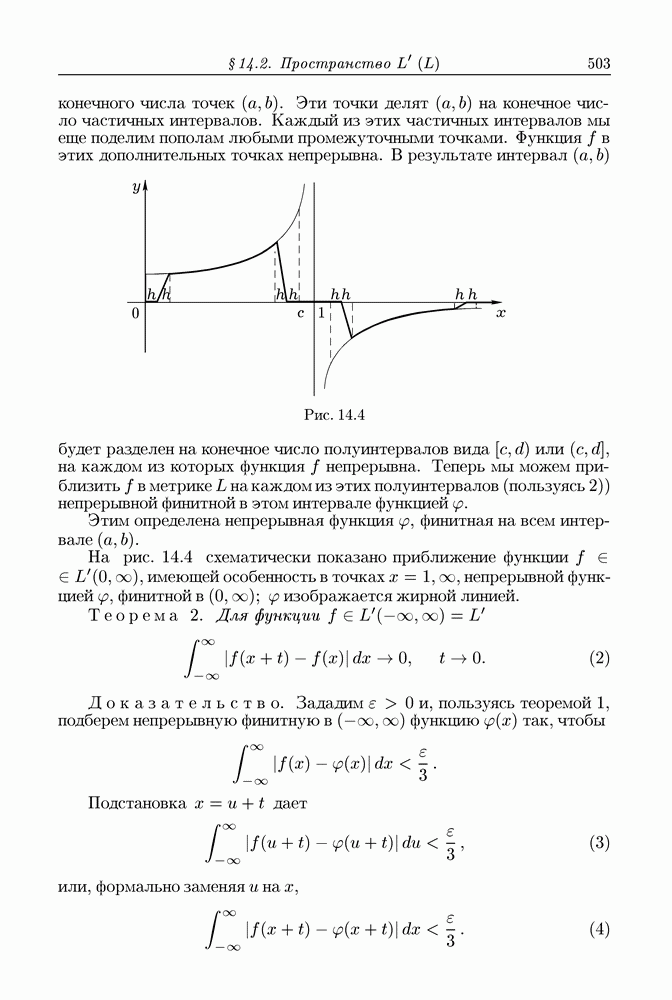
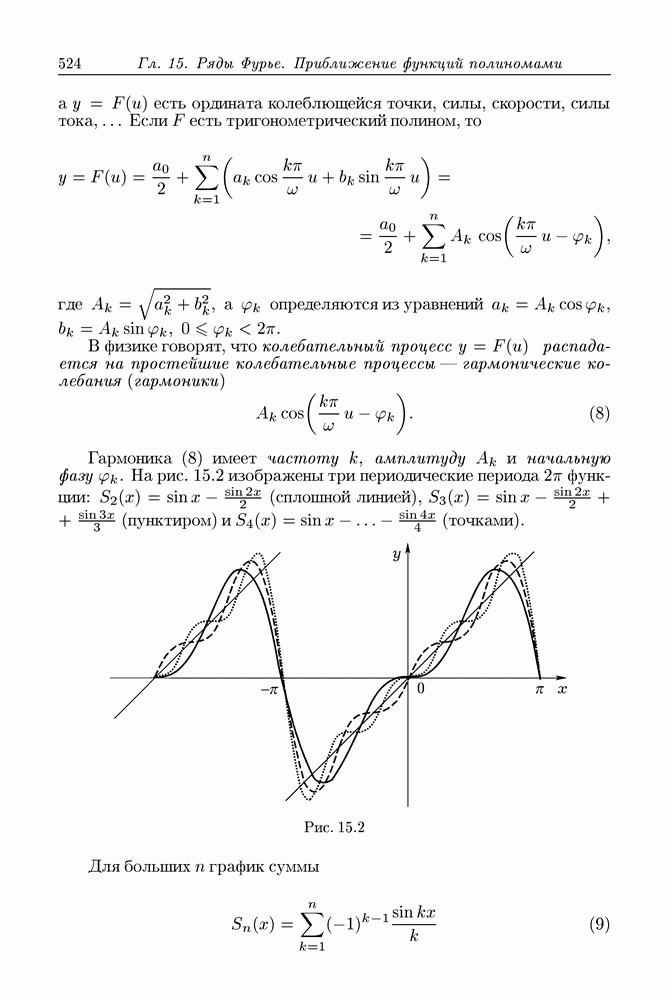
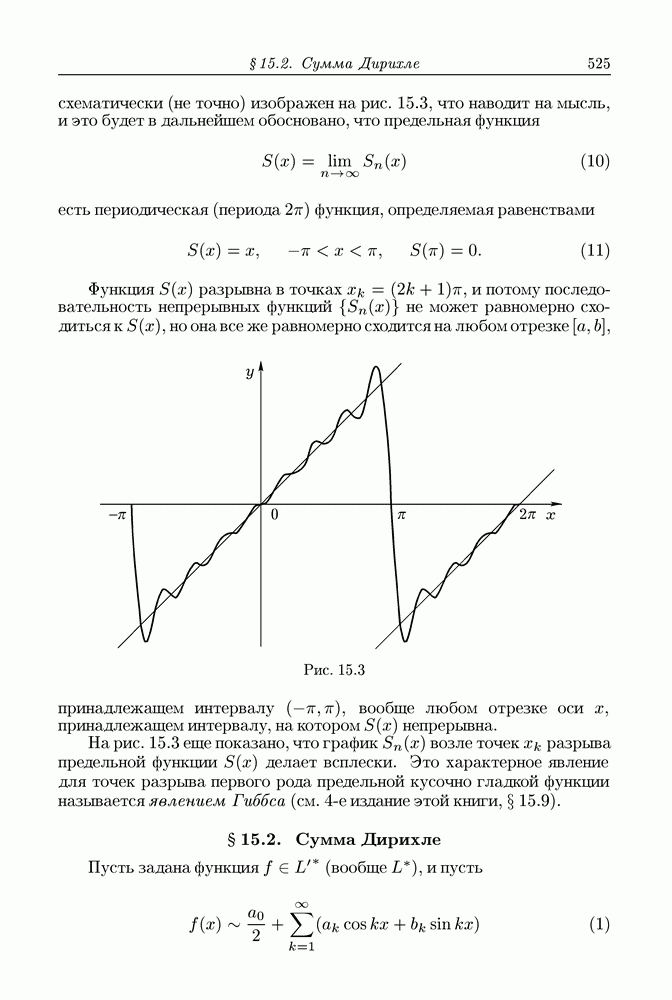
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава 2. ДЕЙСТВИТЕЛЬНОЕ ЧИСЛО
§ 2.1. Рациональные и иррациональные числа
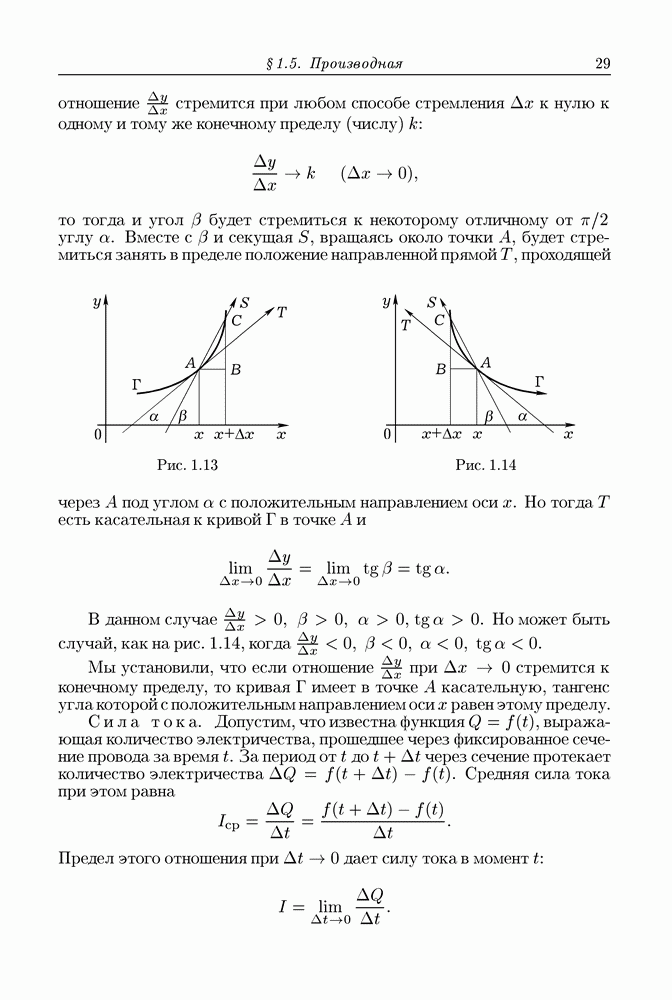
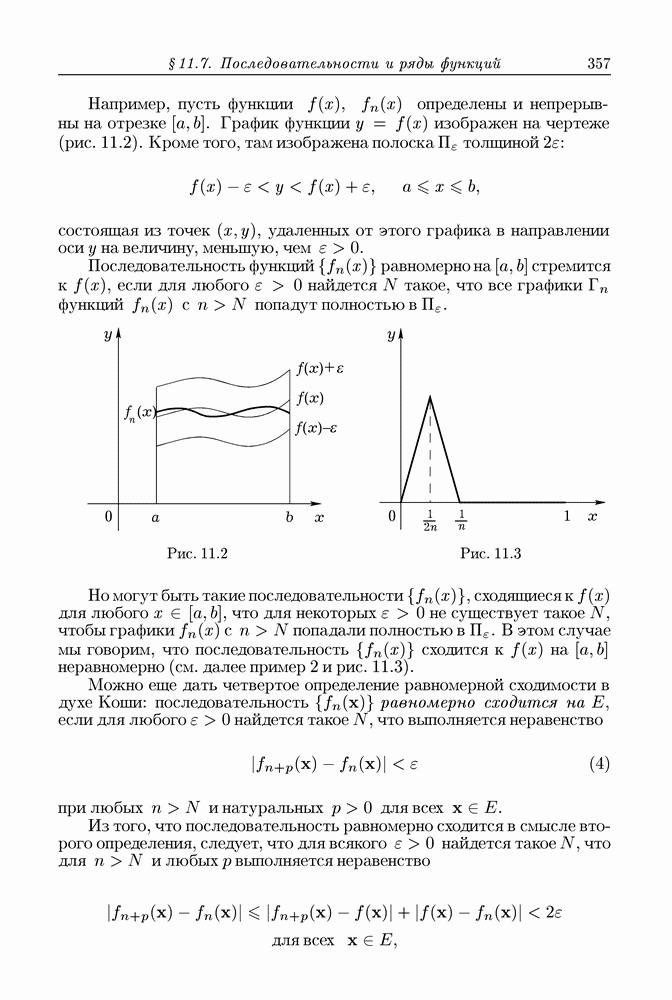
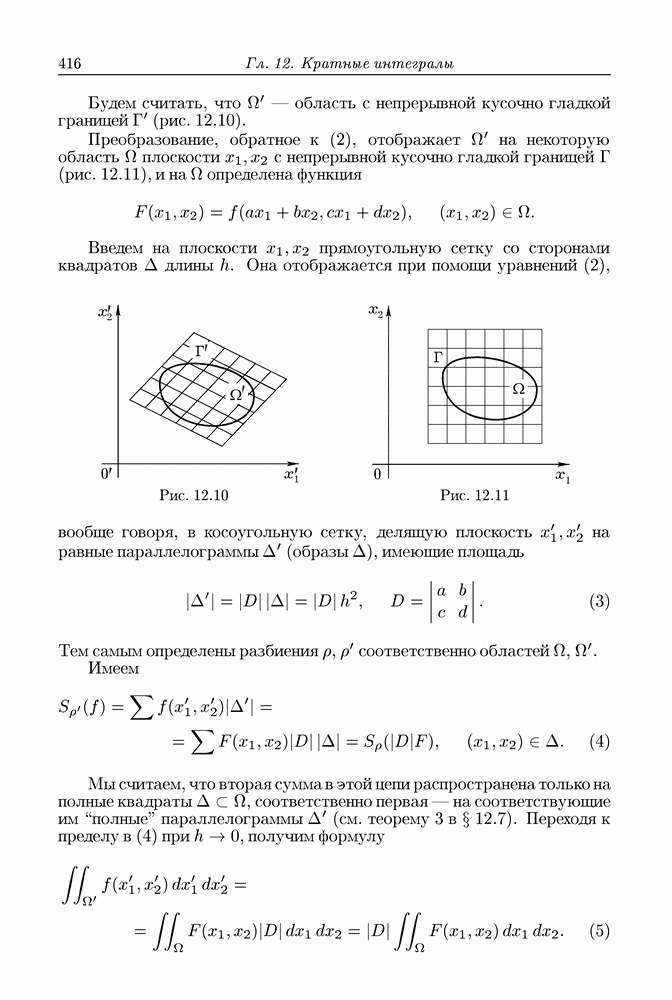
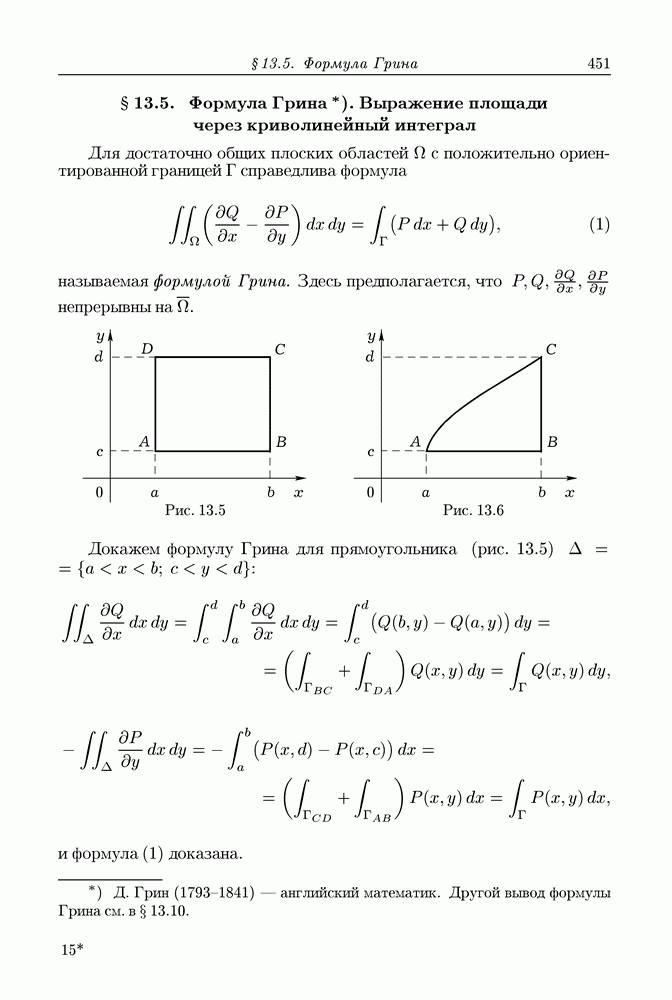
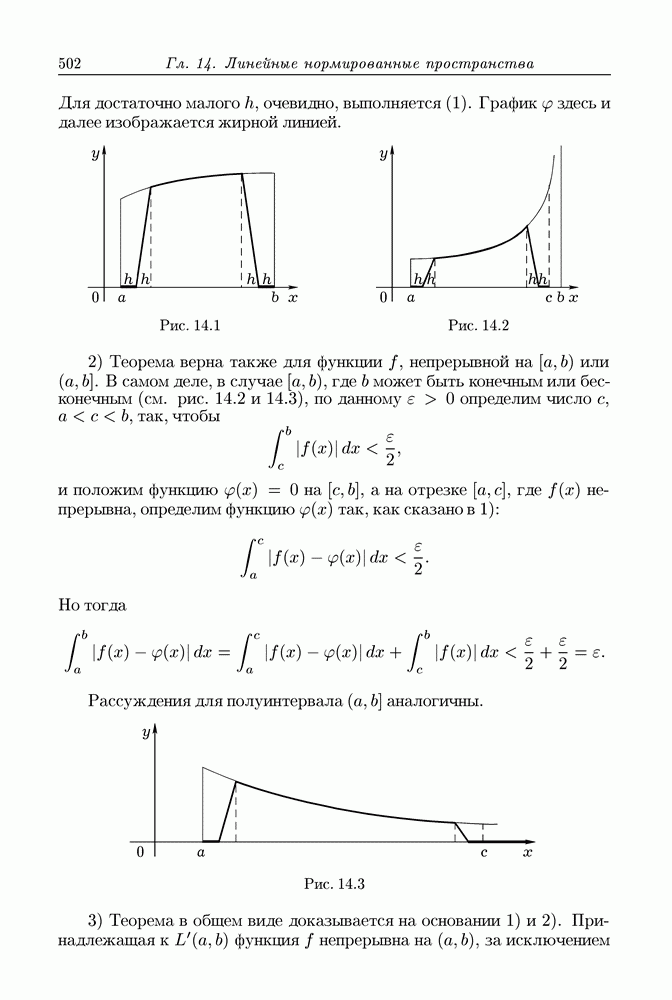
В этой главе мы даем обзор основных свойств (аксиом) действительных чисел. Это уместно, потому что среди этих свойств имеются такие, с которыми мы не имели дела в арифметике и школьном курсе алгебры, где рассматриваются операции над постоянными числами. Между тем эти свойства обнаруживаются при рассмотрении переменных чисел, или, как говорят по традиции, переменных величин.
При изучении функций приходится привлекать свойства чисел во всей их полноте, помимо тех свойств, с которыми мы хорошо знакомы из школьной математики.
Целые числа

можно складывать, вычитать и умножать друг на друга, получая снова целые числа.
Рациональные числа будем записывать в виде  где
где  целые,
целые,  .
.
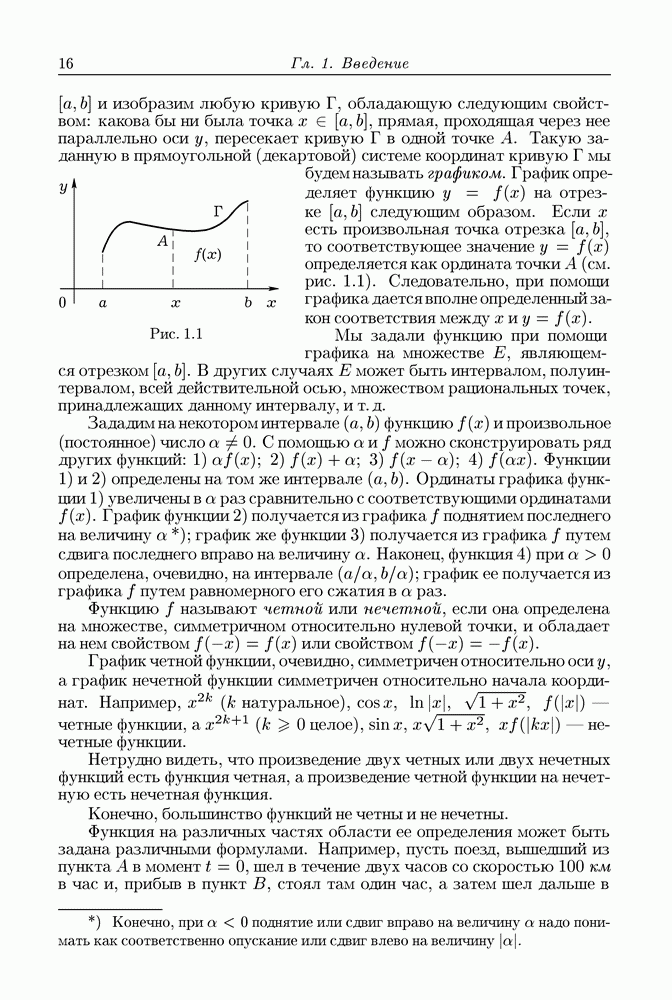
В практических вычислениях вполне достаточно оперировать только рациональными числами. Однако числа нужны еще для целей измерения геометрических и физических величин (длин отрезков, площадей, объемов, температур и т.д.). Мы здесь имеем в виду не практическое приближенное измерение этих величин, а точное (теоретическое) выражение их числами. Для этих целей рациональных чисел уже недостаточно. Рассмотрим, например, отрезок, представляющий собой гипотенузу прямоугольного треугольника с равными катетами длины единица. Если допустить, что длина этого отрезка выражается положительной рациональной дробью  которую будем считать несократимой, то площадь построенного на нем квадрата равна
которую будем считать несократимой, то площадь построенного на нем квадрата равна  а площадь каждого из квадратов, построенных на катетах, равна 1. Тогда в силу теоремы Пифагора получим равенство
а площадь каждого из квадратов, построенных на катетах, равна 1. Тогда в силу теоремы Пифагора получим равенство  Правая его часть есть целое число, делящееся на 2, но тогда левая должна быть четной, а вместе с ней и
Правая его часть есть целое число, делящееся на 2, но тогда левая должна быть четной, а вместе с ней и  Отсюда следует, что левая часть делится на 4, но тогда
Отсюда следует, что левая часть делится на 4, но тогда  делится на 2, откуда также
делится на 2, откуда также  делится на 2. Итак,
делится на 2. Итак,  имеют общий множитель 2, что противоречит предположению, что дробь
имеют общий множитель 2, что противоречит предположению, что дробь  взята несократимой. Таким образом, имеются отрезки, длины которых не выражаются рациональными числами. Их называют несоизмеримыми с единицей. Чтобы
взята несократимой. Таким образом, имеются отрезки, длины которых не выражаются рациональными числами. Их называют несоизмеримыми с единицей. Чтобы
выразить их длины, появилась необходимость в новых числах, называемых иррациональными. Так возникло число  выражающее длину гипотенузы рассмотренного треугольника.
выражающее длину гипотенузы рассмотренного треугольника.
Существуют различные способы введения иррациональных чисел. Покажем, как можно ввести их при помощи бесконечных десятичных дробей.
Зададим произвольное положительное рациональное число  Превратим его по известным правилам арифметики в десятичную дробь. В результате получим
Превратим его по известным правилам арифметики в десятичную дробь. В результате получим

где  целое неотрицательное число, а
целое неотрицательное число, а  цифры. Будем писать
цифры. Будем писать

и называть десятичную дробь в правой части (3) десятичным разложением числа 
Легко показать, что десятичное разложение положительного рационального числа не зависит от способа задания последнего, иначе говоря, при замене в  соответственно
соответственно  где
где  получается в точности то же десятичное разложение
получается в точности то же десятичное разложение  Будем считать, что дробь
Будем считать, что дробь  несократимая.
несократимая.
Хорошо известно, что если знаменатель дроби  имеет вид
имеет вид  где
где  — неотрицательные целые числа, то ее десятичное разложение есть конечная десятичная дробь:
— неотрицательные целые числа, то ее десятичное разложение есть конечная десятичная дробь:

которая, в частности, может оказаться натуральным числом  Если формально приписать справа к этой десятичной дроби бесконечно много нулей, то она превращается в бесконечную десятичную дробь:
Если формально приписать справа к этой десятичной дроби бесконечно много нулей, то она превращается в бесконечную десятичную дробь:

Мы называем ее периодической десятичной дробью с периодом 0, потому что в ней цифра  периодически повторяется.
периодически повторяется.
Пользуются также и другим представлением конечной десятичной дроби (4) в виде периодической десятичной дроби с периодом 9:

хотя оно и не возникает в процессе (2).
Пусть теперь знаменатель положительной дроби  не имеет вид
не имеет вид  Тогда процесс (2) бесконечный — на любом его шаге возникает положительный остаток. Каждый остаток меньше
Тогда процесс (2) бесконечный — на любом его шаге возникает положительный остаток. Каждый остаток меньше  и потому после того, как цифры числа
и потому после того, как цифры числа  снесены, среди первых
снесены, среди первых  остатков окажется по крайней мере два равных между собой. Но как только возникает остаток, который уже был прежде, процесс становится повторяющимся — периодическим. Поэтому десятичное разложение произвольного положительного рационального числа
остатков окажется по крайней мере два равных между собой. Но как только возникает остаток, который уже был прежде, процесс становится повторяющимся — периодическим. Поэтому десятичное разложение произвольного положительного рационального числа  имеет вид
имеет вид

Разложения (5) или (6) можно рассматривать как частные случаи (7). Разложение вида (7) называется положительной десятичной периодической дробью с периодом, представляющим собой группу цифр 
Ниже приводятся частные примеры положительных бесконечных десятичных периодических дробей:

В первом примере периодом является цифра  во втором — группа цифр 142857, в четвертом — группа цифр
во втором — группа цифр 142857, в четвертом — группа цифр 
У положительной десятичной дроби хотя бы одно из чисел  не равно нулю.
не равно нулю.
Итак, каждому положительному рациональному числу  при помощи процесса (2) ставится в соответствие положительная десятичная периодическая дробь с периодом, отличным от 9.
при помощи процесса (2) ставится в соответствие положительная десятичная периодическая дробь с периодом, отличным от 9.
При других вычислениях могут получаться десятичные дроби с периодом 9, но при желании их затем можно записать через соответствующие им конечные десятичные дроби, или, что все равно, десятичные дроби с периодом 0.
Верно и обратное утверждение: каждая положительная десятичная периодическая дробь, если она не имеет периода 9, может быть получена при помощи процесса (2) из некоторой обыкновенной положительной дроби  (единственной).
(единственной).
Например, если дробь подвергнуть процессу (2), то получим десятичную периодическую дробь  Обратно, эта последняя превращается в исходную дробь:
Обратно, эта последняя превращается в исходную дробь:

Отрицательному рациональному числу  приводят в соответствие бесконечное десятичное разложение положительного числа
приводят в соответствие бесконечное десятичное разложение положительного числа  взятое со знаком
взятое со знаком 
Итак, имеется взаимно однозначное соответствие  между не равными нулю рациональными числами и бесконечными десятичными не равными нулю периодическими дробями. Каждому не равному нулю рациональному числу соответствует при помощи указанного выше процесса одно и только одно его десятичное бесконечное периодическое разложение, не имеющее периода 9. Обратно, любое такое разложение соответствует при помощи указанного процесса некоторому не равному нулю рациональному числу (единственному).
между не равными нулю рациональными числами и бесконечными десятичными не равными нулю периодическими дробями. Каждому не равному нулю рациональному числу соответствует при помощи указанного выше процесса одно и только одно его десятичное бесконечное периодическое разложение, не имеющее периода 9. Обратно, любое такое разложение соответствует при помощи указанного процесса некоторому не равному нулю рациональному числу (единственному).
Числу нуль (оно тоже рациональное) естественно привести в соответствие разложение 
Кроме периодических десятичных дробей существуют непериодические, например 
Вот еще пример: если извлекать корень квадратный из 2 по известному правилу, то получим определенную бесконечную непериодическую десятичную дробь  Она определена в том смысле, что любому натуральному числу к соответствует определенная цифра
Она определена в том смысле, что любому натуральному числу к соответствует определенная цифра  разряда числа
разряда числа  однозначно вычисляемая согласно правилу извлечения квадратного корня.
однозначно вычисляемая согласно правилу извлечения квадратного корня.
Математический анализ дает много путей вычисления числа  с любой наперед заданной точностью. Это приводит к вполне определенному бесконечному десятичному разложению
с любой наперед заданной точностью. Это приводит к вполне определенному бесконечному десятичному разложению  которое, как оказывается, не является периодическим.
которое, как оказывается, не является периодическим.
Дадим теперь определение иррационального числа, пока чисто формальное. Иррациональным числом называется произвольная бесконечная непериодическая дробь

где  целое неотрицательное число, а
целое неотрицательное число, а  цифры, знак же равенства
цифры, знак же равенства  выражает, что мы обозначили правую часть (8) через
выражает, что мы обозначили правую часть (8) через  . Впрочем, удобно говорить, что правая часть (8) есть десятичное разложение числа а.
. Впрочем, удобно говорить, что правая часть (8) есть десятичное разложение числа а.
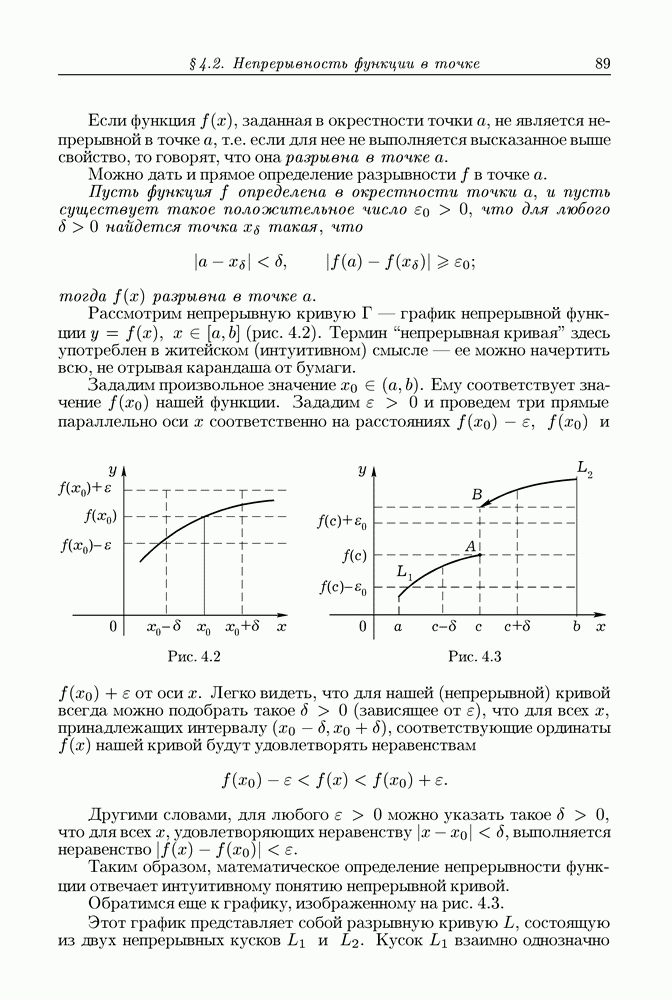
Рациональные и иррациональные числа называются действительными (или вещественными) числами.
Из сказанного следует, что всякое не равное нулю действительное число может быть записано в виде бесконечной десятичной дроби (8). Если оно рационально, то его десятичное разложение есть бесконечная десятичная периодическая дробь. В противном случае согласно нашему определению выражение (8) само определяет иррациональное число.
Число  , где не все
, где не все  равны нулю, называется положительным или отрицательным в зависимости от того, будет ли в (8) фигурировать
равны нулю, называется положительным или отрицательным в зависимости от того, будет ли в (8) фигурировать  или
или  при этом, как обычно,
при этом, как обычно,  будем позволять себе опускать.
будем позволять себе опускать.
Действительные числа определены пока формально, надо еще определить арифметические операции над ними, ввести для них понятие  проверить, что эти операции и понятие
проверить, что эти операции и понятие  согласуются с уже имеющимися соответствующими операциями и понятием
согласуются с уже имеющимися соответствующими операциями и понятием  для рациональных чисел, а также удовлетворяют свойствам, которые мы предъявляем к числам.
для рациональных чисел, а также удовлетворяют свойствам, которые мы предъявляем к числам.
Определение понятия  дается в § 2.2, а определения арифметических операций в § 2.3. В § 2.4 формулируются и доказываются основные свойства действительных чисел, распределенные на пять групп
дается в § 2.2, а определения арифметических операций в § 2.3. В § 2.4 формулируются и доказываются основные свойства действительных чисел, распределенные на пять групп  Первые три группы содержат известные свойства, которыми мы руководствуемся при арифметических вычислениях и решениях неравенств. Группа IV составляет одно свойство (Архимеда). Наконец, группа V также состоит из одного свойства: существования предела у неубывающей ограниченной последовательности. В сущности, для дальнейшего нам будет важно только знать, что действительные числа (десятичные дроби) суть объекты, для которых определены понятие
Первые три группы содержат известные свойства, которыми мы руководствуемся при арифметических вычислениях и решениях неравенств. Группа IV составляет одно свойство (Архимеда). Наконец, группа V также состоит из одного свойства: существования предела у неубывающей ограниченной последовательности. В сущности, для дальнейшего нам будет важно только знать, что действительные числа (десятичные дроби) суть объекты, для которых определены понятие  арифметические операции, удовлетворяющие свойствам
арифметические операции, удовлетворяющие свойствам  Поэтому может быть и такой способ чтения книги, когда читатель систематически читает крупный шрифт, только более или менее ознакомившись с мелким шрифтом, где даются доказательства свойств
Поэтому может быть и такой способ чтения книги, когда читатель систематически читает крупный шрифт, только более или менее ознакомившись с мелким шрифтом, где даются доказательства свойств 
Из свойств  можно получить логически все остальные свойства числа.
можно получить логически все остальные свойства числа.
Существует аксиоматический подход к определению действительного числа, заключающийся в том, что числами называются некоторые объекты (вещи)  удовлетворяющие свойствам
удовлетворяющие свойствам  При таком подходе свойства
При таком подходе свойства  называются аксиомами числа.
называются аксиомами числа.
Аксиоматическое построение понятия числа на первый взгляд может показаться более простым. Однако здесь возникает вопрос, совместны ли аксиомы  Чтобы доказать их совместность, появляется необходимость построить формальные символы, для которых можно определить арифметические операции и понятие
Чтобы доказать их совместность, появляется необходимость построить формальные символы, для которых можно определить арифметические операции и понятие  и проверить, что они удовлетворяют аксиомам
и проверить, что они удовлетворяют аксиомам  Такими символами как раз и могут служить бесконечные десятичные дроби.
Такими символами как раз и могут служить бесконечные десятичные дроби.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1. ВВЕДЕНИЕ
- § 1.2. Множество. Интервал, отрезок
- § 1.3. Функция
- § 1.4. Понятие непрерывности функции
- § 1.5. Производная
- § 1.6. Первообразная. Неопределенный интеграл
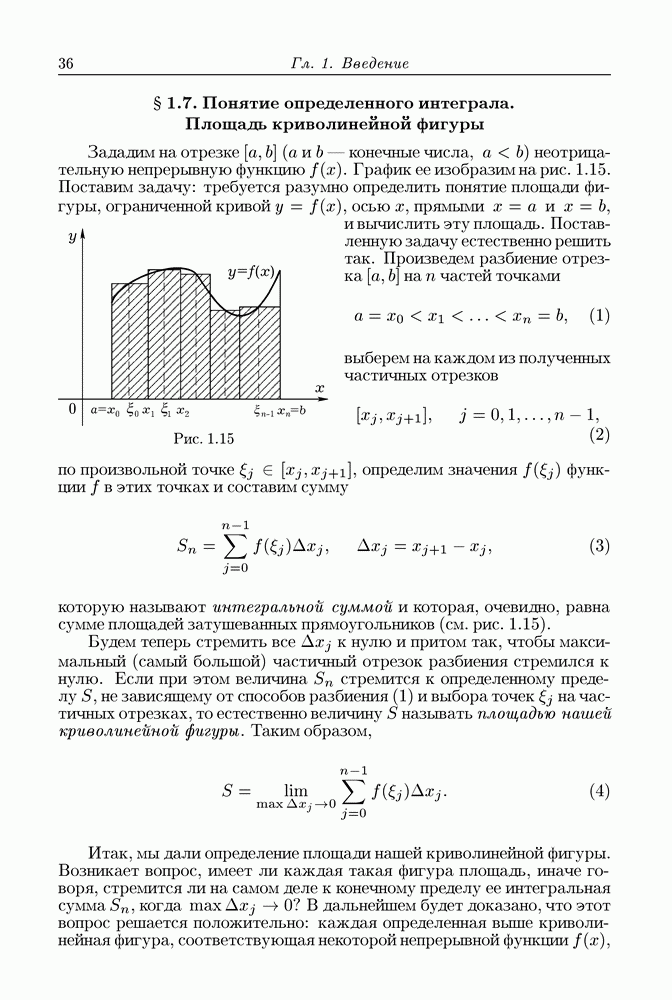
- § 1.7. Понятие определенного интеграла. Площадь криволинейной фигуры
- Глава 2. ДЕЙСТВИТЕЛЬНОЕ ЧИСЛО
- § 2.1. Рациональные и иррациональные числа
- § 2.2. Определение неравенства
- § 2.3. Основная лемма. Определение арифметических действий
- § 2.4. Основные свойства действительных чисел
- § 2.5. Изоморфизм различных представлений действительных чисел. Физические величины
- § 2.6. Неравенства для абсолютных величин
- § 2.7. Точные верхняя и нижняя грани множества
- § 2.8. Символика математической логики
- Глава 3. ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ
- § 3.1. Понятие предела последовательности
- § 3.2. Арифметические действия с пределами
- § 3.3. Бесконечно малая и бесконечно большая величины
- § 3.4. Существование предела у монотонной ограниченной последовательности
- § 3.5. Число е
- § 3.6. Леммы о вложенных отрезках, существовании точных граней множества и сечения во множестве действительных чисел
- § 3.7. Теорема Больцано-Вейерштрасса. Верхний и нижний пределы
- § 3.8. Критерий Коши существования предела
- § 3.9. Счетное множество. Счетность множества рациональных чисел. Несчетность множества действительных чисел
- Глава 4. ПРЕДЕЛ ФУНКЦИИ
- § 4.1. Понятие предела функции
- § 4.2. Непрерывность функции в точке
- § 4.3. Пределы функции справа и слева. Монотонная функция
- § 4.4. Функции, непрерывные на отрезке
- § 4.5. Обратная функция
- § 4.6. Показательная и логарифмическая функции
- § 4.7. Степенная функция x^b
- § 4.8. Еще о числе е
- § 4.9. lim sin oo/oo
- § 4.10. Порядок переменной, эквивалентность (асимптотика)
- Глава 5. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ДЛЯ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ
- § 5.1. Производная
- § 5.2. Дифференциал функции
- § 5.3. Производная функции от функции
- § 5.4. Производная обратной функции
- § 5.6. Производные и дифференциалы высшего порядка
- § 5.7. Возрастание и убывание функции на интервале и в точке. Локальный экстремум
- § 5.8. Теоремы о среднем значении. Критерии возрастания и убывания функции на интервале. Достаточные критерии локальных экстремумов
- § 5.9. Формула Тейлора
- § 5.10. Формулы Тейлора для важнейших элементарных функций
- § 5.11. Ряд Тейлора
- § 5.12. Выпуклость кривой в точке. Точка перегиба
- § 5.13. Выпуклость кривой на отрезке
- § 5.14. Раскрытие неопределенностей
- § 5.15. Асимптота
- § 5.16. Схема построения графика функции
- § 5.17. Кусочно непрерывные и кусочно гладкие функции
- Глава 6. n-МЕРНОЕ ПРОСТРАНСТВО. ГЕОМЕТРИЯ КРИВОЙ
- § 6.1. n-мерное пространство. Линейное множество
- § 6.2. Евклидово n-мерное пространство. Пространство со скалярным произведением
- § 6.3. Линейное нормированное пространство
- § 6.4. Вектор-функция в n-мерном евклидовом пространстве
- § 6.5. Непрерывная кривая. Гладкая кривая
- § 6.6. Геометрический смысл производной вектор-функции
- § 6.7. Длина дуги кривой
- § 6.8. Касательная
- § 6.9. Основной триэдр кривой
- § 6.10. Соприкасающаяся плоскость
- § 6.11. Кривизна и радиус кривизны кривой
- § 6.12. Эволюта
- § 6.13. Формулы Френе. Свойства эволюты
- Глава 7. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ
- § 7.1. Открытое множество
- § 7.2. Предел функции
- § 7.3. Непрерывная функция
- § 7.4. Частные производные и производная по направлению
- § 7.5. Дифференцируемая функция. Касательная плоскость
- § 7.6. Производная сложной функции. Производная по направлению. Градиент
- § 7.7. Независимость от порядка дифференцирования
- § 7.8. Дифференциал функции. Дифференциал высшего порядка
- § 7.9. Теорема Больцано-Вейерштрасса
- § 7.10. Замкнутые и открытые множества
- § 7.11. Функции на множестве. Свойства непрерывных функций на замкнутом ограниченном множестве
- § 7.12. Лемма о вложенных прямоугольниках и лемма Бореля
- § 7.13. Формула Тейлора
- § 7.14. локальный (абсолютный) экстремум функции
- § 7.15. Теоремы существования неявной функции
- § 7.16. Теорема существования решения системы уравнений
- § 7.17. Отображения
- § 7.18. Гладкая поверхность
- § 7.19. Дифференциалы неявных функций. Линеаризация
- § 7.20. Локальный относительный экстремум
- § 7.21. Замена переменных в частных производных
- § 7.22. Система зависимых функций
- Глава 8. НЕОПРЕДЕЛЕННЫЕ ИНТЕГРАЛЫ. АЛГЕБРА МНОГОЧЛЕНОВ
- § 8.1. Введение. Методы замены переменной и интегрирования по частям
- § 8.2. Комплексные числа
- § 8.3. Комплексные функции
- § 8.4. Многочлены
- § 8.5. Разложение рациональной функции на простейшие дроби
- § 8.6. Интегрирование рациональных дробей
- § 8.7. Интегрирование алгебраических иррациональностей
- § 8.8. Подстановки Эйлера
- § 8.9. Биномиальные дифференциалы. Теорема Чебышева
- § 8.10. Интегрирование тригонометрических выражений
- § 8.11. Тригонометрические подстановки
- § 8.12. Несколько важных интегралов, не выражаемых в элементарных функциях
- Глава 9. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ РИМАНА
- § 9.2. Ограниченность интегрируемой функции
- § 9.3. Суммы Дарбу
- § 9.4. Основная теорема
- § 9.5. Теоремы о существовании интеграла от непрерывной и монотонной функции на [a, b]
- § 9.6. Аддитивные и однородные свойства интеграла
- § 9.7. Неравенства и теорема о среднем
- § 9.8. Интеграл как функция верхнего предела. Теорема Ньютона-Лейбница
- § 9.9. Вторая теорема о среднем
- § 9.10. Видоизменение функции
- § 9.11. Несобственные интегралы
- § 9.12. Несобственные интегралы от неотрицательных функций
- § 9.13. Интегрирование по частям
- § 9.14. Несобственный интеграл и ряд
- § 9.15. Несобственные интегралы с особенностями в нескольких точках
- § 9.16. Формула Тейлора с остатком в интегральной форме
- § 9.17. Формулы Валлиса и Стирлинга
- Глава 10. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ ИНТЕГРАЛОВ. ПРИБЛИЖЕННЫЕ МЕТОДЫ
- § 10.1. Площадь в полярных координатах
- § 10.2. Объем тела вращения
- § 10.3. Длина дуги гладкой кривой
- § 10.4. Площадь поверхности тела вращения
- § 10.5. Интерполяционный многочлен Лагранжа
- § 10.6. Квадратурные формулы прямоугольников
- § 10.7. Формула Симпсона
- Глава 11. РЯДЫ
- § 11.1. Понятие ряда
- § 11.2. Действия с рядами
- § 11.3. Ряды с неотрицательными членами
- § 11.4. Ряд Лейбница
- § 11.5. Абсолютно сходящиеся ряды
- § 11.6. Условно и безусловно сходящиеся ряды с действительными членами
- § 11.7. Последовательности и ряды функций. Равномерная сходимость
- § 11.8. Интегрирование и дифференцирование равномерно сходящихся рядов на отрезке
- § 11.9. Кратные ряды. Перемножение абсолютно сходящихся рядов
- § 11.10. Суммирование рядов и последовательностей методом средних арифметических
- § 11.11. Степенные ряды
- § 11.12. Дифференцирование и интегрирование степенных рядов
- § 11.13. Степенные ряды функций e^z, cos z, sinz комплексной переменной
- Глава 12. КРАТНЫЕ ИНТЕГРАЛЫ
- § 12.2. Мера Жордана
- § 12.3. Важные примеры квадрируемых по Жордану множеств
- § 12.4. Еще один критерий измеримости множества. Полярные координаты
- § 12.5. Другие случаи измеримости
- § 12.6. Понятие кратного интеграла
- § 12.7. Верхняя и нижняя интегральные суммы. Основная теорема
- § 12.8. Интегрируемость непрерывной функции на замкнутом измеримом множестве. Другие критерии
- § 12.9. Свойства кратных интегралов
- § 12.10. Сведение кратного интеграла к интегрированию по отдельным переменным
- § 12.11. Непрерывность интеграла по параметру
- § 12.12. Геометрическая интерпретация знака определителя
- § 12.13. Замена переменных в кратном интеграле. Простейший случай
- § 12.14. Замена переменных в кратном интеграле
- § 12.15. Доказательство леммы 1 § 12.14
- § 12.16. Полярные координаты в плоскости
- § 12.17. Полярные и цилиндрические координаты в пространстве
- § 12.18. Гладкая поверхность
- § 12.19. Площадь поверхности
- Глава 13. ТЕОРИЯ ПОЛЯ. ДИФФЕРЕНЦИРОВАНИЕ И ИНТЕГРИРОВАНИЕ ПО ПАРАМЕТРУ. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
- § 13.1. Криволинейный интеграл первого рода
- § 13.2. Криволинейный интеграл второго рода
- § 13.3. Поле потенциала
- § 13.4. Ориентация плоской области
- § 13.5. Формула Грина. Выражение площади через криволинейный интеграл
- § 13.6. Интеграл по поверхности первого рода
- § 13.7. Ориентация поверхностей
- § 13.8. Интеграл по ориентированной плоской области
- § 13.9. Поток вектора через ориентированную поверхность
- § 13.10. Дивергенция. Теорема Гаусса-Остроградского
- § 13.11. Ротор вектора. Формула Стокса
- § 13.12. Дифференцирование интеграла по параметру
- § 13.13. Несобственный интеграл
- § 13.14. Равномерная сходимость несобственного интеграла
- § 13.15. Равномерно сходящийся интеграл для неограниченной области
- Глава 14. ЛИНЕЙНЫЕ НОРМИРОВАННЫЕ ПРОСТРАНСТВА. ОРТОГОНАЛЬНЫЕ СИСТЕМЫ
- § 14.2. Пространство L'(L)
- § 14.3. Пространство L2 (L2)
- § 14.4. Пространство …
- § 14.5. Полнота системы элементов в банаховом пространстве
- § 14.6. Ортогональная система в пространстве со скалярным произведением
- § 14.7. Ортогонализация системы
- § 14.8. Полнота системы функций в …
- Глава 15. РЯДЫ ФУРЬЕ. ПРИБЛИЖЕНИЕ ФУНКЦИЙ ПОЛИНОМАМИ
- § 15.2. Сумма Дирихле
- § 15.3. Формулы для остатка ряда Фурье
- § 15.4. Теоремы об осцилляции
- § 15.5. Критерий сходимости рядов Фурье. Полнота тригонометрической системы функций
- § 15.6. Комплексная форма записи ряда Фурье
- § 15.7. Дифференцирование и интегрирование рядов Фурье
- § 15.8. Оценка остатка ряда Фурье
- § 15.9. Алгебраические многочлены. Многочлены Чебышева
- § 15.10. Теорема Вейерштрасса
- § 15.11. Многочлены Лежандра
- Глава 16. ИНТЕГРАЛ ФУРЬЕ. ОБОБЩЕННЫЕ ФУНКЦИИ
- § 16.1. Понятие интеграла Фурье
- § 16.2. Сходимость простого интеграла Фурье к порождающей его функции
- § 16.3. Преобразование Фурье. Повторный интеграл Фурье. Косинус- и синус-преобразования Фурье
- § 16.4. Производная преобразования Фурье
- § 16.5. Обобщенные функции в смысле D
- § 16.6. Пространство S
- § 16.7. Пространство S обобщенных функций