| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
106. Полиномы Якоби.
Полиномы Лежандра являются лишь частными случаями тех полиномов, которые получаются, когда гипергеометрический ряд обрывается и превращается в полином. Мы исследуем теперь общий случай. Введем следующее обозначение:

и будем считать, что  и q суть фиксированные числа, большие, чем
и q суть фиксированные числа, большие, чем  причем мы всегда будем предполагать, что параметры
причем мы всегда будем предполагать, что параметры  суть числа вещественные. Для того чтобы гипергеометрический ряд оборвался и превратился в полином степени
суть числа вещественные. Для того чтобы гипергеометрический ряд оборвался и превратился в полином степени  мы должны принять а или
мы должны принять а или  равным
равным  . Не ограничивая общности, мы можем считать, например,
. Не ограничивая общности, мы можем считать, например,  и определить затем из (91) значение а и у. Обозначим полученный таким образом полином следующим образом:
и определить затем из (91) значение а и у. Обозначим полученный таким образом полином следующим образом:

где  произвольная постоянная.
произвольная постоянная.
Применяя к написанному гипергеометрическому ряду формулу (64), убедимся в том, что коэффициент при  в полиноме (92) равен
в полиноме (92) равен

Применяя к полиному (92) формулу (77), будем иметь

Определим постоянную  формулой
формулой

При этом для построенного полинома получится формула

Если вместо z ввести  по формуле (80), то получатся полиномы от
по формуле (80), то получатся полиномы от  которые называются полиномами Якоби:
которые называются полиномами Якоби:

При p = q = 0 эти полиномы совпадают с полиномами Лежандра. При  .
.
Из определения  непосредственно следует, что коэффициент при
непосредственно следует, что коэффициент при  в полиноме (92) равен
в полиноме (92) равен

а в полиноме  коэффициент при
коэффициент при  равен
равен

В рассматриваемом случае мы имеем

и функция (92) является решением уравнения

Совершая замену независимой переменной (80), получим для полиномов Якоби уравнение вида

В данном случае полиномы Якоби (93) при  являются решением следующей предельной задачи: найти такие значения параметра X, при которых дифференциальное уравнение
являются решением следующей предельной задачи: найти такие значения параметра X, при которых дифференциальное уравнение

имеет решение, конечное на отрезке (-1, 1), включая его концы. Эти значения параметра будут

а соответствующие решения и суть полиномы Якоби.
Пользуясь уравнением (94) для полиномов Якоби, нетрудно показать, как и в случае полиномов Лежандра, что имеют место следующие равенства 1

Свойства (97) выражают следующим образом: полиномы Якоби ортогональны на промежутке (-1, 1) с весом

Из формулы (93) можно, как и для полиномов Лежандра, заключить, что

Займемся теперь вычислением интеграла 

Пользуясь формулой (93), можем написать

Производя, как и в [105], интегрирование по частям, получим

причем внеинтегральные члены обратятся в нуль в силу  Обозначая, как и выше, через
Обозначая, как и выше, через  коэффициент при
коэффициент при  в полиноме
в полиноме  , получим
, получим

Вводим новую переменную интегрирования 

т. е. 

или, подставляя указанное выше выражение для а и пользуясь формулой (120) из [71],

т. е. имеет место формула 1

При  последнее выражение в силу
последнее выражение в силу  имеет
имеет

Отметим еще один частный случай, а именно тот, когда  Введем для этих полиномов особое обозначение
Введем для этих полиномов особое обозначение

где  некоторые постоянные.
некоторые постоянные.
В силу (93) они определяются следующим соотношением:

Выведем теперь другое выражение для этих полиномов, для чего воспользуемся тем дифференциальным уравнением, которому они должны удовлетворять. Это уравнение получится из уравнения (94), если там положить  . Будем иметь для
. Будем иметь для  уравнение
уравнение

Корни определяющего уравнения в особой точке  будут
будут  и
и  . Первому из них и соответствует решение в виде полинома, а второе решение наверно отлично от полинома. Чтобы найти полином, удовлетворяющий уравнению (103) в удобной форме, введем вместо
. Первому из них и соответствует решение в виде полинома, а второе решение наверно отлично от полинома. Чтобы найти полином, удовлетворяющий уравнению (103) в удобной форме, введем вместо  новую независимую переменную по формуле
новую независимую переменную по формуле

Заменяя дифференцирование по  дифференцированием по
дифференцированием по  , будем иметь по правилу дифференцирования сложных функций
, будем иметь по правилу дифференцирования сложных функций

Подставляя это в уравнение (103), получим

Решения последнего уравнения суть

или для уравнения (ЮЗ) получаем решения вида

Пользуясь известной формулой [I, 174]

убеждаемся, что первое из этих решений есть полином от х, и, следовательно, с точностью до произвольного множителя решение уравнения, представляющееся полиномом, будет

и этот полином называется полиномом Чебышева. При  мы имеем
мы имеем  и, следовательно,
и, следовательно,  с другой стороны, по формуле (99)
с другой стороны, по формуле (99)

и отсюда нетрудно определить постоянный множитель в формуле (101):

| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ К ВОСЬМОМУ ИЗДАНИЮ
- 1. Функции комплексного переменного.
- 2. Производная.
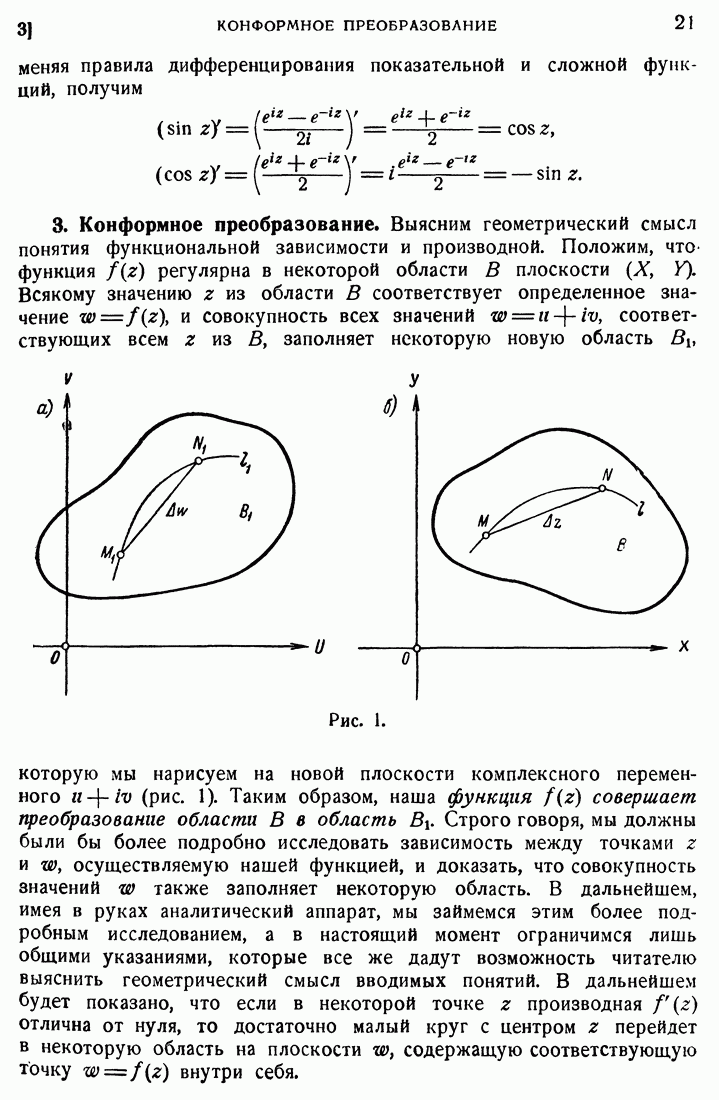
- 3. Конформное преобразование.
- 4. Интеграл.
- 5. Теорема Коши.
- 6. Основная формула интегрального исчисления.
- 7. Формула Коши.
- 8. Интегралы типа Коши.
- 9. Следствия формулы Коши.
- 10. Изолированные особые точки.
- 11. Бесконечные ряды с комплексными членами.
- 12. Теорема Вейерштрасса.
- 13. Степенные ряды.
- 14. Ряд Тейлора.
- 15. Ряд Лорана.
- 16. Примеры.
- 17. Изолированные особые точки. Бесконечно далекая точка.
- 18. Аналитическое продолжение.
- 19. Примеры многозначных функций.
- 20. Особые точки аналитических функций и римановы поверхности.
- 21. Теорема вычетов.
- 22. Теоремы о числе корней.
- 23. Обращение степенного ряда.
- 24. Принцип симметрии.
- 25. Ряд Тейлора на окружности круга сходимости.
- 26. Дополнительные сведения о формуле Коши.
- 27. Главное значение интеграла.
- 28. Главное значение интеграла (продолжение).
- 29. Интегралы типа Коши.
- 30. Интегралы типа Коши (продолжение).
- ГЛАВА II. КОНФОРМНОЕ ПРЕОБРАЗОВАНИЕ И ПЛОСКОЕ ПОЛЕ
- 31. Конформное преобразование.
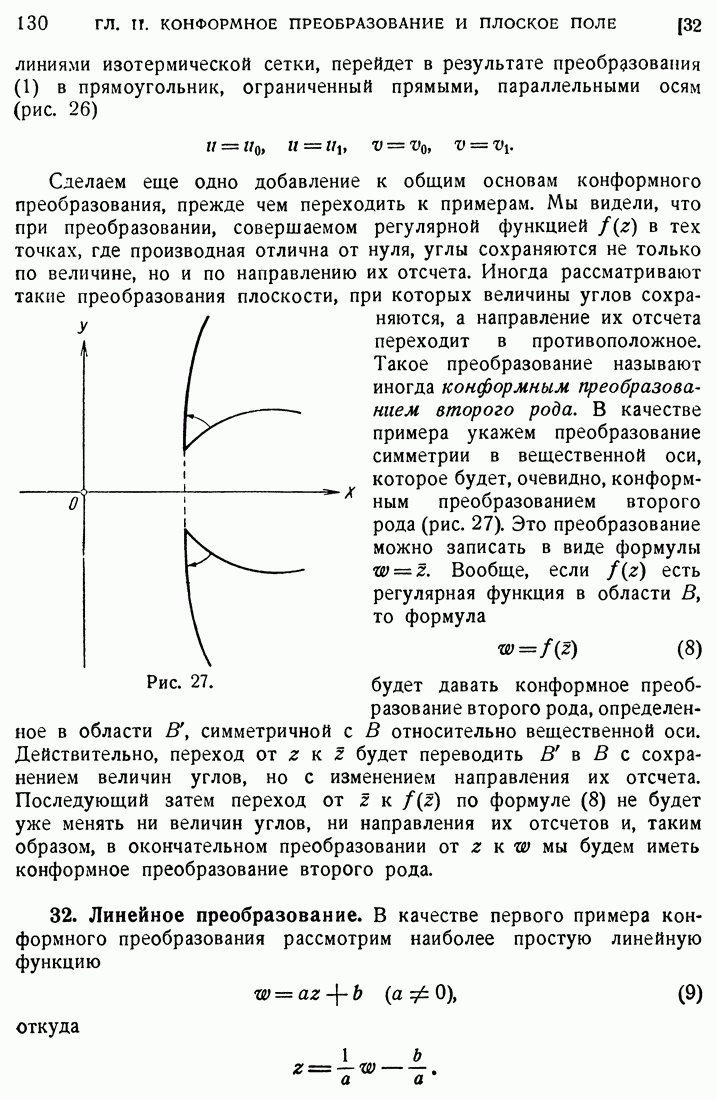
- 32. Линейное преобразование.
- 33. Дробно-линейное преобразование.
- 34. Функция w = z^2.
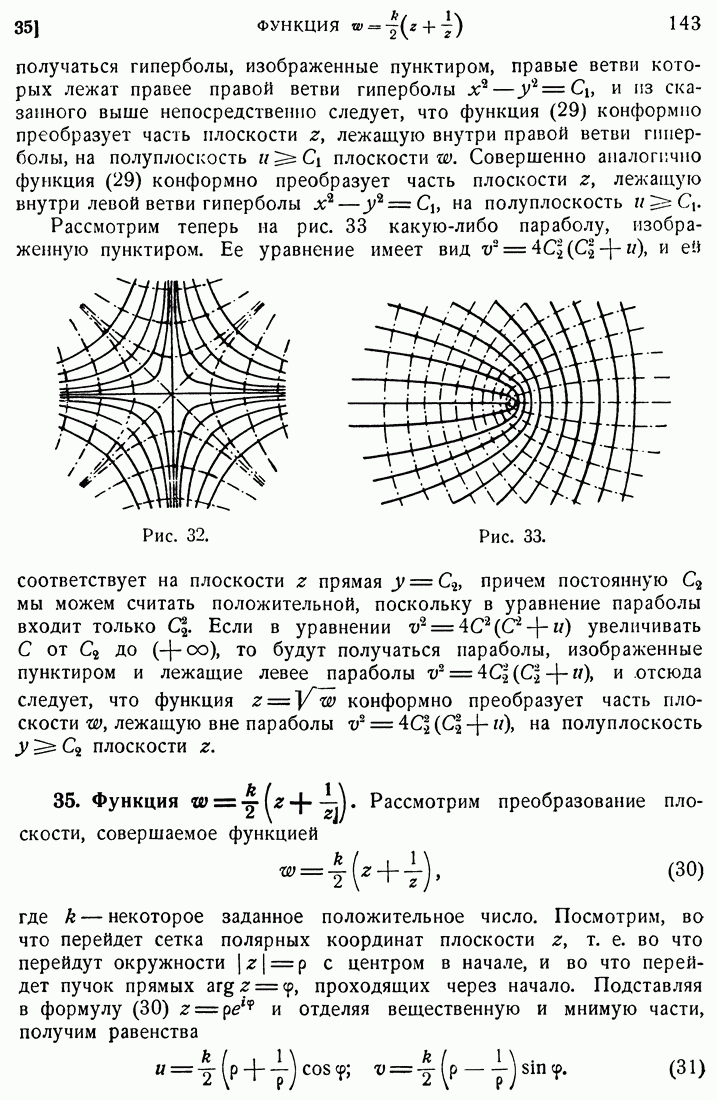
- 35. Функция …
- 36. Двуугольник и полоса.
- 37. Основная теорема.
- 38. Формула Кристоффеля.
- 39. Частные случаи.
- 40. Случай внешности многоугольника.
- 41. Минимальное свойство преобразования на круг.
- 42. Способ сопряженных тригонометрических рядов.
- 43. Плоское установившееся течение жидкости.
- 44. Примеры.
- 45. Задача полного обтекания.
- 46. Формула Н. Е. Жуковского.
- 47. Плоская электростатическая задача.
- 48. Формула Шварца.
- 49. Ядро ctg((s-t)/2).
- 50. Предельные задачи.
- 51. Бигармоническое уравнение.
- 52. Волновое уравнение и аналитические функции.
- 53. Основная теорема.
- 54. Дифракция плоской волны.
- 55. Отражение упругих волн от прямолинейной границы.
- ГЛАВА III. ПРИМЕНЕНИЕ ТЕОРИИ ВЫЧЕТОВ, ЦЕЛЫЕ И ДРОБНЫЕ ФУНКЦИИ
- 56. Интеграл Френеля.
- 57. Интегрирование выражений с тригонометрическими функциями.
- 58. Интегрирование рациональной дроби.
- 59. Некоторые новые типы интегралов с тригонометрическими функциями.
- 60. Лемма Жордана.
- 61. Представление некоторых функций контурными интегралами.
- 62. Примеры интегралов от многозначных функций.
- 63. Интегрирование системы линейных уравнений с постоянными коэффициентами.
- 64. Разложение дробной функции на простейшие дроби.
- 66. Построение мероморфной функции.
- 67. Целые функции.
- 68. Бесконечные произведения.
- 69. Построение целой функции по ее корням.
- 70. Интегралы, зависящие от параметра.
- 71. Эйлеров интеграл второго рода.
- 72. Эйлеров интеграл первого рода.
- 73. Бесконечное произведение для функции …
- 74. Представление Г(z) контурным интегралом.
- 75. Формула Стирлинга.
- 76. Формула суммирования Эйлера.
- 77. Числа Бернулли.
- 78. Метод скорейшего спуска.
- 79. Асимптотическое разложение интеграла.
- 80. Примеры.
- 81. Метод стационарной фазы.
- ГЛАВА IV. АНАЛИТИЧЕСКИЕ ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ И ФУНКЦИИ МАТРИЦ
- 82. Регулярные функции многих переменных.
- 83. Двойной интеграл и формула Коши.
- 84. Степенные ряды.
- 85. Аналитическое продолжение.
- 86. Функции матриц. Предварительные понятия.
- 87. Степенные ряды от одной матрицы.
- 88. Умножение степенных рядов. Обращение степенного ряда.
- 89. Дальнейшее исследование сходимости.
- 90. Интерполяционные полиномы.
- 91. Тождество Кейли. Формула Сильвестра.
- 92. Определение функций одной матрицы формулой Коши.
- 93. Аналитическое продолжение.
- 94. Логарифм матриц.
- 95. Обращение целой функции от матрицы в случае матриц второго порядка.
- 96. Системы линейных уравнений с постоянными коэффициентами.
- 97. Функции нескольких матриц.
- ГЛАВА V. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
- 98. Разложение решения в степенной ряд.
- 99. Аналитическое продолжение решения.
- 100. Окрестность особой точки.
- 101. Регулярная особая точка.
- 102. Уравнения класса Фукса.
- 103. Уравнение Гаусса.
- 104. Гипергеометрический ряд.
- 105. Полиномы Лежандра.
- 106. Полиномы Якоби.
- 107. Конформное преобразование и уравнение Гаусса.
- 108. Преобразование Лапласа.
- 109. Различный выбор решений.
- 110. Уравнение Бесселя.
- 111. Функции Ханкеля и интегральное представление решений уравнения Бесселя.
- 112. Асимптотические разложения.
- 113. Асимптотические разложения решений, полученных преобразованием Лапласа.
- 114. Асимптотические разложения решений уравнения Бесселя.
- 115. Вырождение уравнения Гаусса.
- 116. Формальные ряды в окрестности иррегулярной особой точки.
- 117. Построение асимптотических разложений методом после довательных приближений.
- 118. Функции Эйри.
- 119. Асимптотика при большом значении параметра.
- 120. Уравнения с периодическими коэффициентами.
- 121. Условия устойчивости и неустойчивости для уравнения Хилла.
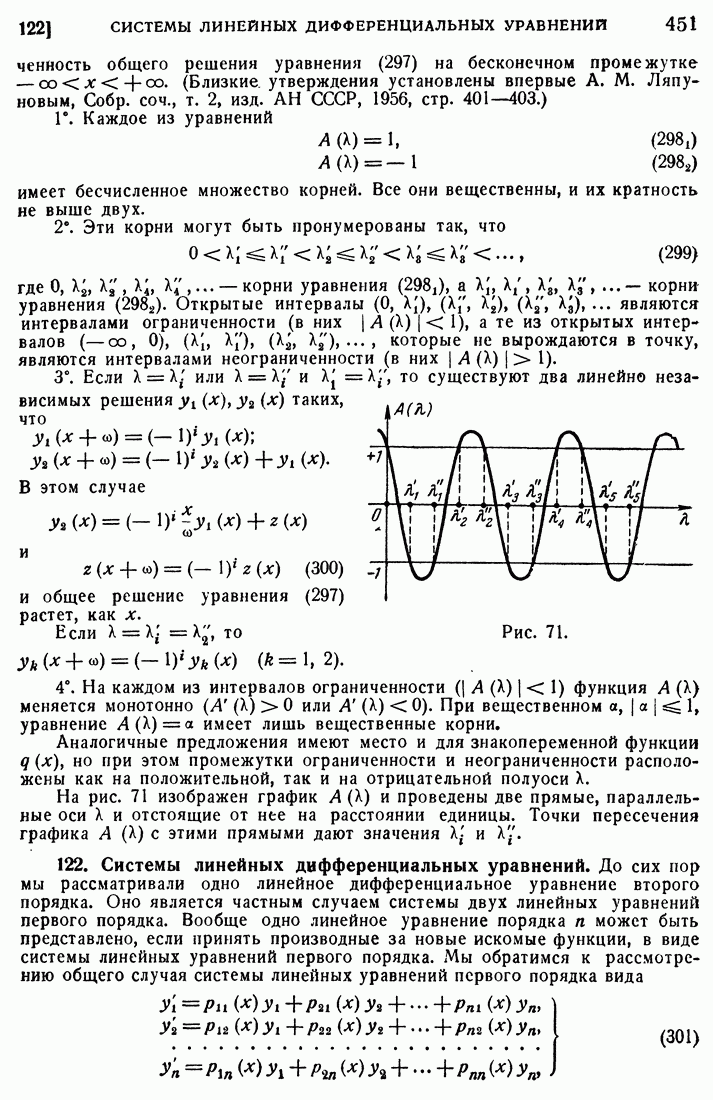
- 122. Системы линейных дифференциальных уравнений.
- 123. Регулярная особая точка.
- 124. Регулярные системы.
- 125. Представление решения в окрестности особой точки.
- 126. Канонические решения.
- 127. Связь с регулярными решениями типа Фукса.
- 128. Случай любых Us.
- 129. Формальные разложения в окрестности иррегулярной особой точки.
- ГЛАВА VI. СПЕЦИАЛЬНЫЕ ФУНКЦИИ
- 130. Определение сферических функций.
- 131. Явные выражения сферических функций.
- 132. Свойство ортогональности.
- 133. Полиномы Лежандра.
- 134. Разложение по сферическим функциям.
- 135. Доказательство сходимости.
- 136. Связь сферических функций с предельными задачами.
- 137. Задачи Дирихле и Неймана.
- 138. Потенциал объемных масс.
- 139. Потенциал сферического слоя.
- 140. Электрон в центральном поле.
- 141. Шаровые функции и линейные представления группы вращения.
- 142. Функция Лежандра.
- 143. Функция Лежандра второго рода.
- § 2. ФУНКЦИИ БЕССЕЛЯ
- 144. Определение функций Бесселя.
- 145. Соотношения между функциями Бесселя.
- 146. Ортогональность функций Бесселя и их корни.
- 147. Производящая функция и интегральное представление.
- 148. Формула Фурье — Бесселя.
- 150. Разложение функций Неймана с целым значком.
- 151. Случай чисто мнимого аргумента.
- 152. Новые интегральные представления.
- 153. Асимптотические представления.
- 154. Функции Бесселя и уравнение Лапласа.
- 155. Волновое уравнение в цилиндрических координатах.
- 156. Волновое уравнение в сферических координатах.
- § 3. ПОЛИНОМЫ ЭРМИТА И ЛАГЕРРА
- 157. Линейный осциллятор и полиномы Эрмита.
- 158. Свойство ортогональности.
- 159. Производящая функция.
- 160. Параболические координаты и функции Эрмита.
- 161. Полиномы Лагерра.
- 162. Связь полиномов Эрмита и Лагерра.
- 163. Асимптотическое выражение полиномов Эрмита.
- 164. Асимптотическое выражение полиномов Лежандра.
- § 4. ЭЛЛИПТИЧЕСКИЕ ИНТЕГРАЛЫ И ЭЛЛИПТИЧЕСКИЕ ФУНКЦИИ
- 165. Приведение эллиптических интегралов к нормальному виду.
- 166. Приведение интегралов к тригонометрической форме.
- 167. Примеры.
- 168. Обращение эллиптического интеграла.
- 169. Общие свойства эллиптических функций.
- 170. Основная лемма.
- 171. Функции Вейерштрасса.
- 172. Дифференциальное уравнение для …
- 173. Функции …
- 174. Разложение целой периодической функции.
- 175. Новые обозначения.
- 176. Функция …
- 177. Функции …
- 178. Свойства функций тэта.
- 179. Выражение чисел … через …
- 180. Эллиптические функции Якоби.
- 181. Основные свойства функций Якоби.
- 182. Дифференциальные уравнения для функций Якоби.
- 183. Формулы сложения.
- 184. Связь функций p(u) и sn(u).
- 185. Эллиптические координаты.
- 186. Введение эллиптических функций.
- 187. Уравнение Лямэ.
- 188. Простой маятник.
- 189. Пример конформного преобразования.
- ДОБАВЛЕНИЕ. ПРИВЕДЕНИЕ МАТРИЦ К КАНОНИЧЕСКОЙ ФОРМЕ
- 191. Случай простых корней.
- 192. Первый этап преобразований в случае кратных корней.
- 193. Приведение к канонической форме.
- 194. Определение структуры канонической формы.
- 196. Пример.