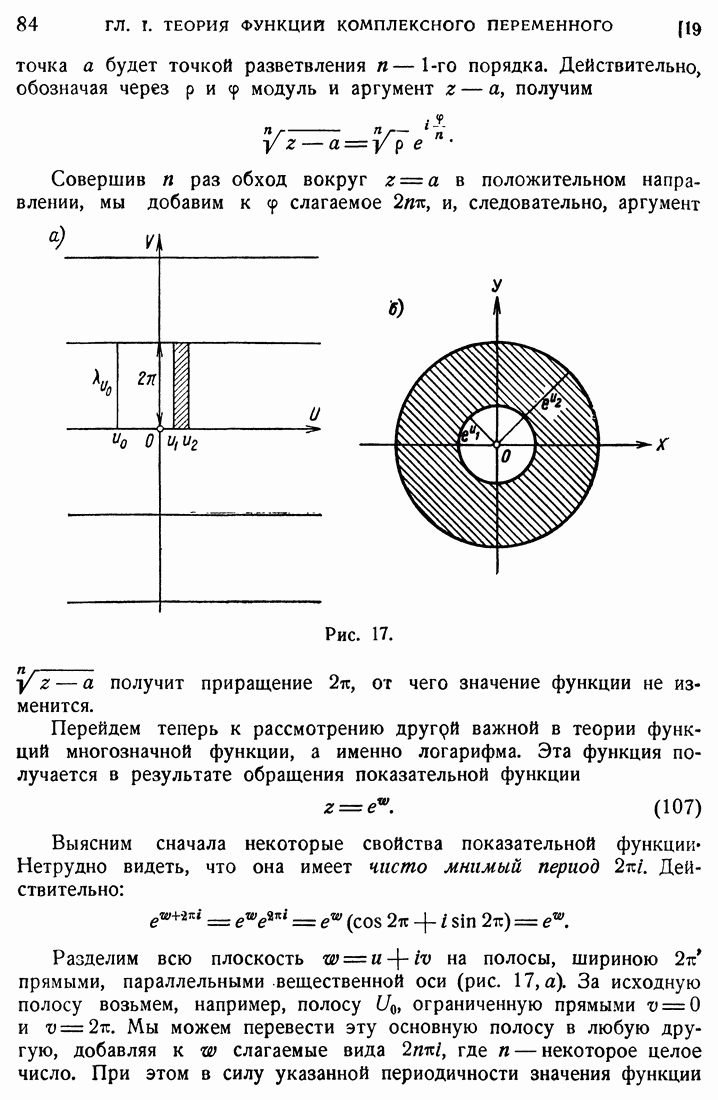
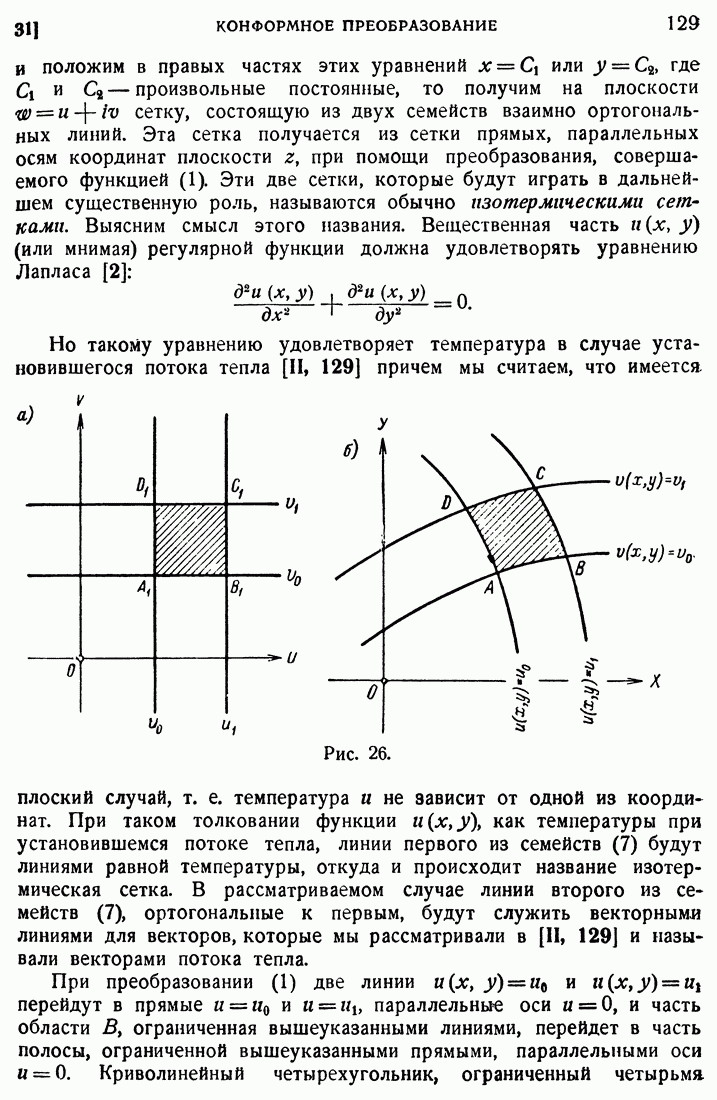
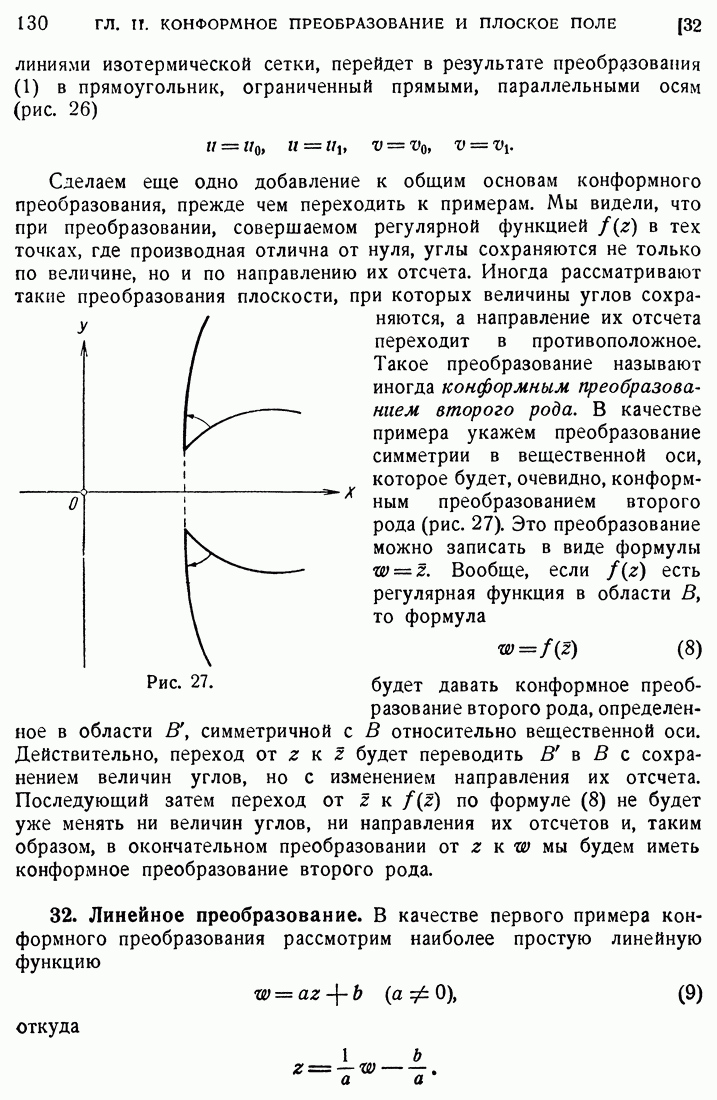
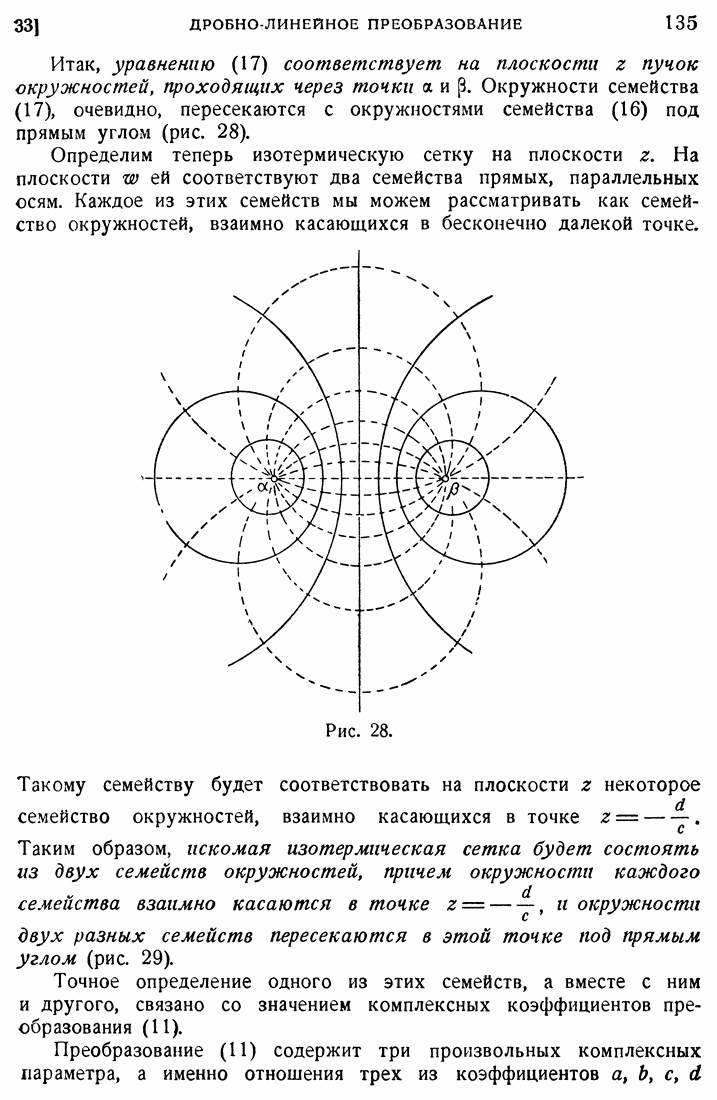
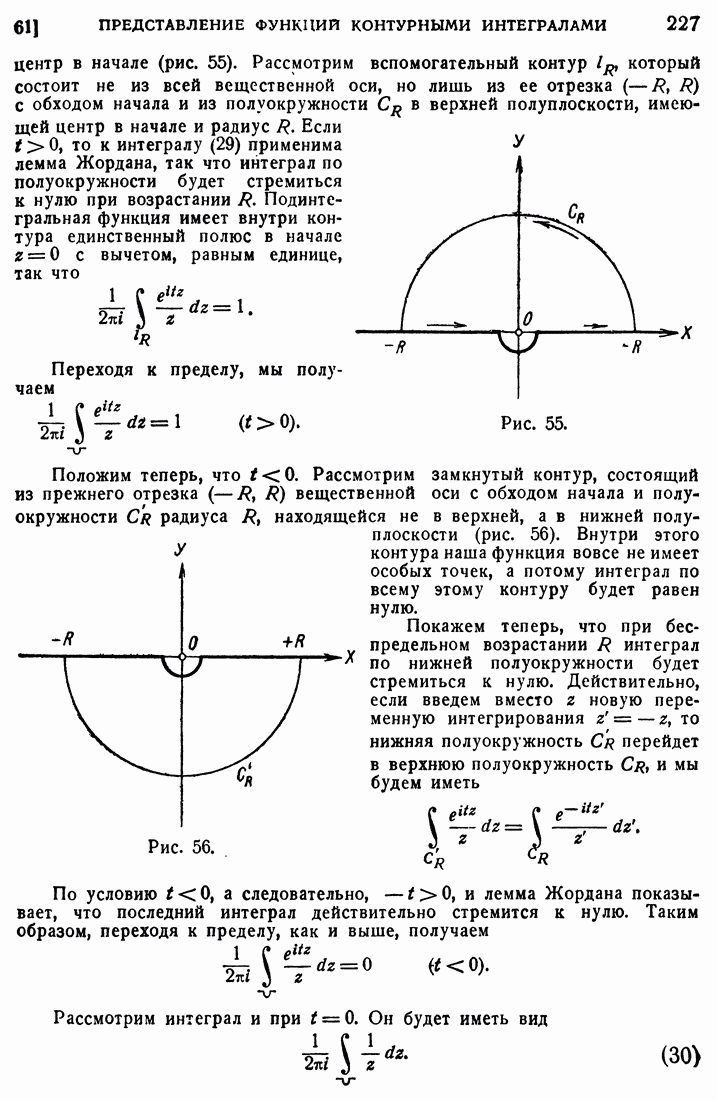
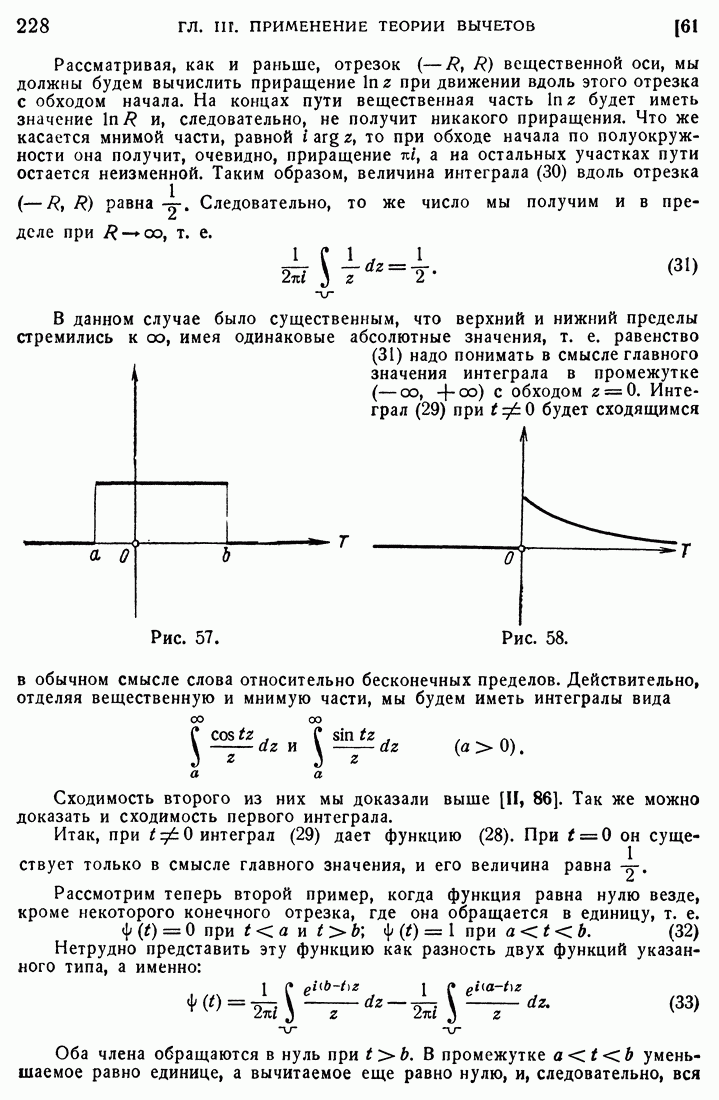
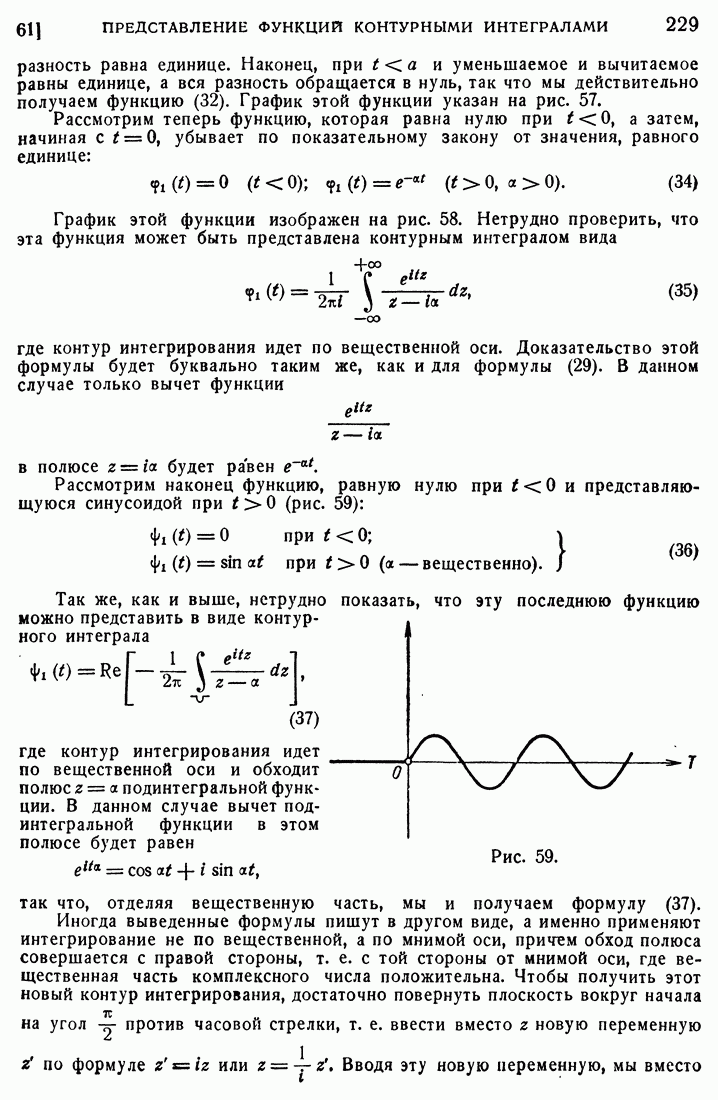
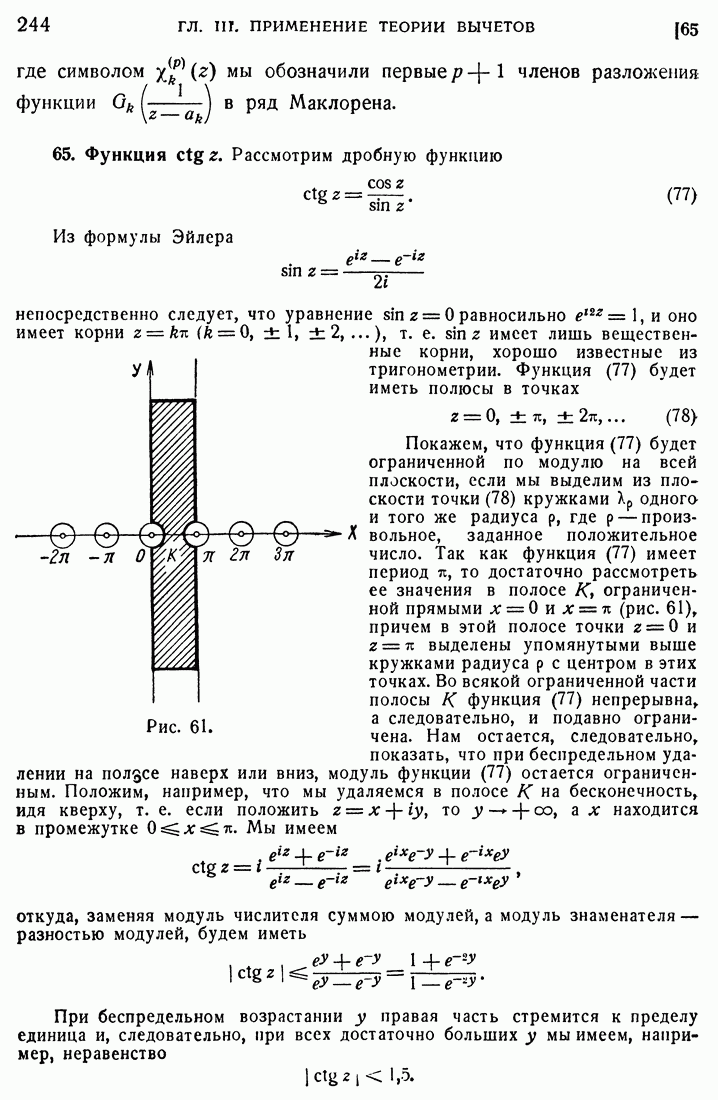
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
29. Интегралы типа Коши.
Рассмотрим интеграл типа Коши [8]

при прежних предположениях относительно  и L. Положим, что
и L. Положим, что  находится не на L. Если L — замкнутый контур, то этот интеграл определяет две различные регулярные функции - внутри и вне b Если контур незамкнутый, то
находится не на L. Если L — замкнутый контур, то этот интеграл определяет две различные регулярные функции - внутри и вне b Если контур незамкнутый, то  регулярна вне L. В обоих случаях
регулярна вне L. В обоих случаях  Если
Если  лежит на контуре, то мы имеем интеграл в смысле главного значения и можем переписать его в виде
лежит на контуре, то мы имеем интеграл в смысле главного значения и можем переписать его в виде

т. е., в силу (161),

Считая сначала, что контур замкнутый, докажем теорему: если  стремится к некоторой точке 6, лежащей на L, то интеграл (166) имеет предел
стремится к некоторой точке 6, лежащей на L, то интеграл (166) имеет предел

причем знак «+» берется, если  изнутри L, и знак «-», если
изнутри L, и знак «-», если  извне. Разберем стремление изнутри. Интеграл (166) мы можем переписать в виде
извне. Разберем стремление изнутри. Интеграл (166) мы можем переписать в виде

или

Исследуем разность

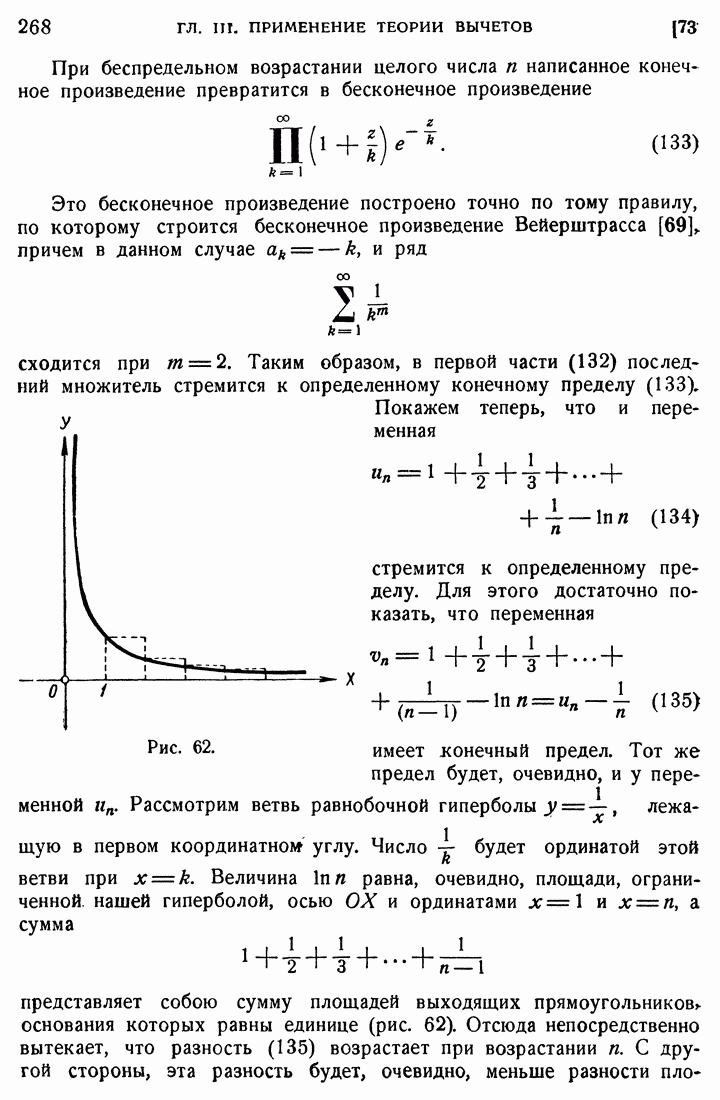
По обе стороны от точки  отложим дуги малой длины
отложим дуги малой длины  Образуемую этими дугами часть контура обозначим через
Образуемую этими дугами часть контура обозначим через  а остальную часть — через 12. Обозначая разность (170) одной буквой
а остальную часть — через 12. Обозначая разность (170) одной буквой  , можем написать
, можем написать

Положим, что z стремится к  по нормали к контуру L. При этом расстояние от z до
по нормали к контуру L. При этом расстояние от z до  будет меньше, чем расстояние от
будет меньше, чем расстояние от  до других точек контура, т. е.
до других точек контура, т. е. 
Кроме того,  причем
причем  Оценивая обычным образом первый из интегралов формулы (171), получим
Оценивая обычным образом первый из интегралов формулы (171), получим

где  соответствует точке
соответствует точке  Принимая во внимание, что отношение длины хорды
Принимая во внимание, что отношение длины хорды  к длине дуги
к длине дуги  стремится к единице, можем утверждать, что последний интеграл будет сходящимся, и, следовательно, при любом заданном положительном
стремится к единице, можем утверждать, что последний интеграл будет сходящимся, и, следовательно, при любом заданном положительном  мы можем выбрать настрлько малым, чтобы модуль интеграла по
мы можем выбрать настрлько малым, чтобы модуль интеграла по  был меньше
был меньше  Закрепив таким образом
Закрепив таким образом  мы будем иметь уже обычный интеграл по
мы будем иметь уже обычный интеграл по  в котором
в котором  остаются ббльшими некоторого положительного числа, а потому интеграл по
остаются ббльшими некоторого положительного числа, а потому интеграл по  будет по модулю меньше при всех z, достаточно близких к
будет по модулю меньше при всех z, достаточно близких к  Ввиду произвольности
Ввиду произвольности  мы можем утверждать, что разность (171) стремится к нулю при
мы можем утверждать, что разность (171) стремится к нулю при  по нормали, т. е.
по нормали, т. е.

или, в силу (161),

и формула (169) дает требуемый результат:

В случае стремления извне доказательство проводится буквально так же, только надо иметь в виду, что  если
если  внутри l,
внутри l,

До сих пор мы предполагали, что  по нормали. Можно показать, что формула (172) сохранит свою силу и при любом стремлении z к
по нормали. Можно показать, что формула (172) сохранит свою силу и при любом стремлении z к  . Для этого достаточно показать, что при предельном переходе на контур по нормали стремление интеграла (166) к пределу (168) имеет место равномерно при всех значениях
. Для этого достаточно показать, что при предельном переходе на контур по нормали стремление интеграла (166) к пределу (168) имеет место равномерно при всех значениях  на контуре L Ограничимся рассмотрением окружности
на контуре L Ограничимся рассмотрением окружности  Пока считаем, что
Пока считаем, что  по нормали. В данном случае
по нормали. В данном случае  Нетрудно показать, что если то
Нетрудно показать, что если то  Пользуясь этим, можно написать
Пользуясь этим, можно написать

и модуль интеграла по L будет меньше

На контуре  если z достаточно близка к
если z достаточно близка к  ,
,

где M — наибольшее значение  на L. Полагая
на L. Полагая  получим
получим

и окончательно

Сначала выбирается  так, чтобы первое слагаемое было меньше и затем при таком фиксированном
так, чтобы первое слагаемое было меньше и затем при таком фиксированном  второе слагаемое будет меньше
второе слагаемое будет меньше  если
если  . В эти оценки не входит
. В эти оценки не входит  , и, следовательно, разность (171) стремится к нулю равномерно относительно
, и, следовательно, разность (171) стремится к нулю равномерно относительно  , когда
, когда  по радиусу стремится к окружности. Следовательно, в формуле (172) предельный переход «также имеет место равномерно относительно
по радиусу стремится к окружности. Следовательно, в формуле (172) предельный переход «также имеет место равномерно относительно  . Отсюда следует, между прочим, что и правая часть формулы (172) и интеграл (166) представляют собой непрерывную функцию от
. Отсюда следует, между прочим, что и правая часть формулы (172) и интеграл (166) представляют собой непрерывную функцию от  мы упоминали о том, что эта функция удовлетворяет условию Липшица.
мы упоминали о том, что эта функция удовлетворяет условию Липшица.
Обозначим правую часть формулы (172) через  и положим, что
и положим, что  любым образом. Пусть
любым образом. Пусть  — переменная точка окружности, лежащая на одном радиусе с z. Очевидно, что
— переменная точка окружности, лежащая на одном радиусе с z. Очевидно, что  Пользуясь доказанным выше утверждением о равномерности предельного перехода в (172) при стремлении
Пользуясь доказанным выше утверждением о равномерности предельного перехода в (172) при стремлении  по радиусу к
по радиусу к  , можем утверждать, что при любом заданном положительном
, можем утверждать, что при любом заданном положительном  для всех z, достаточно близких к
для всех z, достаточно близких к  , будем иметь
, будем иметь

С другой стороны, в силу непрерывности  для всех z, достаточно близких к
для всех z, достаточно близких к  , мы имеем
, мы имеем  а потому
а потому

для всех z, достаточно близких к  . Ввиду произвольности
. Ввиду произвольности  это и показывает, что в формуле (172) предельный переход имеет место при любом законе стремления z к
это и показывает, что в формуле (172) предельный переход имеет место при любом законе стремления z к  изнутри, и притом равномерно относительно
изнутри, и притом равномерно относительно  . Иначе говоря, мы можем утверждать, что функция F(z), определяемая интегралом (166) внутри окружности, будет непрерывной вплоть до окружности, причем ее предельные значения на окружности определяются формулой (172). То же самое справедливо при стремлении извне.
. Иначе говоря, мы можем утверждать, что функция F(z), определяемая интегралом (166) внутри окружности, будет непрерывной вплоть до окружности, причем ее предельные значения на окружности определяются формулой (172). То же самое справедливо при стремлении извне.
Это же свойство интеграла типа Коши может быть доказано и для любого замкнутого контура L при указанных в [28] предположениях относительно  . Можно даже допустить, что L имеет конечное число угловых точек. Пусть М — угловая точка L, и положим, что при обходе по L против часовой стрелки направление касательной поворачивается в точке М на угол
. Можно даже допустить, что L имеет конечное число угловых точек. Пусть М — угловая точка L, и положим, что при обходе по L против часовой стрелки направление касательной поворачивается в точке М на угол  где
где 
При этом, как нетрудно видеть, в правой части формулы (161) вместо  мы будем иметь
мы будем иметь  и выражение (168) мы должны заменить в точке М выражением
и выражение (168) мы должны заменить в точке М выражением

причем одновременно надо брать верхние или нижние знаки.
Если мы обозначим через  предельные значения на контуре L функций (166), определенных внутри и вне Z, то доказанную выше теорему можно записать в виде
предельные значения на контуре L функций (166), определенных внутри и вне Z, то доказанную выше теорему можно записать в виде

Совершенно аналогичную теорему можно доказать и для случая незамкнутого контура. Ограничимся рассмотрением конечного отрезка  вещественной оси:
вещественной оси:

Если  тождественно равна единице, то вместо формулы (168) будем иметь
тождественно равна единице, то вместо формулы (168) будем иметь

где мы должны брать то значение логарифма, которое обращается в нуль при  . Если
. Если  лежит внутри отрезка
лежит внутри отрезка  то вместо формулы (161) будем иметь
то вместо формулы (161) будем иметь

где значение логарифма берется вещественным. Повторяя буквально прежнее рассуждение, получим

Функция (176) имеет разные пределы при стремлении z к  сверху или снизу отрезка
сверху или снизу отрезка  а именно:
а именно:

где верхний знак относится к случаю стремления сверху, т. е. от значений с положительной мнимой частью, а нижний знак — к случаю стремления снизу.
При интегрировании от а до b верхняя полуплоскость находится с левой стороны и стремление  к
к  сверху аналогично стремлению изнутри в случае замкнутой кривой. Точно так же стремление
сверху аналогично стремлению изнутри в случае замкнутой кривой. Точно так же стремление  к
к  снизу аналогично стремлению извне в случае замкнутой кривой. Обозначая через
снизу аналогично стремлению извне в случае замкнутой кривой. Обозначая через  предельные значения функции (175) при стремлении
предельные значения функции (175) при стремлении  к
к  сверху и снизу, будем иметь формулы, аналогичные формулам (174):
сверху и снизу, будем иметь формулы, аналогичные формулам (174):

Если  удовлетворяет на отрезке условиям, указанным в конце
удовлетворяет на отрезке условиям, указанным в конце  а вблизи концов имеет вид (160), то для точек z, близких к концам отрезка, имеют место следующие предложения (см. Н. И. Мусхелишвили):
а вблизи концов имеет вид (160), то для точек z, близких к концам отрезка, имеют место следующие предложения (см. Н. И. Мусхелишвили):
1. Если  то
то

где знак  относится к случаю
относится к случаю  и знак
и знак  к случаю
к случаю  есть ограниченная функция, имеющая определенный предел при
есть ограниченная функция, имеющая определенный предел при  Под
Под  подразумевается любая ветвь, однозначная вблизи
подразумевается любая ветвь, однозначная вблизи  на плоскости с разрезом
на плоскости с разрезом 

где знаки выбираются, как и выше,  обозначает ту однозначную вблизи
обозначает ту однозначную вблизи  на плоскости с разрезом
на плоскости с разрезом  ветвь, у которой на верхнем (левом) берегу разреза
ветвь, у которой на верхнем (левом) берегу разреза  равно тому значению
равно тому значению  которое входит в формулу (165). Далее,
которое входит в формулу (165). Далее,  обладает следующими свойствами: если
обладает следующими свойствами: если  то
то  ограничена и имеет определенный предел при
ограничена и имеет определенный предел при  ; если же
; если же  то
то

где  — постоянные, причем
— постоянные, причем  Используя понятие интеграла Лебега, можно исследовать значения интеграла типа Коши для любой суммируемой функции
Используя понятие интеграла Лебега, можно исследовать значения интеграла типа Коши для любой суммируемой функции  )
)  и для широкого класса контуров (см. И. И. Привалов, Интеграл Коши, 1918).
и для широкого класса контуров (см. И. И. Привалов, Интеграл Коши, 1918).
Отметим один частный случай. Если  суть предельные значения на L функции, регулярной внутри замкнутого контура L и непрерывной вплоть до I, причем со
суть предельные значения на L функции, регулярной внутри замкнутого контура L и непрерывной вплоть до I, причем со  удовлетворяет условию Липшица, то
удовлетворяет условию Липшица, то  и первая из формул (169) показывает, что о
и первая из формул (169) показывает, что о  должна быть решением однородного интегрального уравнения второго рода
должна быть решением однородного интегрального уравнения второго рода

Пусть L, как и выше, — простой замкнутый контур. Главное значение интеграла

переводит любую функцию  заданную на L и удовлетворяющую условию Липшица, в некоторую другую функцию
заданную на L и удовлетворяющую условию Липшица, в некоторую другую функцию  определенную на L и также удовлетворяющую условию Липшица.
определенную на L и также удовлетворяющую условию Липшица.
Иначе говорят, что интеграл (179) является преобразованием или оператором над функцией  . К полученной функции
. К полученной функции  мы можем опять применить оператор с ядром Коши. При этом имеет место формула
мы можем опять применить оператор с ядром Коши. При этом имеет место формула

Иначе говоря, в результате двукратного применения преобразования с ядром Коши мы получаем исходную функцию с коэффициентом Для доказательства (180) перепишем первую из формул (174) в виде

Правая часть дает результат применения к функции  линейного преобразования с ядром Коши. К этой правой части опять применимо линейное преобразование с ядром Коши
линейного преобразования с ядром Коши. К этой правой части опять применимо линейное преобразование с ядром Коши

где  лежит на L и интеграл, как и выше, надо понимать в смысле главного значения. Поскольку
лежит на L и интеграл, как и выше, надо понимать в смысле главного значения. Поскольку  дает предельные значения на L функции, регулярной внутри
дает предельные значения на L функции, регулярной внутри  мы должны иметь в силу (178)
мы должны иметь в силу (178)

С другой стороны, в силу (181)

и окончательно интеграл (182) оказывается равным  т. е. мы имеем формулу (180).
т. е. мы имеем формулу (180).
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К ВОСЬМОМУ ИЗДАНИЮ
- 1. Функции комплексного переменного.
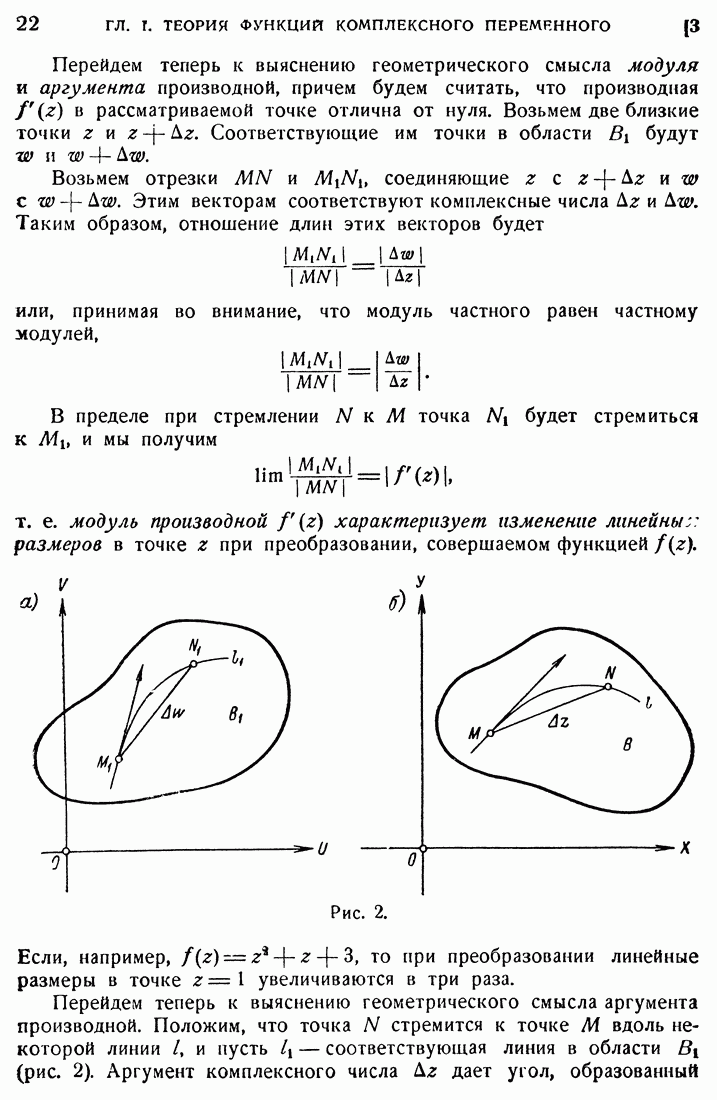
- 2. Производная.
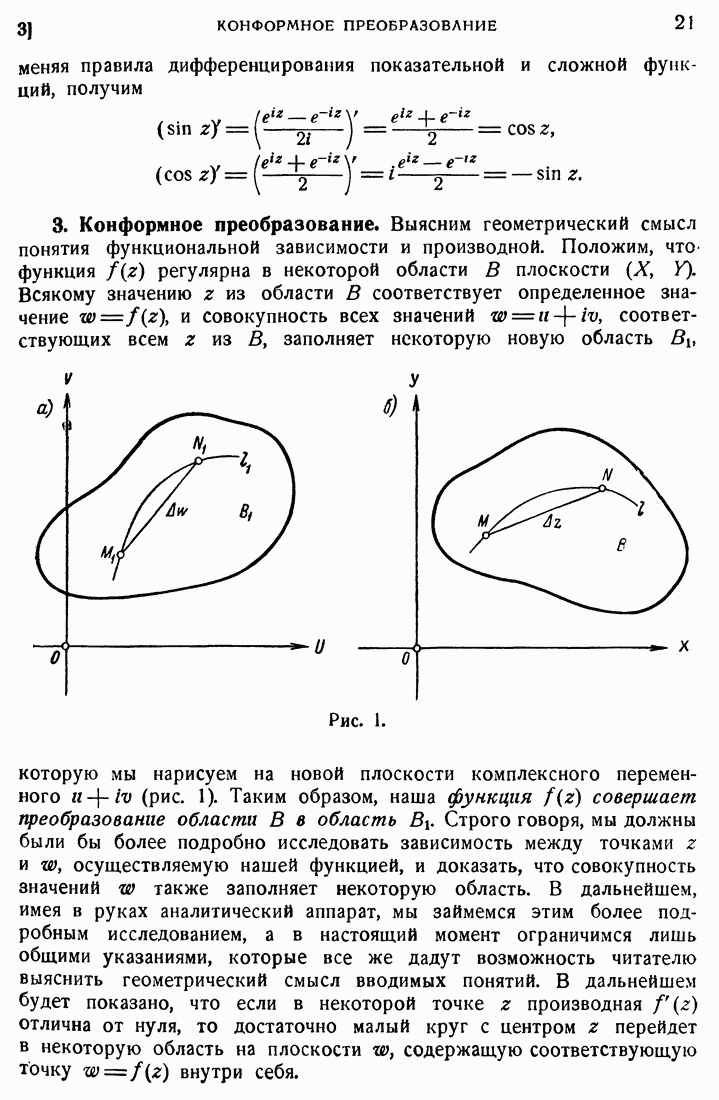
- 3. Конформное преобразование.
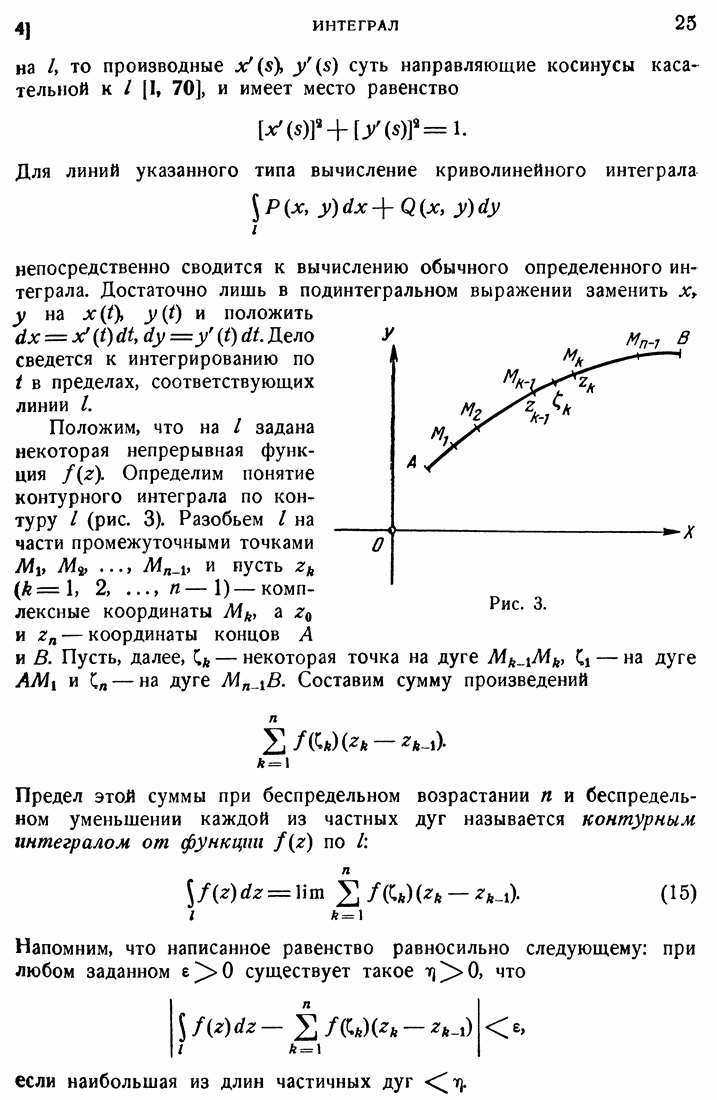
- 4. Интеграл.
- 5. Теорема Коши.
- 6. Основная формула интегрального исчисления.
- 7. Формула Коши.
- 8. Интегралы типа Коши.
- 9. Следствия формулы Коши.
- 10. Изолированные особые точки.
- 11. Бесконечные ряды с комплексными членами.
- 12. Теорема Вейерштрасса.
- 13. Степенные ряды.
- 14. Ряд Тейлора.
- 15. Ряд Лорана.
- 16. Примеры.
- 17. Изолированные особые точки. Бесконечно далекая точка.
- 18. Аналитическое продолжение.
- 19. Примеры многозначных функций.
- 20. Особые точки аналитических функций и римановы поверхности.
- 21. Теорема вычетов.
- 22. Теоремы о числе корней.
- 23. Обращение степенного ряда.
- 24. Принцип симметрии.
- 25. Ряд Тейлора на окружности круга сходимости.
- 26. Дополнительные сведения о формуле Коши.
- 27. Главное значение интеграла.
- 28. Главное значение интеграла (продолжение).
- 29. Интегралы типа Коши.
- 30. Интегралы типа Коши (продолжение).
- ГЛАВА II. КОНФОРМНОЕ ПРЕОБРАЗОВАНИЕ И ПЛОСКОЕ ПОЛЕ
- 31. Конформное преобразование.
- 32. Линейное преобразование.
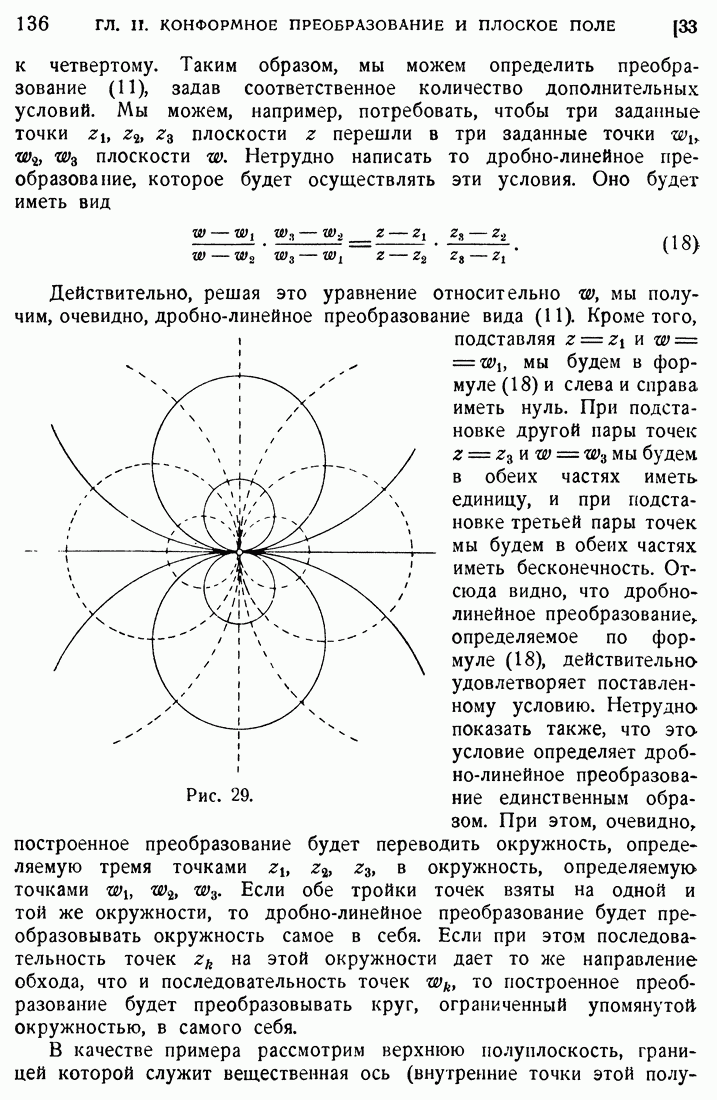
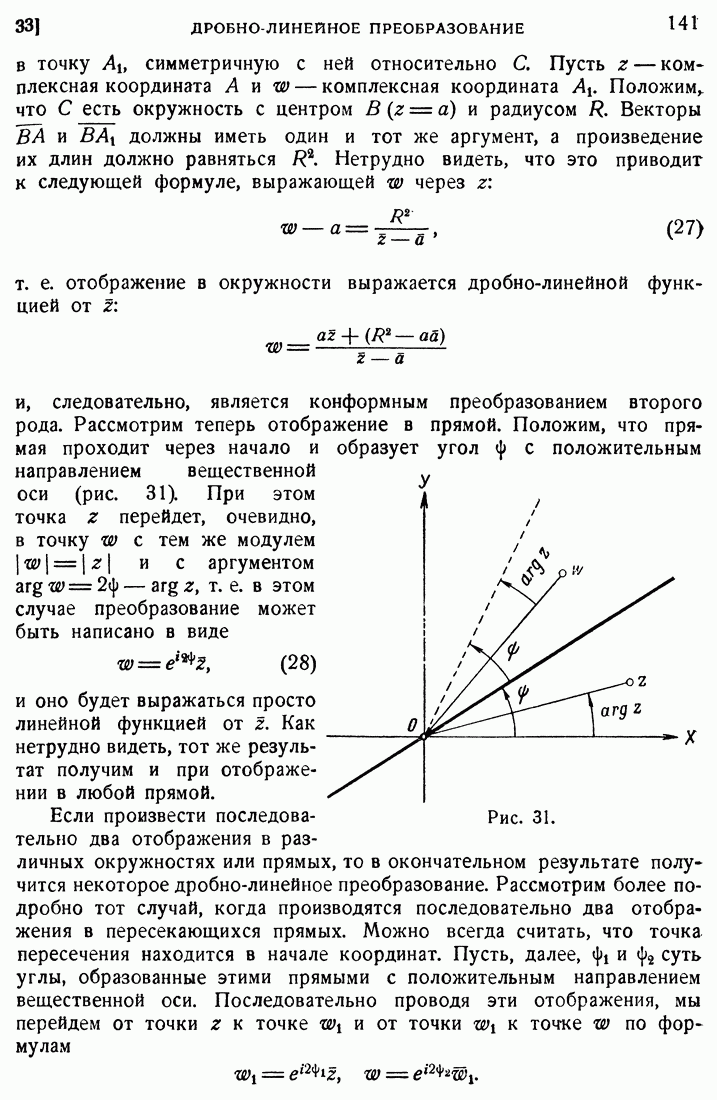
- 33. Дробно-линейное преобразование.
- 34. Функция w = z^2.
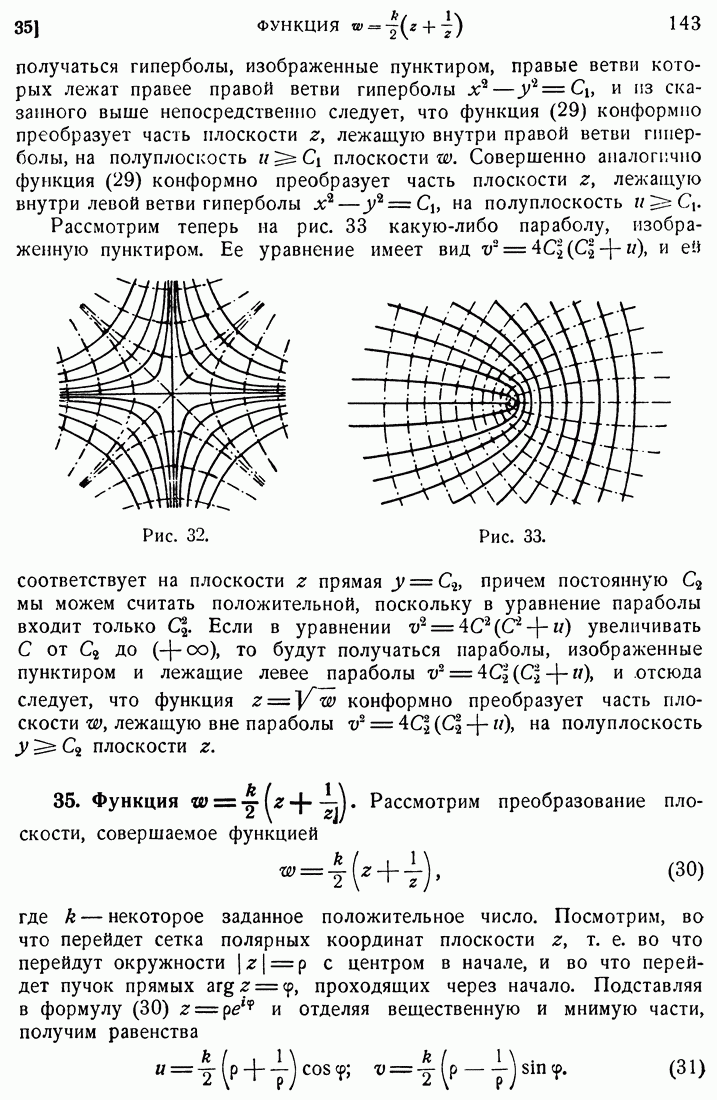
- 35. Функция …
- 36. Двуугольник и полоса.
- 37. Основная теорема.
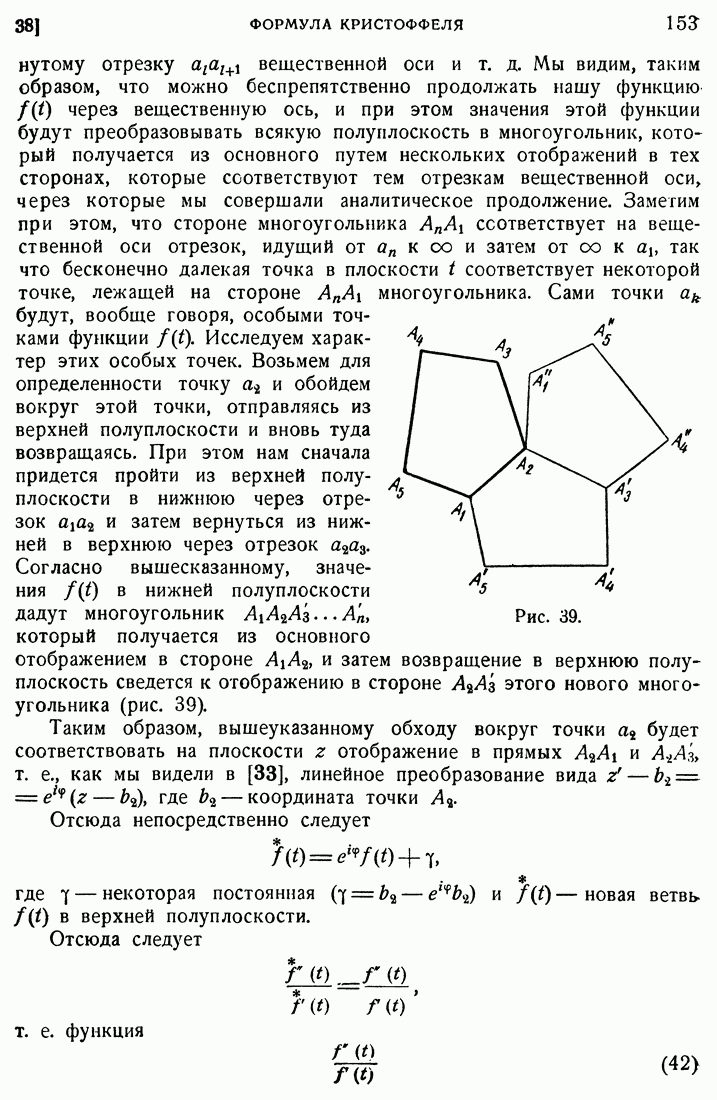
- 38. Формула Кристоффеля.
- 39. Частные случаи.
- 40. Случай внешности многоугольника.
- 41. Минимальное свойство преобразования на круг.
- 42. Способ сопряженных тригонометрических рядов.
- 43. Плоское установившееся течение жидкости.
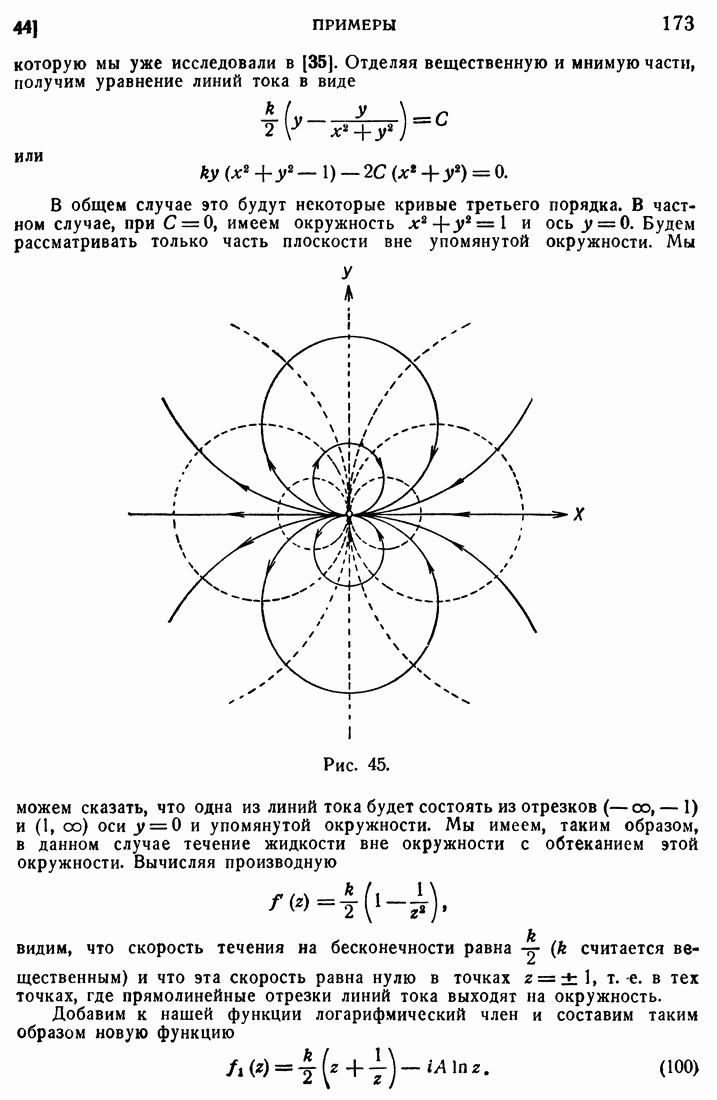
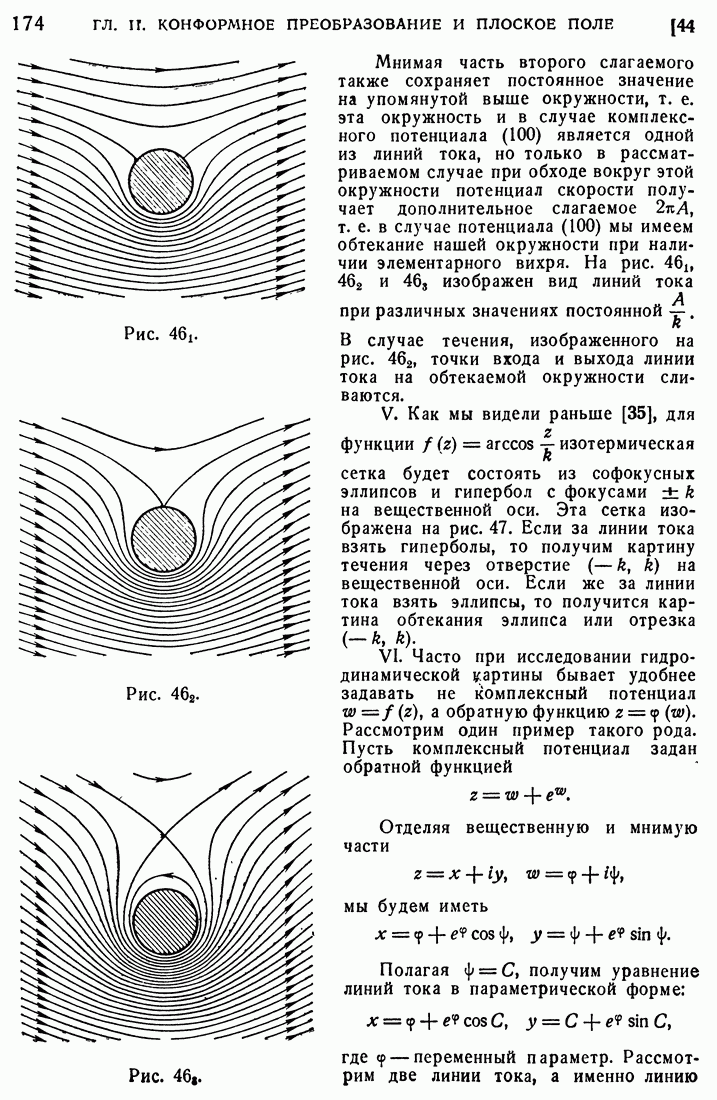
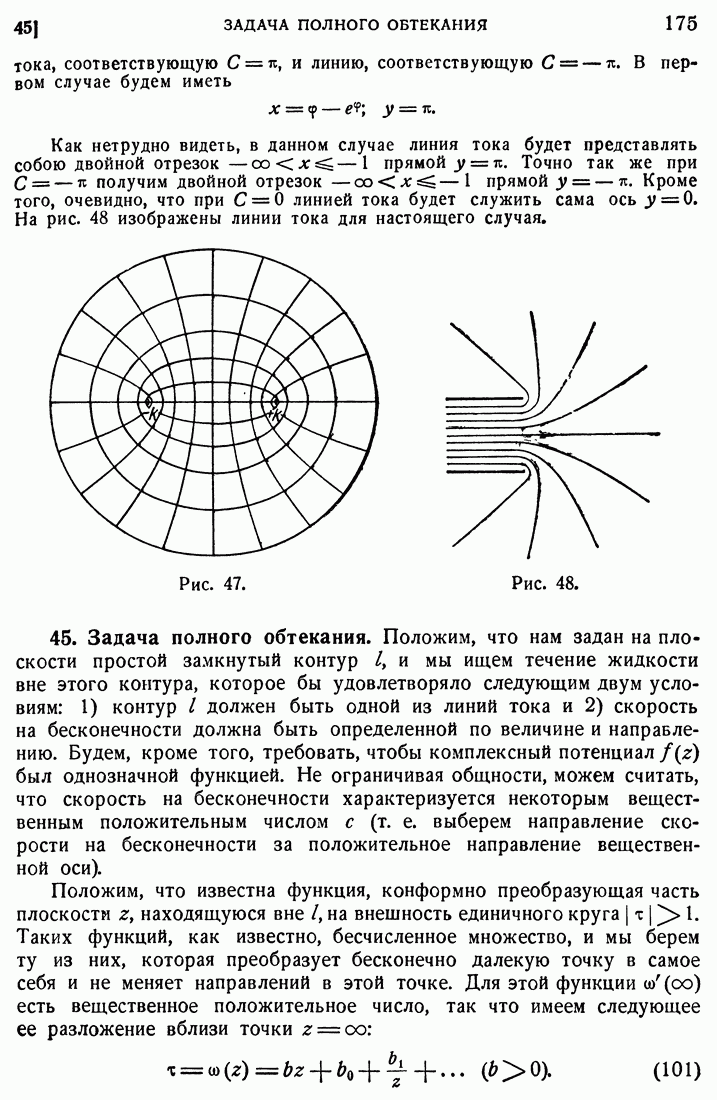
- 44. Примеры.
- 45. Задача полного обтекания.
- 46. Формула Н. Е. Жуковского.
- 47. Плоская электростатическая задача.
- 48. Формула Шварца.
- 49. Ядро ctg((s-t)/2).
- 50. Предельные задачи.
- 51. Бигармоническое уравнение.
- 52. Волновое уравнение и аналитические функции.
- 53. Основная теорема.
- 54. Дифракция плоской волны.
- 55. Отражение упругих волн от прямолинейной границы.
- ГЛАВА III. ПРИМЕНЕНИЕ ТЕОРИИ ВЫЧЕТОВ, ЦЕЛЫЕ И ДРОБНЫЕ ФУНКЦИИ
- 56. Интеграл Френеля.
- 57. Интегрирование выражений с тригонометрическими функциями.
- 58. Интегрирование рациональной дроби.
- 59. Некоторые новые типы интегралов с тригонометрическими функциями.
- 60. Лемма Жордана.
- 61. Представление некоторых функций контурными интегралами.
- 62. Примеры интегралов от многозначных функций.
- 63. Интегрирование системы линейных уравнений с постоянными коэффициентами.
- 64. Разложение дробной функции на простейшие дроби.
- 66. Построение мероморфной функции.
- 67. Целые функции.
- 68. Бесконечные произведения.
- 69. Построение целой функции по ее корням.
- 70. Интегралы, зависящие от параметра.
- 71. Эйлеров интеграл второго рода.
- 72. Эйлеров интеграл первого рода.
- 73. Бесконечное произведение для функции …
- 74. Представление Г(z) контурным интегралом.
- 75. Формула Стирлинга.
- 76. Формула суммирования Эйлера.
- 77. Числа Бернулли.
- 78. Метод скорейшего спуска.
- 79. Асимптотическое разложение интеграла.
- 80. Примеры.
- 81. Метод стационарной фазы.
- ГЛАВА IV. АНАЛИТИЧЕСКИЕ ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ И ФУНКЦИИ МАТРИЦ
- 82. Регулярные функции многих переменных.
- 83. Двойной интеграл и формула Коши.
- 84. Степенные ряды.
- 85. Аналитическое продолжение.
- 86. Функции матриц. Предварительные понятия.
- 87. Степенные ряды от одной матрицы.
- 88. Умножение степенных рядов. Обращение степенного ряда.
- 89. Дальнейшее исследование сходимости.
- 90. Интерполяционные полиномы.
- 91. Тождество Кейли. Формула Сильвестра.
- 92. Определение функций одной матрицы формулой Коши.
- 93. Аналитическое продолжение.
- 94. Логарифм матриц.
- 95. Обращение целой функции от матрицы в случае матриц второго порядка.
- 96. Системы линейных уравнений с постоянными коэффициентами.
- 97. Функции нескольких матриц.
- ГЛАВА V. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
- 98. Разложение решения в степенной ряд.
- 99. Аналитическое продолжение решения.
- 100. Окрестность особой точки.
- 101. Регулярная особая точка.
- 102. Уравнения класса Фукса.
- 103. Уравнение Гаусса.
- 104. Гипергеометрический ряд.
- 105. Полиномы Лежандра.
- 106. Полиномы Якоби.
- 107. Конформное преобразование и уравнение Гаусса.
- 108. Преобразование Лапласа.
- 109. Различный выбор решений.
- 110. Уравнение Бесселя.
- 111. Функции Ханкеля и интегральное представление решений уравнения Бесселя.
- 112. Асимптотические разложения.
- 113. Асимптотические разложения решений, полученных преобразованием Лапласа.
- 114. Асимптотические разложения решений уравнения Бесселя.
- 115. Вырождение уравнения Гаусса.
- 116. Формальные ряды в окрестности иррегулярной особой точки.
- 117. Построение асимптотических разложений методом после довательных приближений.
- 118. Функции Эйри.
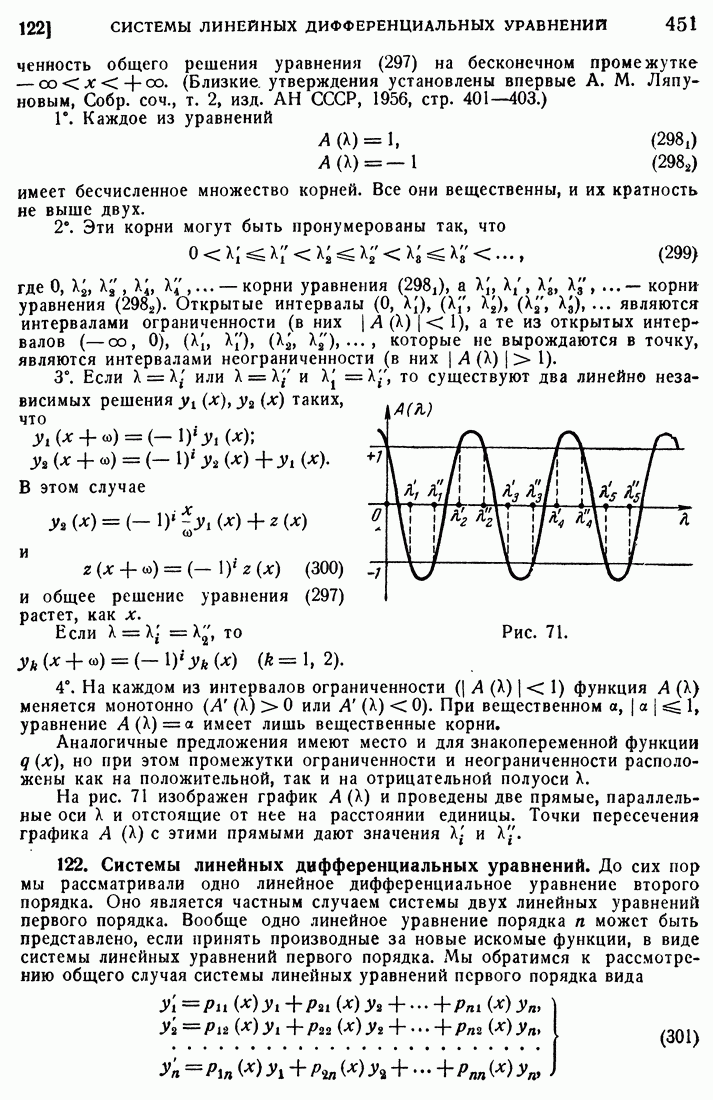
- 119. Асимптотика при большом значении параметра.
- 120. Уравнения с периодическими коэффициентами.
- 121. Условия устойчивости и неустойчивости для уравнения Хилла.
- 122. Системы линейных дифференциальных уравнений.
- 123. Регулярная особая точка.
- 124. Регулярные системы.
- 125. Представление решения в окрестности особой точки.
- 126. Канонические решения.
- 127. Связь с регулярными решениями типа Фукса.
- 128. Случай любых Us.
- 129. Формальные разложения в окрестности иррегулярной особой точки.
- ГЛАВА VI. СПЕЦИАЛЬНЫЕ ФУНКЦИИ
- 130. Определение сферических функций.
- 131. Явные выражения сферических функций.
- 132. Свойство ортогональности.
- 133. Полиномы Лежандра.
- 134. Разложение по сферическим функциям.
- 135. Доказательство сходимости.
- 136. Связь сферических функций с предельными задачами.
- 137. Задачи Дирихле и Неймана.
- 138. Потенциал объемных масс.
- 139. Потенциал сферического слоя.
- 140. Электрон в центральном поле.
- 141. Шаровые функции и линейные представления группы вращения.
- 142. Функция Лежандра.
- 143. Функция Лежандра второго рода.
- § 2. ФУНКЦИИ БЕССЕЛЯ
- 144. Определение функций Бесселя.
- 145. Соотношения между функциями Бесселя.
- 146. Ортогональность функций Бесселя и их корни.
- 147. Производящая функция и интегральное представление.
- 148. Формула Фурье — Бесселя.
- 150. Разложение функций Неймана с целым значком.
- 151. Случай чисто мнимого аргумента.
- 152. Новые интегральные представления.
- 153. Асимптотические представления.
- 154. Функции Бесселя и уравнение Лапласа.
- 155. Волновое уравнение в цилиндрических координатах.
- 156. Волновое уравнение в сферических координатах.
- § 3. ПОЛИНОМЫ ЭРМИТА И ЛАГЕРРА
- 157. Линейный осциллятор и полиномы Эрмита.
- 158. Свойство ортогональности.
- 159. Производящая функция.
- 160. Параболические координаты и функции Эрмита.
- 161. Полиномы Лагерра.
- 162. Связь полиномов Эрмита и Лагерра.
- 163. Асимптотическое выражение полиномов Эрмита.
- 164. Асимптотическое выражение полиномов Лежандра.
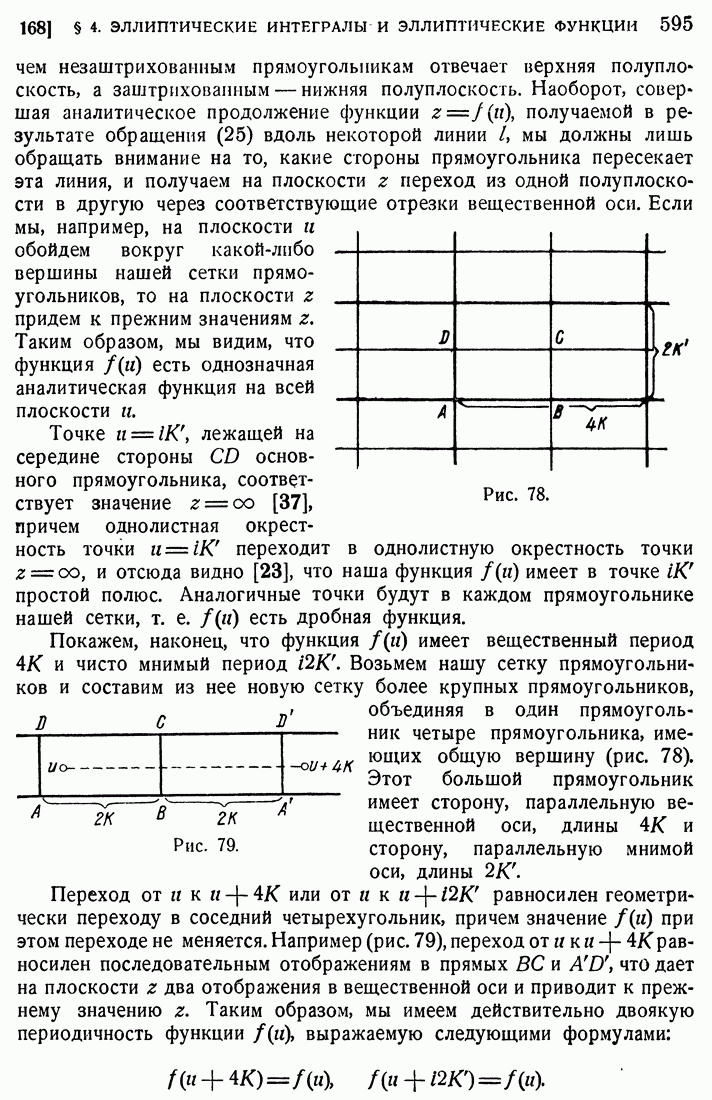
- § 4. ЭЛЛИПТИЧЕСКИЕ ИНТЕГРАЛЫ И ЭЛЛИПТИЧЕСКИЕ ФУНКЦИИ
- 165. Приведение эллиптических интегралов к нормальному виду.
- 166. Приведение интегралов к тригонометрической форме.
- 167. Примеры.
- 168. Обращение эллиптического интеграла.
- 169. Общие свойства эллиптических функций.
- 170. Основная лемма.
- 171. Функции Вейерштрасса.
- 172. Дифференциальное уравнение для …
- 173. Функции …
- 174. Разложение целой периодической функции.
- 175. Новые обозначения.
- 176. Функция …
- 177. Функции …
- 178. Свойства функций тэта.
- 179. Выражение чисел … через …
- 180. Эллиптические функции Якоби.
- 181. Основные свойства функций Якоби.
- 182. Дифференциальные уравнения для функций Якоби.
- 183. Формулы сложения.
- 184. Связь функций p(u) и sn(u).
- 185. Эллиптические координаты.
- 186. Введение эллиптических функций.
- 187. Уравнение Лямэ.
- 188. Простой маятник.
- 189. Пример конформного преобразования.
- ДОБАВЛЕНИЕ. ПРИВЕДЕНИЕ МАТРИЦ К КАНОНИЧЕСКОЙ ФОРМЕ
- 191. Случай простых корней.
- 192. Первый этап преобразований в случае кратных корней.
- 193. Приведение к канонической форме.
- 194. Определение структуры канонической формы.
- 196. Пример.