| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
124. Регулярные системы.
Рассмотрим систему уравнений простейшего вида, коэффициенты которых суть рациональные функции, имеющие полюсы первого порядка на конечном расстоянии и равные нулю на бесконечности. Пусть  есть полюс первого порядка некоторых коэффициентов. Каждый из коэффициентов
есть полюс первого порядка некоторых коэффициентов. Каждый из коэффициентов  имеет в этом полюсе некоторый вычет и эти вычеты образуют некоторую квадратную таблицу
имеет в этом полюсе некоторый вычет и эти вычеты образуют некоторую квадратную таблицу  Мы можем, таким образом, записать нашу систему в следующем виде:
Мы можем, таким образом, записать нашу систему в следующем виде:

где  - матрицы, состоящие из постоянных элементов. Будем искать такое решение системы (318), которое в некоторой точке
- матрицы, состоящие из постоянных элементов. Будем искать такое решение системы (318), которое в некоторой точке  отличной от точек
отличной от точек  обращается в единичную матрицу, и обозначим такое решение символом
обращается в единичную матрицу, и обозначим такое решение символом

Принимая во внимание это начальное условие, можно переписать систему в следующей интегральной форме:

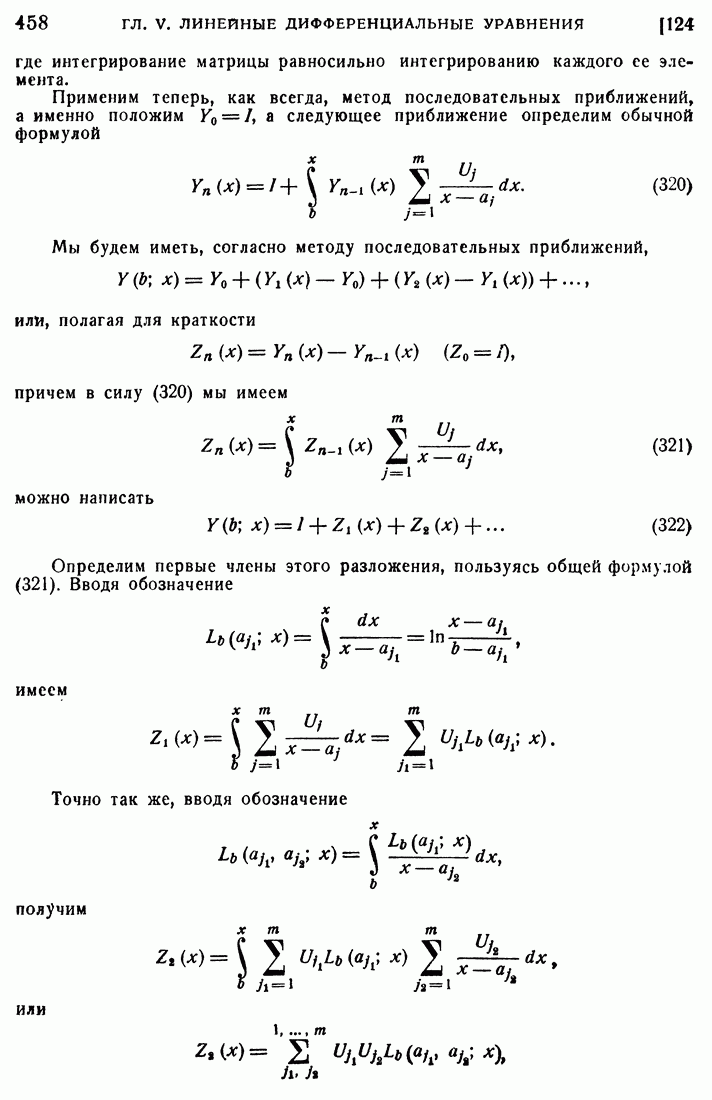
где интегрирование матрицы равносильно интегрированию каждого ее элемента.
Применим теперь, как всегда, метод последовательных приближений, а именно положим  а следующее приближение определим обычной формулой
а следующее приближение определим обычной формулой

Мы будем иметь, согласно методу последовательных приближений,

или, полагая для краткости

причем в силу (320) мы имеем

можно написать

Определим первые члены этого разложения, пользуясь общей формулой (321). Вводя обозначение

имеем

Точно так же, вводя обозначение

получим

или

где суммирование распространяется на значки  и независимо от
и независимо от  до
до  . Продолжая так же и дальше и вводя формулы
. Продолжая так же и дальше и вводя формулы

определяющие последовательно коэффициенты  получим
получим

где суммирование распространяется на все значки, указанные под знаком суммы, причем каждый значок, независимо от других, пробегает целые значения от 1 до  . Окончательно в силу (322) будем иметь следующее представление для нашего решения в виде степенного ряда от матриц
. Окончательно в силу (322) будем иметь следующее представление для нашего решения в виде степенного ряда от матриц 

причем коэффициенты этого ряда определяются рекуррентными соотношениями (323).
Решение  может быть аналитически продолжено по любому пути, не проходящему через особые точки
может быть аналитически продолжено по любому пути, не проходящему через особые точки  и ряд (324) дает это решение во всей области его существования, т. е. при любом аналитическом продолжении. Действительно, покажем сначала, что ряд (324) сходится при любом аналитическом продолжении коэффициентов
и ряд (324) дает это решение во всей области его существования, т. е. при любом аналитическом продолжении. Действительно, покажем сначала, что ряд (324) сходится при любом аналитическом продолжении коэффициентов  Пусть
Пусть  некоторая кривая, выходящая из точки
некоторая кривая, выходящая из точки  и отстоящая на конечном расстоянии от точек
и отстоящая на конечном расстоянии от точек  Пусть b — кратчайшее расстояние от точек а до кривой
Пусть b — кратчайшее расстояние от точек а до кривой  и s — длина дуги на этой кривой, отсчитываемая от точки b. Применяя обычную оценку интеграла по контуру
и s — длина дуги на этой кривой, отсчитываемая от точки b. Применяя обычную оценку интеграла по контуру  мы получаем следующую оценку для коэффициентов ряда (324) на l [4]:
мы получаем следующую оценку для коэффициентов ряда (324) на l [4]:

откуда

и вообще на l

Но степенной ряд

сходится при всяком  и, следовательно, мы можем утверждать, что ряд (324) сходится абсолютно для любых матриц
и, следовательно, мы можем утверждать, что ряд (324) сходится абсолютно для любых матриц  и при любом аналитическом продолжении его коэффициентов [99]. Из предыдущих оценок вытекает также, что сходимость будет и равномерной во всякой конечной области (вообще говоря, многолистной), отстоящей от точек
и при любом аналитическом продолжении его коэффициентов [99]. Из предыдущих оценок вытекает также, что сходимость будет и равномерной во всякой конечной области (вообще говоря, многолистной), отстоящей от точек  на расстоянии большем нуля. Наконец, дифференцируя ряд (324) почленно по
на расстоянии большем нуля. Наконец, дифференцируя ряд (324) почленно по  нетрудно убедиться, что он удовлетворяет и системе. Действительно, мы можем переписать его следующим образом, выделяя одно из суммирований:
нетрудно убедиться, что он удовлетворяет и системе. Действительно, мы можем переписать его следующим образом, выделяя одно из суммирований:

Дифференцируя по  и принимая во внимание, что в силу определения
и принимая во внимание, что в силу определения

и

получим в результате дифференцирования

или

т. е.

Наконец, непосредственно ясно, что построенное решение обращается в единичную матрицу при  так как в силу определения коэффициенты ряда обращаются в нуль при
так как в силу определения коэффициенты ряда обращаются в нуль при  . Предыдущие рассуждения приводят нас к следующей теореме:
. Предыдущие рассуждения приводят нас к следующей теореме:
Теорема. Решение системы (318), которое обращается в единичную матрицу при  определяется рядом (324) во всей области его существования по отношению к
определяется рядом (324) во всей области его существования по отношению к  и при любом выборе матриц
и при любом выборе матриц 
Если на плоскости  проведем из точек
проведем из точек  на бесконечность разрезы
на бесконечность разрезы  так, чтобы они не пересекали друг друга, то на разрезанной таким образом плоскости, которая будет односвязной областью, решение (324) будет одно значной функцией
так, чтобы они не пересекали друг друга, то на разрезанной таким образом плоскости, которая будет односвязной областью, решение (324) будет одно значной функцией  но на противоположных берегах разреза оно будет иметь различные значения, а именно: в результате обхода вокруг каждой точки
но на противоположных берегах разреза оно будет иметь различные значения, а именно: в результате обхода вокруг каждой точки  в положительном направлении наше решение будет умножаться слева на некоторую постоянную матрицу
в положительном направлении наше решение будет умножаться слева на некоторую постоянную матрицу  которую мы назвали выше интегральной
которую мы назвали выше интегральной
матрицей, соответствующей особой точке а. Выведем теперь выражения для интегральных матриц  через матрицы
через матрицы  входящие в коэффициенты заданной системы. В исходной точке
входящие в коэффициенты заданной системы. В исходной точке  наше решение имеет значение
наше решение имеет значение  т. е. обращается в единичную матрицу, и, следовательно, чтобы получить интегральную матрицу
т. е. обращается в единичную матрицу, и, следовательно, чтобы получить интегральную матрицу  нам надо определить значение нашего решения, которое получится при аналитическом продолжении вдоль замкнутого контура
нам надо определить значение нашего решения, которое получится при аналитическом продолжении вдоль замкнутого контура  обходящего вокруг точки
обходящего вокруг точки  и возвращающегося в точку b.
и возвращающегося в точку b.
Это значение может быть получено непосредственно по формуле (324), причем надо только в формулах (323) производить интегрирование по вышеуказанному замкнутому контуру  и при этом, конечно, полученные коэффициенты не будут уже зависеть от
и при этом, конечно, полученные коэффициенты не будут уже зависеть от 
Введем для них следующие обозначения:

и

При этом мы будем иметь представление  в виде степенного ряда от матриц
в виде степенного ряда от матриц  абсолютно сходящегося при любом выборе этих матриц:
абсолютно сходящегося при любом выборе этих матриц:

Теорема. Интегральные матрацы  суть целые функции матриц
суть целые функции матриц  определяемые рядом (327), коэффициенты которого определяются формулами (325) и (326).
определяемые рядом (327), коэффициенты которого определяются формулами (325) и (326).
Вместо формул (326) можно доказать следующие формулы, связывающие величины  для соседних значений т.
для соседних значений т.

Доказательство этих формул мы приводить не будем.
Если совершим аналитическое продолжение построенного решения по какому-либо контуру, выходящему из некоторой точки  и возвращающемуся в эту же точку, то такой замкнутый контур в смысле аналитического продолжения равносилен нескольким обходам вокруг точек
и возвращающемуся в эту же точку, то такой замкнутый контур в смысле аналитического продолжения равносилен нескольким обходам вокруг точек  в положительном или отрицательном направлении. Следовательно, при возвращении в точку
в положительном или отрицательном направлении. Следовательно, при возвращении в точку  наше решение умножится слева на постоянную матрицу, которая представляется в виде произведения множителей
наше решение умножится слева на постоянную матрицу, которая представляется в виде произведения множителей  или
или  . В этом смысле говорят, что интегральные матрицы
. В этом смысле говорят, что интегральные матрицы  образуют группу уравнения (318).
образуют группу уравнения (318).
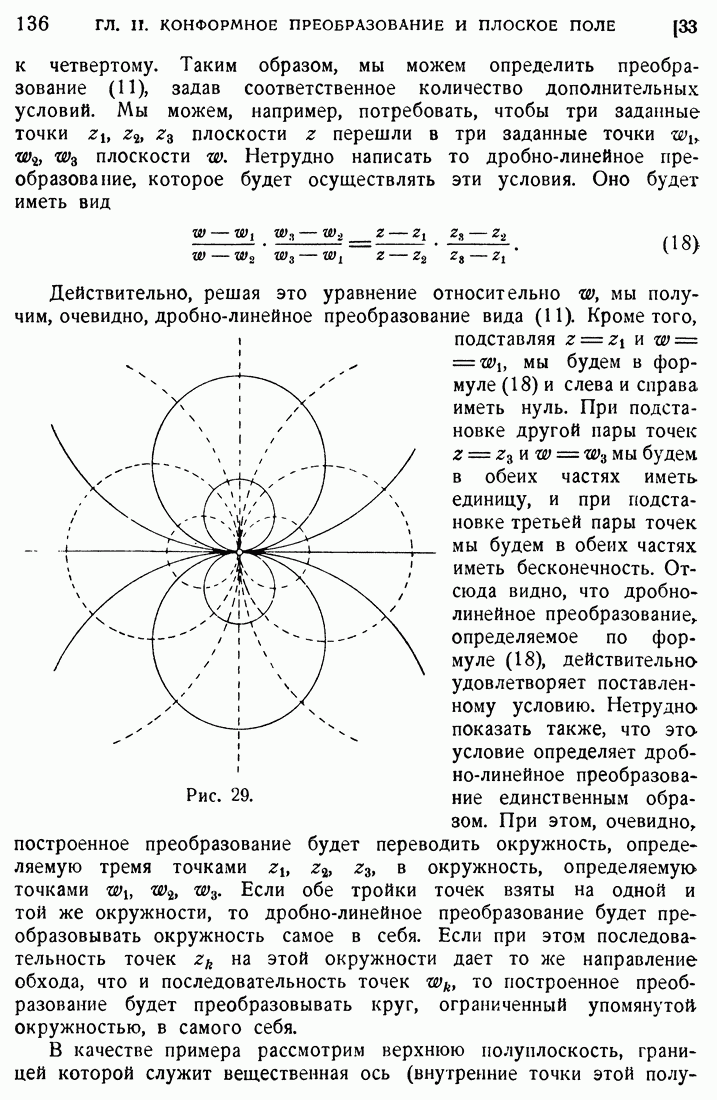
Разъясним сказанное на простом примере. На рис. 72 отмечены особые точки  и сплошной линией указан контур аналитического продолжения. Пунктирные линии сводят этот контур к равносильному в отношении аналитического продолжения контуру, состоящему из ряда обходов вокруг точек
и сплошной линией указан контур аналитического продолжения. Пунктирные линии сводят этот контур к равносильному в отношении аналитического продолжения контуру, состоящему из ряда обходов вокруг точек  причем взято
причем взято 
Первый обход относится к точке  и в результате этого обхода мы придем в точку b с решением
и в результате этого обхода мы придем в точку b с решением  Последующий обход относится к точке
Последующий обход относится к точке  и в результате этого обхода постоянная матрица
и в результате этого обхода постоянная матрица  останется без изменения, а матрица
останется без изменения, а матрица  умножится слева на 1/8, т. е. после второго обхода мы придем в точку b со следующим решением
умножится слева на 1/8, т. е. после второго обхода мы придем в точку b со следующим решением  и, наконец, в результате третьего обхода мы вернемся окончательно в точку b с решением
и, наконец, в результате третьего обхода мы вернемся окончательно в точку b с решением


Рис. 72.
Любое решение  системы (318) отличается от решения
системы (318) отличается от решения  на постоянную матрицу
на постоянную матрицу

и его интегральные матрицы будут, как известно [122],

Рассмотрим теперь матрицу  которая является обратной матрицей для
которая является обратной матрицей для  Эта матрица, как мы видели раньше, удовлетворяет системе линейных уравнений
Эта матрица, как мы видели раньше, удовлетворяет системе линейных уравнений

Применяя к этой системе уравнений метод последовательных приближений, мы получим следующее представление этой матрицы в виде степенного ряда от матриц 

где коэффициенты определяются  формулам
формулам

и

Разложение (329) сходится абсолютно для любых матриц  и при любом аналитическом продолжении относительно переменной
и при любом аналитическом продолжении относительно переменной  . Эти результаты получаются совершенно так же, как и выше. Принимая во внимание, что
. Эти результаты получаются совершенно так же, как и выше. Принимая во внимание, что

мы видим, что матрица  при обходе вокруг особой точки
при обходе вокруг особой точки  помножается справа на матрицу
помножается справа на матрицу  и таким образом можно получить представление
и таким образом можно получить представление  в виде степенного ряда от матриц
в виде степенного ряда от матриц  пользуясь рядом (329) и
пользуясь рядом (329) и
совершая аналитическое продолжение его коэффициентов по замкнутому контуру  обходящему вокруг особой точки
обходящему вокруг особой точки  . Это даст нам ряд вида
. Это даст нам ряд вида

где коэффициенты определяются последовательно по формулам

Отмстим особо один частный случай, когда систему (318) можно проинтегрировать в конечном виде, а именно предположим, что матрицы  попарно коммутируют, т. е. для любых значков
попарно коммутируют, т. е. для любых значков  имеем
имеем

Покажем, что в этом случае решение  системы может быть записано в конечном виде следующим образом:
системы может быть записано в конечном виде следующим образом:

Нетрудно видеть, что написанная функция обращается в единичную матрицу при  . Проверим, что она удовлетворяет и системе уравнений. Дифференцируя по обычному правилу дифференцирования произведения и принимая во внимание, что
. Проверим, что она удовлетворяет и системе уравнений. Дифференцируя по обычному правилу дифференцирования произведения и принимая во внимание, что

получим

Раз матрица  коммутирует с
коммутирует с  , то она коммутирует и с любой функцией
, то она коммутирует и с любой функцией  представляемой степенным рядом от
представляемой степенным рядом от  . Мы можем поэтому написать предыдущую формулу следующим образом:
. Мы можем поэтому написать предыдущую формулу следующим образом:

т. e. матрица (334) действительно удовлетворяет системе. Формула (334) может быть получена из системы, если мы в этой системе совершим чисто формально разделение переменных, не обращая внимания на то, что мы имеем дело с матрицами, а не с численными переменными. В данном случае
это оказывается возможным вследствие того, что матрицы  попарно коммутируют. Правая часть формулы (334) представляет собой просуммированный ряд (324) в предположении, что матрицы
попарно коммутируют. Правая часть формулы (334) представляет собой просуммированный ряд (324) в предположении, что матрицы  попарно коммутируют. Из формулы (334) вытекает, между прочим, что в рассматриваемом случае при обходе точки
попарно коммутируют. Из формулы (334) вытекает, между прочим, что в рассматриваемом случае при обходе точки  матрица
матрица  получает слева постоянный множитель
получает слева постоянный множитель

Это становится ясно, если написать формулу

и воспользоваться известной многозначностью логарифма.
Отметим еще, что в формуле (335) порядок множителей справа не играет роли, так как оба множителя содержат только одну матрицу  , а потому коммутируют.
, а потому коммутируют.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К ВОСЬМОМУ ИЗДАНИЮ
- 1. Функции комплексного переменного.
- 2. Производная.
- 3. Конформное преобразование.
- 4. Интеграл.
- 5. Теорема Коши.
- 6. Основная формула интегрального исчисления.
- 7. Формула Коши.
- 8. Интегралы типа Коши.
- 9. Следствия формулы Коши.
- 10. Изолированные особые точки.
- 11. Бесконечные ряды с комплексными членами.
- 12. Теорема Вейерштрасса.
- 13. Степенные ряды.
- 14. Ряд Тейлора.
- 15. Ряд Лорана.
- 16. Примеры.
- 17. Изолированные особые точки. Бесконечно далекая точка.
- 18. Аналитическое продолжение.
- 19. Примеры многозначных функций.
- 20. Особые точки аналитических функций и римановы поверхности.
- 21. Теорема вычетов.
- 22. Теоремы о числе корней.
- 23. Обращение степенного ряда.
- 24. Принцип симметрии.
- 25. Ряд Тейлора на окружности круга сходимости.
- 26. Дополнительные сведения о формуле Коши.
- 27. Главное значение интеграла.
- 28. Главное значение интеграла (продолжение).
- 29. Интегралы типа Коши.
- 30. Интегралы типа Коши (продолжение).
- ГЛАВА II. КОНФОРМНОЕ ПРЕОБРАЗОВАНИЕ И ПЛОСКОЕ ПОЛЕ
- 31. Конформное преобразование.
- 32. Линейное преобразование.
- 33. Дробно-линейное преобразование.
- 34. Функция w = z^2.
- 35. Функция …
- 36. Двуугольник и полоса.
- 37. Основная теорема.
- 38. Формула Кристоффеля.
- 39. Частные случаи.
- 40. Случай внешности многоугольника.
- 41. Минимальное свойство преобразования на круг.
- 42. Способ сопряженных тригонометрических рядов.
- 43. Плоское установившееся течение жидкости.
- 44. Примеры.
- 45. Задача полного обтекания.
- 46. Формула Н. Е. Жуковского.
- 47. Плоская электростатическая задача.
- 48. Формула Шварца.
- 49. Ядро ctg((s-t)/2).
- 50. Предельные задачи.
- 51. Бигармоническое уравнение.
- 52. Волновое уравнение и аналитические функции.
- 53. Основная теорема.
- 54. Дифракция плоской волны.
- 55. Отражение упругих волн от прямолинейной границы.
- ГЛАВА III. ПРИМЕНЕНИЕ ТЕОРИИ ВЫЧЕТОВ, ЦЕЛЫЕ И ДРОБНЫЕ ФУНКЦИИ
- 56. Интеграл Френеля.
- 57. Интегрирование выражений с тригонометрическими функциями.
- 58. Интегрирование рациональной дроби.
- 59. Некоторые новые типы интегралов с тригонометрическими функциями.
- 60. Лемма Жордана.
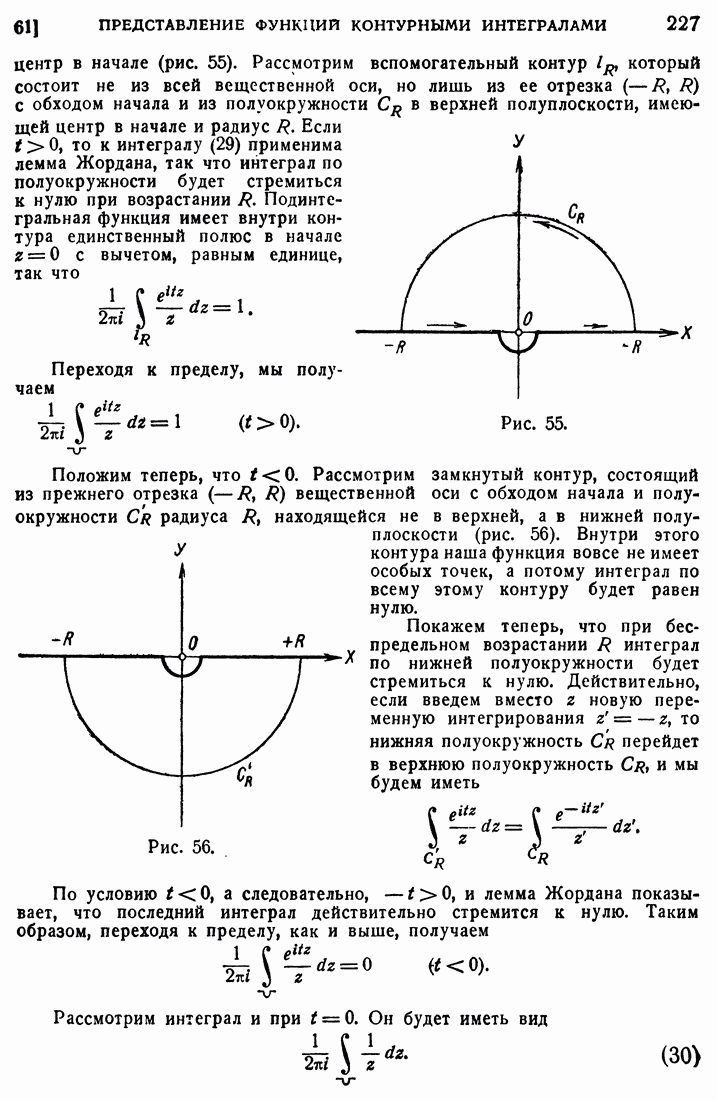
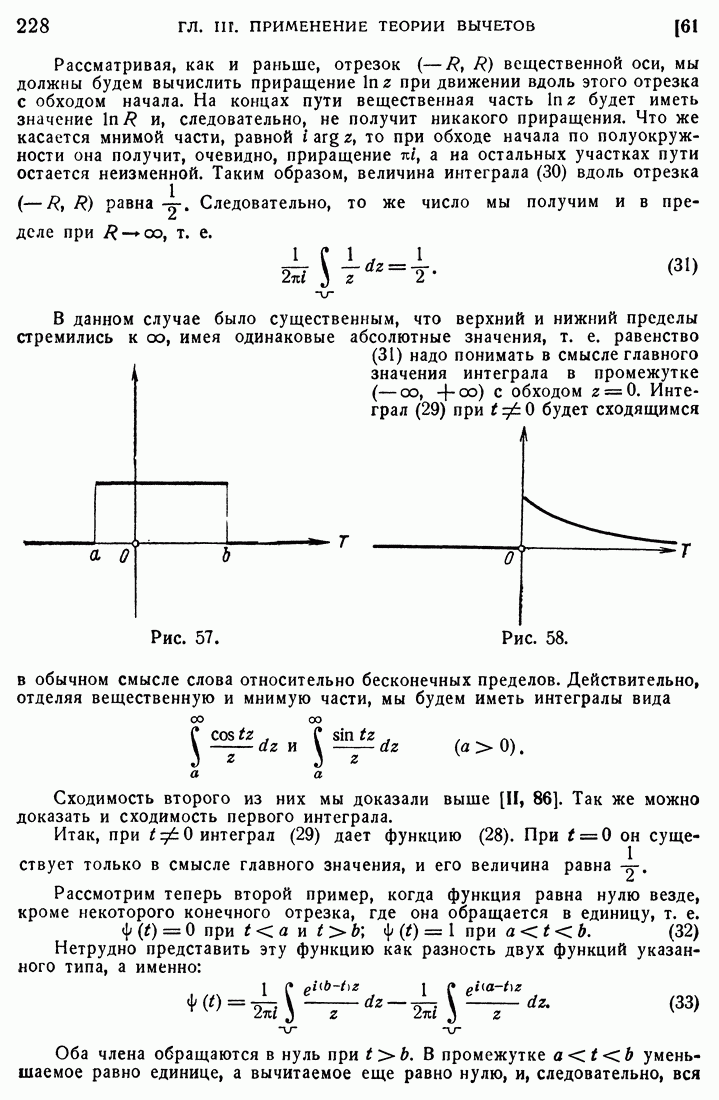
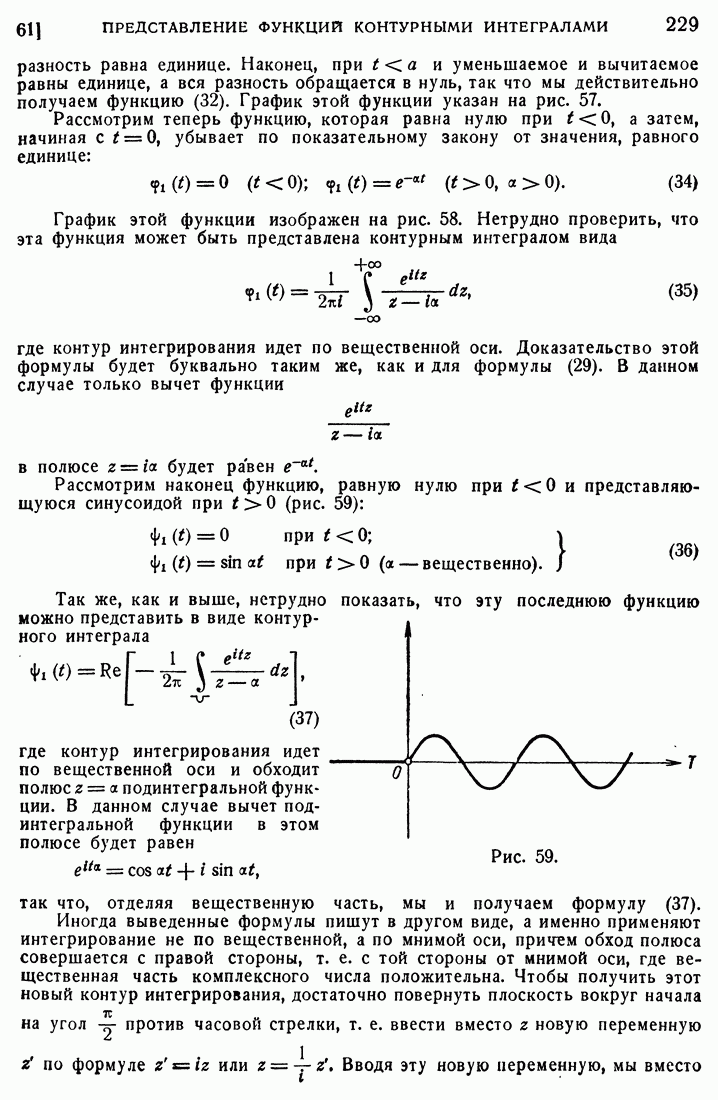
- 61. Представление некоторых функций контурными интегралами.
- 62. Примеры интегралов от многозначных функций.
- 63. Интегрирование системы линейных уравнений с постоянными коэффициентами.
- 64. Разложение дробной функции на простейшие дроби.
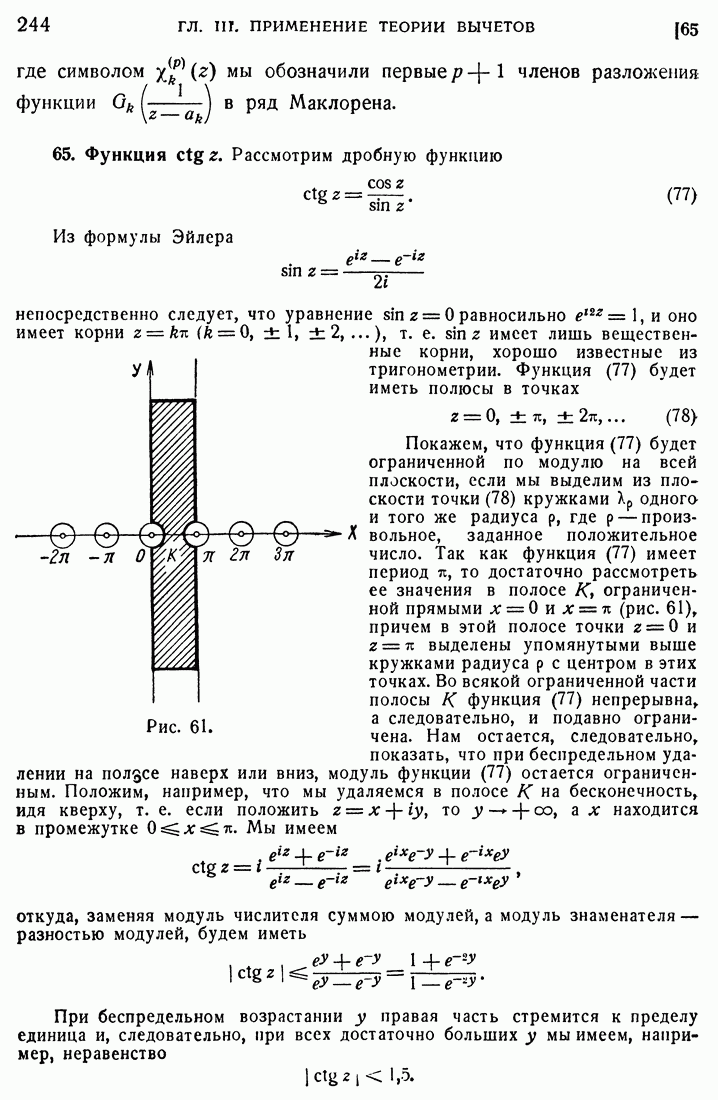
- 66. Построение мероморфной функции.
- 67. Целые функции.
- 68. Бесконечные произведения.
- 69. Построение целой функции по ее корням.
- 70. Интегралы, зависящие от параметра.
- 71. Эйлеров интеграл второго рода.
- 72. Эйлеров интеграл первого рода.
- 73. Бесконечное произведение для функции …
- 74. Представление Г(z) контурным интегралом.
- 75. Формула Стирлинга.
- 76. Формула суммирования Эйлера.
- 77. Числа Бернулли.
- 78. Метод скорейшего спуска.
- 79. Асимптотическое разложение интеграла.
- 80. Примеры.
- 81. Метод стационарной фазы.
- ГЛАВА IV. АНАЛИТИЧЕСКИЕ ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ И ФУНКЦИИ МАТРИЦ
- 82. Регулярные функции многих переменных.
- 83. Двойной интеграл и формула Коши.
- 84. Степенные ряды.
- 85. Аналитическое продолжение.
- 86. Функции матриц. Предварительные понятия.
- 87. Степенные ряды от одной матрицы.
- 88. Умножение степенных рядов. Обращение степенного ряда.
- 89. Дальнейшее исследование сходимости.
- 90. Интерполяционные полиномы.
- 91. Тождество Кейли. Формула Сильвестра.
- 92. Определение функций одной матрицы формулой Коши.
- 93. Аналитическое продолжение.
- 94. Логарифм матриц.
- 95. Обращение целой функции от матрицы в случае матриц второго порядка.
- 96. Системы линейных уравнений с постоянными коэффициентами.
- 97. Функции нескольких матриц.
- ГЛАВА V. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
- 98. Разложение решения в степенной ряд.
- 99. Аналитическое продолжение решения.
- 100. Окрестность особой точки.
- 101. Регулярная особая точка.
- 102. Уравнения класса Фукса.
- 103. Уравнение Гаусса.
- 104. Гипергеометрический ряд.
- 105. Полиномы Лежандра.
- 106. Полиномы Якоби.
- 107. Конформное преобразование и уравнение Гаусса.
- 108. Преобразование Лапласа.
- 109. Различный выбор решений.
- 110. Уравнение Бесселя.
- 111. Функции Ханкеля и интегральное представление решений уравнения Бесселя.
- 112. Асимптотические разложения.
- 113. Асимптотические разложения решений, полученных преобразованием Лапласа.
- 114. Асимптотические разложения решений уравнения Бесселя.
- 115. Вырождение уравнения Гаусса.
- 116. Формальные ряды в окрестности иррегулярной особой точки.
- 117. Построение асимптотических разложений методом после довательных приближений.
- 118. Функции Эйри.
- 119. Асимптотика при большом значении параметра.
- 120. Уравнения с периодическими коэффициентами.
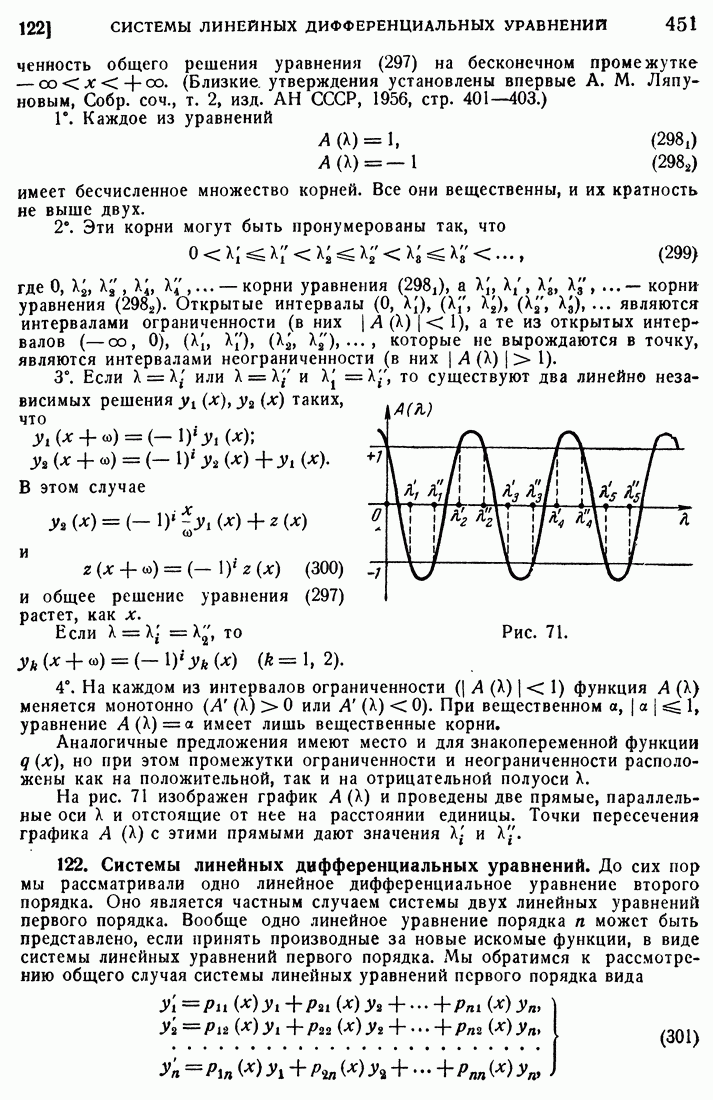
- 121. Условия устойчивости и неустойчивости для уравнения Хилла.
- 122. Системы линейных дифференциальных уравнений.
- 123. Регулярная особая точка.
- 124. Регулярные системы.
- 125. Представление решения в окрестности особой точки.
- 126. Канонические решения.
- 127. Связь с регулярными решениями типа Фукса.
- 128. Случай любых Us.
- 129. Формальные разложения в окрестности иррегулярной особой точки.
- ГЛАВА VI. СПЕЦИАЛЬНЫЕ ФУНКЦИИ
- 130. Определение сферических функций.
- 131. Явные выражения сферических функций.
- 132. Свойство ортогональности.
- 133. Полиномы Лежандра.
- 134. Разложение по сферическим функциям.
- 135. Доказательство сходимости.
- 136. Связь сферических функций с предельными задачами.
- 137. Задачи Дирихле и Неймана.
- 138. Потенциал объемных масс.
- 139. Потенциал сферического слоя.
- 140. Электрон в центральном поле.
- 141. Шаровые функции и линейные представления группы вращения.
- 142. Функция Лежандра.
- 143. Функция Лежандра второго рода.
- § 2. ФУНКЦИИ БЕССЕЛЯ
- 144. Определение функций Бесселя.
- 145. Соотношения между функциями Бесселя.
- 146. Ортогональность функций Бесселя и их корни.
- 147. Производящая функция и интегральное представление.
- 148. Формула Фурье — Бесселя.
- 150. Разложение функций Неймана с целым значком.
- 151. Случай чисто мнимого аргумента.
- 152. Новые интегральные представления.
- 153. Асимптотические представления.
- 154. Функции Бесселя и уравнение Лапласа.
- 155. Волновое уравнение в цилиндрических координатах.
- 156. Волновое уравнение в сферических координатах.
- § 3. ПОЛИНОМЫ ЭРМИТА И ЛАГЕРРА
- 157. Линейный осциллятор и полиномы Эрмита.
- 158. Свойство ортогональности.
- 159. Производящая функция.
- 160. Параболические координаты и функции Эрмита.
- 161. Полиномы Лагерра.
- 162. Связь полиномов Эрмита и Лагерра.
- 163. Асимптотическое выражение полиномов Эрмита.
- 164. Асимптотическое выражение полиномов Лежандра.
- § 4. ЭЛЛИПТИЧЕСКИЕ ИНТЕГРАЛЫ И ЭЛЛИПТИЧЕСКИЕ ФУНКЦИИ
- 165. Приведение эллиптических интегралов к нормальному виду.
- 166. Приведение интегралов к тригонометрической форме.
- 167. Примеры.
- 168. Обращение эллиптического интеграла.
- 169. Общие свойства эллиптических функций.
- 170. Основная лемма.
- 171. Функции Вейерштрасса.
- 172. Дифференциальное уравнение для …
- 173. Функции …
- 174. Разложение целой периодической функции.
- 175. Новые обозначения.
- 176. Функция …
- 177. Функции …
- 178. Свойства функций тэта.
- 179. Выражение чисел … через …
- 180. Эллиптические функции Якоби.
- 181. Основные свойства функций Якоби.
- 182. Дифференциальные уравнения для функций Якоби.
- 183. Формулы сложения.
- 184. Связь функций p(u) и sn(u).
- 185. Эллиптические координаты.
- 186. Введение эллиптических функций.
- 187. Уравнение Лямэ.
- 188. Простой маятник.
- 189. Пример конформного преобразования.
- ДОБАВЛЕНИЕ. ПРИВЕДЕНИЕ МАТРИЦ К КАНОНИЧЕСКОЙ ФОРМЕ
- 191. Случай простых корней.
- 192. Первый этап преобразований в случае кратных корней.
- 193. Приведение к канонической форме.
- 194. Определение структуры канонической формы.
- 196. Пример.