| << Предыдущий параграф | Следующий параграф >> |
Пред.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
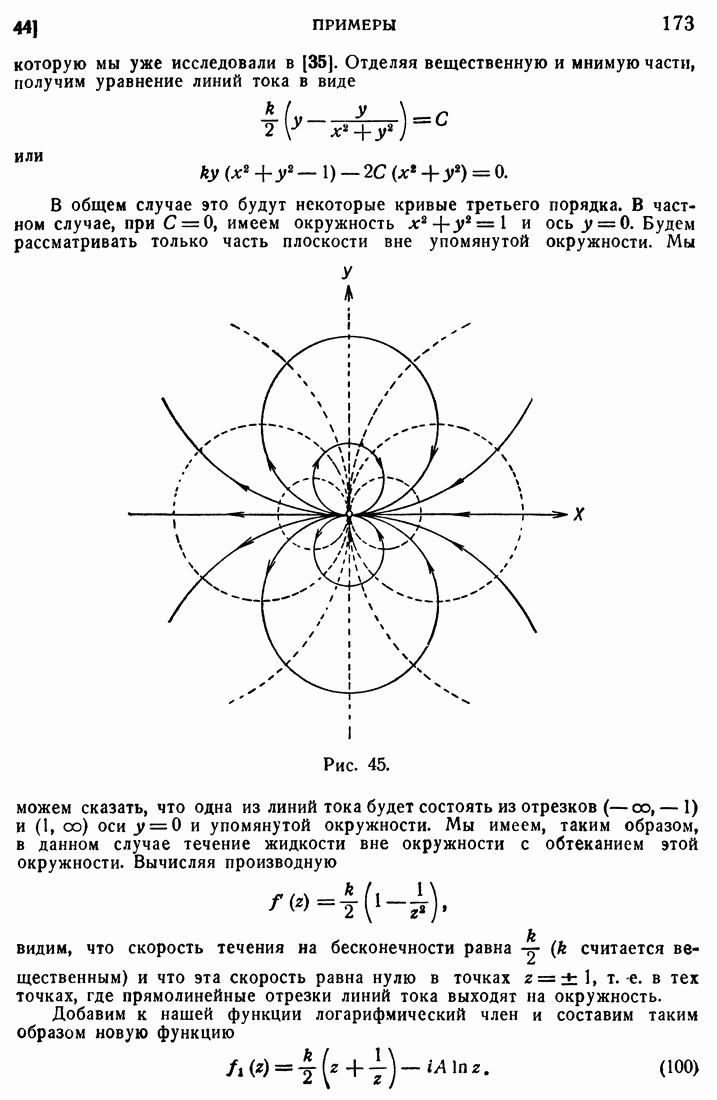
173
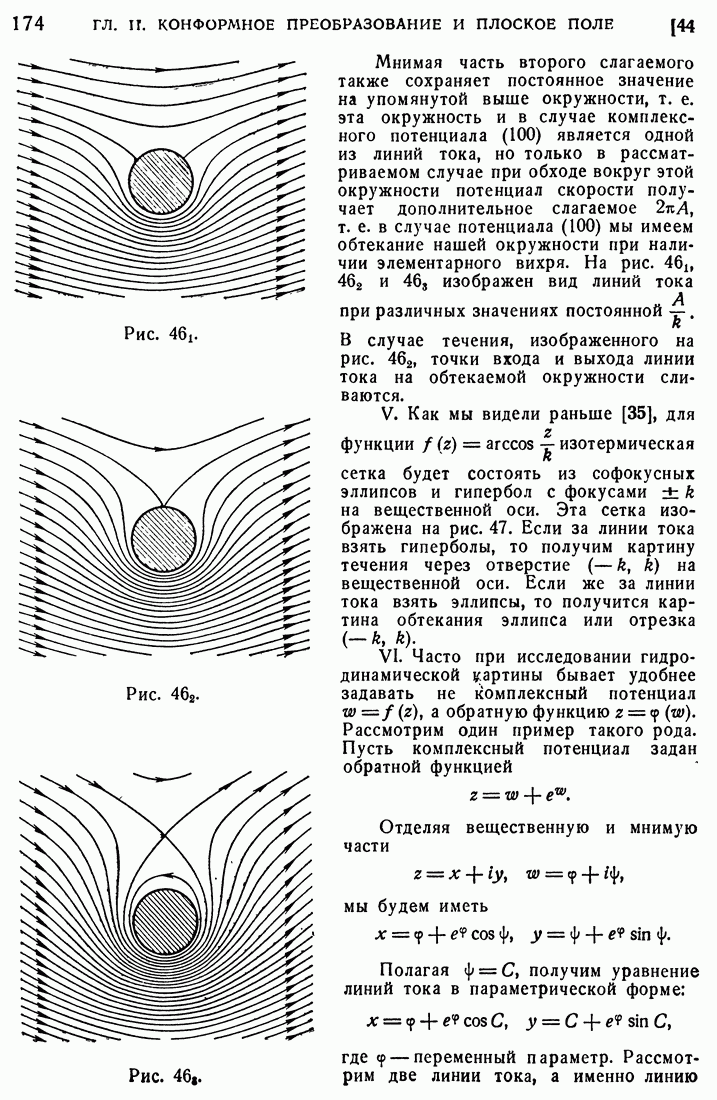
174
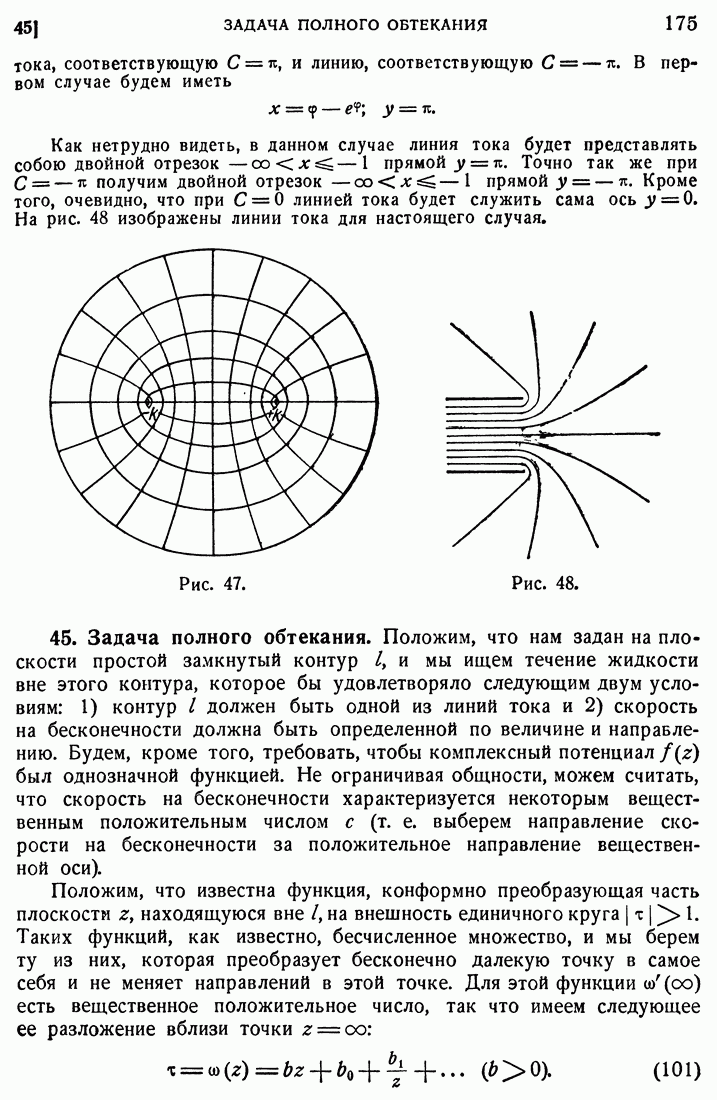
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
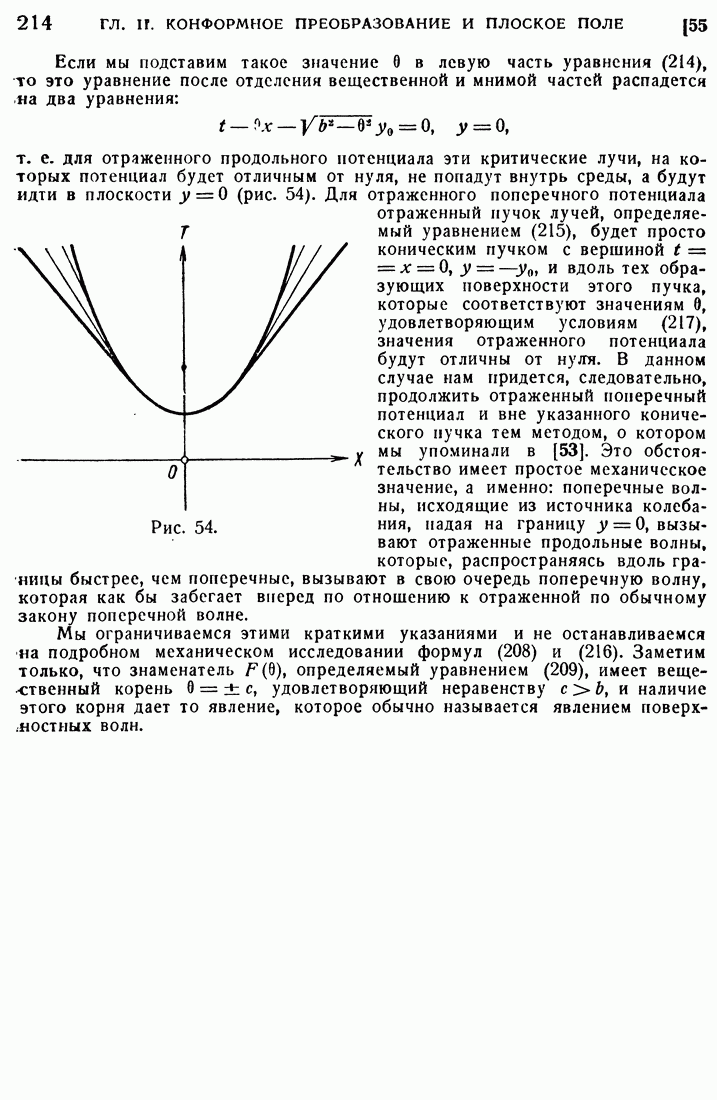
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
353
354
355
356
357
358
359
360
361
362
363
364
365
366
367
368
369
370
371
372
373
374
375
376
377
378
379
380
381
382
383
384
385
386
387
388
389
390
391
392
393
394
395
396
397
398
399
400
401
402
403
404
405
406
407
408
409
410
411
412
413
414
415
416
417
418
419
420
421
422
423
424
425
426
427
428
429
430
431
432
433
434
435
436
437
438
439
440
441
442
443
444
445
446
447
448
449
450
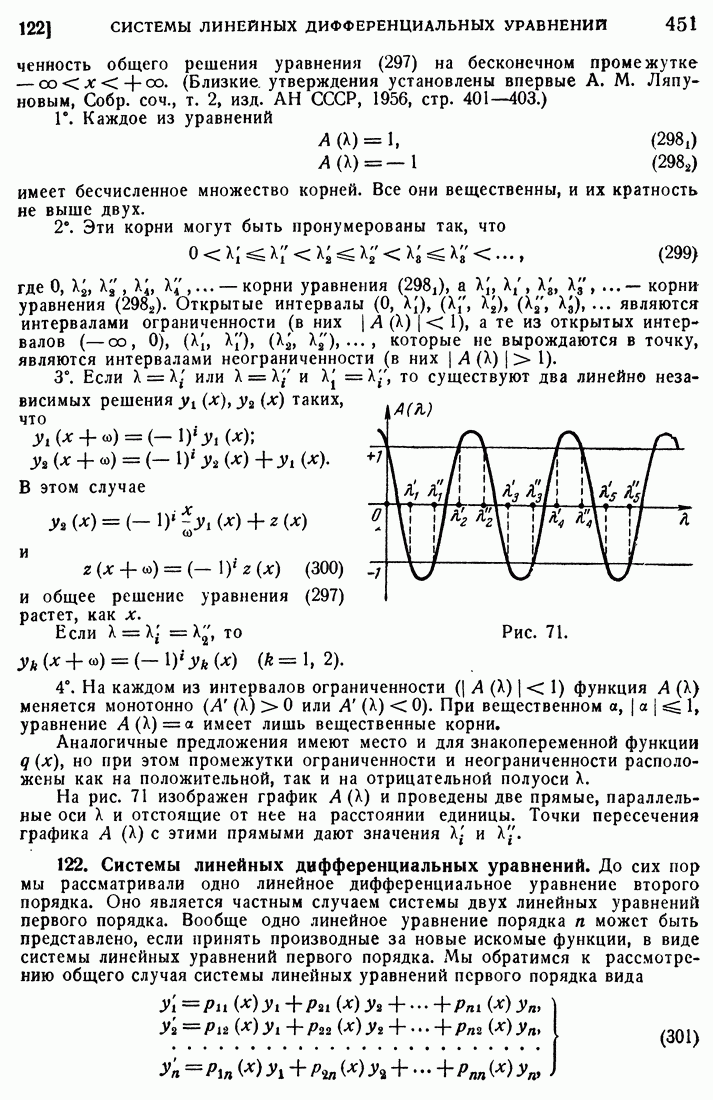
451
452
453
454
455
456
457
458
459
460
461
462
463
464
465
466
467
468
469
470
471
472
473
474
475
476
477
478
479
480
481
482
483
484
485
486
487
488
489
490
491
492
493
494
495
496
497
498
499
500
501
502
503
504
505
506
507
508
509
510
511
512
513
514
515
516
517
518
519
520
521
522
523
524
525
526
527
528
529
530
531
532
533
534
535
536
537
538
539
540
541
542
543
544
545
546
547
548
549
550
551
552
553
554
555
556
557
558
559
560
561
562
563
564
565
566
567
568
569
570
571
572
573
574
575
576
577
578
579
580
581
582
583
584
585
586
587
588
589
590
591
592
593
594
595
596
597
598
599
600
601
602
603
604
605
606
607
608
609
610
611
612
613
614
615
616
617
618
619
620
621
622
623
624
625
626
627
628
629
630
631
632
633
634
635
636
637
638
639
640
641
642
643
644
645
646
647
648
649
650
651
652
653
654
655
656
657
658
659
660
661
662
663
664
665
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
69. Построение целой функции по ее корням.
Пользуясь предыдущими соображениями, мы сможем построить целую функцию по заданным ее корням. Заметим прежде всего, что корни целой функции не могут иметь предельных точек на конечном расстоянии. Если бы такая точка  существовала, т. е. если бы в любом малом круге с центром
существовала, т. е. если бы в любом малом круге с центром  находилось бесчисленное множество корней целой функции, то эта целая функция должна была бы тождественно равняться нулю [18]. Повторяя рассуждения из [64], мы убеждаемся, что во всяком случае корни
находилось бесчисленное множество корней целой функции, то эта целая функция должна была бы тождественно равняться нулю [18]. Повторяя рассуждения из [64], мы убеждаемся, что во всяком случае корни  целой функции могут быть расположены в порядке неубывающего модуля:
целой функции могут быть расположены в порядке неубывающего модуля:

причем  при
при  . Заметим, что если некоторое число а фигурирует q раз среди чисел
. Заметим, что если некоторое число а фигурирует q раз среди чисел  то это значит, что соответствующий корень а должен быть корнем кратности q. Мы пока считаем, кроме того, что
то это значит, что соответствующий корень а должен быть корнем кратности q. Мы пока считаем, кроме того, что  не участвует среди заданных чисел
не участвует среди заданных чисел 
Ограничим нашу задачу рассмотрением одного частного случая, наиболее важного в приложениях, а именно будем считать, что  настолько быстро удаляются на бесконечность, что существует такое целое положительное число
настолько быстро удаляются на бесконечность, что существует такое целое положительное число  что ряд
что ряд

есть ряд сходящийся. Мы будем считать  .
.
Построим бесконечное произведение

и покажем, что оно будет удовлетворять всем условиям, указанным в предыдущем номере. Рассмотрим некоторый круг  Начиная с некоторого значка
Начиная с некоторого значка  числа
числа  будут находиться вне круга
будут находиться вне круга  так что при члены произведения (104) не будут иметь корней в круге С и для всякого
так что при члены произведения (104) не будут иметь корней в круге С и для всякого  принадлежащего
принадлежащего  мы будем иметь
мы будем иметь

где  определенное положительное число, меньшее единицы. Рассмотрим ряд (100) для данного случая:
определенное положительное число, меньшее единицы. Рассмотрим ряд (100) для данного случая:

В силу (105) можно воспользоваться разложением логарифма в степенной ряд и получим при таком выборе значения логарифма для ряда (106) следующую формулу:

Исследуем общий член этого ряда

Мы имеем, очевидно,

или в силу (105), вынося за скобки  и принимая во внимание, что в круге
и принимая во внимание, что в круге 

т. е.

В силу сходимости ряда  положительные числа, стоящие в правой части последнего неравенства, образуют сходящийся ряд, и, следовательно, ряд (106) будет сходиться абсолютно и равномерно в круге
положительные числа, стоящие в правой части последнего неравенства, образуют сходящийся ряд, и, следовательно, ряд (106) будет сходиться абсолютно и равномерно в круге  . Таким образом, мы можем утверждать, что бесконечное произведение (104) представляет собою целую функцию и что корни этой целой функции определяются корнями сомножителей, т. е. что корни этой целой функции суть числа
. Таким образом, мы можем утверждать, что бесконечное произведение (104) представляет собою целую функцию и что корни этой целой функции определяются корнями сомножителей, т. е. что корни этой целой функции суть числа 
Если мы имеем какую-нибудь целую функцию  корни которой суть
корни которой суть  то частное
то частное  будет целой функцией без корней, т. е. это частное будет иметь вид
будет целой функцией без корней, т. е. это частное будет иметь вид  и мы получим таким образом следующее представление для целой функции
и мы получим таким образом следующее представление для целой функции 

где  некоторая целая функция. До сих пор мы предполагали, что точка
некоторая целая функция. До сих пор мы предполагали, что точка  не является корнем функции. Если эта точка есть корень кратности
не является корнем функции. Если эта точка есть корень кратности  , то следует только добавить к правым частям формул (104) и (107) множитель
, то следует только добавить к правым частям формул (104) и (107) множитель 
Рассмотрим в качестве примера функцию  Она имеет простой корень
Она имеет простой корень  и простые корни
и простые корни 
В данном случае имеем  так как ряд
так как ряд

как мы уже упоминали выше, сходится. Применяя формулу  и добавляя множитель z, мы получим
и добавляя множитель z, мы получим

Целая функция  не может быть, конечно, определена из предыдущих общих соображений. Результаты [67] показывают, что в данном случае эта функция равна тождественно нулю.
не может быть, конечно, определена из предыдущих общих соображений. Результаты [67] показывают, что в данном случае эта функция равна тождественно нулю.
Заметим, что если  , т. е. если сходится ряд
, т. е. если сходится ряд

то, рассуждая, как и выше, можно вместо формулы (107) написать формулу

В дальнейшем мы будем иметь еще примеры применения формулы (104), которая называется обычно бесконечным произведением Вейерштрасса.
Может случиться, что числа  заданы так, что ряд (103) расходится при всяком целом положительном
заданы так, что ряд (103) расходится при всяком целом положительном  . Это будет, например, если мы положим
. Это будет, например, если мы положим  Действительно, ряд с общим членом
Действительно, ряд с общим членом  расходится при всяком положительном
расходится при всяком положительном  , так как сумма его первых членов больше, чем
, так как сумма его первых членов больше, чем

а это последнее выражение, как нетрудно показать, применяя хотя бы правило Лопиталя, беспредельно возрастает вместе с k. В случае расходимости ряда (103) при всяком целом положительном  составим бесконечное произведение
составим бесконечное произведение

где

и  будет зависеть от k. Повторяя вышеуказанные оценки, мы убедимся в том, что для сходимости бесконечного произведения (108) достаточна сходимость при всяком
будет зависеть от k. Повторяя вышеуказанные оценки, мы убедимся в том, что для сходимости бесконечного произведения (108) достаточна сходимость при всяком  ряда
ряда

Достаточно для этого взять  . Действительно, применяя признак Коши [I, 121] к ряду
. Действительно, применяя признак Коши [I, 121] к ряду

получим

т. е. ряд действительно сходится. Можно показать, что для сходимости ряда достаточно взять  такими, чтобы имело место неравенство:
такими, чтобы имело место неравенство:  .
.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ К ВОСЬМОМУ ИЗДАНИЮ
- 1. Функции комплексного переменного.
- 2. Производная.
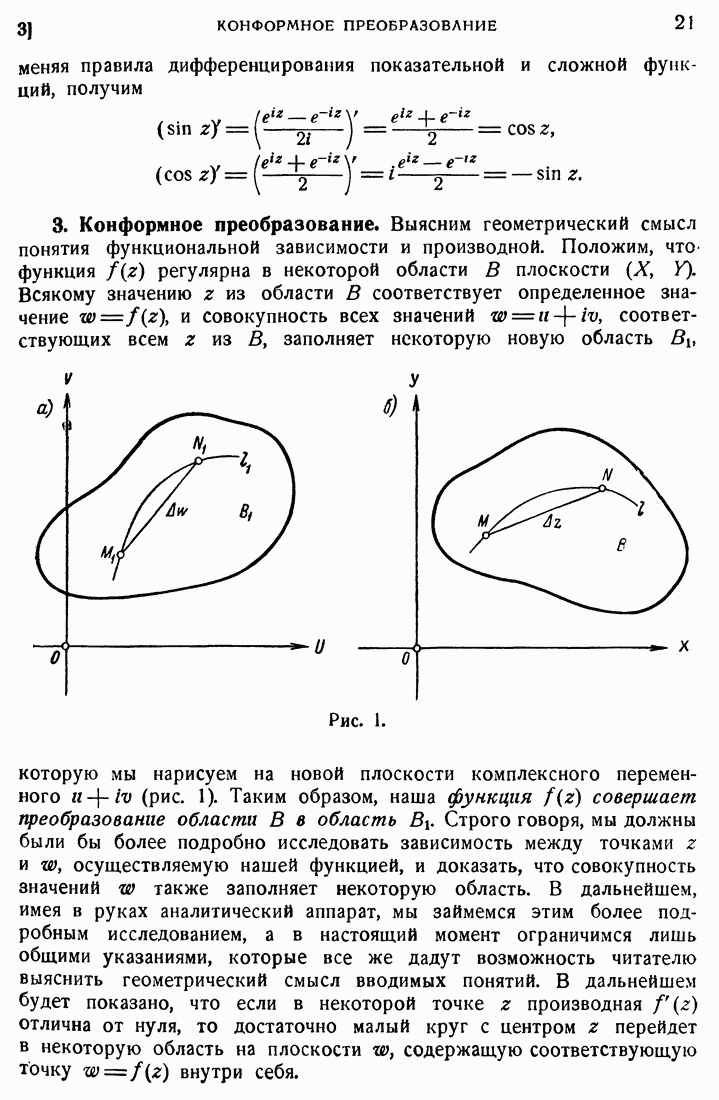
- 3. Конформное преобразование.
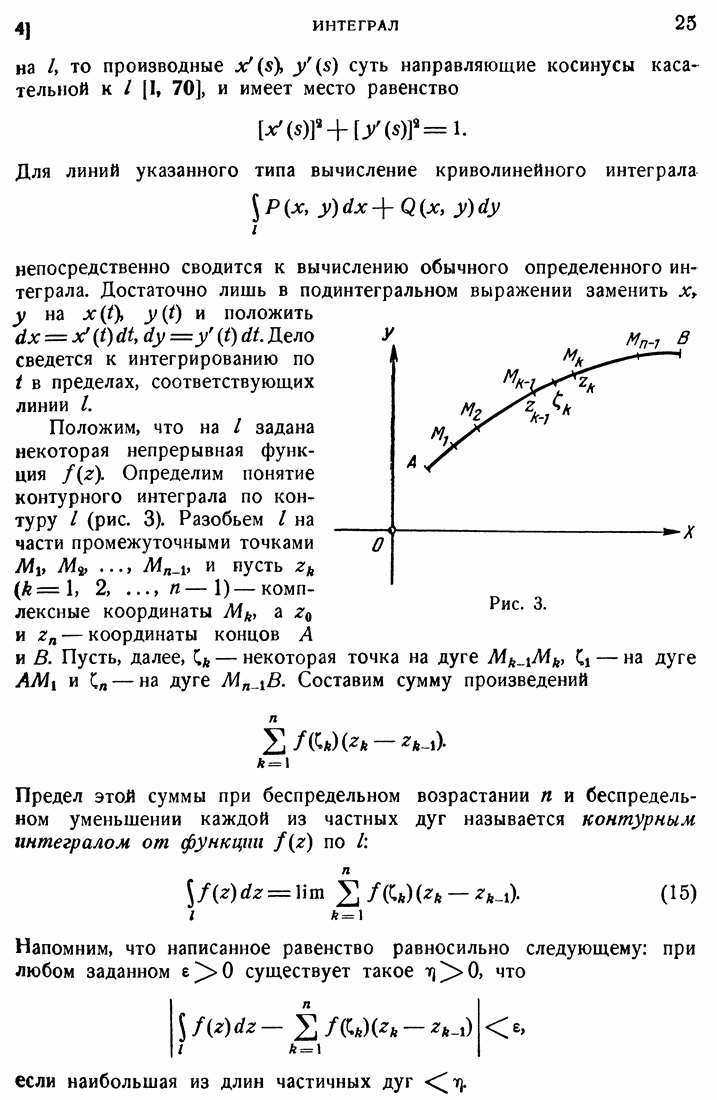
- 4. Интеграл.
- 5. Теорема Коши.
- 6. Основная формула интегрального исчисления.
- 7. Формула Коши.
- 8. Интегралы типа Коши.
- 9. Следствия формулы Коши.
- 10. Изолированные особые точки.
- 11. Бесконечные ряды с комплексными членами.
- 12. Теорема Вейерштрасса.
- 13. Степенные ряды.
- 14. Ряд Тейлора.
- 15. Ряд Лорана.
- 16. Примеры.
- 17. Изолированные особые точки. Бесконечно далекая точка.
- 18. Аналитическое продолжение.
- 19. Примеры многозначных функций.
- 20. Особые точки аналитических функций и римановы поверхности.
- 21. Теорема вычетов.
- 22. Теоремы о числе корней.
- 23. Обращение степенного ряда.
- 24. Принцип симметрии.
- 25. Ряд Тейлора на окружности круга сходимости.
- 26. Дополнительные сведения о формуле Коши.
- 27. Главное значение интеграла.
- 28. Главное значение интеграла (продолжение).
- 29. Интегралы типа Коши.
- 30. Интегралы типа Коши (продолжение).
- ГЛАВА II. КОНФОРМНОЕ ПРЕОБРАЗОВАНИЕ И ПЛОСКОЕ ПОЛЕ
- 31. Конформное преобразование.
- 32. Линейное преобразование.
- 33. Дробно-линейное преобразование.
- 34. Функция w = z^2.
- 35. Функция …
- 36. Двуугольник и полоса.
- 37. Основная теорема.
- 38. Формула Кристоффеля.
- 39. Частные случаи.
- 40. Случай внешности многоугольника.
- 41. Минимальное свойство преобразования на круг.
- 42. Способ сопряженных тригонометрических рядов.
- 43. Плоское установившееся течение жидкости.
- 44. Примеры.
- 45. Задача полного обтекания.
- 46. Формула Н. Е. Жуковского.
- 47. Плоская электростатическая задача.
- 48. Формула Шварца.
- 49. Ядро ctg((s-t)/2).
- 50. Предельные задачи.
- 51. Бигармоническое уравнение.
- 52. Волновое уравнение и аналитические функции.
- 53. Основная теорема.
- 54. Дифракция плоской волны.
- 55. Отражение упругих волн от прямолинейной границы.
- ГЛАВА III. ПРИМЕНЕНИЕ ТЕОРИИ ВЫЧЕТОВ, ЦЕЛЫЕ И ДРОБНЫЕ ФУНКЦИИ
- 56. Интеграл Френеля.
- 57. Интегрирование выражений с тригонометрическими функциями.
- 58. Интегрирование рациональной дроби.
- 59. Некоторые новые типы интегралов с тригонометрическими функциями.
- 60. Лемма Жордана.
- 61. Представление некоторых функций контурными интегралами.
- 62. Примеры интегралов от многозначных функций.
- 63. Интегрирование системы линейных уравнений с постоянными коэффициентами.
- 64. Разложение дробной функции на простейшие дроби.
- 66. Построение мероморфной функции.
- 67. Целые функции.
- 68. Бесконечные произведения.
- 69. Построение целой функции по ее корням.
- 70. Интегралы, зависящие от параметра.
- 71. Эйлеров интеграл второго рода.
- 72. Эйлеров интеграл первого рода.
- 73. Бесконечное произведение для функции …
- 74. Представление Г(z) контурным интегралом.
- 75. Формула Стирлинга.
- 76. Формула суммирования Эйлера.
- 77. Числа Бернулли.
- 78. Метод скорейшего спуска.
- 79. Асимптотическое разложение интеграла.
- 80. Примеры.
- 81. Метод стационарной фазы.
- ГЛАВА IV. АНАЛИТИЧЕСКИЕ ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ И ФУНКЦИИ МАТРИЦ
- 82. Регулярные функции многих переменных.
- 83. Двойной интеграл и формула Коши.
- 84. Степенные ряды.
- 85. Аналитическое продолжение.
- 86. Функции матриц. Предварительные понятия.
- 87. Степенные ряды от одной матрицы.
- 88. Умножение степенных рядов. Обращение степенного ряда.
- 89. Дальнейшее исследование сходимости.
- 90. Интерполяционные полиномы.
- 91. Тождество Кейли. Формула Сильвестра.
- 92. Определение функций одной матрицы формулой Коши.
- 93. Аналитическое продолжение.
- 94. Логарифм матриц.
- 95. Обращение целой функции от матрицы в случае матриц второго порядка.
- 96. Системы линейных уравнений с постоянными коэффициентами.
- 97. Функции нескольких матриц.
- ГЛАВА V. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
- 98. Разложение решения в степенной ряд.
- 99. Аналитическое продолжение решения.
- 100. Окрестность особой точки.
- 101. Регулярная особая точка.
- 102. Уравнения класса Фукса.
- 103. Уравнение Гаусса.
- 104. Гипергеометрический ряд.
- 105. Полиномы Лежандра.
- 106. Полиномы Якоби.
- 107. Конформное преобразование и уравнение Гаусса.
- 108. Преобразование Лапласа.
- 109. Различный выбор решений.
- 110. Уравнение Бесселя.
- 111. Функции Ханкеля и интегральное представление решений уравнения Бесселя.
- 112. Асимптотические разложения.
- 113. Асимптотические разложения решений, полученных преобразованием Лапласа.
- 114. Асимптотические разложения решений уравнения Бесселя.
- 115. Вырождение уравнения Гаусса.
- 116. Формальные ряды в окрестности иррегулярной особой точки.
- 117. Построение асимптотических разложений методом после довательных приближений.
- 118. Функции Эйри.
- 119. Асимптотика при большом значении параметра.
- 120. Уравнения с периодическими коэффициентами.
- 121. Условия устойчивости и неустойчивости для уравнения Хилла.
- 122. Системы линейных дифференциальных уравнений.
- 123. Регулярная особая точка.
- 124. Регулярные системы.
- 125. Представление решения в окрестности особой точки.
- 126. Канонические решения.
- 127. Связь с регулярными решениями типа Фукса.
- 128. Случай любых Us.
- 129. Формальные разложения в окрестности иррегулярной особой точки.
- ГЛАВА VI. СПЕЦИАЛЬНЫЕ ФУНКЦИИ
- 130. Определение сферических функций.
- 131. Явные выражения сферических функций.
- 132. Свойство ортогональности.
- 133. Полиномы Лежандра.
- 134. Разложение по сферическим функциям.
- 135. Доказательство сходимости.
- 136. Связь сферических функций с предельными задачами.
- 137. Задачи Дирихле и Неймана.
- 138. Потенциал объемных масс.
- 139. Потенциал сферического слоя.
- 140. Электрон в центральном поле.
- 141. Шаровые функции и линейные представления группы вращения.
- 142. Функция Лежандра.
- 143. Функция Лежандра второго рода.
- § 2. ФУНКЦИИ БЕССЕЛЯ
- 144. Определение функций Бесселя.
- 145. Соотношения между функциями Бесселя.
- 146. Ортогональность функций Бесселя и их корни.
- 147. Производящая функция и интегральное представление.
- 148. Формула Фурье — Бесселя.
- 150. Разложение функций Неймана с целым значком.
- 151. Случай чисто мнимого аргумента.
- 152. Новые интегральные представления.
- 153. Асимптотические представления.
- 154. Функции Бесселя и уравнение Лапласа.
- 155. Волновое уравнение в цилиндрических координатах.
- 156. Волновое уравнение в сферических координатах.
- § 3. ПОЛИНОМЫ ЭРМИТА И ЛАГЕРРА
- 157. Линейный осциллятор и полиномы Эрмита.
- 158. Свойство ортогональности.
- 159. Производящая функция.
- 160. Параболические координаты и функции Эрмита.
- 161. Полиномы Лагерра.
- 162. Связь полиномов Эрмита и Лагерра.
- 163. Асимптотическое выражение полиномов Эрмита.
- 164. Асимптотическое выражение полиномов Лежандра.
- § 4. ЭЛЛИПТИЧЕСКИЕ ИНТЕГРАЛЫ И ЭЛЛИПТИЧЕСКИЕ ФУНКЦИИ
- 165. Приведение эллиптических интегралов к нормальному виду.
- 166. Приведение интегралов к тригонометрической форме.
- 167. Примеры.
- 168. Обращение эллиптического интеграла.
- 169. Общие свойства эллиптических функций.
- 170. Основная лемма.
- 171. Функции Вейерштрасса.
- 172. Дифференциальное уравнение для …
- 173. Функции …
- 174. Разложение целой периодической функции.
- 175. Новые обозначения.
- 176. Функция …
- 177. Функции …
- 178. Свойства функций тэта.
- 179. Выражение чисел … через …
- 180. Эллиптические функции Якоби.
- 181. Основные свойства функций Якоби.
- 182. Дифференциальные уравнения для функций Якоби.
- 183. Формулы сложения.
- 184. Связь функций p(u) и sn(u).
- 185. Эллиптические координаты.
- 186. Введение эллиптических функций.
- 187. Уравнение Лямэ.
- 188. Простой маятник.
- 189. Пример конформного преобразования.
- ДОБАВЛЕНИЕ. ПРИВЕДЕНИЕ МАТРИЦ К КАНОНИЧЕСКОЙ ФОРМЕ
- 191. Случай простых корней.
- 192. Первый этап преобразований в случае кратных корней.
- 193. Приведение к канонической форме.
- 194. Определение структуры канонической формы.
- 196. Пример.