| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
119. Асимптотика при большом значении параметра.
Прежде чем переходить к аналитической теории систем линейных дифференциальных уравнений, мы рассмотрим два вопроса для линейных уравнений второго порядка без предположения аналитичности коэффициентов уравнений, а именно: асимптотику решений уравнений при больших значениях параметра, входящего в уравнения, и уравнения с периодическими коэффициентами. Начнем с первого вопроса, который мы рассмотрим кратко, не останавливаясь на подробных доказательствах.
Мы будем рассматривать уравнение вида

где функции  вещественные функции, определенные на конечном промежутке
вещественные функции, определенные на конечном промежутке  параметр. Отметим, что уравнение более общего вида
параметр. Отметим, что уравнение более общего вида

приводится к случаю (242) заменой

В дальнейшем будем предполагать, что  непрерывна с производными до второго порядка на замкнутом промежутке
непрерывна с производными до второго порядка на замкнутом промежутке  непрерывная функция. Существенную роль при исследовании решений уравнения (242) при больших значениях X играет знак
непрерывная функция. Существенную роль при исследовании решений уравнения (242) при больших значениях X играет знак 
Рассмотрим сначала тот случай, когда  на промежутке
на промежутке  При больших X коэффициент
При больших X коэффициент  является превалирующим, и целью дальнейшего преобразования уравнения (242) является такое его преобразование, при котором этот превалирующий коэффициент приведется просто к
является превалирующим, и целью дальнейшего преобразования уравнения (242) является такое его преобразование, при котором этот превалирующий коэффициент приведется просто к  Для этого вместо
Для этого вместо  введем новую независимую переменную
введем новую независимую переменную  и вместо у — новую функцию v по формулам
и вместо у — новую функцию v по формулам

Интервал  преобразуете в некоторый новый интервал
преобразуете в некоторый новый интервал  , а уравнение (242), как нетрудно проверить, приводится к виду
, а уравнение (242), как нетрудно проверить, приводится к виду

где

есть непрерывная на  функция. Напомним, что неоднородное уравнение
функция. Напомним, что неоднородное уравнение

имеет общее решение [II, 34]

где  любое фиксированное значение из промежутка
любое фиксированное значение из промежутка  . В случае уравнения (243) роль
. В случае уравнения (243) роль  играет
играет  и уравнение (244) приводится к интегральному уравнению
и уравнение (244) приводится к интегральному уравнению

к решению которого можно применить метод последовательных приближений. В качестве нулевого приближения берем

а последующие поправки определяются формулами

Непрерывная функция  ограничена на промежутке
ограничена на промежутке  где
где  некоторая постоянная. По индукции нетрудно - доказать неравенство
некоторая постоянная. По индукции нетрудно - доказать неравенство

из которого следует, что ряд

равномерно сходится на промежутке  . Его сумма удовлетворяет уравнению (245), т. е. уравнению (243). Далее из оценок (246) следует, что
. Его сумма удовлетворяет уравнению (245), т. е. уравнению (243). Далее из оценок (246) следует, что

равномерно относительно т. Таким образом, имеем

или, возвращаясь к исходным переменным х и у, получаем асимптотику решений уравнения (242) при больших X:

Мы могли бы вместо конечного промежутка  рассматривать и бесконечный промежуток в одну или обе стороны. При этом остаточный член имеет равномерную оценку
рассматривать и бесконечный промежуток в одну или обе стороны. При этом остаточный член имеет равномерную оценку  , где А — положительная постоянная во всяком конечном промежутке изменения
, где А — положительная постоянная во всяком конечном промежутке изменения  но величина А зависит от выбора конечного промежутка и может беспредельно возрастать при его расширении.
но величина А зависит от выбора конечного промежутка и может беспредельно возрастать при его расширении.
В связи со сказанным выше сделаем одно замечание. Рассмотрим уравнение

где  положительная непрерывная периодическая функция на бесконечном промежутке
положительная непрерывная периодическая функция на бесконечном промежутке  Для любого конечного промежутка мы можем применить формулу (248), но нельзя утверждать, что решения уравнения (249) будут ограниченными функциями на всем бесконечном промежутке, хотя первые два слагаемых правой части дают, очевидно, ограниченную функцию на всем бесконечном промежутке, ибо
Для любого конечного промежутка мы можем применить формулу (248), но нельзя утверждать, что решения уравнения (249) будут ограниченными функциями на всем бесконечном промежутке, хотя первые два слагаемых правой части дают, очевидно, ограниченную функцию на всем бесконечном промежутке, ибо  , где
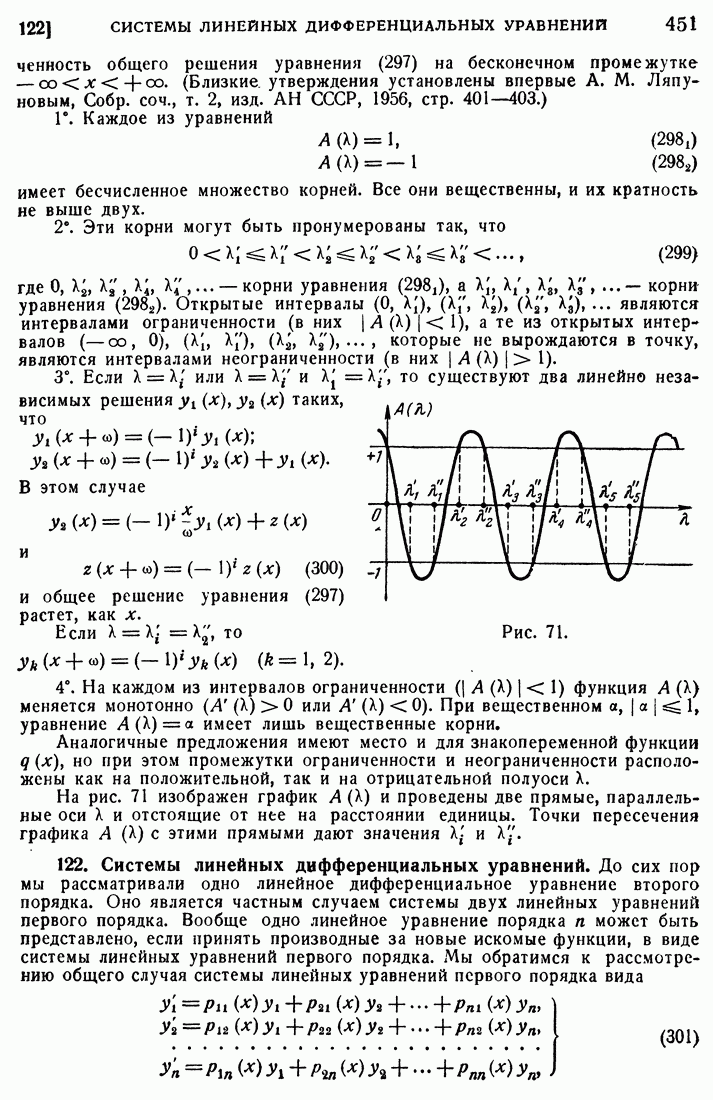
, где  — некоторая постоянная, на всем бесконечном промежутке в силу периодичности. Оказывается, что в рассматриваемом случае может иметь место следующий факт: при одних значениях X все решения уравнения (249) — ограниченные функции на бесконечном промежутке, а при других значениях X этого свойства ограниченности всех решений уже не будет. Более подробно мы об этом будем говорить в дальнейшем, при исследовании уравнений с периодическими коэффициентами.
— некоторая постоянная, на всем бесконечном промежутке в силу периодичности. Оказывается, что в рассматриваемом случае может иметь место следующий факт: при одних значениях X все решения уравнения (249) — ограниченные функции на бесконечном промежутке, а при других значениях X этого свойства ограниченности всех решений уже не будет. Более подробно мы об этом будем говорить в дальнейшем, при исследовании уравнений с периодическими коэффициентами.
Совершенно аналогично случаю  можно рассмотреть и случай
можно рассмотреть и случай  на конечном промежутке
на конечном промежутке  и вместо тригонометрических функций, входящих в формулу (248), получатся показательные функции
и вместо тригонометрических функций, входящих в формулу (248), получатся показательные функции

Переходим теперь к более сложному случаю, когда  в уравнении
в уравнении

меняет знак на рассматриваемом промежутке. Не ограничивая общности можем считать, что  находится внутри
находится внутри  где
где  при
при  . В данном случае основным «эталонным» уравнением является уравнение Эйри
. В данном случае основным «эталонным» уравнением является уравнение Эйри

Относительно гладкости  делаются прежние предположения. Рассмотрим сначала случай
делаются прежние предположения. Рассмотрим сначала случай  Будем искать решение уравнения (251) в виде
Будем искать решение уравнения (251) в виде

где  любое решение уравнения (252), а функции
любое решение уравнения (252), а функции  выбираются так, чтобы в полученном после подстановки в (251) уравнении сократились члены с положительными степенями большого параметра X. Таким путем мы придем к приближенному решению уравнения (251):
выбираются так, чтобы в полученном после подстановки в (251) уравнении сократились члены с положительными степенями большого параметра X. Таким путем мы придем к приближенному решению уравнения (251):

где

Функция (253) в точности удовлетворяет уравнению

где

При любом  уравнение (251) можно записать в виде
уравнение (251) можно записать в виде

где

Функция  непрерывна при
непрерывна при
В дальнейшем мы будем придерживаться и пользоваться результатами и обозначениями из [118].
Теорема 1. Существуют решения уравнения (251), имеющие при  вид
вид

где  непрерывки при
непрерывки при  и имеют место оценки
и имеют место оценки

где постоянная С не зависит ни от  ни от X.
ни от X.
Напомним, что  вещественные решения уравнения (252), причем
вещественные решения уравнения (252), причем  при
при 
Наметим доказательство утверждения для  Для
Для  оно аналогично. Применяя метод вариации произвольных постоянных к уравнению (251 i), получим для решений уравнения (251), которое совпадает с
оно аналогично. Применяя метод вариации произвольных постоянных к уравнению (251 i), получим для решений уравнения (251), которое совпадает с  интегральное уравнение
интегральное уравнение

где  - решения уравнения (254):
- решения уравнения (254):

и  — определитель Вронского этих двух решений. Для него нетрудно получить
— определитель Вронского этих двух решений. Для него нетрудно получить  . Положим
. Положим  и введем в уравнение (257) вместо
и введем в уравнение (257) вместо  новую функцию
новую функцию 

Для  получим уравнение
получим уравнение 

Выбор нижнего предела интегрирования  служит для оценки вычитаемого в квадратной скобке. При доказательстве теоремы для
служит для оценки вычитаемого в квадратной скобке. При доказательстве теоремы для  в уравнении (257) надо положить
в уравнении (257) надо положить  и выбрать нижний предел интегрирования равным нулю. При дальнейшем доказательстве используется следующая
и выбрать нижний предел интегрирования равным нулю. При дальнейшем доказательстве используется следующая
Лемм а. Если в интегральном уравнении на конечном промежутке

с непрерывным в квадрате  ядром и непрерывной функцией
ядром и непрерывной функцией  выполнено условие
выполнено условие 

то уравнение (259) имеет единственное решение  причем
причем

где

Кроме того, если  непрерывно зависит от параметра X, который меняется на конечном или бесконечном промежутке, причем выполнено условие (261) и М не зависит от X, то
непрерывно зависит от параметра X, который меняется на конечном или бесконечном промежутке, причем выполнено условие (261) и М не зависит от X, то  будет непрерывной функцией переменных
будет непрерывной функцией переменных  и X.
и X.
Доказательство леммы легко проводится методом последовательных приближений.
Из упомянутой леммы следует, что для доказательства сформулированной теоремы достаточно установить оценку

где С не зависит ни от  ни от X.
ни от X.
Кратко наметим путь получения этой оценки. Буквой С будем обозначать различные постоянные (не зависящее от X). Из определения  дует, что
дует, что  и, принимая во внимание формулы
и, принимая во внимание формулы  и (237), получаем
и (237), получаем

откуда следует

Интеграл

имеет еще меньший порядок по X. Переходим к его оценке

Положив  , получим
, получим

Легко проверить, что  Используя это и применяя к написанной выше дроби правило Лопиталя, получим, что ее предел при
Используя это и применяя к написанной выше дроби правило Лопиталя, получим, что ее предел при  равен пределу
равен пределу  а в силу (237) этот предел равен нулю. Из указанных выше оценок непосредственно следует и требуемая оценка. Сформулированная выше лемма дает для решения интегрального уравнения (259)
а в силу (237) этот предел равен нулю. Из указанных выше оценок непосредственно следует и требуемая оценка. Сформулированная выше лемма дает для решения интегрального уравнения (259)

откуда в силу (258) следует утверждение теоремы 1.
Для случая  функция
функция  определяется равенством
определяется равенством

На всем промежутке  функция
функция  является гладкой и
является гладкой и 
Функции  входящие в теорему 1, имеют, очевидно, смысл и на промежутке
входящие в теорему 1, имеют, очевидно, смысл и на промежутке  Используя асимптотику, выражаемую формулами (237), получаем:
Используя асимптотику, выражаемую формулами (237), получаем:
Теорема 2. Решения  уравнения (251) имеют при
уравнения (251) имеют при  вид
вид

где  — функции допускающие оценку
— функции допускающие оценку

причем С не зависит ни от  ни от X.
ни от X.
Доказательство этой теоремы, основанное на исследовании интегрального уравнения (257), мы подробно приводить не будем. Отметим лишь, что интегральное уравнение для  имеет вид
имеет вид

и интеграл представляется в виде суммы двух интегралов по промежуткам  . В первом из интегралов можно использовать асимптотику
. В первом из интегралов можно использовать асимптотику  из теоремы 1, после чего этот интеграл приводит к выражению
из теоремы 1, после чего этот интеграл приводит к выражению

а в интеграле по промежутку  вводится вместо
вводится вместо  новая искомая функция:
новая искомая функция:

Замечание. Отметим еще, что появление и  в остаточном члене
в остаточном члене  связано с тем, что в точках
связано с тем, что в точках  где
где  первый член формулы для
первый член формулы для  не является главным.
не является главным.
Можно было бы вместо и  использовать и решения
использовать и решения  уравнения Эйри [118], имеющие комплексные значения при вещественном t. Результат получился бы следующий:
уравнения Эйри [118], имеющие комплексные значения при вещественном t. Результат получился бы следующий:
Теорема 3. При  существуют решения уравнения
существуют решения уравнения  непрерывные при
непрерывные при  и такие, что
и такие, что

 определена формулами
определена формулами  функции Эйри, и
функции Эйри, и  имеют оценку
имеют оценку

Доказательство этой теоремы аналогично доказательству теоремы 1, но несколько проще.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К ВОСЬМОМУ ИЗДАНИЮ
- 1. Функции комплексного переменного.
- 2. Производная.
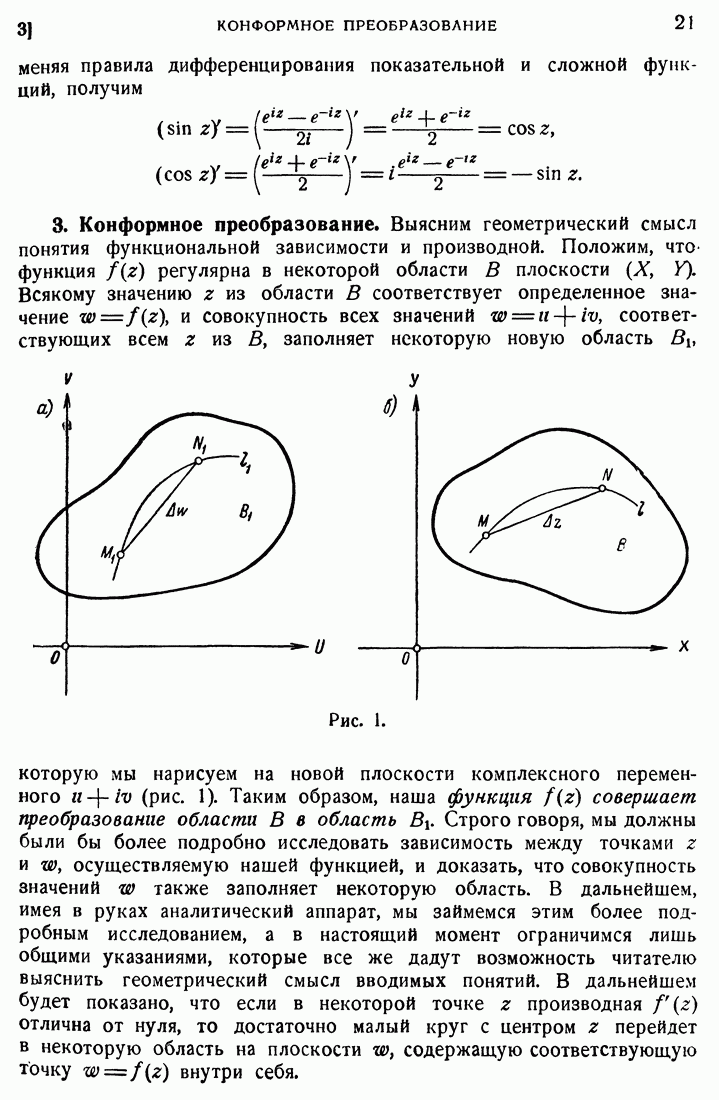
- 3. Конформное преобразование.
- 4. Интеграл.
- 5. Теорема Коши.
- 6. Основная формула интегрального исчисления.
- 7. Формула Коши.
- 8. Интегралы типа Коши.
- 9. Следствия формулы Коши.
- 10. Изолированные особые точки.
- 11. Бесконечные ряды с комплексными членами.
- 12. Теорема Вейерштрасса.
- 13. Степенные ряды.
- 14. Ряд Тейлора.
- 15. Ряд Лорана.
- 16. Примеры.
- 17. Изолированные особые точки. Бесконечно далекая точка.
- 18. Аналитическое продолжение.
- 19. Примеры многозначных функций.
- 20. Особые точки аналитических функций и римановы поверхности.
- 21. Теорема вычетов.
- 22. Теоремы о числе корней.
- 23. Обращение степенного ряда.
- 24. Принцип симметрии.
- 25. Ряд Тейлора на окружности круга сходимости.
- 26. Дополнительные сведения о формуле Коши.
- 27. Главное значение интеграла.
- 28. Главное значение интеграла (продолжение).
- 29. Интегралы типа Коши.
- 30. Интегралы типа Коши (продолжение).
- ГЛАВА II. КОНФОРМНОЕ ПРЕОБРАЗОВАНИЕ И ПЛОСКОЕ ПОЛЕ
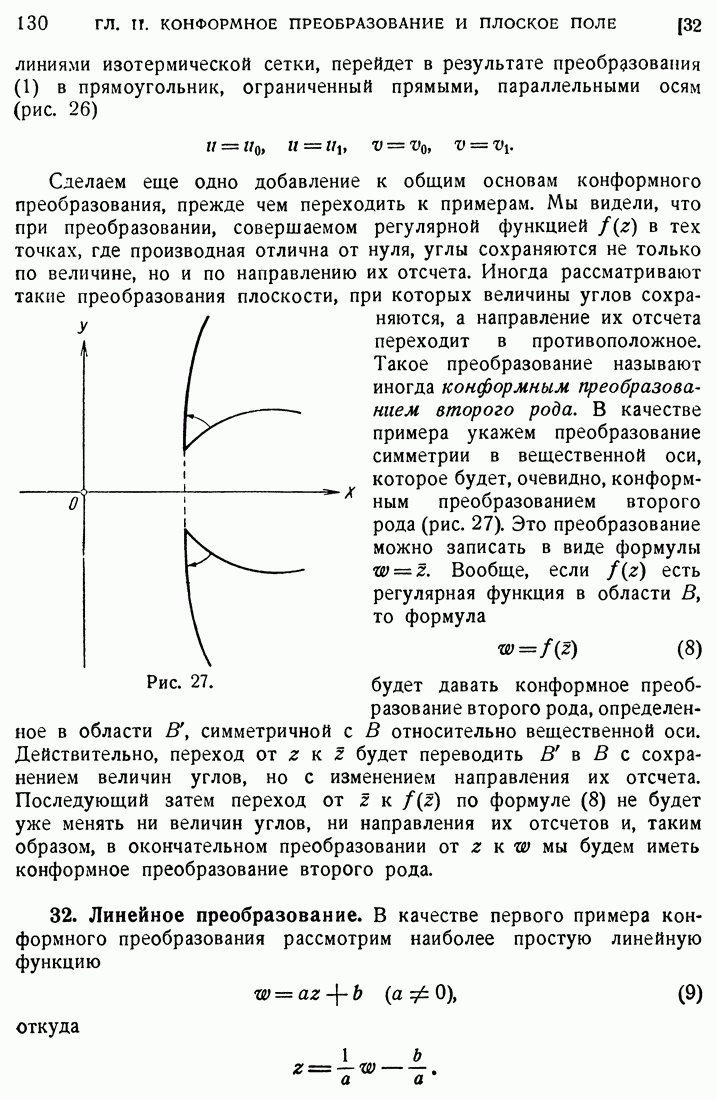
- 31. Конформное преобразование.
- 32. Линейное преобразование.
- 33. Дробно-линейное преобразование.
- 34. Функция w = z^2.
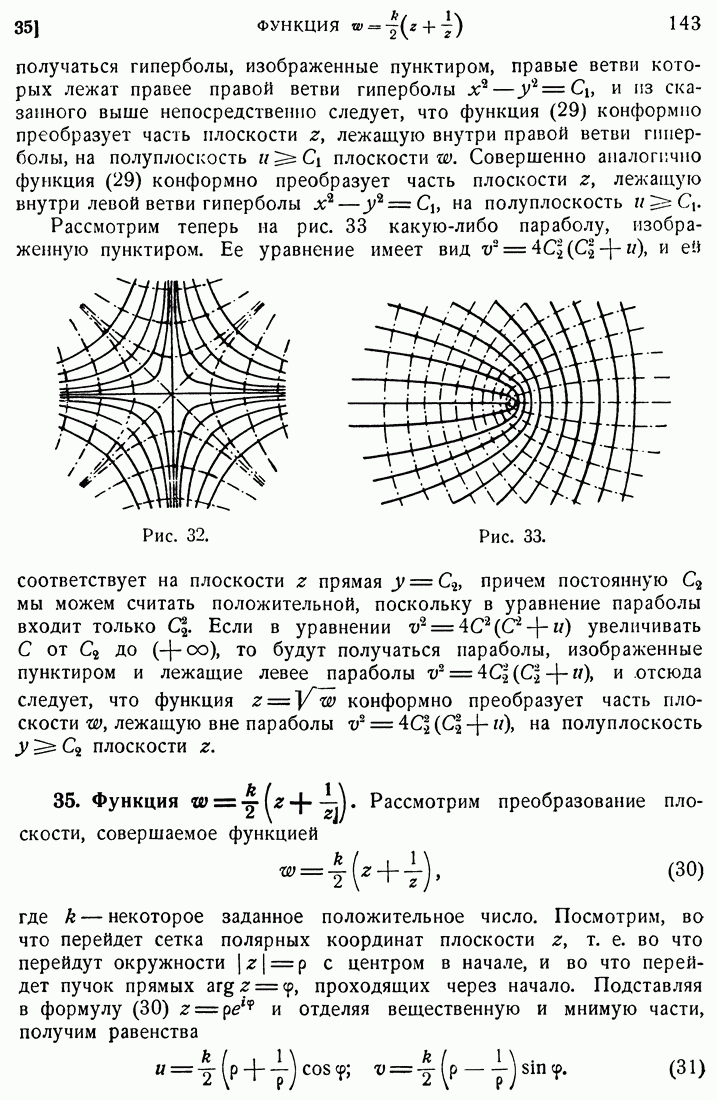
- 35. Функция …
- 36. Двуугольник и полоса.
- 37. Основная теорема.
- 38. Формула Кристоффеля.
- 39. Частные случаи.
- 40. Случай внешности многоугольника.
- 41. Минимальное свойство преобразования на круг.
- 42. Способ сопряженных тригонометрических рядов.
- 43. Плоское установившееся течение жидкости.
- 44. Примеры.
- 45. Задача полного обтекания.
- 46. Формула Н. Е. Жуковского.
- 47. Плоская электростатическая задача.
- 48. Формула Шварца.
- 49. Ядро ctg((s-t)/2).
- 50. Предельные задачи.
- 51. Бигармоническое уравнение.
- 52. Волновое уравнение и аналитические функции.
- 53. Основная теорема.
- 54. Дифракция плоской волны.
- 55. Отражение упругих волн от прямолинейной границы.
- ГЛАВА III. ПРИМЕНЕНИЕ ТЕОРИИ ВЫЧЕТОВ, ЦЕЛЫЕ И ДРОБНЫЕ ФУНКЦИИ
- 56. Интеграл Френеля.
- 57. Интегрирование выражений с тригонометрическими функциями.
- 58. Интегрирование рациональной дроби.
- 59. Некоторые новые типы интегралов с тригонометрическими функциями.
- 60. Лемма Жордана.
- 61. Представление некоторых функций контурными интегралами.
- 62. Примеры интегралов от многозначных функций.
- 63. Интегрирование системы линейных уравнений с постоянными коэффициентами.
- 64. Разложение дробной функции на простейшие дроби.
- 66. Построение мероморфной функции.
- 67. Целые функции.
- 68. Бесконечные произведения.
- 69. Построение целой функции по ее корням.
- 70. Интегралы, зависящие от параметра.
- 71. Эйлеров интеграл второго рода.
- 72. Эйлеров интеграл первого рода.
- 73. Бесконечное произведение для функции …
- 74. Представление Г(z) контурным интегралом.
- 75. Формула Стирлинга.
- 76. Формула суммирования Эйлера.
- 77. Числа Бернулли.
- 78. Метод скорейшего спуска.
- 79. Асимптотическое разложение интеграла.
- 80. Примеры.
- 81. Метод стационарной фазы.
- ГЛАВА IV. АНАЛИТИЧЕСКИЕ ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ И ФУНКЦИИ МАТРИЦ
- 82. Регулярные функции многих переменных.
- 83. Двойной интеграл и формула Коши.
- 84. Степенные ряды.
- 85. Аналитическое продолжение.
- 86. Функции матриц. Предварительные понятия.
- 87. Степенные ряды от одной матрицы.
- 88. Умножение степенных рядов. Обращение степенного ряда.
- 89. Дальнейшее исследование сходимости.
- 90. Интерполяционные полиномы.
- 91. Тождество Кейли. Формула Сильвестра.
- 92. Определение функций одной матрицы формулой Коши.
- 93. Аналитическое продолжение.
- 94. Логарифм матриц.
- 95. Обращение целой функции от матрицы в случае матриц второго порядка.
- 96. Системы линейных уравнений с постоянными коэффициентами.
- 97. Функции нескольких матриц.
- ГЛАВА V. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
- 98. Разложение решения в степенной ряд.
- 99. Аналитическое продолжение решения.
- 100. Окрестность особой точки.
- 101. Регулярная особая точка.
- 102. Уравнения класса Фукса.
- 103. Уравнение Гаусса.
- 104. Гипергеометрический ряд.
- 105. Полиномы Лежандра.
- 106. Полиномы Якоби.
- 107. Конформное преобразование и уравнение Гаусса.
- 108. Преобразование Лапласа.
- 109. Различный выбор решений.
- 110. Уравнение Бесселя.
- 111. Функции Ханкеля и интегральное представление решений уравнения Бесселя.
- 112. Асимптотические разложения.
- 113. Асимптотические разложения решений, полученных преобразованием Лапласа.
- 114. Асимптотические разложения решений уравнения Бесселя.
- 115. Вырождение уравнения Гаусса.
- 116. Формальные ряды в окрестности иррегулярной особой точки.
- 117. Построение асимптотических разложений методом после довательных приближений.
- 118. Функции Эйри.
- 119. Асимптотика при большом значении параметра.
- 120. Уравнения с периодическими коэффициентами.
- 121. Условия устойчивости и неустойчивости для уравнения Хилла.
- 122. Системы линейных дифференциальных уравнений.
- 123. Регулярная особая точка.
- 124. Регулярные системы.
- 125. Представление решения в окрестности особой точки.
- 126. Канонические решения.
- 127. Связь с регулярными решениями типа Фукса.
- 128. Случай любых Us.
- 129. Формальные разложения в окрестности иррегулярной особой точки.
- ГЛАВА VI. СПЕЦИАЛЬНЫЕ ФУНКЦИИ
- 130. Определение сферических функций.
- 131. Явные выражения сферических функций.
- 132. Свойство ортогональности.
- 133. Полиномы Лежандра.
- 134. Разложение по сферическим функциям.
- 135. Доказательство сходимости.
- 136. Связь сферических функций с предельными задачами.
- 137. Задачи Дирихле и Неймана.
- 138. Потенциал объемных масс.
- 139. Потенциал сферического слоя.
- 140. Электрон в центральном поле.
- 141. Шаровые функции и линейные представления группы вращения.
- 142. Функция Лежандра.
- 143. Функция Лежандра второго рода.
- § 2. ФУНКЦИИ БЕССЕЛЯ
- 144. Определение функций Бесселя.
- 145. Соотношения между функциями Бесселя.
- 146. Ортогональность функций Бесселя и их корни.
- 147. Производящая функция и интегральное представление.
- 148. Формула Фурье — Бесселя.
- 150. Разложение функций Неймана с целым значком.
- 151. Случай чисто мнимого аргумента.
- 152. Новые интегральные представления.
- 153. Асимптотические представления.
- 154. Функции Бесселя и уравнение Лапласа.
- 155. Волновое уравнение в цилиндрических координатах.
- 156. Волновое уравнение в сферических координатах.
- § 3. ПОЛИНОМЫ ЭРМИТА И ЛАГЕРРА
- 157. Линейный осциллятор и полиномы Эрмита.
- 158. Свойство ортогональности.
- 159. Производящая функция.
- 160. Параболические координаты и функции Эрмита.
- 161. Полиномы Лагерра.
- 162. Связь полиномов Эрмита и Лагерра.
- 163. Асимптотическое выражение полиномов Эрмита.
- 164. Асимптотическое выражение полиномов Лежандра.
- § 4. ЭЛЛИПТИЧЕСКИЕ ИНТЕГРАЛЫ И ЭЛЛИПТИЧЕСКИЕ ФУНКЦИИ
- 165. Приведение эллиптических интегралов к нормальному виду.
- 166. Приведение интегралов к тригонометрической форме.
- 167. Примеры.
- 168. Обращение эллиптического интеграла.
- 169. Общие свойства эллиптических функций.
- 170. Основная лемма.
- 171. Функции Вейерштрасса.
- 172. Дифференциальное уравнение для …
- 173. Функции …
- 174. Разложение целой периодической функции.
- 175. Новые обозначения.
- 176. Функция …
- 177. Функции …
- 178. Свойства функций тэта.
- 179. Выражение чисел … через …
- 180. Эллиптические функции Якоби.
- 181. Основные свойства функций Якоби.
- 182. Дифференциальные уравнения для функций Якоби.
- 183. Формулы сложения.
- 184. Связь функций p(u) и sn(u).
- 185. Эллиптические координаты.
- 186. Введение эллиптических функций.
- 187. Уравнение Лямэ.
- 188. Простой маятник.
- 189. Пример конформного преобразования.
- ДОБАВЛЕНИЕ. ПРИВЕДЕНИЕ МАТРИЦ К КАНОНИЧЕСКОЙ ФОРМЕ
- 191. Случай простых корней.
- 192. Первый этап преобразований в случае кратных корней.
- 193. Приведение к канонической форме.
- 194. Определение структуры канонической формы.
- 196. Пример.