| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
49. Ядро ctg((s-t)/2).
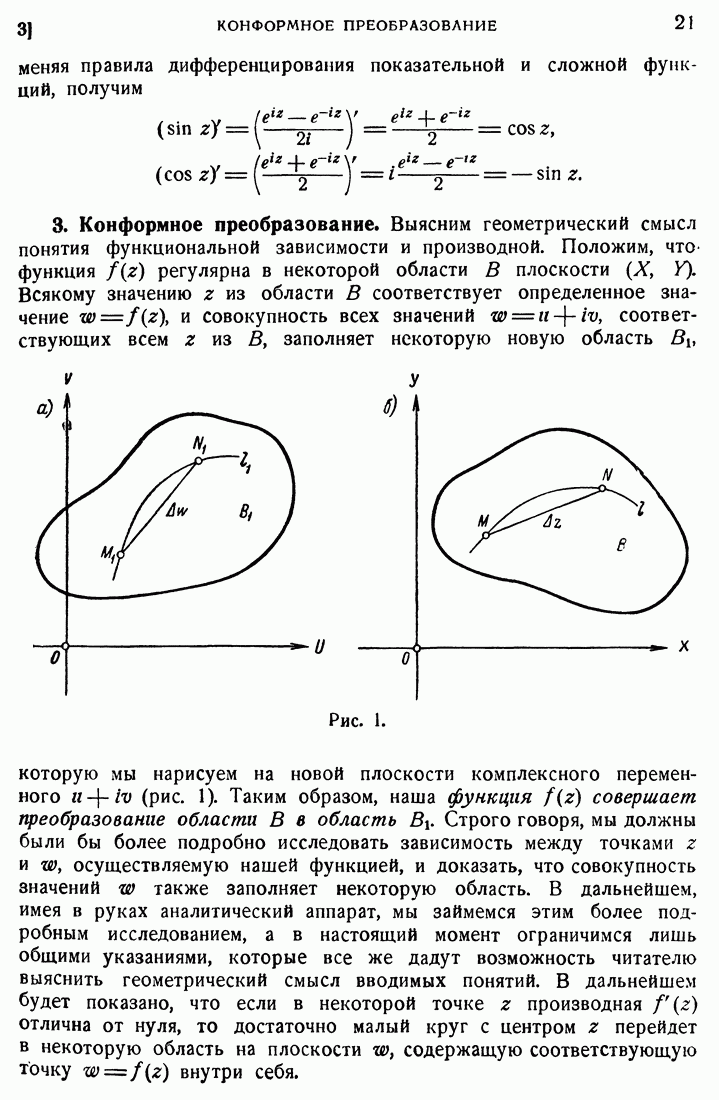
Применим сейчас основную теорему о предельных значениях интеграла типа Коши [29] к случаю окружности  с центром в начале и радиусом единица. Положим, что на этой окружности дана вещественная функция
с центром в начале и радиусом единица. Положим, что на этой окружности дана вещественная функция  , где
, где  удовлетворяющая условию Липшица. Мы можем, пользуясь формулой Шварца [48], построить регулярную внутри окружности функцию, вещественная часть которой имеет предельные значения и
удовлетворяющая условию Липшица. Мы можем, пользуясь формулой Шварца [48], построить регулярную внутри окружности функцию, вещественная часть которой имеет предельные значения и  на самой окружности:
на самой окружности:

или, принимая во внимание, что  ,
,

Полагая  и разбивая наш интеграл на два интеграла получим
и разбивая наш интеграл на два интеграла получим

Положим, что точка  к некоторой точке
к некоторой точке  окружности
окружности  Пользуясь теоремой о предельном значении интеграла типа Коши [29], получим предельное значение нашей функции:
Пользуясь теоремой о предельном значении интеграла типа Коши [29], получим предельное значение нашей функции:

или

но

и, отделяя в формуле (126) мнимую часть, получаем выражение предельных значений мнимой части через вещественную часть:

причем написанный интеграл надо понимать в смысле главного значения. Будем писать  вместо и
вместо и 

Напомним, что формула (125) даст ту регулярную внутри круга  функцию, мнимая часть которой равна нулю в центре круга. Принимая во внимание, что значение гармонической функции в центре круга равно среднему арифметическому ее значений на окружности
функцию, мнимая часть которой равна нулю в центре круга. Принимая во внимание, что значение гармонической функции в центре круга равно среднему арифметическому ее значений на окружности  можем написать
можем написать

Функцию и  можно считать периодической с периодом
можно считать периодической с периодом  и функция
и функция  получается также периодической, а в формуле (127) мы могли бы брать за промежуток интегрирования любой промежуток длины
получается также периодической, а в формуле (127) мы могли бы брать за промежуток интегрирования любой промежуток длины  Функция
Функция  имеет при
имеет при  простой полюс с вычетом, равным единице [21], и мы можем выразить ядро линейного преобразования (127) через ядро Коши:
простой полюс с вычетом, равным единице [21], и мы можем выразить ядро линейного преобразования (127) через ядро Коши:

где  аналитическая регулярная функция во всех точках отрезка
аналитическая регулярная функция во всех точках отрезка  . Совершенно так же, как и в [28], можно показать, что если периодическая функция и
. Совершенно так же, как и в [28], можно показать, что если периодическая функция и  удовлетворяет условию Липшица с показателем
удовлетворяет условию Липшица с показателем  то
то  удовлетворяет также условию Липшица с тем же показателем, если
удовлетворяет также условию Липшица с тем же показателем, если  и с любым показателем, меньшим единицы, если
и с любым показателем, меньшим единицы, если  Согласно (129) это утверждение вытекает также из аналогичного утверждения для ядра Коши.
Согласно (129) это утверждение вытекает также из аналогичного утверждения для ядра Коши.
Мы можем применить к функции  линейное преобразование (127) и получим таким образом некоторую новую функцию
линейное преобразование (127) и получим таким образом некоторую новую функцию  удовлетворяющую условию Липшица:
удовлетворяющую условию Липшица:

Функция  дает предельные значения мнимой части, если за предельные значения вещественной части принять v (?), причем
дает предельные значения мнимой части, если за предельные значения вещественной части принять v (?), причем

С другой стороны, если умножить регулярную функцию (125) на  получим регулярную функцию
получим регулярную функцию  . Но заданием вещественной части мнимая определяется с точностью до постоянного слагаемого и мы можем поэтому написать
. Но заданием вещественной части мнимая определяется с точностью до постоянного слагаемого и мы можем поэтому написать

Для определения постоянной С проинтегрируем обе части этого равенства по промежутку  и примем во внимание (130):
и примем во внимание (130):

и окончательно

т. е. двукратное применение преобразования (127) приводит с точностью до постоянного слагаемого к прежней функции с обратным знаком. Полученный результат мы можем записать в виде следующей формулы:

Это есть известная формула Гильберта, и ядро преобразования (127) естественно назвать ядром Гильберта. Заметим, что в левой части формулы (132) мы, как и в интеграле Фурье, не имеем права менять порядок интегрирования. Обозначая символически преобразование (127) одной буквой А, можем написать формулу (127) в виде  причем в обеих функциях аргумент обозначен буквой s. При этом формула Гильберта (132) запишется в виде
причем в обеих функциях аргумент обозначен буквой s. При этом формула Гильберта (132) запишется в виде

Формулу (127) можно рассматривать как интегральное уравнение относительно и  при заданной функции v (t). Из предыдущих рассуждений следует, что для его разрешимости необходимо выполнение условия (128). Одним из решений этого уравнения будет в силу (131) функция
при заданной функции v (t). Из предыдущих рассуждений следует, что для его разрешимости необходимо выполнение условия (128). Одним из решений этого уравнения будет в силу (131) функция

Это есть то решение уравнения (131), которое удовлетворяет условию

Иначе говоря, это есть та мнимая часть регулярной функции  которая обращается в нуль в начале координат. Если значение функции и
которая обращается в нуль в начале координат. Если значение функции и  в начале координат равно С, то
в начале координат равно С, то

причем и  есть решение однородного уравнения
есть решение однородного уравнения

ибо если и  , то мнимая часть
, то мнимая часть  равная нулю в начале, равна, очевидно, нулю. Формула (134) дает все решения уравнения (127), так как по вещественной части мнимая определяется с точностью до постоянного слагаемого. В предыдущих рассуждениях считалось, что заданная и искомая функции удовлетворяют условию Липшица.
равная нулю в начале, равна, очевидно, нулю. Формула (134) дает все решения уравнения (127), так как по вещественной части мнимая определяется с точностью до постоянного слагаемого. В предыдущих рассуждениях считалось, что заданная и искомая функции удовлетворяют условию Липшица.
Мы можем написать преобразование (127) в виде обычного несобственного интеграла, аналогично тому как это мы делали в случае ядра Коши,
Действительно, принимая во внимание, что

так как однородное уравнение (127) имеет в качестве решения постоянную  можем переписать формулу (127) в виде
можем переписать формулу (127) в виде

Положим, что функция и  имеет непрерывную производную. Принимая во внимание, что
имеет непрерывную производную. Принимая во внимание, что

применяя к интегралу (127) формулу интегрирования по частям на промежутках  и учитывая еще формулу
и учитывая еще формулу

получим для  следующее выражение:
следующее выражение:

причем справа стоит обычный несобственный интеграл.
Если и  удовлетворяет условию Липшица, то функция комплексного переменного
удовлетворяет условию Липшица, то функция комплексного переменного  определенная формулой (125), как мы видели выше, будет непрерывной вплоть до окружности
определенная формулой (125), как мы видели выше, будет непрерывной вплоть до окружности  Пусть
Пусть

есть ряд Фурье функции и  . Для функции
. Для функции  будем иметь ряд Фурье
будем иметь ряд Фурье 

В силу уравнения замкнутости [II, 169]

и, следовательно,

причем знак равенства имеет место тогда и только тогда, когда  Итак, в результате преобразования (127) интеграл от квадрата функции по промежутку
Итак, в результате преобразования (127) интеграл от квадрата функции по промежутку  те) может только уменьшиться. Отметим при этом, что мы считаем функцию и
те) может только уменьшиться. Отметим при этом, что мы считаем функцию и  вещественной. Мы видим, таким образом, что преобразование (127) равносильно переходу от ряда Фурье
вещественной. Мы видим, таким образом, что преобразование (127) равносильно переходу от ряда Фурье  к ряду Фурье (1362).
к ряду Фурье (1362).
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ К ВОСЬМОМУ ИЗДАНИЮ
- 1. Функции комплексного переменного.
- 2. Производная.
- 3. Конформное преобразование.
- 4. Интеграл.
- 5. Теорема Коши.
- 6. Основная формула интегрального исчисления.
- 7. Формула Коши.
- 8. Интегралы типа Коши.
- 9. Следствия формулы Коши.
- 10. Изолированные особые точки.
- 11. Бесконечные ряды с комплексными членами.
- 12. Теорема Вейерштрасса.
- 13. Степенные ряды.
- 14. Ряд Тейлора.
- 15. Ряд Лорана.
- 16. Примеры.
- 17. Изолированные особые точки. Бесконечно далекая точка.
- 18. Аналитическое продолжение.
- 19. Примеры многозначных функций.
- 20. Особые точки аналитических функций и римановы поверхности.
- 21. Теорема вычетов.
- 22. Теоремы о числе корней.
- 23. Обращение степенного ряда.
- 24. Принцип симметрии.
- 25. Ряд Тейлора на окружности круга сходимости.
- 26. Дополнительные сведения о формуле Коши.
- 27. Главное значение интеграла.
- 28. Главное значение интеграла (продолжение).
- 29. Интегралы типа Коши.
- 30. Интегралы типа Коши (продолжение).
- ГЛАВА II. КОНФОРМНОЕ ПРЕОБРАЗОВАНИЕ И ПЛОСКОЕ ПОЛЕ
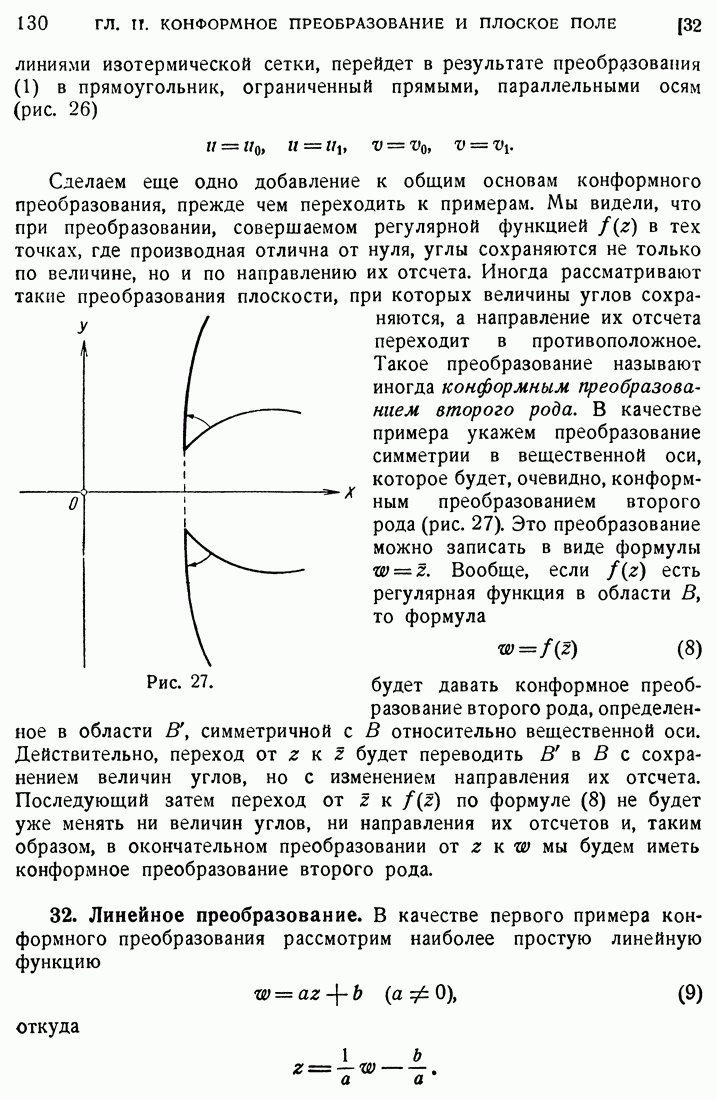
- 31. Конформное преобразование.
- 32. Линейное преобразование.
- 33. Дробно-линейное преобразование.
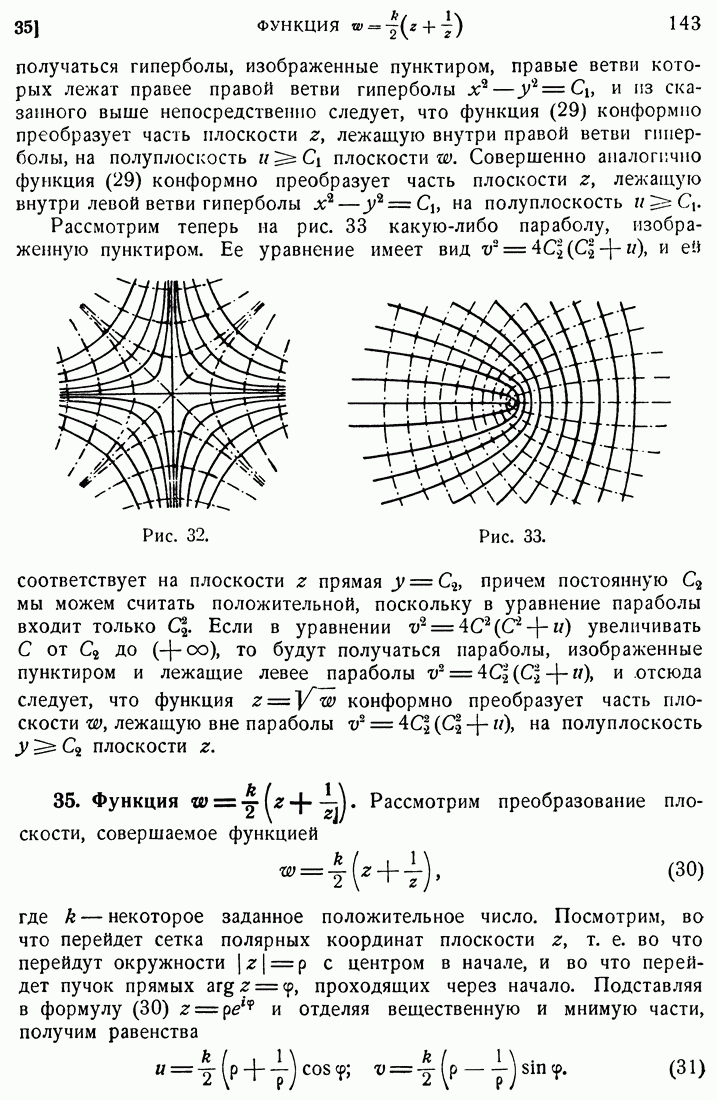
- 34. Функция w = z^2.
- 35. Функция …
- 36. Двуугольник и полоса.
- 37. Основная теорема.
- 38. Формула Кристоффеля.
- 39. Частные случаи.
- 40. Случай внешности многоугольника.
- 41. Минимальное свойство преобразования на круг.
- 42. Способ сопряженных тригонометрических рядов.
- 43. Плоское установившееся течение жидкости.
- 44. Примеры.
- 45. Задача полного обтекания.
- 46. Формула Н. Е. Жуковского.
- 47. Плоская электростатическая задача.
- 48. Формула Шварца.
- 49. Ядро ctg((s-t)/2).
- 50. Предельные задачи.
- 51. Бигармоническое уравнение.
- 52. Волновое уравнение и аналитические функции.
- 53. Основная теорема.
- 54. Дифракция плоской волны.
- 55. Отражение упругих волн от прямолинейной границы.
- ГЛАВА III. ПРИМЕНЕНИЕ ТЕОРИИ ВЫЧЕТОВ, ЦЕЛЫЕ И ДРОБНЫЕ ФУНКЦИИ
- 56. Интеграл Френеля.
- 57. Интегрирование выражений с тригонометрическими функциями.
- 58. Интегрирование рациональной дроби.
- 59. Некоторые новые типы интегралов с тригонометрическими функциями.
- 60. Лемма Жордана.
- 61. Представление некоторых функций контурными интегралами.
- 62. Примеры интегралов от многозначных функций.
- 63. Интегрирование системы линейных уравнений с постоянными коэффициентами.
- 64. Разложение дробной функции на простейшие дроби.
- 66. Построение мероморфной функции.
- 67. Целые функции.
- 68. Бесконечные произведения.
- 69. Построение целой функции по ее корням.
- 70. Интегралы, зависящие от параметра.
- 71. Эйлеров интеграл второго рода.
- 72. Эйлеров интеграл первого рода.
- 73. Бесконечное произведение для функции …
- 74. Представление Г(z) контурным интегралом.
- 75. Формула Стирлинга.
- 76. Формула суммирования Эйлера.
- 77. Числа Бернулли.
- 78. Метод скорейшего спуска.
- 79. Асимптотическое разложение интеграла.
- 80. Примеры.
- 81. Метод стационарной фазы.
- ГЛАВА IV. АНАЛИТИЧЕСКИЕ ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ И ФУНКЦИИ МАТРИЦ
- 82. Регулярные функции многих переменных.
- 83. Двойной интеграл и формула Коши.
- 84. Степенные ряды.
- 85. Аналитическое продолжение.
- 86. Функции матриц. Предварительные понятия.
- 87. Степенные ряды от одной матрицы.
- 88. Умножение степенных рядов. Обращение степенного ряда.
- 89. Дальнейшее исследование сходимости.
- 90. Интерполяционные полиномы.
- 91. Тождество Кейли. Формула Сильвестра.
- 92. Определение функций одной матрицы формулой Коши.
- 93. Аналитическое продолжение.
- 94. Логарифм матриц.
- 95. Обращение целой функции от матрицы в случае матриц второго порядка.
- 96. Системы линейных уравнений с постоянными коэффициентами.
- 97. Функции нескольких матриц.
- ГЛАВА V. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
- 98. Разложение решения в степенной ряд.
- 99. Аналитическое продолжение решения.
- 100. Окрестность особой точки.
- 101. Регулярная особая точка.
- 102. Уравнения класса Фукса.
- 103. Уравнение Гаусса.
- 104. Гипергеометрический ряд.
- 105. Полиномы Лежандра.
- 106. Полиномы Якоби.
- 107. Конформное преобразование и уравнение Гаусса.
- 108. Преобразование Лапласа.
- 109. Различный выбор решений.
- 110. Уравнение Бесселя.
- 111. Функции Ханкеля и интегральное представление решений уравнения Бесселя.
- 112. Асимптотические разложения.
- 113. Асимптотические разложения решений, полученных преобразованием Лапласа.
- 114. Асимптотические разложения решений уравнения Бесселя.
- 115. Вырождение уравнения Гаусса.
- 116. Формальные ряды в окрестности иррегулярной особой точки.
- 117. Построение асимптотических разложений методом после довательных приближений.
- 118. Функции Эйри.
- 119. Асимптотика при большом значении параметра.
- 120. Уравнения с периодическими коэффициентами.
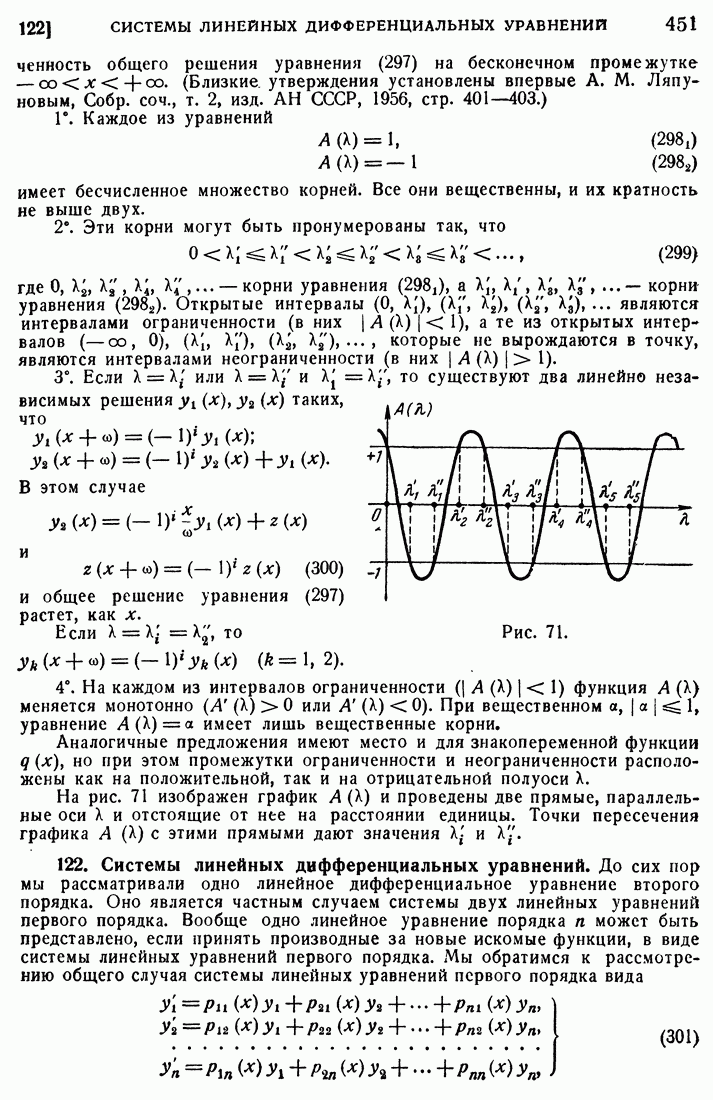
- 121. Условия устойчивости и неустойчивости для уравнения Хилла.
- 122. Системы линейных дифференциальных уравнений.
- 123. Регулярная особая точка.
- 124. Регулярные системы.
- 125. Представление решения в окрестности особой точки.
- 126. Канонические решения.
- 127. Связь с регулярными решениями типа Фукса.
- 128. Случай любых Us.
- 129. Формальные разложения в окрестности иррегулярной особой точки.
- ГЛАВА VI. СПЕЦИАЛЬНЫЕ ФУНКЦИИ
- 130. Определение сферических функций.
- 131. Явные выражения сферических функций.
- 132. Свойство ортогональности.
- 133. Полиномы Лежандра.
- 134. Разложение по сферическим функциям.
- 135. Доказательство сходимости.
- 136. Связь сферических функций с предельными задачами.
- 137. Задачи Дирихле и Неймана.
- 138. Потенциал объемных масс.
- 139. Потенциал сферического слоя.
- 140. Электрон в центральном поле.
- 141. Шаровые функции и линейные представления группы вращения.
- 142. Функция Лежандра.
- 143. Функция Лежандра второго рода.
- § 2. ФУНКЦИИ БЕССЕЛЯ
- 144. Определение функций Бесселя.
- 145. Соотношения между функциями Бесселя.
- 146. Ортогональность функций Бесселя и их корни.
- 147. Производящая функция и интегральное представление.
- 148. Формула Фурье — Бесселя.
- 150. Разложение функций Неймана с целым значком.
- 151. Случай чисто мнимого аргумента.
- 152. Новые интегральные представления.
- 153. Асимптотические представления.
- 154. Функции Бесселя и уравнение Лапласа.
- 155. Волновое уравнение в цилиндрических координатах.
- 156. Волновое уравнение в сферических координатах.
- § 3. ПОЛИНОМЫ ЭРМИТА И ЛАГЕРРА
- 157. Линейный осциллятор и полиномы Эрмита.
- 158. Свойство ортогональности.
- 159. Производящая функция.
- 160. Параболические координаты и функции Эрмита.
- 161. Полиномы Лагерра.
- 162. Связь полиномов Эрмита и Лагерра.
- 163. Асимптотическое выражение полиномов Эрмита.
- 164. Асимптотическое выражение полиномов Лежандра.
- § 4. ЭЛЛИПТИЧЕСКИЕ ИНТЕГРАЛЫ И ЭЛЛИПТИЧЕСКИЕ ФУНКЦИИ
- 165. Приведение эллиптических интегралов к нормальному виду.
- 166. Приведение интегралов к тригонометрической форме.
- 167. Примеры.
- 168. Обращение эллиптического интеграла.
- 169. Общие свойства эллиптических функций.
- 170. Основная лемма.
- 171. Функции Вейерштрасса.
- 172. Дифференциальное уравнение для …
- 173. Функции …
- 174. Разложение целой периодической функции.
- 175. Новые обозначения.
- 176. Функция …
- 177. Функции …
- 178. Свойства функций тэта.
- 179. Выражение чисел … через …
- 180. Эллиптические функции Якоби.
- 181. Основные свойства функций Якоби.
- 182. Дифференциальные уравнения для функций Якоби.
- 183. Формулы сложения.
- 184. Связь функций p(u) и sn(u).
- 185. Эллиптические координаты.
- 186. Введение эллиптических функций.
- 187. Уравнение Лямэ.
- 188. Простой маятник.
- 189. Пример конформного преобразования.
- ДОБАВЛЕНИЕ. ПРИВЕДЕНИЕ МАТРИЦ К КАНОНИЧЕСКОЙ ФОРМЕ
- 191. Случай простых корней.
- 192. Первый этап преобразований в случае кратных корней.
- 193. Приведение к канонической форме.
- 194. Определение структуры канонической формы.
- 196. Пример.