| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
20. Особые точки аналитических функций и римановы поверхности.
В предыдущем пункте мы разобрали ряд примеров многозначных функций и построили соответствующие им римановы поверхности, на которых они однозначны. Рассмотрим соответствующие вопросы в общем случае. Мы не будем при этом за недостатком места входить в детали и ограничимся общими указаниями. Предварительно» выясним понятие об изолированной особой точке при аналитическом продолжении.

Рис. 18.
Пусть в точке  задан начальный элемент аналитической функции
задан начальный элемент аналитической функции  который мы затем продолжаем вдоль линии
который мы затем продолжаем вдоль линии  . Положим, что аналитическое продолжение возможно до точки
. Положим, что аналитическое продолжение возможно до точки  исключительно, но не дальше, так что точка
исключительно, но не дальше, так что точка  является особой точкой при аналитическом продолжении вдоль I [18]. Пусть существует круг К с центром
является особой точкой при аналитическом продолжении вдоль I [18]. Пусть существует круг К с центром  такой, что элементы функции
такой, что элементы функции  соответствующие точкам участка
соответствующие точкам участка  линии I (рис. 18), лежащего внутри К, можно аналитически продолжать вдоль любой линии, лежащей внутри К и не проходящей через точку
линии I (рис. 18), лежащего внутри К, можно аналитически продолжать вдоль любой линии, лежащей внутри К и не проходящей через точку  . В этом случае точка
. В этом случае точка  называется изолированной особой точкой f(z) (соответствующей пути l). Упомянутое аналитическое продолжение по всевозможным линиям внутри К может привести к однозначной или многозначной функции внутри К. В первом случае полученная однозначная внутри К функция будет регулярной везде внутри
называется изолированной особой точкой f(z) (соответствующей пути l). Упомянутое аналитическое продолжение по всевозможным линиям внутри К может привести к однозначной или многозначной функции внутри К. В первом случае полученная однозначная внутри К функция будет регулярной везде внутри  кроме
кроме  будет разлагаться в ряд Лорана по целым степеням (z — b), и точка
будет разлагаться в ряд Лорана по целым степеням (z — b), и точка  будет или полюсом или существенно особой точкой нашей аналитической функции f(z) (при аналитическом продолжении вдоль l). Во втором случае, при многозначности получаемой внутри К функции, точка
будет или полюсом или существенно особой точкой нашей аналитической функции f(z) (при аналитическом продолжении вдоль l). Во втором случае, при многозначности получаемой внутри К функции, точка  называется точкой разветвления.
называется точкой разветвления.
Положим, что при всевозможных аналитических продолжениях внутри К мы получаем в некоторой точке  внутри К конечное число различных элементов. Обозначим это число через
внутри К конечное число различных элементов. Обозначим это число через  . Нетрудно видеть, что в любой другой точке
. Нетрудно видеть, что в любой другой точке  , принадлежащей
, принадлежащей  , мы получим тоже
, мы получим тоже  различных элементов. Это непосредственно следует из того, что при аналитическом продолжении из а в
различных элементов. Это непосредственно следует из того, что при аналитическом продолжении из а в  или из
или из  в а различных исходных элементов по одному и тому же пути в конечной точке получаются различные элементы. В рассматриваемом случае точка z = b называется точкой разветвления порядка (
в а различных исходных элементов по одному и тому же пути в конечной точке получаются различные элементы. В рассматриваемом случае точка z = b называется точкой разветвления порядка ( ). Если число различных элементов, получаемых при аналитическом продолжении внутри К, в каждой точке К не конечно, то z = b называется точкой разветвления бесконечного порядка.
). Если число различных элементов, получаемых при аналитическом продолжении внутри К, в каждой точке К не конечно, то z = b называется точкой разветвления бесконечного порядка.
Рассмотрим подробнее случай точки разветвления конечного порядка ( ). По условию аналитическое продолжение внутри К выполнимо, исключая точку z = b. Такой круг К с исключенной точкой z = b есть двусвязная область. Возьмем
). По условию аналитическое продолжение внутри К выполнимо, исключая точку z = b. Такой круг К с исключенной точкой z = b есть двусвязная область. Возьмем  экземпляров круга К и разрежем каждый из этих экземпляров вдоль одного и того же радиуса. Такой разрезанный вдоль радиуса круг
экземпляров круга К и разрежем каждый из этих экземпляров вдоль одного и того же радиуса. Такой разрезанный вдоль радиуса круг  будет односвязной областью. Возьмем внутри каждого экземпляра одну и ту же точку
будет односвязной областью. Возьмем внутри каждого экземпляра одну и ту же точку  . Мы имеем в этой точке
. Мы имеем в этой точке  элементов нашей аналитической функции. Возьмем в каждом экземпляре в точке z = а определенный элемент и будем его аналитически продолжать внутри По теореме однозначности [18] получим в каждом экземпляре определенную однозначную функцию. Будем называть один из берегов разреза в каждом экземпляре левым, а другой — правым. Например, назовем правым берегом такой берег, что из его точек можно попасть на левый берег, двигаясь внутри
элементов нашей аналитической функции. Возьмем в каждом экземпляре в точке z = а определенный элемент и будем его аналитически продолжать внутри По теореме однозначности [18] получим в каждом экземпляре определенную однозначную функцию. Будем называть один из берегов разреза в каждом экземпляре левым, а другой — правым. Например, назовем правым берегом такой берег, что из его точек можно попасть на левый берег, двигаясь внутри  и обходя z = b против часовой стрелки. Возьмем некоторый экземпляр круга
и обходя z = b против часовой стрелки. Возьмем некоторый экземпляр круга  с определенной на нём однозначной функцией. Назовем этот экземпляр первым, а определенную на нем однозначную функцию обозначим через
с определенной на нём однозначной функцией. Назовем этот экземпляр первым, а определенную на нем однозначную функцию обозначим через  . Значения
. Значения  на левом берегу разреза будут совпадать со значениями нашей функции на правом берегу разреза в некотором другом экземпляре
на левом берегу разреза будут совпадать со значениями нашей функции на правом берегу разреза в некотором другом экземпляре  . Назовем этот последний экземпляр
. Назовем этот последний экземпляр  вторым, а определенную на нем функцию обозначим через
вторым, а определенную на нем функцию обозначим через  . Соединим мысленно левый берег первого экземпляра с правым берегом второго. Значения
. Соединим мысленно левый берег первого экземпляра с правым берегом второго. Значения  на левом берегу второго экземпляра будут совпадать со значениями нашей функции на правом берегу разреза в некотором другом экземпляре
на левом берегу второго экземпляра будут совпадать со значениями нашей функции на правом берегу разреза в некотором другом экземпляре  . Назовем этот экземпляр третьим, а определенную на нем функцию обозначим через
. Назовем этот экземпляр третьим, а определенную на нем функцию обозначим через  . Соединим мысленно левый берег второго экземпляра с правым берегом третьего экземпляра. Продолжая так и дальше, дойдем до последнего экземпляра с номером
. Соединим мысленно левый берег второго экземпляра с правым берегом третьего экземпляра. Продолжая так и дальше, дойдем до последнего экземпляра с номером  . Нетрудно видеть, что значения
. Нетрудно видеть, что значения  на левом берегу этого
на левом берегу этого  -го экземпляра должны совпадать со значениями
-го экземпляра должны совпадать со значениями  на правом берегу первого экземпляра. Соединим мысленно эти два берега.
на правом берегу первого экземпляра. Соединим мысленно эти два берега.
Таким образом мы получим  -листный круг L с точкой разветвления
-листный круг L с точкой разветвления  порядка
порядка  . Эта точка считается совпадающей на всех экземплярах. На
. Эта точка считается совпадающей на всех экземплярах. На  - листном круге наша функция будет однозначной и регулярной везде за исключением точки z = b. Введем вместо z новую независимую переменную
- листном круге наша функция будет однозначной и регулярной везде за исключением точки z = b. Введем вместо z новую независимую переменную

где  причем
причем  фиксировано определенным образом в некоторой точке L. Точка z = b перейдет в
фиксировано определенным образом в некоторой точке L. Точка z = b перейдет в  Общее изменение аргумента на L при обходе
Общее изменение аргумента на L при обходе  равно
равно  а при обходе
а при обходе  общее изменение аргумента будет
общее изменение аргумента будет  Круг I, имеющий
Круг I, имеющий  листов, перейдет на плоскости
листов, перейдет на плоскости  в однолистный круг С с центром
в однолистный круг С с центром  и радиусом где R есть радиус L. В этом однолистном круге С наша функция будет однозначной и регулярной, кроме, может быть, точки
и радиусом где R есть радиус L. В этом однолистном круге С наша функция будет однозначной и регулярной, кроме, может быть, точки  Следовательно, она будет разлагаться внутри С в ряд Лорана:
Следовательно, она будет разлагаться внутри С в ряд Лорана:

или, если вернуться к прежней переменной:

т. е. в окрестности точки разветвления порядка  функция разлагается по целым степеням аргумента (112). Можно произвольным, но определенным образом фиксировать значение аргумента (112) в некоторой точке z из окрестности точки
функция разлагается по целым степеням аргумента (112). Можно произвольным, но определенным образом фиксировать значение аргумента (112) в некоторой точке z из окрестности точки  . Могут представиться различные случаи в отношении разложения (113). Может случиться, что в этом разложении вовсе не будет членов с отрицательными значениями
. Могут представиться различные случаи в отношении разложения (113). Может случиться, что в этом разложении вовсе не будет членов с отрицательными значениями  :
:

При этом, очевидно,  при
при  причем z может стремиться к b любым образом, оставаясь лишь в L. В рассматриваемом случае полагаем
причем z может стремиться к b любым образом, оставаясь лишь в L. В рассматриваемом случае полагаем  и назовем
и назовем  точкой разветвления регулярного типа. Если разложение (113) содержит лишь конечное число членов с отрицательными значениями
точкой разветвления регулярного типа. Если разложение (113) содержит лишь конечное число членов с отрицательными значениями  , то
, то  при
при  . В этом случае полагаем
. В этом случае полагаем  и называем
и называем  точкой разветвления полярного типа. Если разложение (113) содержит бесчисленное множество членов с отрицательными значениями
точкой разветвления полярного типа. Если разложение (113) содержит бесчисленное множество членов с отрицательными значениями  , то назовем
, то назовем  точкой разветвления существенно особого типа.
точкой разветвления существенно особого типа.
Все предыдущие определения можно перенести и на бесконечно далекую точку. Положим, что совершается аналитическое продолжение  вдоль контура l и существует такая окрестность
вдоль контура l и существует такая окрестность  бесконечно далекой точки (рис. 19), что элементы функции
бесконечно далекой точки (рис. 19), что элементы функции  соответствующие точкам дуги
соответствующие точкам дуги  принадлежащей
принадлежащей  можно аналитически продолжать по любому пути, лежащему внутри
можно аналитически продолжать по любому пути, лежащему внутри 
Если это аналитическое продолжение дает однозначную функцию, то точка  будет или регулярной точкой для
будет или регулярной точкой для  или полюсом, или существенно особой точкой [10]. При многозначности упомянутого аналитического продолжения
или полюсом, или существенно особой точкой [10]. При многозначности упомянутого аналитического продолжения  называют точкой разветвления. Если эта точка разветвления будет конечного порядка
называют точкой разветвления. Если эта точка разветвления будет конечного порядка  то в ее окрестности будет иметь место разложение
то в ее окрестности будет иметь место разложение

причем дословно можно повторить все, что сказано выше о таком разложении. Характер точки  может зависеть, конечно, от того пути аналитического продолжения
может зависеть, конечно, от того пути аналитического продолжения  которым мы приходим в окрестность бесконечно далекой точки.
которым мы приходим в окрестность бесконечно далекой точки.

Рис. 19.
Выясним теперь в основных чертах понятие римановой поверхности для данной многозначной аналитической функции  Положим, что при аналитическом продолжении исходного элемента мы пришли в некоторую точку
Положим, что при аналитическом продолжении исходного элемента мы пришли в некоторую точку  Мы будем иметь в этой точке некоторый элемент, т. е. ряд, расположенный по целым положительным степеням (
Мы будем иметь в этой точке некоторый элемент, т. е. ряд, расположенный по целым положительным степеням ( ). Этот ряд может быть перестроен по целым положительным степеням (
). Этот ряд может быть перестроен по целым положительным степеням ( ), где Р — любая точка из окрестности точки
), где Р — любая точка из окрестности точки  т. е. элемент в точке
т. е. элемент в точке  дает и элементы во всех точках, достаточно «близких к а. Каждому такому элементу мы сопоставляем точку
дает и элементы во всех точках, достаточно «близких к а. Каждому такому элементу мы сопоставляем точку  являющуюся центром соответственного круга сходимости степенного ряда (элемента). Упомянутому элементу с центром
являющуюся центром соответственного круга сходимости степенного ряда (элемента). Упомянутому элементу с центром  мы сопоставляем именно эту точку а. Тем элементам, которые из него получаются в близких точках
мы сопоставляем именно эту точку а. Тем элементам, которые из него получаются в близких точках  мы сопоставляем точки
мы сопоставляем точки  принадлежащие окрестности
принадлежащие окрестности  Совершая аналитическое продолжение, мы получаем все новые и новые элементы, а тем самым — все новые и новые точки z римановой поверхности. Если при возвращении в точку
Совершая аналитическое продолжение, мы получаем все новые и новые элементы, а тем самым — все новые и новые точки z римановой поверхности. Если при возвращении в точку  получится элемент функции, который уже имелся раньше, то мы отождествим ее с прежней точкой
получится элемент функции, который уже имелся раньше, то мы отождествим ее с прежней точкой  . Если же при аналитическом продолжении при возвращении в точку
. Если же при аналитическом продолжении при возвращении в точку  получим аналитический элемент (ряд, расположенный по целым неотрицательным степеням
получим аналитический элемент (ряд, расположенный по целым неотрицательным степеням  отличный от исходного, то полученная точка
отличный от исходного, то полученная точка  считается отличной от исходной.
считается отличной от исходной.
Значения функции и ее нескольких последовательных производных могут и совпадать в этих точках z = а. Речь идет о различии ряда Тейлора, рассматриваемого в целом. Как мы указывали выше, можно совершать аналитическое продолжение через полюс и бесконечно далекую точку. На полученной таким образом римановой поверхности полученная аналитическим продолжением функция однозначна. К этой поверхности причисляют полюсы и точки разветвления конечного порядка регулярного или полярного типа. В этих последних точках функция имеет определенное конечное или бесконечное значение.
Кратко говоря, аналитическое продолжение создает риманову поверхность. Полная полученная таким образом поверхность может состоять из бесчисленного множества листов. Заметим, что риманова поверхность аналитической функции  , естественно, не всегда может быть получена путем преобразования плоскости w при помощи однозначной функции
, естественно, не всегда может быть получена путем преобразования плоскости w при помощи однозначной функции  как это имело место в простейших примерах из [19].
как это имело место в простейших примерах из [19].
Отметим, что мы лишь в самых общих чертах коснулись понятия римановой поверхности многозначной аналитической функции. Строгое изложение можно найти, например, в книгах: Н. Wеу 1, Die Idee der Riemannschen Flache; А. Гуpвиц, P. Курант, Теория функций, «Наука», 1968.
В заключение настоящего пункта обратим внимание на то, что при аналитическом продолжении особые точки могут быть и неизолированными. Например, может случиться, что исходный степенной ряд непродолжим, т. е. что всякая точка окружности его круга сходимости является особой точкой. Примером такого непродолжимого степенного ряда является ряд

радиус сходимости которого равен единице.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К ВОСЬМОМУ ИЗДАНИЮ
- 1. Функции комплексного переменного.
- 2. Производная.
- 3. Конформное преобразование.
- 4. Интеграл.
- 5. Теорема Коши.
- 6. Основная формула интегрального исчисления.
- 7. Формула Коши.
- 8. Интегралы типа Коши.
- 9. Следствия формулы Коши.
- 10. Изолированные особые точки.
- 11. Бесконечные ряды с комплексными членами.
- 12. Теорема Вейерштрасса.
- 13. Степенные ряды.
- 14. Ряд Тейлора.
- 15. Ряд Лорана.
- 16. Примеры.
- 17. Изолированные особые точки. Бесконечно далекая точка.
- 18. Аналитическое продолжение.
- 19. Примеры многозначных функций.
- 20. Особые точки аналитических функций и римановы поверхности.
- 21. Теорема вычетов.
- 22. Теоремы о числе корней.
- 23. Обращение степенного ряда.
- 24. Принцип симметрии.
- 25. Ряд Тейлора на окружности круга сходимости.
- 26. Дополнительные сведения о формуле Коши.
- 27. Главное значение интеграла.
- 28. Главное значение интеграла (продолжение).
- 29. Интегралы типа Коши.
- 30. Интегралы типа Коши (продолжение).
- ГЛАВА II. КОНФОРМНОЕ ПРЕОБРАЗОВАНИЕ И ПЛОСКОЕ ПОЛЕ
- 31. Конформное преобразование.
- 32. Линейное преобразование.
- 33. Дробно-линейное преобразование.
- 34. Функция w = z^2.
- 35. Функция …
- 36. Двуугольник и полоса.
- 37. Основная теорема.
- 38. Формула Кристоффеля.
- 39. Частные случаи.
- 40. Случай внешности многоугольника.
- 41. Минимальное свойство преобразования на круг.
- 42. Способ сопряженных тригонометрических рядов.
- 43. Плоское установившееся течение жидкости.
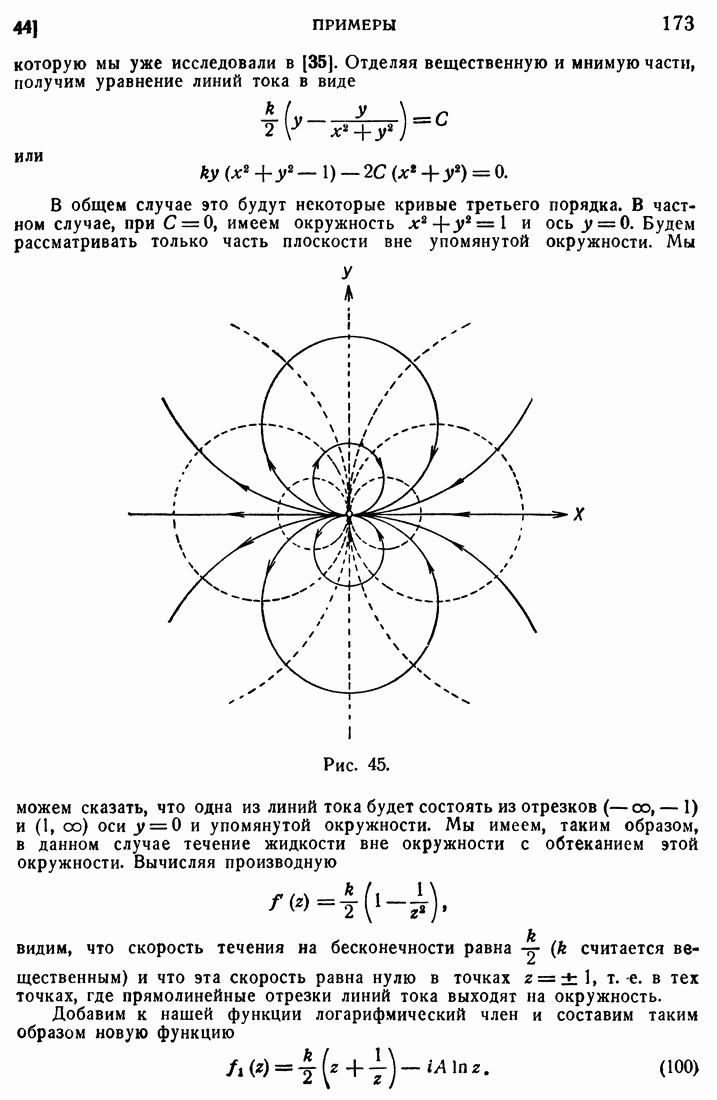
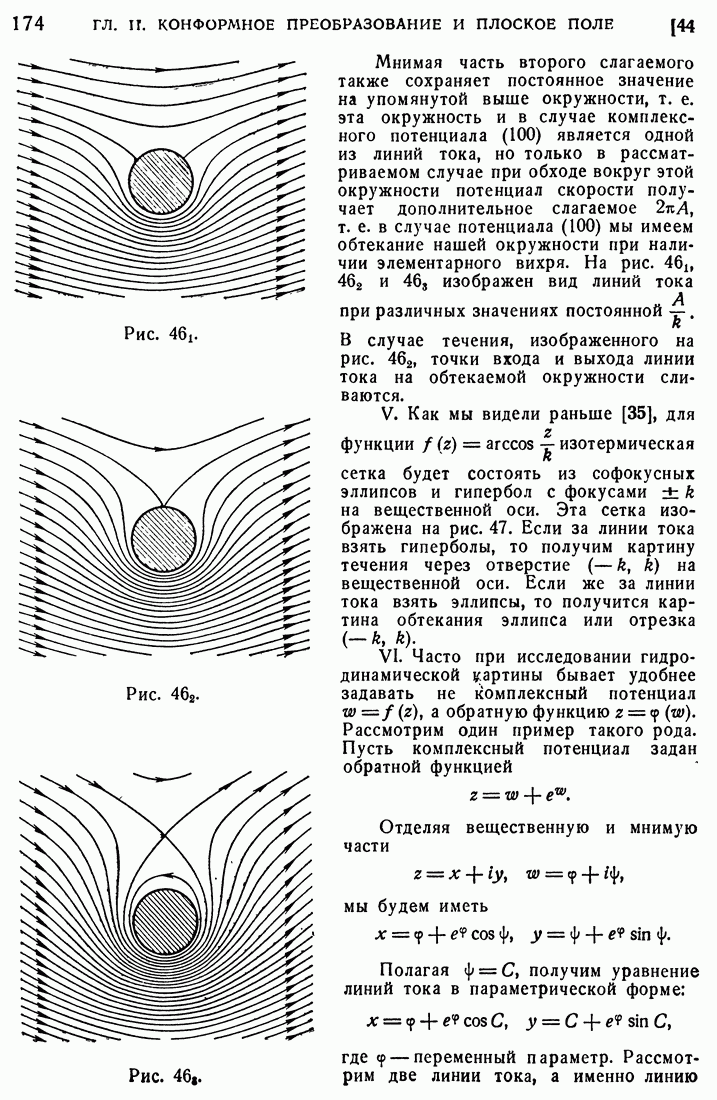
- 44. Примеры.
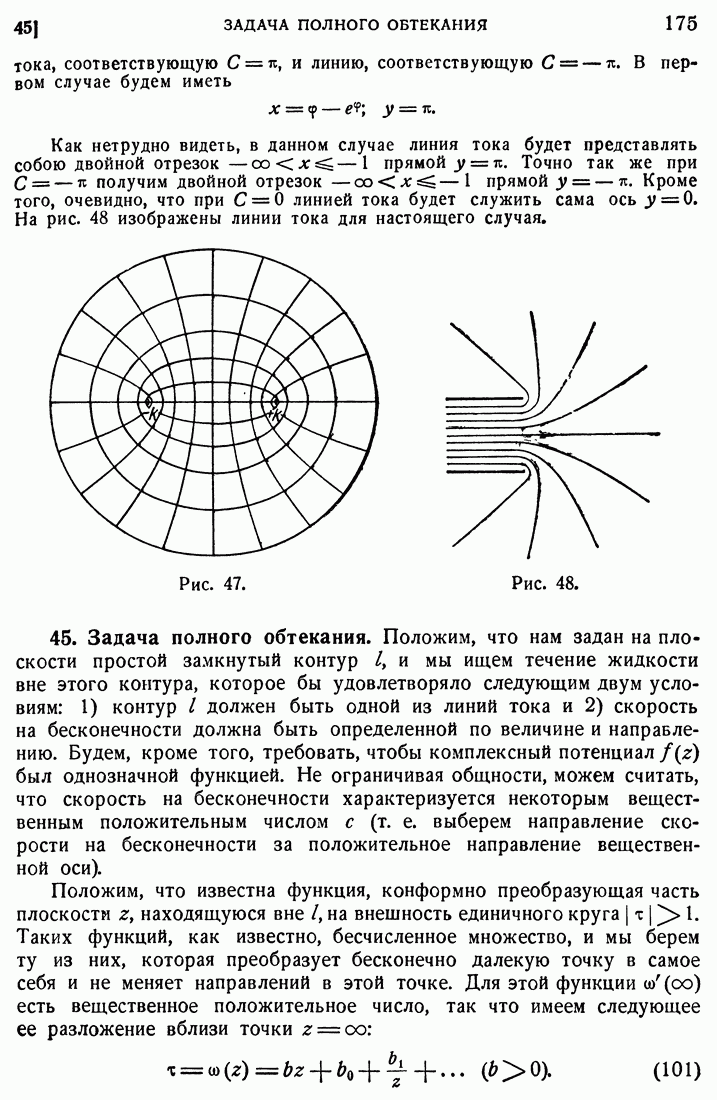
- 45. Задача полного обтекания.
- 46. Формула Н. Е. Жуковского.
- 47. Плоская электростатическая задача.
- 48. Формула Шварца.
- 49. Ядро ctg((s-t)/2).
- 50. Предельные задачи.
- 51. Бигармоническое уравнение.
- 52. Волновое уравнение и аналитические функции.
- 53. Основная теорема.
- 54. Дифракция плоской волны.
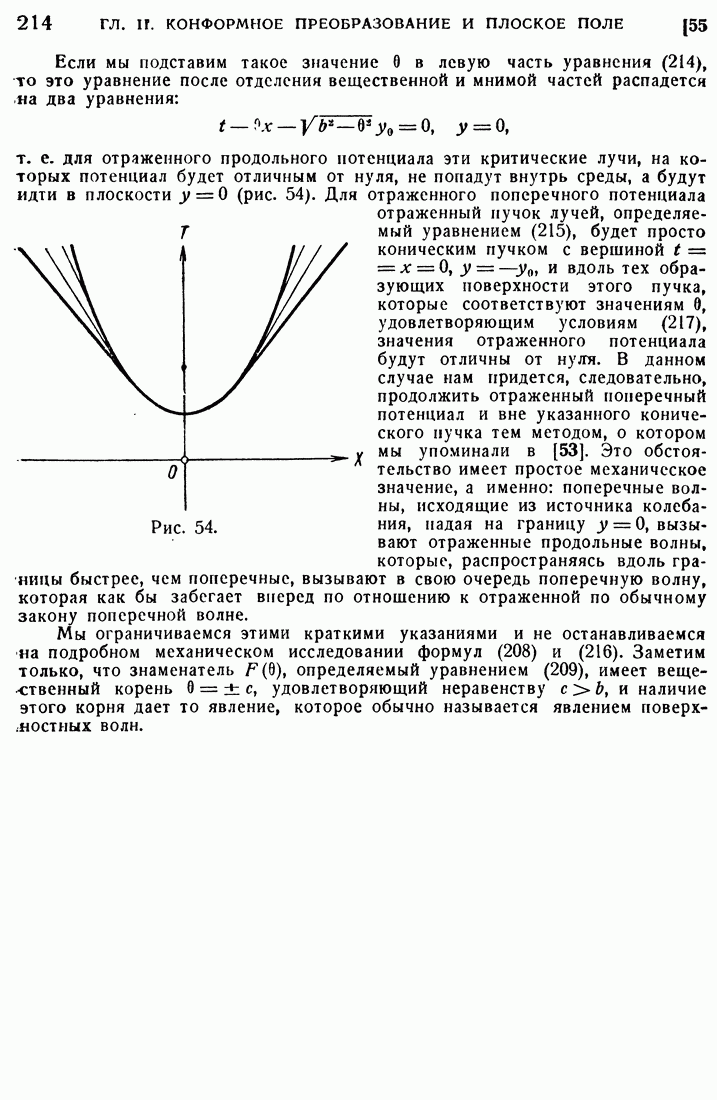
- 55. Отражение упругих волн от прямолинейной границы.
- ГЛАВА III. ПРИМЕНЕНИЕ ТЕОРИИ ВЫЧЕТОВ, ЦЕЛЫЕ И ДРОБНЫЕ ФУНКЦИИ
- 56. Интеграл Френеля.
- 57. Интегрирование выражений с тригонометрическими функциями.
- 58. Интегрирование рациональной дроби.
- 59. Некоторые новые типы интегралов с тригонометрическими функциями.
- 60. Лемма Жордана.
- 61. Представление некоторых функций контурными интегралами.
- 62. Примеры интегралов от многозначных функций.
- 63. Интегрирование системы линейных уравнений с постоянными коэффициентами.
- 64. Разложение дробной функции на простейшие дроби.
- 66. Построение мероморфной функции.
- 67. Целые функции.
- 68. Бесконечные произведения.
- 69. Построение целой функции по ее корням.
- 70. Интегралы, зависящие от параметра.
- 71. Эйлеров интеграл второго рода.
- 72. Эйлеров интеграл первого рода.
- 73. Бесконечное произведение для функции …
- 74. Представление Г(z) контурным интегралом.
- 75. Формула Стирлинга.
- 76. Формула суммирования Эйлера.
- 77. Числа Бернулли.
- 78. Метод скорейшего спуска.
- 79. Асимптотическое разложение интеграла.
- 80. Примеры.
- 81. Метод стационарной фазы.
- ГЛАВА IV. АНАЛИТИЧЕСКИЕ ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ И ФУНКЦИИ МАТРИЦ
- 82. Регулярные функции многих переменных.
- 83. Двойной интеграл и формула Коши.
- 84. Степенные ряды.
- 85. Аналитическое продолжение.
- 86. Функции матриц. Предварительные понятия.
- 87. Степенные ряды от одной матрицы.
- 88. Умножение степенных рядов. Обращение степенного ряда.
- 89. Дальнейшее исследование сходимости.
- 90. Интерполяционные полиномы.
- 91. Тождество Кейли. Формула Сильвестра.
- 92. Определение функций одной матрицы формулой Коши.
- 93. Аналитическое продолжение.
- 94. Логарифм матриц.
- 95. Обращение целой функции от матрицы в случае матриц второго порядка.
- 96. Системы линейных уравнений с постоянными коэффициентами.
- 97. Функции нескольких матриц.
- ГЛАВА V. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
- 98. Разложение решения в степенной ряд.
- 99. Аналитическое продолжение решения.
- 100. Окрестность особой точки.
- 101. Регулярная особая точка.
- 102. Уравнения класса Фукса.
- 103. Уравнение Гаусса.
- 104. Гипергеометрический ряд.
- 105. Полиномы Лежандра.
- 106. Полиномы Якоби.
- 107. Конформное преобразование и уравнение Гаусса.
- 108. Преобразование Лапласа.
- 109. Различный выбор решений.
- 110. Уравнение Бесселя.
- 111. Функции Ханкеля и интегральное представление решений уравнения Бесселя.
- 112. Асимптотические разложения.
- 113. Асимптотические разложения решений, полученных преобразованием Лапласа.
- 114. Асимптотические разложения решений уравнения Бесселя.
- 115. Вырождение уравнения Гаусса.
- 116. Формальные ряды в окрестности иррегулярной особой точки.
- 117. Построение асимптотических разложений методом после довательных приближений.
- 118. Функции Эйри.
- 119. Асимптотика при большом значении параметра.
- 120. Уравнения с периодическими коэффициентами.
- 121. Условия устойчивости и неустойчивости для уравнения Хилла.
- 122. Системы линейных дифференциальных уравнений.
- 123. Регулярная особая точка.
- 124. Регулярные системы.
- 125. Представление решения в окрестности особой точки.
- 126. Канонические решения.
- 127. Связь с регулярными решениями типа Фукса.
- 128. Случай любых Us.
- 129. Формальные разложения в окрестности иррегулярной особой точки.
- ГЛАВА VI. СПЕЦИАЛЬНЫЕ ФУНКЦИИ
- 130. Определение сферических функций.
- 131. Явные выражения сферических функций.
- 132. Свойство ортогональности.
- 133. Полиномы Лежандра.
- 134. Разложение по сферическим функциям.
- 135. Доказательство сходимости.
- 136. Связь сферических функций с предельными задачами.
- 137. Задачи Дирихле и Неймана.
- 138. Потенциал объемных масс.
- 139. Потенциал сферического слоя.
- 140. Электрон в центральном поле.
- 141. Шаровые функции и линейные представления группы вращения.
- 142. Функция Лежандра.
- 143. Функция Лежандра второго рода.
- § 2. ФУНКЦИИ БЕССЕЛЯ
- 144. Определение функций Бесселя.
- 145. Соотношения между функциями Бесселя.
- 146. Ортогональность функций Бесселя и их корни.
- 147. Производящая функция и интегральное представление.
- 148. Формула Фурье — Бесселя.
- 150. Разложение функций Неймана с целым значком.
- 151. Случай чисто мнимого аргумента.
- 152. Новые интегральные представления.
- 153. Асимптотические представления.
- 154. Функции Бесселя и уравнение Лапласа.
- 155. Волновое уравнение в цилиндрических координатах.
- 156. Волновое уравнение в сферических координатах.
- § 3. ПОЛИНОМЫ ЭРМИТА И ЛАГЕРРА
- 157. Линейный осциллятор и полиномы Эрмита.
- 158. Свойство ортогональности.
- 159. Производящая функция.
- 160. Параболические координаты и функции Эрмита.
- 161. Полиномы Лагерра.
- 162. Связь полиномов Эрмита и Лагерра.
- 163. Асимптотическое выражение полиномов Эрмита.
- 164. Асимптотическое выражение полиномов Лежандра.
- § 4. ЭЛЛИПТИЧЕСКИЕ ИНТЕГРАЛЫ И ЭЛЛИПТИЧЕСКИЕ ФУНКЦИИ
- 165. Приведение эллиптических интегралов к нормальному виду.
- 166. Приведение интегралов к тригонометрической форме.
- 167. Примеры.
- 168. Обращение эллиптического интеграла.
- 169. Общие свойства эллиптических функций.
- 170. Основная лемма.
- 171. Функции Вейерштрасса.
- 172. Дифференциальное уравнение для …
- 173. Функции …
- 174. Разложение целой периодической функции.
- 175. Новые обозначения.
- 176. Функция …
- 177. Функции …
- 178. Свойства функций тэта.
- 179. Выражение чисел … через …
- 180. Эллиптические функции Якоби.
- 181. Основные свойства функций Якоби.
- 182. Дифференциальные уравнения для функций Якоби.
- 183. Формулы сложения.
- 184. Связь функций p(u) и sn(u).
- 185. Эллиптические координаты.
- 186. Введение эллиптических функций.
- 187. Уравнение Лямэ.
- 188. Простой маятник.
- 189. Пример конформного преобразования.
- ДОБАВЛЕНИЕ. ПРИВЕДЕНИЕ МАТРИЦ К КАНОНИЧЕСКОЙ ФОРМЕ
- 191. Случай простых корней.
- 192. Первый этап преобразований в случае кратных корней.
- 193. Приведение к канонической форме.
- 194. Определение структуры канонической формы.
- 196. Пример.