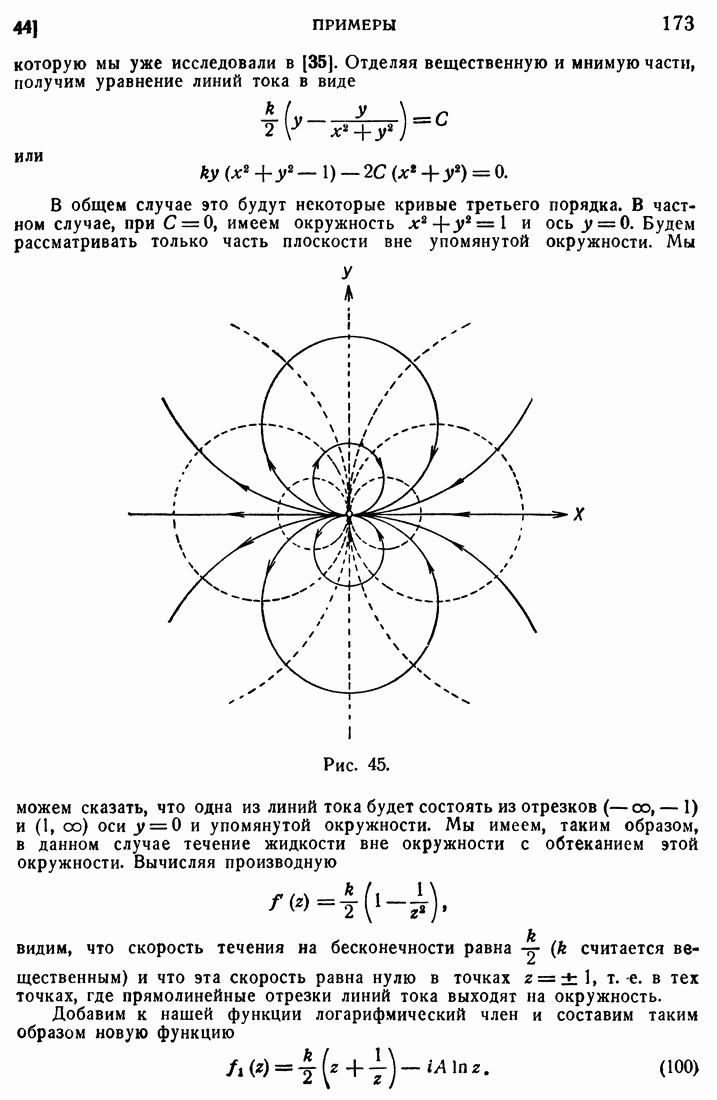
110. Уравнение Бесселя.

Уравнение Бесселя

при помощи преобразования

приводится к уравнению

которое имеет вид (112). В данном случае

Уравнение (117) имеет вид и мы получаем

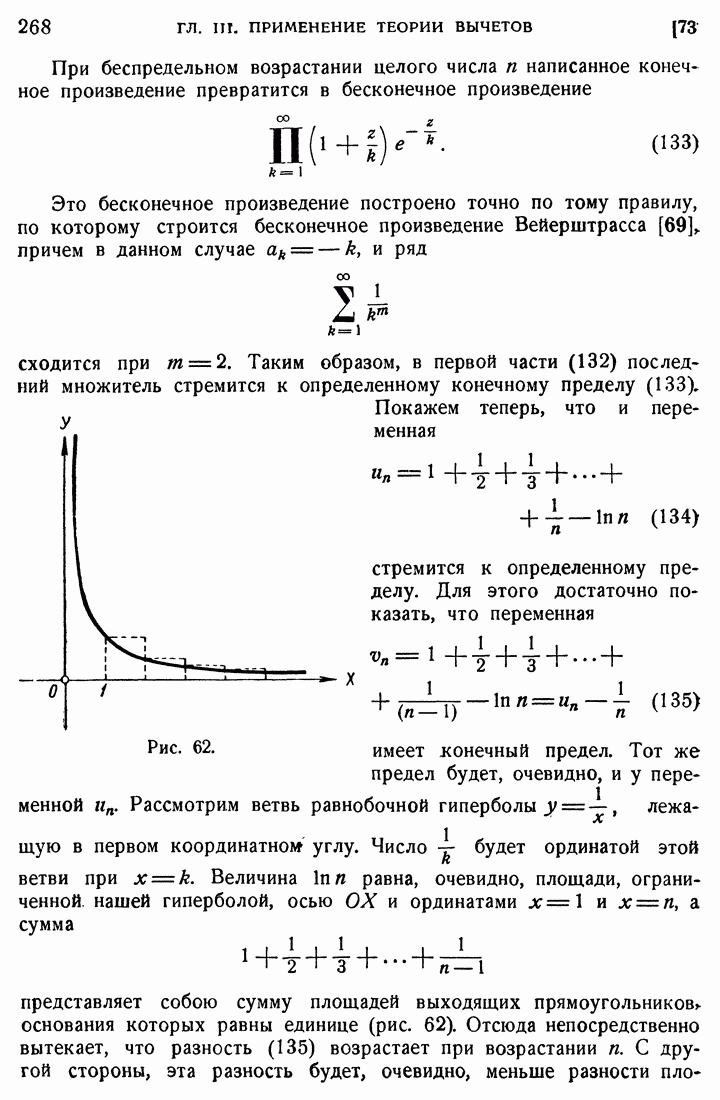
Решения уравнения (133) имеют вид

Согласно сказанному в при при , откуда следует, что при вещественных

Иногда пишут решения несколько в ином виде, а именно вводят вместо новую переменную интегрирования по формуле , что соответствует повороту плоскости z на угол

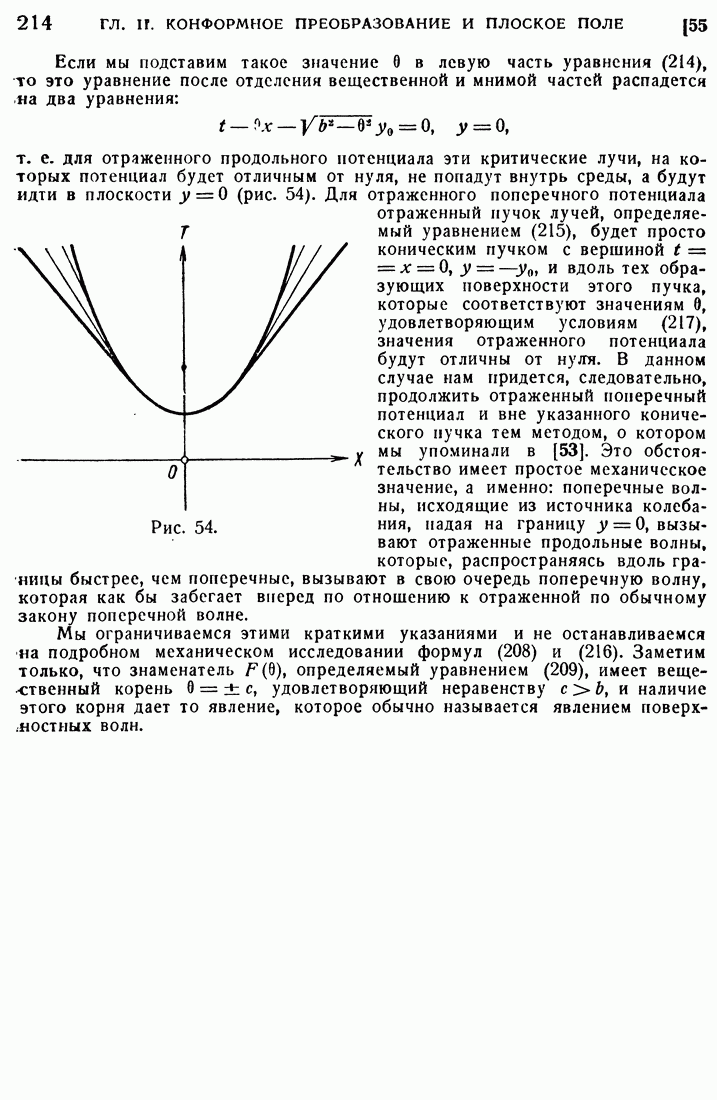
где — контуры, выходящие из точки и обходящие вокруг точек и при чисто мнимых , которые соответствуют вещественнным или, что тоже, при . Полагая получим вместо (136)

где

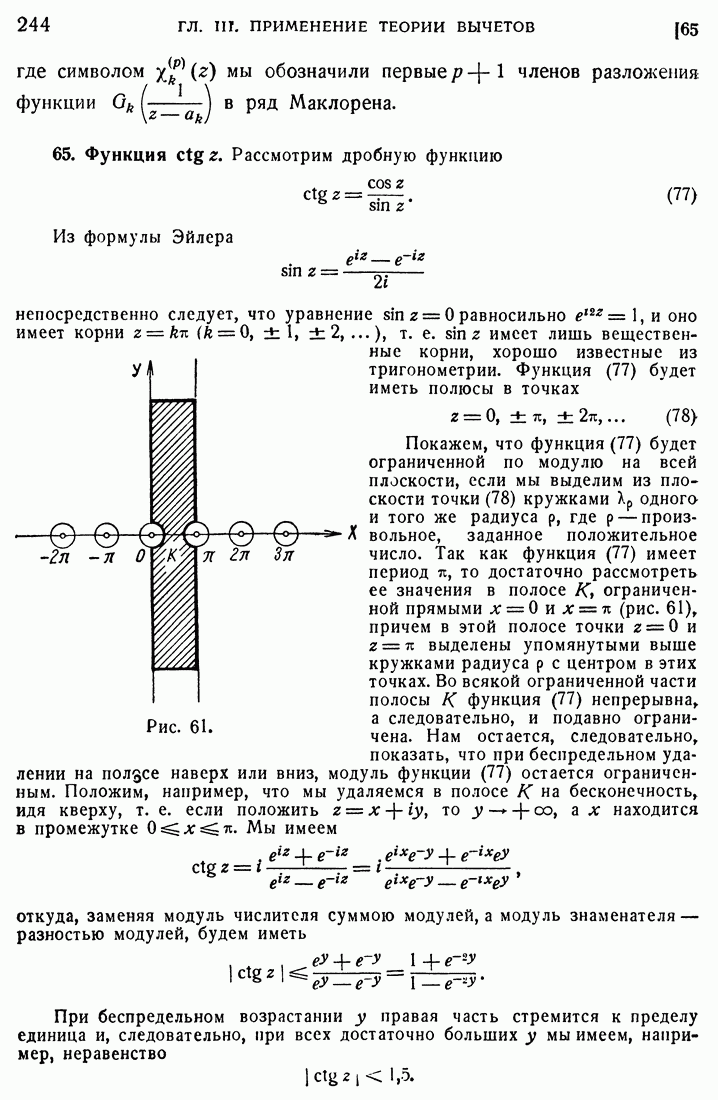
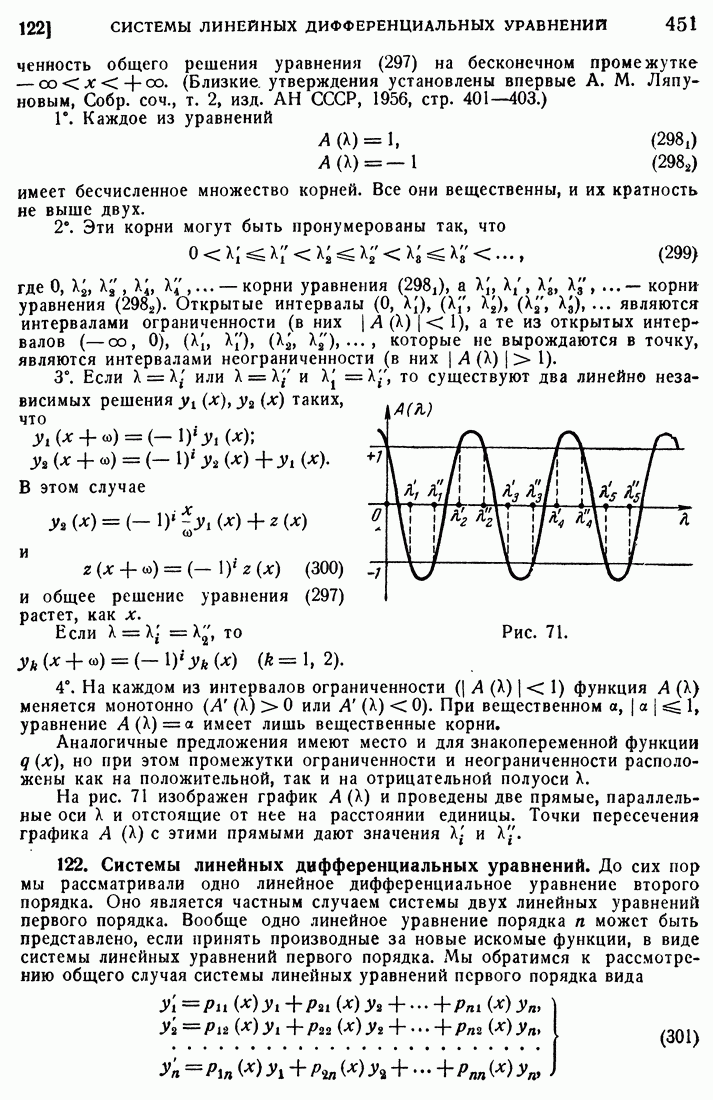
Рис. 68.

Соответствующие решения уравнения (131) будут

Вместо второго решения введем так что

Разность — w дает решение уравнения Бесселя, имеющее вблизи начала вид [109]

Мы уже знаем, что такое решение уравнения Бесселя определяется следующим рядом [II, 48]:

При этом считается, что не есть целое отрицательное число. Если целое, то, как указывалось раньше, полагают причем, как обычно, Таким образом, функция Бесселя с целым неотрицательным значком определяется рядом

или, пользуясь формулой для можем написать

При любом , отличном от целого отрицательного числа, при определении полагают

т. е.

или, в силу формулы получаем при указанных значениях формулу (141). Правая часть этой формулы сохраняет смысл и при целых отрицательных . Заменяя в ней на и принимая во внимание, что при получаем

Заменяя переменную суммирования новой: , и вынося за знак суммы получаем

т. е.

Разность даег нам функцию Бесселя (141) лишь с точностью до постоянного множителя. Мы будем искать теперь множитель а, на который надо умножить разность чтобы получить в точности функцию Бесселя. Учитывая формулу (132) и факт, что мы сводим задачу к следующей: найти постоянную а из того условия, чтобы полусумма решений уравнения Бесселя

давала функцию Бесселя (141). Выше мы предполагали, что не есть целое число . Последний случай мы рассмотрим при подробном изложении функций Бесселя.