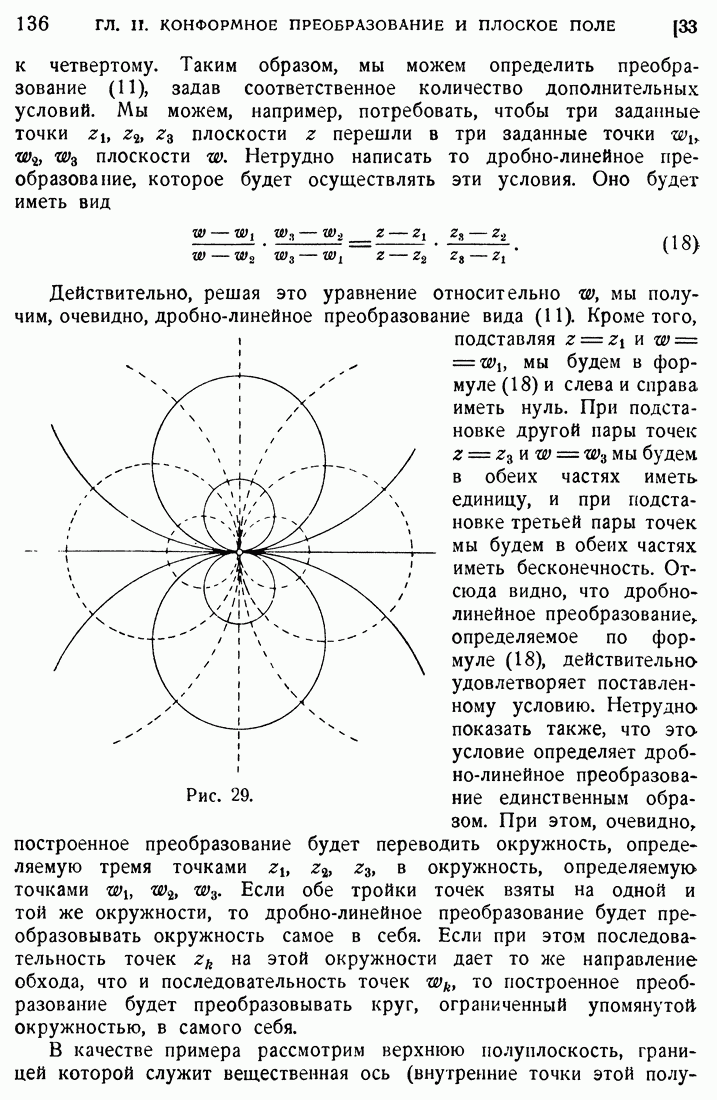
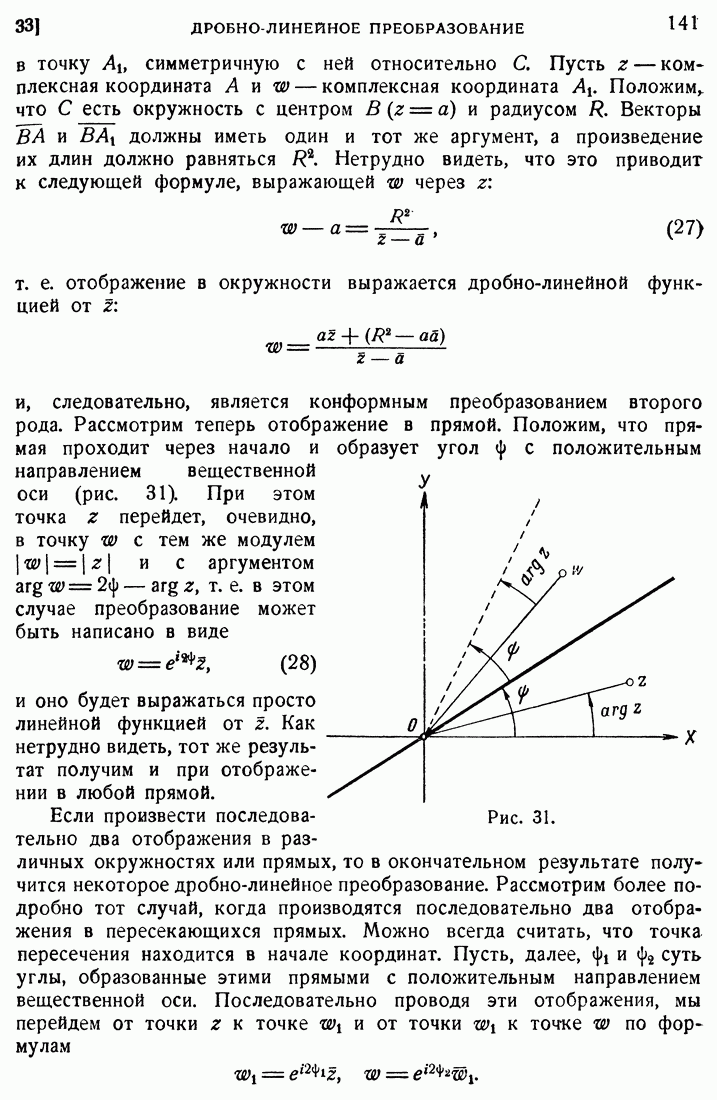
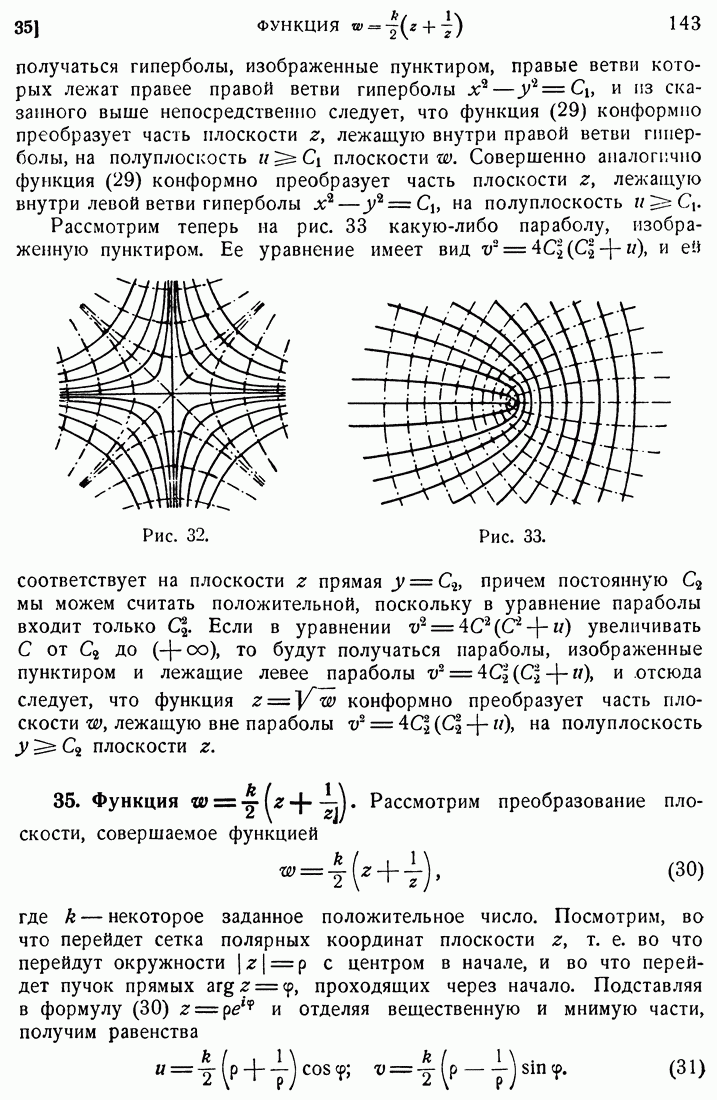
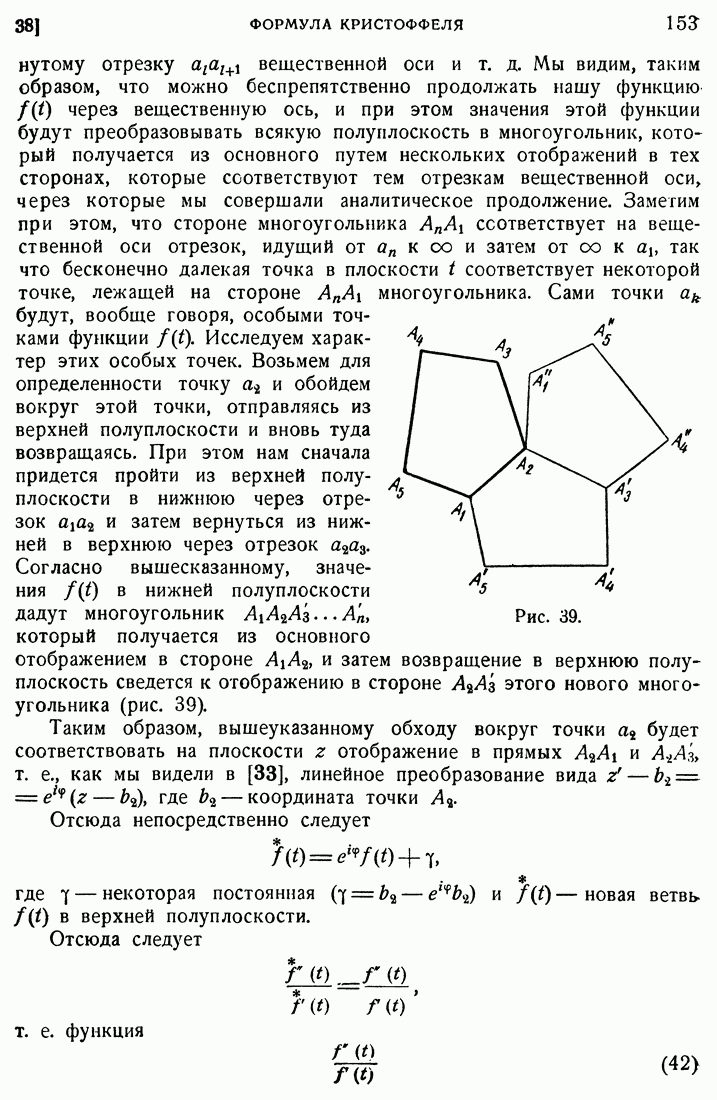
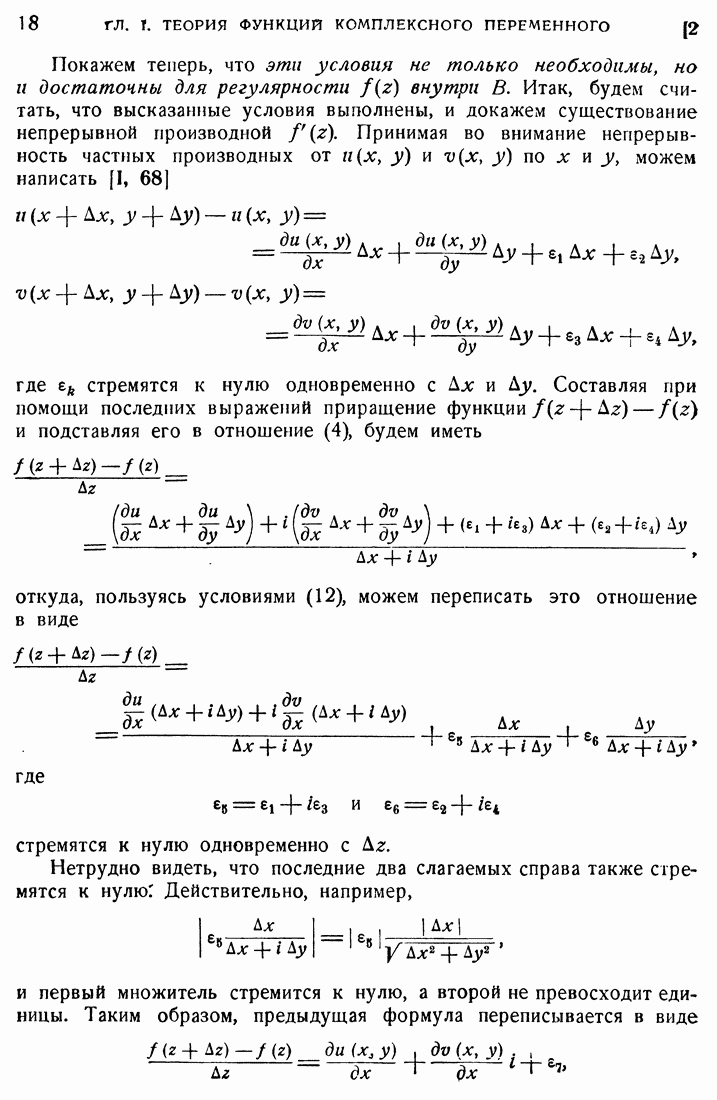| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
53. Основная теорема.
Если в некоторой области В пространства (S) уравнение (174) при условии (175) определяет  как комплексную функцию переменных t, x и у, то вещественная и мнимая части любой аналитической функции
как комплексную функцию переменных t, x и у, то вещественная и мнимая части любой аналитической функции  дают решение уравнения (173). Если же
дают решение уравнения (173). Если же  в некоторой области есть вещественная функция
в некоторой области есть вещественная функция  то произвольная вещественная функция от
то произвольная вещественная функция от  с непрерывными производными до второго порядка дает решение уравнения (173).
с непрерывными производными до второго порядка дает решение уравнения (173).
Если  то, деля обе части (174) на
то, деля обе части (174) на  можем считать
можем считать  Кроме того, мы можем принять
Кроме того, мы можем принять  за новую комплексную переменную
за новую комплексную переменную  При этом условие (175) даст
При этом условие (175) даст  так что уравнение (174) может быть переписано, например, в форме
так что уравнение (174) может быть переписано, например, в форме

где  любая аналитическая функция 0. Вместо
любая аналитическая функция 0. Вместо  мы должны писать, конечно, при этом
мы должны писать, конечно, при этом 
Остановимся более подробно на рассмотрении того частного случая, когда  . В этом случае уравнение (176) имеет вид
. В этом случае уравнение (176) имеет вид

и отсюда  определяется как функция лишь от двух аргументов:
определяется как функция лишь от двух аргументов:

В данном случае и построенные нами решения  уравнения (173) будут функциями аргументов (178), т. е. это будут однородные функции
уравнения (173) будут функциями аргументов (178), т. е. это будут однородные функции  и у нулевого измерения. Такие функции, как известно, определяются соотношением
и у нулевого измерения. Такие функции, как известно, определяются соотношением

которое должно иметь место тождественно. Можно показать, что и, наоборот, любое такое однородное решение уравнения (173) может быть получено указанным выше путем. Будем называть в дальнейшем эти решения просто однородными решениями.
Исследуем более подробно уравнение (177). Входящий в него радикал  будет, как мы знаем [19], однозначной функцией на плоскости
будет, как мы знаем [19], однозначной функцией на плоскости  с разрезом
с разрезом  вдоль вещественной оси. Фиксируем значение упомянутого радикала условием, чтобы он был положительным на верхней части мнимой оси, т. е. при
вдоль вещественной оси. Фиксируем значение упомянутого радикала условием, чтобы он был положительным на верхней части мнимой оси, т. е. при  где
где  . Это условие равносильно тому, чтобы упомянутый радикал был отрицательно мнимым при
. Это условие равносильно тому, чтобы упомянутый радикал был отрицательно мнимым при  или положительно мнимым при
или положительно мнимым при  на вещественной оси. В этом нетрудно убедиться, следя за непрерывным изменением аргумента упомянутого радикала. Уравнение (177) мы можем переписать в виде
на вещественной оси. В этом нетрудно убедиться, следя за непрерывным изменением аргумента упомянутого радикала. Уравнение (177) мы можем переписать в виде

Освобождаясь от радикала и решая полученное квадратное уравнение, получим для  выражение
выражение

Мы считаем при этом, что имеет место неравенство

или, что то же,

В формуле (180) радикал надо понимать арифметически. В этом легко убедиться, пользуясь самим уравнением (179), где радикал должен иметь определенное значение. Действительно, если мы положим в уравнении  то для
то для  получим чисто мнимые значения, и в силу (179) знак радикала
получим чисто мнимые значения, и в силу (179) знак радикала  должен быть противоположным знаку
должен быть противоположным знаку  т. е. если, например,
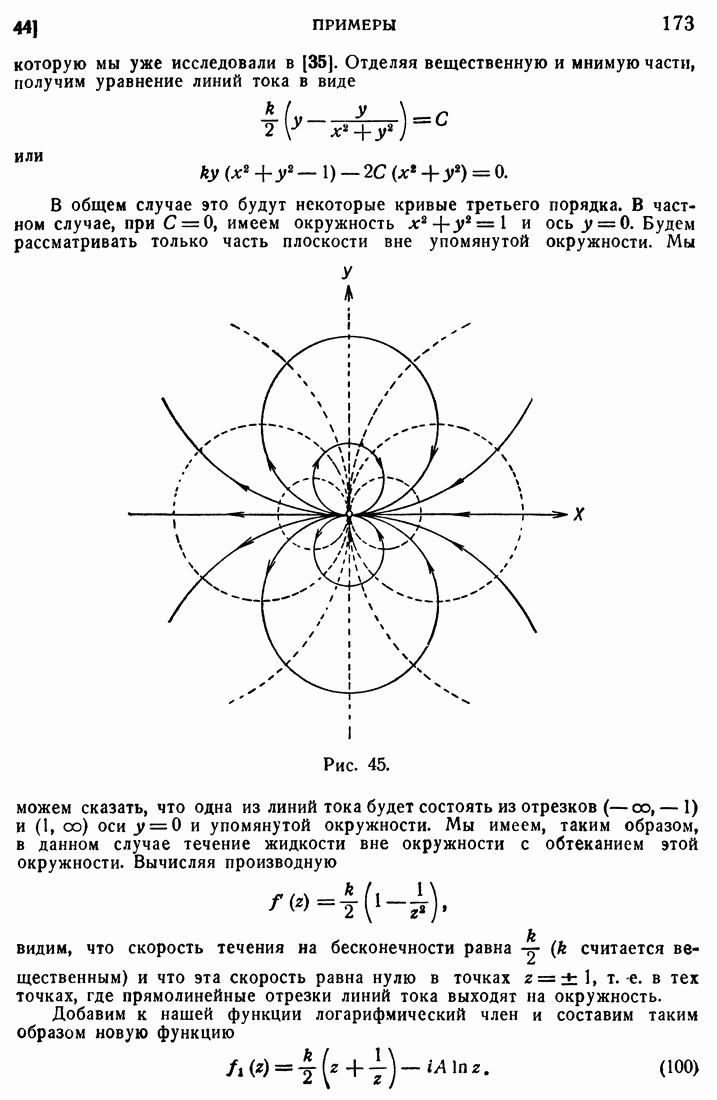
т. е. если, например,  то согласно поставленному выше условию
то согласно поставленному выше условию  должно находиться на верхней части мнимой оси, что и совпадает с тем выбором знака в формуле (180), который мы сделали, считая радикал в этой формуле положительным.
должно находиться на верхней части мнимой оси, что и совпадает с тем выбором знака в формуле (180), который мы сделали, считая радикал в этой формуле положительным.
При фиксированных значениях  мы имеем в силу (178) прямую пространства (5), проходящую через начало. Будем рассматривать только ту часть этой прямой, на которой
мы имеем в силу (178) прямую пространства (5), проходящую через начало. Будем рассматривать только ту часть этой прямой, на которой  , и назовем такую полупрямую лучом. В силу условия (181) или (182) эти лучи образуют конический пучок с вершиной в начале и с углом
, и назовем такую полупрямую лучом. В силу условия (181) или (182) эти лучи образуют конический пучок с вершиной в начале и с углом  вершине, причем осью пучка является ось t Уравнение (179) или (180) приводит в соответствие лучам этого пучка комплексные значения плоскости
вершине, причем осью пучка является ось t Уравнение (179) или (180) приводит в соответствие лучам этого пучка комплексные значения плоскости  с разрезом
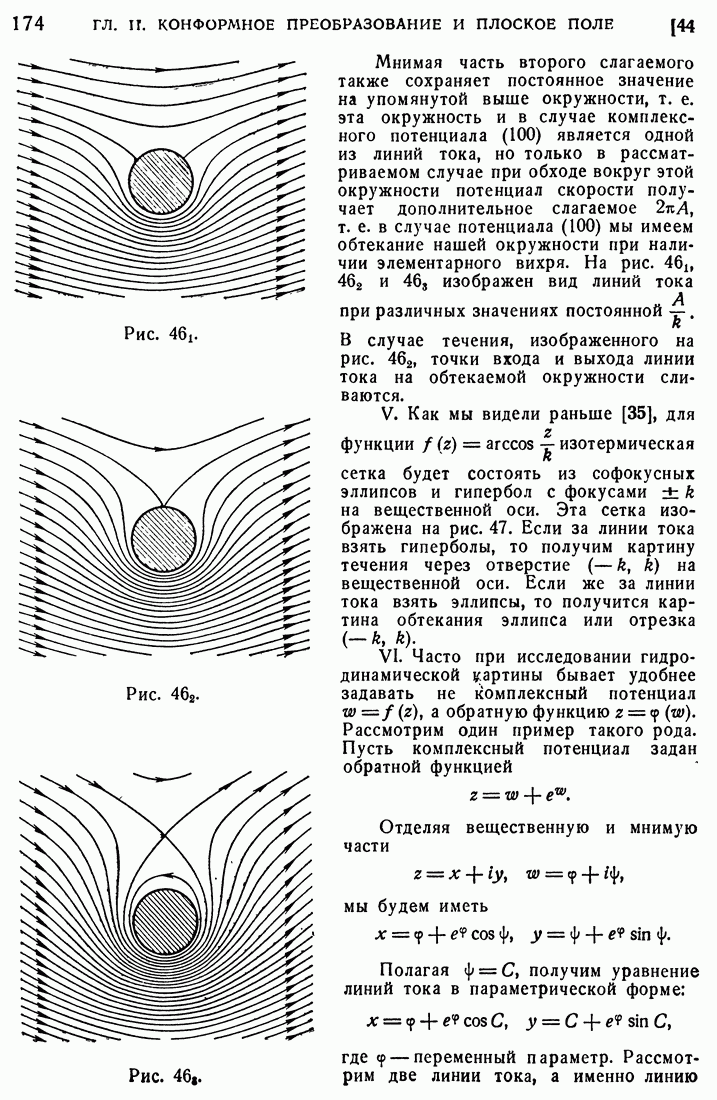
с разрезом  . Пользуясь формулой (180), нетрудно проследить это соответствие более подробно. Отметим некоторые существенные факты, непосредственно вытекающие из формулы (180). Прежде всего, отметим, что лучам, образующим поверхность конического пучка, т. е. лучам, которые удовлетворяют равенству
. Пользуясь формулой (180), нетрудно проследить это соответствие более подробно. Отметим некоторые существенные факты, непосредственно вытекающие из формулы (180). Прежде всего, отметим, что лучам, образующим поверхность конического пучка, т. е. лучам, которые удовлетворяют равенству

соответствуют точки разреза плоскости 6. Оси нашего конического пучка, которая характеризуется значениями  или
или  соответствует бесконечно далекая точка плоскости 0. Наконец, отметим еще, что тем лучам, которые находятся в плоскости
соответствует бесконечно далекая точка плоскости 0. Наконец, отметим еще, что тем лучам, которые находятся в плоскости  и для которых
и для которых  соответствуют вещественные значения 0, по абсолютному значению большие а, т. е. соответствуют точки, лежащие на вещественной оси плоскости 0 и находящиеся вне разреза
соответствуют вещественные значения 0, по абсолютному значению большие а, т. е. соответствуют точки, лежащие на вещественной оси плоскости 0 и находящиеся вне разреза  .
.
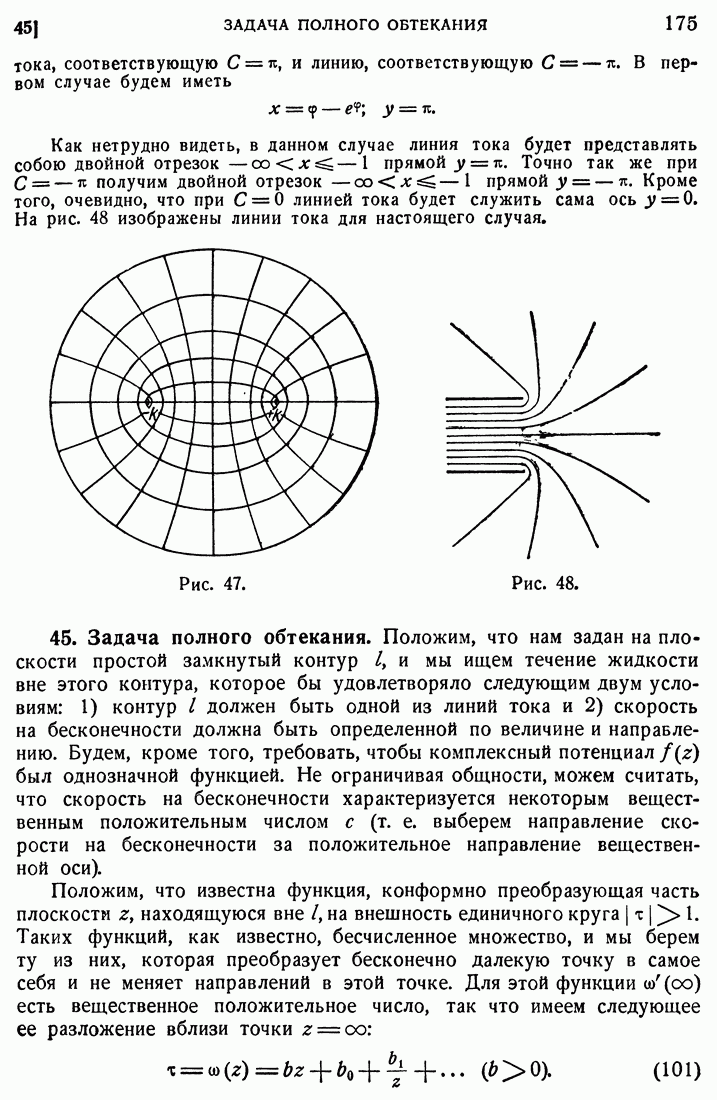
Если мы разделим наш конический пучок плоскостью  на две части, то одной из них будет соответствовать верхняя полуплоскость
на две части, то одной из них будет соответствовать верхняя полуплоскость  и другой — нижняя полуплоскость, а именно: той половине, где
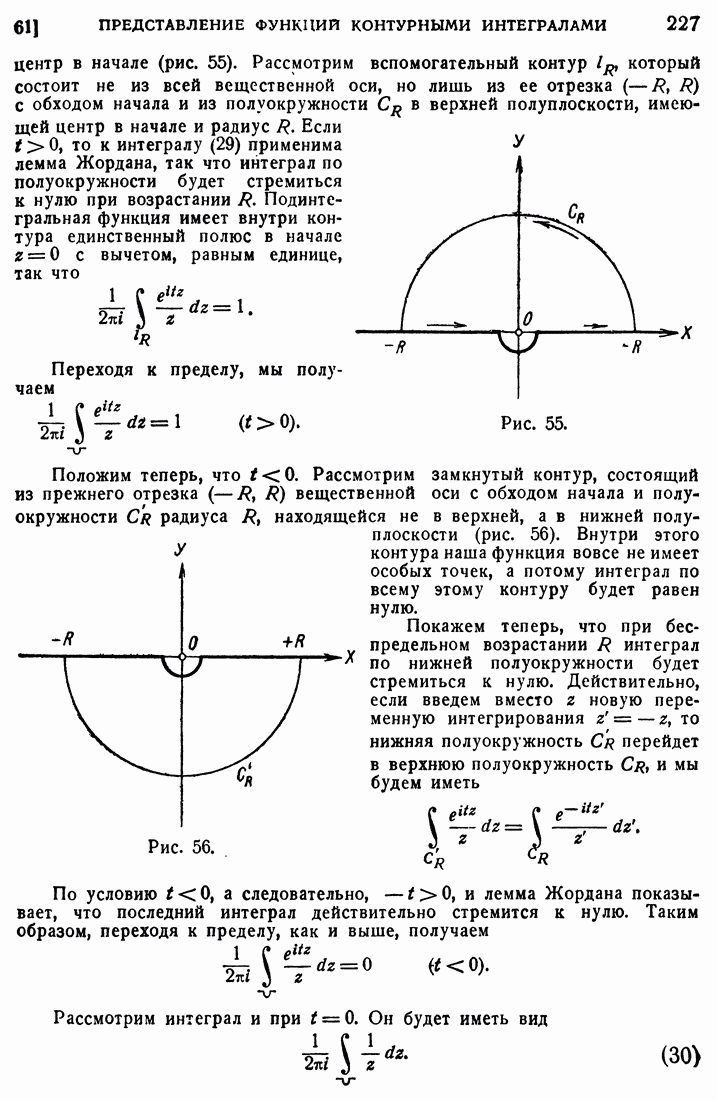
и другой — нижняя полуплоскость, а именно: той половине, где  будет соответствовать нижняя полуплоскость, а там, где
будет соответствовать нижняя полуплоскость, а там, где  , — верхняя полуплоскость.
, — верхняя полуплоскость.
Если мы возьмем решение уравнения (173), построенное указанным выше способом, т. е. являющееся вещественной частью некоторой аналитической функции  то такое решение будет иметь постоянное значение на каждом из вышеуказанных лучей.
то такое решение будет иметь постоянное значение на каждом из вышеуказанных лучей.
Исследуем теперь значения  для точек пространства (5), которые лежаг вне упомянутого конического пучка, т. е. для всех точек в которых выполнено неравенство
для точек пространства (5), которые лежаг вне упомянутого конического пучка, т. е. для всех точек в которых выполнено неравенство

Уравнение (179) даст нам при этом два вещественных корня, принадлежащих отрезку  :
:

Этот отрезок  является разрезом на плоскости, и на противоположных берегах этого разреза радикал
является разрезом на плоскости, и на противоположных берегах этого разреза радикал  имеет противоположные знаки, так что в уравнении (179) мы должны в данном случае принимать во внимание двойной знак радикала и вместе с тем в формуле (183) брать также оба знака у радикала. Пусть
имеет противоположные знаки, так что в уравнении (179) мы должны в данном случае принимать во внимание двойной знак радикала и вместе с тем в формуле (183) брать также оба знака у радикала. Пусть  некоторая точка вне нашего конического пучка,
некоторая точка вне нашего конического пучка,  и
и  — соответствующие значения
— соответствующие значения  , получаемые из формулы (183). Если мы подставим эти значения
, получаемые из формулы (183). Если мы подставим эти значения  и
и  в левую часть уравнения (179), то у нас получатся два вещественных уравнения первой степени относительно
в левую часть уравнения (179), то у нас получатся два вещественных уравнения первой степени относительно  и у, и, следовательно, мы будем иметь две плоскости, проходящие через точку
и у, и, следовательно, мы будем иметь две плоскости, проходящие через точку  Мы можем выразить это и иначе, а именно: всякому значению
Мы можем выразить это и иначе, а именно: всякому значению  находящемуся на разрезе
находящемуся на разрезе  , соответствует некоторая плоскость Р пространства (5). Пусть
, соответствует некоторая плоскость Р пространства (5). Пусть  образующая нашего конического пучка, которая соответствует точке
образующая нашего конического пучка, которая соответствует точке  разреза. Плоскость Р должна, очевидно, содержать в себе эту образующую X. Нетрудно показать, что плоскость Р будет касательной плоскостью к поверхности нашего конического пучка вдоль образующей X. Действительно, если бы плоскость Р не была касательной к поверхности конуса вдоль X, то она пересеклась бы с этой поверхностью и часть плоскости попала бы внутрь конического пучка. Но тогда мы получили бы, что точкам, лежащим внутри конического пучка, соответствует вещественное
разреза. Плоскость Р должна, очевидно, содержать в себе эту образующую X. Нетрудно показать, что плоскость Р будет касательной плоскостью к поверхности нашего конического пучка вдоль образующей X. Действительно, если бы плоскость Р не была касательной к поверхности конуса вдоль X, то она пересеклась бы с этой поверхностью и часть плоскости попала бы внутрь конического пучка. Но тогда мы получили бы, что точкам, лежащим внутри конического пучка, соответствует вещественное  из промежутка.
из промежутка.  что, как мы видели выше, не имеет места. Итак, каждому вещественному
что, как мы видели выше, не имеет места. Итак, каждому вещественному  , находящемуся на разрезе
, находящемуся на разрезе  , в силу
, в силу  - соответствует плоскость, касательная к поверхности контеского
- соответствует плоскость, касательная к поверхности контеского
пучка вдоль той образующей, которая отвечает взятому значению  .
.
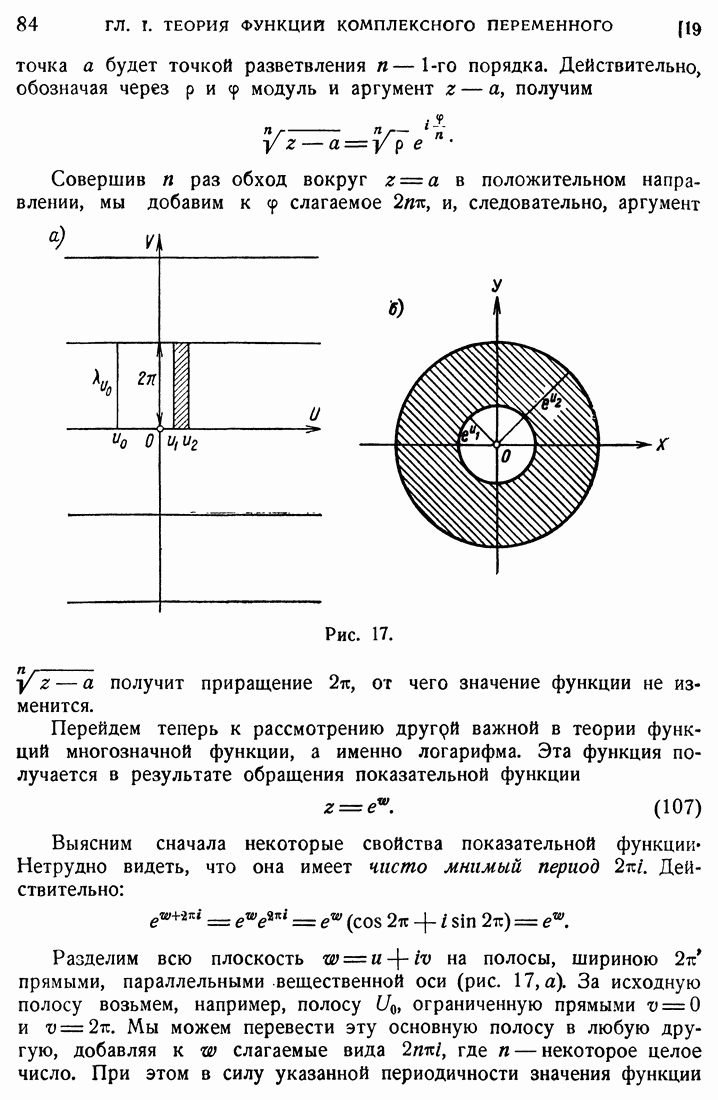
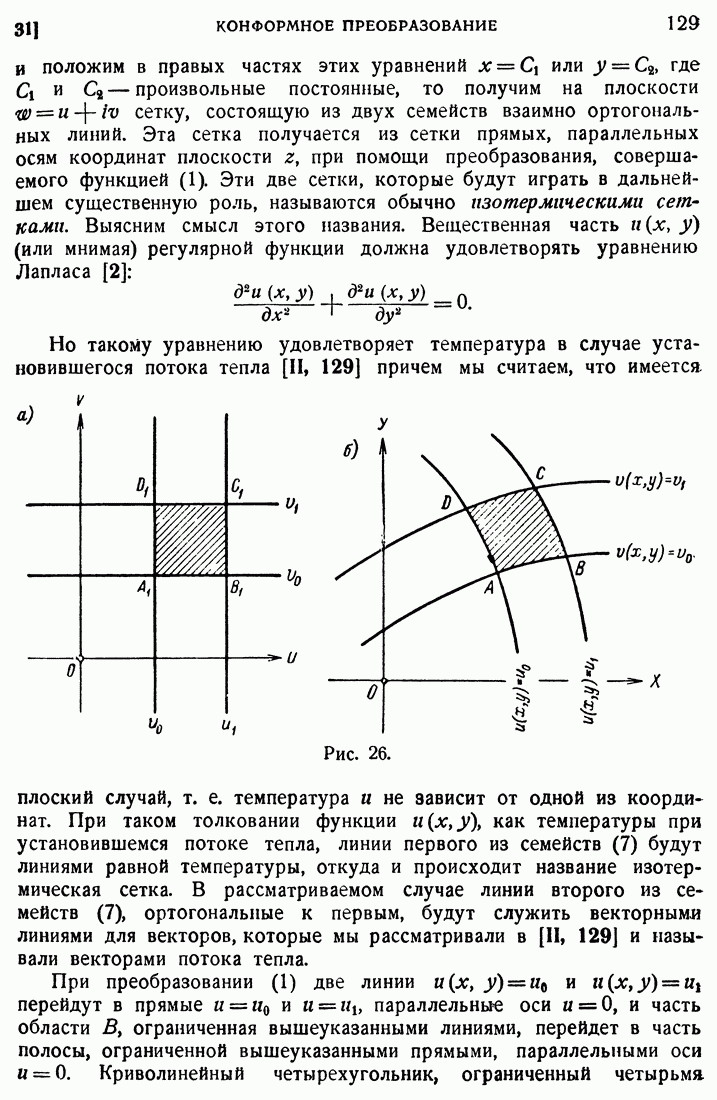
Вместо того чтобы говорить о коническом пучке и касательных плоскостях к его поверхности, мы можем пользоваться и плоским чертежом, а именно мы можем пересечь наш конический пучок некоторой плоскостью, перпендикулярной к оси t. При этом сам конический пучок изобразится некоторым кругом, а касательные плоскости изобразятся касательными к окружности этого круга. В частности, мы можем воспользоваться переменными Е и  для того, чтобы перейти к плоскому чертежу. Вместо конического пучка мы будем иметь на плоскости
для того, чтобы перейти к плоскому чертежу. Вместо конического пучка мы будем иметь на плоскости  круг К:
круг К:

так что каждой точке этого круга будет соответствовать определенный луч нашего пучка, и наоборот. Касательной к окружности нашего круга будет соответствовать упомянутая выше касательная плоскость к поверхности пучка. Полуплоскости  будет соответствовать та часть пространства, где
будет соответствовать та часть пространства, где  . Оси
. Оси  будет соответствовать плоскость
будет соответствовать плоскость 
Пусть  аналитическая однозначная функция на плоскости
аналитическая однозначная функция на плоскости  с разрезом
с разрезом  . Возьмем соответствующее решение уравнения (173):
. Возьмем соответствующее решение уравнения (173):


Рис. 49.
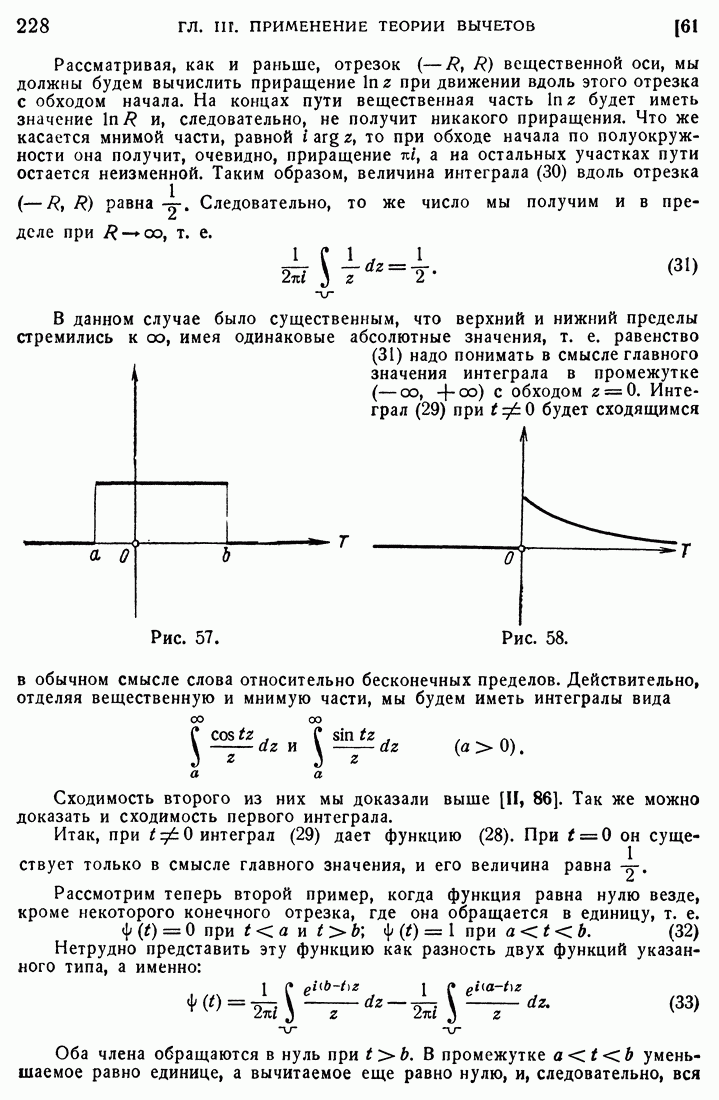
Это решение будет определено внутри нашего конического пучка или, для случая плоскости  в круге (184). Укажем один, важный в приложениях, способ продолжения этого решения вне конического пучка. Для этой цели проведем семейство касательных полуплоскостей к поверхности нашего конического пучка так, чтобы эти касательные полуплоскости шли в одном и том же направлении, т. е. соответствующие им касательные к окружности
в круге (184). Укажем один, важный в приложениях, способ продолжения этого решения вне конического пучка. Для этой цели проведем семейство касательных полуплоскостей к поверхности нашего конического пучка так, чтобы эти касательные полуплоскости шли в одном и том же направлении, т. е. соответствующие им касательные к окружности

имели вид, указанный на рис. 49. Эти касательные полуплоскости не будут пересекаться друг с другом и заполнят часть пространства (S), лежащую вне конического пучка. На каждой из таких полуплоскостей  сохраняет постоянное значение, и мы можем определить однозначным образом решение и вне конического пучка, пользуясь той же самой формулой (185), которая нам давала решение внутри конического пучка. В данном случае вне пучка решение будет
сохраняет постоянное значение, и мы можем определить однозначным образом решение и вне конического пучка, пользуясь той же самой формулой (185), которая нам давала решение внутри конического пучка. В данном случае вне пучка решение будет
сохранять постоянное значение уже не на лучах, а на полуплоскостях. Заметим, что мы можем, очевидно, двояким образом определять направление касательных к окружности (186) и, значит, получим два различных способа продолжения решения по указанному выше методу.
Соответствующие поверхности конического пучка  принадлежат разрезу
принадлежат разрезу  а. Мы можем при этом разбить значение и, определяемое формулой (185), на два вещественных слагаемых:
а. Мы можем при этом разбить значение и, определяемое формулой (185), на два вещественных слагаемых:  и продолжать одно из них по полукасательным
и продолжать одно из них по полукасательным  (рис. 49), а другое — по полукасательным 11. Это даст нам тоже некоторое решение уравнения вне круга. Мы имеем, таким образом, но существу, бесчисленное множество различных способов продолжения, причем при всех этих продолжениях сохраняется непрерывность решения и при переходе через окружность. В конкретных задачах способ продолжения определяется из рассмотрения движения фронта волны.
(рис. 49), а другое — по полукасательным 11. Это даст нам тоже некоторое решение уравнения вне круга. Мы имеем, таким образом, но существу, бесчисленное множество различных способов продолжения, причем при всех этих продолжениях сохраняется непрерывность решения и при переходе через окружность. В конкретных задачах способ продолжения определяется из рассмотрения движения фронта волны.

Рис. 50.
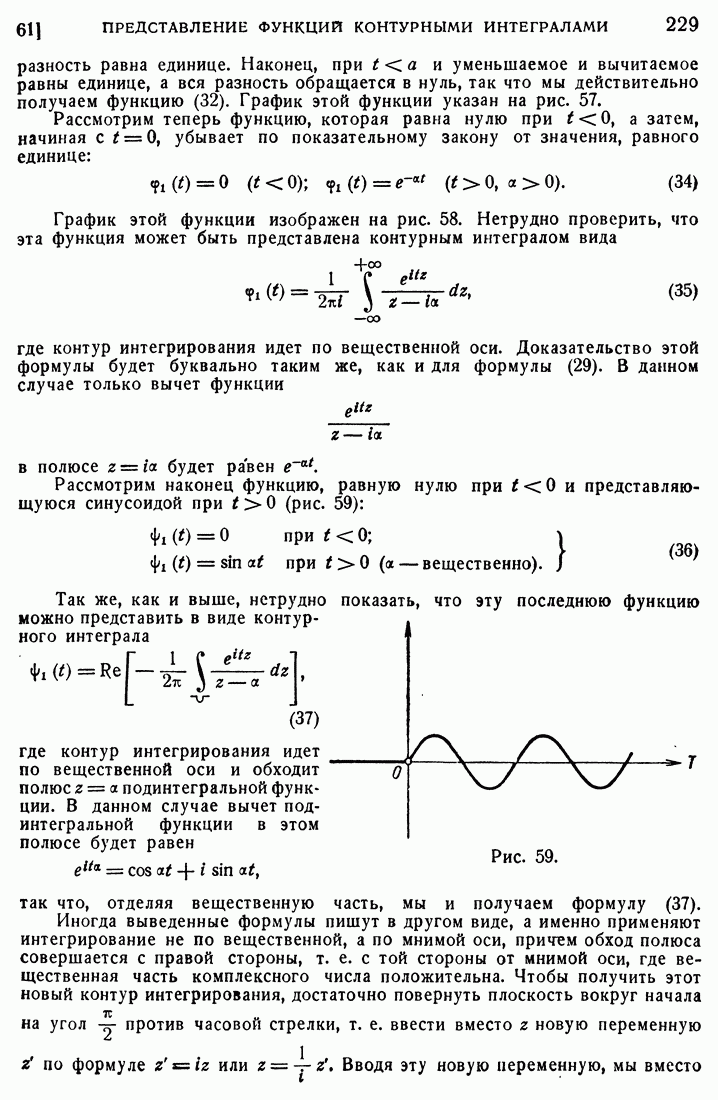
Все предыдущее относилось к тому случаю, когда мы рассматривали решение во всем пространстве (5). Положим теперь, что нас интересует только полупространство  или на плоскости
или на плоскости  только полуплоскость
только полуплоскость  Положим, что формула (185) дает нам решение в полукруге, причем это решение обращается в нуль на некоторой дуге АВ полуокружности так, как это изображено на рис. 50. В данном случае во многих задачах, связанных с распространением колебаний, мы приходим к однозначному продолжению решения (185), пользуясь полукасательными к окружности, изображенными на рис. 50, т. е. соответствующими полуплоскостями, касательными к поверхности конического пучка. При этом решение будет равно нулю вне контура
Положим, что формула (185) дает нам решение в полукруге, причем это решение обращается в нуль на некоторой дуге АВ полуокружности так, как это изображено на рис. 50. В данном случае во многих задачах, связанных с распространением колебаний, мы приходим к однозначному продолжению решения (185), пользуясь полукасательными к окружности, изображенными на рис. 50, т. е. соответствующими полуплоскостями, касательными к поверхности конического пучка. При этом решение будет равно нулю вне контура 
Соображения, аналогичные предыдущим, применимы и к общему случаю уравнения (176), но при этом, конечно, вместо конического пучка мы будем иметь более сложный геометрический образ (семейство прямых с двумя параметрами), связанный с выбором функции 
Мы можем в уравнениях (176) или (177) выбирать вместо  другую комплексную переменную
другую комплексную переменную  связанную с
связанную с  некоторой аналитической функциональной зависимостью. Укажем на один особенно удобный выбор комплексной переменной. Пусть z связана с 0 формулой
некоторой аналитической функциональной зависимостью. Укажем на один особенно удобный выбор комплексной переменной. Пусть z связана с 0 формулой

При этом, как мы знаем [35], вместо плоскости 0 с разрезом  мы будем иметь для переменной z единичный круг
мы будем иметь для переменной z единичный круг  . Пользуясь формулой (187), нетрудно видеть, что при нашем выборе значения радикала будет иметь место формула
. Пользуясь формулой (187), нетрудно видеть, что при нашем выборе значения радикала будет иметь место формула

Исследуем в данном случае более подробно уравнение (177). Оно будет иметь вид

или

что можно переписать следующим образом:

Введем для круга (184) полярные координаты по формулам

Уравнение (189) перепишется при этом так:

и мы имеем, очевидно, для z решение вида  где
где  определяется из квадратного уравнения
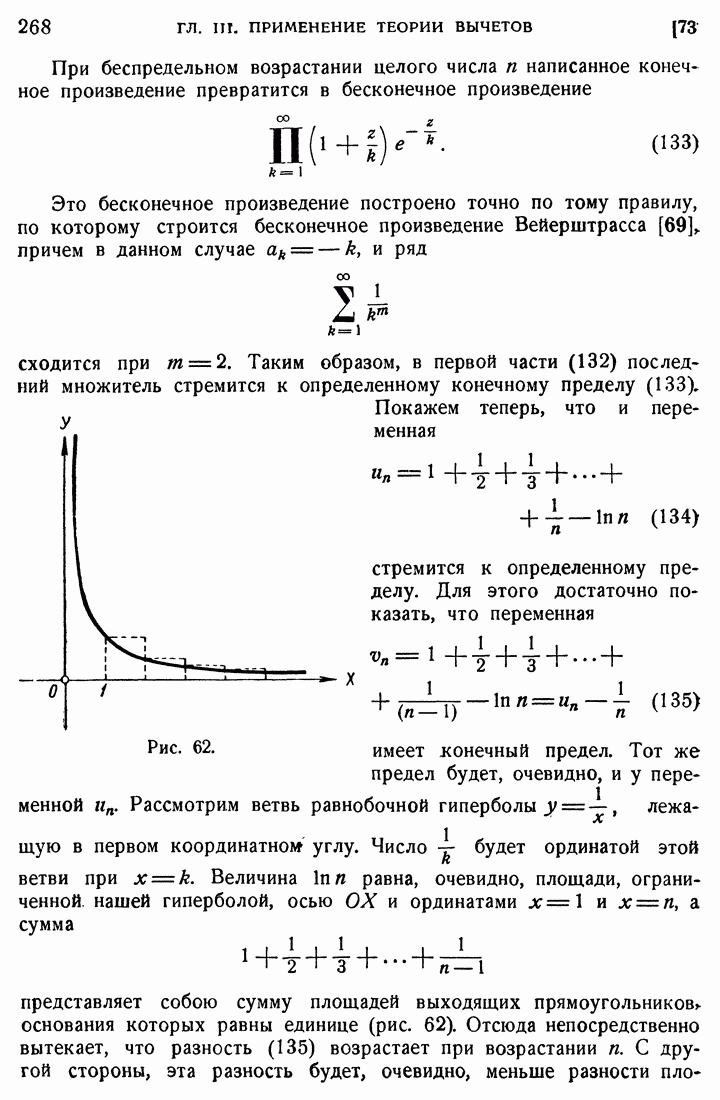
определяется из квадратного уравнения

т. е. в данном случае каждой точке круга (184) (т. е. лучу) соответствует значение комплексного переменного  с тем же самым аргументом и точкам окружности круга (186) соответствуют точки единичной окружности с тем же самым аргументом. Иначе говоря, всякому радиусу круга (184) соответствует радиус единичного круга
с тем же самым аргументом и точкам окружности круга (186) соответствуют точки единичной окружности с тем же самым аргументом. Иначе говоря, всякому радиусу круга (184) соответствует радиус единичного круга  с тем же самым полярным углом.
с тем же самым полярным углом.
Указанные в настоящем пункте основные идеи приложения теории функций комплексного переменного к решению волнового уравнения
(173) имеют обширные приложения в задачах распространения колебаний (акустических, электромагнитных), связанных с волновым уравнением, а также в более сложных задачах распространения упругих колебаний. Предыдущий метод дает только некоторый класс решений уравнения (173), но, как оказывается, в этот класс входят решения, имеющие важное физическое значение, и, пользуясь этим классом решений, можно доводить до конца в виде, удобном для вычисления, задачи, связанные с отражением и дифракцией волн.
Уравнение (173) есть волновое уравнение для плоского случая (цилиндрические волны), но, пользуясь принципом наложения, можно из решений указанного выше типа составлять новые решения и исследовать таким образом волновое уравнение и в общем случае трехмерного пространства. Обоснование изложенного выше метода можно найти в работах С. Л. Соболева и автора, напечатанных в «Трудах Сейсмологического института Академии наук СССР». Его применение к конкретным задачам находится в работах Е. А. Нарышкиной и С. Л. Соболева. Не вдаваясь в подробности, которые завели бы нас слишком далеко и потребовали бы много места, мы изложим весьма кратко применение этого метода к двум задачам: к задаче дифракции плоской волны и к задаче отражения упругих колебаний от плоской границы.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К ВОСЬМОМУ ИЗДАНИЮ
- 1. Функции комплексного переменного.
- 2. Производная.
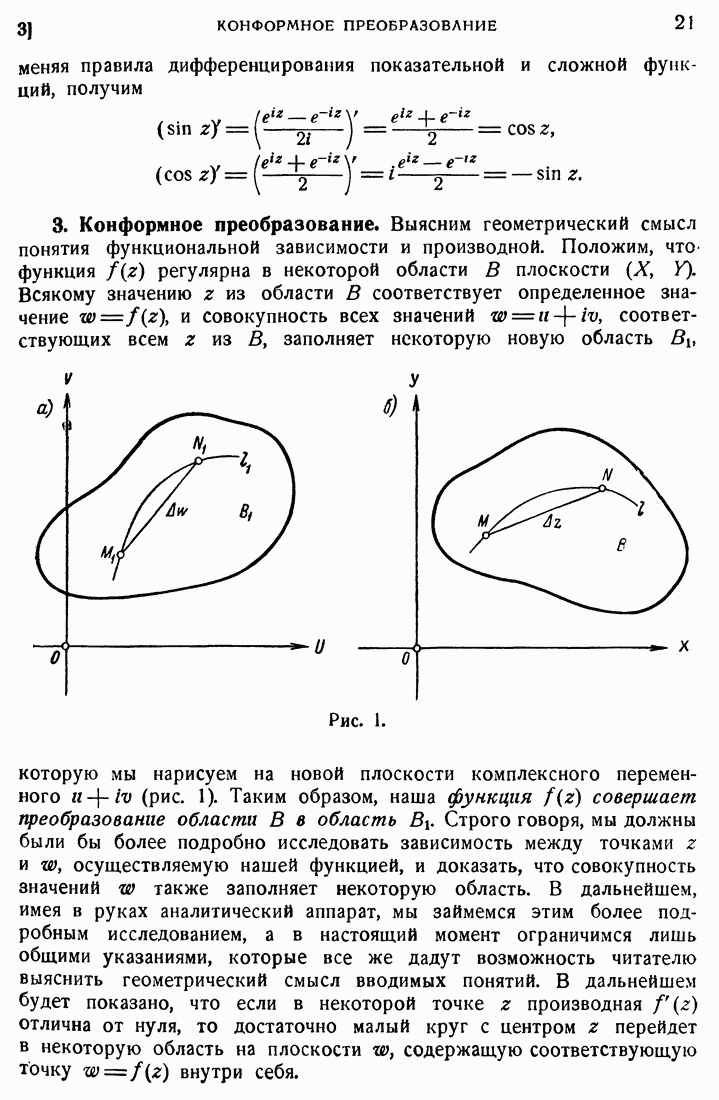
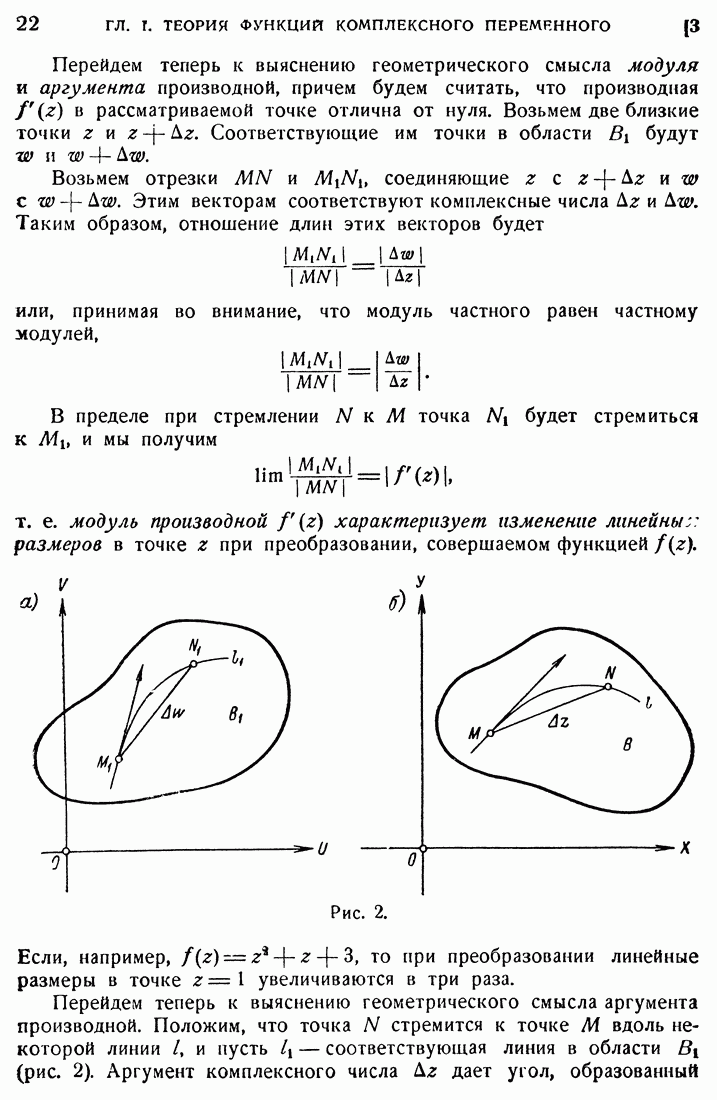
- 3. Конформное преобразование.
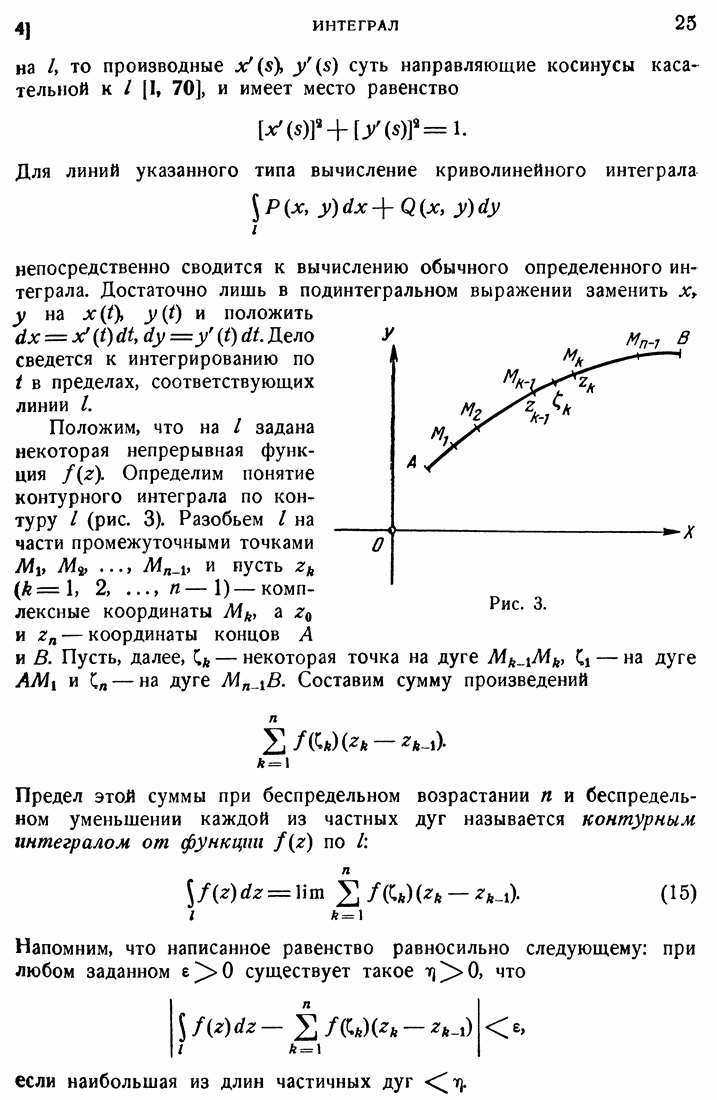
- 4. Интеграл.
- 5. Теорема Коши.
- 6. Основная формула интегрального исчисления.
- 7. Формула Коши.
- 8. Интегралы типа Коши.
- 9. Следствия формулы Коши.
- 10. Изолированные особые точки.
- 11. Бесконечные ряды с комплексными членами.
- 12. Теорема Вейерштрасса.
- 13. Степенные ряды.
- 14. Ряд Тейлора.
- 15. Ряд Лорана.
- 16. Примеры.
- 17. Изолированные особые точки. Бесконечно далекая точка.
- 18. Аналитическое продолжение.
- 19. Примеры многозначных функций.
- 20. Особые точки аналитических функций и римановы поверхности.
- 21. Теорема вычетов.
- 22. Теоремы о числе корней.
- 23. Обращение степенного ряда.
- 24. Принцип симметрии.
- 25. Ряд Тейлора на окружности круга сходимости.
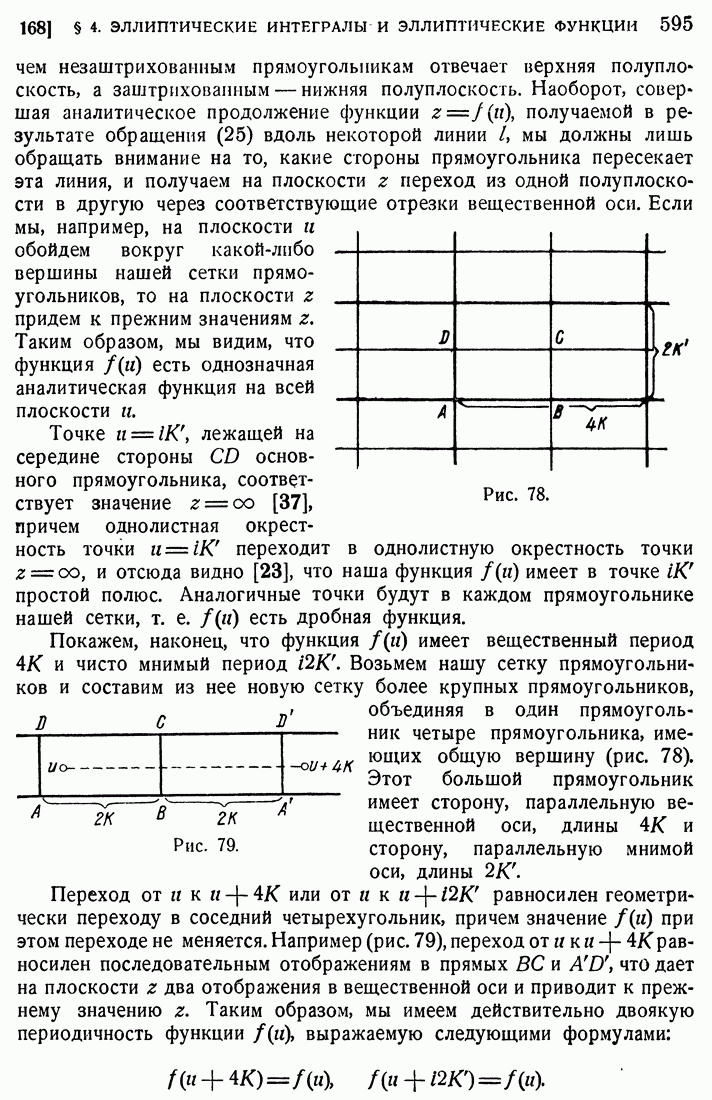
- 26. Дополнительные сведения о формуле Коши.
- 27. Главное значение интеграла.
- 28. Главное значение интеграла (продолжение).
- 29. Интегралы типа Коши.
- 30. Интегралы типа Коши (продолжение).
- ГЛАВА II. КОНФОРМНОЕ ПРЕОБРАЗОВАНИЕ И ПЛОСКОЕ ПОЛЕ
- 31. Конформное преобразование.
- 32. Линейное преобразование.
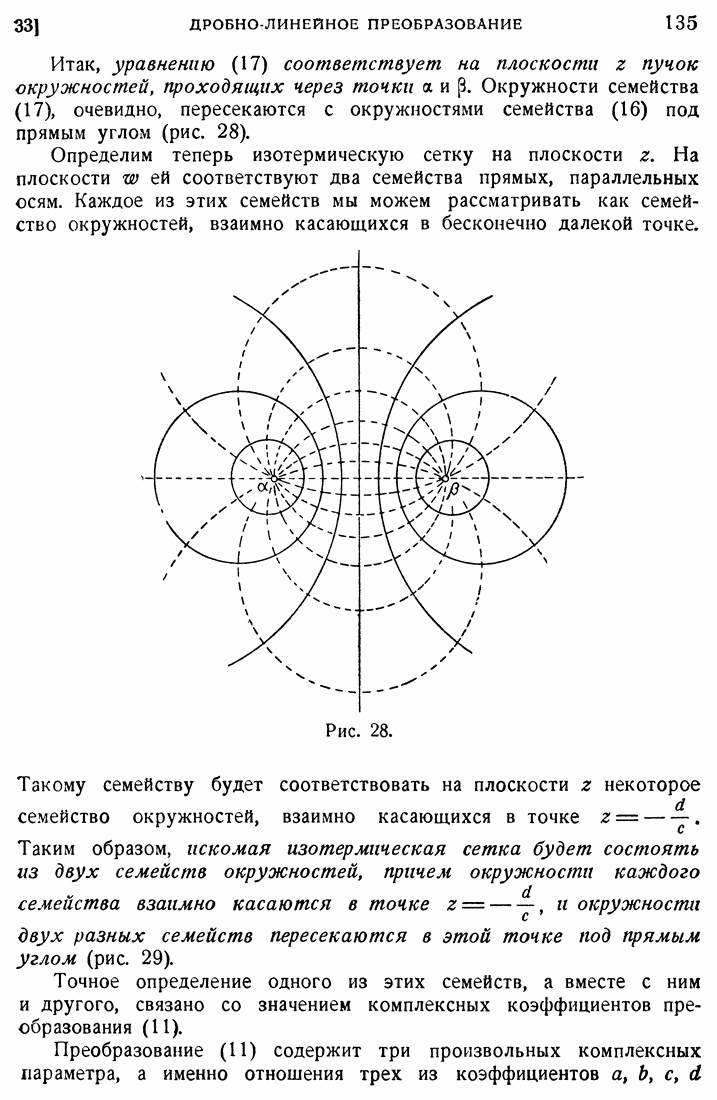
- 33. Дробно-линейное преобразование.
- 34. Функция w = z^2.
- 35. Функция …
- 36. Двуугольник и полоса.
- 37. Основная теорема.
- 38. Формула Кристоффеля.
- 39. Частные случаи.
- 40. Случай внешности многоугольника.
- 41. Минимальное свойство преобразования на круг.
- 42. Способ сопряженных тригонометрических рядов.
- 43. Плоское установившееся течение жидкости.
- 44. Примеры.
- 45. Задача полного обтекания.
- 46. Формула Н. Е. Жуковского.
- 47. Плоская электростатическая задача.
- 48. Формула Шварца.
- 49. Ядро ctg((s-t)/2).
- 50. Предельные задачи.
- 51. Бигармоническое уравнение.
- 52. Волновое уравнение и аналитические функции.
- 53. Основная теорема.
- 54. Дифракция плоской волны.
- 55. Отражение упругих волн от прямолинейной границы.
- ГЛАВА III. ПРИМЕНЕНИЕ ТЕОРИИ ВЫЧЕТОВ, ЦЕЛЫЕ И ДРОБНЫЕ ФУНКЦИИ
- 56. Интеграл Френеля.
- 57. Интегрирование выражений с тригонометрическими функциями.
- 58. Интегрирование рациональной дроби.
- 59. Некоторые новые типы интегралов с тригонометрическими функциями.
- 60. Лемма Жордана.
- 61. Представление некоторых функций контурными интегралами.
- 62. Примеры интегралов от многозначных функций.
- 63. Интегрирование системы линейных уравнений с постоянными коэффициентами.
- 64. Разложение дробной функции на простейшие дроби.
- 66. Построение мероморфной функции.
- 67. Целые функции.
- 68. Бесконечные произведения.
- 69. Построение целой функции по ее корням.
- 70. Интегралы, зависящие от параметра.
- 71. Эйлеров интеграл второго рода.
- 72. Эйлеров интеграл первого рода.
- 73. Бесконечное произведение для функции …
- 74. Представление Г(z) контурным интегралом.
- 75. Формула Стирлинга.
- 76. Формула суммирования Эйлера.
- 77. Числа Бернулли.
- 78. Метод скорейшего спуска.
- 79. Асимптотическое разложение интеграла.
- 80. Примеры.
- 81. Метод стационарной фазы.
- ГЛАВА IV. АНАЛИТИЧЕСКИЕ ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ И ФУНКЦИИ МАТРИЦ
- 82. Регулярные функции многих переменных.
- 83. Двойной интеграл и формула Коши.
- 84. Степенные ряды.
- 85. Аналитическое продолжение.
- 86. Функции матриц. Предварительные понятия.
- 87. Степенные ряды от одной матрицы.
- 88. Умножение степенных рядов. Обращение степенного ряда.
- 89. Дальнейшее исследование сходимости.
- 90. Интерполяционные полиномы.
- 91. Тождество Кейли. Формула Сильвестра.
- 92. Определение функций одной матрицы формулой Коши.
- 93. Аналитическое продолжение.
- 94. Логарифм матриц.
- 95. Обращение целой функции от матрицы в случае матриц второго порядка.
- 96. Системы линейных уравнений с постоянными коэффициентами.
- 97. Функции нескольких матриц.
- ГЛАВА V. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
- 98. Разложение решения в степенной ряд.
- 99. Аналитическое продолжение решения.
- 100. Окрестность особой точки.
- 101. Регулярная особая точка.
- 102. Уравнения класса Фукса.
- 103. Уравнение Гаусса.
- 104. Гипергеометрический ряд.
- 105. Полиномы Лежандра.
- 106. Полиномы Якоби.
- 107. Конформное преобразование и уравнение Гаусса.
- 108. Преобразование Лапласа.
- 109. Различный выбор решений.
- 110. Уравнение Бесселя.
- 111. Функции Ханкеля и интегральное представление решений уравнения Бесселя.
- 112. Асимптотические разложения.
- 113. Асимптотические разложения решений, полученных преобразованием Лапласа.
- 114. Асимптотические разложения решений уравнения Бесселя.
- 115. Вырождение уравнения Гаусса.
- 116. Формальные ряды в окрестности иррегулярной особой точки.
- 117. Построение асимптотических разложений методом после довательных приближений.
- 118. Функции Эйри.
- 119. Асимптотика при большом значении параметра.
- 120. Уравнения с периодическими коэффициентами.
- 121. Условия устойчивости и неустойчивости для уравнения Хилла.
- 122. Системы линейных дифференциальных уравнений.
- 123. Регулярная особая точка.
- 124. Регулярные системы.
- 125. Представление решения в окрестности особой точки.
- 126. Канонические решения.
- 127. Связь с регулярными решениями типа Фукса.
- 128. Случай любых Us.
- 129. Формальные разложения в окрестности иррегулярной особой точки.
- ГЛАВА VI. СПЕЦИАЛЬНЫЕ ФУНКЦИИ
- 130. Определение сферических функций.
- 131. Явные выражения сферических функций.
- 132. Свойство ортогональности.
- 133. Полиномы Лежандра.
- 134. Разложение по сферическим функциям.
- 135. Доказательство сходимости.
- 136. Связь сферических функций с предельными задачами.
- 137. Задачи Дирихле и Неймана.
- 138. Потенциал объемных масс.
- 139. Потенциал сферического слоя.
- 140. Электрон в центральном поле.
- 141. Шаровые функции и линейные представления группы вращения.
- 142. Функция Лежандра.
- 143. Функция Лежандра второго рода.
- § 2. ФУНКЦИИ БЕССЕЛЯ
- 144. Определение функций Бесселя.
- 145. Соотношения между функциями Бесселя.
- 146. Ортогональность функций Бесселя и их корни.
- 147. Производящая функция и интегральное представление.
- 148. Формула Фурье — Бесселя.
- 150. Разложение функций Неймана с целым значком.
- 151. Случай чисто мнимого аргумента.
- 152. Новые интегральные представления.
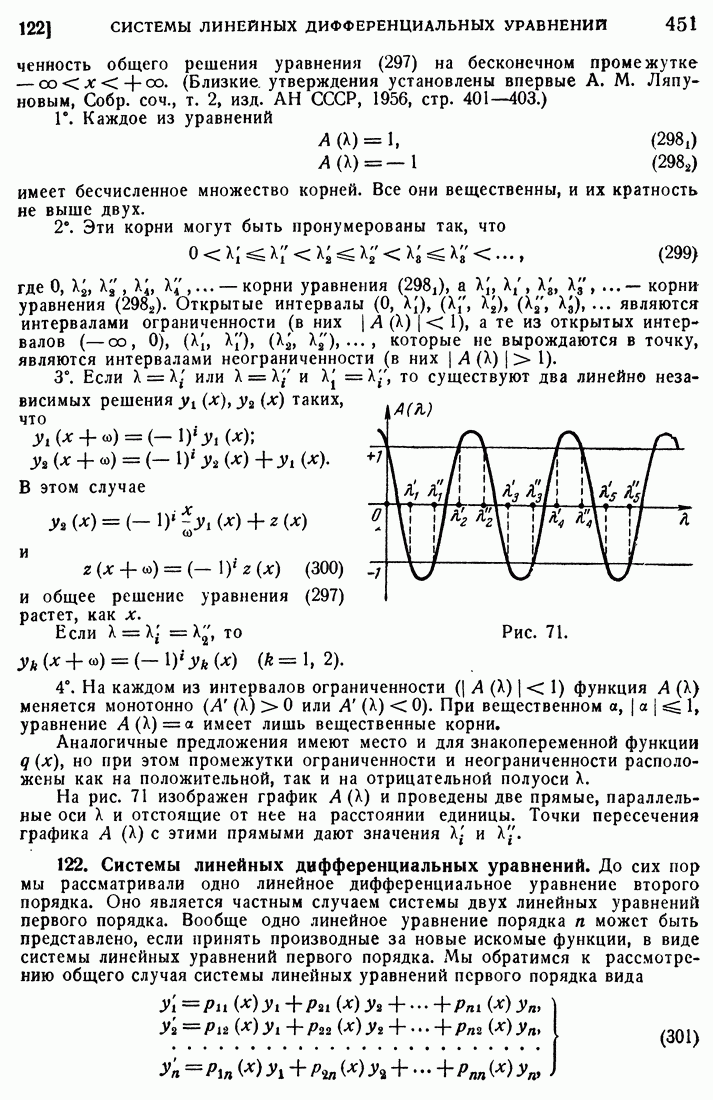
- 153. Асимптотические представления.
- 154. Функции Бесселя и уравнение Лапласа.
- 155. Волновое уравнение в цилиндрических координатах.
- 156. Волновое уравнение в сферических координатах.
- § 3. ПОЛИНОМЫ ЭРМИТА И ЛАГЕРРА
- 157. Линейный осциллятор и полиномы Эрмита.
- 158. Свойство ортогональности.
- 159. Производящая функция.
- 160. Параболические координаты и функции Эрмита.
- 161. Полиномы Лагерра.
- 162. Связь полиномов Эрмита и Лагерра.
- 163. Асимптотическое выражение полиномов Эрмита.
- 164. Асимптотическое выражение полиномов Лежандра.
- § 4. ЭЛЛИПТИЧЕСКИЕ ИНТЕГРАЛЫ И ЭЛЛИПТИЧЕСКИЕ ФУНКЦИИ
- 165. Приведение эллиптических интегралов к нормальному виду.
- 166. Приведение интегралов к тригонометрической форме.
- 167. Примеры.
- 168. Обращение эллиптического интеграла.
- 169. Общие свойства эллиптических функций.
- 170. Основная лемма.
- 171. Функции Вейерштрасса.
- 172. Дифференциальное уравнение для …
- 173. Функции …
- 174. Разложение целой периодической функции.
- 175. Новые обозначения.
- 176. Функция …
- 177. Функции …
- 178. Свойства функций тэта.
- 179. Выражение чисел … через …
- 180. Эллиптические функции Якоби.
- 181. Основные свойства функций Якоби.
- 182. Дифференциальные уравнения для функций Якоби.
- 183. Формулы сложения.
- 184. Связь функций p(u) и sn(u).
- 185. Эллиптические координаты.
- 186. Введение эллиптических функций.
- 187. Уравнение Лямэ.
- 188. Простой маятник.
- 189. Пример конформного преобразования.
- ДОБАВЛЕНИЕ. ПРИВЕДЕНИЕ МАТРИЦ К КАНОНИЧЕСКОЙ ФОРМЕ
- 191. Случай простых корней.
- 192. Первый этап преобразований в случае кратных корней.
- 193. Приведение к канонической форме.
- 194. Определение структуры канонической формы.
- 196. Пример.