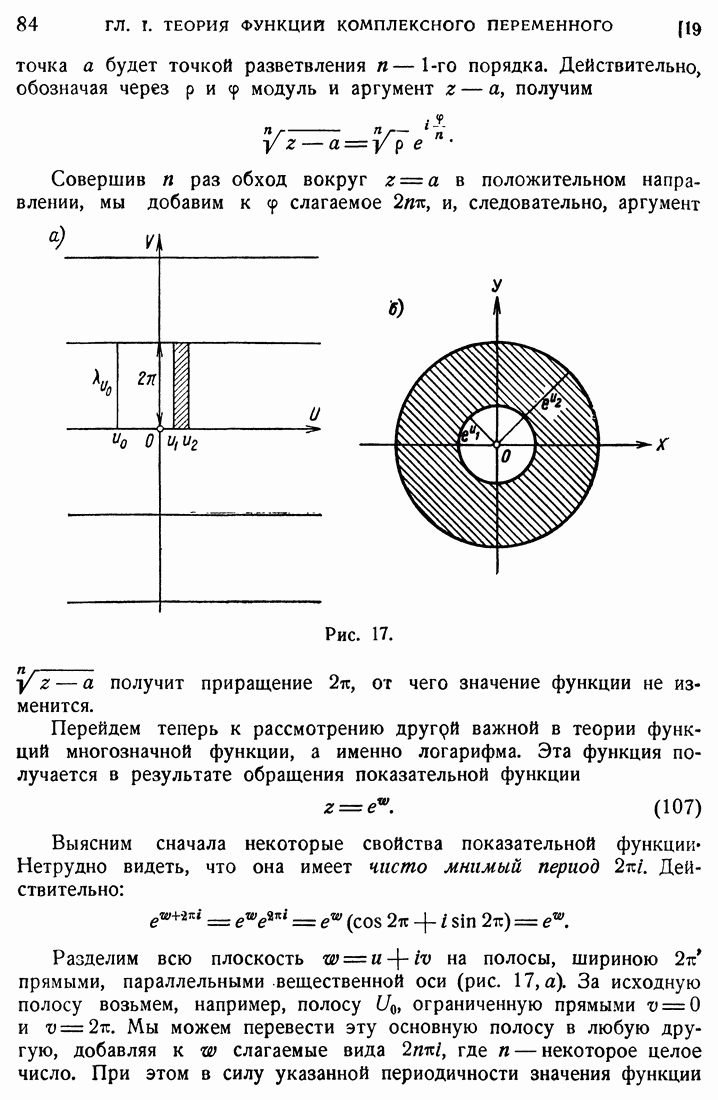
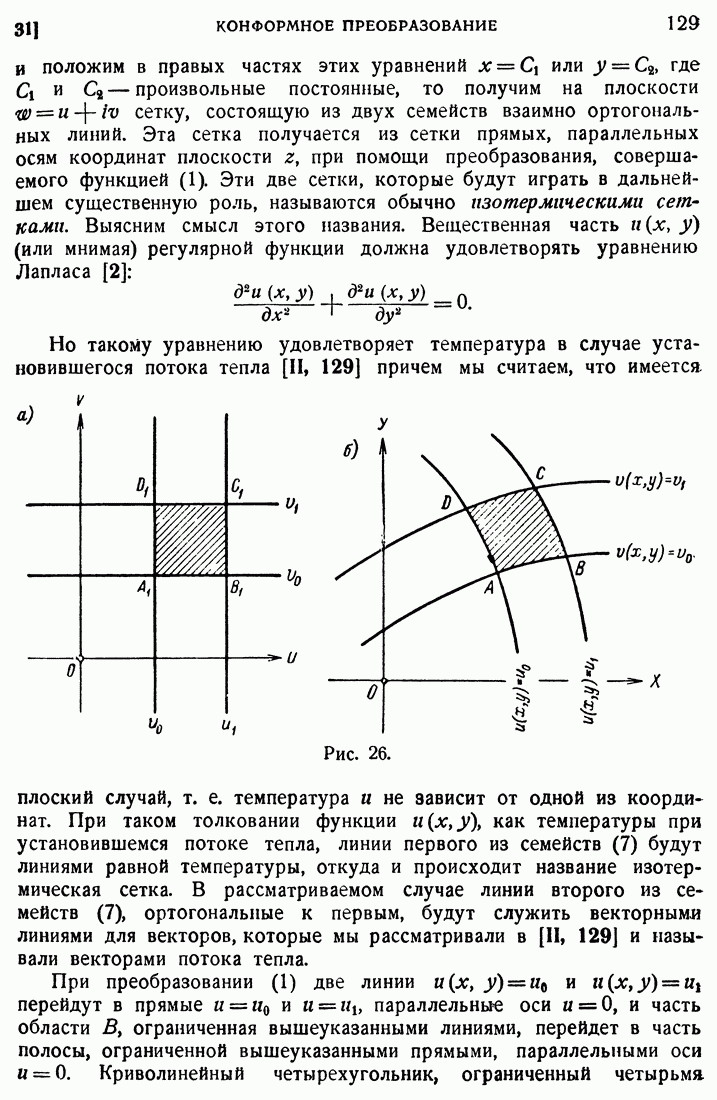
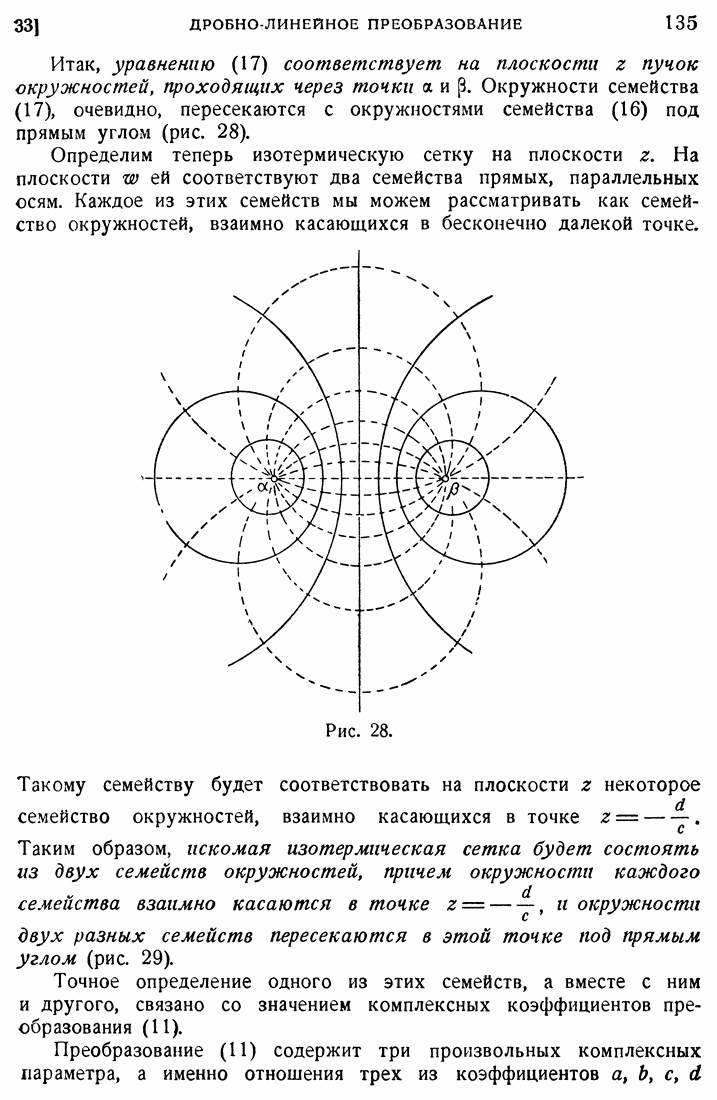
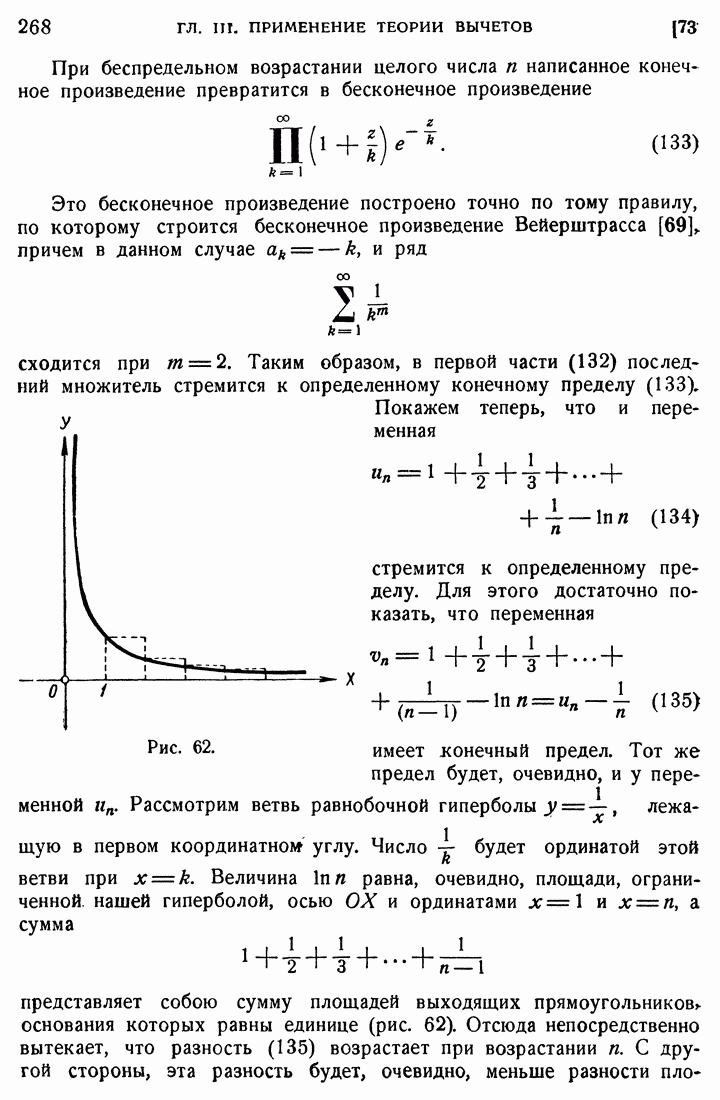
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДОБАВЛЕНИЕ. ПРИВЕДЕНИЕ МАТРИЦ К КАНОНИЧЕСКОЙ ФОРМЕ
190. Вспомогательные предложения.
Целью настоящего добавления является доказательство предложения, приведенного нами без доказательства в  Прежде всего, сформулируем это предложение. Если А есть некоторая матрица, то всегда можно найти такую матрицу V с определителем, отличным от нуля, что матрица
Прежде всего, сформулируем это предложение. Если А есть некоторая матрица, то всегда можно найти такую матрицу V с определителем, отличным от нуля, что матрица  , подобная матрице А, будет иметь квазидиагональную (или диагональную) форму
, подобная матрице А, будет иметь квазидиагональную (или диагональную) форму

где матрицы  имеют вид
имеют вид

Нижний значок  указывает порядок матрицы и аргумент X дает число, стоящее на главной диагонали. Если
указывает порядок матрицы и аргумент X дает число, стоящее на главной диагонали. Если  то матрица
то матрица  приводится к числу X. В результате доказательства этого предложения мы дополним его в некоторых существенных пунктах.
приводится к числу X. В результате доказательства этого предложения мы дополним его в некоторых существенных пунктах.
Напомним, прежде всего, геометрический смысл перехода к подобной матрице. Матрица А порядка  является оператором в
является оператором в  -мерном пространстве в том смысле, что она совершает некоторое линейное преобразование этого пространства. Вид матрицы А зависит, как мы видели
-мерном пространстве в том смысле, что она совершает некоторое линейное преобразование этого пространства. Вид матрицы А зависит, как мы видели  от выбора координат, т. е. основных ортов. Если матрица А выражает линейное преобразование при определенном выборе ортов и если мы совершаем преобразование координат, при котором новые составляющие каждого вектора выражаются через его прежние составляющие при помощи преобразования V, то в новой координатной системе наше линейное преобразование будет
от выбора координат, т. е. основных ортов. Если матрица А выражает линейное преобразование при определенном выборе ортов и если мы совершаем преобразование координат, при котором новые составляющие каждого вектора выражаются через его прежние составляющие при помощи преобразования V, то в новой координатной системе наше линейное преобразование будет
выражаться матрицей  Таким образом, формулированная нами задача сводится, по. существу, к выбору ортов, в некотором смысле наиболее естественных для линейного преобразования, осуществляемого в прежней системе координат матрицей А, а именно к такому выбору ортов, при котором наше линейное преобразование выражается матрицей, имеющей форму, указанную в правой части равенства (1).
Таким образом, формулированная нами задача сводится, по. существу, к выбору ортов, в некотором смысле наиболее естественных для линейного преобразования, осуществляемого в прежней системе координат матрицей А, а именно к такому выбору ортов, при котором наше линейное преобразование выражается матрицей, имеющей форму, указанную в правой части равенства (1).
Прежде чем переходить к решению этой задачи, мы предварительно выясним некоторые вспомогательные предложения, которыми нам придется пользоваться. Большая часть этих предложений выяснена ранее, но для цельности картины мы соберем их здесь в одном месте.
Прежде всего мы остановимся на выяснении понятия подпространства, с которым мы часто имели дело и раньше. Если  суть k линейно независимых векторов пространства, причем
суть k линейно независимых векторов пространства, причем  то совокупность векторов, определяемых формулой
то совокупность векторов, определяемых формулой

где  произвольные числа, мы называли подпространством измерения k, образованным вышеуказанными векторами. В случае
произвольные числа, мы называли подпространством измерения k, образованным вышеуказанными векторами. В случае  подпространство совпадает со всем пространством. Можно дать другое определение подпространства, эквивалентное только что указанному, а именно: подпространством называется совокупность векторов, обладающих следующими двумя свойствами. Если некоторый вектор
подпространство совпадает со всем пространством. Можно дать другое определение подпространства, эквивалентное только что указанному, а именно: подпространством называется совокупность векторов, обладающих следующими двумя свойствами. Если некоторый вектор  принадлежит этой совокупности, то и вектор
принадлежит этой совокупности, то и вектор  где с — произвольное число, также принадлежит совокупности, и если два вектора
где с — произвольное число, также принадлежит совокупности, и если два вектора  и принадлежат совокупности, то и их сумма также принадлежит совокупности. Иначе говоря, совершая действие умножения на число и сложение над векторами совокупности, мы не выходим из этой совокупности.
и принадлежат совокупности, то и их сумма также принадлежит совокупности. Иначе говоря, совершая действие умножения на число и сложение над векторами совокупности, мы не выходим из этой совокупности.
В дальнейшем мы будем иметь дело с двумя способами определения подпространства, которые мы сейчас и укажем. Пусть Р — некоторая матрица порядка  их — произвольный переменный вектор в
их — произвольный переменный вектор в  -мерном пространстве. Совокупность векторов, определяемых формулой
-мерном пространстве. Совокупность векторов, определяемых формулой

является, очевидно, некоторым подпространством, которое может совпадать и с полным пространством. Действительно, если к указанной совокупности принадлежит некоторый вектор  то к этой же совокупности принадлежит и вектор
то к этой же совокупности принадлежит и вектор  и если к нашей совокупности принадлежат два вектора
и если к нашей совокупности принадлежат два вектора  то к этой совокупности принадлежит, очевидно, и вектор
то к этой совокупности принадлежит, очевидно, и вектор  и, таким образом, формула (4) при произвольном переменном векторе
и, таким образом, формула (4) при произвольном переменном векторе  действительно определяет некоторое подпространство. Как мы уже упоминали [III, 15], число измерений этого подпространства равно рангу матрицы Р.
действительно определяет некоторое подпространство. Как мы уже упоминали [III, 15], число измерений этого подпространства равно рангу матрицы Р.
Укажем теперь второй способ определения подпространства. Пуаь Q есть некоторая матрица порядка  , и мы рассматриваем совокупность векторов, удовлетворяющих уравнению
, и мы рассматриваем совокупность векторов, удовлетворяющих уравнению

Совершенно так же, как и выше, можно показать, что эта совокупность векторов образует некоторое подпространство. Как мы видели выше  это подпространство будет иметь измерение
это подпространство будет иметь измерение  где
где  матрицы
матрицы 
Говоря о подпространстве, мы, конечно, всегда предполагаем, что оно не пустое, т. е. что оно содержит действительно векторы, отличные от нуля. Посмотрим, в каком случае формула (4) определяет пустое подпространство, т. е. в каком случае для любого  из нашего пространства формула (4) дает вектор, равный нулю. Принимая во внимание самый вид линейного преобразования, мы можем утверждать, что это будет иметь место в том и только в том случае, когда матрица Р равна пулю, т. е. когда все ее элементы равны нулю.
из нашего пространства формула (4) дает вектор, равный нулю. Принимая во внимание самый вид линейного преобразования, мы можем утверждать, что это будет иметь место в том и только в том случае, когда матрица Р равна пулю, т. е. когда все ее элементы равны нулю.
Пусть  некоторые подпространства. Мы будем говорить, что они образуют полную систему подпространств, если всякий вектор
некоторые подпространства. Мы будем говорить, что они образуют полную систему подпространств, если всякий вектор  нашего пространства может быть представлен единственным образом в виде суммы векторов
нашего пространства может быть представлен единственным образом в виде суммы векторов

принадлежащих указанным выше подпространствам. Отметим значение условия единственности представления. Из этого условия непосредственно вытекает, что вектор, равный нулю, не может быть представлен в виде суммы (6), среди слагаемых которой есть отличные от нуля, а это в свою очередь равносильно тому факту, что между векторами упомянутых выше подпространств не может существовать линейной зависимости. В качестве примера рассмотрим обычное вещественное трехмерное пространство, образованное векторами, имеющими начало в некоторой точке О. В качестве полной системы подпространств мы можем взять некоторую плоскость L, проходящую через О, и некоторую прямую  проходящую через О и не лежащую в плоскости L. Первое подпространство будет двух измерений и может быть образовано двумя произвольными векторами, лежащими в плоскости L и не находящимися на одной прямой. Второе подпространство будет одного измерения и может быть образовано любым вектором, лежащим на прямой
проходящую через О и не лежащую в плоскости L. Первое подпространство будет двух измерений и может быть образовано двумя произвольными векторами, лежащими в плоскости L и не находящимися на одной прямой. Второе подпространство будет одного измерения и может быть образовано любым вектором, лежащим на прямой  Всякий вектор нашего трехмерного пространства может быть единственным образом представлен как сумма векторов, лежащих в плоскости L и на прямой
Всякий вектор нашего трехмерного пространства может быть единственным образом представлен как сумма векторов, лежащих в плоскости L и на прямой 
Пусть А есть некоторая матрица, осуществляющая линейное преобразование пространства. Положим, что нам удалось найти такую полную систему подпространств  измерения
измерения  что каждое из этих подпространств будет инвариантным по отношению
что каждое из этих подпространств будет инвариантным по отношению
шению к линейному преобразованию, осуществляемому матрицей  , т. е., иначе говоря, любой вектор подпространства
, т. е., иначе говоря, любой вектор подпространства  в результате линейного преобразования, осуществляемого матрицей
в результате линейного преобразования, осуществляемого матрицей  , перейдет в вектор того же подпространства. В данном случае мы имеем следующий естественный выбор ортов, при котором матрица А принимает квазидиагональпую форму структуры
, перейдет в вектор того же подпространства. В данном случае мы имеем следующий естественный выбор ортов, при котором матрица А принимает квазидиагональпую форму структуры  . Берем за первые
. Берем за первые  , ортов какие-либо
, ортов какие-либо  линейно независимых векторов, образующих подпространство
линейно независимых векторов, образующих подпространство  за следующие
за следующие  , ортов выбираем какие-нибудь
, ортов выбираем какие-нибудь  линейно независимых векторов, образующих подпространство
линейно независимых векторов, образующих подпространство  и т. д. Раз
и т. д. Раз  образует полную систему подпространств, мы имеем, очевидно,
образует полную систему подпространств, мы имеем, очевидно,  Нетрудно видеть, что при таком выборе ортов наша матрица А действительно будет квазидиагоналыюй формы. Остановимся на этом подробнее и для простоты письма ограничимся случаем
Нетрудно видеть, что при таком выборе ортов наша матрица А действительно будет квазидиагоналыюй формы. Остановимся на этом подробнее и для простоты письма ограничимся случаем  Пусть
Пусть  некоторый вектор и
некоторый вектор и  - новый вектор, получаемый из него при помощи нашего линейного преобразования. В силу инвариантности подпространства
- новый вектор, получаемый из него при помощи нашего линейного преобразования. В силу инвариантности подпространства  и сделанного выбора ортов мы должны иметь При
и сделанного выбора ортов мы должны иметь При  и точно так же, в силу инвариантности
и точно так же, в силу инвариантности  если
если  то
то  Отсюда непосредственно следует, что при сделанном выборе ортов наше линейное преобразование осуществляется квазидиагональной матрицей вида
Отсюда непосредственно следует, что при сделанном выборе ортов наше линейное преобразование осуществляется квазидиагональной матрицей вида

Отметим еще, что выбор основных ортов внутри каждого подпространства остается совершенно произвольным, и в дальнейшем мы используем этот произвол для того, чтобы привести каждую из отдельных матриц А и  входящих в квазидиагональпую матрицу (7), к наиболее простой в некотором смысле форме.
входящих в квазидиагональпую матрицу (7), к наиболее простой в некотором смысле форме.
Мы переходим сейчас к следующим предложениям, которыми нам придется пользоваться в дальнейшем.
Пусть  есть некоторый полином
есть некоторый полином

Подставляя вместо  некоторую матрицу А, мы получаем полином от матрицы
некоторую матрицу А, мы получаем полином от матрицы

В результате действий, указанных в правой части, мы получим некоторую новую матрицу, т. е. всякий полином от матрицы  есть также некоторая матрица. Отметим, что коэффициенты полинома
есть также некоторая матрица. Отметим, что коэффициенты полинома  суть некоторые числа. Поскольку целые положительные степени одной и той же матрицы
суть некоторые числа. Поскольку целые положительные степени одной и той же матрицы  коммутируют друг с другом и с любыми числами, мы можем утверждать, что не только сложение, но и умножение полиномов от одной и той же матрицы А производится по правилам обычной алгебры так же, как это делается с полиномами от численного аргумента. Таким образом, если мы имеем некоторое тождество, связывающее несколько полиномов от численного аргумента и содержащее действия сложения и умножения, то же самое тождество будет иметь место, если вместо аргумента
коммутируют друг с другом и с любыми числами, мы можем утверждать, что не только сложение, но и умножение полиномов от одной и той же матрицы А производится по правилам обычной алгебры так же, как это делается с полиномами от численного аргумента. Таким образом, если мы имеем некоторое тождество, связывающее несколько полиномов от численного аргумента и содержащее действия сложения и умножения, то же самое тождество будет иметь место, если вместо аргумента  мы подставим любую матрицу А.
мы подставим любую матрицу А.
Основную роль в вопросе приведения матриц к каноническому виду играет характеристическое уравнение

где  элементы матрицы А. Это уравнение может быть записано в виде
элементы матрицы А. Это уравнение может быть записано в виде

где символ  означает определитель матрицы U. Как мы показали выше [91], имеет место следующее тождество Кейли:
означает определитель матрицы U. Как мы показали выше [91], имеет место следующее тождество Кейли:

т. е. если в характеристический полином  матрицы А вместо аргумента X вставить матрицу А, то в результате получится матрица, равная нулю.
матрицы А вместо аргумента X вставить матрицу А, то в результате получится матрица, равная нулю.
Нам остается еще отметить два простых предложения. Как известно, корни уравнения (9) называются характеристическими числами матрицы А. Докажем следующую теорему: если  суть характеристические числа матрицы А, то у матрицы
суть характеристические числа матрицы А, то у матрицы  где s — целое положительное число, характеристические числа будут
где s — целое положительное число, характеристические числа будут 
Принимая во внимание, что в полиноме  старший член равен
старший член равен  мы можем написать тождество относительно X:
мы можем написать тождество относительно X:

Пусть  - корень степени s из единицы. Мы имеем очевидное тождество [I, 175]:
- корень степени s из единицы. Мы имеем очевидное тождество [I, 175]:

Принимая во внимание, что определитель произведения матриц равен произведению определителей и тождеств (12) и (13), мы можем написать

или

Отсюда, в силу тождества (13), получим

т. е.

что и доказывает высказанную теорему.
В дальнейшем нам придется вычислять определитель матриц, имеющих квазидиагональную форму

Нетрудно видеть, что он равен произведению определителей матриц А, т. е.

Для простоты письма ограничимся случаем  . Мы имеем в силу закона умножения
. Мы имеем в силу закона умножения

откуда

Применяя разложение определителя по элементам некоторого столбца или строки, мы получим, например,

откуда и вытекает непосредственно формула (14).
В заключение напомним, что подобные матрицы имеют одинаковые характеристические числа.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К ВОСЬМОМУ ИЗДАНИЮ
- 1. Функции комплексного переменного.
- 2. Производная.
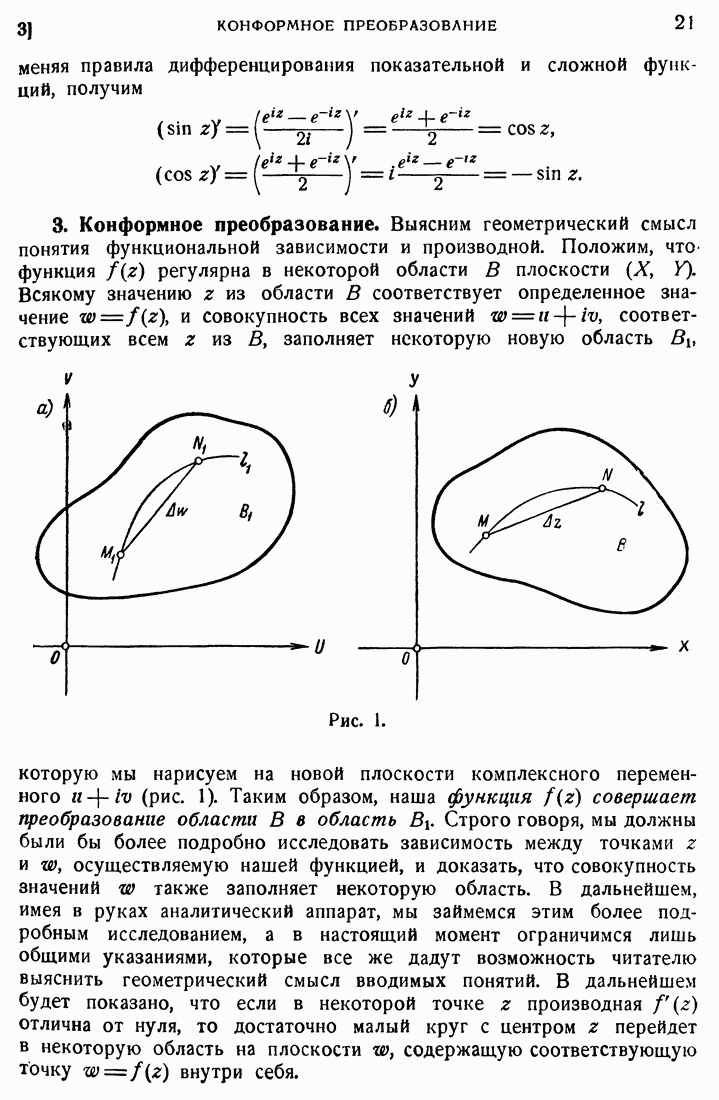
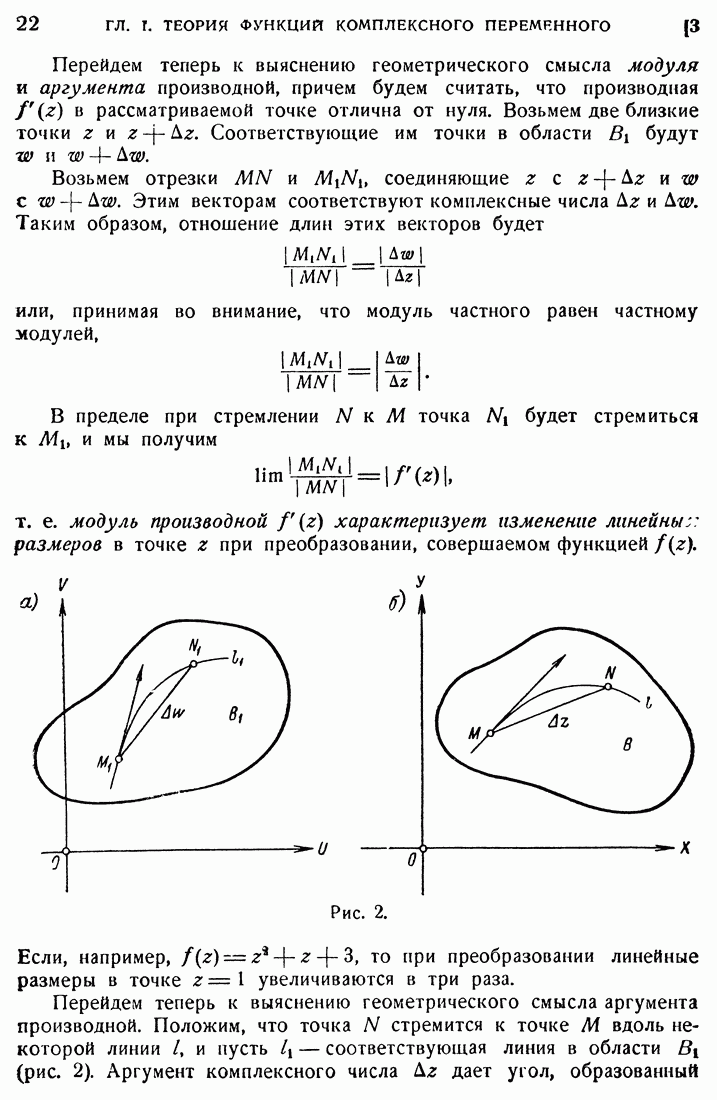
- 3. Конформное преобразование.
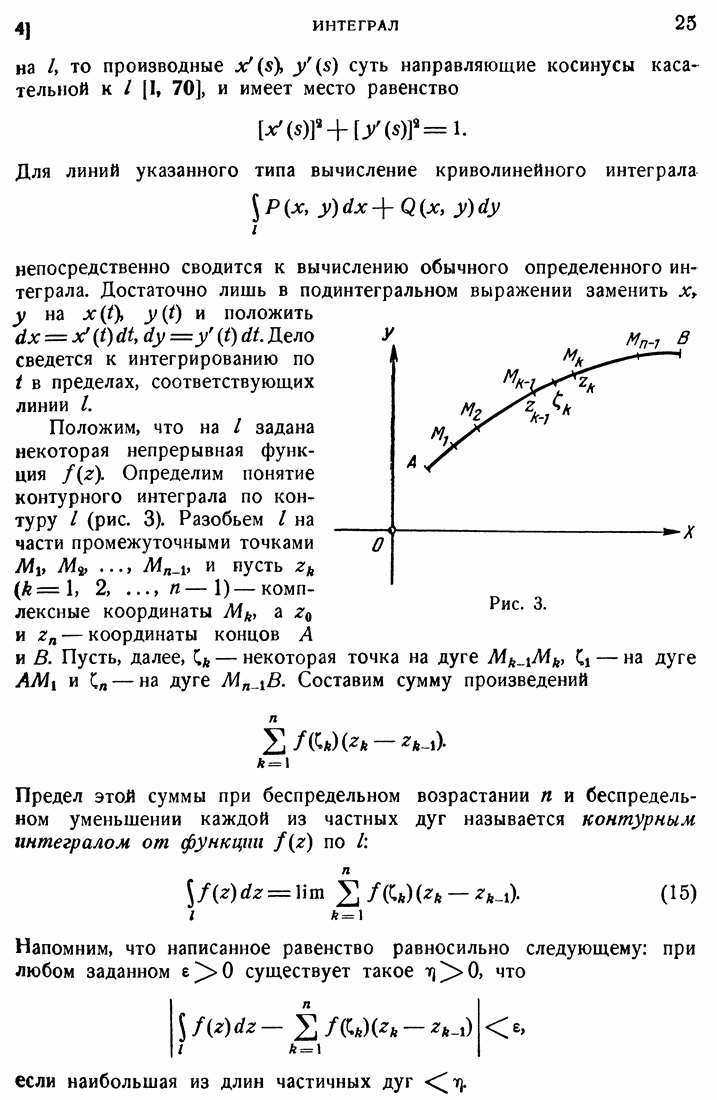
- 4. Интеграл.
- 5. Теорема Коши.
- 6. Основная формула интегрального исчисления.
- 7. Формула Коши.
- 8. Интегралы типа Коши.
- 9. Следствия формулы Коши.
- 10. Изолированные особые точки.
- 11. Бесконечные ряды с комплексными членами.
- 12. Теорема Вейерштрасса.
- 13. Степенные ряды.
- 14. Ряд Тейлора.
- 15. Ряд Лорана.
- 16. Примеры.
- 17. Изолированные особые точки. Бесконечно далекая точка.
- 18. Аналитическое продолжение.
- 19. Примеры многозначных функций.
- 20. Особые точки аналитических функций и римановы поверхности.
- 21. Теорема вычетов.
- 22. Теоремы о числе корней.
- 23. Обращение степенного ряда.
- 24. Принцип симметрии.
- 25. Ряд Тейлора на окружности круга сходимости.
- 26. Дополнительные сведения о формуле Коши.
- 27. Главное значение интеграла.
- 28. Главное значение интеграла (продолжение).
- 29. Интегралы типа Коши.
- 30. Интегралы типа Коши (продолжение).
- ГЛАВА II. КОНФОРМНОЕ ПРЕОБРАЗОВАНИЕ И ПЛОСКОЕ ПОЛЕ
- 31. Конформное преобразование.
- 32. Линейное преобразование.
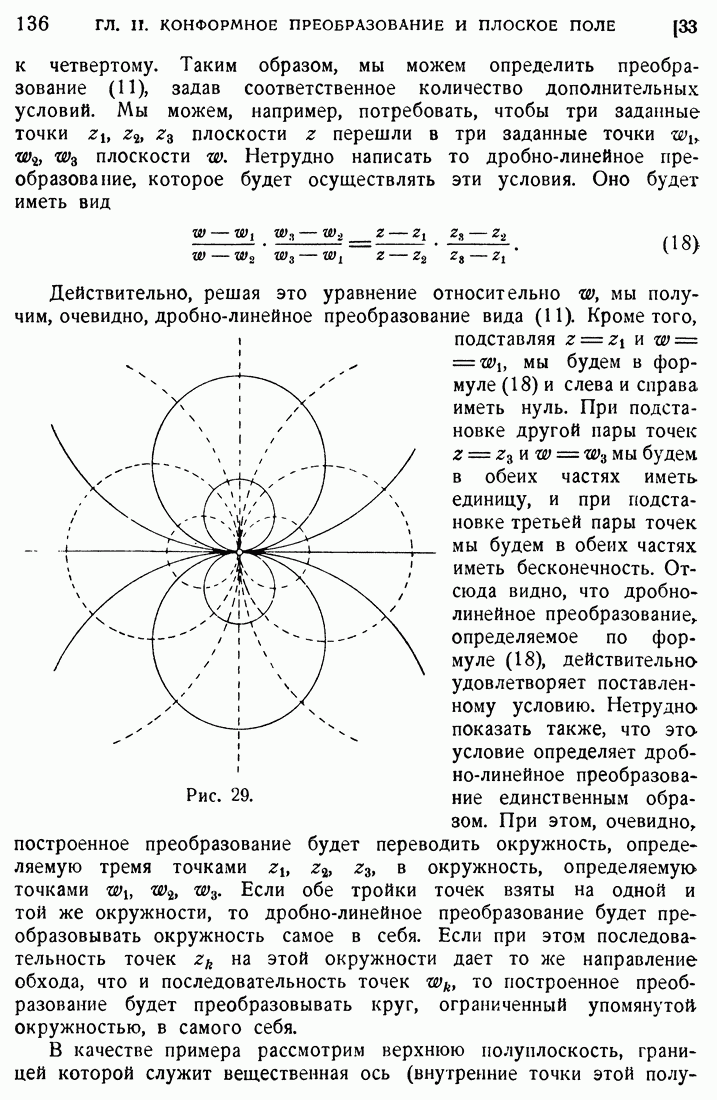
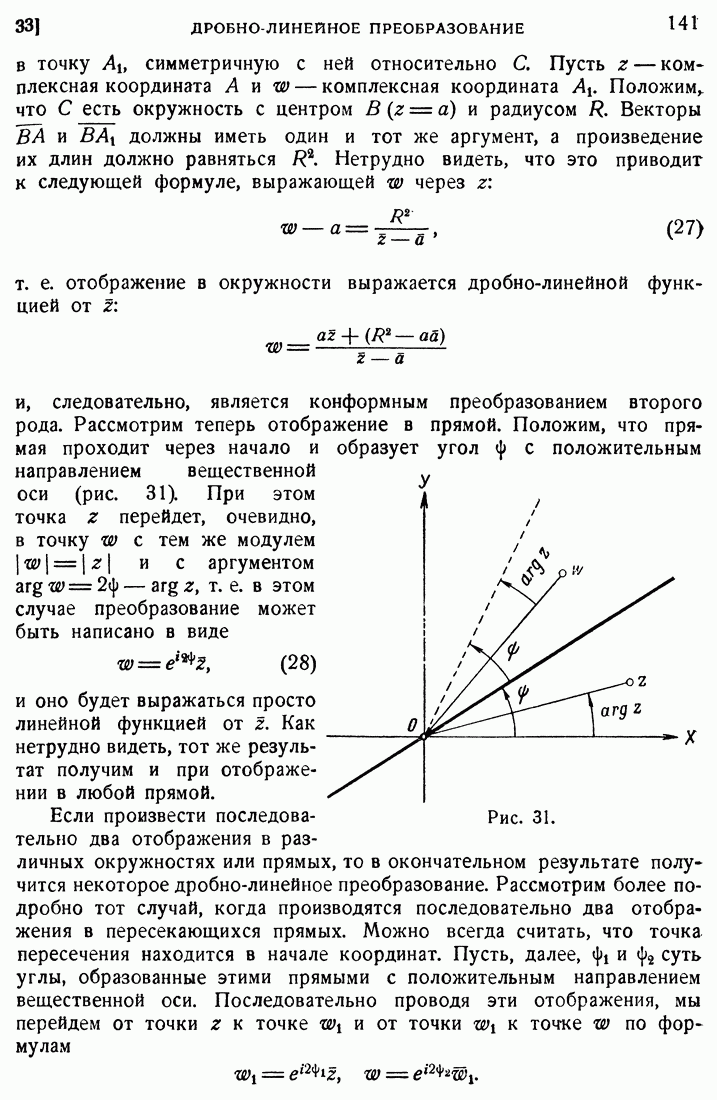
- 33. Дробно-линейное преобразование.
- 34. Функция w = z^2.
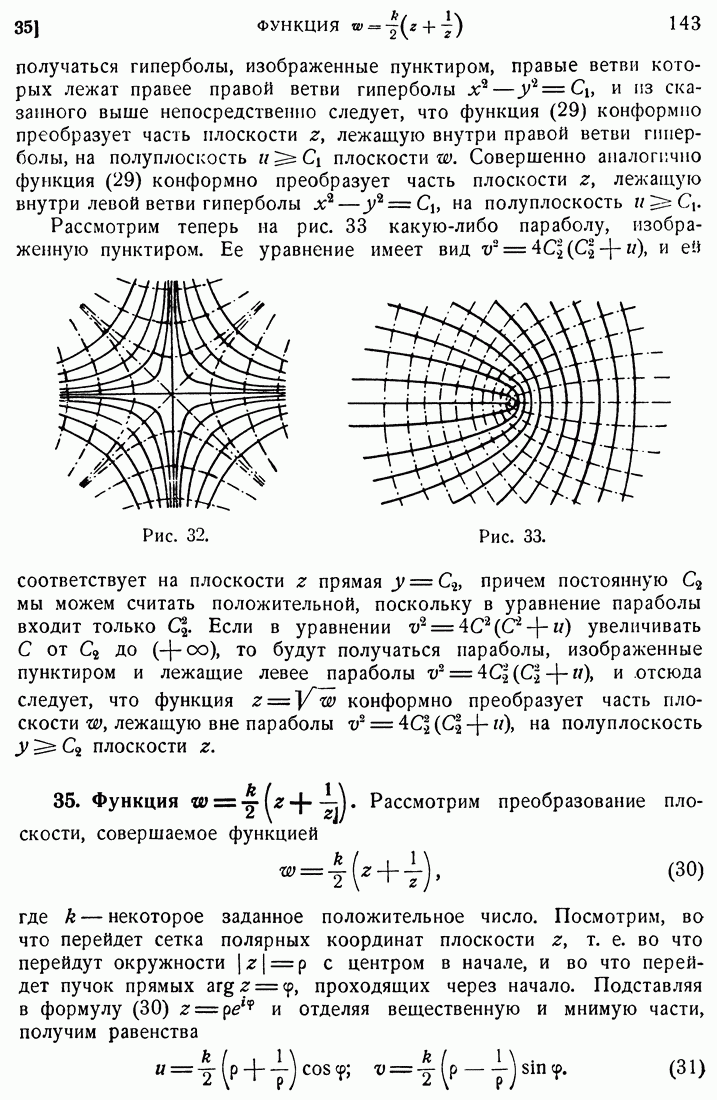
- 35. Функция …
- 36. Двуугольник и полоса.
- 37. Основная теорема.
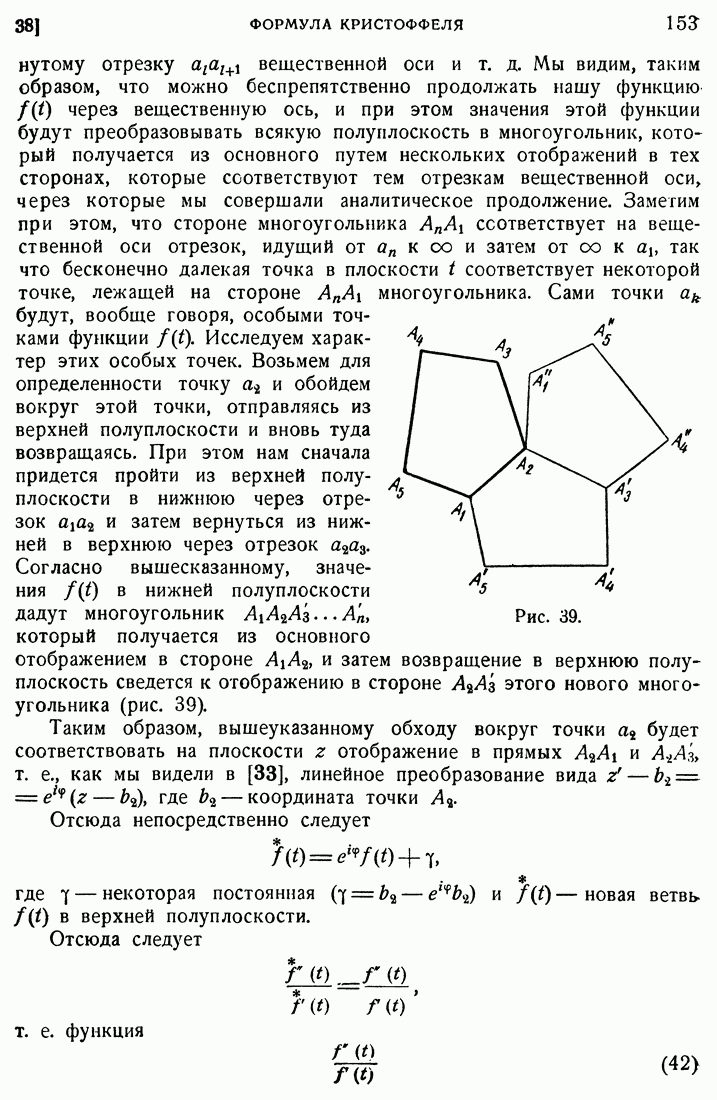
- 38. Формула Кристоффеля.
- 39. Частные случаи.
- 40. Случай внешности многоугольника.
- 41. Минимальное свойство преобразования на круг.
- 42. Способ сопряженных тригонометрических рядов.
- 43. Плоское установившееся течение жидкости.
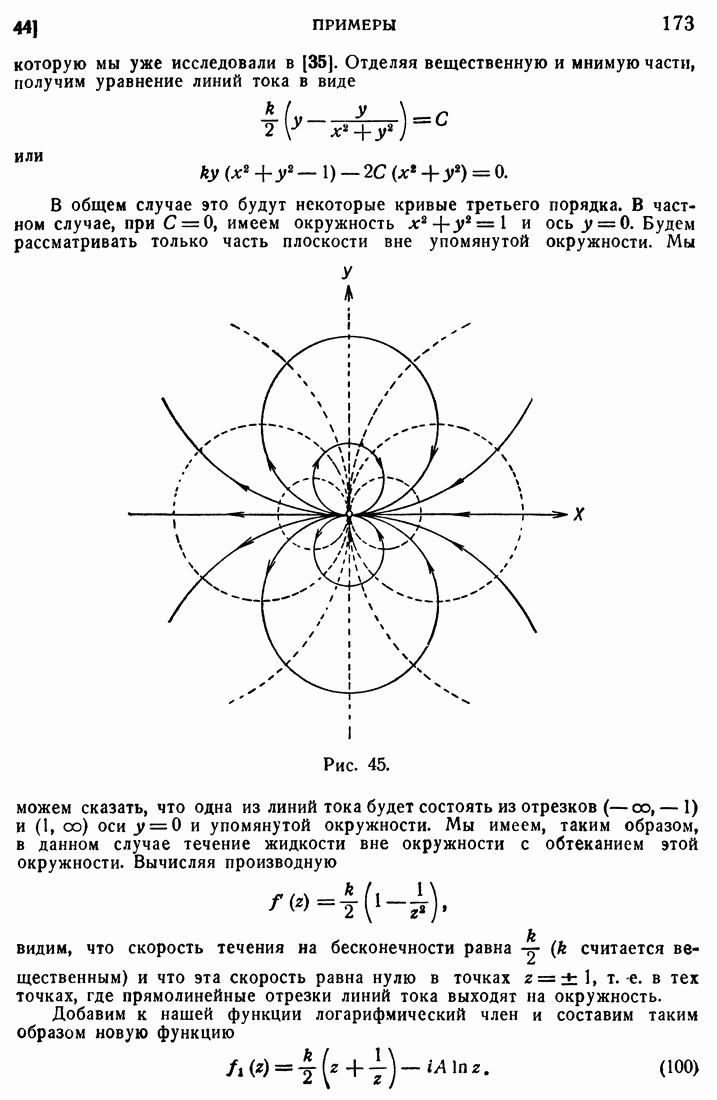
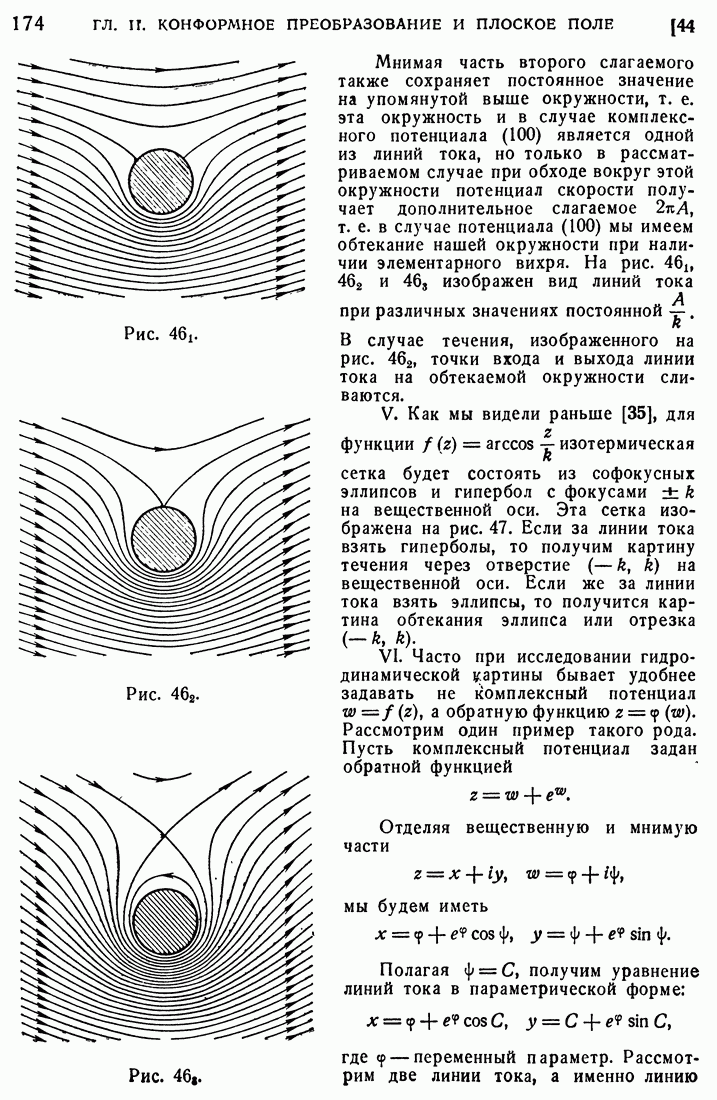
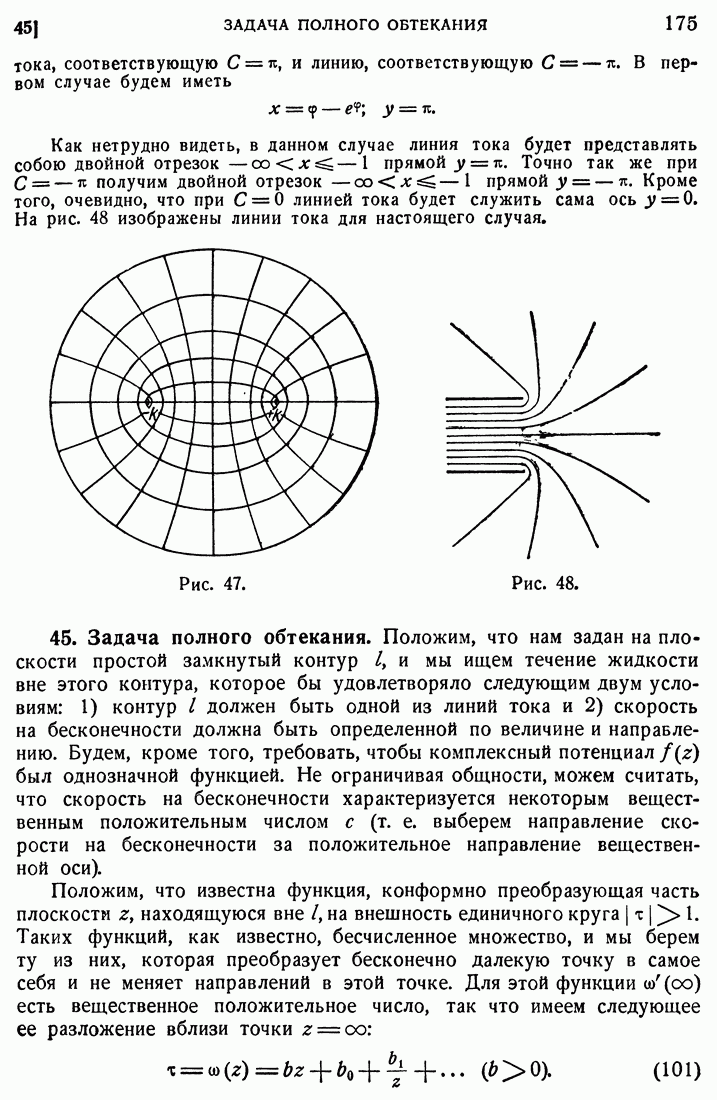
- 44. Примеры.
- 45. Задача полного обтекания.
- 46. Формула Н. Е. Жуковского.
- 47. Плоская электростатическая задача.
- 48. Формула Шварца.
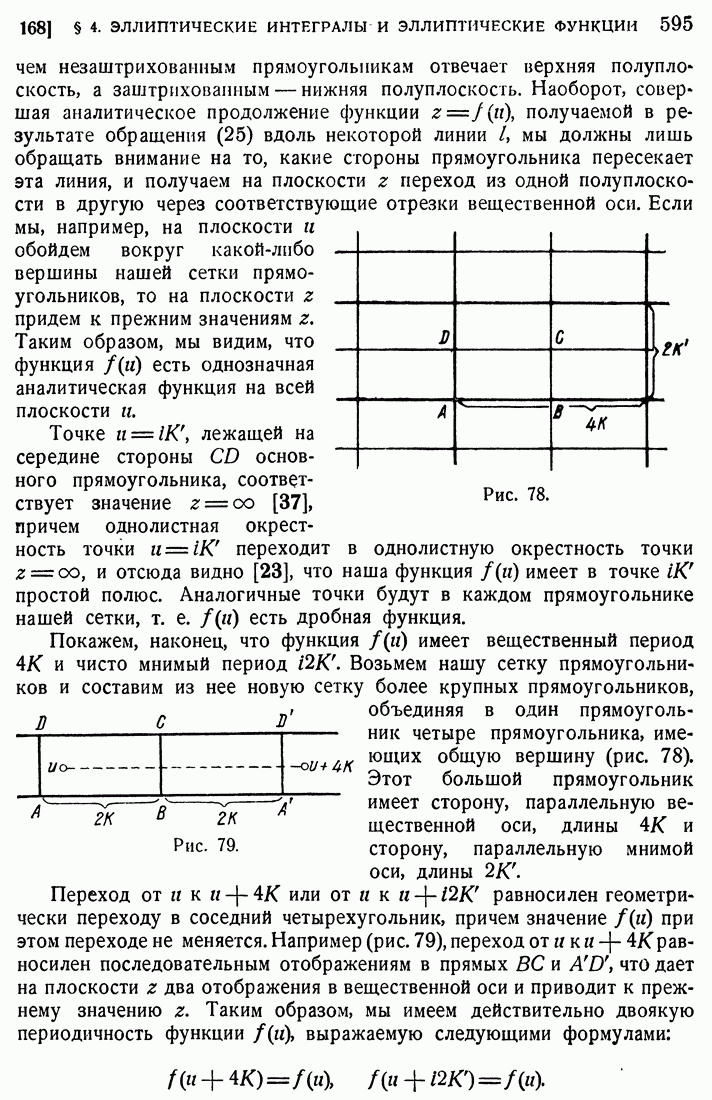
- 49. Ядро ctg((s-t)/2).
- 50. Предельные задачи.
- 51. Бигармоническое уравнение.
- 52. Волновое уравнение и аналитические функции.
- 53. Основная теорема.
- 54. Дифракция плоской волны.
- 55. Отражение упругих волн от прямолинейной границы.
- ГЛАВА III. ПРИМЕНЕНИЕ ТЕОРИИ ВЫЧЕТОВ, ЦЕЛЫЕ И ДРОБНЫЕ ФУНКЦИИ
- 56. Интеграл Френеля.
- 57. Интегрирование выражений с тригонометрическими функциями.
- 58. Интегрирование рациональной дроби.
- 59. Некоторые новые типы интегралов с тригонометрическими функциями.
- 60. Лемма Жордана.
- 61. Представление некоторых функций контурными интегралами.
- 62. Примеры интегралов от многозначных функций.
- 63. Интегрирование системы линейных уравнений с постоянными коэффициентами.
- 64. Разложение дробной функции на простейшие дроби.
- 66. Построение мероморфной функции.
- 67. Целые функции.
- 68. Бесконечные произведения.
- 69. Построение целой функции по ее корням.
- 70. Интегралы, зависящие от параметра.
- 71. Эйлеров интеграл второго рода.
- 72. Эйлеров интеграл первого рода.
- 73. Бесконечное произведение для функции …
- 74. Представление Г(z) контурным интегралом.
- 75. Формула Стирлинга.
- 76. Формула суммирования Эйлера.
- 77. Числа Бернулли.
- 78. Метод скорейшего спуска.
- 79. Асимптотическое разложение интеграла.
- 80. Примеры.
- 81. Метод стационарной фазы.
- ГЛАВА IV. АНАЛИТИЧЕСКИЕ ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ И ФУНКЦИИ МАТРИЦ
- 82. Регулярные функции многих переменных.
- 83. Двойной интеграл и формула Коши.
- 84. Степенные ряды.
- 85. Аналитическое продолжение.
- 86. Функции матриц. Предварительные понятия.
- 87. Степенные ряды от одной матрицы.
- 88. Умножение степенных рядов. Обращение степенного ряда.
- 89. Дальнейшее исследование сходимости.
- 90. Интерполяционные полиномы.
- 91. Тождество Кейли. Формула Сильвестра.
- 92. Определение функций одной матрицы формулой Коши.
- 93. Аналитическое продолжение.
- 94. Логарифм матриц.
- 95. Обращение целой функции от матрицы в случае матриц второго порядка.
- 96. Системы линейных уравнений с постоянными коэффициентами.
- 97. Функции нескольких матриц.
- ГЛАВА V. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
- 98. Разложение решения в степенной ряд.
- 99. Аналитическое продолжение решения.
- 100. Окрестность особой точки.
- 101. Регулярная особая точка.
- 102. Уравнения класса Фукса.
- 103. Уравнение Гаусса.
- 104. Гипергеометрический ряд.
- 105. Полиномы Лежандра.
- 106. Полиномы Якоби.
- 107. Конформное преобразование и уравнение Гаусса.
- 108. Преобразование Лапласа.
- 109. Различный выбор решений.
- 110. Уравнение Бесселя.
- 111. Функции Ханкеля и интегральное представление решений уравнения Бесселя.
- 112. Асимптотические разложения.
- 113. Асимптотические разложения решений, полученных преобразованием Лапласа.
- 114. Асимптотические разложения решений уравнения Бесселя.
- 115. Вырождение уравнения Гаусса.
- 116. Формальные ряды в окрестности иррегулярной особой точки.
- 117. Построение асимптотических разложений методом после довательных приближений.
- 118. Функции Эйри.
- 119. Асимптотика при большом значении параметра.
- 120. Уравнения с периодическими коэффициентами.
- 121. Условия устойчивости и неустойчивости для уравнения Хилла.
- 122. Системы линейных дифференциальных уравнений.
- 123. Регулярная особая точка.
- 124. Регулярные системы.
- 125. Представление решения в окрестности особой точки.
- 126. Канонические решения.
- 127. Связь с регулярными решениями типа Фукса.
- 128. Случай любых Us.
- 129. Формальные разложения в окрестности иррегулярной особой точки.
- ГЛАВА VI. СПЕЦИАЛЬНЫЕ ФУНКЦИИ
- 130. Определение сферических функций.
- 131. Явные выражения сферических функций.
- 132. Свойство ортогональности.
- 133. Полиномы Лежандра.
- 134. Разложение по сферическим функциям.
- 135. Доказательство сходимости.
- 136. Связь сферических функций с предельными задачами.
- 137. Задачи Дирихле и Неймана.
- 138. Потенциал объемных масс.
- 139. Потенциал сферического слоя.
- 140. Электрон в центральном поле.
- 141. Шаровые функции и линейные представления группы вращения.
- 142. Функция Лежандра.
- 143. Функция Лежандра второго рода.
- § 2. ФУНКЦИИ БЕССЕЛЯ
- 144. Определение функций Бесселя.
- 145. Соотношения между функциями Бесселя.
- 146. Ортогональность функций Бесселя и их корни.
- 147. Производящая функция и интегральное представление.
- 148. Формула Фурье — Бесселя.
- 150. Разложение функций Неймана с целым значком.
- 151. Случай чисто мнимого аргумента.
- 152. Новые интегральные представления.
- 153. Асимптотические представления.
- 154. Функции Бесселя и уравнение Лапласа.
- 155. Волновое уравнение в цилиндрических координатах.
- 156. Волновое уравнение в сферических координатах.
- § 3. ПОЛИНОМЫ ЭРМИТА И ЛАГЕРРА
- 157. Линейный осциллятор и полиномы Эрмита.
- 158. Свойство ортогональности.
- 159. Производящая функция.
- 160. Параболические координаты и функции Эрмита.
- 161. Полиномы Лагерра.
- 162. Связь полиномов Эрмита и Лагерра.
- 163. Асимптотическое выражение полиномов Эрмита.
- 164. Асимптотическое выражение полиномов Лежандра.
- § 4. ЭЛЛИПТИЧЕСКИЕ ИНТЕГРАЛЫ И ЭЛЛИПТИЧЕСКИЕ ФУНКЦИИ
- 165. Приведение эллиптических интегралов к нормальному виду.
- 166. Приведение интегралов к тригонометрической форме.
- 167. Примеры.
- 168. Обращение эллиптического интеграла.
- 169. Общие свойства эллиптических функций.
- 170. Основная лемма.
- 171. Функции Вейерштрасса.
- 172. Дифференциальное уравнение для …
- 173. Функции …
- 174. Разложение целой периодической функции.
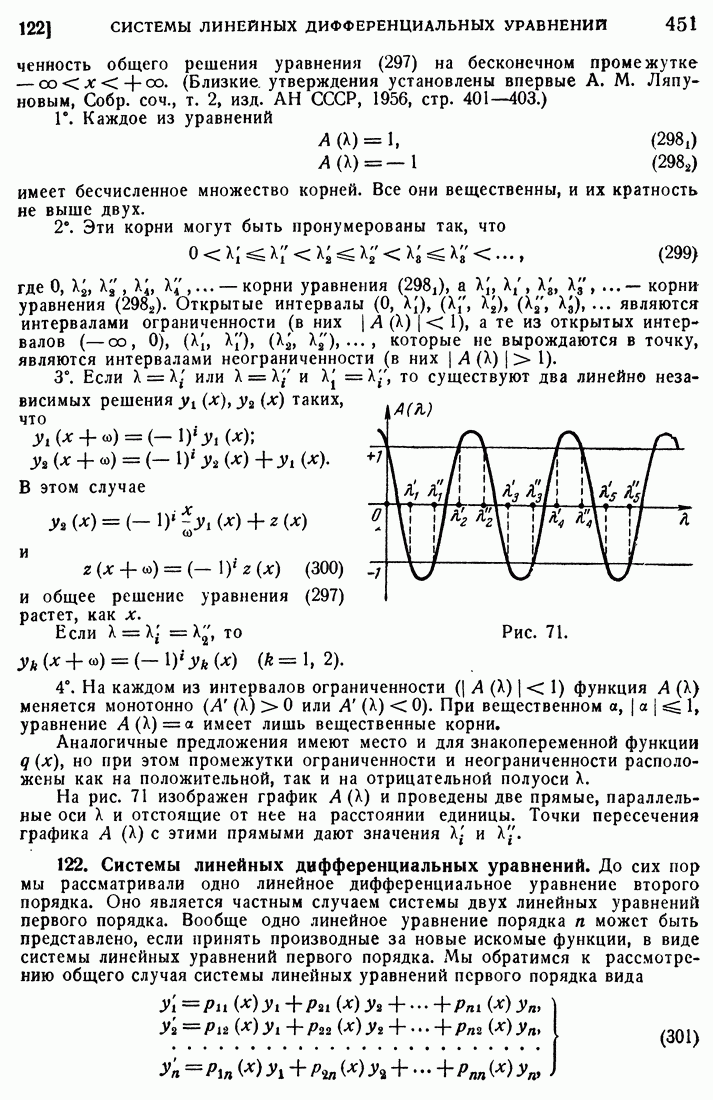
- 175. Новые обозначения.
- 176. Функция …
- 177. Функции …
- 178. Свойства функций тэта.
- 179. Выражение чисел … через …
- 180. Эллиптические функции Якоби.
- 181. Основные свойства функций Якоби.
- 182. Дифференциальные уравнения для функций Якоби.
- 183. Формулы сложения.
- 184. Связь функций p(u) и sn(u).
- 185. Эллиптические координаты.
- 186. Введение эллиптических функций.
- 187. Уравнение Лямэ.
- 188. Простой маятник.
- 189. Пример конформного преобразования.
- ДОБАВЛЕНИЕ. ПРИВЕДЕНИЕ МАТРИЦ К КАНОНИЧЕСКОЙ ФОРМЕ
- 191. Случай простых корней.
- 192. Первый этап преобразований в случае кратных корней.
- 193. Приведение к канонической форме.
- 194. Определение структуры канонической формы.
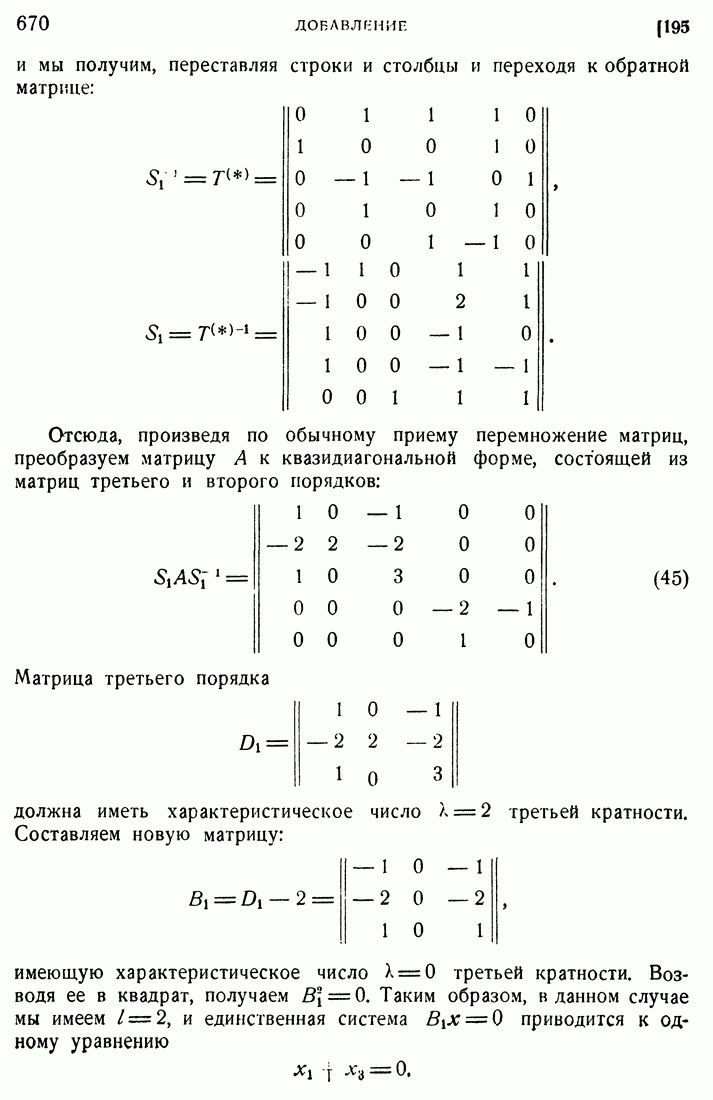
- 196. Пример.