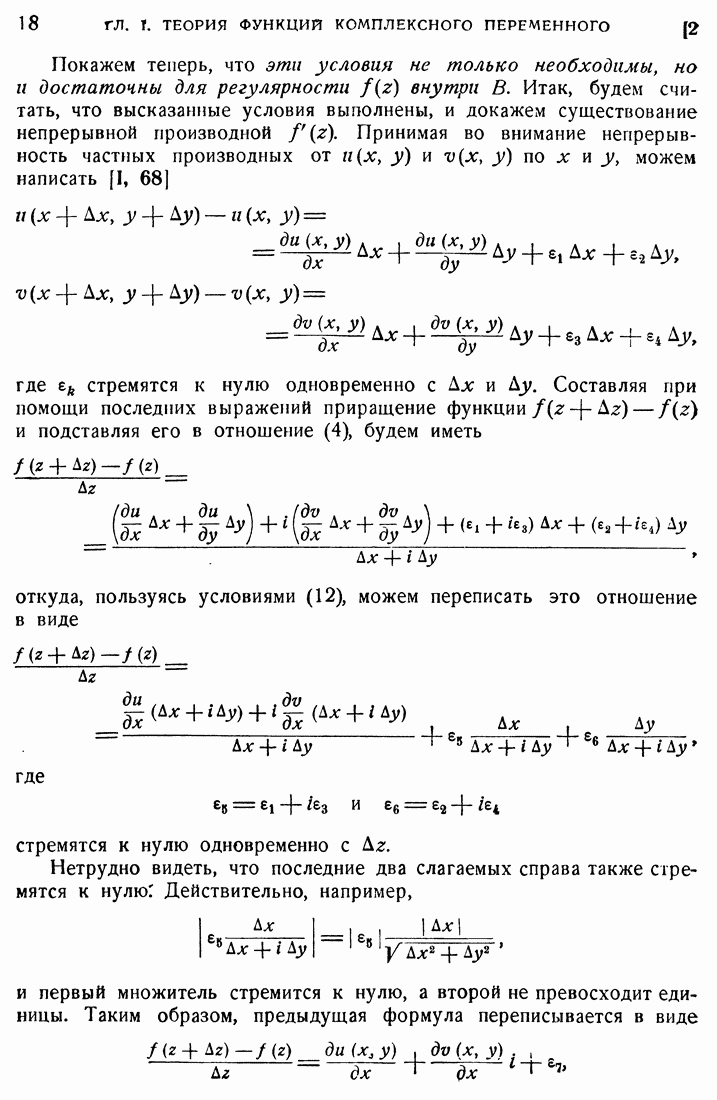| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
121. Условия устойчивости и неустойчивости для уравнения Хилла.
Выше было показано, что для уравнения Хилла имеет место устойчивость (все решения ограничены при если для постоянной Ляпунова А выполнено неравенство  или неустойчивость показательного типа, если
или неустойчивость показательного типа, если  Однако обычно нельзя различить эти случаи без численного интегрирования, так как А выражается лишь через решения уравнения (275) по формуле (279).
Однако обычно нельзя различить эти случаи без численного интегрирования, так как А выражается лишь через решения уравнения (275) по формуле (279).
Далее мы выведем простые достаточные условия устойчивости и неустойчивости, принадлежащие А. М. Ляпунову и Н. Е. Жуковскому выраженные непосредственно через функцию  . Для этого нам понадобятся некоторые леммы, первая из которых непосредственна связана с содержанием [II, 31].
. Для этого нам понадобятся некоторые леммы, первая из которых непосредственна связана с содержанием [II, 31].
Лемма 1. Пусть в уравнениях

коэффициенты — вещественные непрерывные функции на всей оси  . Тогда между двумя корнями любого решения второго из уравнений лежит по крайней мере один корень любого решения первого из уравнений (285). Пусть, далее, имеются начальные условия
. Тогда между двумя корнями любого решения второго из уравнений лежит по крайней мере один корень любого решения первого из уравнений (285). Пусть, далее, имеются начальные условия

и при  решение
решение  положительно. Тогда на указанном промежутке
положительно. Тогда на указанном промежутке 
Доказательство первого утверждения указано в  Переходим к доказательству второго утверждения.
Переходим к доказательству второго утверждения.
Умножая первое из уравнений на  второе на
второе на  и вычитая полученные уравнения почленно, получим
и вычитая полученные уравнения почленно, получим

На промежутке  решения
решения  удовлетворяющие условиям
удовлетворяющие условиям  положительны в силу первого утверждения, и отношение
положительны в силу первого утверждения, и отношение  равное единице при
равное единице при  в силу (286) возрастает, откуда и следует второе утверждение леммы.
в силу (286) возрастает, откуда и следует второе утверждение леммы.
Лемма 2. Если  и уравнение Хилла имеет не обращающееся в нуль апериодическое решение
и уравнение Хилла имеет не обращающееся в нуль апериодическое решение  то
то

Доказательство. Подставляя  и интегрируя по частям, получим
и интегрируя по частям, получим

В силу периодичности  внеинтегральный член исчезает, и из полученной формулы следует (287).
внеинтегральный член исчезает, и из полученной формулы следует (287).
Введем понятие выпуклого множества функций. Множество М вещественных непрерывных функций  называется выпуклым при соблюдении следующего условия: если функции
называется выпуклым при соблюдении следующего условия: если функции  принадлежат
принадлежат  , то и функция
, то и функция

при всех s, удовлетворяющих условию  также принадлежит М. Переходим к основной для дальнейших доказательств лемме.
также принадлежит М. Переходим к основной для дальнейших доказательств лемме.
Лемма 3. Пусть М — некоторое выпуклое множество  -периодических, вещественных и непрерывных функций
-периодических, вещественных и непрерывных функций  такое, что
такое, что
(1) для  из М уравнение (275) не имеет апериодических и
из М уравнение (275) не имеет апериодических и  -антипериодических решений; (11) множество М содержит функцию
-антипериодических решений; (11) множество М содержит функцию  тождественно равную положительной постоянной. Тогда при
тождественно равную положительной постоянной. Тогда при  из М для соответствующей характеристической постоянной Ляпунова выполнено неравенство
из М для соответствующей характеристической постоянной Ляпунова выполнено неравенство 
Доказательство. Пусть  из М. Положим
из М. Положим  Выпуклость множества М означает, что
Выпуклость множества М означает, что  тоже из М при
тоже из М при  . Для уравнения (275) с коэффициентом
. Для уравнения (275) с коэффициентом  постоянная
постоянная  является функцией 5. Покажем, что
является функцией 5. Покажем, что  Фудет непрерывной функцией s. Любое решение
Фудет непрерывной функцией s. Любое решение  уравнения (275) с начальными значениями
уравнения (275) с начальными значениями  не зависящими от s, будет непрерывной (и даже целой) функцией s. Это сразу следует из равномерной при
не зависящими от s, будет непрерывной (и даже целой) функцией s. Это сразу следует из равномерной при  ), сходимости к решению
), сходимости к решению  последовательности
последовательности  определенной соотношениями [II, 50]
определенной соотношениями [II, 50]

При этом  будут непрерывными (и даже целыми) функциями s. Следовательно, непрерывными (и даже целыми) функциями s будут
будут непрерывными (и даже целыми) функциями s. Следовательно, непрерывными (и даже целыми) функциями s будут  , а значит, и определенная формулой (279) функция
, а значит, и определенная формулой (279) функция  .
.
Как было показано в предыдущем пункте, из предположения (I) следует, что при выполнено  Из предположений (I) и (II) следует, что
Из предположений (I) и (II) следует, что  так как для уравнения (275) с коэффициентом
так как для уравнения (275) с коэффициентом  имеем
имеем  Выше было показано, что для уравнения с коэффициентом
Выше было показано, что для уравнения с коэффициентом  выполнено
выполнено  Итак,
Итак,  при Следовательно,
при Следовательно,  при
при  и, в частности,
и, в частности,  что и утверждалось.
что и утверждалось.
Отметим, что утверждение леммы 3 остается справедливым при более общих предположениях, например, когда условие выпуклости множества М заменено условием связности. Для дальнейшего, однако, достаточно сформулированного утверждения.
Критерий Н. Е. Жуковского. Если для некоторого  выполнено
выполнено

то все решения уравнения (275) ограничены при  и для этого уравнения
и для этого уравнения 
Доказательство. Множество М вещественных  -периодических функций
-периодических функций  удовлетворяющих соотношениям (288), очевидно,
удовлетворяющих соотношениям (288), очевидно,
выпукло, и выполнено также условие (II) леммы 3. Покажем, что выполнено условие (I). Пусть  решение уравнения (275) для некоторого
решение уравнения (275) для некоторого  из М такое, что
из М такое, что  . Решение
. Решение  непременно имеет нули. Действительно, если
непременно имеет нули. Действительно, если  то
то  меняет знак и, следовательно, имеет нули. Если
меняет знак и, следовательно, имеет нули. Если  , то
, то  имеет нули по лемме
имеет нули по лемме  . Пусть
. Пусть  какие-либо два последовательных нуля функции
какие-либо два последовательных нуля функции  . Будем считать для определенности, что
. Будем считать для определенности, что  при
при  Построим решения
Построим решения  и
и  уравнения (275) с коэффициентами
уравнения (275) с коэффициентами  и с начальными условиями
и с начальными условиями


Рис. 70.
Расстояния между соседними нулями у решений  будут, очевидно, - и
будут, очевидно, - и  По лемме
По лемме  графики функций
графики функций  расположены так, как показано на рис. 70, т. е.
расположены так, как показано на рис. 70, т. е.

Таким образом, расстояние d между любыми соседними нулями решения  удовлетворяет неравенству
удовлетворяет неравенству

Поскольку  то на интервале
то на интервале  длины
длины  укладывается целое число (обозначим его через k) отрезков между соседними нулями решения
укладывается целое число (обозначим его через k) отрезков между соседними нулями решения  . Длины
. Длины  этих отрезков должны удовлетворять соотношению (289). Легко убедиться в том, что это невозможно. Действительно, имеем
этих отрезков должны удовлетворять соотношению (289). Легко убедиться в том, что это невозможно. Действительно, имеем  Складывая соответствующие неравенства (289), получим
Складывая соответствующие неравенства (289), получим  что невозможно, так как k — целое число.
что невозможно, так как k — целое число.
Итак, выполнено условие (I) леммы 3. Из леммы 3 поэтому следует справедливость критерия Жуковского.
Отметим, что, несколько уточняя приведенные рассуждения, легко заменить (288) более общим условием, а именно заменить в (288) знаки на но при этом потребовать, чтобы  . При этом по-прежнему
. При этом по-прежнему 
В работе В. А. Якубовича (Матем. сб., т. 37 (79), вып. 1, 1965) установлено следующее обобщение критерия Н. Е. Жуковского: неравенство  имеет место, если выполнено неравенство
имеет место, если выполнено неравенство

где  — какие-либо произвольные, дважды непрерывно дифференцируемые
— какие-либо произвольные, дважды непрерывно дифференцируемые  -периодические положительные функции, нормированные условием
-периодические положительные функции, нормированные условием

При этом предполагается, что  не совпадает тождественно ни с левой, ни с правой частью неравенства (290). Исторически первым достаточным условием устойчивости для уравнения Хилла было следующее условие, установленное А. М. Ляпуновым (см. А. М. Ляпунов, Общая задача об устойчивости движения, 1894):
не совпадает тождественно ни с левой, ни с правой частью неравенства (290). Исторически первым достаточным условием устойчивости для уравнения Хилла было следующее условие, установленное А. М. Ляпуновым (см. А. М. Ляпунов, Общая задача об устойчивости движения, 1894):
Неравенство  имеет место, если
имеет место, если

При этом считается, что 
Лемма 4. Пусть  последовательные нули произвольного решения уравнения (275), в котором
последовательные нули произвольного решения уравнения (275), в котором  . Тогда
. Тогда

Доказательство. Предполагается, очевидно, что  . Можно считать, что
. Можно считать, что  при а
при а  и пусть
и пусть 

Существуют точки  принадлежащие промежуткам
принадлежащие промежуткам  и такие, что
и такие, что
При  имеем
имеем  и, интегрируя, получим
и, интегрируя, получим 

В подинтегральном выражении  , а знаменатель мы заменили его максимумом
, а знаменатель мы заменили его максимумом  . При этом вместо мы поставили
. При этом вместо мы поставили  Оправдаем это. Если бы вместо стоял знак =, то в силу
Оправдаем это. Если бы вместо стоял знак =, то в силу
непрерывности  мы должны были бы иметь в промежутке
мы должны были бы иметь в промежутке  , и надо привести это тождество к противоречию. Из указанного тождества следует, что в точках промежутка i или
, и надо привести это тождество к противоречию. Из указанного тождества следует, что в точках промежутка i или  , или
, или  . Докажем, что у = 0 внутри
. Докажем, что у = 0 внутри  , а тем самым и на концах. Пусть существует такая точка
, а тем самым и на концах. Пусть существует такая точка  , в которой
, в которой  . Мы должны при этом иметь
. Мы должны при этом иметь  при всех х, достаточно близких к
при всех х, достаточно близких к  . При этом из формулы Тейлора
. При этом из формулы Тейлора  , следует, что при х, близких к
, следует, что при х, близких к  и отличных от
и отличных от  , мы имеем
, мы имеем  , что противоречит указанному выше тождеству, и, следовательно, из него следует, что
, что противоречит указанному выше тождеству, и, следовательно, из него следует, что  при
при  , т. е. в этом промежутке
, т. е. в этом промежутке  , что противоречит (293). Таким образом, доказано наличие знака в (294). Используя (293) и (294), получим
, что противоречит (293). Таким образом, доказано наличие знака в (294). Используя (293) и (294), получим

При изменении с в промежутке  правая часть достигает минимального значения
правая часть достигает минимального значения  в случае
в случае  , т. е.
, т. е.

откуда и следует (292).
Переходим к доказательству критерия (291). Применим лемму 3. Множество функций  , удовлетворяющих условиям (291), очевидно, выпукло. Условие (II) леммы выполнено. Покажем, что и условие (I) выполнено. Предположим, что имеется
, удовлетворяющих условиям (291), очевидно, выпукло. Условие (II) леммы выполнено. Покажем, что и условие (I) выполнено. Предположим, что имеется  -периодическое или
-периодическое или  -антипериодическое решение
-антипериодическое решение  и приведем это предположение к противоречию. Согласно лемме
и приведем это предположение к противоречию. Согласно лемме  имеет нули и расстояние d между соседними нулями а и b удовлетворяет неравенству
имеет нули и расстояние d между соседними нулями а и b удовлетворяет неравенству  . Согласно лемме 4
. Согласно лемме 4

По второму из условий (291) правая часть не меньше  , откуда
, откуда  . Это противоречие указывает на выполнение условия (11) леммы 3, и из последней следует достаточность критерия (291) для выполнения условия
. Это противоречие указывает на выполнение условия (11) леммы 3, и из последней следует достаточность критерия (291) для выполнения условия  .
.
Как показал М. Г. Крейн, для выполнения неравенства  вместо (291) достаточны следующие менее ограничительные условия:
вместо (291) достаточны следующие менее ограничительные условия:

где

и предполагается, что  Этот критерий доказывается по той же схеме, что и выше.
Этот критерий доказывается по той же схеме, что и выше.
Приведем еще следующие критерии (В. А. Якубович, ДАН СССР, т. 74, № 5, 1950), являющиеся по своему характеру промежуточными между критериями А. М. Ляпунова и Н. Е. Жуковского: если для некоторого  выполнено
выполнено

или

и

то  . Для
. Для  первый из критериев переходит в критерий A. М. Ляпунова. Можно показать, что эти критерии являются точными: при сколь угодно малом увеличении постоянных в правых частях неравенств, содержащих интегралы, всегда можно найти функцию
первый из критериев переходит в критерий A. М. Ляпунова. Можно показать, что эти критерии являются точными: при сколь угодно малом увеличении постоянных в правых частях неравенств, содержащих интегралы, всегда можно найти функцию  для которой выполнены соответствующие условия, но
для которой выполнены соответствующие условия, но 
Другие критерии устойчивости уравнения Хилла получены М. Г. Крейном, М. Г. Нейгауз, В. Б. Лидским, Ж. Боргом и В. А. Якубовичем. Эти условия можно найти в обзоре B. М. Старжинского (ПММ, т. 18, в. 4, 1954).
Условий неустойчивости уравнения Хилла, достаточно эффективных и просто формулируемых, известно немного. Приведем следующий простой критерий, установленный А. М. Ляпуновым:
Если в уравнении Хилла  , то
, то  и, следовательно, числа
и, следовательно, числа  различны и положительны.
различны и положительны.
Доказательство. Пусть  решение нашего уравнения, удовлетворяющее начальным условиям
решение нашего уравнения, удовлетворяющее начальным условиям  Интегрируя уравнение Хилла и принимая во внимание последнее начальное условие, мы можем написать
Интегрируя уравнение Хилла и принимая во внимание последнее начальное условие, мы можем написать

При значениях  близких к нулю и положительных,
близких к нулю и положительных,  близко к единице, и, следовательно,
близко к единице, и, следовательно,  в силу
в силу  возрастает. В силу соотношения
возрастает. В силу соотношения  могло бы стать отрицательным только после того, как
могло бы стать отрицательным только после того, как  станет отрицательным. Но, с другой стороны, для того чтобы
станет отрицательным. Но, с другой стороны, для того чтобы  стало отрицательным, необходимо, чтобы оно предварительно начало убывать, т. е. необходимо, чтобы до этого
стало отрицательным, необходимо, чтобы оно предварительно начало убывать, т. е. необходимо, чтобы до этого  стало отрицательным. Мы приходим, таким образом, к противоречию и можем утверждать, что при всяком
стало отрицательным. Мы приходим, таким образом, к противоречию и можем утверждать, что при всяком  будет
будет  и, в частности, имеем
и, в частности, имеем  Возьмем теперь решение
Возьмем теперь решение  удовлетворяющее начальным условиям
удовлетворяющее начальным условиям  Интегрируя уравнение Хилла, получим
Интегрируя уравнение Хилла, получим

При X близких к нулю,  близко к единице и, следовательно, положительно, а потому
близко к единице и, следовательно, положительно, а потому  возрастает и больше нуля, ибо
возрастает и больше нуля, ибо  Формула (296) показывает, что
Формула (296) показывает, что  может стать отрицательным только после того, как
может стать отрицательным только после того, как  станет отрицательным. Но, с другой стороны,
станет отрицательным. Но, с другой стороны,  может стать отрицательным, лишь предварительно убывая, т. е. после того, как
может стать отрицательным, лишь предварительно убывая, т. е. после того, как  станет отрицательным. Это противоречие показывает нам, что при всяком положительном
станет отрицательным. Это противоречие показывает нам, что при всяком положительном  мы имеем
мы имеем  и, в частности,
и, в частности,  Доказанные неравенства для
Доказанные неравенства для  дают нам
дают нам

что и утверждалось.
Несколько уточняя предыдущие рассуждения, мы могли бы условие  заменить условием
заменить условием 
Рассмотрим в заключение уравнение Хилла, содержащее параметр X:

где, как и раньше,  - периодическая функция и
- периодическая функция и  - комплексный параметр. Как мы видели раньше, вопрос об ограниченности или неограниченности решений уравнения (297) при вещественных значениях X решается величиной характеристической постоянной Ляпунова
- комплексный параметр. Как мы видели раньше, вопрос об ограниченности или неограниченности решений уравнения (297) при вещественных значениях X решается величиной характеристической постоянной Ляпунова

Эта постоянная в случае уравнения (297) зависит от параметра X, и мы ее обозначим через Л (X). Учитывая равномерную сходимость метода последовательных приближений при построении решений  можно утверждать, что
можно утверждать, что  целая функция X, вещественная при вещественных X. Как известно, при этом, если
целая функция X, вещественная при вещественных X. Как известно, при этом, если  то все решения уравнения ограничены при
то все решения уравнения ограничены при  если
если  то общее решение уравнения не ограничено, а при
то общее решение уравнения не ограничено, а при  общее решение может быть как ограниченным, так и неограниченным.
общее решение может быть как ограниченным, так и неограниченным.
Сформулируем некоторые общие результаты, касающиеся промежутков изменения X, для которых будет иметь место ограниченность или неограниченность
общего решения уравнения (297) на бесконечном промежутке -  (Близкие, утверждения установлены впервые А. М. Ляпуновым, Собр. соч., т. 2, изд. АН СССР, 1956, стр.
(Близкие, утверждения установлены впервые А. М. Ляпуновым, Собр. соч., т. 2, изд. АН СССР, 1956, стр.  )
)
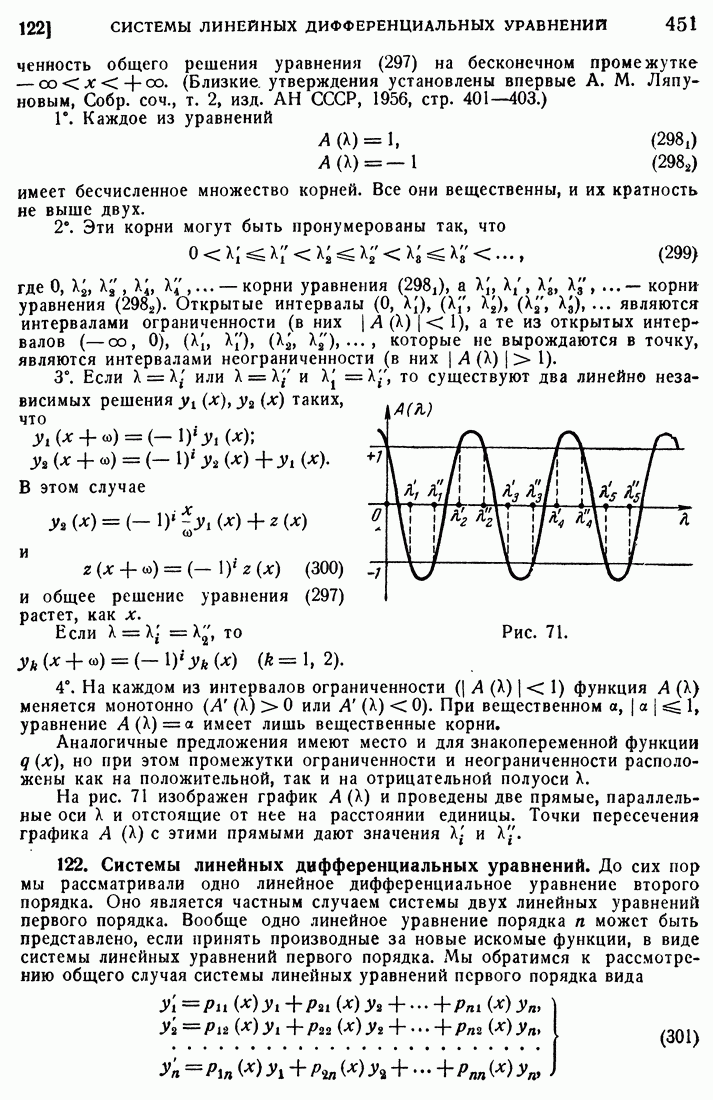
1°. Каждое из уравнений

имеет бесчисленное множество корней. Все они вещественны, и их кратность не выше двух.
2°. Эти корни могут быть пронумерованы так, что

где  - корни уравнения
- корни уравнения  корни уравнения (298). Открытые интервалы
корни уравнения (298). Открытые интервалы  являются интервалами ограниченности (в них
являются интервалами ограниченности (в них  ), а те из открытых интервалов
), а те из открытых интервалов  которые не вырождаются в точку, являются интервалами неограниченности (в них
которые не вырождаются в точку, являются интервалами неограниченности (в них 
Если
4°. На каждом из интервалов ограниченности (| А (X) | < 1) функция А (X) меняется монотонно (А (X) > 0 или  то существуют два линейно независимых решения
то существуют два линейно независимых решения  таких, что
таких, что

В этом случае

и

и общее решение уравнения (297) растет, как 

Рис. 71.
Если  , то
, то

4. На каждом из интервалов ограниченности  функция
функция  меняется монотонно
меняется монотонно  или
или  При вещественном а,
При вещественном а,  уравнение
уравнение  имеет лишь вещественные корни.
имеет лишь вещественные корни.
Аналогичные предложения имеют место и для знакопеременной функции  но при этом промежутки ограниченности и неограниченности расположены как на положительной, так и на отрицательной полуоси X.
но при этом промежутки ограниченности и неограниченности расположены как на положительной, так и на отрицательной полуоси X.
На рис. 71 изображен график  и проведены две прямые, параллельные оси
и проведены две прямые, параллельные оси  и отстоящие от нее на расстоянии единицы. Точки пересечения графика
и отстоящие от нее на расстоянии единицы. Точки пересечения графика  с этими прямыми дают значения
с этими прямыми дают значения  и
и  .
.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К ВОСЬМОМУ ИЗДАНИЮ
- 1. Функции комплексного переменного.
- 2. Производная.
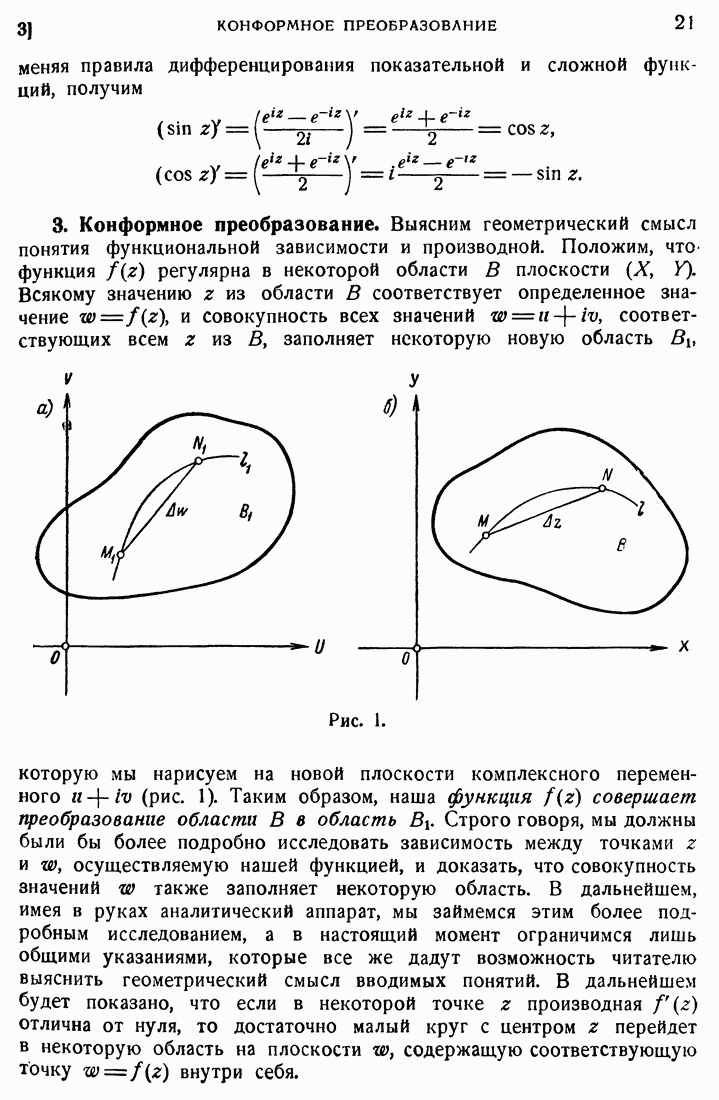
- 3. Конформное преобразование.
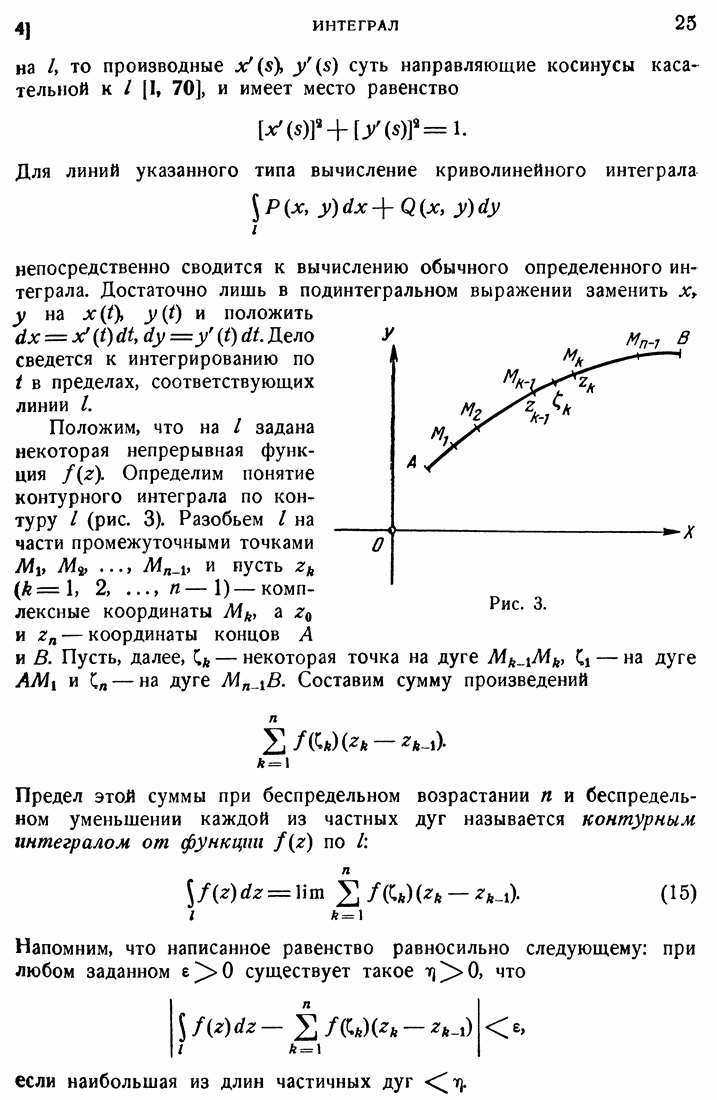
- 4. Интеграл.
- 5. Теорема Коши.
- 6. Основная формула интегрального исчисления.
- 7. Формула Коши.
- 8. Интегралы типа Коши.
- 9. Следствия формулы Коши.
- 10. Изолированные особые точки.
- 11. Бесконечные ряды с комплексными членами.
- 12. Теорема Вейерштрасса.
- 13. Степенные ряды.
- 14. Ряд Тейлора.
- 15. Ряд Лорана.
- 16. Примеры.
- 17. Изолированные особые точки. Бесконечно далекая точка.
- 18. Аналитическое продолжение.
- 19. Примеры многозначных функций.
- 20. Особые точки аналитических функций и римановы поверхности.
- 21. Теорема вычетов.
- 22. Теоремы о числе корней.
- 23. Обращение степенного ряда.
- 24. Принцип симметрии.
- 25. Ряд Тейлора на окружности круга сходимости.
- 26. Дополнительные сведения о формуле Коши.
- 27. Главное значение интеграла.
- 28. Главное значение интеграла (продолжение).
- 29. Интегралы типа Коши.
- 30. Интегралы типа Коши (продолжение).
- ГЛАВА II. КОНФОРМНОЕ ПРЕОБРАЗОВАНИЕ И ПЛОСКОЕ ПОЛЕ
- 31. Конформное преобразование.
- 32. Линейное преобразование.
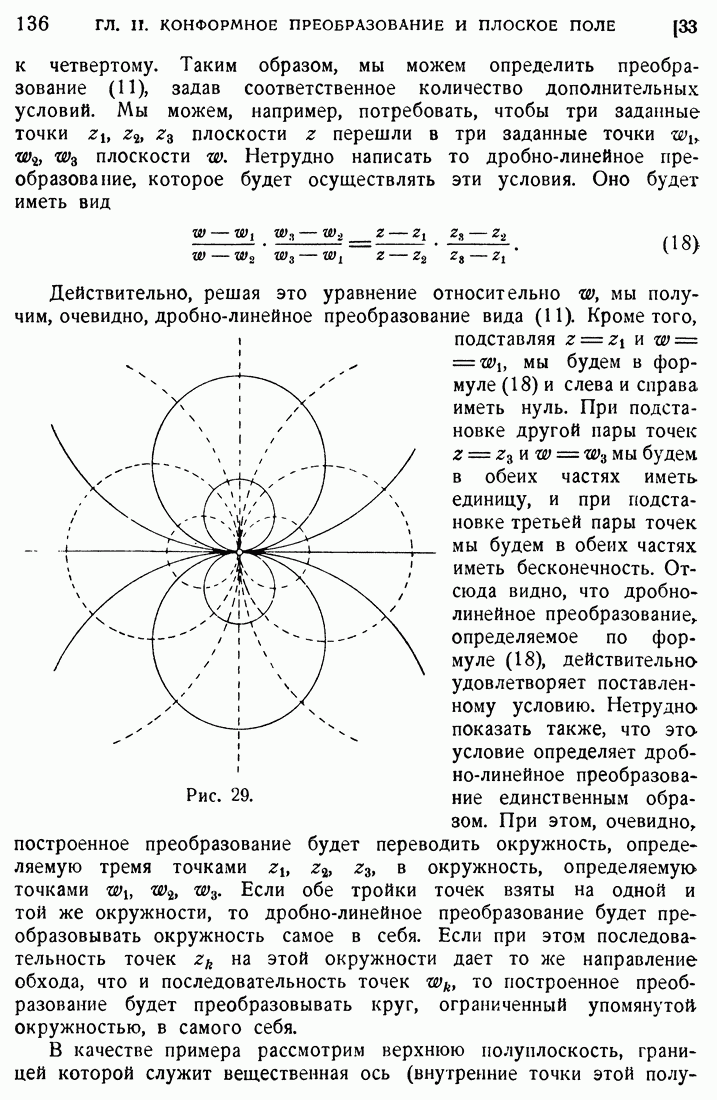
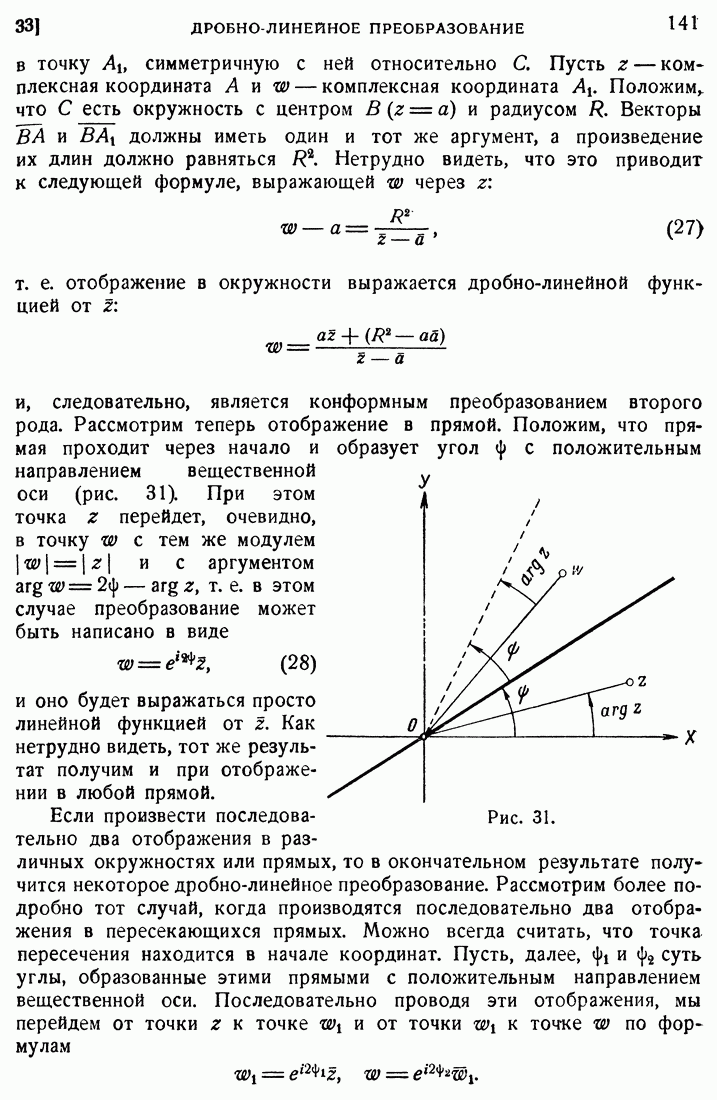
- 33. Дробно-линейное преобразование.
- 34. Функция w = z^2.
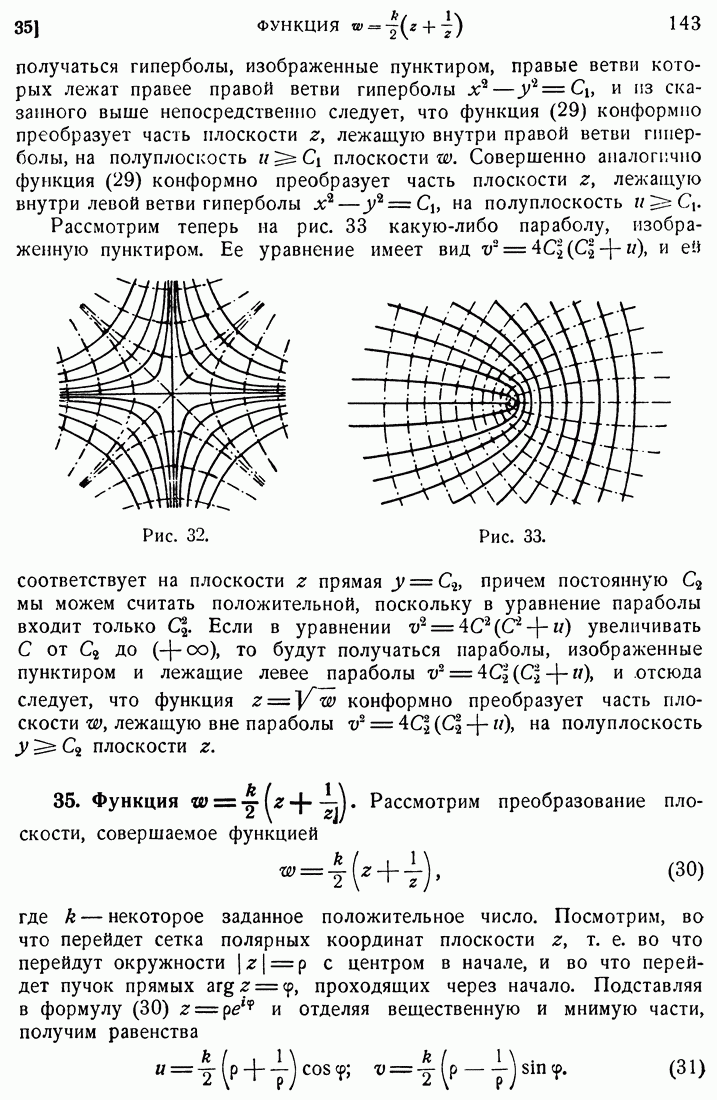
- 35. Функция …
- 36. Двуугольник и полоса.
- 37. Основная теорема.
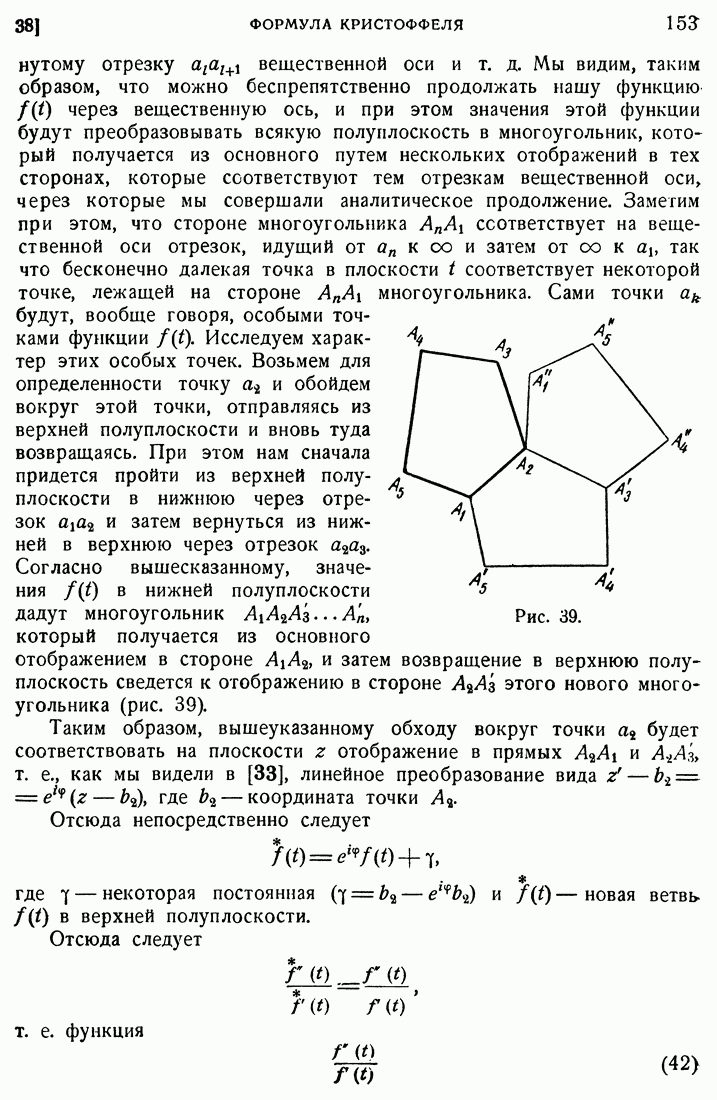
- 38. Формула Кристоффеля.
- 39. Частные случаи.
- 40. Случай внешности многоугольника.
- 41. Минимальное свойство преобразования на круг.
- 42. Способ сопряженных тригонометрических рядов.
- 43. Плоское установившееся течение жидкости.
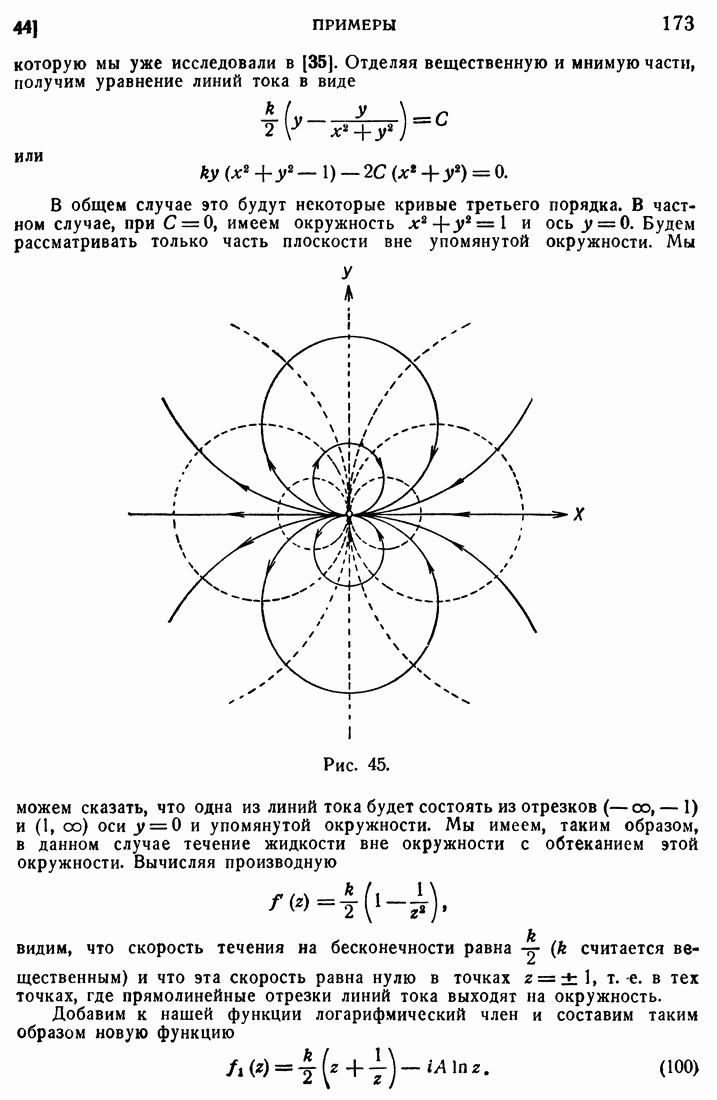
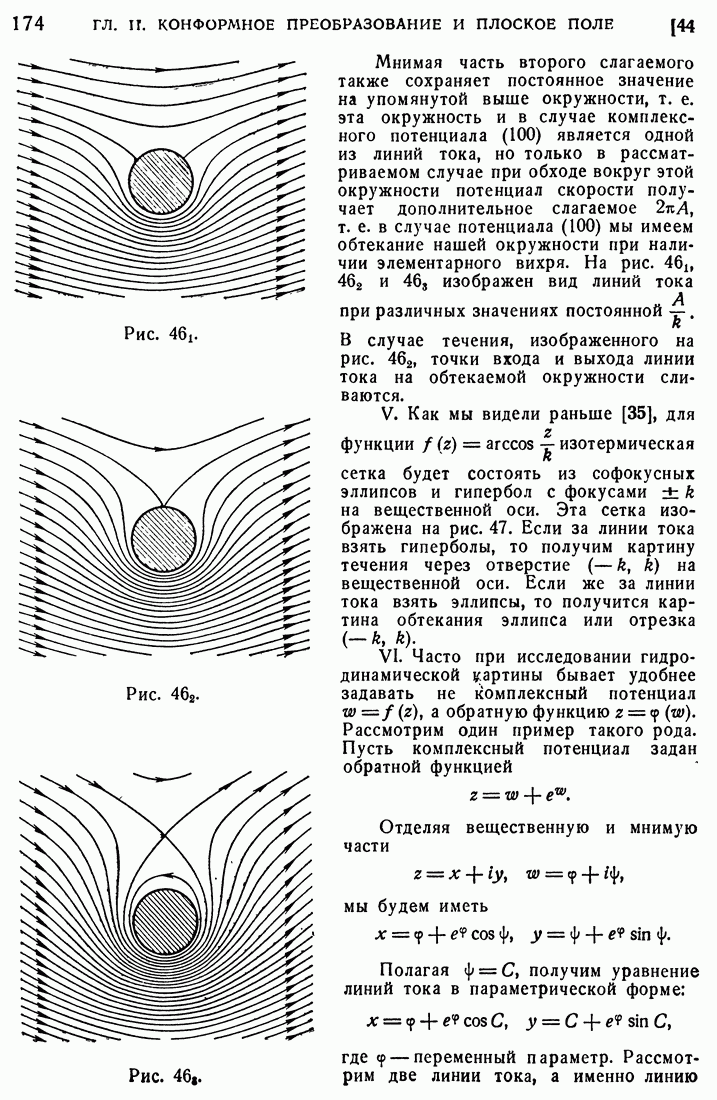
- 44. Примеры.
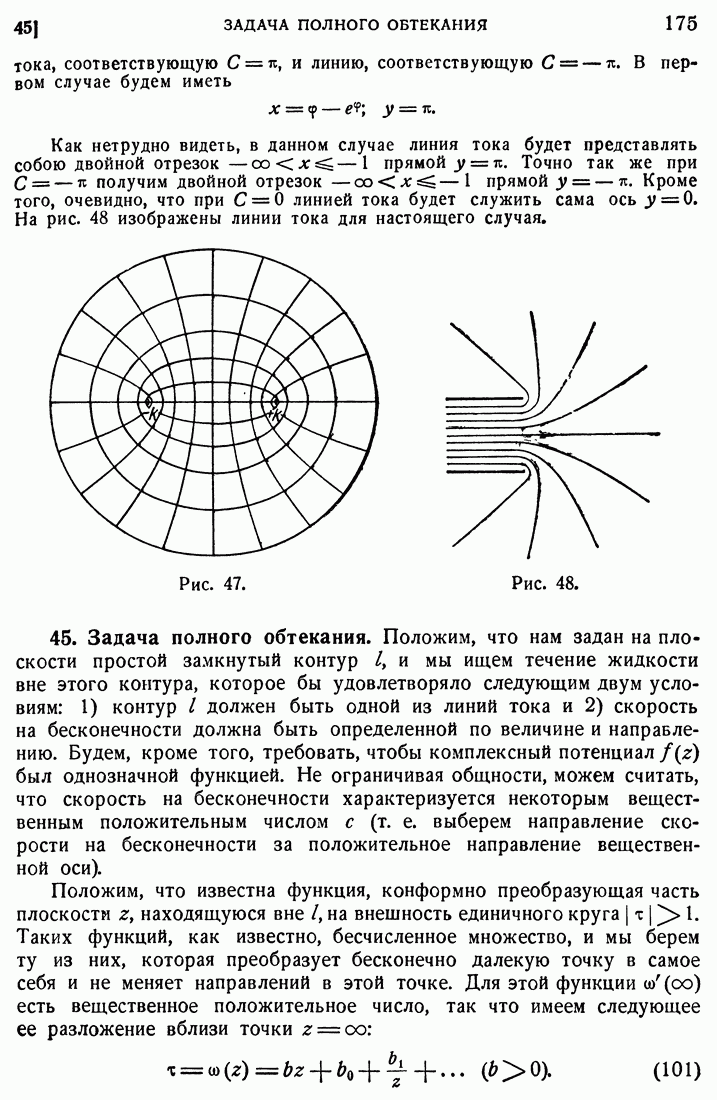
- 45. Задача полного обтекания.
- 46. Формула Н. Е. Жуковского.
- 47. Плоская электростатическая задача.
- 48. Формула Шварца.
- 49. Ядро ctg((s-t)/2).
- 50. Предельные задачи.
- 51. Бигармоническое уравнение.
- 52. Волновое уравнение и аналитические функции.
- 53. Основная теорема.
- 54. Дифракция плоской волны.
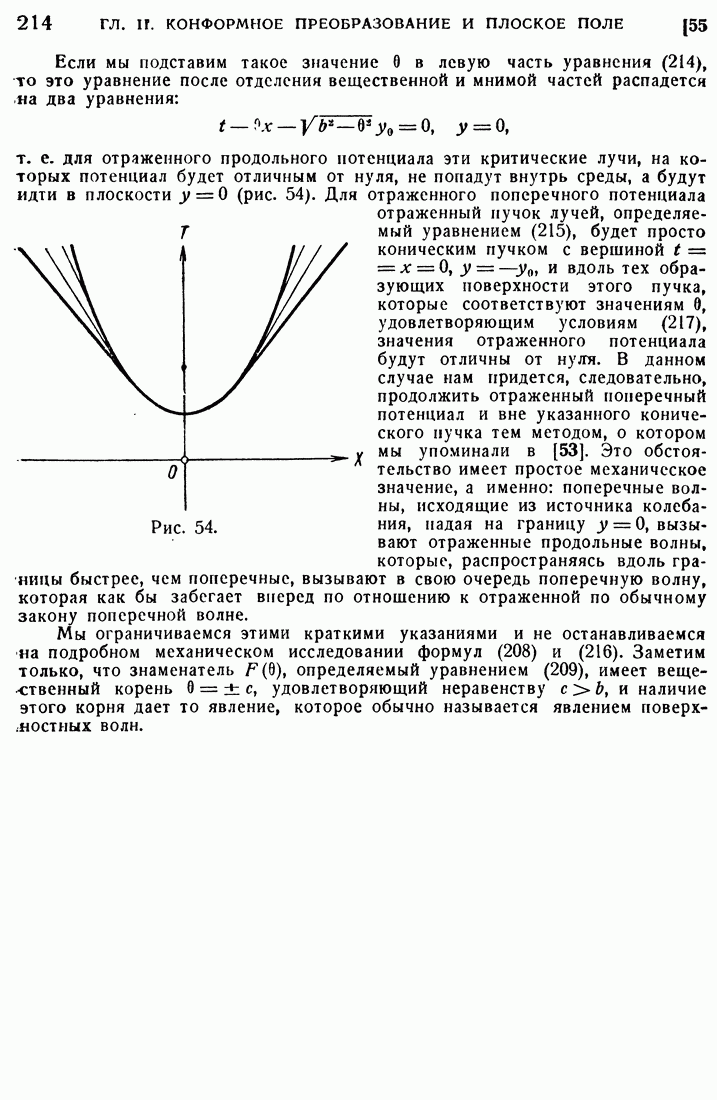
- 55. Отражение упругих волн от прямолинейной границы.
- ГЛАВА III. ПРИМЕНЕНИЕ ТЕОРИИ ВЫЧЕТОВ, ЦЕЛЫЕ И ДРОБНЫЕ ФУНКЦИИ
- 56. Интеграл Френеля.
- 57. Интегрирование выражений с тригонометрическими функциями.
- 58. Интегрирование рациональной дроби.
- 59. Некоторые новые типы интегралов с тригонометрическими функциями.
- 60. Лемма Жордана.
- 61. Представление некоторых функций контурными интегралами.
- 62. Примеры интегралов от многозначных функций.
- 63. Интегрирование системы линейных уравнений с постоянными коэффициентами.
- 64. Разложение дробной функции на простейшие дроби.
- 66. Построение мероморфной функции.
- 67. Целые функции.
- 68. Бесконечные произведения.
- 69. Построение целой функции по ее корням.
- 70. Интегралы, зависящие от параметра.
- 71. Эйлеров интеграл второго рода.
- 72. Эйлеров интеграл первого рода.
- 73. Бесконечное произведение для функции …
- 74. Представление Г(z) контурным интегралом.
- 75. Формула Стирлинга.
- 76. Формула суммирования Эйлера.
- 77. Числа Бернулли.
- 78. Метод скорейшего спуска.
- 79. Асимптотическое разложение интеграла.
- 80. Примеры.
- 81. Метод стационарной фазы.
- ГЛАВА IV. АНАЛИТИЧЕСКИЕ ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ И ФУНКЦИИ МАТРИЦ
- 82. Регулярные функции многих переменных.
- 83. Двойной интеграл и формула Коши.
- 84. Степенные ряды.
- 85. Аналитическое продолжение.
- 86. Функции матриц. Предварительные понятия.
- 87. Степенные ряды от одной матрицы.
- 88. Умножение степенных рядов. Обращение степенного ряда.
- 89. Дальнейшее исследование сходимости.
- 90. Интерполяционные полиномы.
- 91. Тождество Кейли. Формула Сильвестра.
- 92. Определение функций одной матрицы формулой Коши.
- 93. Аналитическое продолжение.
- 94. Логарифм матриц.
- 95. Обращение целой функции от матрицы в случае матриц второго порядка.
- 96. Системы линейных уравнений с постоянными коэффициентами.
- 97. Функции нескольких матриц.
- ГЛАВА V. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
- 98. Разложение решения в степенной ряд.
- 99. Аналитическое продолжение решения.
- 100. Окрестность особой точки.
- 101. Регулярная особая точка.
- 102. Уравнения класса Фукса.
- 103. Уравнение Гаусса.
- 104. Гипергеометрический ряд.
- 105. Полиномы Лежандра.
- 106. Полиномы Якоби.
- 107. Конформное преобразование и уравнение Гаусса.
- 108. Преобразование Лапласа.
- 109. Различный выбор решений.
- 110. Уравнение Бесселя.
- 111. Функции Ханкеля и интегральное представление решений уравнения Бесселя.
- 112. Асимптотические разложения.
- 113. Асимптотические разложения решений, полученных преобразованием Лапласа.
- 114. Асимптотические разложения решений уравнения Бесселя.
- 115. Вырождение уравнения Гаусса.
- 116. Формальные ряды в окрестности иррегулярной особой точки.
- 117. Построение асимптотических разложений методом после довательных приближений.
- 118. Функции Эйри.
- 119. Асимптотика при большом значении параметра.
- 120. Уравнения с периодическими коэффициентами.
- 121. Условия устойчивости и неустойчивости для уравнения Хилла.
- 122. Системы линейных дифференциальных уравнений.
- 123. Регулярная особая точка.
- 124. Регулярные системы.
- 125. Представление решения в окрестности особой точки.
- 126. Канонические решения.
- 127. Связь с регулярными решениями типа Фукса.
- 128. Случай любых Us.
- 129. Формальные разложения в окрестности иррегулярной особой точки.
- ГЛАВА VI. СПЕЦИАЛЬНЫЕ ФУНКЦИИ
- 130. Определение сферических функций.
- 131. Явные выражения сферических функций.
- 132. Свойство ортогональности.
- 133. Полиномы Лежандра.
- 134. Разложение по сферическим функциям.
- 135. Доказательство сходимости.
- 136. Связь сферических функций с предельными задачами.
- 137. Задачи Дирихле и Неймана.
- 138. Потенциал объемных масс.
- 139. Потенциал сферического слоя.
- 140. Электрон в центральном поле.
- 141. Шаровые функции и линейные представления группы вращения.
- 142. Функция Лежандра.
- 143. Функция Лежандра второго рода.
- § 2. ФУНКЦИИ БЕССЕЛЯ
- 144. Определение функций Бесселя.
- 145. Соотношения между функциями Бесселя.
- 146. Ортогональность функций Бесселя и их корни.
- 147. Производящая функция и интегральное представление.
- 148. Формула Фурье — Бесселя.
- 150. Разложение функций Неймана с целым значком.
- 151. Случай чисто мнимого аргумента.
- 152. Новые интегральные представления.
- 153. Асимптотические представления.
- 154. Функции Бесселя и уравнение Лапласа.
- 155. Волновое уравнение в цилиндрических координатах.
- 156. Волновое уравнение в сферических координатах.
- § 3. ПОЛИНОМЫ ЭРМИТА И ЛАГЕРРА
- 157. Линейный осциллятор и полиномы Эрмита.
- 158. Свойство ортогональности.
- 159. Производящая функция.
- 160. Параболические координаты и функции Эрмита.
- 161. Полиномы Лагерра.
- 162. Связь полиномов Эрмита и Лагерра.
- 163. Асимптотическое выражение полиномов Эрмита.
- 164. Асимптотическое выражение полиномов Лежандра.
- § 4. ЭЛЛИПТИЧЕСКИЕ ИНТЕГРАЛЫ И ЭЛЛИПТИЧЕСКИЕ ФУНКЦИИ
- 165. Приведение эллиптических интегралов к нормальному виду.
- 166. Приведение интегралов к тригонометрической форме.
- 167. Примеры.
- 168. Обращение эллиптического интеграла.
- 169. Общие свойства эллиптических функций.
- 170. Основная лемма.
- 171. Функции Вейерштрасса.
- 172. Дифференциальное уравнение для …
- 173. Функции …
- 174. Разложение целой периодической функции.
- 175. Новые обозначения.
- 176. Функция …
- 177. Функции …
- 178. Свойства функций тэта.
- 179. Выражение чисел … через …
- 180. Эллиптические функции Якоби.
- 181. Основные свойства функций Якоби.
- 182. Дифференциальные уравнения для функций Якоби.
- 183. Формулы сложения.
- 184. Связь функций p(u) и sn(u).
- 185. Эллиптические координаты.
- 186. Введение эллиптических функций.
- 187. Уравнение Лямэ.
- 188. Простой маятник.
- 189. Пример конформного преобразования.
- ДОБАВЛЕНИЕ. ПРИВЕДЕНИЕ МАТРИЦ К КАНОНИЧЕСКОЙ ФОРМЕ
- 191. Случай простых корней.
- 192. Первый этап преобразований в случае кратных корней.
- 193. Приведение к канонической форме.
- 194. Определение структуры канонической формы.
- 196. Пример.