| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
3. Конформное преобразование.
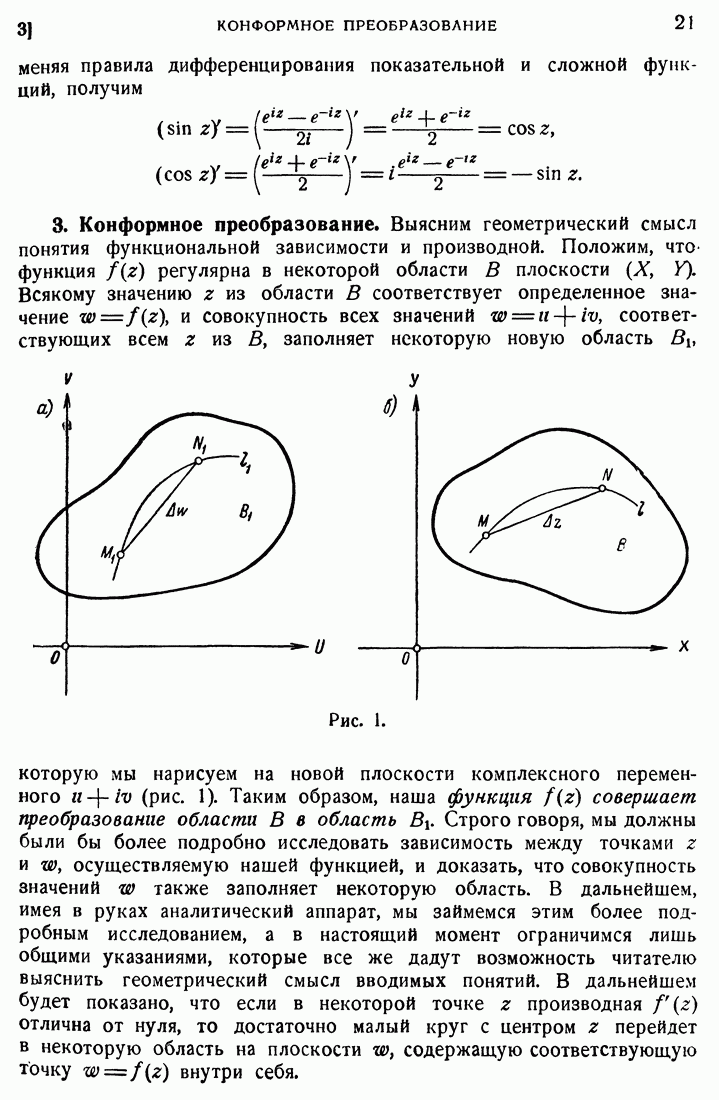
Выясним геометрический смысл понятия функциональной зависимости и производной. Положим, что функция  регулярна в некоторой области В плоскости
регулярна в некоторой области В плоскости  . Всякому значению z из области В соответствует определенное значение
. Всякому значению z из области В соответствует определенное значение  и совокупность всех значений
и совокупность всех значений  соответствующих всем
соответствующих всем  из В, заполняет некоторую новую область
из В, заполняет некоторую новую область  которую мы нарисуем на новой плоскости комплексного переменного
которую мы нарисуем на новой плоскости комплексного переменного 

Рис. 1.
Таким образом, наша функция  совершает преобразование области В в область
совершает преобразование области В в область  Строго говоря, мы должны были бы более подробно исследовать зависимость между точками
Строго говоря, мы должны были бы более подробно исследовать зависимость между точками  , осуществляемую нашей функцией, и доказать, что совокупность значений w также заполняет некоторую область. В дальнейшем, имея в руках аналитический аппарат, мы займемся этим более подробным исследованием, а в настоящий момент ограничимся лишь общими указаниями, которые все же дадут возможность читателю выяснить геометрический смысл вводимых понятий. В дальнейшем будет показано, что если в некоторой точке z производная f(z) отлична от нуля, то достаточно малый круг с центром z перейдет в некоторую область на плоскости w, содержащую соответствующую точку
, осуществляемую нашей функцией, и доказать, что совокупность значений w также заполняет некоторую область. В дальнейшем, имея в руках аналитический аппарат, мы займемся этим более подробным исследованием, а в настоящий момент ограничимся лишь общими указаниями, которые все же дадут возможность читателю выяснить геометрический смысл вводимых понятий. В дальнейшем будет показано, что если в некоторой точке z производная f(z) отлична от нуля, то достаточно малый круг с центром z перейдет в некоторую область на плоскости w, содержащую соответствующую точку  внутри себя.
внутри себя.
Перейдем теперь к выяснению геометрического смысла модуля и аргумента производной, причем будем считать, что производная f(z) в рассматриваемой точке отлична от нуля. Возьмем две близкие точки z и  Соответствующие им точки в области
Соответствующие им точки в области  будут
будут 
Возьмем отрезки MN и  соединяющие z с
соединяющие z с  Этим векторам соответствуют комплексные числа
Этим векторам соответствуют комплексные числа  Таким образом, отношение длин этих векторов будет
Таким образом, отношение длин этих векторов будет

или, принимая во внимание, что модуль частного равен частному модулей,

 пределе при стремлении N к М точка
пределе при стремлении N к М точка  будет стремиться к
будет стремиться к  и мы получим
и мы получим

т. е. модуль производной  характеризует изменение линейных размеров в точке z при преобразовании, совершаемом функцией
характеризует изменение линейных размеров в точке z при преобразовании, совершаемом функцией 

Рис. 2.
Если, например,  то при преобразовании линейные размеры в точке
то при преобразовании линейные размеры в точке  увеличиваются в три раза.
увеличиваются в три раза.
Перейдем теперь к выяснению геометрического смысла аргумента производной. Положим, что точка N стремится к точке М вдоль некоторой линии  и пусть
и пусть  соответствующая линия в области
соответствующая линия в области  . Аргумент комплексного числа
. Аргумент комплексного числа  дает угол, образованный вектором MN с вещественной осью, и точно так же
дает угол, образованный вектором MN с вещественной осью, и точно так же  дает угол, образованный вектором
дает угол, образованный вектором  с вещественной осью.
с вещественной осью.
Разность, указанных аргументов, т. е.

представляет собою угол, образованный направлением вектора MNV с направлением вектора MN, причем этот угол отсчитывается от вектора MN противоположно часовой стрелке. Принимая во внимание, что аргумент частного равен разности аргументов делимого и делителя, можем написать

В пределе направление вектора MN совпадает с направлением касательной к кривой I в точке  , а направление вектора
, а направление вектора  совпадает с направлением касательной к кривой
совпадает с направлением касательной к кривой  в точке
в точке 
Переходя в предыдущей формуле к пределу, мы видим, что аргумент производной  дает угол поворота в данной точке z в результате преобразования, совершаемого функцией
дает угол поворота в данной точке z в результате преобразования, совершаемого функцией  Иными словами, если провести через z какую-нибудь кривую I, имеющую в точке z определенную касательную, то в результате преобразования получится новая кривая
Иными словами, если провести через z какую-нибудь кривую I, имеющую в точке z определенную касательную, то в результате преобразования получится новая кривая  касательная к которой в соответствующей точке w будет образовывать с вышеуказанной касательной угол, равный аргументу производной. Если мы возьмем в области В две кривые, пересекающиеся в точке z под некоторым углом, то в результате преобразования касательные к этим кривым повернутся на один и тот же угол, равный аргументу производной, и, следовательно, угол между преобразованными кривыми будет прежним как по величине, так и по направлению, т. е. преобразование, совершаемое регулярной функцией, сохраняет углы во всех точках, где производная этой функции отлична от нуля. Такое преобразование, сохраняющее углы, называется обычно конформным.
касательная к которой в соответствующей точке w будет образовывать с вышеуказанной касательной угол, равный аргументу производной. Если мы возьмем в области В две кривые, пересекающиеся в точке z под некоторым углом, то в результате преобразования касательные к этим кривым повернутся на один и тот же угол, равный аргументу производной, и, следовательно, угол между преобразованными кривыми будет прежним как по величине, так и по направлению, т. е. преобразование, совершаемое регулярной функцией, сохраняет углы во всех точках, где производная этой функции отлична от нуля. Такое преобразование, сохраняющее углы, называется обычно конформным.
Если мы нанесем в области В плоскости ХУ некоторую сетку кривых, то в результате преобразования получим также сетку кривых, но уже, конечно, других, причем углы между кривыми сохраняются, кроме тех точек, где производная равна нулю. Если мы возьмем, например в области В, сетку прямых, параллельных осям, то в области  получим уже криволинейную, вообще говоря, сетку, но углы между кривыми останутся по-прежнему прямыми, т. е. сетка останется ортогональной. Больше того, если мы покроем область В малыми одинаковыми квадратами, то каждый такой квадрат превратится в области
получим уже криволинейную, вообще говоря, сетку, но углы между кривыми останутся по-прежнему прямыми, т. е. сетка останется ортогональной. Больше того, если мы покроем область В малыми одинаковыми квадратами, то каждый такой квадрат превратится в области  в малый криволинейный прямоугольник, стороны которого приближенно будут равны произведению длины стороны квадрата на модуль производной в какой-либо из точек этого квадрата, т. е. упомянутый выше криволинейный прямоугольник будет также с точностью до малых высших порядков квадратом, но так как значение
в малый криволинейный прямоугольник, стороны которого приближенно будут равны произведению длины стороны квадрата на модуль производной в какой-либо из точек этого квадрата, т. е. упомянутый выше криволинейный прямоугольник будет также с точностью до малых высших порядков квадратом, но так как значение  в разных точках будет разное, то эти криволинейные квадраты, заполняющие
в разных точках будет разное, то эти криволинейные квадраты, заполняющие  будут иметь различные по длине стороны.
будут иметь различные по длине стороны.
Пусть точка  принадлежит области регулярности В функции
принадлежит области регулярности В функции  . При этом можно утверждать, как будет потом доказано, что
. При этом можно утверждать, как будет потом доказано, что  преобразует некоторую окрестность
преобразует некоторую окрестность  точки
точки  в некоторую окрестность
в некоторую окрестность  точки
точки  находится внутри В, так что в
находится внутри В, так что в  существует однозначная обратная функция
существует однозначная обратная функция  преобразующая
преобразующая  в BQ. При этом
в BQ. При этом  регулярна в
регулярна в  и имеет место правило дифференцирования обратной функции
и имеет место правило дифференцирования обратной функции

Окрестность BQ точки  во всяком случае должна быть такой, что во всех ее точках
во всяком случае должна быть такой, что во всех ее точках  . В дальнейшем мы исследуем и тот случай, когда
. В дальнейшем мы исследуем и тот случай, когда  обращается в нуль, и более подробно рассмотрим вопрос об обратной функции.
обращается в нуль, и более подробно рассмотрим вопрос об обратной функции.
Остановимся кратко на понятии сложной функции  где
где  Пусть
Пусть  регулярна внутри некоторой области В и преобразует ее в некоторую область
регулярна внутри некоторой области В и преобразует ее в некоторую область  плоскости w. Положим, далее, что
плоскости w. Положим, далее, что  регулярна в В. При этом сложная функция
регулярна в В. При этом сложная функция  - регулярная функция от
- регулярная функция от  в
в  для нее имеет место правило дифференцирования, выражаемое формулой (6).
для нее имеет место правило дифференцирования, выражаемое формулой (6).
Отметим, что это правило справедливо и в том случае, когда функция  такова, что в В нет однозначной обратной, т. е. при различных z из В могут получаться одинаковые w из В и под В подразумевается множество значений
такова, что в В нет однозначной обратной, т. е. при различных z из В могут получаться одинаковые w из В и под В подразумевается множество значений  когда z меняется в В. Как мы увидим в дальнейшем,
когда z меняется в В. Как мы увидим в дальнейшем,  есть некоторая открытая область на плоскости w. B упомянутых случаях обычно не говорят, что
есть некоторая открытая область на плоскости w. B упомянутых случаях обычно не говорят, что  преобразует В и
преобразует В и  . Этот вопрос будет выяснен в дальнейшем.
. Этот вопрос будет выяснен в дальнейшем.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ К ВОСЬМОМУ ИЗДАНИЮ
- 1. Функции комплексного переменного.
- 2. Производная.
- 3. Конформное преобразование.
- 4. Интеграл.
- 5. Теорема Коши.
- 6. Основная формула интегрального исчисления.
- 7. Формула Коши.
- 8. Интегралы типа Коши.
- 9. Следствия формулы Коши.
- 10. Изолированные особые точки.
- 11. Бесконечные ряды с комплексными членами.
- 12. Теорема Вейерштрасса.
- 13. Степенные ряды.
- 14. Ряд Тейлора.
- 15. Ряд Лорана.
- 16. Примеры.
- 17. Изолированные особые точки. Бесконечно далекая точка.
- 18. Аналитическое продолжение.
- 19. Примеры многозначных функций.
- 20. Особые точки аналитических функций и римановы поверхности.
- 21. Теорема вычетов.
- 22. Теоремы о числе корней.
- 23. Обращение степенного ряда.
- 24. Принцип симметрии.
- 25. Ряд Тейлора на окружности круга сходимости.
- 26. Дополнительные сведения о формуле Коши.
- 27. Главное значение интеграла.
- 28. Главное значение интеграла (продолжение).
- 29. Интегралы типа Коши.
- 30. Интегралы типа Коши (продолжение).
- ГЛАВА II. КОНФОРМНОЕ ПРЕОБРАЗОВАНИЕ И ПЛОСКОЕ ПОЛЕ
- 31. Конформное преобразование.
- 32. Линейное преобразование.
- 33. Дробно-линейное преобразование.
- 34. Функция w = z^2.
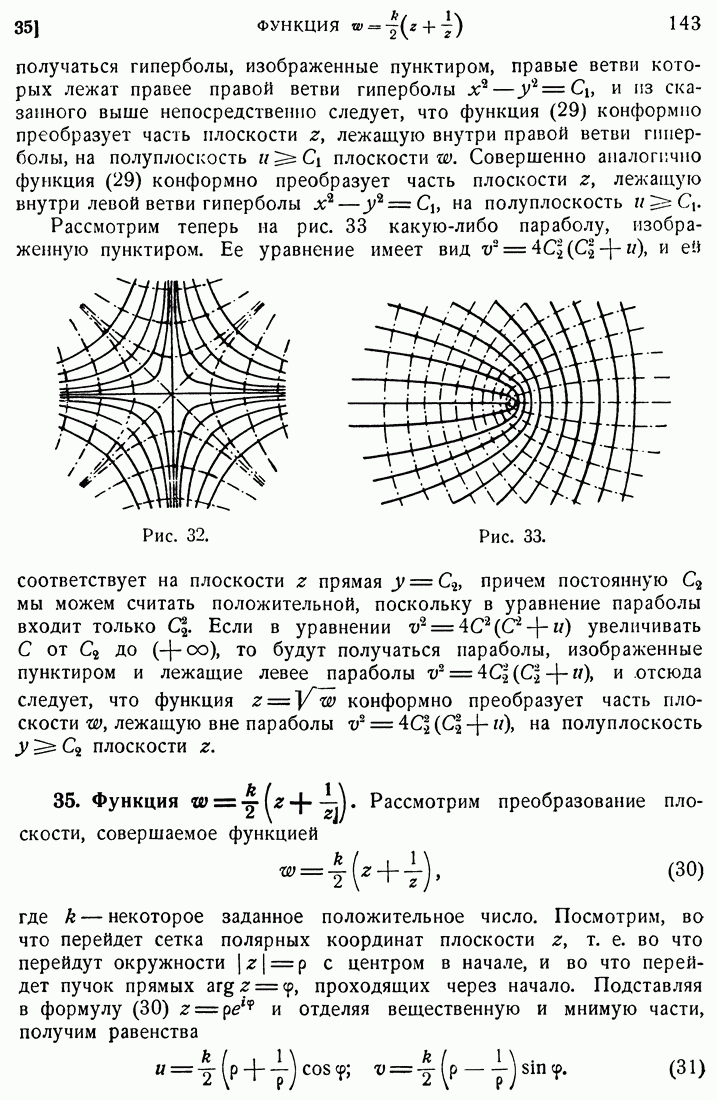
- 35. Функция …
- 36. Двуугольник и полоса.
- 37. Основная теорема.
- 38. Формула Кристоффеля.
- 39. Частные случаи.
- 40. Случай внешности многоугольника.
- 41. Минимальное свойство преобразования на круг.
- 42. Способ сопряженных тригонометрических рядов.
- 43. Плоское установившееся течение жидкости.
- 44. Примеры.
- 45. Задача полного обтекания.
- 46. Формула Н. Е. Жуковского.
- 47. Плоская электростатическая задача.
- 48. Формула Шварца.
- 49. Ядро ctg((s-t)/2).
- 50. Предельные задачи.
- 51. Бигармоническое уравнение.
- 52. Волновое уравнение и аналитические функции.
- 53. Основная теорема.
- 54. Дифракция плоской волны.
- 55. Отражение упругих волн от прямолинейной границы.
- ГЛАВА III. ПРИМЕНЕНИЕ ТЕОРИИ ВЫЧЕТОВ, ЦЕЛЫЕ И ДРОБНЫЕ ФУНКЦИИ
- 56. Интеграл Френеля.
- 57. Интегрирование выражений с тригонометрическими функциями.
- 58. Интегрирование рациональной дроби.
- 59. Некоторые новые типы интегралов с тригонометрическими функциями.
- 60. Лемма Жордана.
- 61. Представление некоторых функций контурными интегралами.
- 62. Примеры интегралов от многозначных функций.
- 63. Интегрирование системы линейных уравнений с постоянными коэффициентами.
- 64. Разложение дробной функции на простейшие дроби.
- 66. Построение мероморфной функции.
- 67. Целые функции.
- 68. Бесконечные произведения.
- 69. Построение целой функции по ее корням.
- 70. Интегралы, зависящие от параметра.
- 71. Эйлеров интеграл второго рода.
- 72. Эйлеров интеграл первого рода.
- 73. Бесконечное произведение для функции …
- 74. Представление Г(z) контурным интегралом.
- 75. Формула Стирлинга.
- 76. Формула суммирования Эйлера.
- 77. Числа Бернулли.
- 78. Метод скорейшего спуска.
- 79. Асимптотическое разложение интеграла.
- 80. Примеры.
- 81. Метод стационарной фазы.
- ГЛАВА IV. АНАЛИТИЧЕСКИЕ ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ И ФУНКЦИИ МАТРИЦ
- 82. Регулярные функции многих переменных.
- 83. Двойной интеграл и формула Коши.
- 84. Степенные ряды.
- 85. Аналитическое продолжение.
- 86. Функции матриц. Предварительные понятия.
- 87. Степенные ряды от одной матрицы.
- 88. Умножение степенных рядов. Обращение степенного ряда.
- 89. Дальнейшее исследование сходимости.
- 90. Интерполяционные полиномы.
- 91. Тождество Кейли. Формула Сильвестра.
- 92. Определение функций одной матрицы формулой Коши.
- 93. Аналитическое продолжение.
- 94. Логарифм матриц.
- 95. Обращение целой функции от матрицы в случае матриц второго порядка.
- 96. Системы линейных уравнений с постоянными коэффициентами.
- 97. Функции нескольких матриц.
- ГЛАВА V. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
- 98. Разложение решения в степенной ряд.
- 99. Аналитическое продолжение решения.
- 100. Окрестность особой точки.
- 101. Регулярная особая точка.
- 102. Уравнения класса Фукса.
- 103. Уравнение Гаусса.
- 104. Гипергеометрический ряд.
- 105. Полиномы Лежандра.
- 106. Полиномы Якоби.
- 107. Конформное преобразование и уравнение Гаусса.
- 108. Преобразование Лапласа.
- 109. Различный выбор решений.
- 110. Уравнение Бесселя.
- 111. Функции Ханкеля и интегральное представление решений уравнения Бесселя.
- 112. Асимптотические разложения.
- 113. Асимптотические разложения решений, полученных преобразованием Лапласа.
- 114. Асимптотические разложения решений уравнения Бесселя.
- 115. Вырождение уравнения Гаусса.
- 116. Формальные ряды в окрестности иррегулярной особой точки.
- 117. Построение асимптотических разложений методом после довательных приближений.
- 118. Функции Эйри.
- 119. Асимптотика при большом значении параметра.
- 120. Уравнения с периодическими коэффициентами.
- 121. Условия устойчивости и неустойчивости для уравнения Хилла.
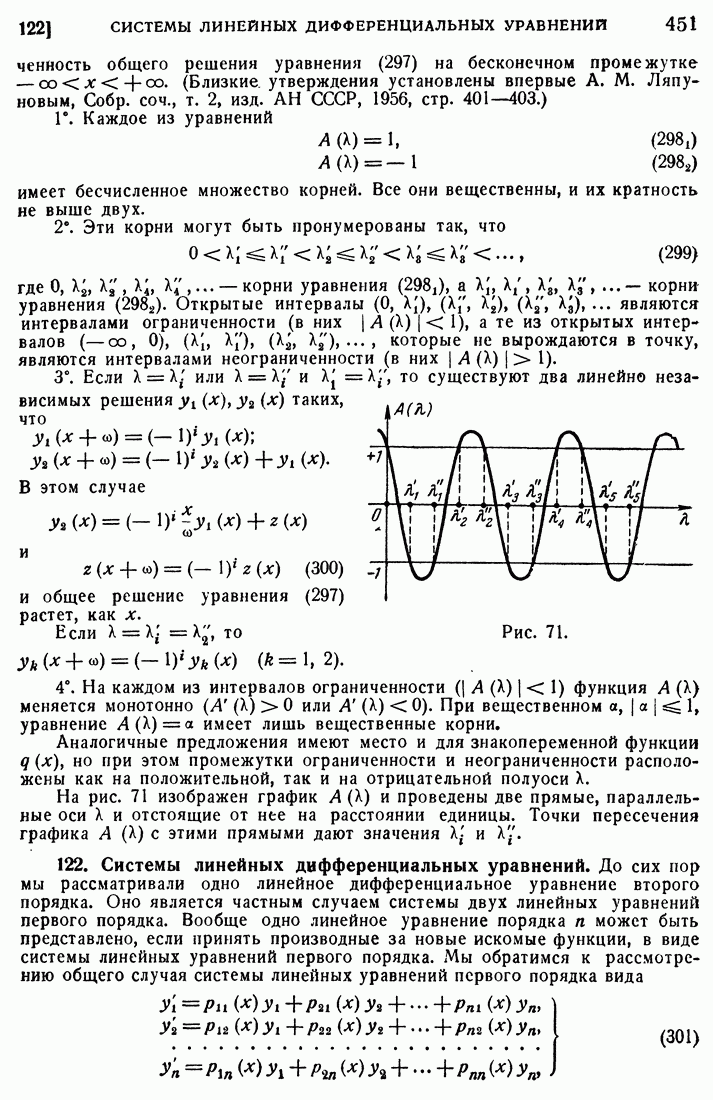
- 122. Системы линейных дифференциальных уравнений.
- 123. Регулярная особая точка.
- 124. Регулярные системы.
- 125. Представление решения в окрестности особой точки.
- 126. Канонические решения.
- 127. Связь с регулярными решениями типа Фукса.
- 128. Случай любых Us.
- 129. Формальные разложения в окрестности иррегулярной особой точки.
- ГЛАВА VI. СПЕЦИАЛЬНЫЕ ФУНКЦИИ
- 130. Определение сферических функций.
- 131. Явные выражения сферических функций.
- 132. Свойство ортогональности.
- 133. Полиномы Лежандра.
- 134. Разложение по сферическим функциям.
- 135. Доказательство сходимости.
- 136. Связь сферических функций с предельными задачами.
- 137. Задачи Дирихле и Неймана.
- 138. Потенциал объемных масс.
- 139. Потенциал сферического слоя.
- 140. Электрон в центральном поле.
- 141. Шаровые функции и линейные представления группы вращения.
- 142. Функция Лежандра.
- 143. Функция Лежандра второго рода.
- § 2. ФУНКЦИИ БЕССЕЛЯ
- 144. Определение функций Бесселя.
- 145. Соотношения между функциями Бесселя.
- 146. Ортогональность функций Бесселя и их корни.
- 147. Производящая функция и интегральное представление.
- 148. Формула Фурье — Бесселя.
- 150. Разложение функций Неймана с целым значком.
- 151. Случай чисто мнимого аргумента.
- 152. Новые интегральные представления.
- 153. Асимптотические представления.
- 154. Функции Бесселя и уравнение Лапласа.
- 155. Волновое уравнение в цилиндрических координатах.
- 156. Волновое уравнение в сферических координатах.
- § 3. ПОЛИНОМЫ ЭРМИТА И ЛАГЕРРА
- 157. Линейный осциллятор и полиномы Эрмита.
- 158. Свойство ортогональности.
- 159. Производящая функция.
- 160. Параболические координаты и функции Эрмита.
- 161. Полиномы Лагерра.
- 162. Связь полиномов Эрмита и Лагерра.
- 163. Асимптотическое выражение полиномов Эрмита.
- 164. Асимптотическое выражение полиномов Лежандра.
- § 4. ЭЛЛИПТИЧЕСКИЕ ИНТЕГРАЛЫ И ЭЛЛИПТИЧЕСКИЕ ФУНКЦИИ
- 165. Приведение эллиптических интегралов к нормальному виду.
- 166. Приведение интегралов к тригонометрической форме.
- 167. Примеры.
- 168. Обращение эллиптического интеграла.
- 169. Общие свойства эллиптических функций.
- 170. Основная лемма.
- 171. Функции Вейерштрасса.
- 172. Дифференциальное уравнение для …
- 173. Функции …
- 174. Разложение целой периодической функции.
- 175. Новые обозначения.
- 176. Функция …
- 177. Функции …
- 178. Свойства функций тэта.
- 179. Выражение чисел … через …
- 180. Эллиптические функции Якоби.
- 181. Основные свойства функций Якоби.
- 182. Дифференциальные уравнения для функций Якоби.
- 183. Формулы сложения.
- 184. Связь функций p(u) и sn(u).
- 185. Эллиптические координаты.
- 186. Введение эллиптических функций.
- 187. Уравнение Лямэ.
- 188. Простой маятник.
- 189. Пример конформного преобразования.
- ДОБАВЛЕНИЕ. ПРИВЕДЕНИЕ МАТРИЦ К КАНОНИЧЕСКОЙ ФОРМЕ
- 191. Случай простых корней.
- 192. Первый этап преобразований в случае кратных корней.
- 193. Приведение к канонической форме.
- 194. Определение структуры канонической формы.
- 196. Пример.