| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 13. Уравнение эволюции средних значений и соотношение неопределенности время-энергия
Исходя из «представления» Гейзенберга, особенно просто написать дифференциальное уравнение для среднего значения заданной наблюдаемой  Действительно, поскольку
Действительно, поскольку  не зависит от времени, имеем
не зависит от времени, имеем

Пользуясь уравнением Гейзенберга, вновь получаем уравнение (V. 72)

Если же воспользоваться системой (I), то получаются уравнения Эренфеста (§ VI. 2).
В качестве приложения уравнения (43) дадим точный вывод соотношения неопределенности время-энергия (см. § IV. 10). Рассмотрим систему, гамильтониан которой не зависит явно от времени, и пусть А есть некоторая другая наблюдаемая этой системы, также не зависящая от времени. Мы анализируем динамическое состояние системы в заданный момент времени  . Пусть
. Пусть  есть вектор, представляющий это состояние. Обозначим с помощью
есть вектор, представляющий это состояние. Обозначим с помощью  средние квадратичные отклонения А и Н соответственно. Применим неравенство Шварца к векторам
средние квадратичные отклонения А и Н соответственно. Применим неравенство Шварца к векторам  и повторим слово в слово рассуждения § 4. Мы найдем после вычислений, что
и повторим слово в слово рассуждения § 4. Мы найдем после вычислений, что

причем равенство реализуется, если  удовлетворяет уравнению
удовлетворяет уравнению

где  — некоторые вещественные постоянные (ср. уравнение (10)). Однако согласно уравнению (43)
— некоторые вещественные постоянные (ср. уравнение (10)). Однако согласно уравнению (43)

неравенство (44) можно поэтому записать в форме

или

если положить

где  — характеристическое время эволюции статистического распределения А. Это время, необходимое для того, чтобы центр
— характеристическое время эволюции статистического распределения А. Это время, необходимое для того, чтобы центр  распределения сместился на ширину распределения
распределения сместился на ширину распределения  , т. е. время, необходимое для заметного изменения распределения. Таким образом, для каждой динамической переменной можно ввести характеристическое время эволюции.
, т. е. время, необходимое для заметного изменения распределения. Таким образом, для каждой динамической переменной можно ввести характеристическое время эволюции.
Пусть теперь  есть наименьшее из так определенных характеристических времен;
есть наименьшее из так определенных характеристических времен;  можно рассматривать как характеристическое время эволюции самой физической системы: каким бы ни было измерение, осуществляемое в системе в момент времени его статистическое распределение будет практически одинаковым с распределением измерения в момент
можно рассматривать как характеристическое время эволюции самой физической системы: каким бы ни было измерение, осуществляемое в системе в момент времени его статистическое распределение будет практически одинаковым с распределением измерения в момент  если разность.
если разность.  меньше
меньше  .
.
Согласно неравенству (45),  удовлетворяют соотношению неопределенности время-энергия
удовлетворяют соотношению неопределенности время-энергия

Если, в частности, система находится в стационарном состоянии, то  каким бы ни было А и, следовательно,
каким бы ни было А и, следовательно,  бесконечно велико; при этом
бесконечно велико; при этом  в согласии с соотношением (47).
в согласии с соотношением (47).
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ К РУССКОМУ ПЕРЕВОДУ
- ПРЕДИСЛОВИЕ
- ЧАСТЬ I. ФОРМАЛИЗМ И ЕГО ИНТЕРПРЕТАЦИЯ
- ГЛАВА I. ИСТОКИ КВАНТОВОЙ ТЕОРИИ
- Раздел I. КОНЕЦ КЛАССИЧЕСКОГО ПЕРИОДА
- § 2. Классическая теоретическая физика
- § 3. Успехи в изучении микроскопических явлений и появление квантов в физике
- Раздел II. СВЕТОВЫЕ КВАНТЫ, ИЛИ ФОТОНЫ
- § 5. Эффект Комптона
- § 6. Световые кванты и явления интерференции
- § 7. Заключение
- Раздел III. КВАНТОВАНИЕ В АТОМНЫХ СИСТЕМАХ
- § 8. Атомная спектроскопия и трудности классической модели Резерфорда
- § 9. Квантование энергетических уровней атомов
- § 10. Другие примеры квантования: пространственное квантование
- Раздел IV. ПРИНЦИП СООТВЕТСТВИЯ И СТАРАЯ КВАНТОВАЯ ТЕОРИЯ
- § 11. Недостаточность классической корпускулярной теории
- § 12. Принцип соответствия
- § 13. Применение принципа соответствия при вычислении постоянной Ридберга
- § 14. Лагранжева и гамильтонова формы уравнений к лассической механики
- § 15. Правила квантования Бора — Зоммерфельда
- § 16. Достижения и ограниченность старой теории квантов
- § 17. Заключение
- ГЛАВА II. ВОЛНЫ ВЕЩЕСТВА И УРАВНЕНИЕ ШРЕДИНГЕРА
- Раздел I. ВОЛНЫ ВЕЩЕСТВА
- § 3. Свободный волновой пакет. Фазовая и групповая скорости
- § 4. Волновой пакет в медленно меняющемся поле
- § 5. Квантование уровней энергии атомов
- § 6. Дифракция волн вещества
- § 7. Корпускулярная структура вещества
- § 8. Универсальный характер дуализма волна — частица
- Раздел II. УРАВНЕНИЕ ШРЕДИНГЕРА
- § 9. Закон сохранения числа частиц вещества
- § 10. Необходимость волнового уравнения и условия, которым оно должно удовлетворять
- § 11. Понятие оператора
- § 12. Волновое уравнение для свободной частицы
- § 13. Частица в области действия скалярного потенциала
- § 14. Заряженная частица в электромагнитном поле
- § 15. Общее правило построения уравнения Шредингера по принципу соответствия
- Раздел III. СТАЦИОНАРНОЕ УРАВНЕНИЕ ШРЕДИНГЕРА
- § 16. Исследование стационарных состояний
- § 17. Общие свойства уравнения. Структура энергетического спектра
- ГЛАВА III. КВАНТОВЫЕ СИСТЕМЫ В ОДНОМ ИЗМЕРЕНИИ
- Раздел I. ПРЯМОУГОЛЬНЫЕ ПОТЕНЦИАЛЫ
- § 3. Скачок потенциала. Отражение и прохождение волн
- § 4. Бесконечно высокий потенциальный барьер
- § 5. Бесконечно глубокая потенциальная яма. Дискретный спектр
- § 6. Конечная потенциальная яма. Резонансы
- § 7. Прохождение прямоугольного потенциального барьера. Туннельный эффект
- Раздел II. ОБЩИЕ СВОЙСТВА ОДНОМЕРНОГО УРАВНЕНИЯ ШРЕДИНГЕРА
- § 8. Свойства вронскиана
- § 9. Асимптотическое поведение решений
- § 10. Структура спектра собственных значений
- § 11. Состояния непрерывного спектра: отражение и прохождение волн
- § 12. Число узлов связанных состояний
- § 13. Соотношения ортогональности
- § 14. Замечание по поводу четности
- ГЛАВА IV. СТАТИСТИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ КОРПУСКУЛЯРНО-ВОЛНОВОГО ДУАЛИЗМА И СООТНОШЕНИЯ НЕОПРЕДЕЛЕННОСТИ
- Раздел I. СТАТИСТИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ ВОЛНОВЫХ ФУНКЦИИ В ВОЛНОВОЙ МЕХАНИКЕ
- § 2. Вероятности результатов измерения координаты и импульса частицы
- § 3. Сохранение нормы во времени
- § 4. Понятие потока
- § 5. Средние значения функций от r и от p
- § 6. Системы многих частиц
- Раздел II. СООТНОШЕНИЯ НЕОПРЕДЕЛЕННОСТИ ГЕЙЗЕНБЕРГА
- § 7. Соотношения неопределенности координата-импульс квантовой частицы
- § 8. Точное выражение соотношений неопределенности координата-импульс
- § 9. Обобщение: соотношения неопределенности для сопряженных переменных
- § 10. Соотношение неопределенности время-энергия
- § 11. Соотношения неопределенности для фотонов
- Раздел III. СООТНОШЕНИЯ НЕОПРЕДЕЛЕННОСТИ И МЕХАНИЗМ ИЗМЕРЕНИЯ
- § 12. Неконтролируемое возмущение в процессе измерения
- § 13. Измерения положения в пространстве
- § 14. Измерения импульса
- Раздел IV. ОПИСАНИЕ ЯВЛЕНИЙ В КВАНТОВОЙ ТЕОРИИ. ДОПОЛНИТЕЛЬНОСТЬ И ПРИЧИННОСТЬ
- § 16. Описание микроскопических явлений и дополнительность
- § 17. Дополнительные переменные. Совместные переменные
- § 18. Корпускулярно-волновой дуализм и дополнительность
- § 19. Дополнительность и причинность
- ГЛАВА V. ФОРМАЛИЗМ ВОЛНОВОЙ МЕХАНИКИ И ЕГО ИСТОЛКОВАНИЕ
- Раздел I. ЭРМИТОВЫ ОПЕРАТОРЫ И ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ
- § 2. Пространство волновых функций
- § 3. Определение средних значений
- § 4. Отсутствие флуктуаций и проблема собственных значений
- Раздел II. ИССЛЕДОВАНИЕ ДИСКРЕТНОГО СПЕКТРА
- § 5. Собственные значения и собственные функции эрмитового оператора
- § 6. Разложение волновой функции в ряд по ортонормированным собственным функциям
- § 7. Статистическое распределение результатов измерений величины, оператор которой обладает полной системой собственных функций с конечной нормой
- Раздел III. СТАТИСТИКА ИЗМЕРЕНИЙ В ОБЩЕМ СЛУЧАЕ
- § 8. Трудности описания непрерывного спектра. Введение дельта-функции Дирака
- § 9. Разложение по собственным функциям в общем случае. Условие замкнутости
- § 10. Статистическое распределение результатов измерения в общем случае
- § 11. Другие методы исследования непрерывного спектра
- § 12. Комментарии и примеры
- Раздел IV. ОПРЕДЕЛЕНИЕ ВОЛНОВОЙ ФУНКЦИИ
- § 13. Операция измерения и редукция волнового пакета. Идеальные измерения
- § 14. Коммутирующие наблюдаемые и совместные переменные
- § 15. Полные наборы коммутирующих наблюдаемых
- § 16. Чистые и смешанные состояния
- Раздел V. АЛГЕБРА КОММУТАТОРОВ И ЕЕ ПРИЛОЖЕНИЯ
- § 17. Алгебра коммутаторов и основные свойства коммутаторов
- § 18. Соотношения коммутации для момента импульса
- § 19. Изменение статистического распределения во времени. Интегралы движения
- § 20. Примеры интегралов движения. Энергия. Четность
- ГЛАВА VI. КЛАССИЧЕСКОЕ ПРИБЛИЖЕНИЕ И МЕТОД ВКБ
- Раздел I. КЛАССИЧЕСКИЙ ПРЕДЕЛ ВОЛНОВОЙ МЕХАНИКИ
- § 2. Теорема Эренфеста
- § 3. Движение и расплывание волновых пакетов
- § 4. Классический предел уравнения Шредингера
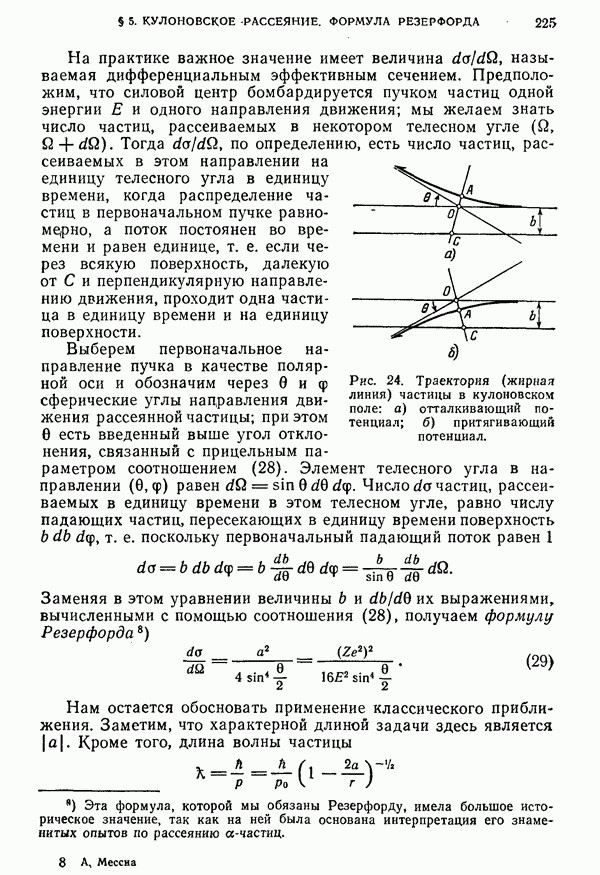
- § 5. Кулоновское рассеяние. Формула Резерфорда
- Раздел II. МЕТОД ВКБ
- § 7. Решения ВКБ в одном измерении
- § 8. Условия применимости приближения ВКБ
- § 9. Граничные точки и формулы согласования
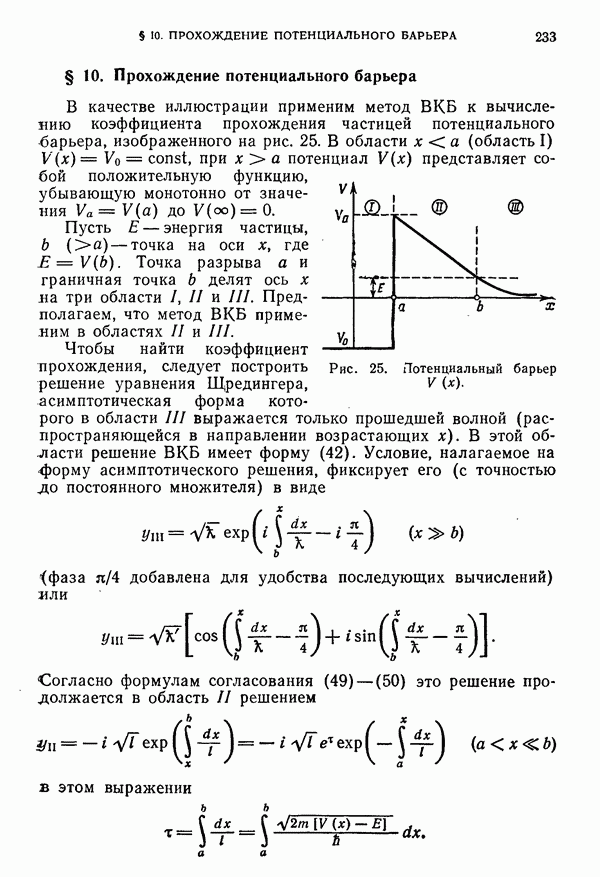
- § 10. Прохождение потенциального барьера
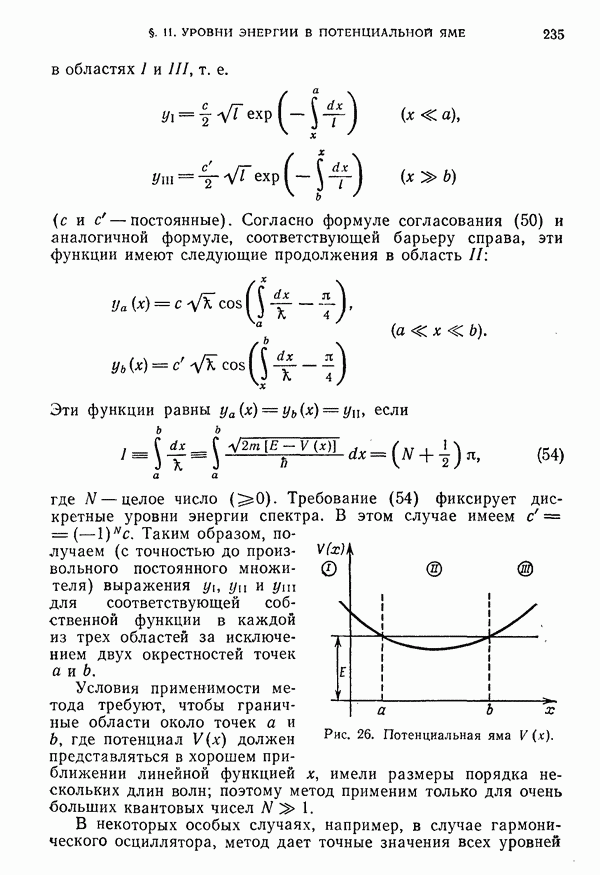
- § 11. Уровни энергии в потенциальной яме
- ГЛАВА VII. ОБЩИЙ ФОРМАЛИЗМ КВАНТОВОЙ ТЕОРИИ А. МАТЕМАТИЧЕСКИЙ АППАРАТ
- § 1. Принцип суперпозиции и представление динамических состояний векторами
- Раздел I. ВЕКТОРЫ И ОПЕРАТОРЫ
- § 2. Векторное пространство. Кет-векторы
- § 3. Дуальное пространство. Бра-векторы
- § 4. Скалярное произведение
- § 5. Линейные операторы
- § 6. Тензорное произведение двух векторных пространств
- Раздел II. ЭРМИТОВЫ ОПЕРАТОРЫ, ПРОЕКТОРЫ И НАБЛЮДАЕМЫЕ
- § 7. Сопряженные операторы и правила сопряжения
- § 8. Эрмитовы (самосопряженные) операторы, положительна определенные операторы, унитарные операторы
- § 9. Проблема собственных значений и наблюдаемые
- § 10. Проекторы (или операторы проектирования)
- § 11. Алгебра проекторов
- § 12. Наблюдаемые, обладающие только дискретным спектром
- § 13. Наблюдаемые в общем случае и обобщенное соотношение замкнутости
- § 14. Функции наблюдаемых
- § 15. Операторы, коммутирующие с наблюдаемой. Коммутирующие наблюдаемые
- Раздел III. ТЕОРИЯ ПРЕДСТАВЛЕНИЙ
- § 16. Общее понятие о конечных матрицах
- § 17. Квадратные матрицы
- § 18. Бесконечные матрицы
- § 19. Представление векторов и операторов матрицами
- § 20. Преобразования матриц
- § 21. Смена представления
- § 22. Унитарные преобразования операторов и векторов
- ГЛАВА VIII. ОБЩИЙ ФОРМАЛИЗМ КВАНТОВОЙ ТЕОРИИ Б. ОПИСАНИЕ ФИЗИЧЕСКИХ ЯВЛЕНИЙ
- Раздел I. ДИНАМИЧЕСКИЕ СОСТОЯНИЯ И ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ
- § 2. Определение вероятностей. Постулаты измерения
- § 3. Наблюдаемые квантовой системы и соотношения коммутации
- § 4. Соотношения неопределенности Гейзенберга
- § 5. Определение состояний и построение пространства
- § 6. Квантовая одномерная система, обладающая классическим аналогом
- § 7. Построение пространства состояний путем тензорного умножения более простых пространств
- Раздел II. УРАВНЕНИЯ ДВИЖЕНИЯ
- § 8. Оператор эволюции и уравнение Шредингера
- § 9. «Представление» Шредингера
- § 10. «Представление» Гейзенберга
- § 11. «Представление» Гейзенберга и принцип соответствия
- § 12. Интегралы движения
- § 13. Уравнение эволюции средних значений и соотношение неопределенности время-энергия
- § 14. Промежуточные «представления»
- Раздел III. РАЗЛИЧНЫЕ ПРЕДСТАВЛЕНИЯ ТЕОРИИ
- § 16. Волновая механика
- § 17. Представление {р}
- § 18. Пример: движение свободного волнового пакета
- § 19. Другие представления. Представление, в котором диагональна энергия
- Раздел IV. КВАНТОВАЯ СТАТИСТИКА
- § 20. Системы с неполной информацией и смешанные состояния
- § 21. Матрица плотности
- § 22. Эволюция смешанного состояния во времени
- § 23. Характеристические свойства матрицы плотности
- § 24. Чистые состояния
- § 25. Классическая статистика и квантовая статистика
- ЧАСТЬ II. ПРОСТЫЕ СИСТЕМЫ
- ГЛАВА IX. РЕШЕНИЕ УРАВНЕНИЯ ШРЕДИНГЕРА МЕТОДОМ РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ. ЦЕНТРАЛЬНО-СИММЕТРИЧНЫЙ ПОТЕНЦИАЛ
- Раздел I. ЧАСТИЦА В ЦЕНТРАЛЬНО-СИММЕТРИЧНОМ ПОТЕНЦИАЛЬНОМ ПОЛЕ. ОБЩЕЕ РАССМОТРЕНИЕ ПРОБЛЕМЫ
- § 2. Гамильтониан частицы в сферических координатах
- § 3. Отделение угловых переменных. Сферические функции
- § 4. Радиальное уравнение
- § 5. Собственные решения радиального уравнения. Структура спектра.
- § 6. Заключение
- Раздел II. ЦЕНТРАЛЬНО-СИММЕТРИЧНЫЙ ПРЯМОУГОЛЬНЫЙ ПОТЕНЦИАЛ. СВОБОДНАЯ ЧАСТИЦА
- § 7. Сферические функции Бесселя
- § 8. Свободная частица. Свободные плоские и сферические волны
- § 9. Разложение плоской волны по сферическим функциям
- § 10. Сферическая прямоугольная яма
- Раздел III. ЗАДАЧА ДВУХ ТЕЛ. ОТДЕЛЕНИЕ ДВИЖЕНИЯ ЦЕНТРА МАСС
- § 11. Отделение движения центра масс в классической механике
- § 12. Отделение движения центра масс квантовой системы двух частиц
- § 13. Система многих частиц
- ГЛАВА X. ПРОБЛЕМА РАССЕЯНИЯ. ЦЕНТРАЛЬНЫЙ ПОТЕНЦИАЛ И МЕТОД ФАЗОВЫХ СДВИГОВ
- Раздел I. ЭФФЕКТИВНЫЕ СЕЧЕНИЯ И АМПЛИТУДЫ РАССЕЯНИЯ
- § 3. Стационарная волна рассеяния
- § 4. Описание рассеяния при помощи пучка волновых пакетов
- § 5. Рассеяние волнового пакета на потенциале
- § 6. Вычисление эффективных сечений
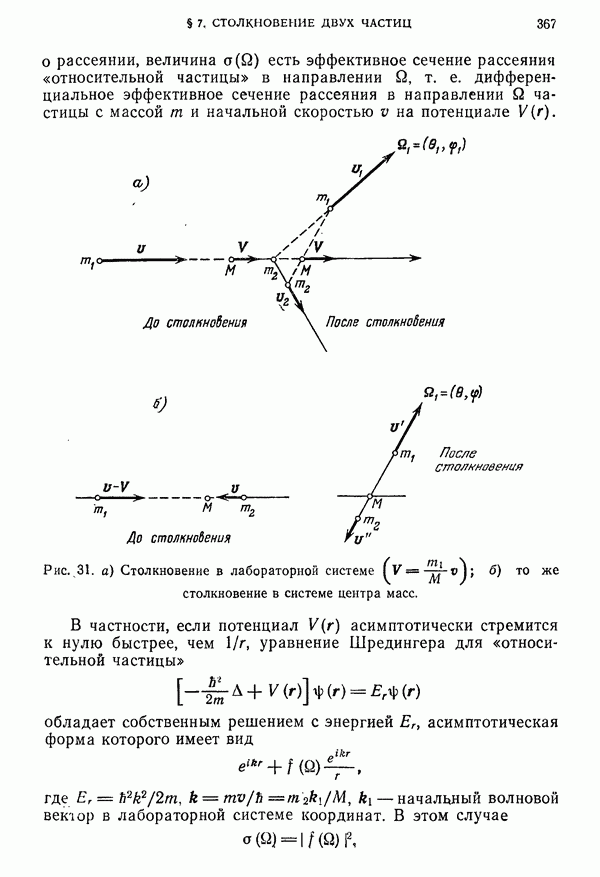
- § 7. Столкновение двух частиц. Лабораторная система и система центра масс
- Раздел II. РАССЕЯНИЕ ЦЕНТРАЛЬНЫМ ПОТЕНЦИАЛОМ. ФАЗОВЫЕ СДВИГИ
- § 8. Разложение по парциальным волнам. Метод фазовых сдвигов
- § 9. Квазиклассическое представление рассеяния. Прицельный параметр
- Раздел III. ПОТЕНЦИАЛ ОГРАНИЧЕННОГО РАДИУСА ДЕЙСТВИЯ
- § 10. Сдвиг фазы и логарифмическая производная
- § 11. Сдвиги фаз при низких энергиях
- § 12. Парциальные волны более высокого порядка. Сходимость ряда
- § 13. Рассеяние на твердой сфере
- Раздел IV. РЕЗОНАНСНОЕ РАССЕЯНИЕ
- § 14. Рассеяние глубокой прямоугольной потенциальной ямой
- § 15. Общий закон резонансного рассеяния. Метастабильные состояния
- § 16. Наблюдение времени жизни метастабильных состояний
- Раздел V. РАЗЛИЧНЫЕ ФОРМУЛЫ И СВОЙСТВА
- § 17. Интегральные представления фазовых сдвигов
- § 18. Зависимость фазовых сдвигов от формы потенциала
- § 19. Приближение Борна
- § 20. Теория эффективного радиуса действия. Формула Бете
- ГЛАВА XI. КУЛОНОВСКОЕ ВЗАИМОДЕЙСТВИЕ
- Раздел I. АТОМ ВОДОРОДА
- § 2. Уравнение Шредингера для атома водорода
- § 3. Порядок величины энергии связи основного состояния
- § 4. Решение уравнения Шредингера в сферических координатах
- § 5. Спектр энергии. Вырождение
- § 6. Собственные функции связанных состояний
- Раздел II. КУЛОНОВСКОЕ РАССЕЯНИЕ
- § 7. Кулоновская функция рассеяния
- § 8. Формула Резерфорда
- § 9. Разложение по парциальным волнам
- § 10. Разложение по сферическим функциям
- § 11. Модификация кулоновского потенциала короткодействующим взаимодействием
- ГЛАВА XII. ГАРМОНИЧЕСКИЙ ОСЦИЛЛЯТОР
- Раздел I. СОБСТВЕННЫЕ СОСТОЯНИЯ И СОБСТВЕННЫЕ ВЕКТОРЫ ГАМИЛЬТОНИАНА
- § 3. Введение операторов
- § 4. Спектр и базисная система оператора N
- § 5. Представление [N]
- § 6. Операторы рождения и уничтожения
- § 7. Представление {Q}. Полиномы Эрмита
- Раздел II. ПРИЛОЖЕНИЯ И РАЗЛИЧНЫЕ СВОЙСТВА
- § 8. Производящая функция собственных функций
- § 9. Интегрирование уравнений Гейзенберга
- § 10. Классический и квантовый осцилляторы
- § 11. Движение минимизирующего волнового пакета и классический предел
- § 12. Гармонические осцилляторы в термодинамическом равновесии
- Раздел III. ИЗОТРОПНЫЕ МНОГОМЕРНЫЕ ГАРМОНИЧЕСКИЕ ОСЦИЛЛЯТОРЫ
- § 13. Общее исследование изотропного осциллятора в р измерениях
- § 14. Изотропный осциллятор в двух измерениях
- § 15. Изотропный осциллятор в трех измерениях
- ДОПОЛНЕНИЕ А ОБОБЩЕННЫЕ ФУНКЦИИ, «ФУНКЦИЯ» ДЕЛЬТА И ПРЕОБРАЗОВАНИЕ ФУРЬЕ
- § 1. Понятие функционала и строгий подход к проблеме непрерывного спектра
- § 2. Определение обобщенных функций
- § 3. Линейная комбинация обобщенных функций
- § 4. Произведение двух обобщенных функций
- § 5. Ряды и интегралы обобщенных функций
- § 6. Дифференцирование обобщенных функций
- Раздел II. СВОЙСТВА «ФУНКЦИИ» ДЕЛЬТА
- § 8. Представление в виде предела ядра интегрального оператора
- § 9. Основные свойства
- § 10. Производные
- Раздел III. ПРЕОБРАЗОВАНИЕ ФУРЬЕ
- § 11. Преобразование Фурье. Определение
- § 12. Абсолютно интегрируемые функции f(x)
- § 13. Функции «хи» (основные функции)
- § 14. Преобразование Фурье обобщенных функций. Определение
- § 15. Обобщенные функции медленного роста
- § 16. Квадратично интегрируемые функции
- § 17. Преобразование свертки
- ДОПОЛНЕНИЕ Б. СПЕЦИАЛЬНЫЕ ФУНКЦИИ И СВЯЗАННЫЕ С НИМИ ФОРМУЛЫ
- § 1. Уравнение Лапласа и вырожденная гипергеометрическая функция
- § 2. Полиномы Лагерра
- § 3. Собственные функции водородоподобных атомов (теория Шредингера)
- § 4. Чисто кулоновская волна
- § 5. Сферические кулоновские функции
- Раздел II. СФЕРИЧЕСКИЕ ФУНКЦИИ БЕССЕЛЯ
- § 6. Сферические функции Бесселя
- Раздел III. ГАРМОНИЧЕСКИЙ ОСЦИЛЛЯТОР И ПОЛИНОМЫ ЭРМИТА
- § 7. Полиномы Эрмита
- § 8. Собственные функции гармонического осциллятора
- Раздел IV. ПОЛИНОМЫ И ФУНКЦИИ ЛЕЖАНДРА, СФЕРИЧЕСКИЕ ФУНКЦИИ
- § 9. Полиномы и функции Лежандра
- § 10. Сферические функции
- Раздел V РАЗЛОЖЕНИЯ И РАЗЛИЧНЫЕ ФОРМУЛЫ