| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 14. Измерения импульса
Аналогичным образом импульс частицы может a priori быть измерен с любой наперед заданной точностью, но операция измерения всегда сопровождается возмущением, которое увеличивает неопределенность в знании координаты, измеряющей положение, так что соотношения неопределенности всегда выполнены. Покажем это на двух примерах.
а) Отклонение в магнитном поле. Импульс заряженной частицы обычно измеряется по отклонению в постоянном магнитном поле. Количество движения  связано с радиусом кривизны
связано с радиусом кривизны  траектории частицы хорошо известным соотношением
траектории частицы хорошо известным соотношением

где  — величина магнитного поля,
— величина магнитного поля,  заряд частицы.
заряд частицы.
Исследуем процесс измерения импульса электрона этим методом. На рис. 20 представлена схема эксперимента. Электрон попадает в поле магнита через диафрагму А и покидает его через диафрагму В после отклонения на 180° (этот угол отклонения выбран для удобства рассуждений). В момент, непосредственно предшествующий началу измерения (т. е. непосредственно
перед прохождением диафрагмы), направление движения (ось Оу) и координата электрона в этом направлении  по предположению точно известны. Эти начальные условия
по предположению точно известны. Эти начальные условия  в принципе всегда могут быть реализованы с помощью коллиматора, снабженного обтюратором с достаточно коротким «временем пропускания». Радиус кривизны равен половине расстояния между двумя диафрагмами: если
в принципе всегда могут быть реализованы с помощью коллиматора, снабженного обтюратором с достаточно коротким «временем пропускания». Радиус кривизны равен половине расстояния между двумя диафрагмами: если  соответствующие ширины этих диафрагм, то
соответствующие ширины этих диафрагм, то  измеряется с точностью до
измеряется с точностью до  Таким образом, импульс электрона известен с точностью до
Таким образом, импульс электрона известен с точностью до


Рис. 20. Измерение импульса методом отклонения в магнитном поле.
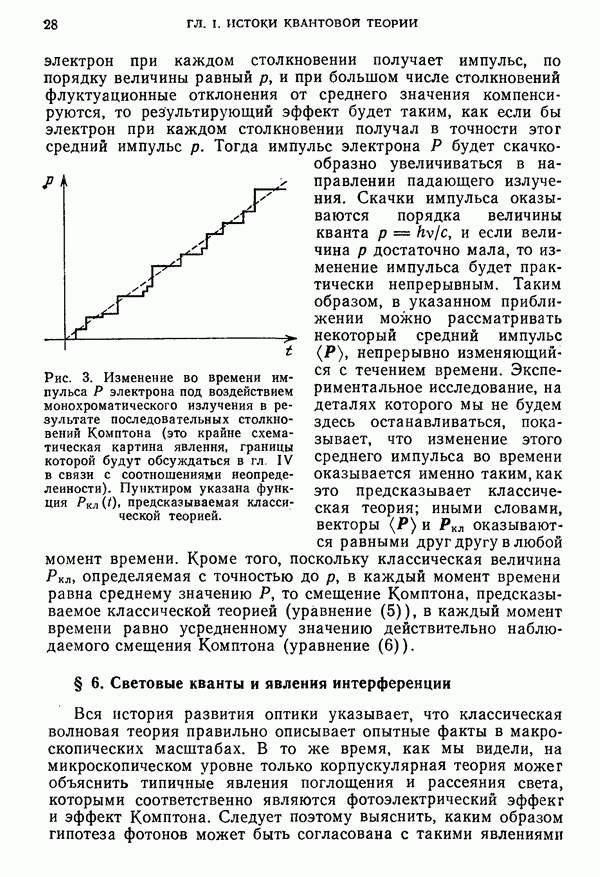
Измеряемой в опыте величиной является составляющая импульса в направлении оси  Покажем, что в результате измерения координата электрона у будет характеризоваться неопределенностью А у, причем
Покажем, что в результате измерения координата электрона у будет характеризоваться неопределенностью А у, причем  Квантовым эффектом, существенным в этом опыте, является дифракция электронной волны при прохождении диафрагмы А (читатель без труда убедится в том, что дифракция на диафрагме В роли не играет). Если бы указанного эффекта не было, то импульс электрона на входе в область действия поля был бы строго направлен по
Квантовым эффектом, существенным в этом опыте, является дифракция электронной волны при прохождении диафрагмы А (читатель без труда убедится в том, что дифракция на диафрагме В роли не играет). Если бы указанного эффекта не было, то импульс электрона на входе в область действия поля был бы строго направлен по  далее электрон описывал бы полукруг, и время движения от А к В, равное
далее электрон описывал бы полукруг, и время движения от А к В, равное  не зависело бы от величины
не зависело бы от величины  Квантовый эффект дифракции приводит к тому, что угол между направлением импульса на входе и осью
Квантовый эффект дифракции приводит к тому, что угол между направлением импульса на входе и осью  характеризуется неопределенностью
характеризуется неопределенностью  траектория электрона (в приближении геометрической оптики) есть дуга окружности, определяемая с точностью до
траектория электрона (в приближении геометрической оптики) есть дуга окружности, определяемая с точностью до  ; момент прихода в В характеризуется неопределенностью
; момент прихода в В характеризуется неопределенностью  а неопределенность
а неопределенность  в
в  раз больше, следовательно
раз больше, следовательно

Отсюда получаем

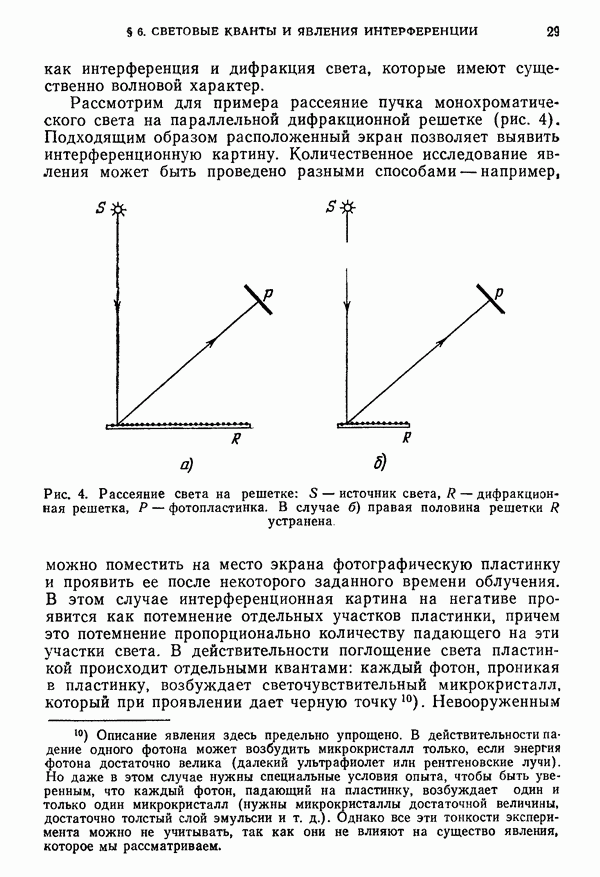
б) Столкновение с фотоном. Следующий метод измерения импульса основан на изучении процесса столкновения
рассматризаемой частицы с другой частицей, например, с фотоном, начальный импульс которого известен точно; измеряется импульс, передаваемый при столкновении второй частице. Рассмотрим электрон из предшествующей задачи с начальными данными  Для определения импульса электрона
Для определения импульса электрона  будем облучать его идеально монохроматическим светом частоты
будем облучать его идеально монохроматическим светом частоты  распространяющимся параллельно оси у. Один из световых фотонов испытывает комптоновское столкновение и измеряется его конечный импульс. Чтобы упростить рассуждения, предположим, что конечный импульс фотона также параллелен оси у, но направлен в противоположную сторону (рис. 21). Пусть
распространяющимся параллельно оси у. Один из световых фотонов испытывает комптоновское столкновение и измеряется его конечный импульс. Чтобы упростить рассуждения, предположим, что конечный импульс фотона также параллелен оси у, но направлен в противоположную сторону (рис. 21). Пусть  — частота фотона после столкновения; теория комптоновского рассеяния позволяет выразить начальный
— частота фотона после столкновения; теория комптоновского рассеяния позволяет выразить начальный  и конечный
и конечный  импульсы электрона через частоты
импульсы электрона через частоты  и
и  Предположим, что реализуются условия нерелятивистского приближения
Предположим, что реализуются условия нерелятивистского приближения  . В результате вычислений находим
. В результате вычислений находим

причем точность определения этих величин связана с точностью определения  соотношением
соотношением


Рис. 21. Измерение импульса электрона при комптоновском столкновении с фотоном. Схема столкновения
Положение у электрона после измерения может быть вычислено, исходя из того, что в начальный момент  , скорость электрона до столкновения равна
, скорость электрона до столкновения равна  а после столкновения
а после столкновения  Если положение и импульс рассеянного фотона можно было бы измерить одновременно с большой точностью, то был бы строго определен и момент столкновения, а тогда неопределенности в значениях
Если положение и импульс рассеянного фотона можно было бы измерить одновременно с большой точностью, то был бы строго определен и момент столкновения, а тогда неопределенности в значениях  и у могли бы быть сделаны одновременно сколь угодно малыми. Читатель проверит это без труда. Однако измерение
и у могли бы быть сделаны одновременно сколь угодно малыми. Читатель проверит это без труда. Однако измерение  есть измерение частоты; чем точнее это измерение, тем больше неопределенность в определении момента прохождения фотоном какой-либо точки, в частности в определении момента столкновения:
есть измерение частоты; чем точнее это измерение, тем больше неопределенность в определении момента прохождения фотоном какой-либо точки, в частности в определении момента столкновения:  же время неопределенность А у в положении электрона после столкновения равна по меньшей мере произведению
же время неопределенность А у в положении электрона после столкновения равна по меньшей мере произведению 
на изменение скорости, т. е.

что дает 
В этой измерительной операции, как и в предшествующей, измеряемая величина  сама меняется в процессе измерения. Это изменение не следует смешивать с непредсказуемым и неконтролируемым возмущением, испытываемым системой при измерении. Действительно, указанное изменение известно точно, во всяком случае значения
сама меняется в процессе измерения. Это изменение не следует смешивать с непредсказуемым и неконтролируемым возмущением, испытываемым системой при измерении. Действительно, указанное изменение известно точно, во всяком случае значения  величины
величины  до и после столкновения известны с одинаковой точностью, которая может быть сделана сколь угодно большой. Напротив, ввиду невозможности предсказать и контролировать возмущение, испытываемое частицей при осуществлении измерения (неопределенность в определении момента передачи импульса и энергии), величина у после столкновения известна только с неопределенностью А у, причем эта неопределенность тем больше, чем точнее измерение
до и после столкновения известны с одинаковой точностью, которая может быть сделана сколь угодно большой. Напротив, ввиду невозможности предсказать и контролировать возмущение, испытываемое частицей при осуществлении измерения (неопределенность в определении момента передачи импульса и энергии), величина у после столкновения известна только с неопределенностью А у, причем эта неопределенность тем больше, чем точнее измерение 
Подчеркнем еще раз универсальность характера соотношений неопределенности. Действительно, что бы произошло, если, величина кванта действия для фотонов была бы равна некоторой величине  значительно меньшей
значительно меньшей  Все наши рассуждения относительно измерения типа б) можно было бы повторить, заменяя всюду
Все наши рассуждения относительно измерения типа б) можно было бы повторить, заменяя всюду  на
на  это привело бы нас к соотношению
это привело бы нас к соотношению  Соотношения неопределенности оказались бы нарушенными и вся развиваемая нами статистическая интерпретация теории пришла бы в противоречие с опытом.
Соотношения неопределенности оказались бы нарушенными и вся развиваемая нами статистическая интерпретация теории пришла бы в противоречие с опытом.
Оба метода измерения импульса, обсуждавшиеся выше, требуют некоторого временного интервала. Этот интервал может быть вообще говоря уменьшен (при увеличении поля  в первом случае, при увеличении частоты
в первом случае, при увеличении частоты  во втором; см. задачу 7) без изменения точности измерения
во втором; см. задачу 7) без изменения точности измерения  Но как бы то ни было, вероятности, определенные в §§ 2, 5, вычисляются с помощью волновой функции, заданной в момент времени
Но как бы то ни было, вероятности, определенные в §§ 2, 5, вычисляются с помощью волновой функции, заданной в момент времени  Поскольку само измерение не мгновенно, следует точно определить этот момент времени:
Поскольку само измерение не мгновенно, следует точно определить этот момент времени:  есть момент начала измерения, так что распределение вероятностей, данное в § 2 (уравнение (6)) относится к импульсу
есть момент начала измерения, так что распределение вероятностей, данное в § 2 (уравнение (6)) относится к импульсу  т. е. к импульсу до измерения.
т. е. к импульсу до измерения.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ К РУССКОМУ ПЕРЕВОДУ
- ПРЕДИСЛОВИЕ
- ЧАСТЬ I. ФОРМАЛИЗМ И ЕГО ИНТЕРПРЕТАЦИЯ
- ГЛАВА I. ИСТОКИ КВАНТОВОЙ ТЕОРИИ
- Раздел I. КОНЕЦ КЛАССИЧЕСКОГО ПЕРИОДА
- § 2. Классическая теоретическая физика
- § 3. Успехи в изучении микроскопических явлений и появление квантов в физике
- Раздел II. СВЕТОВЫЕ КВАНТЫ, ИЛИ ФОТОНЫ
- § 5. Эффект Комптона
- § 6. Световые кванты и явления интерференции
- § 7. Заключение
- Раздел III. КВАНТОВАНИЕ В АТОМНЫХ СИСТЕМАХ
- § 8. Атомная спектроскопия и трудности классической модели Резерфорда
- § 9. Квантование энергетических уровней атомов
- § 10. Другие примеры квантования: пространственное квантование
- Раздел IV. ПРИНЦИП СООТВЕТСТВИЯ И СТАРАЯ КВАНТОВАЯ ТЕОРИЯ
- § 11. Недостаточность классической корпускулярной теории
- § 12. Принцип соответствия
- § 13. Применение принципа соответствия при вычислении постоянной Ридберга
- § 14. Лагранжева и гамильтонова формы уравнений к лассической механики
- § 15. Правила квантования Бора — Зоммерфельда
- § 16. Достижения и ограниченность старой теории квантов
- § 17. Заключение
- ГЛАВА II. ВОЛНЫ ВЕЩЕСТВА И УРАВНЕНИЕ ШРЕДИНГЕРА
- Раздел I. ВОЛНЫ ВЕЩЕСТВА
- § 3. Свободный волновой пакет. Фазовая и групповая скорости
- § 4. Волновой пакет в медленно меняющемся поле
- § 5. Квантование уровней энергии атомов
- § 6. Дифракция волн вещества
- § 7. Корпускулярная структура вещества
- § 8. Универсальный характер дуализма волна — частица
- Раздел II. УРАВНЕНИЕ ШРЕДИНГЕРА
- § 9. Закон сохранения числа частиц вещества
- § 10. Необходимость волнового уравнения и условия, которым оно должно удовлетворять
- § 11. Понятие оператора
- § 12. Волновое уравнение для свободной частицы
- § 13. Частица в области действия скалярного потенциала
- § 14. Заряженная частица в электромагнитном поле
- § 15. Общее правило построения уравнения Шредингера по принципу соответствия
- Раздел III. СТАЦИОНАРНОЕ УРАВНЕНИЕ ШРЕДИНГЕРА
- § 16. Исследование стационарных состояний
- § 17. Общие свойства уравнения. Структура энергетического спектра
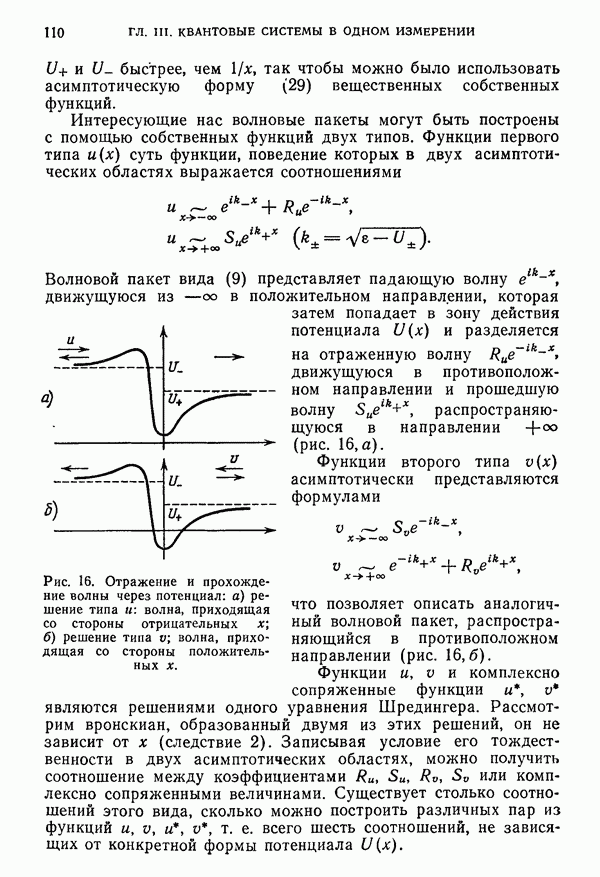
- ГЛАВА III. КВАНТОВЫЕ СИСТЕМЫ В ОДНОМ ИЗМЕРЕНИИ
- Раздел I. ПРЯМОУГОЛЬНЫЕ ПОТЕНЦИАЛЫ
- § 3. Скачок потенциала. Отражение и прохождение волн
- § 4. Бесконечно высокий потенциальный барьер
- § 5. Бесконечно глубокая потенциальная яма. Дискретный спектр
- § 6. Конечная потенциальная яма. Резонансы
- § 7. Прохождение прямоугольного потенциального барьера. Туннельный эффект
- Раздел II. ОБЩИЕ СВОЙСТВА ОДНОМЕРНОГО УРАВНЕНИЯ ШРЕДИНГЕРА
- § 8. Свойства вронскиана
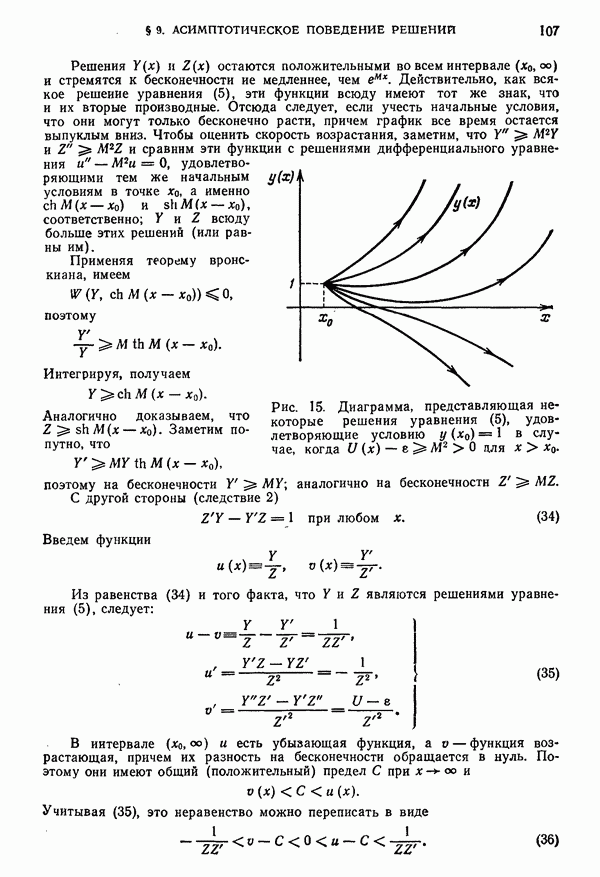
- § 9. Асимптотическое поведение решений
- § 10. Структура спектра собственных значений
- § 11. Состояния непрерывного спектра: отражение и прохождение волн
- § 12. Число узлов связанных состояний
- § 13. Соотношения ортогональности
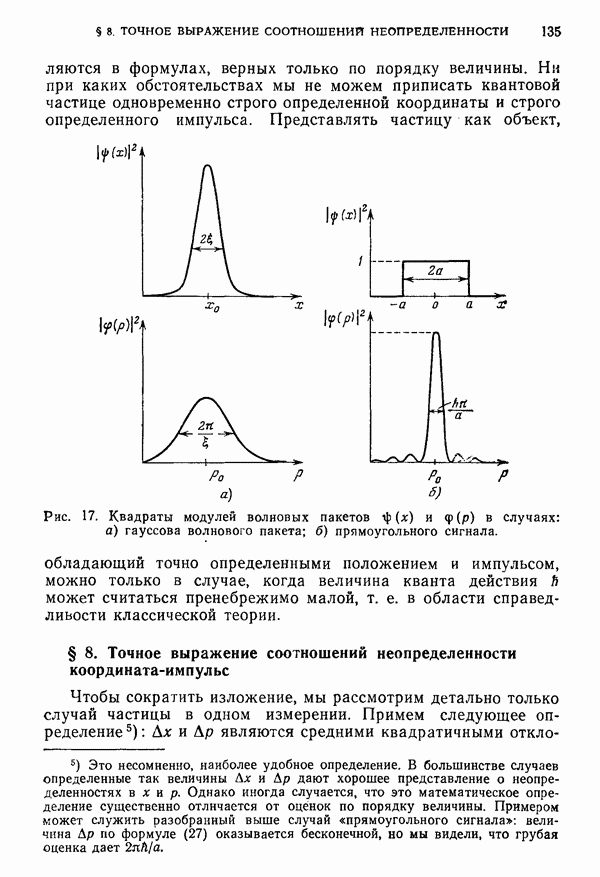
- § 14. Замечание по поводу четности
- ГЛАВА IV. СТАТИСТИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ КОРПУСКУЛЯРНО-ВОЛНОВОГО ДУАЛИЗМА И СООТНОШЕНИЯ НЕОПРЕДЕЛЕННОСТИ
- Раздел I. СТАТИСТИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ ВОЛНОВЫХ ФУНКЦИИ В ВОЛНОВОЙ МЕХАНИКЕ
- § 2. Вероятности результатов измерения координаты и импульса частицы
- § 3. Сохранение нормы во времени
- § 4. Понятие потока
- § 5. Средние значения функций от r и от p
- § 6. Системы многих частиц
- Раздел II. СООТНОШЕНИЯ НЕОПРЕДЕЛЕННОСТИ ГЕЙЗЕНБЕРГА
- § 7. Соотношения неопределенности координата-импульс квантовой частицы
- § 8. Точное выражение соотношений неопределенности координата-импульс
- § 9. Обобщение: соотношения неопределенности для сопряженных переменных
- § 10. Соотношение неопределенности время-энергия
- § 11. Соотношения неопределенности для фотонов
- Раздел III. СООТНОШЕНИЯ НЕОПРЕДЕЛЕННОСТИ И МЕХАНИЗМ ИЗМЕРЕНИЯ
- § 12. Неконтролируемое возмущение в процессе измерения
- § 13. Измерения положения в пространстве
- § 14. Измерения импульса
- Раздел IV. ОПИСАНИЕ ЯВЛЕНИЙ В КВАНТОВОЙ ТЕОРИИ. ДОПОЛНИТЕЛЬНОСТЬ И ПРИЧИННОСТЬ
- § 16. Описание микроскопических явлений и дополнительность
- § 17. Дополнительные переменные. Совместные переменные
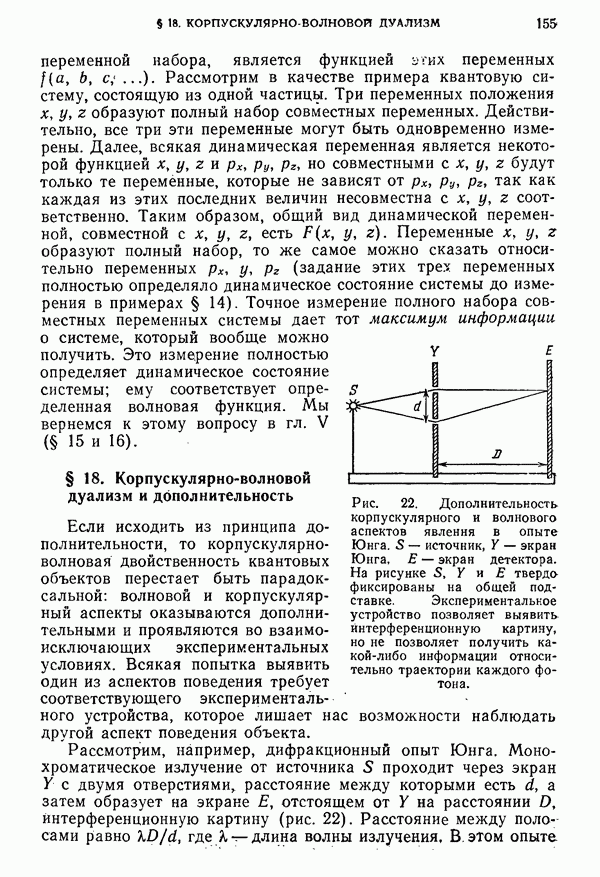
- § 18. Корпускулярно-волновой дуализм и дополнительность
- § 19. Дополнительность и причинность
- ГЛАВА V. ФОРМАЛИЗМ ВОЛНОВОЙ МЕХАНИКИ И ЕГО ИСТОЛКОВАНИЕ
- Раздел I. ЭРМИТОВЫ ОПЕРАТОРЫ И ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ
- § 2. Пространство волновых функций
- § 3. Определение средних значений
- § 4. Отсутствие флуктуаций и проблема собственных значений
- Раздел II. ИССЛЕДОВАНИЕ ДИСКРЕТНОГО СПЕКТРА
- § 5. Собственные значения и собственные функции эрмитового оператора
- § 6. Разложение волновой функции в ряд по ортонормированным собственным функциям
- § 7. Статистическое распределение результатов измерений величины, оператор которой обладает полной системой собственных функций с конечной нормой
- Раздел III. СТАТИСТИКА ИЗМЕРЕНИЙ В ОБЩЕМ СЛУЧАЕ
- § 8. Трудности описания непрерывного спектра. Введение дельта-функции Дирака
- § 9. Разложение по собственным функциям в общем случае. Условие замкнутости
- § 10. Статистическое распределение результатов измерения в общем случае
- § 11. Другие методы исследования непрерывного спектра
- § 12. Комментарии и примеры
- Раздел IV. ОПРЕДЕЛЕНИЕ ВОЛНОВОЙ ФУНКЦИИ
- § 13. Операция измерения и редукция волнового пакета. Идеальные измерения
- § 14. Коммутирующие наблюдаемые и совместные переменные
- § 15. Полные наборы коммутирующих наблюдаемых
- § 16. Чистые и смешанные состояния
- Раздел V. АЛГЕБРА КОММУТАТОРОВ И ЕЕ ПРИЛОЖЕНИЯ
- § 17. Алгебра коммутаторов и основные свойства коммутаторов
- § 18. Соотношения коммутации для момента импульса
- § 19. Изменение статистического распределения во времени. Интегралы движения
- § 20. Примеры интегралов движения. Энергия. Четность
- ГЛАВА VI. КЛАССИЧЕСКОЕ ПРИБЛИЖЕНИЕ И МЕТОД ВКБ
- Раздел I. КЛАССИЧЕСКИЙ ПРЕДЕЛ ВОЛНОВОЙ МЕХАНИКИ
- § 2. Теорема Эренфеста
- § 3. Движение и расплывание волновых пакетов
- § 4. Классический предел уравнения Шредингера
- § 5. Кулоновское рассеяние. Формула Резерфорда
- Раздел II. МЕТОД ВКБ
- § 7. Решения ВКБ в одном измерении
- § 8. Условия применимости приближения ВКБ
- § 9. Граничные точки и формулы согласования
- § 10. Прохождение потенциального барьера
- § 11. Уровни энергии в потенциальной яме
- ГЛАВА VII. ОБЩИЙ ФОРМАЛИЗМ КВАНТОВОЙ ТЕОРИИ А. МАТЕМАТИЧЕСКИЙ АППАРАТ
- § 1. Принцип суперпозиции и представление динамических состояний векторами
- Раздел I. ВЕКТОРЫ И ОПЕРАТОРЫ
- § 2. Векторное пространство. Кет-векторы
- § 3. Дуальное пространство. Бра-векторы
- § 4. Скалярное произведение
- § 5. Линейные операторы
- § 6. Тензорное произведение двух векторных пространств
- Раздел II. ЭРМИТОВЫ ОПЕРАТОРЫ, ПРОЕКТОРЫ И НАБЛЮДАЕМЫЕ
- § 7. Сопряженные операторы и правила сопряжения
- § 8. Эрмитовы (самосопряженные) операторы, положительна определенные операторы, унитарные операторы
- § 9. Проблема собственных значений и наблюдаемые
- § 10. Проекторы (или операторы проектирования)
- § 11. Алгебра проекторов
- § 12. Наблюдаемые, обладающие только дискретным спектром
- § 13. Наблюдаемые в общем случае и обобщенное соотношение замкнутости
- § 14. Функции наблюдаемых
- § 15. Операторы, коммутирующие с наблюдаемой. Коммутирующие наблюдаемые
- Раздел III. ТЕОРИЯ ПРЕДСТАВЛЕНИЙ
- § 16. Общее понятие о конечных матрицах
- § 17. Квадратные матрицы
- § 18. Бесконечные матрицы
- § 19. Представление векторов и операторов матрицами
- § 20. Преобразования матриц
- § 21. Смена представления
- § 22. Унитарные преобразования операторов и векторов
- ГЛАВА VIII. ОБЩИЙ ФОРМАЛИЗМ КВАНТОВОЙ ТЕОРИИ Б. ОПИСАНИЕ ФИЗИЧЕСКИХ ЯВЛЕНИЙ
- Раздел I. ДИНАМИЧЕСКИЕ СОСТОЯНИЯ И ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ
- § 2. Определение вероятностей. Постулаты измерения
- § 3. Наблюдаемые квантовой системы и соотношения коммутации
- § 4. Соотношения неопределенности Гейзенберга
- § 5. Определение состояний и построение пространства
- § 6. Квантовая одномерная система, обладающая классическим аналогом
- § 7. Построение пространства состояний путем тензорного умножения более простых пространств
- Раздел II. УРАВНЕНИЯ ДВИЖЕНИЯ
- § 8. Оператор эволюции и уравнение Шредингера
- § 9. «Представление» Шредингера
- § 10. «Представление» Гейзенберга
- § 11. «Представление» Гейзенберга и принцип соответствия
- § 12. Интегралы движения
- § 13. Уравнение эволюции средних значений и соотношение неопределенности время-энергия
- § 14. Промежуточные «представления»
- Раздел III. РАЗЛИЧНЫЕ ПРЕДСТАВЛЕНИЯ ТЕОРИИ
- § 16. Волновая механика
- § 17. Представление {р}
- § 18. Пример: движение свободного волнового пакета
- § 19. Другие представления. Представление, в котором диагональна энергия
- Раздел IV. КВАНТОВАЯ СТАТИСТИКА
- § 20. Системы с неполной информацией и смешанные состояния
- § 21. Матрица плотности
- § 22. Эволюция смешанного состояния во времени
- § 23. Характеристические свойства матрицы плотности
- § 24. Чистые состояния
- § 25. Классическая статистика и квантовая статистика
- ЧАСТЬ II. ПРОСТЫЕ СИСТЕМЫ
- ГЛАВА IX. РЕШЕНИЕ УРАВНЕНИЯ ШРЕДИНГЕРА МЕТОДОМ РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ. ЦЕНТРАЛЬНО-СИММЕТРИЧНЫЙ ПОТЕНЦИАЛ
- Раздел I. ЧАСТИЦА В ЦЕНТРАЛЬНО-СИММЕТРИЧНОМ ПОТЕНЦИАЛЬНОМ ПОЛЕ. ОБЩЕЕ РАССМОТРЕНИЕ ПРОБЛЕМЫ
- § 2. Гамильтониан частицы в сферических координатах
- § 3. Отделение угловых переменных. Сферические функции
- § 4. Радиальное уравнение
- § 5. Собственные решения радиального уравнения. Структура спектра.
- § 6. Заключение
- Раздел II. ЦЕНТРАЛЬНО-СИММЕТРИЧНЫЙ ПРЯМОУГОЛЬНЫЙ ПОТЕНЦИАЛ. СВОБОДНАЯ ЧАСТИЦА
- § 7. Сферические функции Бесселя
- § 8. Свободная частица. Свободные плоские и сферические волны
- § 9. Разложение плоской волны по сферическим функциям
- § 10. Сферическая прямоугольная яма
- Раздел III. ЗАДАЧА ДВУХ ТЕЛ. ОТДЕЛЕНИЕ ДВИЖЕНИЯ ЦЕНТРА МАСС
- § 11. Отделение движения центра масс в классической механике
- § 12. Отделение движения центра масс квантовой системы двух частиц
- § 13. Система многих частиц
- ГЛАВА X. ПРОБЛЕМА РАССЕЯНИЯ. ЦЕНТРАЛЬНЫЙ ПОТЕНЦИАЛ И МЕТОД ФАЗОВЫХ СДВИГОВ
- Раздел I. ЭФФЕКТИВНЫЕ СЕЧЕНИЯ И АМПЛИТУДЫ РАССЕЯНИЯ
- § 3. Стационарная волна рассеяния
- § 4. Описание рассеяния при помощи пучка волновых пакетов
- § 5. Рассеяние волнового пакета на потенциале
- § 6. Вычисление эффективных сечений
- § 7. Столкновение двух частиц. Лабораторная система и система центра масс
- Раздел II. РАССЕЯНИЕ ЦЕНТРАЛЬНЫМ ПОТЕНЦИАЛОМ. ФАЗОВЫЕ СДВИГИ
- § 8. Разложение по парциальным волнам. Метод фазовых сдвигов
- § 9. Квазиклассическое представление рассеяния. Прицельный параметр
- Раздел III. ПОТЕНЦИАЛ ОГРАНИЧЕННОГО РАДИУСА ДЕЙСТВИЯ
- § 10. Сдвиг фазы и логарифмическая производная
- § 11. Сдвиги фаз при низких энергиях
- § 12. Парциальные волны более высокого порядка. Сходимость ряда
- § 13. Рассеяние на твердой сфере
- Раздел IV. РЕЗОНАНСНОЕ РАССЕЯНИЕ
- § 14. Рассеяние глубокой прямоугольной потенциальной ямой
- § 15. Общий закон резонансного рассеяния. Метастабильные состояния
- § 16. Наблюдение времени жизни метастабильных состояний
- Раздел V. РАЗЛИЧНЫЕ ФОРМУЛЫ И СВОЙСТВА
- § 17. Интегральные представления фазовых сдвигов
- § 18. Зависимость фазовых сдвигов от формы потенциала
- § 19. Приближение Борна
- § 20. Теория эффективного радиуса действия. Формула Бете
- ГЛАВА XI. КУЛОНОВСКОЕ ВЗАИМОДЕЙСТВИЕ
- Раздел I. АТОМ ВОДОРОДА
- § 2. Уравнение Шредингера для атома водорода
- § 3. Порядок величины энергии связи основного состояния
- § 4. Решение уравнения Шредингера в сферических координатах
- § 5. Спектр энергии. Вырождение
- § 6. Собственные функции связанных состояний
- Раздел II. КУЛОНОВСКОЕ РАССЕЯНИЕ
- § 7. Кулоновская функция рассеяния
- § 8. Формула Резерфорда
- § 9. Разложение по парциальным волнам
- § 10. Разложение по сферическим функциям
- § 11. Модификация кулоновского потенциала короткодействующим взаимодействием
- ГЛАВА XII. ГАРМОНИЧЕСКИЙ ОСЦИЛЛЯТОР
- Раздел I. СОБСТВЕННЫЕ СОСТОЯНИЯ И СОБСТВЕННЫЕ ВЕКТОРЫ ГАМИЛЬТОНИАНА
- § 3. Введение операторов
- § 4. Спектр и базисная система оператора N
- § 5. Представление [N]
- § 6. Операторы рождения и уничтожения
- § 7. Представление {Q}. Полиномы Эрмита
- Раздел II. ПРИЛОЖЕНИЯ И РАЗЛИЧНЫЕ СВОЙСТВА
- § 8. Производящая функция собственных функций
- § 9. Интегрирование уравнений Гейзенберга
- § 10. Классический и квантовый осцилляторы
- § 11. Движение минимизирующего волнового пакета и классический предел
- § 12. Гармонические осцилляторы в термодинамическом равновесии
- Раздел III. ИЗОТРОПНЫЕ МНОГОМЕРНЫЕ ГАРМОНИЧЕСКИЕ ОСЦИЛЛЯТОРЫ
- § 13. Общее исследование изотропного осциллятора в р измерениях
- § 14. Изотропный осциллятор в двух измерениях
- § 15. Изотропный осциллятор в трех измерениях
- ДОПОЛНЕНИЕ А ОБОБЩЕННЫЕ ФУНКЦИИ, «ФУНКЦИЯ» ДЕЛЬТА И ПРЕОБРАЗОВАНИЕ ФУРЬЕ
- § 1. Понятие функционала и строгий подход к проблеме непрерывного спектра
- § 2. Определение обобщенных функций
- § 3. Линейная комбинация обобщенных функций
- § 4. Произведение двух обобщенных функций
- § 5. Ряды и интегралы обобщенных функций
- § 6. Дифференцирование обобщенных функций
- Раздел II. СВОЙСТВА «ФУНКЦИИ» ДЕЛЬТА
- § 8. Представление в виде предела ядра интегрального оператора
- § 9. Основные свойства
- § 10. Производные
- Раздел III. ПРЕОБРАЗОВАНИЕ ФУРЬЕ
- § 11. Преобразование Фурье. Определение
- § 12. Абсолютно интегрируемые функции f(x)
- § 13. Функции «хи» (основные функции)
- § 14. Преобразование Фурье обобщенных функций. Определение
- § 15. Обобщенные функции медленного роста
- § 16. Квадратично интегрируемые функции
- § 17. Преобразование свертки
- ДОПОЛНЕНИЕ Б. СПЕЦИАЛЬНЫЕ ФУНКЦИИ И СВЯЗАННЫЕ С НИМИ ФОРМУЛЫ
- § 1. Уравнение Лапласа и вырожденная гипергеометрическая функция
- § 2. Полиномы Лагерра
- § 3. Собственные функции водородоподобных атомов (теория Шредингера)
- § 4. Чисто кулоновская волна
- § 5. Сферические кулоновские функции
- Раздел II. СФЕРИЧЕСКИЕ ФУНКЦИИ БЕССЕЛЯ
- § 6. Сферические функции Бесселя
- Раздел III. ГАРМОНИЧЕСКИЙ ОСЦИЛЛЯТОР И ПОЛИНОМЫ ЭРМИТА
- § 7. Полиномы Эрмита
- § 8. Собственные функции гармонического осциллятора
- Раздел IV. ПОЛИНОМЫ И ФУНКЦИИ ЛЕЖАНДРА, СФЕРИЧЕСКИЕ ФУНКЦИИ
- § 9. Полиномы и функции Лежандра
- § 10. Сферические функции
- Раздел V РАЗЛОЖЕНИЯ И РАЗЛИЧНЫЕ ФОРМУЛЫ