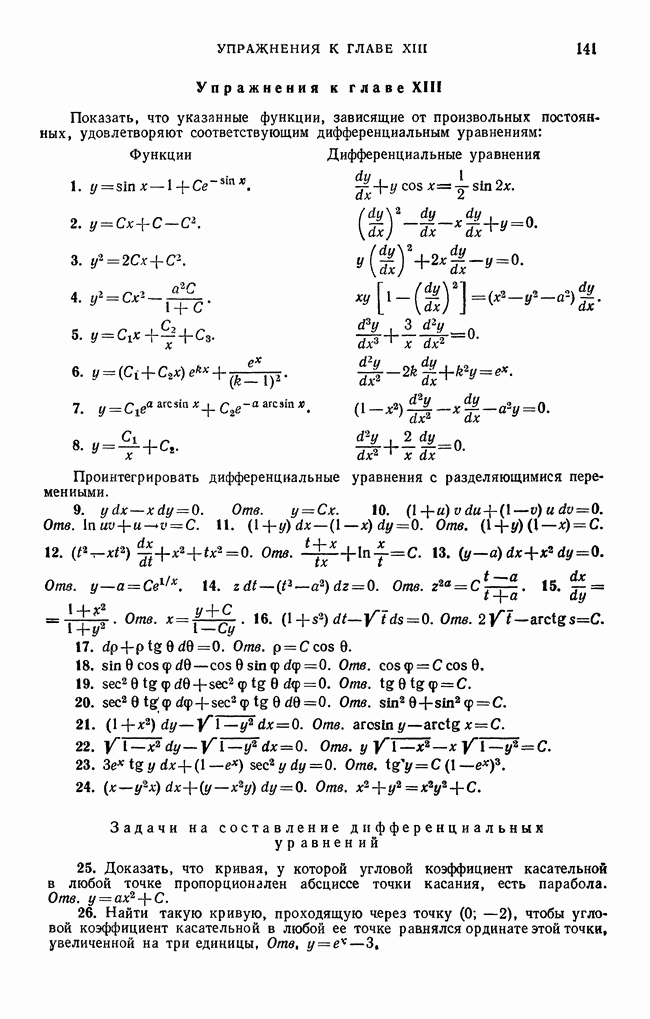| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 4. Свойство линейности изображения
Теорема. Изображение суммы нескольких функций, умноженных на постоянные, равняется сумме изображений этих функций, умноженных на соответствующие постоянные, т. е. вела

(с - постоянные) и

то

Доказательство. Умножая все члены равенства (14) на и интегрируя по  в пределах
в пределах  до
до  (вынося множители за знак интеграла), получаем равенство (14).
(вынося множители за знак интеграла), получаем равенство (14).
Пример 1. Найти изображение функции

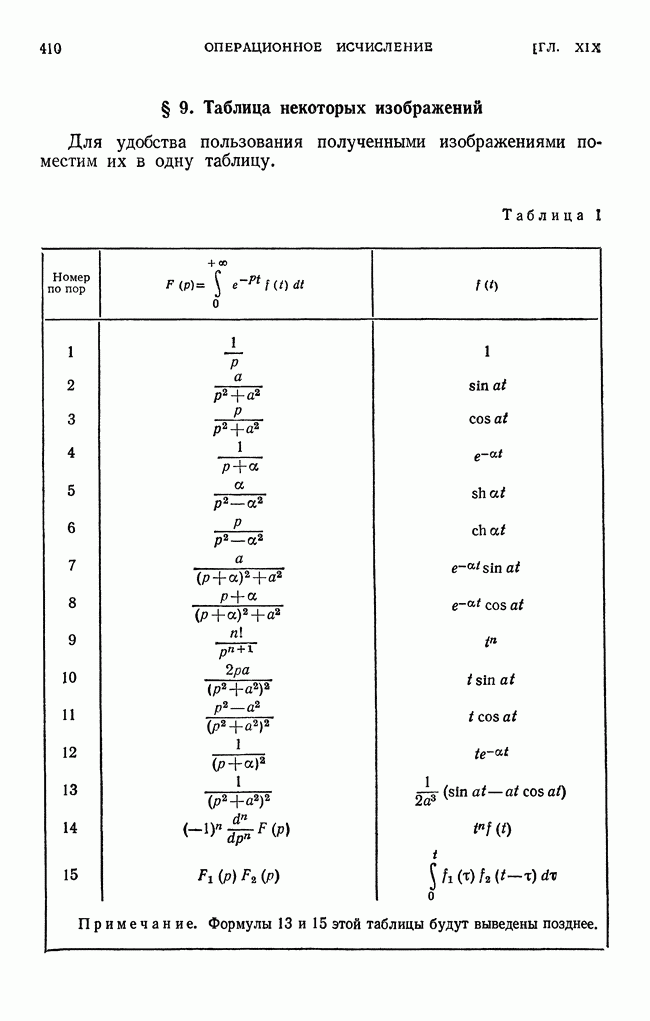
Решение. На основании формул (12), (13) и (14) получаем

Пример 2. Найти начальную функцию, изображение которой выражается формулой

Решение. Представим  так:
так:

Следовательно, на основании формул (12), (13) и (14) получаем

Из теоремы единственности в § 1 следует, что это единственная начальная функция, соответствующая данной  .
.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ К ДЕВЯТОМУ ИЗДАНИЮ
- ПРЕДИСЛОВИЕ К ПЯТОМУ ИЗДАНИЮ
- ГЛАВА XIII. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
- § 1. Постановка задачи. Уравнение движения тела при сопротивлении среды, пропорциональном скорости. Уравнение цепной линии
- § 2. Определения
- § 3. Дифференциальные уравнения первого порядка (общие понятия)
- § 4. Уравнения с разделенными и разделяющимися переменными. Задача о распаде радия
- § 5. Однородные уравнения первого порядка
- § 6. Уравнения, приводящиеся к однородным
- § 7. Линейные уравнения первого порядка
- § 8. Уравнение Бернулли
- § 9. Уравнение в полных дифференциалах
- § 10. Интегрирующий множитель
- § 11. Огибающая семейства кривых
- § 12. Особые решения дифференциального уравнения первого порядка
- § 13. Уравнение Клеро
- § 14. Уравнение Лагранжа
- § 15. Ортогональные и изогональные траектории
- § 16. Дифференциальные уравнения высших порядков (общие понятия)
- § 17. Уравнение вида y^(n) = f(x)
- § 18. Некоторые типы дифференциальных уравнений второго порядка, приводимых к уравнениям первого порядка. Задача о второй космической скорости
- § 19. Графический метод интегрирования дифференциального уравнения второго порядка
- § 20. Линейные однородные уравнения. Определения и общие свойства
- § 21. Линейные однородные уравнения второго порядка с постоянными коэффициентами
- § 22. Линейные однородные уравнения n-го порядка с постоянными коэффициентами
- § 23. Неоднородные линейные уравнения второго порядка
- § 24. Неоднородные линейные уравнения второго порядка с постоянными коэффициентами
- § 25. Неоднородные линейные уравнения высших порядков
- § 26. Дифференциальное уравнение механических колебаний
- § 27. Свободные колебания. Векторное и комплексное изображение гармонических колебаний
- § 28. Вынужденные колебания
- § 29. Системы обыкновенных дифференциальных уравнений
- § 30. Системы линейных дифференциальных уравнений с постоянными коэффициентами
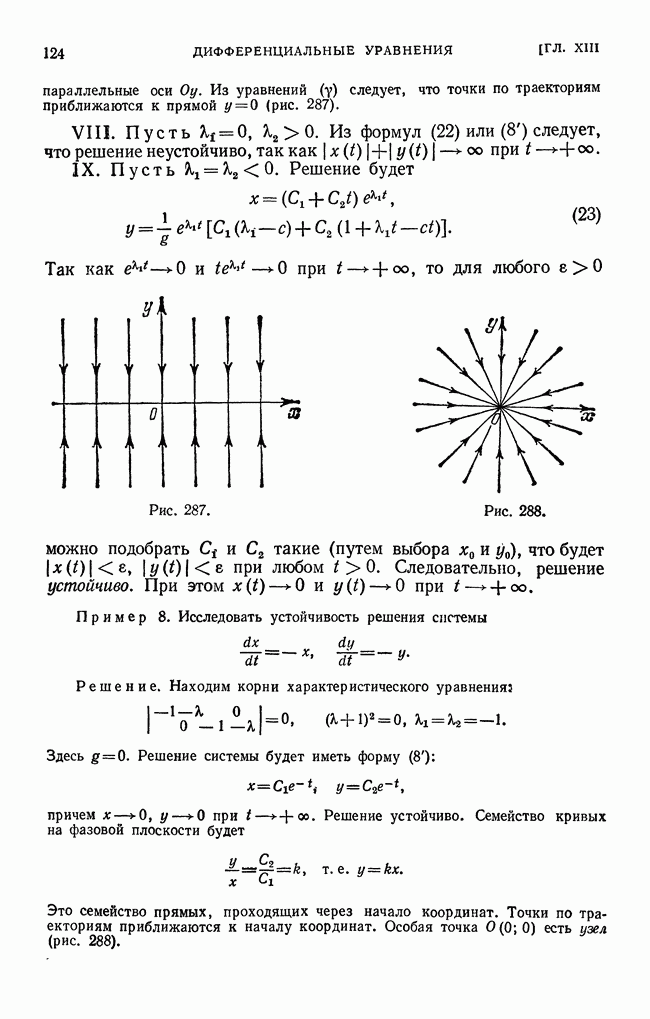
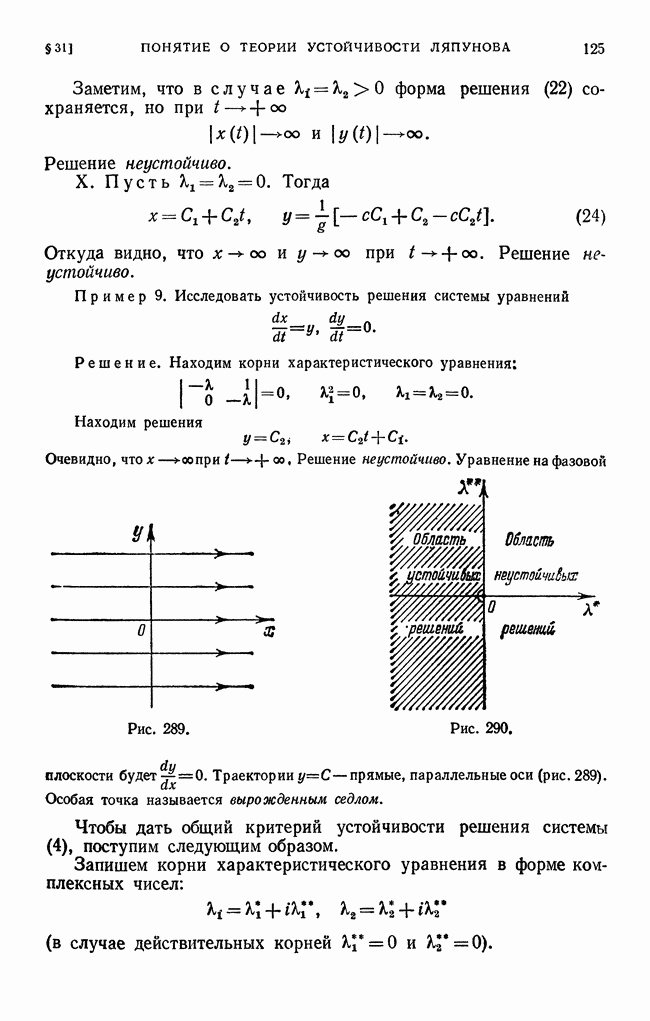
- § 31. Понятие о теории устойчивости Ляпунова. Поведение траектории дифференциального уравнения в окрестности особой точки
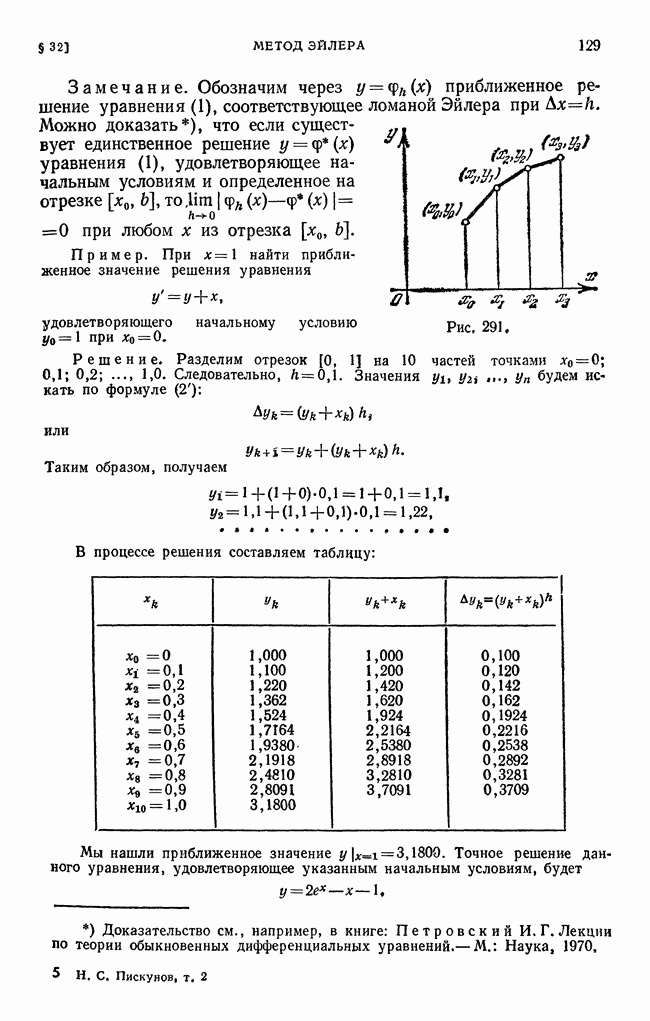
- § 32. Приближенное решение дифференциальных уравнений первого порядка методом Эйлера
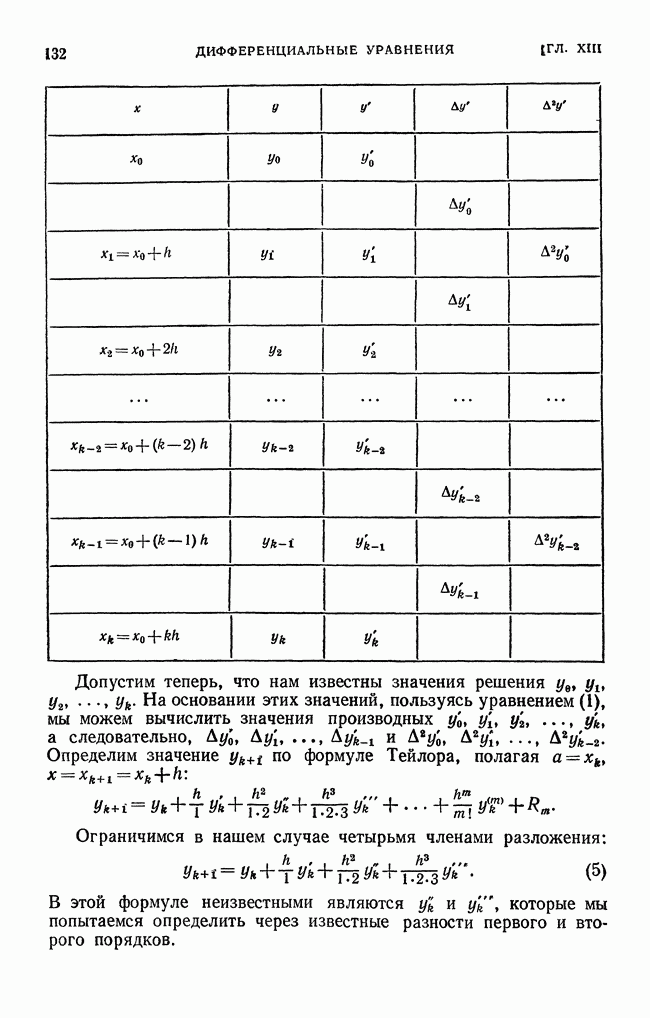
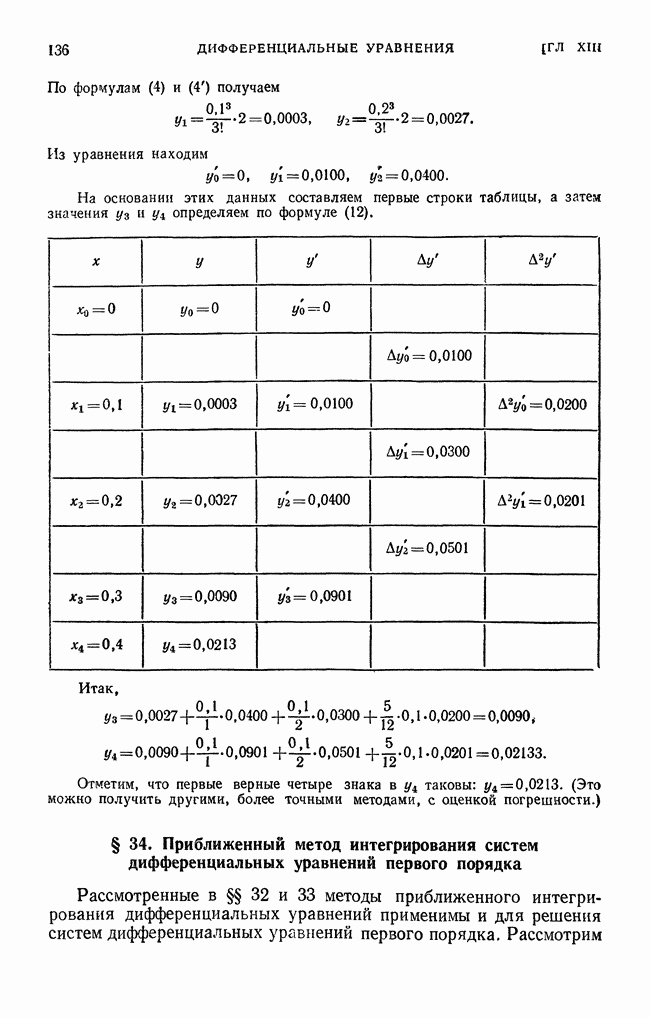
- § 33. Разностный метод приближенного решения дифференциальных уравнений, основанный на применении формулы Тейлора.. Метод Адамса
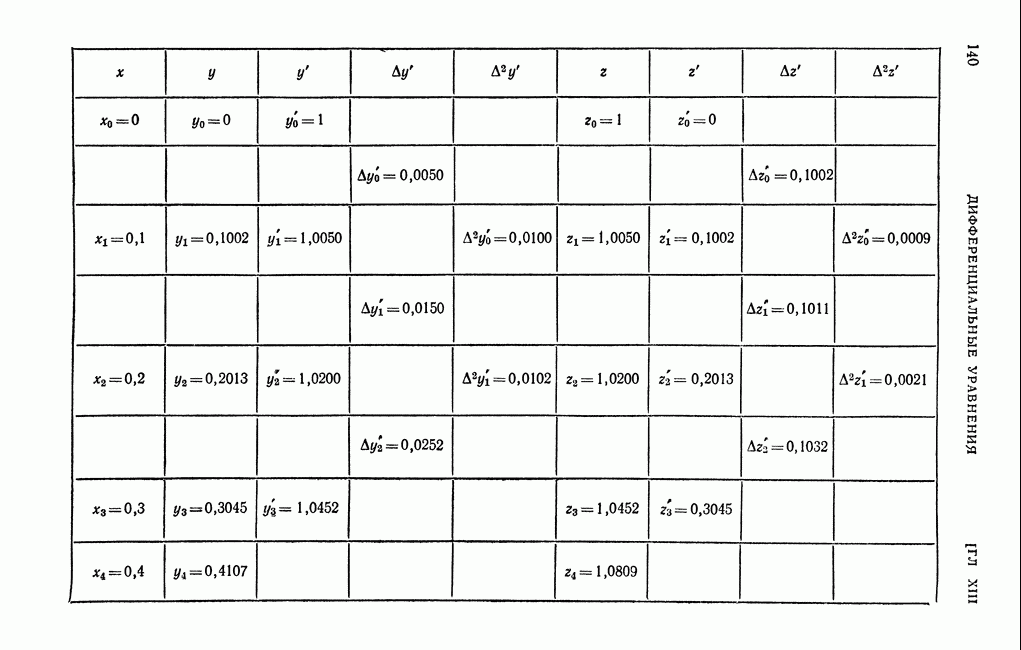
- § 34. Приближенный метод интегрирования систем дифференциальных уравнений первого порядка
- Упражнения к главе XIII
- ГЛАВА XIV. КРАТНЫЕ ИНТЕГРАЛЫ
- § 2. Вычисление двойного интеграла
- § 3. Вычисление двойного интеграла (продолжение)
- § 4. Вычисление площадей и объемов с помощью двойных интегралов
- § 5. Двойной интеграл в полярных координатах
- § 6. Замена переменных в двойном интеграле (общий случай)
- § 7. Вычисление площади поверхности
- § 9. Момент инерции площади плоской фигуры
- § 10. Координаты центра масс площади плоской фигуры
- § 11. Тройной интеграл
- § 12. Вычисление тройного интеграла
- § 13. Замена переменных в тройном интеграле
- § 14. Момент инерции и координаты центра масс тела
- § 15. Вычисление интегралов, зависящих от параметра
- Упражнения к главе XIV
- ГЛАВА XV. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ И ИНТЕГРАЛЫ ПО ПОВЕРХНОСТИ
- § 2. Вычисление криволинейного интеграла
- § 3. Формула Грина
- § 4. Условия независимости криволинейного интеграла от пути интегрирования
- § 5. Поверхностный интеграл
- § 6. Вычисление поверхностного интеграла
- § 7. Формула Стокса
- § 9. Оператор Гамильтона. Некоторые его применения
- Упражнения к главе XV
- ГЛАВА XVI. РЯДЫ
- § 1. Ряд. Сумма ряда
- § 2. Необходимый признак сходимости ряда
- § 3. Сравнение рядов с положительными членами
- § 4. Признак Даламбера
- § 5. Признак Коши
- § 6. Интегральный признак сходимости ряда
- § 7. Знакочередующиеся ряды. Теорема Лейбница
- § 8. Знакопеременные ряды. Абсолютная и условная сходимость
- § 9. Функциональные ряды
- § 10. Мажорируемые ряды
- § 11. Непрерывность суммы ряда
- § 12. Интегрирование и дифференцирование рядов
- § 13. Степенные ряды. Интервал сходимости
- § 14. Дифференцирование степенных рядов
- § 15. Ряды по степеням x-a
- § 16. Ряды Тейлора и Маклорена
- § 17. Примеры разложения функций в ряды
- § 18. Формула Эйлера
- § 19. Биномиальный ряд
- § 20. Разложение функции ln(1+x) в степенной ряд. Вычисление логарифмов
- § 21. Вычисление определенных интегралов с помощью рядов
- § 22. Интегрирование дифференциальных уравнений с помощью рядов
- § 23. Уравнение Бесселя
- § 24. Ряды с комплексными членами
- § 25. Степенные ряды с комплексной переменной
- § 26. Решение дифференциального уравнения первого порядка методом последовательных приближений (метод итераций)
- § 27. Доказательство существования решения дифференциального уравнения. Оценка погрешности при приближенном решении
- § 28. Теорема единственности решения дифференциального уравнения
- Упражнения к главе XVI
- ГЛАВА XVII. РЯДЫ ФУРЬЕ
- § 2. Примеры разложения функций в ряды Фурье
- § 3. Одно, замечание о разложении периодической функции в ряд Фурье
- § 4. Ряды Фурье для четных и нечетных функций
- § 5. Ряд Фурье для функции с периодом 2l
- § 6. О разложении непериодической функции в ряд Фурье
- § 7. Приближение в среднем заданной функции с помощью тригонометрического многочлена
- § 8. Интеграл Дирихле
- § 9. Сходимость ряда Фурье в данной точке
- § 10. Некоторые достаточные условия сходимости ряда Фурье
- § 11. Практический гармонический анализ
- § 12. Ряд Фурье в комплексной форме
- § 13. Интеграл Фурье
- § 14. Интеграл Фурье в комплексной форме
- § 15. Ряд Фурье по ортогональной системе функций
- § 16. Понятие о линейном функциональном пространстве. Аналогия между разложением функций в ряд Фурье и разложением векторов
- Упражнения к главе XVII
- ГЛАВА XVIII. УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ
- § 1. Основные типы уравнений математической физики
- § 2. Вывод уравнения колебаний струны. Формулировка краевой задачи. Вывод уравнений электрических колебаний в проводах
- § 3. Решение уравнения колебаний струны методом разделения переменных (методом Фурье)
- § 4. Уравнение распространения тепла в стержне. Формулировка краевой задачи
- § 5. Распространение тепла в пространстве
- § 6. Решение первой краевой задачи для уравнения теплопроводности методом конечных разностей
- § 7. Распространение тепла в неограниченном стержне
- § 8. Задачи, приводящие к исследованию решений уравнения Лапласа. Формулировка краевых задач
- § 9. Уравнение Лапласа в цилиндрических координатах. Решение задачи Дирихле для кольца с постоянными значениями искомой функции на внутренней и внешней окружностях
- § 10. Решение задачи Дирихле для круга
- § 11. Решение задачи Дирихле методом конечных разностей
- Упражнения к главе XVIII
- ГЛАВА XIX. ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ И НЕКОТОРЫЕ ЕГО ПРИЛОЖЕНИЯ
- § 1. Начальная функция и ее изображение
- § 2. Изображение функций …
- § 3. Изображение функции с измененным масштабом независимой переменной. Изображение функций sin at, cos at
- § 4. Свойство линейности изображения
- § 5. Теорема смещения
- § 6. Изображение функций …
- § 7. Дифференцирование изображения
- § 8. Изображение производных
- § 9. Таблица некоторых изображений
- § 10. Вспомогательное уравнение для данного дифференциального уравнения
- § 11. Теорема разложения
- § 12. Примеры решения дифференциальных уравнений и систем дифференциальных уравнений операционным методом
- § 13. Теорема свертывания
- § 14. Дифференциальные уравнения механических колебаний. Дифференциальные уравнения теории электрических цепей
- § 15. Решение дифференциального уравнения колебаний
- § 16. Исследование свободных колебаний
- § 17. Исследование механических и электрических колебаний в случае периодической внешней силы
- § 18. Решение уравнения колебаний в случае резонанса
- § 19. Теорема запаздывания
- § 20. Дельта-функция и ее изображение
- Упражнения к главе XIX
- ГЛАВА XX. ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
- § 1. Случайное событие. Относительная частота случайного события. Вероятность события. Предмет теории вероятностей
- § 2. Классическое определение вероятности и непосредственный подсчет вероятностей
- § 3. Сложение вероятностей. Противоположные случайные события
- § 4. Умножение вероятностей независимых событий
- § 5. Зависимые события. Условная вероятность. Полная вероятность
- § 6. Вероятность гипотез. Формула Байеса
- § 7. Дискретная случайная величина. Закон распределения дискретной случайной величины
- § 8. Относительная частота и вероятность относительной частоты при повторных испытаниях
- § 9. Математическое ожидание дискретной случайной величины
- § 10. Дисперсия. Среднеквадратичное отклонение. Понятие о моментах
- § 11. Функции от случайных величин
- § 12. Непрерывная случайная величина. Плотность распределения непрерывной случайной величины. Вероятность попадания случайной величины в заданный интервал
- § 13. Функция распределения, или интегральный закон распределения. Закон равномерного распределения вероятностей
- § 14. Числовые характеристики непрерывной случайной величины
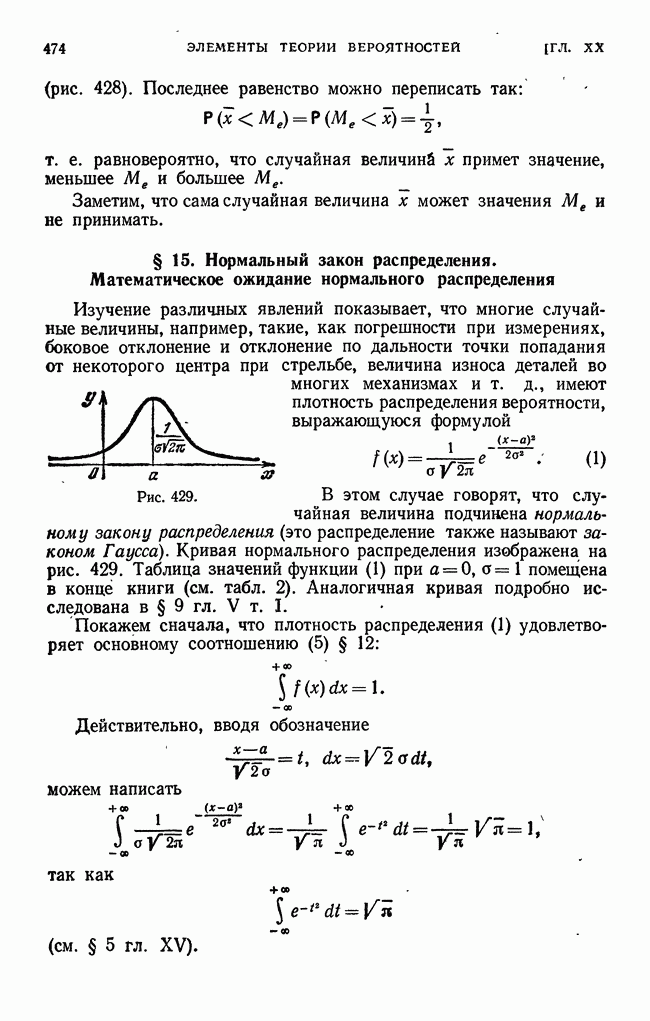
- § 15. Нормальный закон распределения. Математическое ожидание нормального распределения
- § 16. Дисперсия и среднеквадратичное отклонение случайной величины, подчиненной нормальному закону распределения
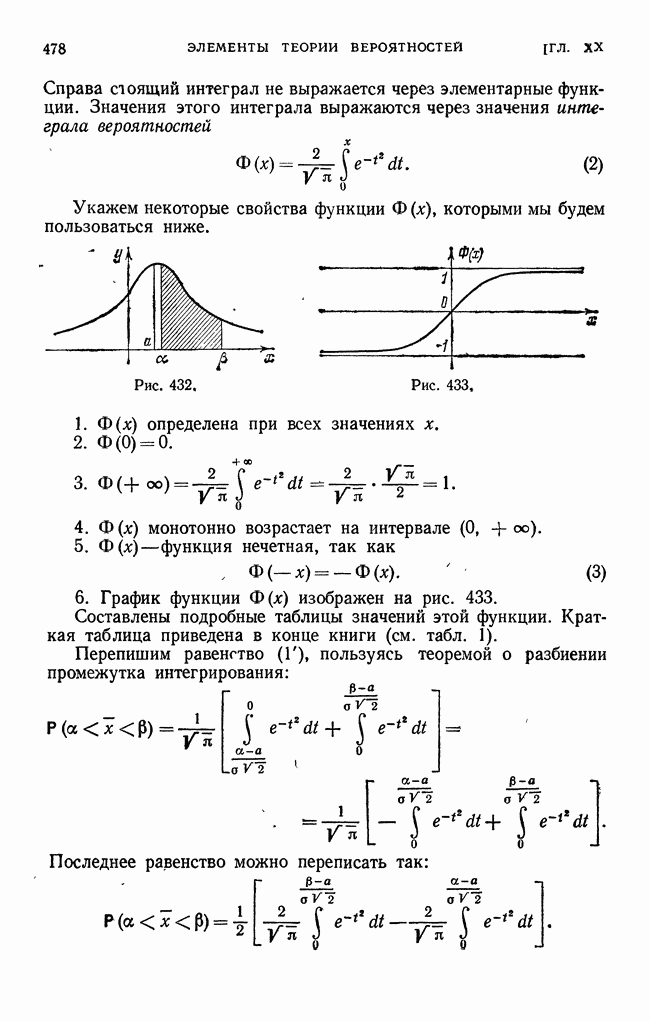
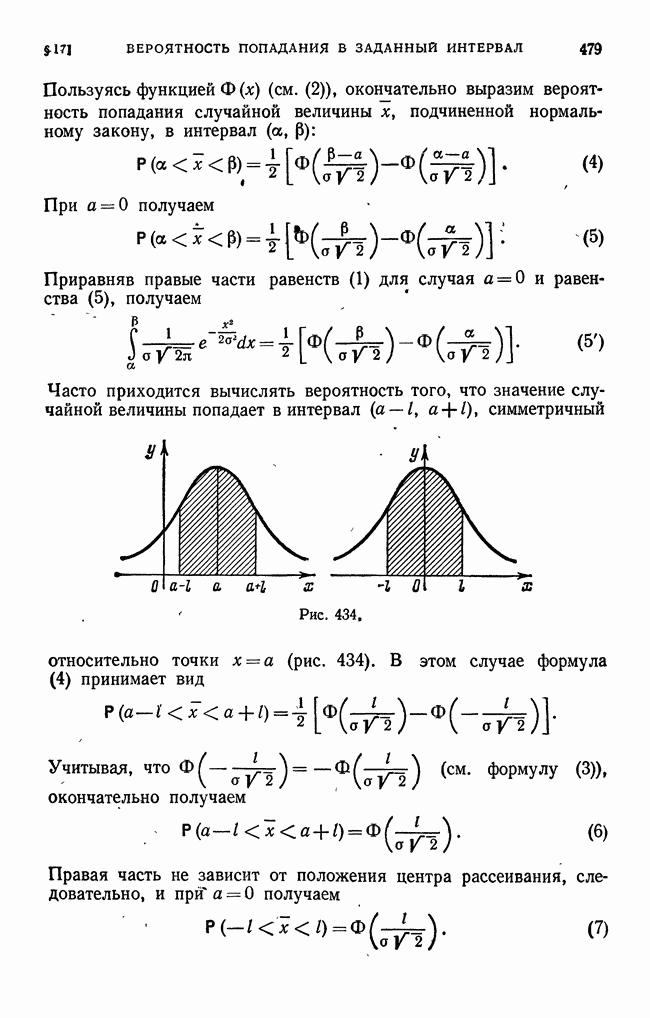
- § 17. Вероятность попадания значения случайной величины в заданный интервал. Функция Лапласа. Интегральная функция распределения для нормального закона
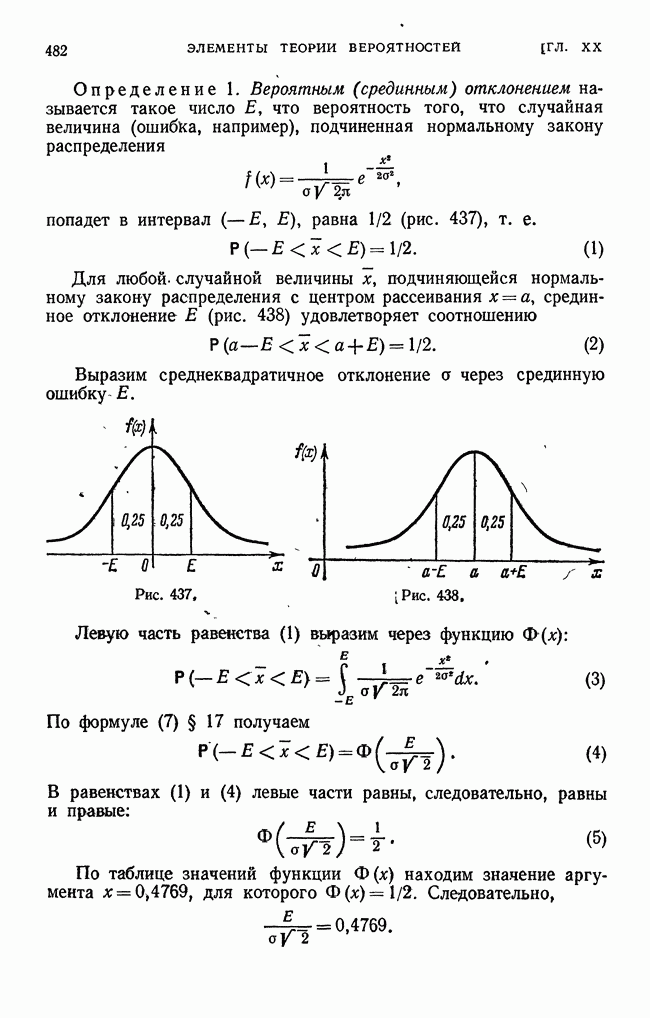
- § 18. Вероятное (срединное) отклонение или срединная ошибка
- § 19. Выражение нормального закона распределения через срединное отклонение. Приведенная функция Лапласа
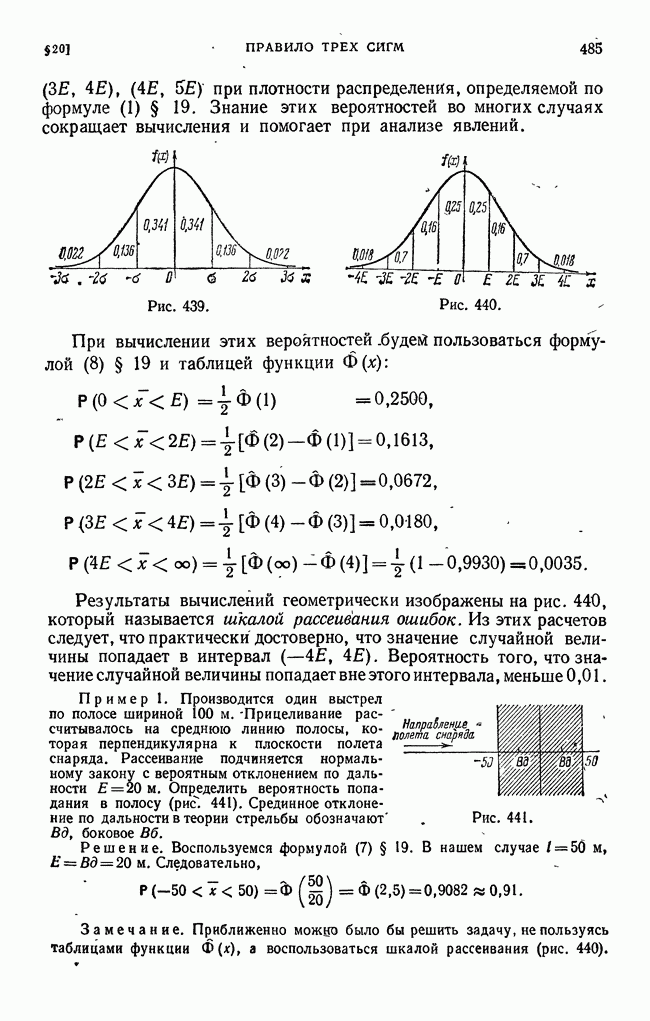
- § 20. Правило трех сигм. Шкала вероятностей распределения ошибок
- § 21. Среднеарифметическая ошибка
- § 22. Мера точности. Соотношение между характеристиками распределения ошибок
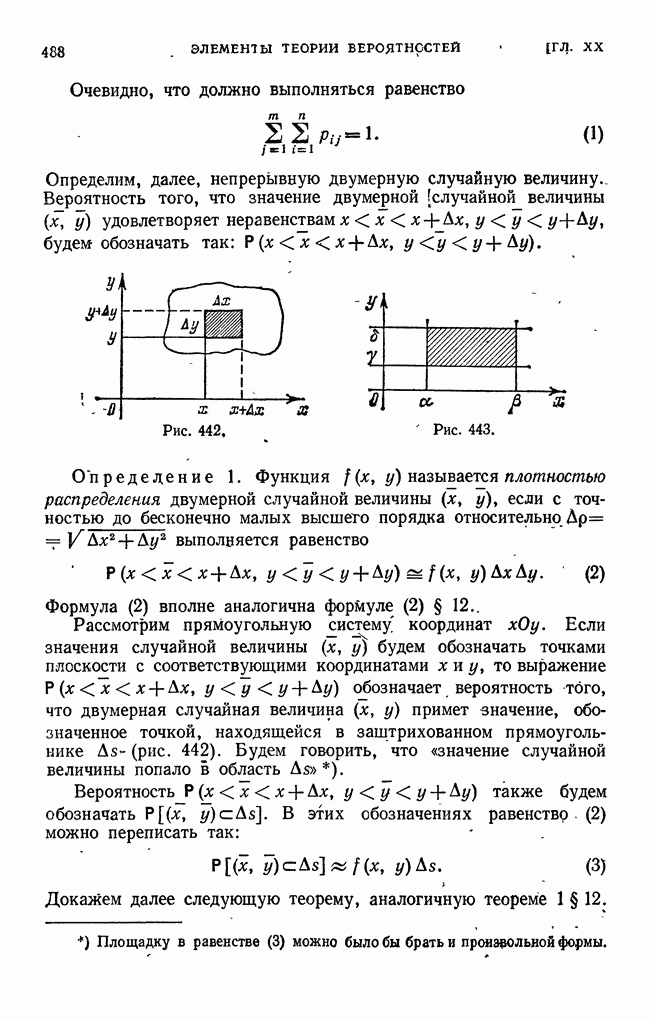
- § 23. Двумерная случайная величина
- § 24. Нормальный закон распределения на плоскости
- § 25. Вероятность попадания двумерной случайной величины в прямоугольник со сторонами, параллельными главным осям рассеивания, при нормальном законе распределения
- § 26. Вероятность попадания двумерной случайной величины в эллипс рассеивания
- § 27. Задачи математической статистики. Статистический материал
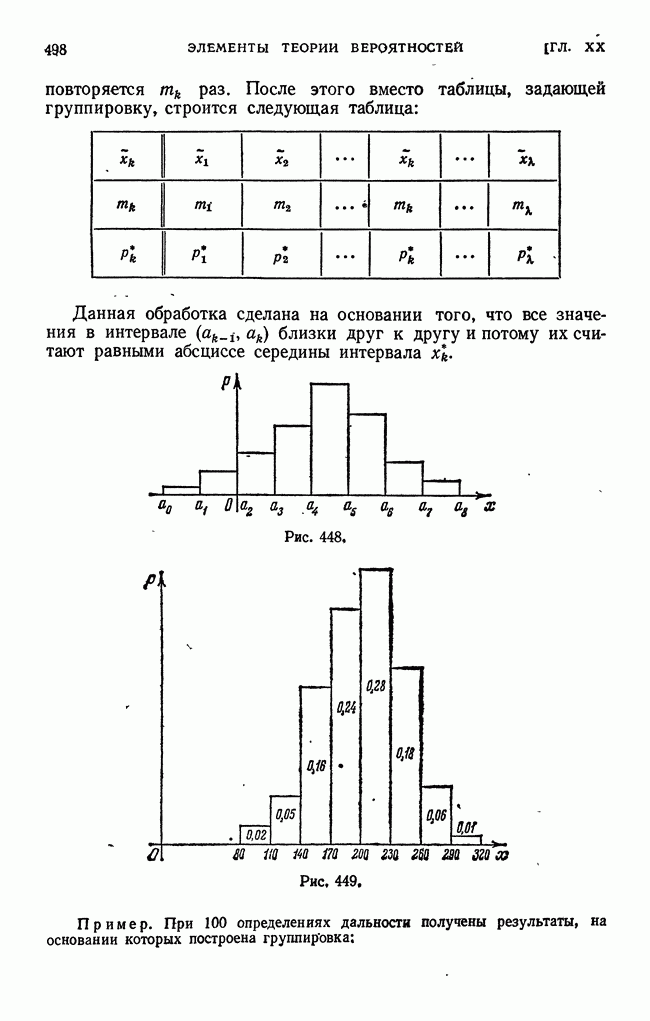
- § 28. Статистический ряд. Гистограмма
- § 29. Определение подходящего значения измеряемой величины
- § 30. Определение параметров закона распределения. Теорема Ляпунова. Теорема Лапласа
- Упражнения к главе XX
- ГЛАВА XXI. МАТРИЦЫ. МАТРИЧНАЯ ЗАПИСЬ СИСТЕМ И РЕШЕНИЙ СИСТЕМ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
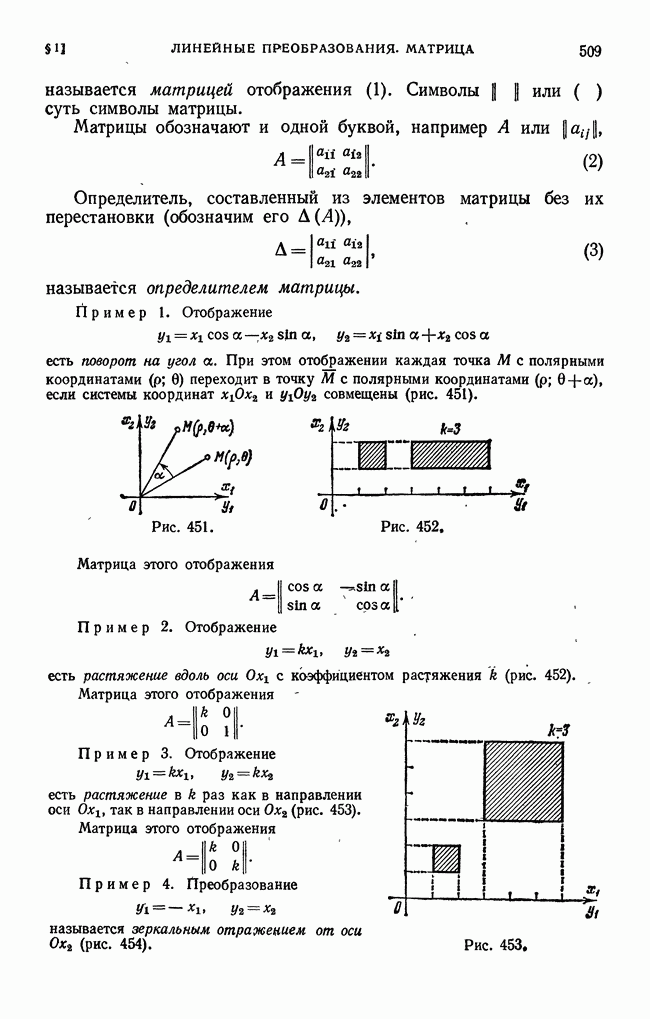
- § 1. Линейные преобразования. Матрица
- § 2. Общие определения, связанные с понятием матрицы
- § 3. Обратное преобразование
- § 4. Действия над матрицами. Сложение матриц
- § 5. Преобразование вектора в другой вектор с помощью матрицы
- § 6. Обратная матрица
- § 7. Нахождение матрицы, обратной данной
- § 8. Матричная запись системы линейных уравнений
- § 9. Решение системы линейных уравнений матричным методом
- § 10. Ортогональные отображения. Ортогональные матрицы
- § 11. Собственный вектор линейного преобразования
- § 12. Матрица линейного преобразования, при котором базисные векторы являются собственными векторами
- § 13. Преобразование матрицы линейного преобразования при переходе от одного базиса к другому
- § 14. Квадратичные формы и их преобразования
- § 15. Ранг матрицы. Существование решений системы линейных уравнений
- § 16. Дифференцирование и интегрирование матриц
- § 17. Матричная запись системы дифференциальных уравнений и решений системы дифференциальных уравнений с постоянными коэффициентами
- § 18. Матричная запись линейного уравнения n-го порядка
- § 19. Решение систем линейных дифференциальных уравнений с переменными коэффициентами методом последовательных приближений с использованием матричной записи
- Упражнения к главе XXI
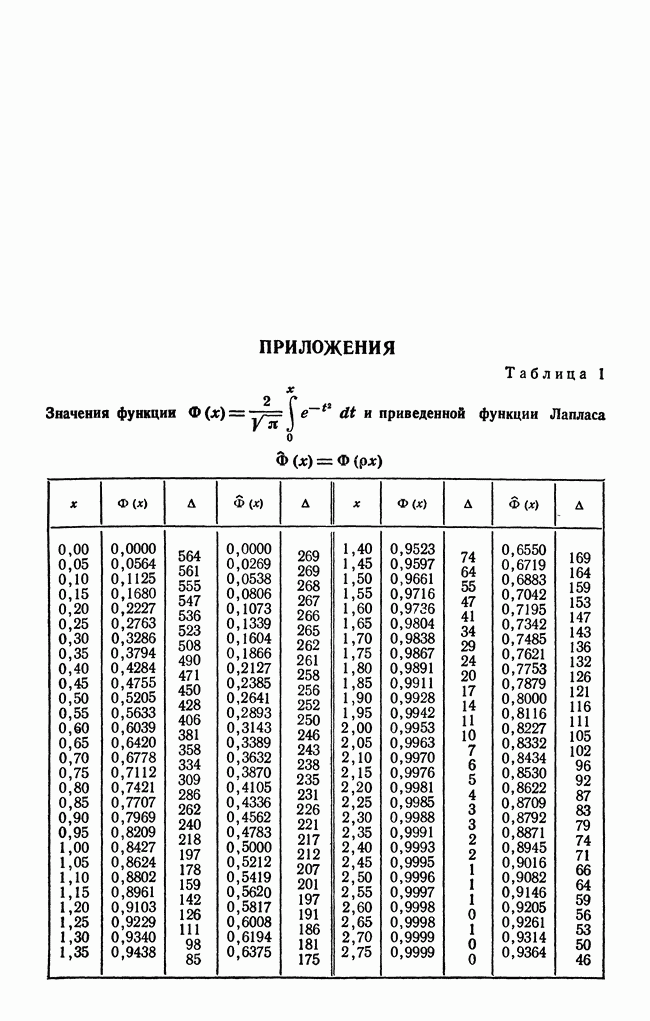
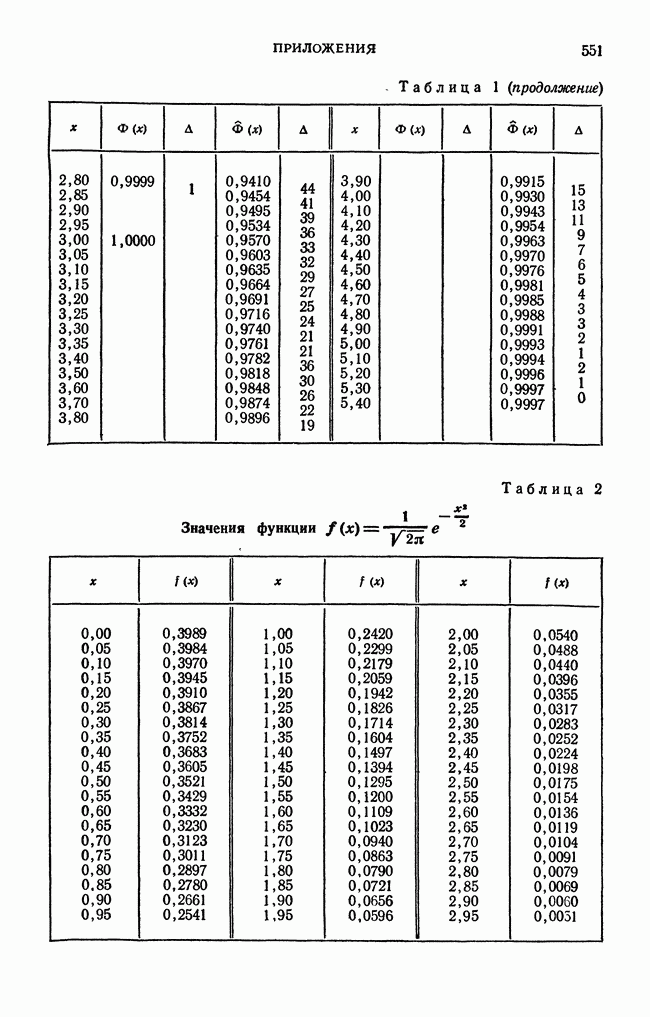
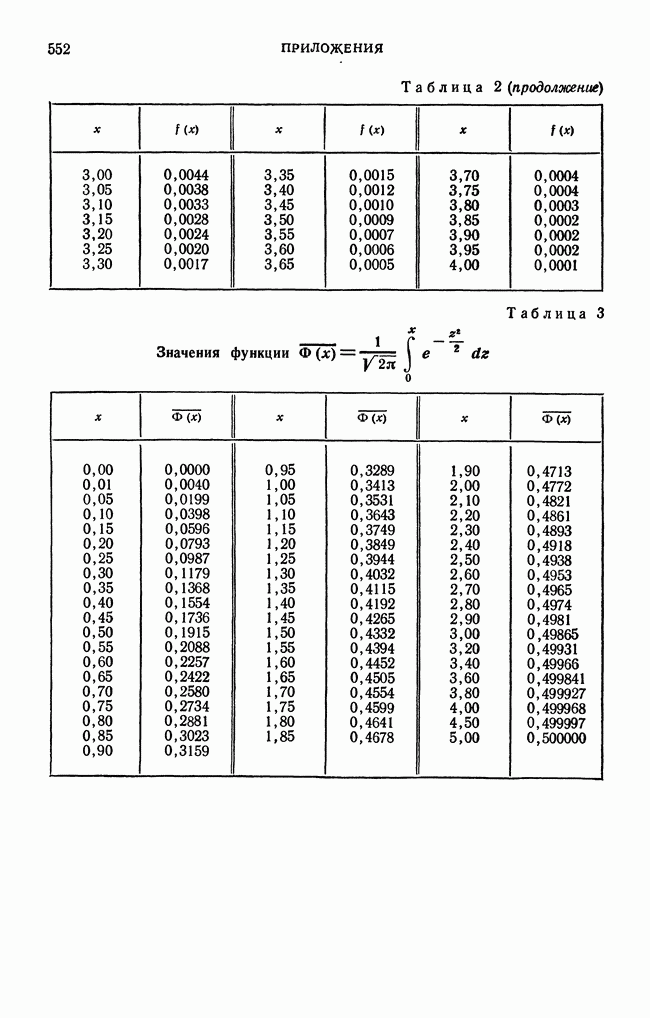
- ПРИЛОЖЕНИЯ