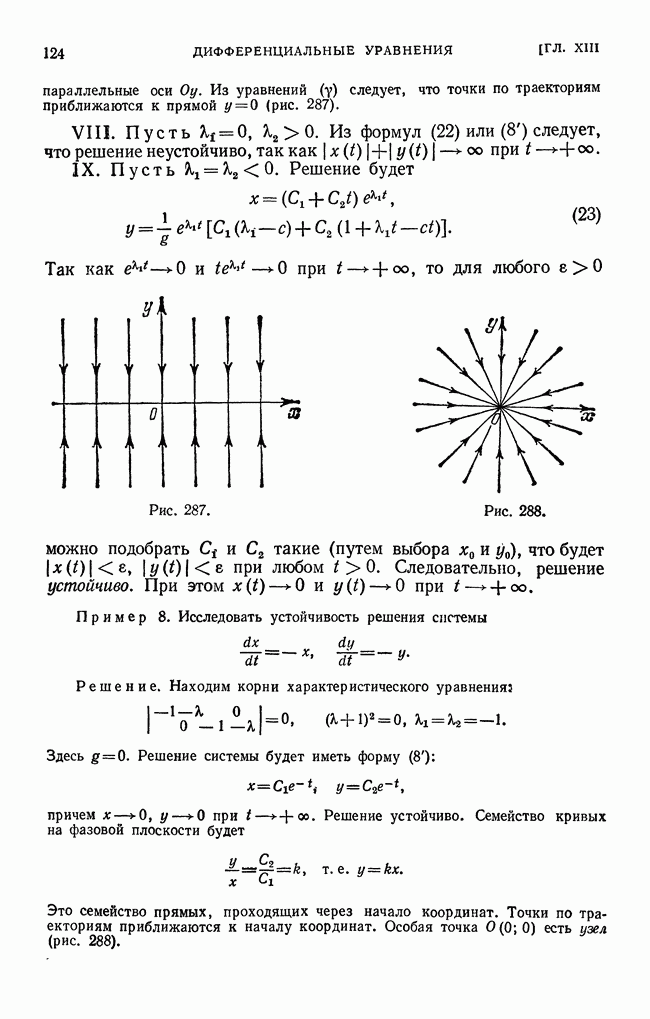
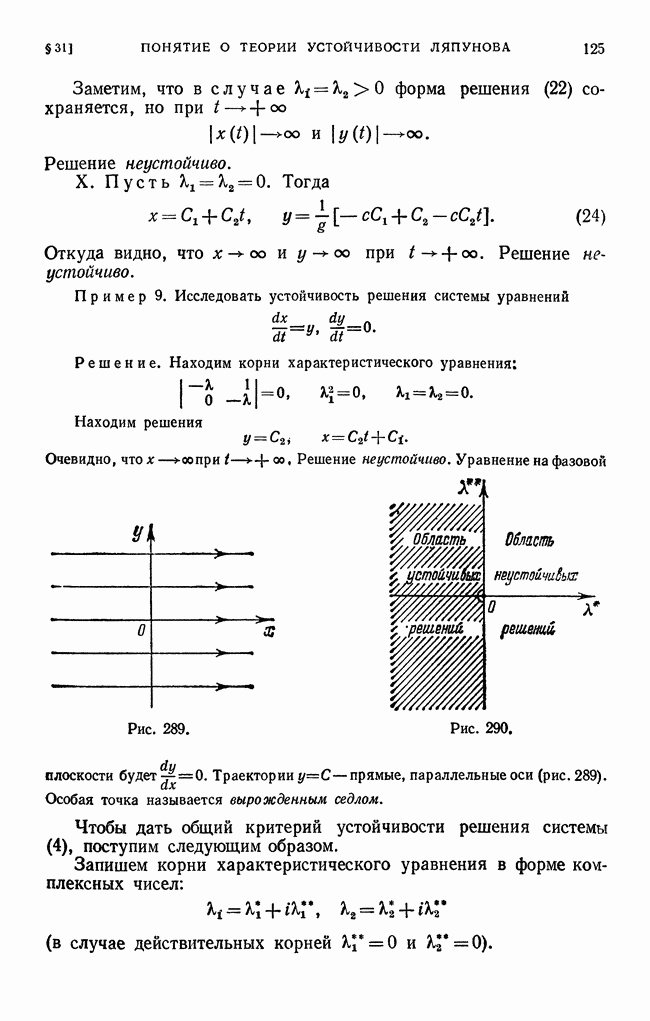
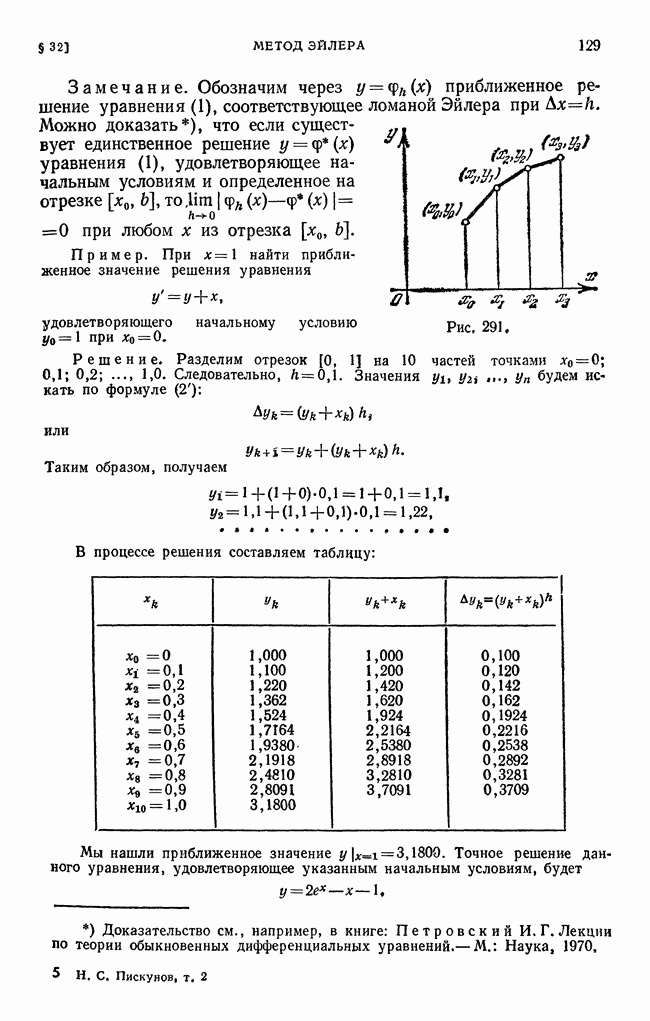
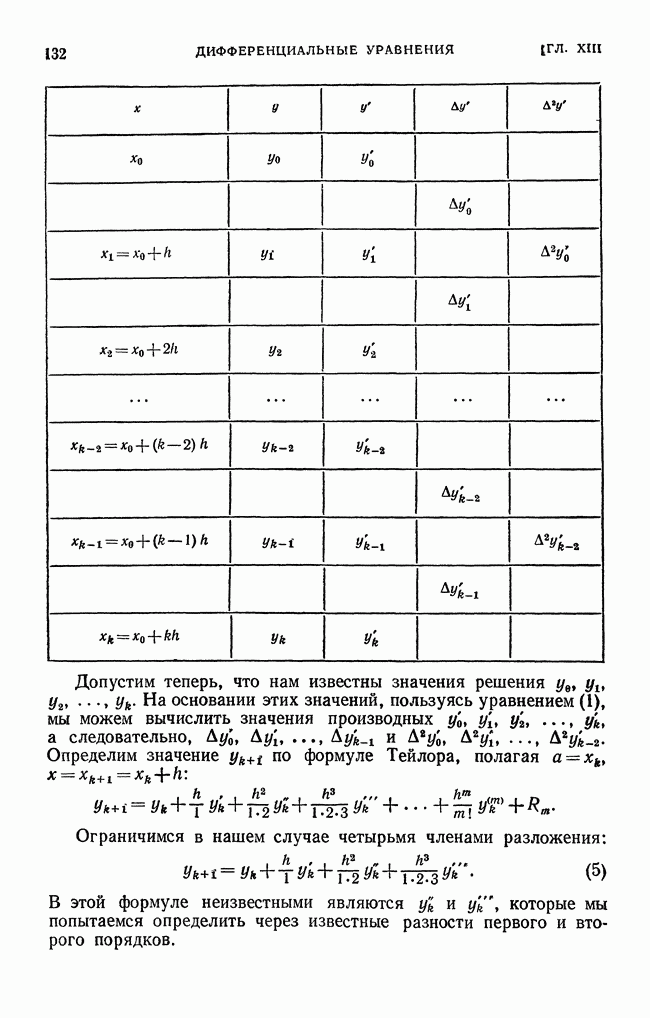
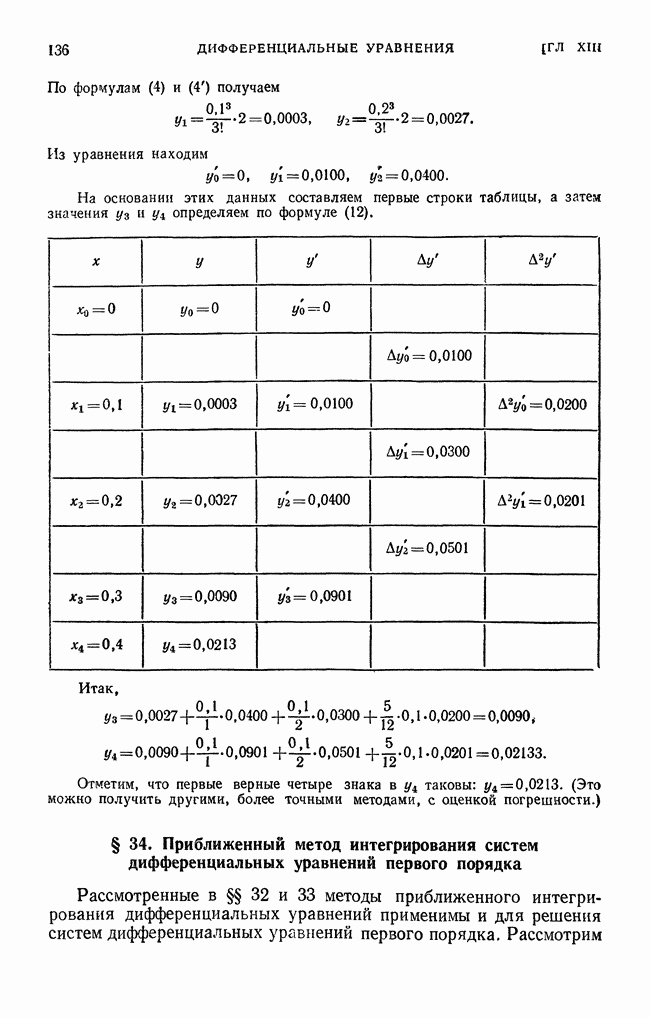
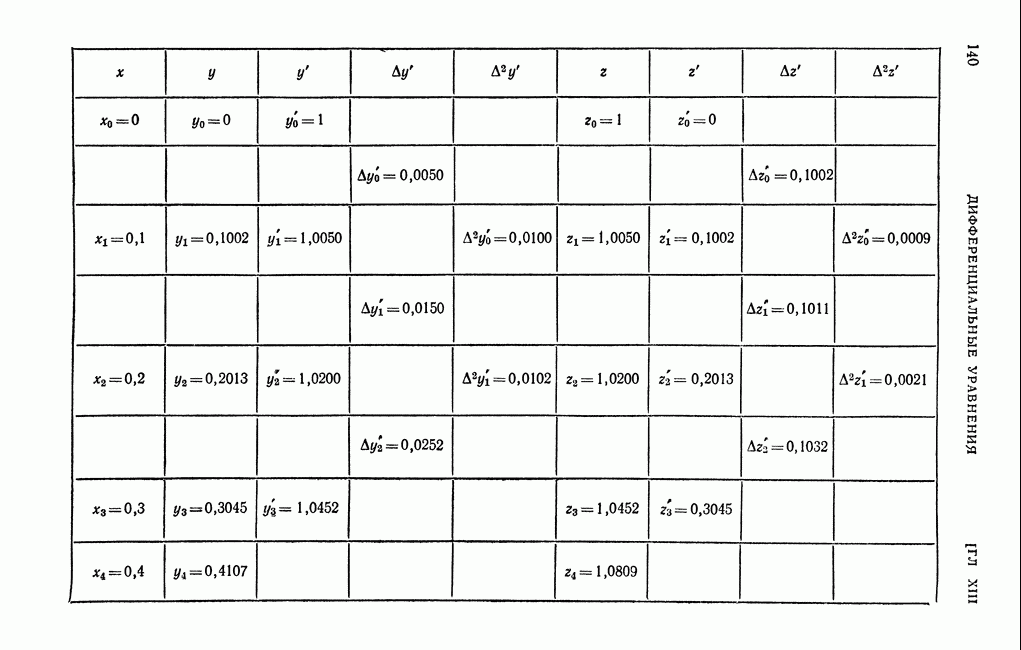
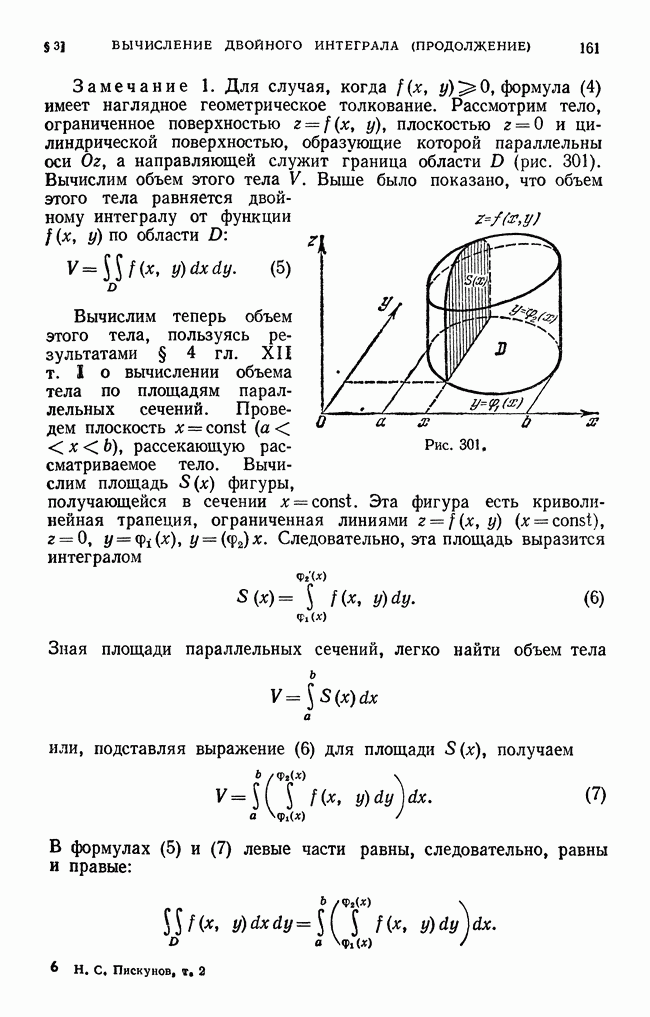
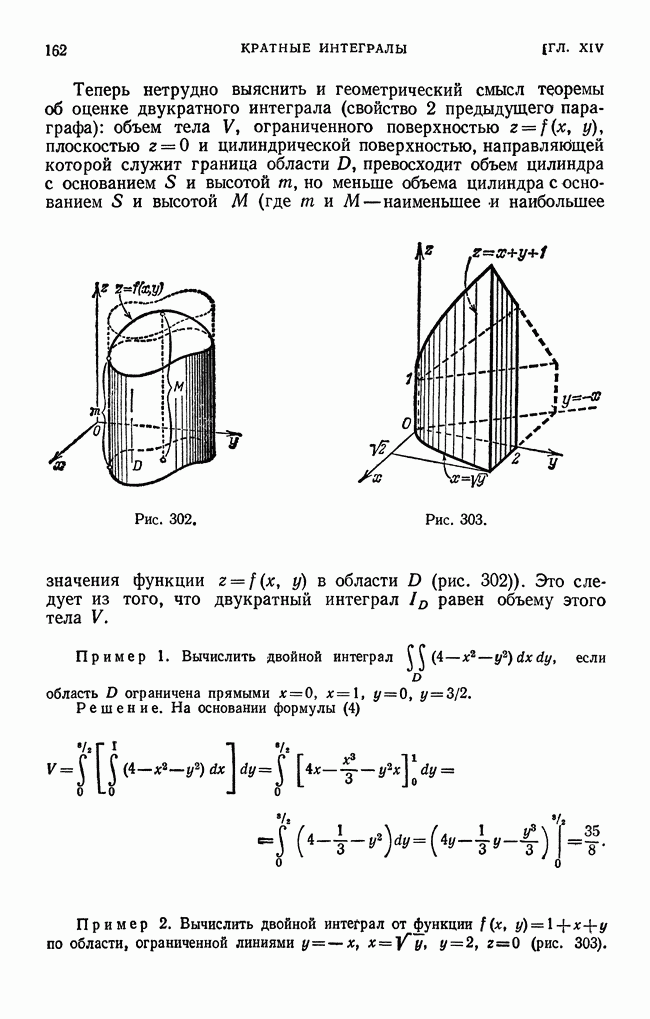
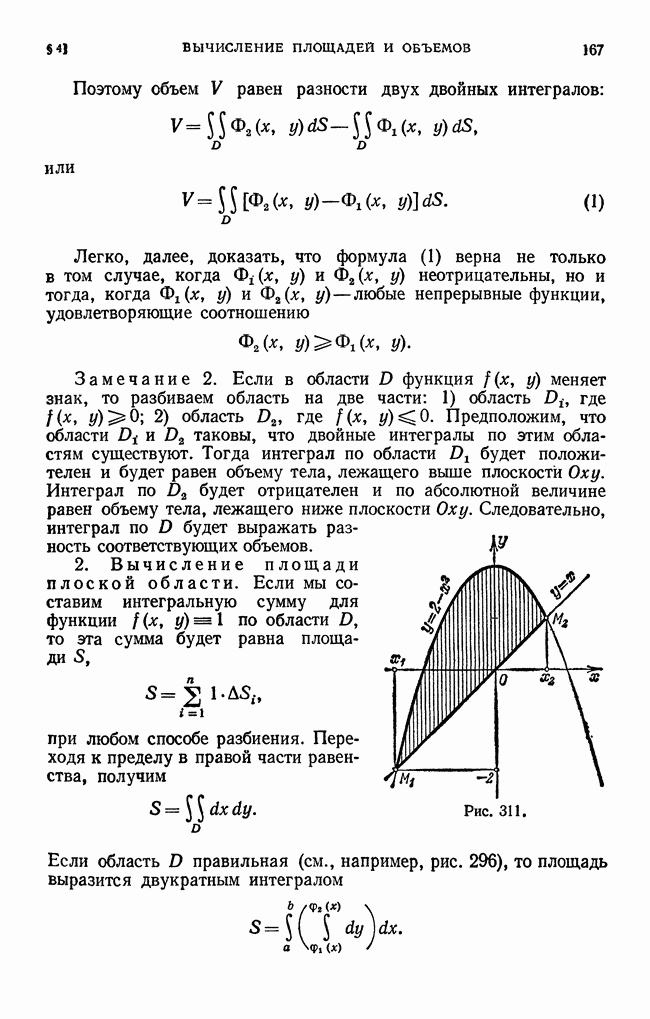
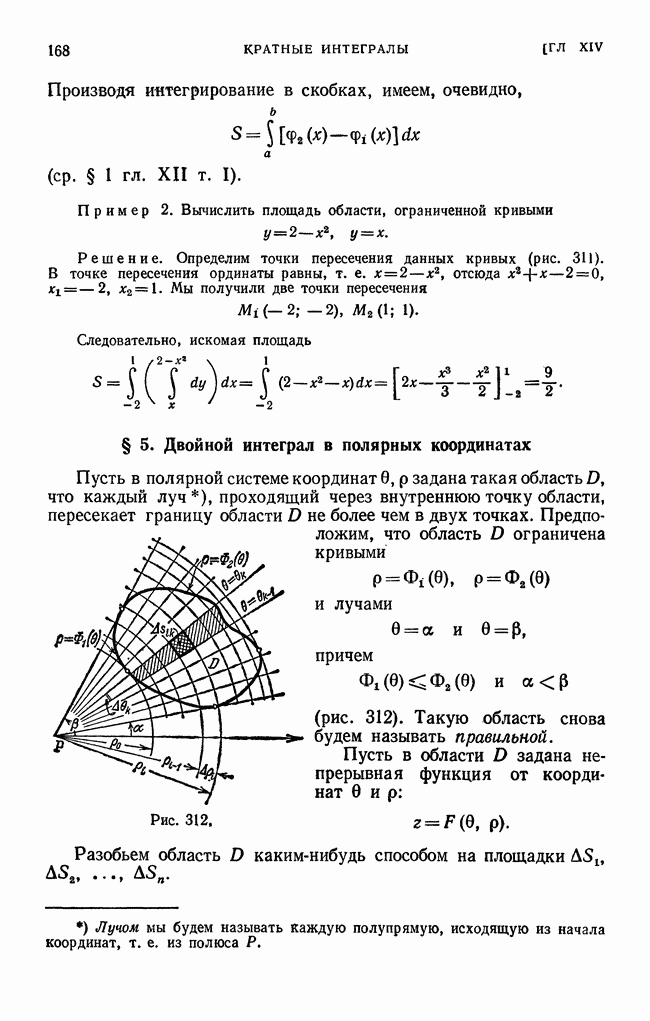
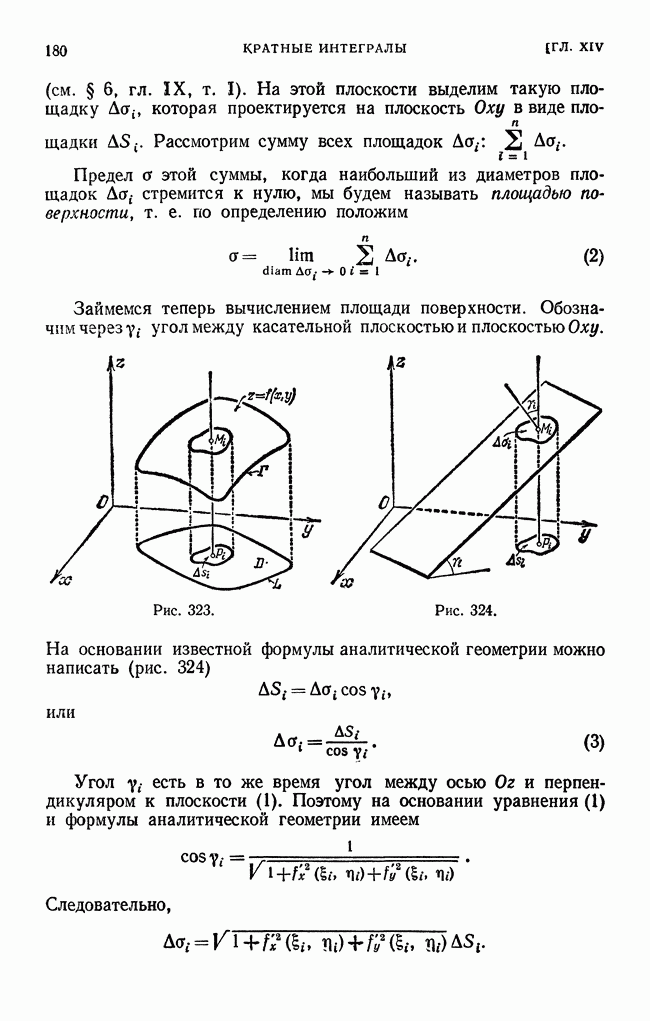
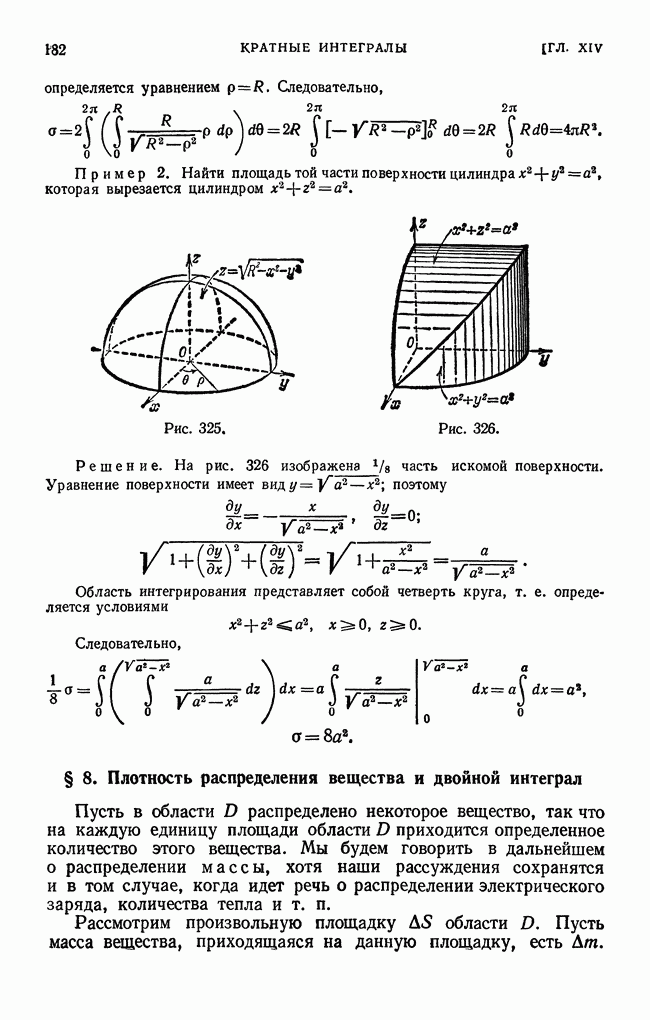
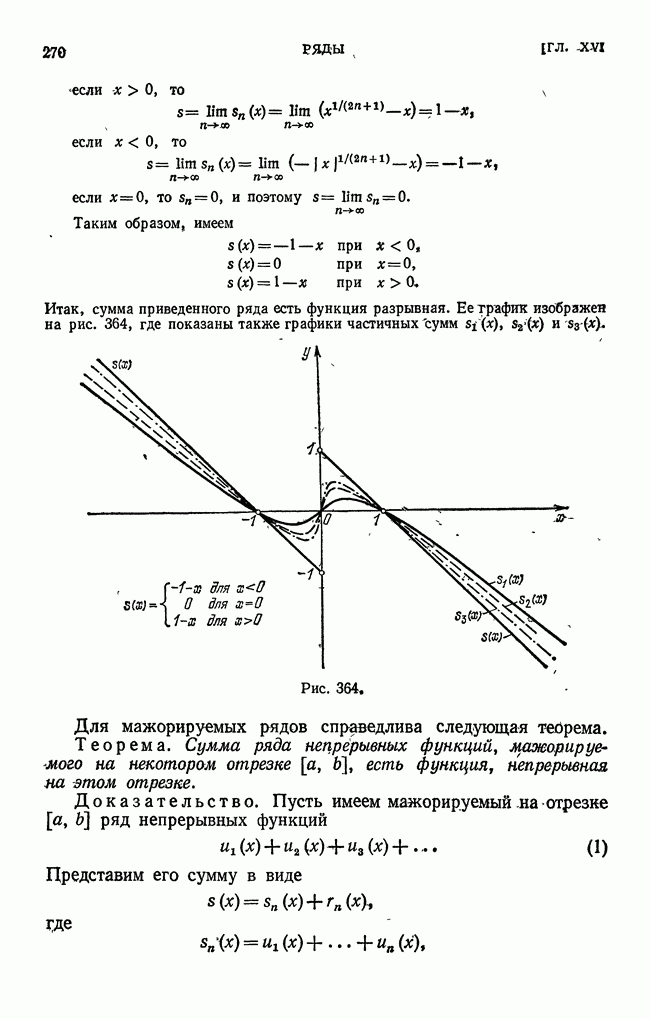
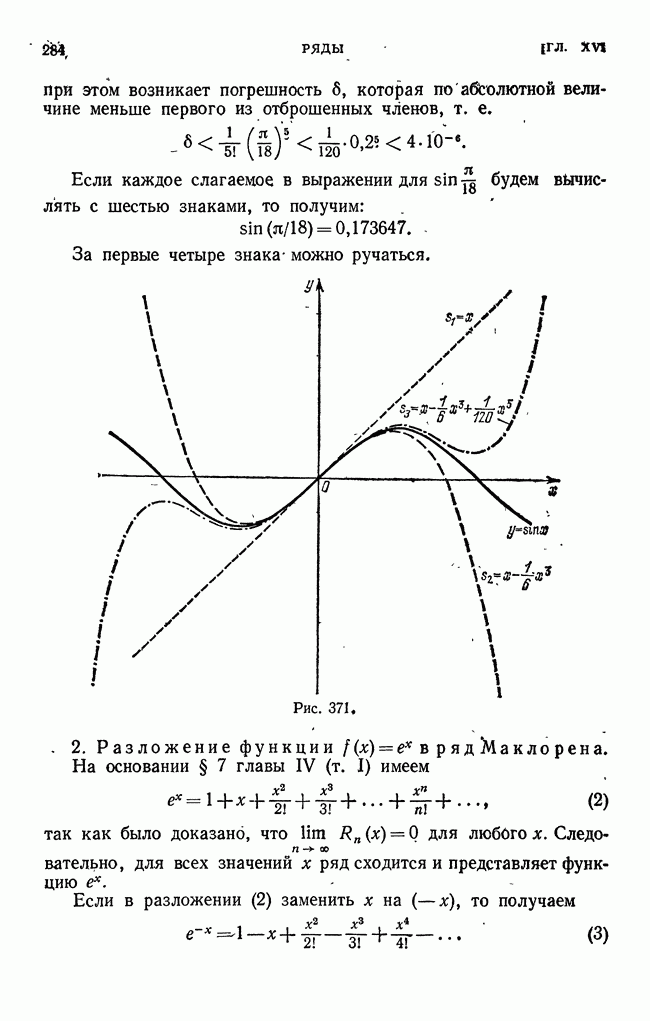
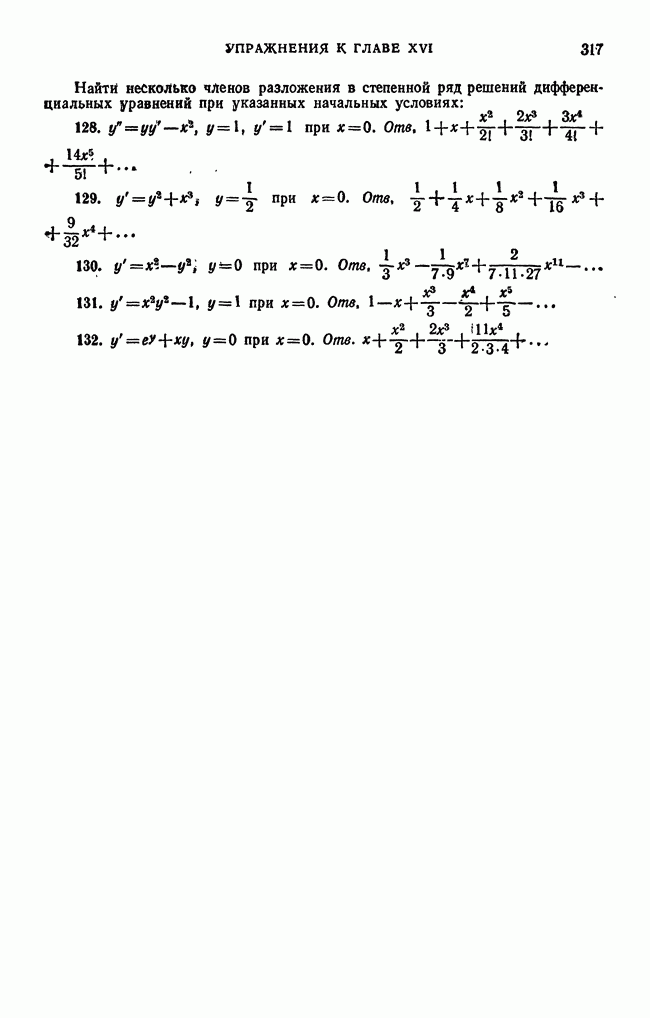| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 4. Признак Даламбера
Теорема (признак Даламбера). Если в ряде с положительными членами

отношение  члена к
члена к  при
при  имеет (конечный) предел I, т. е.
имеет (конечный) предел I, т. е. 

то:
1) ряд сходится в случае 
2) ряд расходится в случае 
(случае  ответа на вопрос о сходимости или расходимости ряда теорема не дает.)
ответа на вопрос о сходимости или расходимости ряда теорема не дает.)
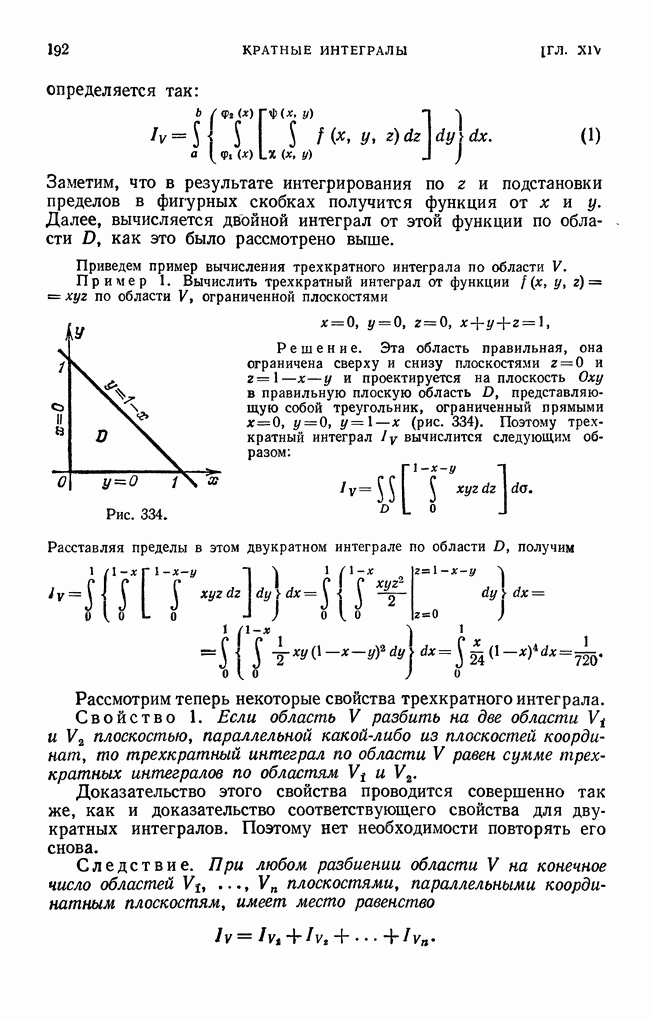
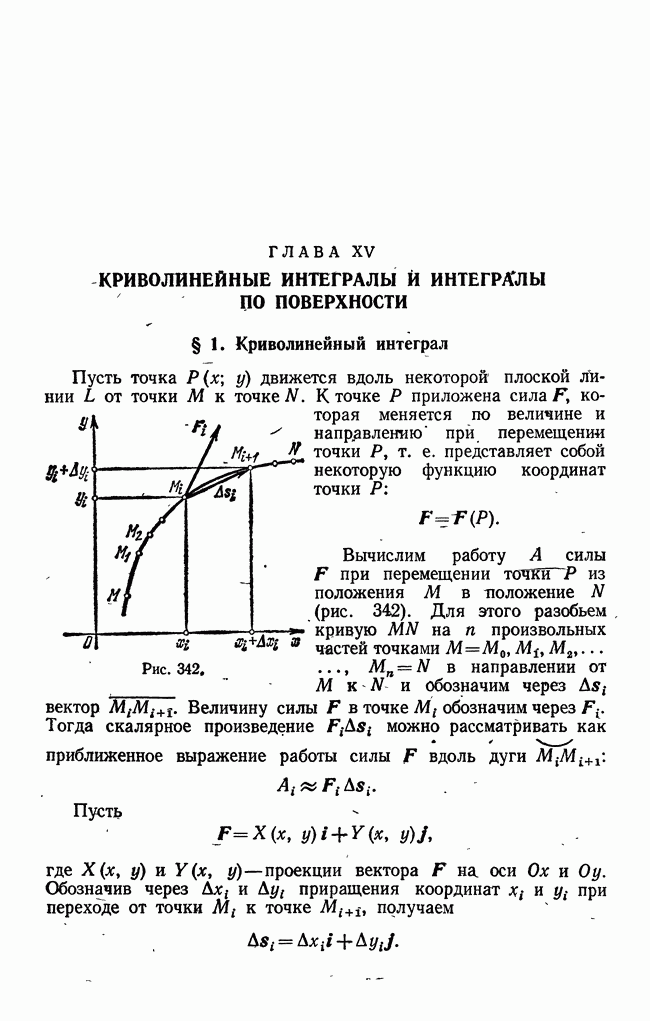
Доказательство. 1) Пусть К 1. Рассмотрим число q, удовлетворяющее соотношению  (рис. 358).
(рис. 358).
Из определения предела и соотношения (2) следует, что для всех значений  , начиная с некоторого номера N, т. е. для
, начиная с некоторого номера N, т. е. для  будет иметь место неравенство
будет иметь место неравенство

Действительно, так как величина стремится к пределу  , то разность между величиной ±1 и числом I может быть сделана (начиная с некоторого номера N) по абсолютному значению меньше любого положительного числа, в частности, меньше
, то разность между величиной ±1 и числом I может быть сделана (начиная с некоторого номера N) по абсолютному значению меньше любого положительного числа, в частности, меньше  , т. е.
, т. е.


Рис. 358.
Из последнего неравенства и следует неравенство (2). Записывая неравенство (2) для различных значений  , начиная с номера N, получим
, начиная с номера N, получим

Рассмотрим теперь два ряда

Ряд (1) есть геометрическая прогрессия с положительным знаменателем  Следовательно, этот ряд сходится. Члены ряда (1), начиная с
Следовательно, этот ряд сходится. Члены ряда (1), начиная с  меньше членов ряда
меньше членов ряда  . На основании теоремы 1 § 3 и теоремы 1 § 1 следует, что ряд (1) сходится.
. На основании теоремы 1 § 3 и теоремы 1 § 1 следует, что ряд (1) сходится.
2) Пусть  Тогда из равенства
Тогда из равенства  (где
(где  ) следует, что, начиная с некоторого номера N, т. е. для
) следует, что, начиная с некоторого номера N, т. е. для  будет имет место неравенство
будет имет место неравенство

(рис. 359), или  для всех
для всех  Но это означает, что члены ряда возрастают, начиная с номера
Но это означает, что члены ряда возрастают, начиная с номера  и поэтому общий член ряда не стремится к нулю. Следовательно, ряд расходится.
и поэтому общий член ряда не стремится к нулю. Следовательно, ряд расходится.

Рис. 359.
Замечание 1. Ряд будет расходиться и в том случае, когда  . Это следует из того, что если
. Это следует из того, что если  , то, начиная с некоторого номера
, то, начиная с некоторого номера  будет иметь место неравенство
будет иметь место неравенство
Пример 1. Исследовать сходимость ряда

Решение. Здесь

Следовательно,

Ряд сходится.
Пример 2. Исследовать сходимость ряда

Решение. Здесь

Ряд расходится, причем его общий член  стремится к бесконечности.
стремится к бесконечности.
Замечание 2. Признак Даламбера дает ответ на вопрос о том, сходится ли данный положительный ряд, только в том случае, когда  существует и отличен от 1. Если же этот предел не существует или существует, но
существует и отличен от 1. Если же этот предел не существует или существует, но  то признак Даламбера не дает возможности установить, сходится ряд или расходится, так как в этом случае ряд может оказаться и сходящимся и расходящимся. Для решения вопроса о сходимости таких рядов надо применить какой-либо другой признак.
то признак Даламбера не дает возможности установить, сходится ряд или расходится, так как в этом случае ряд может оказаться и сходящимся и расходящимся. Для решения вопроса о сходимости таких рядов надо применить какой-либо другой признак.
Замечание 3. Если  но отношение для всех номеров
но отношение для всех номеров  начиная с некоторого, больше единицы, то ряд
начиная с некоторого, больше единицы, то ряд
расходится. Это следует из того, что если  то
то  и общий член не стремится к нулю при
и общий член не стремится к нулю при 
Рассмотрим примеры, иллюстрирующие сказанное.
Пример 3. Исследовать сходимость ряда

Решение. Здесь

В данном случае ряд расходится так как  для всех
для всех 

Пример 4. Применяя признак Даламбера к гармоническому ряду  что
что  и, следовательно,
и, следовательно,  . Значит, на основании признака Даламбера
. Значит, на основании признака Даламбера

нельзя установить сходимость или расходимость данного ряда. Но ранее мы установили другим путем, что гармонический ряд расходится.
Пример 5. Исследовать сходимость ряда

Решение. Здесь

На основании признака Даламбера сделать заключения о сходимости ряда нельзя, однако, исходя из других соображений, можно установить, что этот ряд сходится. Заметив, что  мы можем записать
мы можем записать  данный ряд в виде
данный ряд в виде

Частичная сумма  первых членов после раскрытия скобок и сокращения будет равна
первых членов после раскрытия скобок и сокращения будет равна

т. e. ряд сходится и его сумма равна 1.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ К ДЕВЯТОМУ ИЗДАНИЮ
- ПРЕДИСЛОВИЕ К ПЯТОМУ ИЗДАНИЮ
- ГЛАВА XIII. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
- § 1. Постановка задачи. Уравнение движения тела при сопротивлении среды, пропорциональном скорости. Уравнение цепной линии
- § 2. Определения
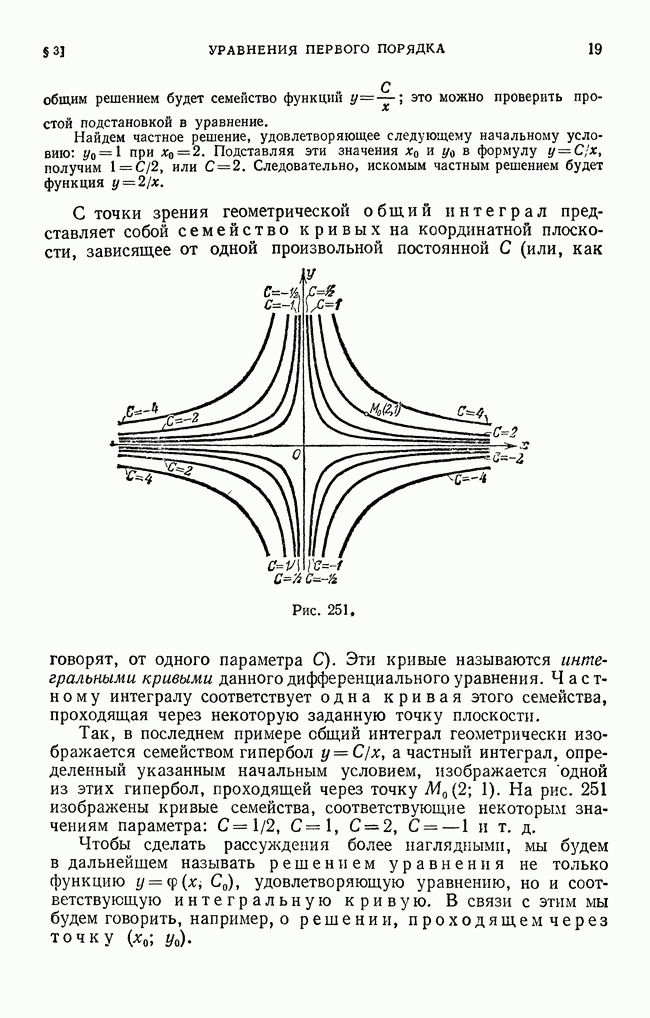
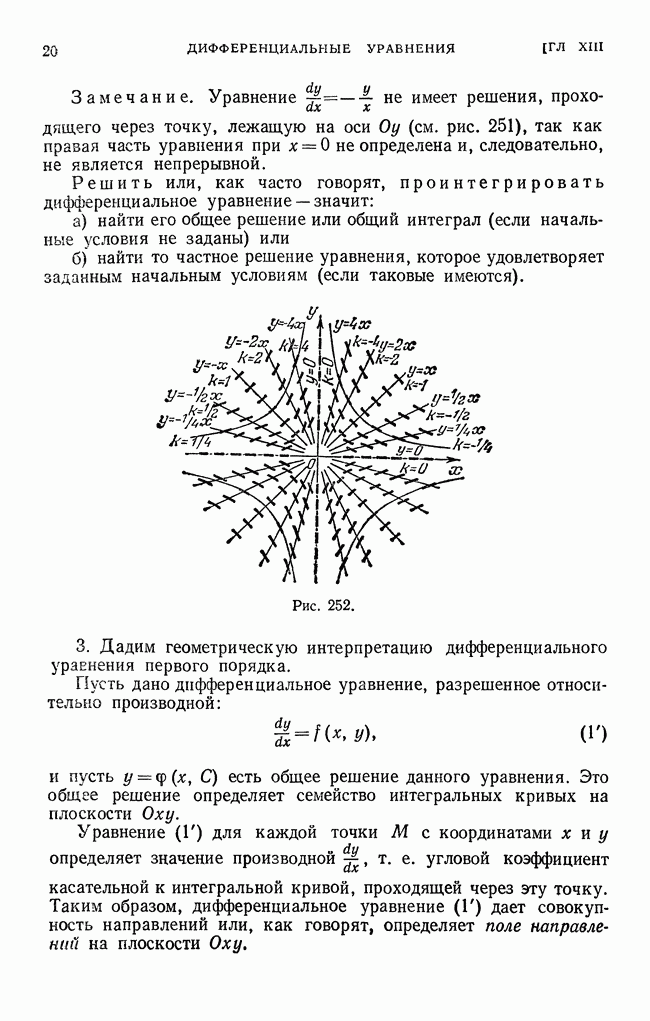
- § 3. Дифференциальные уравнения первого порядка (общие понятия)
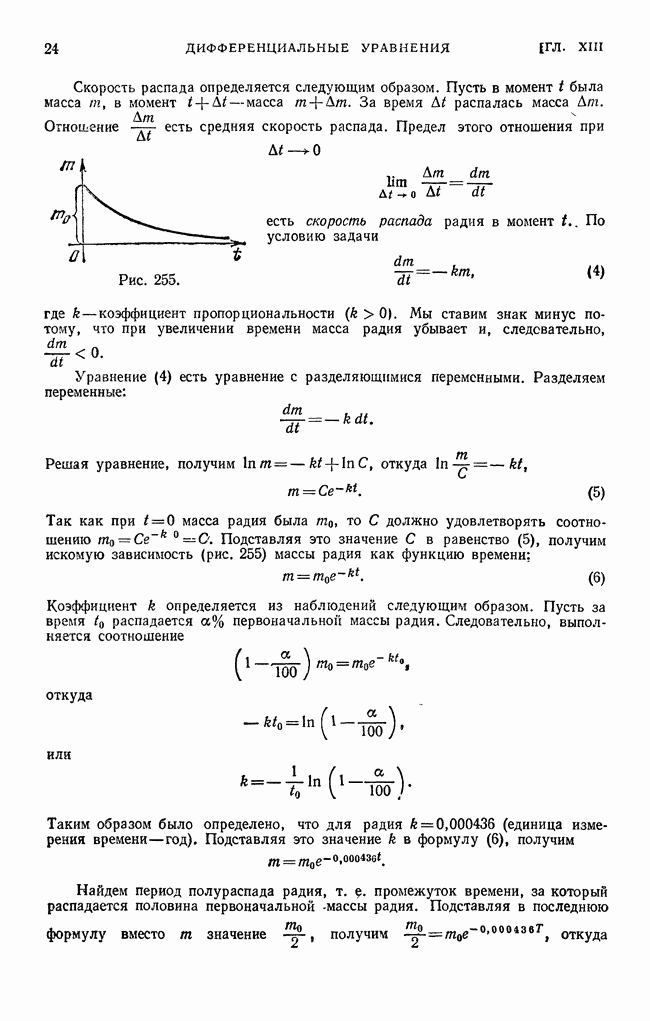
- § 4. Уравнения с разделенными и разделяющимися переменными. Задача о распаде радия
- § 5. Однородные уравнения первого порядка
- § 6. Уравнения, приводящиеся к однородным
- § 7. Линейные уравнения первого порядка
- § 8. Уравнение Бернулли
- § 9. Уравнение в полных дифференциалах
- § 10. Интегрирующий множитель
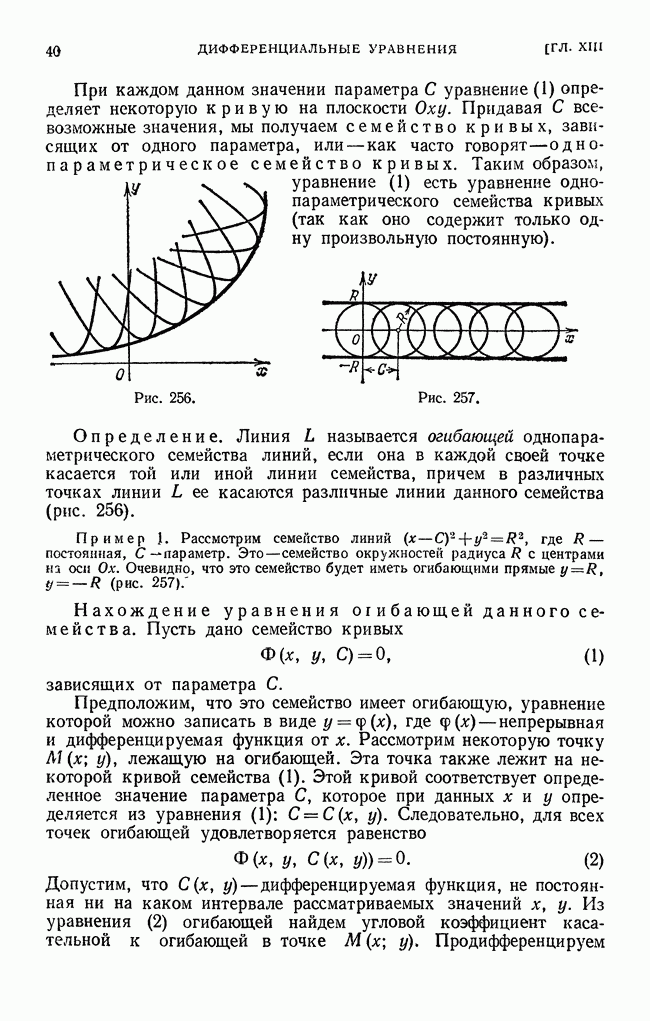
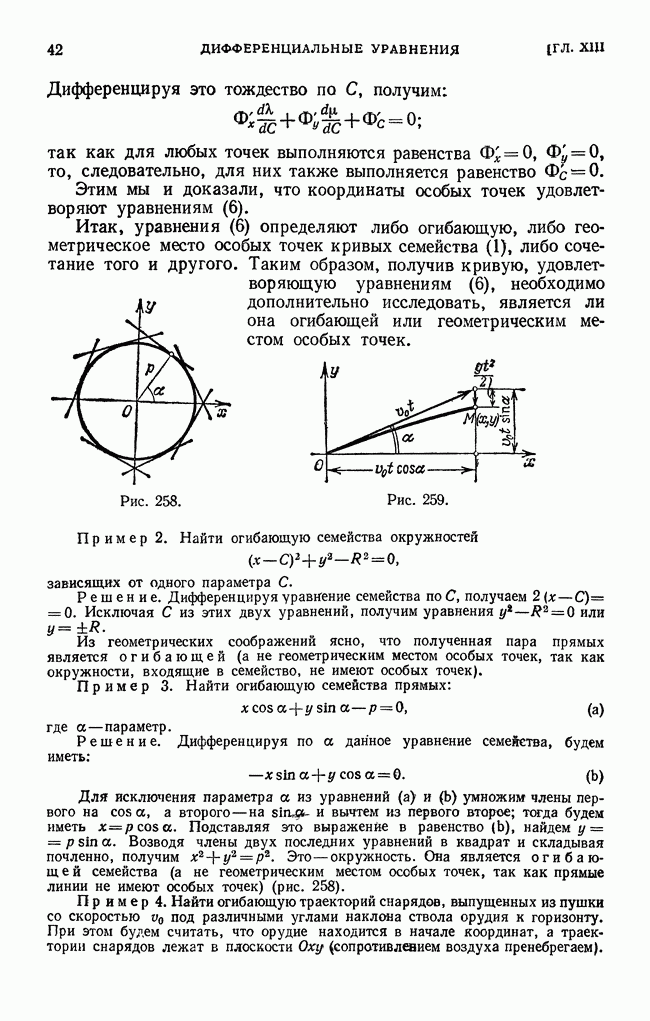
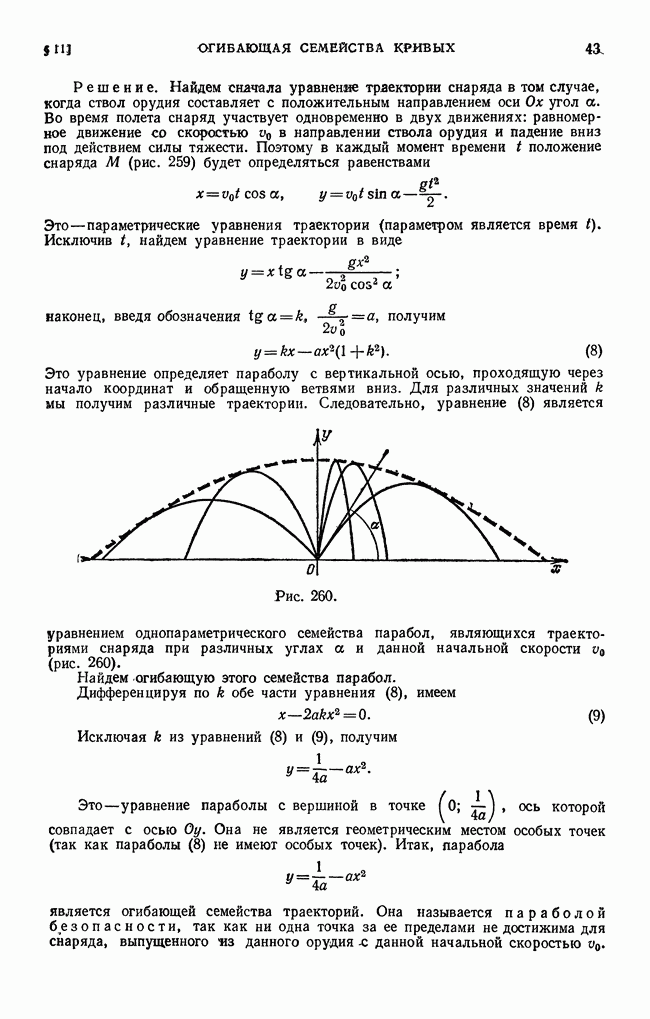
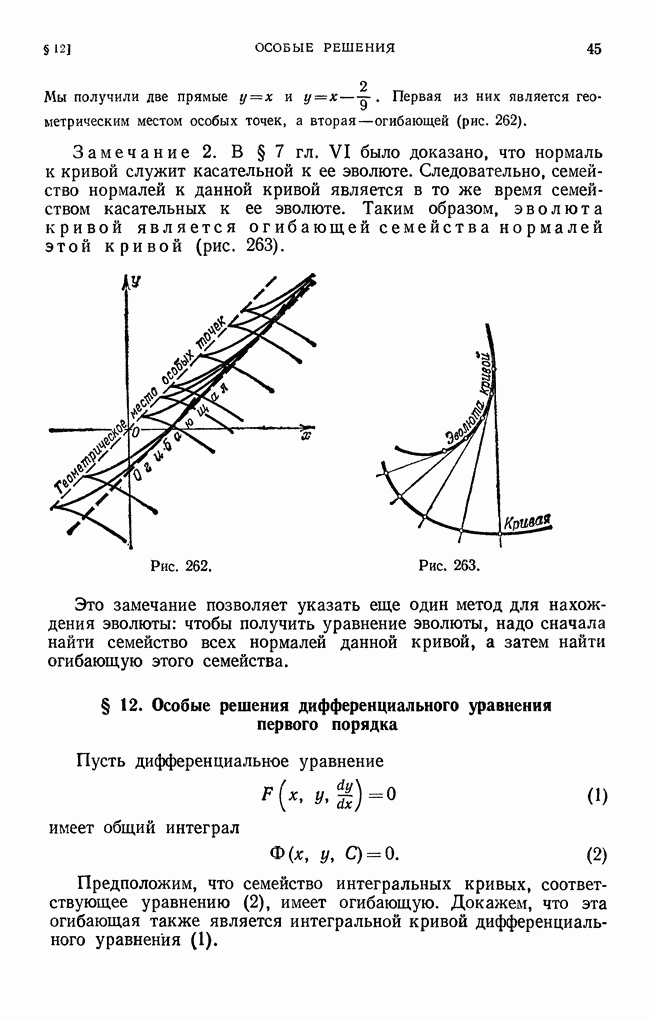
- § 11. Огибающая семейства кривых
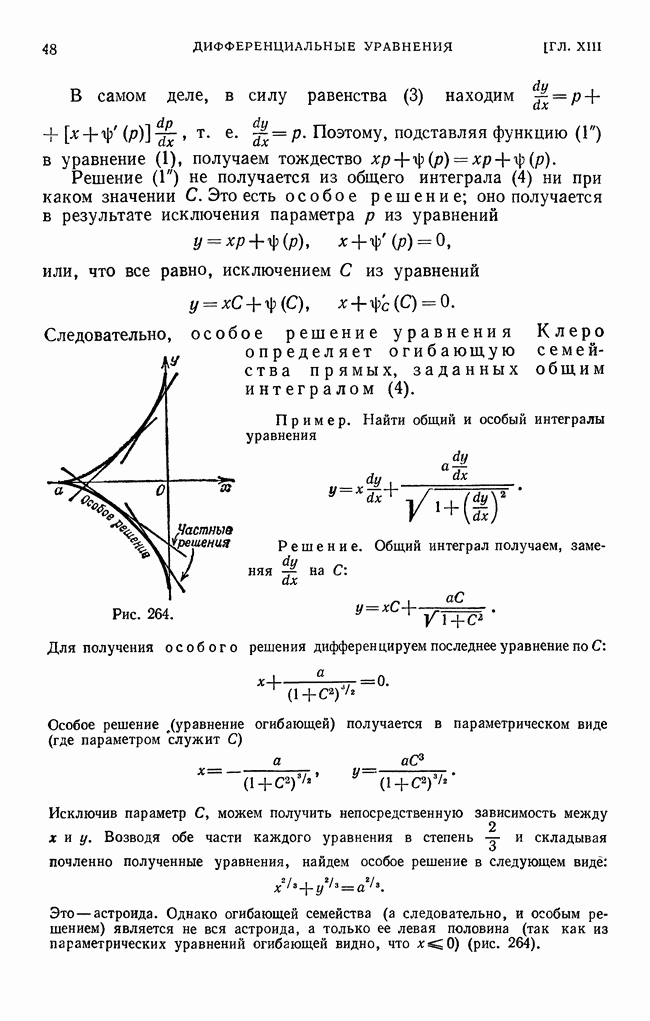
- § 12. Особые решения дифференциального уравнения первого порядка
- § 13. Уравнение Клеро
- § 14. Уравнение Лагранжа
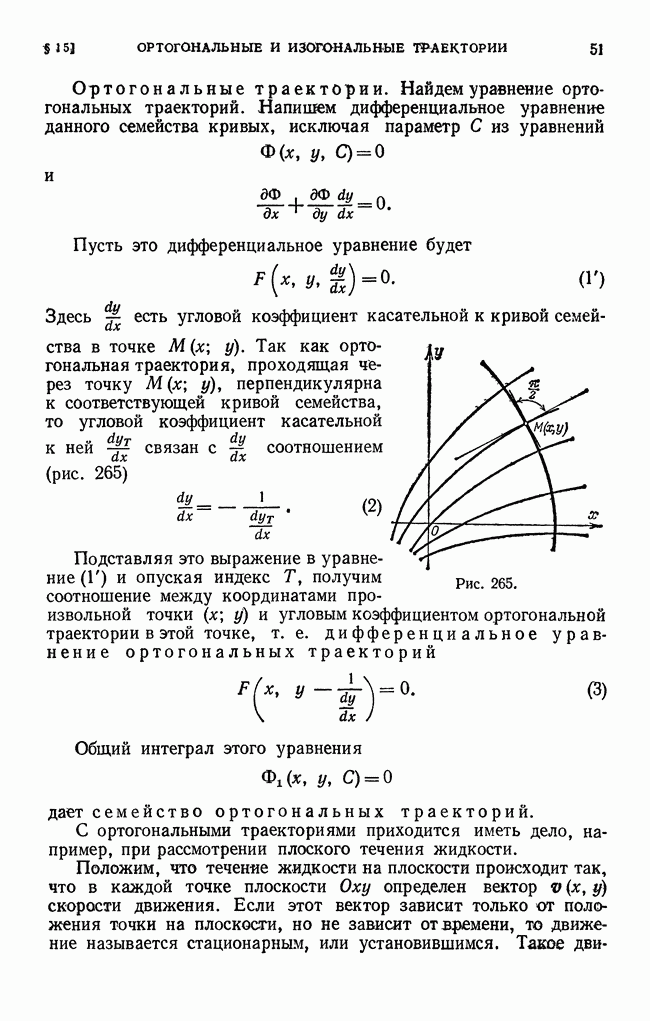
- § 15. Ортогональные и изогональные траектории
- § 16. Дифференциальные уравнения высших порядков (общие понятия)
- § 17. Уравнение вида y^(n) = f(x)
- § 18. Некоторые типы дифференциальных уравнений второго порядка, приводимых к уравнениям первого порядка. Задача о второй космической скорости
- § 19. Графический метод интегрирования дифференциального уравнения второго порядка
- § 20. Линейные однородные уравнения. Определения и общие свойства
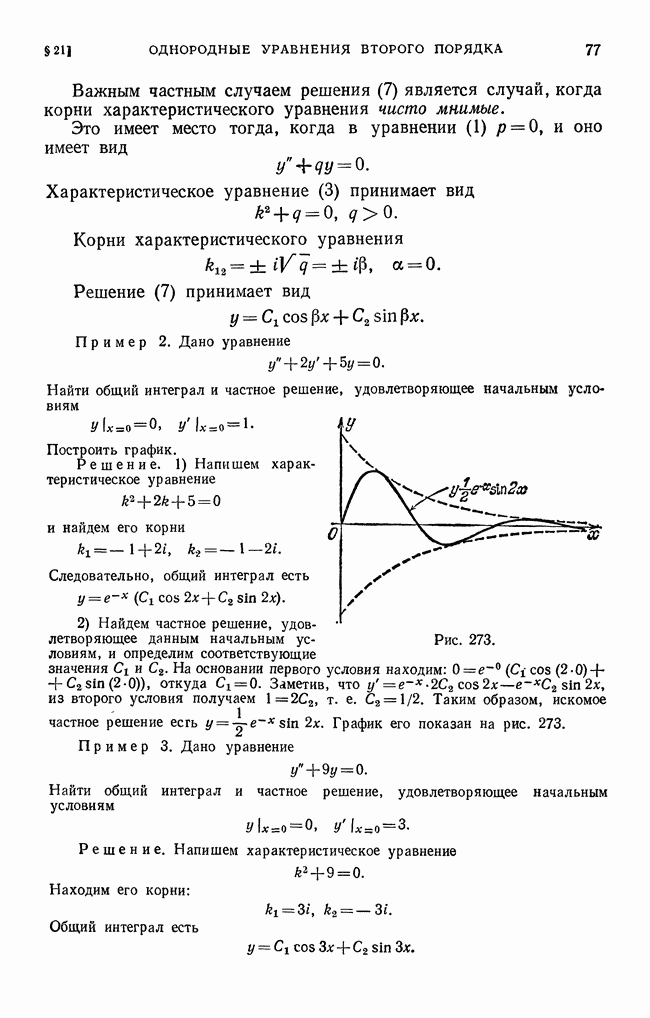
- § 21. Линейные однородные уравнения второго порядка с постоянными коэффициентами
- § 22. Линейные однородные уравнения n-го порядка с постоянными коэффициентами
- § 23. Неоднородные линейные уравнения второго порядка
- § 24. Неоднородные линейные уравнения второго порядка с постоянными коэффициентами
- § 25. Неоднородные линейные уравнения высших порядков
- § 26. Дифференциальное уравнение механических колебаний
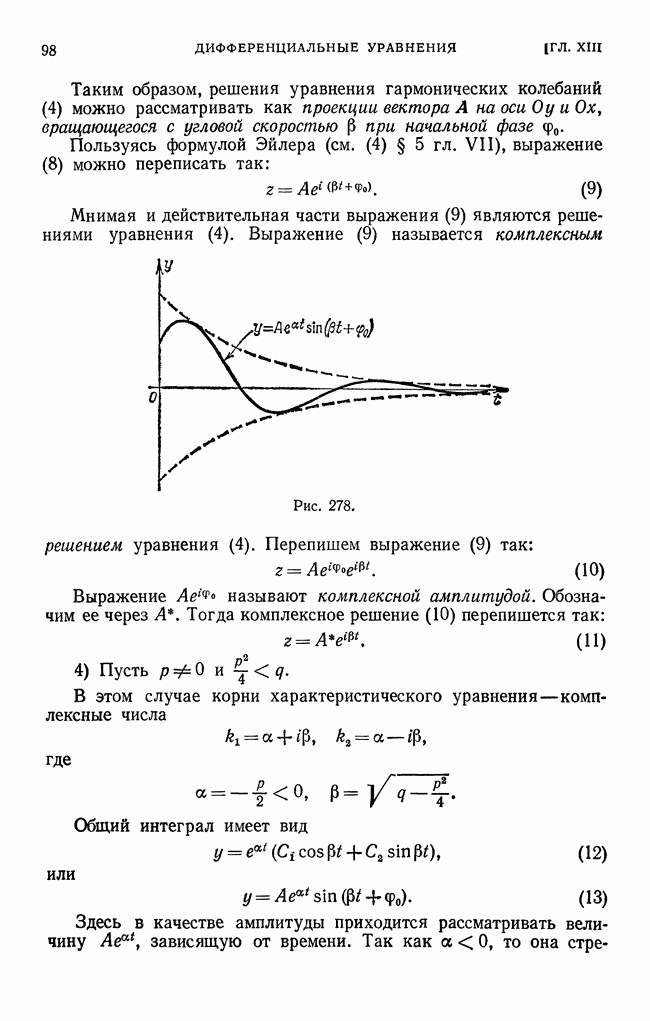
- § 27. Свободные колебания. Векторное и комплексное изображение гармонических колебаний
- § 28. Вынужденные колебания
- § 29. Системы обыкновенных дифференциальных уравнений
- § 30. Системы линейных дифференциальных уравнений с постоянными коэффициентами
- § 31. Понятие о теории устойчивости Ляпунова. Поведение траектории дифференциального уравнения в окрестности особой точки
- § 32. Приближенное решение дифференциальных уравнений первого порядка методом Эйлера
- § 33. Разностный метод приближенного решения дифференциальных уравнений, основанный на применении формулы Тейлора.. Метод Адамса
- § 34. Приближенный метод интегрирования систем дифференциальных уравнений первого порядка
- Упражнения к главе XIII
- ГЛАВА XIV. КРАТНЫЕ ИНТЕГРАЛЫ
- § 2. Вычисление двойного интеграла
- § 3. Вычисление двойного интеграла (продолжение)
- § 4. Вычисление площадей и объемов с помощью двойных интегралов
- § 5. Двойной интеграл в полярных координатах
- § 6. Замена переменных в двойном интеграле (общий случай)
- § 7. Вычисление площади поверхности
- § 9. Момент инерции площади плоской фигуры
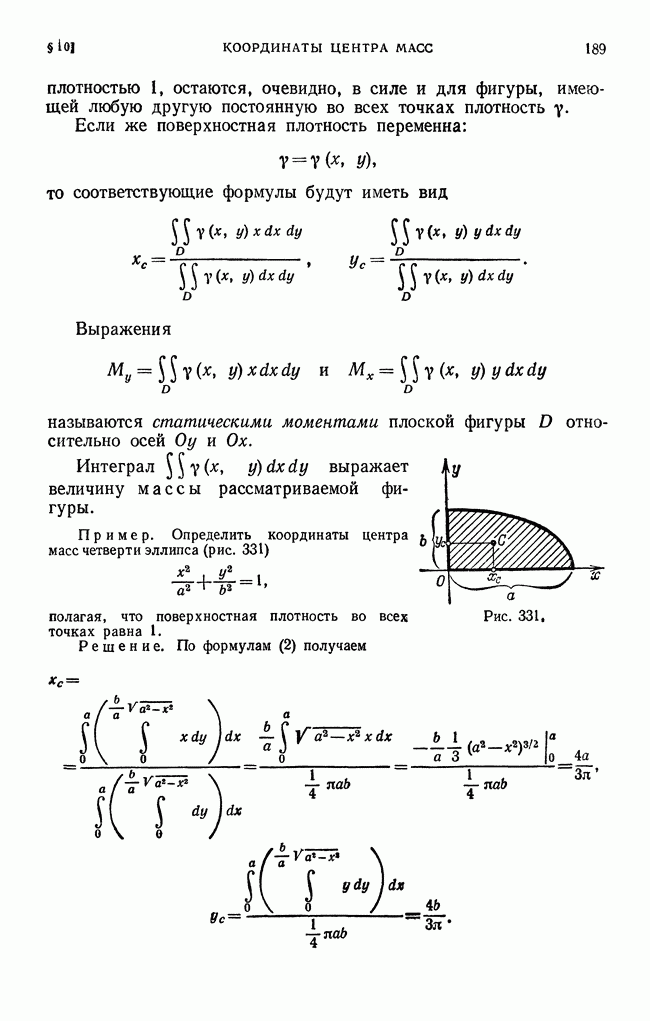
- § 10. Координаты центра масс площади плоской фигуры
- § 11. Тройной интеграл
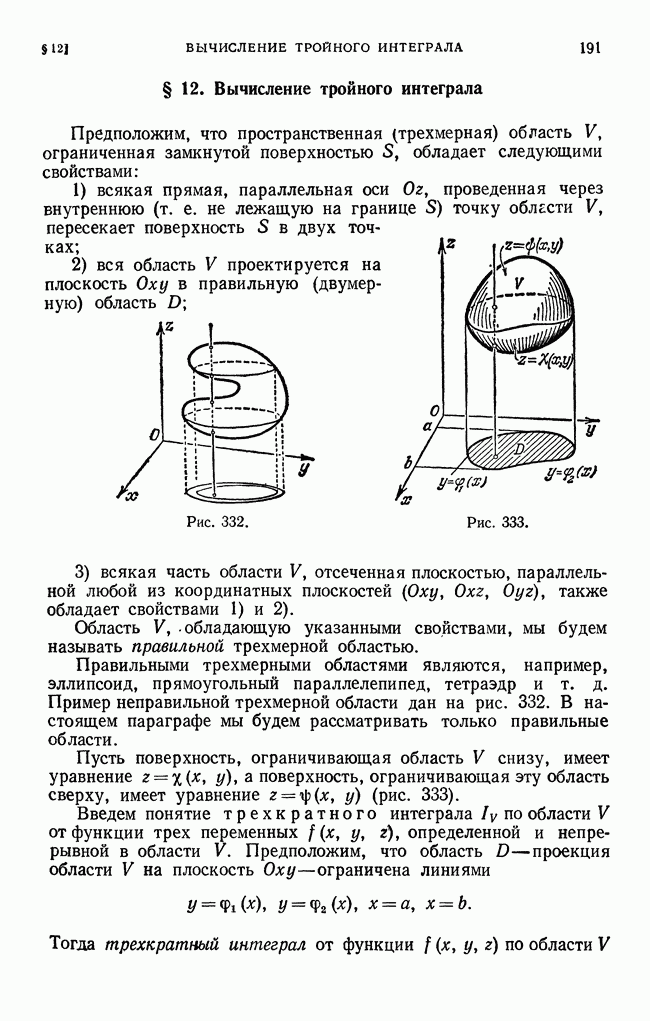
- § 12. Вычисление тройного интеграла
- § 13. Замена переменных в тройном интеграле
- § 14. Момент инерции и координаты центра масс тела
- § 15. Вычисление интегралов, зависящих от параметра
- Упражнения к главе XIV
- ГЛАВА XV. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ И ИНТЕГРАЛЫ ПО ПОВЕРХНОСТИ
- § 2. Вычисление криволинейного интеграла
- § 3. Формула Грина
- § 4. Условия независимости криволинейного интеграла от пути интегрирования
- § 5. Поверхностный интеграл
- § 6. Вычисление поверхностного интеграла
- § 7. Формула Стокса
- § 9. Оператор Гамильтона. Некоторые его применения
- Упражнения к главе XV
- ГЛАВА XVI. РЯДЫ
- § 1. Ряд. Сумма ряда
- § 2. Необходимый признак сходимости ряда
- § 3. Сравнение рядов с положительными членами
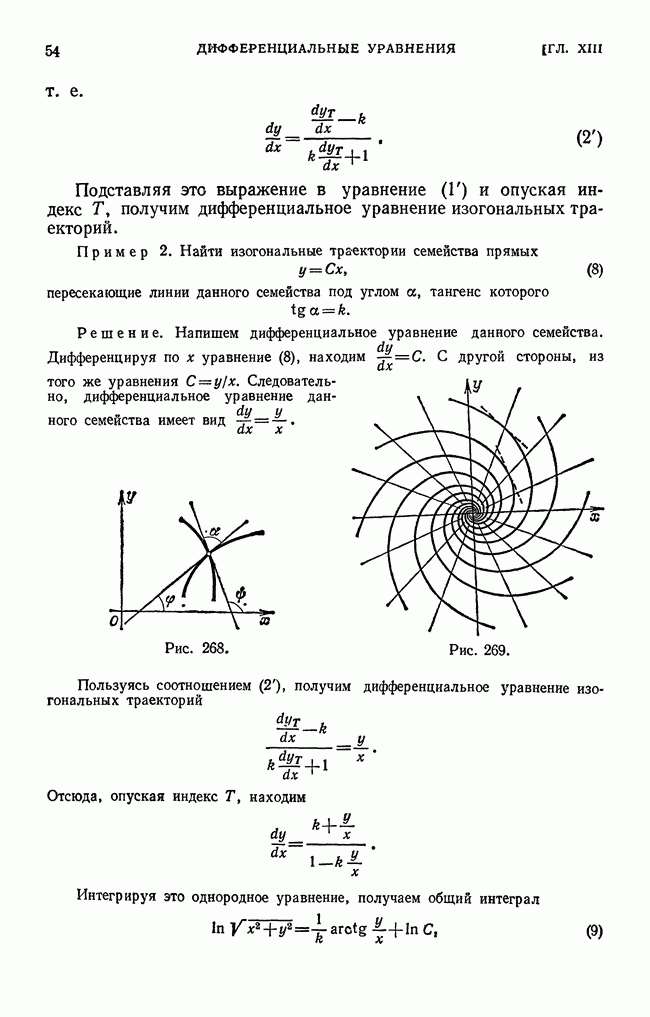
- § 4. Признак Даламбера
- § 5. Признак Коши
- § 6. Интегральный признак сходимости ряда
- § 7. Знакочередующиеся ряды. Теорема Лейбница
- § 8. Знакопеременные ряды. Абсолютная и условная сходимость
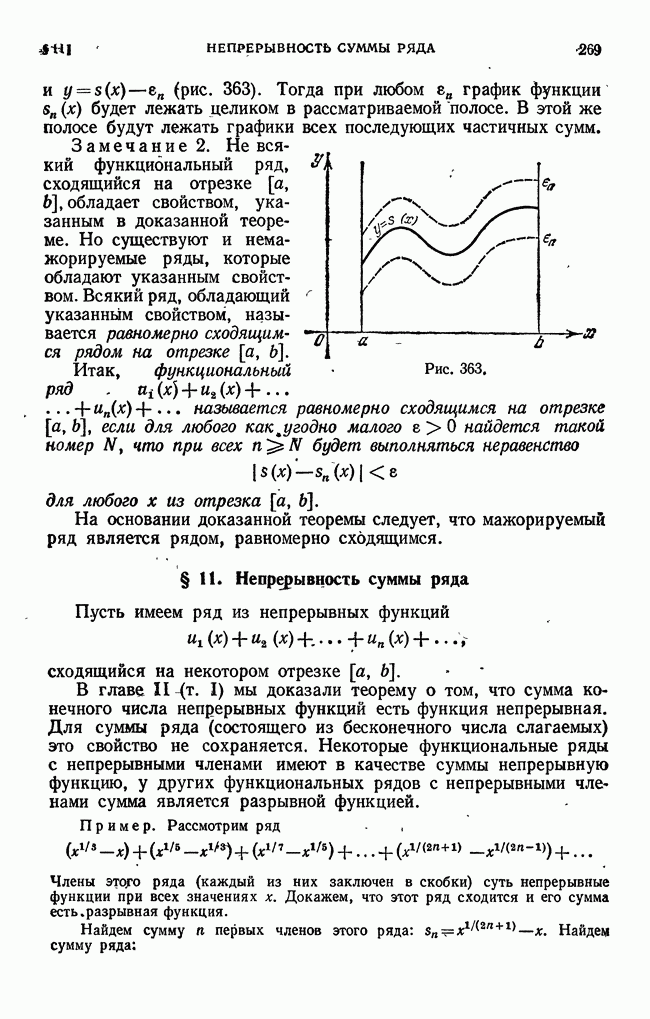
- § 9. Функциональные ряды
- § 10. Мажорируемые ряды
- § 11. Непрерывность суммы ряда
- § 12. Интегрирование и дифференцирование рядов
- § 13. Степенные ряды. Интервал сходимости
- § 14. Дифференцирование степенных рядов
- § 15. Ряды по степеням x-a
- § 16. Ряды Тейлора и Маклорена
- § 17. Примеры разложения функций в ряды
- § 18. Формула Эйлера
- § 19. Биномиальный ряд
- § 20. Разложение функции ln(1+x) в степенной ряд. Вычисление логарифмов
- § 21. Вычисление определенных интегралов с помощью рядов
- § 22. Интегрирование дифференциальных уравнений с помощью рядов
- § 23. Уравнение Бесселя
- § 24. Ряды с комплексными членами
- § 25. Степенные ряды с комплексной переменной
- § 26. Решение дифференциального уравнения первого порядка методом последовательных приближений (метод итераций)
- § 27. Доказательство существования решения дифференциального уравнения. Оценка погрешности при приближенном решении
- § 28. Теорема единственности решения дифференциального уравнения
- Упражнения к главе XVI
- ГЛАВА XVII. РЯДЫ ФУРЬЕ
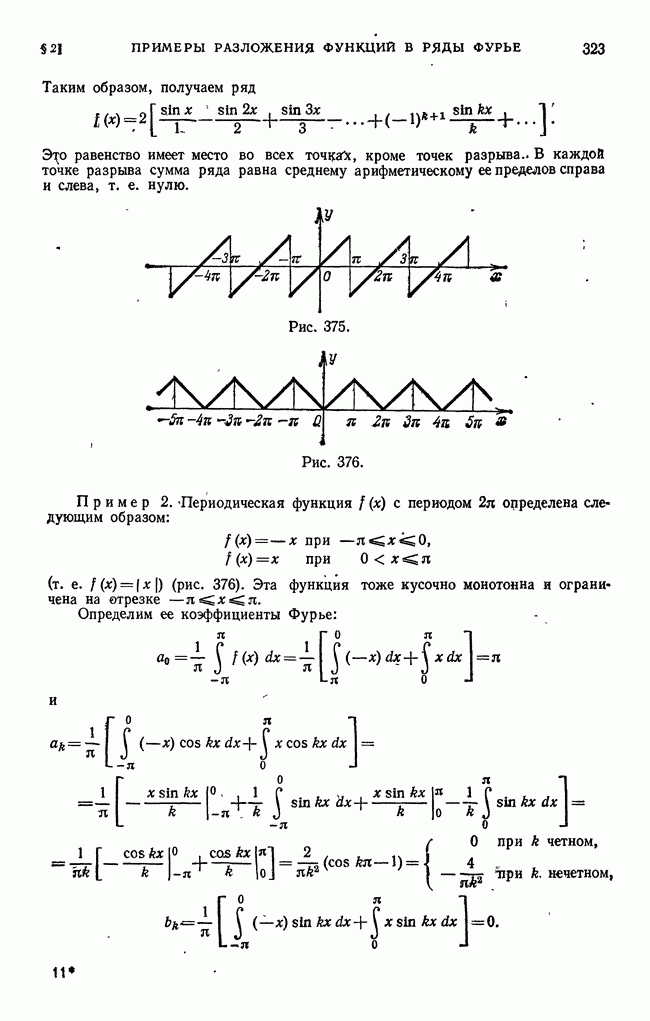
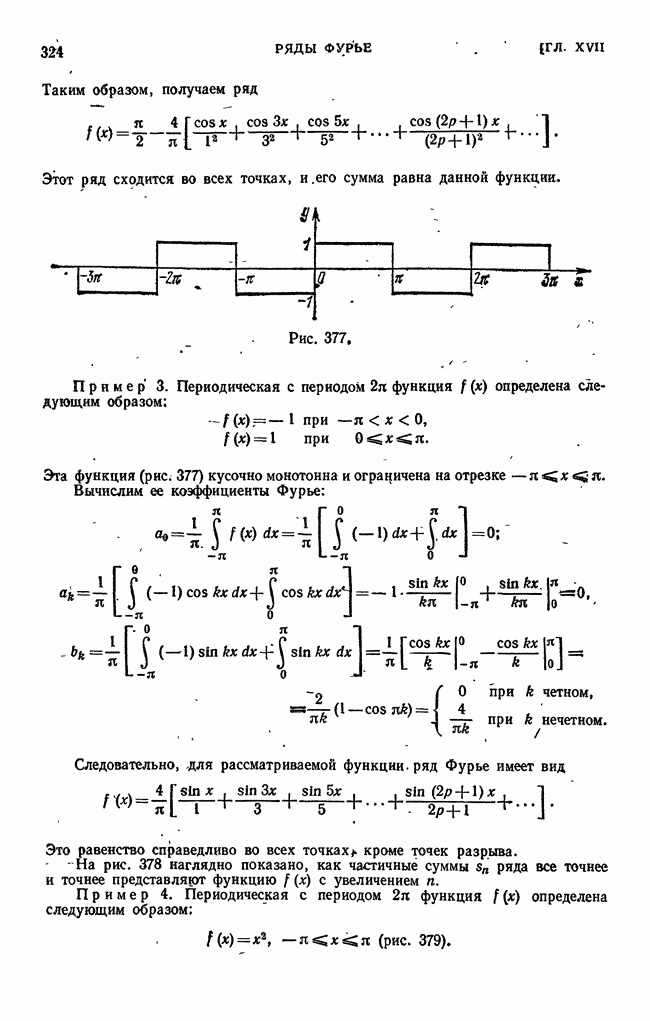
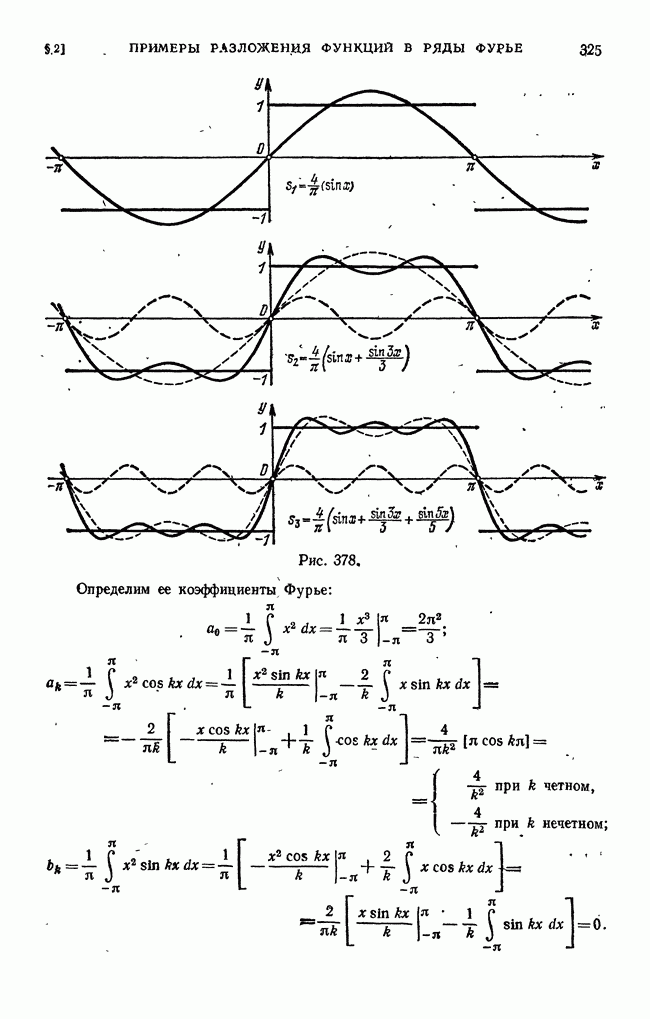
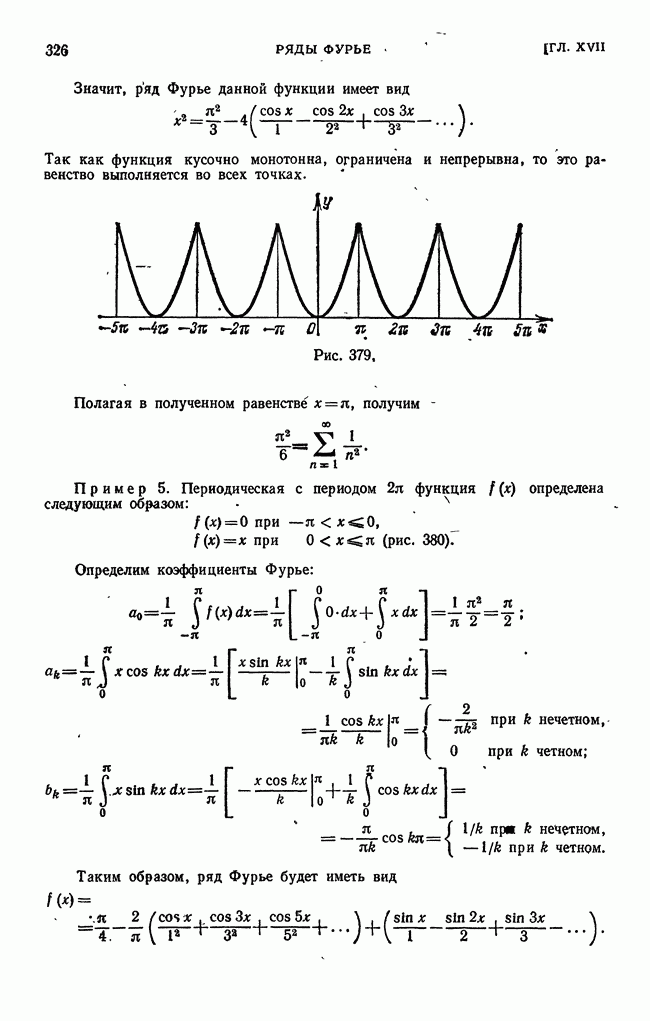
- § 2. Примеры разложения функций в ряды Фурье
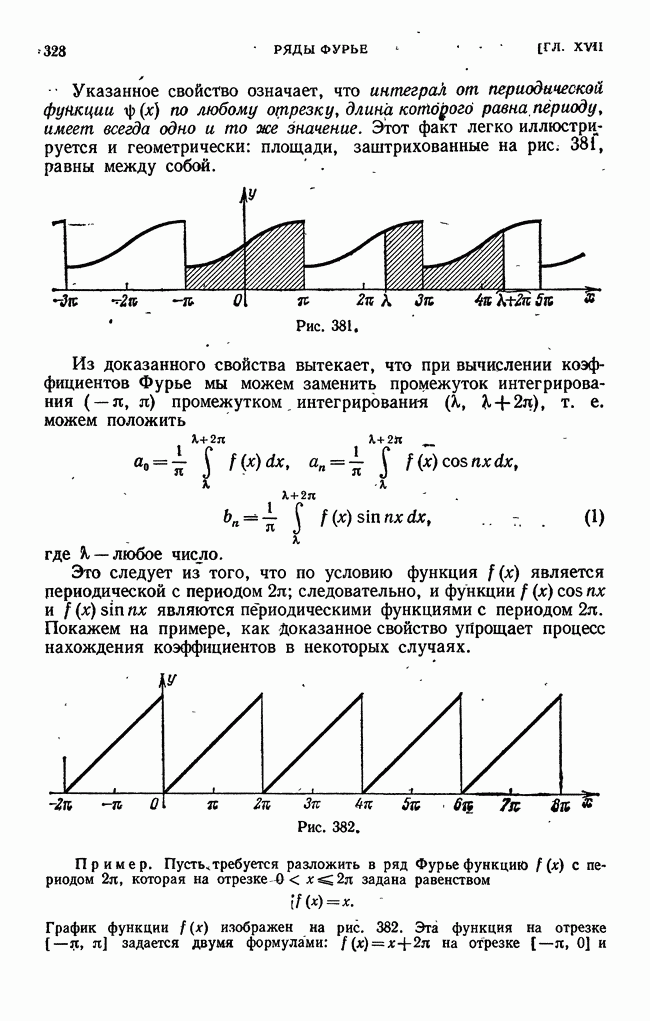
- § 3. Одно, замечание о разложении периодической функции в ряд Фурье
- § 4. Ряды Фурье для четных и нечетных функций
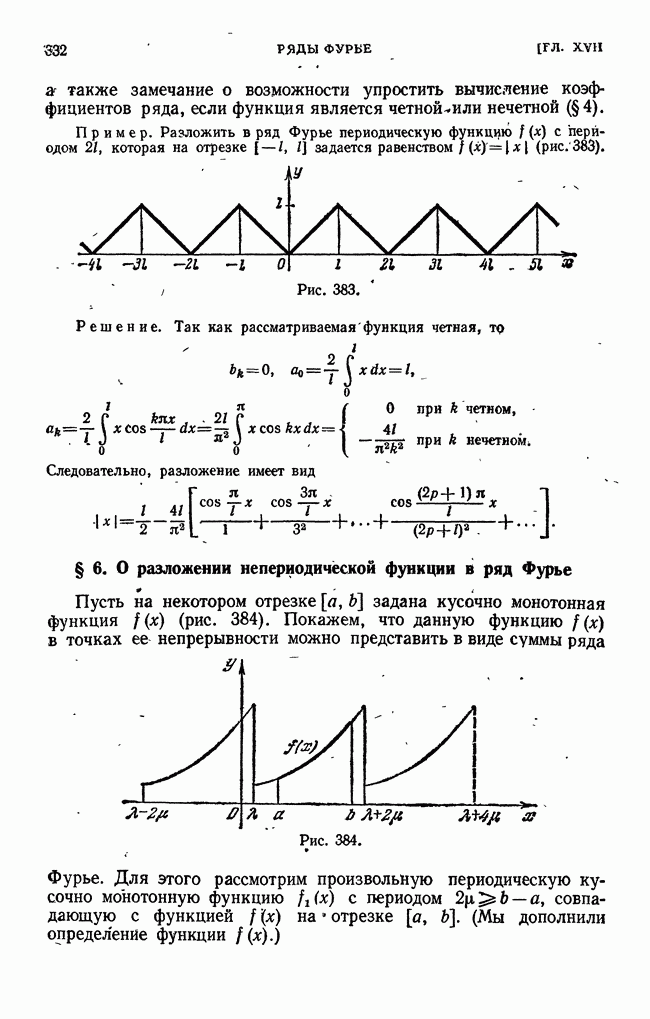
- § 5. Ряд Фурье для функции с периодом 2l
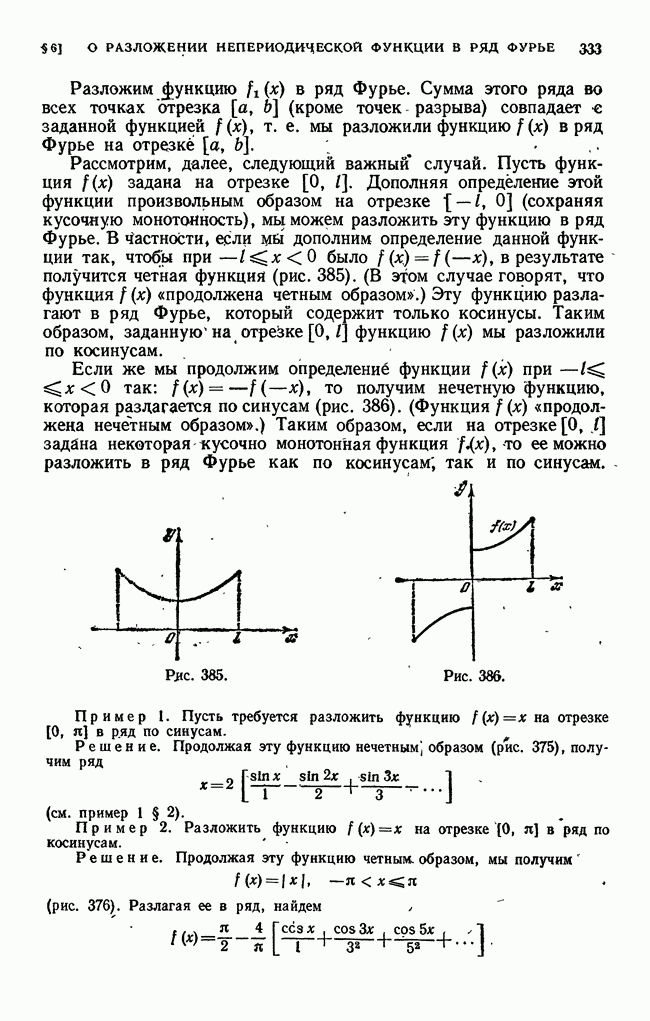
- § 6. О разложении непериодической функции в ряд Фурье
- § 7. Приближение в среднем заданной функции с помощью тригонометрического многочлена
- § 8. Интеграл Дирихле
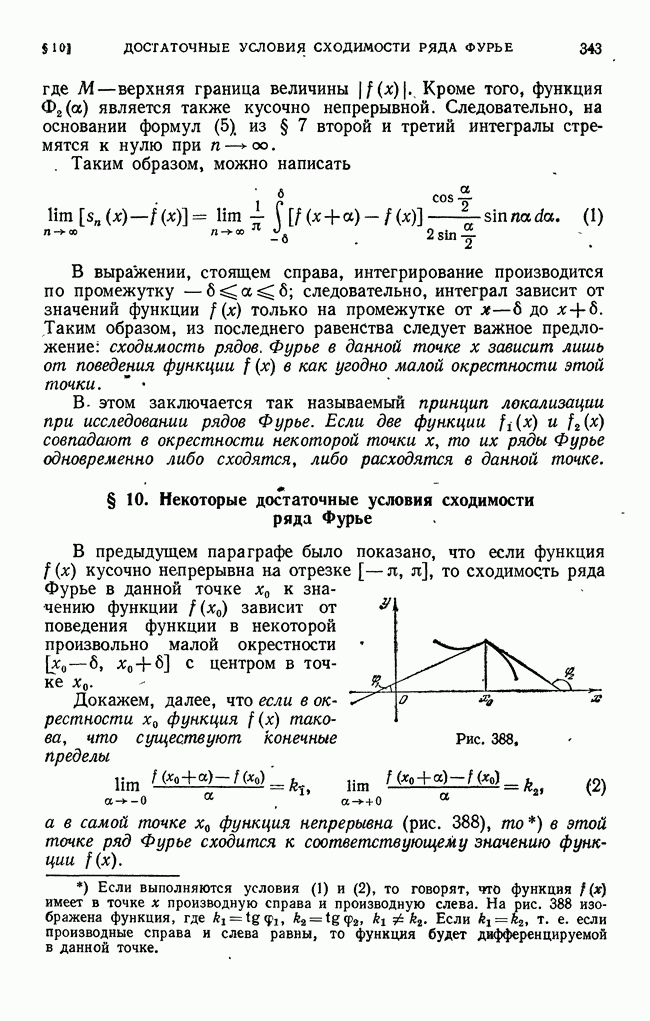
- § 9. Сходимость ряда Фурье в данной точке
- § 10. Некоторые достаточные условия сходимости ряда Фурье
- § 11. Практический гармонический анализ
- § 12. Ряд Фурье в комплексной форме
- § 13. Интеграл Фурье
- § 14. Интеграл Фурье в комплексной форме
- § 15. Ряд Фурье по ортогональной системе функций
- § 16. Понятие о линейном функциональном пространстве. Аналогия между разложением функций в ряд Фурье и разложением векторов
- Упражнения к главе XVII
- ГЛАВА XVIII. УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ
- § 1. Основные типы уравнений математической физики
- § 2. Вывод уравнения колебаний струны. Формулировка краевой задачи. Вывод уравнений электрических колебаний в проводах
- § 3. Решение уравнения колебаний струны методом разделения переменных (методом Фурье)
- § 4. Уравнение распространения тепла в стержне. Формулировка краевой задачи
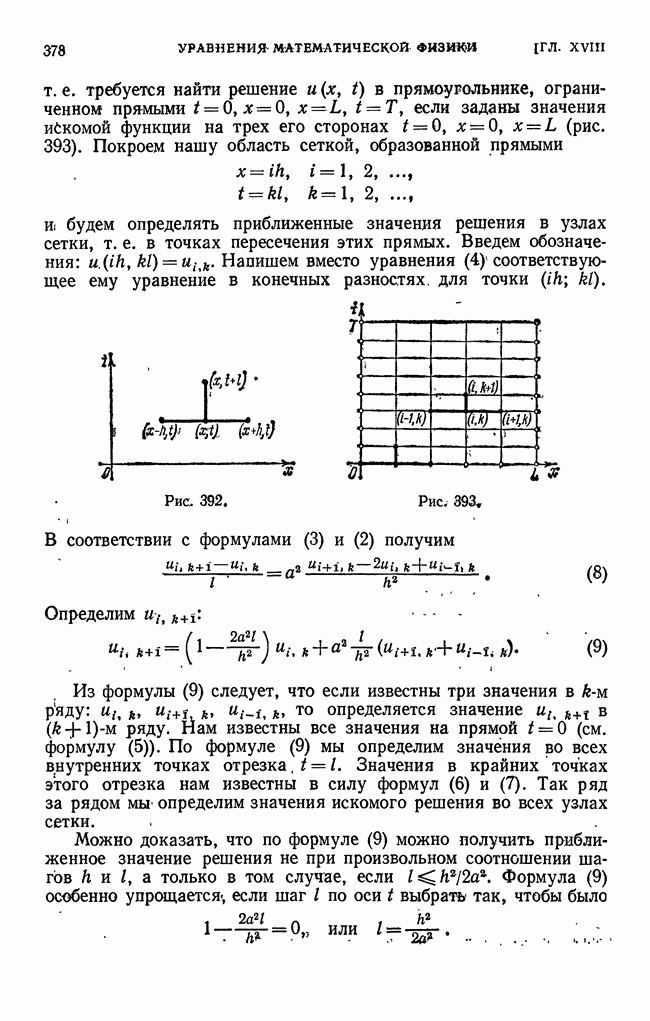
- § 5. Распространение тепла в пространстве
- § 6. Решение первой краевой задачи для уравнения теплопроводности методом конечных разностей
- § 7. Распространение тепла в неограниченном стержне
- § 8. Задачи, приводящие к исследованию решений уравнения Лапласа. Формулировка краевых задач
- § 9. Уравнение Лапласа в цилиндрических координатах. Решение задачи Дирихле для кольца с постоянными значениями искомой функции на внутренней и внешней окружностях
- § 10. Решение задачи Дирихле для круга
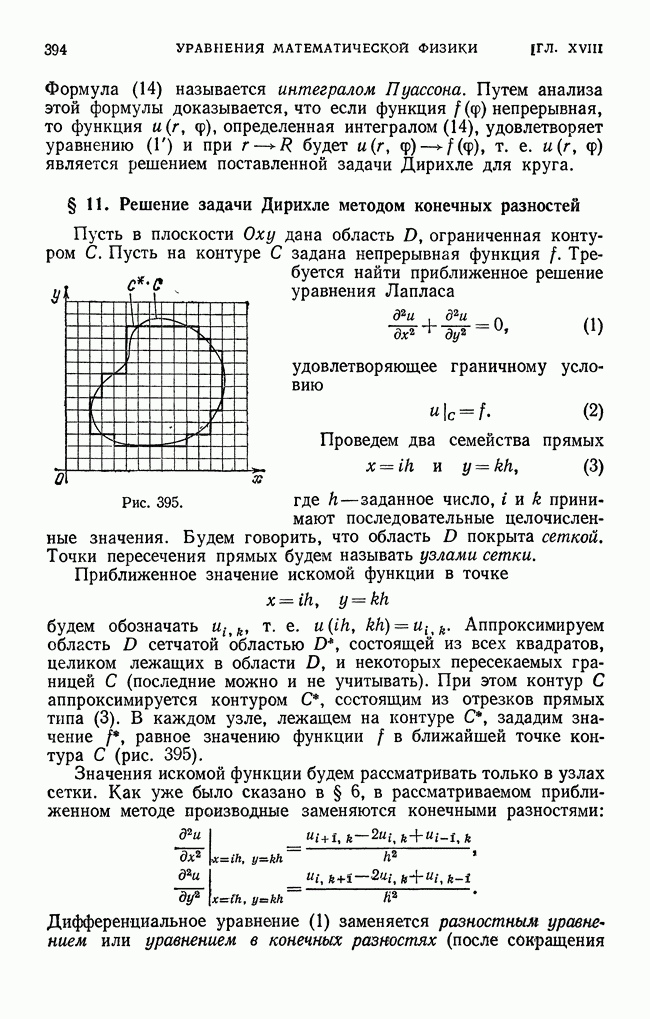
- § 11. Решение задачи Дирихле методом конечных разностей
- Упражнения к главе XVIII
- ГЛАВА XIX. ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ И НЕКОТОРЫЕ ЕГО ПРИЛОЖЕНИЯ
- § 1. Начальная функция и ее изображение
- § 2. Изображение функций …
- § 3. Изображение функции с измененным масштабом независимой переменной. Изображение функций sin at, cos at
- § 4. Свойство линейности изображения
- § 5. Теорема смещения
- § 6. Изображение функций …
- § 7. Дифференцирование изображения
- § 8. Изображение производных
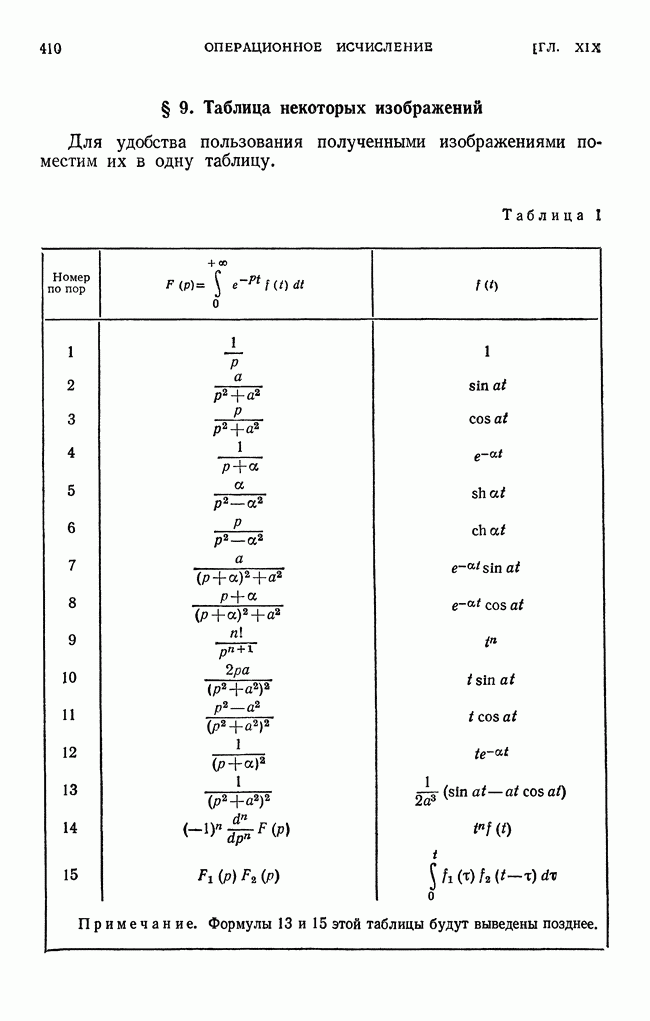
- § 9. Таблица некоторых изображений
- § 10. Вспомогательное уравнение для данного дифференциального уравнения
- § 11. Теорема разложения
- § 12. Примеры решения дифференциальных уравнений и систем дифференциальных уравнений операционным методом
- § 13. Теорема свертывания
- § 14. Дифференциальные уравнения механических колебаний. Дифференциальные уравнения теории электрических цепей
- § 15. Решение дифференциального уравнения колебаний
- § 16. Исследование свободных колебаний
- § 17. Исследование механических и электрических колебаний в случае периодической внешней силы
- § 18. Решение уравнения колебаний в случае резонанса
- § 19. Теорема запаздывания
- § 20. Дельта-функция и ее изображение
- Упражнения к главе XIX
- ГЛАВА XX. ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
- § 1. Случайное событие. Относительная частота случайного события. Вероятность события. Предмет теории вероятностей
- § 2. Классическое определение вероятности и непосредственный подсчет вероятностей
- § 3. Сложение вероятностей. Противоположные случайные события
- § 4. Умножение вероятностей независимых событий
- § 5. Зависимые события. Условная вероятность. Полная вероятность
- § 6. Вероятность гипотез. Формула Байеса
- § 7. Дискретная случайная величина. Закон распределения дискретной случайной величины
- § 8. Относительная частота и вероятность относительной частоты при повторных испытаниях
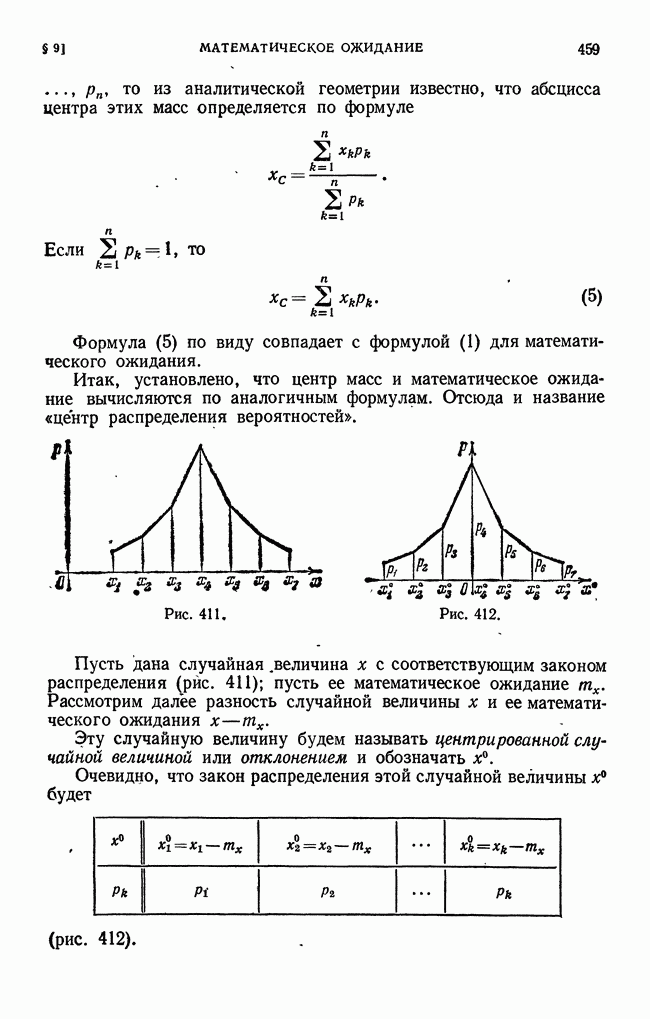
- § 9. Математическое ожидание дискретной случайной величины
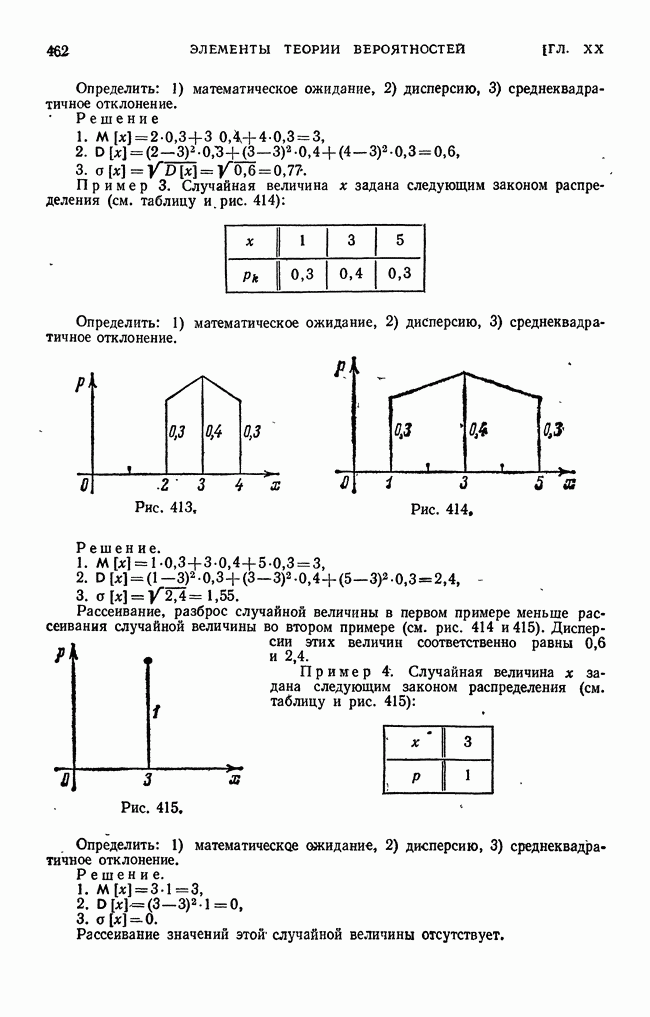
- § 10. Дисперсия. Среднеквадратичное отклонение. Понятие о моментах
- § 11. Функции от случайных величин
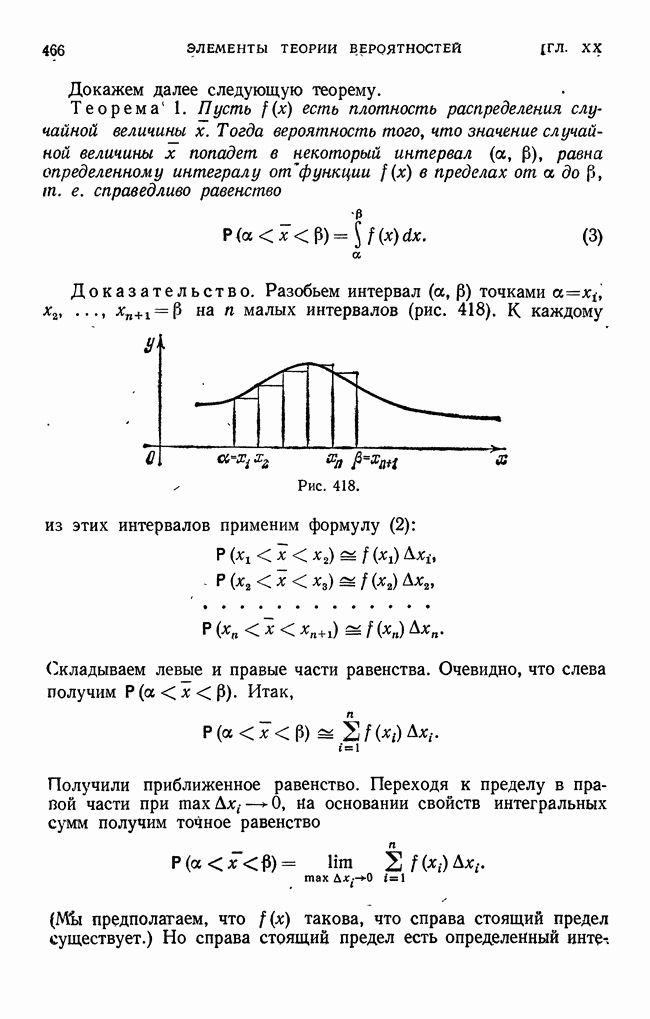
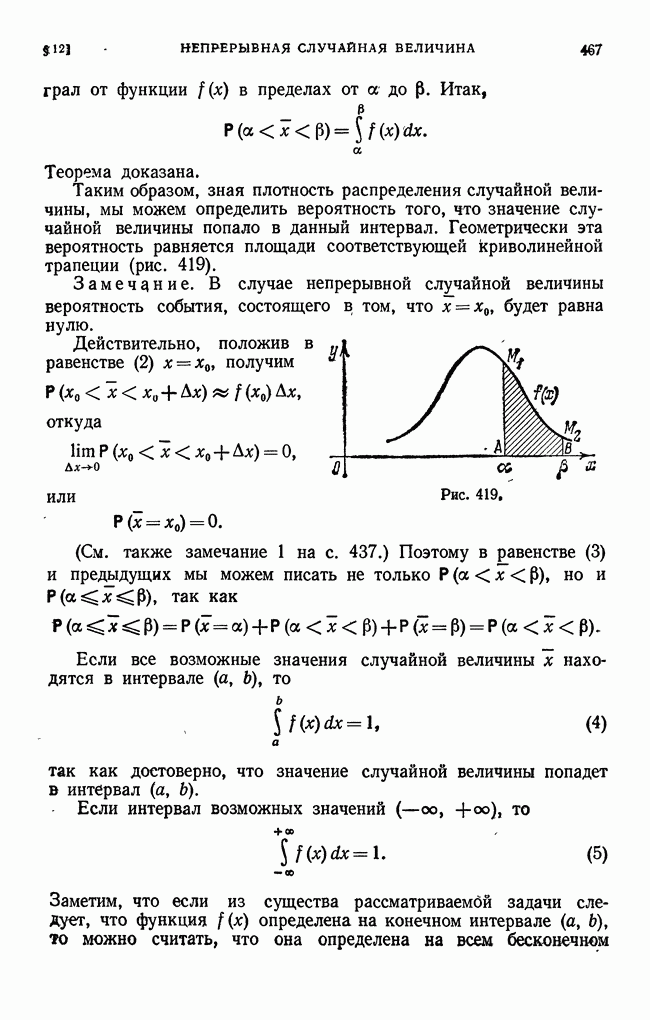
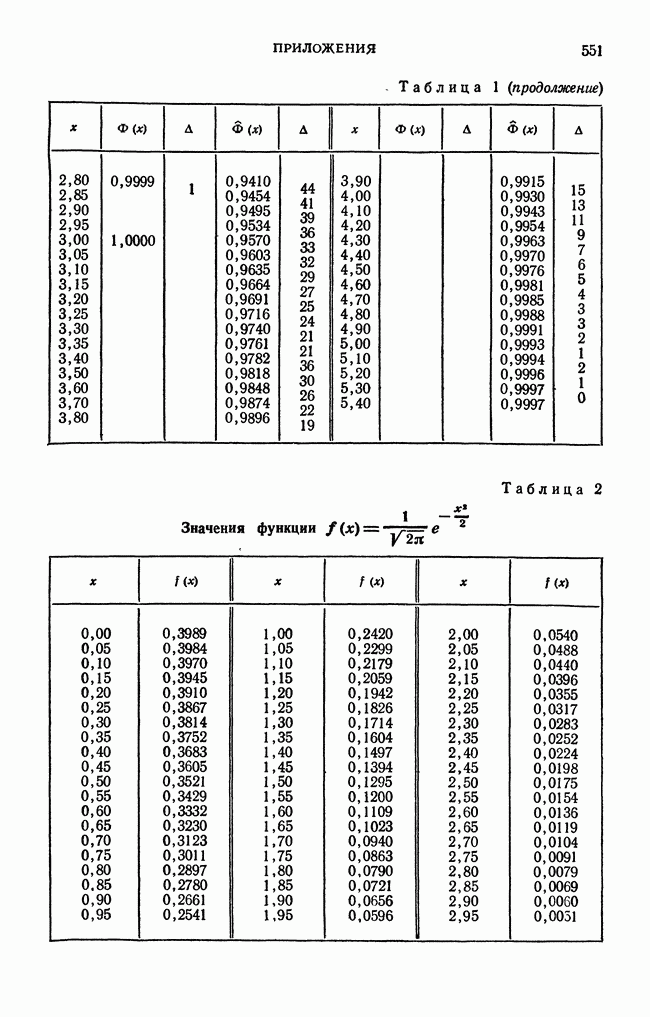
- § 12. Непрерывная случайная величина. Плотность распределения непрерывной случайной величины. Вероятность попадания случайной величины в заданный интервал
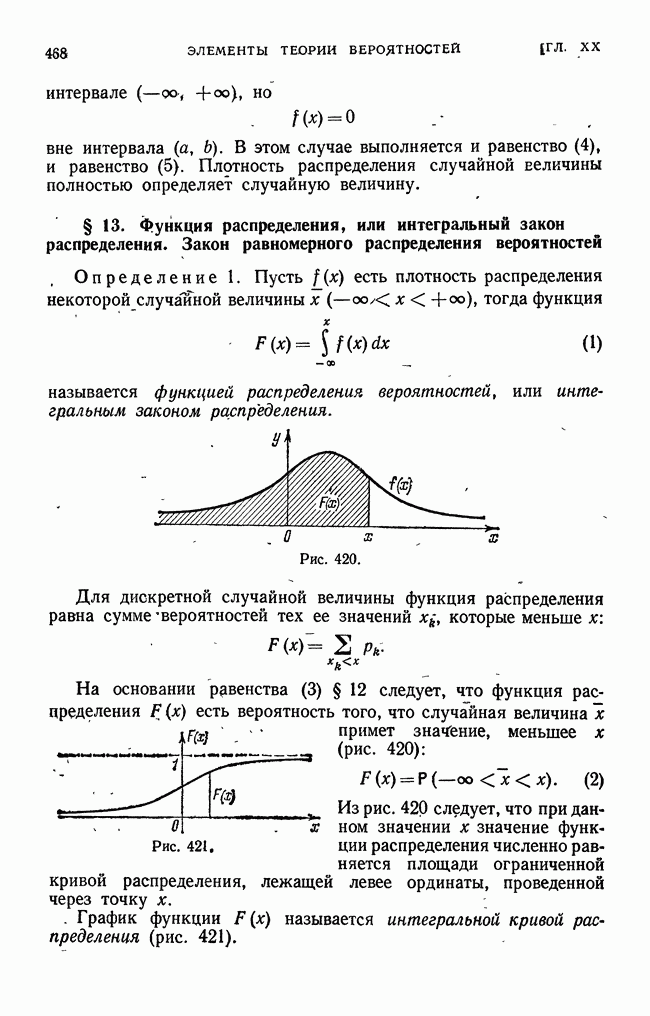
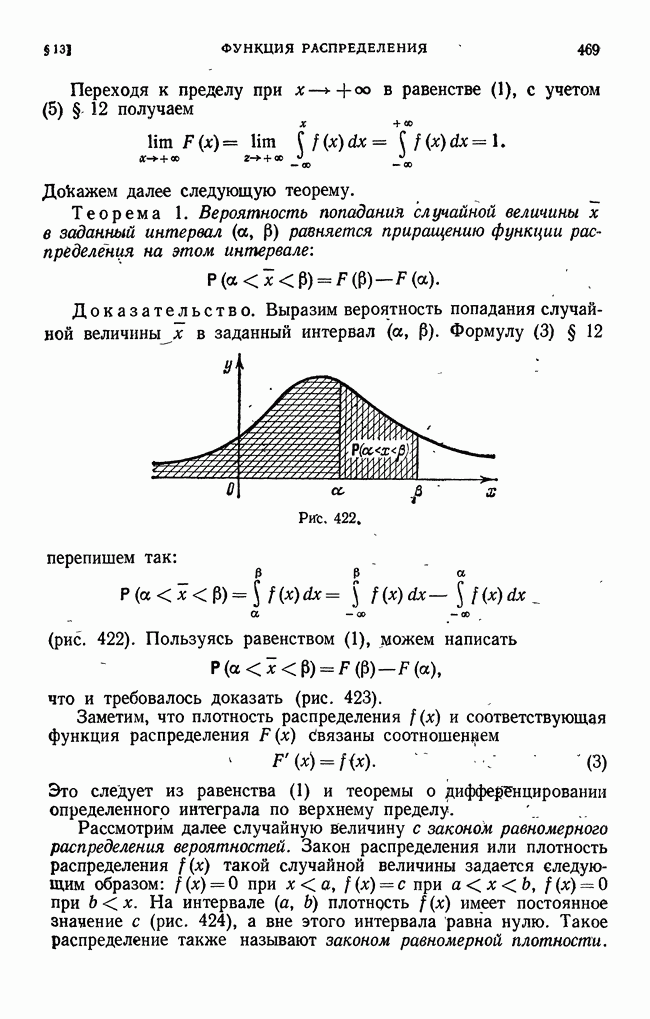
- § 13. Функция распределения, или интегральный закон распределения. Закон равномерного распределения вероятностей
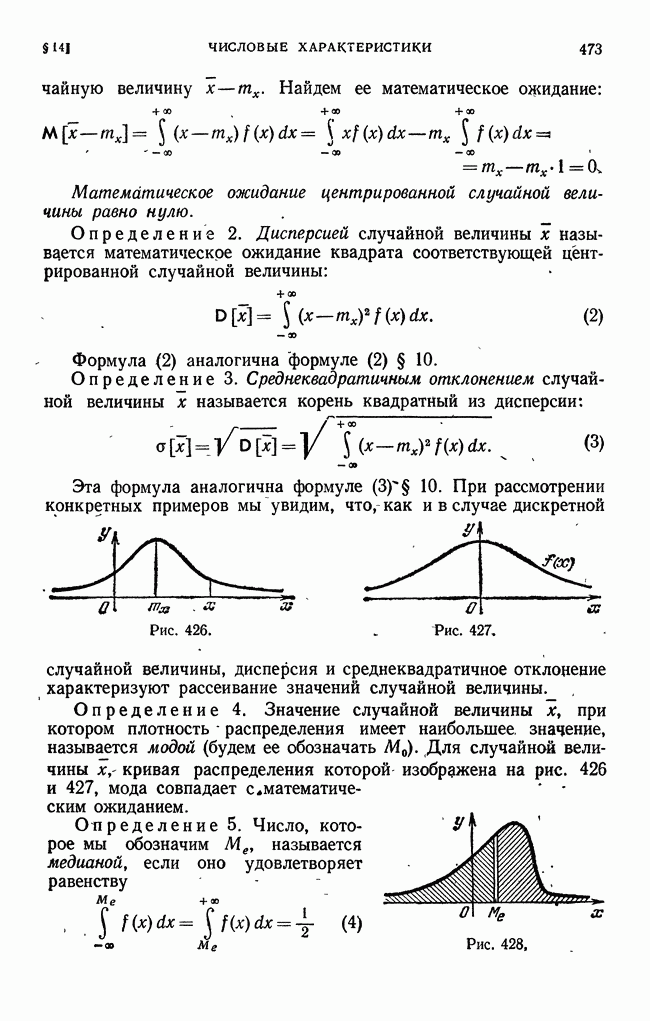
- § 14. Числовые характеристики непрерывной случайной величины
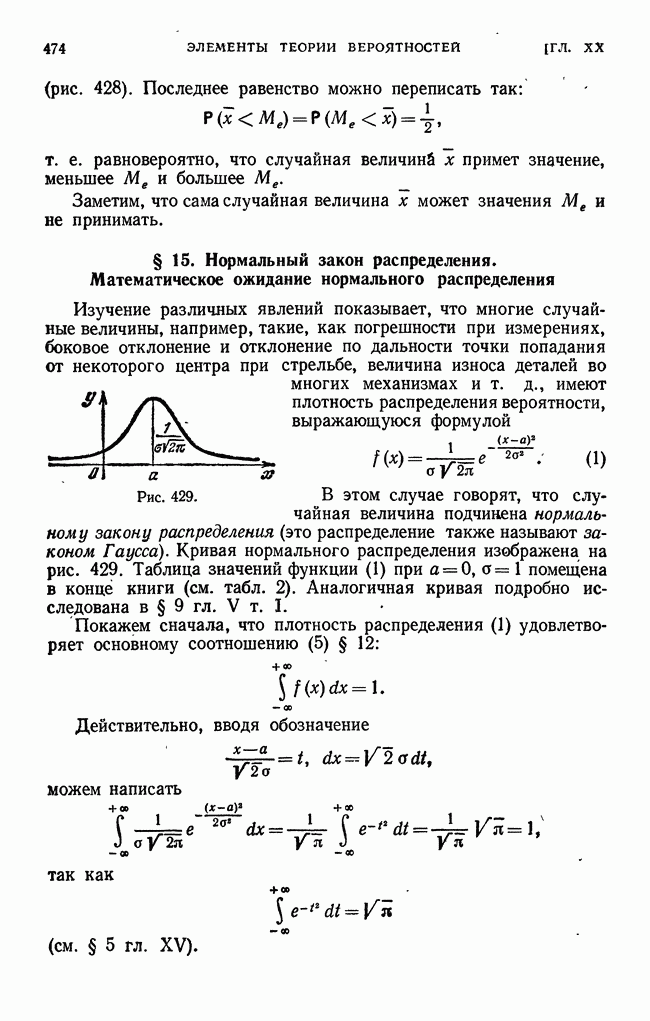
- § 15. Нормальный закон распределения. Математическое ожидание нормального распределения
- § 16. Дисперсия и среднеквадратичное отклонение случайной величины, подчиненной нормальному закону распределения
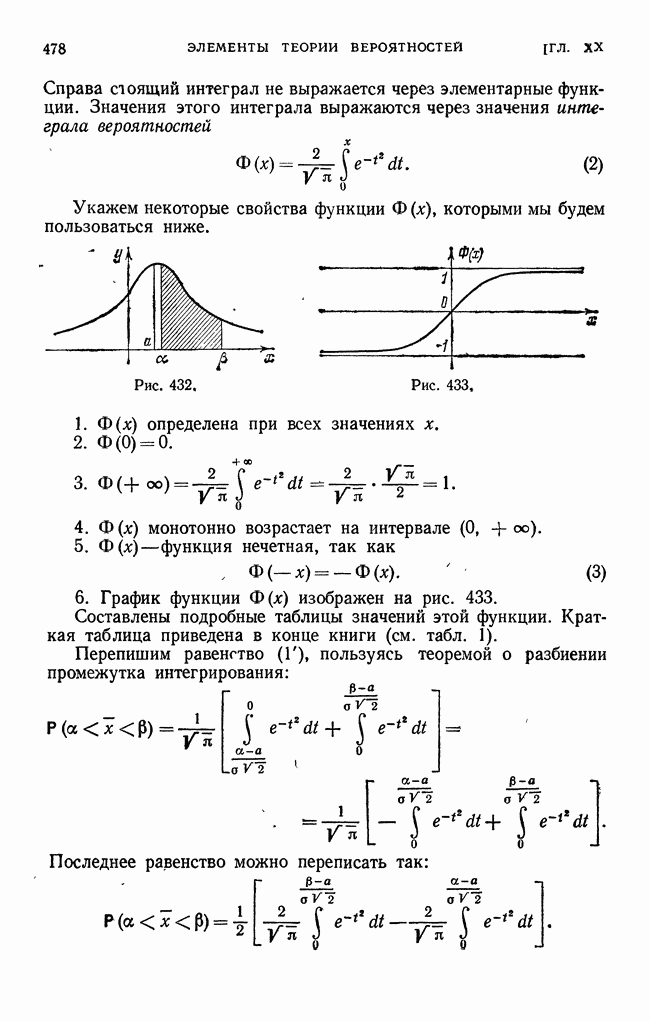
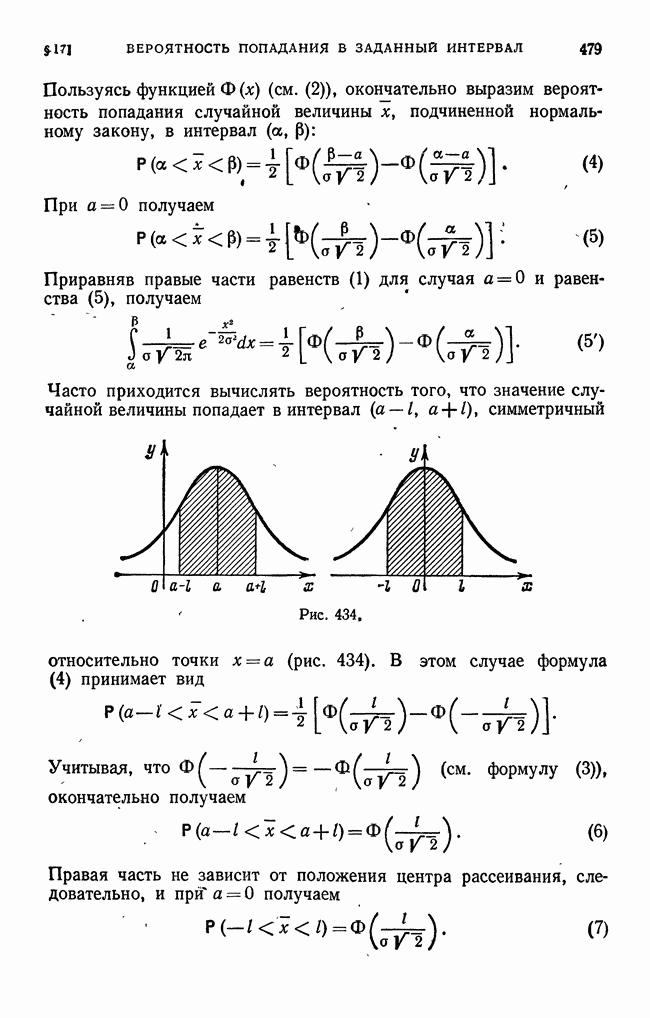
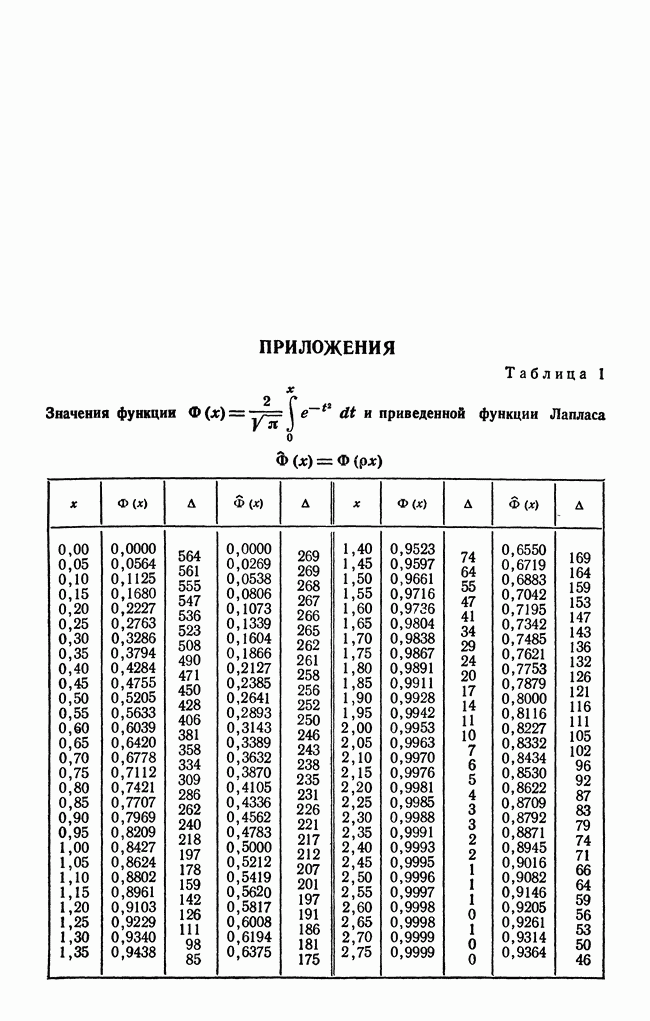
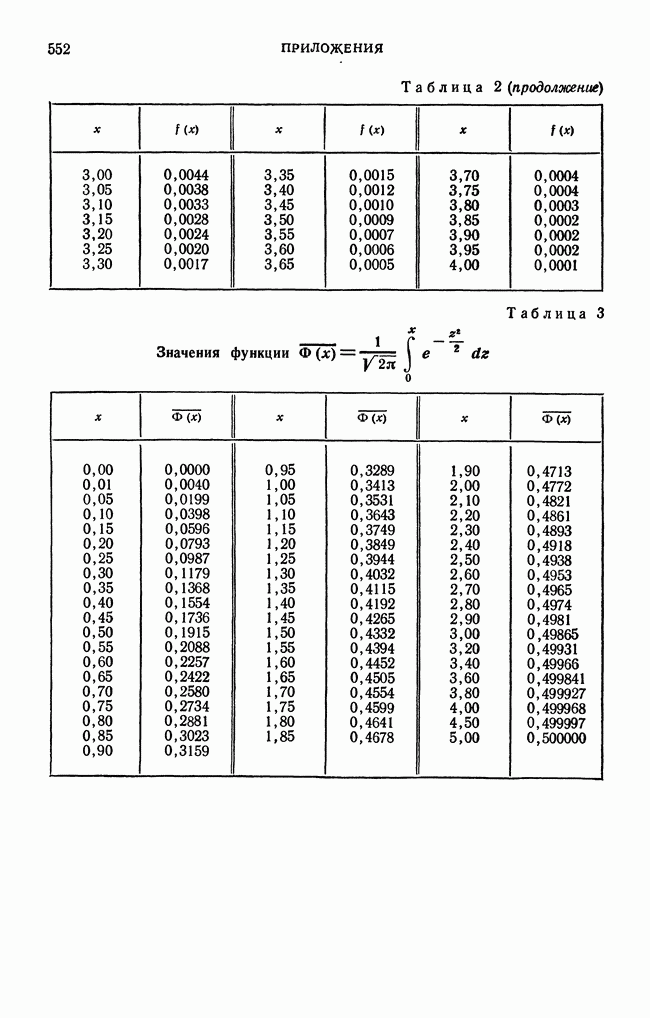
- § 17. Вероятность попадания значения случайной величины в заданный интервал. Функция Лапласа. Интегральная функция распределения для нормального закона
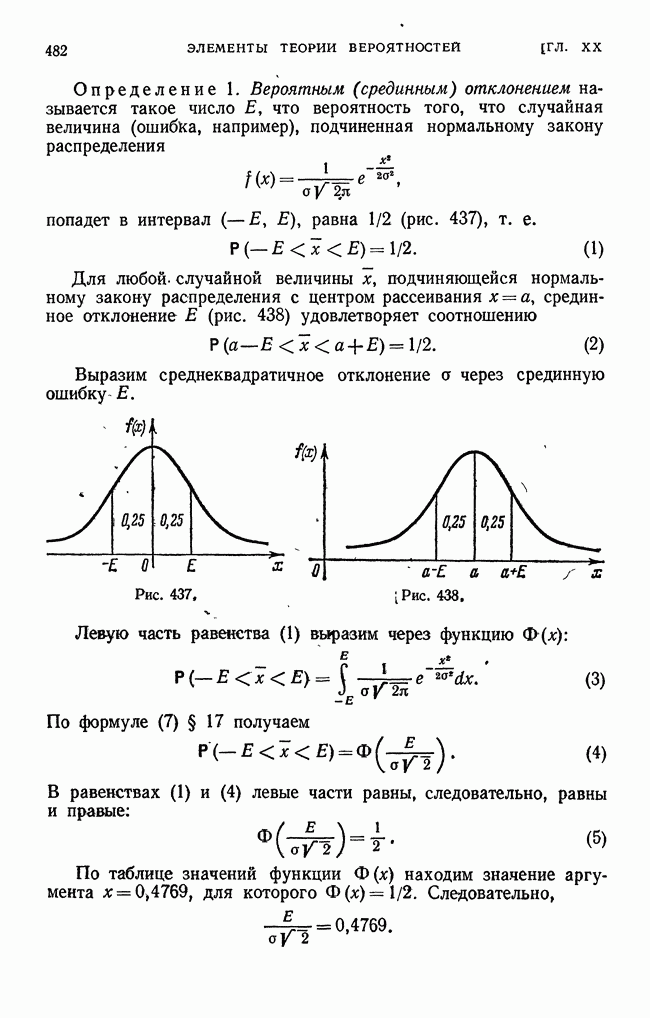
- § 18. Вероятное (срединное) отклонение или срединная ошибка
- § 19. Выражение нормального закона распределения через срединное отклонение. Приведенная функция Лапласа
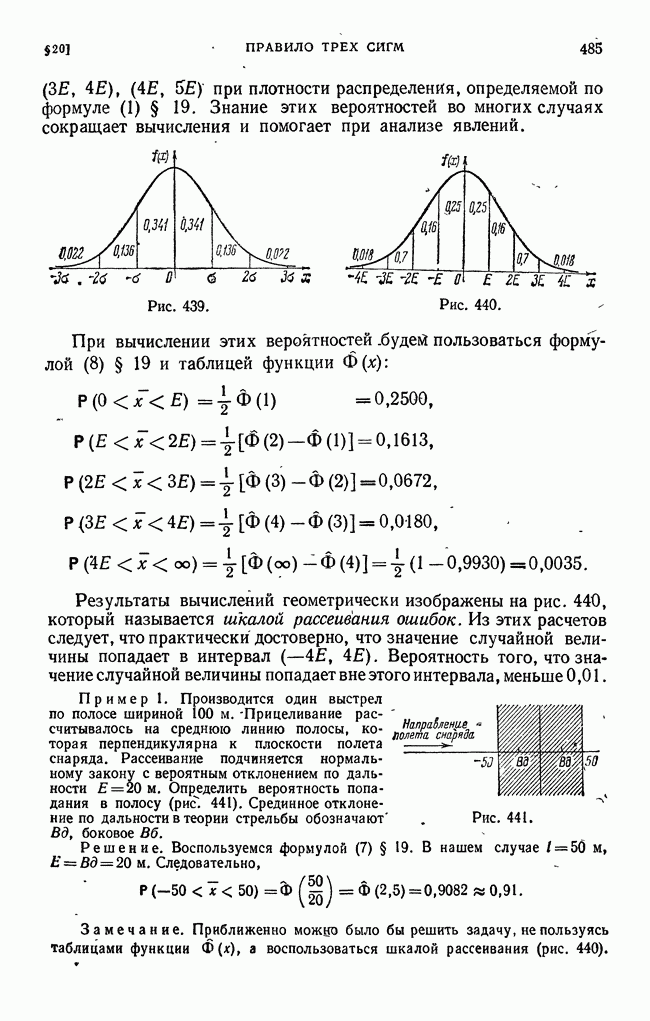
- § 20. Правило трех сигм. Шкала вероятностей распределения ошибок
- § 21. Среднеарифметическая ошибка
- § 22. Мера точности. Соотношение между характеристиками распределения ошибок
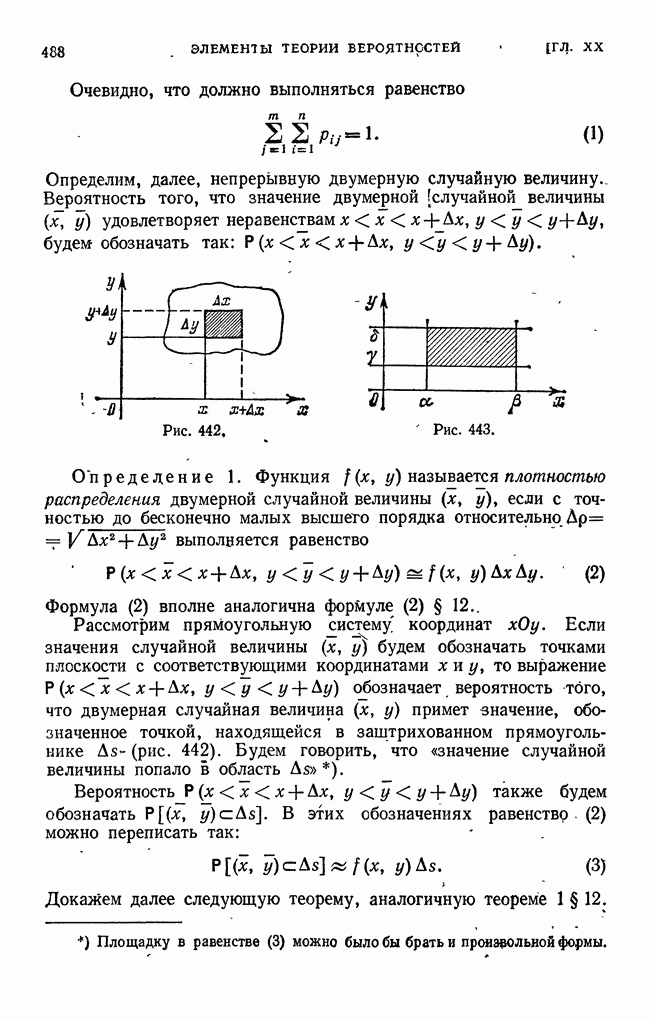
- § 23. Двумерная случайная величина
- § 24. Нормальный закон распределения на плоскости
- § 25. Вероятность попадания двумерной случайной величины в прямоугольник со сторонами, параллельными главным осям рассеивания, при нормальном законе распределения
- § 26. Вероятность попадания двумерной случайной величины в эллипс рассеивания
- § 27. Задачи математической статистики. Статистический материал
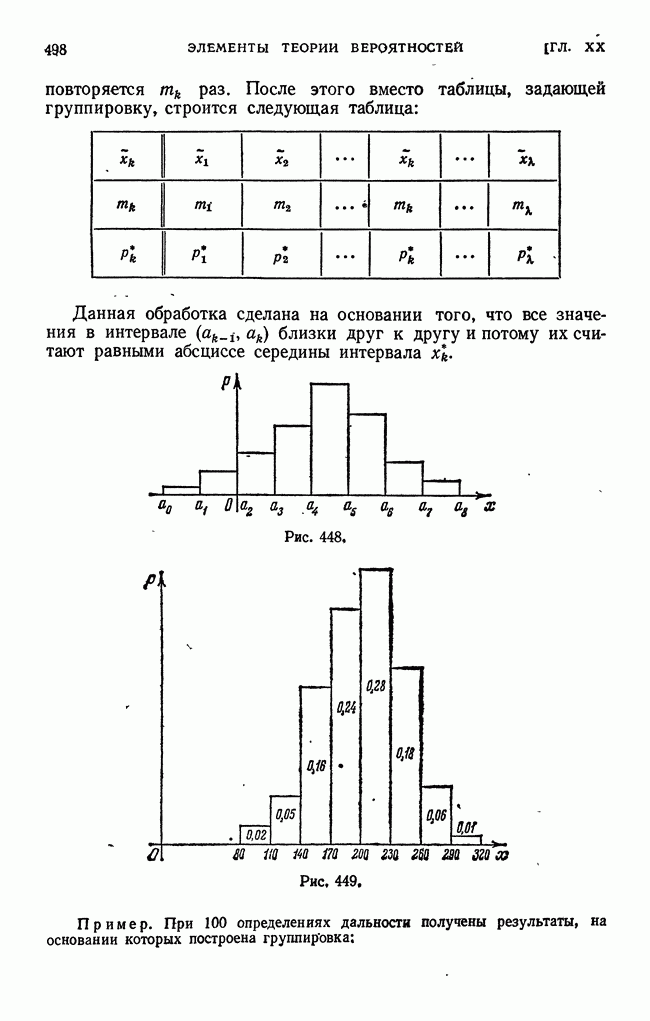
- § 28. Статистический ряд. Гистограмма
- § 29. Определение подходящего значения измеряемой величины
- § 30. Определение параметров закона распределения. Теорема Ляпунова. Теорема Лапласа
- Упражнения к главе XX
- ГЛАВА XXI. МАТРИЦЫ. МАТРИЧНАЯ ЗАПИСЬ СИСТЕМ И РЕШЕНИЙ СИСТЕМ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
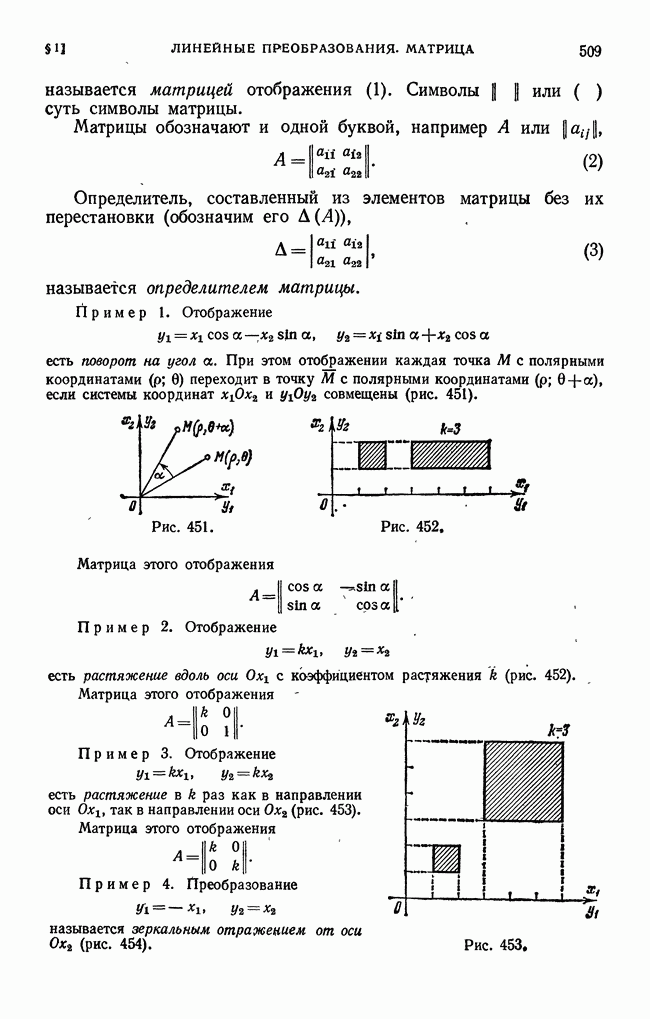
- § 1. Линейные преобразования. Матрица
- § 2. Общие определения, связанные с понятием матрицы
- § 3. Обратное преобразование
- § 4. Действия над матрицами. Сложение матриц
- § 5. Преобразование вектора в другой вектор с помощью матрицы
- § 6. Обратная матрица
- § 7. Нахождение матрицы, обратной данной
- § 8. Матричная запись системы линейных уравнений
- § 9. Решение системы линейных уравнений матричным методом
- § 10. Ортогональные отображения. Ортогональные матрицы
- § 11. Собственный вектор линейного преобразования
- § 12. Матрица линейного преобразования, при котором базисные векторы являются собственными векторами
- § 13. Преобразование матрицы линейного преобразования при переходе от одного базиса к другому
- § 14. Квадратичные формы и их преобразования
- § 15. Ранг матрицы. Существование решений системы линейных уравнений
- § 16. Дифференцирование и интегрирование матриц
- § 17. Матричная запись системы дифференциальных уравнений и решений системы дифференциальных уравнений с постоянными коэффициентами
- § 18. Матричная запись линейного уравнения n-го порядка
- § 19. Решение систем линейных дифференциальных уравнений с переменными коэффициентами методом последовательных приближений с использованием матричной записи
- Упражнения к главе XXI
- ПРИЛОЖЕНИЯ