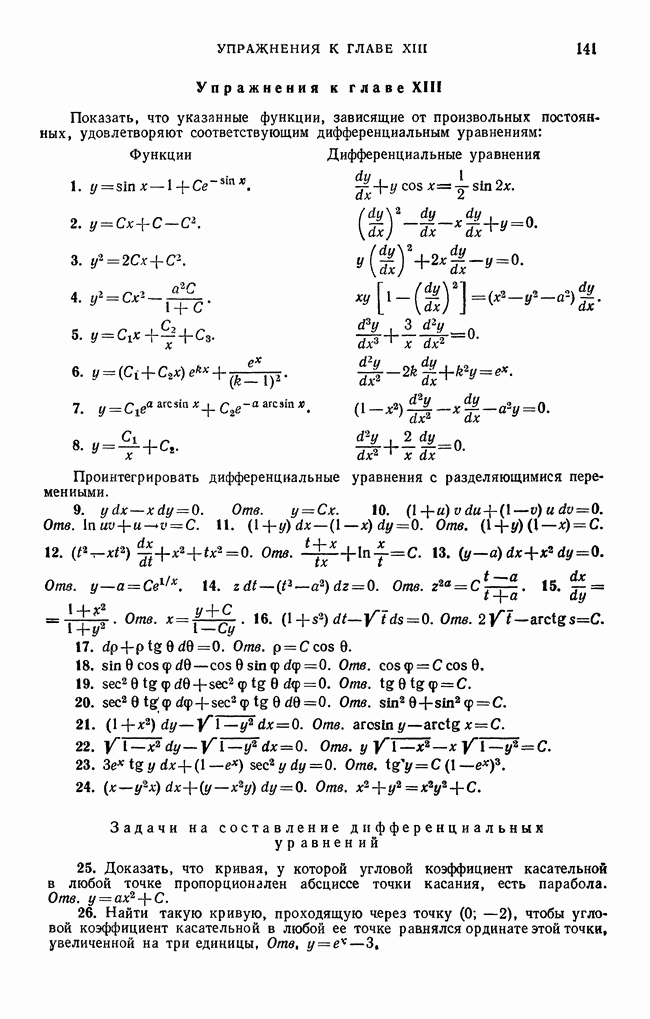| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 31. Понятие о теории устойчивости Ляпунова. Поведение траектории дифференциального уравнения в окрестности особой точки
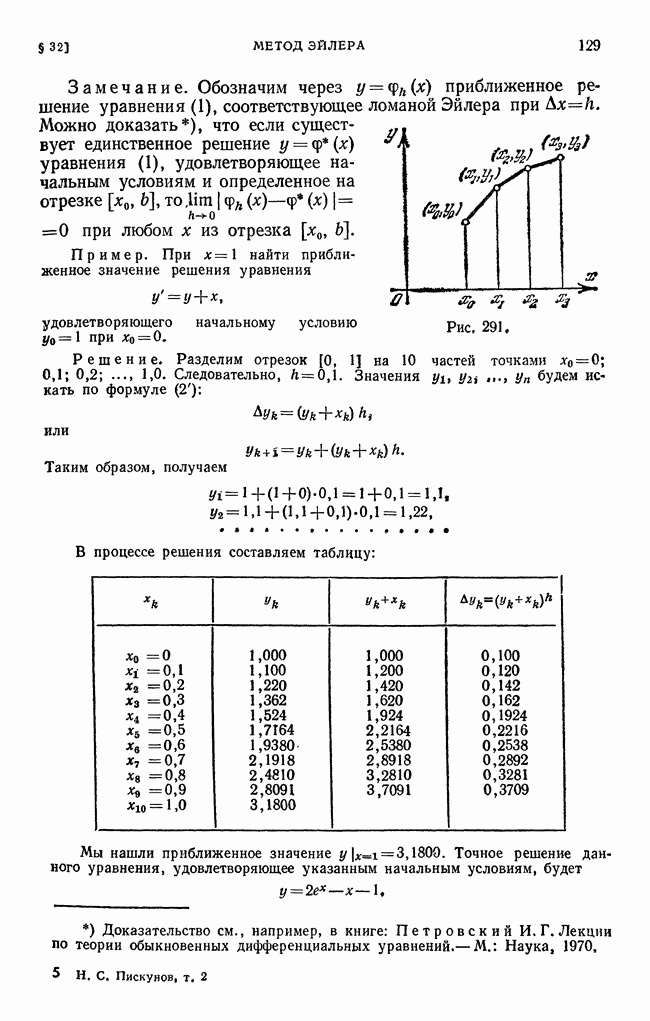
Так как решения большинства дифференциальных уравнений и систем уравнений не выражаются через элементарные функции или квадратуры, то в этих случаях при решении конкретных дифференциальных уравнений применяются приближенные методы интегрирования. Понятие об этих методах было дано в § 3; кроме того, некоторые из этих методов будут рассмотрены в §§ 32—34, а также в главе XVI.
Недостаток этих методов заключается в том, что они дают только одно частное решение; чтобы получить другие частные решения, нужно все вычисления проводить снова. Зная одно частное решение, нельзя сделать заключение о характере других решений.
Во многих задачах механики и техники бывает важно знать не конкретные значения решения при данном конкретном значении аргумента, а характер поведения решения при изменении аргумента и, в частности, при неограниченном возрастании аргумента. Например, бывает важно знать, являются ли решения, удовлетворяющие данным начальным условиям, периодическими, приближаются ли они асимптотически к какой-либо известной функция и т. д. Этими вопросами занимается качественная теория дифференциальных уравнений.
Одним из основных вопросов качественной теории является вопрос об устойчивости решения или об устойчивости движения; этот вопрос был подробно исследован знаменитым русским математиком А. М. Ляпуновым (1857—1918).
Пусть дана система дифференциальных уравнений

Пусть  — решения этой системы, удовлетворяющие начальным условиям
— решения этой системы, удовлетворяющие начальным условиям

Пусть далее,  решения уравнения (1), удовлетворяющие начальным условиям
решения уравнения (1), удовлетворяющие начальным условиям

Определение. Решения  удовлетворяющие уравнениям (1) и начальным условиям
удовлетворяющие уравнениям (1) и начальным условиям  , называются устойчивыми по Ляпунову при
, называются устойчивыми по Ляпунову при  если для каждого как угодно малого
если для каждого как угодно малого  можно указать
можно указать  такое, что при всех значениях
такое, что при всех значениях  будут выполняться неравенства
будут выполняться неравенства

если начальные данные удовлетворяют неравенствам

Выясним смысл этого определения. Из неравенств (2) и (3) следует, что при малых изменениях начальных условий мало отличаются соответствующие решения при всех положительных значениях t. Если система дифференциальных уравнений является системой, описывающей некоторое движение, то в случае устойчивости решений характер движений мало изменяется при малом изменении начальных данных.
Разберем это на примере одного уравнения первого порядка.
Пусть дано дифференциальное уравнение

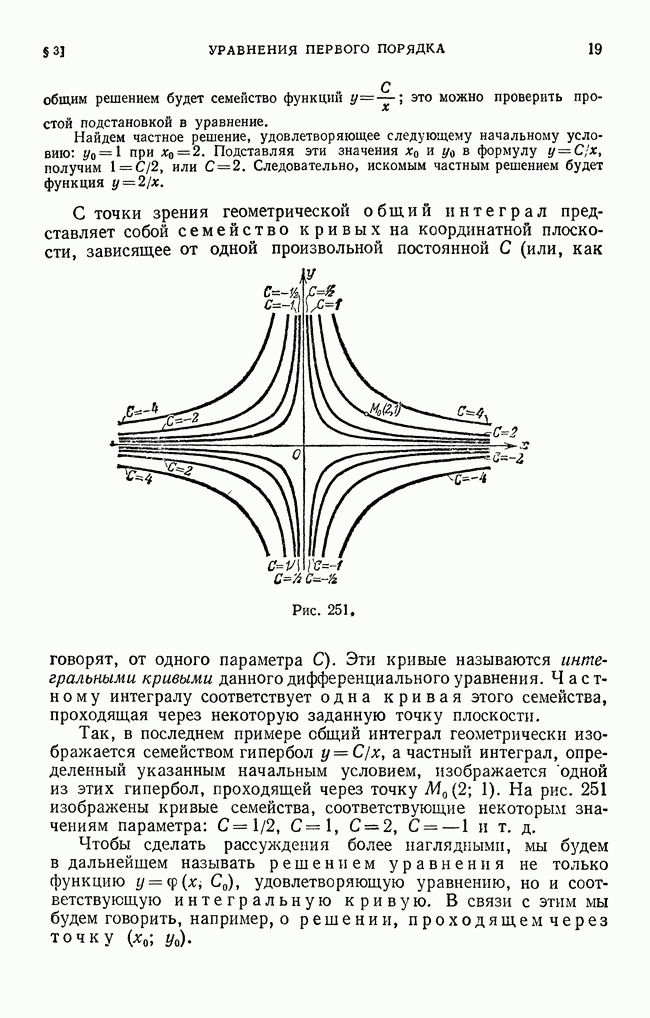
Общим решением этого уравнения является функция

Найдем частное решение, удовлетворяющее начальному условию

Очевидно, что это решение  получится при
получится при  (рис. 281). Найдем, далее, частное решение, удовлетворяющее начальному условию
(рис. 281). Найдем, далее, частное решение, удовлетворяющее начальному условию

Найдем значение С из уравнения (6):

откуда

Подставляя это значение С в равенство (6), получаем

Очевидно, решение  является устойчивым. Действительно,
является устойчивым. Действительно,


Рис. 281.
Следовательно, при произвольном  будет выполняться неравенство (3), если будет выполняться неравенство
будет выполняться неравенство (3), если будет выполняться неравенство

Если уравнения (1) описывают движение, где аргумент t есть время, и при этом уравнения не содержат явно времени t, т. е. имеют вид

то эта система называется автономной.
Рассмотрим, далее, систему линейных дифференциальных уравнений

Будем предполагать, что коэффициенты а, b, с, g постоянные, при этом очевидно, что х = 0, у = 0 есть решение системы (4), в чем убеждаемся непосредственной подстановкой. Исследуем вопрос о том, каким условиям должны удовлетворять коэффициенты системы, чтобы решение х = 0, у = 0 было устойчиво. Эта исследование проводится так.
Дифференцируем первое уравнение и исключаем у и на основании уравнений системы:

или

Характеристическое уравнение дифференциального уравнения (5) имеет вид

Это уравнение принято записывать в виде определителя

(см. уравнение (4) § 30).
Обозначим корни характеристического уравнения (7) через и  . Как мы увидим ниже, устойчивость или неустойчивость решений системы (4) определяется характером корней
. Как мы увидим ниже, устойчивость или неустойчивость решений системы (4) определяется характером корней  . Рассмотрим все возможные случаи,
. Рассмотрим все возможные случаи,
I. Корни характеристического уравнения действительные, отрицательные и различные:  Из уравнения (5) находим
Из уравнения (5) находим

Зная  из первого уравнения (4) находим у. Таким образом, решение системы (4) имеет вид
из первого уравнения (4) находим у. Таким образом, решение системы (4) имеет вид

Замечание. Если  , то уравнение (5) мы составим для функции у. Найдя у, из второго уравнения системы (4) находим х. Структура решений (8) сохранится. Если же
, то уравнение (5) мы составим для функции у. Найдя у, из второго уравнения системы (4) находим х. Структура решений (8) сохранится. Если же  , то решение системы уравнений принимает вид:
, то решение системы уравнений принимает вид:

Анализ характера решений в этом случае производится проще.
Подберем  так, чтобы решения (8) удовлетворяли начальным условиям
так, чтобы решения (8) удовлетворяли начальным условиям

Решение, удовлетворяющее начальным условиям, будет

Из последних равенств следует, что при любом  можно выбирать
можно выбирать  столь малыми, что для всех
столь малыми, что для всех  будет
будет  так как
так как 
Отметим, что в данном случае

Рассмотрим плоскость  Для системы дифференциальных уравнений (4) и дифференциального уравнения (5) эта плоскость называется фазовой плоскостью. Решения (8) и (9) системы (4) будем рассматривать как параметрические уравнения некоторой кривой на фазовой плоскости
Для системы дифференциальных уравнений (4) и дифференциального уравнения (5) эта плоскость называется фазовой плоскостью. Решения (8) и (9) системы (4) будем рассматривать как параметрические уравнения некоторой кривой на фазовой плоскости 

Эти кривые являются интегральными кривыми, или траекториями дифференциального уравнения

которое получается из системы (4) путем деления друг на друга правых и левых частей.
Начало координат  является особой точкой для дифференциального уравнения (13), так как эта точка не принадлежит к области существования и единственности решения.
является особой точкой для дифференциального уравнения (13), так как эта точка не принадлежит к области существования и единственности решения.
Характер решений (9) и вообще решений системы (4) наглядно иллюстрируется расположением интегральных кривых

образующих общий интеграл дифференциального уравнения (13). Постоянная С определяется из начального условия  . После подстановки значения С получаем уравнение семейства в форме
. После подстановки значения С получаем уравнение семейства в форме

В случае решений (9) особая точка называется устойчивым узлом. Говорят, что точка, двигаясь по траектории, неограниченно приближается к особой точке при 
Очевидно, что соотношение (14) может быть получено путем исключения параметра t из системы (12). Не производя в дальнейшем полного анализа характера расположения интегральных кривых вблизи особой точки на фазовой плоскости при всех возможных случаях корней характеристического уравнения, ограничимся иллюстрацией этого на простейших примерах, не требующих проведения громоздких вычислений. Отметим, что характер поведения траекторий уравнения (13) вблизи начала координат при произвольных коэффициентах качественно такой же, какой будет рассмотрен в примерах.
Пример 1. Исследовать устойчивость решения  системы уравнений
системы уравнений

Решение. Характеристическое уравнение будет

Корни характеристического уравнения

Решения (8) в данном случае будут

Решения (9) будут

Очевидно, что  при
при  Решение
Решение  устойчиво. Обратимся теперь к фазовой плоскости. Исключая параметр t из уравнений (а), получаем уравнение вида (14)
устойчиво. Обратимся теперь к фазовой плоскости. Исключая параметр t из уравнений (а), получаем уравнение вида (14)

Это семейство парабол (рис. 282).

Рис. 282.
Уравнение вида (13) для данного примера будет

Интегрируя, получаем  Определим С из условия
Определим С из условия

Подставляя найденное значение  в (в), получаем решение (б). Особая точка
в (в), получаем решение (б). Особая точка  есть устойчивый узел.
есть устойчивый узел.
II. Корни характеристического у равнения действительные, положительные, различные:  , В этом случае решения выражаются также формулами (8) и соответственно (9). Но в данном случае при как угодно малых
, В этом случае решения выражаются также формулами (8) и соответственно (9). Но в данном случае при как угодно малых  будет
будет  при
при  так как
так как  при
при  . На фазовой плоскости особая точка — неустойчивый узел: при
. На фазовой плоскости особая точка — неустойчивый узел: при  точка на траектории удаляется от точки покоя
точка на траектории удаляется от точки покоя 
Пример 2. Исследовать устойчивость решений системы 

Решение. Характеристическое уравнение будет

его решения

Решение будет

Решение неустойчиво, так как  при
при  Исключая t, получаем
Исключая t, получаем

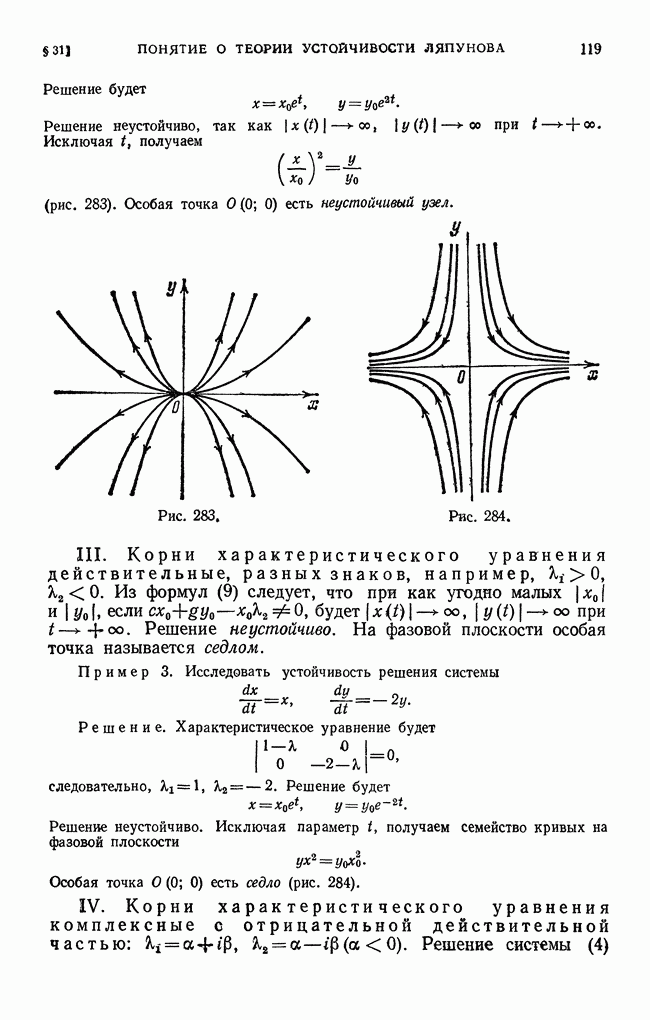
(рис. 283). Особая точка  есть неустойчивый узел.
есть неустойчивый узел.

Рис. 283,

Рис. 284.
III. Корни характеристического уравнения действительные, разных знаков, например,  . Из формул (9) следует, что при как угодно малых
. Из формул (9) следует, что при как угодно малых  если
если  , будет
, будет  при
при  . Решение неустойчиво. На фазовой плоскости особая точка называется седлом.
. Решение неустойчиво. На фазовой плоскости особая точка называется седлом.
Пример 3. Исследовать устойчивость решения системы 

Решение. Характеристическое уравнение будет

следовательно,  . Решение будет
. Решение будет

Решение неустойчиво. Исключая параметр t, получаем семейство кривых на фазовой плоскости

Особая точка  есть седло (рис. 284).
есть седло (рис. 284).
IV. Корни характеристического уравнения комплексные с отрицательной действительной частью:  . Решение системы (4)
. Решение системы (4)
будет

Если ввести обозначение

то уравнения (15) можно переписать в виде  ,
,

где  - произвольные постоянные, которые определяются из начальных условий
- произвольные постоянные, которые определяются из начальных условий  при
при  причем
причем

откуда находим

Снова заметим, что если  то вид решения будет несколько иной, но характер анализа не изменится.
то вид решения будет несколько иной, но характер анализа не изменится.
Очевидно, что при любом  при достаточно малых
при достаточно малых  будут выполняться соотношения
будут выполняться соотношения

Решение устойчиво. В данном случае при 

неограниченное число раз меняя знаки. На фазовой плоскости особая точка называется устойчивым фокусом.
Пример 4. Исследовать устойчивость решения системы уравнений 

Решение. Составляем характеристическое уравнение и находим его корни:

Находим  по формулам
по формулам  Подставляя в (15), получаем
Подставляя в (15), получаем

Очевидно, что при любых значениях 

При  имеем
имеем  . Решение устойчиво.
. Решение устойчиво.
Выясним характер расположения кривых на фазовой плоскости в этом случае. Преобразуем выражения (А). Пусть

Тогда равенства (А) примут вид

На фазовой плоскости перейдем к полярным координатам  и установим зависимость
и установим зависимость  Уравнения (В) принимают вид
Уравнения (В) принимают вид

Возведя в квадрат правые и левые части и складывая, получим

или

Установим зависимость t от 0. Деля члены нижнего из равенств (С) на соответствующие члены верхнего равенства, получим

откуда

Подставляя в (D), получаем

или

Обозначая  окончательно получаем
окончательно получаем

Это семейство логарифмических спиралей. В этом случае при  точка по траектории приближается к началу координат. Особая точка
точка по траектории приближается к началу координат. Особая точка  есть устойчивый фокус.
есть устойчивый фокус.
V. Корни характеристического уравнения комплексные с положительной действительной частью:  . В этом случае решение также выразится формулами (15), где
. В этом случае решение также выразится формулами (15), где  При любых начальных условиях
При любых начальных условиях  и при
и при  величины
величины  могут принимать как угодно большие значения, решение неустойчиво. На фазовой плоскости особая точка называется неустойчивым фокусом. Точка по траектории неограниченно удаляется от начала координат.
могут принимать как угодно большие значения, решение неустойчиво. На фазовой плоскости особая точка называется неустойчивым фокусом. Точка по траектории неограниченно удаляется от начала координат.
Пример 5. Исследовать устойчивость решения системы уравнений

Решение. Составим характеристическое уравнение:

Решение (15) с учетом (17) в данном случае будет

На фазовой плоскости получим кривую в полярных координатах

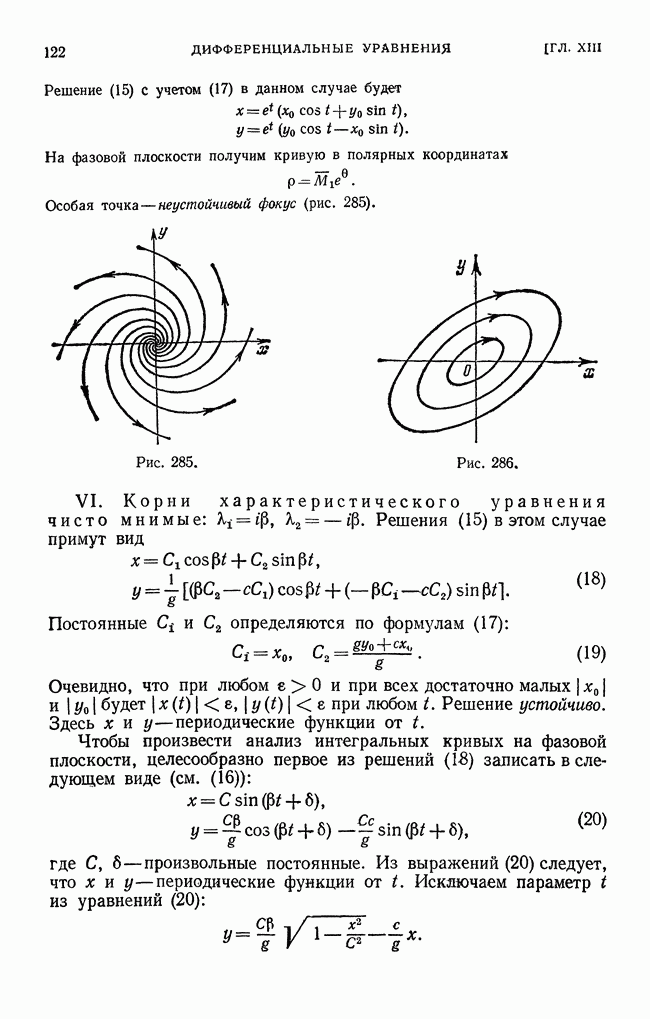
Особая точка — неустойчивый фокус (рис. 285).

Рис. 285.

Рис. 286.
VI. Корни характеристического уравнения чисто мнимые:  . Решения (15) в этом случае примут вид
. Решения (15) в этом случае примут вид

Постоянные Q и  определяются по формулам (17):
определяются по формулам (17):

Очевидно, что при любом  и при всех достаточно малых
и при всех достаточно малых  будет
будет  при любом t. Решение устойчиво. Здесь х и у — периодические функции от t.
при любом t. Решение устойчиво. Здесь х и у — периодические функции от t.
Чтобы произвести анализ интегральных кривых на фазовой плоскости, целесообразно первое из решений (1-8) записать в следующем виде (см. (16)):

где  — произвольные постоянные. Из выражений (20) следует, что х и у — периодические функции от t. Исключаем параметр t из уравнений (20):
— произвольные постоянные. Из выражений (20) следует, что х и у — периодические функции от t. Исключаем параметр t из уравнений (20):

Освобождаясь от радикала, получим

Это семейство кривых  порядка (кривые действительные), зависящих от произвольной постоянной С. Каждая из них не имеет неограниченно удаленных точек. Следовательно, это семейство эллипсов, окружающих начало координат
порядка (кривые действительные), зависящих от произвольной постоянной С. Каждая из них не имеет неограниченно удаленных точек. Следовательно, это семейство эллипсов, окружающих начало координат  эллипсов параллельны осям координат). Особая точка называется центром (рис. 286).
эллипсов параллельны осям координат). Особая точка называется центром (рис. 286).
Пример 6. Исследовать устойчивость решения системы уравнений 

Решение. Составим характеристическое уравнение и найдем его корни:

Решения (20) будут

Уравнение (21) будет иметь вид

На фазовой плоскости имеем систему эллипсов. Особая точка — центр.
VII. Пусть  Решение (8) в этом случае принимает вид
Решение (8) в этом случае принимает вид

Очевидно, что при любом  и при достаточно малых
и при достаточно малых  будет
будет  при
при  . Следовательно, решение устойчиво.
. Следовательно, решение устойчиво.
Пример 7. Исследовать устойчивость решения системы

Решение. Находим корни характеристического уравнения;

Здесь  Решения находим непосредственно, решая систему, не пользуясь формулами (22):
Решения находим непосредственно, решая систему, не пользуясь формулами (22):

Решение, удовлетворяющее начальным условиям  при
при  будет
будет

Очевидно, что решение устойчиво. Дифференциальное уравнение на фазовой плоскости будет  Общий интеграл будет
Общий интеграл будет  . Траектории — прямые,
. Траектории — прямые,
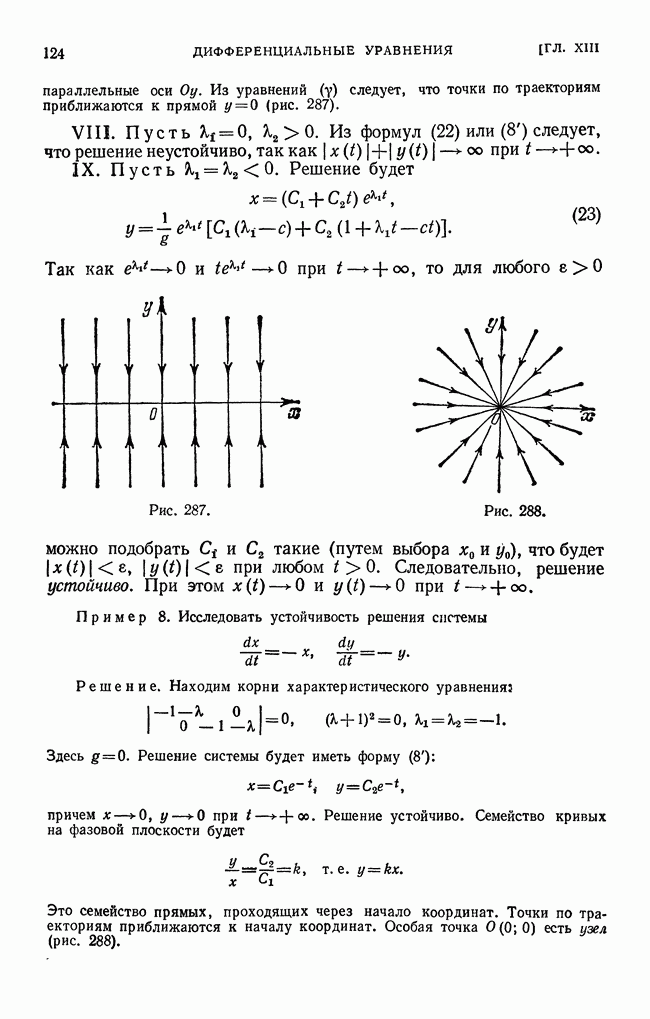
параллельные оси Оу. Из уравнений  следует, что точки по траекториям приближаются к прямой у = 0 (рис. 287).
следует, что точки по траекториям приближаются к прямой у = 0 (рис. 287).
VIII. Пусть  . Из формул (22) или (8) следует, что решение неустойчиво, так как
. Из формул (22) или (8) следует, что решение неустойчиво, так как  при
при 
Пусть  Решение будет
Решение будет

Так как  при
при  , то для любого е>0 можно подобрать
, то для любого е>0 можно подобрать  такие (путем выбора
такие (путем выбора  что будет
что будет  при любом
при любом 

Рис. 287.

Рис. 288.
Следовательно, решение устойчиво. При этом  при
при 
Пример 8. Исследовать устойчивость решения системы 

Решение. Находим корни характеристического уравнения;

Здесь  Решение системы будет иметь форму (8):
Решение системы будет иметь форму (8):

причем  при
при  Решение устойчиво. Семейство кривых на фазовой плоскости будет
Решение устойчиво. Семейство кривых на фазовой плоскости будет
т.е.

Это семейство прямых, проходящих через начало координат. Точки по траекториям приближаются к началу координат. Особая точка  есть узел (рис. 288).
есть узел (рис. 288).
Заметим, что в случае  форма решения (22) сохраняется, но при
форма решения (22) сохраняется, но при 

Решение неустойчиво.
X. Пусть  . Тогда
. Тогда

Откуда видно, что  при
при  . Решение неустойчиво.
. Решение неустойчиво.
Пример 9. Исследовать устойчивость решения системы уравнений

Решение. Находим корни характеристического уравнения:

Находим решения

Очевидно, что  Решение неустойчиво. Уравнение на фазовой плоскости будет
Решение неустойчиво. Уравнение на фазовой плоскости будет 

Рис. 289.

Рис. 290.
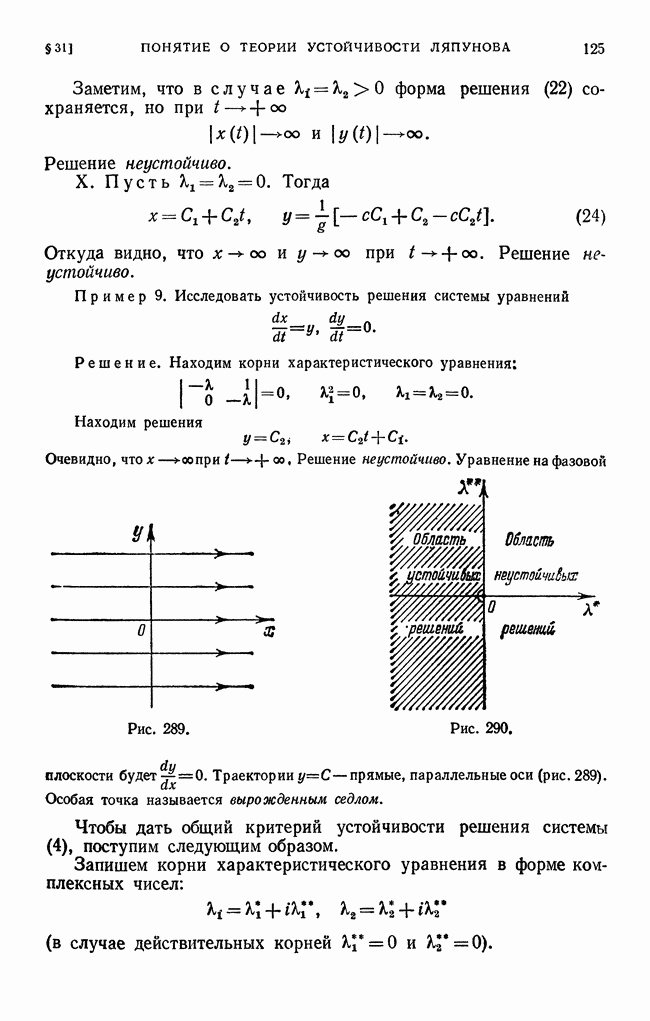
Траектории  прямые, параллельные оси (рис. 289). Особая точка называется вырожденным седлом.
прямые, параллельные оси (рис. 289). Особая точка называется вырожденным седлом.
Чтобы дать общий критерий устойчивости решения системы (4), поступим следующим образом.
Запишем корни характеристического уравнения в форме комплексных чисел:

(в случае действительных корней  ).
).
Возьмем плоскость  комплексной переменной и будем изображать корни характеристического уравнения точками на этой плоскости. Тогда на основании рассмотренных случаев условие устойчивости решения системы (4) можно сформулировать следующим образом.
комплексной переменной и будем изображать корни характеристического уравнения точками на этой плоскости. Тогда на основании рассмотренных случаев условие устойчивости решения системы (4) можно сформулировать следующим образом.
Если ни один из корней  , характеристического уравнения (6) не лежит справа от мнимой оси, причем хотя бы один корень отличен от нуля, то решение устойчиво; если же хотя бы один корень лежит справа от мнимой оси или оба корня равны нулю, то решение неустойчиво (рис. 290).
, характеристического уравнения (6) не лежит справа от мнимой оси, причем хотя бы один корень отличен от нуля, то решение устойчиво; если же хотя бы один корень лежит справа от мнимой оси или оба корня равны нулю, то решение неустойчиво (рис. 290).
Рассмотрим теперь более общую систему уравнений

Решение такой системы, кроме исключительных случаев, не выражается через элементарные функции и квадратуры.
Для того чтобы установить, устойчивы или неустойчивы решения этой системы, ее сравнивают о решениями линейной системы. Предположим, что при  функции
функции  также стремятся к нулю и притом быстрее, чем
также стремятся к нулю и притом быстрее, чем  , где
, где  иными словами,
иными словами,

Тогда можно доказать, что, кроме исключительного случая, решение системы (25) будет устойчиво тогда, когда устойчиво решение системы

и неустойчиво, когда решение системы (4) неустойчиво. Исключение составляет тот случай, когда оба корня характеристического уравнения лежат на мнимой оси; в этом случае вопрос об устойчивости или неустойчивости решения системы (25) решается значительно сложнее.
А. М. Ляпунов исследовал вопрос об устойчивости решений систем уравнений при довольно общих предположениях относительно вида этих уравнений.
В теории колебаний часто рассматривают уравнение

Обозначим

Фазовой плоскостью для этой системы будет плоскость  Траектории на фазовой плоскости дают геометрическое изображение зависимости скорости v от координаты х и наглядно качественно характеризуют изменение х и v. Если точка
Траектории на фазовой плоскости дают геометрическое изображение зависимости скорости v от координаты х и наглядно качественно характеризуют изменение х и v. Если точка  является особой точкой, то она определяет положение равновесия.
является особой точкой, то она определяет положение равновесия.
Так, например, если особая точка системы уравнений есть центр, т. е. траектории на фазовой плоскости представляют собой замкнутые линии, окружающие начало координат, то движения, определяемые уравнением  незатухающие колебательные движения. Если особая точка фазовой плоскости есть фокус (при этом
незатухающие колебательные движения. Если особая точка фазовой плоскости есть фокус (при этом  при
при  то движения, определяемые уравнением
то движения, определяемые уравнением  затухающие колебания. Если особая точка есть узел или седло (и это единственная особая точка), то
затухающие колебания. Если особая точка есть узел или седло (и это единственная особая точка), то  при
при  . В этом случае движущаяся материальная точка уходит в бесконечность.
. В этом случае движущаяся материальная точка уходит в бесконечность.

Если уравнение (26) линейное вида то система  имеет вид
имеет вид

Это система вида (4). Точка  есть особая точка, она определяет положение равновесия. Отметим, что переменная
есть особая точка, она определяет положение равновесия. Отметим, что переменная  не обязательно механическое перемещение точки. Она может иметь различный физический смысл, например, обозначать величину, характеризующую электрические колебания.
не обязательно механическое перемещение точки. Она может иметь различный физический смысл, например, обозначать величину, характеризующую электрические колебания.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К ДЕВЯТОМУ ИЗДАНИЮ
- ПРЕДИСЛОВИЕ К ПЯТОМУ ИЗДАНИЮ
- ГЛАВА XIII. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
- § 1. Постановка задачи. Уравнение движения тела при сопротивлении среды, пропорциональном скорости. Уравнение цепной линии
- § 2. Определения
- § 3. Дифференциальные уравнения первого порядка (общие понятия)
- § 4. Уравнения с разделенными и разделяющимися переменными. Задача о распаде радия
- § 5. Однородные уравнения первого порядка
- § 6. Уравнения, приводящиеся к однородным
- § 7. Линейные уравнения первого порядка
- § 8. Уравнение Бернулли
- § 9. Уравнение в полных дифференциалах
- § 10. Интегрирующий множитель
- § 11. Огибающая семейства кривых
- § 12. Особые решения дифференциального уравнения первого порядка
- § 13. Уравнение Клеро
- § 14. Уравнение Лагранжа
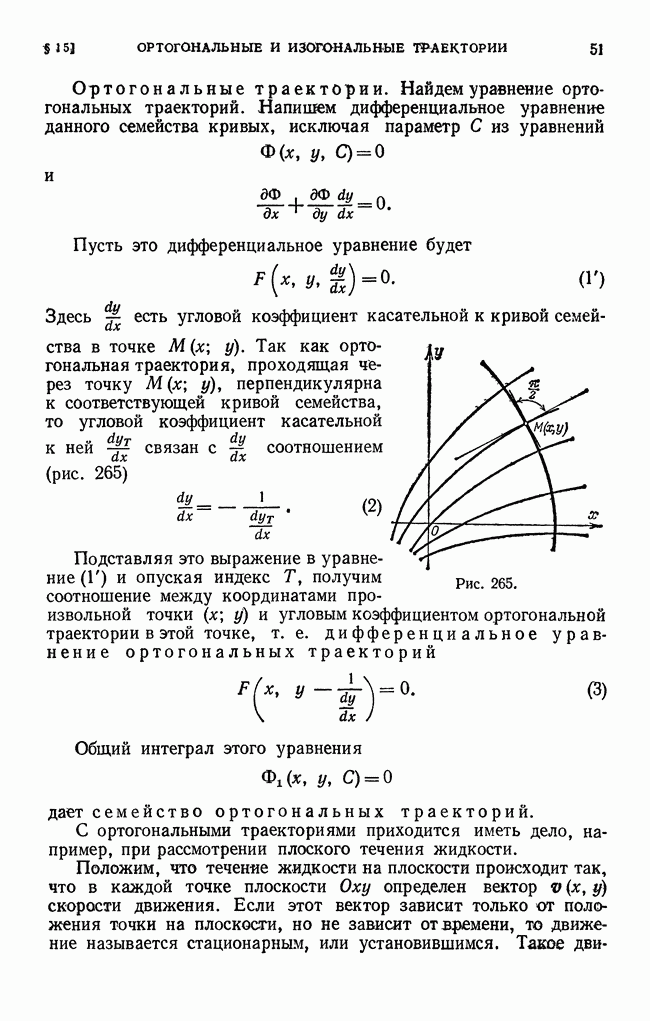
- § 15. Ортогональные и изогональные траектории
- § 16. Дифференциальные уравнения высших порядков (общие понятия)
- § 17. Уравнение вида y^(n) = f(x)
- § 18. Некоторые типы дифференциальных уравнений второго порядка, приводимых к уравнениям первого порядка. Задача о второй космической скорости
- § 19. Графический метод интегрирования дифференциального уравнения второго порядка
- § 20. Линейные однородные уравнения. Определения и общие свойства
- § 21. Линейные однородные уравнения второго порядка с постоянными коэффициентами
- § 22. Линейные однородные уравнения n-го порядка с постоянными коэффициентами
- § 23. Неоднородные линейные уравнения второго порядка
- § 24. Неоднородные линейные уравнения второго порядка с постоянными коэффициентами
- § 25. Неоднородные линейные уравнения высших порядков
- § 26. Дифференциальное уравнение механических колебаний
- § 27. Свободные колебания. Векторное и комплексное изображение гармонических колебаний
- § 28. Вынужденные колебания
- § 29. Системы обыкновенных дифференциальных уравнений
- § 30. Системы линейных дифференциальных уравнений с постоянными коэффициентами
- § 31. Понятие о теории устойчивости Ляпунова. Поведение траектории дифференциального уравнения в окрестности особой точки
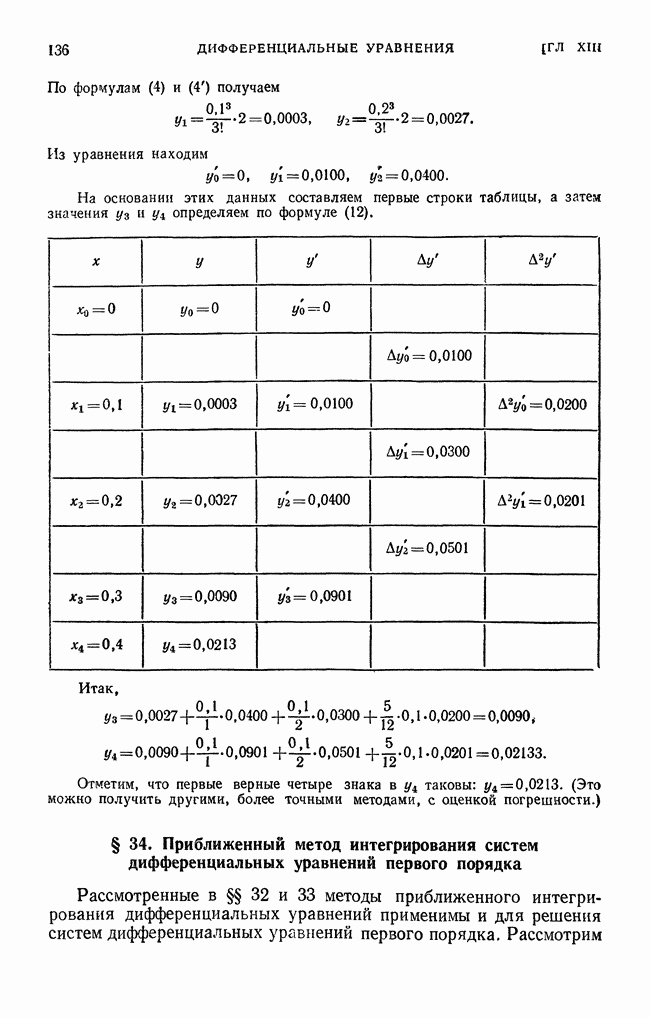
- § 32. Приближенное решение дифференциальных уравнений первого порядка методом Эйлера
- § 33. Разностный метод приближенного решения дифференциальных уравнений, основанный на применении формулы Тейлора.. Метод Адамса
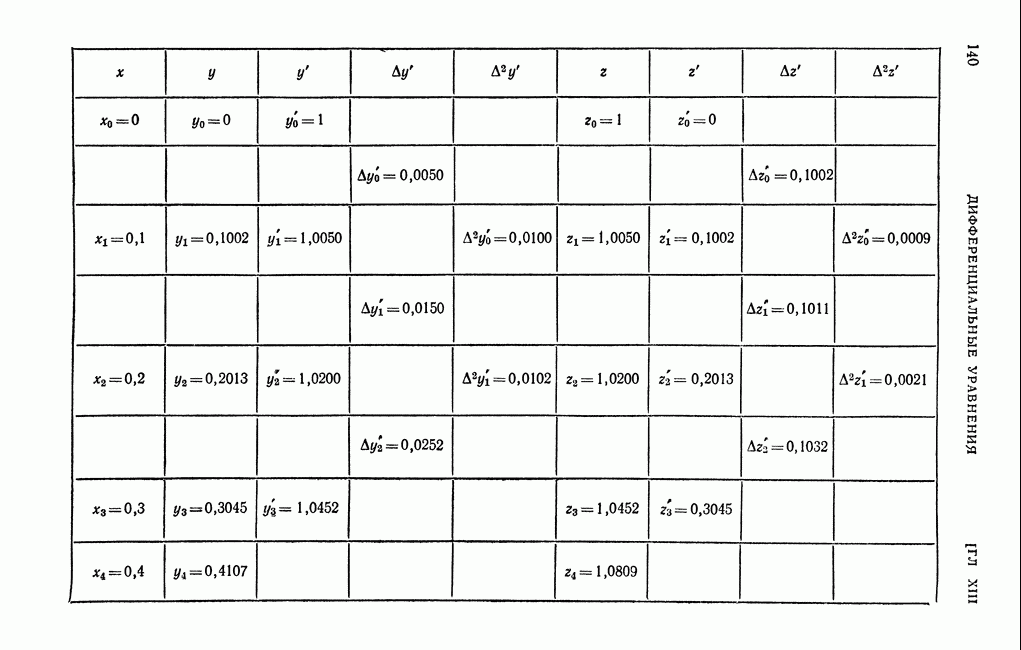
- § 34. Приближенный метод интегрирования систем дифференциальных уравнений первого порядка
- Упражнения к главе XIII
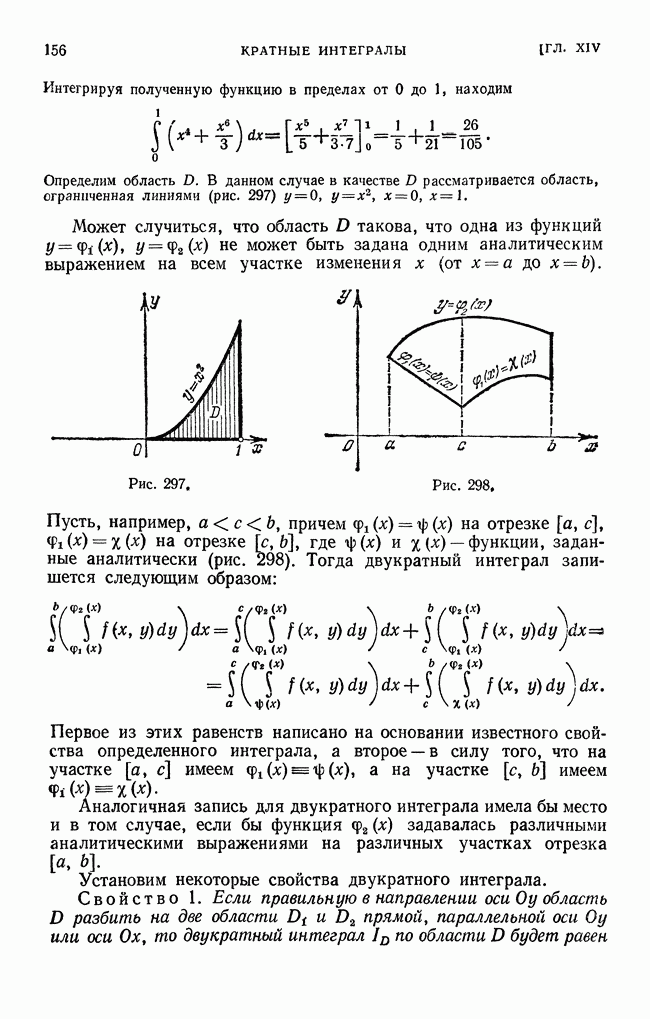
- ГЛАВА XIV. КРАТНЫЕ ИНТЕГРАЛЫ
- § 2. Вычисление двойного интеграла
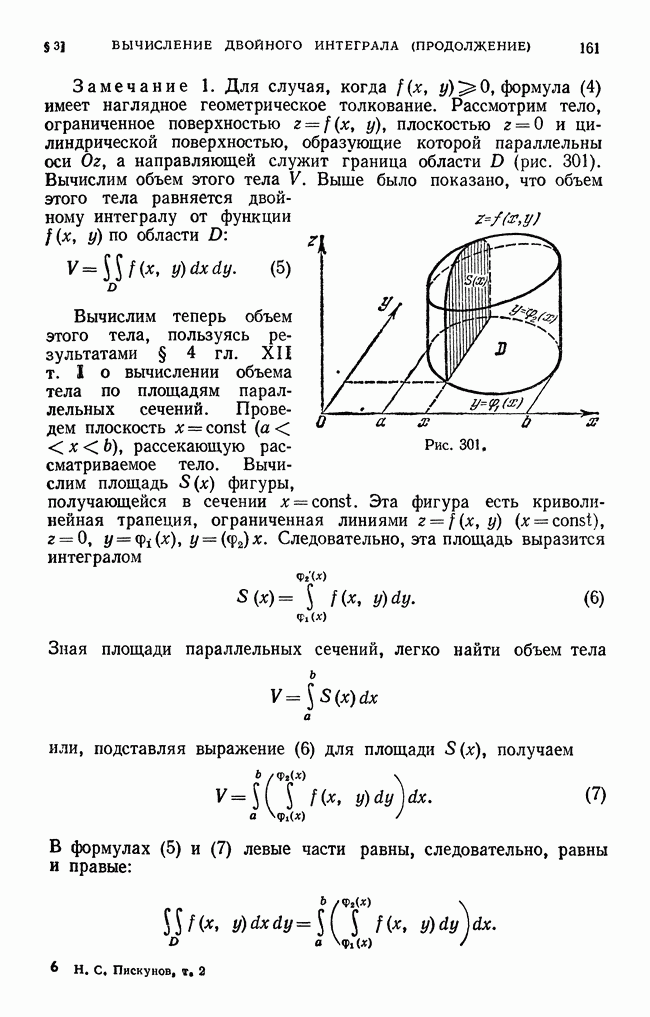
- § 3. Вычисление двойного интеграла (продолжение)
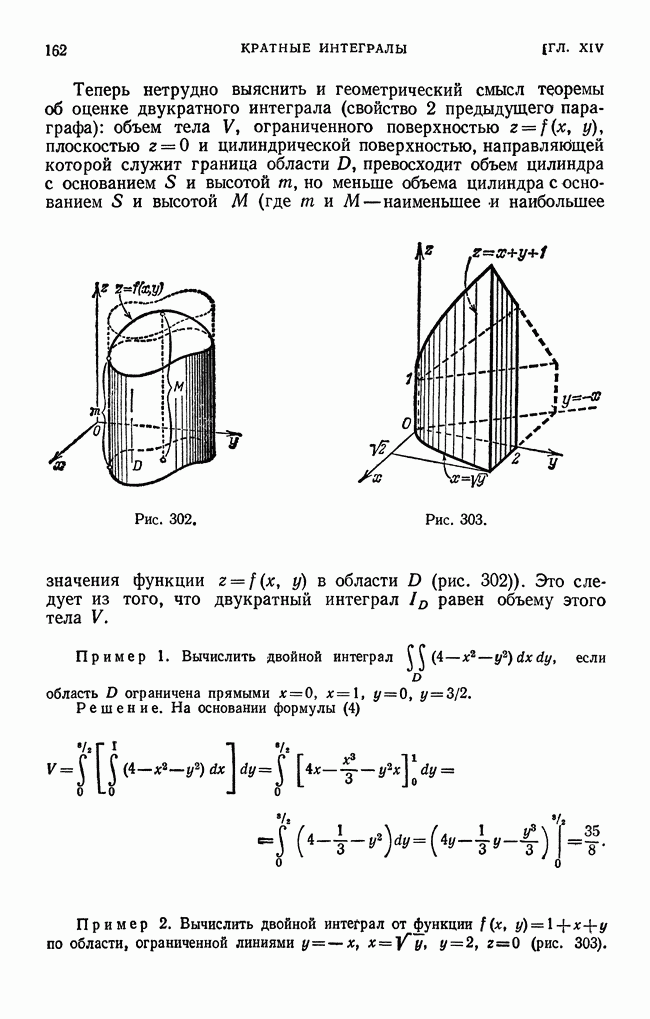
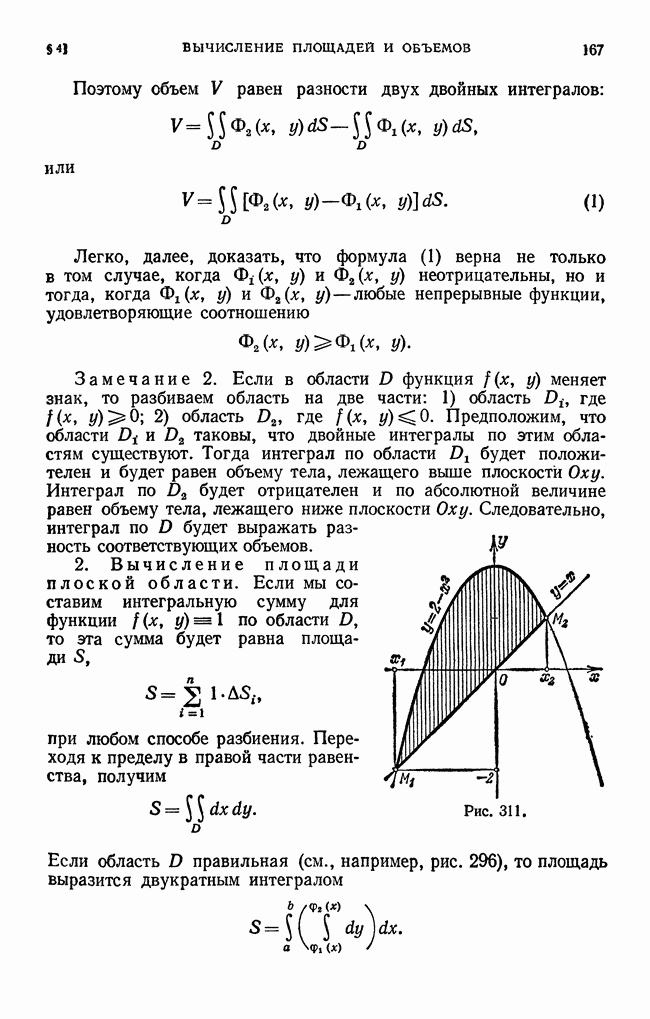
- § 4. Вычисление площадей и объемов с помощью двойных интегралов
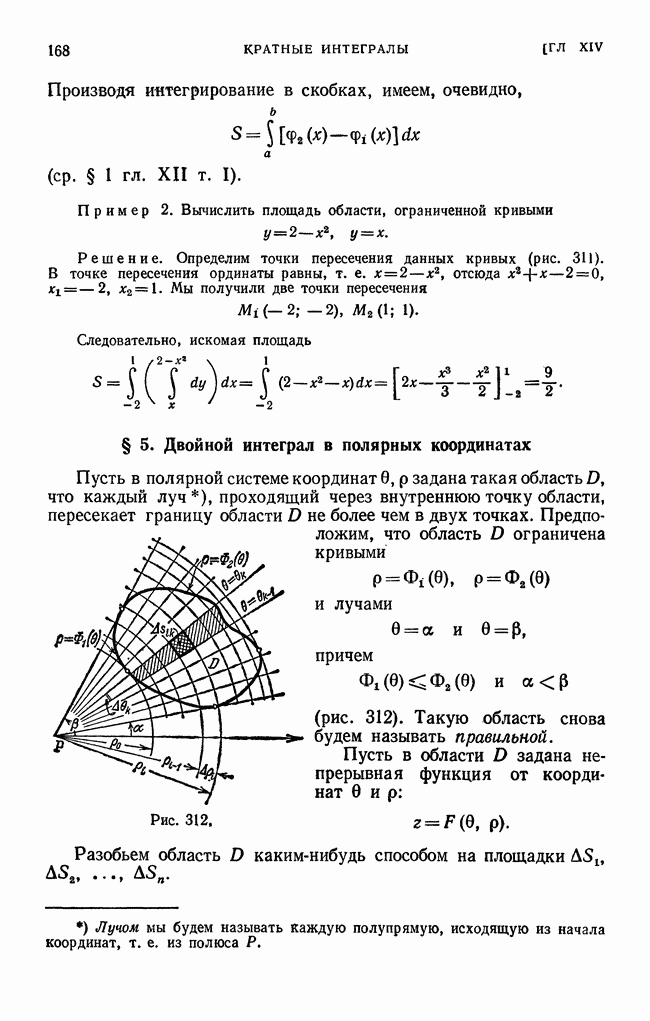
- § 5. Двойной интеграл в полярных координатах
- § 6. Замена переменных в двойном интеграле (общий случай)
- § 7. Вычисление площади поверхности
- § 9. Момент инерции площади плоской фигуры
- § 10. Координаты центра масс площади плоской фигуры
- § 11. Тройной интеграл
- § 12. Вычисление тройного интеграла
- § 13. Замена переменных в тройном интеграле
- § 14. Момент инерции и координаты центра масс тела
- § 15. Вычисление интегралов, зависящих от параметра
- Упражнения к главе XIV
- ГЛАВА XV. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ И ИНТЕГРАЛЫ ПО ПОВЕРХНОСТИ
- § 2. Вычисление криволинейного интеграла
- § 3. Формула Грина
- § 4. Условия независимости криволинейного интеграла от пути интегрирования
- § 5. Поверхностный интеграл
- § 6. Вычисление поверхностного интеграла
- § 7. Формула Стокса
- § 9. Оператор Гамильтона. Некоторые его применения
- Упражнения к главе XV
- ГЛАВА XVI. РЯДЫ
- § 1. Ряд. Сумма ряда
- § 2. Необходимый признак сходимости ряда
- § 3. Сравнение рядов с положительными членами
- § 4. Признак Даламбера
- § 5. Признак Коши
- § 6. Интегральный признак сходимости ряда
- § 7. Знакочередующиеся ряды. Теорема Лейбница
- § 8. Знакопеременные ряды. Абсолютная и условная сходимость
- § 9. Функциональные ряды
- § 10. Мажорируемые ряды
- § 11. Непрерывность суммы ряда
- § 12. Интегрирование и дифференцирование рядов
- § 13. Степенные ряды. Интервал сходимости
- § 14. Дифференцирование степенных рядов
- § 15. Ряды по степеням x-a
- § 16. Ряды Тейлора и Маклорена
- § 17. Примеры разложения функций в ряды
- § 18. Формула Эйлера
- § 19. Биномиальный ряд
- § 20. Разложение функции ln(1+x) в степенной ряд. Вычисление логарифмов
- § 21. Вычисление определенных интегралов с помощью рядов
- § 22. Интегрирование дифференциальных уравнений с помощью рядов
- § 23. Уравнение Бесселя
- § 24. Ряды с комплексными членами
- § 25. Степенные ряды с комплексной переменной
- § 26. Решение дифференциального уравнения первого порядка методом последовательных приближений (метод итераций)
- § 27. Доказательство существования решения дифференциального уравнения. Оценка погрешности при приближенном решении
- § 28. Теорема единственности решения дифференциального уравнения
- Упражнения к главе XVI
- ГЛАВА XVII. РЯДЫ ФУРЬЕ
- § 2. Примеры разложения функций в ряды Фурье
- § 3. Одно, замечание о разложении периодической функции в ряд Фурье
- § 4. Ряды Фурье для четных и нечетных функций
- § 5. Ряд Фурье для функции с периодом 2l
- § 6. О разложении непериодической функции в ряд Фурье
- § 7. Приближение в среднем заданной функции с помощью тригонометрического многочлена
- § 8. Интеграл Дирихле
- § 9. Сходимость ряда Фурье в данной точке
- § 10. Некоторые достаточные условия сходимости ряда Фурье
- § 11. Практический гармонический анализ
- § 12. Ряд Фурье в комплексной форме
- § 13. Интеграл Фурье
- § 14. Интеграл Фурье в комплексной форме
- § 15. Ряд Фурье по ортогональной системе функций
- § 16. Понятие о линейном функциональном пространстве. Аналогия между разложением функций в ряд Фурье и разложением векторов
- Упражнения к главе XVII
- ГЛАВА XVIII. УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ
- § 1. Основные типы уравнений математической физики
- § 2. Вывод уравнения колебаний струны. Формулировка краевой задачи. Вывод уравнений электрических колебаний в проводах
- § 3. Решение уравнения колебаний струны методом разделения переменных (методом Фурье)
- § 4. Уравнение распространения тепла в стержне. Формулировка краевой задачи
- § 5. Распространение тепла в пространстве
- § 6. Решение первой краевой задачи для уравнения теплопроводности методом конечных разностей
- § 7. Распространение тепла в неограниченном стержне
- § 8. Задачи, приводящие к исследованию решений уравнения Лапласа. Формулировка краевых задач
- § 9. Уравнение Лапласа в цилиндрических координатах. Решение задачи Дирихле для кольца с постоянными значениями искомой функции на внутренней и внешней окружностях
- § 10. Решение задачи Дирихле для круга
- § 11. Решение задачи Дирихле методом конечных разностей
- Упражнения к главе XVIII
- ГЛАВА XIX. ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ И НЕКОТОРЫЕ ЕГО ПРИЛОЖЕНИЯ
- § 1. Начальная функция и ее изображение
- § 2. Изображение функций …
- § 3. Изображение функции с измененным масштабом независимой переменной. Изображение функций sin at, cos at
- § 4. Свойство линейности изображения
- § 5. Теорема смещения
- § 6. Изображение функций …
- § 7. Дифференцирование изображения
- § 8. Изображение производных
- § 9. Таблица некоторых изображений
- § 10. Вспомогательное уравнение для данного дифференциального уравнения
- § 11. Теорема разложения
- § 12. Примеры решения дифференциальных уравнений и систем дифференциальных уравнений операционным методом
- § 13. Теорема свертывания
- § 14. Дифференциальные уравнения механических колебаний. Дифференциальные уравнения теории электрических цепей
- § 15. Решение дифференциального уравнения колебаний
- § 16. Исследование свободных колебаний
- § 17. Исследование механических и электрических колебаний в случае периодической внешней силы
- § 18. Решение уравнения колебаний в случае резонанса
- § 19. Теорема запаздывания
- § 20. Дельта-функция и ее изображение
- Упражнения к главе XIX
- ГЛАВА XX. ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
- § 1. Случайное событие. Относительная частота случайного события. Вероятность события. Предмет теории вероятностей
- § 2. Классическое определение вероятности и непосредственный подсчет вероятностей
- § 3. Сложение вероятностей. Противоположные случайные события
- § 4. Умножение вероятностей независимых событий
- § 5. Зависимые события. Условная вероятность. Полная вероятность
- § 6. Вероятность гипотез. Формула Байеса
- § 7. Дискретная случайная величина. Закон распределения дискретной случайной величины
- § 8. Относительная частота и вероятность относительной частоты при повторных испытаниях
- § 9. Математическое ожидание дискретной случайной величины
- § 10. Дисперсия. Среднеквадратичное отклонение. Понятие о моментах
- § 11. Функции от случайных величин
- § 12. Непрерывная случайная величина. Плотность распределения непрерывной случайной величины. Вероятность попадания случайной величины в заданный интервал
- § 13. Функция распределения, или интегральный закон распределения. Закон равномерного распределения вероятностей
- § 14. Числовые характеристики непрерывной случайной величины
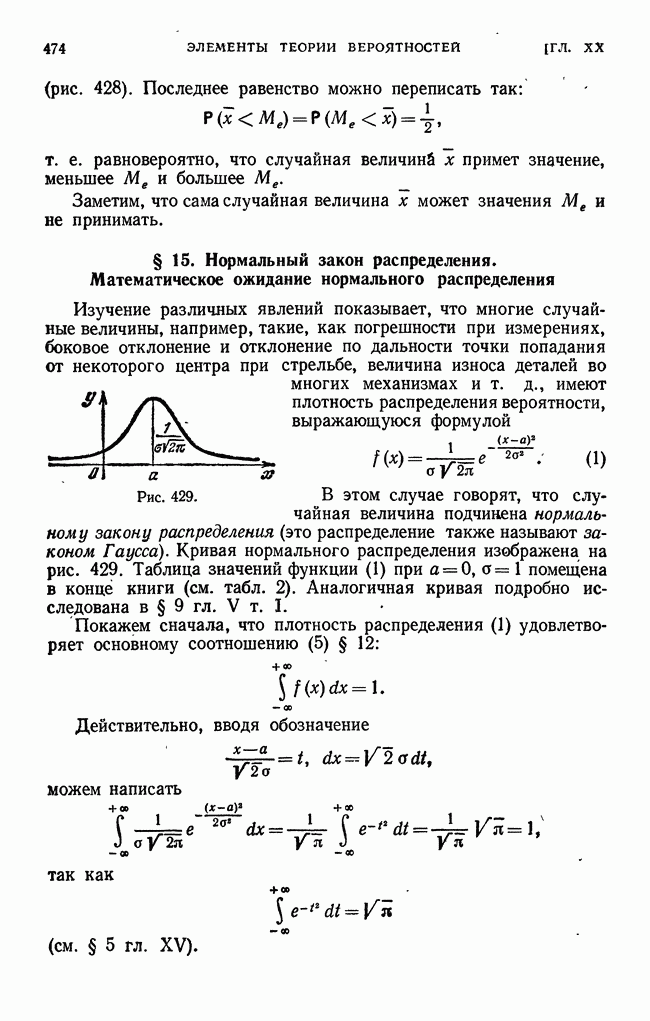
- § 15. Нормальный закон распределения. Математическое ожидание нормального распределения
- § 16. Дисперсия и среднеквадратичное отклонение случайной величины, подчиненной нормальному закону распределения
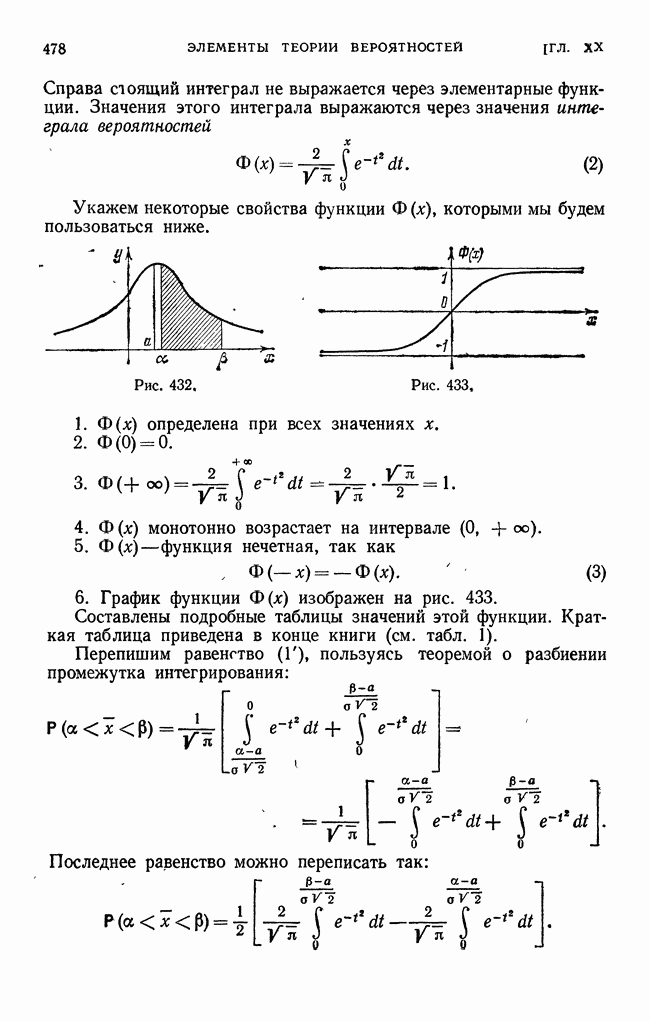
- § 17. Вероятность попадания значения случайной величины в заданный интервал. Функция Лапласа. Интегральная функция распределения для нормального закона
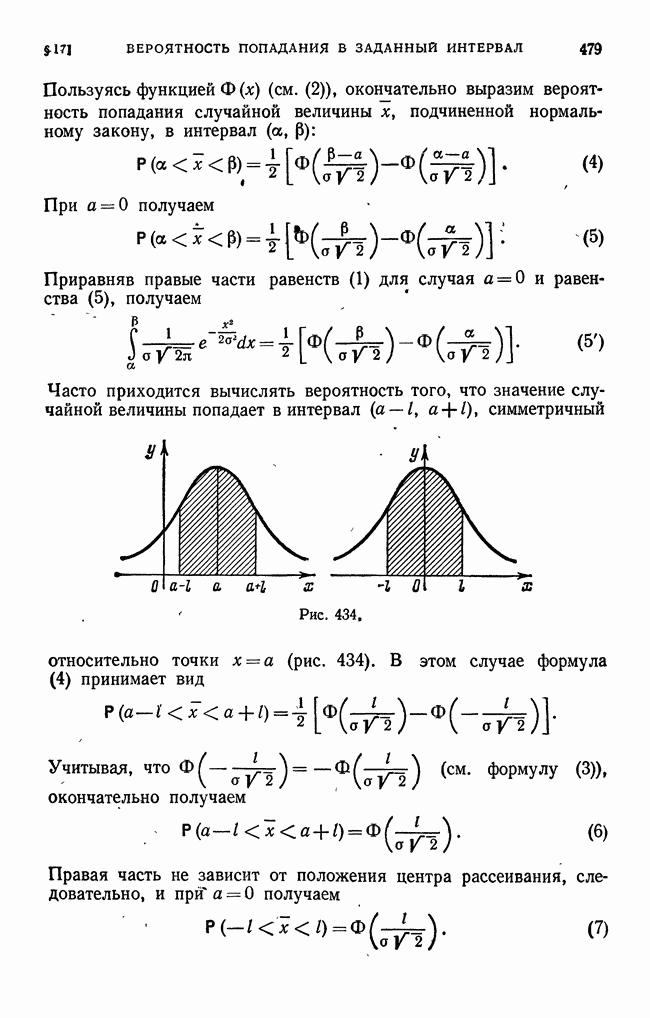
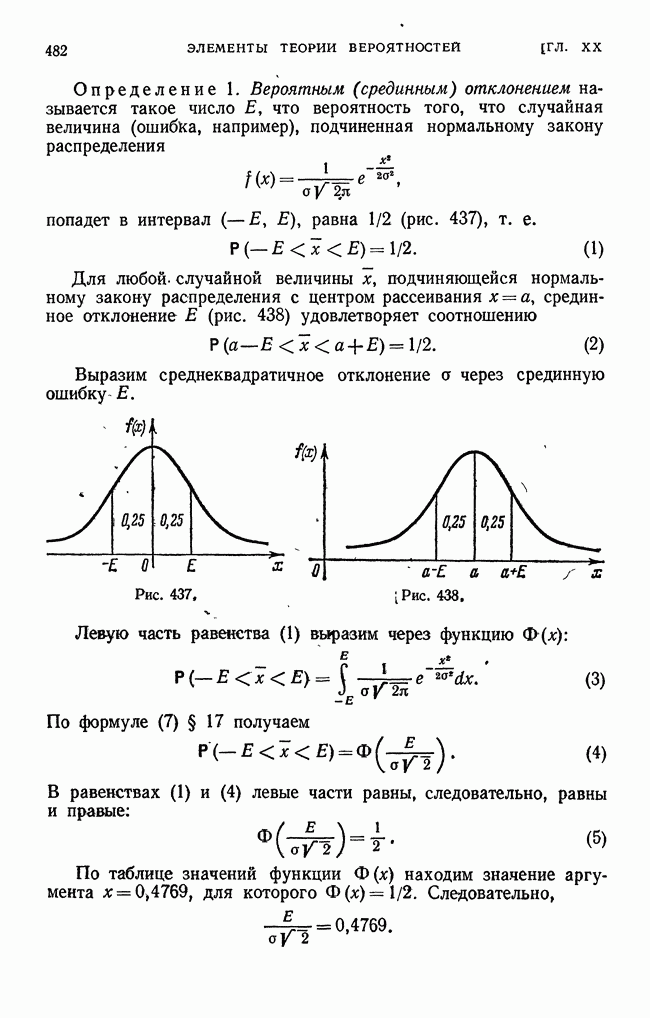
- § 18. Вероятное (срединное) отклонение или срединная ошибка
- § 19. Выражение нормального закона распределения через срединное отклонение. Приведенная функция Лапласа
- § 20. Правило трех сигм. Шкала вероятностей распределения ошибок
- § 21. Среднеарифметическая ошибка
- § 22. Мера точности. Соотношение между характеристиками распределения ошибок
- § 23. Двумерная случайная величина
- § 24. Нормальный закон распределения на плоскости
- § 25. Вероятность попадания двумерной случайной величины в прямоугольник со сторонами, параллельными главным осям рассеивания, при нормальном законе распределения
- § 26. Вероятность попадания двумерной случайной величины в эллипс рассеивания
- § 27. Задачи математической статистики. Статистический материал
- § 28. Статистический ряд. Гистограмма
- § 29. Определение подходящего значения измеряемой величины
- § 30. Определение параметров закона распределения. Теорема Ляпунова. Теорема Лапласа
- Упражнения к главе XX
- ГЛАВА XXI. МАТРИЦЫ. МАТРИЧНАЯ ЗАПИСЬ СИСТЕМ И РЕШЕНИЙ СИСТЕМ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- § 1. Линейные преобразования. Матрица
- § 2. Общие определения, связанные с понятием матрицы
- § 3. Обратное преобразование
- § 4. Действия над матрицами. Сложение матриц
- § 5. Преобразование вектора в другой вектор с помощью матрицы
- § 6. Обратная матрица
- § 7. Нахождение матрицы, обратной данной
- § 8. Матричная запись системы линейных уравнений
- § 9. Решение системы линейных уравнений матричным методом
- § 10. Ортогональные отображения. Ортогональные матрицы
- § 11. Собственный вектор линейного преобразования
- § 12. Матрица линейного преобразования, при котором базисные векторы являются собственными векторами
- § 13. Преобразование матрицы линейного преобразования при переходе от одного базиса к другому
- § 14. Квадратичные формы и их преобразования
- § 15. Ранг матрицы. Существование решений системы линейных уравнений
- § 16. Дифференцирование и интегрирование матриц
- § 17. Матричная запись системы дифференциальных уравнений и решений системы дифференциальных уравнений с постоянными коэффициентами
- § 18. Матричная запись линейного уравнения n-го порядка
- § 19. Решение систем линейных дифференциальных уравнений с переменными коэффициентами методом последовательных приближений с использованием матричной записи
- Упражнения к главе XXI
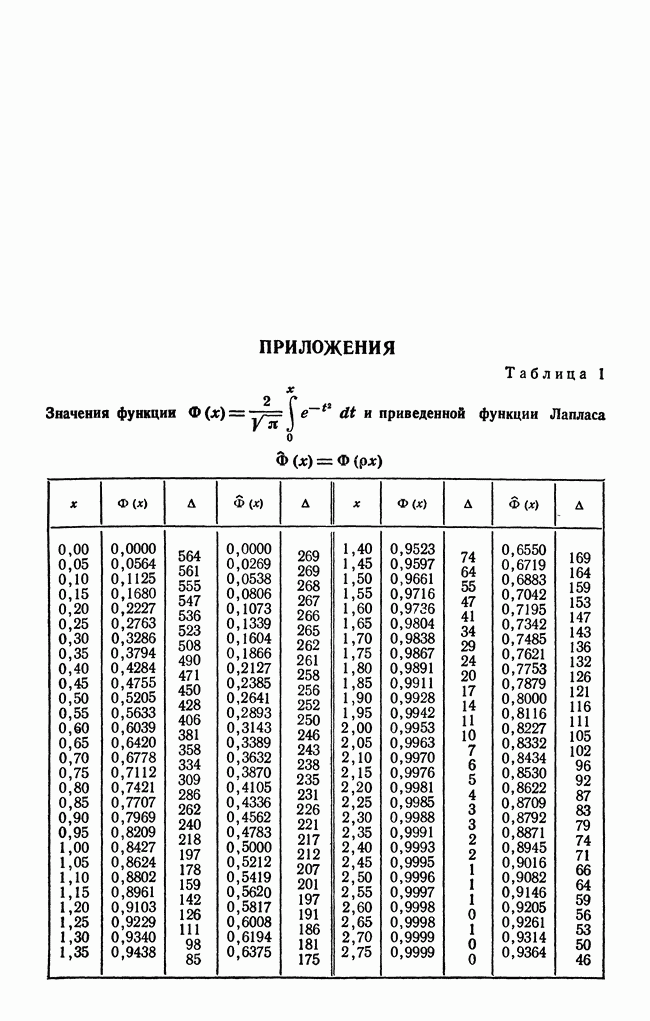
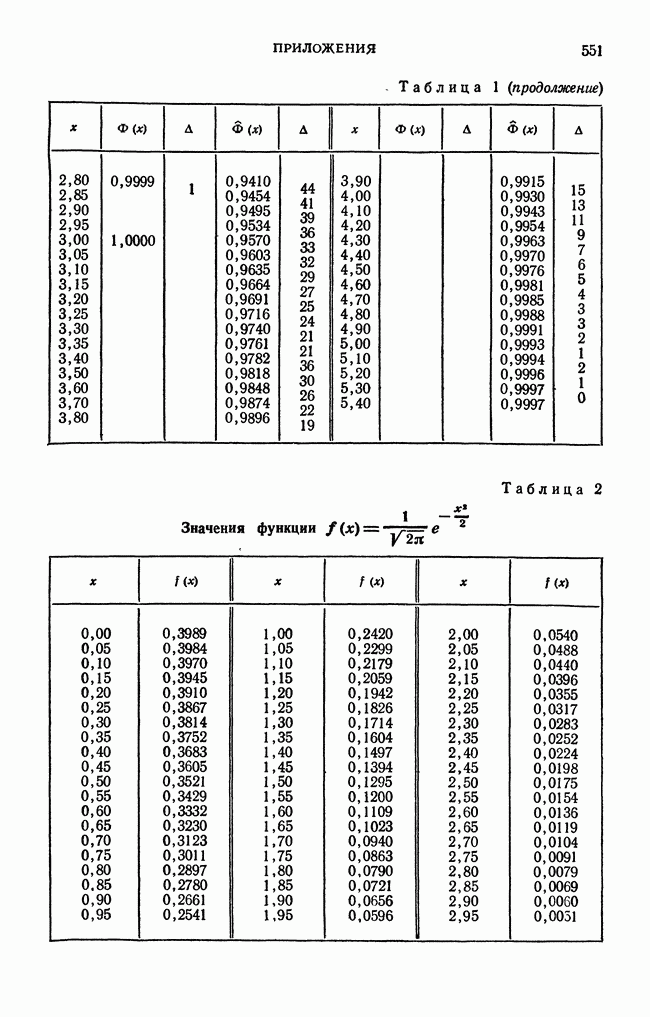
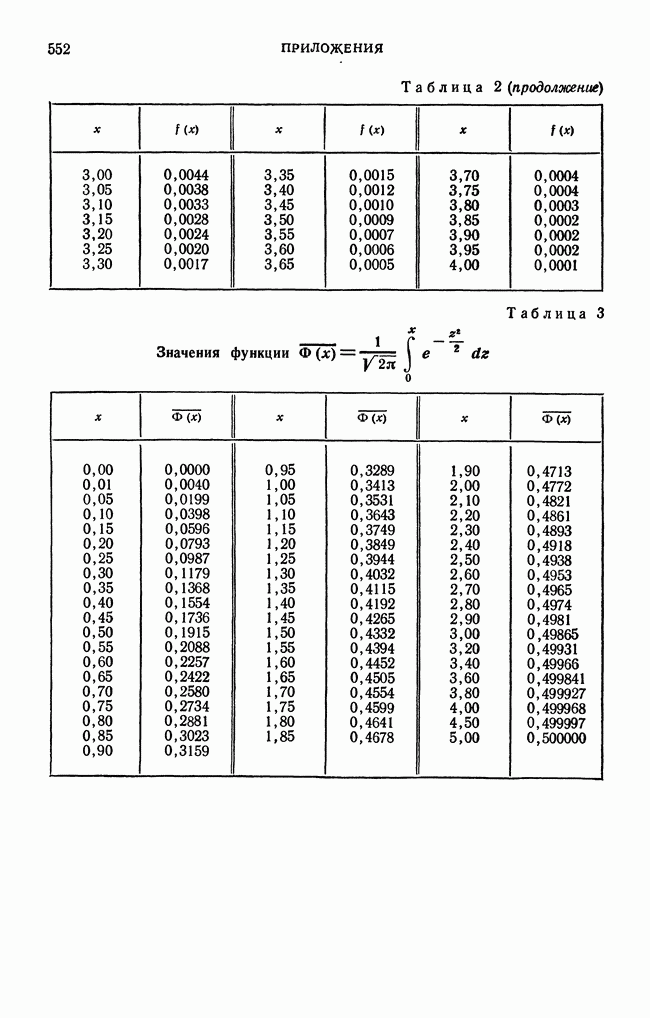
- ПРИЛОЖЕНИЯ