| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Соответствие Клейна
Исследуем геометрическую связь между  и проективным твисторным пространством
и проективным твисторным пространством  точки которого являются классами эквивалентности пропорциональных (ненулевых) твисторов
точки которого являются классами эквивалентности пропорциональных (ненулевых) твисторов  Пространство
Пространство  обладает структурой комплексного проективного 3-пространства
обладает структурой комплексного проективного 3-пространства  и может быть параметризовано с помощью трех независимых комплексных отношений
и может быть параметризовано с помощью трех независимых комплексных отношений  Как следует из абзаца, содержащего формулу (6.2.15), комплексные линейные 2-пространства в твисторном пространстве Т (по меньшей мере те, для которых не все твисторы имеют пропорциональные проекционные части) представляют точки в комплексифицированном пространстве Минковского
Как следует из абзаца, содержащего формулу (6.2.15), комплексные линейные 2-пространства в твисторном пространстве Т (по меньшей мере те, для которых не все твисторы имеют пропорциональные проекционные части) представляют точки в комплексифицированном пространстве Минковского  Кроме того из абзаца, содержащего формулу
Кроме того из абзаца, содержащего формулу  следует, что эти 2-пространства Могут быть представлены как классы эквивалентности пропорциональных (не равных нулю) простых кососимметричных твисторов
следует, что эти 2-пространства Могут быть представлены как классы эквивалентности пропорциональных (не равных нулю) простых кососимметричных твисторов  . В пространстве
. В пространстве  эти 2-пространства можно рассматривать как комплексные проективные прямые [каждая из них является пространством
эти 2-пространства можно рассматривать как комплексные проективные прямые [каждая из них является пространством  ]. Следовательно, эти прямые представляют в
]. Следовательно, эти прямые представляют в  точки пространства
точки пространства  Но, чтобы получить некую конечную точку пространства
Но, чтобы получить некую конечную точку пространства  мы требуем, чтобы прямая, представляющая ее в
мы требуем, чтобы прямая, представляющая ее в  не пересекалась с прямой
не пересекалась с прямой  которая задается уравнением
которая задается уравнением  Дело в том, что прямой
Дело в том, что прямой  определяется система твисторов
определяется система твисторов  с равной нулю проекционной частью, а поэтому прямая в
с равной нулю проекционной частью, а поэтому прямая в  пересекающаяся с I, представляет линейное 2-пространство в Т, содержащее твистор с равной нулю проекционной частью, откуда следует, что проекционные части всех твисторов в 2-пространстве обязательно пропорциональны друг другу. Тем не менее такая прямая, будучи представлена простым кососимметричным твистором
пересекающаяся с I, представляет линейное 2-пространство в Т, содержащее твистор с равной нулю проекционной частью, откуда следует, что проекционные части всех твисторов в 2-пространстве обязательно пропорциональны друг другу. Тем не менее такая прямая, будучи представлена простым кососимметричным твистором  должна соответствовать точке пространства
должна соответствовать точке пространства  Следовательно, она соответствует точке конуса
Следовательно, она соответствует точке конуса  , а сама прямая I — вершине
, а сама прямая I — вершине  конуса У. Мы видим, что точками пространства
конуса У. Мы видим, что точками пространства  представляются линии пространства
представляются линии пространства  Такого рода соответствие, при котором линии проективного 3-пространства представляются точками квадрики в проективном
Такого рода соответствие, при котором линии проективного 3-пространства представляются точками квадрики в проективном  -пространстве, называется соответствием
-пространстве, называется соответствием
(представлением) Клейна. Оно лежит в основе всей твисторной геометрии.
Теперь рассмотрим обратное соответствие. Нам нужно выяснить, как представить точку  пространства
пространства  в пространстве
в пространстве  Проанализируем поведение прямых в
Проанализируем поведение прямых в  проходящих через точку
проходящих через точку  Они входят в 2-комплексно-параметрическое семейство (которое называется связкой прямых), соответствующее комплексной 2-поверхности
Они входят в 2-комплексно-параметрическое семейство (которое называется связкой прямых), соответствующее комплексной 2-поверхности  в
в  Этой 2-поверхностью и можно воспользоваться для представления точки
Этой 2-поверхностью и можно воспользоваться для представления точки  Чтобы установить, каков характер этой 2-поверхности, вернемся к формуле (6.2.2) как основе уравнения (6.2.15), которое связывает радиус-вектор
Чтобы установить, каков характер этой 2-поверхности, вернемся к формуле (6.2.2) как основе уравнения (6.2.15), которое связывает радиус-вектор  точки
точки  пространства
пространства  с линейным 2-пространством твисторов. Уравнение (6.2.2) есть условие инцидентности между точками пространства
с линейным 2-пространством твисторов. Уравнение (6.2.2) есть условие инцидентности между точками пространства  и твисторами. Так, мы говорим, что точка
и твисторами. Так, мы говорим, что точка  инцидентна твистору
инцидентна твистору  если
если

где  — радиус-вектор точки
— радиус-вектор точки  относительно любой точки, в которой вычисляются спинорные поля
относительно любой точки, в которой вычисляются спинорные поля  (Для определенности будем вычислять все интересующие нас соотношения в фиксированной начальной точке О.) Если зафиксировать в соотношении (9.3.12) радиус-вектор
(Для определенности будем вычислять все интересующие нас соотношения в фиксированной начальной точке О.) Если зафиксировать в соотношении (9.3.12) радиус-вектор  и позволить изменяться твистору
и позволить изменяться твистору  то мы получим линейное 2-пространство в Т, о котором говорилось выше и которым представляется точка
то мы получим линейное 2-пространство в Т, о котором говорилось выше и которым представляется точка  в твисторном описании. Если же зафиксировать
в твисторном описании. Если же зафиксировать  и менять
и менять  то мы получим искомый локус
то мы получим искомый локус  которым представляется
которым представляется  в
в  При условии, что
При условии, что  т. е. что
т. е. что  , уравнение (9.3.12) имеет как минимум одно комплексное решение
, уравнение (9.3.12) имеет как минимум одно комплексное решение 

Рис. 9.8. Всякая  -плоскость в пространстве
-плоскость в пространстве  вполне изотропна. Разность двух радиус-векторов, проведенных к двум ее точкам, — это комплексный изотропный вектор
вполне изотропна. Разность двух радиус-векторов, проведенных к двум ее точкам, — это комплексный изотропный вектор  причем спинор
причем спинор  фиксирован, а
фиксирован, а  изменяется. Аналогичным свойством обладает
изменяется. Аналогичным свойством обладает  -плоскость, но роли спиноров
-плоскость, но роли спиноров  и
и  меняются.
меняются.
(в чем легко убедиться, рассмотрев это уравнение в компонентной форме записи). Обозначим это решение через  Тогда остальные решения должны удовлетворять уравнению
Тогда остальные решения должны удовлетворять уравнению  и в силу формулы (3.5.17) имеют вид
и в силу формулы (3.5.17) имеют вид

где областью изменения спинора  является все многообразие
является все многообразие  Комплексные векторы
Комплексные векторы  в точке О при фиксированных
в точке О при фиксированных  и меняющихся
и меняющихся  образуют
образуют  (комплексно) мерное векторное пространство, все элементы которого изотропны и взаимно ортогональны. Следовательно, пространство
(комплексно) мерное векторное пространство, все элементы которого изотропны и взаимно ортогональны. Следовательно, пространство  — это 2-плоскость в
— это 2-плоскость в  (рис. 9.8) и все ее касательные векторы изотропны и взаимно ортогональны. Стало быть, расстояние между двумя любыми точками на
(рис. 9.8) и все ее касательные векторы изотропны и взаимно ортогональны. Стало быть, расстояние между двумя любыми точками на  равно нулю, т. е. тождественно равна нулю индуцированная на
равно нулю, т. е. тождественно равна нулю индуцированная на  метрика.
метрика.
В пространстве  имеются два семейства плоскостей, обладающих таким свойством. Второе получается, когда спиноры
имеются два семейства плоскостей, обладающих таким свойством. Второе получается, когда спиноры  меняются ролями, т. е. когда выполняется соотношение (9.3.13), но
меняются ролями, т. е. когда выполняется соотношение (9.3.13), но  остается фиксированным, а
остается фиксированным, а  изменяется
изменяется  с формулой (3.2.22) и далее]. Плоскости первого типа называются
с формулой (3.2.22) и далее]. Плоскости первого типа называются  -плоскостями, а второго —
-плоскостями, а второго —  -плоскостями. (Эта терминология согласуется с принятой в гл. 6, § 2 и гл. 7, § 4.) Итак, мы только что доказали, что представлением точки
-плоскостями. (Эта терминология согласуется с принятой в гл. 6, § 2 и гл. 7, § 4.) Итак, мы только что доказали, что представлением точки  пространства
пространства  (при
(при  ) в
) в  является
является  -плоскость. Если же рассматривать
-плоскость. Если же рассматривать  -плоскости в
-плоскости в  то от ограничения
то от ограничения  можно отказаться. Это сразу же следует из полной
можно отказаться. Это сразу же следует из полной
однородности пространства  и из конформной инвариантности (которую мы сейчас докажем) а-плоскости.
и из конформной инвариантности (которую мы сейчас докажем) а-плоскости.
В самом деле,  -плоскость есть комплексная 2-поверхность, все касательные векторы к которой в любой данной точке имеют при некотором
-плоскость есть комплексная 2-поверхность, все касательные векторы к которой в любой данной точке имеют при некотором  форму Алял [это эквивалентно утверждению, что касательные бивекторы самодуальны и изотропны, поскольку имеют вид елвяляв; см. формулу (3.4.39)] и касательные пространства которой при параллельном переносе вдоль касательных направлений переходят в себя (т. е. поверхности плоские). Последнее условие при некоторых
форму Алял [это эквивалентно утверждению, что касательные бивекторы самодуальны и изотропны, поскольку имеют вид елвяляв; см. формулу (3.4.39)] и касательные пространства которой при параллельном переносе вдоль касательных направлений переходят в себя (т. е. поверхности плоские). Последнее условие при некоторых  и при любых
и при любых  можно записать в виде
можно записать в виде

т. е. для всех  и выполняется уравнение
и выполняется уравнение

а значит, и уравнение

которое, как следует из формулы (7.4.56), является конформноинвариантным, если приписать спинору  конформный вес, равный 1. [Сходство между уравнениями (9.3.15) и (7.3.1) не случайно: см. предложение (7.3.18).] Уравнение (9.3.15) оказывается фактически следствием того, что все касательные к поверхности векторы имеют вид Ялял [с определенным спинором
конформный вес, равный 1. [Сходство между уравнениями (9.3.15) и (7.3.1) не случайно: см. предложение (7.3.18).] Уравнение (9.3.15) оказывается фактически следствием того, что все касательные к поверхности векторы имеют вид Ялял [с определенным спинором  в каждой точке в силу условия со скобками Ли, при котором касательными плоскостями определяется поверхность; см. формулу (7.3.17)]: при некоторых
в каждой точке в силу условия со скобками Ли, при котором касательными плоскостями определяется поверхность; см. формулу (7.3.17)]: при некоторых  имеем
имеем

свертка обеих частей этого равенства с  дает
дает

откуда снова получается уравнение (9.3.15) и его следствие (9.3.14).
Что касается  -плоскостей, то они появляются совершенно аналогичным образом, если заменить только что рассмотреныый
-плоскостей, то они появляются совершенно аналогичным образом, если заменить только что рассмотреныый  -твистор
-твистор  дуальным
дуальным  -твистором
-твистором  и поменять ролями штрихованные и нештрихованные спинорные индексы. Условие инцидентности (9.3.12) заменяется уравнением
и поменять ролями штрихованные и нештрихованные спинорные индексы. Условие инцидентности (9.3.12) заменяется уравнением

Решения этого уравнения имеют, как и раньше, вид (9.3.13), но теперь спинор  фиксирован, а
фиксирован, а  изменяется. Отсюда следует, что
изменяется. Отсюда следует, что  -плоскость можно рассматривать как представление проективного дуального твистора в
-плоскость можно рассматривать как представление проективного дуального твистора в  или
или  Но проективный дуальный твистор можно также представить комплексной проективной 2-плоскостью
Но проективный дуальный твистор можно также представить комплексной проективной 2-плоскостью  (т. е. пространством
(т. е. пространством  в
в  поскольку твистор
поскольку твистор  можно с точностью до пропорциональности представить системой
можно с точностью до пропорциональности представить системой  точек
точек  для которых
для которых

Уравнение (9.3.17) указывает на инцидентность между плоскостью  и точкой
и точкой  в
в  т. е. между дуальным твистором
т. е. между дуальным твистором  и твистором
и твистором  Условие инцидентности (9.3.12) в чисто твисторной форме имеет вид
Условие инцидентности (9.3.12) в чисто твисторной форме имеет вид

Из этих формул следует, что в  точка
точка  лежит на прямой
лежит на прямой  (представленной твистором
(представленной твистором  Если
Если  то этот дуальный твистор можно рассматривать как представление плоскости, связывающей
то этот дуальный твистор можно рассматривать как представление плоскости, связывающей  с
с  в
в  Соответственно этому условие инцидентности (9.3.16) можно переписать в виде
Соответственно этому условие инцидентности (9.3.16) можно переписать в виде

Это означает, что в  прямая
прямая  лежит в плоскости
лежит в плоскости  . И аналогично если
. И аналогично если  , то этот твистор является представлением точки пересечения прямой
, то этот твистор является представлением точки пересечения прямой  с плоскостью
с плоскостью 
Итак, в пространстве  точка
точка  прямая
прямая  и плоскость
и плоскость  представляются
представляются  -плоскостью
-плоскостью  точкой
точкой  и
и  -плоскостью
-плоскостью  Инцидентность между
Инцидентность между  и
и  в
в  переходит в инцидентность между
переходит в инцидентность между  и
и  в
в  точка
точка  лежит на
лежит на  -плоскости
-плоскости  Инцидентность между
Инцидентность между  и
и  в
в  переходит в инцидентность между
переходит в инцидентность между  и
и  в
в  точка
точка  лежит на
лежит на  -плоскости
-плоскости  Инцидентность между
Инцидентность между  и
и  в
в  переходит в инцидентность между
переходит в инцидентность между  и
и  в
в  -плоскость
-плоскость  пересекается с
пересекается с  -плоскостью
-плоскостью  . В справедливости последнего утверждения можно убедиться,
. В справедливости последнего утверждения можно убедиться,
либо снова обратившись к формулам (9.3.12), (9.3.16) и (9.3.17) и построив рассуждения так, чтобы охватить случаи, когда точка  лежит на 9 или в точке
лежит на 9 или в точке  либо просто приняв во внимание, что если точка
либо просто приняв во внимание, что если точка  лежит на плоскости
лежит на плоскости  то существует прямая
то существует прямая  которая одновременно лежит на плоскости
которая одновременно лежит на плоскости  и проходит через точку
и проходит через точку  т. е. существует точка
т. е. существует точка  которая лежит одновременно на
которая лежит одновременно на  -плоскости
-плоскости  и на
и на  -плоскости
-плоскости  Заметим, что если это условие выполняется, то существует не одна прямая
Заметим, что если это условие выполняется, то существует не одна прямая  а целое однопараметрическое семейство таких прямых, лежащих в плоскости
а целое однопараметрическое семейство таких прямых, лежащих в плоскости  и проходящих через точку
и проходящих через точку  т. е. плоский пучок прямых. В
т. е. плоский пучок прямых. В  можно указать кривую пересечения
можно указать кривую пересечения  -плоскости
-плоскости  с
с  -плоскостью
-плоскостью  — комплексную изотропную геодезическую в конформной метрике пространства
— комплексную изотропную геодезическую в конформной метрике пространства  ибо это изотропная прямая в
ибо это изотропная прямая в  (потому, например, что параметрическое уравнение этой кривой имеет вид линейной функции
(потому, например, что параметрическое уравнение этой кривой имеет вид линейной функции  . И обратно, всякая комплексная изотропная геодезическая в
. И обратно, всякая комплексная изотропная геодезическая в  появляется именно таким путем, так что справедливо следующее предложение.
появляется именно таким путем, так что справедливо следующее предложение.
Предложение
Через всякую изотропную геодезическую пространства  проходит единственная
проходит единственная  -плоскость и единственная
-плоскость и единственная  -плоскость-, линия пересечения
-плоскость-, линия пересечения  -плоскости с
-плоскости с  -плоскостью всегда является изотропной геодезической.
-плоскостью всегда является изотропной геодезической.
В то же время две любые разные  -плоскости всегда имеют в
-плоскости всегда имеют в  единственную общую точку, ибо две разные точки на
единственную общую точку, ибо две разные точки на  связаны между собой единственной прямой; аналогично две любые разные
связаны между собой единственной прямой; аналогично две любые разные  -плоскости всегда имеют в
-плоскости всегда имеют в  единственную общую точку, так как две разные плоскости в
единственную общую точку, так как две разные плоскости в  имеют единственную общую прямую. («Инцидентность» между двумя а-плоскостями или между двумя
имеют единственную общую прямую. («Инцидентность» между двумя а-плоскостями или между двумя  -плоскостями — это обязательно «совпадение».) Две прямые в
-плоскостями — это обязательно «совпадение».) Две прямые в  в общем случае не пересекаются (они «скрещиваются»), но если пересекаются, то лежат в одной плоскости. Таким образом, пересекающиеся прямые в
в общем случае не пересекаются (они «скрещиваются»), но если пересекаются, то лежат в одной плоскости. Таким образом, пересекающиеся прямые в  соответствуют изотропно-разделенным точкам в
соответствуют изотропно-разделенным точкам в  Итак, справедливо следующее предложение.
Итак, справедливо следующее предложение.
Предложение
(см. скан)

Рис. 9.9. Основное геометрическое соответствие — соответствие Клейна, — связывающее отношения инцидентности точек, плоскостей и прямых в пространстве  (комплексном проективном 3-пространстве) с отношениями инцидентности
(комплексном проективном 3-пространстве) с отношениями инцидентности  -плоскостей, р-плоскостей и точек (в комплексной проективной 4-квадрике)
-плоскостей, р-плоскостей и точек (в комплексной проективной 4-квадрике) 
Взаимосвязи геометрий пространств  и
и  приведены на рис. 9.9 и в таблице (9.3.22).
приведены на рис. 9.9 и в таблице (9.3.22).
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие редактора перевода
- Предисловие
- Краткое содержание тома 1
- § 5 (гл. 1). Спинорные объекты и спиновая структура
- § 2 (гл. 2). Формализм абстрактных индексов в тензорной алгебре
- § 3 (гл. 3). Операции симметрии
- Переход от спинорной к тензорной форме записи, и наоборот; преобразование дуальности
- Некоторые свойства тензоров и спиноров в точке
- Активные лоренцевы и спиновые преобразования
- Ковариантная производная
- Спиновые коэффициенты
- Спинорная форма кривизны
- Тождества для спинора Риччи
- Спинорные тождества Бианки
- Компоненты спинорной кривизны
- Модифицированный формализм спиновых коэффициентов
- Уравнения для модифицированных спиновых коэффициентов
- Геометрия пространственноподобных 2-поверхностей
- На изотропной гиперповерхности
- § 15 (гл. 4). Функции на метрической сфере
- Производные заряженных полей
- Поля Янга — Миллса
- Конформные изменения масштаба
- Безмассовые свободные поля
- Другие полевые уравнения
- Данные на изотропной гиперповерхности
- 6. Твисторы
- § 1. Твисторное уравнение и пространство его решений
- Твисторное уравнение
- Пространство твисторов
- Дуальные твисторы
- Твисторы высшей валентности
- Конформная инвариантность спиральности и скалярного произведения
- § 2. Некоторые геометрические аспекты твисторной алгебры
- Поле флагштоков спинора: конгруэнция Робинсона
- Отношение взаимности твисторов
- Комплексная геометрия
- Представление точек с помощью простых кососимметричных твисторов
- § 3. Твисторы и момент импульса
- Момент импульса произвольной системы
- Представление твистора с помощью одноиндексных твисторов
- § 4. Симметричные твисторы и безмассовые поля
- Общий случай, потенциалы
- Повышение спина
- Другие виды потенциалов; связь с оператором
- § 5. Конформные векторы Киллинга; сохраняющиеся величины и точные последовательности
- Спиноры: Законы сохранения
- Твисторное описание
- Связь с интегралами от источников в линейной гравитации
- Точные последовательности
- Последовательности моментов
- Интегралы в линейной теории гравитации
- Спиноры: Десять интегралов, равных нулю
- Роль дуальности в последовательностях момента
- § 6. Производные Ли спиноров
- Связь с теорией твисторов
- § 7. Интегралы движения частиц; конформно-инвариантные операторы
- Спиноры Киллинга для вакуумных решений типа (22)
- Свойства решения Керра
- Конформно-инвариантные первые производные
- Твисторные решения различных уравнений
- Повторные операции; разрешения уравнений
- § 8. Кривизна и конформные преобразования
- Конформные свойства величин
- Конформные отображения плоских пространств
- Конформно-инвариантное волновое уравнение и оператор
- Конформно-инвариантный тензор Баха
- § 9. Локальные твисторы
- Условие совместности для твисторного уравнения
- Определение локального твистора
- Перенос локального твистора
- Кривизна в пространстве локальных твисторов
- Нулевая кривизна Вейля как свойство конформно-плоского пространства
- § 10. Безмассовые поля и когомологии твисторов
- Спиноры: Непроективное представление
- Квантование твисторов
- Спиральность
- Интегралы для спиральности противоположного знака
- Повышение и понижение спиральности
- Массивные твисторные волновые функции
- Геометрия контурных интегралов
- Положительно-частотные поля
- Введение когомологий
- Понятие 1-функции
- r-Функции общего вида
- Нелинейные 1-функции
- Конструкция Уорда
- Пример конструкции Уорда
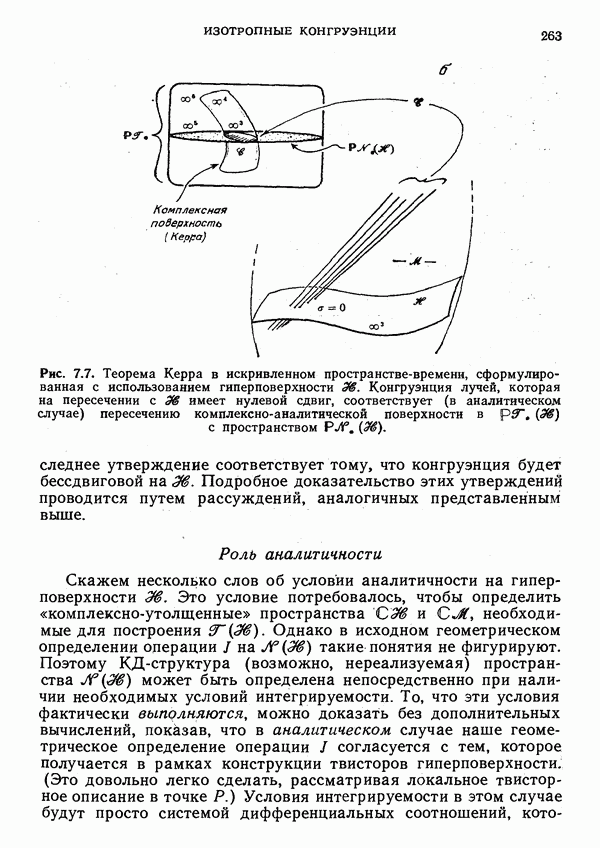
- 7. Изотропные конгруэнции
- § 1. Изотропные конгруэнции и спиновые коэффициенты
- Интерпретация величин; изопараметричность лучей
- Ортогональность гиперповерхности; изотропные гиперповерхности
- Изопараметричность в теории твисторов
- § 2. Изотропные конгруэнции и кривизна пространства-времени
- Изопараметрические лучи; уравнения Сакса
- Неизопараметрические лучи
- Описание в трехмерном пространстве Минковского
- § 3. Бессдвиговые конгруэнции лучей
- Обобщенная теорема Голдберга — Сакса
- Координаты Керра
- § 4. БСК, твисторы и геометрия лучей
- Твисторная форма теоремы Керра
- Линейные и квадратичные функции твисторов, момент импульса
- Связь с твисторными функциями безмассовых полей
- Пространства и инвариантная контактная структура
- Комплексная структура и КД-структура
- Твисторы гиперповерхности
- Спиноры: Роль аналитичности
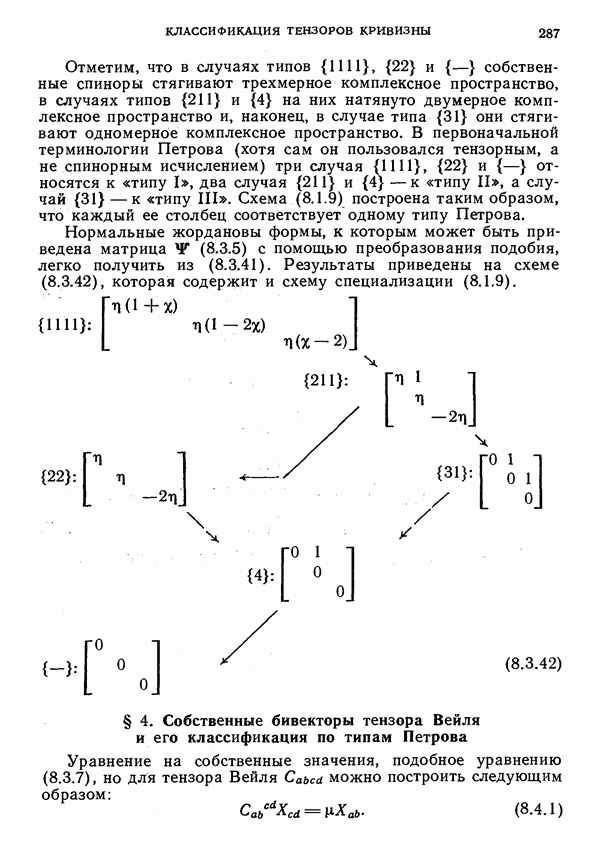
- 8. Классификация тензоров кривизны
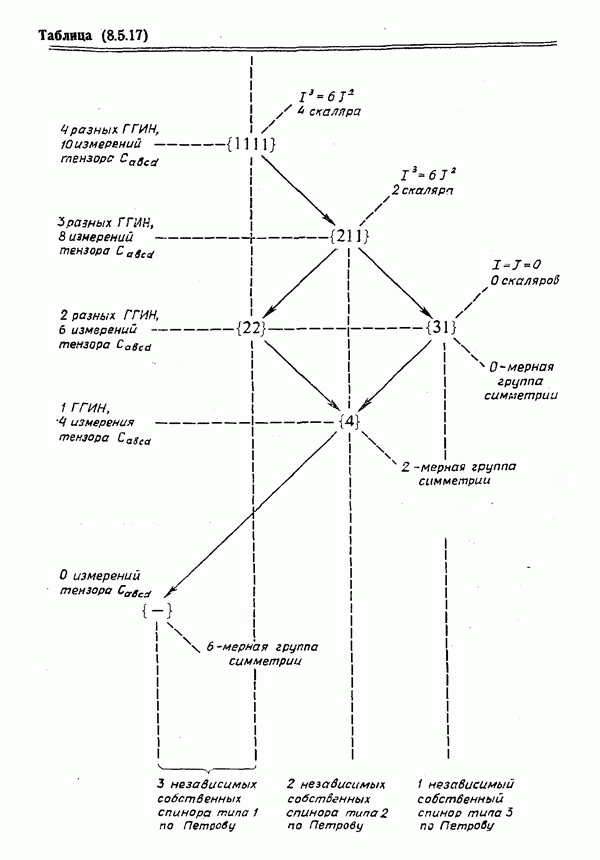
- Спиноры: Схема специализации
- § 2. Представление спинора Вейля на сфере S+
- ГГИН в пространстве-времени высокой симметрии
- «Картина» тензора Вейля на S+
- § 3. Собственные спиноры спинора Вейля
- Соотношение между собственными значениями и двойными отношениями
- Частные случаи
- § 4. Собственные бивекторы тензора Вейля и его классификация по типам Петрова
- Компоненты тензора Вейля в бивекторном базисе
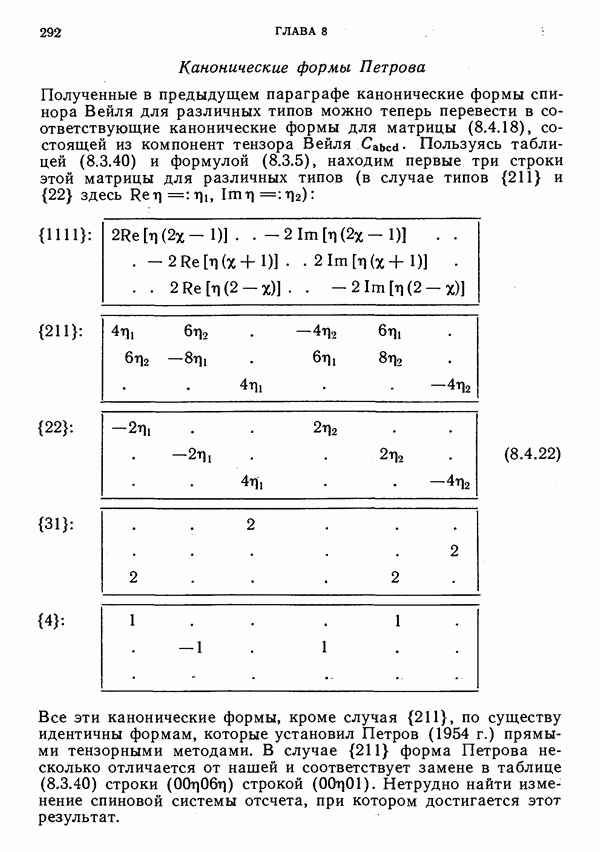
- Канонические формы Петрова
- § 5. Геометрия и симметрия вейлевской кривизны
- Дисфеноид для типа {1111}
- Симметрии в частных случаях типа {1111}
- Тип (211)
- О размерностях групп симметрий
- Классификация тензора Максвелла
- § 6. Коварианты кривизны
- Инварианты полной кривизны
- Система полей Эйнштейна — Максвелла
- § 7. Классификационная схема для спиноров с любым числом индексов
- Приводимость локуса
- Комплексные (р, q) — кривые на CS+
- Процедура классификации спинора
- Структура кривой w (ее кратные точки)
- Кратные точки кривой w
- Локус Rw на S+
- Знак спинора, черный и белый цвета сферы S+
- § 8. Классификация спинора Риччи
- Тип спинора по Плебаньскому
- Физические тензоры энергии-импульса
- 9. Конформная бесконечность
- § 1. Бесконечность в случае пространства Минковского
- ГНП и ГНБ
- § 2. Компактифицированное пространство Минковского
- Описание в пространстве Р5
- O(2,4) и конформная группа
- § 3. Комплексифицированное компактифицированное пространство Минковского и твисторная геометрия
- Соответствие Клейна
- Твисторное отношение дуальности
- Действительная структура
- Различные типы комплексных точек в СМ*
- § 4. Четырехзначность твисторов и индекс Гржина
- Две спиновые структуры на М*
- Поведение спинора
- Твисторные спин-расслоения над М*
- Конформные плотности на М*; индекс Гржина
- Теорема Гржина
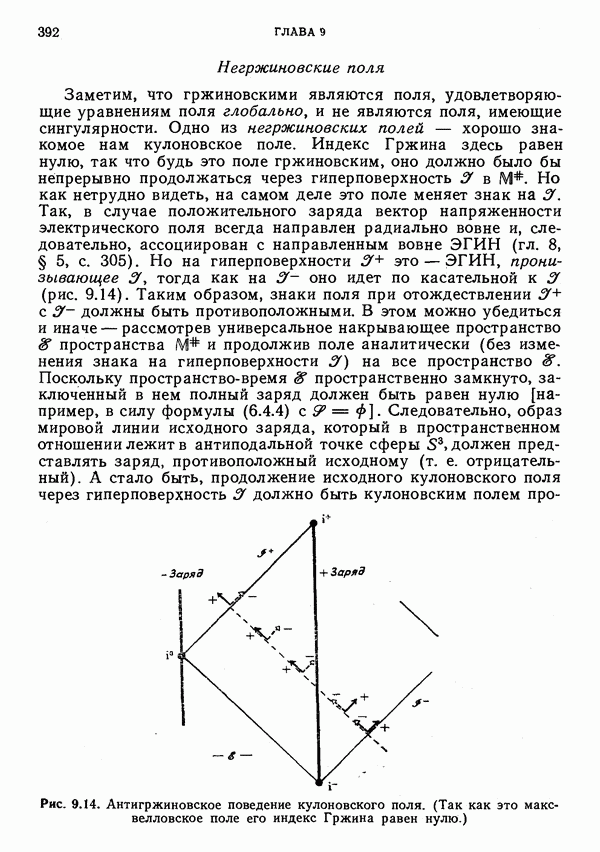
- Негржиновские поля
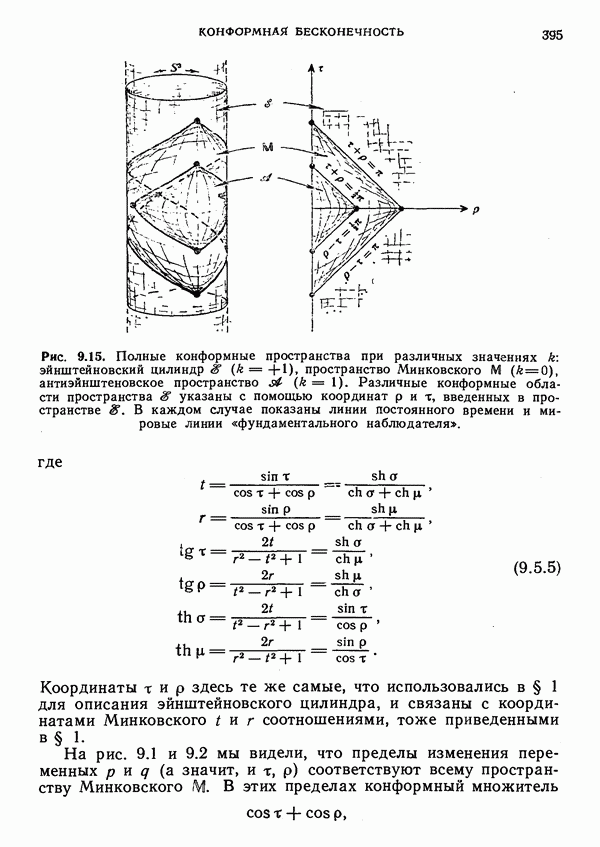
- § 5. Космологические модели и соответствующие твисторы
- Космологические горизонты
- Описание в пространстве Р5
- Деситтеровская и антидеситтеровская модели; твисторы …
- Функции для конформно-плоского пространства-времени
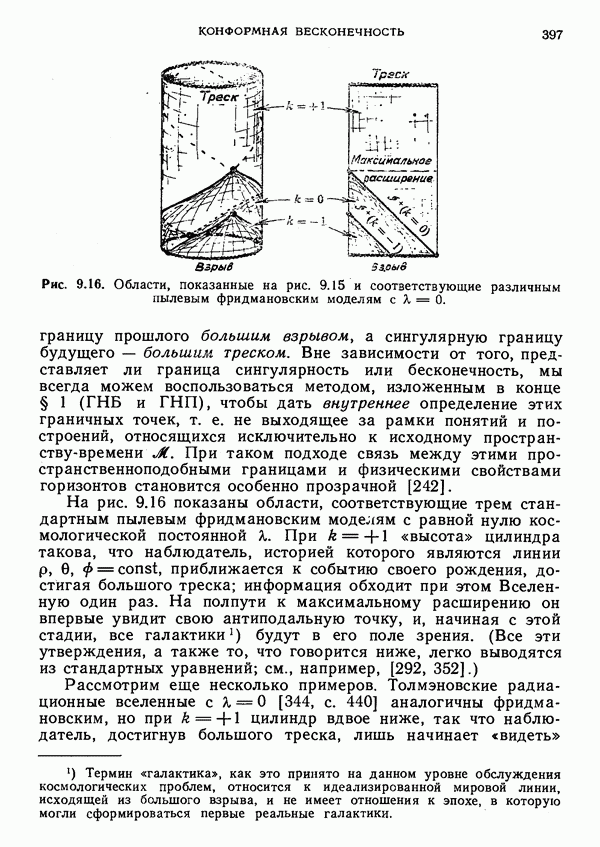
- Модели ФРУ, соответствующие твисторы начальной и конечной сингулярностей
- Явные выражения для функции I
- § 6. Асимптотически простое пространство-время
- Асимптотически-простое пространство-время
- Обращение в нуль тензора Вейля на границе J
- § 7. Последовательное вырождение
- Параллельно переносимые спиновые системы отсчета
- Сравнение аффинных параметров
- Сравнение спиновых систем отсчета
- Доказательство свойства последовательного вырождения
- Поля излучений
- § 8. Группа БМС и структура гиперповерхности J+
- Группа Бонди — Метцнера — Сакса
- Связь между сильной конформной геометрией и твистором
- Интерпретация изотропных углов
- Структура группы БМС
- Сдвиговая структура гиперповерхности J+
- H-пространство и асимптотическое твисторное пространство
- Отношение группы БМС к импульсу и моменту импульса
- Асимптотические разложения в теории Эйнштейна — Максвелла
- § 9. Энергия-импульс и момент импульса
- Усложнения в случае искривленного пространства-времени
- Твисторы двумерной поверхности
- Контортные двумерные поверхности
- Квазилокальный твистор момента импульса
- Определение множителя
- Асимптотическое спиновое пространство
- Свойства нормы на J+
- Эрмитовость твистора на 4-импульс Бонди — Сакса
- Альтернативные выражения для массы Бонди — Сакса
- Пространство Минковского как пространство «начал»
- Момент импульса на J+
- § 10. Потери массы Бонди — Сакса и положительность энергии
- Нелокальность энергии гравитационных волн
- НП-константы
- Подход Виттена в доказательстве положительности массы
- Связь с 4-импульсом Бонди — Сакса
- Спинор в подходе Людвигсена — Виккерса
- 3-форма Спарлинга
- Приложение. Спиноры в n измерениях
- 2-валентные e-спиноры
- Переход от тензоров к спинорам
- Геометрия фундаментальных спиноров
- Условие фундаментальности; структура спинового пространства
- Индуктивное построение спинового пространства
- Некоторые физически интересные случаи; триальность
- Спинорные поля; твисторы в n измерениях
- Послесловие авторов
- Литература