| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Понятие 1-функции
Отсюда следует, что нужно рассматривать не просто функции на  , но функции
, но функции  по модулю функций, голоморфных на
по модулю функций, голоморфных на  или на У. Другими словами, две функции на
или на У. Другими словами, две функции на  будут считаться эквивалентными, если они различаются суммой функций, которые допускают голоморфное продолжение либо на
будут считаться эквивалентными, если они различаются суммой функций, которые допускают голоморфное продолжение либо на  , либо на
, либо на  (Суть этого отношения эквивалентности в том, что интеграл от разности эквивалентных в таком смысле функций очевидным образом обращается в нуль в силу стягиваемости контура.) Например, функция, определенная соотношением (6.10.54), эквивалентна нулю. Указанные классы эквивалентности функций образуют первую группу когомологий голоморфных пучков по отношению к покрытию
(Суть этого отношения эквивалентности в том, что интеграл от разности эквивалентных в таком смысле функций очевидным образом обращается в нуль в силу стягиваемости контура.) Например, функция, определенная соотношением (6.10.54), эквивалентна нулю. Указанные классы эквивалентности функций образуют первую группу когомологий голоморфных пучков по отношению к покрытию  пространства
пространства  Такие классы эквивалентности мы будем называть 1-функциями по отношению к покрытию
Такие классы эквивалентности мы будем называть 1-функциями по отношению к покрытию  При этом обычные функции мы будем называть
При этом обычные функции мы будем называть  -функциями.
-функциями.
Мы сразу же вынуждены распространить определение 1-функций на более сложные покрытия  а затем и вовсе устранить зависимость от специального выбора покрытия. Ведь даже простейшая задача сложения 1-функций, определенных на разных парах покрытий
а затем и вовсе устранить зависимость от специального выбора покрытия. Ведь даже простейшая задача сложения 1-функций, определенных на разных парах покрытий  приводит к рассмотрению 1-функций на общем подпокрытии [см. далее формулу (6.10.62)] этих покрытий. Поэтому мы будем рассматривать открытые покрытия пространства
приводит к рассмотрению 1-функций на общем подпокрытии [см. далее формулу (6.10.62)] этих покрытий. Поэтому мы будем рассматривать открытые покрытия пространства  общего вида (открытыми множествами) с дополнительным ограничением локальной конечности покрытий, которое означает, что всякая точка принадлежит конечному числу покрывающих множеств. (Отметим, что некомпактные множества, такие, как
общего вида (открытыми множествами) с дополнительным ограничением локальной конечности покрытий, которое означает, что всякая точка принадлежит конечному числу покрывающих множеств. (Отметим, что некомпактные множества, такие, как  допускают локально-конечные покрытия, содержащие бесконечное число множеств.) На рис. 6.13 показано покрытие пространства
допускают локально-конечные покрытия, содержащие бесконечное число множеств.) На рис. 6.13 показано покрытие пространства  состоящее из большого
состоящее из большого  даже, может быть, бесконечно большого) числа
даже, может быть, бесконечно большого) числа

Рис. 6.13. Покрытие пространства  имеющее вид большого числа (которое может быть бесконечно большим) открытых множеств, образующих локально-конечную систему. Интегрирование проводится по разветвленному контуру.
имеющее вид большого числа (которое может быть бесконечно большим) открытых множеств, образующих локально-конечную систему. Интегрирование проводится по разветвленному контуру.
открытых множеств  Для такого покрытия потребуется ввести целое семейство
Для такого покрытия потребуется ввести целое семейство  голоморфных функций, определенных на пересечениях пар открытых множеств из этого набора:
голоморфных функций, определенных на пересечениях пар открытых множеств из этого набора:
Функция  определена на пересечении
определена на пересечении 
Далее, прямая  будучи компактным множеством, пересекает локально-конечную систему только по конечному числу множеств
будучи компактным множеством, пересекает локально-конечную систему только по конечному числу множеств  так что лишь конечное число функций
так что лишь конечное число функций  имеет непустое ограничение на
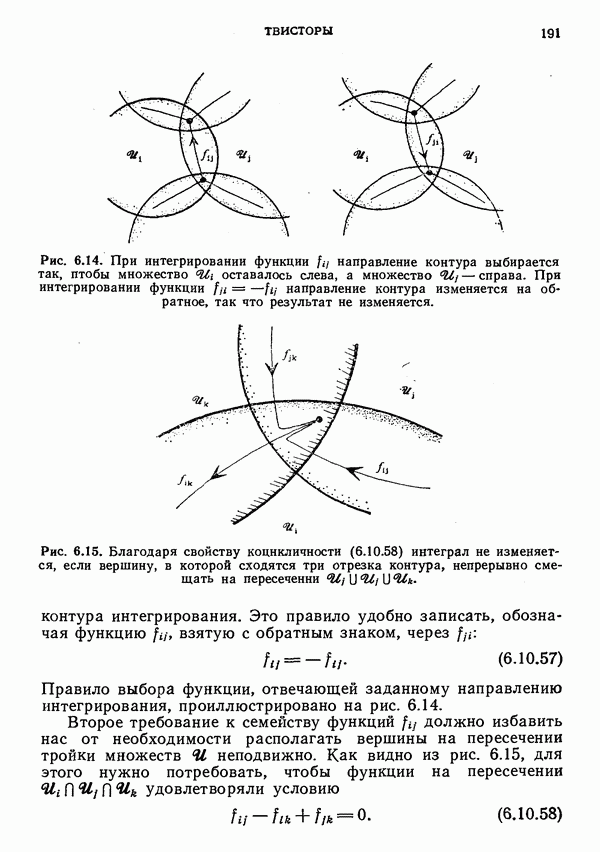
имеет непустое ограничение на  Мы должны теперь обобщить интегральные формулы так, чтобы они были пригодны в рассматриваемой ситуациии. Наглядное представление об этой процедуре можно получить из рис. 6.13: мы переходим к интегралу по разветвленному контуру в виде сетки из отдельных ориентированных отрезков. Каждый отрезок принадлежит пересечению двух множеств покрытия, и соответствующий интеграл вычисляется от функции вида (6.10.56). Каждый отрезок начинается и оканчивается вершиной (если он не является замкнутой петлей), лежащей на пересечении трех множеств
Мы должны теперь обобщить интегральные формулы так, чтобы они были пригодны в рассматриваемой ситуациии. Наглядное представление об этой процедуре можно получить из рис. 6.13: мы переходим к интегралу по разветвленному контуру в виде сетки из отдельных ориентированных отрезков. Каждый отрезок принадлежит пересечению двух множеств покрытия, и соответствующий интеграл вычисляется от функции вида (6.10.56). Каждый отрезок начинается и оканчивается вершиной (если он не является замкнутой петлей), лежащей на пересечении трех множеств  каждая вершина принадлежит трем и только трем отрезкам, а каждый отрезок — двум из трех указанных множеств. В силу свойств контурных интегралов результат интегрирования не изменится, если любой из отрезков деформировать непрерывно на заданном пересечении пары множеств
каждая вершина принадлежит трем и только трем отрезкам, а каждый отрезок — двум из трех указанных множеств. В силу свойств контурных интегралов результат интегрирования не изменится, если любой из отрезков деформировать непрерывно на заданном пересечении пары множеств  при условии, что конечные точки остаются неподвижными (если все пересечения имеют евклидову топологию, то слово «непрерывно» можно опустить).
при условии, что конечные точки остаются неподвижными (если все пересечения имеют евклидову топологию, то слово «непрерывно» можно опустить).
Чтобы рассматриваемый интеграл был определен однозначно, следует ввести два дополнительных требования к семейству функций  Во-первых, поскольку интеграл вдоль данного отрезка можно вычислять в любом направлении, вклад в полный интеграл оказывается неопределенным и зависящим от этого выбора. Чтобы устранить эту неопределенность, будем считать, что знак функции изменяется, когда изменяется направление
Во-первых, поскольку интеграл вдоль данного отрезка можно вычислять в любом направлении, вклад в полный интеграл оказывается неопределенным и зависящим от этого выбора. Чтобы устранить эту неопределенность, будем считать, что знак функции изменяется, когда изменяется направление

Рис. 6.14. При интегрировании функции направление контура выбирается так, птобы множество  оставалось слева, а множество
оставалось слева, а множество  справа. При интегрировании функции
справа. При интегрировании функции  направление контура изменяется на обратное, так что результат не изменяется.
направление контура изменяется на обратное, так что результат не изменяется.

Рис. 6.15. Благодаря свойству коцнкличности (6.10.58) интеграл не изменяется, если вершину, в которой сходятся три отрезка контура, непрерывно смещать на пересечении 
контура интегрирования. Это правило удобно записать, обозначая функцию  взятую с обратным знаком, через
взятую с обратным знаком, через 

Правило выбора функции, отвечающей заданному направлению интегрирования, проиллюстрировано на рис. 6.14.
Второе требование к семейству функций  должно избавить нас от необходимости располагать вершины на пересечении тройки множеств 41 неподвижно. Как видно из рис. 6.15, для этого нужно потребовать, чтобы функции на пересечении
должно избавить нас от необходимости располагать вершины на пересечении тройки множеств 41 неподвижно. Как видно из рис. 6.15, для этого нужно потребовать, чтобы функции на пересечении  удовлетворяли условию
удовлетворяли условию

Всякое семейство функций  определенных на пересечениях
определенных на пересечениях  пар открытых множеств открытого покрытия
пар открытых множеств открытого покрытия  удовлетворяющее условиям (6.10.57) и (6.10.58), называется 1-коциклом по отношению к данному покрытию. Хотя мы ввели коциклы в связи с контурными интегралами, это — более широкое понятие, которое возникает во многих математических построениях, не связанных с интегралами. Нам также потребуется ввести понятие 1-кограницы и определить факторпространство 1-коциклов по 1-кограницам. (Это приводит к обобщению ранее приведенного определения 1-функций на случай покрытия, состоящего только из двух множеств. Итак, 1-кограницей некоторого семейства функций (в данном контексте голоморфных) будем называть 1-коцикл, который можно представить в виде
удовлетворяющее условиям (6.10.57) и (6.10.58), называется 1-коциклом по отношению к данному покрытию. Хотя мы ввели коциклы в связи с контурными интегралами, это — более широкое понятие, которое возникает во многих математических построениях, не связанных с интегралами. Нам также потребуется ввести понятие 1-кограницы и определить факторпространство 1-коциклов по 1-кограницам. (Это приводит к обобщению ранее приведенного определения 1-функций на случай покрытия, состоящего только из двух множеств. Итак, 1-кограницей некоторого семейства функций (в данном контексте голоморфных) будем называть 1-коцикл, который можно представить в виде

где

причем в соотношение (6.10.59) входят ограничения функций  на пересечение
на пересечение  Очевидно, что 1-кограница удовлетворяет условиям 1-коцикла (6.10.57) и (6.10.58).
Очевидно, что 1-кограница удовлетворяет условиям 1-коцикла (6.10.57) и (6.10.58).
Определим теперь 1-функцию (или элемент первой группы когомологий) по отношению к выбранному покрытию как класс эквивалентности 1-коциклов. Два коцикла считаются эквивалентными, если их разность есть 1-кограница (всюду подразумевается, что фиксировано определенное покрытие  Выгоды такого перехода к факторпространству 1-коциклов можно понять, возвращаясь к задаче вычисления контурных интегралов. Из рис. 6.16 интуитивно ясно (в предположении евклидовой топологии всех множеств 2), что интеграл от (голоморфной)
Выгоды такого перехода к факторпространству 1-коциклов можно понять, возвращаясь к задаче вычисления контурных интегралов. Из рис. 6.16 интуитивно ясно (в предположении евклидовой топологии всех множеств 2), что интеграл от (голоморфной)
1-кограницы равен нулю.
Ранее мы упоминали, что переход к рассмотрению более сложных покрытий  (чем покрытие, образованное только двумя множествами 41 и У) отчасти обусловлен желанием иметь возможность складывать 1-функции, определенные по отношению к различным покрытиям. Сейчас мы уже достаточно подготовлены, чтобы рассмотреть этот вопрос. Для удобства обозначим ограничение функции определенной на пересечении
(чем покрытие, образованное только двумя множествами 41 и У) отчасти обусловлен желанием иметь возможность складывать 1-функции, определенные по отношению к различным покрытиям. Сейчас мы уже достаточно подготовлены, чтобы рассмотреть этот вопрос. Для удобства обозначим ограничение функции определенной на пересечении  на подмножество
на подмножество  через
через

Пусть теперь  — два коцикла, определенные по отношению к покрытиям
— два коцикла, определенные по отношению к покрытиям  соответственно, на
соответственно, на  Определим покрытие
Определим покрытие  которое назовем общим подпокрытием
которое назовем общим подпокрытием

Рис. 6.16. Когда выполняется условие кограницы, интеграл сводится к интегралу по набору стягиваемых замкнутых контуров и оказывается равным нулю.
покрытий 

где I — собирательный индекс, заменяющий два независимых индекса  (Аналогично мы будем обозначать через
(Аналогично мы будем обозначать через  пару индексов
пару индексов  Введем также обозначения
Введем также обозначения

Легко видеть, что после перехода к подпокрытию кограница остается кограницей, а также выполняются условия коцикла (6.10.57) и (6.10.58) для функций в (6.10.63) (роль обычных индексов будут играть собирательные индексы). Однако может случиться так, что новые кограницы, возникающие в подпокрытии, приведут к такому расширению классов эквивалентности, что 1-функции, отличные от нуля в исходных покрытиях, окажутся равными нулю в подпокрытии. Относя 1-функции к подпокрытию, мы можем их складывать: сумме величин  отвечает сумма
отвечает сумма  Поскольку некоторые из 1-функций могут обращаться в нуль при переходе к подпокрытию, можно определить 1-функцию на всем пространстве (в данном случае на пространстве
Поскольку некоторые из 1-функций могут обращаться в нуль при переходе к подпокрытию, можно определить 1-функцию на всем пространстве (в данном случае на пространстве  не зависящую от выбора покрытия, как прямой предел при переходе ко все более тонкому покрытию. (Проще говоря, это означает, что всякую 1-функцию можно представить с помощью 1-коцикла на некотором покрытии, но
не зависящую от выбора покрытия, как прямой предел при переходе ко все более тонкому покрытию. (Проще говоря, это означает, что всякую 1-функцию можно представить с помощью 1-коцикла на некотором покрытии, но
чтобы выяснить, определяют ли два коцикла, взятые в одном и том же или в различных покрытиях, одну и ту же 1-функцию, нам, быть может, придется обратиться к подпокрытию этого покрытия.) Подводя итог всему изложенному, с учетом данного определения можно сказать, что твисторная волновая функция безмассовой частицы в состоянии с определенной спираль-ностью есть голоморфная однородная 1-функция в пространстве 
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие редактора перевода
- Предисловие
- Краткое содержание тома 1
- § 5 (гл. 1). Спинорные объекты и спиновая структура
- § 2 (гл. 2). Формализм абстрактных индексов в тензорной алгебре
- § 3 (гл. 3). Операции симметрии
- Переход от спинорной к тензорной форме записи, и наоборот; преобразование дуальности
- Некоторые свойства тензоров и спиноров в точке
- Активные лоренцевы и спиновые преобразования
- Ковариантная производная
- Спиновые коэффициенты
- Спинорная форма кривизны
- Тождества для спинора Риччи
- Спинорные тождества Бианки
- Компоненты спинорной кривизны
- Модифицированный формализм спиновых коэффициентов
- Уравнения для модифицированных спиновых коэффициентов
- Геометрия пространственноподобных 2-поверхностей
- На изотропной гиперповерхности
- § 15 (гл. 4). Функции на метрической сфере
- Производные заряженных полей
- Поля Янга — Миллса
- Конформные изменения масштаба
- Безмассовые свободные поля
- Другие полевые уравнения
- Данные на изотропной гиперповерхности
- 6. Твисторы
- § 1. Твисторное уравнение и пространство его решений
- Твисторное уравнение
- Пространство твисторов
- Дуальные твисторы
- Твисторы высшей валентности
- Конформная инвариантность спиральности и скалярного произведения
- § 2. Некоторые геометрические аспекты твисторной алгебры
- Поле флагштоков спинора: конгруэнция Робинсона
- Отношение взаимности твисторов
- Комплексная геометрия
- Представление точек с помощью простых кососимметричных твисторов
- § 3. Твисторы и момент импульса
- Момент импульса произвольной системы
- Представление твистора с помощью одноиндексных твисторов
- § 4. Симметричные твисторы и безмассовые поля
- Общий случай, потенциалы
- Повышение спина
- Другие виды потенциалов; связь с оператором
- § 5. Конформные векторы Киллинга; сохраняющиеся величины и точные последовательности
- Спиноры: Законы сохранения
- Твисторное описание
- Связь с интегралами от источников в линейной гравитации
- Точные последовательности
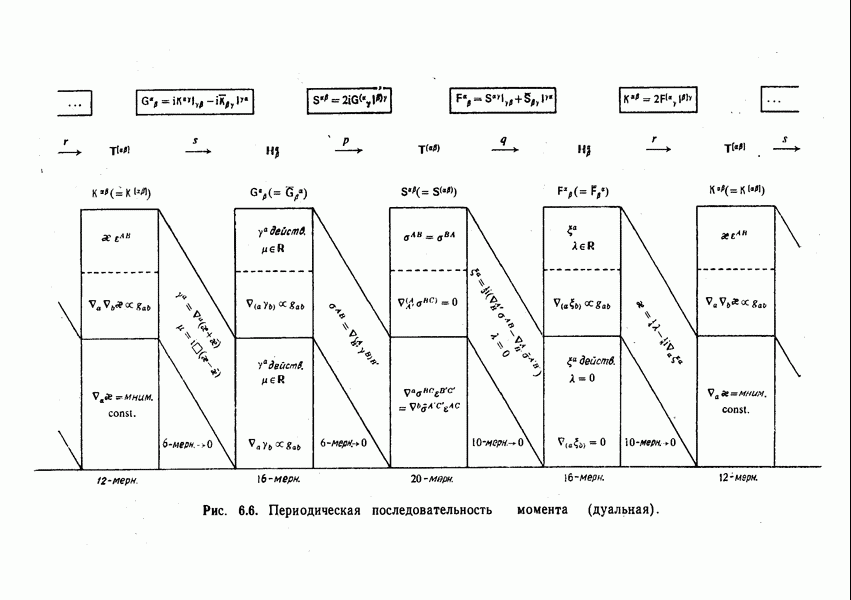
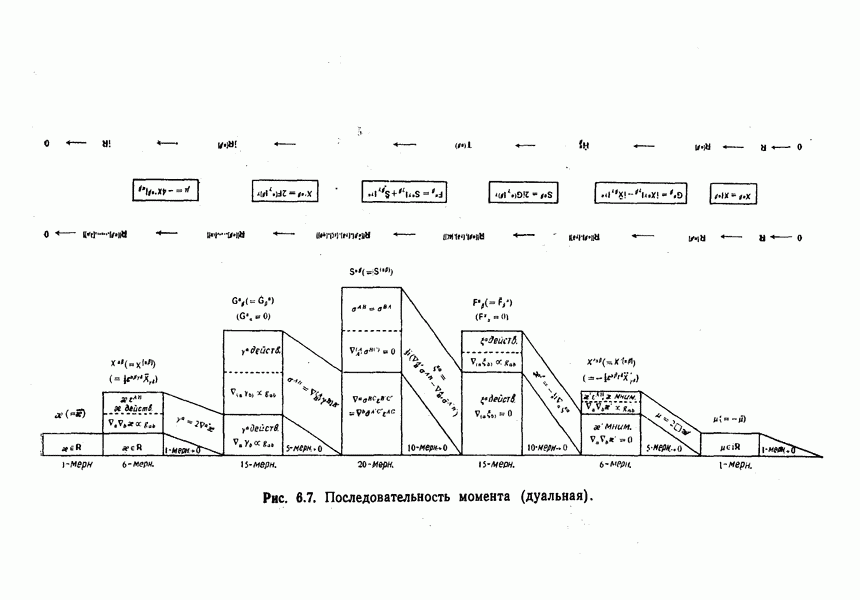
- Последовательности моментов
- Интегралы в линейной теории гравитации
- Спиноры: Десять интегралов, равных нулю
- Роль дуальности в последовательностях момента
- § 6. Производные Ли спиноров
- Связь с теорией твисторов
- § 7. Интегралы движения частиц; конформно-инвариантные операторы
- Спиноры Киллинга для вакуумных решений типа (22)
- Свойства решения Керра
- Конформно-инвариантные первые производные
- Твисторные решения различных уравнений
- Повторные операции; разрешения уравнений
- § 8. Кривизна и конформные преобразования
- Конформные свойства величин
- Конформные отображения плоских пространств
- Конформно-инвариантное волновое уравнение и оператор
- Конформно-инвариантный тензор Баха
- § 9. Локальные твисторы
- Условие совместности для твисторного уравнения
- Определение локального твистора
- Перенос локального твистора
- Кривизна в пространстве локальных твисторов
- Нулевая кривизна Вейля как свойство конформно-плоского пространства
- § 10. Безмассовые поля и когомологии твисторов
- Спиноры: Непроективное представление
- Квантование твисторов
- Спиральность
- Интегралы для спиральности противоположного знака
- Повышение и понижение спиральности
- Массивные твисторные волновые функции
- Геометрия контурных интегралов
- Положительно-частотные поля
- Введение когомологий
- Понятие 1-функции
- r-Функции общего вида
- Нелинейные 1-функции
- Конструкция Уорда
- Пример конструкции Уорда
- 7. Изотропные конгруэнции
- § 1. Изотропные конгруэнции и спиновые коэффициенты
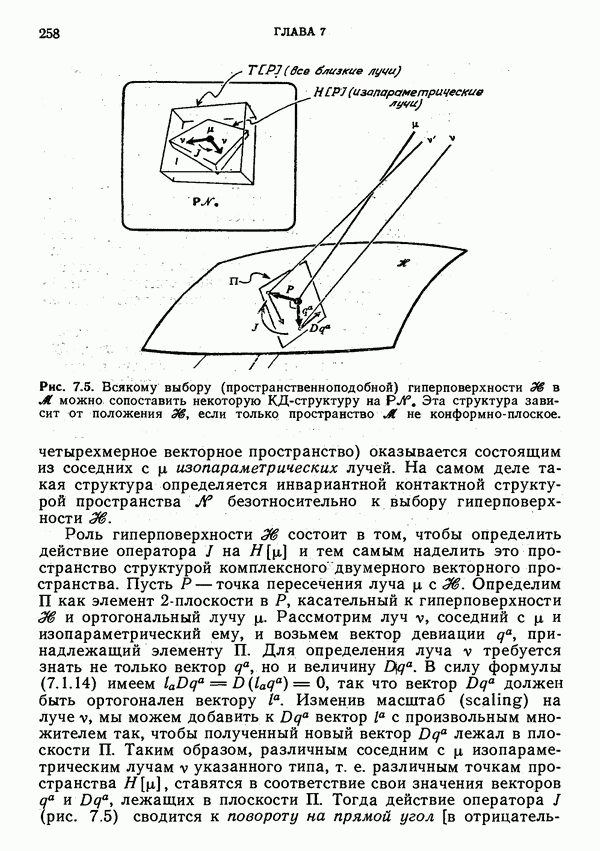
- Интерпретация величин; изопараметричность лучей
- Ортогональность гиперповерхности; изотропные гиперповерхности
- Изопараметричность в теории твисторов
- § 2. Изотропные конгруэнции и кривизна пространства-времени
- Изопараметрические лучи; уравнения Сакса
- Неизопараметрические лучи
- Описание в трехмерном пространстве Минковского
- § 3. Бессдвиговые конгруэнции лучей
- Обобщенная теорема Голдберга — Сакса
- Координаты Керра
- § 4. БСК, твисторы и геометрия лучей
- Твисторная форма теоремы Керра
- Линейные и квадратичные функции твисторов, момент импульса
- Связь с твисторными функциями безмассовых полей
- Пространства и инвариантная контактная структура
- Комплексная структура и КД-структура
- Твисторы гиперповерхности
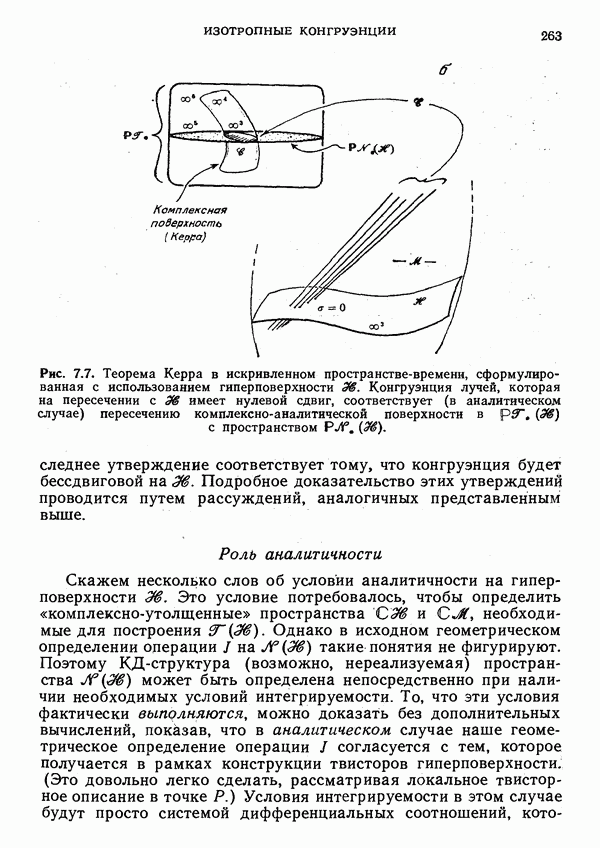
- Спиноры: Роль аналитичности
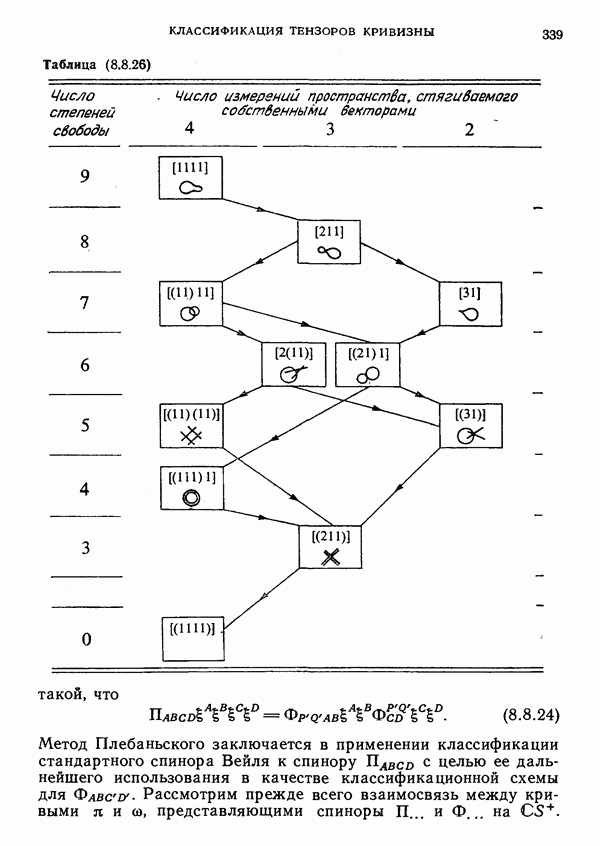
- 8. Классификация тензоров кривизны
- Спиноры: Схема специализации
- § 2. Представление спинора Вейля на сфере S+
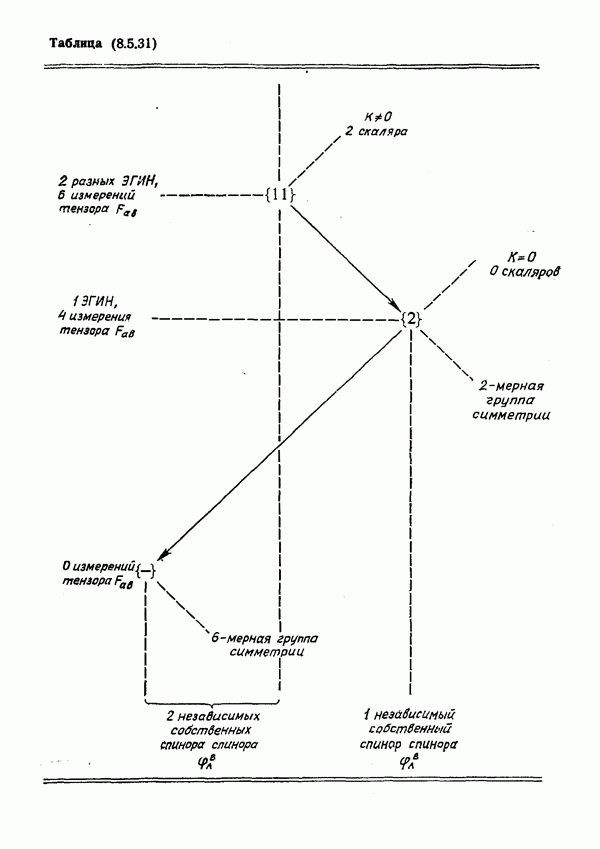
- ГГИН в пространстве-времени высокой симметрии
- «Картина» тензора Вейля на S+
- § 3. Собственные спиноры спинора Вейля
- Соотношение между собственными значениями и двойными отношениями
- Частные случаи
- § 4. Собственные бивекторы тензора Вейля и его классификация по типам Петрова
- Компоненты тензора Вейля в бивекторном базисе
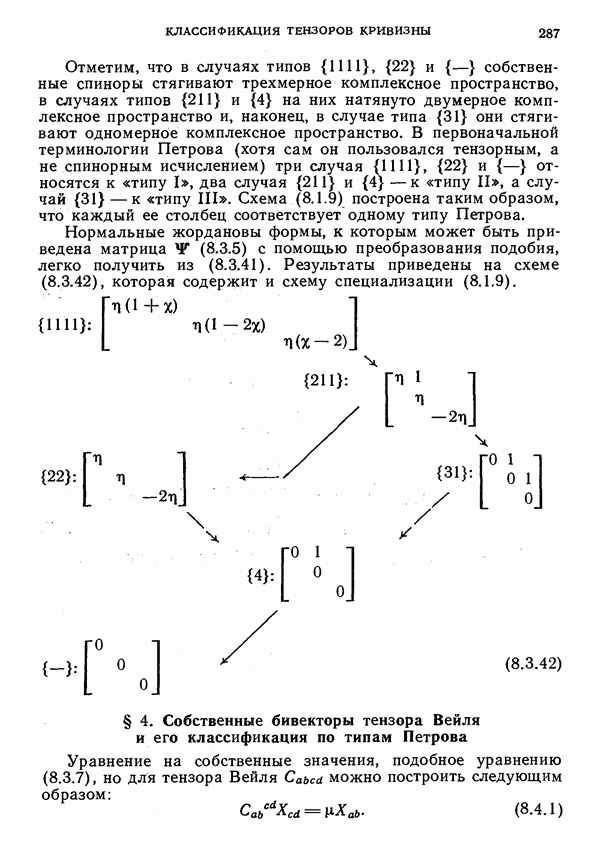
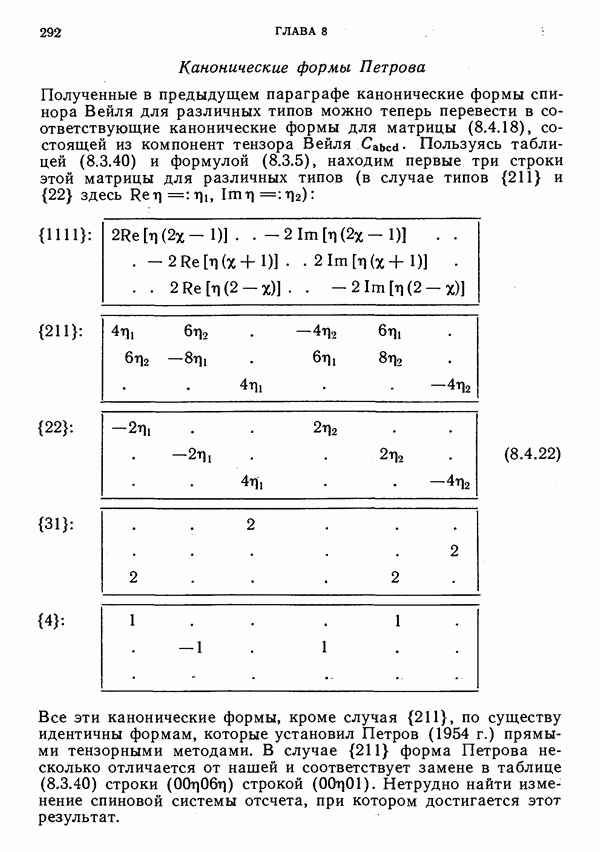
- Канонические формы Петрова
- § 5. Геометрия и симметрия вейлевской кривизны
- Дисфеноид для типа {1111}
- Симметрии в частных случаях типа {1111}
- Тип (211)
- О размерностях групп симметрий
- Классификация тензора Максвелла
- § 6. Коварианты кривизны
- Инварианты полной кривизны
- Система полей Эйнштейна — Максвелла
- § 7. Классификационная схема для спиноров с любым числом индексов
- Приводимость локуса
- Комплексные (р, q) — кривые на CS+
- Процедура классификации спинора
- Структура кривой w (ее кратные точки)
- Кратные точки кривой w
- Локус Rw на S+
- Знак спинора, черный и белый цвета сферы S+
- § 8. Классификация спинора Риччи
- Тип спинора по Плебаньскому
- Физические тензоры энергии-импульса
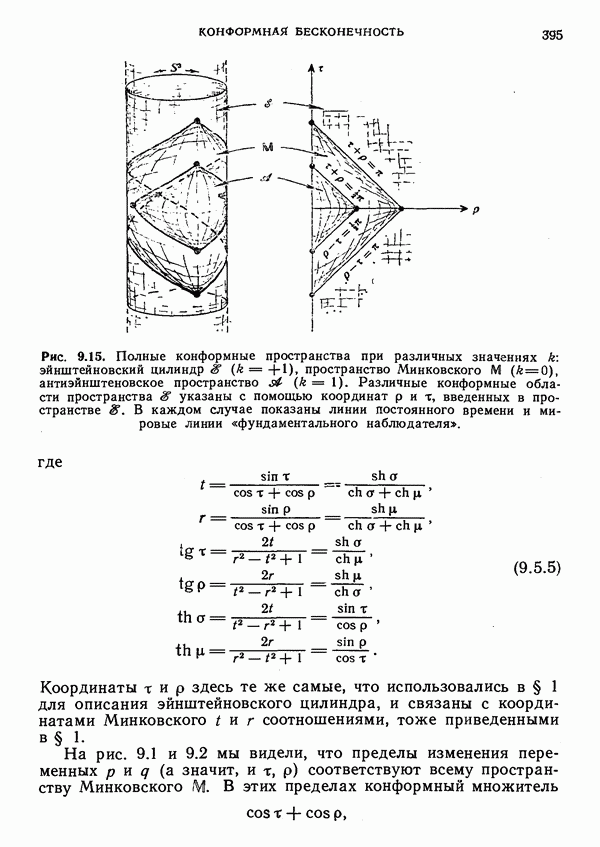
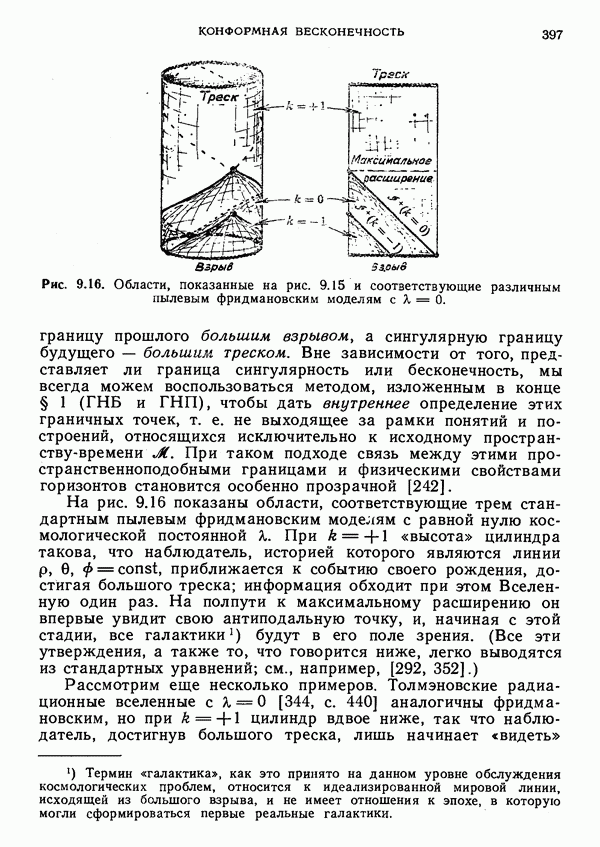
- 9. Конформная бесконечность
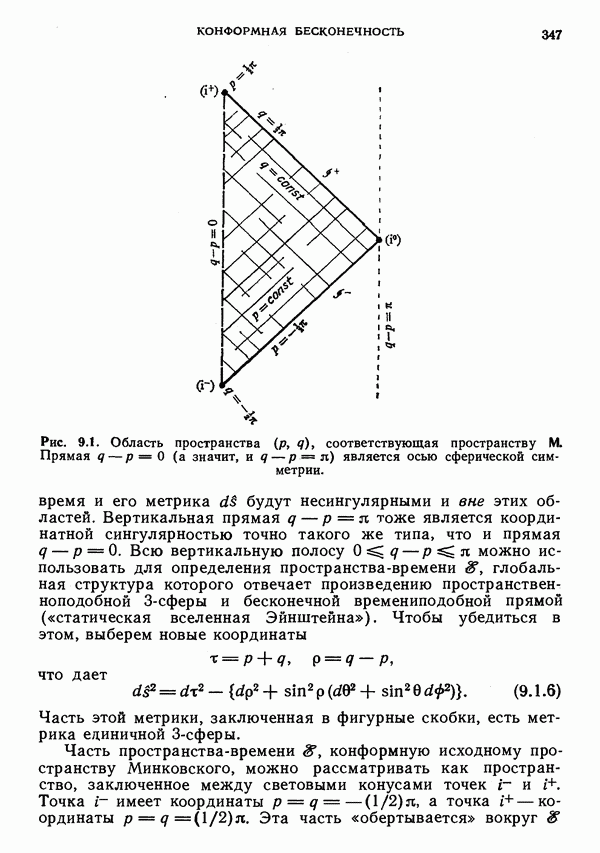
- § 1. Бесконечность в случае пространства Минковского
- ГНП и ГНБ
- § 2. Компактифицированное пространство Минковского
- Описание в пространстве Р5
- O(2,4) и конформная группа
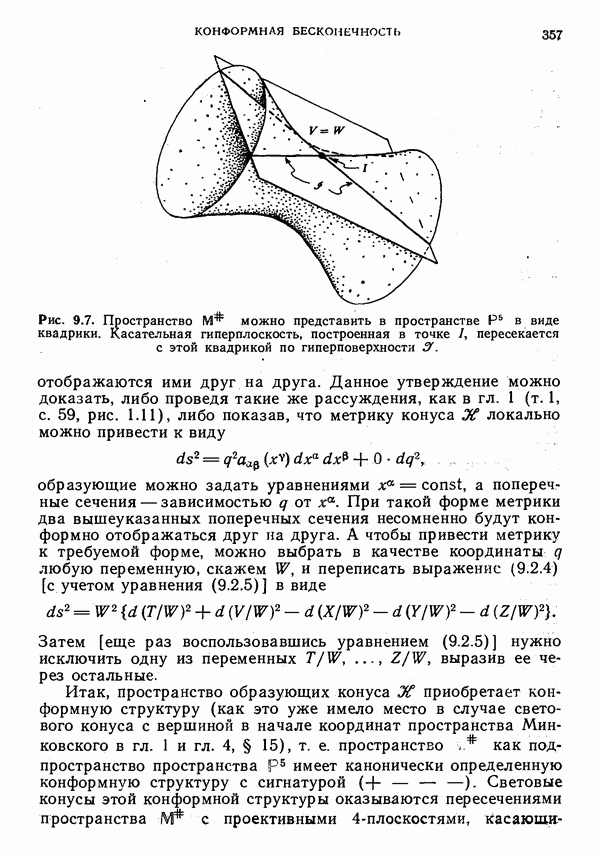
- § 3. Комплексифицированное компактифицированное пространство Минковского и твисторная геометрия
- Соответствие Клейна
- Твисторное отношение дуальности
- Действительная структура
- Различные типы комплексных точек в СМ*
- § 4. Четырехзначность твисторов и индекс Гржина
- Две спиновые структуры на М*
- Поведение спинора
- Твисторные спин-расслоения над М*
- Конформные плотности на М*; индекс Гржина
- Теорема Гржина
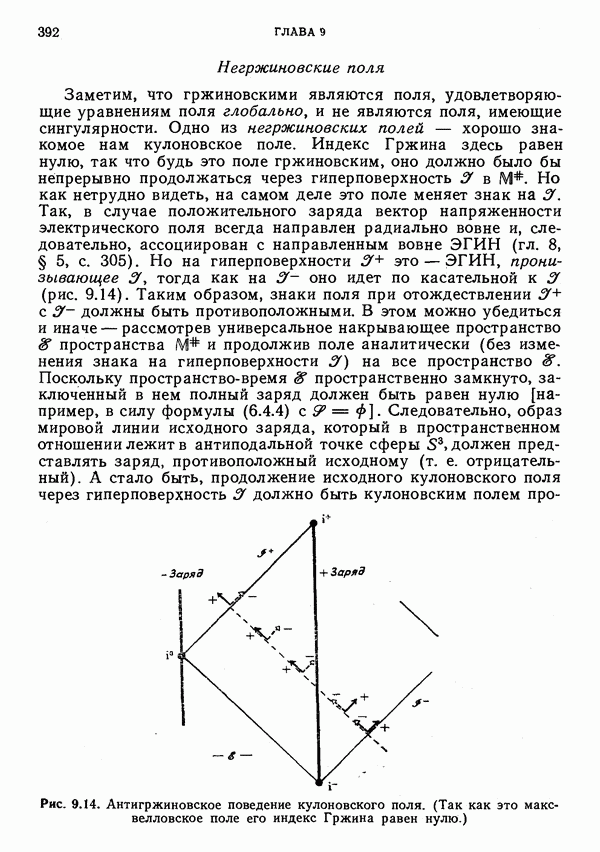
- Негржиновские поля
- § 5. Космологические модели и соответствующие твисторы
- Космологические горизонты
- Описание в пространстве Р5
- Деситтеровская и антидеситтеровская модели; твисторы …
- Функции для конформно-плоского пространства-времени
- Модели ФРУ, соответствующие твисторы начальной и конечной сингулярностей
- Явные выражения для функции I
- § 6. Асимптотически простое пространство-время
- Асимптотически-простое пространство-время
- Обращение в нуль тензора Вейля на границе J
- § 7. Последовательное вырождение
- Параллельно переносимые спиновые системы отсчета
- Сравнение аффинных параметров
- Сравнение спиновых систем отсчета
- Доказательство свойства последовательного вырождения
- Поля излучений
- § 8. Группа БМС и структура гиперповерхности J+
- Группа Бонди — Метцнера — Сакса
- Связь между сильной конформной геометрией и твистором
- Интерпретация изотропных углов
- Структура группы БМС
- Сдвиговая структура гиперповерхности J+
- H-пространство и асимптотическое твисторное пространство
- Отношение группы БМС к импульсу и моменту импульса
- Асимптотические разложения в теории Эйнштейна — Максвелла
- § 9. Энергия-импульс и момент импульса
- Усложнения в случае искривленного пространства-времени
- Твисторы двумерной поверхности
- Контортные двумерные поверхности
- Квазилокальный твистор момента импульса
- Определение множителя
- Асимптотическое спиновое пространство
- Свойства нормы на J+
- Эрмитовость твистора на 4-импульс Бонди — Сакса
- Альтернативные выражения для массы Бонди — Сакса
- Пространство Минковского как пространство «начал»
- Момент импульса на J+
- § 10. Потери массы Бонди — Сакса и положительность энергии
- Нелокальность энергии гравитационных волн
- НП-константы
- Подход Виттена в доказательстве положительности массы
- Связь с 4-импульсом Бонди — Сакса
- Спинор в подходе Людвигсена — Виккерса
- 3-форма Спарлинга
- Приложение. Спиноры в n измерениях
- 2-валентные e-спиноры
- Переход от тензоров к спинорам
- Геометрия фундаментальных спиноров
- Условие фундаментальности; структура спинового пространства
- Индуктивное построение спинового пространства
- Некоторые физически интересные случаи; триальность
- Спинорные поля; твисторы в n измерениях
- Послесловие авторов
- Литература