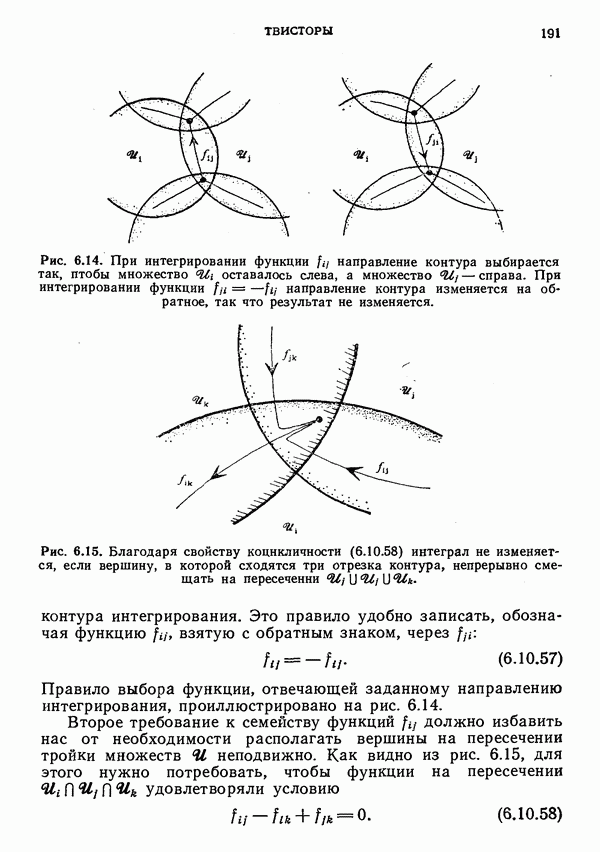
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 3. Бессдвиговые конгруэнции лучей
Изотропную конгруэнцию, т. е. изотропное векторное поле (или ассоциированное с ним поле спин-векторов), которое является геодезическим, а также характеризуется нулевым сдвигом, будем называть бессдвиговой конгруэнцией (БСК). Условия «бессдвиговости» конгруэнции таковы:

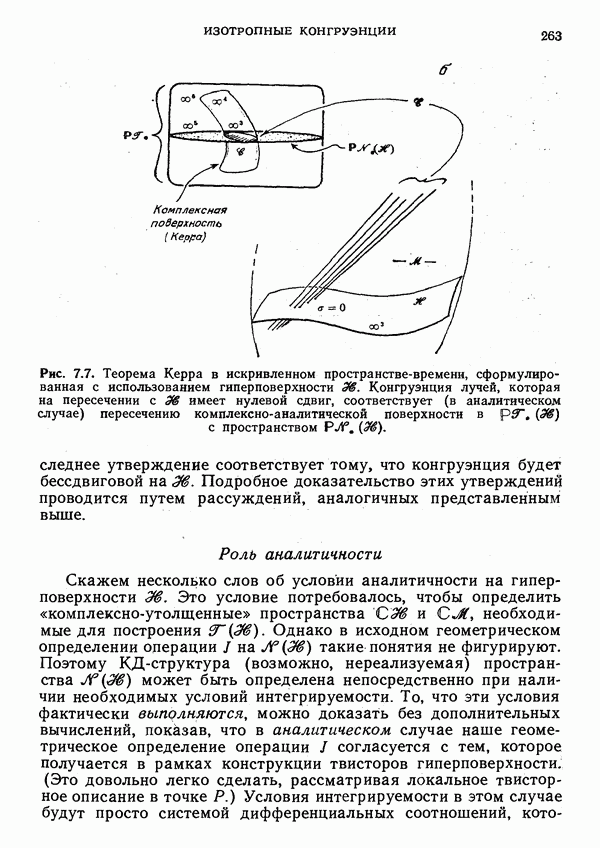
БСК играют важную роль в теории относительности. Они возникают в связи с решениями безмассовых полевых уравнений и особенно важны в теории твисторов. Здесь мы в основном остановимся на связи БСК с безмассовыми полями. В § 4 мы проиллюстрируем роль БСК в теории твисторов и помимо прочего покажем, как можно использовать твисторы, чтобы получать БСК общего вида в пространстве Минковского (теорема Керра). Здесь же можно отметить, что всякое спинорное поле  которое удовлетворяет твисторному уравнению (6.1.1), автоматически удовлетворяет условию БСК (7.3.1); другими словами, конгруэнции Робинсона являются БСК (см. с. 76).
которое удовлетворяет твисторному уравнению (6.1.1), автоматически удовлетворяет условию БСК (7.3.1); другими словами, конгруэнции Робинсона являются БСК (см. с. 76).
Связь с ГИН; вполне изотропные комплексные 2-поверхности
Сначала отметим два результата предварительного характера, касающихся БСК. В качестве альтернативной формулировки утверждения (7.2.14) имеем

т. е.  , что, разумеется, очевидно уже из уравнений (7.2.12). Если дополнительно
, что, разумеется, очевидно уже из уравнений (7.2.12). Если дополнительно  как, например, в плоском пространстве или в пространстве Эйнштейна, то остаются в силе вычисления, приводящие к формулам (7.2.23). Напишем результат для случая
как, например, в плоском пространстве или в пространстве Эйнштейна, то остаются в силе вычисления, приводящие к формулам (7.2.23). Напишем результат для случая 

В частности, замечаем, что если поле  есть БСК, то
есть БСК, то

Напомним, что безмассовыв поля со спином  описываются симметричными спинорами
описываются симметричными спинорами  валентности 0], так что имеет место каноническое разложение (3.5.18):
валентности 0], так что имеет место каноническое разложение (3.5.18):

Если два или более ГИН спинора  (т. е. направления флагштоков спиноров
(т. е. направления флагштоков спиноров  ) совпадают, то поле
) совпадают, то поле  называется алгебраически специальным («вдоль» кратных
называется алгебраически специальным («вдоль» кратных  Если все
Если все  ГИН совпадают
ГИН совпадают  то поле называется изотропным («вдоль» совпадающих ГИН). Напомним, что, как следует из соотношения (3.5.29), в случае электромагнитного поля изотропность эквивалентна обращению в нуль комплексного скалярного инварианта:
то поле называется изотропным («вдоль» совпадающих ГИН). Напомним, что, как следует из соотношения (3.5.29), в случае электромагнитного поля изотропность эквивалентна обращению в нуль комплексного скалярного инварианта:

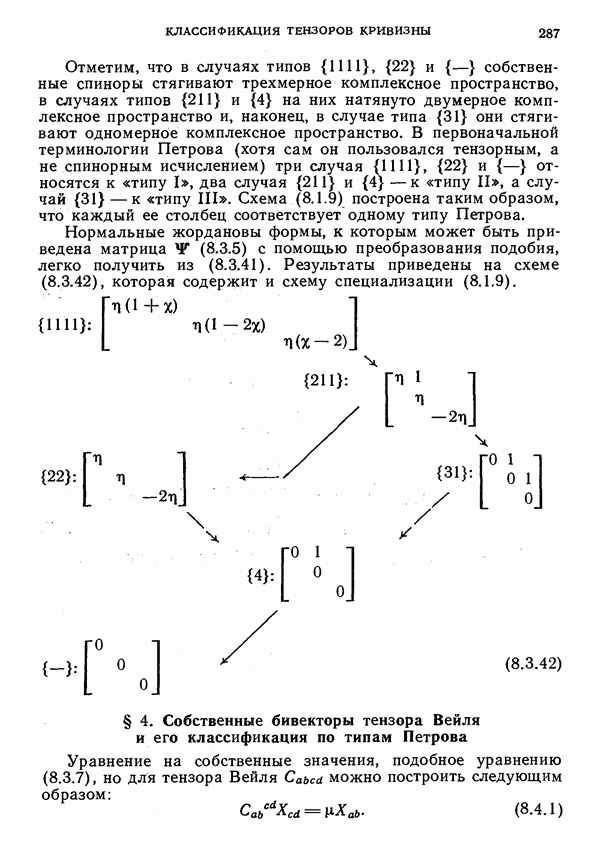
(т. е. двух его действительных скалярных инвариантов). Соответствующие условия для случая, когда спин равен 2, будут приведены в формуле (8.6.3). ГИН спинора  называются гравитационными главными изотропными направлениями (ГГИН).
называются гравитационными главными изотропными направлениями (ГГИН).
Из (3.5.26) следуют два предложения:

Как явствует из этих предложений, алгебраически специальные и изотропные поля тесно связаны с БСК. Предположим, что спинор удовлетворяет уравнению (4.14.42) для свободного безмассового поля.
Предложение
Если выполняется уравнение  и спинор
и спинор  является алгебраически специальным вдоль
является алгебраически специальным вдоль  , то (в области, где
, то (в области, где  поле
поле  есть БСК.
есть БСК.
Доказательство. Рассмотрим открытую область, в которой  будет
будет  -кратным ГИН спинора
-кратным ГИН спинора  (границу между такими областями мы не рассматриваем; условие БСК продолжается по непрерывности). В силу предложения (3.5.26) имеем
(границу между такими областями мы не рассматриваем; условие БСК продолжается по непрерывности). В силу предложения (3.5.26) имеем

где спинор  встречается
встречается  раз, тогда как в уравнении [формула (3.5.24)]
раз, тогда как в уравнении [формула (3.5.24)]

где  левая часть содержит
левая часть содержит  множителей
множителей  а правая
а правая  таких множителей. Дифференцируя равенство (7.3.10) и выполняя свертку по индексу
таких множителей. Дифференцируя равенство (7.3.10) и выполняя свертку по индексу  (эта операция определена, так как
(эта операция определена, так как  получаем
получаем

с учетом равенства (7.3.11). Поскольку  имеем равенство
имеем равенство

и, сравнив его с (7.3.1), получаем требуемый результат (см. также работы [203, 188, 156]).
Мы увидим также, что при  справедиво утверждение, обратное предложению (7.3.9) (теорема Робинсона [294]:
справедиво утверждение, обратное предложению (7.3.9) (теорема Робинсона [294]:  есть
есть  существует такой спинор
существует такой спинор  . В случае когда
. В случае когда  оно справедливо лишь при дополнительных жестких ограничениях на кривизну, которые следуют из соотношений Бухдала — Плебаньского (5.8.2) и составляют содержание следующего предложения.
оно справедливо лишь при дополнительных жестких ограничениях на кривизну, которые следуют из соотношений Бухдала — Плебаньского (5.8.2) и составляют содержание следующего предложения.
Предложение
Если безмассовое свободное поле  со спином
со спином  изотропно вдоль
изотропно вдоль  , то спинор Вейля будет алгебраически специальным вдоль
, то спинор Вейля будет алгебраически специальным вдоль  (в области, где
(в области, где  ).
).
Доказательство. Полагая в (5.8.2)  и
и

получаем

откуда в силу предложения (3.5.15) находим

В силу этого равенства требуемый результат следует из (7.3.7) при 
Теперь можно сформулировать утверждение, обратное предложениям (7.3.9) и (7.3.13).
Теорема [294, 316]
Если поле векторов  определяет БСК и аналитично, то существует ненулевое решение уравнений Максвелла
определяет БСК и аналитично, то существует ненулевое решение уравнений Максвелла  которое изотропно вдоль
которое изотропно вдоль  ; кроме того, если спинор Вейля является алгебраически специальным вдоль
; кроме того, если спинор Вейля является алгебраически специальным вдоль  , то при всех значениях спина
, то при всех значениях спина  существует ненулевое симметричное решение уравнения
существует ненулевое симметричное решение уравнения  изотропное вдоль
изотропное вдоль  . В обоих случаях произвол в выборе решения параметризуется одной голоморфной функцией двух комплексных переменных.
. В обоих случаях произвол в выборе решения параметризуется одной голоморфной функцией двух комплексных переменных.
Прежде чем перейти к доказательству [которое мы проводим, следуя Соммерсу [316], по аналогии с рассуждениями, идущими после равенства (7.3.22)], рассмотрим некоторые леммы о свойствах БСК. Они оказываются важными в другом контексте и имеют отношение к задаче построения точных решений уравнений Эйнштейна, а также к теории твисторов. Первая лемма фактически та же, что и в работе [294] [если спинор  удовлетворяет уравнению (7.3.14), то последнему удовлетворяет и величина
удовлетворяет уравнению (7.3.14), то последнему удовлетворяет и величина 
Лемма
Пусть  — аналитическая БСК. Тогда существуют функционально независимые комплексные скаляры
— аналитическая БСК. Тогда существуют функционально независимые комплексные скаляры  такие, что
такие, что

и всякое решение со уравнения  является голоморфной функцией величин и
является голоморфной функцией величин и 
(В качестве важного приложения этого результата отметим, что из мнимых и действительных частей величин  можно выбрать три удобные координаты в
можно выбрать три удобные координаты в  «привязанные» к БСК. Все они постоянны вдоль лучей БСК, а потому четвертая координата должна быть введена иным способом. Отметим, что градиент каждой из величины
«привязанные» к БСК. Все они постоянны вдоль лучей БСК, а потому четвертая координата должна быть введена иным способом. Отметим, что градиент каждой из величины  имеет вид
имеет вид  а поэтому в любой точке можно образовать линейную комбинацию
а поэтому в любой точке можно образовать линейную комбинацию
градиентов, равную В конце данного параграфа мы покажем, что можно выбрать  естественным образом, если пространство
естественным образом, если пространство  вакуумное.)
вакуумное.)
Доказательство. Сначала комплексифицируем пространство  позволив координатам принимать комплексные значения в открытых аналитических множествах. Поскольку все рассматриваемые величины аналитичны, мы получаем (при достаточно малых мнимых частях координат) комплексное многообразие
позволив координатам принимать комплексные значения в открытых аналитических множествах. Поскольку все рассматриваемые величины аналитичны, мы получаем (при достаточно малых мнимых частях координат) комплексное многообразие  с голоморфной метрикой и голоморфным полем БСК [Напомним, что при «комплексификации» величин, которые и так уже комплексны, мы рассматриваем комплексно-сопряженные им величины как независимые; см. текст после формулы (6.9.1)
с голоморфной метрикой и голоморфным полем БСК [Напомним, что при «комплексификации» величин, которые и так уже комплексны, мы рассматриваем комплексно-сопряженные им величины как независимые; см. текст после формулы (6.9.1)
Далее мы вводим аналитический спинорный базис  на
на  и считаем его тоже комплексифицированным, так что он будет голоморфным на
и считаем его тоже комплексифицированным, так что он будет голоморфным на  Рассмотрим теперь голоморфные векторные поля
Рассмотрим теперь голоморфные векторные поля

Мы хотим показать, что существует комплексно-двухпараметрическое семейство комплексных 2-поверхностей  таких, что поля
таких, что поля  являются касательными к ним. В этом случае, выбирая в качестве параметров, постоянных на каждой поверхности 2, величины
являются касательными к ним. В этом случае, выбирая в качестве параметров, постоянных на каждой поверхности 2, величины  имеем
имеем  , откуда следует лемма (7.3.15). Необходимое и достаточное условие, при котором
, откуда следует лемма (7.3.15). Необходимое и достаточное условие, при котором  и V связаны с системой 2-поверхностей, указано в следующей лемме [165].
и V связаны с системой 2-поверхностей, указано в следующей лемме [165].
Лемма

Доказательство:  следовательно,
следовательно,  в силу условия
в силу условия  Из последнего равенства заключаем, что коммутатор
Из последнего равенства заключаем, что коммутатор  имеет вид где
имеет вид где  — некоторый голоморфный спинор, и, следовательно, должен быть голоморфной линейной комбинацией полей
— некоторый голоморфный спинор, и, следовательно, должен быть голоморфной линейной комбинацией полей  и V, что и требовалось доказать.
и V, что и требовалось доказать.
Тем самым мы доказали следующее предложение.
Предложение
Аналитическое поле  есть БСК при том и только при том условии, что все векторы вида
есть БСК при том и только при том условии, что все векторы вида  (где поле
(где поле  аналитически продолжено на
аналитически продолжено на  ) являются
) являются
касательными к некоторому комплексно-двухпараметрическому семейству комплексных 2-поверхностей в 
Это, по-видимому, основное свойство поля  удовлетворяющего условию
удовлетворяющего условию 
В этой связи нам потребуются еще две леммы.
Лемма
Система дифференциальных уравнений  [формула (4.1.40)], где
[формула (4.1.40)], где  — поля на
— поля на  интегрируема, если
интегрируема, если  где
где  — те же величины, что и в формуле (7.3.17).
— те же величины, что и в формуле (7.3.17).
Доказательство. Это стандартный результат [165]. Ход рассуждений таков: интегрируем уравнение  на некоторой линии, принадлежащей 2-поверхности
на некоторой линии, принадлежащей 2-поверхности  ; затем продолжаем решение вне линии в направлении V, решая уравнение
; затем продолжаем решение вне линии в направлении V, решая уравнение  Если
Если  то имеем
то имеем

откуда  на
на  . (Эти рассуждения носят локальный характер и могут быть неверными для семейства в целом.)
. (Эти рассуждения носят локальный характер и могут быть неверными для семейства в целом.)
Лемма
Уравнение  интегрируемо относительно (комплексного) х (для аналитической
интегрируемо относительно (комплексного) х (для аналитической  если
если  Общее решение, отвечающее данному частному решению
Общее решение, отвечающее данному частному решению  имеет вид:
имеет вид:  где
где  — голоморфная функция, а
— голоморфная функция, а  — такие же, как в лемме (7.3.15).
— такие же, как в лемме (7.3.15).
Доказательство. Условие интегрируемости этого уравнения в компонентах, отнесенных к базису  , то же, что и в лемме (7.3.19) при
, то же, что и в лемме (7.3.19) при  Таким образом, аналог условия интегрируемости (7.3.19) имеет вид
Таким образом, аналог условия интегрируемости (7.3.19) имеет вид

где X и  удовлетворяют уравнению
удовлетворяют уравнению

Сворачивая это уравнение с  и сравнивая результат с (7.3.21), находим
и сравнивая результат с (7.3.21), находим

что после некоторых преобразований приводит к искомому условию интегрируемости. Относительно общего решения см. лемму (7.3.15).
Теперь мы можем доказать теорему (7.3.14). Пусть  есть заданная БСК. Нам потребуется отличное от нуля решение безмассового полевого уравнения вида
есть заданная БСК. Нам потребуется отличное от нуля решение безмассового полевого уравнения вида  т. е.
т. е.

где  определяется как коэффициент пропорциональности в уравнении
определяется как коэффициент пропорциональности в уравнении

которое получается из (7.3.1). Таким образом, требуется решить уравнение

Подставим его правую часть вместо  в условия интегрируемости леммы (7.3.20). Используя уравнение (7.3.24), после некоторых преобразований приведем полученное уравнение к виду
в условия интегрируемости леммы (7.3.20). Используя уравнение (7.3.24), после некоторых преобразований приведем полученное уравнение к виду

Чтобы проверить, выполняются ли эти условия интегрируемости, удобно воспользоваться следующим представлением входящих сюда величин (Соммерс):

Выражение (7.3.27) получаем следующим образом:

где использовано уравнение (7.3.24), а на последнем шаге — уравнение (4.9.15). Чтобы получить выражение (7.3.28), возьмем производную обеих частей последнего равенства в формуле

С учетом формулы (2.5.23) и (4.9.15) первое слагаемое во второй строке может быть записано в виде

Аналогично соотношению (7.3.24) введем величину с помощью первого из следующих равенств:

Таким образом,

Тогда последнее слагаемое в уравнении (7.3.29) преобразуется к виду

В силу равенства (7.3.29) сумму в правых частях равенств (7.3.30) и (7.3.33) можно положить равной нулю, а отсюда следует выражение (7.3.28). Теперь с учетом равенств (7.3.27) и (7.3.28) условие интегрируемости (7.3.26) непосредственно преобразуется к виду

чем доказывается основная часть предложения (7.3.14). Оставшаяся часть, а именно степень произвола в выборе решения, может быть установлена с помощью леммы (7.3.20): к  [формула (7.3.25)] можно добавлять любую голоморфную функцию величин со 1 и
[формула (7.3.25)] можно добавлять любую голоморфную функцию величин со 1 и  а следовательно, саму функцию можно умножать на такую функцию.
а следовательно, саму функцию можно умножать на такую функцию.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие редактора перевода
- Предисловие
- Краткое содержание тома 1
- § 5 (гл. 1). Спинорные объекты и спиновая структура
- § 2 (гл. 2). Формализм абстрактных индексов в тензорной алгебре
- § 3 (гл. 3). Операции симметрии
- Переход от спинорной к тензорной форме записи, и наоборот; преобразование дуальности
- Некоторые свойства тензоров и спиноров в точке
- Активные лоренцевы и спиновые преобразования
- Ковариантная производная
- Спиновые коэффициенты
- Спинорная форма кривизны
- Тождества для спинора Риччи
- Спинорные тождества Бианки
- Компоненты спинорной кривизны
- Модифицированный формализм спиновых коэффициентов
- Уравнения для модифицированных спиновых коэффициентов
- Геометрия пространственноподобных 2-поверхностей
- На изотропной гиперповерхности
- § 15 (гл. 4). Функции на метрической сфере
- Производные заряженных полей
- Поля Янга — Миллса
- Конформные изменения масштаба
- Безмассовые свободные поля
- Другие полевые уравнения
- Данные на изотропной гиперповерхности
- 6. Твисторы
- § 1. Твисторное уравнение и пространство его решений
- Твисторное уравнение
- Пространство твисторов
- Дуальные твисторы
- Твисторы высшей валентности
- Конформная инвариантность спиральности и скалярного произведения
- § 2. Некоторые геометрические аспекты твисторной алгебры
- Поле флагштоков спинора: конгруэнция Робинсона
- Отношение взаимности твисторов
- Комплексная геометрия
- Представление точек с помощью простых кососимметричных твисторов
- § 3. Твисторы и момент импульса
- Момент импульса произвольной системы
- Представление твистора с помощью одноиндексных твисторов
- § 4. Симметричные твисторы и безмассовые поля
- Общий случай, потенциалы
- Повышение спина
- Другие виды потенциалов; связь с оператором
- § 5. Конформные векторы Киллинга; сохраняющиеся величины и точные последовательности
- Спиноры: Законы сохранения
- Твисторное описание
- Связь с интегралами от источников в линейной гравитации
- Точные последовательности
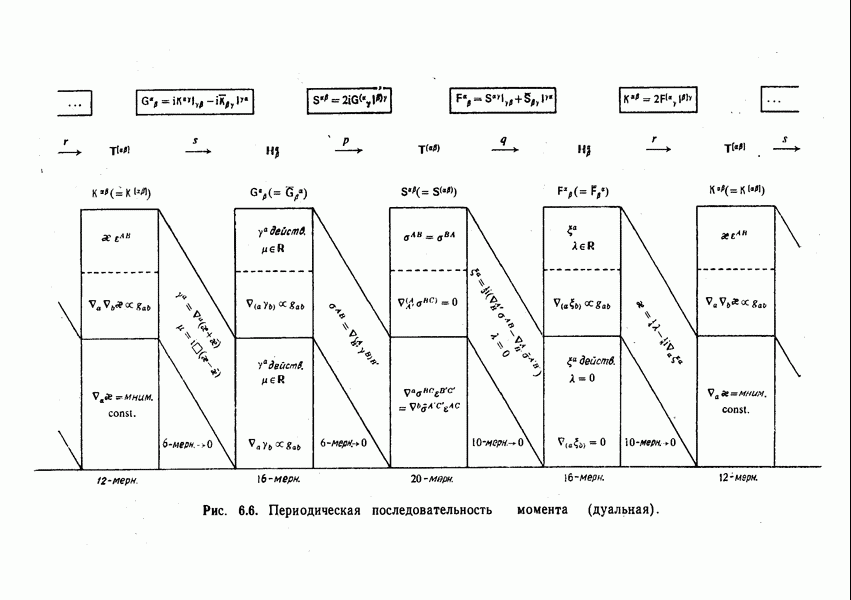
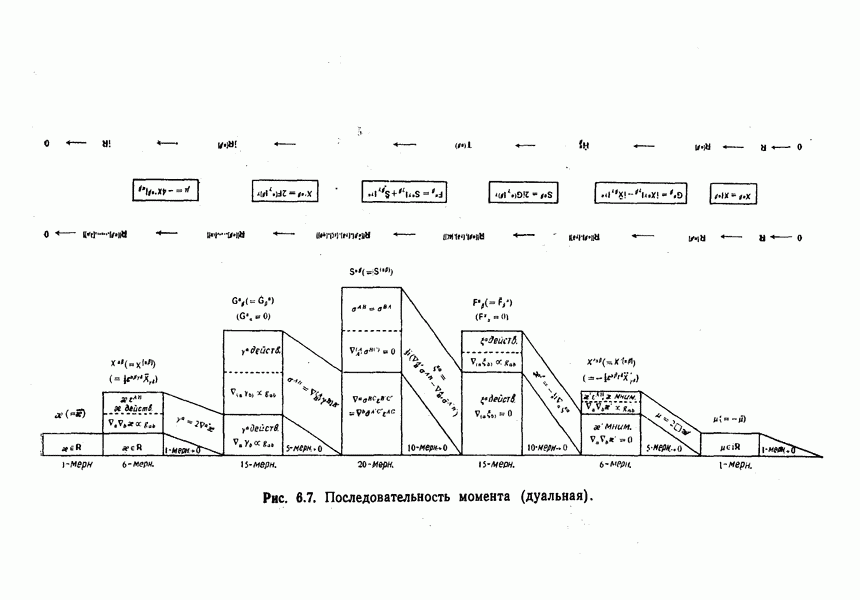
- Последовательности моментов
- Интегралы в линейной теории гравитации
- Спиноры: Десять интегралов, равных нулю
- Роль дуальности в последовательностях момента
- § 6. Производные Ли спиноров
- Связь с теорией твисторов
- § 7. Интегралы движения частиц; конформно-инвариантные операторы
- Спиноры Киллинга для вакуумных решений типа (22)
- Свойства решения Керра
- Конформно-инвариантные первые производные
- Твисторные решения различных уравнений
- Повторные операции; разрешения уравнений
- § 8. Кривизна и конформные преобразования
- Конформные свойства величин
- Конформные отображения плоских пространств
- Конформно-инвариантное волновое уравнение и оператор
- Конформно-инвариантный тензор Баха
- § 9. Локальные твисторы
- Условие совместности для твисторного уравнения
- Определение локального твистора
- Перенос локального твистора
- Кривизна в пространстве локальных твисторов
- Нулевая кривизна Вейля как свойство конформно-плоского пространства
- § 10. Безмассовые поля и когомологии твисторов
- Спиноры: Непроективное представление
- Квантование твисторов
- Спиральность
- Интегралы для спиральности противоположного знака
- Повышение и понижение спиральности
- Массивные твисторные волновые функции
- Геометрия контурных интегралов
- Положительно-частотные поля
- Введение когомологий
- Понятие 1-функции
- r-Функции общего вида
- Нелинейные 1-функции
- Конструкция Уорда
- Пример конструкции Уорда
- 7. Изотропные конгруэнции
- § 1. Изотропные конгруэнции и спиновые коэффициенты
- Интерпретация величин; изопараметричность лучей
- Ортогональность гиперповерхности; изотропные гиперповерхности
- Изопараметричность в теории твисторов
- § 2. Изотропные конгруэнции и кривизна пространства-времени
- Изопараметрические лучи; уравнения Сакса
- Неизопараметрические лучи
- Описание в трехмерном пространстве Минковского
- § 3. Бессдвиговые конгруэнции лучей
- Обобщенная теорема Голдберга — Сакса
- Координаты Керра
- § 4. БСК, твисторы и геометрия лучей
- Твисторная форма теоремы Керра
- Линейные и квадратичные функции твисторов, момент импульса
- Связь с твисторными функциями безмассовых полей
- Пространства и инвариантная контактная структура
- Комплексная структура и КД-структура
- Твисторы гиперповерхности
- Спиноры: Роль аналитичности
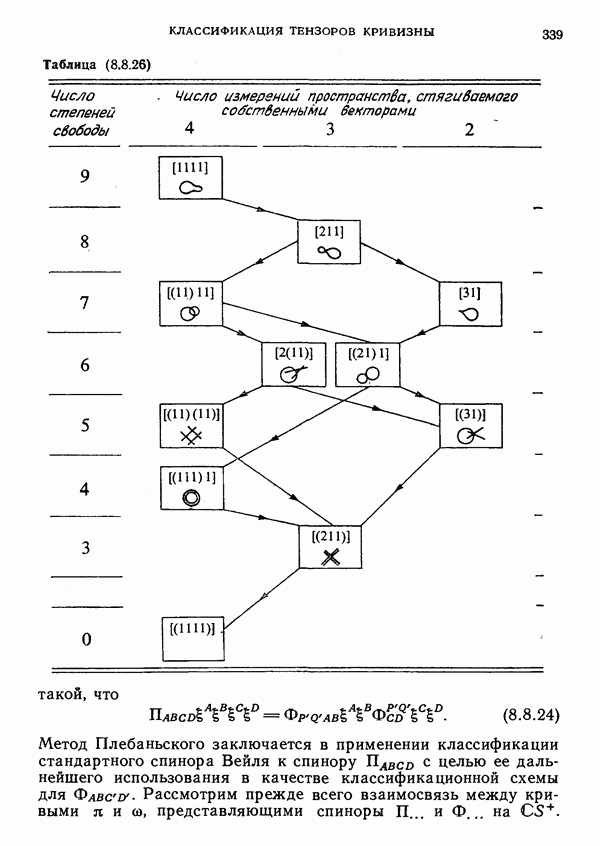
- 8. Классификация тензоров кривизны
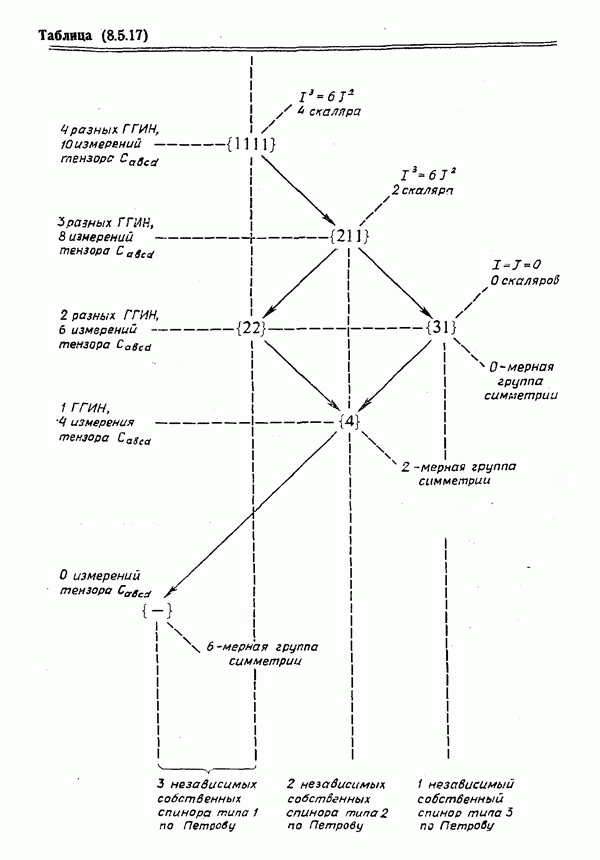
- Спиноры: Схема специализации
- § 2. Представление спинора Вейля на сфере S+
- ГГИН в пространстве-времени высокой симметрии
- «Картина» тензора Вейля на S+
- § 3. Собственные спиноры спинора Вейля
- Соотношение между собственными значениями и двойными отношениями
- Частные случаи
- § 4. Собственные бивекторы тензора Вейля и его классификация по типам Петрова
- Компоненты тензора Вейля в бивекторном базисе
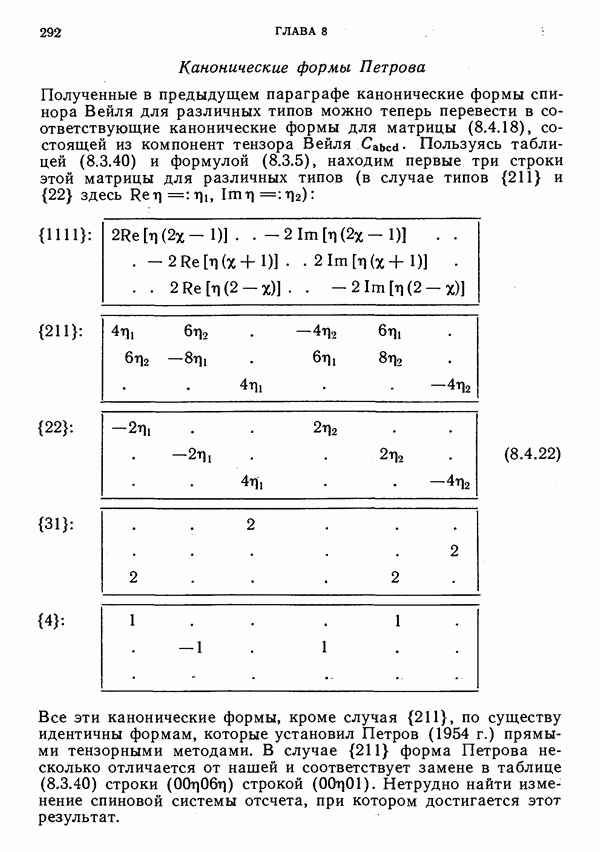
- Канонические формы Петрова
- § 5. Геометрия и симметрия вейлевской кривизны
- Дисфеноид для типа {1111}
- Симметрии в частных случаях типа {1111}
- Тип (211)
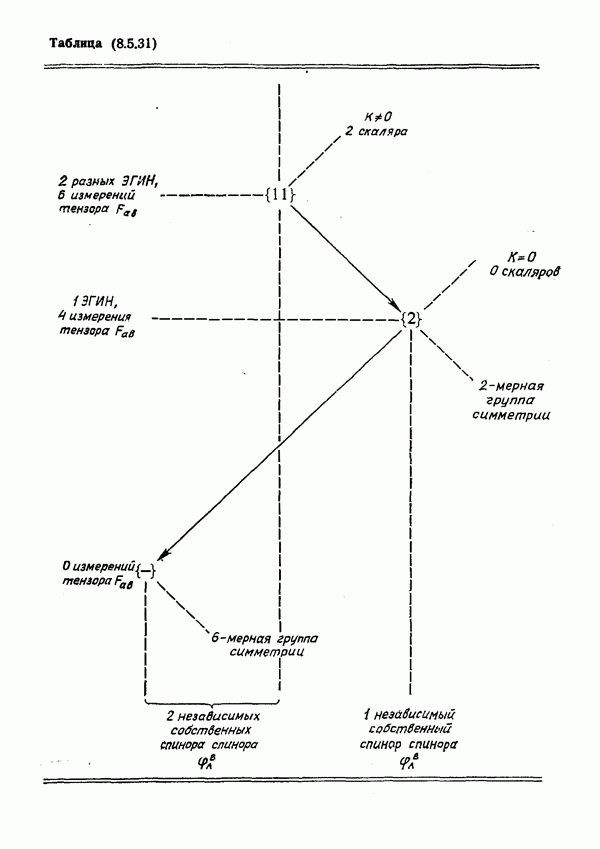
- О размерностях групп симметрий
- Классификация тензора Максвелла
- § 6. Коварианты кривизны
- Инварианты полной кривизны
- Система полей Эйнштейна — Максвелла
- § 7. Классификационная схема для спиноров с любым числом индексов
- Приводимость локуса
- Комплексные (р, q) — кривые на CS+
- Процедура классификации спинора
- Структура кривой w (ее кратные точки)
- Кратные точки кривой w
- Локус Rw на S+
- Знак спинора, черный и белый цвета сферы S+
- § 8. Классификация спинора Риччи
- Тип спинора по Плебаньскому
- Физические тензоры энергии-импульса
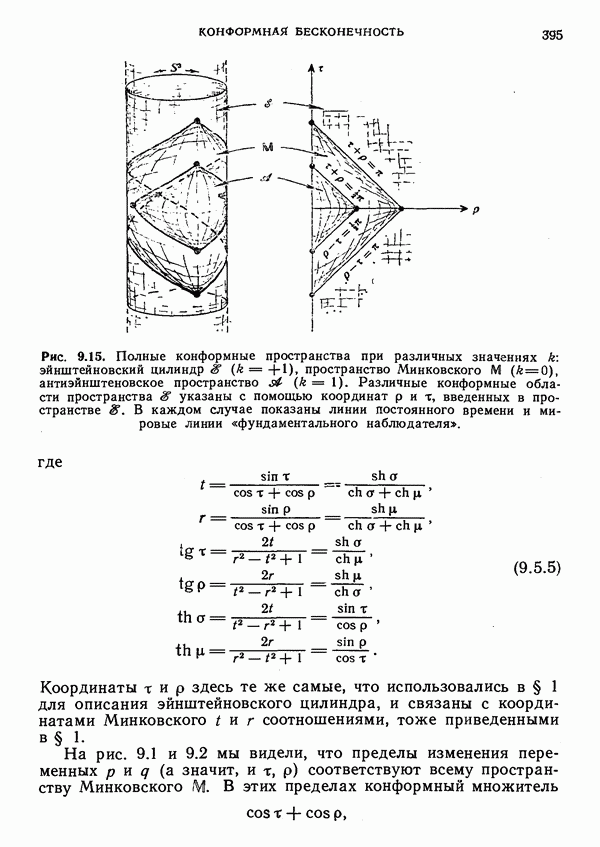
- 9. Конформная бесконечность
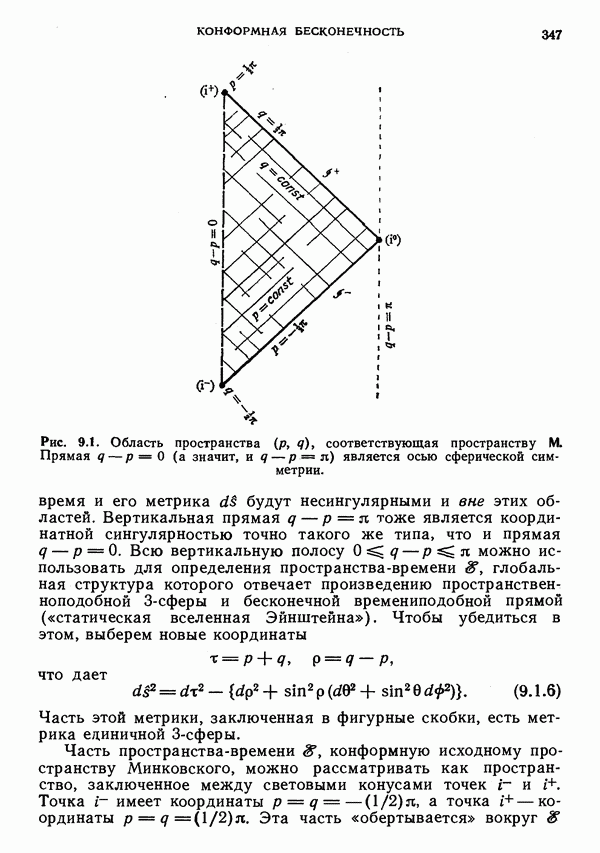
- § 1. Бесконечность в случае пространства Минковского
- ГНП и ГНБ
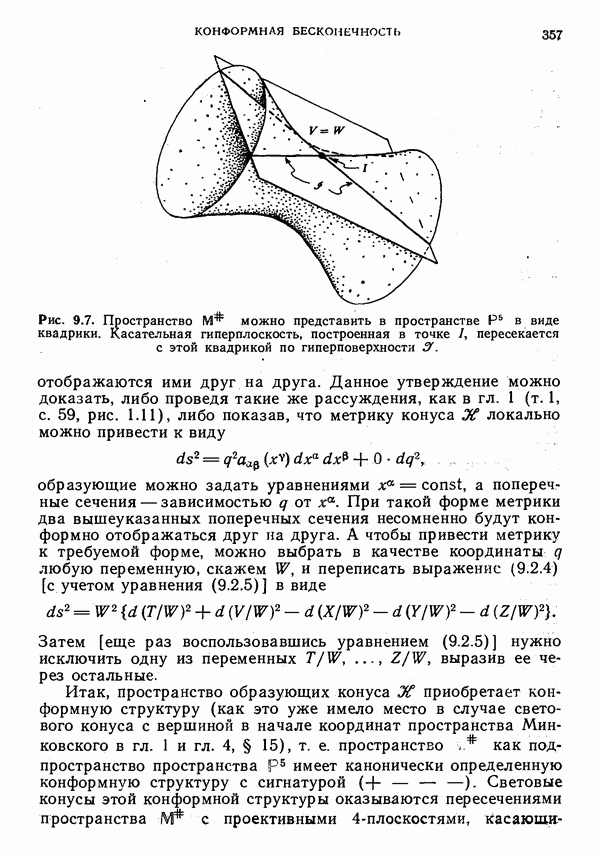
- § 2. Компактифицированное пространство Минковского
- Описание в пространстве Р5
- O(2,4) и конформная группа
- § 3. Комплексифицированное компактифицированное пространство Минковского и твисторная геометрия
- Соответствие Клейна
- Твисторное отношение дуальности
- Действительная структура
- Различные типы комплексных точек в СМ*
- § 4. Четырехзначность твисторов и индекс Гржина
- Две спиновые структуры на М*
- Поведение спинора
- Твисторные спин-расслоения над М*
- Конформные плотности на М*; индекс Гржина
- Теорема Гржина
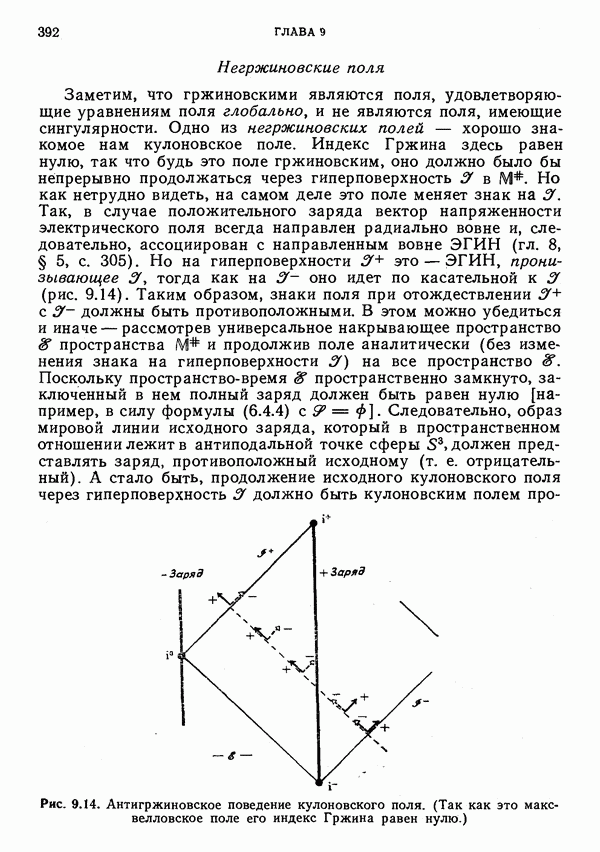
- Негржиновские поля
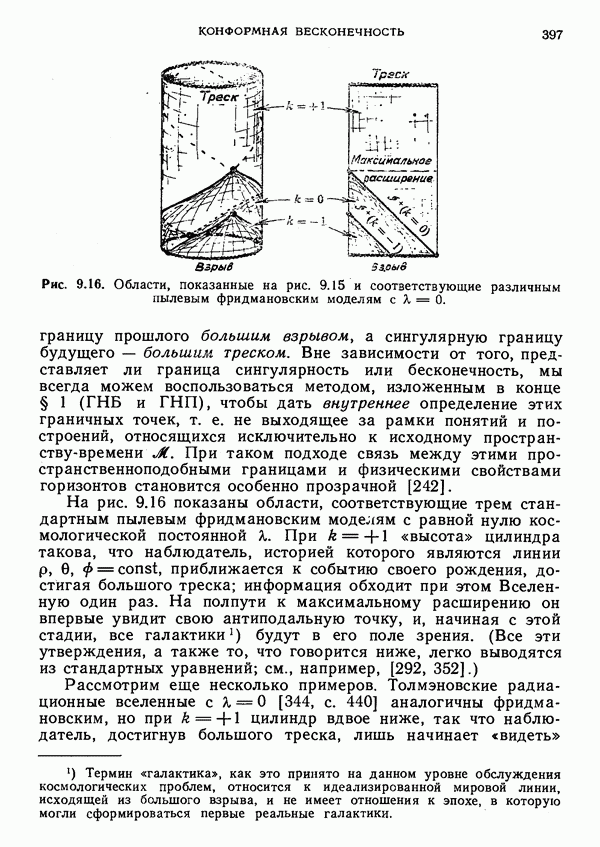
- § 5. Космологические модели и соответствующие твисторы
- Космологические горизонты
- Описание в пространстве Р5
- Деситтеровская и антидеситтеровская модели; твисторы …
- Функции для конформно-плоского пространства-времени
- Модели ФРУ, соответствующие твисторы начальной и конечной сингулярностей
- Явные выражения для функции I
- § 6. Асимптотически простое пространство-время
- Асимптотически-простое пространство-время
- Обращение в нуль тензора Вейля на границе J
- § 7. Последовательное вырождение
- Параллельно переносимые спиновые системы отсчета
- Сравнение аффинных параметров
- Сравнение спиновых систем отсчета
- Доказательство свойства последовательного вырождения
- Поля излучений
- § 8. Группа БМС и структура гиперповерхности J+
- Группа Бонди — Метцнера — Сакса
- Связь между сильной конформной геометрией и твистором
- Интерпретация изотропных углов
- Структура группы БМС
- Сдвиговая структура гиперповерхности J+
- H-пространство и асимптотическое твисторное пространство
- Отношение группы БМС к импульсу и моменту импульса
- Асимптотические разложения в теории Эйнштейна — Максвелла
- § 9. Энергия-импульс и момент импульса
- Усложнения в случае искривленного пространства-времени
- Твисторы двумерной поверхности
- Контортные двумерные поверхности
- Квазилокальный твистор момента импульса
- Определение множителя
- Асимптотическое спиновое пространство
- Свойства нормы на J+
- Эрмитовость твистора на 4-импульс Бонди — Сакса
- Альтернативные выражения для массы Бонди — Сакса
- Пространство Минковского как пространство «начал»
- Момент импульса на J+
- § 10. Потери массы Бонди — Сакса и положительность энергии
- Нелокальность энергии гравитационных волн
- НП-константы
- Подход Виттена в доказательстве положительности массы
- Связь с 4-импульсом Бонди — Сакса
- Спинор в подходе Людвигсена — Виккерса
- 3-форма Спарлинга
- Приложение. Спиноры в n измерениях
- 2-валентные e-спиноры
- Переход от тензоров к спинорам
- Геометрия фундаментальных спиноров
- Условие фундаментальности; структура спинового пространства
- Индуктивное построение спинового пространства
- Некоторые физически интересные случаи; триальность
- Спинорные поля; твисторы в n измерениях
- Послесловие авторов
- Литература