| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
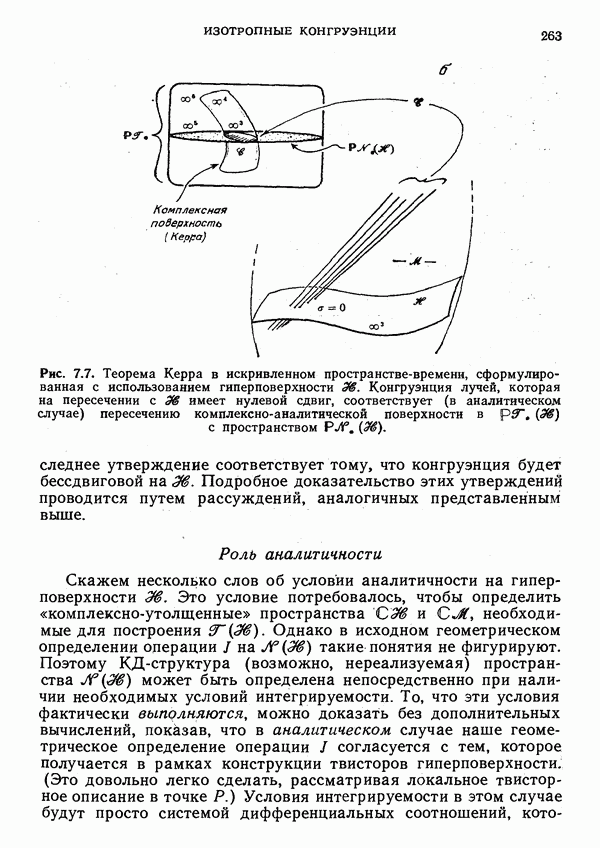
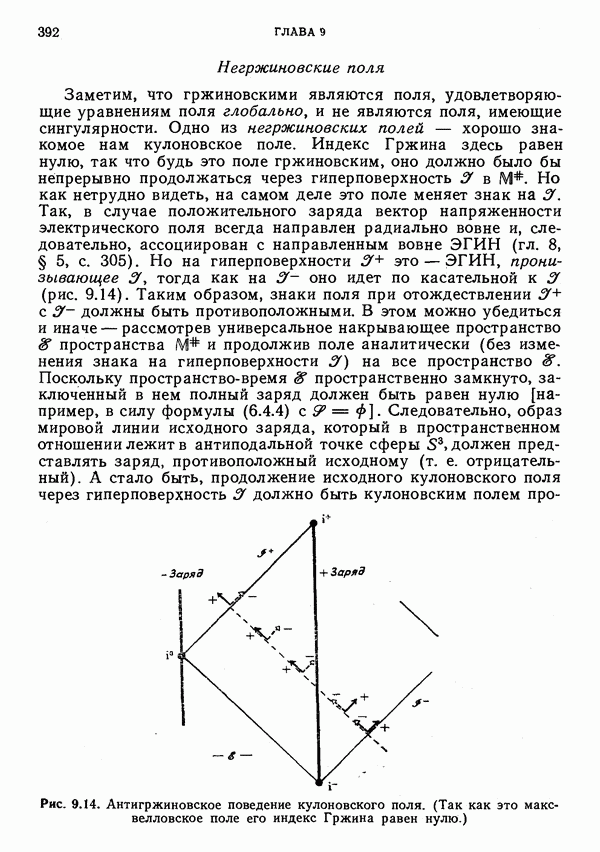
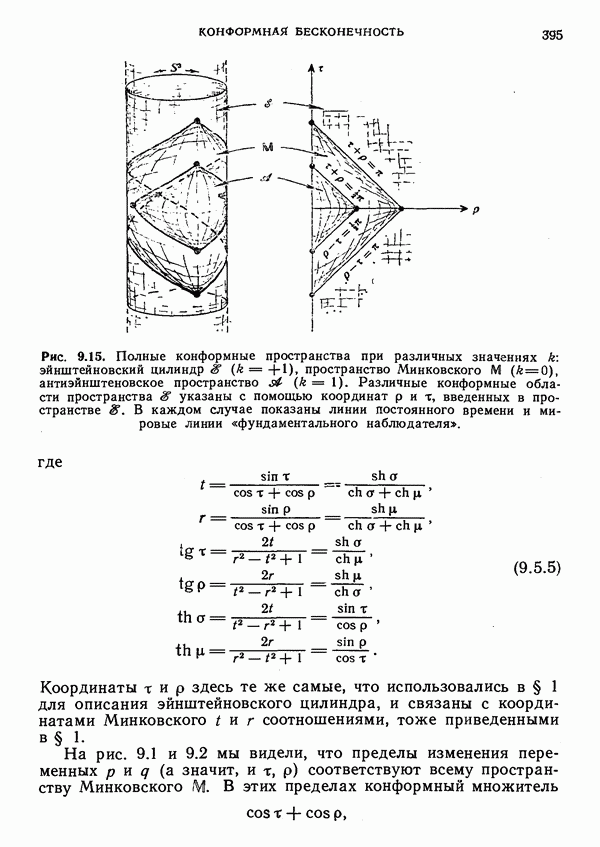
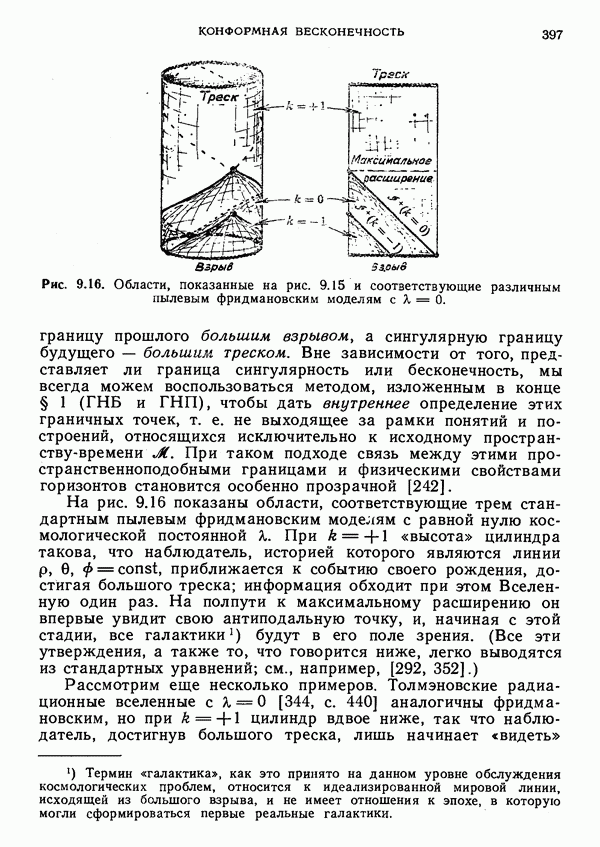
Сдвиговая структура гиперповерхности J+
Из сказанного следует, что, имея дело с групповой структурой одной лишь группы  , невозможно единственным образом выделить ограниченную группу Пуанкаре как подгруппу. (И проблема, как мы видели, не в том, чтобы отличить трансляции от супертрансляций, а в том, чтобы выяснить, что следует понимать под «бессупертранляционным» лоренцевым поворотом.) В случае пространства М на гиперповерхности
, невозможно единственным образом выделить ограниченную группу Пуанкаре как подгруппу. (И проблема, как мы видели, не в том, чтобы отличить трансляции от супертрансляций, а в том, чтобы выяснить, что следует понимать под «бессупертранляционным» лоренцевым поворотом.) В случае пространства М на гиперповерхности  есть некая дополнительная структура, а именно определение «хорошего среза», который позволяет выделить единственную подгруппу Ф. Напрашивается вывод, что для получения подходящего единственного аналога подгруппы 9 в случае искривленного пространства
есть некая дополнительная структура, а именно определение «хорошего среза», который позволяет выделить единственную подгруппу Ф. Напрашивается вывод, что для получения подходящего единственного аналога подгруппы 9 в случае искривленного пространства  следовало бы и здесь ввести соответствующее понятие «хорошего среза».
следовало бы и здесь ввести соответствующее понятие «хорошего среза».
Однако при этом возникают серьезные трудности. По ряду причин не годится брать в качестве хороших срезов просто пересечения настоящих световых конусов в  (Например, вследствие вида каустик и областей пересечения на конусе такие «срезы» вовсе не обязаны быть сечениями гиперповерхности
(Например, вследствие вида каустик и областей пересечения на конусе такие «срезы» вовсе не обязаны быть сечениями гиперповерхности  и даже те из них, которые являются ими, в общем случае не преобразуются друг в друга в соответствии с подгруппой группы Я.) Правильнее было бы принять определение, «локальное» на
и даже те из них, которые являются ими, в общем случае не преобразуются друг в друга в соответствии с подгруппой группы Я.) Правильнее было бы принять определение, «локальное» на  (а следовательно, полностью асимптотическое в Ж). В пространстве М световые конусы (будущего) выделяются по признаку их расходимости и равенства нулю сдвига
(а следовательно, полностью асимптотическое в Ж). В пространстве М световые конусы (будущего) выделяются по признаку их расходимости и равенства нулю сдвига  (см. гл. 7, § 1). Значит, в пространстве М, чтобы установить, что срез
(см. гл. 7, § 1). Значит, в пространстве М, чтобы установить, что срез
хороший, нужно лишь исследовать сдвиг на самом срезе. Полагая флагштоки спинора о ортогональными срезу (как это имеет место в стандартной трактовке пространственноподобных 2-поверхностей, данной в гл. 4, § 14), можно вычислить а на срезе, и если обнаружится, что  всюду на этом срезе, то можно утверждать, что это хороший срез.
всюду на этом срезе, то можно утверждать, что это хороший срез.
Такой подход допустим не только в пространстве  но и в некоторых других пространствах-временах
но и в некоторых других пространствах-временах  особенно если они стационарны. Однако при наличии гравитационного излучения возникают трудности фундаментального характера. Чтобы выяснить, как это происходит, нужно вывести еще ряд формул. Для начала предположим, что имеется гладкая координата и на
особенно если они стационарны. Однако при наличии гравитационного излучения возникают трудности фундаментального характера. Чтобы выяснить, как это происходит, нужно вывести еще ряд формул. Для начала предположим, что имеется гладкая координата и на  которая соответствующим образом возрастает на образующих этой гиперповерхности, но не обязательно является параметром времени Бонди. Выберем
которая соответствующим образом возрастает на образующих этой гиперповерхности, но не обязательно является параметром времени Бонди. Выберем  -флагштоки так, чтобы они, как и выше, были ортогональны срезам
-флагштоки так, чтобы они, как и выше, были ортогональны срезам  Тогда (если и — величина типа
Тогда (если и — величина типа  имеем
имеем

Применив к и коммутатор (4.12.34), мы с учетом условий (9.8.25) получим слабое равенство

которое в силу равенства (9.8.69) сводится к формуле

Далее будем считать, что выполняются условия (9.8.33). Тогда условие (9.8.30), гарантирующее, что и — координата времени Бонди (ассоциированная с выбранным для  масштабом), приводится к виду
масштабом), приводится к виду  что вместе с (9.8.28) позволяет свести слабое равенство (9.8.70) к виду
что вместе с (9.8.28) позволяет свести слабое равенство (9.8.70) к виду

[Этот вывод частично обратим: если выполняется условие (9.8.71) и предполагаются справедливыми условия (9.8.33), то и является функцией такого рода ассоциированной координаты времени Бонди, так что и последняя и первая будут постоянными на одних и тех же срезах.] Будем называть о-флагштоки, связанные указанным способом с параметром времени Бонди, ассоциированным с выбранным масштабом для гиперповерхности  системой Бонди. Тогда справедливо следующее предложение.
системой Бонди. Тогда справедливо следующее предложение.
Предложение
Условием существования системы Бонди является слабое равенство 
Уравнение (4.12.32 д) дает

где

есть комплексная функция новостей Бонди — Сакса, очень важная связь которой с потоком энергии гравитационного поля будет рассматриваться в § 9. В системе Бонди соотношение (9.8.73) принимает вид 

Вспомним, что как часть сильного асимптотического эйнштейновского условия для пространства  должно выполняться слабое равенство
должно выполняться слабое равенство

т. е.

В результате из формул (4.12.32а) и (4.12.32г) следует, что

Теперь нам потребуются тождества Бианки на  Принимая во внимание, что поле со спином 2
Принимая во внимание, что поле со спином 2

является гладким класса  на
на  [при наших начальных предположениях на
[при наших начальных предположениях на  ; см. теорему (9.6.41)], получаем
; см. теорему (9.6.41)], получаем

[формула (9.6.42)]. С учетом равенств (9.8.77) это дает

(тогда как  Следовательно, принимая во внимание (4.12.39), получаем
Следовательно, принимая во внимание (4.12.39), получаем

Кроме того, воспользовавшись комбинацией соотношений (4.12.38) +(4.12.41)+(4.12.38) и замечая, что, согласно формуле  » можно получить слабое равенство
» можно получить слабое равенство

Нас также интересует обобщение равенства (9.8.83), которое получается, когда предполагается выполненным только условие  а второе условие (9.8.33) не привлекается. Следовательно, на
а второе условие (9.8.33) не привлекается. Следовательно, на  выполняется такое масштабное преобразование, что
выполняется такое масштабное преобразование, что  срезы этой гиперповерхности изометрически отображаются
срезы этой гиперповерхности изометрически отображаются
друг на друга ее образующими, но не обязательно являются метрическими сферами. В результате получается слабое равенство

где

Согласно формуле (4.14.20), эта действительная величина К представляет собой половину гауссовой кривизны срезов. Пока что мы положим  и тогда соотношение (9.8.84) сведется к (9.8.83).
и тогда соотношение (9.8.84) сведется к (9.8.83).
Затем, вычитая (4.12.37) из комплексно-сопряженного ему выражения, мы получаем

тогда как из формулы (4.12.32г) следует, что

При выводе формулы (9.8.87) использовалось равенство

в котором [формулы (4.14.2) и (7.1.58)] выражается то обстоятельство, что элементы 2-плоскостей на  ортогональные о-флагштокам, являются поверхность-образующими (а именно касательны к срезам
ортогональные о-флагштокам, являются поверхность-образующими (а именно касательны к срезам  ). Кроме того, в силу формулы (4.12.35) и действительного характера величины К величина
). Кроме того, в силу формулы (4.12.35) и действительного характера величины К величина  тоже действительна, так что, подставив (9.8.87) в (9.8.86), мы получим условие действительности
тоже действительна, так что, подставив (9.8.87) в (9.8.86), мы получим условие действительности

которое нам понадобится в § 9.
Между прочим отметим, что приведенная в (6.8.17) форма тождеств Бианки

 позволяет получить слабое равенство
позволяет получить слабое равенство

из которого следует много других выражений для  [С его помощью можно дать другой вывод соотношений (9.8.82), (9.8.84) и (9.8.86), хотя это и не тривиально; в этой связи отметим, что соотношения (9.8.78) и (9.8.85) можно скомбинировать в одно соотношение
[С его помощью можно дать другой вывод соотношений (9.8.82), (9.8.84) и (9.8.86), хотя это и не тривиально; в этой связи отметим, что соотношения (9.8.78) и (9.8.85) можно скомбинировать в одно соотношение 
Наибольший интерес для нас сейчас представляют соотношения (9.8.82) и (9.8.75), которые вместе означают, что в
системе Бонди мы имеем

Согласно сказанному в § 7, величина  на
на  является мерой уходящего гравитационного излучения (т. е. это
является мерой уходящего гравитационного излучения (т. е. это  физического поля вейлевой кривизны). Таким образом, одно из следствий соотношения (9.8.91) таково: когда имеется уходящее гравитационное излучение, невозможно сохранить условие «хорошего срезам
физического поля вейлевой кривизны). Таким образом, одно из следствий соотношения (9.8.91) таково: когда имеется уходящее гравитационное излучение, невозможно сохранить условие «хорошего срезам  во всей системе Бонди. Суть системы Бонди состоит в том, что все срезы
во всей системе Бонди. Суть системы Бонди состоит в том, что все срезы  являются трансляциями во времени относительно фиксированного «временного направления» (а именно такого, которое определяется выбором масштаба единичной сферы срезов) наперед заданного среза (скажем, среза, соответствующего значению параметра
являются трансляциями во времени относительно фиксированного «временного направления» (а именно такого, которое определяется выбором масштаба единичной сферы срезов) наперед заданного среза (скажем, среза, соответствующего значению параметра  Здесь в сущности обнаруживается, что трансляция хорошего среза — в общем случае плохой срез. (Термин «трансляция» в данном контексте означает, что второй срез — это БМС-трансляция первого, но само пространство-время, включая
Здесь в сущности обнаруживается, что трансляция хорошего среза — в общем случае плохой срез. (Термин «трансляция» в данном контексте означает, что второй срез — это БМС-трансляция первого, но само пространство-время, включая  при этом не движется.)
при этом не движется.)
Таким образом, в системе с уходящим гравитационным излучением гиперповерхность  обладает «структурой хорошего среза», которая отличается от аналогичной структуры для пространства М, и мы уже не можем использовать методы, развитые ранее для выделения частной ограниченной подгруппы Пуанкаре
обладает «структурой хорошего среза», которая отличается от аналогичной структуры для пространства М, и мы уже не можем использовать методы, развитые ранее для выделения частной ограниченной подгруппы Пуанкаре  группы
группы  . Более подходящей «структурой хорошего среза» для
. Более подходящей «структурой хорошего среза» для  является сдвиговая структура, которая любому срезу гиперповерхности
является сдвиговая структура, которая любому срезу гиперповерхности  ставит в соответствие
ставит в соответствие  —
— -скалярную функцию а, определенную на этом срезе. Такая сдвиговая структура на одну ступень более «внутренняя», чем сильная конформная геометрия гиперповерхности
-скалярную функцию а, определенную на этом срезе. Такая сдвиговая структура на одну ступень более «внутренняя», чем сильная конформная геометрия гиперповерхности  (хотя, что называть «внутренним» или «внешним», особенно в случае изотропной гиперповерхности, это в известной степени вопрос соглашения [247]). Ибо она относится к сдвигу на
(хотя, что называть «внутренним» или «внешним», особенно в случае изотропной гиперповерхности, это в известной степени вопрос соглашения [247]). Ибо она относится к сдвигу на  изотропных гиперповерхностей в
изотропных гиперповерхностей в  Из сказанного следует, что сдвиговая структура гиперповерхности
Из сказанного следует, что сдвиговая структура гиперповерхности  пространства М отличается от сдвиговой структуры такой гиперповерхности в общем пространстве
пространства М отличается от сдвиговой структуры такой гиперповерхности в общем пространстве  Фактически сдвиговая структура гиперповерхности
Фактически сдвиговая структура гиперповерхности  эквивалентна (по модулю, самое большее, двух постоянных интегрирования на каждой образующей гиперповерхности
эквивалентна (по модулю, самое большее, двух постоянных интегрирования на каждой образующей гиперповерхности  информации об уходящем гравитационном излучении. Подгруппа группы 38 в случае пространства М является группой, сохраняющей в дополнение к сильной конформной геометрии гиперповерхности
информации об уходящем гравитационном излучении. Подгруппа группы 38 в случае пространства М является группой, сохраняющей в дополнение к сильной конформной геометрии гиперповерхности  ее сдвиговую структуру. В случае произвольного пространства
ее сдвиговую структуру. В случае произвольного пространства  в котором поле
в котором поле  лишено симметрий на
лишено симметрий на  ими не обладает и сдвиговая структура гиперповерхности
ими не обладает и сдвиговая структура гиперповерхности  Так что мы вернулись туда же, где были в начале этого
Так что мы вернулись туда же, где были в начале этого
обсуждения: в случае произвольного пространства  группа симметрий, сохраняющая сдвиговую структуру, состоит лишь из тождественного элемента.
группа симметрий, сохраняющая сдвиговую структуру, состоит лишь из тождественного элемента.
Сдвиговой структурой гиперповерхности  конечно, определяются хорошие срезы, а именно те, для которых
конечно, определяются хорошие срезы, а именно те, для которых  . Но в общем случае никакие хорошие срезы не нужны! Это объясняется главным образом тем, что а — комплексная величина на сфере, тогда как свободе в выборе среза отвечает одна действительная функция, определенная на сфере, а именно значение параметра и, соответствующее пересечению с каждой образующей. Легко показать [299], что в случае пространства М разница между значением
. Но в общем случае никакие хорошие срезы не нужны! Это объясняется главным образом тем, что а — комплексная величина на сфере, тогда как свободе в выборе среза отвечает одна действительная функция, определенная на сфере, а именно значение параметра и, соответствующее пересечению с каждой образующей. Легко показать [299], что в случае пространства М разница между значением  на одном срезе и значением
на одном срезе и значением  на другом, полученном из первого в результате супертрансляции
на другом, полученном из первого в результате супертрансляции  в формуле (9.8.9) (2), определяется слабым равенством
в формуле (9.8.9) (2), определяется слабым равенством

В пространстве М все срезы являются супертрансляциями некоторого хорошего среза  так что действительный характер функции Н в формуле (9.8.92) указывает на то, что все срезы удовлетворяют условию
так что действительный характер функции Н в формуле (9.8.92) указывает на то, что все срезы удовлетворяют условию

которое называется чисто электрическим [219], и этим эффективная свобода комплексной функции а сводится к свободе действительной функции на сфере. Однако в случае произвольного пространства  в соотношении (9.8.92) добавляется член, содержащий интеграл по и от
в соотношении (9.8.92) добавляется член, содержащий интеграл по и от  (или от
(или от  в силу чего условие (9.8.93), вообще говоря, не выполняется.
в силу чего условие (9.8.93), вообще говоря, не выполняется.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие редактора перевода
- Предисловие
- Краткое содержание тома 1
- § 5 (гл. 1). Спинорные объекты и спиновая структура
- § 2 (гл. 2). Формализм абстрактных индексов в тензорной алгебре
- § 3 (гл. 3). Операции симметрии
- Переход от спинорной к тензорной форме записи, и наоборот; преобразование дуальности
- Некоторые свойства тензоров и спиноров в точке
- Активные лоренцевы и спиновые преобразования
- Ковариантная производная
- Спиновые коэффициенты
- Спинорная форма кривизны
- Тождества для спинора Риччи
- Спинорные тождества Бианки
- Компоненты спинорной кривизны
- Модифицированный формализм спиновых коэффициентов
- Уравнения для модифицированных спиновых коэффициентов
- Геометрия пространственноподобных 2-поверхностей
- На изотропной гиперповерхности
- § 15 (гл. 4). Функции на метрической сфере
- Производные заряженных полей
- Поля Янга — Миллса
- Конформные изменения масштаба
- Безмассовые свободные поля
- Другие полевые уравнения
- Данные на изотропной гиперповерхности
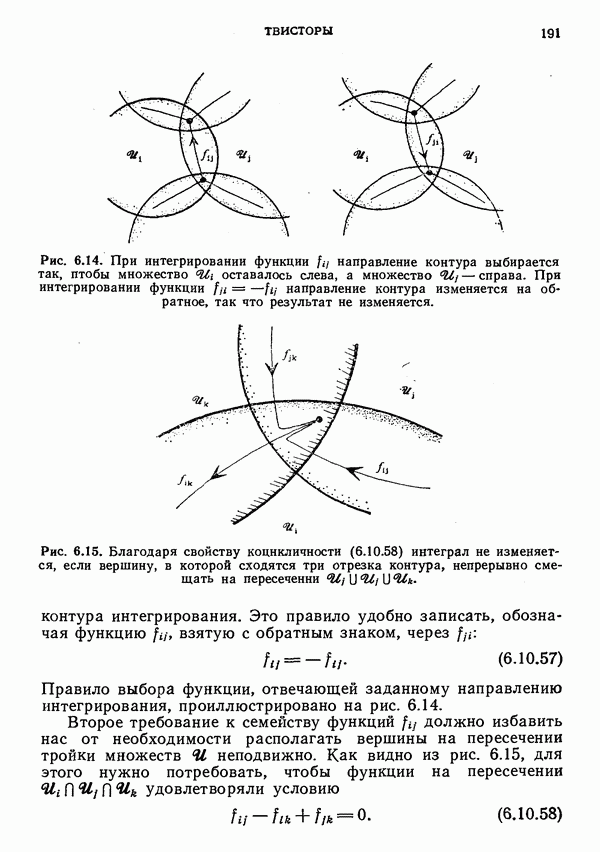
- 6. Твисторы
- § 1. Твисторное уравнение и пространство его решений
- Твисторное уравнение
- Пространство твисторов
- Дуальные твисторы
- Твисторы высшей валентности
- Конформная инвариантность спиральности и скалярного произведения
- § 2. Некоторые геометрические аспекты твисторной алгебры
- Поле флагштоков спинора: конгруэнция Робинсона
- Отношение взаимности твисторов
- Комплексная геометрия
- Представление точек с помощью простых кососимметричных твисторов
- § 3. Твисторы и момент импульса
- Момент импульса произвольной системы
- Представление твистора с помощью одноиндексных твисторов
- § 4. Симметричные твисторы и безмассовые поля
- Общий случай, потенциалы
- Повышение спина
- Другие виды потенциалов; связь с оператором
- § 5. Конформные векторы Киллинга; сохраняющиеся величины и точные последовательности
- Спиноры: Законы сохранения
- Твисторное описание
- Связь с интегралами от источников в линейной гравитации
- Точные последовательности
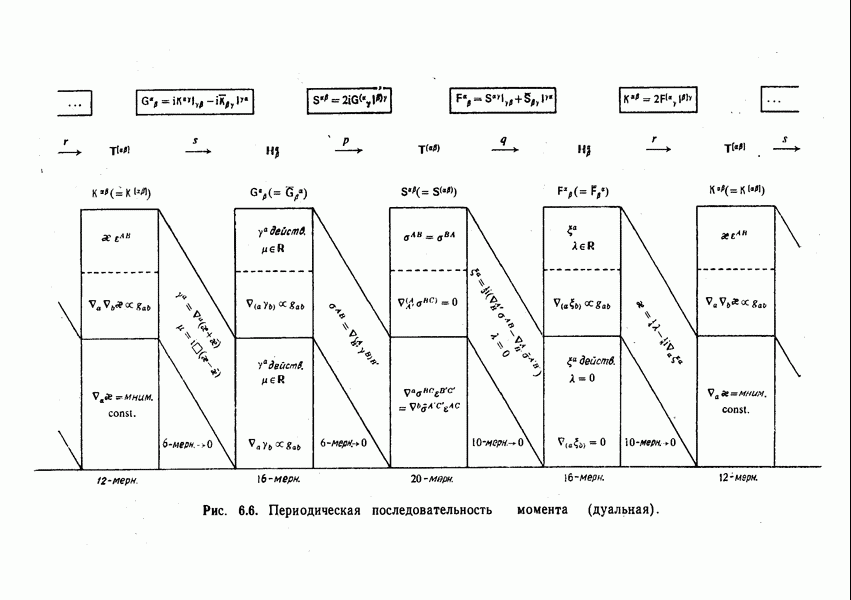
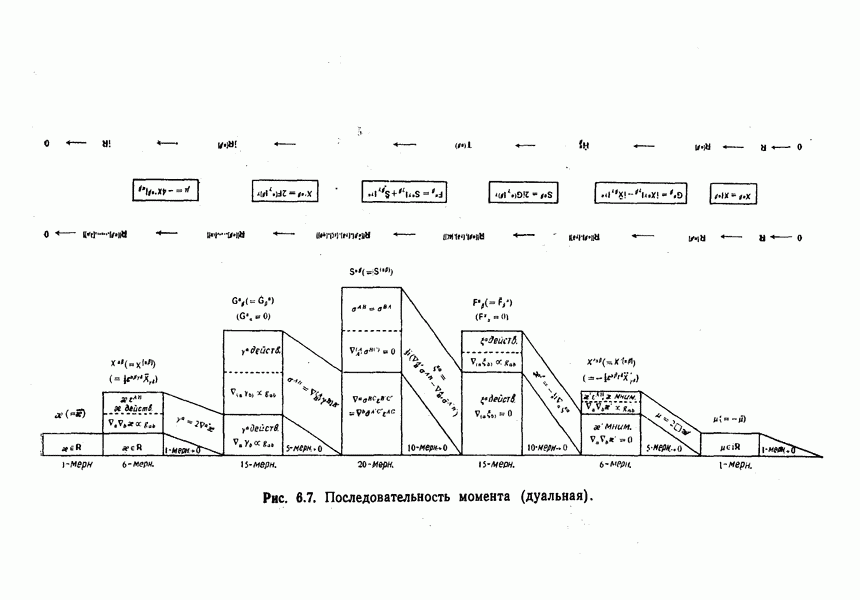
- Последовательности моментов
- Интегралы в линейной теории гравитации
- Спиноры: Десять интегралов, равных нулю
- Роль дуальности в последовательностях момента
- § 6. Производные Ли спиноров
- Связь с теорией твисторов
- § 7. Интегралы движения частиц; конформно-инвариантные операторы
- Спиноры Киллинга для вакуумных решений типа (22)
- Свойства решения Керра
- Конформно-инвариантные первые производные
- Твисторные решения различных уравнений
- Повторные операции; разрешения уравнений
- § 8. Кривизна и конформные преобразования
- Конформные свойства величин
- Конформные отображения плоских пространств
- Конформно-инвариантное волновое уравнение и оператор
- Конформно-инвариантный тензор Баха
- § 9. Локальные твисторы
- Условие совместности для твисторного уравнения
- Определение локального твистора
- Перенос локального твистора
- Кривизна в пространстве локальных твисторов
- Нулевая кривизна Вейля как свойство конформно-плоского пространства
- § 10. Безмассовые поля и когомологии твисторов
- Спиноры: Непроективное представление
- Квантование твисторов
- Спиральность
- Интегралы для спиральности противоположного знака
- Повышение и понижение спиральности
- Массивные твисторные волновые функции
- Геометрия контурных интегралов
- Положительно-частотные поля
- Введение когомологий
- Понятие 1-функции
- r-Функции общего вида
- Нелинейные 1-функции
- Конструкция Уорда
- Пример конструкции Уорда
- 7. Изотропные конгруэнции
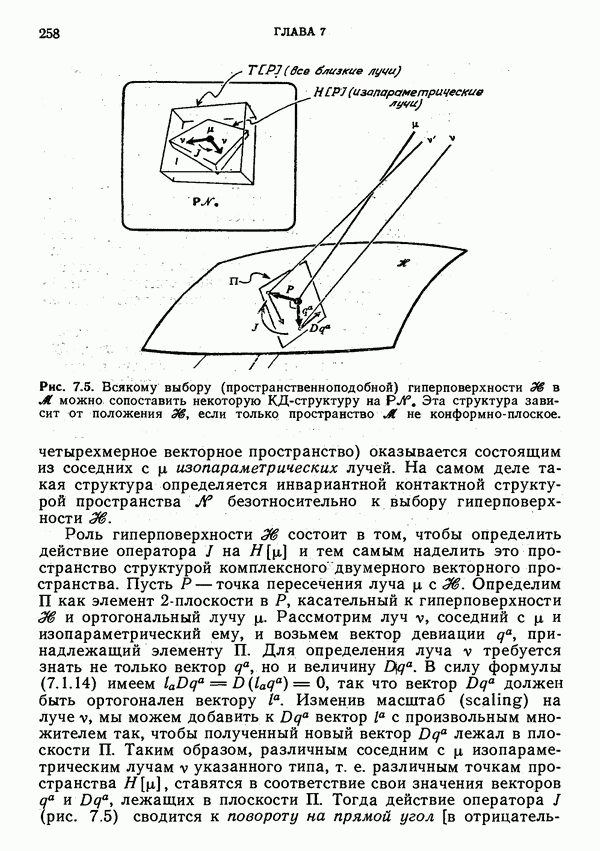
- § 1. Изотропные конгруэнции и спиновые коэффициенты
- Интерпретация величин; изопараметричность лучей
- Ортогональность гиперповерхности; изотропные гиперповерхности
- Изопараметричность в теории твисторов
- § 2. Изотропные конгруэнции и кривизна пространства-времени
- Изопараметрические лучи; уравнения Сакса
- Неизопараметрические лучи
- Описание в трехмерном пространстве Минковского
- § 3. Бессдвиговые конгруэнции лучей
- Обобщенная теорема Голдберга — Сакса
- Координаты Керра
- § 4. БСК, твисторы и геометрия лучей
- Твисторная форма теоремы Керра
- Линейные и квадратичные функции твисторов, момент импульса
- Связь с твисторными функциями безмассовых полей
- Пространства и инвариантная контактная структура
- Комплексная структура и КД-структура
- Твисторы гиперповерхности
- Спиноры: Роль аналитичности
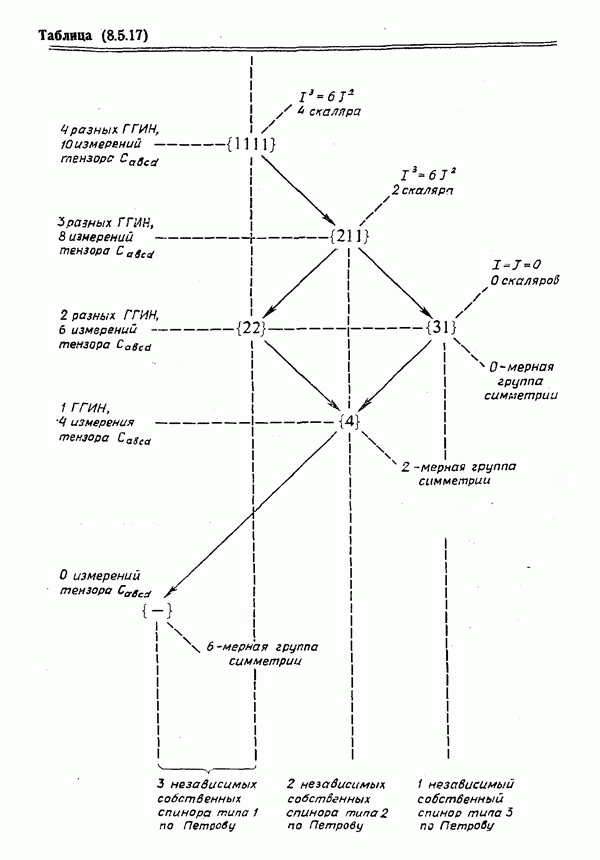
- 8. Классификация тензоров кривизны
- Спиноры: Схема специализации
- § 2. Представление спинора Вейля на сфере S+
- ГГИН в пространстве-времени высокой симметрии
- «Картина» тензора Вейля на S+
- § 3. Собственные спиноры спинора Вейля
- Соотношение между собственными значениями и двойными отношениями
- Частные случаи
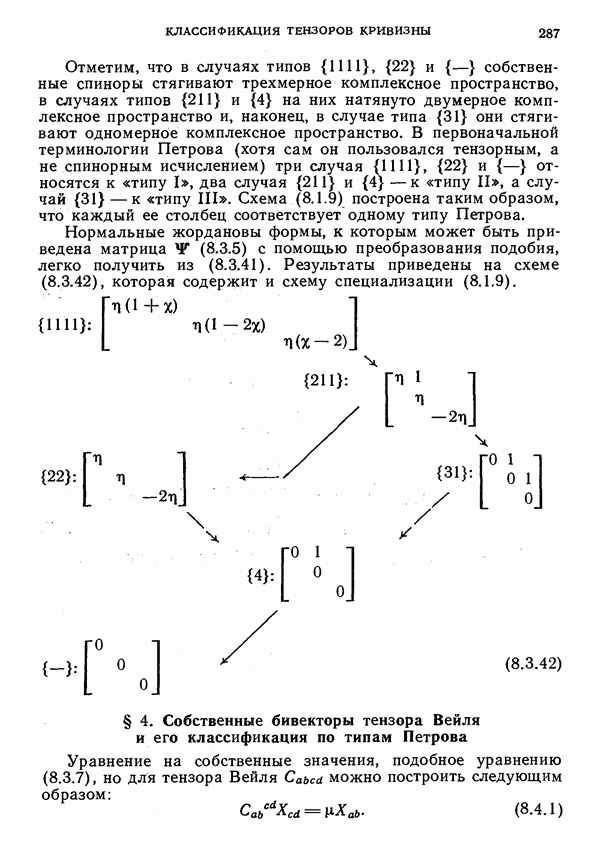
- § 4. Собственные бивекторы тензора Вейля и его классификация по типам Петрова
- Компоненты тензора Вейля в бивекторном базисе
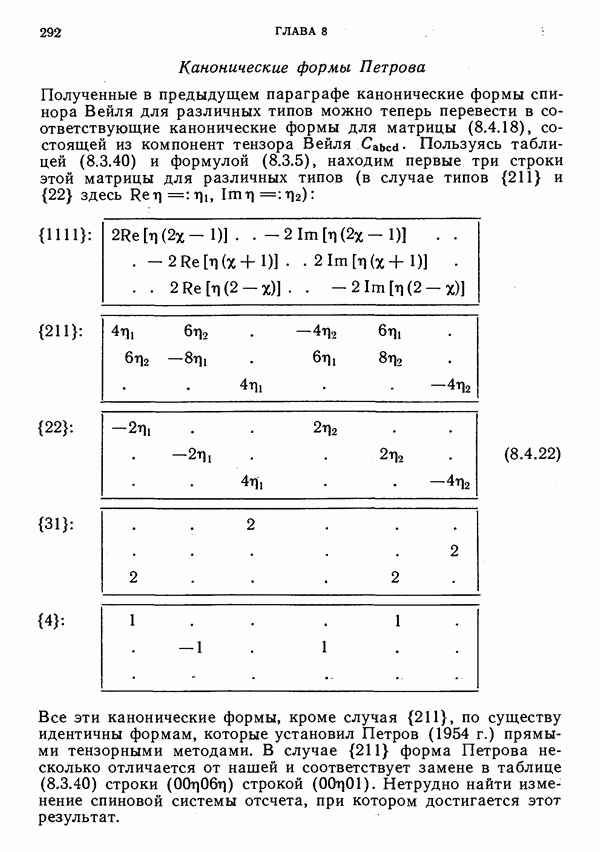
- Канонические формы Петрова
- § 5. Геометрия и симметрия вейлевской кривизны
- Дисфеноид для типа {1111}
- Симметрии в частных случаях типа {1111}
- Тип (211)
- О размерностях групп симметрий
- Классификация тензора Максвелла
- § 6. Коварианты кривизны
- Инварианты полной кривизны
- Система полей Эйнштейна — Максвелла
- § 7. Классификационная схема для спиноров с любым числом индексов
- Приводимость локуса
- Комплексные (р, q) — кривые на CS+
- Процедура классификации спинора
- Структура кривой w (ее кратные точки)
- Кратные точки кривой w
- Локус Rw на S+
- Знак спинора, черный и белый цвета сферы S+
- § 8. Классификация спинора Риччи
- Тип спинора по Плебаньскому
- Физические тензоры энергии-импульса
- 9. Конформная бесконечность
- § 1. Бесконечность в случае пространства Минковского
- ГНП и ГНБ
- § 2. Компактифицированное пространство Минковского
- Описание в пространстве Р5
- O(2,4) и конформная группа
- § 3. Комплексифицированное компактифицированное пространство Минковского и твисторная геометрия
- Соответствие Клейна
- Твисторное отношение дуальности
- Действительная структура
- Различные типы комплексных точек в СМ*
- § 4. Четырехзначность твисторов и индекс Гржина
- Две спиновые структуры на М*
- Поведение спинора
- Твисторные спин-расслоения над М*
- Конформные плотности на М*; индекс Гржина
- Теорема Гржина
- Негржиновские поля
- § 5. Космологические модели и соответствующие твисторы
- Космологические горизонты
- Описание в пространстве Р5
- Деситтеровская и антидеситтеровская модели; твисторы …
- Функции для конформно-плоского пространства-времени
- Модели ФРУ, соответствующие твисторы начальной и конечной сингулярностей
- Явные выражения для функции I
- § 6. Асимптотически простое пространство-время
- Асимптотически-простое пространство-время
- Обращение в нуль тензора Вейля на границе J
- § 7. Последовательное вырождение
- Параллельно переносимые спиновые системы отсчета
- Сравнение аффинных параметров
- Сравнение спиновых систем отсчета
- Доказательство свойства последовательного вырождения
- Поля излучений
- § 8. Группа БМС и структура гиперповерхности J+
- Группа Бонди — Метцнера — Сакса
- Связь между сильной конформной геометрией и твистором
- Интерпретация изотропных углов
- Структура группы БМС
- Сдвиговая структура гиперповерхности J+
- H-пространство и асимптотическое твисторное пространство
- Отношение группы БМС к импульсу и моменту импульса
- Асимптотические разложения в теории Эйнштейна — Максвелла
- § 9. Энергия-импульс и момент импульса
- Усложнения в случае искривленного пространства-времени
- Твисторы двумерной поверхности
- Контортные двумерные поверхности
- Квазилокальный твистор момента импульса
- Определение множителя
- Асимптотическое спиновое пространство
- Свойства нормы на J+
- Эрмитовость твистора на 4-импульс Бонди — Сакса
- Альтернативные выражения для массы Бонди — Сакса
- Пространство Минковского как пространство «начал»
- Момент импульса на J+
- § 10. Потери массы Бонди — Сакса и положительность энергии
- Нелокальность энергии гравитационных волн
- НП-константы
- Подход Виттена в доказательстве положительности массы
- Связь с 4-импульсом Бонди — Сакса
- Спинор в подходе Людвигсена — Виккерса
- 3-форма Спарлинга
- Приложение. Спиноры в n измерениях
- 2-валентные e-спиноры
- Переход от тензоров к спинорам
- Геометрия фундаментальных спиноров
- Условие фундаментальности; структура спинового пространства
- Индуктивное построение спинового пространства
- Некоторые физически интересные случаи; триальность
- Спинорные поля; твисторы в n измерениях
- Послесловие авторов
- Литература