| << Предыдущий параграф | Следующий параграф >> |
Пред.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
353
354
355
356
357
358
359
360
361
362
363
364
365
366
367
368
369
370
371
372
373
374
375
376
377
378
379
380
381
382
383
384
385
386
387
388
389
390
391
392
393
394
395
396
397
398
399
400
401
402
403
404
405
406
407
408
409
410
411
412
413
414
415
416
417
418
419
420
421
422
423
424
425
426
427
428
429
430
431
432
433
434
435
436
437
438
439
440
441
442
443
444
445
446
447
448
449
450
451
452
453
454
455
456
457
458
459
460
461
462
463
464
465
466
467
468
469
470
471
472
473
474
475
476
477
478
479
480
481
482
483
484
485
486
487
488
489
490
491
492
493
494
495
496
497
498
499
500
501
502
503
504
505
506
507
508
509
510
511
512
513
514
515
516
517
518
519
520
521
522
523
524
525
526
527
528
529
530
531
532
533
534
535
536
537
538
539
540
541
542
543
544
545
546
547
548
549
550
551
552
553
554
555
556
557
558
559
560
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
ГНП и ГНБ
При исследовании кривых в пространстве Минковского вопрос о достигаемых ими концевых точках несколько усложняется. Например, винтовая линия  хотя и является изотропной кривой, имеет концевую точку прошлого в точке
хотя и является изотропной кривой, имеет концевую точку прошлого в точке  , а концевую точку будущего — в точке
, а концевую точку будущего — в точке  (и в обеих концевых точках полная кривая не является гладкой). Времениподобная же кривая
(и в обеих концевых точках полная кривая не является гладкой). Времениподобная же кривая  гладко достигает концевой точки прошлого на границе
гладко достигает концевой точки прошлого на границе  и концевой точки будущего на границе
и концевой точки будущего на границе  . К тому же легко найти пространственноподобные кривые, достигающие концевых точек либо на обеих границах
. К тому же легко найти пространственноподобные кривые, достигающие концевых точек либо на обеих границах  , либо в точке
, либо в точке  Если ограничиться только причинными кривыми (т. е. кривыми, которые всюду либо времениподобны, либо изотропны; а это в обоих случаях единственные кривые, вдоль которых распространяются частицы и информация), то можно указать очень простой критерий (целиком опирающийся на характеристики самого пространства Минковского М), позволяющий определить, достигают ли две такие кривые одной и той же концевой
Если ограничиться только причинными кривыми (т. е. кривыми, которые всюду либо времениподобны, либо изотропны; а это в обоих случаях единственные кривые, вдоль которых распространяются частицы и информация), то можно указать очень простой критерий (целиком опирающийся на характеристики самого пространства Минковского М), позволяющий определить, достигают ли две такие кривые одной и той же концевой
точки прошлого или концевой точки будущего и лежат ли эти точки на границе  или в точке
или в точке
Чтобы установить этот критерий, рассмотрим произвольное множество точек 2 в пространстве (VI и обозначим через  подмножество пространства М, состоящее только из тех точек, которые могут быть достигнуты направленной в будущее времениподобной кривой, выходящей из некоторых точек множества 2. Иными словами,
подмножество пространства М, состоящее только из тех точек, которые могут быть достигнуты направленной в будущее времениподобной кривой, выходящей из некоторых точек множества 2. Иными словами,  — это (открытое) будущее множества 2. (О том, почему оно будет открытым множеством в М, см. работы [245, 125].) Аналогично, пусть
— это (открытое) будущее множества 2. (О том, почему оно будет открытым множеством в М, см. работы [245, 125].) Аналогично, пусть  прошлое множества 2. Тогда если а — любая причинная кривая с (конечной) концевой точкой прошлого Р в М, то будущее точки Р совпадает с множеством
прошлое множества 2. Тогда если а — любая причинная кривая с (конечной) концевой точкой прошлого Р в М, то будущее точки Р совпадает с множеством  Этим свойством не обладает никакая другая точка в
Этим свойством не обладает никакая другая точка в  (в чем читателю нетрудно будет убедиться самому; полное доказательство можно найти в работе [104]). Таким образом, любая другая причинная кривая
(в чем читателю нетрудно будет убедиться самому; полное доказательство можно найти в работе [104]). Таким образом, любая другая причинная кривая  тоже имеет в точке Р свою концевую точку прошлого только в том случае, если
тоже имеет в точке Р свою концевую точку прошлого только в том случае, если  Преимущество этого критерия состоит в том, что он применим и в случае, когда
Преимущество этого критерия состоит в том, что он применим и в случае, когда  — кривые, бесконцевые в прошлом (т. е. неограниченно продолжимые в прошлое и не достигающие конечных концевых точек прошлого в М): такие кривые
— кривые, бесконцевые в прошлом (т. е. неограниченно продолжимые в прошлое и не достигающие конечных концевых точек прошлого в М): такие кривые  достигают одних и тех же концевых точек прошлого, лежащих на
достигают одних и тех же концевых точек прошлого, лежащих на  или совпадающих с
или совпадающих с  только в том случае, когда
только в том случае, когда  (рис. 9.3). (Они, очевидно, не могут иметь концевые точки прошлого в
(рис. 9.3). (Они, очевидно, не могут иметь концевые точки прошлого в  или на
или на  Отсюда следует, что бесконцевая в прошлом причинная кривая а достигает концевой точки прошлого в точке
Отсюда следует, что бесконцевая в прошлом причинная кривая а достигает концевой точки прошлого в точке  или на
или на  в зависимости от того, является ли
в зависимости от того, является ли

Рис. 9.3. Две причинные кривые  и имеют одну и ту же концевую точку на гиперповерхности
и имеют одну и ту же концевую точку на гиперповерхности  в том и только в том случае, когда у них одинаковое будущее.
в том и только в том случае, когда у них одинаковое будущее.
множество  всем пространством М или нет (так, например, будущим оси времени
всем пространством М или нет (так, например, будущим оси времени  является все пространство М). Точно так же бесконцевая в будущем причинная кривая а достигает точки
является все пространство М). Точно так же бесконцевая в будущем причинная кривая а достигает точки  или точки на
или точки на  в зависимости от того, является ли
в зависимости от того, является ли  всем пространством М или нет; более того, бесконцевая в будущем кривая
всем пространством М или нет; более того, бесконцевая в будущем кривая  достигает на бесконечности той же точки, что и кривая
достигает на бесконечности той же точки, что и кривая  в том и только в том случае, если
в том и только в том случае, если 
Эти критерии особенно ценны тем, что они применимы и в искривленном пространстве. Множества типа  где а — бесконцевая в прошлом причинная кривая, называются граничными неразложимыми множествами будущего
где а — бесконцевая в прошлом причинная кривая, называются граничными неразложимыми множествами будущего  множества же типа
множества же типа  с бесконцевой в будущем причинной кривой а называются граничными неразложимыми множествами прошлого
с бесконцевой в будущем причинной кривой а называются граничными неразложимыми множествами прошлого  Ими можно воспользоваться для того, чтобы дать определения прошлых/будущих границ в пространстве-времени самого общего вида [307,104]. Границы ГНБ и
Ими можно воспользоваться для того, чтобы дать определения прошлых/будущих границ в пространстве-времени самого общего вида [307,104]. Границы ГНБ и  тоже представляют определенный интерес. Они порождаются лучами, которые являются бесконцевыми в будущем или прошлом, соответственно [245, 125]. В случае пространства Минковского (VI эти границы (если они не пустые) являются изотропными гиперплоскостями в М, т. е. множествами, описываемыми уравнениями типа
тоже представляют определенный интерес. Они порождаются лучами, которые являются бесконцевыми в будущем или прошлом, соответственно [245, 125]. В случае пространства Минковского (VI эти границы (если они не пустые) являются изотропными гиперплоскостями в М, т. е. множествами, описываемыми уравнениями типа  где
где  и В — постоянные и
и В — постоянные и  — изотропный вектор. Это будет иметь существенное значение в следующем параграфе.
— изотропный вектор. Это будет иметь существенное значение в следующем параграфе.
Итак, требуемое конформное многообразие (с границей) (VI состоит из исходного пространства Минковского (VI с его конформной метрикой и двух граничных 3-поверхностей  и Однако точки
и Однако точки  исключаются из М, ибо граница не была бы в этих точках гладкой. Мы видим, что границы
исключаются из М, ибо граница не была бы в этих точках гладкой. Мы видим, что границы  имеют топологию
имеют топологию  где сфера
где сфера  параметризована сферическими полярными углами
параметризована сферическими полярными углами  а пространство
а пространство  — запаздывающим временем и в случае границы
— запаздывающим временем и в случае границы  и опережающим временем
и опережающим временем  в случае границы
в случае границы 
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие редактора перевода
- Предисловие
- Краткое содержание тома 1
- § 5 (гл. 1). Спинорные объекты и спиновая структура
- § 2 (гл. 2). Формализм абстрактных индексов в тензорной алгебре
- § 3 (гл. 3). Операции симметрии
- Переход от спинорной к тензорной форме записи, и наоборот; преобразование дуальности
- Некоторые свойства тензоров и спиноров в точке
- Активные лоренцевы и спиновые преобразования
- Ковариантная производная
- Спиновые коэффициенты
- Спинорная форма кривизны
- Тождества для спинора Риччи
- Спинорные тождества Бианки
- Компоненты спинорной кривизны
- Модифицированный формализм спиновых коэффициентов
- Уравнения для модифицированных спиновых коэффициентов
- Геометрия пространственноподобных 2-поверхностей
- На изотропной гиперповерхности
- § 15 (гл. 4). Функции на метрической сфере
- Производные заряженных полей
- Поля Янга — Миллса
- Конформные изменения масштаба
- Безмассовые свободные поля
- Другие полевые уравнения
- Данные на изотропной гиперповерхности
- 6. Твисторы
- § 1. Твисторное уравнение и пространство его решений
- Твисторное уравнение
- Пространство твисторов
- Дуальные твисторы
- Твисторы высшей валентности
- Конформная инвариантность спиральности и скалярного произведения
- § 2. Некоторые геометрические аспекты твисторной алгебры
- Поле флагштоков спинора: конгруэнция Робинсона
- Отношение взаимности твисторов
- Комплексная геометрия
- Представление точек с помощью простых кососимметричных твисторов
- § 3. Твисторы и момент импульса
- Момент импульса произвольной системы
- Представление твистора с помощью одноиндексных твисторов
- § 4. Симметричные твисторы и безмассовые поля
- Общий случай, потенциалы
- Повышение спина
- Другие виды потенциалов; связь с оператором
- § 5. Конформные векторы Киллинга; сохраняющиеся величины и точные последовательности
- Спиноры: Законы сохранения
- Твисторное описание
- Связь с интегралами от источников в линейной гравитации
- Точные последовательности
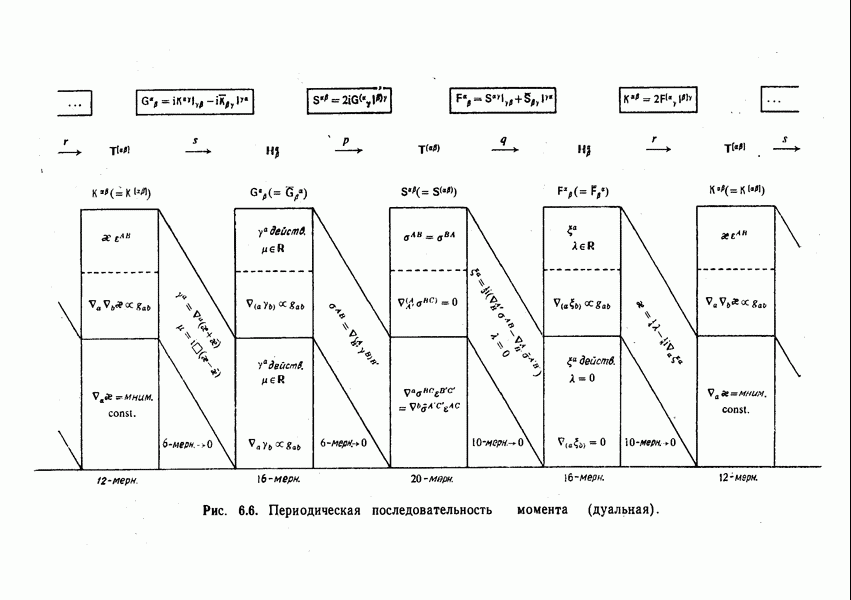
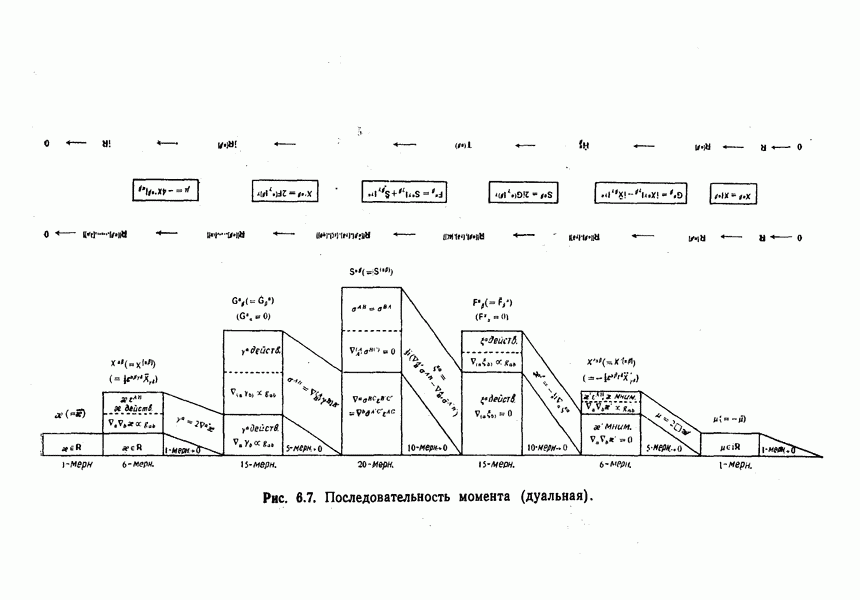
- Последовательности моментов
- Интегралы в линейной теории гравитации
- Спиноры: Десять интегралов, равных нулю
- Роль дуальности в последовательностях момента
- § 6. Производные Ли спиноров
- Связь с теорией твисторов
- § 7. Интегралы движения частиц; конформно-инвариантные операторы
- Спиноры Киллинга для вакуумных решений типа (22)
- Свойства решения Керра
- Конформно-инвариантные первые производные
- Твисторные решения различных уравнений
- Повторные операции; разрешения уравнений
- § 8. Кривизна и конформные преобразования
- Конформные свойства величин
- Конформные отображения плоских пространств
- Конформно-инвариантное волновое уравнение и оператор
- Конформно-инвариантный тензор Баха
- § 9. Локальные твисторы
- Условие совместности для твисторного уравнения
- Определение локального твистора
- Перенос локального твистора
- Кривизна в пространстве локальных твисторов
- Нулевая кривизна Вейля как свойство конформно-плоского пространства
- § 10. Безмассовые поля и когомологии твисторов
- Спиноры: Непроективное представление
- Квантование твисторов
- Спиральность
- Интегралы для спиральности противоположного знака
- Повышение и понижение спиральности
- Массивные твисторные волновые функции
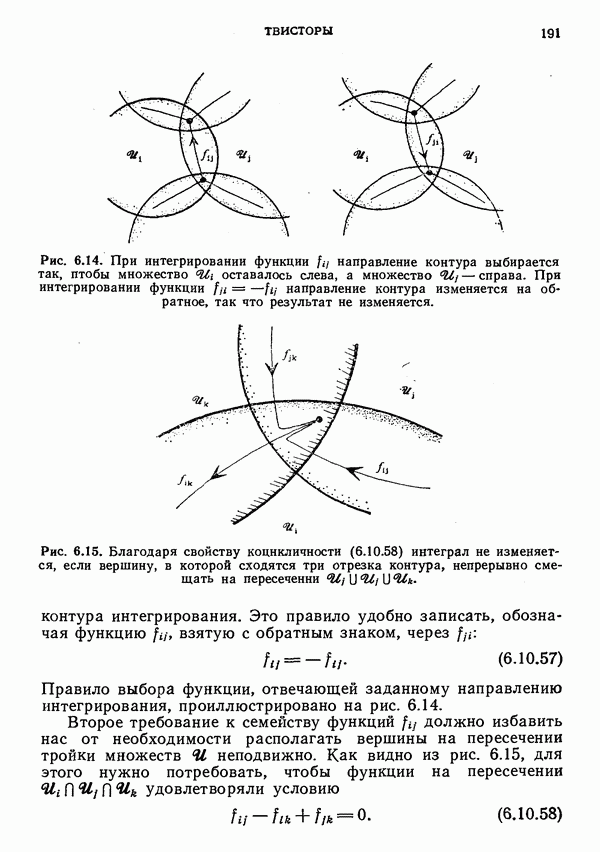
- Геометрия контурных интегралов
- Положительно-частотные поля
- Введение когомологий
- Понятие 1-функции
- r-Функции общего вида
- Нелинейные 1-функции
- Конструкция Уорда
- Пример конструкции Уорда
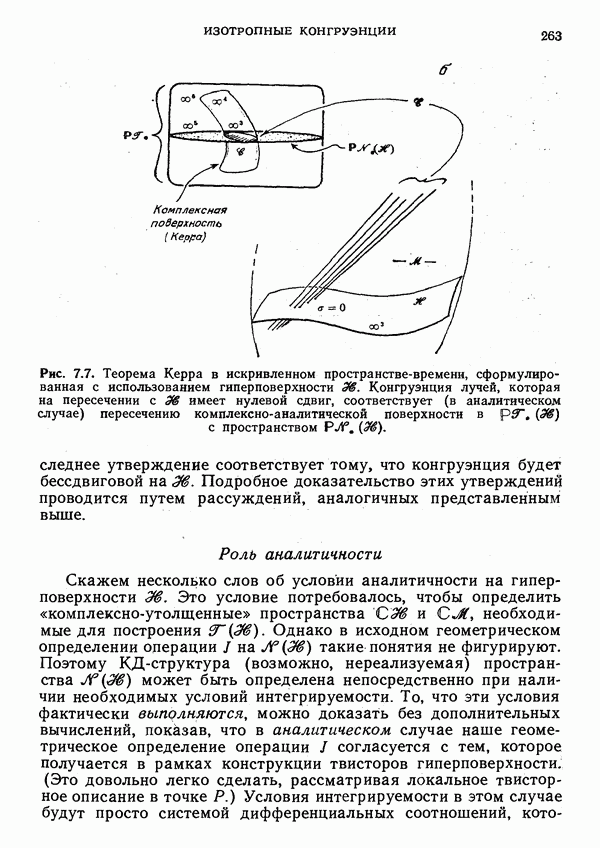
- 7. Изотропные конгруэнции
- § 1. Изотропные конгруэнции и спиновые коэффициенты
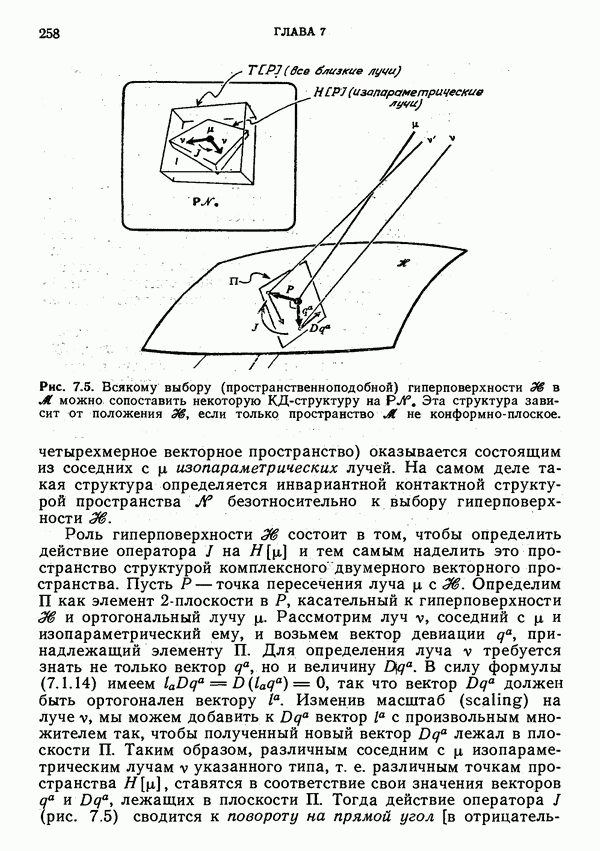
- Интерпретация величин; изопараметричность лучей
- Ортогональность гиперповерхности; изотропные гиперповерхности
- Изопараметричность в теории твисторов
- § 2. Изотропные конгруэнции и кривизна пространства-времени
- Изопараметрические лучи; уравнения Сакса
- Неизопараметрические лучи
- Описание в трехмерном пространстве Минковского
- § 3. Бессдвиговые конгруэнции лучей
- Обобщенная теорема Голдберга — Сакса
- Координаты Керра
- § 4. БСК, твисторы и геометрия лучей
- Твисторная форма теоремы Керра
- Линейные и квадратичные функции твисторов, момент импульса
- Связь с твисторными функциями безмассовых полей
- Пространства и инвариантная контактная структура
- Комплексная структура и КД-структура
- Твисторы гиперповерхности
- Спиноры: Роль аналитичности
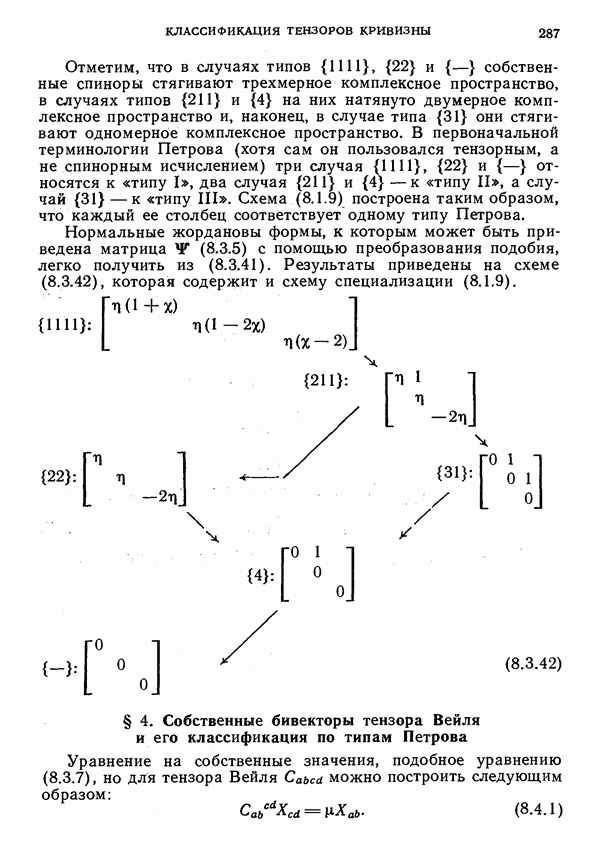
- 8. Классификация тензоров кривизны
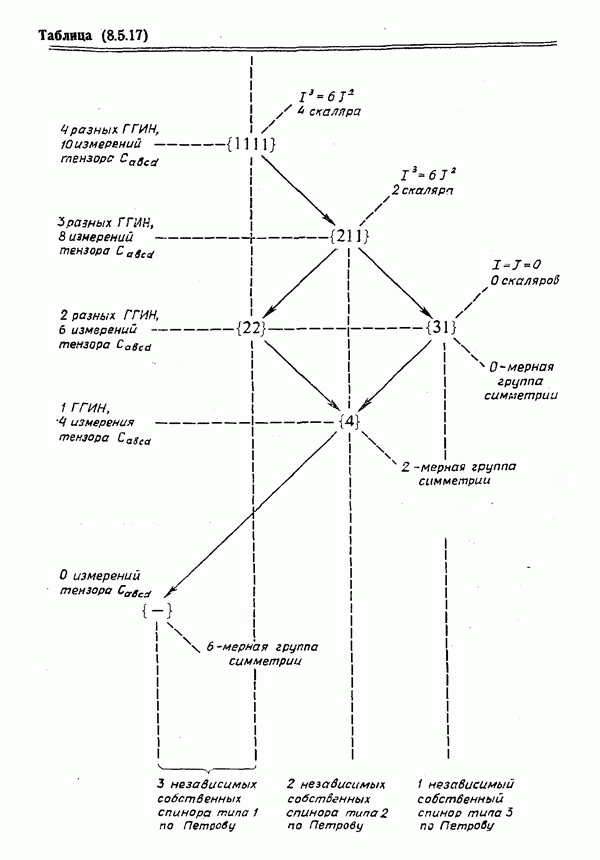
- Спиноры: Схема специализации
- § 2. Представление спинора Вейля на сфере S+
- ГГИН в пространстве-времени высокой симметрии
- «Картина» тензора Вейля на S+
- § 3. Собственные спиноры спинора Вейля
- Соотношение между собственными значениями и двойными отношениями
- Частные случаи
- § 4. Собственные бивекторы тензора Вейля и его классификация по типам Петрова
- Компоненты тензора Вейля в бивекторном базисе
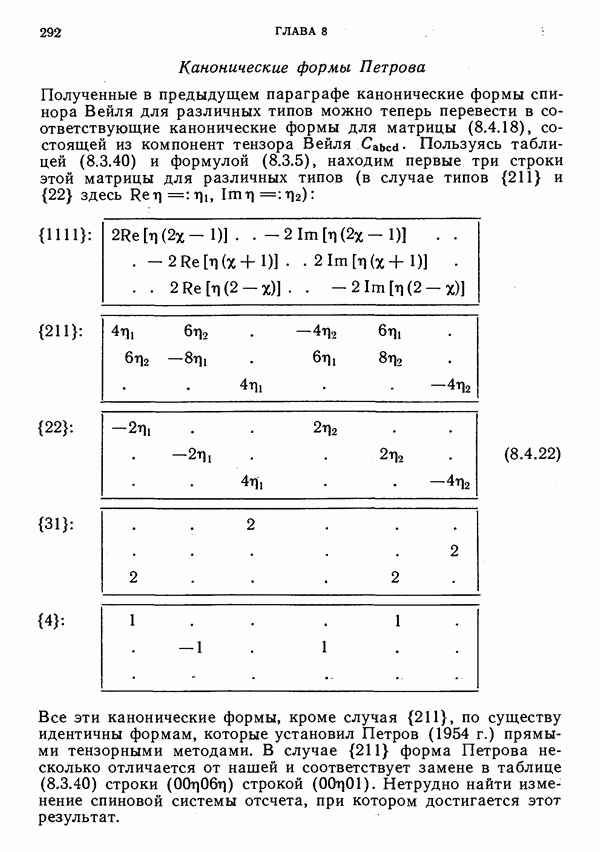
- Канонические формы Петрова
- § 5. Геометрия и симметрия вейлевской кривизны
- Дисфеноид для типа {1111}
- Симметрии в частных случаях типа {1111}
- Тип (211)
- О размерностях групп симметрий
- Классификация тензора Максвелла
- § 6. Коварианты кривизны
- Инварианты полной кривизны
- Система полей Эйнштейна — Максвелла
- § 7. Классификационная схема для спиноров с любым числом индексов
- Приводимость локуса
- Комплексные (р, q) — кривые на CS+
- Процедура классификации спинора
- Структура кривой w (ее кратные точки)
- Кратные точки кривой w
- Локус Rw на S+
- Знак спинора, черный и белый цвета сферы S+
- § 8. Классификация спинора Риччи
- Тип спинора по Плебаньскому
- Физические тензоры энергии-импульса
- 9. Конформная бесконечность
- § 1. Бесконечность в случае пространства Минковского
- ГНП и ГНБ
- § 2. Компактифицированное пространство Минковского
- Описание в пространстве Р5
- O(2,4) и конформная группа
- § 3. Комплексифицированное компактифицированное пространство Минковского и твисторная геометрия
- Соответствие Клейна
- Твисторное отношение дуальности
- Действительная структура
- Различные типы комплексных точек в СМ*
- § 4. Четырехзначность твисторов и индекс Гржина
- Две спиновые структуры на М*
- Поведение спинора
- Твисторные спин-расслоения над М*
- Конформные плотности на М*; индекс Гржина
- Теорема Гржина
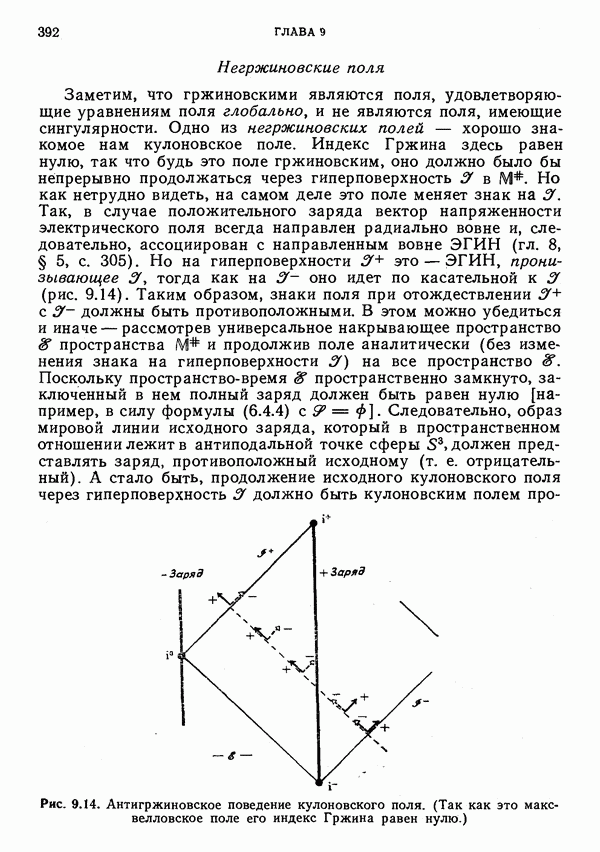
- Негржиновские поля
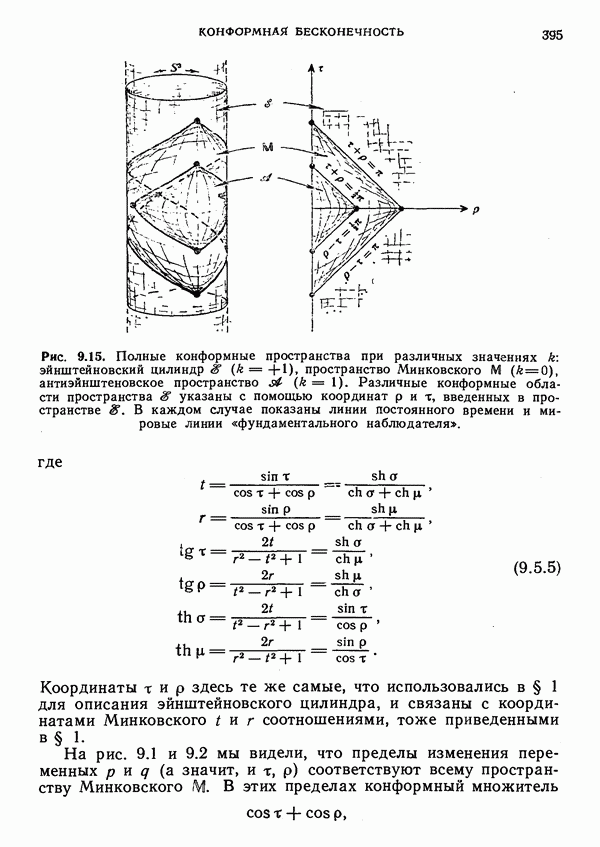
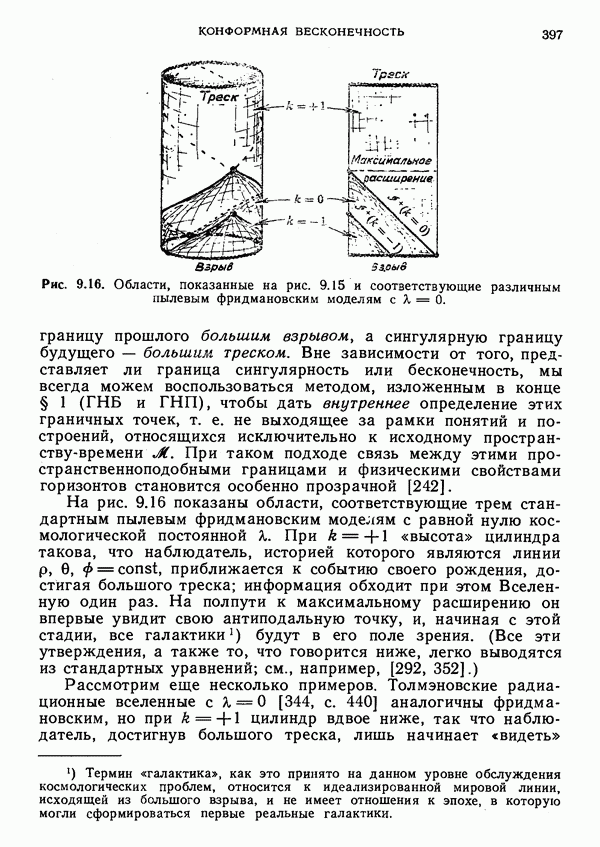
- § 5. Космологические модели и соответствующие твисторы
- Космологические горизонты
- Описание в пространстве Р5
- Деситтеровская и антидеситтеровская модели; твисторы …
- Функции для конформно-плоского пространства-времени
- Модели ФРУ, соответствующие твисторы начальной и конечной сингулярностей
- Явные выражения для функции I
- § 6. Асимптотически простое пространство-время
- Асимптотически-простое пространство-время
- Обращение в нуль тензора Вейля на границе J
- § 7. Последовательное вырождение
- Параллельно переносимые спиновые системы отсчета
- Сравнение аффинных параметров
- Сравнение спиновых систем отсчета
- Доказательство свойства последовательного вырождения
- Поля излучений
- § 8. Группа БМС и структура гиперповерхности J+
- Группа Бонди — Метцнера — Сакса
- Связь между сильной конформной геометрией и твистором
- Интерпретация изотропных углов
- Структура группы БМС
- Сдвиговая структура гиперповерхности J+
- H-пространство и асимптотическое твисторное пространство
- Отношение группы БМС к импульсу и моменту импульса
- Асимптотические разложения в теории Эйнштейна — Максвелла
- § 9. Энергия-импульс и момент импульса
- Усложнения в случае искривленного пространства-времени
- Твисторы двумерной поверхности
- Контортные двумерные поверхности
- Квазилокальный твистор момента импульса
- Определение множителя
- Асимптотическое спиновое пространство
- Свойства нормы на J+
- Эрмитовость твистора на 4-импульс Бонди — Сакса
- Альтернативные выражения для массы Бонди — Сакса
- Пространство Минковского как пространство «начал»
- Момент импульса на J+
- § 10. Потери массы Бонди — Сакса и положительность энергии
- Нелокальность энергии гравитационных волн
- НП-константы
- Подход Виттена в доказательстве положительности массы
- Связь с 4-импульсом Бонди — Сакса
- Спинор в подходе Людвигсена — Виккерса
- 3-форма Спарлинга
- Приложение. Спиноры в n измерениях
- 2-валентные e-спиноры
- Переход от тензоров к спинорам
- Геометрия фундаментальных спиноров
- Условие фундаментальности; структура спинового пространства
- Индуктивное построение спинового пространства
- Некоторые физически интересные случаи; триальность
- Спинорные поля; твисторы в n измерениях
- Послесловие авторов
- Литература