| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
Перенос локального твистора
Далее мы определим процедуру, позволяющую сравнивать локальные твисторы в разных точках [т. е. построим связность в расслоении, см. формулы (5.4.17) — (5.4.19)]. При этом мы будем исходить из двух требований. Во-первых, мы хотим сохранить соответствие с теорией глобальных твисторов. Это поможет нам определить процедуру параллельного переноса, которую будем называть переносом локального твистора. Для всякой гладкой кривой  соединяющей точки Р и
соединяющей точки Р и  локальному твистору
локальному твистору  в точке Р сопоставим определенный локальный твистор в точке
в точке Р сопоставим определенный локальный твистор в точке  Это соответствие не зависит от пути только в случае конформно-плоского пространства-времени. Именно в этом случае мы потребуем соответствия с понятием глобального твистора; локальный твистор, который в указанном смысле
Это соответствие не зависит от пути только в случае конформно-плоского пространства-времени. Именно в этом случае мы потребуем соответствия с понятием глобального твистора; локальный твистор, который в указанном смысле
переносится «параллельно» во все точки, должен совпадать с глобальным твистором. Во-вторых, мы потребуем инвариантности относительно конформных преобразований. Отметим, что параллельный перенос твистора  понимаемый как параллельный перенос его спинорных компонент, не удовлетворяет указанным выше требованиям.
понимаемый как параллельный перенос его спинорных компонент, не удовлетворяет указанным выше требованиям.
Вначале еще раз проанализируем понятие глобального твистора, введенное в § 1, с точки зрения теории локальных твисторов. Глобальный твистор  в конформно-плоском пространстве-времени отождествляется со спинорным полем
в конформно-плоском пространстве-времени отождествляется со спинорным полем  удовлетворяющим твисторному уравнению
удовлетворяющим твисторному уравнению

Определим спинор  с помощью соотношения
с помощью соотношения

которое в совокупности с уравнением (6.9.8) эквивалентно соотношению (6.1.9). Из (6.8.11) немедленно находим, что

[где  — величина, определяемая формулой (6.8.12)]. Таким образом, глобальный твистор представляется парой (сол,
— величина, определяемая формулой (6.8.12)]. Таким образом, глобальный твистор представляется парой (сол,  полей, удовлетворяющих уравнениям
полей, удовлетворяющих уравнениям

[В частном случае плоского пространства-времени эти уравнения сводятся к соотношению (6.1.9).]
Воспользуемся системой (6.9.10) для определения понятия параллельного переноса локальных твисторов в произвольном пространстве-времени  Будем называть локальный твистор
Будем называть локальный твистор  постоянным на
постоянным на  (и совпадающим с глобальным твистором), если выполняются уравнения (6.9.10). В произвольном пространстве-времени в общем случае не существует нетривиальных локальных твисторов, удовлетворяющих уравнениям (6.9.10) во всех точках
(и совпадающим с глобальным твистором), если выполняются уравнения (6.9.10). В произвольном пространстве-времени в общем случае не существует нетривиальных локальных твисторов, удовлетворяющих уравнениям (6.9.10) во всех точках  Но, сворачивая (6.9.10) с вектором
Но, сворачивая (6.9.10) с вектором  мы получаем более слабые равенства
мы получаем более слабые равенства

которые выражают свойство постоянства твистора  в направлении
в направлении  Пусть в
Пусть в  задана кривая
задана кривая  с касательным вектором
с касательным вектором  Тогда твистор
Тогда твистор  называется постоянным вдоль кривой
называется постоянным вдоль кривой  (т. е. на
(т. е. на  задан перенос локального твистора), если уравнения
задан перенос локального твистора), если уравнения
(6.9.11) выполняются в каждой точке кривой  . Ясно, что, выбрав (произвольно) начальные значения спиноров пары
. Ясно, что, выбрав (произвольно) начальные значения спиноров пары  , с помощью уравнений переноса (6.9.11) мы можем однозначно определить твистор
, с помощью уравнений переноса (6.9.11) мы можем однозначно определить твистор  в каждой точке кривой
в каждой точке кривой  . (При этом предполагается, что кривая
. (При этом предполагается, что кривая  не имеет самопересечений и вектор
не имеет самопересечений и вектор  всюду отличен от нуля.)
всюду отличен от нуля.)
От определения локального твистора, постоянного вдоль кривой, естественно перейти к понятию вариации твистора  вдоль кривой
вдоль кривой  . Вводя для этой величины обозначение
. Вводя для этой величины обозначение  мы определяем
мы определяем

Далее, используя формулу (6.8.14), непосредственно убеждаемся, что  удовлетворяет закону преобразования (6.9.5), (6.9.6), если ему удовлетворяет твистор
удовлетворяет закону преобразования (6.9.5), (6.9.6), если ему удовлетворяет твистор  Таким образом, величина
Таким образом, величина  будет локальным твистором в каждой точке кривой
будет локальным твистором в каждой точке кривой  . По существу это можно рассматривать как свойстео конформной инвариантности оператора V в указанном смысле. Поскольку определения (6.9.11) и (6.9.12) относятся к произвольному пространству-времени, как следствие такой инвариантности оператора V мы получаем конформную инвариантность переноса локального твистора. Постоянный локальный твистор, определенный на всем многообразии
. По существу это можно рассматривать как свойстео конформной инвариантности оператора V в указанном смысле. Поскольку определения (6.9.11) и (6.9.12) относятся к произвольному пространству-времени, как следствие такой инвариантности оператора V мы получаем конформную инвариантность переноса локального твистора. Постоянный локальный твистор, определенный на всем многообразии  (т. е. глобальный твистор), должен удовлетворять уравнению
(т. е. глобальный твистор), должен удовлетворять уравнению  в каждой точке многообразия
в каждой точке многообразия  для произвольного вектора
для произвольного вектора 
До сих пор мы рассматривали только локальные твисторы типа  Обобщение на случай
Обобщение на случай  -локальных твисторов осуществляется по стандартному образцу. Наряду с локальными твисторами в фиксированной точке многообразия
-локальных твисторов осуществляется по стандартному образцу. Наряду с локальными твисторами в фиксированной точке многообразия  можно рассматривать поля локальных твисторов на
можно рассматривать поля локальных твисторов на  . В первом случае
. В первом случае  -локальные твисторы образуют четырехмерное векторное пространство над С, а во втором — вполне рефлексивный четырехмерный модуль над комплексными скалярными полями
-локальные твисторы образуют четырехмерное векторное пространство над С, а во втором — вполне рефлексивный четырехмерный модуль над комплексными скалярными полями  Определение умножения твистора на число
Определение умножения твистора на число  и
и
суммы твисторов  очевидно. Система абстрактных индексов и общая схема построения величин произвольной валентности, приведенная в гл. 2, применимы и в этом случае; разложение величин на спинорные части (и соответствующие обозначения) выполняются по той же схеме, что и в случае глобальных твисторов (см. § 1). Так же как для глобальных твисторов, определена операция комплексного сопряжения, которая переводит
очевидно. Система абстрактных индексов и общая схема построения величин произвольной валентности, приведенная в гл. 2, применимы и в этом случае; разложение величин на спинорные части (и соответствующие обозначения) выполняются по той же схеме, что и в случае глобальных твисторов (см. § 1). Так же как для глобальных твисторов, определена операция комплексного сопряжения, которая переводит  -твистор в
-твистор в  -твистор. Продемонстрируем это в частном случае
-твистор. Продемонстрируем это в частном случае  и проанализируем связь этой операции с понятием переноса локального твистора. Если твистор
и проанализируем связь этой операции с понятием переноса локального твистора. Если твистор  выбран в соответствии с условиями (6.9.5), имеем
выбран в соответствии с условиями (6.9.5), имеем  по аналогии с (6.1.31), так что, заменяя метрику
по аналогии с (6.1.31), так что, заменяя метрику  на
на  получаем новое представление
получаем новое представление  Таким образом, из представления
Таким образом, из представления

 -локальных твисторов в метрике
-локальных твисторов в метрике  находим представление в метрике
находим представление в метрике 

где

Отсюда находим, что, например, спинорные части  -локального твистора
-локального твистора  преобразуются по закону
преобразуются по закону

и аналогично для твисторов с другим набором индексов.
Из выражения, комплексно-сопряженного выражению (6.9.12), следует, что

Так же как в случае  -твисторов, находим, что оператор должен быть конформно-инвариантным в том смысле, что величина
-твисторов, находим, что оператор должен быть конформно-инвариантным в том смысле, что величина  удовлетворяет правильному закону преобразования (6.9.13) локального твистора при конформных отображениях, если этому закону удовлетворяет сам твистор
удовлетворяет правильному закону преобразования (6.9.13) локального твистора при конформных отображениях, если этому закону удовлетворяет сам твистор  Более того, инвариантом конформного преобразования будет скалярное произведение
Более того, инвариантом конформного преобразования будет скалярное произведение  [что явствует из сходства
[что явствует из сходства
формул (6.9.6) и (6.9.13) с аналогичными выражениями (6.1.75) и (6.1.76) для глобального твистора], и это произведение удовлетворяет соотношению

в чем легко убедиться, используя формулы (6.9.12) и (6.9.14). Левая часть этого равенства имеет смысл обычной производной по направлению  от скаляра [формула (4.3.31)]. Одним из следствий соотношения (6.9.15) является то, что спиральность
от скаляра [формула (4.3.31)]. Одним из следствий соотношения (6.9.15) является то, что спиральность  локального твистора не изменяется при параллельном переносе. И в частности, изотропный твистор остается изотропным. Это свойство имеет аналог в римановой геометрии: норма и скалярное произведение векторов остаются неизменными при параллельном переносе. В теории твисторов роль, аналогичную римановой метрике, играет операция комплексного сопряжения: перенос локального твистора коммутирует с комплексным сопряжением твистора.
локального твистора не изменяется при параллельном переносе. И в частности, изотропный твистор остается изотропным. Это свойство имеет аналог в римановой геометрии: норма и скалярное произведение векторов остаются неизменными при параллельном переносе. В теории твисторов роль, аналогичную римановой метрике, играет операция комплексного сопряжения: перенос локального твистора коммутирует с комплексным сопряжением твистора.
Определение оператора V распространяется на локальные твисторы произвольной валентности с учетом обычных требований аддитивности и выполнения правила Лейбница. Проиллюстрируем общую схему частным примером:

| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие редактора перевода
- Предисловие
- Краткое содержание тома 1
- § 5 (гл. 1). Спинорные объекты и спиновая структура
- § 2 (гл. 2). Формализм абстрактных индексов в тензорной алгебре
- § 3 (гл. 3). Операции симметрии
- Переход от спинорной к тензорной форме записи, и наоборот; преобразование дуальности
- Некоторые свойства тензоров и спиноров в точке
- Активные лоренцевы и спиновые преобразования
- Ковариантная производная
- Спиновые коэффициенты
- Спинорная форма кривизны
- Тождества для спинора Риччи
- Спинорные тождества Бианки
- Компоненты спинорной кривизны
- Модифицированный формализм спиновых коэффициентов
- Уравнения для модифицированных спиновых коэффициентов
- Геометрия пространственноподобных 2-поверхностей
- На изотропной гиперповерхности
- § 15 (гл. 4). Функции на метрической сфере
- Производные заряженных полей
- Поля Янга — Миллса
- Конформные изменения масштаба
- Безмассовые свободные поля
- Другие полевые уравнения
- Данные на изотропной гиперповерхности
- 6. Твисторы
- § 1. Твисторное уравнение и пространство его решений
- Твисторное уравнение
- Пространство твисторов
- Дуальные твисторы
- Твисторы высшей валентности
- Конформная инвариантность спиральности и скалярного произведения
- § 2. Некоторые геометрические аспекты твисторной алгебры
- Поле флагштоков спинора: конгруэнция Робинсона
- Отношение взаимности твисторов
- Комплексная геометрия
- Представление точек с помощью простых кососимметричных твисторов
- § 3. Твисторы и момент импульса
- Момент импульса произвольной системы
- Представление твистора с помощью одноиндексных твисторов
- § 4. Симметричные твисторы и безмассовые поля
- Общий случай, потенциалы
- Повышение спина
- Другие виды потенциалов; связь с оператором
- § 5. Конформные векторы Киллинга; сохраняющиеся величины и точные последовательности
- Спиноры: Законы сохранения
- Твисторное описание
- Связь с интегралами от источников в линейной гравитации
- Точные последовательности
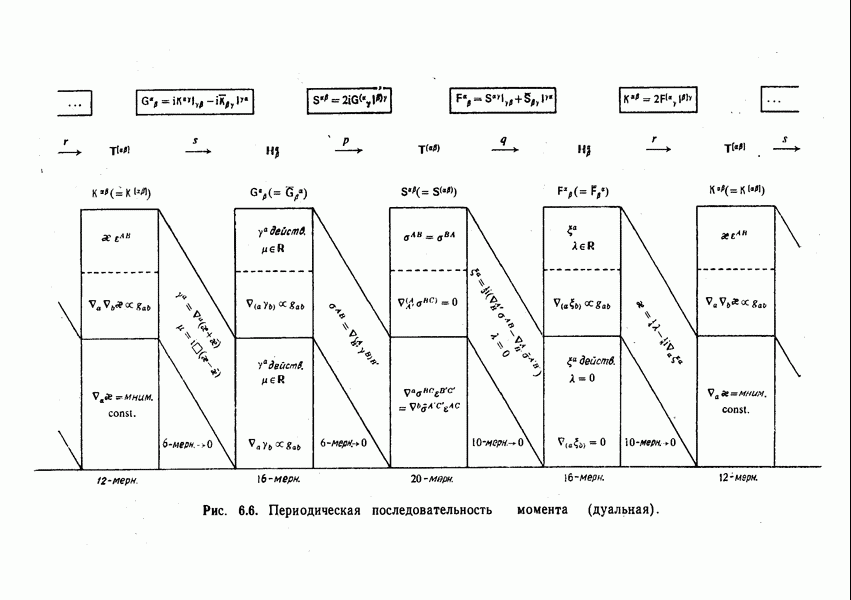
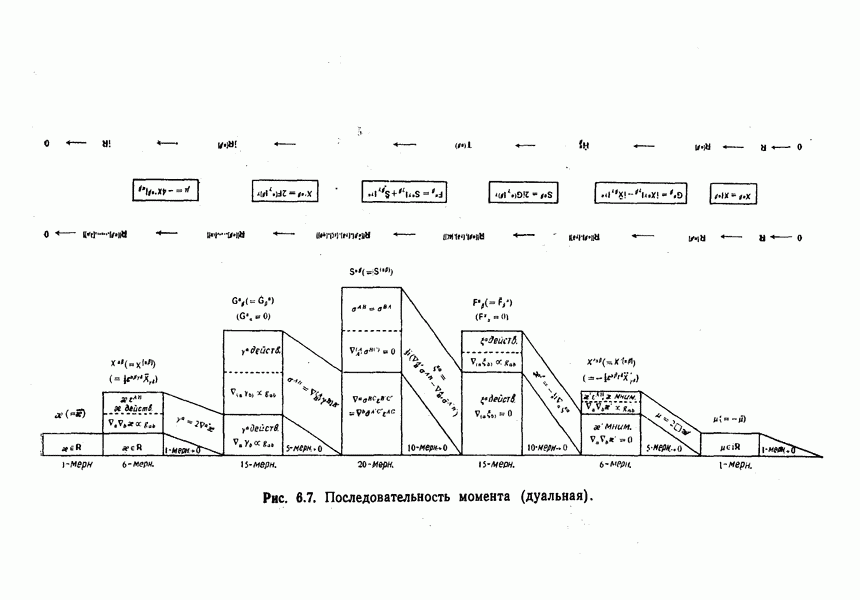
- Последовательности моментов
- Интегралы в линейной теории гравитации
- Спиноры: Десять интегралов, равных нулю
- Роль дуальности в последовательностях момента
- § 6. Производные Ли спиноров
- Связь с теорией твисторов
- § 7. Интегралы движения частиц; конформно-инвариантные операторы
- Спиноры Киллинга для вакуумных решений типа (22)
- Свойства решения Керра
- Конформно-инвариантные первые производные
- Твисторные решения различных уравнений
- Повторные операции; разрешения уравнений
- § 8. Кривизна и конформные преобразования
- Конформные свойства величин
- Конформные отображения плоских пространств
- Конформно-инвариантное волновое уравнение и оператор
- Конформно-инвариантный тензор Баха
- § 9. Локальные твисторы
- Условие совместности для твисторного уравнения
- Определение локального твистора
- Перенос локального твистора
- Кривизна в пространстве локальных твисторов
- Нулевая кривизна Вейля как свойство конформно-плоского пространства
- § 10. Безмассовые поля и когомологии твисторов
- Спиноры: Непроективное представление
- Квантование твисторов
- Спиральность
- Интегралы для спиральности противоположного знака
- Повышение и понижение спиральности
- Массивные твисторные волновые функции
- Геометрия контурных интегралов
- Положительно-частотные поля
- Введение когомологий
- Понятие 1-функции
- r-Функции общего вида
- Нелинейные 1-функции
- Конструкция Уорда
- Пример конструкции Уорда
- 7. Изотропные конгруэнции
- § 1. Изотропные конгруэнции и спиновые коэффициенты
- Интерпретация величин; изопараметричность лучей
- Ортогональность гиперповерхности; изотропные гиперповерхности
- Изопараметричность в теории твисторов
- § 2. Изотропные конгруэнции и кривизна пространства-времени
- Изопараметрические лучи; уравнения Сакса
- Неизопараметрические лучи
- Описание в трехмерном пространстве Минковского
- § 3. Бессдвиговые конгруэнции лучей
- Обобщенная теорема Голдберга — Сакса
- Координаты Керра
- § 4. БСК, твисторы и геометрия лучей
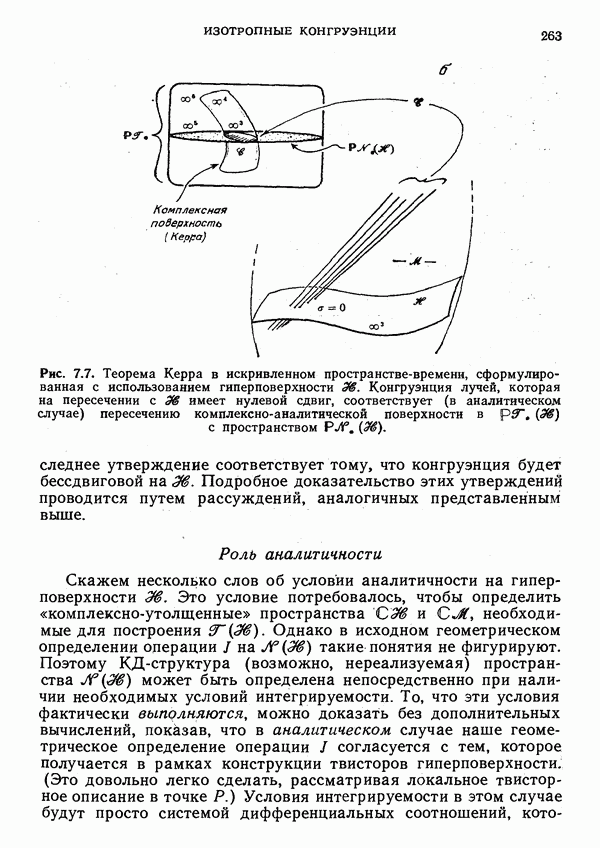
- Твисторная форма теоремы Керра
- Линейные и квадратичные функции твисторов, момент импульса
- Связь с твисторными функциями безмассовых полей
- Пространства и инвариантная контактная структура
- Комплексная структура и КД-структура
- Твисторы гиперповерхности
- Спиноры: Роль аналитичности
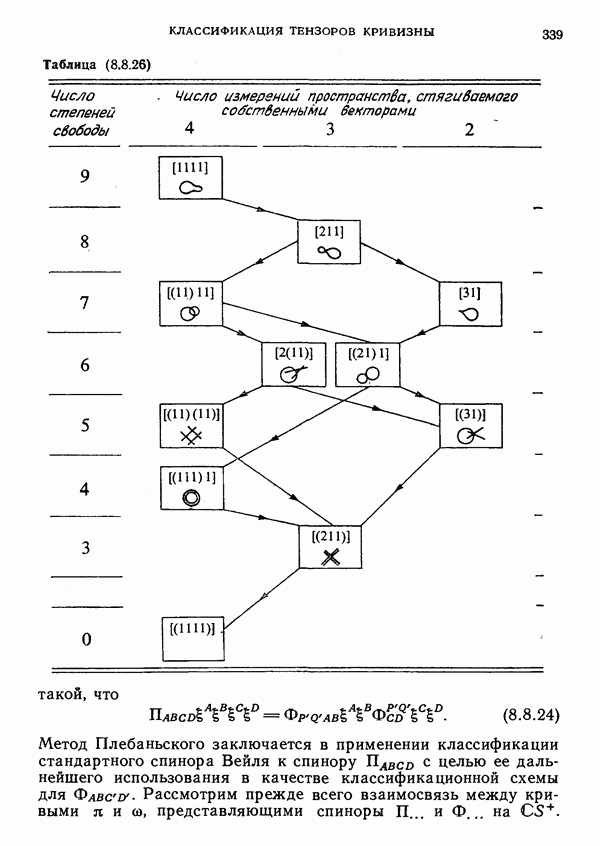
- 8. Классификация тензоров кривизны
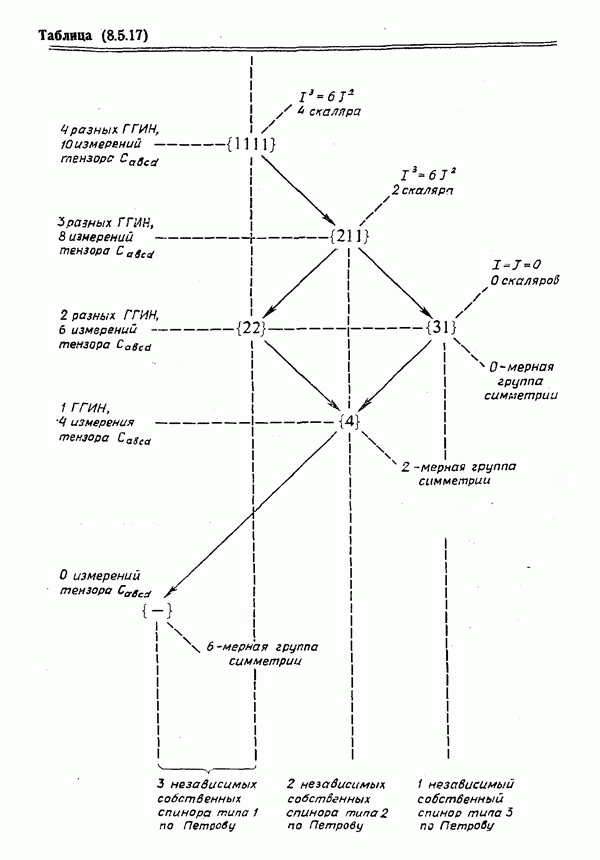
- Спиноры: Схема специализации
- § 2. Представление спинора Вейля на сфере S+
- ГГИН в пространстве-времени высокой симметрии
- «Картина» тензора Вейля на S+
- § 3. Собственные спиноры спинора Вейля
- Соотношение между собственными значениями и двойными отношениями
- Частные случаи
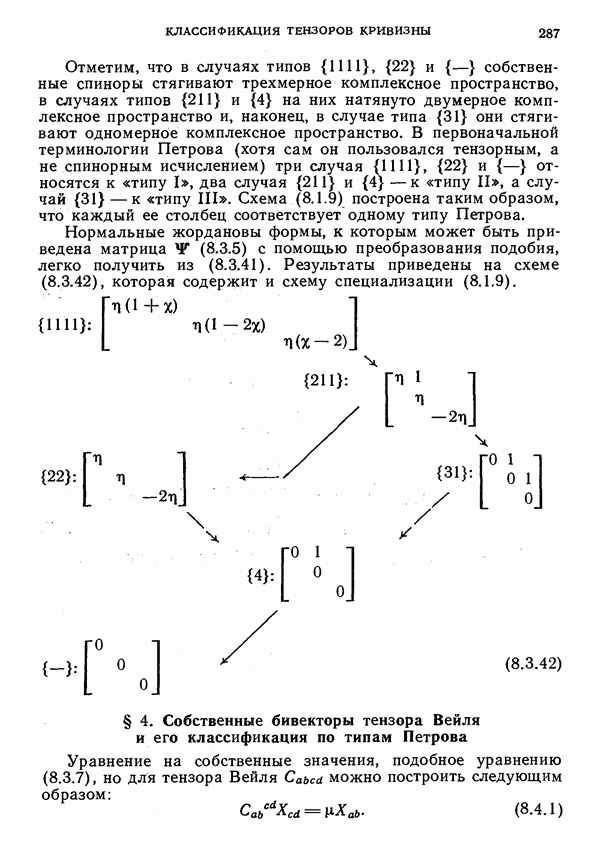
- § 4. Собственные бивекторы тензора Вейля и его классификация по типам Петрова
- Компоненты тензора Вейля в бивекторном базисе
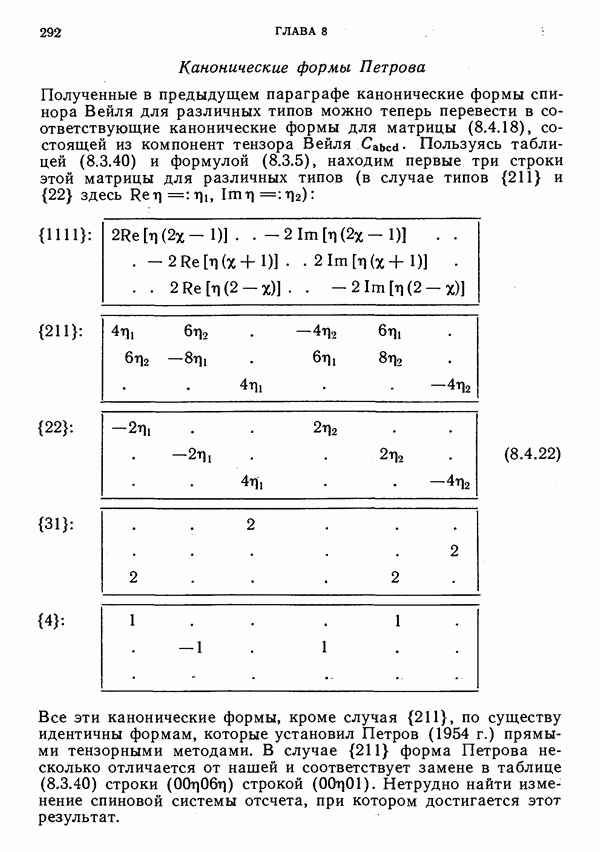
- Канонические формы Петрова
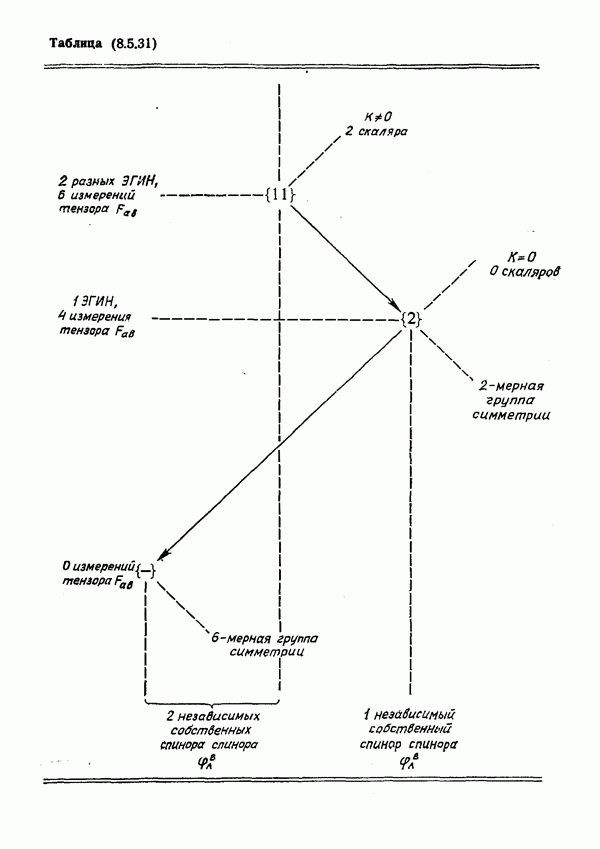
- § 5. Геометрия и симметрия вейлевской кривизны
- Дисфеноид для типа {1111}
- Симметрии в частных случаях типа {1111}
- Тип (211)
- О размерностях групп симметрий
- Классификация тензора Максвелла
- § 6. Коварианты кривизны
- Инварианты полной кривизны
- Система полей Эйнштейна — Максвелла
- § 7. Классификационная схема для спиноров с любым числом индексов
- Приводимость локуса
- Комплексные (р, q) — кривые на CS+
- Процедура классификации спинора
- Структура кривой w (ее кратные точки)
- Кратные точки кривой w
- Локус Rw на S+
- Знак спинора, черный и белый цвета сферы S+
- § 8. Классификация спинора Риччи
- Тип спинора по Плебаньскому
- Физические тензоры энергии-импульса
- 9. Конформная бесконечность
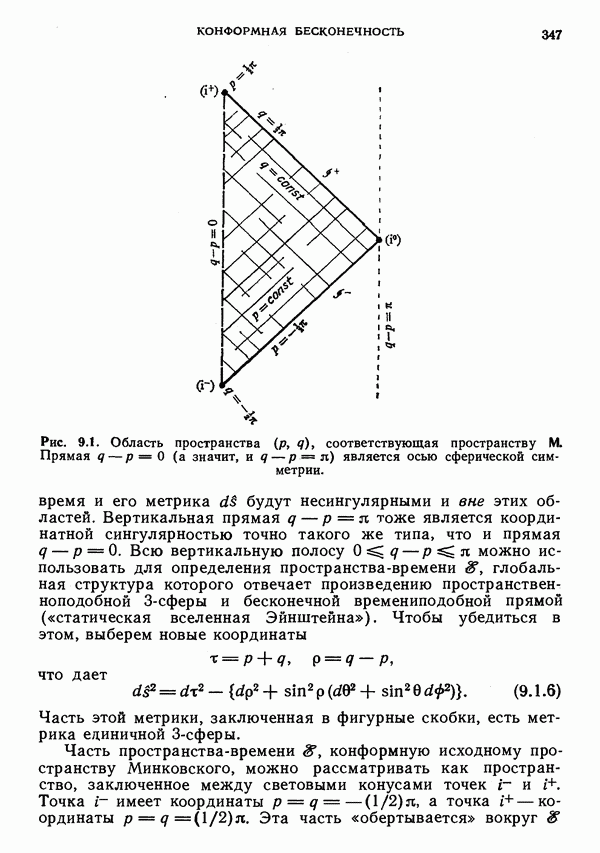
- § 1. Бесконечность в случае пространства Минковского
- ГНП и ГНБ
- § 2. Компактифицированное пространство Минковского
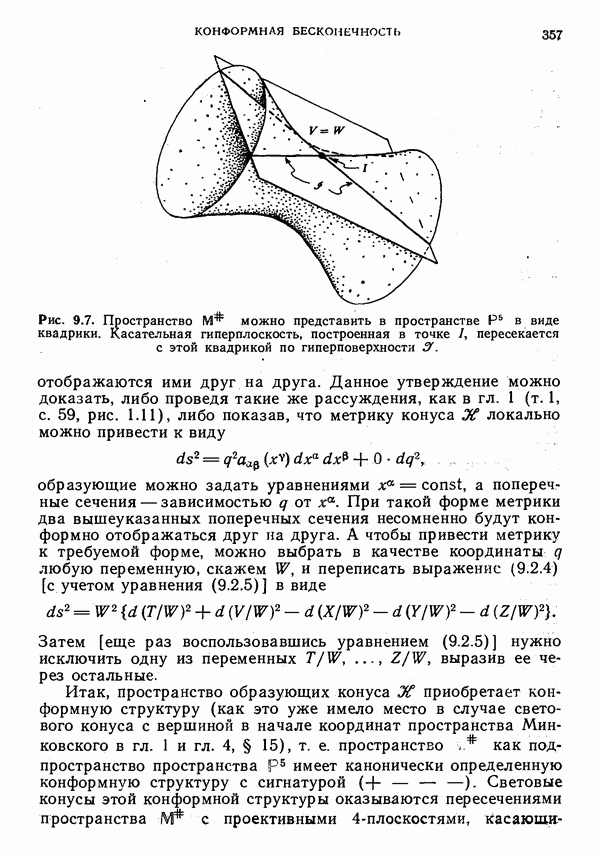
- Описание в пространстве Р5
- O(2,4) и конформная группа
- § 3. Комплексифицированное компактифицированное пространство Минковского и твисторная геометрия
- Соответствие Клейна
- Твисторное отношение дуальности
- Действительная структура
- Различные типы комплексных точек в СМ*
- § 4. Четырехзначность твисторов и индекс Гржина
- Две спиновые структуры на М*
- Поведение спинора
- Твисторные спин-расслоения над М*
- Конформные плотности на М*; индекс Гржина
- Теорема Гржина
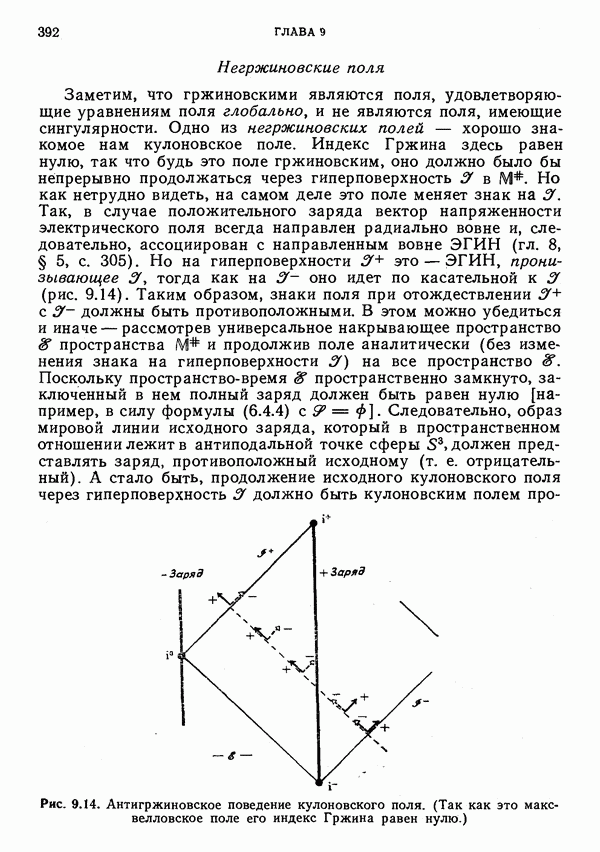
- Негржиновские поля
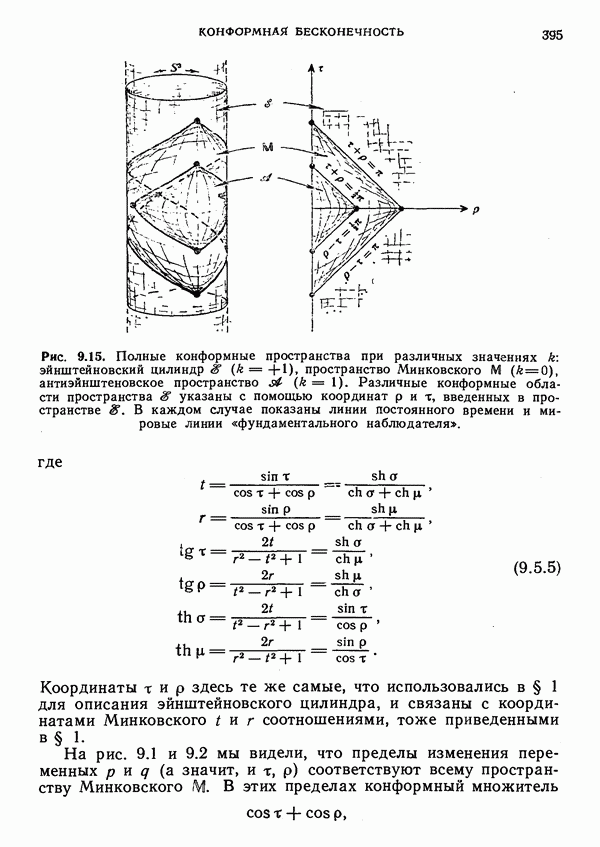
- § 5. Космологические модели и соответствующие твисторы
- Космологические горизонты
- Описание в пространстве Р5
- Деситтеровская и антидеситтеровская модели; твисторы …
- Функции для конформно-плоского пространства-времени
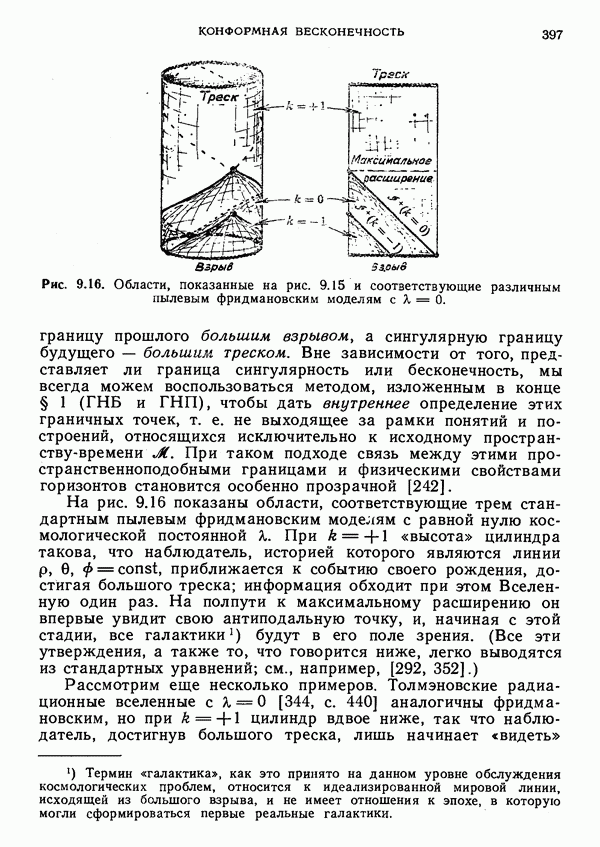
- Модели ФРУ, соответствующие твисторы начальной и конечной сингулярностей
- Явные выражения для функции I
- § 6. Асимптотически простое пространство-время
- Асимптотически-простое пространство-время
- Обращение в нуль тензора Вейля на границе J
- § 7. Последовательное вырождение
- Параллельно переносимые спиновые системы отсчета
- Сравнение аффинных параметров
- Сравнение спиновых систем отсчета
- Доказательство свойства последовательного вырождения
- Поля излучений
- § 8. Группа БМС и структура гиперповерхности J+
- Группа Бонди — Метцнера — Сакса
- Связь между сильной конформной геометрией и твистором
- Интерпретация изотропных углов
- Структура группы БМС
- Сдвиговая структура гиперповерхности J+
- H-пространство и асимптотическое твисторное пространство
- Отношение группы БМС к импульсу и моменту импульса
- Асимптотические разложения в теории Эйнштейна — Максвелла
- § 9. Энергия-импульс и момент импульса
- Усложнения в случае искривленного пространства-времени
- Твисторы двумерной поверхности
- Контортные двумерные поверхности
- Квазилокальный твистор момента импульса
- Определение множителя
- Асимптотическое спиновое пространство
- Свойства нормы на J+
- Эрмитовость твистора на 4-импульс Бонди — Сакса
- Альтернативные выражения для массы Бонди — Сакса
- Пространство Минковского как пространство «начал»
- Момент импульса на J+
- § 10. Потери массы Бонди — Сакса и положительность энергии
- Нелокальность энергии гравитационных волн
- НП-константы
- Подход Виттена в доказательстве положительности массы
- Связь с 4-импульсом Бонди — Сакса
- Спинор в подходе Людвигсена — Виккерса
- 3-форма Спарлинга
- Приложение. Спиноры в n измерениях
- 2-валентные e-спиноры
- Переход от тензоров к спинорам
- Геометрия фундаментальных спиноров
- Условие фундаментальности; структура спинового пространства
- Индуктивное построение спинового пространства
- Некоторые физически интересные случаи; триальность
- Спинорные поля; твисторы в n измерениях
- Послесловие авторов
- Литература