| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Структура группы БМС
Выше мы проанализировали геометрический смысл сильной конформной геометрии на  а тем самым и группы БМС, являющейся группой движений гиперповерхности
а тем самым и группы БМС, являющейся группой движений гиперповерхности  сохраняющей эту геометрическую структуру. Однако в отличие от преобразований Пуанкаре преобразования БМС не сохраняют в
сохраняющей эту геометрическую структуру. Однако в отличие от преобразований Пуанкаре преобразования БМС не сохраняют в
каком-либо очевидном смысле «физику». (Эта трудность в наиболее очевидной форме проявляется в плоском пространстве-времени.) Все дело, конечно, в том, что группа  все еще слишком «велика», являясь функционально-пространственной группой (бесконечномерной), а значит, даже не группой Ли. Естественно спросить себя, не существует ли некое дополнительное геометрическое ограничение, которое, не устраняя полностью эту функциональную свободу, позволило бы в конечном итоге получить подгруппу, изоморфную ограниченной группе Пуанкаре.
все еще слишком «велика», являясь функционально-пространственной группой (бесконечномерной), а значит, даже не группой Ли. Естественно спросить себя, не существует ли некое дополнительное геометрическое ограничение, которое, не устраняя полностью эту функциональную свободу, позволило бы в конечном итоге получить подгруппу, изоморфную ограниченной группе Пуанкаре.
«Размер» группы  зависит от функции Я в выражении (9.8.10) [см. также (9.8.11)]. В случае пространства Минковского М ограниченные движения Пуанкаре индуцируют преобразования гиперповерхности
зависит от функции Я в выражении (9.8.10) [см. также (9.8.11)]. В случае пространства Минковского М ограниченные движения Пуанкаре индуцируют преобразования гиперповерхности  которые можно записать в виде преобразований (9.8.9), ограниченных условиями (9.8.10) и (9.8.11) с функцией Я вида
которые можно записать в виде преобразований (9.8.9), ограниченных условиями (9.8.10) и (9.8.11) с функцией Я вида

причем «матрица»  постоянна и эрмитова. Чтобы получить это выражение, переменную и нужно считать разновидностью координаты времени Бонди, такой, что значением
постоянна и эрмитова. Чтобы получить это выражение, переменную и нужно считать разновидностью координаты времени Бонди, такой, что значением  определяется пересечение некоторого светового конуса
определяется пересечение некоторого светового конуса  с гиперповерхностью
с гиперповерхностью  Возьмем вершину этого конуса за начало отсчета О и выберем единичный времениподобный вектор будущего Т в точке О, обладающий тем свойством, что ассоциированный с ним выбор масштаба (анти-) небесной сферы, делающий ее единичной сферой, согласуется с выбором масштаба, который определяется координатой времени Бонди и [см. текст после формулы (9.8.31)]. Тогда выяснится, что и — это просто стандартный параметр запаздывающего времени инерциального наблюдателя с началом отсчета в точке О и осью времени Та (рис. 9.24). Иначе говоря, заданное значение и времени Бонди на
Возьмем вершину этого конуса за начало отсчета О и выберем единичный времениподобный вектор будущего Т в точке О, обладающий тем свойством, что ассоциированный с ним выбор масштаба (анти-) небесной сферы, делающий ее единичной сферой, согласуется с выбором масштаба, который определяется координатой времени Бонди и [см. текст после формулы (9.8.31)]. Тогда выяснится, что и — это просто стандартный параметр запаздывающего времени инерциального наблюдателя с началом отсчета в точке О и осью времени Та (рис. 9.24). Иначе говоря, заданное значение и времени Бонди на  достигается там, где световой конус будущего с вершиной в точке с радиус-вектором
достигается там, где световой конус будущего с вершиной в точке с радиус-вектором  в пространстве М пересекается с гиперповерхностью
в пространстве М пересекается с гиперповерхностью  Снабдив М стандартными координатами Минковского, легко убедиться, что частная форма преобразований БМС (9.8.9) [с (9.8.10)], при которой функция
Снабдив М стандартными координатами Минковского, легко убедиться, что частная форма преобразований БМС (9.8.9) [с (9.8.10)], при которой функция  имеет вид (9.8.51), дается активными (ограниченными) движениями Пуанкаре (записанными с помощью радиус-вектора, исходящего из считающейся фиксированной точки О):
имеет вид (9.8.51), дается активными (ограниченными) движениями Пуанкаре (записанными с помощью радиус-вектора, исходящего из считающейся фиксированной точки О):


Рис. 9.24. Чтобы получить стандартную координату времени Бонди в пространстве М, нужно взять времениподобную прямую в М и принять за и собственное время наблюдателя, история которого описывается данной мировой линией. При этом значения и остаются постоянными вдоль световых конусов будущего, исходящих из точек этой линии.
где  — спиноры, стандартными компонентами которых [формула (3.3.31)] являются величины
— спиноры, стандартными компонентами которых [формула (3.3.31)] являются величины  из (9.8.51) и
из (9.8.51) и

из формулы (9.8.9) (1), соответственно. Выражение (9.8.51) можно представить в следующей более «инвариантной» форме:

где величина

есть вектор, которым в точке О (или в любой другой точке пространства М) определяется изотропное направление образующей (с параметром  гиперповерхности
гиперповерхности
Укажем, что, когда преобразование (9.8.9) (1) является тождественным [т. е., когда матрица (9.8.53) является единичной], преобразования (9.8.52) представляют собой простые трансляции пространства М. В связи с этим всякий раз, когда преобразования (9.8.9) (1) являются тождественными [так что в формуле (9.8.11) мы имеем  а
а  имеет вид (9.8.51), соответствующие преобразования БМС даже в случае искривленного пространства
имеет вид (9.8.51), соответствующие преобразования БМС даже в случае искривленного пространства  называют трансляциями и говорят, что они образуют 4-параметрическую подгруппу трансляций
называют трансляциями и говорят, что они образуют 4-параметрическую подгруппу трансляций  группы
группы  Более общий вид преобразований, когда преобразования (9.8.9) (1) по-прежнему остаются тождественными (а значит,
Более общий вид преобразований, когда преобразования (9.8.9) (1) по-прежнему остаются тождественными (а значит,
 но функция Н является гладкой функцией общего вида на сфере, называют супертрансляциями — они образуют бесконечнопараметрическую подгруппу группы 38. Таким образом,
но функция Н является гладкой функцией общего вида на сфере, называют супертрансляциями — они образуют бесконечнопараметрическую подгруппу группы 38. Таким образом,

Подчеркнем, что в определении трансляции (и супертрансляции) фактически не существен выбор координаты времени Бонди и и нет зависимости от нее. То, что форма функции (9.8.51) сохраняется, когда  подвергается преобразованию (9.8.9) (1), а и соответственно изменяется как произведение
подвергается преобразованию (9.8.9) (1), а и соответственно изменяется как произведение  [с
[с  из формулы (9.8.11)], следует из того, что преобразования (9.8.52) образуют группу. (Это легко проверить и непосредственно.) Более того, трансляция оказывает на «супертранслированную» координату времени Бонди
из формулы (9.8.11)], следует из того, что преобразования (9.8.52) образуют группу. (Это легко проверить и непосредственно.) Более того, трансляция оказывает на «супертранслированную» координату времени Бонди  точно такое же влияние, как и на исходную координату и. На этом основании можно сделать вывод, что данное определение трансляции, как уже говорилось, БМС-инвариантно. (Супертрансляциями мы сейчас займемся.)
точно такое же влияние, как и на исходную координату и. На этом основании можно сделать вывод, что данное определение трансляции, как уже говорилось, БМС-инвариантно. (Супертрансляциями мы сейчас займемся.)
Сказанное выше можно сформулировать и иначе. Пусть 91 — группа лоренцевых вращений [т. е. преобразований (9.8.9), ограниченных условиями (9.8.11) и  в формуле (9.8.10)]. Тогда
в формуле (9.8.10)]. Тогда

Кроме того,

(Поскольку все супертрансляции коммутируют, подгруппа  во втором случае сохраняется поэлементно.) Из формы преобразований (9.8.9) следует, что каждый элемент группы
во втором случае сохраняется поэлементно.) Из формы преобразований (9.8.9) следует, что каждый элемент группы  имеет вид
имеет вид  , т. е. что
, т. е. что

Комбинируя это соотношение с (9.8.57) и (9.8.58), получаем

т. е.  — это нормальный делитель группы 38. Аналогично можно показать, что
— это нормальный делитель группы 38. Аналогично можно показать, что  тоже нормальный делитель группы
тоже нормальный делитель группы 

Таким образом, данное выше определение супертрансляции также БМС-инвариантно. Кроме того, получен следующий результат [299], который мы приводим без доказательства.
Теорема
Подгруппа трансляций группы БМС является ее единственным 4-параметрическим нормальным делителем.
Инвариантность определения трансляции — это по существу пример феномена, уже отмечавшегося в гл. 4, § 15. В общем случае супертрансляции определяются произвольной (гладкой) функцией Я на 2-сфере, а из выражения (9.8.51) и из формул, приведенных в конце гл. 4, § 15, вытекает следующее предложение.
Предложение
Трансляции — это супертрансляции, для которых функция  построена только из сферических гармоник с
построена только из сферических гармоник с  и
и 
(Спин-вес здесь равен нулю.) Из таблицы (4.15.60) видно, что такое условие для  можно записать в виде
можно записать в виде

Мы рассматриваем  - 2-сферу как пространство образующих гиперповерхности
- 2-сферу как пространство образующих гиперповерхности  (т. е. как фактор-пространство гиперповерхности
(т. е. как фактор-пространство гиперповерхности  при ее образующих). Под действием группы
при ее образующих). Под действием группы  (или, разумеется, группы 38) функции
(или, разумеется, группы 38) функции  ведут себя как конформно-взвешенные скаляры с весом
ведут себя как конформно-взвешенные скаляры с весом  Это связано с тем, что дифференциал
Это связано с тем, что дифференциал  параметра и имеет [согласно (9.8.20)] конформный вес
параметра и имеет [согласно (9.8.20)] конформный вес  хотя сами параметры не являются конформно-взвешенными объектами. Из сказанного в гл. 4, § 15, следует, что части таких скаляров с
хотя сами параметры не являются конформно-взвешенными объектами. Из сказанного в гл. 4, § 15, следует, что части таких скаляров с  при конформных движениях сферы преобразуются друг в друга, тогда как части с более высокими значениями
при конформных движениях сферы преобразуются друг в друга, тогда как части с более высокими значениями  этим свойством не обладают (т. е. при таких движениях они могут «подхватывать» части с
этим свойством не обладают (т. е. при таких движениях они могут «подхватывать» части с  или
или  ). Таким образом, хотя определение трансляции лоренц-инвариантно, справедливо следующее предложение.
). Таким образом, хотя определение трансляции лоренц-инвариантно, справедливо следующее предложение.
Предложение
Свойство супертрансляций не иметь трансляций не обладает лоренц-инвариантностью.
В этом предложении слова «лоренц-инвариантность» при желании можно было бы заменить словами «БМС-инвариантность». Интересующие нас преобразования Лоренца — это просто конформные движения  -сферы. Следовательно, такая
-сферы. Следовательно, такая
(ограниченная) группа Лоренца  может быть интерпретирована как фактор-группа группы
может быть интерпретирована как фактор-группа группы 

Однако группа Лоренца не появляется канонически как подгруппа группы  . Подгруппа
. Подгруппа  группы
группы  изоморфна группе
изоморфна группе  но выделяется совершенно не канонически. Предположим, что
но выделяется совершенно не канонически. Предположим, что  — это любой элемент группы
— это любой элемент группы  тогда группа
тогда группа

будет еще одной подгруппой группы и тоже изоморфной ограниченной группе Лоренца, да к тому же (в рамках групповой структуры группы  совершенно равноправна с группой
совершенно равноправна с группой  . Отличительным свойством группы
. Отличительным свойством группы  является то, что она состоит из элементов, оставляющих без изменения частное сечение гиперповерхности
является то, что она состоит из элементов, оставляющих без изменения частное сечение гиперповерхности  Гладкие сечения гиперповерхности
Гладкие сечения гиперповерхности  называют срезами
называют срезами  Инвариантным относительно действия группы
Инвариантным относительно действия группы  остается срез Г, который в заданной системе координат определяется уравнением
остается срез Г, который в заданной системе координат определяется уравнением  . Супертрансляция
. Супертрансляция  переводит Г в некоторый другой срез
переводит Г в некоторый другой срез  и из (9.8.66) следует, что
и из (9.8.66) следует, что  — это подгруппа группы
— это подгруппа группы  оставляющая срез Г без изменения. Только в том случае, когда
оставляющая срез Г без изменения. Только в том случае, когда  — тождественный элемент 1, группы
— тождественный элемент 1, группы  будут представлять собой одно и то же; если же
будут представлять собой одно и то же; если же  пробегает все значения в
пробегает все значения в  , то инвариантный срез пробегает все возможные срезы.
, то инвариантный срез пробегает все возможные срезы.
Разумеется, нельзя ожидать, что (ограниченная) группа Лоренца будет естественным образом возникать как подгруппа. Такие надежды необоснованы даже в связи с обычной (ограниченной) группой Пуанкаре пространства  где она также возникает естественным образом только как фактор-группа. (Как подгруппа она зависит от выбора произвольного начала отсчета в пространстве М.) Но, что касается группы Я, то здесь ситуация еще хуже, ибо в общем случае даже ограниченная группа Пуанкаре
где она также возникает естественным образом только как фактор-группа. (Как подгруппа она зависит от выбора произвольного начала отсчета в пространстве М.) Но, что касается группы Я, то здесь ситуация еще хуже, ибо в общем случае даже ограниченная группа Пуанкаре  не возникает естественным образом как подгруппа (или хотя бы как фактор-группа) этой группы
не возникает естественным образом как подгруппа (или хотя бы как фактор-группа) этой группы 
Чтобы правильно оценить сложившуюся ситуацию, рассмотрим сначала случай, когда группа  относится к гиперповерхности
относится к гиперповерхности  пространства М. Группу
пространства М. Группу  можно рассматривать в качестве подгруппы группы
можно рассматривать в качестве подгруппы группы  генерируемой трансляциями и лоренцевыми вращениями
генерируемой трансляциями и лоренцевыми вращениями  с формулой (9.8.59)]:
с формулой (9.8.59)]:

В то время как группа  не выделяется канонически в семейство групп лоренцевых поворотов вокруг всевозможных различных начал отсчета в пространстве М выделяется. Любая такая подгруппа Лоренца группы
не выделяется канонически в семейство групп лоренцевых поворотов вокруг всевозможных различных начал отсчета в пространстве М выделяется. Любая такая подгруппа Лоренца группы  возникает как подгруппа
возникает как подгруппа
группы  оставляющая без изменения определенный тип среза, называемого хорошим срезом и представляющего собой пересечение светового конуса некоторой точки пространства М с гиперповерхностью
оставляющая без изменения определенный тип среза, называемого хорошим срезом и представляющего собой пересечение светового конуса некоторой точки пространства М с гиперповерхностью  Хорошие срезы, образующие 4-пара-метрические системы, получаются один из другого в результате трансляций; однако супертрансляции, не являющиеся трансляциями, всегда переводят хороший срез в плохой (т. е. не являющийся хорошим). Следовательно, определение хорошего среза не инвариантно относительно преобразований группы БСМ. Если операция
Хорошие срезы, образующие 4-пара-метрические системы, получаются один из другого в результате трансляций; однако супертрансляции, не являющиеся трансляциями, всегда переводят хороший срез в плохой (т. е. не являющийся хорошим). Следовательно, определение хорошего среза не инвариантно относительно преобразований группы БСМ. Если операция  из формулы (9.8.66) не является трансляцией, то определяющая ее группа Ы? должна быть взята вне Аналогично, для такого рода супертрансляции десятипараметрическая подгруппа группы Я
из формулы (9.8.66) не является трансляцией, то определяющая ее группа Ы? должна быть взята вне Аналогично, для такого рода супертрансляции десятипараметрическая подгруппа группы Я

должна отличаться от  хотя и изоморфна ей. Фактически, в случае самого общего элемента
хотя и изоморфна ей. Фактически, в случае самого общего элемента  подгруппы и 9 вместе обладают только трансляциями
подгруппы и 9 вместе обладают только трансляциями 
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие редактора перевода
- Предисловие
- Краткое содержание тома 1
- § 5 (гл. 1). Спинорные объекты и спиновая структура
- § 2 (гл. 2). Формализм абстрактных индексов в тензорной алгебре
- § 3 (гл. 3). Операции симметрии
- Переход от спинорной к тензорной форме записи, и наоборот; преобразование дуальности
- Некоторые свойства тензоров и спиноров в точке
- Активные лоренцевы и спиновые преобразования
- Ковариантная производная
- Спиновые коэффициенты
- Спинорная форма кривизны
- Тождества для спинора Риччи
- Спинорные тождества Бианки
- Компоненты спинорной кривизны
- Модифицированный формализм спиновых коэффициентов
- Уравнения для модифицированных спиновых коэффициентов
- Геометрия пространственноподобных 2-поверхностей
- На изотропной гиперповерхности
- § 15 (гл. 4). Функции на метрической сфере
- Производные заряженных полей
- Поля Янга — Миллса
- Конформные изменения масштаба
- Безмассовые свободные поля
- Другие полевые уравнения
- Данные на изотропной гиперповерхности
- 6. Твисторы
- § 1. Твисторное уравнение и пространство его решений
- Твисторное уравнение
- Пространство твисторов
- Дуальные твисторы
- Твисторы высшей валентности
- Конформная инвариантность спиральности и скалярного произведения
- § 2. Некоторые геометрические аспекты твисторной алгебры
- Поле флагштоков спинора: конгруэнция Робинсона
- Отношение взаимности твисторов
- Комплексная геометрия
- Представление точек с помощью простых кососимметричных твисторов
- § 3. Твисторы и момент импульса
- Момент импульса произвольной системы
- Представление твистора с помощью одноиндексных твисторов
- § 4. Симметричные твисторы и безмассовые поля
- Общий случай, потенциалы
- Повышение спина
- Другие виды потенциалов; связь с оператором
- § 5. Конформные векторы Киллинга; сохраняющиеся величины и точные последовательности
- Спиноры: Законы сохранения
- Твисторное описание
- Связь с интегралами от источников в линейной гравитации
- Точные последовательности
- Последовательности моментов
- Интегралы в линейной теории гравитации
- Спиноры: Десять интегралов, равных нулю
- Роль дуальности в последовательностях момента
- § 6. Производные Ли спиноров
- Связь с теорией твисторов
- § 7. Интегралы движения частиц; конформно-инвариантные операторы
- Спиноры Киллинга для вакуумных решений типа (22)
- Свойства решения Керра
- Конформно-инвариантные первые производные
- Твисторные решения различных уравнений
- Повторные операции; разрешения уравнений
- § 8. Кривизна и конформные преобразования
- Конформные свойства величин
- Конформные отображения плоских пространств
- Конформно-инвариантное волновое уравнение и оператор
- Конформно-инвариантный тензор Баха
- § 9. Локальные твисторы
- Условие совместности для твисторного уравнения
- Определение локального твистора
- Перенос локального твистора
- Кривизна в пространстве локальных твисторов
- Нулевая кривизна Вейля как свойство конформно-плоского пространства
- § 10. Безмассовые поля и когомологии твисторов
- Спиноры: Непроективное представление
- Квантование твисторов
- Спиральность
- Интегралы для спиральности противоположного знака
- Повышение и понижение спиральности
- Массивные твисторные волновые функции
- Геометрия контурных интегралов
- Положительно-частотные поля
- Введение когомологий
- Понятие 1-функции
- r-Функции общего вида
- Нелинейные 1-функции
- Конструкция Уорда
- Пример конструкции Уорда
- 7. Изотропные конгруэнции
- § 1. Изотропные конгруэнции и спиновые коэффициенты
- Интерпретация величин; изопараметричность лучей
- Ортогональность гиперповерхности; изотропные гиперповерхности
- Изопараметричность в теории твисторов
- § 2. Изотропные конгруэнции и кривизна пространства-времени
- Изопараметрические лучи; уравнения Сакса
- Неизопараметрические лучи
- Описание в трехмерном пространстве Минковского
- § 3. Бессдвиговые конгруэнции лучей
- Обобщенная теорема Голдберга — Сакса
- Координаты Керра
- § 4. БСК, твисторы и геометрия лучей
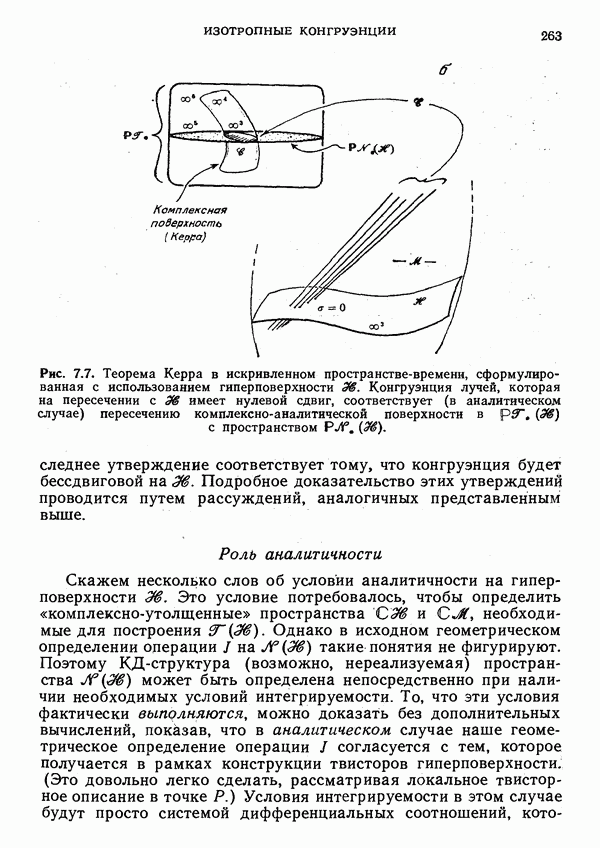
- Твисторная форма теоремы Керра
- Линейные и квадратичные функции твисторов, момент импульса
- Связь с твисторными функциями безмассовых полей
- Пространства и инвариантная контактная структура
- Комплексная структура и КД-структура
- Твисторы гиперповерхности
- Спиноры: Роль аналитичности
- 8. Классификация тензоров кривизны
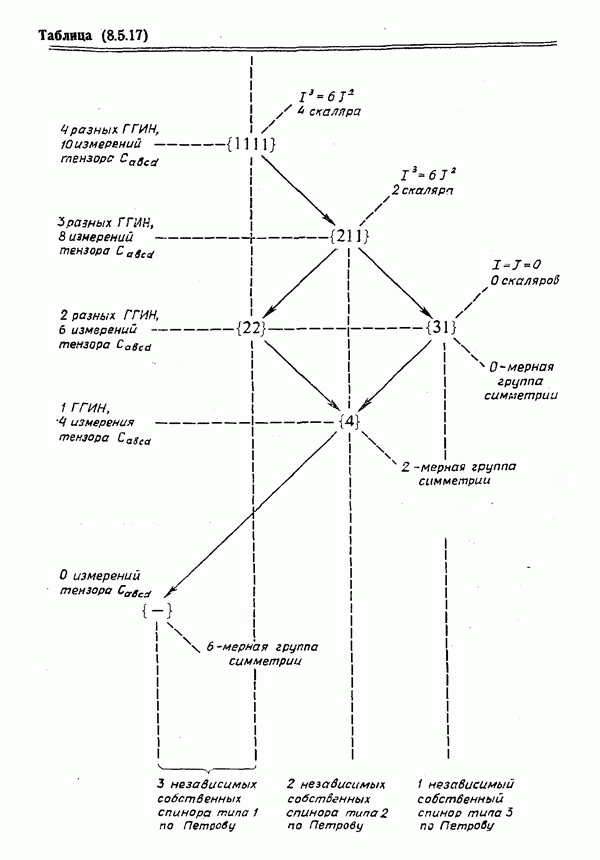
- Спиноры: Схема специализации
- § 2. Представление спинора Вейля на сфере S+
- ГГИН в пространстве-времени высокой симметрии
- «Картина» тензора Вейля на S+
- § 3. Собственные спиноры спинора Вейля
- Соотношение между собственными значениями и двойными отношениями
- Частные случаи
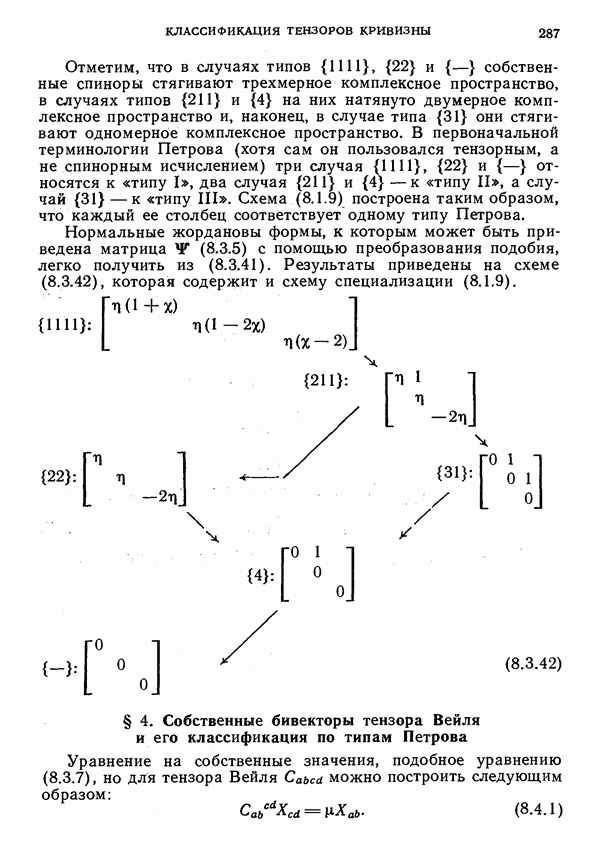
- § 4. Собственные бивекторы тензора Вейля и его классификация по типам Петрова
- Компоненты тензора Вейля в бивекторном базисе
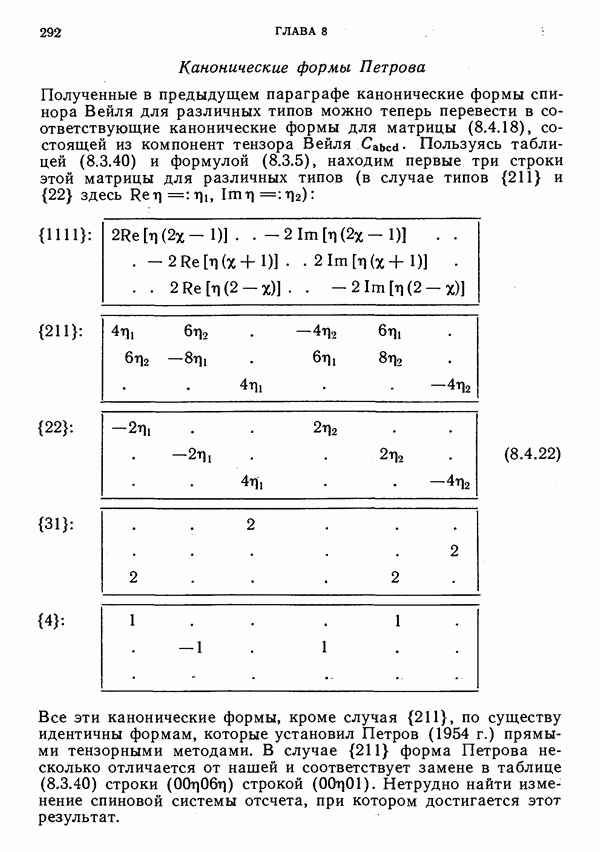
- Канонические формы Петрова
- § 5. Геометрия и симметрия вейлевской кривизны
- Дисфеноид для типа {1111}
- Симметрии в частных случаях типа {1111}
- Тип (211)
- О размерностях групп симметрий
- Классификация тензора Максвелла
- § 6. Коварианты кривизны
- Инварианты полной кривизны
- Система полей Эйнштейна — Максвелла
- § 7. Классификационная схема для спиноров с любым числом индексов
- Приводимость локуса
- Комплексные (р, q) — кривые на CS+
- Процедура классификации спинора
- Структура кривой w (ее кратные точки)
- Кратные точки кривой w
- Локус Rw на S+
- Знак спинора, черный и белый цвета сферы S+
- § 8. Классификация спинора Риччи
- Тип спинора по Плебаньскому
- Физические тензоры энергии-импульса
- 9. Конформная бесконечность
- § 1. Бесконечность в случае пространства Минковского
- ГНП и ГНБ
- § 2. Компактифицированное пространство Минковского
- Описание в пространстве Р5
- O(2,4) и конформная группа
- § 3. Комплексифицированное компактифицированное пространство Минковского и твисторная геометрия
- Соответствие Клейна
- Твисторное отношение дуальности
- Действительная структура
- Различные типы комплексных точек в СМ*
- § 4. Четырехзначность твисторов и индекс Гржина
- Две спиновые структуры на М*
- Поведение спинора
- Твисторные спин-расслоения над М*
- Конформные плотности на М*; индекс Гржина
- Теорема Гржина
- Негржиновские поля
- § 5. Космологические модели и соответствующие твисторы
- Космологические горизонты
- Описание в пространстве Р5
- Деситтеровская и антидеситтеровская модели; твисторы …
- Функции для конформно-плоского пространства-времени
- Модели ФРУ, соответствующие твисторы начальной и конечной сингулярностей
- Явные выражения для функции I
- § 6. Асимптотически простое пространство-время
- Асимптотически-простое пространство-время
- Обращение в нуль тензора Вейля на границе J
- § 7. Последовательное вырождение
- Параллельно переносимые спиновые системы отсчета
- Сравнение аффинных параметров
- Сравнение спиновых систем отсчета
- Доказательство свойства последовательного вырождения
- Поля излучений
- § 8. Группа БМС и структура гиперповерхности J+
- Группа Бонди — Метцнера — Сакса
- Связь между сильной конформной геометрией и твистором
- Интерпретация изотропных углов
- Структура группы БМС
- Сдвиговая структура гиперповерхности J+
- H-пространство и асимптотическое твисторное пространство
- Отношение группы БМС к импульсу и моменту импульса
- Асимптотические разложения в теории Эйнштейна — Максвелла
- § 9. Энергия-импульс и момент импульса
- Усложнения в случае искривленного пространства-времени
- Твисторы двумерной поверхности
- Контортные двумерные поверхности
- Квазилокальный твистор момента импульса
- Определение множителя
- Асимптотическое спиновое пространство
- Свойства нормы на J+
- Эрмитовость твистора на 4-импульс Бонди — Сакса
- Альтернативные выражения для массы Бонди — Сакса
- Пространство Минковского как пространство «начал»
- Момент импульса на J+
- § 10. Потери массы Бонди — Сакса и положительность энергии
- Нелокальность энергии гравитационных волн
- НП-константы
- Подход Виттена в доказательстве положительности массы
- Связь с 4-импульсом Бонди — Сакса
- Спинор в подходе Людвигсена — Виккерса
- 3-форма Спарлинга
- Приложение. Спиноры в n измерениях
- 2-валентные e-спиноры
- Переход от тензоров к спинорам
- Геометрия фундаментальных спиноров
- Условие фундаментальности; структура спинового пространства
- Индуктивное построение спинового пространства
- Некоторые физически интересные случаи; триальность
- Спинорные поля; твисторы в n измерениях
- Послесловие авторов
- Литература