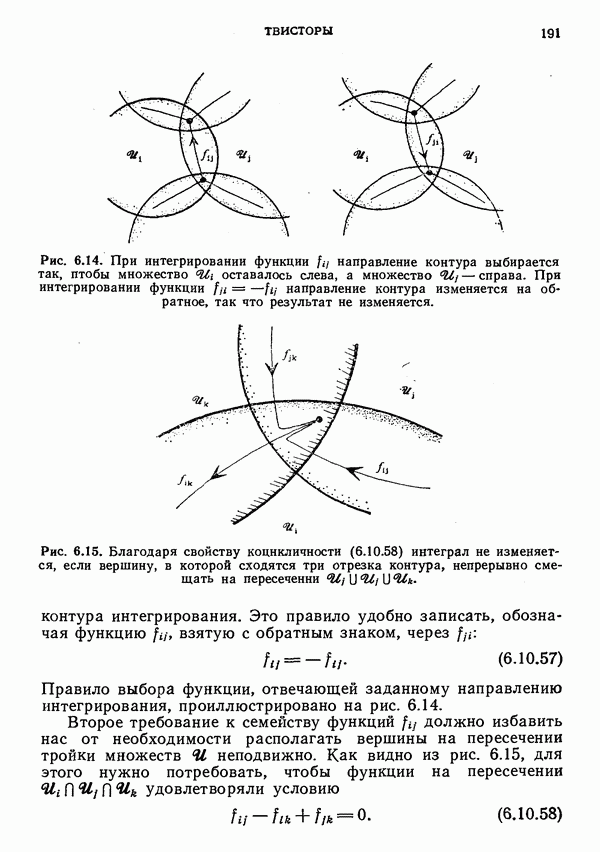
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Твисторы высшей валентности
Рассмотрим теперь прямое (тензорное) произведение  двух твисторов вида
двух твисторов вида

или, выписывая явную зависимость от точки О,

Сравнивая это представление с (6.1.20), находим, что компоненты произведения  выражаются через все компоненты следующих четырех спиноров, взятых в точке О:
выражаются через все компоненты следующих четырех спиноров, взятых в точке О:

Спинорные поля (6.1.40) представляют собой спинорные части произведения  а их зависимость от точки определяется соотношением (6.1.10) [примененным к твисторам (6.1.38)]. Произвольный
а их зависимость от точки определяется соотношением (6.1.10) [примененным к твисторам (6.1.38)]. Произвольный  -твистор
-твистор  будучи суммой произведений вида
будучи суммой произведений вида  полностью характеризуется четырьмя независимыми спинорами, взятыми в точке О, а именно значениями в точке О четырех полей
полностью характеризуется четырьмя независимыми спинорами, взятыми в точке О, а именно значениями в точке О четырех полей

Мы говорим, что они образуют спинорные части твистора  Это особые выделенные взаимосвязанные величины, которые равны суммам произведений вида (6.1.40), сомножители которых определяются выражениями (6.1.38), а зависимость от точки — соотношениями (6.1.10).
Это особые выделенные взаимосвязанные величины, которые равны суммам произведений вида (6.1.40), сомножители которых определяются выражениями (6.1.38), а зависимость от точки — соотношениями (6.1.10).
Используя обозначения (6.1.41), важно сохранять неизменный порядок спинорных индексов, т. е. нельзя писать  отличие от обычных обозначений, см. (2.5.33)]
отличие от обычных обозначений, см. (2.5.33)]  поскольку этот порядок — наше единственное указание в обозначениях на то, какая из спинорных частей имеется в виду. Но эти обозначения могут приводить к путанице, когда индексы поднимаются и опускаются с помощью
поскольку этот порядок — наше единственное указание в обозначениях на то, какая из спинорных частей имеется в виду. Но эти обозначения могут приводить к путанице, когда индексы поднимаются и опускаются с помощью  -символа. Поэтому, если в вычислениях постоянно используются спинорные части определенного твистора, удобнее ввести для них отдельные символы,
-символа. Поэтому, если в вычислениях постоянно используются спинорные части определенного твистора, удобнее ввести для них отдельные символы,
При общем же изложении теории твисторов используемые обозначения оказываются очень экономными. Мы часто пишем

По аналогии находим типичные представления для  и
и  -твисторов:
-твисторов:

 Ясно, что в общем случае
Ясно, что в общем случае  -твистор имеет
-твистор имеет  спинорных частей, которые, однако, не удается записать в таких же удобных обозначениях, как выше. Например,
спинорных частей, которые, однако, не удается записать в таких же удобных обозначениях, как выше. Например,  -твистор
-твистор  имеет восемь независимых спинорных частей вида
имеет восемь независимых спинорных частей вида

Спинорная часть, все индексы которой расположены в верхней позиции (в предыдущем случае  называется главной спинорной частью твистора. Часть, все индексы которой находятся в нижних позициях, называется проекционной
называется главной спинорной частью твистора. Часть, все индексы которой находятся в нижних позициях, называется проекционной 
Определение (6.1.23) произведения  приводит к определениям сверток произвольных твисторов. Практически они сводятся к свертке «соответствующих» спинорных частей по индексам А и А для каждого сворачиваемого твисторного индекса а. Например:
приводит к определениям сверток произвольных твисторов. Практически они сводятся к свертке «соответствующих» спинорных частей по индексам А и А для каждого сворачиваемого твисторного индекса а. Например:

Теперь по аналогии с формулами (6.1.21) и (6.1.37) легко вычислить компоненты произвольных твисторов в базисе (6.1.17). Рассматривая в качестве примера твистор

мы находим [компоненты спинорного поля должны быть взяты в точке О в соответствии с замечанием, сделанным после формулы (6.1.21)]

Здесь левая часть каждого из равенств — компонента твистора, а правая — компонента спинорной части. Поскольку твисторные индексы не штрихованы, а спинорные никогда не принимают значений 2 и 3, вторая строка в соотношениях (6.1.47) определена однозначно. Может показаться, что неоднозначность имеется в первой строке, но это не так. В самом деле, мы имеем следующее правило:

Далее выясним зависимость спинорных частей (6.1.41)  -твистора
-твистора  от точки. Зависимостью от точки и от отношения взаимности (полевых) спинорных частей 1-валентных твисторов определяется вид (полевых) спинорных частей всех твисторов. В случае твистора
от точки. Зависимостью от точки и от отношения взаимности (полевых) спинорных частей 1-валентных твисторов определяется вид (полевых) спинорных частей всех твисторов. В случае твистора  это можно вывести из требования, чтобы (скалярное) поле
это можно вывести из требования, чтобы (скалярное) поле

образованное из двух произвольных  -твисторов
-твисторов  было постоянным и, следовательно, равнялось своему значению в начале координат. Действуя далее так же, как при выводе формулы (6.1.25), мы легко находим требуемые соотношения. Чтобы записать их в удобном виде, введем более конкретные обозначения для спинорных частей твистора
было постоянным и, следовательно, равнялось своему значению в начале координат. Действуя далее так же, как при выводе формулы (6.1.25), мы легко находим требуемые соотношения. Чтобы записать их в удобном виде, введем более конкретные обозначения для спинорных частей твистора  а именно
а именно

(хотя вполне можно было бы использовать обозначения компонент  Определенные таким образом спинорные части связаны между собой следующими соотношениями:
Определенные таким образом спинорные части связаны между собой следующими соотношениями:

Информация, которую несут эти равенства, содержится также в следующих дифференциальных уравнениях [см. формулы

Это можно показать, вычислив производные обеих частей равенств (6.1.51) в начале координат; поскольку выбор начала координат произволен, мы приходим к выводу, что уравнения (6.1.52) выполняются в любой точке. В этом специальном случае твистор  полностью определяется одним полем, а именно главной спинорной частью
полностью определяется одним полем, а именно главной спинорной частью  Первое уравнение системы
Первое уравнение системы

откуда находим и  . Затем, используя второе или третье уравнение системы (6.1.52), находим
. Затем, используя второе или третье уравнение системы (6.1.52), находим 
Соотношения, аналогичные соотношениям (6.1.51) и (6.1.52), очевидно, имеют место для твисторов любой валентности и могут быть получены тем же способом. Рассмотрим еще один специальный случай, а именно случай  -твистора
-твистора  вида (6.1.43), для полевых спинорных частей которого мы тоже введем свои обозначения:
вида (6.1.43), для полевых спинорных частей которого мы тоже введем свои обозначения:

Для таких полей находим

что [аналогично случаю равенств (6.1.51) и (6.1.52)] эквивалентно уравнениям

Замечая, что преобразование

не меняет уравнений (6.1.55), мы видим, что главная спинорная часть твистора  определяет его однозначно. Преобразование (6.1.57) изменяет след
определяет его однозначно. Преобразование (6.1.57) изменяет след

этого твистора:

Только при условии, что след известен (например, равен нулю), твистор  однозначно восстанавливается по его главной спинорной части
однозначно восстанавливается по его главной спинорной части 
Уравнения, аналогичные уравнениям (6.1.51) и (6.1.55), выполняются для всех твисторов. Определенный класс твисторов, например  полностью определяется заданием их главной части. Однако пример твистора
полностью определяется заданием их главной части. Однако пример твистора  показывает, что это не всегда справедливо. Один класс твисторов, которые полностью определяются своей главной частью, состоит из бесследовых симметричных твисторов:
показывает, что это не всегда справедливо. Один класс твисторов, которые полностью определяются своей главной частью, состоит из бесследовых симметричных твисторов:

Уравнение, которому удовлетворяет главная часть этого твистора  имеет вид
имеет вид

Другой предельный случай — альтернирующие твисторы еаруб, удовлетворяющие уравнениям

Каждый такой твистор имеет шестнадцать спинорных частей, причем лишь шесть из них отличны от нуля. Это спинорные части с двумя штрихованными и двумя нештрихованными индексами, они имеют вид

для 

для  Главная часть в этих случаях равна нулю. (Она
Главная часть в этих случаях равна нулю. (Она  нулю также в случае антисимметричного твистора
нулю также в случае антисимметричного твистора  Оказывается, что только бесследовые симметричные твисторы восстанавливаются однозначно по единственному
Оказывается, что только бесследовые симметричные твисторы восстанавливаются однозначно по единственному
спинорному полю (а именно по главной спинорной части), удовлетворяющему одному дифференциальному уравнению первого порядка. В некоторых других случаях (например, в случае кососимметричного  -твистора) главная спинорная часть все же определяет твистор полностью, но для ее вычисления недостаточно одного дифференциального уравнения первого порядка. В большинстве же случаев твистор не определяется главной спинорной частью. Например, главная часть симметричного твистора (6.1.60), след которого отличен от нуля, удовлетворяет уравнению (6.1.62), но различные слагаемые, входящие в определение следа, скажем выражения вида
-твистора) главная спинорная часть все же определяет твистор полностью, но для ее вычисления недостаточно одного дифференциального уравнения первого порядка. В большинстве же случаев твистор не определяется главной спинорной частью. Например, главная часть симметричного твистора (6.1.60), след которого отличен от нуля, удовлетворяет уравнению (6.1.62), но различные слагаемые, входящие в определение следа, скажем выражения вида  не определяются главной частью (т. е. выражения такого вида можно добавлять к
не определяются главной частью (т. е. выражения такого вида можно добавлять к  не изменяя главной части).
не изменяя главной части).
Особый интерес для нас будут представлять симметричные, кососимметричные и эрмитовы 2-валентные твисторы. Твистор  вида (6.1.50) будет симметричным, если
вида (6.1.50) будет симметричным, если  т. е. если выполняются соотношения
т. е. если выполняются соотношения

Из уравнений (6.1.52) видно, что для выполнения второго и третьего равенств (6.1.66) достаточно потребовать, чтобы симметрия спинорной части  имела место во всех точках-, следовательно, это свойство является достаточным для симметрии твистора
имела место во всех точках-, следовательно, это свойство является достаточным для симметрии твистора  . В случае кососимметричного твистора
. В случае кососимметричного твистора  уравнениях (6.1.66) следует поставить знак минус в правой части. Аналогично можно показать, что из требования кососимметричности спинорной части
уравнениях (6.1.66) следует поставить знак минус в правой части. Аналогично можно показать, что из требования кососимметричности спинорной части  во всех точках автоматически следуют второе и третье уравнения.
во всех точках автоматически следуют второе и третье уравнения.
Мы говорим, что твистор  вида (6.1.54) эрмитов, если
вида (6.1.54) эрмитов, если

т. е.

Используя уравнение (6.1.55), можно показать, так же как и в случае симметричных спиноров, что эрмитовостью спинорной части  во всех точках обеспечивается выполнение второго из уравнений (6.1.68), однако левая и правая части третьего уравнения допускают при этом сдвиг на спинор
во всех точках обеспечивается выполнение второго из уравнений (6.1.68), однако левая и правая части третьего уравнения допускают при этом сдвиг на спинор  умноженный на мнимое число. Поэтому из требования эрмитовости спинорной части эрмитовость твистора
умноженный на мнимое число. Поэтому из требования эрмитовости спинорной части эрмитовость твистора  следует только в том случае, когда след его равен нулю.
следует только в том случае, когда след его равен нулю.
В дальнейшем для нас будет важно следующее обстоятельство: главная спинорная часть  любого твистора
любого твистора  автоматически удовлетворяет дифференциальному уравнению
автоматически удовлетворяет дифференциальному уравнению

что явствует из первого уравнения (6.1.52). Кроме того, главная спинорная часть  любого твистора
любого твистора  автоматически удовлетворяет дифференциальному уравнению
автоматически удовлетворяет дифференциальному уравнению

(которое по существу есть конформное уравнение Киллинга, см. § 5), что следует из первого уравнения (6.1.56). По аналогии с уравнением (6.1.1), которому удовлетворяет главная спинорная часть твистора  эти два уравнения также конформно-инвариантны при
эти два уравнения также конформно-инвариантны при

(на что в случае конформно-плоского пространства указывает их твисторное происхождение). Так же как и относительно уравнения (6.1.1), это можно показать, не делая предположения, что пространство-время является плоским. Более того, так же как при выводе уравнений (6.1.10), можно показать, что общие решения уравнений (6.1.69) и (6.1.70) в  в предположении симметрии спинорной части
в предположении симметрии спинорной части  определяются четвертыми уравнениями (6.1.51) и (6.1.55), соответственно. Отметим, что уравнения (6.1.69) и (6.1.70) — это частные случаи уравнения (6.1.62), которое также конформно-инвариантно [формула (5.6.15)], причем
определяются четвертыми уравнениями (6.1.51) и (6.1.55), соответственно. Отметим, что уравнения (6.1.69) и (6.1.70) — это частные случаи уравнения (6.1.62), которое также конформно-инвариантно [формула (5.6.15)], причем

К обсуждению уравнений (6.1.69), (6.1.70) и (6.1.62) мы вернемся позже [§ 7; формула (6.4.1)]. В § 7 будет показано, что все симметричные решения уравнения (6.1.62) есть главные части бесследовых симметричных твисторов.
Рассмотрим теперь вопрос о комплексном сопряжении твистора общего вида. Соответствующее правило по существу следует из определения (6.1.31) для 1-валентных твисторов, а также из требования, чтобы операция комплексного сопряжения коммутировала с операциями умножения и сложения, например:

В частности, рассмотрим твистор

В соответствии с нашим определением имеем

Поскольку в общем случае  -твистор есть сумма твисторов типа
-твистор есть сумма твисторов типа  и аналогично можно рассматривать
и аналогично можно рассматривать  -твистор самого общего вида, мы формулируем следующее общее правило:
-твистор самого общего вида, мы формулируем следующее общее правило:
Чтобы выполнить комплексное сопряжение твистора, следует выполнить комплексное сопряжение всех его спинорных частей, расположив их затем в правильном порядке, соответствующем твистору со всеми индексами исходного твистора, перенесенными на противоположный уровень.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие редактора перевода
- Предисловие
- Краткое содержание тома 1
- § 5 (гл. 1). Спинорные объекты и спиновая структура
- § 2 (гл. 2). Формализм абстрактных индексов в тензорной алгебре
- § 3 (гл. 3). Операции симметрии
- Переход от спинорной к тензорной форме записи, и наоборот; преобразование дуальности
- Некоторые свойства тензоров и спиноров в точке
- Активные лоренцевы и спиновые преобразования
- Ковариантная производная
- Спиновые коэффициенты
- Спинорная форма кривизны
- Тождества для спинора Риччи
- Спинорные тождества Бианки
- Компоненты спинорной кривизны
- Модифицированный формализм спиновых коэффициентов
- Уравнения для модифицированных спиновых коэффициентов
- Геометрия пространственноподобных 2-поверхностей
- На изотропной гиперповерхности
- § 15 (гл. 4). Функции на метрической сфере
- Производные заряженных полей
- Поля Янга — Миллса
- Конформные изменения масштаба
- Безмассовые свободные поля
- Другие полевые уравнения
- Данные на изотропной гиперповерхности
- 6. Твисторы
- § 1. Твисторное уравнение и пространство его решений
- Твисторное уравнение
- Пространство твисторов
- Дуальные твисторы
- Твисторы высшей валентности
- Конформная инвариантность спиральности и скалярного произведения
- § 2. Некоторые геометрические аспекты твисторной алгебры
- Поле флагштоков спинора: конгруэнция Робинсона
- Отношение взаимности твисторов
- Комплексная геометрия
- Представление точек с помощью простых кососимметричных твисторов
- § 3. Твисторы и момент импульса
- Момент импульса произвольной системы
- Представление твистора с помощью одноиндексных твисторов
- § 4. Симметричные твисторы и безмассовые поля
- Общий случай, потенциалы
- Повышение спина
- Другие виды потенциалов; связь с оператором
- § 5. Конформные векторы Киллинга; сохраняющиеся величины и точные последовательности
- Спиноры: Законы сохранения
- Твисторное описание
- Связь с интегралами от источников в линейной гравитации
- Точные последовательности
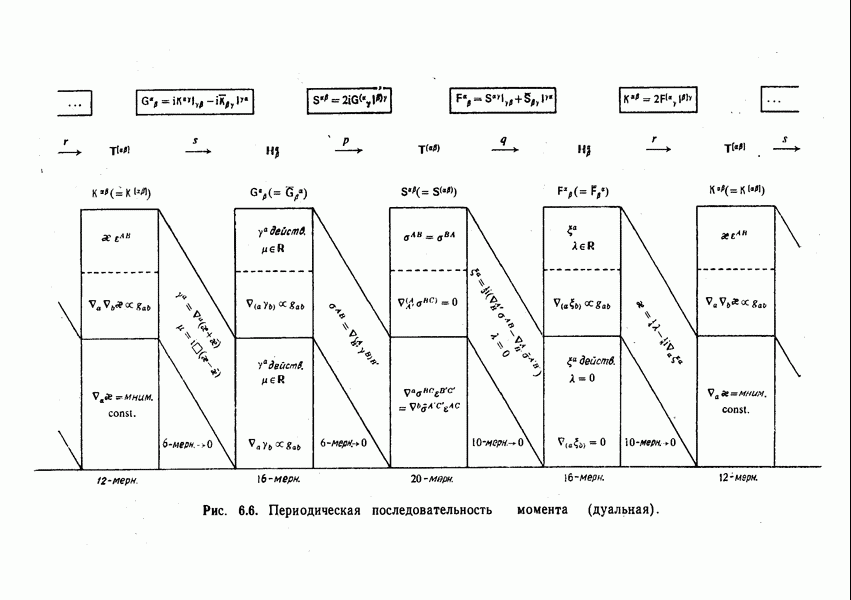
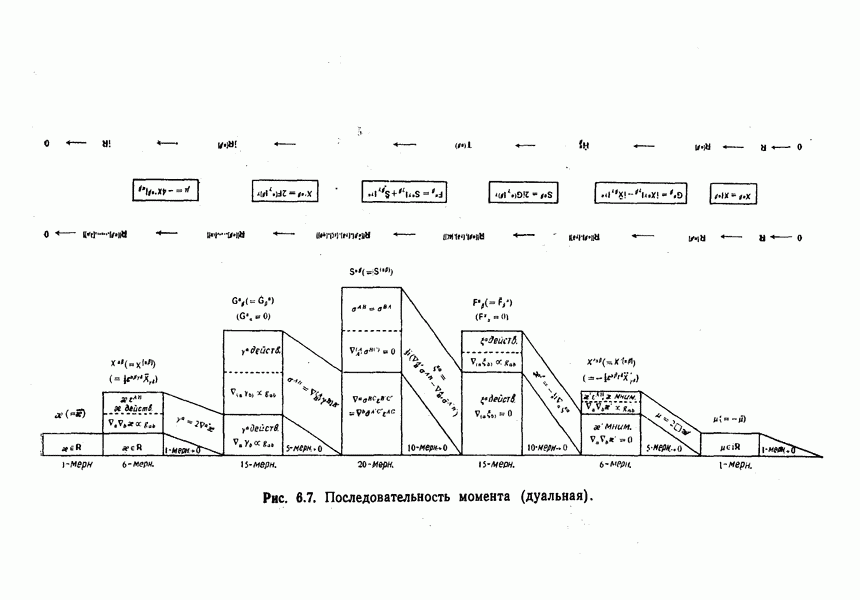
- Последовательности моментов
- Интегралы в линейной теории гравитации
- Спиноры: Десять интегралов, равных нулю
- Роль дуальности в последовательностях момента
- § 6. Производные Ли спиноров
- Связь с теорией твисторов
- § 7. Интегралы движения частиц; конформно-инвариантные операторы
- Спиноры Киллинга для вакуумных решений типа (22)
- Свойства решения Керра
- Конформно-инвариантные первые производные
- Твисторные решения различных уравнений
- Повторные операции; разрешения уравнений
- § 8. Кривизна и конформные преобразования
- Конформные свойства величин
- Конформные отображения плоских пространств
- Конформно-инвариантное волновое уравнение и оператор
- Конформно-инвариантный тензор Баха
- § 9. Локальные твисторы
- Условие совместности для твисторного уравнения
- Определение локального твистора
- Перенос локального твистора
- Кривизна в пространстве локальных твисторов
- Нулевая кривизна Вейля как свойство конформно-плоского пространства
- § 10. Безмассовые поля и когомологии твисторов
- Спиноры: Непроективное представление
- Квантование твисторов
- Спиральность
- Интегралы для спиральности противоположного знака
- Повышение и понижение спиральности
- Массивные твисторные волновые функции
- Геометрия контурных интегралов
- Положительно-частотные поля
- Введение когомологий
- Понятие 1-функции
- r-Функции общего вида
- Нелинейные 1-функции
- Конструкция Уорда
- Пример конструкции Уорда
- 7. Изотропные конгруэнции
- § 1. Изотропные конгруэнции и спиновые коэффициенты
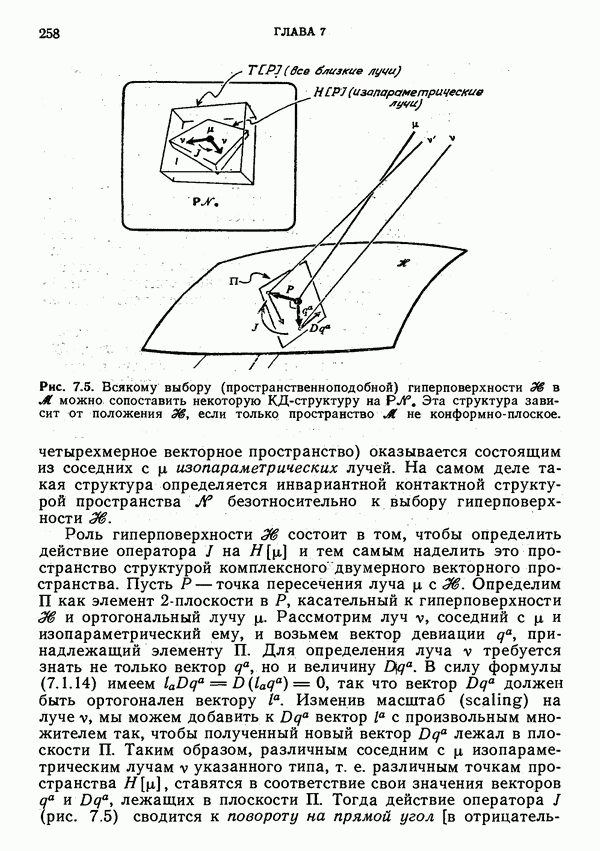
- Интерпретация величин; изопараметричность лучей
- Ортогональность гиперповерхности; изотропные гиперповерхности
- Изопараметричность в теории твисторов
- § 2. Изотропные конгруэнции и кривизна пространства-времени
- Изопараметрические лучи; уравнения Сакса
- Неизопараметрические лучи
- Описание в трехмерном пространстве Минковского
- § 3. Бессдвиговые конгруэнции лучей
- Обобщенная теорема Голдберга — Сакса
- Координаты Керра
- § 4. БСК, твисторы и геометрия лучей
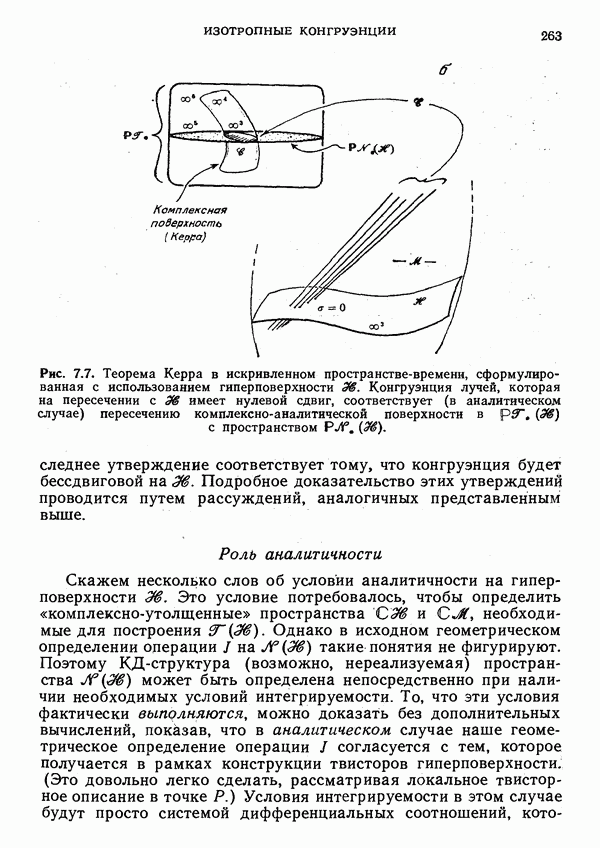
- Твисторная форма теоремы Керра
- Линейные и квадратичные функции твисторов, момент импульса
- Связь с твисторными функциями безмассовых полей
- Пространства и инвариантная контактная структура
- Комплексная структура и КД-структура
- Твисторы гиперповерхности
- Спиноры: Роль аналитичности
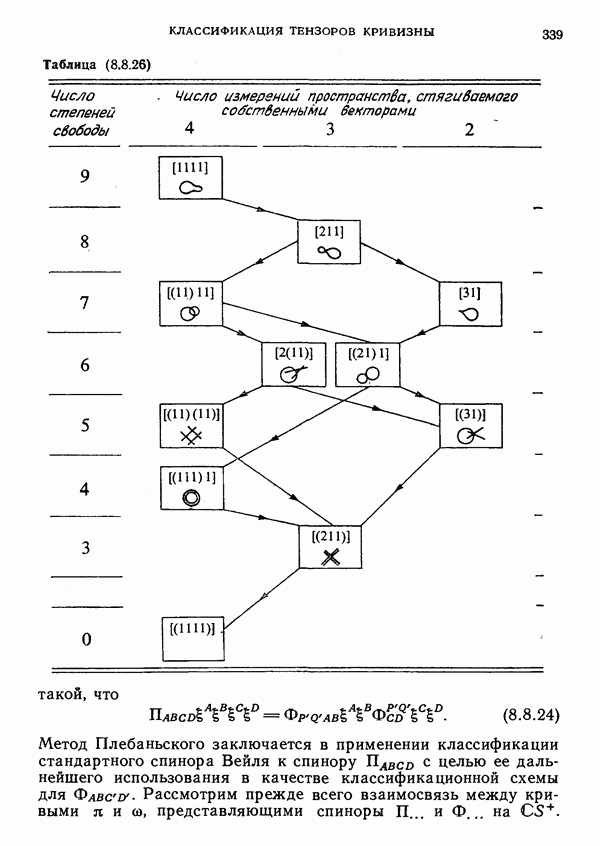
- 8. Классификация тензоров кривизны
- Спиноры: Схема специализации
- § 2. Представление спинора Вейля на сфере S+
- ГГИН в пространстве-времени высокой симметрии
- «Картина» тензора Вейля на S+
- § 3. Собственные спиноры спинора Вейля
- Соотношение между собственными значениями и двойными отношениями
- Частные случаи
- § 4. Собственные бивекторы тензора Вейля и его классификация по типам Петрова
- Компоненты тензора Вейля в бивекторном базисе
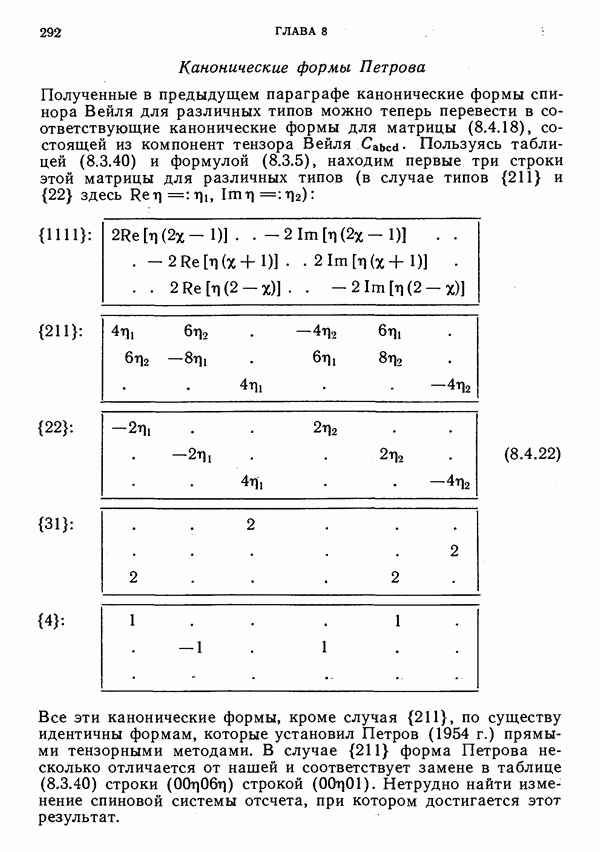
- Канонические формы Петрова
- § 5. Геометрия и симметрия вейлевской кривизны
- Дисфеноид для типа {1111}
- Симметрии в частных случаях типа {1111}
- Тип (211)
- О размерностях групп симметрий
- Классификация тензора Максвелла
- § 6. Коварианты кривизны
- Инварианты полной кривизны
- Система полей Эйнштейна — Максвелла
- § 7. Классификационная схема для спиноров с любым числом индексов
- Приводимость локуса
- Комплексные (р, q) — кривые на CS+
- Процедура классификации спинора
- Структура кривой w (ее кратные точки)
- Кратные точки кривой w
- Локус Rw на S+
- Знак спинора, черный и белый цвета сферы S+
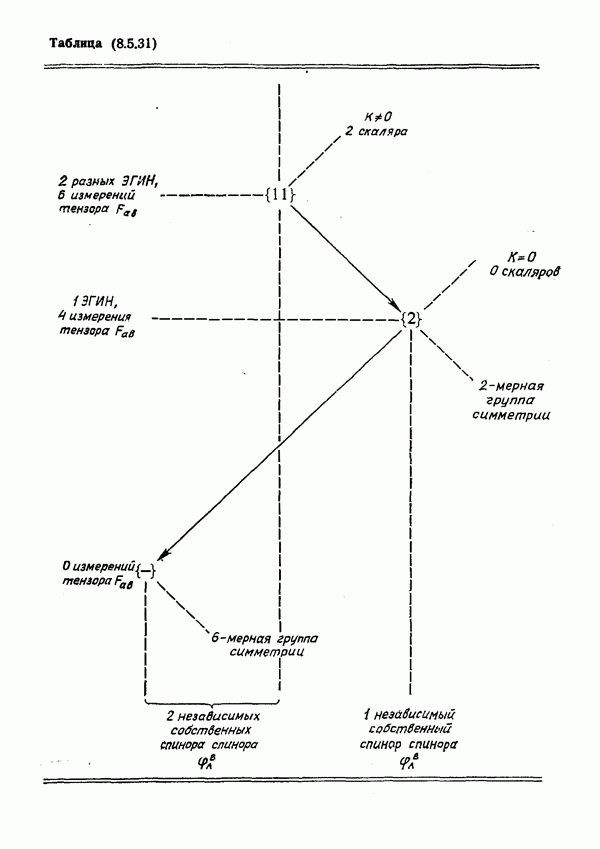
- § 8. Классификация спинора Риччи
- Тип спинора по Плебаньскому
- Физические тензоры энергии-импульса
- 9. Конформная бесконечность
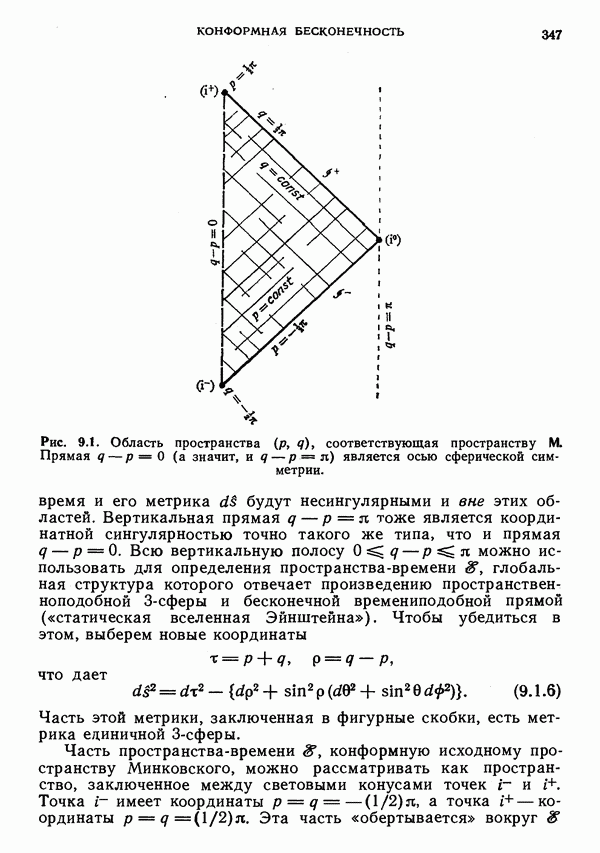
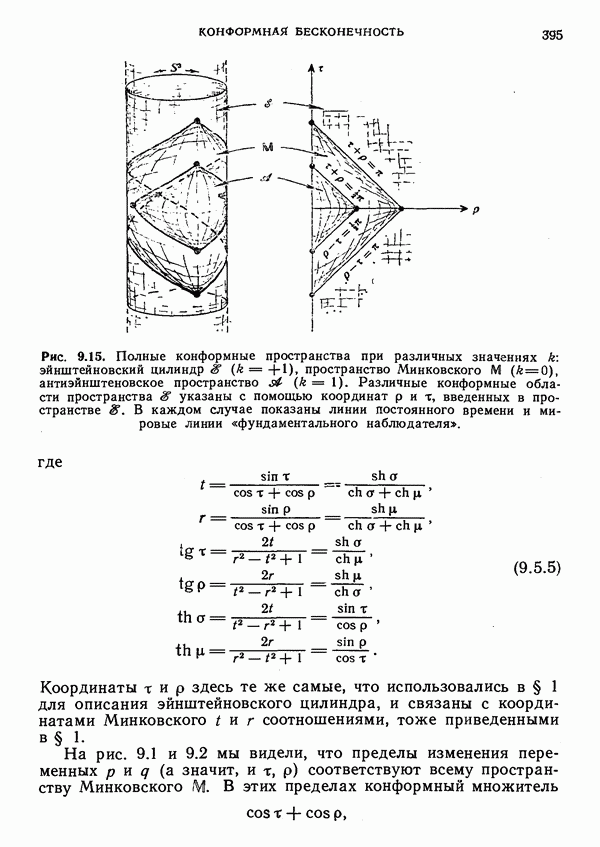
- § 1. Бесконечность в случае пространства Минковского
- ГНП и ГНБ
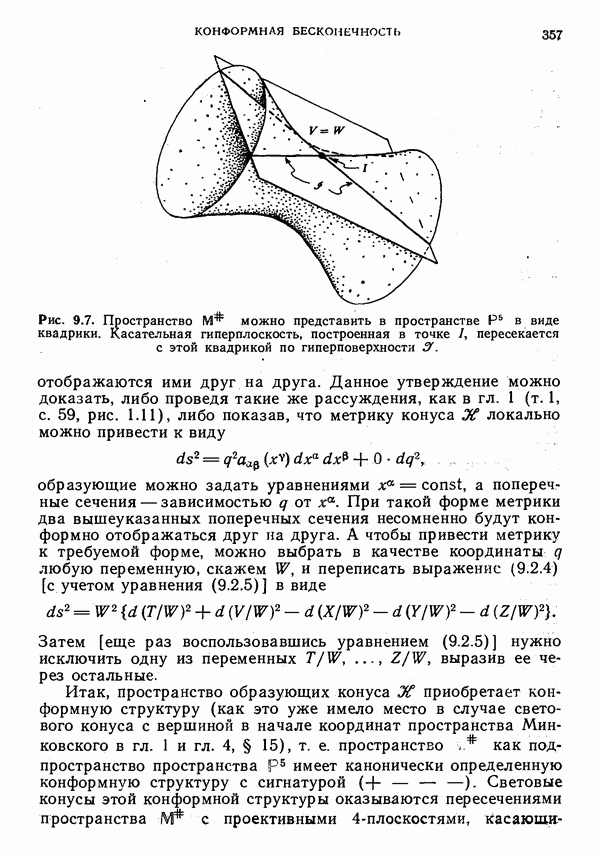
- § 2. Компактифицированное пространство Минковского
- Описание в пространстве Р5
- O(2,4) и конформная группа
- § 3. Комплексифицированное компактифицированное пространство Минковского и твисторная геометрия
- Соответствие Клейна
- Твисторное отношение дуальности
- Действительная структура
- Различные типы комплексных точек в СМ*
- § 4. Четырехзначность твисторов и индекс Гржина
- Две спиновые структуры на М*
- Поведение спинора
- Твисторные спин-расслоения над М*
- Конформные плотности на М*; индекс Гржина
- Теорема Гржина
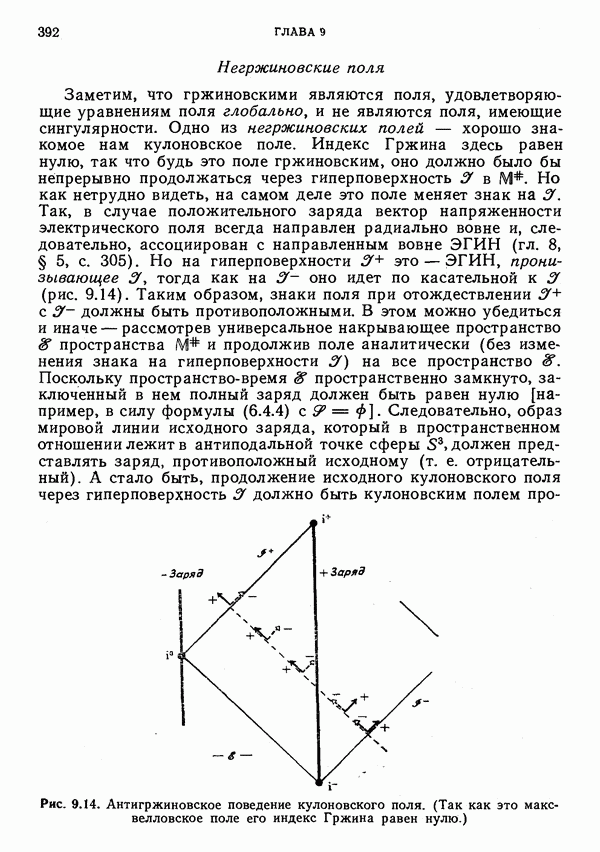
- Негржиновские поля
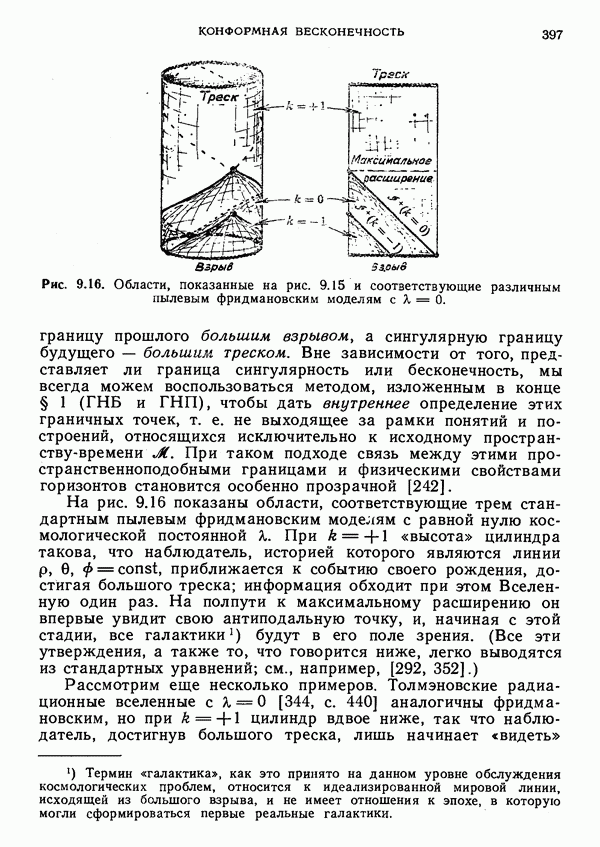
- § 5. Космологические модели и соответствующие твисторы
- Космологические горизонты
- Описание в пространстве Р5
- Деситтеровская и антидеситтеровская модели; твисторы …
- Функции для конформно-плоского пространства-времени
- Модели ФРУ, соответствующие твисторы начальной и конечной сингулярностей
- Явные выражения для функции I
- § 6. Асимптотически простое пространство-время
- Асимптотически-простое пространство-время
- Обращение в нуль тензора Вейля на границе J
- § 7. Последовательное вырождение
- Параллельно переносимые спиновые системы отсчета
- Сравнение аффинных параметров
- Сравнение спиновых систем отсчета
- Доказательство свойства последовательного вырождения
- Поля излучений
- § 8. Группа БМС и структура гиперповерхности J+
- Группа Бонди — Метцнера — Сакса
- Связь между сильной конформной геометрией и твистором
- Интерпретация изотропных углов
- Структура группы БМС
- Сдвиговая структура гиперповерхности J+
- H-пространство и асимптотическое твисторное пространство
- Отношение группы БМС к импульсу и моменту импульса
- Асимптотические разложения в теории Эйнштейна — Максвелла
- § 9. Энергия-импульс и момент импульса
- Усложнения в случае искривленного пространства-времени
- Твисторы двумерной поверхности
- Контортные двумерные поверхности
- Квазилокальный твистор момента импульса
- Определение множителя
- Асимптотическое спиновое пространство
- Свойства нормы на J+
- Эрмитовость твистора на 4-импульс Бонди — Сакса
- Альтернативные выражения для массы Бонди — Сакса
- Пространство Минковского как пространство «начал»
- Момент импульса на J+
- § 10. Потери массы Бонди — Сакса и положительность энергии
- Нелокальность энергии гравитационных волн
- НП-константы
- Подход Виттена в доказательстве положительности массы
- Связь с 4-импульсом Бонди — Сакса
- Спинор в подходе Людвигсена — Виккерса
- 3-форма Спарлинга
- Приложение. Спиноры в n измерениях
- 2-валентные e-спиноры
- Переход от тензоров к спинорам
- Геометрия фундаментальных спиноров
- Условие фундаментальности; структура спинового пространства
- Индуктивное построение спинового пространства
- Некоторые физически интересные случаи; триальность
- Спинорные поля; твисторы в n измерениях
- Послесловие авторов
- Литература