| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Квазилокальный твистор момента импульса
Одно из возможных определений 2-формы  на
на  , применимое в полной общей теории относительности [259], получается подстановкой выражения (9.9.14) в (9.9.3), а затем полученного тензора
, применимое в полной общей теории относительности [259], получается подстановкой выражения (9.9.14) в (9.9.3), а затем полученного тензора  вместе с полной кривизной — в формулу (9.9.1):
вместе с полной кривизной — в формулу (9.9.1):

Действительно, имеются довольно убедительные доказательства [337] того, что в случае неконтортной поверхности  это определение дает меру массы-энергии в общей теории относительности, превосходно (и даже замечательно) согласующуюся с физическими требованиями. Но в настоящее время имеются основания считать (как указывают и работы Тода, Келли и Вудхауса), что в общем случае контортной поверхности
это определение дает меру массы-энергии в общей теории относительности, превосходно (и даже замечательно) согласующуюся с физическими требованиями. Но в настоящее время имеются основания считать (как указывают и работы Тода, Келли и Вудхауса), что в общем случае контортной поверхности  следует не просто проинтегрировать выражение (9.9.15) по 3? [как требует стандартная процедура (4.3.24)], но ввести дополнительный множитель. Напишем
следует не просто проинтегрировать выражение (9.9.15) по 3? [как требует стандартная процедура (4.3.24)], но ввести дополнительный множитель. Напишем

где [в силу формул (9.9.15), (9.9.3) и (3.4.22)]

[ср. с формулой (4.6.38)]. Вместо того чтобы интегрировать 0 по  , мы интегрируем 2-форму
, мы интегрируем 2-форму

где  — комплексная скалярная величина на
— комплексная скалярная величина на  предлагаемое определение которой будет дано ниже. Если поверхность неконтортна, то следует положить
предлагаемое определение которой будет дано ниже. Если поверхность неконтортна, то следует положить  и это будет справедливо и для контортных сечений гиперповерхности
и это будет справедливо и для контортных сечений гиперповерхности  Получим [обозначив через
Получим [обозначив через  -форму элемента поверхности, как в формуле (4.14.65)]
-форму элемента поверхности, как в формуле (4.14.65)]

в соответствии с формулами (4.14.53), (4.14.66), где  определяется формулой (9.9.14).
определяется формулой (9.9.14).
Напомним теперь о дуальности твистора  и твистора момента-импульса
и твистора момента-импульса  обсуждавшейся в гл. 6, § 5.
обсуждавшейся в гл. 6, § 5.
Приравнивая (6.5.53) и (6.5.51), применительно к рассматриваемой ситуации будем иметь

откуда (в силу нелинейности)

Здесь  — произвольные элементы пространства
— произвольные элементы пространства  соответствующие решениям
соответствующие решениям  уравнения (9.9.13). Соотношение (9.9.19) определяет величину
уравнения (9.9.13). Соотношение (9.9.19) определяет величину  как «твистор момента-импульса», описывающий суммарный источник гравитационного поля, окруженный поверхностью
как «твистор момента-импульса», описывающий суммарный источник гравитационного поля, окруженный поверхностью  .
.
Заметим, что в соответствии с определением (9.9.19) величина  имеет десять компонент (поскольку пространство
имеет десять компонент (поскольку пространство  комплексно-десятимерно). Но чтобы данная ее физическая интерпретация была полностью удовлетворительна, необходимо, как можно полагать, дополнительно наложить некоторое аналогичное условию (6.3.12) условие эрмитовости типа
комплексно-десятимерно). Но чтобы данная ее физическая интерпретация была полностью удовлетворительна, необходимо, как можно полагать, дополнительно наложить некоторое аналогичное условию (6.3.12) условие эрмитовости типа

сводящее десять комплексных компонент к десяти действительным. Однако точная форма такого условия пока не найдена. Чтобы хотя бы сказать, что должно означать условие типа (9.9.20), необходимы два момента. Во-первых, нужно ввести операцию (инволюции) твисторного комплексного сопряжения для  переводящего это пространство в дуальное пространство:
переводящего это пространство в дуальное пространство:

так чтобы получающееся скалярное произведение  имело сигнатуру
имело сигнатуру  Во-вторых, очевидно, необходим (простой? твисторно-действительный?) элемент
Во-вторых, очевидно, необходим (простой? твисторно-действительный?) элемент

который должен входить в условие (9.9.20).
Возможный путь реализации этого таков: ввести локальное твисторное поле  на 9 (см. гл. 6, § 9) для каждого
на 9 (см. гл. 6, § 9) для каждого  положив
положив

причем вместе с (9.9.13) эти соотношения являются тангенциальными частями на М уравнения (6.1.9). Нетрудно убедиться, что формулы преобразования (6.9.6) локальных твисторов при конформном изменении масштаба выполняются. Однако твистор  вообще говоря, не будет постоянным при локальном твисторном переносе (6.9.10), если не считать случая, когда пространство
вообще говоря, не будет постоянным при локальном твисторном переносе (6.9.10), если не считать случая, когда пространство  конформно-плоское. Построим теперь конформно-инвариантное скалярное поле на
конформно-плоское. Построим теперь конформно-инвариантное скалярное поле на 

поскольку величины  действительны. До тех пор пока величина (9.9.24) постоянна на
действительны. До тех пор пока величина (9.9.24) постоянна на  это будет конформно-инвариантное число, которое нужным образом задает эрмитову твисторную норму
это будет конформно-инвариантное число, которое нужным образом задает эрмитову твисторную норму  для
для  Однако в общем случае выражение
Однако в общем случае выражение  не постоянно на
не постоянно на  причем условием постоянства для всех
причем условием постоянства для всех  является неконтортность поверхности 9 (см., например, работу [155]). В случае контортной поверхности
является неконтортность поверхности 9 (см., например, работу [155]). В случае контортной поверхности  можно пытаться преодолеть возникающую трудность усреднением
можно пытаться преодолеть возникающую трудность усреднением

или, возможно, иначе:

где  — гауссова кривизна поверхности
— гауссова кривизна поверхности  [см. формулы (4.14.20), (4.14.21),
[см. формулы (4.14.20), (4.14.21),  или же использовать некоторое выражение, содержащее
или же использовать некоторое выражение, содержащее  Это дает два (или более) способа введения произведения, осуществляющего отображение (9.9.21). Но ни один из них не обеспечивает конформной инвариантности.
Это дает два (или более) способа введения произведения, осуществляющего отображение (9.9.21). Но ни один из них не обеспечивает конформной инвариантности.
С соотношением (9.9.22) возникают на первый взгляд аналогичные проблемы. Например, можно было бы ввести скалярное поле на  :
:

но оно опять в общем случае непостоянно (даже для неконтортной поверхности  Если усреднить это выражение по
Если усреднить это выражение по  , то соображения, связанные с конформной инвариантностью, перестают быть существенными. Однако получающаяся величина
, то соображения, связанные с конформной инвариантностью, перестают быть существенными. Однако получающаяся величина  в общем случае не оказывается простой [в смысле предложений (3.5.30) и (3.5.35)]. Такой твистор
в общем случае не оказывается простой [в смысле предложений (3.5.30) и (3.5.35)]. Такой твистор  не
не
удовлетворяющий указанному критерию простоты, все же можно было бы использовать в условии (9.9.20); более того, есть веские основания полагать, что в общем случае необходимо использовать такой твистор  «деситтеровского» типа. Пока не известно, действительно ли соотношение (9.9.20) выполняется с таким твистором
«деситтеровского» типа. Пока не известно, действительно ли соотношение (9.9.20) выполняется с таким твистором  возможно дополнительно модифицированным некоторым членом (или членами) с
возможно дополнительно модифицированным некоторым членом (или членами) с  .
.
Разрешение этих трудностей требует дальнейших исследований. Как мы увидим вскоре, ситуация на  намного приятней. Более того, как было показано Шоу [310], в предельном случае, когда стремится к пространственноподобной бесконечности
намного приятней. Более того, как было показано Шоу [310], в предельном случае, когда стремится к пространственноподобной бесконечности  приемлемое определение
приемлемое определение  и соответствующей нормы существует и условие (9.9.20) выполняется, если только кривизна удовлетворяет подходящим условиям убывания. В этом случае достигается полное согласие с определением массы Арновитта — Дезера — Мизнера [4] и определением Аштекара — Хансена [7] момента импульса. Прежде чем обратиться к случаю
и соответствующей нормы существует и условие (9.9.20) выполняется, если только кривизна удовлетворяет подходящим условиям убывания. В этом случае достигается полное согласие с определением массы Арновитта — Дезера — Мизнера [4] и определением Аштекара — Хансена [7] момента импульса. Прежде чем обратиться к случаю  следует сделать некоторые замечания, касающиеся общего случая произвольной поверхности Заметим сначала, что в пространстве М справедлива формула
следует сделать некоторые замечания, касающиеся общего случая произвольной поверхности Заметим сначала, что в пространстве М справедлива формула

для квадрата массы покоя  которая без труда получается из (6.3.11), причем здесь требуется только операция твисторного комплексного сопряжения, но не нужно введение
которая без труда получается из (6.3.11), причем здесь требуется только операция твисторного комплексного сопряжения, но не нужно введение  Таким образом, можно воспользоваться соотношениями (9.9.25) или (9.9.26) и предложить два возможных альтернативных определения «квазилокальной массы покоя» в общей теории относительности (т. е. массы покоя, заключенной внутри конечной замкнутой двумерной поверхности). Тодом [337] была также предложена модификация формулы (9.9.28), в которой используется определитель твистора
Таким образом, можно воспользоваться соотношениями (9.9.25) или (9.9.26) и предложить два возможных альтернативных определения «квазилокальной массы покоя» в общей теории относительности (т. е. массы покоя, заключенной внутри конечной замкнутой двумерной поверхности). Тодом [337] была также предложена модификация формулы (9.9.28), в которой используется определитель твистора  вместо нормы.
вместо нормы.
Отметим также указанное Тодом [337] соотношение, которое справедливо при  а именно выражение (9.9.19), переписанное в замечательно простой форме
а именно выражение (9.9.19), переписанное в замечательно простой форме

[При доказательстве используются соотношения (9.9.13), (9.9.23), (4.12.32д), (4.12.35) и формула интегрирования по частям (4.14.71); доказательство оказывается простым, если начать с формулы (9.9.29).] Имеется интригующее сходство между формулами (9.9.29) и (9.9.27), указывающее на то, что
соотношение типа (9.9.20) можно было бы получить, если найти подходящие определения. Выражение (9.9.29) окажется для нас важным в конце этого параграфа. Если  то формула (9.9.29) модифицируется путем замены каждого множителя
то формула (9.9.29) модифицируется путем замены каждого множителя  величиной
величиной  а каждого множителя
а каждого множителя  величиной
величиной  и добавления члена
и добавления члена  где
где 
Чтобы обосновать введение величины  в формулу (9.9.19) и ее определение, к которому мы перейдем далее, полезно привести некоторые результаты, полученные Тодом [337] в различных случаях неконтортных поверхностей
в формулу (9.9.19) и ее определение, к которому мы перейдем далее, полезно привести некоторые результаты, полученные Тодом [337] в различных случаях неконтортных поверхностей  . Будем рассматривать квазилокальную массу покоя
. Будем рассматривать квазилокальную массу покоя  определяемую формулой (9.9.28); она однозначна, поскольку во всех случаях неконтортности норма (9.9.24) постоянна на
определяемую формулой (9.9.28); она однозначна, поскольку во всех случаях неконтортности норма (9.9.24) постоянна на 
Для пространства-времени Шварцшильда получен замечательный результат: в случае поверхности  , лежащей на любой гиперповерхности
, лежащей на любой гиперповерхности  сферической симметрии (определяемой в обычных шварцшильдовых координатах некоторым соотношением, фиксирующим функциональную зависимость
сферической симметрии (определяемой в обычных шварцшильдовых координатах некоторым соотношением, фиксирующим функциональную зависимость  и
и  , масса
, масса  оказывается в точности шварцшильдовой массой, если
оказывается в точности шварцшильдовой массой, если  охватывает источник (и только один раз), и
охватывает источник (и только один раз), и  если 9? не охватывает источник. (Сама поверхность 9 не обладает сферической симметрией гиперповерхности
если 9? не охватывает источник. (Сама поверхность 9 не обладает сферической симметрией гиперповерхности  и может произвольно располагаться внутри
и может произвольно располагаться внутри  Такая поверхность неконтортна).
Такая поверхность неконтортна).
Похожие результаты получаются в произвольном вакуумном пространстве-времени, содержащем конформно-плоскую гиперповерхность  симметричную во времени, причем
симметричную во времени, причем  может содержать «источники» либо в виде заполненных материей областей, либо в виде «кротовых нор» [207] Снова, при условии
может содержать «источники» либо в виде заполненных материей областей, либо в виде «кротовых нор» [207] Снова, при условии  масса
масса  зависит только от того, охватывает ли поверхность
зависит только от того, охватывает ли поверхность  источники, независимо от ее конкретного положения в
источники, независимо от ее конкретного положения в  Если обозначить через
Если обозначить через  значение
значение  получаемое, когда 97 охватывает только
получаемое, когда 97 охватывает только  источник (один раз), и через
источник (один раз), и через  значение, получаемое, когда
значение, получаемое, когда  охватывает
охватывает  источники (по одному разу каждый), то мы получим физически приемлемый результат
источники (по одному разу каждый), то мы получим физически приемлемый результат

Это указывает на то, что вклад гравитационной потенциальной энергии уже содержится в определениях (9.9.19), (9.9.28) [причем вклад гравитационного излучения равен нулю в  Действительно, в пределе слабого поля разность
Действительно, в пределе слабого поля разность 
оказывается в точности равной ньютоновскому  -члену потенциальной энергии.
-члену потенциальной энергии.
[Эти результаты были получены с помощью введенного Тодом понятия твистора 3-мерной поверхности, которое вводится применительно к гиперповерхности  с нормалью
с нормалью  обладающей теми свойствами, что 1) магнитная часть
обладающей теми свойствами, что 1) магнитная часть

тензора Вейля равна нулю на  и 2) магнитная часть
и 2) магнитная часть

нормальной производной тензора Вейля также равна нулю на  (Второе условие в вакууме можно сформулировать как обращение в нуль ротора электрической части тензора Саьса на
(Второе условие в вакууме можно сформулировать как обращение в нуль ротора электрической части тензора Саьса на  , который определен подобно тензору
, который определен подобно тензору  но без дуализации.) Такая гиперповерхность «неконтортна» в том смысле, что может быть погружена в конформно-плоское пространство-время с той же внутренней метрикой и внешней кривизной для
но без дуализации.) Такая гиперповерхность «неконтортна» в том смысле, что может быть погружена в конформно-плоское пространство-время с той же внутренней метрикой и внешней кривизной для  и любая 2-поверхность
и любая 2-поверхность  , лежащая в
, лежащая в  тоже будет неконтортна. Свойством такой гиперповерхности
тоже будет неконтортна. Свойством такой гиперповерхности  является возможность задания на ней твисторов 3-мерной поверхности, которые являются решением частей уравнения (9.9.12), содержащих производные, которые действуют лишь внутри
является возможность задания на ней твисторов 3-мерной поверхности, которые являются решением частей уравнения (9.9.12), содержащих производные, которые действуют лишь внутри  а именно
а именно

(Фактически они являются также твисторами гиперповерхности для  см. текст, относящийся к соотношению (7.4.52), которое является в определенном смысле дуальным приведенному уравнению, так что величины
см. текст, относящийся к соотношению (7.4.52), которое является в определенном смысле дуальным приведенному уравнению, так что величины  постоянны вдоль
постоянны вдоль  -кривых. Здесь
-кривых. Здесь 
Выражения для квазилокальной массы можно также применять, если поверхность 9 лежит внутри областей, заполненных материей. В частности, в случае сферически-симметричного (электровакуумного) пространства-времени Райсснера — Нордстрема
величина  теперь определяется не только тем, охватывается ли поверхностью источник массы, но и вкладом в массу энергии электромагнитного поля. Модели Фридмана — Робертсона — Уокера (см. § 5), будучи конформно-плоскими, относительно легко исследовать. В частности,
теперь определяется не только тем, охватывается ли поверхностью источник массы, но и вкладом в массу энергии электромагнитного поля. Модели Фридмана — Робертсона — Уокера (см. § 5), будучи конформно-плоскими, относительно легко исследовать. В частности,  показал, что если поверхность 91 обладает вращательной симметрией, то величина
показал, что если поверхность 91 обладает вращательной симметрией, то величина  равна массе, которая была бы окружена сферой равной площади в евклидовом пространстве, заполненном жидкостью той же плотности, что и в исследуемой модели. Таким образом, в частности, в случае пространственно-замкнутой модели величина
равна массе, которая была бы окружена сферой равной площади в евклидовом пространстве, заполненном жидкостью той же плотности, что и в исследуемой модели. Таким образом, в частности, в случае пространственно-замкнутой модели величина  возрастает по мере того как сфера расширяется, достигает максимального значения для «экваториальной» сферы и затем уменьшается до нуля по мере того как сфера сжимается в точку. Это показывает, что полная масса в данной модели равна нулю в согласии с выводами других подходов [207]. Отрицательными вкладами потенциальной энергии в точности компенсируется вклад материи. Более того, весьма общим свойством нашей конструкции является то, что полная масса любой модели замкнутой вселенной равна нулю. Это частный случай еще более общего свойства масса по одну сторону любой конечной поверхности
возрастает по мере того как сфера расширяется, достигает максимального значения для «экваториальной» сферы и затем уменьшается до нуля по мере того как сфера сжимается в точку. Это показывает, что полная масса в данной модели равна нулю в согласии с выводами других подходов [207]. Отрицательными вкладами потенциальной энергии в точности компенсируется вклад материи. Более того, весьма общим свойством нашей конструкции является то, что полная масса любой модели замкнутой вселенной равна нулю. Это частный случай еще более общего свойства масса по одну сторону любой конечной поверхности  должна быть равна массе по другую сторону, что непосредственно видно из симметрии выражения (9.9.19).
должна быть равна массе по другую сторону, что непосредственно видно из симметрии выражения (9.9.19).
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие редактора перевода
- Предисловие
- Краткое содержание тома 1
- § 5 (гл. 1). Спинорные объекты и спиновая структура
- § 2 (гл. 2). Формализм абстрактных индексов в тензорной алгебре
- § 3 (гл. 3). Операции симметрии
- Переход от спинорной к тензорной форме записи, и наоборот; преобразование дуальности
- Некоторые свойства тензоров и спиноров в точке
- Активные лоренцевы и спиновые преобразования
- Ковариантная производная
- Спиновые коэффициенты
- Спинорная форма кривизны
- Тождества для спинора Риччи
- Спинорные тождества Бианки
- Компоненты спинорной кривизны
- Модифицированный формализм спиновых коэффициентов
- Уравнения для модифицированных спиновых коэффициентов
- Геометрия пространственноподобных 2-поверхностей
- На изотропной гиперповерхности
- § 15 (гл. 4). Функции на метрической сфере
- Производные заряженных полей
- Поля Янга — Миллса
- Конформные изменения масштаба
- Безмассовые свободные поля
- Другие полевые уравнения
- Данные на изотропной гиперповерхности
- 6. Твисторы
- § 1. Твисторное уравнение и пространство его решений
- Твисторное уравнение
- Пространство твисторов
- Дуальные твисторы
- Твисторы высшей валентности
- Конформная инвариантность спиральности и скалярного произведения
- § 2. Некоторые геометрические аспекты твисторной алгебры
- Поле флагштоков спинора: конгруэнция Робинсона
- Отношение взаимности твисторов
- Комплексная геометрия
- Представление точек с помощью простых кососимметричных твисторов
- § 3. Твисторы и момент импульса
- Момент импульса произвольной системы
- Представление твистора с помощью одноиндексных твисторов
- § 4. Симметричные твисторы и безмассовые поля
- Общий случай, потенциалы
- Повышение спина
- Другие виды потенциалов; связь с оператором
- § 5. Конформные векторы Киллинга; сохраняющиеся величины и точные последовательности
- Спиноры: Законы сохранения
- Твисторное описание
- Связь с интегралами от источников в линейной гравитации
- Точные последовательности
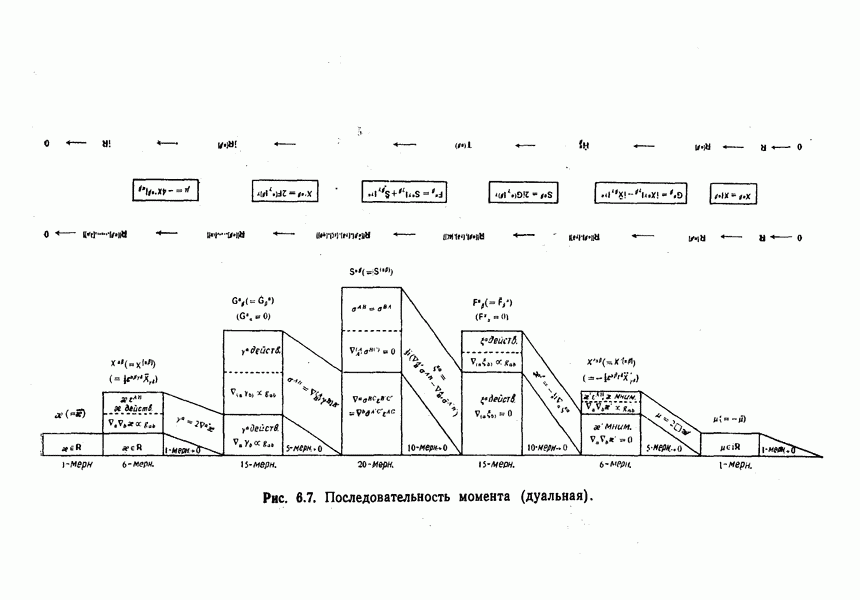
- Последовательности моментов
- Интегралы в линейной теории гравитации
- Спиноры: Десять интегралов, равных нулю
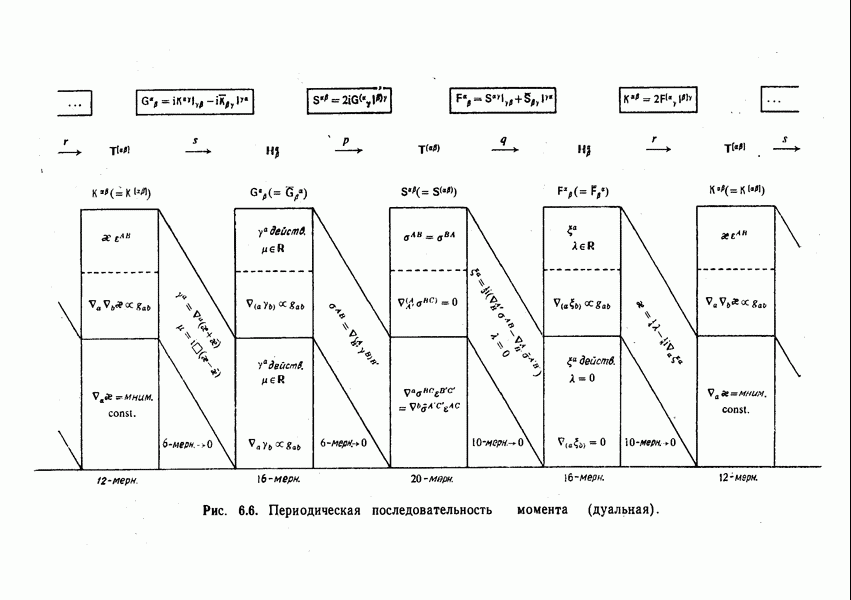
- Роль дуальности в последовательностях момента
- § 6. Производные Ли спиноров
- Связь с теорией твисторов
- § 7. Интегралы движения частиц; конформно-инвариантные операторы
- Спиноры Киллинга для вакуумных решений типа (22)
- Свойства решения Керра
- Конформно-инвариантные первые производные
- Твисторные решения различных уравнений
- Повторные операции; разрешения уравнений
- § 8. Кривизна и конформные преобразования
- Конформные свойства величин
- Конформные отображения плоских пространств
- Конформно-инвариантное волновое уравнение и оператор
- Конформно-инвариантный тензор Баха
- § 9. Локальные твисторы
- Условие совместности для твисторного уравнения
- Определение локального твистора
- Перенос локального твистора
- Кривизна в пространстве локальных твисторов
- Нулевая кривизна Вейля как свойство конформно-плоского пространства
- § 10. Безмассовые поля и когомологии твисторов
- Спиноры: Непроективное представление
- Квантование твисторов
- Спиральность
- Интегралы для спиральности противоположного знака
- Повышение и понижение спиральности
- Массивные твисторные волновые функции
- Геометрия контурных интегралов
- Положительно-частотные поля
- Введение когомологий
- Понятие 1-функции
- r-Функции общего вида
- Нелинейные 1-функции
- Конструкция Уорда
- Пример конструкции Уорда
- 7. Изотропные конгруэнции
- § 1. Изотропные конгруэнции и спиновые коэффициенты
- Интерпретация величин; изопараметричность лучей
- Ортогональность гиперповерхности; изотропные гиперповерхности
- Изопараметричность в теории твисторов
- § 2. Изотропные конгруэнции и кривизна пространства-времени
- Изопараметрические лучи; уравнения Сакса
- Неизопараметрические лучи
- Описание в трехмерном пространстве Минковского
- § 3. Бессдвиговые конгруэнции лучей
- Обобщенная теорема Голдберга — Сакса
- Координаты Керра
- § 4. БСК, твисторы и геометрия лучей
- Твисторная форма теоремы Керра
- Линейные и квадратичные функции твисторов, момент импульса
- Связь с твисторными функциями безмассовых полей
- Пространства и инвариантная контактная структура
- Комплексная структура и КД-структура
- Твисторы гиперповерхности
- Спиноры: Роль аналитичности
- 8. Классификация тензоров кривизны
- Спиноры: Схема специализации
- § 2. Представление спинора Вейля на сфере S+
- ГГИН в пространстве-времени высокой симметрии
- «Картина» тензора Вейля на S+
- § 3. Собственные спиноры спинора Вейля
- Соотношение между собственными значениями и двойными отношениями
- Частные случаи
- § 4. Собственные бивекторы тензора Вейля и его классификация по типам Петрова
- Компоненты тензора Вейля в бивекторном базисе
- Канонические формы Петрова
- § 5. Геометрия и симметрия вейлевской кривизны
- Дисфеноид для типа {1111}
- Симметрии в частных случаях типа {1111}
- Тип (211)
- О размерностях групп симметрий
- Классификация тензора Максвелла
- § 6. Коварианты кривизны
- Инварианты полной кривизны
- Система полей Эйнштейна — Максвелла
- § 7. Классификационная схема для спиноров с любым числом индексов
- Приводимость локуса
- Комплексные (р, q) — кривые на CS+
- Процедура классификации спинора
- Структура кривой w (ее кратные точки)
- Кратные точки кривой w
- Локус Rw на S+
- Знак спинора, черный и белый цвета сферы S+
- § 8. Классификация спинора Риччи
- Тип спинора по Плебаньскому
- Физические тензоры энергии-импульса
- 9. Конформная бесконечность
- § 1. Бесконечность в случае пространства Минковского
- ГНП и ГНБ
- § 2. Компактифицированное пространство Минковского
- Описание в пространстве Р5
- O(2,4) и конформная группа
- § 3. Комплексифицированное компактифицированное пространство Минковского и твисторная геометрия
- Соответствие Клейна
- Твисторное отношение дуальности
- Действительная структура
- Различные типы комплексных точек в СМ*
- § 4. Четырехзначность твисторов и индекс Гржина
- Две спиновые структуры на М*
- Поведение спинора
- Твисторные спин-расслоения над М*
- Конформные плотности на М*; индекс Гржина
- Теорема Гржина
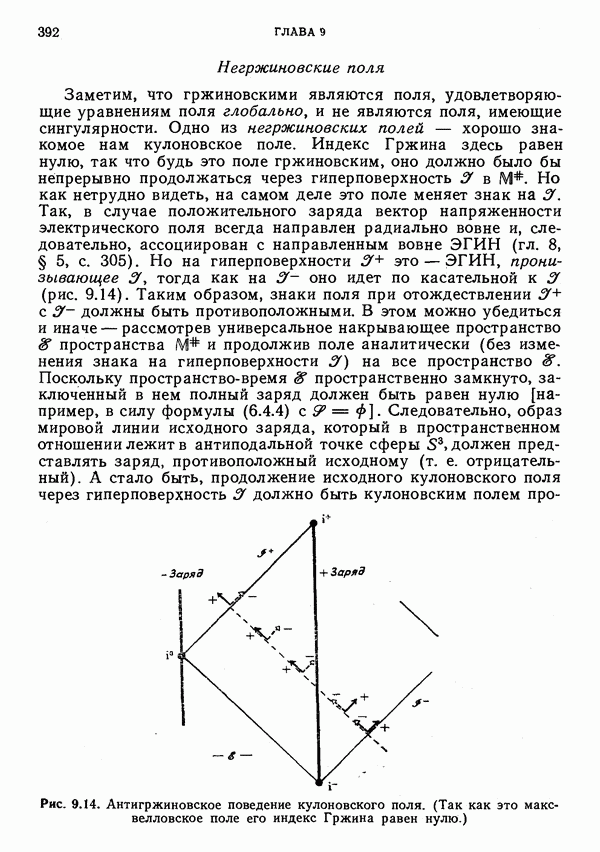
- Негржиновские поля
- § 5. Космологические модели и соответствующие твисторы
- Космологические горизонты
- Описание в пространстве Р5
- Деситтеровская и антидеситтеровская модели; твисторы …
- Функции для конформно-плоского пространства-времени
- Модели ФРУ, соответствующие твисторы начальной и конечной сингулярностей
- Явные выражения для функции I
- § 6. Асимптотически простое пространство-время
- Асимптотически-простое пространство-время
- Обращение в нуль тензора Вейля на границе J
- § 7. Последовательное вырождение
- Параллельно переносимые спиновые системы отсчета
- Сравнение аффинных параметров
- Сравнение спиновых систем отсчета
- Доказательство свойства последовательного вырождения
- Поля излучений
- § 8. Группа БМС и структура гиперповерхности J+
- Группа Бонди — Метцнера — Сакса
- Связь между сильной конформной геометрией и твистором
- Интерпретация изотропных углов
- Структура группы БМС
- Сдвиговая структура гиперповерхности J+
- H-пространство и асимптотическое твисторное пространство
- Отношение группы БМС к импульсу и моменту импульса
- Асимптотические разложения в теории Эйнштейна — Максвелла
- § 9. Энергия-импульс и момент импульса
- Усложнения в случае искривленного пространства-времени
- Твисторы двумерной поверхности
- Контортные двумерные поверхности
- Квазилокальный твистор момента импульса
- Определение множителя
- Асимптотическое спиновое пространство
- Свойства нормы на J+
- Эрмитовость твистора на 4-импульс Бонди — Сакса
- Альтернативные выражения для массы Бонди — Сакса
- Пространство Минковского как пространство «начал»
- Момент импульса на J+
- § 10. Потери массы Бонди — Сакса и положительность энергии
- Нелокальность энергии гравитационных волн
- НП-константы
- Подход Виттена в доказательстве положительности массы
- Связь с 4-импульсом Бонди — Сакса
- Спинор в подходе Людвигсена — Виккерса
- 3-форма Спарлинга
- Приложение. Спиноры в n измерениях
- 2-валентные e-спиноры
- Переход от тензоров к спинорам
- Геометрия фундаментальных спиноров
- Условие фундаментальности; структура спинового пространства
- Индуктивное построение спинового пространства
- Некоторые физически интересные случаи; триальность
- Спинорные поля; твисторы в n измерениях
- Послесловие авторов
- Литература