| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 8. Группа БМС и структура гиперповерхности J+
Пространство-время Минковского М и рассмотренные в § 5 космологические модели допускают группы изометрий, представляющие значительный практический интерес. Правда, группа изометрий на произвольном пространстве-времени  - это просто тождественное преобразование, так что ее наличие не дает никакой существенной информации. Но группы симметрий имеют большое значение в физике; в частности, группа Пуанкаре, описывающая изометрии пространства М, играет важную роль в стандартных определениях энергии-импульса и момента импульса. Уже одно это может служить основанием для поисков обобщения концепции группы изометрии, пригодного в искривленных пространствах-временах с теми или иными отклонениями от регулярности.
- это просто тождественное преобразование, так что ее наличие не дает никакой существенной информации. Но группы симметрий имеют большое значение в физике; в частности, группа Пуанкаре, описывающая изометрии пространства М, играет важную роль в стандартных определениях энергии-импульса и момента импульса. Уже одно это может служить основанием для поисков обобщения концепции группы изометрии, пригодного в искривленных пространствах-временах с теми или иными отклонениями от регулярности.
В случае произвольного пространства-времени  вместо группы Пуанкаре по историческим причинам часто рассматривают группу (или псевдогруппу), называемую «общей координатной группой» (или, что эквивалентно, «группой диффеоморфизмов»). Однако в данном контексте она практически бесполезна, ибо слишком «велика» и сохраняет лишь дифференцируемую структуру пространства
вместо группы Пуанкаре по историческим причинам часто рассматривают группу (или псевдогруппу), называемую «общей координатной группой» (или, что эквивалентно, «группой диффеоморфизмов»). Однако в данном контексте она практически бесполезна, ибо слишком «велика» и сохраняет лишь дифференцируемую структуру пространства  а не те или иные важные физические свойства этого пространства. Значительно больший интерес представляет концепция группы асимптотической симметрии. Она применима в любом пространстве-времени
а не те или иные важные физические свойства этого пространства. Значительно больший интерес представляет концепция группы асимптотической симметрии. Она применима в любом пространстве-времени  которое на бесконечности соответствующим образом стремится либо к пространству-времени Минковского М, либо к подходящей космологической модели Фридмана — Робертсона — Уокера.
которое на бесконечности соответствующим образом стремится либо к пространству-времени Минковского М, либо к подходящей космологической модели Фридмана — Робертсона — Уокера.
Суть этой концепции заключается в том, что, присоединив к  подходящую конформную границу
подходящую конформную границу  или
или  либо всю границу
либо всю границу  мы можем получить такого рода асимптотические симметрии в виде конформных движений границы, поскольку наличие нужной нам группы симметрий у границы более вероятно, чем у самого пространства
мы можем получить такого рода асимптотические симметрии в виде конформных движений границы, поскольку наличие нужной нам группы симметрий у границы более вероятно, чем у самого пространства  . (Любая изометрия пространства
. (Любая изометрия пространства  проявляется, очевидно, как конформное движение границы, но конформные движения границы не обязательно должно продолжаться в
проявляется, очевидно, как конформное движение границы, но конформные движения границы не обязательно должно продолжаться в  каким-либо имеющим определенный смысл образом.)
каким-либо имеющим определенный смысл образом.)
Параметры Бонди
Мы будем рассматривать лишь подходящие нам асимптоти-чески-плоские пространства  Возьмем пространство
Возьмем пространство  с 3-асимптотической простотой будущего (см. § 6) и с изотропной гиперповерхностью
с 3-асимптотической простотой будущего (см. § 6) и с изотропной гиперповерхностью  и пусть на нем выполняется сильное асимптотическое эйнштейновское условие [формула (9.6.21) вместе со слабым равенством
и пусть на нем выполняется сильное асимптотическое эйнштейновское условие [формула (9.6.21) вместе со слабым равенством  а также следующее условие [103]: образующие гиперповерхности
а также следующее условие [103]: образующие гиперповерхности  имеют бесконечную протяженность. [Это дополнительное условие в данной главе уже упоминалось после определения
имеют бесконечную протяженность. [Это дополнительное условие в данной главе уже упоминалось после определения  Дадим следующие определения.
Дадим следующие определения.
Определение
Образующая у гиперповерхности  называется бесконечно протяженной, если параметр Бонди на у принимает на у все значения в интервале
называется бесконечно протяженной, если параметр Бонди на у принимает на у все значения в интервале 
Определение
Увеличивающийся в направлении будущего действительный параметр ”и” на образующей у гиперповерхности  называется параметром Бонди, если в случае вектора
называется параметром Бонди, если в случае вектора  , касательного к образующим гиперповерхности
, касательного к образующим гиперповерхности  выполняется уравнение
выполняется уравнение

записанное в компактных обозначениях для спиновых коэффициентов (т. 1, гл. 4, § 5, 12).
Параметр и имеет тип  так что величина
так что величина  имеет тип
имеет тип  вследствие чего [с учетом формулы (4.12.15)] уравнение в определении (9.8.2) означает, что
вследствие чего [с учетом формулы (4.12.15)] уравнение в определении (9.8.2) означает, что

Если к тому же потребовать, чтобы параметр и имел конформный вес, равный нулю, то, воспользовавшись обозначениями из
(5.6.33), уравнение из определения (9.8.2) можно будет переписать в виде

Уравнение (9.8.4) явно конформно-инвариантно [формула (5.6.34)], на основании чего можно утверждать, что определение параметра Бонди не связано с конформным множителем  (и, разумеется, с выбором масштаба для вектора
(и, разумеется, с выбором масштаба для вектора  ). Если выбрать такой множитель
). Если выбрать такой множитель  чтобы выполнялось условие
чтобы выполнялось условие  [см. текст после формулы (9.6.31)] и такой масштаб вектора па, чтобы он параллельно переносился вдоль луча 7, то уравнение (9.8.3) можно будет привести к виду
[см. текст после формулы (9.6.31)] и такой масштаб вектора па, чтобы он параллельно переносился вдоль луча 7, то уравнение (9.8.3) можно будет привести к виду

откуда со всей очевидностью следует, что различные параметры Бонди на у связаны друг с другом соотношением

где  — действительные постоянные и
— действительные постоянные и 
Подчеркнем, что при обсуждении определения (9.8.2) мы опустили «шляпки» над величинами, определенными на  Мы будем поступать так и в дальнейшем, поскольку большая часть расчетов будет связана с величинами, определенными на гиперповерхности
Мы будем поступать так и в дальнейшем, поскольку большая часть расчетов будет связана с величинами, определенными на гиперповерхности  Так, в частности (и в противоположность обозначениям двух предыдущих параграфов)
Так, в частности (и в противоположность обозначениям двух предыдущих параграфов)  будет обозначать «нефизическую» регулярную на
будет обозначать «нефизическую» регулярную на  метрику, конформную физической метрике. Если же случится иметь дело с величинами, относящимися к «физическому» пространству-времени, то мы будем отмечать их тильдой сверху. Итак, конформное изменение масштаба теперь будет выглядеть следующим образом;
метрику, конформную физической метрике. Если же случится иметь дело с величинами, относящимися к «физическому» пространству-времени, то мы будем отмечать их тильдой сверху. Итак, конформное изменение масштаба теперь будет выглядеть следующим образом;

Материал этого и следующего параграфов изложен в применении к гиперповерхности  Но совершенно очевидно, что все полученные в них результаты будут применимы и к
Но совершенно очевидно, что все полученные в них результаты будут применимы и к  если, конечно, именно на будут выполняться подходящие асимптотические условия. Что касается физических проблем, то результаты, полученные на
если, конечно, именно на будут выполняться подходящие асимптотические условия. Что касается физических проблем, то результаты, полученные на  как правило, представляют больший интерес, чем результаты на
как правило, представляют больший интерес, чем результаты на  Для этого есть причины двоякого рода. Во-первых, физические соображения вынуждают интересоваться больше запаздывающим излучением, которое связано со структурой гиперповерхности
Для этого есть причины двоякого рода. Во-первых, физические соображения вынуждают интересоваться больше запаздывающим излучением, которое связано со структурой гиперповерхности  чем опережающим связанным со структурой если бы она имелась. Во-вторых, в случае гиперповерхности
чем опережающим связанным со структурой если бы она имелась. Во-вторых, в случае гиперповерхности  гораздо труднее, чем в случае
гораздо труднее, чем в случае  объяснить, почему в «физически приемлемых» ситуациях на ней должны выполняться требуемые асимптотические условия (см., например, работы [355, 283, 96, 97]).
объяснить, почему в «физически приемлемых» ситуациях на ней должны выполняться требуемые асимптотические условия (см., например, работы [355, 283, 96, 97]).
Группа Ньюмена — Унти
Как показано в § 6 [см. (9.6.31)], при подходящем выборе конформного множителя  метрика гиперповерхности
метрика гиперповерхности  (со знаком минус) может быть представлена в виде
(со знаком минус) может быть представлена в виде

 как в формуле (1.2.10)]. Не вызывает сомнений [формула (1.2.17)], что эта (вырожденная) метрика для гиперповерхности
как в формуле (1.2.10)]. Не вызывает сомнений [формула (1.2.17)], что эта (вырожденная) метрика для гиперповерхности  конформно сохраняется при действии активных точечных преобразований
конформно сохраняется при действии активных точечных преобразований

где  и
и  — комплексные постоянные (причем
— комплексные постоянные (причем  ), a F - функция, (достаточно) гладкая на всей гиперповерхности
), a F - функция, (достаточно) гладкая на всей гиперповерхности  (так что можно рассматривать и
(так что можно рассматривать и  кроме того, при каждом значении
кроме того, при каждом значении  величина
величина  должна быть монотонно возрастающей функцией переменной и, отображающей всю область изменения и для каждой образующей
должна быть монотонно возрастающей функцией переменной и, отображающей всю область изменения и для каждой образующей  на себя и имеющей отличную от нуля производную по и (чтобы обратное преобразование тоже было гладким). Первое преобразование (9.8.9) — это конформные движения
на себя и имеющей отличную от нуля производную по и (чтобы обратное преобразование тоже было гладким). Первое преобразование (9.8.9) — это конформные движения  -пространства образующих гиперповерхности
-пространства образующих гиперповерхности  без отражений (конформная структура адекватно определяется любым из сечений этой гиперповерхности), а второе преобразование (9.8.9) в случае, когда первая является тождественным преобразованием
без отражений (конформная структура адекватно определяется любым из сечений этой гиперповерхности), а второе преобразование (9.8.9) в случае, когда первая является тождественным преобразованием  определяет общие гладкие движения образующих в себя без отражений. Группа преобразований (9.8.9) называется группой Ньюмена — Унти
определяет общие гладкие движения образующих в себя без отражений. Группа преобразований (9.8.9) называется группой Ньюмена — Унти  или ограниченной группой
или ограниченной группой  но мы предпочитаем не рассматривать здесь преобразования отражения и будем называть «группой
но мы предпочитаем не рассматривать здесь преобразования отражения и будем называть «группой  тождественно-связанные преобразования (9.8.9) без отражений. Следовательно, группу
тождественно-связанные преобразования (9.8.9) без отражений. Следовательно, группу  можно считать группой движений гиперповерхности
можно считать группой движений гиперповерхности  без отражений, сохраняющей внутреннюю (вырожденную) конформную метрику этой гиперповерхности.
без отражений, сохраняющей внутреннюю (вырожденную) конформную метрику этой гиперповерхности.
Всякий раз, когда пространство М в результате ограниченного движения Пуанкаре отображается на себя, граничная гиперповерхность  пространства М претерпевает преобразования вида (9.8.9). Это происходит из-за того, что конформная структура гиперповерхности
пространства М претерпевает преобразования вида (9.8.9). Это происходит из-за того, что конформная структура гиперповерхности  определяется конформной структурой пространства М, а последняя, конечно, сохраняется при движениях Пуанкаре. Следовательно, ограниченную группу
определяется конформной структурой пространства М, а последняя, конечно, сохраняется при движениях Пуанкаре. Следовательно, ограниченную группу
Пуанкаре можно считать подгруппой  . Однако последняя явно намного «больше» первой, ибо является функционально-пространственной (и, значит, бесконечномерной), а не просто десяти мерной группой.
. Однако последняя явно намного «больше» первой, ибо является функционально-пространственной (и, значит, бесконечномерной), а не просто десяти мерной группой.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие редактора перевода
- Предисловие
- Краткое содержание тома 1
- § 5 (гл. 1). Спинорные объекты и спиновая структура
- § 2 (гл. 2). Формализм абстрактных индексов в тензорной алгебре
- § 3 (гл. 3). Операции симметрии
- Переход от спинорной к тензорной форме записи, и наоборот; преобразование дуальности
- Некоторые свойства тензоров и спиноров в точке
- Активные лоренцевы и спиновые преобразования
- Ковариантная производная
- Спиновые коэффициенты
- Спинорная форма кривизны
- Тождества для спинора Риччи
- Спинорные тождества Бианки
- Компоненты спинорной кривизны
- Модифицированный формализм спиновых коэффициентов
- Уравнения для модифицированных спиновых коэффициентов
- Геометрия пространственноподобных 2-поверхностей
- На изотропной гиперповерхности
- § 15 (гл. 4). Функции на метрической сфере
- Производные заряженных полей
- Поля Янга — Миллса
- Конформные изменения масштаба
- Безмассовые свободные поля
- Другие полевые уравнения
- Данные на изотропной гиперповерхности
- 6. Твисторы
- § 1. Твисторное уравнение и пространство его решений
- Твисторное уравнение
- Пространство твисторов
- Дуальные твисторы
- Твисторы высшей валентности
- Конформная инвариантность спиральности и скалярного произведения
- § 2. Некоторые геометрические аспекты твисторной алгебры
- Поле флагштоков спинора: конгруэнция Робинсона
- Отношение взаимности твисторов
- Комплексная геометрия
- Представление точек с помощью простых кососимметричных твисторов
- § 3. Твисторы и момент импульса
- Момент импульса произвольной системы
- Представление твистора с помощью одноиндексных твисторов
- § 4. Симметричные твисторы и безмассовые поля
- Общий случай, потенциалы
- Повышение спина
- Другие виды потенциалов; связь с оператором
- § 5. Конформные векторы Киллинга; сохраняющиеся величины и точные последовательности
- Спиноры: Законы сохранения
- Твисторное описание
- Связь с интегралами от источников в линейной гравитации
- Точные последовательности
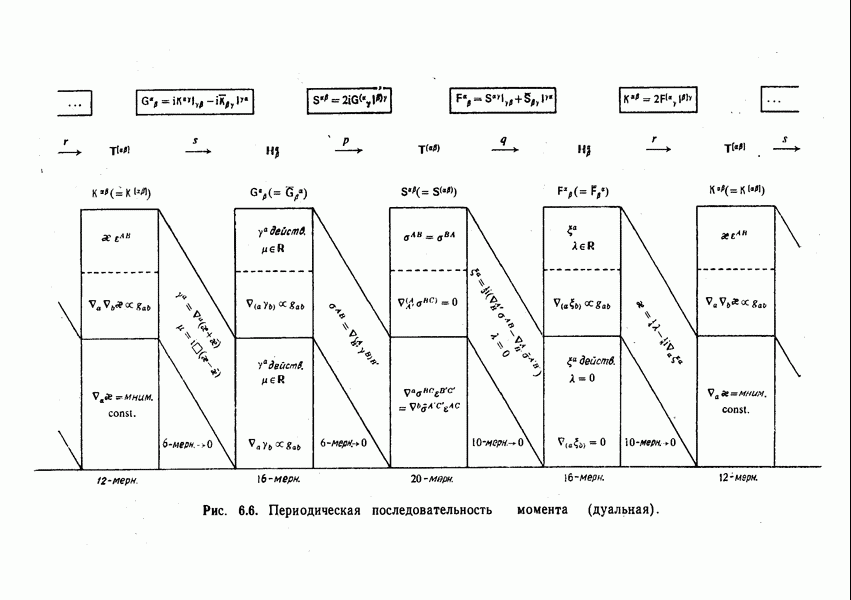
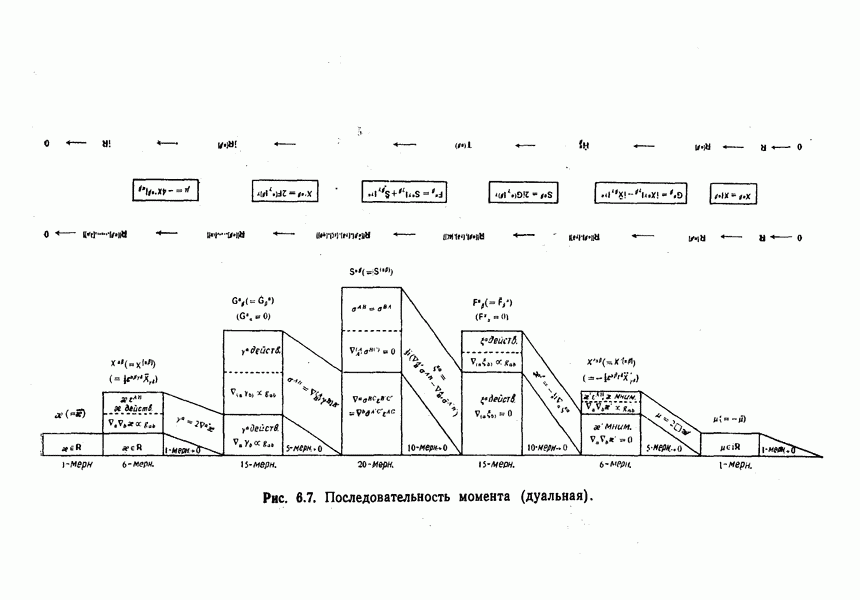
- Последовательности моментов
- Интегралы в линейной теории гравитации
- Спиноры: Десять интегралов, равных нулю
- Роль дуальности в последовательностях момента
- § 6. Производные Ли спиноров
- Связь с теорией твисторов
- § 7. Интегралы движения частиц; конформно-инвариантные операторы
- Спиноры Киллинга для вакуумных решений типа (22)
- Свойства решения Керра
- Конформно-инвариантные первые производные
- Твисторные решения различных уравнений
- Повторные операции; разрешения уравнений
- § 8. Кривизна и конформные преобразования
- Конформные свойства величин
- Конформные отображения плоских пространств
- Конформно-инвариантное волновое уравнение и оператор
- Конформно-инвариантный тензор Баха
- § 9. Локальные твисторы
- Условие совместности для твисторного уравнения
- Определение локального твистора
- Перенос локального твистора
- Кривизна в пространстве локальных твисторов
- Нулевая кривизна Вейля как свойство конформно-плоского пространства
- § 10. Безмассовые поля и когомологии твисторов
- Спиноры: Непроективное представление
- Квантование твисторов
- Спиральность
- Интегралы для спиральности противоположного знака
- Повышение и понижение спиральности
- Массивные твисторные волновые функции
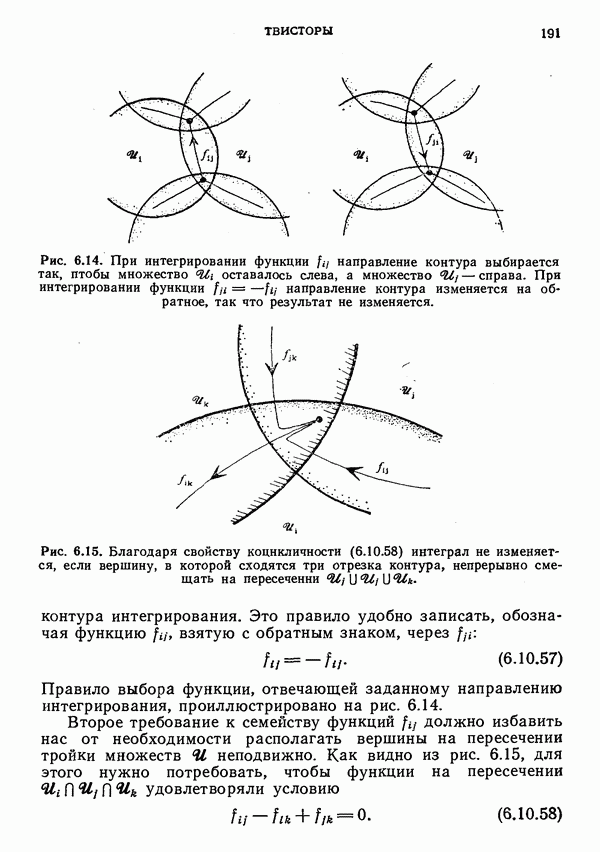
- Геометрия контурных интегралов
- Положительно-частотные поля
- Введение когомологий
- Понятие 1-функции
- r-Функции общего вида
- Нелинейные 1-функции
- Конструкция Уорда
- Пример конструкции Уорда
- 7. Изотропные конгруэнции
- § 1. Изотропные конгруэнции и спиновые коэффициенты
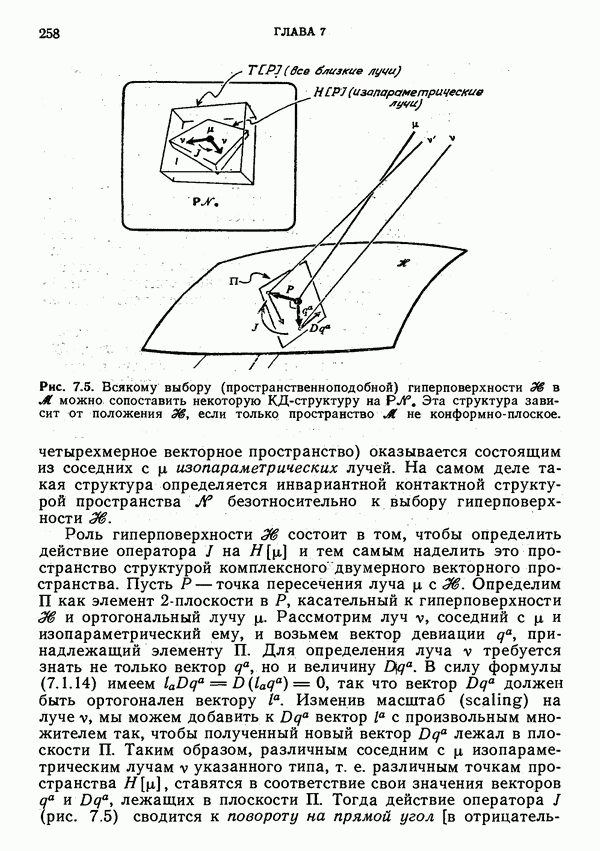
- Интерпретация величин; изопараметричность лучей
- Ортогональность гиперповерхности; изотропные гиперповерхности
- Изопараметричность в теории твисторов
- § 2. Изотропные конгруэнции и кривизна пространства-времени
- Изопараметрические лучи; уравнения Сакса
- Неизопараметрические лучи
- Описание в трехмерном пространстве Минковского
- § 3. Бессдвиговые конгруэнции лучей
- Обобщенная теорема Голдберга — Сакса
- Координаты Керра
- § 4. БСК, твисторы и геометрия лучей
- Твисторная форма теоремы Керра
- Линейные и квадратичные функции твисторов, момент импульса
- Связь с твисторными функциями безмассовых полей
- Пространства и инвариантная контактная структура
- Комплексная структура и КД-структура
- Твисторы гиперповерхности
- Спиноры: Роль аналитичности
- 8. Классификация тензоров кривизны
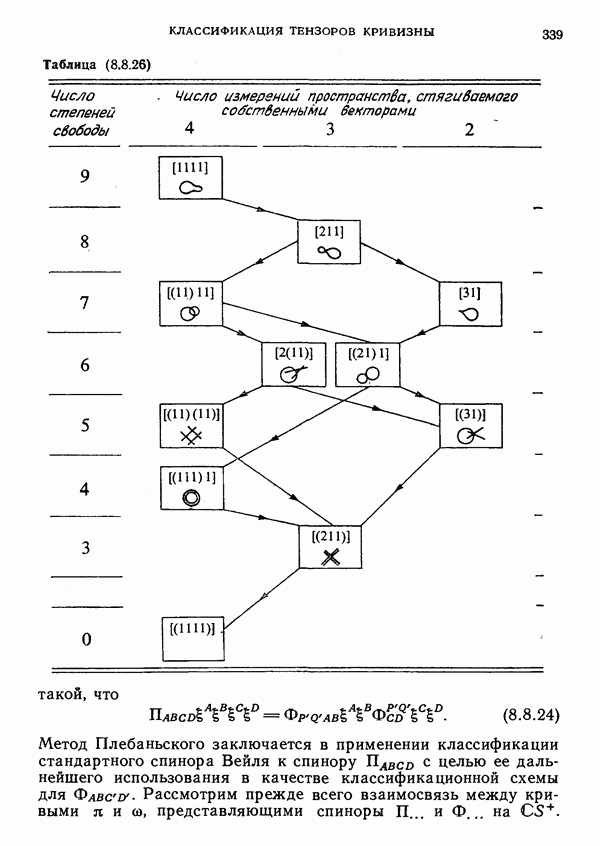
- Спиноры: Схема специализации
- § 2. Представление спинора Вейля на сфере S+
- ГГИН в пространстве-времени высокой симметрии
- «Картина» тензора Вейля на S+
- § 3. Собственные спиноры спинора Вейля
- Соотношение между собственными значениями и двойными отношениями
- Частные случаи
- § 4. Собственные бивекторы тензора Вейля и его классификация по типам Петрова
- Компоненты тензора Вейля в бивекторном базисе
- Канонические формы Петрова
- § 5. Геометрия и симметрия вейлевской кривизны
- Дисфеноид для типа {1111}
- Симметрии в частных случаях типа {1111}
- Тип (211)
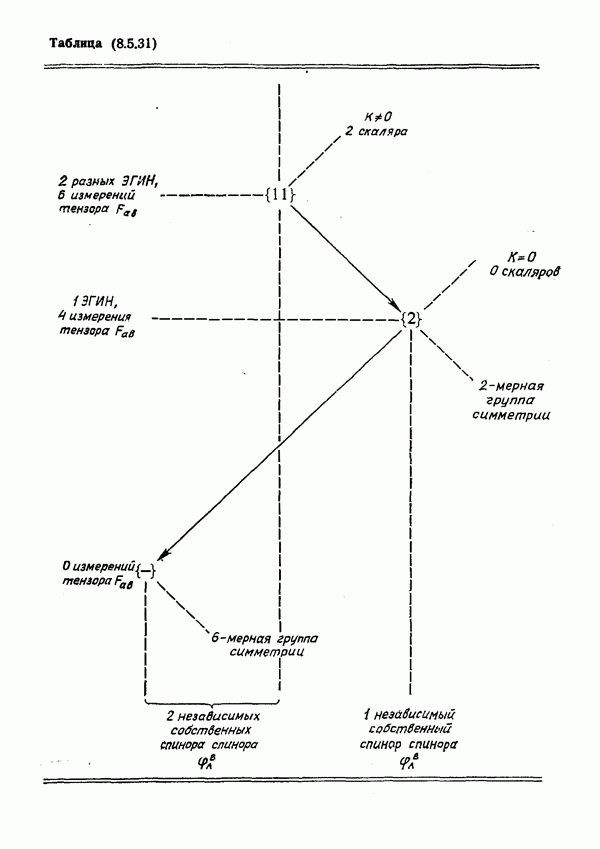
- О размерностях групп симметрий
- Классификация тензора Максвелла
- § 6. Коварианты кривизны
- Инварианты полной кривизны
- Система полей Эйнштейна — Максвелла
- § 7. Классификационная схема для спиноров с любым числом индексов
- Приводимость локуса
- Комплексные (р, q) — кривые на CS+
- Процедура классификации спинора
- Структура кривой w (ее кратные точки)
- Кратные точки кривой w
- Локус Rw на S+
- Знак спинора, черный и белый цвета сферы S+
- § 8. Классификация спинора Риччи
- Тип спинора по Плебаньскому
- Физические тензоры энергии-импульса
- 9. Конформная бесконечность
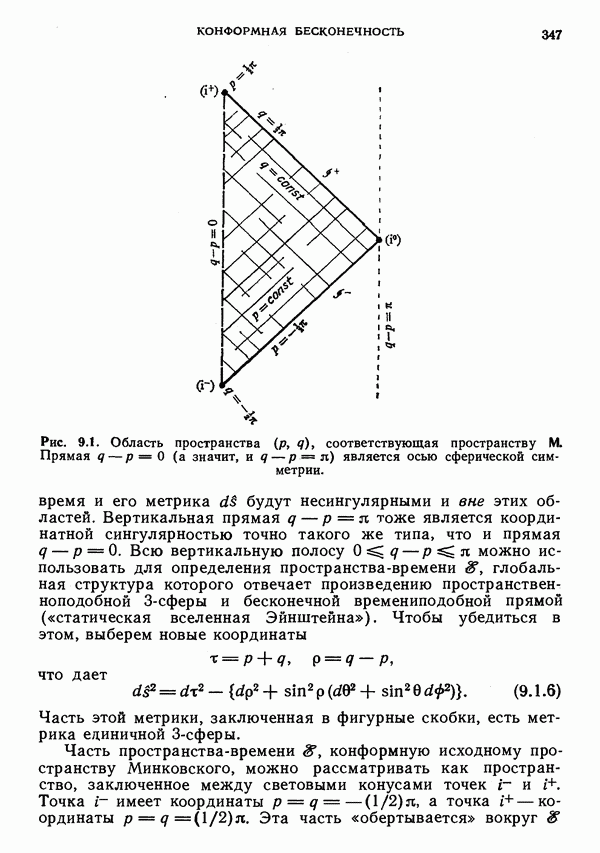
- § 1. Бесконечность в случае пространства Минковского
- ГНП и ГНБ
- § 2. Компактифицированное пространство Минковского
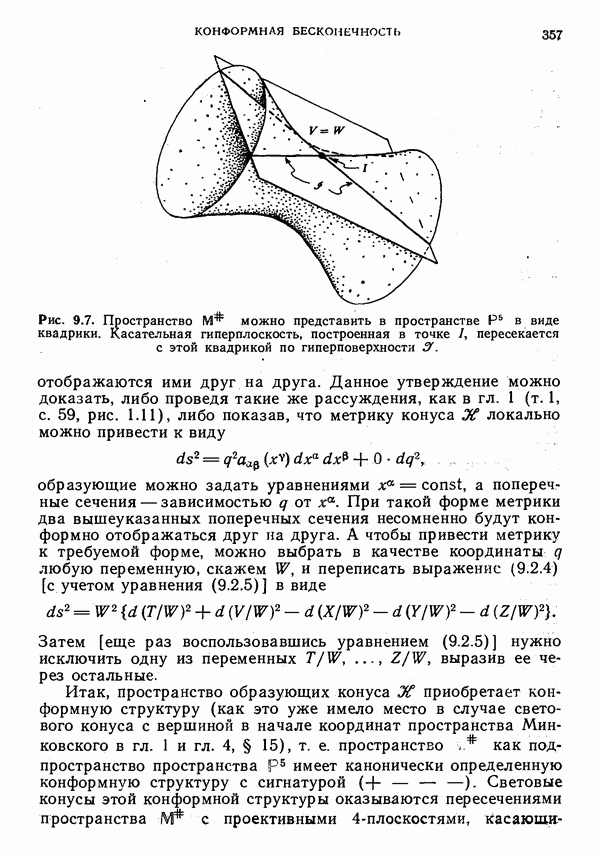
- Описание в пространстве Р5
- O(2,4) и конформная группа
- § 3. Комплексифицированное компактифицированное пространство Минковского и твисторная геометрия
- Соответствие Клейна
- Твисторное отношение дуальности
- Действительная структура
- Различные типы комплексных точек в СМ*
- § 4. Четырехзначность твисторов и индекс Гржина
- Две спиновые структуры на М*
- Поведение спинора
- Твисторные спин-расслоения над М*
- Конформные плотности на М*; индекс Гржина
- Теорема Гржина
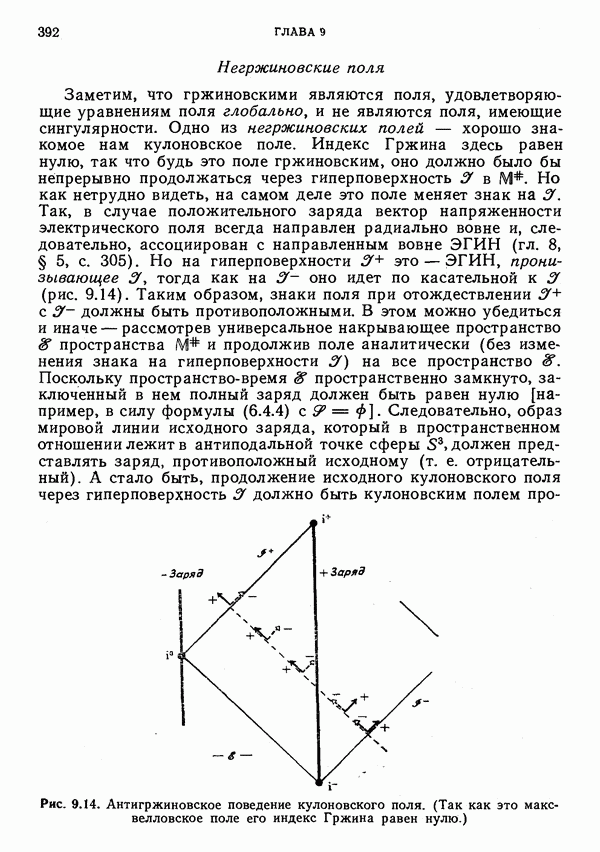
- Негржиновские поля
- § 5. Космологические модели и соответствующие твисторы
- Космологические горизонты
- Описание в пространстве Р5
- Деситтеровская и антидеситтеровская модели; твисторы …
- Функции для конформно-плоского пространства-времени
- Модели ФРУ, соответствующие твисторы начальной и конечной сингулярностей
- Явные выражения для функции I
- § 6. Асимптотически простое пространство-время
- Асимптотически-простое пространство-время
- Обращение в нуль тензора Вейля на границе J
- § 7. Последовательное вырождение
- Параллельно переносимые спиновые системы отсчета
- Сравнение аффинных параметров
- Сравнение спиновых систем отсчета
- Доказательство свойства последовательного вырождения
- Поля излучений
- § 8. Группа БМС и структура гиперповерхности J+
- Группа Бонди — Метцнера — Сакса
- Связь между сильной конформной геометрией и твистором
- Интерпретация изотропных углов
- Структура группы БМС
- Сдвиговая структура гиперповерхности J+
- H-пространство и асимптотическое твисторное пространство
- Отношение группы БМС к импульсу и моменту импульса
- Асимптотические разложения в теории Эйнштейна — Максвелла
- § 9. Энергия-импульс и момент импульса
- Усложнения в случае искривленного пространства-времени
- Твисторы двумерной поверхности
- Контортные двумерные поверхности
- Квазилокальный твистор момента импульса
- Определение множителя
- Асимптотическое спиновое пространство
- Свойства нормы на J+
- Эрмитовость твистора на 4-импульс Бонди — Сакса
- Альтернативные выражения для массы Бонди — Сакса
- Пространство Минковского как пространство «начал»
- Момент импульса на J+
- § 10. Потери массы Бонди — Сакса и положительность энергии
- Нелокальность энергии гравитационных волн
- НП-константы
- Подход Виттена в доказательстве положительности массы
- Связь с 4-импульсом Бонди — Сакса
- Спинор в подходе Людвигсена — Виккерса
- 3-форма Спарлинга
- Приложение. Спиноры в n измерениях
- 2-валентные e-спиноры
- Переход от тензоров к спинорам
- Геометрия фундаментальных спиноров
- Условие фундаментальности; структура спинового пространства
- Индуктивное построение спинового пространства
- Некоторые физически интересные случаи; триальность
- Спинорные поля; твисторы в n измерениях
- Послесловие авторов
- Литература